Weighted Random Forests to Improve Arrhythmia Classification
Abstract
1. Introduction
- Boosting aimed at building multiple models (also typically of the same type) in a sequence. Each model learns to fix the prediction errors of a prior/preceding model (e.g., AdaBoost [6] and Gradient tree Boosting [7]). Base estimators are built sequentially and in each step the last one added tries to reduce the bias of the combined estimator;
- Voting (also called stacking) aimed at building multiple models (typically of different types). Uses simple statistics (like calculating the mean) to combine predictions [4]. It is also possible to take the output of the base learners on the training data and apply another learning algorithm on them to predict the response values [8].
- Does the proposed weighting method introduce improvements to the standard Random Forest algorithm?
- To what extent is it possible to outperform previous results of reducing false arrhythmia alarms?
- What is the effect of different tuning parameters as part of finding optimized ensembles on the quality of predictions?
- Can the results be generalized over different arrhythmia types (datasets of different characteristics)?
2. Literature Review
3. Weighted Random Forest
- Ranking the pre-defined criterion () according to their importance (performance of the tree derived using Formula (4));
- Weighting the criteria from their ranks using some rank order weighting approach.
| Algorithm 1. Weighted Random Forest algorithm pseudocode. |
| input: Number of Trees (), random subset of the features (), training dataset () output: Random Forest () 1: is empty 2: for each to do 3: = Bootstrap Sample () 4: = Random Decision Tree (, ) 5: = 6: end 7: for each to do 8: Compute using Formula (5) 9: end 10: for each to do 11: = 12: end 13: for each to do 14: Compute using Formula (9) 15: end 16: for each to do 17: Compute final prediction using Formula (3) 18: end 19: return |
4. Research Framework and Settings
4.1. Feature Vector
4.2. Numerical Implementation
4.3. Performance Measures
4.4. Benchmarking Methods
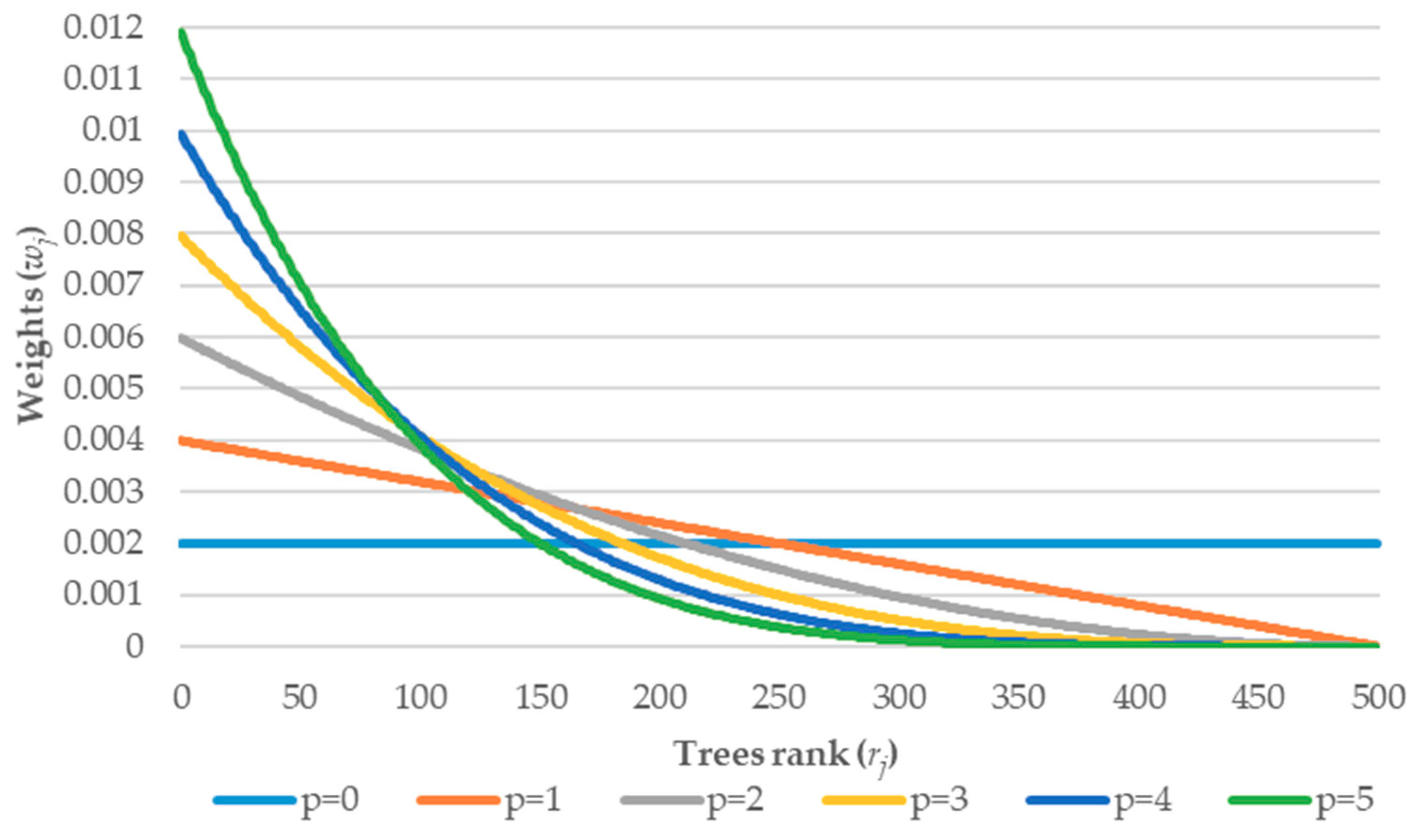
4.5. Tuning of the Weighting Parameters
- —controlling the importance of the first (model stability) or the second (small error on the unseen dataset) term in Formula (4).
- —which is the exponential parameter describing the strength of the weights (distribution).
5. Empirical Analysis
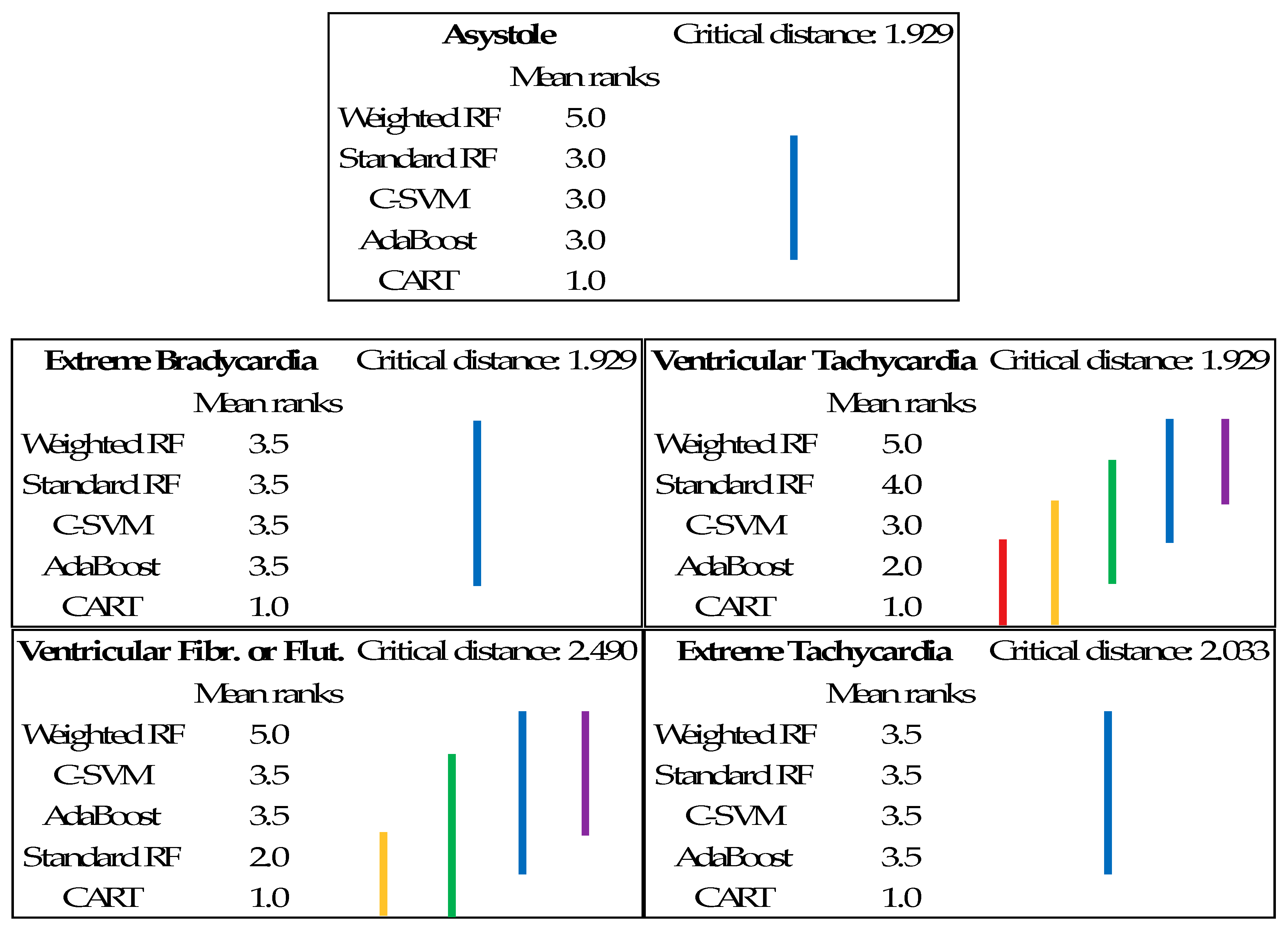
- 31.9 for Ventricular Tachycardia—accuracy of the model was improved in comparison to RPART (27.7), C-SVM (30.5), and AdaBoost (29.9);
- 86.1 for Ventricular Fibrillation or Flutter—accuracy of the model was improved in comparison to RPART (29.4), C-SVM (50.1), and AdaBoost (50.1);
- 80.7 for Asystole—accuracy of the model was improved in comparison to RPART (52.1), C-SVM (61.7), and AdaBoost (61.7).
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L.; Suganthan, P.N. Ensemble Classification and Regression-Recent Developments, Applications and Future Directions. IEEE Comput. Intell. Mag. 2016, 11, 41–53. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G.; Pham, H. Optimizing Ensemble Weights and Hyperparameters of Machine Learning Models for Regression Problems. arXiv 2019, arXiv:1908.05287. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 261–277. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Large, J.; Lines, J.; Bagnall, A. A probabilistic classifier ensemble weighting scheme based on cross-validated accuracy estimates. Data Min. Knowl. Discov. 2019, 33, 1674–1709. [Google Scholar] [CrossRef]
- Bhasuran, B.; Murugesan, G.; Abdulkadhar, S.; Natarajan, J. Stacked ensemble combined with fuzzy matching for biomedical named entity recognition of diseases. J. Biomed. Inform. 2016, 64, 1–9. [Google Scholar] [CrossRef]
- Ekbal, A.; Saha, S. Stacked ensemble coupled with feature selection for biomedical entity extraction. Knowl. -Based Syst. 2013, 46, 22–32. [Google Scholar] [CrossRef]
- Winham, S.J.; Freimuth, R.R.; Biernacka, J.M. A weighted random forests approach to improve predictive performance. Stat. Anal. Data Min. ASA Data Sci. J. 2013, 6, 496–505. [Google Scholar] [CrossRef]
- Martínez-Muñoz, G.; Suárez, A. Using boosting to prune bagging ensembles. Pattern Recognit. Lett. 2007, 28, 156–165. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, H. Search for the smallest random forest. Stat. Interface 2009, 2, 381–388. [Google Scholar] [CrossRef] [PubMed]
- Pham, H.; Olafsson, S. Bagged ensembles with tunable parameters. Comput. Intell. 2019, 35, 184–203. [Google Scholar] [CrossRef]
- Byeon, H.; Cha, S.; Lim, K. Exploring Factors Associated with Voucher Program for Speech Language Therapy for the Preschoolers of Parents with Communication Disorder using Weighted Random Forests. Int. J. Adv. Comput. Sci. Appl. 2019, 10. [Google Scholar] [CrossRef]
- Xuan, S.; Liu, G.; Li, Z. Refined Weighted Random Forest and Its Application to Credit Card Fraud Detection. Lect. Notes Comput. Sci. 2018, 11280, 343–355. [Google Scholar] [CrossRef]
- Kulkarni, V.Y.; Sinha, P.K. Effective learning and classification using random forest algorithm. Int. J. Eng. Innov. Technol. 2014, 3, 267–273. [Google Scholar]
- Gajowniczek, K.; Grzegorczyk, I.; Ząbkowski, T. Reducing False Arrhythmia Alarms Using Different Methods of Probability and Class Assignment in Random Forest Learning Methods. Sensors 2019, 19, 1588. [Google Scholar] [CrossRef]
- Clifford, G.D.; Silva, I.; Moody, B.; Li, Q.; Kella, D.; Shahin, A.; Kooistra, T.L.; Perry, D.; Mark, R.G. The PhysioNet/computing in cardiology challenge 2015: Reducing false arrhythmia alarms in the ICU. In Proceedings of the 2015 Computing in Cardiology Conference (CinC), Nice, France, 6–9 September 2015; pp. 273–276. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Rodríguez, J.J. A weighted voting framework for classifiers ensembles. Knowl. Inf. Syst. 2012, 38, 259–275. [Google Scholar] [CrossRef]
- Filmus, Y.; Oren, J.; Zick, Y.; Bachrach, Y. Analyzing Power in Weighted Voting Games with Super-Increasing Weights. Theory Comput. Syst. 2018, 63, 150–174. [Google Scholar] [CrossRef]
- Pham, H.; Olafsson, S. On Cesaro averages for weighted trees in the random forest. J. Classif. 2019, 1–14. [Google Scholar] [CrossRef]
- Booth, A.; Gerding, E.; McGroarty, F. Automated trading with performance weighted random forests and seasonality. Expert Syst. Appl. 2014, 41, 3651–3661. [Google Scholar] [CrossRef]
- Utkin, L.V.; Konstantinov, A.V.; Chukanov, V.S.; Kots, M.V.; Ryabinin, M.A.; Meldo, A.A. A weighted random survival forest. Knowl.-Based Syst. 2019, 177, 136–144. [Google Scholar] [CrossRef]
- Sunil Babu, M.; Vijayalakshmi, V. An Effective Approach for Sub-acute Ischemic Stroke Lesion Segmentation by Adopting Meta-Heuristics Feature Selection Technique Along with Hybrid Naive Bayes and Sample-Weighted Random Forest Classification. Sens. Imaging 2019, 20. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, L.; Tang, H.; Li, Q.; Wei, S.; Li, J. Life-threatening false alarm rejection in ICU: Using the rule-based and multi-channel information fusion method. Physiol. Meas. 2016, 37, 1298–1312. [Google Scholar] [CrossRef]
- Silva, I.; Moody, B.; Behar, J.; Johnson, A.; Oster, J.; Clifford, G.D.; Moody, G.B. Robust detection of heart beats in multimodal data. Physiol. Meas. 2015, 36, 1629–1644. [Google Scholar] [CrossRef]
- Behar, J.; Johnson, A.; Clifford, G.D.; Oster, J. A comparison of single channel fetal ECG extraction methods. Ann. Biomed. Eng. 2014, 42, 1340–1353. [Google Scholar] [CrossRef]
- Gierałtowski, J.; Grzegorczyk, I.; Ciuchciński, K.; Kośna, K.; Soliński, M.; Podziemski, P. Algorithm for life-threatening arrhythmias detection with reduced false alarms. In Proceedings of the 2015 Computing in Cardiology Conference (CinC), Nice, France, 6–9 September 2015; pp. 1201–1204. [Google Scholar] [CrossRef]
- Krasteva, V.; Jekova, I.; Leber, R.; Schmid, R.; Abächerli, R. Superiority of classification tree versus cluster, fuzzy and discriminant models in a heartbeat classification system. PLoS ONE 2015, 10, e0140123. [Google Scholar] [CrossRef]
- Rooijakkers, M.J.; Rabotti, C.; Oei, S.G.; Mischi, M. Low-complexity R-peak detection for ambulatory fetal monitoring. Physiol. Meas. 2012, 33, 1135–1150. [Google Scholar] [CrossRef]
- Gierałtowski, J.; Ciuchciński, K.; Grzegorczyk, I.; Kośna, K.; Soliński, M.; Podziemski, P. RS slope detection algorithm for extraction of heart rate from noisy, multimodal recordings. Physiol. Meas. 2015, 36, 1743–1761. [Google Scholar] [CrossRef]
- Sedghamiz, H. Matlab Implementation of Pan Tompkins ECG QRS Detector. Code Available at the File Exchange Site of MathWorks. 2014. Available online: https://fr.mathworks.com/matlabcentral/fileexchange/45840-complete-pan-tompkins-implementationecg-qrs-detector (accessed on 25 February 2019).
- Antink, C.H.; Leonhardt, S.; Walter, M. Reducing false alarms in the ICU by quantifying self-similarity of multimodal biosignals. Physiol. Meas. 2016, 37, 1233–1252. [Google Scholar] [CrossRef] [PubMed]
- Kalidas, V.; Tamil, L.S. Cardiac arrhythmia classification using multi-modal signal analysis. Physiol. Meas. 2016, 37, 1253. [Google Scholar] [CrossRef] [PubMed]
- Sadr, N.; Huvanandana, J.; Nguyen, D.T.; Kalra, C.; McEwan, A.; de Chazal, P. Reducing false arrhythmia alarms in the ICU using multimodal signals and robust QRS detection. Physiol. Meas. 2016, 37, 1340. [Google Scholar] [CrossRef] [PubMed]
- Plesinger, F.; Klimes, P.; Halamek, J.; Jurak, P. Taming of the monitors: Reducing false alarms in intensive care units. Physiol. Meas. 2016, 37, 1313–1325. [Google Scholar] [CrossRef] [PubMed]
- Khadra, L.; Al-Fahoum, A.S.; Al-Nashash, H. Detection of life-threatening cardiac arrhythmias using the wavelet transformation. Med. Biol. Eng. Comput. 1997, 35, 626–632. [Google Scholar] [CrossRef] [PubMed]
- Christov, I.I. Real time electrocardiogram QRS detection using combined adaptive threshold. Biomed. Eng. Online 2004, 3, 28. [Google Scholar] [CrossRef]
- Arzeno, N.M.; Deng, Z.D.; Poon, C.-S. Analysis of First-Derivative Based QRS Detection Algorithms. IEEE Trans. Biomed. Eng. 2008, 55, 478–484. [Google Scholar] [CrossRef]
- Mjahad, A.; Rosado-Muñoz, A.; Bataller-Mompeán, M.; Francés-Víllora, J.V.; Guerrero-Martínez, J.F. Ventricular Fibrillation and Tachycardia detection from surface ECG using time-frequency representation images as input dataset for machine learning. Comput. Methods Programs Biomed. 2017, 141, 119–127. [Google Scholar] [CrossRef]
- Prabhakararao, E.; Manikandan, M.S. Efficient and robust ventricular tachycardia and fibrillation detection method for wearable cardiac health monitoring devices. Healthc. Technol. Lett. 2016, 3, 239–246. [Google Scholar] [CrossRef]
- Fallet, S.; Yazdani, S.; Vesin, J.M. A multimodal approach to reduce false arrhythmia alarms in the intensive care unit. In Proceedings of the 2015 Computing in Cardiology Conference (CinC), Nice, France, 6–9 September 2015; pp. 277–280. [Google Scholar] [CrossRef]
- Chen, S.; Thakor, N.V.; Mower, M.M. Ventricular fibrillation detection by a regression test on the autocorrelation function. Med. Biol. Eng. Comput. 1987, 25, 241–249. [Google Scholar] [CrossRef]
- Balasundaram, K.; Masse, S.; Nair, K.; Farid, T.; Nanthakumar, K.; Umapathy, K. Wavelet-based features for characterizing ventricular arrhythmias in optimizing treatment options. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011. [Google Scholar] [CrossRef]
- Li, H.; Han, W.; Hu, C.; Meng, M.Q.-H. Detecting ventricular fibrillation by fast algorithm of dynamic sample entropy. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009. [Google Scholar] [CrossRef]
- Alonso-Atienza, F.; Morgado, E.; Fernandez-Martinez, L.; Garcia-Alberola, A.; Rojo-Alvarez, J.L. Detection of Life-Threatening Arrhythmias Using Feature Selection and Support Vector Machines. IEEE Trans. Biomed. Eng. 2014, 61, 832–840. [Google Scholar] [CrossRef] [PubMed]
- Anas, E.; Lee, S.Y.; Hasan, M.K. Sequential algorithm for life threatening cardiac pathologies detection based on mean signal strength and EMD functions. Biomed. Eng. Online 2010, 9, 43. [Google Scholar] [CrossRef]
- Asadi, F.; Mollakazemi, M.J.; Ghiasi, S.; Sadati, S.H. Enhancement of life-threatening arrhythmia discrimination in the intensive care unit with morphological features and interval feature extraction via random forest classifier. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 57–60. [Google Scholar] [CrossRef]
- Eerikäinen, L.M.; Vanschoren, J.; Rooijakkers, M.J.; Vullings, R.; Aarts, R.M. Reduction of false arrhythmia alarms using signal selection and machine learning. Physiol. Meas. 2016, 37, 1204–1216. [Google Scholar] [CrossRef] [PubMed]
- Gajowniczek, K.; Orłowski, A.; Ząbkowski, T. Entropy Based Trees to Support Decision Making for Customer Churn Management. Acta Phys. Pol. A 2016, 129, 971–979. [Google Scholar] [CrossRef]
- Li, H.B.; Wang, W.; Ding, H.W.; Dong, J. Trees weighting random forest method for classifying high-dimensional noisy data. In Proceedings of the 2010 IEEE 7th International Conference on E-Business Engineering, Shanghai, China, 10–12 November 2010; pp. 160–163. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Orłowski, A.; Ząbkowski, T. Simulation Study on the Application of the Generalized Entropy Concept in Artificial Neural Networks. Entropy 2018, 20, 249. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. arXiv 2019, arXiv:1908.09635. [Google Scholar]
- Hocking, T. WeightedROC: Fast, Weighted ROC Curves. R package Version 2018.10.1. 2018. Available online: https://CRAN.R-project.org/package=WeightedROC (accessed on 10 October 2019).
- Roszkowska, E. Rank ordering criteria weighting methods—A comparative overview, Optimum. Studia Ekon. 2013, 5. [Google Scholar] [CrossRef]
- Stillwell, W.G.; Seaver, D.A.; Edwards, W. A comparison of weight approximation techniques in multiattribute utility decision making. Organ. Behav. Hum. Perform. 1981, 28, 62–77. [Google Scholar] [CrossRef]
- The R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Wright, M.N.; Ziegler, A. ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77. [Google Scholar] [CrossRef]
- Youden, W.J. An index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R using the caret Package. J. Stat. Softw. 2008, 28. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Karpio, K.; Łukasiewicz, P.; Orłowski, A.; Ząbkowski, T. Q-Entropy Approach to Selecting High Income Households. Acta Phys. Pol. A 2015, 127, A-38–A-44. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth Statistics/Probability Series; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Ząbkowski, T.; Sodenkamp, M. Revealing Household Characteristics from Electricity Meter Data with Grade Analysis and Machine Learning Algorithms. Appl. Sci. 2018, 8, 1654. [Google Scholar] [CrossRef]
- Pohlert, T. The Pairwise Multiple Comparison of Mean Ranks Package (PMCMR). R Package. Available online: https://cran.r-project.org/web/packages/PMCMR/vignettes/PMCMR.pdf (accessed on 29 December 2019).
| Work | Method Applied | Conclusion |
|---|---|---|
| [11] | Tree-level weights in Random Forest. | Method does not dramatically improve predictive ability in high-dimensional genetic data, but it may improve performance in other domains. |
| [14] | Tunable weighted bagged ensemble using CART, Naïve Bayes, KNN, SVM, ANN and Logistic Regression. | Approach can usually outperform pure bagging, however, there are some cons in terms of time considerations in effectively choosing tunable parameters aside from a grid search. |
| [15] | Variable importance-weighted Random Forest. | Better prediction power in comparison to existing random forests granting the same weight to all tree models. |
| [16] | Refined weighted Random Forest (assigning different weights to different decision trees). | Better prediction power in comparison to standard random forests due to the following: (1) all training data including in-bag data and Out-of-Bag data is used and (2) the margin between probability of predicting true class and false class label applied. |
| [20] | Optimality conditions for four combination methods: majority vote (MV), weighted majority vote (WMV), the recall combiner (REC) and Naive Bayes (NB). | Experiments revealed that there is no dominant combiner. NB was the most successful but the differences with MV and WMV were not found to be statistically significant. |
| [22] | Weighting each tree by replacing the regular average with a Cesaro average (CRF—Cesaro Random Forest). | Although the Cesaro random forest appears to be competitive to the classical RF, it has limitations i.e., the way to determine the sequencing of trees (what impacts the results) and the probability estimates of class membership are not available. |
| [23] | Variable performance-weighted and Recency-weighted random forests. | The results show that recency-weighted ensembles of random forests produce superior results in terms of both profitability and prediction accuracy compared with other ensemble techniques. |
| [24] | Weighted random survival forest by assigning weights to survival decision trees or to their subsets. | Numerical examples with real data illustrate the outperformance of the proposed model in comparison with the original random survival forest. |
| Arrhythmia/Complex | Method | Work |
|---|---|---|
| QRS Detection | Pan-Tompkins (filtering techniques); Threshold-based detection; Multimodal data methods; Gradient calculations; Based on Peak energy; Markov-model; RS Slope detection; Low-complexity R-peak detector. | [26,27,28,29,30,31,32,33,34,35] |
| Asystole | Short term autocorrelation analysis; Flat line artefacts definition; Frequency domain analysis; Signal quality based rules. | [35,36,37] |
| Bradycardia and Tachycardia | Threshold +Support vector machine; Beat-to-beat Correlogram 2D. | [35,36] |
| Ventricular Tachycardia | Time-frequency representation images; Spectral characteristics of ECG; Spectra purity index; Autocorrelation function. | [31,36,38,39,40,41,42,43,44] |
| Ventricular Flutter or Fibrillation | Autocorrelation analysis; Wavelet transformations; Sample entropy; Machine learning methods with features derived from signal morphology and analysis of power spectrum; Time-frequency representation images; Empirical mode decomposition; The zero crossing rate combined with base noise suppression with discrete cosine transform and beat-to-beat intervals. | [39,42,43,45,46,47,48,49] |
| All types | Rule based methods; Regular-activity test; Single- and multichannel fusion rules; Machine learning algorithms; SVM—Support Vector Machines; LDA—Linear discriminant analysis; Random Forest classifiers. | [27,35,38,50,51] |
| Tree No. | Equation (4) | Ranking | Nominator (p = 2) | Final Weights | ||
|---|---|---|---|---|---|---|
| 1 | 0.70 | 0.70 | 0.350 | 3 | 4 | 0.133 |
| 2 | 0.65 | 0.55 | 0.325 | 4 | 1 | 0.034 |
| 3 | 0.90 | 0.80 | 0.450 | 1 | 16 | 0.533 |
| 4 | 0.85 | 0.80 | 0.425 | 2 | 9 | 0.300 |
| Base | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC = 0.93 | 0 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.050 | 0.050 |
| 0.1 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.050 | |
| 0.2 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.050 | |
| 0.3 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.050 | |
| 0.4 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.050 | |
| 0.5 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.050 | |
| 0.6 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.050 | |
| 0.7 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | |
| 0.8 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | |
| 0.9 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.060 | 0.060 | |
| 1 | 0.000 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.055 | 0.060 | 0.060 | 0.060 | 0.060 | |
| SCORE = 61.75 | 0 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 |
| 0.1 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.2 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.3 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.4 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.5 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.6 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.7 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.8 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 0.9 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| 1 | 0.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | 19.00 | |
| Base | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC = 0.95 | 0 | 0.000 | 0.000 | −0.005 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 |
| 0.1 | 0.000 | 0.000 | −0.005 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | |
| 0.2 | 0.000 | 0.000 | −0.005 | −0.005 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | |
| 0.3 | 0.000 | 0.001 | −0.005 | −0.005 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | −0.011 | |
| 0.4 | 0.000 | 0.001 | −0.005 | −0.005 | −0.005 | −0.011 | −0.011 | −0.011 | −0.005 | −0.005 | −0.005 | |
| 0.5 | 0.000 | 0.001 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | |
| 0.6 | 0.000 | 0.001 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | |
| 0.7 | 0.000 | 0.001 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | |
| 0.8 | 0.000 | 0.001 | 0.001 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | |
| 0.9 | 0.000 | 0.001 | 0.001 | 0.001 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | |
| 1 | 0.000 | 0.001 | 0.001 | 0.001 | 0.001 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | −0.005 | |
| SCORE = 77.73 | 0 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −1.27 | −1.27 | −1.27 | −1.27 | −1.27 | −1.27 |
| 0.1 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −1.27 | −1.27 | −1.27 | −1.27 | −1.27 | |
| 0.2 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −1.27 | −1.27 | −1.27 | −1.27 | −1.27 | |
| 0.3 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −1.27 | −1.27 | −1.27 | −1.27 | |
| 0.4 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −1.27 | −1.27 | −1.27 | |
| 0.5 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −1.27 | |
| 0.6 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | |
| 0.7 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | |
| 0.8 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | |
| 0.9 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | |
| 1 | 0.00 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | |
| Base | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC = 0.99 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.1 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.008 | −0.008 | −0.008 | |
| 0.2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.008 | −0.008 | −0.008 | |
| 0.3 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.008 | −0.008 | |
| 0.4 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.008 | −0.008 | |
| 0.5 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.001 | −0.001 | |
| 0.6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.001 | −0.001 | |
| 0.7 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.001 | |
| 0.8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.008 | |
| 0.9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | −0.008 | |
| 1 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.008 | −0.008 | −0.008 | |
| SCORE = 81.08 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.4 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −9.25 | |
| 0.7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Base | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC = 0.97 | 0 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 |
| 0.1 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.2 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.3 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.4 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.5 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.6 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.7 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.8 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 0.9 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | |
| 1 | 0.000 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.030 | 0.009 | |
| SCORE = 30.56 | 0 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 |
| 0.1 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.2 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.3 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.4 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.5 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.6 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.7 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.8 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 0.9 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| 1 | 0.00 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 55.55 | 54.51 | 54.51 | 54.51 | |
| Base | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC = 0.87 | 0 | 0.000 | −0.001 | 0.000 | 0.003 | 0.001 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.003 |
| 0.1 | 0.000 | −0.001 | 0.000 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.001 | 0.000 | 0.002 | |
| 0.2 | 0.000 | −0.002 | 0.000 | 0.001 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.002 | |
| 0.3 | 0.000 | −0.002 | 0.001 | 0.001 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.003 | |
| 0.4 | 0.000 | −0.002 | 0.001 | 0.000 | 0.002 | 0.002 | 0.001 | 0.001 | 0.000 | 0.001 | 0.003 | |
| 0.5 | 0.000 | −0.002 | 0.001 | 0.000 | 0.001 | 0.002 | 0.002 | 0.002 | 0.001 | 0.001 | 0.002 | |
| 0.6 | 0.000 | −0.002 | 0.001 | 0.000 | 0.001 | 0.002 | 0.002 | 0.001 | 0.002 | 0.002 | 0.003 | |
| 0.7 | 0.000 | −0.002 | 0.000 | 0.000 | 0.001 | 0.002 | 0.002 | 0.002 | 0.001 | 0.001 | 0.003 | |
| 0.8 | 0.000 | −0.002 | 0.001 | 0.000 | 0.001 | 0.001 | 0.002 | 0.002 | 0.001 | 0.003 | 0.002 | |
| 0.9 | 0.000 | −0.002 | 0.000 | 0.001 | 0.001 | 0.001 | 0.002 | 0.001 | 0.000 | 0.002 | 0.002 | |
| 1 | 0.000 | −0.002 | −0.001 | 0.000 | 0.001 | 0.001 | 0.002 | 0.001 | 0.000 | 0.001 | 0.001 | |
| SCORE = 31.54 | 0 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.31 | 0.31 | 0.21 | 0.21 | 0.21 |
| 0.1 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.31 | 0.21 | 0.21 | 0.21 | 0.21 | |
| 0.2 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 | 0.31 | 0.21 | 0.21 | |
| 0.3 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 | 0.31 | 0.31 | 0.31 | |
| 0.4 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.42 | 0.31 | 0.31 | 0.31 | 0.31 | |
| 0.5 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 | 0.31 | 0.31 | 0.31 | |
| 0.6 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.42 | 0.31 | 0.31 | 0.31 | 0.31 | |
| 0.7 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.42 | 0.31 | 1.01 | 1.01 | 0.33 | |
| 0.8 | 0.00 | −0.26 | 1.11 | 0.42 | 0.42 | 0.42 | 0.42 | 1.01 | 1.01 | 0.33 | 0.33 | |
| 0.9 | 0.00 | −0.26 | 0.44 | 0.42 | 0.42 | 0.42 | 1.11 | 1.01 | 0.33 | 0.33 | 0.33 | |
| 1 | 0.00 | −0.26 | 0.44 | 0.42 | 0.42 | 1.11 | 1.11 | 0.33 | 0.33 | 0.23 | 0.23 | |
| Arrhythmia Type | Method | AUC | Score |
|---|---|---|---|
| Asystole | Weighted RF ( = 4.5) | (98.5 ± 3.1) | (80.7 ± 8.7) |
| Standard RF | (92.5 ± 3.5) | (61.7 ± 9.2) | |
| CART (cp = 0.065) | (86.0 ± 4.2) | (52.1 ± 10.9) | |
| C-SVM (polynomial = 2, = 0.3, = 0.4) | (92.0 ± 3.7) | (61.7 ± 9.2) | |
| AdaBoost | (91.9 ± 3.9) | (61.7 ± 9.2) | |
| Extreme Bradycardia | Weighted RF ( = 0.5) | (95.6 ± 4.4) | (77.7 ± 9.7) |
| Standard RF | (95.0 ± 4.5) | (77.7 ± 9.7) | |
| CART (cp = 0.083) | (87.5 ± 4.4) | (63.1 ± 10.5) | |
| C-SVM (polynomial = 2, = 0.3, C = 0.4) | (95.2 ± 4.5) | (77.7 ± 9.7) | |
| AdaBoost | (95.1 ± 4.6) | (77.7 ± 9.7) | |
| Ventricular Tachycardia | Weighted RF ( = 5.0) | (87.5 ± 3.5) | (31.9 ± 2.7) |
| Standard RF | (87.3 ± 3.5) | (31.5 ± 2.7) | |
| CART (cp = 0.011) | (72.6 ± 4.2) | (27.7 ± 4.2) | |
| C-SVM (radial = 0.1, = 0.1, = 0.8) | (86.1 ± 3.7) | (30.5 ± 3.7) | |
| AdaBoost | (83.1 ± 3.9) | (29.9 ± 3.7) | |
| Ventricular Fibrillation or Flutter | Weighted RF ( = 1.0) | (99.9 ± 0.1) | (86.1 ± 7.7) |
| Standard RF | (97.0 ± 2.1) | (30.6 ± 13.9) | |
| CART (cp = 0.017) | (89.9 ± 8.7) | (29.4 ± 16.6) | |
| C-SVM (radial = 0.5, = 0.1, = 0.8) | (97.5 ± 5.3) | (50.1 ± 12.8) | |
| AdaBoost | (97.5 ± 5.3) | (50.1 ± 12.8) | |
| Extreme Tachycardia | Weighted RF ( = 1.0) | (99.2 ± 0.1) | (81.1 ± 7.7) |
| Standard RF | (99.2 ± 0.1) | (81.1 ± 7.7) | |
| CART (cp = 0.090) | (64.2 ± 8.6) | (53.6 ± 9.9) | |
| C-SVM (polynomial = 3, = 0.5, = 0.6) | (99.2 ± 0.1) | (81.1 ± 7.7) | |
| AdaBoost | (99.2 ± 0.1) | (81.1 ± 7.7) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajowniczek, K.; Grzegorczyk, I.; Ząbkowski, T.; Bajaj, C. Weighted Random Forests to Improve Arrhythmia Classification. Electronics 2020, 9, 99. https://doi.org/10.3390/electronics9010099
Gajowniczek K, Grzegorczyk I, Ząbkowski T, Bajaj C. Weighted Random Forests to Improve Arrhythmia Classification. Electronics. 2020; 9(1):99. https://doi.org/10.3390/electronics9010099
Chicago/Turabian StyleGajowniczek, Krzysztof, Iga Grzegorczyk, Tomasz Ząbkowski, and Chandrajit Bajaj. 2020. "Weighted Random Forests to Improve Arrhythmia Classification" Electronics 9, no. 1: 99. https://doi.org/10.3390/electronics9010099
APA StyleGajowniczek, K., Grzegorczyk, I., Ząbkowski, T., & Bajaj, C. (2020). Weighted Random Forests to Improve Arrhythmia Classification. Electronics, 9(1), 99. https://doi.org/10.3390/electronics9010099






