Abstract
This paper presents a novel efficient encoding method and a high-throughput low-complexity encoder architecture for quasi-cyclic low-density parity-check (QC-LDPC) codes for the 5th-generation (5G) New Radio (NR) standard. By storing the quantized value of the permutation information for each submatrix instead of the whole parity check matrix, the required memory storage size is considerably reduced. In addition, sharing techniques are employed to reduce the hardware complexity. The encoding complexity of the proposed method was analyzed, and indicated a substantial reduction in the required area as well as memory storage when compared with existing state-of-the-art encoding approaches. The proposed method requires only 61% gate area, and 11% ROM storage when compared with a similar LDPC encoder using the Richardson–Urbanke method. Synthesis results on TSMC 65-nm complementary metal-oxide semiconductor (CMOS) technology with different submatrix sizes were carried out, which confirmed that the design methodology is flexible and can be adapted for multiple submatrix sizes. For all the considered submatrix sizes, the throughput ranged from 22.1–202.4 Gbps, which sufficiently meets the throughput requirement for the 5G NR standard.
1. Introduction
Low-density parity-check (LDPC) codes [1], which were first proposed by Gallager in the early 1960s and rediscovered by MacKay and Neal [2] in 1996, have attracted widespread attention thanks to their remarkable error correction capabilities near the Shannon limit, with advancements in very large-scale integration (VLSI). Moreover, LDPC codes are among the most widely used types of forward error correction (FEC) codes in several communications standards such as the wireless local area network (WLAN, IEEE 802.11n), wireless radio access network (WRAN, IEEE 802.22), digital video broadcast (DVB), and the Advanced Television System Committee (ATSC). Recently, the fifth generation (5G) communication has been a hotspot of research and development [3]. More specially, LDPC codes play an important role in 5G communication and have been selected as the coding scheme for the 5G enhanced Mobile Broad Band (eMBB) data channel [4]. To support compatible rate and scalable data transmission, 3rd Generation Partnership Project (3GPP) has agreed to consider two rate-compatible base graphs, BG1 and BG2, for the channel coding [5]. Accordingly, several studies have been conducted on the 5G LDPC codes. In [6], a low-cost and flexible demonstration platform is designed and implemented to evaluate the real-time performance of LDPC over the air interface as defined by 5G New Radio (NR) specifications. An algebra-assisted method for constructing 5G LDPC codes is presented in [7].
Over recent years, research on LDPC codes has been focused on structured LDPC codes known as quasi-cyclic low-density parity-check (QC-LDPC) codes [8,9,10,11,12], which exhibit advantages over other types of LDPC codes with respect to the hardware implementations of encoding and decoding using simple shift registers and logic circuits. A low-complexity encoder can be realized by using QC-LDPC codes, due to the sparseness of the parity check matrix. However, it is not straightforward to encode with low complexity as LDPC codes are defined by their parity check matrix, and the generator matrix is generally unknown. Various approaches have been suggested to improve the hardware complexity of LDPC encoders [13,14,15,16,17,18,19,20,21]. One of the most conventional approaches is systematic encoding, in which the generator matrix is derived from the parity check matrix by exploiting Gaussian elimination. The main drawback related to this method is that the storage overhead is dramatically increased for large block sizes, which limits its practical applicability. The Richardson–Urbanke (RU) algorithm is a widely-used LDPC codes encoding scheme developed by Richardson and Urbanke [13]. The underlying principle of the method is the transformation of the parity check matrix into an approximate lower triangular (ALT) form by using only row and column permutations, which preserves the sparseness of the matrix. This method suffers from a long critical path, which could make the LDPC encoder unsuitable for high throughput applications. To overcome the limitations of the previous approaches, the design proposed in this paper, which is referred to as a low-complexity high-throughput LDPC encoder architecture for the 5G standard, requires significantly less area and memory storage while maintaining a high throughput.
This paper targets the design of low-complexity high-throughput QC-LDPC encoders for the 5G NR standard. In LDPC encoders, the memory and interconnecting blocks are considered as the major influencing factors of the overall area, delay, and power performance of the hardware design. Hence, the size of the read only memory (ROM) was decreased by storing the quantized value of the permutation information for each submatrix instead of the entire parity check matrix H. The proposed architecture requires less matrix multiplications than the RU method, by exploiting the characteristics of the 5G NR base matrix. In addition, the proposed algorithm does not require the inverse of the component matrix, which presents a primary advantage over the RU method. Moreover, block-memories are not required to store the generator matrix G, and the number of required components is reduced. The ROM size of the proposed method is 98.2% and 88.9% lower than those of the G matrix method and RU method, respectively.
To assess the benefits of the proposed encoding approach, we further implement and synthesize several QC-LDPC encoder architectures with different submatrix sizes Z = 30, 64, 96, 144, and 352. The application specific integrated circuit (ASIC) post synthesis implementation results on TSMC 65-nm complementary metal-oxide semiconductor (CMOS) technology revealed an area efficiency up to 597 Gbps/mm when the proposed encoding method was implemented. Hence, it can be concluded that a promising encoding architecture design for 5G NR LDPC codes was developed in this study.
The remainder of this paper is organized as follows. Section 2 gives a brief overview of the characteristics of 5G NR QC-LDPC codes. In Section 3, two conventional LDPC encoding algorithms from the literature are outlined. A novel 5G NR QC-LDPC encoding approach and a low-complexity high-throughput QC-LDPC encoder architecture are described in Section 4. Section 5 presents the implementation and comparison results, followed by the conclusions in Section 6.
2. 5G NR QC-LDPC Codes
The NR access technology marks a transition in FEC coding for the 3GPP of cellular technologies [22]. In this section, the QC-LDPC codes are reviewed, and the characteristics of standard 5G QC-LDPC codes are summarized. In addition, procedures are presented for the construction of the parity check matrix of the target LDPC codes.
2.1. Preliminary
Let Z be the size of a circulant permutation matrix and be the shift value. For any integer value , , a circulant permutation matrix shifts the identity matrix I to the right by times for the -th non-zero element in a base matrix. This binary circulant permutation matrix is denoted as . Considering as an example,
For simple notation, denotes the null matrix (all elements equal to zero) of the same size.
2.2. Introduction to QC-LDPC Codes
A binary QC-LDPC code can be characterized by the null space of an array of sparse circulants of the same size [7,23,24]. Taking into account the implementation, the parity-check matrix H of a QC-LDPC code can be defined by its base graph and shift coefficients . Elements 1s and 0s in the base graph are replaced by a circulant permutation matrix and a zero matrix of size , respectively. For two positive integers and , with , consider the QC-LDPC code expressed by the following array of circulants over GF(2):
The exponent matrix of H, which is , has the following form:
Each entry in the matrix E is referred to as a shift value. It should be noted that the parity check matrix H in Equation (2) can be constructed by expanding the exponent matrix . This procedure is referred to as protograph construction [25].
2.3. 5G NR QC-LDPC Characteristics
As mentioned above, QC-LDPC codes play an important role in 5G communications and have been accepted as the channel coding scheme for the 5G eMBB data channel in 3GPP standard meeting. Figure 1 illustrates the general structure of the NR QC-LDPC base graph. The columns are divided into three parts: information columns, core parity columns, and extension parity columns. The rows are partitioned into two parts: core check rows and extension check rows. As shown in the figure, the base matrix is composed of five submatrices, namely, A, B, O, C, and I [22]. Submatrix A corresponds to systematic bits. In addition, B corresponds to the first set of parity bits and is a square matrix with a dual-diagonal structure: its first column is of weight 3, whereas the submatrix composed of other columns after the first column has an upper dual-diagonal structure. Submatrix O is an all-zero matrix. For the efficient support of incremental redundancy hybrid automatic repeat request (IR-HARQ), a single parity-check (SPC) based extension is used to support lower rates, as shown in Figure 1. Submatrix C corresponds to SPC rows, and I is an identity matrix that corresponds to the second set of parity bits, i.e., the SPC extension. The combination of A and B is referred to as the kernel, and the other parts (O, C, and I) are referred to as extensions. This code structure is similar to the Raptor-like extension, as described in [26].
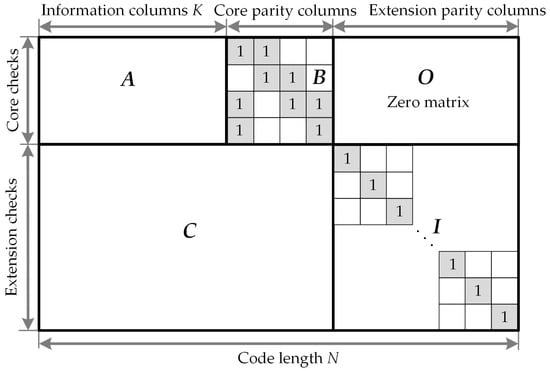
Figure 1.
Sketch of base parity check structure for the 5G NR QC-LDPC codes.
The 3GPP agreed to consider two rate-compatible base graphs, denoted by BG1 and BG2, for the channel coding. Base graphs BG1 and BG2 have similar structures. However, BG1 is targeted for larger block lengths and higher rates , whereas BG2 is targeted for smaller block lengths and lower rates . The actual base graph usage and the definition of the two matrices are detailed in the NR standard specification TS 38.212 [27]. The base graph that supports should support the following set of shift sizes Z, where for and .
For base graphs BG1 and BG2, the number of shift coefficient designs is 8. All lift sizes are divided into eight sets based on parameter a, where a is used for the definition of the lifting-size . The set of shift coefficients are listed in Table 1.

Table 1.
Relationship between exponent matrices and sets of lifting size.
The shift value can be calculated using the function , where is the shift coefficient of the -th element in the corresponding shift design. The function f is defined as Equation (4), in which denotes the modulo arithmetic:
The following procedures are the steps of constructing the parity check matrix of the target QC-LDPC code with a given information block size K and code rate . For a base graph, denotes the number of information circulant columns; thus, if the lifting size is Z, nominally.
- Step 1:
- Obtain the base graph BG1 or BG2 and determine the value of for the given K and R.
- –
- For BG1: .
- –
- For BG2: if ; if ; if ; and
- Step 2:
 Table 2. Lifting size Z supported by standard 5G QC-LDPC codes.
Table 2. Lifting size Z supported by standard 5G QC-LDPC codes.- Step 3:
- After the lifting size Z is determined, the corresponding shift coefficient matrix is then selected from Table 1 {Set 1, Set 2,⋯, Set 8} according to set Z.
- Step 4:
- Calculate the shifting coefficient value by the modular Z operation, as discussed in Equation (4).
- Step 5:
- Replace each entry in the final exponent matrix with the corresponding circulant permutation matrix or zero matrix of size . The QC-LDPC code construction is completed and a parity check matrix H of size is obtained. In 5G QC-LDPC codes, shortening and puncturing is carried out to obtain the desired information lengths and rate adaption. Figure 2 presents an illustration of the encoding process of these codes
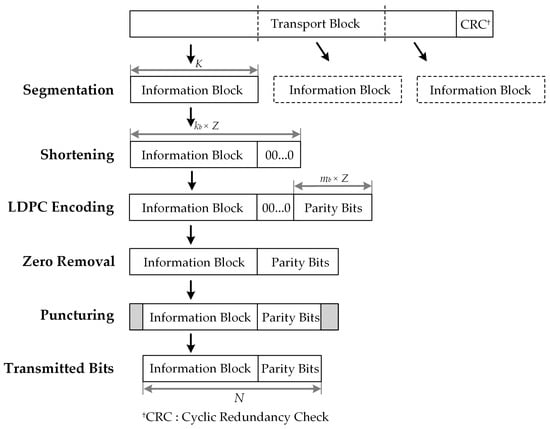 Figure 2. Shortening by zero padding and puncturing of standard 5G QC-LDPC codes.
Figure 2. Shortening by zero padding and puncturing of standard 5G QC-LDPC codes.
3. LDPC Encoding Algorithms
Given a parity check matrix H, the objective of LDPC encoding is to solve parity equations:
where C is the systematic codeword, which consists of the information bit vector S and parity code vector P.
This section presents a review on two generic encoding methodologies for the implementation of the LDPC encoder: the Gaussian elimination method and the RU method.
3.1. LDPC Encoding with Gaussian Elinination
The Gaussian elimination is the most conventional method of encoding LDPC codes, which is carried out by the multiplication of the generator matrix G, and contains a complexity quadratic in the block length [19]. The unknown generator matrix G can be derived from the parity check matrix H. A generator matrix for code with a parity check matrix H can be obtained by carrying out Gauss–Jordan elimination on H in the following form:
where A is an binary matrix and is the identity matrix of order . The generator matrix is as follows:
The codeword C is then obtained by multiplying the generator matrix G by the systematic bits S as follows:
The sequential LDPC encoder based on the multiplication of the G matrix requires a ROM to store the generator matrix used to compute the codeword C. The main drawback of this approach is that, unlike parity check matrix H, the corresponding generator matrix G will most likely not be sparse. The complexity of this straightforward encoding algorithm is , where N is the number of bits in a codeword. Therefore, the implementation of the matrix multiplication at the encoder results in a very high complexity. For an arbitrary parity check matrix, the construction of G should be avoided and encoding should be carried out using back substitution with H.
3.2. LDPC Encoding with the RU Method
Instead of determining a generator matrix for H, an LDPC code can be directly encoded using the parity check matrix by transforming it into a lower triangular form and applying back substitution. The RU encoding method, which was proposed by Richardson and Urbanke [13], is a linear time encoding method for sparse parity check matrices. The underlying principle is transformation using only row and column permutations, to reformulate a parity check matrix H into a sparse matrix. Therefore, this approach can reduce the complexity more than the G matrix multiplication method. The RU algorithm consists of two steps: a pre-processing step and actual encoding step.
First, in the pre-processing step, the parity check matrix H is converted into the approximate lower triangular (ALT) form, as shown in Figure 3. The parity check matrix H is given by the matrix, where N is the block length of the code and M is the number of parity check equations. Given that the matrix transformation is realized solely by row and column permutations, the H matrix remains a sparse matrix:
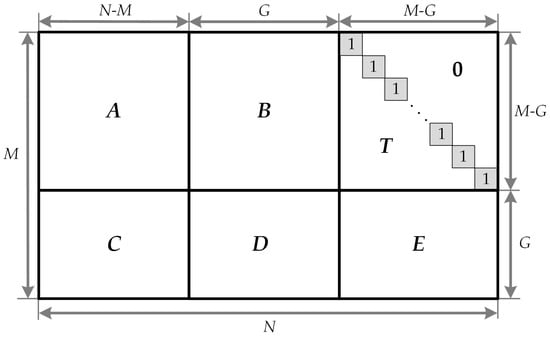
Figure 3.
The parity check matrix H in approximate lower triangular form.
Here, the matrix T has a lower triangular form with 1s along the diagonal, and all the entries above the diagonal are 0s. By multiplying H from the left by
the following is obtained:
where
The actual encoding step is performed by matrix-multiplication, forward-substitution and vector addition operations. Let the codeword where s represents the information bits, denotes the first G parity check bits, and contains the remaining parity check bits. The codeword C must satisfy the parity check equation . The two equations are then expressed by:
Using the RU method, the calculation of the parity bits in the first parity portion is only dependent on the information bits, given that E was cleared. Hence, it can be calculated independently of the parity bits in . If is non singular, then can be obtained from Equation (13):
If is singular in GF(2), then it is necessary to further permute the columns of to eliminate this singularity. Once is known, can be determined using Equation (13):
Given that T is the lower triangular form, can be found using back substitution. The complexity of this encoding procedure can be kept low since A, B and T are sparse. Table 3 and Table 4 present the complexity of calculation of and , respectively. The complexity of the RU algorithm is given by , where N is the block length and G is the gap to linear encoding. The gap is actually the number of rows of the parity check matrix that cannot be set into a triangular form using only row and column permutations. With a small gap G, the lower encoding complexity for the code is achieved.

Table 3.
Complexity analysis of calculation.

Table 4.
Complexity analysis of calculation.
The disadvantage of encoding using the RU method is that there is no exact programmable step-by-step algorithm. The multiple matrix calculations in this algorithm significantly limit the development of a rapid flexible encoder [28]. In addition, the RU method is subjected to a long critical path and odd constraints, which could render the LDPC encoder non-systematic [19].
4. Proposed 5G NR QC-LDPC Encoder Design
4.1. Proposed QC-LDPC Encoding Algorithm
This section presents an efficient scheme developed in this study for the construction of efficient encoders for 5G NR QC-LDPC codes. The proposed encoding method is based on the special characteristics of 5G NR QC-LDPC codes, which are presented in Figure 1. The proposed architectures target low-complexity, while ensuring high-throughput. As reported in the literature review, base graphs BG1 and BG2 have similar structures. In this paper, we focus our description on BG1 with a size of ( = 46, and = 68), which is the main 5G NR high rate base graph.
Let the codeword , where s denotes the systematic portion, which is divided into 22 groups of Z bits, since the base graph BG1 has information bit columns. Moreover, , where each element of s is a vector of length Z. The information messages received by the encoder are stored in registers that are organized by blocks, denoted by , which correspond to the systematic blocks, where each consists of Z bits. Given that the encoder was designed to read Z bits per clock cycle, it requires cycles to store all the information blocks. Moreover, the parity sequence can be grouped into sets of Z bits. Suppose that the parity portion of each message p is split into two sub-components as follows: the first parity bits , and the remaining parity bits . More precisely, the encoded codeword can be expressed as:
The parity check matrix H of 5G NR QC-LDPC codes can be partitioned into six matrices and presented in the following form:
where A is , B is , is , and is . Moreover, I is an identity matrix with dimensions of . The encoding of LDPC codes is carried out using the following defining equation:
Equation (18) can also be expressed as:
The proposed algorithm is performed in two steps. In the initial step, the parity bits in the first portion are computed by solving Equation (20). The second step in the encoding process includes the computation of the parity portions using Equation (21).
The first step in the encoder implementation is the determination of the part. Initially, Equation (20) is re-written in block form as follows:
This can then be expanded into the following set of equations:
where denotes the (right) cyclic shifted version of for . By adding up all the above equations, the following is obtained:
It should be noted that a straightforward implementation of can be done with the use of Z-bit cyclic shifters. Since is a circular right shift of with the shift coefficient defined by , the hardware complexity is trivial. Based on the definition below,
the following can be obtained:
From Equation (28), each value is computed by accumulating all the values. In Modulo 2, is obtained by carrying out XOR operations on all the elements of . The values can be estimated per clock cycle in cycles. The first block of the parity bits is then calculated by accumulating all the values. The remaining parity bits can be obtained using a method that can be easily derived from Equations (30)–(32). This process can be done in two clock cycles since there is dependency between and . All the parity bits in the first parity portion are stored in registers.
In a second step, the portion can be easily determined based on Equation (21), where matrices and are given by
Upon the application of Equation (21), the elements of can be computed using the following equations:
Similarly, represents a circular shift of with the shift coefficient defined by , and represents a circular shift of with the shift coefficient defined by . As soon as and have been obtained, they can be used to determine the value of the corresponding parity bits in the second parity portion . This step can be performed in a single clock cycle. Hence, all the parity bits can be acquired in clock cycles. The encoded codeword is then a combination of the original message s and the two calculated parity portions and .
4.2. Proposed QC-LDPC Encoder Architecture
Figure 4 details the overall block diagram for the proposed low complexity 5G NR QC-LDPC code encoder. The hardware architectures were designed to conduct the encoding process through steps defined in Equations (29)–(32) and (34). In the first step, the computation of the parity bits in the first portion is carried out. From Equation (28), each value is computed by accumulating all the cyclic shift results of . Since the information message s consists of blocks of Z bits, a total of barrel shifters of size Z, which are denoted by , , are required for the circular shift process. The vector addition of all the components is then carried out by the XOR trees. Each intermediate value corresponding to Equation (28) can be estimated per clock cycle and stored in the to be used later. Thus, the value of can be obtained in clock cycles when all values are obtained and stored in memory. The remaining parity bits of can be obtained in 2 clock cycles with the use of XOR gates.The objective of the second step is the calculation of the parity bits in the second portion . According to (34), the parity blocks can be achieved by the vector addition of and . The value of is also computed by accumulating all the cyclic shift results of . In this step, the overall hardware complexity can be further decreased by exploiting the sharing technique. More specifically, the barrel shifters and XOR trees are reused for the computation of in this step. Control signals are generated by the controller block. The value of is estimated by accumulating all the cyclic shift results of . The required number of Z–bit barrel shifters is . The main blocks of the proposed architecture can be described as follows.
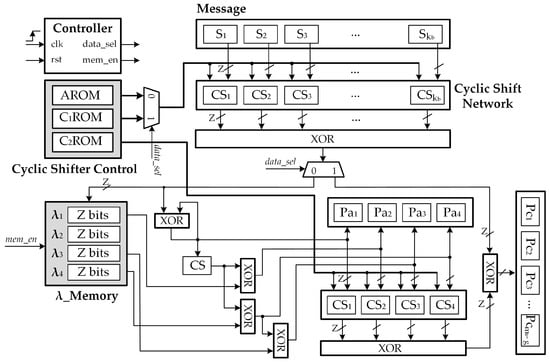
Figure 4.
Low-complexity high-throughput encoder architecture for 5G NR QC-LDPC code.
(1) Input/ Output Buffer: the input buffer, which is implemented as a number of serial input parallel output shift registers, is exploited to store the input systematic bits received by the encoder. The output buffer is used to store the encoded codeword.
(2) Memory Blocks: two memory blocks are utilized, namely, one for the submatrix permutation values, and the others for the accumulated values that correspond to matrix A. In Figure 4, the AROM, CROM, and CROM correspond to the ROMs that store the coefficients of matrix A, matrix , and matrix , respectively. Under the assumption that bits represent the required word length to store the permutation information for each submatrix: , , and bits are required to store matrix A, , and , respectively. A significant portion of the hardware complexity of the LDPC encoder consists of the memory required to store the parity check matrix. Unlike the RU method, the proposed algorithm does not require the inverse of the component matrix, which reflects its primary advantage over the RU method. Compared with the Gaussian method, the proposed architecture does not require for block-memories to store the generator matrix G, which further decreases the number of required components. The is implemented as a dual port random access memory (RAM) for storing messages . Each memory word consists of Z bits, corresponding to one accumulated message of matrix A. Moreover, a total of bits of are required for the proposed encoder.
(3) Barrel Shifters: barrel shifters are used to implement the cyclic shift permutations, according to the shift values provided by the cyclic shifter controllers. It should be noted that the number of cyclic shifters is equal to the number of message blocks, and the size of the barrel shifters is equal to submatrix size Z.
(4) XOR Trees: in Modulo 2, the addition implementation is obtained by carrying out an XOR operation on all the elements.
(5) Controller: this block generates control signals, such as to indicate the step being processed; and , to enable write access to the .
5. Performance Analysis and Comparison
This section reports the implementation results of the proposed LDPC encoder architecture as well as a detailed comparison between the proposed method and other encoder implementations in terms of area and speed for 5G NR standard. First, the design characteristics of different LDPC code encoders are discussed. Thereafter, an analysis of the proposed LDPC encoder, with respect to its implementation on ASIC, is presented.
Table 5 presents a comparison between the area and speed of the proposed encoding method and those of other state-of-the-art approaches. As shown in Table 5, the matrix size was utilized to determine the ROM storage, and the Hamming weights of the matrices were used in computing the gate count. Since all the systematic bits and parity check bits in the first parity portion are stored in registers, the number of flip-flops required was estimated by the bit sizes of K and . In Table 5, the time interval between input frames was exploited in order to compare the processing speed of different encoding methods. The time between two consecutive input frames is based on the total number of clock cycles between the arrivals of the first Z bits of a frame up to the cycle wherein the encoder is ready to receive another frame.

Table 5.
Comparison between Gaussian method, RU method, and proposed method.
To make it clear, a target LDPC code with a base graph BG1 and submatrix size was considered in Table 6. As can be observed from Table 6, the proposed encoder gains a significant reduction in the storage overhead. In the Gaussian elimination method, the entire generator matrix G is stored in the memory. In the RU method, the location of the edges (ones) of each row is stored, with an extra bit indicating the end of a row. By only storing the values of shift coefficients for each submatrix, the proposed method dramatically reduces the ROM size by 98.2% and 88.9% when compared with the G matrix method and RU method, respectively. Moreover, the proposed encoder reduces the number of XOR logic gate counts by 1.65 times compared with the RU method. This leads to a significant reduction in the hardware complexity for the proposed encoder as these components are the main contributors of logic resources in the encoder architecture. Hence, the proposed encoding structure shows a significant advantage over other LDPC encoding methods with respect to hardware complexity. As can be seen from Table 6, the Gaussian elimination approach requires only 23 clock cycles to generate the encoded codeword for a given LDPC code. However, this method suffers from a significant storage overhead which makes it less of an idea for implementation. From the analysis of the RU design, it was found to require 471 clock cycles per codeword. This is significantly higher than that of the proposed encoder, which only requires 70 clock cycles. From Table 6, it can be observed that the number of clock cycles required per codeword for the encoding of the proposed encoder design decreased to 14.8% of that of RU method.

Table 6.
Comparison between Gaussian method, RU method, and proposed method for submatrix size .
The ASIC post synthesis implementation results on TSMC 65–nm CMOS technology are shown in Table 7, for various QC-LDPC encoders with expansion factors Z = 30, 64, 96, 144, and 352, which are indicated in the table as BG1-Z30, BG1-Z64, BG1-Z96, BG1-Z144, and BG1-Z352, respectively. In Table 7, size denotes the word length required to store the shift sizes while stands for the number of clock cycles required per codeword for encoding. Note that all input data bits were assumed to be available for encoding, and the serialization factors are not included in the results. In the proposed design, the is equal to the maximum number of clock cycles required for the calculation of the and parity check bits. The computation of requires clock cycles, in which g clock cycles are used to compute all the values and , and two extra clock cycles are required for estimation of the remaining parity bits in the portion. The computation of requires clock cycles. Hence, this method requires clock cycles in total. The information throughput reported in Table 7 is given by the formula
where is the maximum operating frequency (post synthesis). For different submatrix sizes, the throughput varied from 22.1–202.4 Gbps. In Table 7, the occupied areas are also reported. It should be noted that there is a significant increase in the core area when processing higher submatrix sizes. Since encoder architecture of a higher submatrix size Z requires a higher size, additional memory and hardware components are required. It is shown that the encoding complexity of the proposed design is linearly proportional to the submatrix size Z of the code. To keep the throughput comparison on equal basis, the throughput-to-area ratio metric was further defined as . For all the considered submatrix sizes in Table 7, the ranged from 520–597 Gbps/mm.

Table 7.
ASIC implementation results of LDPC encoders for different lifting sizes 30, 64, 96, 144, and 352.
Based on the implementation results presented above, it is clear that the design methodology is applicable to different submatrix sizes and offers a significantly high area efficiency and high information throughput, which is more than enough to satisfy the throughput requirement for the 5G NR standard.
6. Conclusions
In this paper, a novel low-complexity high-throughput encoder approach for the 5G NR standard is proposed. Based on the proposed encoding algorithm, five encoder architectures with different submatrix sizes were implemented. The derived architecture exhibited a significantly lower hardware complexity, as it decreased the memory and logic component requirements. The proposed design demonstrates a superior performance to the alternative methods. Moreover, the synthesis results revealed that the proposed design is appropriate for the high throughput 5G standard.
Author Contributions
T.T.B.N. conceptualized the idea of this research, conducted experiments, collected data, and prepared the original version. T.N.T. reviewed, analyzed data, and updated the manuscript. H.L. supervised, validated, reviewed, and supported the research with funding.
Funding
This work was supported by the INHA UNIVERSITY Research Grant.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gallager, R.G. Low-Density Parity-Check Codes; MIT Press: Cambridge, MA, USA, 1963. [Google Scholar]
- MacKay, D.J.C.; Neal, R.M. Near Shannon Limit Performance of Low-Density Parity-Check Codes. Electron. Lett. 1996, 32, 1645–1646. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Xu, W. 5G Cellular User Equipment: From Theory to Practical Hardware Design. IEEE Access 2017, 5, 13992–14010. [Google Scholar] [CrossRef]
- Session Chairman (Nokia). Chairman’s Notes of Agenda Item 7.1.5 Channel Coding and Modulation, 3GPP TSG RAN WG1 Meeting No. 87, R1-1613710 (2016). Available online: https://portal.3gpp.org/ngppapp/CreateTdoc.aspx?mode=view&contributionId=752413 (accessed on 22 May 2019).
- Richardson, T.; Kudekar, S. Design of Low-Density Parity Check Codes for 5G New Radio. IEEE Commun. Mag. 2018, 56, 28–34. [Google Scholar] [CrossRef]
- Ji, W.; Wu, Z.; Zheng, K.; Zhao, L.; Liu, Y. Design and Implementation of a 5G NR System Based on LDPC in Open Source SDR. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Tang, H.; Xu, J.; Kou, Y.; Lin, S.; Abdel-Ghaffar, K. On Algebraic Construction of Gallager and Circulant Low-Density Parity-Check Codes. IEEE Trans. Inf. Theory 2004, 50, 1269–1279. [Google Scholar] [CrossRef]
- Ajaz, S.; Nguyen, T.T.B.; Lee, H. An Area-Efficient Half-Row Pipelined Layered LDPC Decoder Architecture. J. Semicond. Technol. Sci. 2017, 17, 845–853. [Google Scholar] [CrossRef]
- Nguyen, T.T.B.; Lee, H. Low-Complexity Multi-mode Multi-way Split-row Layered LDPC Decoder for Gigabit Wireless Communications. Integration 2018. [Google Scholar] [CrossRef]
- Ajaz, S.; Lee, H. Efficient multi-Gb/s multi-mode LDPC decoder architecture for IEEE 802.11ad applications. Integration 2015, 51, 21–36. [Google Scholar] [CrossRef]
- Ajaz, S.; Lee, H. An efficient radix-4 Quasi-cyclic shift network for QC-LDPC decoders. IEICE Electron. Express 2014, 11, 1–6. [Google Scholar] [CrossRef][Green Version]
- Ajaz, S.; Lee, H. Reduced-complexity Local Switch Based Multi-mode QC-LDPC Decoder Architecture for Gigabit Wireless Communications. IET Electron. Lett. 2013, 49, 1246–1248. [Google Scholar] [CrossRef]
- Richardson, T.J.; Urbanke, R.L. Efficient Encoding of Low-density Parity-check Codes. IEEE Trans. Inf. Theory 2001, 47, 638–656. [Google Scholar] [CrossRef]
- Khodaiemehr, H.; Kiani, D. Construction and Encoding of QC-LDPC Codes Using Group Rings. IEEE Trans. Inf. Theory 2017, 63, 2039–2060. [Google Scholar] [CrossRef]
- Huang, Q.; Tang, L.; He, S.; Xiong, Z.; Wang, Z. Low-Complexity Encoding of Quasi-Cyclic Codes Based on Galois Fourier Transform. IEEE Trans. Commun. 2014, 62, 1757–1767. [Google Scholar] [CrossRef]
- Li, Z.; Chen, L.; Zeng, L.; Lin, S.; Fong, W. Efficient Encoding of Quasi-cyclic Low-density Parity-check Codes. IEEE Trans. Commun. 2006, 54, 71–81. [Google Scholar] [CrossRef]
- Ilani, I. Designing and Encoding QC-LDPC Codes Using Matrices over Commutative Rings. In Proceedings of the 2016 IEEE International Conference on the Science of Electrical Engineering (ICSEE), Eilat, Israel, 16–18 November 2016; pp. 1–5. [Google Scholar]
- Jung, Y.; Chung, C.; Jung, Y.; Kim, J. 7.7 Gbps Encoder Design for IEEE 802.11ac QC-LDPC Codes. J. Semicond. Technol. Sci. 2014, 14, 419–425. [Google Scholar] [CrossRef]
- Cohen, A.E.; Parhi, K.K. A Low-Complexity Hybrid LDPC Code Encoder for IEEE 802.3an (10GBase-T) Ethernet. IEEE Trans. Signal Process. 2009, 57, 4085–4094. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, C.; Jiang, L. Efficient Encoding of QC-LDPC Codes Based on Rotate-left-accumulator Circuits. Electron. Lett. 2013, 49, 810–812. [Google Scholar] [CrossRef]
- Jung, Y.; Kim, J. Memory-efficient and High-speed LDPC Encoder. Electron. Lett. 2010, 46, 1035–1036. [Google Scholar] [CrossRef]
- Li, H.; Bai, B.; Mu, X.; Zhang, J.; Xu, H. Algebra-Assisted Construction of Quasi-Cyclic LDPC Codes for 5G New Radio. IEEE Access 2018, 6, 50229–50244. [Google Scholar] [CrossRef]
- Chen, L.; Xu, J.; Djurdjevic, I.; Lin, S. Near-Shannon-limit Quasi- cyclic Low-density Parity-check Codes. IEEE Trans. Commun. 2004, 52, 1038–1042. [Google Scholar] [CrossRef]
- Chen, L.; Lan, L.; Djurdjevic, I.; Lin, S.; Abdel-Ghaffar, K. An Algebraic Method for Constructing Quasi-cyclic LDPC Codes. In Proceedings of the International Symposium on Information Theory and Its Applications, Parma, Italy, 10–13 October 2004; pp. 535–539. [Google Scholar]
- Li, J.; Lin, S.; Abdel-Ghaffar, K.; Ryan, W.; Costello, D.J., Jr. LDPC Code Designs, Constructions, and Unification; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Chen, T.; Vakilinia, K.; Divsalar, D.; Wesel, R.D. Protograph Based Raptor-like LDPC Codes. IEEE Trans. Commun. 2015, 63, 1522–1532. [Google Scholar] [CrossRef]
- Ad-Hoc chair (Nokia). Chairman’s Notes of Agenda Item 7.1.4. Channel Coding, 3GPP TSG RAN WG1 Meeting AH 2, R1-1711982 (2017). Available online: https://portal.3gpp.org/ngppapp/CreateTdoc.aspx?mode=view&contributionId=805088 (accessed on 22 May 2019).
- Yasotharan, H.; Carusone, A.C. A Flexible Hardware Encoder for Systematic Low-density Parity-check Codes. In Proceedings of the 52nd IEEE International Midwest Symposium on Circuits and Systems, Cancun, Mexico, 2–5 August 2009; pp. 54–57. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).