Guided Modes in a Double-Well Asymmetric Potential of a Graphene Waveguide

Abstract

The analogy between the electron wave nature in graphene electronics and the electromagnetic waves in dielectrics has suggested a series of optical-like phenomena, which is of great importance for graphene-based electronic devices. In this paper, we propose an asymmetric double-well potential on graphene as an electronic waveguide to confine the graphene electrons. The guided modes in this graphene waveguide are investigated using a modified transfer matrix method. It is found that there are two types of guided modes. The first kind is confined in one well, which is similar to the asymmetric quantum well graphene waveguide. The second kind can appear in two potential wells with double-degeneracy. Characteristics of all the possible guide modes are presented.

1. Introduction

A two-dimensional layer of carbon atoms known as graphene [1] has been investigated widely both theoretically and experimentally. Graphene has a unique band structure for which the electron and hole bands meet at two inequivalent points in the Brillouin zone. At these Dirac points, the electrons behave like quasi-particles according to the massless Dirac equation, which leads to a linear dispersion relation. The analogy between the electron wave nature in graphene electronics and the electromagnetic waves in dielectrics has suggested a series of optical-like phenomena, such as the Goos–Hänchen effect [2,3], negative refraction [4], collimation [5], birefringence [6], and the Bragg reflection [7] reported in recent papers.

Another analogy is the graphene-based electron waveguides [8,9,10,11,12,13,14,15,16,17,18], which will be useful for various graphene-based devices, such as electronic fiber [19]. The crux of such an electronic waveguide is the confinement of Dirac fermions in graphene. There are many schemes to confine electrons in graphene, e.g., electric confinement [20,21], magnetic confinement [22] and strain-induced confinement [16,17,18]. By having a quantum well in graphene to confine massless Dirac fermions, the guided modes in graphene-based waveguides with quantum well structure induced by an external electrical field have been investigated in detail [8,9,10]. Experimentally, gate-controlled electron guiding in graphene by tuning the carrier type and its density using local electrostatic fields has been achieved [12]. However, the confinement of the quasi-particles is not strong enough due to the Klein tunneling.

Another effective way to confine the electrons in graphene is by applying a uniform magnetic field [22] and the characteristics of magnetic waveguides in graphene have also been studied [13,14]. Recently, the strain-induced graphene waveguides has also attracted much attention [16,17,18]. Contrary to the electric or magnetic waveguide in graphene, the strain-induced waveguide confines electrons without any external fields. It confines the quasi-particles with the pseudo-magnetic field [23], which arises from the applied mechanical strain. The bound states of the strain-induced waveguides are dependent on the valleys, which is different from the electric and magnetic waveguides (valley independent). Furthermore, smooth one-dimensional potential [15,24,25,26] and velocity barriers [27] have been proposed to confine the Dirac fermions in graphene. Electrons can also be guided in nano-structured graphene, such as graphene nano-ribbons [28] and antidot lattice [29]. Recently, Allen et al. demonstrated the confinement of electron waves in graphene with the use of superconducting interferometry in a graphene Josephson junction [30].

For a given graphene waveguide with quantum well structures, the dispersion equation for its guided modes is normally determined by applying the continuity of wave function at the interfaces of the quantum well. This method is easy for one quantum well structure, but not for multiple or more complicated quantum well structures, e.g., a double-well potential. In this paper, we will apply a transfer matrix method [31,32,33] to deduce the dispersion equation for guided modes in a double-well potential structure. From the calculation, we will present the characteristics of the guided modes in detail, and report its novel properties as compared to other graphene-based waveguides.

In the present work, we focus on the properties of guided modes in a double-well asymmetric potential that acts as a slab waveguide for electron waves (based on Dirac solution) in a form similar to that in integrated optics. However, it should be noted that the optical properties or optical waves in graphene have also been investigated [34,35,36,37,38,39,40,41]. This work shows an analogy between the electron wave nature in graphene electronics and the electromagnetic waves in dielectrics.

2. Guided Mode and Dispersion Equation for a Double-Well Potential

In the presence of an electrostatic potential V(x), electrons inside a monolayer graphene can be described by the Dirac-like equation:

$$[-i\hslash v_F\overrightarrow{\sigma }·\nabla +V(x)]\mathsf{\Psi }(x,y)=E\mathsf{\Psi }(x,y),$$

(1)

where $\overrightarrow{\sigma }=({\sigma }_x,{\sigma }_y)$ are the Pauli matrices, and $v_F={10}^6$ m/s is the Fermi velocity. $\mathsf{\Psi }={({\tilde{\mathsf{\Psi }}}_A,{\tilde{\mathsf{\Psi }}}_B)}^T$ is a two-component pseudo-spinor wave function, and ${\tilde{\mathsf{\Psi }}}_{A,B}$ are the smooth enveloping functions for two triangular sublattices in graphene, which can be expressed as ${\tilde{\mathsf{\Psi }}}_{A,B}(x,y)={\mathsf{\Psi }}_{A,B}(x)e^{i{k}_{y}y}$ due to its translation invariance in the direction. In terms of ${\mathsf{\Psi }}_{A,B}$, Equation (1) is written as

$$\frac{d{\mathsf{\Psi }}_{A,B}}{dx}\mp k_y{\mathsf{\Psi }}_{A,B}=i\frac{E-V(x)}{\hslash v_F}{\mathsf{\Psi }}_{B,A}.$$

(2)

By using the transfer matrix method [31,32,33], we obtain a matrix M to connect the wave functions ${\mathsf{\Psi }}_{A,B}(x)$ at the two boundaries at $x=0$ and $x=d$:

$$\left(\begin{array}{c}{\mathsf{\Psi }}_A(d)\\ {\mathsf{\Psi }}_B(d)\end{array}\right)=M\left(\begin{array}{c}{\mathsf{\Psi }}_A(0)\\ {\mathsf{\Psi }}_B(0)\end{array}\right),$$

(3)

$$M=\left(\begin{array}{cc}{\displaystyle \frac{cos(k_{x}d-\theta )}{cos\theta }}& {\displaystyle s\frac{isin(k_{x}d)}{cos\theta }}\\ & \\ {\displaystyle s\frac{isin(k_{x}d)}{cos\theta }}& {\displaystyle \frac{cos(k_{x}d+\theta )}{cos\theta }}\end{array}\right),$$

(4)

where $s=\text{sgn}(E-V)$, $k=|E-V|/\hslash v_F$, $(k_x,k_y)=k(cos\theta ,sin\theta )$. By solving Equation (3), one can immediately obtain the dispersion equation of a graphene waveguide (see below).

Here, we consider a double-well asymmetric potential for graphene waveguide as plotted in Figure 1a, where its potential distribution $V(x)$ is denoted by

$$V(x)=\left\{\begin{array}{cc}{V}_1\hfill & x<0\hfill \\ V_2\hfill & 0<x<h_1\hfill \\ V_3\hfill & h_1<x<(h_1+h_2)\hfill \\ V_4\hfill & x>(h_1+h_2)\hfill \end{array}\right..$$

(5)

Figure 1. Schematic diagram of (a) a double-well potential on graphene; (b) guided modes in the region $(0,h_1)$; (c) guided modes in the region $(0,h_1+h_2)$.

The proposed waveguide configuration can be realized by applying four gate-tunable potential barriers on single-layer graphene [42]. By tuning the applied voltage on the gate, a double-well asymmetric potential can be formed on graphene. For simplicity, we have $V_1=V_4$ unless it is specified elsewhere. In this model, we have neglected the microscopic details of the interaction effects such as the inter-valley coupling [43,44] and inter-valley scattering in the potential steps [44,45]. The electron wave incident into the quantum well (region 2) with an angle θ respect to the x-axis, and the guided modes are propagating in the y-direction. The critical angle of the incident electron waves from region i to region j is defined by

$${\theta }_{ij}=arcsin(|E-V_j|/|E-V_i|),$$

(6)

where $i,j=1,2,3,4(i\ne j)$, E is the energy of incident electron and $V_{i(j)}$ is the electrostatic potential in the respective region $i(j)$. The critical angle ${\theta }_{ij}$ is shown in Figure 2 as a function of the incidence energy E for $V_1=V_4=100\text{meV}$, $V_2=0\text{meV}$, $V_3=60\text{meV}$, $h_1=100\text{nm}$, and $h_2=80\text{nm}$.

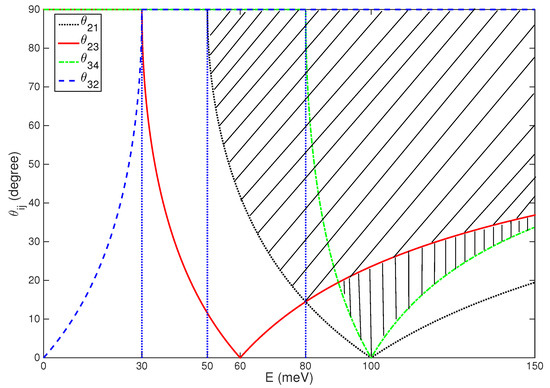
Figure 2. The critical angle ${\theta }_{ij}$ as a function of the incidence energy E. The physical parameters are: $V_1=V_4=100$ meV, $V_2=0$ meV, $V_3=60$ meV, $h_1=100$ nm, $h_2=80$ nm.

For a given guided mode, there will be total internal reflection of electron waves at both the two interfaces of a waveguide. For example, at large incidence angles $\theta >max({\theta }_{21},{\theta }_{23})$, total reflection occurs in a specific range (marked with “slanted lines”) as plotted in Figure 2. In this range, the electron waves will be reflected at the interfaces back and forth with an angle of in region 2 ($0<x<h_1$) with a guided wave propagating in the axis as shown in Figure 1b.

For the angle within ${\theta }_{23}>\theta >{\theta }_{21}$ in region 2 and the angle ${\theta }_3>{\theta }_{34}$ in region 3, which lies in a range marked with “vertical lines” in Figure 2, the electron waves will refract into region 3, and total internal reflection occurs at the interface $x=h_1+h_2$. The electron wave will oscillate in the region of $0<x<h_1+h_2$ as shown in Figure 1c. It is important to note that there are no guided modes within $h_1<x<h_1+h_2$, as there is no angle θ to fulfill the condition ${\theta }_3>max({\theta }_{32},{\theta }_{34})$. Thus, there are only two types of guided modes in a double-well potential. The first one is the guided modes in $0<x<h_1$, and the other is the guided modes in $0<x<h_1+h_2$.

To derive the dispersion equation, the electron wave function ${\mathsf{\Psi }}_{AB}(x)$ in the double-well potential can be written as:

$${\mathsf{\Psi }}_A(x)=\left\{\begin{array}{cc}{A}_1{e}^{{\alpha }_{1}x}\hfill & x<0\hfill \\ A_2{e}^{i{k}_{2x}(x-h_1)}+B_2{e}^{-i{k}_{2x}(x-h_1)}\hfill & 0<x<h_1\hfill \\ A_3{e}^{i{k}_{3x}(x-h_1-h_2)}+B_3{e}^{-i{k}_{3x}(x-h_1-h_2)}\hfill & h_1<x<(h_1+h_2)\hfill \\ A_4{e}^{-{\alpha }_4(x-h_1-h_2)}\hfill & x>(h_1+h_2)\hfill \end{array}\right.,$$

(7)

$${\mathsf{\Psi }}_B(x)=\left\{\begin{array}{cc}{c}_1{A}_1{e}^{{\alpha }_{1}x}\hfill & x<0\hfill \\ c_2{A}_2{e}^{i{k}_{2x}(x-h_1)}-d_2{B}_2{e}^{-i{k}_{2x}(x-h_1)}\hfill & 0<x<h_1\hfill \\ c_3{A}_3{e}^{i{k}_{3x}(x-h_1-h_2)}-d_3{B}_3{e}^{-i{k}_{3x}(x-h_1-h_2)}\hfill & h_1<x<(h_1+h_2)\hfill \\ c_4{A}_4{e}^{-{\alpha }_4(x-h_1-h_2)}\hfill & x>(h_1+h_2)\hfill \end{array}\right..$$

(8)

Here, we have $k_i=|E-V_i|/\hslash v_F$, $s_i=\text{sgn}(E-V_i)$$(i=1,2,3,4)$, $k_y=k_{2}sin\theta$, $k_{2x}=\sqrt{k_2^2-k_y^2}$, $k_{3x}=\sqrt{k_3^2-k_y^2}$, ${\alpha }_1={\alpha }_4=\sqrt{k_y^2-k_1^2}$. And $c_1=-i{s}_1({\alpha }_1-k_y)/k_1$, $c_2=-i{s}_2(i{k}_{2x}-k_y)/k_2$, $c_3=-i{s}_3(i{k}_{3x}-k_y)/k_3$, $c_4=i{s}_4({\alpha }_4+k_y)/k_4$, $d_2=-i{s}_2(i{k}_{2x}+k_y)/k_2$, $d_3=-i{s}_3(i{k}_{3x}+k_y)/k_3$.

Based on the transfer matrix method, we have:

$$\left(\begin{array}{c}1\\ c_4\end{array}\right)A_4=\left(\begin{array}{c}{\mathsf{\Psi }}_A(h_1+h_2)\\ {\mathsf{\Psi }}_B(h_1+h_2)\end{array}\right)=M_3{M}_2\left(\begin{array}{c}{\mathsf{\Psi }}_A(0)\\ {\mathsf{\Psi }}_B(0)\end{array}\right)=M_3{M}_2\left(\begin{array}{c}1\\ c_1\end{array}\right)A_1,$$

(9)

where $M_{2(3)}=\left(\begin{array}{cc}{\displaystyle \frac{cos\left(k_{2x(3x)}{h}_{1(2)}-{\theta }_{2(3)}\right)}{cos{\theta }_{2(3)}}}\hfill & {\displaystyle s_{2(3)}\frac{isin\left(k_{2x(3x)}{h}_{1(2)}\right)}{cos{\theta }_{2(3)}}}\hfill \\ \\ {\displaystyle s_{2(3)}\frac{isin\left(k_{2x(3x)}{h}_{1(2)}\right)}{cos{\theta }_{2(3)}}}\hfill & {\displaystyle \frac{cos\left(k_{2x(3x)}{h}_{1(2)}+{\theta }_{2(3)}\right)}{cos{\theta }_{2(3)}}}\hfill \end{array}\right)$, and $sin{\theta }_{2(3)}=k_y/k_{2(3)}$.

By multiplying Equation (9) with matrix $(-c_4,1)$, we obtain

$$\left(\begin{array}{cc}-c_4& 1\end{array}\right)M_3{M}_2\left(\begin{array}{c}1\\ c_1\end{array}\right)=0.$$

(10)

From Equation (10), we obtain the dispersion equation for the guided modes in a double-well potential, which is

$$tan(k_{2x}{h}_1)=\frac{(k_{2x}{h}_1)tan(k_{3x}{h}_2)f_2-s_1{s}_{3}tan(k_{3x}{h}_2)f_3+(k_{2x}{h}_1)(k_{3x}{h}_1)f_1}{s_1{s}_2{f}_4-(k_{3x}{h}_2)f_2-tan(k_{3x}{h}_2)f_1{f}_2+s_2{s}_3(k_2{h}_1)(k_3{h}_1)tan(k_{3x}{h}_2)f_1}=F(k_{2x}{h}_1),$$

(11)

and $f_1=\sqrt{{(k_2{h}_1)}^2-{(k_{2x}{h}_1)}^2-{(k_1{h}_1)}^2}$, $f_2={(k_2{h}_1)}^2-{(k_{2x}{h}_1)}^2$, $f_3=(k_1{h}_1)(k_{2x}{h}_1)(k_3{h}_1)$, $f_4=(k_1{h}_1)(k_2{h}_1)(k_{3x}{h}_1)$, and $k_{3x}{h}_2=\sqrt{{(k_3{h}_1)}^2-{(k_2{h}_1)}^2+{(k_{2x}{h}_1)}^2}{h}_2/h_1$. The dispersion equation for the guided modes obtained with the transfer matrix method is more convenient than the usual method that solving the Dirac equations from the continuity of wave function at the interfaces of quantum wells. The dispersion equation (Equation (11)) obtained for the double-well asymmetric potential can be recovered to that of the symmetric quantum well-based graphene waveguide by setting $V_3=V_4=V_1$ and $h_2=0\text{nm}$. Thus, we have

$$tan(k_{2x}{h}_1)=\frac{s_1\sqrt{{(k_2{h}_1)}^2-{(k_{2x}{h}_1)}^2-{(k_1{h}_1)}^2}(k_{2x}{h}_1)}{s_2(k_1{h}_1)(k_2{h}_1)-s_1\left({(k_2{h}_1)}^2-{(k_{2x}{h}_1)}^2\right)}=F(k_{2x}{h}_1),$$

(12)

which is the dispersion equation for a symmetric quantum well, as reported in Ref. [8]. Equation (12) can also be directly obtained by using the transfer matrix method:

$$\left(\begin{array}{c}{\mathsf{\Psi }}_A(h_1)\\ {\mathsf{\Psi }}_B(h_1)\end{array}\right)=M_2\left(\begin{array}{c}{\mathsf{\Psi }}_A(0)\\ {\mathsf{\Psi }}_B(0)\end{array}\right).$$

(13)

3. Characteristics of the Guided Modes in a Double-Well Potential

For the guided mode in the region $0<x<h_1$, the electron waves are evanescent in the other three regions, namely $k_y^2>k_3^2$, where $k_{3x}=\sqrt{k_3^2-k_y^2}$ is an imaginary number, and $k_{2x}$, ${\alpha }_1={\alpha }_4$ are real. Thus, we have the following conditions:

$$\left\{\begin{array}{c}{k}_{2x}<\sqrt{k_2^2-k_1^2}\hfill \\ k_{2x}<\sqrt{k_2^2-k_3^2}\hfill \end{array}\right.,$$

(14)

which is used to determine the range of $k_{2x}$.

There are three energy ranges for a guided mode in this region: (i) $E<V_3$; (ii) $V_3<E<V_1$; and (iii) $E>V_1$, as shown Figure 2 (marked with oblique lines). To show the values of $k_{2x}{h}_1$, Equation (11) (LHS: $tan(k_{2x}{h}_1)$ and RHS: $F(k_{2x}{h}_1)$) are plotted in Figure 3 as a function of $k_{2x}{h}_1$ for three energy levels: $E=56$, 94 and 110 meV. The intersections of $tan(k_{2x}{h}_1)$ and $F(k_{2x}{h}_1)$ give the specific values for the guided modes.

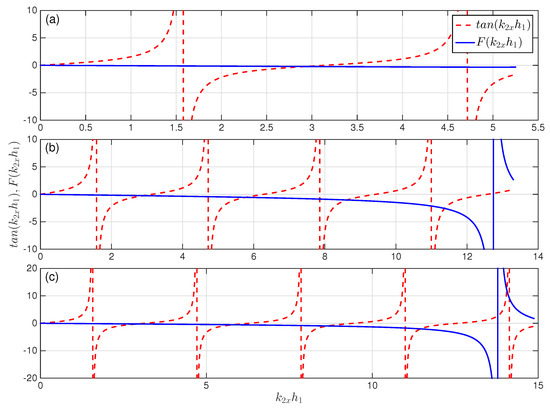
Figure 3. Graphical determination of $k_{2x}{h}_1$ for guided modes in $(0,h_1)$. The red and blue curves correspond to $tan(k_{2x}{h}_1)$ and $F(k_{2x}{h}_1)$, respectively. The energy of incident electron is (a) $E=56$ meV; (b) $E=94$ meV; and (c) $E=110$ meV. The other parameters are the same as those in Figure 2.

For the $E<V_3$ case, we have $s_1=s_3=s_4=-1$ and $s_2=1$, which corresponds to the regime of Klein tunneling. Here, we set $E=56$ meV, and there is only one intersection ($k_{2x}{h}_1=2.9257$), as shown in Figure 3a. The corresponding wave function distribution is plotted in Figure 4a. Similar to the optical waveguide, the guided modes is defined by the number of the nodes of the spinor wave function ${({\mathsf{\Psi }}_A,-i{\mathsf{\Psi }}_B)}^T$. The spinor components ${\mathsf{\Psi }}_A$ and $-i{\mathsf{\Psi }}_B$ represent electron and hole states, respectively. It is clearly seen from Figure 4a that there is no fundamental mode in this case since only Klein tunneling occurs in the double-well potential. The probability current density of the guided mode is plotted in Figure 4b, which can be calculated by the definition in the Dirac equation, $J_y=v_F{\mathsf{\Psi }}^{+}{\sigma }_y\mathsf{\Psi }$ with ${\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right)$, $\mathsf{\Psi }=\left(\begin{array}{c}{\mathsf{\Psi }}_A(x)\\ {\mathsf{\Psi }}_B(x)\end{array}\right)e^{i{k}_{y}y}$. This finding indicates that the Dirac fermions can be well-localized in the double-well potential.

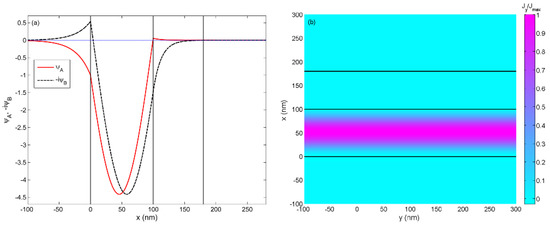
Figure 4. (a) the wave function of guided modes as a function of distance corresponding to the intersection $(k_{2x}{h}_1=2.9257,\theta ={69.8694}^{\mathrm{o}})$ in Figure 3a. The solid curve and the dashed lines corresponds to ${\mathsf{\Psi }}_A$ and $-i{\mathsf{\Psi }}_B$, respectively. The vertical lines represent the boundaries of the waveguide; and (b) the corresponding probability current density within the graphene waveguide for the guided mode. The solid black lines represent boundaries of the waveguide.

For the $V_3<E<V_1$ case, we have $s_1=s_4=-1$, $s_2=s_3=1$. Both Klein tunneling and classical motion are present in the double-well potential. Here, we choose $E=94$ meV, and there are four intersections, as shown in Figure 3b. The corresponding wave functions of the four guided modes are presented in Figure 5: (a) $k_{2x}{h}_1=2.8959$; (b) $k_{2x}{h}_1=5.7775$; (c) $k_{2x}{h}_1=8.6220$; and (d) $k_{2x}{h}_1=11.3661$. The figure shows different mode structures and characteristics between ${\mathsf{\Psi }}_A$ and $-i{\mathsf{\Psi }}_B$. For ${\mathsf{\Psi }}_A$, the double-well potential can support the fundamental mode, first-order mode, second-order mode, and third-order mode. However, there is no fundamental mode in the waveguide for $-i{\mathsf{\Psi }}_B$ (see Figure 5a, a small peak appears in wave functions for $-i{\mathsf{\Psi }}_B$ on the left interface of the waveguide), and it only supports first-order mode, second-order mode, third-order mode, and fourth-order mode. This finding suggests that the electrons and holes have different behaviors under the same conditions, which is similar to the mixing case of classical motion and Klein tunneling that appeared in an asymmetric quantum well graphene waveguide [9,10].

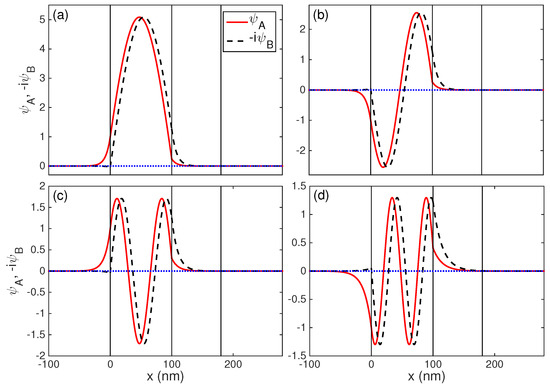
Figure 5. The wave function ${\mathsf{\Psi }}_A$ (solid) and $-i{\mathsf{\Psi }}_B$ (dashed) of guided modes as a function of distance corresponding to the intersections in Figure 3b: (a) $k_{2x}{h}_1=2.8959$, $\theta ={78.2908}^{\mathrm{o}}$; (b) $k_{2x}{h}_1=5.7775$, $\theta ={66.1160}^{\mathrm{o}}$; (c) $k_{2x}{h}_1=8.6220$, $\theta ={52.8267}^{\mathrm{o}}$; and (d) $k_{2x}{h}_1=11.3661$, $\theta ={37.1996}^{\mathrm{o}}$.

For large electron energy $E=110$ meV in the $E>V_1$ case, we have $s_1=s_2=s_3=s_4=1$. The dependencies of $tan(k_{2x}{h}_1)$ and $F(k_{2x}{h}_1)$ on $k_{2x}{h}_1$ are shown in Figure 3c. In this case, it is clearly seen from Figure 6 that the wave functions ${\mathsf{\Psi }}_A$ and $-i{\mathsf{\Psi }}_B$ of guided modes for the five intersection points: (a) $k_{2x}{h}_1=2.9025$; (b) $k_{2x}{h}_1=5.7934$; (c) $k_{2x}{h}_1=8.6556$; (d) $k_{2x}{h}_1=11.4531$; and (e) $k_{2x}{h}_1=14.0545$ have very similar characteristics. The waveguide can support the fundamental mode, first-order mode, second-order mode, third-order mode, and fourth-order mode for the electrons and the holes. It must be pointed out that the guided modes in region 2 have similar characteristics with those in asymmetric quantum well graphene waveguide [9,10].

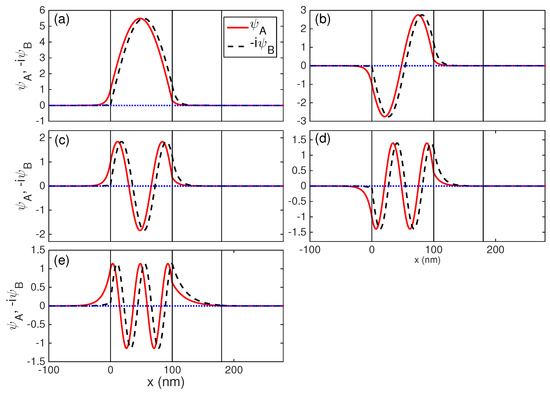
Figure 6. The wave function ${\mathsf{\Psi }}_A$ (solid) and $-i{\mathsf{\Psi }}_B$ (dashed) of guided modes as a function of distance corresponding to the intersections in Figure 3c: (a) $k_{2x}{h}_1=2.9025$, $\theta ={79.9900}^{\mathrm{o}}$; (b) $k_{2x}{h}_1=5.7934$, $\theta ={69.6994}^{\mathrm{o}}$; (c) $k_{2x}{h}_1=8.6556$, $\theta ={58.7782}^{\mathrm{o}}$; (d) $k_{2x}{h}_1=11.4531$, $\theta ={46.6948}^{\mathrm{o}}$; and (e) $k_{2x}{h}_1=14.0545$, $\theta ={32.6828}^{\mathrm{o}}$.

For the guided modes in the region of $0<x<h_1+h_2$, $k_{2x}=\sqrt{k_2^2-k_y^2}$, $k_{3x}=\sqrt{k_3^2-k_y^2}$ and ${\alpha }_1={\alpha }_4$ should be real. The transverse wavenumber $k_{2x}$ in region 2 must fulfills the following condition:

$$\sqrt{k_2^2-k_3^2}<k_{2x}<\sqrt{k_2^2-k_1^2}.$$

(15)

For the incident electrons with low energy $E=56$ meV, the double-well potential cannot support a guided mode. Thus, only a dispersion equation at higher energy $E=94$ meV and $E=110$ meV are plotted in Figure 7a,b, respectively. Each of them has three intersection points. For $E=94$ meV (from Figure 7a), the intersections are (a) $k_{2x}{h}_1=13.4848$; (b) $k_{2x}{h}_1=14.0965$; and (c) $k_{2x}{h}_1=14.2552$, which are plotted in Figure 8. For $E=110$ meV (from Figure 7b), we have (a) $k_{2x}{h}_1=15.2567$; (b) $k_{2x}{h}_1=16.0201$; and (c) $k_{2x}{h}_1=16.6082$, which are plotted in Figure 9.

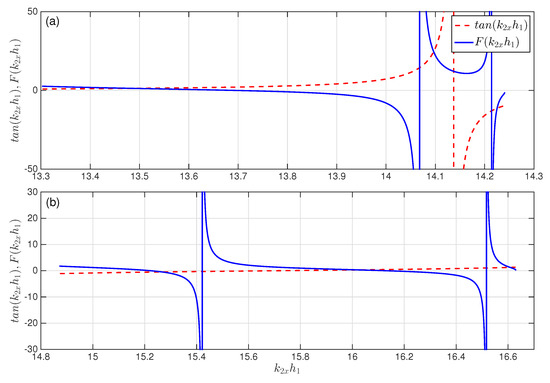
Figure 7. Graphical determination of $k_{2x}{h}_1$ for guided modes in $(0,h_1+h_2)$. The red and blue curves correspond to $tan(k_{2x}{h}_1)$ and $F(k_{2x}{h}_1)$, respectively. The energy of incident electron is (a) $E=94$ meV and (b) $E=110$ meV. The other parameters are the same as those in Figure 2.

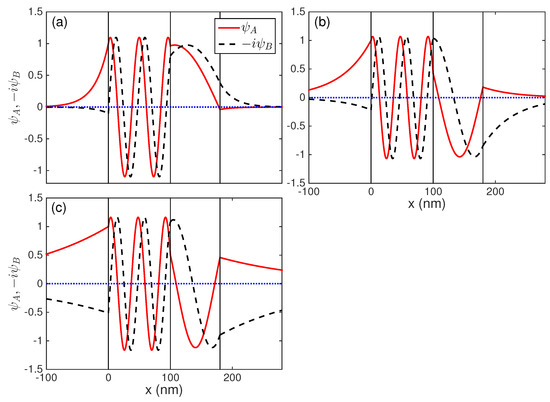
Figure 8. The wave function ${\mathsf{\Psi }}_A$ (solid) and $-i{\mathsf{\Psi }}_B$ (dashed) of guided modes as a function of distance corresponding to the intersections in Figure 7a: (a) $k_{2x}{h}_1=13.4848$, $\theta ={19.0890}^{\mathrm{o}}$; (b) $k_{2x}{h}_1=14.0965$, $\theta ={8.9296}^{\mathrm{o}}$; and (c) $k_{2x}{h}_1=14.2552$, $\theta ={4.5134}^{\mathrm{o}}$.

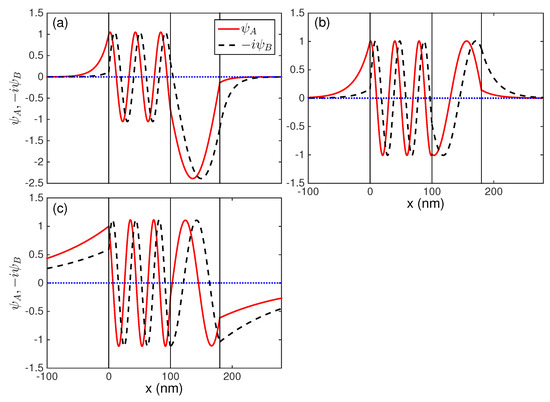
Figure 9. The wave function ${\mathsf{\Psi }}_A$ (solid) and $-i{\mathsf{\Psi }}_B$ (dashed) of guided modes as a function of distance corresponding to the intersections in Figure 7b: (a) $k_{2x}{h}_1=15.2675$, $\theta ={23.8914}^{\mathrm{o}}$; (b) $k_{2x}{h}_1=16.0201$, $\theta ={16.3885}^{\mathrm{o}}$; and (c) $k_{2x}{h}_1=16.6082$, $\theta ={5.9544}^{\mathrm{o}}$.

From the figure, we see that the electrons and holes have similar mode structure and motion characteristics. For the $E=94$ meV case, the double-well potential is able to support a higher order mode, such as the sixth-order mode (Figure 8b,c). This is known as mode double-degeneracy, which is similar to the oscillating guided modes in a symmetric five-layer left-handed waveguide [46]. For $E=110$ meV, we have fifth-order mode, sixth-order mode, and seventh-order mode, as shown in Figure 9. For completeness, the probability current density of some specific guided modes is plotted in Figure 10, which shows good confinement.

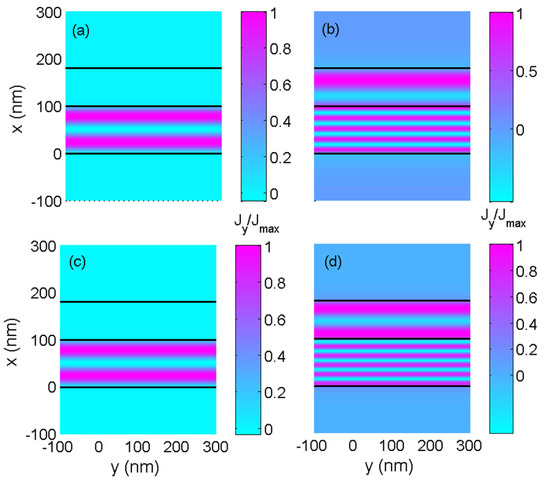
Figure 10. Probability current density within the graphene waveguide for the guided modes: (a) $E=94$ meV, $k_{2x}{h}_1=5.7775$; (b) $E=94$ meV, $k_{2x}{h}_1=14.0965$; (c) $E=110$ meV, $k_{2x}{h}_1=5.7934$; and (d) $E=110$ meV, $k_{2x}{h}_1=16.0201$.

In general, for the electrons in this graphene waveguide with $E=94$ meV, the double-well potential supports the fundamental mode, first-order mode, second-order mode, third-order mode, fifth-order mode and sixth-order mode for ${\mathsf{\Psi }}_A$, while it supports the first-order mode, second-order mode, third-order mode, fourth-order mode, fifth-order mode and sixth-order mode for $-i{\mathsf{\Psi }}_B$. The fourth-order mode is absent for ${\mathsf{\Psi }}_A$, while the fundamental mode is absent for $-i{\mathsf{\Psi }}_B$. Mode double-degeneracy appears for the sixth-order mode for both ${\mathsf{\Psi }}_A$ and $-i{\mathsf{\Psi }}_B$. The order of the guided modes is dependent on the incident energy and incidence angle for a given quantum well electron waveguide. The reason for the absence of some guided modes is that the incident energy is not sufficiently large with respect to the critical angle for the certain guided mode [8]. The absence of guided modes is similar to the situations in negative-refractive-index waveguides [46,47]. For the $E=110$ meV case, the guided modes for ${\mathsf{\Psi }}_A$ and $-i{\mathsf{\Psi }}_B$ have similar mode structure. The waveguide can support the fundamental mode, first-order mode, second-order mode, and up to the seventh-order mode for the electrons and the holes. There is no mode absent in this condition.

For many applications, it is desired to have mode tuning either by potential, the incident energy, or the well width. In Figure 11, the solutions to the guided modes at different values of well width $h_2=0$, 40, 100, 160 nm are presented. For the guided modes in $0<x<h_1$, the results (see Figure 11a) show that changing $h_2$ has no effect on the number of guided modes. However, for the guided modes in $0<x<h_1+h_2$, we have more guide modes at higher $h_2$, as shown in Figure 11b. For example, at $h_2=160$ nm, we have three guided modes in the region $0<x<h_1+h_2$, which is higher than two modes for $h_2=100$ nm, and only one mode for $h_2=40$ nm. Obviously, there are no intersections for guided modes in the region $0<x<h_1+h_2$ with $h_2=0$ nm. In comparison with the quantum well graphene waveguide, the double-well graphene waveguide can support some higher order guided modes in a wider range.

Figure 11. Graphical determination of $tan(k_{2x}{h}_1)$ and $F(k_{2x}{h}_1)$ for guided modes in (a) $(0,h_1)$ and (b) $(0,h_1+h_2)$ with different values of $h_2$. Here, the incident energy of electrons is fixed at $E=94$ meV. The other parameters are the same as those in Figure 2.

4. Conclusions

We have determined the guided modes in a double-well asymmetry potential with a transfer matrix method over a wide range of parameters. Two types of guide modes were found in the proposed structures, one of which was similar to the characteristics with those in the graphene waveguide with asymmetric quantum well structure. It was found that the proposed graphene based electron waveguides can support some higher order nodes (up to the 7th order). Mode double-degeneracy appeared under some conditions. For some given incident energy of electrons, some modes are absent. Furthermore, the tuning of the number of guided modes by the well width was also studied. These novel properties of the guided modes in the double-well potential may provide potential applications for various graphene-based electronic devices. Electron waveguides are examples of various graphene-based electronic devices; however, the transfer matrix method may not be suitable for simulating other graphene-based electronic devices, such as graphene-based field effect transistors. Hence, we will seek other methods to solve the Dirac equation in graphene in order to simulate graphene-based electronic devices in our future research work.