Analysis of a Multilevel Dual Active Bridge (ML-DAB) DC-DC Converter Using Symmetric Modulation

Abstract

Dual active bridge (DAB) converters have been popular in high voltage, low and medium power DC-DC applications, as well as an intermediate high frequency link in solid state transformers. In this paper, a multilevel DAB (ML-DAB) has been proposed in which two active bridges produce two-level (2L)-5L, 5L-2L and 3L-5L voltage waveforms across the high frequency transformer. The proposed ML-DAB has the advantage of being used in high step-up/down converters, which deal with higher voltages, as compared to conventional two-level DABs. A three-level neutral point diode clamped (NPC) topology has been used in the high voltage bridge, which enables the semiconductor switches to be operated within a higher voltage range without the need for cascaded bridges or multiple two-level DAB converters. A symmetric modulation scheme, based on the least number of angular parameters rather than the duty-ratio, has been proposed for a different combination of bridge voltages. This ML-DAB is also suitable for maximum power point tracking (MPPT) control in photovoltaic applications. Steady-state analysis of the converter with symmetric phase-shift modulation is presented and verified using simulation and hardware experiments.

2. ML-DAB Topologies with Symmetric Phase-Shift Modulation

In this ML-DAB configuration, two bridges are assumed to have different dc voltage levels (i.e., $V_s$ and $V_P,$ where $V_P>V_s$) where $V_P$ and $V_s$ are high and low dc bus voltages, respectively. Figure 1 and Figure 2 show voltage step-up and step-down schematics of NPC-based 2L-5L DAB, respectively. Most DAB-based power electronic converters deal with different voltage levels at the two ends of the converter, and this ML-DAB is very suitable for such applications. If the required voltage level is much higher than the dc bus voltage $V_P$, a higher voltage may be achieved by cascading multiple ML-DABs, which, in turn, facilitates conversion of large-scale (in the order of megawatts) power with a fewer number of ML-DAB modules. This methodology improves the overall efficiency and increases the power density.

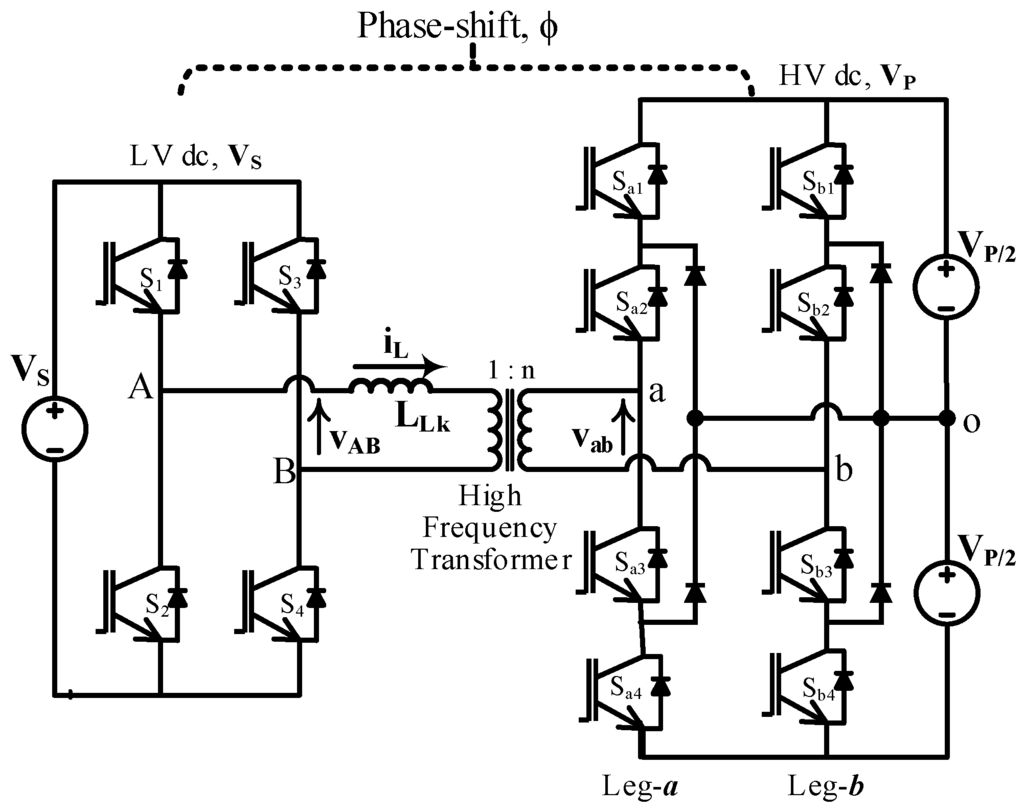
Figure 1. Boost configuration (V_p > V_s) of a multilevel dual active bridge (ML-DAB), where the transformer primary voltage (v_AB) is two-level (2L) and the secondary (v_ab) of 5L.

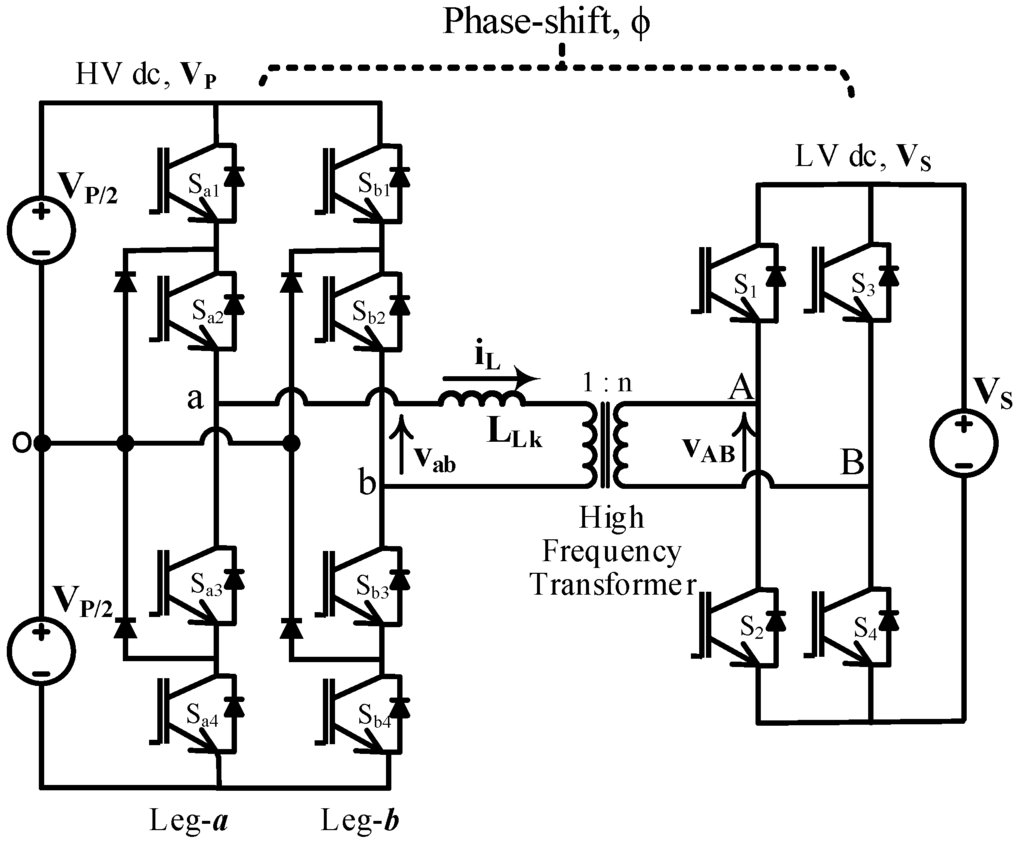
Figure 2. Buck configuration (V_s < V_p) of the ML-DAB where the transformer primary voltage (v_ab) is of 5L and the secondary (v_AB) is of 2L.

2.1. Neutral Point Diode Clamped Configuration

The neutral point diode clamp (NPC) is one of the most popular and widely-used multilevel topologies in medium and high voltage industrial applications. In this ML-DAB, three-level (3L) diode clamped legs (leg-a, b in Figure 1 and Figure 2) are used to produce a leg-to-leg five-level (5L) voltage waveform $v_{ab}$. The low voltage bridge is switched so as to produce a two-level (2L) square waveform $v_{AB}$ across the transformer. Compared to the 2L voltage source converter, the 3L-NPC configuration employs clamping diodes to connect the phase output to the neutral point “o”, as shown in Figure 1 and Figure 2, which produces a 3L voltage at each NPC leg. The voltage sources (i.e., $V_s,\frac{V_P}{2}$) shown in Figure 1 and Figure 2 are practically replaced by bulk capacitors, and the input and/or the output of the ML-DAB usually are followed by a source, a load or other converters in real applications. This ML-DAB can be configured for single phase or three phases with bi-directional power-flow capability by using current bi-directional switches and a suitable modulation scheme. In this paper, we are analyzing different cases of ML-DAB assuming a single-phase transformer with unidirectional power flow from the 2L bridge to the 5L bridge. The bi-directional power flow can easily be controlled with the phase-shift angle ($\varphi$) between the active bridges. Power always flows from the voltage-leading bridge to the voltage-lagging bridge.

2.2. Switching States of the 3L-NPC Bridge

The NPC inverter concept was first proposed in 1980 [15]. Since then, researchers have contributed to several aspects of this converter, such as various modulation schemes, the number of voltage levels, capacitor voltage balancing, harmonics mitigation and active clamping instead of diodes. Switching and modulation details of a 3L-NPC as a three-phase inverter are studied in detail in [16]. In ML-DAB operation, the switching pattern of NPC is slightly different from that in conventional inverters. Unlike 3L-NPC line frequency (i.e., 50 or 60 Hz) inverters, the switching frequency is considered the fundamental frequency in an ML-DAB. Table 1 shows how a three-level voltage is synthesized in a 3L-NPC leg for both positive ($i_a>0$) and negative ($i_a<0$) current flow.

Table 1. Switching states in a 3L-NPC leg.

Switching States	Status of the Switches in 3L-NPC Leg-a				3-Level LEG Voltage, vao
	Sa1	Sa2	Sa3	Sa4
+	ON	ON	OFF	OFF	+ $\frac{V_P}{2}$
0	OFF	ON	ON	OFF	0
−	OFF	OFF	ON	ON	− $\frac{V_P}{2}$

Table 1. Switching states in a 3L-NPC leg.

Switching States	Status of the Switches in 3L-NPC Leg-a				3-Level LEG Voltage, vao
	Sa1	Sa2	Sa3	Sa4
+	ON	ON	OFF	OFF	+ $\frac{V_P}{2}$
0	OFF	ON	ON	OFF	0
−	OFF	OFF	ON	ON	− $\frac{V_P}{2}$

Figure 3 shows some major switching states to form a 3L (i.e., $+\frac{V_P}{2},0,-\frac{V_P}{2}$) voltage waveform $v_{ao}$. The main advantage of the 3L-NPC is that all of the switching devices in a leg withstand only half (i.e., $\frac{V_P}{2}$) of the dc bus voltage (i.e., $V_P$) during commutation between states, which also yields lower $\frac{dv}{dt}$ in comparison to the two-level inverter. Switching between “+” and “−” states are not considered, because this scheme involves all four switches ($S_{a1}to{S}_{a4}$) in a leg, two being turned on and the other two being commutated off, during which dynamic voltage on each switch may not be kept the same [16]. This also causes double the switching losses. A small dead time is allowed between different states. The leg-b is also switched in a similar pattern to create a 3L voltage waveform $v_{bo}$. In this proposed modulation scheme, $v_{bo}$ is phase-shifted from $v_{ao}$ by an amount $(\alpha +\beta )$ to produce a leg-to-leg 5L voltage waveform $v_{ab}$ across the transformer (Figure 4).

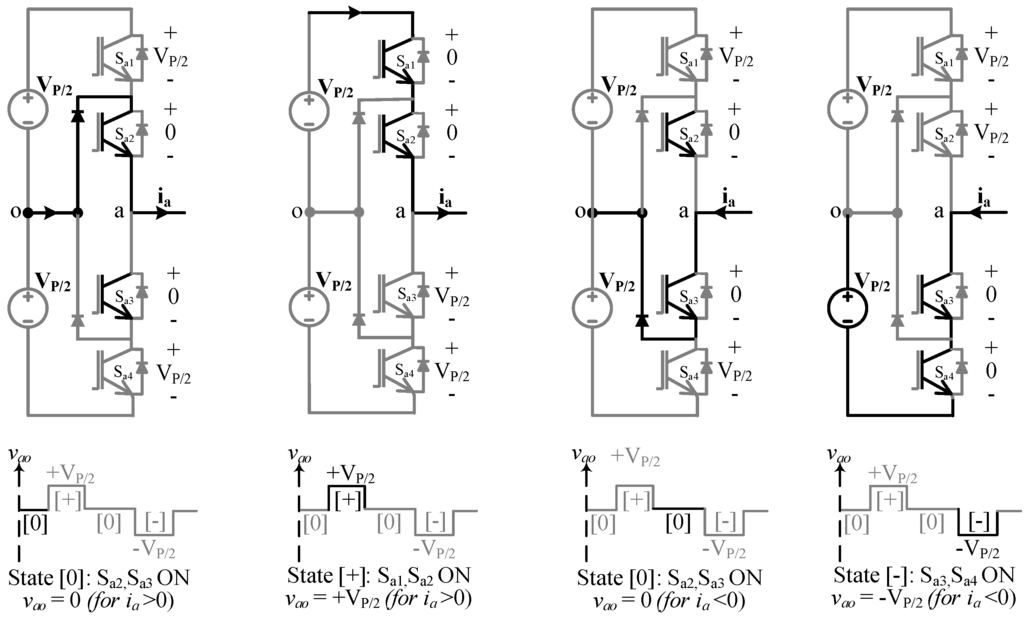
Figure 3. Switching states and corresponding 3L voltage (v_ao) synthesized from leg-a of a 3L-NPC bridge.

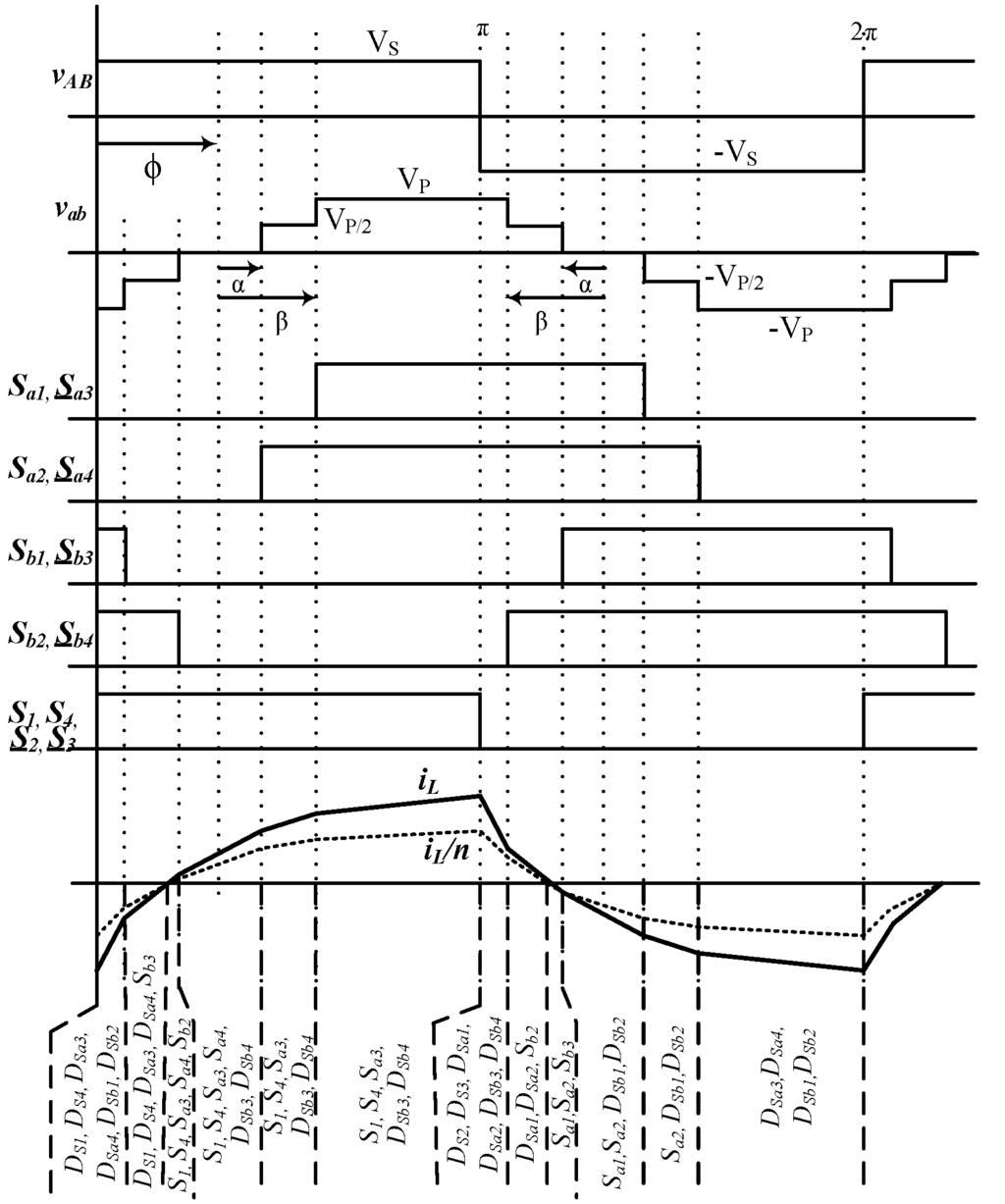
Figure 4. Switch pulses and corresponding voltage waveforms and primary current in a 2L-5L DAB boost topology.

The two-level bridge has two legs, each having two complementary switches operating with a 50% duty cycle. When $S_1,S_4$ are turned on, the leg-to-leg square wave voltage $v_{AB}=+V_s$, and when $S_2,S_3$ are turned on, $v_{AB}=-V_s$. Gate pulses for all twelve switches (i.e., $S_1\text{ to }{S}_4\text{ and }{S}_{a1}\text{to }{S}_{a4},S_{b1}\text{ to }{S}_{b4}$) for both 2L and 5L bridges in a boost topology are shown in Figure 4 with the resulting voltage waveforms ($v_{AB},v_{ab}$) across the high frequency transformer and the current ($i_L\text{ and}\frac{i_L}{n}$) through the leakage inductor.

2.3. Symmetric Modulation

In order to synthesize the 5L voltage $v_{ab}$, the switching pulses and the resulting voltage waveform are defined with respect to angular distances (i.e., $\alpha ,\beta$) instead of the duty cycle. These angles $\alpha ,\beta$ are measured symmetrically at zero, $\text{π}$ and $2\text{π}$ within a switching period (Figure 5). The zero and $\pi$ are considered at the mid-point of the zero voltage level of the 5L voltage $v_{ab}$. Defining $v_{ab}$ in such a symmetrical way is advantageous in terms of the minimum numbers of parameters ($\alpha ,\beta$) required, which, in turn, easily describe and derive a simple mathematical expression for power flow in the ML-DAB. These parameters $\alpha \text{ and }\beta$ shape the multilevel voltage waveform and can be utilized in the improvement of the total harmonic distortion (THD) and voltage balancing of the capacitors [14]. The phase-shift angle $\varphi$ is independent of $\alpha ,\beta$ and acts as the control parameter to control the power flow in the ML-DAB.

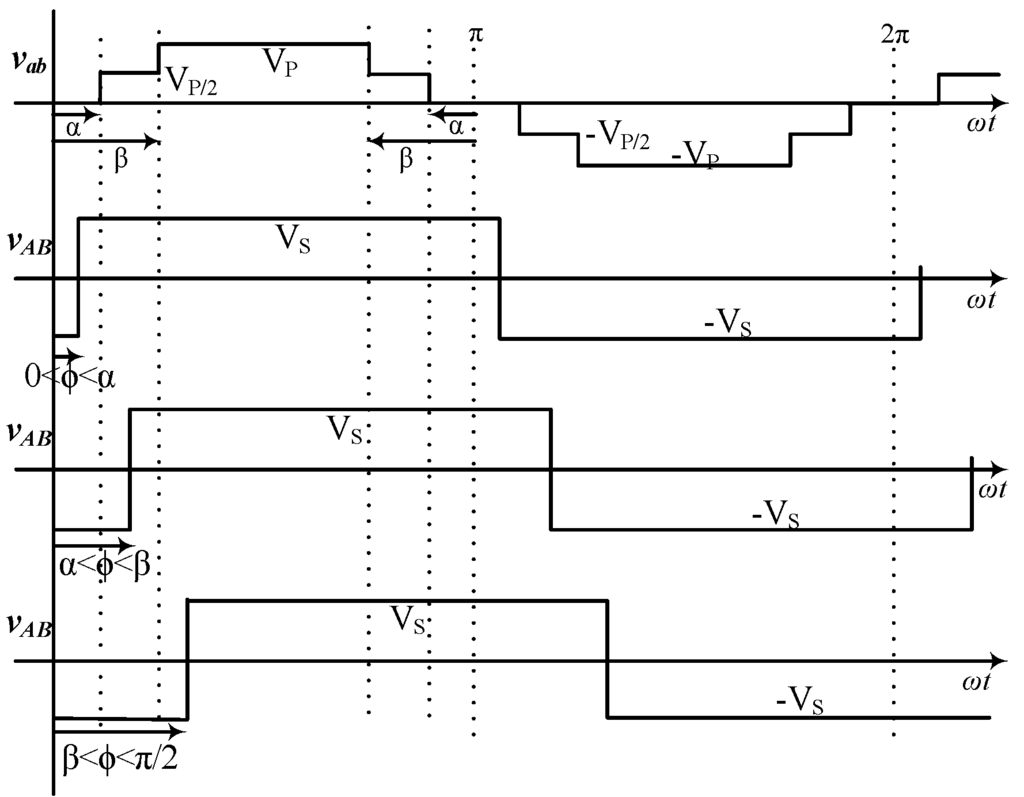
Figure 5. Voltage waveforms in a 5L-2L DAB for three different cases of buck topology when v_AB is formed using $D=0.5$.

In order to produce a zero-average symmetric alternating waveform, the low-voltage ($V_s$) bridge legs should be switched complementarily at the duty cycle (D) in a range of zero to 50% ($0<D\le 0.5$). If $D=0.5$, a 2L ($v_{AB}\equiv +V_s,-V_s$) voltage $v_{AB}$ will be formed, and if $D<0.5$, a 3L ($v_{AB}\equiv +V_s,0,-V_s$) voltage will be produced (Figure 6). This 3L voltage at the low voltage bridge is also generated symmetrically, equally spaced from zero $\text{and }\pi$ by an angle $\gamma$. This single parameter $\gamma$ can define the 3L $v_{AB}$ for the whole range of $D<0.5$.

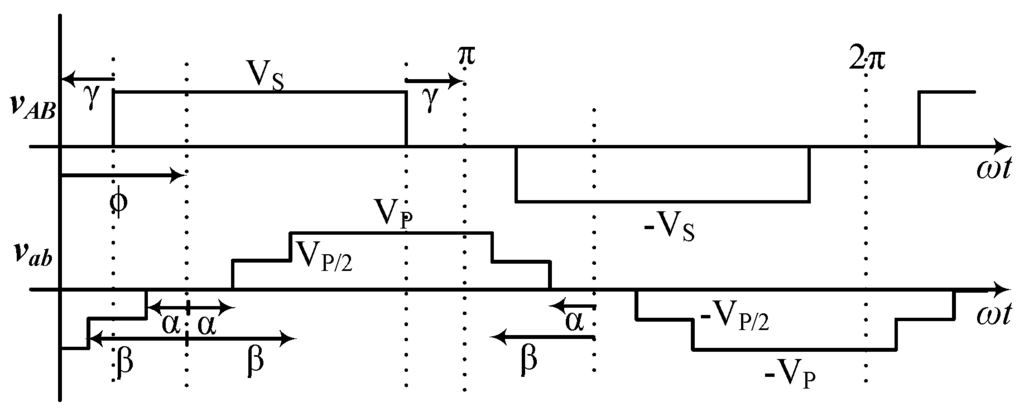
Figure 6. Voltage waveforms in a 3L-5L DAB boost topology when v_AB is formed using $D<0.5$.

3. Power Flow Equations and Soft Switching in ML-DAB

In ML-DAB, power flow is controlled by the phase-shift angle ($\varphi$) between $v_{AB}$ and $v_{ab}$, like conventional DAB. The leakage inductance of the high frequency transformer acts as the main energy transfer element. This primary referred leakage inductance is assumed externally as $L_{Lk}$ in Figure 1 and Figure 2. In order to analyze the power flow through each type of ML-DAB shown in Figure 4, Figure 5 and Figure 6, we will analyze the current $i_L$ through the leakage inductor for each topology.

3.1. 2L-5L DAB Boost Topology

The switching and modulation for a 2L-5L DAB boost topology is shown in Figure 4. The 2L $v_{AB}$ is assumed to start at angle zero, and 5L $v_{ab}$ is lagging $v_{AB}$ by the phase-shift angle $\varphi ,\left(0<\varphi <\frac{\pi }{2}\right)$. From the basic inductor voltage relation we get,

$$\begin{array}{c}{v}_L=L.\frac{{di}_L}{dt}\\ or,i_L\left(t\right)=\frac{1}{L}.{{\displaystyle \int }}_{t_1}^{t_2}{v}_L.dt\\ or,i_L(\theta )=\frac{1}{\omega L}.{{\displaystyle \int }}_{{\theta }_1}^{{\theta }_2}{v}_L.d\theta ;\text{ where},\theta =\omega t\end{array}$$

(1)

One switching cycle time period has been converted to 2π radians in the following equations. Now, writing this i_L(θ) equation for each segment of v_L from zero to π as shown in Figure 4, we get, $\text{for }0<\theta <\left(\varphi -\beta \right):$

$$i_L\left(\theta \right)=\frac{V_s+\frac{V_P}{n}}{\omega L}.\theta +i_L\left(0\right);i_L\left(\varphi -\beta \right)=\frac{V_s+\frac{V_P}{n}}{\omega L}.\left(\varphi -\beta \right)+i_L\left(0\right),$$

(2)

$\text{for }\left(\varphi -\beta \right)<\theta <\left(\varphi -\alpha \right):$

$$i_L\left(\varphi -\alpha \right)=\frac{V_s+\frac{V_P}{2n}}{\omega L}.\left(\varphi -\alpha -\varphi +\beta \right)+i_L\left(\varphi -\beta \right),$$

(3)

$\text{for }\left(\varphi -\alpha \right)<\theta <\left(\varphi +\alpha \right):$

$$i_L\left(\varphi +\alpha \right)=\frac{V_s}{\omega L}.\left(\varphi +\alpha -\varphi +\alpha \right)+i_L\left(\varphi -\alpha \right),$$

(4)

$\text{for }\left(\varphi +\alpha \right)<\theta <\left(\varphi +\beta \right):$

$$i_L\left(\varphi +\beta \right)=\frac{V_s-\frac{V_P}{2n}}{\omega L}.\left(\varphi +\beta -\varphi -\alpha \right)+i_L\left(\varphi +\alpha \right),$$

(5)

$\text{for }\left(\varphi +\beta \right)<\theta <\pi :$

$$i_L\left(\pi \right)=\frac{V_s-\frac{V_P}{n}}{\omega L}.\left(\pi -\varphi -\beta \right)+\frac{V_s-\frac{V_P}{2n}}{\omega L}.\left(\beta -\alpha \right)+\frac{V_s}{\omega L}.\left(2\alpha \right)+\frac{V_s+\frac{V_P}{2n}}{\omega L}.\left(\beta -\alpha \right)+\frac{V_s+\frac{V_P}{n}}{\omega L}.\left(\varphi -\beta \right)+i_L\left(0\right),$$

(6)

Assuming zero average current through the transformer, $i_L\left(0\right)=-i_L(\pi )$:

$$\begin{array}{c}or,-2i_L\left(0\right)=\frac{V_s}{\omega L}.\left(\pi \right)-\frac{V_P}{2n\omega L}.(2\pi -4\varphi )\\ or,i_L\left(0\right)=\frac{V_P}{n\omega L}.\left(\frac{\pi }{2}-\varphi \right)-\frac{V_s}{\omega L}.\left(\frac{\pi }{2}\right)\end{array}$$

(7)

Putting this expression of $i_L\left(zero\right)$ in the above equations, we can get the $i_L\left(\theta \right)$ at different points,

$$\begin{array}{c}{i}_L\left(\varphi -\beta \right)=\frac{V_s}{\omega L}.\left(\varphi -\beta -\frac{\pi }{2}\right)+\frac{V_P}{n\omega L}.\left(\frac{\pi }{2}-\beta \right),\\ i_L\left(\varphi -\alpha \right)=\frac{V_s}{\omega L}.\left(\varphi -\alpha -\frac{\pi }{2}\right)+\frac{V_P}{n\omega L}.\left(\frac{\pi }{2}-\frac{\alpha }{2}-\frac{\beta }{2}\right),\\ i_L\left(\varphi +\alpha \right)=\frac{V_s}{\omega L}.\left(\varphi +\alpha -\frac{\pi }{2}\right)+\frac{V_P}{n\omega L}.\left(\frac{\pi }{2}-\frac{\alpha }{2}-\frac{\beta }{2}\right),\\ i_L\left(\varphi +\beta \right)=\frac{V_s}{\omega L}.\left(\varphi +\beta -\frac{\pi }{2}\right)+\frac{V_P}{n\omega L}.\left(\frac{\pi }{2}-\beta \right).\end{array}\}$$

(8)

The average power flow expression from the primary to secondary bridge through the leakage inductance can be written as follows:

$$\begin{array}{c}{P}_o=\frac{1}{\pi }\underset{0}{\overset{\pi }{{\displaystyle \int }}}{v}_{AB}\left(\theta \right).i_L\left(\theta \right).d\theta \\ or,P_o=\frac{V_s}{2\pi }\left[\right\{i_L\left(0\right)+i_L\left(\varphi -\beta \right)\}.\left(\varphi -\beta \right)+\left\{i_L\left(\varphi -\beta \right)+i_L\left(\varphi -\alpha \right)\right\}.\left(\beta -\alpha \right)+\left\{i_L\left(\varphi -\alpha \right)+i_L\left(\varphi +\alpha \right)\right\}.\left(2\alpha \right)+\left\{i_L\left(\varphi +\beta \right)+i_L\left(\varphi +\alpha \right)\right\}.\left(\beta -\alpha \right)+\left\{i_L\left(\varphi +\beta \right)+i_L\left(\pi \right)\right\}.\left(\pi -\varphi -\beta \right)]\end{array}$$

(9)

After calculating the above power equation using (3), we get the simplified power equation as follows,

$$P_o=\frac{V_P{V}_s}{n\omega L}.\left(\varphi -\frac{{\varphi }^2}{\pi }-\frac{{\alpha }^2}{2\pi }-\frac{{\beta }^2}{2\pi }\right)$$

(10)

$$or,P_{o_{p.u.}}=m\left(\varphi -\frac{{\varphi }^2}{\pi }-\frac{{\alpha }^2}{2\pi }-\frac{{\beta }^2}{2\pi }\right);wherem=\frac{V_P}{n{V}_s},P_{base}=\frac{V_s^2}{\omega L}$$

(11)

where $P_o$ is the average power ($P_{o_{p.u.}}$ is the per unit power) measured at the output of the converter with the variables defined as, $\omega =2\pi f_s$, where $f_s$ is the switching frequency, n is the transformer turns ratio, m is the voltage conversion ratio defined as $m=\frac{V_P}{n{V}_s}$ and L is the primary referred inductance ($L_{Lk}$) used at the high frequency link. The per unit power vs.$\varphi \text{ and }\beta$, while α is chosen to be fixed at ${10}^0$, is shown in Figure 7 for different m values. Power vs.$\varphi \text{ and }\beta$ planes with different m-values for a 2L-5L DAB boost topology are shown in Figure 7.

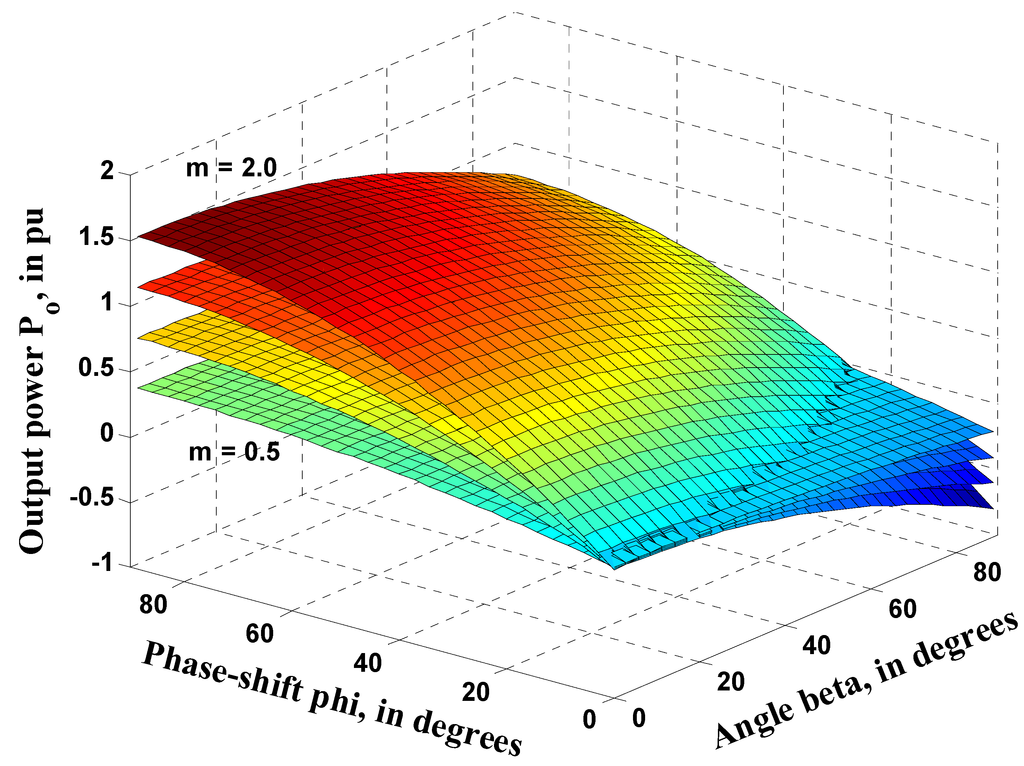
Figure 7. ML-DAB output power $P_{o_{p.u.}}vs.\varphi \text{ and }\beta \text{ with }\alpha ={10}^0$for $m=0.5,1,1.5\text{ and }2.$

3.2. 5L-2L DAB Buck Topology

The voltage waveforms for a 5L-2L DAB buck topology are shown in Figure 5. The 5L v_ab is assumed to start at angle zero, and 2L v_AB is lagging by the phase-shift angle ϕ. In this topology, based on the value of ϕ, there may be three cases, such as $\text{Case I}:0<\varphi <\alpha ,\text{ Case II}:\alpha <\varphi <\beta \text{ and }$$\text{Case III}:\beta <\varphi <\frac{\pi }{2}$. Each case has been analyzed to formulate a power flow equation using the same procedure described from (1) to (11).

$$\text{Case I}:P_o=\frac{V_P{V}_s}{n\omega L}\varphi \left(1-\frac{\alpha }{\pi }-\frac{\beta }{\pi }\right);0<\varphi \le \alpha$$

(12)

$$\text{Case II}:P_o=\frac{V_P{V}_s}{n\omega L}\left(\varphi -\frac{{\varphi }^2}{\pi }-\frac{{\alpha }^2}{2\pi }-\frac{\varphi \beta }{\pi }\right);\alpha <\varphi \le \beta$$

(13)

$$\text{Case III}:P_o=\frac{V_P{V}_s}{n\omega L}\left(\varphi -\frac{{\varphi }^2}{\pi }-\frac{{\alpha }^2}{2\pi }-\frac{{\beta }^2}{2\pi }\right);\beta <\varphi \le \frac{\pi }{2}$$

(14)

Equation (14) may be considered as the generalized one and can be rewritten as follows,

$$P_o=m\frac{V_s^2}{\omega L}\left(\varphi -\frac{{\varphi }^2}{\pi }-\frac{{\alpha }^2}{2\pi }-\frac{{\beta }^2}{2\pi }\right);\text{ where }m=\frac{V_P}{n{V}_s}$$

(15)

Equations (10) and (15) are the same, which also validates the bi-directional power-flow capability of this ML-DAB converter only based on the phase-shift between primary and secondary side bridge voltages. Figure 8 shows the power flow from the 5L to 2L bridge for the three different cases described above.

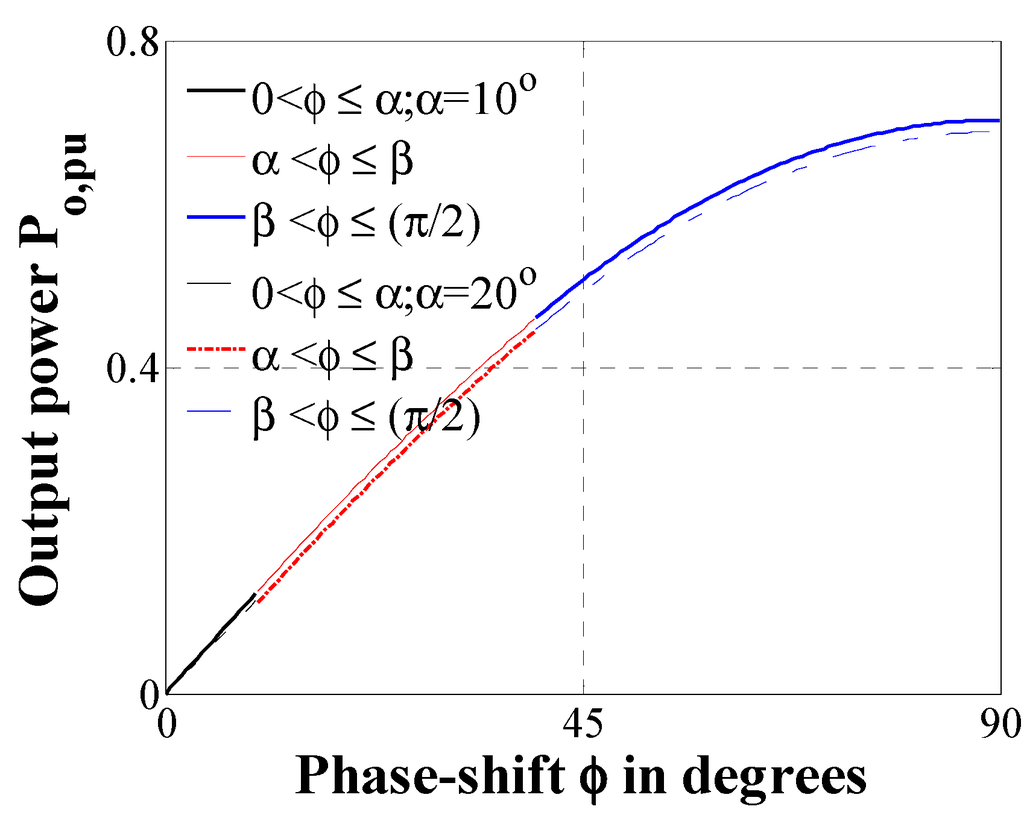
Figure 8. Power flow through DAB for all three cases (12) to (14), with respect to phase-shift ϕ; here, $\alpha ={10}^{0}and{20}^0,\beta ={40}^0$ are assumed for calculation.

3.3. 3L-5L DAB Boost Topology

The primary and secondary voltage waveforms for a 3L-5L DAB boost topology are shown in Figure 9. The 3L v_AB is assumed to start at angle γ after the zero, and 5L v_ab is lagging v_AB by the phase-shift angle ϕ The pulse-width of 3L waveform is assumed symmetrically reduced by an angle of γ which actually results from switch duty cycles D < 5. Using the same sector-wise inductor current analysis, as shown in (1) to (10), the power flow equation for this topology has been derived as,

$$P_{o_{p.u}}=\left[m\left\{\left(\varphi -\frac{{\varphi }^2}{\pi }+\frac{\beta \gamma }{\pi }+\frac{\gamma }{2}-\frac{{\beta }^2}{2\pi }-\frac{{\alpha }^2}{2\pi }\right)\right\}+\gamma \left\{\frac{\pi +\beta -\varphi -\gamma }{2\pi }\right\}\right]$$

(16)

If we put $\gamma =0$ in (16), it reduces to the 2L-5L power equation in (11). Similarly, if the condition is such that $\alpha =\beta =0$, Equations (11) and (16) reduce to the conventional two-level DAB onverter equations [1].

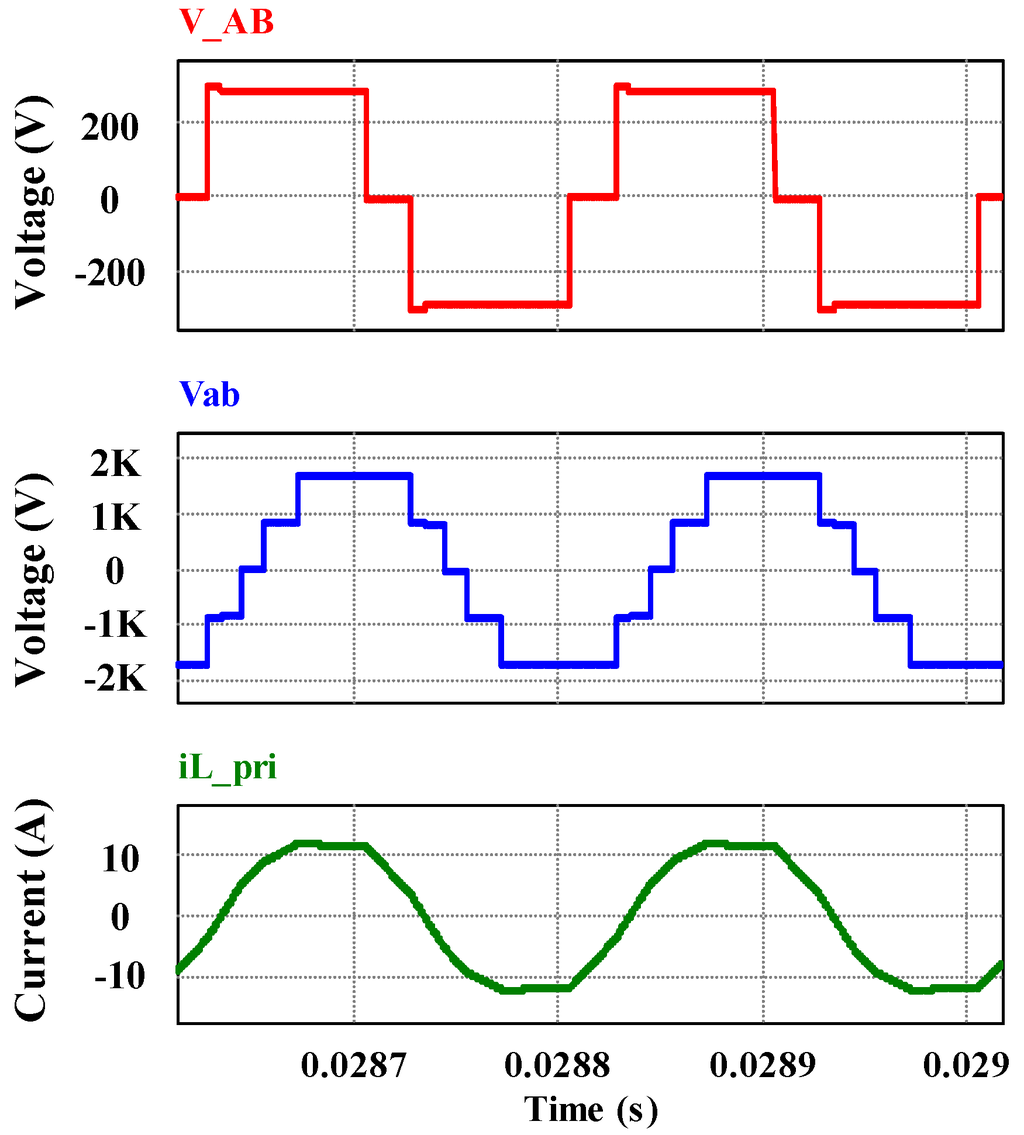
Figure 9. Primary 3L voltage v_AB secondary 5L voltage v_ab and current through the primary referred leakage inductance i_L; where $V_s=290\text{ V},V_P=1,868\text{ V},\alpha ={10}^0,\beta ={40}^0,$$\text{γ}={20}^0\text{ and }\varphi ={60}^0.$

3.4. Soft Switching

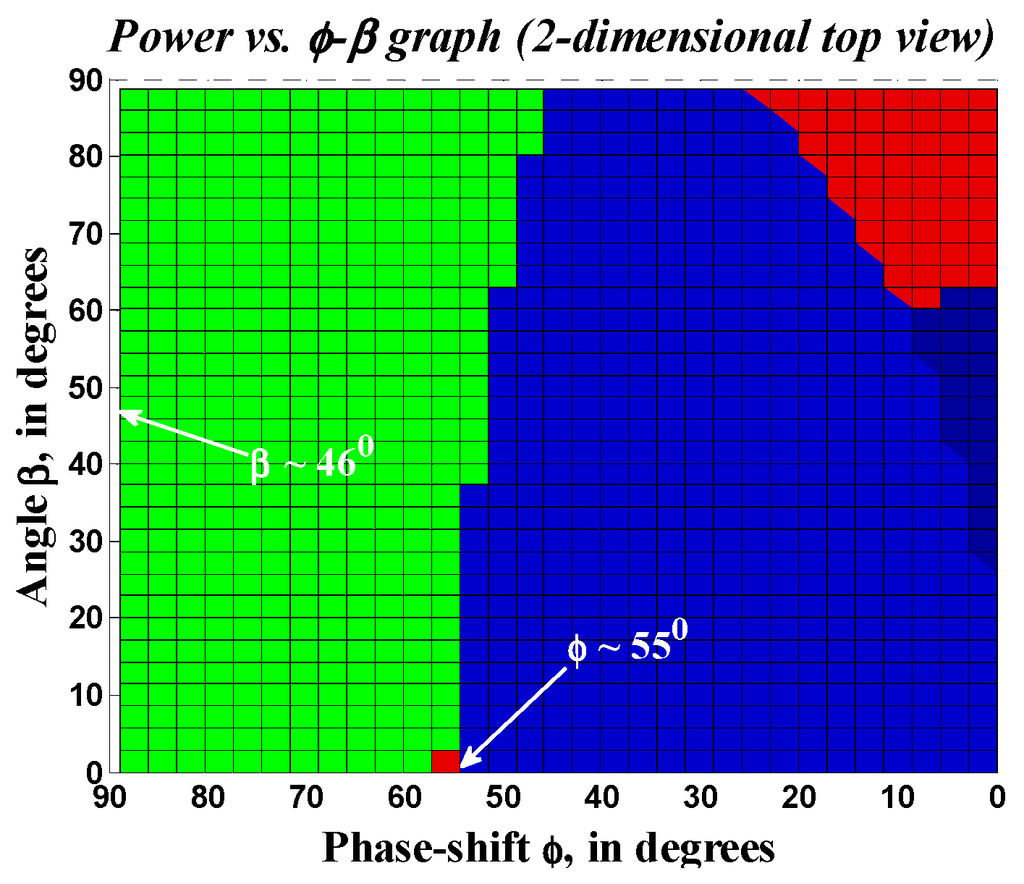
The per unit output power vs. $\varphi -\beta$ characteristics is shown in Figure 10 (15), where $\alpha$ is chosen as ${15}^0$, as this value gives the minimum THD in five-level $v_{ab}$ [14]. In Figure 11, the two-dimensional view of $\varphi$-$\beta$ planes ease the visualization of the boundary values of $\varphi >{55}^0\text{ and }\beta \ge {46}^0$ for achieving soft-switching both in primary (2L) and secondary (5L) bridges, as described in the following subsections.

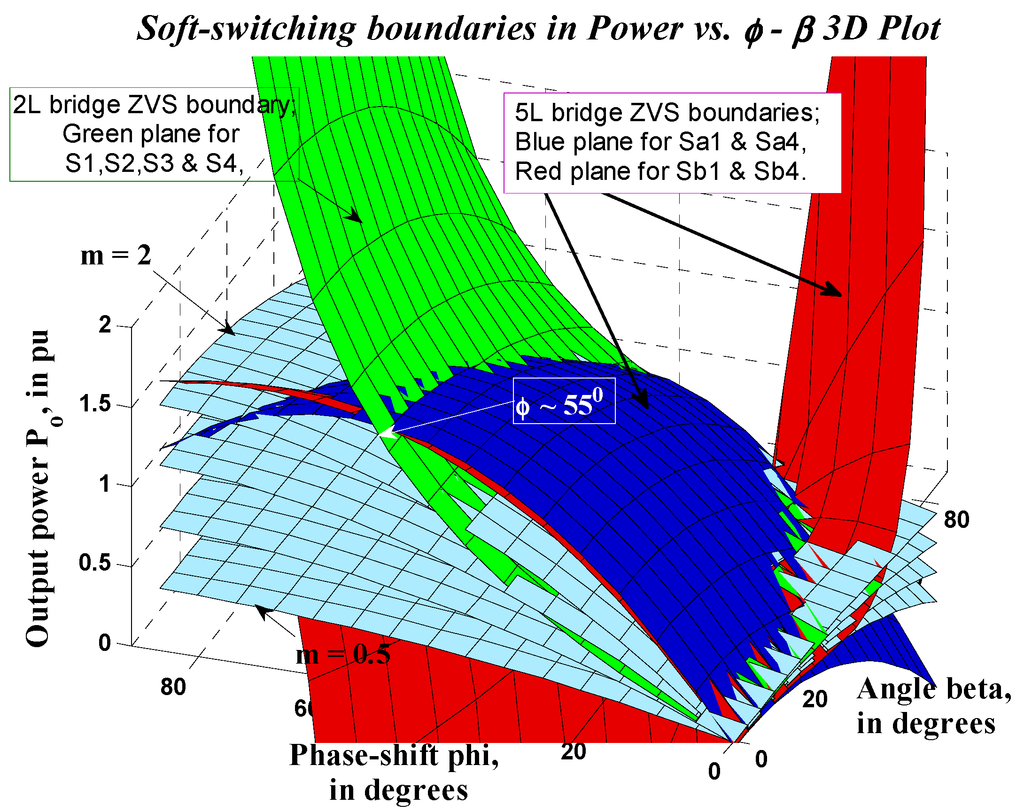
Figure 10. Soft switching boundaries shown in three-dimensional power vs. $\varphi$-$\beta$ planes (where $\alpha ={15}^0,0<\beta <{90}^0\text{ and }0<\varphi <{90}^0$); the grey planes (15) show the power vs. phi-beta relations for m = 0.5, 1, 1.5, 2; the green plane (17) is for two-level bridge, and the zero voltage switching (ZVS) is possible while operating under this plane; the blue (18) and red (19) planes are for five-level bridge leg-a and leg-b, respectively.

Figure 11. Two-dimensional view of Figure 10 showing the ZVS boundaries of ϕ and β.

The conventional 2L DAB topology can achieve zero voltage switching (ZVS) for all switches in the entire power range when m is equal to unity. The switching pulses for the 2L-5L DAB switches are shown in Figure 4. It is possible to achieve the same in the primary bridge (S₁ to S₄ with the condition of $i_L\left(0\right)<0$ as shown in Figure 12.

3.4.1. Soft-Switching Conditions for the Two-Level (V_s) Bridge

From the current and voltage waveform of the switches in the primary two-level (V_s) bridge (Figure 12), we can say that the condition for soft-switching in the primary bridge should be,

$$\begin{array}{c}{i}_L\left(0\right)<0\\ or,\frac{V_P}{n\omega L}.\left(\frac{\pi }{2}-\varphi \right)-\frac{V_s}{\omega L}.\left(\frac{\pi }{2}\right)<0\\ or,\frac{V_P}{n{V}_s}\equiv m<\frac{\left(\frac{\pi }{2}\right)}{\left(\frac{\pi }{2}-\varphi \right)}\end{array}$$

(17)

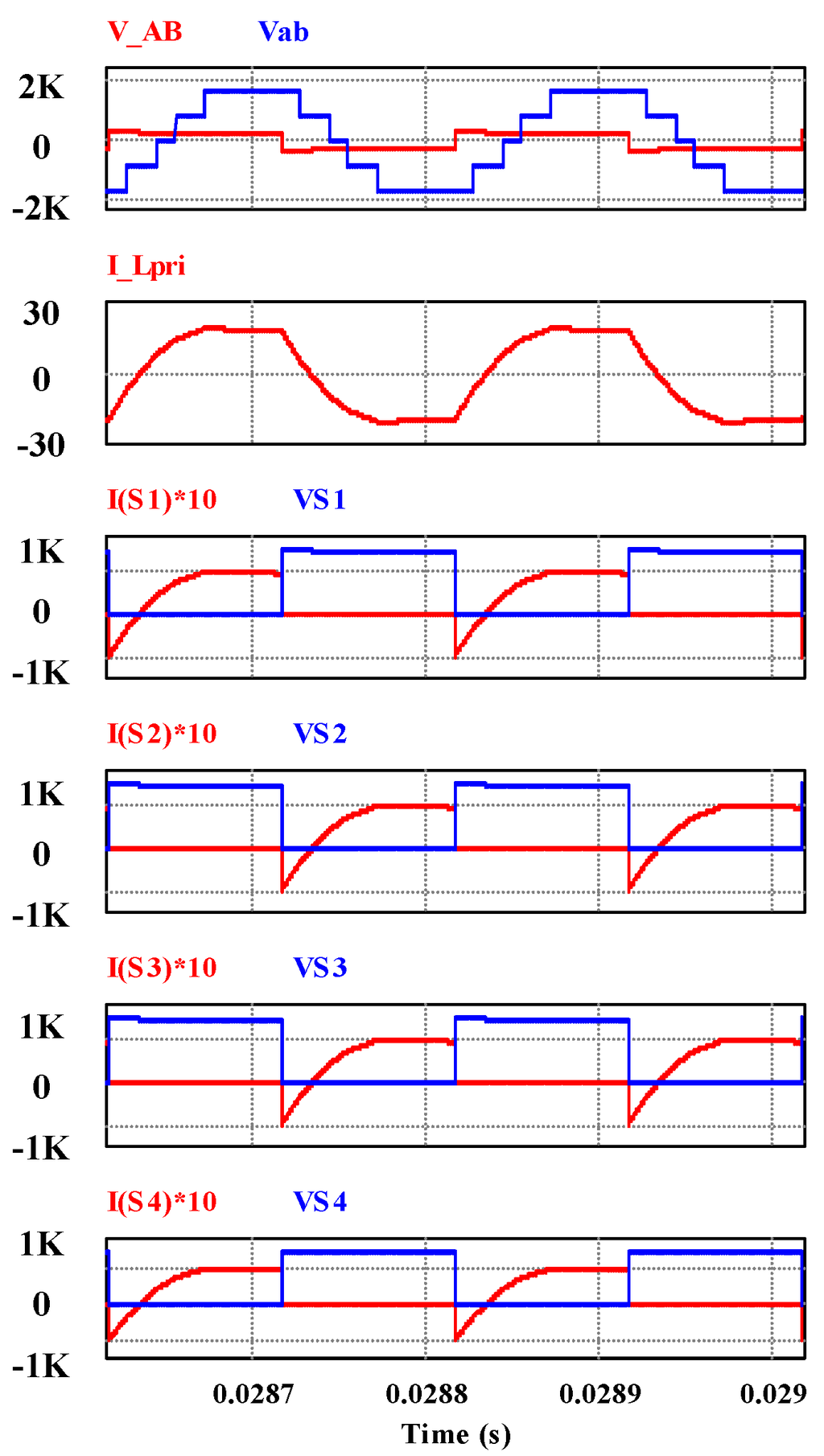
Figure 12. Voltage across the transformer v_AB and v_ab, inductor current i_L and switch currents and voltages for S₁ to S₄.

3.4.2. Soft-Switching Conditions for the Leg-a of NPC (Five-Level) Bridge

Condition for S_a1 and S_a4 to be turned-on at ZVS: $i_L\left(\varphi +\beta \right)>0$

$$or,m>\frac{\left\{\pi -2\left(\varphi +\beta \right)\right\}}{\left(\pi -2\beta \right)}$$

(18)

Boundary condition for S_b1 and S_b4 to be turned-on at ZVS: $i_L\left(\varphi -\alpha \right)=0$

$$or,m=\frac{\left\{\pi -2\left(\varphi -\alpha \right)\right\}}{\left\{\pi -\left(\alpha +\beta \right)\right\}}$$

(19)

In the NPC bridge, ZVS happens in the switches $S_{a1},S_{a4},S_{b1},S_{b4}$ during turn-on at $m=1$. The rest of the switches $(S_{a2},S_{a3},S_{b2},S_{b3})$ are also turned on at a favorable condition when the current through the switch is already zero, as shown in Figure 13 and Figure 14.

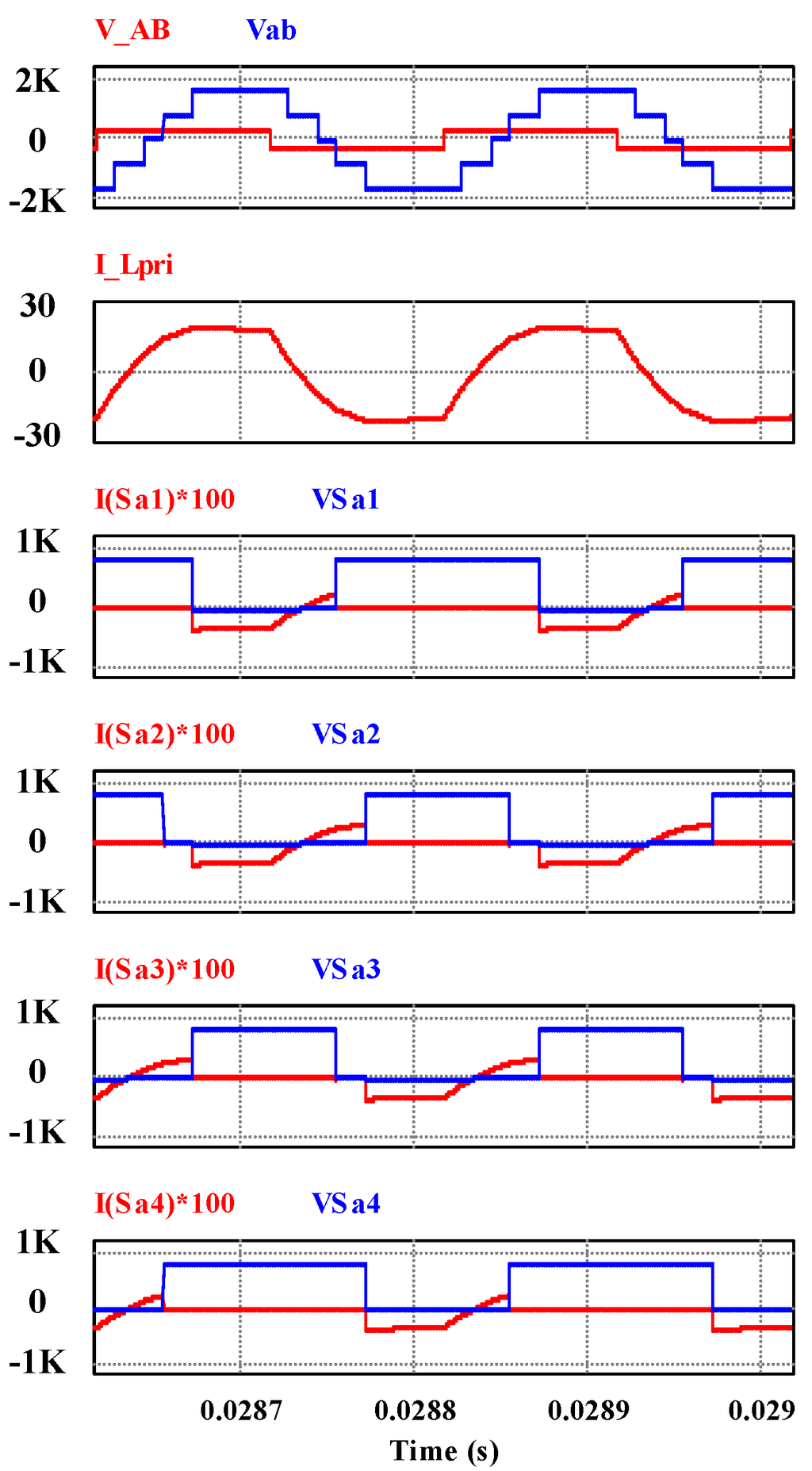
Figure 13. Voltage across the transformer $v_{AB}\text{ and }{v}_{ab}$, inductor current $i_L$ and switch currents and voltages for $S_{a1}$ to $S_{a4}$.

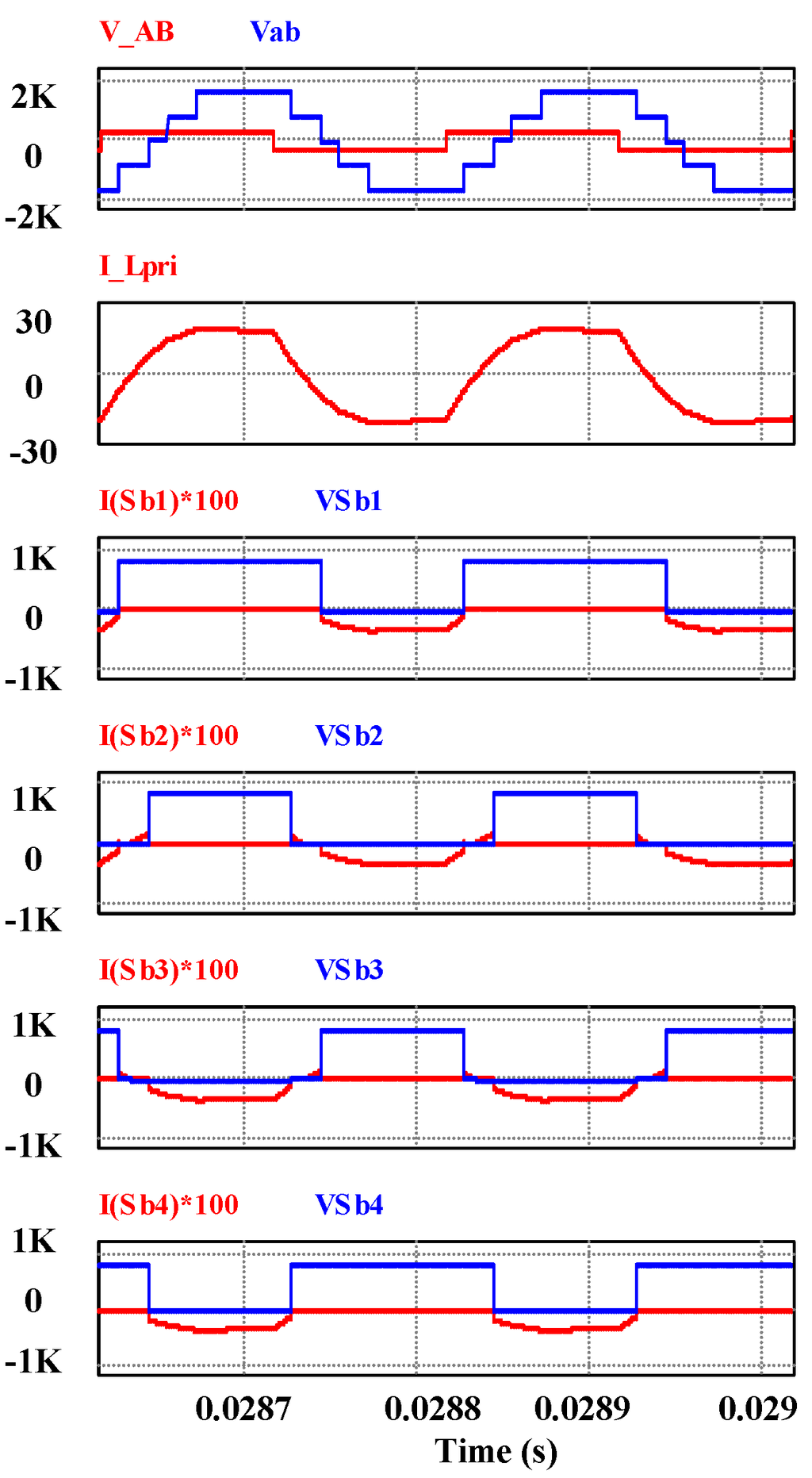
Figure 14. Voltage across the transformer v_AB v_ab, inductor current i_L and switch currents and voltages for S_b1 to S_b4.

3.5. Transformer Design

Considering the operating frequency and loss profile, various core materials, such as silicon steel, amorphous alloy and nano-crystalline, are used as the transformer core. For frequencies less than 10 kHz, the amorphous metglas material shows better performance. For this ML-DAB converter, amorphous metglas alloy 2605SA1 material has been chosen in the transformer core, because of its high permeability, low core losses, high saturation flux density and narrow hysteresis curve. The design of a 3.4-kVA transformer core and winding wires has been calculated using the area-product method as shown below:

The transformer core area product is defined as,

$$A_p=A_{core}{A}_{window}=\frac{k_{conv}\left(V_1{I}_{1_{rms}}+V_2{I}_{2_{rms}}\right)}{k_w{B}_{mx}{J}_{mx}{f}_s}$$

(20)

where

• $V_1\approx V_s=292V,V_2\approx V_P=1,667V,$ switching frequency $f_s=5kHz,$
• $I_{1_{rms}}=16.2A,I_{2_{rms}}=2.9A$ (RMS values calculated from simulation results),
• $k_{conv}=0.5$ (this factor value is chosen based on the converter topology),
• $k_w=0.4$ (this is the fill-factor having values usually within range of 0.3 to 0.6),
• $B_{mx}=1T$ (chosen based on the maximum saturation flux density being 1.56 T),
• $J_{mx}=6A/m{m}^2$ (peak current density with the use of litz wire).

From Equation (20), we get $A_p=398,650m{m}^4$. By using metglass 2605SA1 AMCC-50 core specification, we get, $A_p=462,000m{m}^4,A_{core}=330m{m}^2,A_w=1,400m{m}^2$.

The conductor cross-section can be found as $A_{con{d}_1}=\frac{I_{1_{rms}}}{J_{mx}}=2.7m{m}^2,and{A}_{con{d}_2}=0.48m{m}^2.$ The number of turns in the transformer is calculated as, $N_1=\frac{k_{conv}{V}_1}{A_{core}{f}_s{B}_{mx}}=89turns,$ and similarly $N_2=509turns.$ AWG 12 259/36 and AWG 20 38/30 Type 2 litz wire have been chosen for transformer primary and secondary windings, respectively.

4. Applications for ML-DAB

The proposed ML-DAB could find some suitable applications in a solid state transformer (SST), a front-end DC-DC converter in a photovoltaic (PV) system, a high step-up voltage DC-DC or an intermediate stage in ac-ac applications. Figure 15 shows a block diagram of the ML-DAB in a grid-connected large-scale PV system. The ML-DAB module along with inverter stage can act as a building block to be cascaded in order to achieve the 13.8-kV distribution voltage requirement.

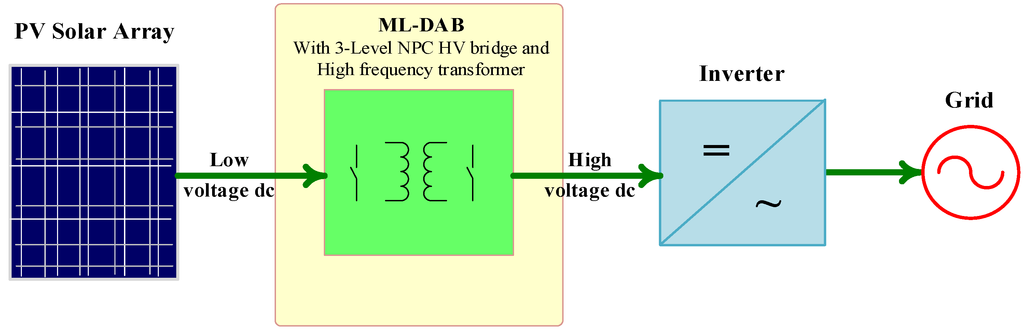
Figure 15. ML-DAB module in a grid-connected photovoltaic (PV) power converter.

This ML-DAB can control maximum power point tracking (MPPT) by controlling the phase-shift ($\varphi$) between two active bridges. This topology has the advantage of being modular and replacing the bulky line frequency transformer at the grid-end with a smaller high frequency power electronic transformer. Figure 16, Figure 17 show the MPPT performance in an ML-DAB in PV applications.

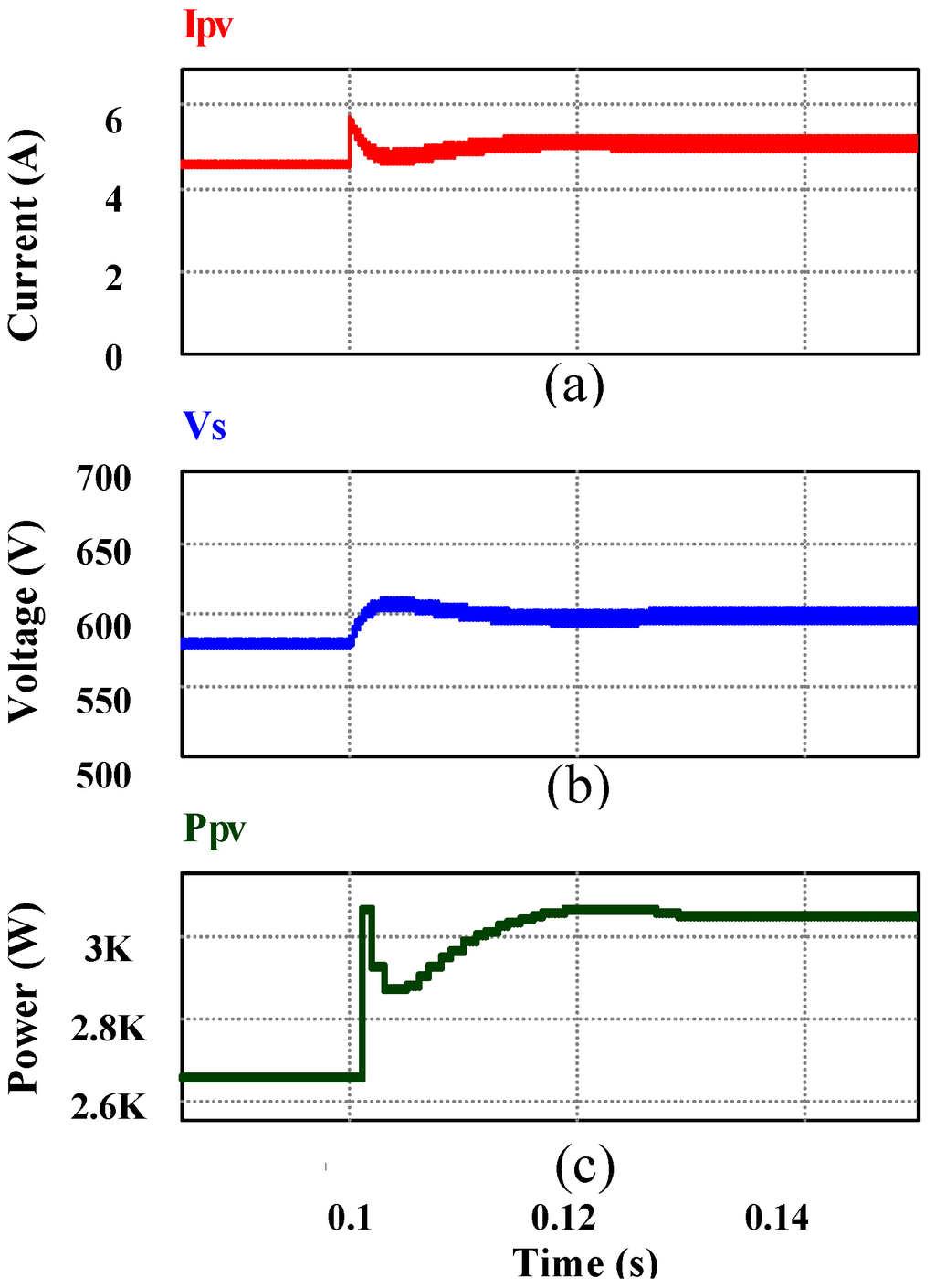
Figure 16. (From top to bottom) (a) Change in PV output current I_pv due to the change in light intensity from 800 W/m² to 1,000 W/m²; (b) corresponding change in voltage V_pv because of maximum power point tracking (MPPT) and (c) power P_pv.

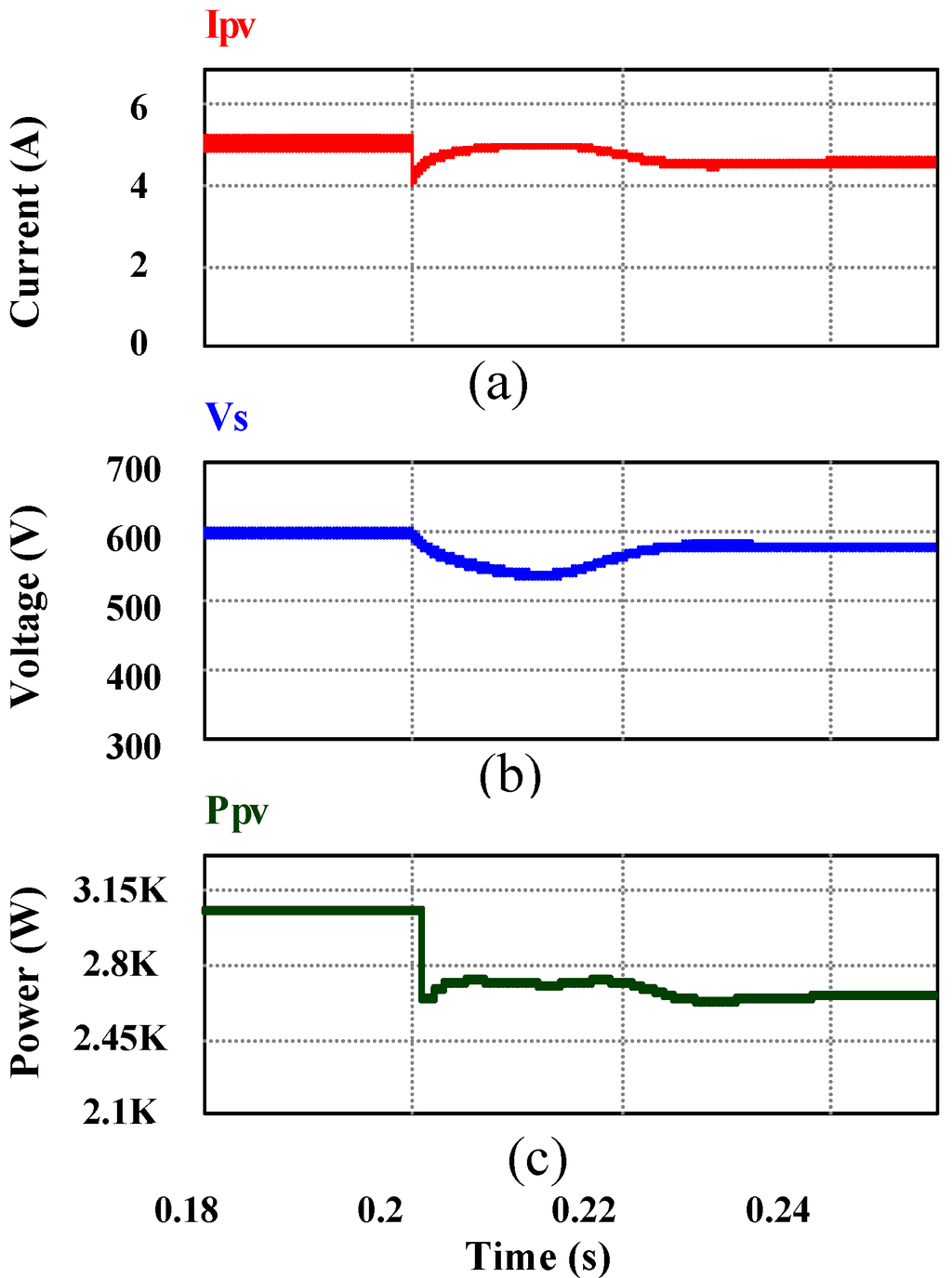
Figure 17. (From top to bottom) (a) Change in PV output current I_pv due to the change in light intensity from 1,000 W/m² to 800 W/m²; (b) corresponding change in voltage V_pv because of MPPT and (c) power P_pv.

5. Simulation and Experimental Results

A 3.34-kW ML-DAB module with a single phase high frequency transformer has been simulated in PSIM^®. The design parameters of the ML-DAB are listed in Table 2. Based on the soft-switching constraints for the ML-DAB switches, as shown in (16) to (19), a good choice for modulation parameters is used for simulation, which are $\alpha =10,\beta ={30}^0$ and $\varphi ={70}^0$. For the PV application explained in Section 4, 1,200-V or 1,700-V rated IGBTs are needed for ML-DAB. There are limitations in the switching characteristics of commercially available IGBTs when operated above 20 kHz. Hence, we have chosen 5 kHz for the proposed ML-DAB. The minimum input capacitor value has been theoretically calculated as 39 uF based on the ML-DAB parameters in Table 2. In the prototype, we have used a 100-uF polypropylene capacitor with a high ripple current carrying capacity.

As per (10) and Table 2, the key simulation results are shown in Figure 18 and Figure 19 for a 2L-5L DAB in the steady state. The corresponding voltage and current waveforms for the 3L-5L ML-DAB have been shown in Figure 9 for the same input, output dc voltage and power rating as shown in Table 2. The phase-shift ϕ is actually the control parameter that is controlled by a proportional-integral (PI) controller sensing the variation in input (e.g., the PV panel’s output) or output (e.g., the input voltage of an inverter) dc voltages of the ML-DAB. Figure 18 and Figure 19 show the input and output voltage, current and average power of the ML-DAB obtained from simulation.

Table 2. Parameter values for a 3.34-kW ML-DAB based on the 2L-5L topology.

Item Description	Nominal Value
Power rating of a ML-DAB module, Po	3.34 kW
Vs = Vdc(2L)	292 V
VP = Vdc(5L)	1,668 V
ML-DAB high frequency transformer’s turns ratio, $\mathit{n}=\frac{{\mathit{V}}_{\mathit{P}}}{{\mathit{V}}_{\mathit{s}}}$	5.716
${\mathit{I}}_{{\mathit{L}}_{\mathit{2}\mathit{L}}}$	11.4 A
${\mathit{I}}_{{\mathit{L}}_{\mathit{5}\mathit{L}}}$	2 A
${\mathit{I}}_{{\mathit{L}}_{\mathit{2}\mathit{L}(\mathit{r}\mathit{m}\mathit{s})}}$	17 A
Switching frequency, fs	5 kHz
Leakage Inductance for ML-DAB transformer, L (value calculated as per Equation 14)	0.5 mH
2-level PV side bridge IGBT’s VCE	600 V (49% of Vs)
3-level NPC bridge IGBT’s VCE	1,200 V (70% of $\frac{V_P}{2}$)

Table 2. Parameter values for a 3.34-kW ML-DAB based on the 2L-5L topology.

Item Description	Nominal Value
Power rating of a ML-DAB module, Po	3.34 kW
Vs = Vdc(2L)	292 V
VP = Vdc(5L)	1,668 V
ML-DAB high frequency transformer’s turns ratio, $\mathit{n}=\frac{{\mathit{V}}_{\mathit{P}}}{{\mathit{V}}_{\mathit{s}}}$	5.716
${\mathit{I}}_{{\mathit{L}}_{\mathit{2}\mathit{L}}}$	11.4 A
${\mathit{I}}_{{\mathit{L}}_{\mathit{5}\mathit{L}}}$	2 A
${\mathit{I}}_{{\mathit{L}}_{\mathit{2}\mathit{L}(\mathit{r}\mathit{m}\mathit{s})}}$	17 A
Switching frequency, fs	5 kHz
Leakage Inductance for ML-DAB transformer, L (value calculated as per Equation 14)	0.5 mH
2-level PV side bridge IGBT’s VCE	600 V (49% of Vs)
3-level NPC bridge IGBT’s VCE	1,200 V (70% of $\frac{V_P}{2}$)

Soft-switching results for semiconductor switches in the converter are shown in Figure 12, Figure 13 and Figure 14 showing zero voltage switching (ZVS) and zero current switching (ZCS) performance. Infineon 1,200-V IGBT modules FF100R12YT3 are modeled in the simulation to estimate the losses and efficiency. In the simulation, the conduction losses have been modelled based on the IGBT datasheet parameters and assuming linear switching characteristics. The efficiency is 96.42%, as seen in the simulation.

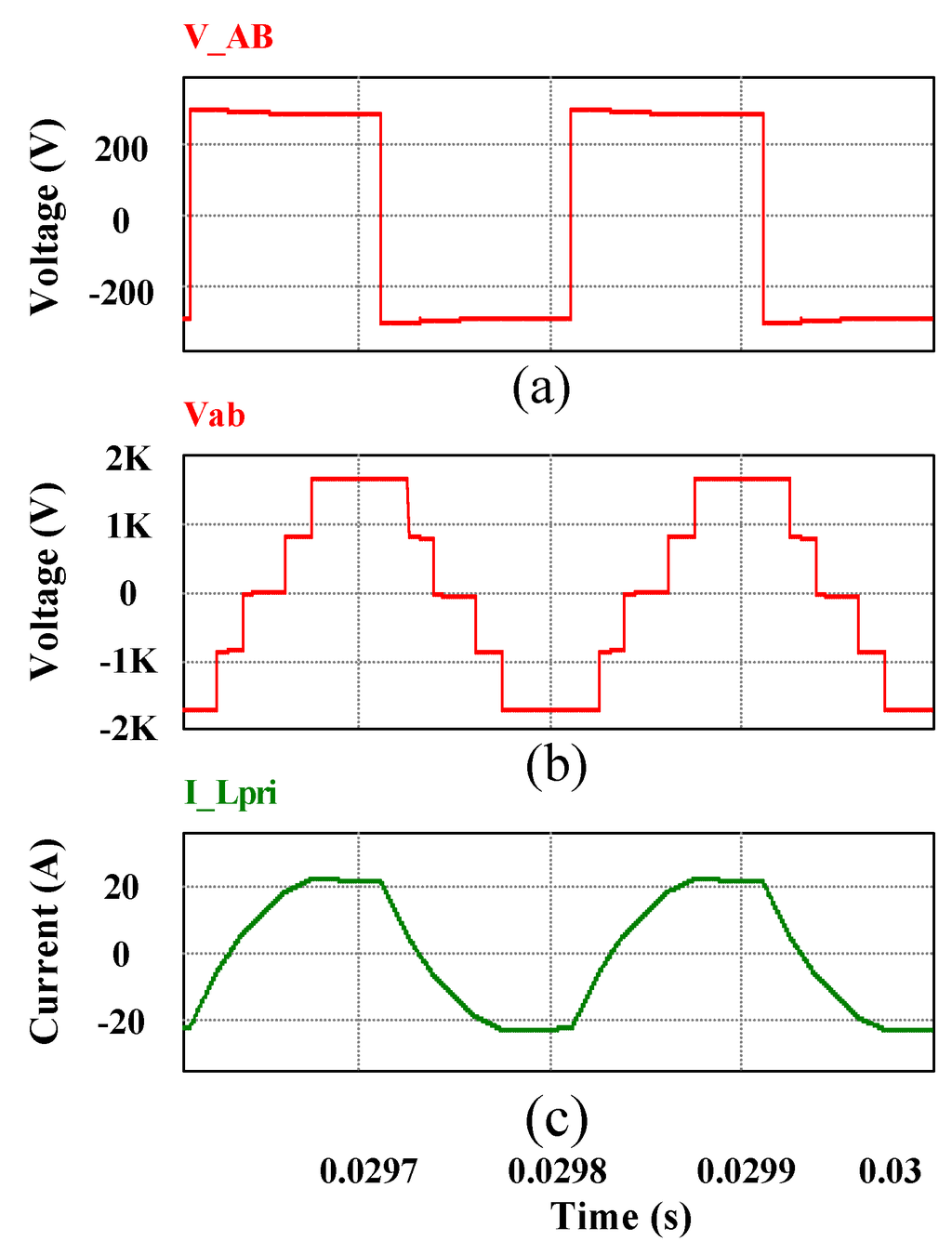
Figure 18. (From top to bottom) (a) Primary 2L voltage v_AB; (b) secondary 5L voltage v_ab; and (c) current through the primary referred leakage inductor i_L.

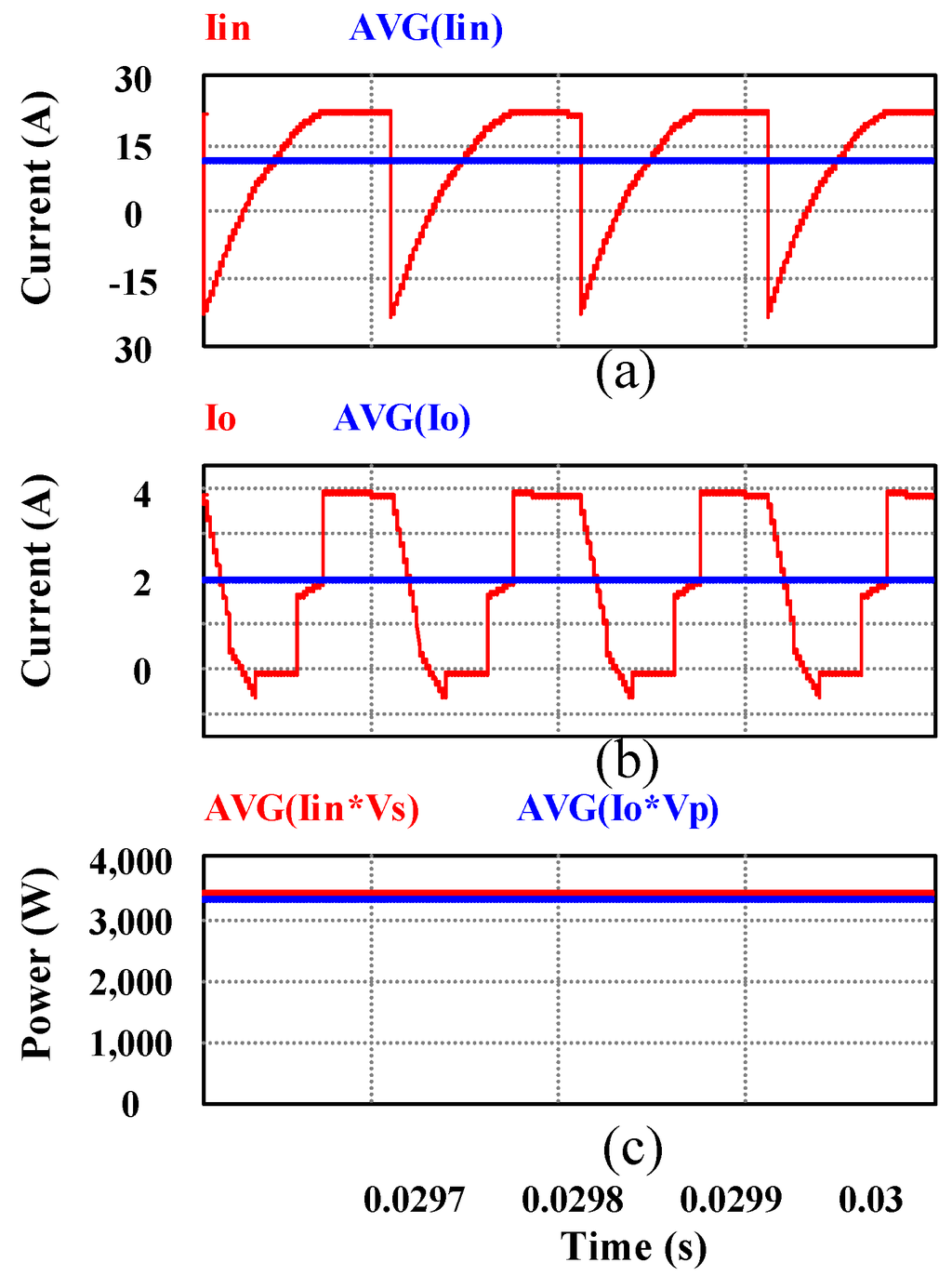
Figure 19. (From top to bottom) (a) ML-DAB input current I_in and its average; (b) output current I_out and its average; and (c) average input and output power $P_{in}=AVG\left(I_{in}*V_s\right)\text{ and }{P}_{out}=AVG(I_o*V_P)$.

Simulation and experimental results also verify the functionality of the proposed ML-DAB and the symmetric modulation technique. A hardware prototype (Figure 20) has been built and tested with a scaled-down input voltage ($V_s=120\text{ V},f_s=5\text{ kHz}$) to verify the power flow and open-loop control. The gate signal for all the twelve IGBTs used in the ML-DAB is shown in Figure 21.The experimental voltage and current waveforms shown in Figure 22 and Figure 23 have a close match with the simulation results shown in Figure 18 and Figure 19. Figure 24 shows the output voltage and current waveforms when the ML-DAB is connected to a full-bridge inverter and a resistive-inductive (R-L) load. In the hardware prototype, an overall efficiency of 88% (Figure 25) has been observed for a 120-V input voltage and 638 W (which is 20% of the rated power of the converter) of input power (Table 3). At full rated power, it is expected that the observed efficiency will closely match with the theoretical and simulated efficiency figures.

Figure 20. ML-DAB prototype hardware setup for laboratory testing.

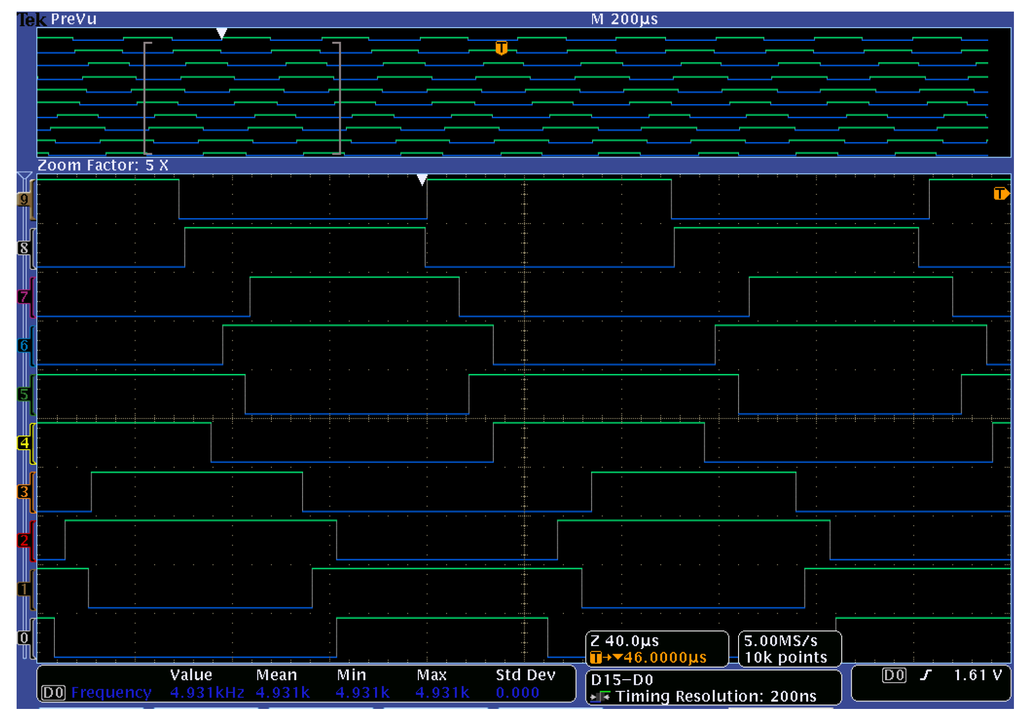
Figure 21. Gate pulses for the ML-DAB IGBTs (from top to bottom: $S_{1,4},S_{2,3}\text{ and }{S}_{a1},S_{a2},S_{a3},S_{a4}\text{ and }{S}_{b1},S_{b2},S_{b3},S_{b4})$.

Table 3. Experimental efficiency and losses for the prototype ML-DAB.

Vs	Vp	Pin	Pout	$P_{los{s}_{trans}}$	$P_{los{s}_{total}}$	Efftrans	Efftotal
(V)	(V)	(w)	(w)	(w)	(w)	(%)	(%)
60	310	161	133	14	28	90	83
80	416	284	239	27	45	90	84
100	521	443	373	45	70	89	84
120	626	638	561	42	77	93	88

Table 3. Experimental efficiency and losses for the prototype ML-DAB.

Vs	Vp	Pin	Pout	$P_{los{s}_{trans}}$	$P_{los{s}_{total}}$	Efftrans	Efftotal
(V)	(V)	(w)	(w)	(w)	(w)	(%)	(%)
60	310	161	133	14	28	90	83
80	416	284	239	27	45	90	84
100	521	443	373	45	70	89	84
120	626	638	561	42	77	93	88

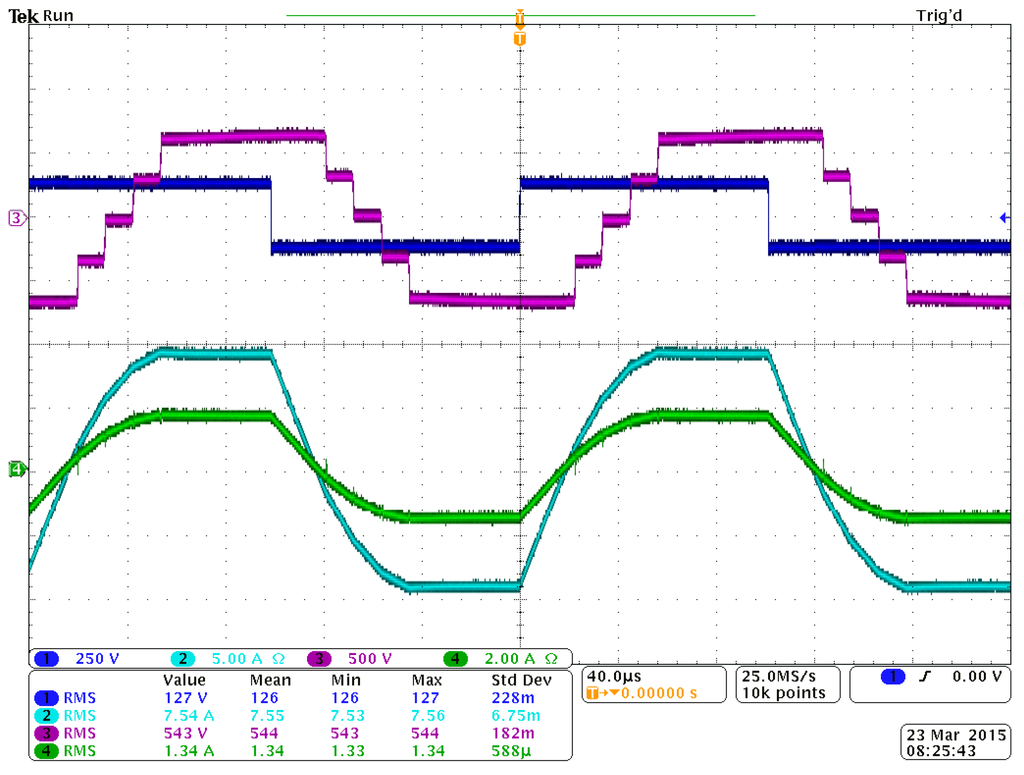
Figure 22. ML-DAB 2L voltage v_AB, 5L voltage v_ab and current through the 2L and 5L side of the transformers $i_{L_{pri}}\text{and }{i}_{L_{sec}}$; where $V_s=125\text{ V},V_P=650\text{ V},n=5.71,\alpha ={10}^0,$$\beta ={30}^0\text{ and }\varphi ={70}^0.$

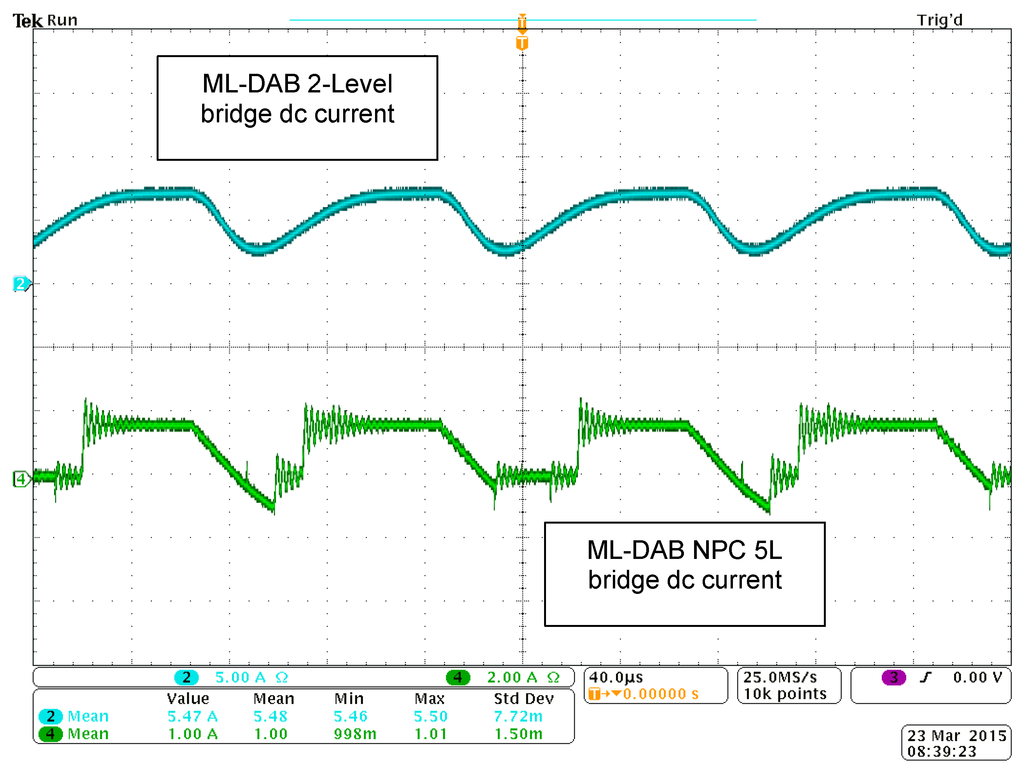
Figure 23. ML-DAB input (2L bridge) and output (5L bridge) dc current waveforms $I_{d{c}_{2L}}$ and $I_{d{c}_{5L}}.$

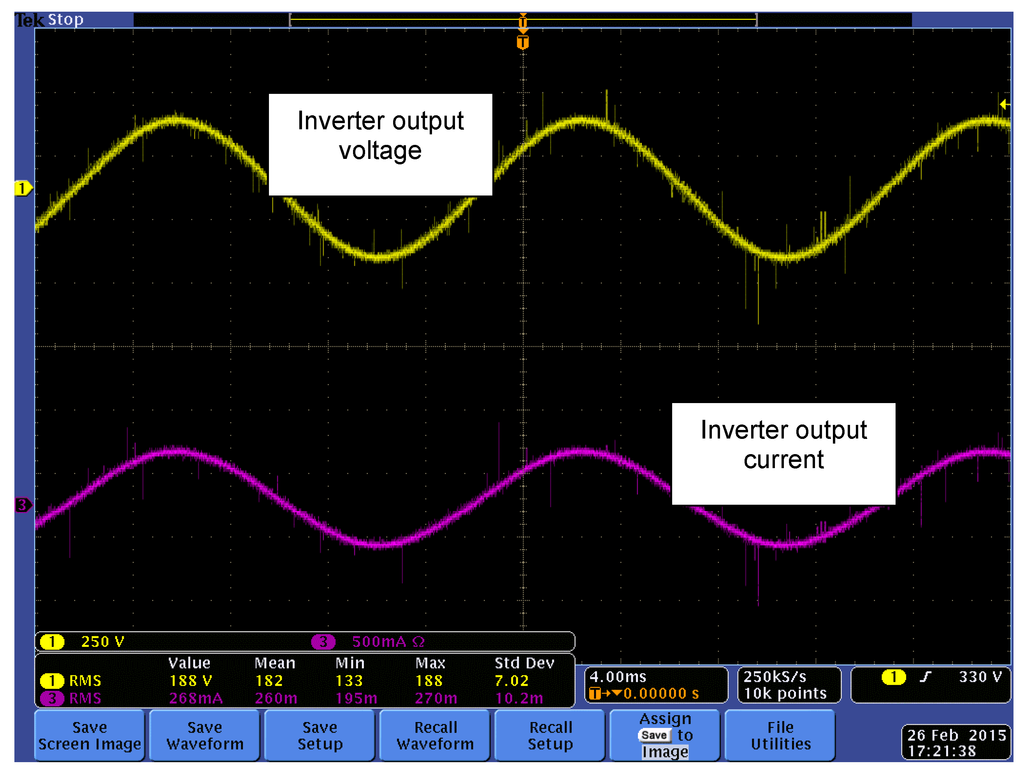
Figure 24. Output voltage and current waveforms when the ML-DAB is connected to a full-bridge inverter and a resistive-inductive (R-L) load.

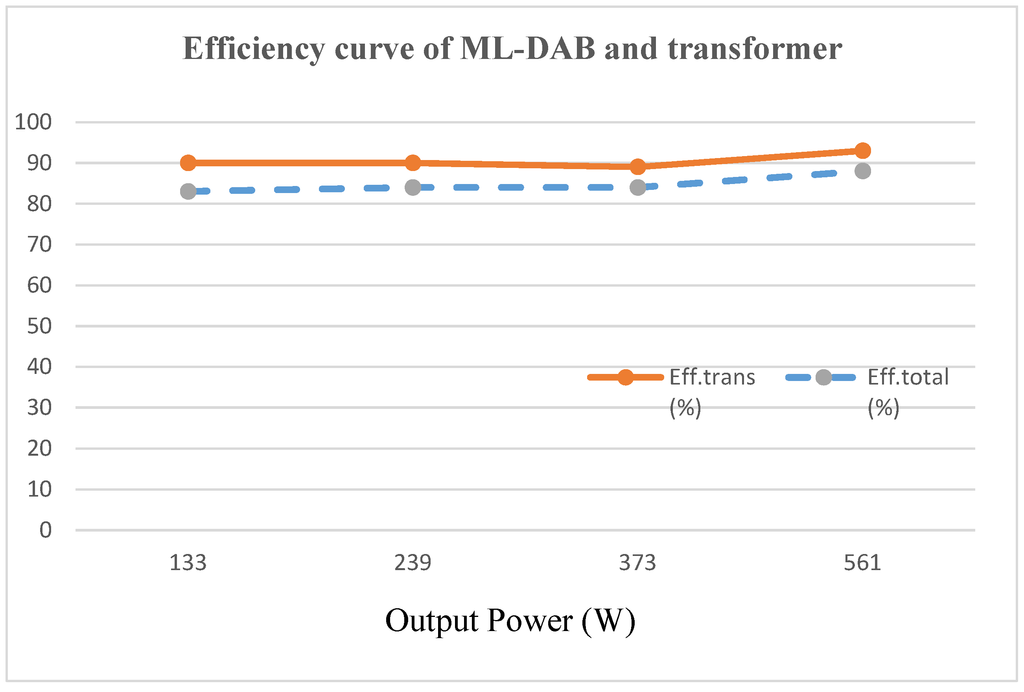
Figure 25. Efficiency curve of the transformer and ML-DAB with output power variation.

6. Conclusions

In this paper, a multilevel DAB (ML-DAB) dc-dc converter has been proposed for its use in high step-up/down, high-voltage applications. The boost and buck configurations of the ML-DAB have been explained in detail. A symmetric modulation technique has been proposed, which allows for independent control of the phase-shift from the control parameters that shape the multilevel voltage waveforms. The paper analyzes in detail the 2L-5L, 5L-2L and 3L-5L voltage waveforms across the high frequency transformer and derives expressions for the power flow. A soft-switching analysis along with boundary conditions is presented. The converter is designed and simulated in PSIM^®. A hardware prototype is built and tested to verify the proposed ML-DAB performance with the symmetric modulation scheme. Experimental results have been presented to validate the proposed modulation and power flow in the ML-DAB.