Abstract
Event–event causal relation extraction (ECRE) represents a critical yet challenging task in natural language processing. Existing studies primarily focus on extracting causal sentences and events, despite the use of joint extraction methods for both tasks. However, both pipeline methods and joint extraction approaches often overlook the impact of document-level event temporal sequences on causal relations. To address this limitation, we propose a model that incorporates document-level event temporal order information to enhance the extraction of implicit causal relations between events. The proposed model comprises two channels: an event–event causal relation extraction channel (ECC) and an event–event temporal relation extraction channel (ETC). Temporal features provide critical support for modeling node weights in the causal graph, thereby improving the accuracy of causal reasoning. An Association Link Network (ALN) is introduced to construct an Event Causality Graph (ECG), incorporating an innovative design that computes node weights using Kullback–Leibler divergence and Gaussian kernels. The experimental results indicate that our model significantly outperforms baseline models in terms of accuracy and weighted average F1 scores.
1. Introduction
Causal relations are among the most fundamental and crucial semantic relation types in natural language. They are essential for understanding the inherent logical connections between events and play a central role in advanced tasks such as recommendation systems [1], event prediction [2], and causal reasoning [3]. Similarly, temporal relations are crucial for understanding the order and dependencies between events. Determining the timing, sequence, and temporal dependencies of events is critical for tasks such as question answering [4], information retrieval [5], and text generation [6]. The study of temporal and causal relations dates back to Granger’s pioneering work on Granger causality [7].
In real-world scenarios, however, causal and temporal relations are frequently intertwined. Causal chains between events often imply temporal precedence, while temporal sequences frequently indicate causal links. This phenomenon is particularly prominent at the document level, where multiple relationships intertwine and event connections span sentences or even entire documents. Hence, extracting implicit causal relations embedded in temporal relations at the document level is not only a significant challenge in natural language processing but also a fundamental step toward achieving comprehensive event understanding. Figure 1 includes the following textual example: “ The Battle of Sultanabad occurred on February 13, 1812. The Persians won the battle by moving faster than the Russians and attacking them near their camp. In the end, however, the Persians lost the invasion due to the Russian maneuvering around the Aras River”. In this example, the event Battle of Sultanabad occurred before lost, attacking preceded lost, moving occurred before attacking, and maneuvering took place prior to lost. Additionally, maneuvering is identified as the cause of lost.

Figure 1.
An example for document-level ECRE in MAVEN-ERE.
Currently, most studies address event–event causal relation extraction (ECRE) and event–event temporal relation extraction (ETRE) as two independent tasks. Traditional approaches to ECRE often rely on pattern matching and handcrafted features, requiring extensive manual annotations of linguistic characteristics, including syntax, lexicon, and semantic patterns, to effectively extract causal events. Traditional methods can be broadly classified into three categories: rule-based methods [8], statistical methods [9], and deep learning-based methods [10]. While these methods perform well on sentences with simple structures, they encounter substantial challenges in handling long-distance dependencies and intricate semantics. The diversity of semantics in natural language frequently results in errors during template matching, as these methods rely on local cues and lack the capacity to fully capture the deeper causal logic within context.
Recent years have witnessed remarkable progress in causal relation extraction through deep learning-based models. These models learn text features automatically, enabling them to capture latent causality patterns with minimal manual intervention. Bidirectional Long Short-Term Memory network (BiLSTM) [11], by integrating forward and backward information, effectively captures contextual dependencies, demonstrating superior performance in causal relation extraction tasks. Convolutional Neural Network (CNN) [12] extracts causal features from different contextual segments through convolutional layers and classifies them using fully connected layers, enabling automated event causality extraction. Graph Convolutional Network (GCN) [13] enhances the ability to model complex dependencies and provide a flexible framework for representing multi-level event relationships. Recurrent Neural Network (RNN) [14,15] excels in capturing causal dependencies in complex contexts, particularly for sequential events.
Moreover, pre-trained language models such as BERT [16] have significantly advanced causal relation extraction. Leveraging the self-attention mechanism [17], BERT captures deeper contextual representations, allowing it to identify implicit causal relations in complex linguistic phenomena. Likewise, multi-head self-attention not only improves extraction accuracy but also significantly enhances the model’s capability to handle intricate event relationships. As attention mechanisms continue to evolve, multi-head self-attention is expected to play a pivotal role in complex causal reasoning and multimodal event relationships.
Event–event temporal relation extraction (ETRE) aims to identify temporal relations between events and temporal expressions. This task primarily involves recognizing temporal expressions and modeling the temporal attributes of events, such as the time of occurrence, order, and duration [18,19,20]. For temporal relations, we follow the perspective of O’ Gorman et al. [21]. In natural language processing (NLP), ETRE is a critical task as it provides essential information for constructing event chains and inferring dependencies among events [22]. Accurately determining the temporal attributes of events is vital for tasks like temporal reasoning, event sequencing, and contextual understanding. In addition to identifying temporal expressions, ETRE requires addressing the problem of temporal ordering, which involves determining the sequence of events [23] and the potential dependencies between them [24]. By employing event embeddings and contextual modeling, temporal ordering can effectively capture the sequence relations among events, thereby supporting higher-level event reasoning tasks [25]. Specifically, Graph Neural Network (GNN) [26] has been utilized to construct temporal event graphs. These leverage connections and adjacent relationships among event nodes to infer and capture the temporal sequences and logical dependencies in event chains.
However, despite the significant progress made by deep learning-based models in ECRE and ETRE, several limitations remain. Firstly, these models often focus primarily on directly extracting causal cues while neglecting the strong interconnection between causal relations and temporal order. In many cases, accurately identifying causal relations requires incorporating temporal information, as the chronological order of events frequently dictates the rationality of causal chains. Secondly, deep learning models typically rely on large amounts of annotated data for training, yet annotating causal relations is both time-consuming and costly. Consequently, these models’ generalization ability is limited in scenarios with scarce annotated data. Lastly, previous research has struggled to comprehensively model document-level causal relations, particularly under the constraints of event temporal order. In this research, we construct a document-level event graph structure and extract implicit causal relations within temporal event relations. The main contributions of this paper include the following:
- Document-level event temporal and causal structure modeling: We employ an event–event temporal relation extraction channel (ETC) to assist the event–event causal relation extraction channel (ECC) in modeling document-level causal events. A single-channel model can only capture explicit causal relations and struggles to effectively incorporate temporal information. In contrast, the dual-channel model enhances robustness in handling implicit causal relations by separately modeling temporal and causal relations through the event–event temporal relation extraction channel (ETC) and the event–event causal relation extraction channel (ECC), followed by their integration. By explicitly incorporating temporal order and leveraging a Gaussian kernel function to adjust causal edge weights, the model ensures that the predicted causal relations align with temporal logic.
- ECG modeling based on Association Link Network (ALN) and Graph-based Weight Assignment: In ECC, ALN constructs a richer event association network, enabling better handling of causal inference across sentences and paragraphs. ALN provides a framework for building event association networks, allowing our model to flexibly combine event semantics, temporal order, and causal features, thereby enhancing the accuracy of causal relation extraction. To determine the direction of edges in the initial event graph, improved Gaussian kernel function is employed to integrate features from both channels. This approach leverages temporal information of events to construct a hierarchical and sequential causal association network.
- Dual-level GCN: We adopt a dual-level GCN architecture in ETC. The first level focuses on modeling and learning explicit causal event pairs using a conventional GCN structure. In the second level, we incorporate Kullback–Leibler (KL) divergence to compute the directional dependency of cross-sentence causal events, improving the ability to capture document-level implicit causal events. This structure fully exploits temporal relations between events.
- Our model demonstrates outstanding performance on the MAVEN-ERE and EventStoryLine datasets, achieving significant improvements in extracting relational facts that were unseen in the training set.
We conducted extensive experimental evaluations on the publicly available datasets MAVEN-ERE and EventStoryLine, comparing our model against multiple benchmark models. The experimental results demonstrate that our model achieves significant improvements in event–event causal relation extraction (ECRE), particularly in texts with complex interwoven causal and temporal relations. The model shows notable gains in accuracy and average weighted F1 score.
The structure of this paper is organized as follows: Section 2. Related Work reviews the research progress in event–event causal relation extraction (ECRE) and event–event temporal relation extraction (ETRE). Section 3. Methodology provides a detailed description of the design and implementation of the proposed dual-channel extraction model. Section 4. Experiment introduces the experimental setup, datasets, and evaluation metrics, and presents the results and comparative analyses, including the ablation study on different model components. Finally, Section 5. Conclusions and Future Work summarizes the research contributions and discusses potential directions for future improvements. We have appended all abbreviations used in this paper at the end.
2. Related Work
In this section, we provide a detailed overview of the development of research on document-level relation extraction, including the progress in event–event causal relation extraction (ECRE) and event–event temporal relation extraction (ETRE). Those include early rule-based and statistical methods, as well as the extensive contributions made by researchers in the field of deep learning in recent years.
2.1. Document-Level Relation Extraction
Relation extraction plays a crucial role in the field of information extraction (IE) and serves as a key technology for building complex intelligent systems such as knowledge graphs or recommendation systems. While sentence-level causal relation extraction has achieved remarkable success [21,27,28,29,30], real-world causal relations often appear in a cross-sentence format within documents. Benefiting from the rise of deep learning techniques, numerous DocRE (Document Relation Extraction) models based on deep learning have been proposed [31,32,33,34,35,36,37]. These models can be broadly categorized into three types: sequence-based models, attention-based models, and graph-based models.
Sequence-based models, which utilize CNN or RNN as the core encoding layers, were among the earliest methods applied to DocRE. These approaches rely on feature engineering to extract document-level features. Drawing from the experience of sentence-level causal relation extraction, these models incorporate inter-entity dependencies within documents during the preprocessing stage. Specifically, Zhou et al. [36] proposed a hybrid system that integrates feature engineering, Tree Kernel-based models, and neural networks, leveraging syntactic and semantic information to significantly enhance relation extraction performance. Gu et al. [35] constructed a maximum entropy classifier based on multiple features, including lexical features, dependency features, and hyper-category filtering. Their approach extracts features at both intra-sentence and cross-sentence levels, merging results at the entity-pair level to generate final document-level relations, thus achieving automatic relation extraction. However, the structural limitations of these models make it challenging to capture long-distance contextual dependencies, preventing them from effectively modeling inter-sentence structural dependencies between entities.
Attention-based models aim to comprehensively and deeply model the structural dependency information between entities within a document. For instance, Verga et al. [34] proposed a Bi-affine Relation Attention Network (BRAN) based on self-attention mechanisms. This model scores all entity pairs in a document simultaneously, combining multi-instance learning and multi-task training to capture cross-sentence and long-distance entity relations. Huang et al. [33], through a joint design of entity-guided and evidence-guided mechanisms, achieved state-of-the-art performance in relation extraction and evidence prediction on the DocRED dataset while significantly enhancing model interpretability. This method provides an efficient, intuitive, and interpretable solution for document-level relation extraction tasks.
Recently, graph-based DocRE algorithms have become the dominant trend, as their graph structures have been shown to provide significant advantages in encoding long-distance dependencies and inter-sentence information. Specifically, Guo et al. [32] combined attention-guided layers and dense connection layers to achieve outstanding performance in relation extraction tasks, particularly in scenarios requiring cross-sentence reasoning and capturing long-distance dependencies. This approach introduces new ideas for graph-based natural language processing tasks. Christopoulou et al. [31] proposed the Edge-oriented Graph (EoG), which performs well in document-level relation extraction tasks by modeling multi-type nodes and edges and incorporating iterative reasoning mechanisms to effectively capture entity relationships in complex documents. Nan et al. [37] developed a GNN with structured attention units, which generates task-specific dependency structures and progressively aggregates relevant information to capture non-local interactions between entities.
The extraction of document-level causal relations remains a significant challenge in current research. It not only involves multiple sentences but also spans cross-sentence and even cross-document event causal relations. Therefore, developing effective models to establish relationships among document-level events has become a key focus in this field. To the best of our knowledge, we are the first to utilize an Event Causality Graph (ECG) on document-level inputs to uncover implicit causal relations from temporally related events.
2.2. Event–Event Causal Relation Extraction
Event causality extraction is a significant research area in natural language processing (NLP), aiming to identify and extract causal relations between events from text. Early research primarily focused on rule-based and statistical machine learning methods, as well as neural network models that emerged alongside the rise of deep learning.
Early research heavily relied on pattern matching and manually designed features. Girju et al. [38] conducted one of the earliest studies leveraging causal trigger words and syntactic patterns to identify causal relations. Khoo et al. [39] further proposed a dependency analysis method based on causal markers to recognize causal relations. Do et al. [27] introduced Causal Association (CEA) statistics. Although these methods achieved good results in simple sentence structures, they were limited to capturing local causal clues, making it challenging to fully understand deep causal logic within the context of long-distance dependencies and complex semantics.
With the advent of deep learning techniques, researchers gradually shifted to using neural networks to automatically learn text features, reducing reliance on manually designed features. Following the pioneering work of Collobert et al. [12], Kim et al. [28] were the first to introduce Convolutional Neural Networks (CNNs) into event causality extraction, leveraging convolutional kernels to automatically extract causal features from input text. CNNs excelled at capturing local features and detecting causal trigger words. For example, in the study by Kruengkrai et al. [40], Multi-Column Convolutional Neural Networks (MCNNs) significantly improved the accuracy of causal relation extraction. However, CNN was limited in handling long-distance dependencies in causal relations.
To address these limitations, Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network were introduced into causality extraction tasks. For instance, an LSTM model [29] was employed to capture long-distance dependencies in lengthy texts. For implicit causal events that lacked direct causal trigger words, Javed et al. [30] adopted BiLSTM to simultaneously capture forward and backward contextual information, enabling comprehensive modeling of causal relations between events. Li et al. [41] proposed a causality extraction model that combines BiLSTM with an attention mechanism. The attention mechanism weights important causal signals within sentences, significantly enhancing causal relation recognition performance. Beyond improving the model’s understanding of complex semantics, the attention mechanism also provided interpretability by highlighting the words or phrases the model focused on when making causal judgments.
In the field of event–event causal relation extraction (ECRE), multi-task learning methods have garnered significant attention for their ability to effectively handle diverse yet related tasks. By promoting knowledge sharing across tasks, these methods enhance generalization and improve overall performance. For example, Shang et al. [42] proposed a span-based dynamic local attention model for sequential sentence classification. This model explicitly captures latent paragraph structures in documents and integrates an auxiliary span-level classification task, achieving performance on benchmark datasets that is either superior to or on par with state-of-the-art methods.
In a pioneering study, Gao et al. [43] employed a dynamic attention mechanism to integrate a Textual Enhancement Channel (TEC) and a Knowledge Enhancement Channel (KEC), with both channels collaborating to extract event causality labels. Shen et al. [44] proposed a novel derivational prompt-based joint learning model for event causality identification, which enhances the extraction of both explicit and implicit causal relations through dual prompting tasks. Liu et al. [45] described a method for event causality identification by incorporating external knowledge bases and masking generalization. This strategy demonstrated strong adaptability to unseen scenarios and significant improvements in causal reasoning applications. Hashimoto et al. [46] proposed a weakly supervised method for extracting causal knowledge from Wikipedia by leveraging multilingual descriptions and textual redundancy. This approach achieved remarkable results in both precision and recall, effectively addressing the dispersion of cross-lingual causal information. Additionally, Man et al. [47] reframed event causality identification (ECI) as a generative task, focusing on generating causal and dependency path terms from input sentences. Moreover, GCN has shown tremendous potential in constructing Event Causality Graphs (ECGs). GCN applies convolutional operations to graph-structured data, capturing complex node relationships and improving the accuracy of event–event causal relation extraction (ECRE). In ECRE tasks, GCN builds event relation graphs from document-level data, allowing for detailed analysis of event dependencies and interactions [48]. These relation graphs enable GCN to learn context-aware document representations, facilitating the extraction of causal relations between events.
Compared with traditional methods, deep learning models leverage sequence modeling to flexibly learn contextual relationships between events, making causal relation extraction more adaptable and robust. However, as semantic structures are often limited to the sentence level, previous studies have struggled to comprehensively model document-level contextual information related to events. Additionally, implicit causal events involving temporal relations are often difficult to predict accurately. Temporal relations between events are also a sufficient condition for causal relations to exist. This is why we incorporate temporal relations as an additional channel, which effectively improves the accuracy of implicit event causality extraction.
2.3. Event–Event Temporal Relation Extraction
Allen [49] was the first to propose a temporal interval reasoning model which implemented event reasoning through the use of a temporal interval transitivity table. Specifically, if event occurs before event , and event occurs before event , it can be inferred that event also occurs before event . This concept of temporal logic transitivity laid the foundation for subsequent research on temporal relation reasoning, enabling complex temporal reasoning between events. Such logical reasoning has shown significant value in text comprehension and event chain construction, providing theoretical support for the development of more comprehensive and systematic temporal relation models.
With the increasing demand for temporal relation reasoning, supervised learning methods have gradually been applied to temporal event extraction tasks. Chambers et al. [50] and Mani et al. [51] were among the first to attempt classifying temporal relations using supervised learning, formalizing it as a classification task. However, manually designed features struggled to account for all possible scenarios. To address this limitation, Tatu and Srikanth [52] leveraged external temporal resources to construct training data, thereby enhancing the model’s ability to understand temporal features. These external resources included specially annotated temporal corpora and knowledge bases, providing additional contextual information that enabled the model to more accurately capture the temporal order between events.
In addition, Chambers et al. [50] enhanced the transitivity constraints of temporal logic by incorporating external information, thereby improving the performance of event pair classification. However, due to the lack of sufficiently annotated temporal relations in the training data, these methods fail to infer implicit causal relations from existing events. This limitation becomes particularly pronounced in scenarios where explicit temporal markers are absent. Amigo et al. [53] proposed a reasoning method based on temporal graphs. These methods represent events and temporal entities using temporal graphs, with edges in the graph denoting temporal relations between events. By utilizing temporal graphs, the sequential order of events in complex texts can be effectively captured, while also providing an intuitive visualization of relationships between events. Temporal graphs address the issue of data scarcity, providing a foundation for systematically representing complex event relationships and enhancing the modeling of event temporal relations.
In the context of the rise of deep learning, Han et al. [54] proposed a neural network model for jointly extracting events and temporal relations, leveraging a shared neural representation layer to simultaneously extract events and their temporal order. The model captures the complex dependencies between events and temporal relations through a shared feature embedding layer and improves extraction accuracy by incorporating a multi-task learning approach, thereby reducing error propagation issues commonly seen in traditional pipeline methods. Similarly, Huang et al. [55] proposed a unified framework for extracting event temporal relations. This framework integrates shared representation learning with structured reasoning methods to simultaneously capture events and their temporal labels, thereby mitigating error propagation in traditional pipeline methods. A multi-task learning strategy was also introduced to enhance the modeling of event temporal relations. However, these methods focus solely on extracting temporal event relations, overlooking the implicit causal relations embedded in temporally related events. Temporal relations are inherently linear and possess transitivity, indicating a high likelihood of causal connections among events aligned on the same timeline.
When a temporal relation exists between a pair of events, this relation significantly influences whether a causal connection exists between them. Maisonnave et al. [56] conducted a comparative study on various time-series causality learning methods for extracting causal graphs from news texts. However, the input of this method relies entirely on the filtering accuracy of topic-relevant sentences, making it incapable of extracting causal relations from a global document-level perspective. Consequently, the model lacks the ability to effectively handle implicit causal relations. These complex causal relations are often more prevalent in real-world scenarios.
3. Methodology
In this section, we introduce the architecture of our model, as shown in Figure 2. For both the event–event causal relation extraction channel (ECC) and the event–event temporal relation extraction channel (ETC), we employ BERT as the token encoder.
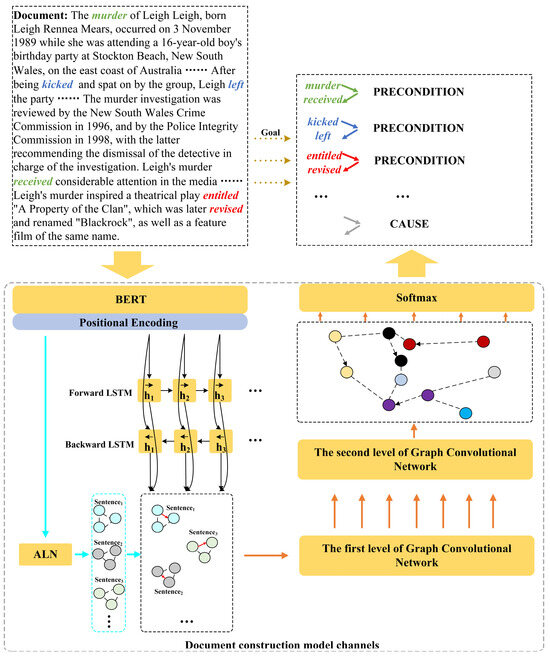
Figure 2.
The overall framework of the proposed model is shown. The blue arrows represent the ETC (event–event temporal relation extraction channel), while the black arrows represent the ECC (event–event causal relation extraction channel). The temporal relations between events are extracted using a BiLSTM, which aids in the extraction of causal relations. By modeling each sentence in the document as a graph structure, a dual-level GCN is employed to train the graph, and finally, a softmax is used to extract causal labels.
3.1. Feature Encoder
When extracting causal events involving temporal relations, we adopt a joint extraction approach. We define the sentences in the same document as . In ECRE, each token is assigned a causal label . The label “O” represents other event entities. CAUSE is defined as “the tail event is inevitable given the head event,” while PRECONDITION is defined as “the tail event would not have happened if the head event had not happened” [57]. The label “B_C” indicates the beginning of a CAUSE, and “I_C” represents the continuation of a CAUSE. Similarly, the label “B_P” marks the beginning of a PRECONDITION, while “I_P” represents the continuation of a PRECONDITION. Likewise, in event–event temporal relation extraction, each token is assigned a temporal label . The label “O” represents other entities, “B_BEFORE” indicates that the event occurred earlier, and “I_BEFORE” indicates that the event occurred later.
Leveraging the outstanding performance of Transformer models in natural language processing, text information is mapped to a high-dimensional space to achieve a quantified representation of text features. On this basis, BERT [16] was proposed as a pre-trained language representation model. Unlike traditional pre-training methods that rely on unidirectional language models or the shallow concatenation of two unidirectional models, BERT emphasizes the use of a novel Masked Language Model (MLM) to generate deep bidirectional language representations. BERT aims to pre-train deep bidirectional representations by jointly conditioning on context from all layers. In this study, the BERT pre-training model is employed to extract both local and global semantic information from text, with the goal of enhancing the model’s performance in ECRE and ETRE tasks. The pre-training mechanism of BERT involves a pair of distinctive tokens, where each input sentence begins with a [CLS] token and is separated by a [SEP] token. The [CLS] token semantically represents the entire sentence and assists the model in distinguishing semantic information between different sentences. This facilitates event position encoding and the construction of causal relation graphs. We use a BERT base uncased from Hugging Face Transformers. The model has 12 layers and 768 hidden dimensions.
3.2. Event–Event Causal Relation Extraction Channel
Traditional event causality extraction methods are mostly designed for extracting sentence-level causal relations [40]. As a result, they are unable to extract causal events across paragraphs and often compromise the integrity of the Event Causality Graph (ECG) by overlooking potential causal relations between events. To address this issue, we use the Association Link Network (ALN) in the event–event causal relation extraction channel to model the ECG for all input sentences. ALN is capable of processing triplet structures, (token1, relation, token2), extracted from the input text. Based on our research, these triplets are configured as causal triplet structures, (token1, CAUSE/PRECONDITION, token2). Finally, the modeled ECG is used as input to the dual-level GCN for model training.
3.2.1. Association Link Network
The Association Link Network (ALN) [58] is a structured approach designed to establish complex semantic associations between event nodes. The core idea of the ALN is to construct a semantic network using nodes and edges, effectively capturing and representing complex relationships between pieces of information. It demonstrates exceptional performance, particularly in causal relation modeling. Through this graph structure, the ALN can accurately describe the multi-level semantic connections within a document, thereby enhancing the understanding and reasoning of complex inter-event relationships. The generation process of the Association Link Network (ALN) begins by extracting event entities and causal indicators from the text, which are typically obtained through information extraction tools or annotations in the original dataset. Next, semantic association algorithms are used to establish connections between implicit causal relations, referred to as association links, to represent the causal correlations between different nodes. Each edge is then assigned a weight to indicate the strength of the relationship between nodes. Finally, all nodes and edges are integrated to construct the event causality network.
In this study, our input consists of a set of sentences , where each sentence undergoes preprocessing, including tokenization, syntactic parsing, and event extraction. Each sentence is decomposed into a sequence of events , where represents the -th event, which is also treated as the -th token in this study. The extracted events are represented as a node set , and the annotated causal relations are represented as a set . We use the dependency parsing tool AllenNLP to generate the dependency graph for each sentence from which the causal dependencies of each event are extracted to form the initial event node set . Each node in the initial event set represents an event, which can be specifically described in the form of a triplet , where is the unique identifier of the document containing the sentence, represents the position of the sentence in the document, and represents the position of the event in the sentence. By analyzing the contextual relationships and causal cues between nodes, the cosine similarity is used to evaluate the connection between two nodes, which determines whether an edge should be established, as shown in Equation (1):
Here, and represent the embedding vectors from the BERT outputs for nodes and respectively. A threshold is set, and if , an edge is established between the two nodes. Therefore, the initial construction of the ECG is defined as shown in Equation (2):
Here, represents the event network graph composed of the node set and the edge set .
3.2.2. Dual-Level GCN
We use the ALN to construct an initial ECG based on the output of BERT, improving the accuracy of semantic dependency graph construction. The edges of the ECG form a set of candidate causal relations, which are used as an adjacency matrix input to the GCN to further enhance the accuracy of causal relations between events. As shown in Figure 3, we design a dual-level GCN. Each GCN level consists of two hidden layers, with each hidden layer employing the ReLU activation function. The output nodes of the hidden layers are calculated using Equation (3) and are denoted by :
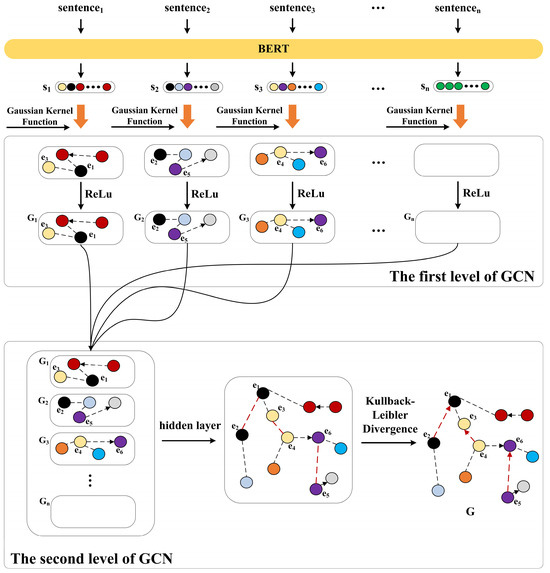
Figure 3.
The structure of the dual-level GCN is illustrated. After the document input is processed through token embedding, the output from the temporal relation extraction channel assists the causal relation extraction channel via the Gaussian kernel function, thereby enhancing the ALN’s modeling of the event feature graph. The two levels of GCN employ different strategies to compute the causal direction between event nodes.
represents the output of node in the -th hidden layer, which incorporates the features of all nodes from the previous layer. denotes the weight of the -th layer. The feature vector of node is initially aggregated with its neighboring nodes to extract relevant feature information. Since the number of neighboring nodes is related to the ECG, the set includes all neighboring nodes of node . Feature transformation is then performed by combining the bias term and multiplying it with the weight matrix , thereby altering the representation space of the feature vector. Finally, the application of the ReLU function strengthens the causal connections between nodes in the ECG, enhancing the feature adaptability for subsequent tasks. This adjustment is essential because linear models often struggle to effectively capture complex data structures and relationships.
Although the first-level GCN can identify explicit causal relations between certain event pairs, its ability to extract event pairs across sentences is limited. To enhance the detection of implicit causal event pairs and long-distance causal relations within the text, we introduce a second-level GCN into the model, thereby improving its overall robustness. The second-level GCN focuses on information from neighboring nodes in different sentences, facilitating the capture of implicit causality and causal relations across sentences. The hidden layer formula of the second-level GCN is expressed as follows:
Here, represents the weight of node in the -th layer, is the output feature of the -th layer, and is the bias of the -th layer. This formula facilitates information propagation between the hidden layers of the model. In the second-level GCN, we normalize the output of the first-level GCN to ensure that the feature representations of the nodes are valid probability distributions.
The edge weight quantifies the strength of the causal relation between two events. To accurately characterize this causal relation, the second-level GCN employs KL divergence (Kullback–Leibler divergence) to compute the edge weights. KL divergence measures the difference between two probability distributions and has a significant advantage in capturing directional relationships, making it effective for identifying causal associations between events. In the ECG, edge weights not only represent the direct associations between events but also enable the construction and reasoning of event chains through weighted path analysis, thereby facilitating more complex causal network analyses.
We represent the features of each node as a probability distribution. Each node has a feature vector , where denotes the dimensionality of the features. To transform the feature vector into a probability distribution, we apply the softmax function for normalization, converting the feature vector of the node into a probability distribution . The formula is expressed as follows:
Here, represents the probability value of node at feature dimension , denotes the -th feature value of node , is the dimensionality of the feature vector, The function exp represents the exponential function, which ensures that all feature values are positive and subsequently normalizes them into a probability distribution through the softmax function. The feature vector of each node is represented as a probability distribution, describing the importance of the node across different feature dimensions. This probabilistic representation facilitates the calculation of relationships between nodes, enabling the effective propagation of each node’s information within the graph structure.
KL divergence is used to measure the degree of difference between two probability distributions. Specifically, if nodes and have feature distributions and , respectively, their KL divergence is defined as shown in Equation (6):
Here, represents the probability value of node at feature dimension , and represents the probability value of node at feature dimension . The dimensionality of the feature distribution is denoted as . The logarithmic function log is used to measure the difference between and at feature dimension . The larger the KL divergence value, the greater the difference between the feature distributions of the two nodes. Since KL divergence is asymmetric, i.e., , it can effectively represent the directionality of causal relations. After obtaining the KL divergence between nodes, it can be further converted into the initial edge weight , which describes the strength of the causal relation between nodes and . The specific calculation formula is as follows:
Here, represents the initial weight of the edge from node to node in layer , denotes the KL divergence between nodes and , and the exponential function exp is used to convert the KL divergence into edge weights. Since KL divergence is sensitive to small probabilities, we apply Laplace smoothing () to prevent numerical instability. Additionally, we use exponential normalization when computing causal weights to ensure that the weights remain within a stable range, preventing the gradient explosion problem. Consequently, converges to the interval (0, 1], ensuring the stability of causal inference. The degree of difference in KL divergence is mapped to the initial edge weight. A smaller KL divergence value indicates that the feature distributions of the two nodes are more similar, resulting in a larger initial edge weight , which suggests a stronger causal relation. Conversely, when the KL divergence is larger, the initial edge weight is smaller, indicating a weaker causal relation between the nodes. Since KL divergence can measure causal directionality, it enables the model to distinguish between the effects of and . Compared to the Wasserstein distance, KL divergence has a lower computational complexity, making it more suitable for document-level causal relation modeling. During GCN propagation, the event representation is treated as a probability distribution, and KL divergence effectively captures variations between event distributions.
Finally, the output of the second level of GCN is employed to extract the causal relations between each event pair using a softmax function. The dimensionality of the final output vector is determined by the length of each causal event token. As shown in Figure 4, we provide an example from the dataset to illustrate the output of our model. Here, represents the set of all possible causal label sequences within a sentence.
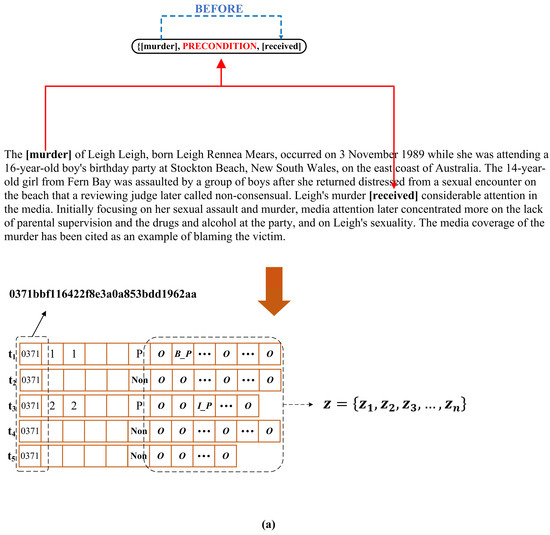
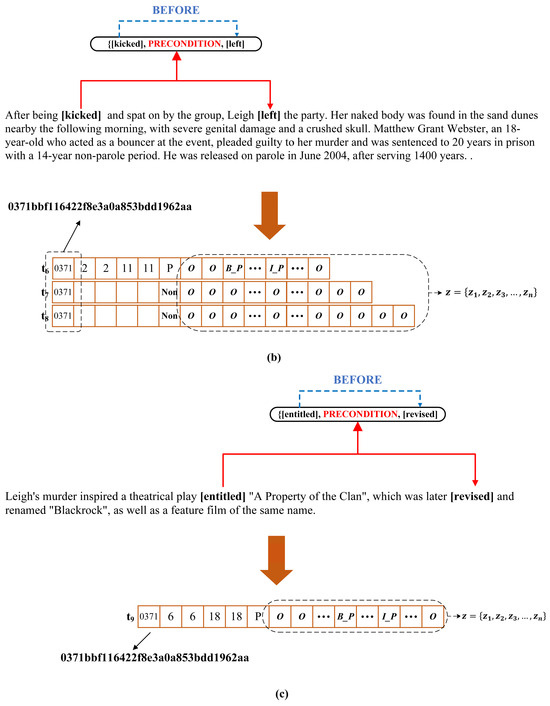
Figure 4.
A schematic diagram illustrating the structure of the model’s output labels is provided. The textual content in (a–c) is extracted from a document in the dataset. The length of each vector does not correspond to the actual length of the sentence but is instead used solely to illustrate the labeling process of the proposed model. Each output vector t represents a sentence in the document, with its corresponding event model annotated accordingly. From left to right, the first position contains the unique document identifier, the second, the third, the fourth, and fifth positions denote the beginning and inside tokens of the “CAUSE” tag event or the beginning and inside tokens of the “PRECONDITION” tag event. The sixth position indicates whether the sentence contains a causal relation and specifies the type of causal tag. The annotations of all events in the sentence follow the sixth position. Specifically, “B_C” and “I_C” represent the beginning and inside tokens of the “CAUSE” tag, “B_P” and “I_P” denote the beginning and inside tokens of the “PRECONDITION” tag, and “O” represents other types.
3.3. Event–Event Temporal Relation Extraction Channel
For event pairs with temporal relations, we set up another channel, event–event temporal relation extraction channel (ETC), which shares the embedding layer with the event–event causal relation extraction channel (ECC). In the ETC, we enhance the directionality and consistency of causal reasoning by incorporating temporal context information, ensuring that the inferred causal relations align with the chronological sequence of events. This method includes using BERT and positional encoding (PE) to represent event features, extracting temporal features through BiLSTM, constructing causal graphs with ALN, and ultimately adjusting the edge weights in the graph based on the time differences between events. This ensures that causal reasoning adheres to temporal logical consistency.
3.3.1. Multi-Tasking Auxiliary Structure
The output of the shared embedding layer from BERT contains only the semantic information of the token and the information of the token itself. We use relative positional encoding to represent the information about the sequence of event occurrences. The specific formula is as follows:
Here, Embedding is a learnable lookup table that maps relative position indices to a vector of dimension . and refer to event indices, representing two events from the document. Finally, the features extracted by BERT are concatenated with positional encoding:
refers to the embedding of the event , which is derived from BERT’s last layer. We use the BiLSTM model to capture the temporal context information of each event. Given an input sequence of events, BiLSTM outputs the hidden representation of each event, capturing both forward and backward contextual information. The process is divided into a forward LSTM and a backward LSTM, and their respective computations are shown as follows:
The final hidden state represents event as a vector, incorporating contextual information from the temporal sequence in both directions and , as processed by the BiLSTM. It is formed by concatenating the hidden states from the forward and backward directions.
3.3.2. Adjustment of Node Weight
If the time difference between two events is small, the weight of their causal relation is enhanced, indicating a closer causal connection between the two events. However, this introduces a challenge: if the time difference between two events is large, the causal weight theoretically weakens. In practice, however, these two causally related events may not exhibit an obvious temporal relation. Alternatively, two events with a small time difference may, in fact, lack a causal relation. To address these issues, we use a Gaussian kernel function to adjust the strength and direction of the causal relation. The formula for the Gaussian kernel function is as follows:
Here, is derived from the output vectors of BERT and represents the semantic similarity between events and . The Gaussian kernel function is used to measure this similarity. Smaller indicates greater semantic similarity between the events, implying a stronger causal relation. represents the result obtained by applying softmax to the concatenation of BiLSTM outputs and ():
When the temporal similarity is high (), the function retains a larger causal weight, ensuring that event pairs occurring close in time exhibit stronger causal relations. Conversely, when the temporal gap is large ((), the function gradually reduces the causal weight, preventing events with long time spans from being mistakenly considered as directly causal. However, in some cases, temporal relations and causal relations may not always be consistent. Events with significant temporal gaps can still exhibit causal dependencies, while temporally proximate events may not necessarily have causal relations (e.g., consecutively occurring but unrelated news events).
controls the width of the Gaussian kernel, which we set to 15, indicating the impact of semantic similarity on the strength of the causal relation. and are hyperparameters used to adjust the strength of the causal relation. We refer to as the temporal adjustment term. The model can regulate the influence of temporal similarity on causal inference, preventing events that are temporally close but lack causal relations from being incorrectly linked. When the BERT outputs and of two events and become more similar, this value approaches 1, indicating a stronger causal relation between them. When is large, the temporal difference term approaches 1, maintaining a strong causal relation. Conversely, when is small, the distance term gradually decreases smoothly but does not completely vanish. By adjusting the parameters and , we control the influence of temporal similarity on the causal relation. Therefore, the final edge weight is defined as follows:
represents the initial edge weight calculated based on the ALN, while is the temporal enhancement function. This function combines the contextual representations from BERT’s output with temporal similarity between events to adjust the edge weights.
4. Experiment
4.1. Datasets
Given the limited availability and small scale of datasets annotated with event causal relations and temporal relations, this study selected two large-scale datasets with comprehensive annotations, namely MAVEN-ERE [57] and EventStoryLine [59], for experimental comparison. Both datasets include annotations for event causal relations as well as event temporal relations. We conducted experiments on these benchmark datasets to validate the effectiveness of our approach. MAVEN-ERE is a large-scale, state-of-the-art, and uniformly annotated event relation extraction (ERE) dataset designed to address the limitations of existing datasets in terms of the quantity of causal and temporal annotations. This dataset includes a variety of event relationships, such as coreference, temporal, causal, and sub-event relations, making it the largest dataset for causal relations among all existing ERE datasets. EventStoryLine is a comprehensively annotated dataset that includes 258 documents, 22 topics, 5334 events, and 1770 internal as well as 3885 external causal relation pairs. Since this dataset is primarily derived from story collections, which are rich in temporal relations, the chronological order of events greatly facilitates the extraction of causal event pairs. Similarly, MAVEN-ERE is a state-of-the-art dataset for event relation prediction, containing 57,992 causal relation pairs and 1,042,709 event pairs annotated with “BEFORE” relations.
We first performed an initial cleaning of the MAVEN-ERE dataset, retaining only the data with causal and temporal order annotations to fit the requirements of our task. Each row of data in the dataset follows the structure outlined below:
[unique identifier for the document, the document of content,
[event 1, the sentence of content, the position of the sentence in the document, the start position of event 1, the end position of event 1],
[event 2, the sentence of content, the position of the sentence in the document, the start position of event 2, the end position of event 2],
CAUSE/PRECONDITION/BEFORE].
Since the test set for this dataset has not yet been released, we partitioned the original dataset into 10% for the validation set, 70% for the training set, and the remaining 20% for the test set.
For the EventStoryLine dataset, inspired by Tao et al. [60], we labeled “FALLING_ACTION” and “PRECONDITION” as causal event pairs. Consistent with the processing of MAVEN-ERE, 10% of EventStoryLine was used as the validation set, 70% as the training set, and 20% as the test set.
Negative examples were generated by randomly selecting event pairs that do not have an explicit causal or temporal relation in the dataset. Additionally, we ensured that the sampled negative pairs were balanced against the positive pairs to prevent model bias.
4.2. Baseline Models
To demonstrate the superior performance of our model compared to other models, we employed several different methods and conducted experiments uniformly on the MAVEN-ERE and EventStoryLine datasets:
- BiLSTM+CRF: This is a fundamental information extraction model that utilizes BiLSTM to capture the sequential and contextual information in the text and employs CRF to decode the resulting label sequence.
- CNN+BiLSTM+CRF [43]: The model employs CNN to extract multiple n-gram semantic features and utilizes a BiLSTM+CRF layer to capture dependencies between the features.
- BERT+SCITE [41]: This method integrates multiple prior knowledge sources into the embedding representations to generate hybrid embeddings and employs a multi-head attention mechanism to learn dependencies between causal words. Instead of using hybrid embeddings, we utilize BERT to encode sentences.
- Hierarchical dependency tree (HDT) [61]: A model based on the hierarchical dependency tree (HDT) was proposed to efficiently capture global semantics and contextual information across sentences in a document. The document is divided into four layers: document layer, sentence layer, context layer, and entity layer, to capture multi-granular features. This training approach enables the model to better capture and utilize the structural causal relations between events.
- CSNN [62]: The model integrates CNN to capture local features, a self-attention mechanism to enhance semantic associations between features, and BiLSTM to handle long dependencies in causal relations. CRF is employed to predict word-level labels, ensuring global consistency in causal relation annotations.
4.3. Experimental Settings
The model parameters are listed in Table 1. This experiment was conducted using the PyTorch 1.7.0 deep learning framework (Table 2). To address the issue of class imbalance, we assigned weights based on the ratio of positive to negative samples, which is 1:1. The number of training epochs was set to 50. To ensure the reliability of the experimental results, all data were divided into training, validation, and test sets in a ratio of 70%, 10%, and 20%, respectively. Due to the large size of the dataset, the validation set was evaluated in mini-batches, and the weighted average F1 score across all batches was used to represent the overall performance on the validation set.

Table 1.
Model parameter configuration.

Table 2.
Experiment setup.
4.4. Experimental Results and Analysis
We evaluated a total of five baseline models, as shown in Table 3. Accuracy, Precision, Recall, and F1 score were used to compare the performance of six models on two datasets. Our model demonstrated significant advantages across all four metrics compared to the other five models, especially when contrasted with BERT+SCITE and BiLSTM+CRF, which do not employ graph structures for modeling. The performance metrics of our model were notably higher. However, the HDT model leverages the structure of hierarchical dependency trees to divide Document Nodes, Sentence Nodes, Context Nodes, and Entity Nodes into distinct levels. While it shows slight advantages in Precision and Accuracy, we further plotted the learning curves of these six models on the MAVEN and EventStoryLine datasets, as shown in Figure 5 and Figure 6. The HDT model is the only one that exhibits a noticeably slow upward trend and achieves a higher average weighted F1 score compared to the other four baseline models. We hypothesize that this is closely related to the model’s use of hierarchical dependency trees at different levels. However, the average weighted F1 score of our model is significantly higher. This is because both the ETC and ECC components in our model have the ability to perceive global contextual information. ETC extracts temporal relation features within the document using BiLSTM, while the dual-level GCN in ECC incorporates global event causal relation transformation information. Therefore, the assistance of ETC to ECC enables the model to capture more global dependency information from the document, enhancing its performance on the ECE task. Although our model achieved significant advantages on both datasets, there remain some notable issues. During the first 20 epochs, the model’s performance curves exhibited significant fluctuations before stabilizing after epoch 20. We speculate that this may be related to the design of our model architecture. In future work, we will continue to refine the model to ensure a more stable and efficient training process.

Table 3.
Experimental findings of six baseline models on multiple datasets (%).
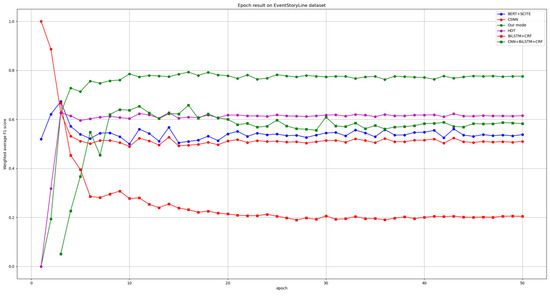
Figure 5.
The learning curve of different methods on the EventStoryLine dataset. The curve of our model is represented by the green solid line.
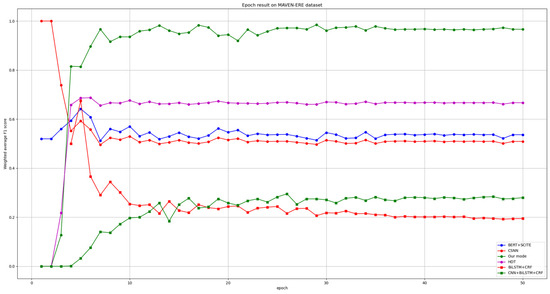
Figure 6.
The learning curve of different methods on the MAVEN-ERE dataset. The curve of our model is represented by the green solid line.
4.5. Ablation Experiment
To comprehensively evaluate the contribution of each component to the overall performance of the model, we conducted systematic ablation experiments. The primary objective of ablation analysis is to quantify the impact of specific modules on the causal relation extraction task by removing them one by one. To achieve this, we designed multiple ablation experiments targeting different model components and observed their effects on overall model performance after the removal of each component. This approach allows us to gain a deeper understanding of the unique role and contribution of each module.
In the ablation experiments, only one module was altered while all other modules remained unchanged, as shown in Table 4. The experimental configurations are summarized as follows:

Table 4.
Ablation experiment results.
- w/o BERT: We removed the BERT embedding layer and replaced it with randomly initialized embeddings while keeping the positional encoding unchanged.
- w/o event–event temporal relation extraction channel (ETC): We removed the temporal relation extraction channel while keeping the ECC unchanged.
- w/o event–event causal relation extraction channel (ECC): We removed the causal relation extraction channel while keeping the temporal relation extraction channel unchanged.
- w/o positional encoding: We removed the positional encoding method and directly constructed the graph structure using the original dataset after passing it through the BERT embedding layer.
- w/o dual-level GCN: For the dual-level GCN, we separately removed the first level of GCN and the second level of GCN to evaluate the individual contribution of each level.
- w/o adjustment of node weight: We removed the process of using the Gaussian kernel function to assist in graph structure construction and directly passed the output of ETC to the dual-level GCN.
- w/o Gaussian kernel function: We used semantic similarity to compute causal relations while keeping all other components unchanged.
- w/o temporal adjustment term: We only used
The experimental results show that each component has a significant impact on the overall performance of the model. The ETC has a notable influence on causal relation extraction, as temporal features provide abundant temporal cues for causal reasoning. These features help the model better capture the sequential information and temporal constraints between events, thereby enhancing its ability to identify and predict causal relations. Temporal features provide the model with critical information about the sequence of events, ensuring the rationality of causal relations along the timeline. When the dual-level GCN is removed, the model’s perception ability decreases. Both the first level of GCN and the second level of GCN play indispensable roles, as they are responsible for aggregating local features and high-order features, respectively. Removing either level results in a decline in performance. The adjustment of node weights based on temporal features ensures temporal consistency in causal reasoning, highlighting the critical role of temporal features in dynamically adjusting causal relations. By dynamically modifying edge weights, temporal features ensure the temporal consistency of causal relations, enabling the model to allocate causal weights more reasonably according to the chronological order when modeling causal chains. When this strategy is removed, the model fails to accurately capture the impact of temporal features on causal weights, resulting in a decline in overall reasoning accuracy. This further validates the core role of temporal features in dynamically adjusting edge weights and modeling temporal consistency. The results of removing the Gaussian kernel function indicate an increased proportion of misclassified causal relations, highlighting the indispensable role of temporal information in causal inference. The temporal adjustment term plays a crucial role in capturing implicit causal relations over long time spans.
Through systematic ablation experiments on the two datasets, we reached the following key conclusion: each module plays an indispensable role in the overall performance. The temporal and causal extraction channels, dual-level GCN, and the node weight adjustment strategy based on temporal features significantly improve the extraction of temporal and causal relations. The rich contextual information and semantic understanding provided by BERT form a solid foundation for the model. The dual-channel structure effectively integrates temporal and causal information, while positional encoding ensures the perception of event order. Notably, the dual-level GCN and the weight adjustment based on temporal features enhance the depth of relationship modeling through multi-level feature aggregation, ensuring the temporal consistency of causal relations. The Gaussian kernel function is not only used for modeling temporal similarity but also effectively enhances the rationality of causal inference, ensuring that the extracted causal relations align with real-world temporal logic. This enables the model to allocate causal weights more reasonably according to chronological order when modeling causal chains, thereby maintaining the causal relations under temporal constraints.
5. Conclusions and Future Work
This paper proposes an innovative event temporal relation-assisted event causality extraction model, which adopts a dual-channel architecture to separately handle event causality and event temporal relations, enhancing the model’s ability to extract implicit causal relations. The core innovation of the model lies in leveraging the event–event temporal relation extraction channel (ETC) to assist the event–event causal relation extraction channel (ECC), constructing an Event Causality Graph (ECG) based on the Association Link Network (ALN), and employing a dual-level GCN to extract deep features of event relations. The experimental results demonstrate that the proposed model significantly improves the accuracy and weighted F1 score for causal relation extraction tasks on the public datasets MAVEN-ERE and EventStoryLine, particularly excelling in document-level structures. The model exhibits strong robustness and generalization capability in handling diverse textual contexts. Through systematic ablation experiments, we validated the independent roles and combined contributions of various modules in the model. The results indicate that the temporal and causal event channels, the node weight adjustment based on temporal features, and the dual-level GCN all play indispensable roles in enhancing the model’s performance.
Future research will focus on the following areas for improvement: First, we plan to conduct experiments on larger and more diverse datasets to further evaluate the model’s generalization ability and cross-domain adaptability. Different datasets encompass texts from various domains and languages, enabling a comprehensive assessment of the model’s robustness and transferability in multilingual and multi-domain scenarios. Second, we will incorporate additional external knowledge bases to enhance the background knowledge in causal reasoning. This is particularly important for detecting implicit relationships between causal events. The introduction of external knowledge bases can significantly improve the model’s reasoning capability for cross-domain causal relations. For instance, knowledge graphs from medical or legal domains can provide rich contextual information, further boosting the model’s performance in these specific areas. Moreover, the current model relies on static embeddings to model node relationships. In the future, we will explore dynamic embeddings and sequential graph learning to more flexibly capture temporal dynamics and the evolution of causal relations. To further improve the model’s performance in complex causal relation modeling, we plan to explore novel network architectures, such as integrating Temporal Graph Neural Networks (TGNNs) and Relational Graph Convolutional Networks (R-GCNs), to capture multi-level causal relations. This integration will enable the model to more effectively learn temporal and causal dependencies between events and capture their dynamic changes. Additionally, we aim to develop more efficient node relationship inference algorithms to meet the demands of real-time applications. In intelligent dialog systems, for instance, user inputs often contain complex causal and temporal information, making real-time causal reasoning particularly critical. Future research will focus on optimizing the computational efficiency of GCN and improving the edge weight adjustment mechanism to achieve more efficient causal reasoning in real-time applications.
Author Contributions
Z.L.: conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, visualization, writing—original draft, writing—editing; Y.L.: funding acquisition, supervision, writing—review, project administration; W.N.: funding acquisition, supervision, writing—review. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Shandong Provincial Natural Science Joint Foundation (No. ZR2022LZH014), the Shandong Provincial Natural Science Foundation (No. ZR2022MF319), and the Open Foundation of Key Laboratory of Blockchain Agricultural Applications, Ministry of Agriculture and Rural Affairs (No. 2023KLABA01).
Data Availability Statement
The data presented in this study are available in MAVEN-ERE at https://doi.org/10.18653/v1/2022.emnlp-main.60. These data were derived from the following resources available in the public domain: https://github.com/THU-KEG/MAVEN-ERE accessed on 20 February 2025.
Conflicts of Interest
The authors affirm that they have no identifiable financial conflicts of interest or personal relationships that may have influenced the work presented in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| ALN | Association Link Network |
| BERT | Bidirectional encoder representations from transformers |
| BiLSTM | Bidirectional Long Short-Term Memory network |
| BRAN | Bi-affine Relation Attention Network |
| CEA | Cause–effect association |
| CNN | Convolutional Neural Network |
| CRF | Conditional random field |
| CSNN | Cascaded multi-structure neural network |
| ECC | Event–event causal relation extraction channel |
| ECE | Event causality extraction |
| ECG | Event Causality Graph |
| ECI | Event causality identification |
| ECRE | Event–event causal relation extraction |
| EoG | Edge-oriented graph |
| ERE | Event relation extraction |
| ETC | Event–event temporal relation extraction channel |
| ETRE | Event–event temporal relation extraction |
| GCN | Graph Convolutional Network |
| GNN | Graph Neural Network |
| HDT | Hierarchical dependency tree |
| IE | Information extraction |
| KEC | Knowledge Enhancement Channel |
| KL | Kullback–Leibler |
| LSTM | Long Short-Term Memory network |
| MCNN | Multi-column Convolutional Neural Network |
| MLM | Masked Language Model |
| NLP | Natural language processing |
| PE | Positional encoding |
| R-GCN | Relational Graph Convolutional Network |
| RNN | Recurrent Neural Network |
| SCITE | Self-attentive BiLSTM-CRF with transferred embeddings |
| TEC | Textual Enhancement Channel |
| TGNN | Temporal Graph Neural Network |
References
- Wang, Y.; Liang, D.; Charlin, L.; Blei, D.M. Causal inference for recommender systems. In Proceedings of the 14th ACM Conference on Recommender Systems, New York, NY, USA, 22–26 September 2020; pp. 426–431. [Google Scholar] [CrossRef]
- van Geloven, N.; Swanson, S.A.; Ramspek, C.L.; Luijken, K.; van Diepen, M.; Morris, T.P.; Groenwold, R.H.H.; van Houwelingen, H.C.; Putter, H.; le Cessie, S. Prediction meets causal inference: The role of treatment in clinical prediction models. Eur. J. Epidemiol. 2020, 35, 619–630. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Chu, Z.; Li, S.; Li, Y.; Gao, J.; Zhang, A. A survey on causal inference. ACM Trans. Knowl. Discov. Data 2021, 15, 74. [Google Scholar] [CrossRef]
- Wang, A.; Cho, K.; Lewis, M. Asking and answering questions to evaluate the factual consistency of summaries. arXiv 2020, arXiv:2004.04228. [Google Scholar]
- Guo, J.; Fan, Y.; Pang, L.; Yang, L.; Ai, Q.; Zamani, H.; Wu, C.; Croft, W.B.; Cheng, X. A deep look into neural ranking models for information retrieval. Inf. Process. Manag. 2019, 57, 102067. [Google Scholar] [CrossRef]
- Dong, C.; Li, Y.; Gong, H.; Chen, M.; Li, J.; Shen, Y.; Yang, M. A survey of natural language generation. ACM Comput. Surv. 2022, 55, 173. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Khoo, C.S.; Kornfilt, J.; Oddy, R.N.; Myaeng, S.H. Automatic extraction of cause-effect information from newspaper text without knowledge-based inferencing. Lit. Linguistic Comput. 1998, 13, 177–186. [Google Scholar] [CrossRef]
- Blanco, N.E.; Castell, D. Moldovan, Causal relation extraction. In Proceedings of the Sixth International Conference on Language Resources and Evaluation (LREC’08), Marrakech, Morocco, 28–30 May 2008. [Google Scholar]
- Wang, Z.; Wang, H.; Luo, X.; Gao, J. Back to prior knowledge: Joint event-event causal relation extraction via convolutional semantic infusion. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Delhi, India, 11–14 May 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 346–357. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P. Natural language processing (almost) from scratch. J. Mach. Learn. Res. 2011, 12, 2493–2537. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. Advances in Neural Information Processing Systems (NeurIPS). arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Zhao, L.; Sun, Q.; Ye, J.; Chen, F.; Lu, C.-T.; Ramakrishnan, N. Multi-task learning for spatio-temporal event forecasting. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; ACM: New York, NY, USA, 2015; pp. 1503–1512. [Google Scholar] [CrossRef]
- Wongsuphasawat, K.; Gotz, D. Exploring flow, factors, and outcomes of temporal event sequences with the outflow visualization. IEEE Trans. Vis. Comput. Graph. 2012, 18, 2659–2668. [Google Scholar] [CrossRef]
- Sinha, C.; Sinha, V.D.S.; Zinken, J.; Sampaio, W. When time is not space: The social and linguistic construction of time intervals and temporal event relations in an Amazonian culture. Lang. Cogn. 2011, 3, 137–169. [Google Scholar] [CrossRef]
- O'Gorman, T.; Wright-Bettner, K.; Palmer, M. Richer event description: Integrating event coreference with temporal, causal and bridging annotation. In Proceedings of the CNS, Jeju, Republic of Korea, 2–7 July 2016; pp. 47–56. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Zhang, P. A framework for mining sequential patterns from spatio-temporal event data sets. IEEE Trans. Knowl. Data Eng. 2008, 20, 433–448. [Google Scholar] [CrossRef]
- Boogaart, R. Aspect and Temporal Ordering. A Contrastive Analysis of Dutch and English; LOT: Warsaw, Poland, 1999. [Google Scholar]
- Mani, I.; Schiffman, B.; Zhang, J. Inferring temporal ordering of events in news. In Companion Volume of the Proceedings of HLT-NAACL 2003-Short Papers; ACL: Stroudsburg, PA, USA, 2003; pp. 55–57. [Google Scholar]
- Haffar, N.; Ayadi, R.; Hkiri, E.; Zrigui, M. Temporal ordering of events via deep neural networks. In Document Analysis and Recognition, Proceedings of the ICDAR 2021: 16th International Conference, Lausanne, Switzerland, 5–10 September 2021; Springer: Berlin/Heidelberg, Germany, 2021; Part II 16; pp. 762–777. [Google Scholar] [CrossRef]
- Zhou, H.; Zheng, D.; Nisa, I.; Ioannidis, V.; Song, X.; Karypis, G. Tgl: A general framework for temporal gnn training on billion-scale graphs. arXiv 2022, arXiv:2203.14883. [Google Scholar] [CrossRef]
- Do, Q.; Chan, Y.S.; Roth, D. Minimally supervised event causality identification. In Proceedings of the 2011 Conference on Empirical Methods in Natural Language Processing, Edinburgh, UK, 27–29 July 2011; pp. 294–303. [Google Scholar]
- Kim, Y. Convolutional neural networks for sentence classification. In Proceedings of the EMNLP, Doha, Qatar, 25–29 October 2014; pp. 1746–1751. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Z.; Jin, X.; Bai, L.; Guan, S.; Guo, J.; Cheng, X. Semantic structure enhanced event causality identification. arXiv 2023, arXiv:2305.12792. [Google Scholar]
- Aved, U.; Ijaz, K.; Jawad, M.; Khosa, I.; Ansari, E.A.; Zaidi, K.S.; Rafiq, M.N.; Shabbir, N. A novel short receptive field based dilated causal convolutional network integrated with Bidirectional LSTM for short-term load forecasting. Expert Syst. Appl. 2022, 205, 117689. [Google Scholar] [CrossRef]
- Christopoulou, F.; Miwa, M.; Ananiadou, S. Connecting the dots: Document-level neural relation extraction with edge-oriented graphs. arXiv 2019, arXiv:1909.00228. [Google Scholar]
- Guo, Z.; Zhang, Y.; Lu, W. Attention guided graph convolutional networks for relation extraction. arXiv 2019, arXiv:1906.07510. [Google Scholar]
- Huang, K.; Wang, G.; Ma, T.; Huang, J. Entity and evidence guided relation extraction for docred. arXiv 2020, arXiv:2008.12283. [Google Scholar]
- Verga, P.; Strubell, E.; McCallum, A. Simultaneously self-attending to all mentions for full-abstract biological relation extraction. arXiv 2018, arXiv:1802.10569. [Google Scholar]
- Gu, J.; Qian, L.; Zhou, G. Chemical-induced disease relation extraction with various linguistic features. Database 2016, 2016, baw042. [Google Scholar] [CrossRef]
- Zhou, H.; Deng, H.; Chen, L.; Yang, Y.; Jia, C.; Huang, D. Exploiting syntactic and semantics information for chemical–disease relation extraction. Database 2016, 2016, baw048. [Google Scholar] [CrossRef] [PubMed]
- Nan, G.; Guo, Z.; Sekulić, I.; Lu, W. Reasoning with latent structure refinement for document-level relation extraction. arXiv 2020, arXiv:2005.06312. [Google Scholar]
- Girju, R. Automatic detection of causal relations for question answering. In Proceedings of the ACL 2003 Workshop on Multilingual Summarization and Question Answering, Sapporo, Japan, 7–12 July 2003; pp. 76–83. [Google Scholar] [CrossRef]
- Khoo, C.S.; Chan, S.; Niu, Y. Extracting causal knowledge from a medical database using graphical patterns. In Proceedings of the 38th Annual Meeting of the Association for Computational Linguistics, Hong Kong, China, 3–6 October 2020; pp. 336–343. [Google Scholar] [CrossRef]
- Kruengkrai, C.; Torisawa, K.; Hashimoto, C.; Kloetzer, J.; Oh, J.H.; Tanaka, M. Improving event causality recognition with multiple background knowledge sources using multi-column convolutional neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q.; Zou, X.; Ren, J. Causality extraction based on self-attentive BiLSTM-CRF with transferred embeddings. Neurocomputing 2021, 423, 207–219. [Google Scholar] [CrossRef]
- Shang, X.; Ma, Q.; Lin, Z.; Yan, J.; Chen, Z. A span-based dynamic local attention model for sequential sentence classification. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, Online, 1–6 August 2021; ACL: Stroudsburg, PA, USA, 2021; Volume 2, pp. 198–203. [Google Scholar] [CrossRef]
- Gao, J.; Yu, H.; Zhang, S. Joint event-event causal relation extraction using dual-channel enhanced neural network. Knowl. Based Syst. 2022, 258, 109935. [Google Scholar] [CrossRef]
- Shen, S.; Zhou, H.; Wu, T.; Qi, G. Event causality identification via derivative prompt joint learning. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 2288–2299. [Google Scholar]
- Liu, J.; Chen, Y.; Zhao, J. Knowledge enhanced event causality identification with mention masking generalizations. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 3608–3614. [Google Scholar] [CrossRef]
- Hashimoto, C. Weakly supervised multilingual causality extraction from Wikipedia. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Proceedings of the 2019 Conference on Empirical Methods in Natural Language, Hong Kong, China, 3–7 November 2019; ACL: Stroudsburg, PA, USA, 2019; pp. 2988–2999. [Google Scholar] [CrossRef]
- An, H.; Nguyen, M.; Nguyen, T.H. Event causality identification via generation of important context words. In Proceedings of the 11th Joint Conference on Lexical and Computational Semantics, Seattle, WA, USA, 14–15 July 2022; pp. 323–330. [Google Scholar] [CrossRef]
- Phu, M.T.; Nguyen, T.H. Graph convolutional networks for event causality identification with rich document-level structures. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Online, 6–11 June 2021; pp. 3480–3490. [Google Scholar] [CrossRef]
- Allen, J.F. Maintaining knowledge about temporal intervals. Commun. ACM 1983, 26, 832–843. [Google Scholar] [CrossRef]
- Chambers, N.; Jurafsky, D. Jointly combining implicit constraints improves temporal ordering. In Proceedings of the Conference on Empirical Methods for Natural Language Processing (EMNLP 2008), Honolulu, HA, USA, 25–27 October 2008; pp. 698–706. [Google Scholar]
- Mani Inderjeet Wellner, B.; Verhagen, M.; Pustejovsky, J. Three Approaches to Learning Tlinks in Timeml; Technical Report CS-07-268; Brandeis University: Waltham, MA, USA, 2007. [Google Scholar]
- Marta, T.; Srikanth, M. Experiments with reasoning for temporal relations between events. In Proceedings of the 22nd International Conference on Computational Linguistics (COLING 2008), Manchester, UK, 18–22 August 2008; COLING 2008 Organizing Committee: Manchester, UK, 2008; pp. 857–864. [Google Scholar]
- Amigo, E.; Artiles, J.; Li, Q.; Ji, H. An evaluation framework for aggregated temporal information extraction. In Proceedings of the SIGIR workshop on entity-oriented, Taipei, Taiwan, 23–27 July 2023; ACM: New York, NY, USA, 2011. [Google Scholar]
- Han, R.; Ning, Q.; Peng, N. Joint event and temporal relation extraction with shared representations and structured prediction. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Proceedings of the 2019 Conference on Empirical Methods in Natural Language, Hong Kong, China, 3–7 November 2019; ACL: Stroudsburg, PA, USA, 2019; pp. 434–444. [Google Scholar] [CrossRef]
- Huang, Q.; Hu, Y.; Zhu, S.; Feng, Y.; Liu, C.; Zhao, D. More than classification: A unified framework for event temporal relation extraction. arXiv 2023, arXiv:2305.17607. [Google Scholar]
- Maisonnave, M.; Delbianco, F.; Tohme, F.; Milios, E.; Maguitman, A.G. Causal graph extraction from news: A comparative study of time-series causality learning techniques. PeerJ Comput. Sci. 2022, 8, e1066. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, Y.; Ding, N.; Peng, H.; Wang, Z.; Lin, Y.; Han, X.; Hou, L.; Li, J.; Liu, Z.; et al. Maven-ere: A unified large-scale dataset for event coreference, temporal, causal, and subevent relation extraction. arXiv 2022, arXiv:2211.07342. [Google Scholar]
- Liu, Y.; Borhan, N.; Luo, X.; Zhang, H.; He, X. Association link network based core events discovery on the web. In Proceedings of the 2013 IEEE 16th International Conference on Computational Science and Engineering, Sydney, Australia, 3–5 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 553–560. [Google Scholar] [CrossRef]
- Caselli, T.; Vossen, P. The EventStoryLine Corpus: A new benchmark for causal and temporal relation extraction. In Proceedings of the Events and Stories in the News Workshop, Vancouver, BC, Canada, 4 August 2017; pp. 77–86. [Google Scholar] [CrossRef]
- Tao, Z.; Jin, Z.; Bai, X.; Zhao, H.; Dou, C.; Zhao, Y.; Wang, F.; Tao, C. SEAG: Structure-aware event causality generation. In Findings of the Association for Computational Linguistics, Proceedings of the ACL 2023, Toronto, ON, Canada, 9–14 July 2023; ACL: Stroudsburg, PA, USA, 2023; pp. 4631–4644. [Google Scholar] [CrossRef]
- Wan, Q.; Du, S.; Liu, Y.; Fang, J.; Wei, L.; Liu, S. Document-level relation extraction with hierarchical dependency tree and bridge path. Knowl. Based Syst. 2023, 278, 110873. [Google Scholar] [CrossRef]
- Jin, X.; Wang, X.; Luo, X.; Huang, S.; Gu, S. Inter-sentence and implicit causality extraction from Chinese corpus. In Proceedings of the PAKDD 2020. LNCS (LNAI), Singapore, 11–14 May 2020; Lauw, H.W., Wong, R.C.-W., Ntoulas, A., Lim, E.-P., Ng, S.-K., Pan, S.J., Eds.; Springer: Cham, Switzerland, 2020; Volume 12084, pp. 739–751. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).