PPRD-FL: Privacy-Preserving Federated Learning Based on Randomized Parameter Selection and Dynamic Local Differential Privacy
Abstract
1. Introduction
- We propose a novel randomized parameter selection strategy (R-PSS), which selects parameters for global aggregation based on their importance in the network, while incorporating controlled randomness to further enhance the process. This strategy effectively mitigates privacy budget dilution, improving the trade-off between privacy and model usability;
- We introduce a dynamic local differential privacy mechanism, where the standard deviation of the perturbation mechanism varies dynamically with global aggregation. This adaptive approach ensures robust privacy protection while minimizing noise, addressing the key privacy challenges in federated learning;
- We conducted a comprehensive privacy analysis to demonstrate the feasibility of the proposed approach. Compared to existing methods, the proposed approach achieves better privacy protection while preserving model performance.
2. Related Work
2.1. Privacy-Preserving Techniques in Federated Learning
2.2. Challenges and Applications in Local Differential Privacy
3. Preliminaries
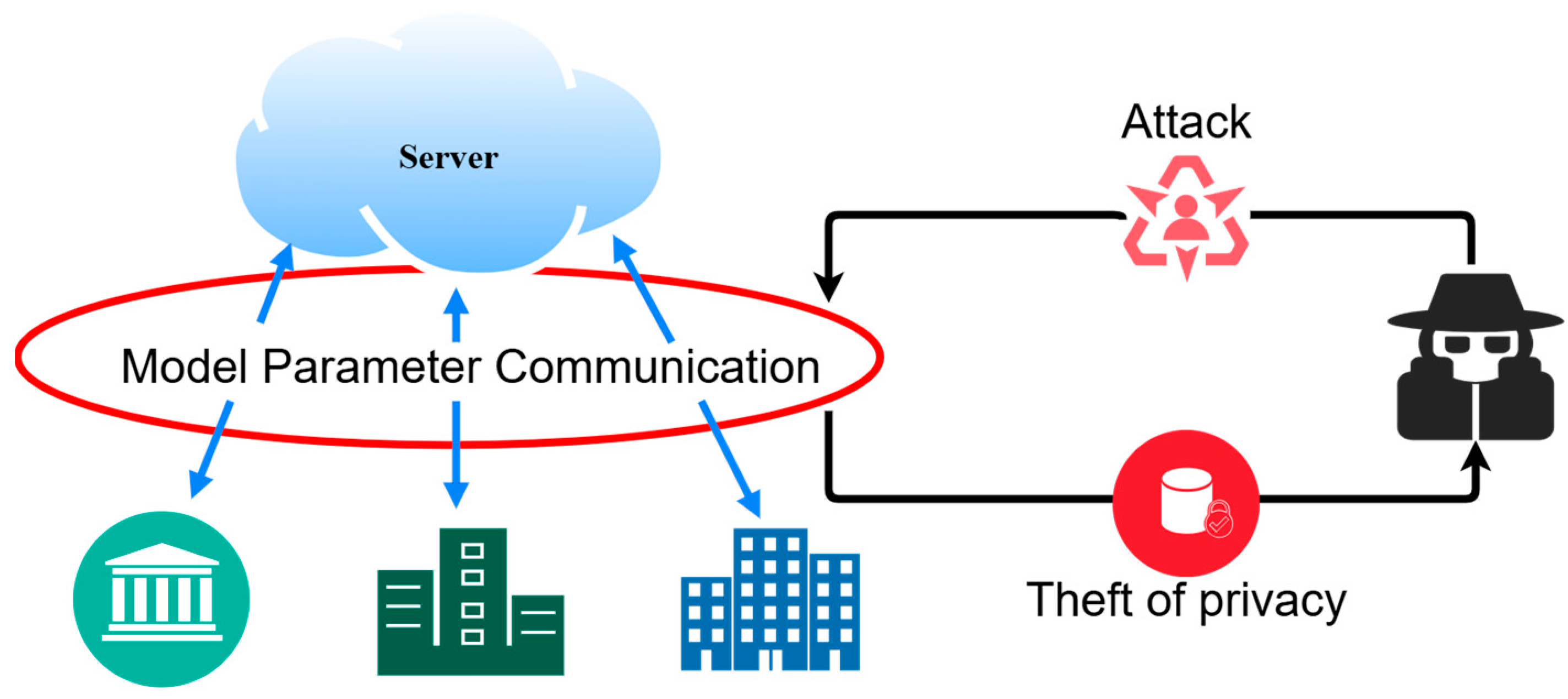
3.1. Federated Learning
3.2. Potential Threats
- An attacker can eavesdrop on the communication in the system to obtain sensitive data from participants;
- A compromised server may attempt to reconstruct participant data regarding the participants from the parameters uploaded by them;
- Participants controlled by attackers may try to extract private data about fellow participants from the perturbed data.
3.3. Local Differential Privacy
4. Method
4.1. PPRD-FL
| Algorithm 1 PPRD-FL |
| Input: the number of participants, the global model’s initial parameter , global training rounds , local iteration rounds of participants, the sum of all participant datasets, and the size of the participant’s local dataset, learning rate . |
| Output: global model parameters |
| 1 Parameter server generates global model weights ; |
| 2 The weight is broadcast to all participants; |
| 3 Global training: |
| 4 for global epoch do: |
| 5 for do: |
| 6 Accept global weight ; |
| 7 Perform rounds of local updates using Adam optimization; |
| 8 for epoch do |
| 9 Update the parameters of participant : |
| 10 ; |
| 11 Clip the parameters of participant : |
| 12 |
| 13 Apply R-PSS to filter parameters: ; |
| 14 Add dynamic LDP noise: ; |
| 15 Send the noised local weight to the server; |
| 16 End |
| 17 Global model aggregation: |
| 18 Collect the added noise weights for all participants; |
| 19 Calculate global model weights: |
| 20 |
| 21 End |
| 22 return |
4.2. Filtering Using Randomized Parameter Selection Strategy
| Algorithm 2 R-PSS |
| Input: the weight parameter of the participant , a filter threshold , near zero threshold |
| Output: Weight parameters after final filtering |
| 1 Initialize a with the same structure as ; |
| 2 Obtain the absolute values of all parameters of and arrange them in descending order to obtain a list ; |
| 3 Calculate the value which is the value of the last parameter in the top 50% of based on absolute values; |
| 4 for do: |
| 5 If , then: |
| 6 Mark as and add to the corresponding position of ; |
| 7 Else if and , then: |
| 8 Generate a random binary ; |
| 9 If , then: |
| 10 Mark as and add to the corresponding position of ; |
| 11 If , then: |
| 12 Do not process , and add to the corresponding position of ; |
| 13 Else if , then: |
| 14 Do not process , and add to the corresponding position of ; |
| 15 End |
| 16 Return |
4.3. Dynamic Perturbation Mechanism
5. Results
5.1. Experimental Setting
- MNIST Dataset: Consists of 70,000 grayscale images of hand-written digits ranging from 0 to 9, each with a resolution of 28 × 28 pixels. Among these, 60,000 images are used for training and 10,000 for testing. It is a widely adopted benchmark for evaluating image classification algorithms;
- Fashion-MNIST: The dataset contains 70,000 grayscale images across 10 fashion-related categories, such as clothing and shoes. The dataset is divided into 60,000 training images and 10,000 testing images, with each image sized at 28 × 28 pixels. It is designed as a more challenging and advanced alternative to the MNIST dataset;
- CIFAR-10 Dataset: The dataset includes 60,000 color images divided into 10 classes, with each image having a resolution of 32 × 32 pixels. It is split into 50,000 training images and 10,000 testing images. This dataset is widely used in deep learning for object recognition and image classification tasks.
5.2. Result Evaluation and Analysis
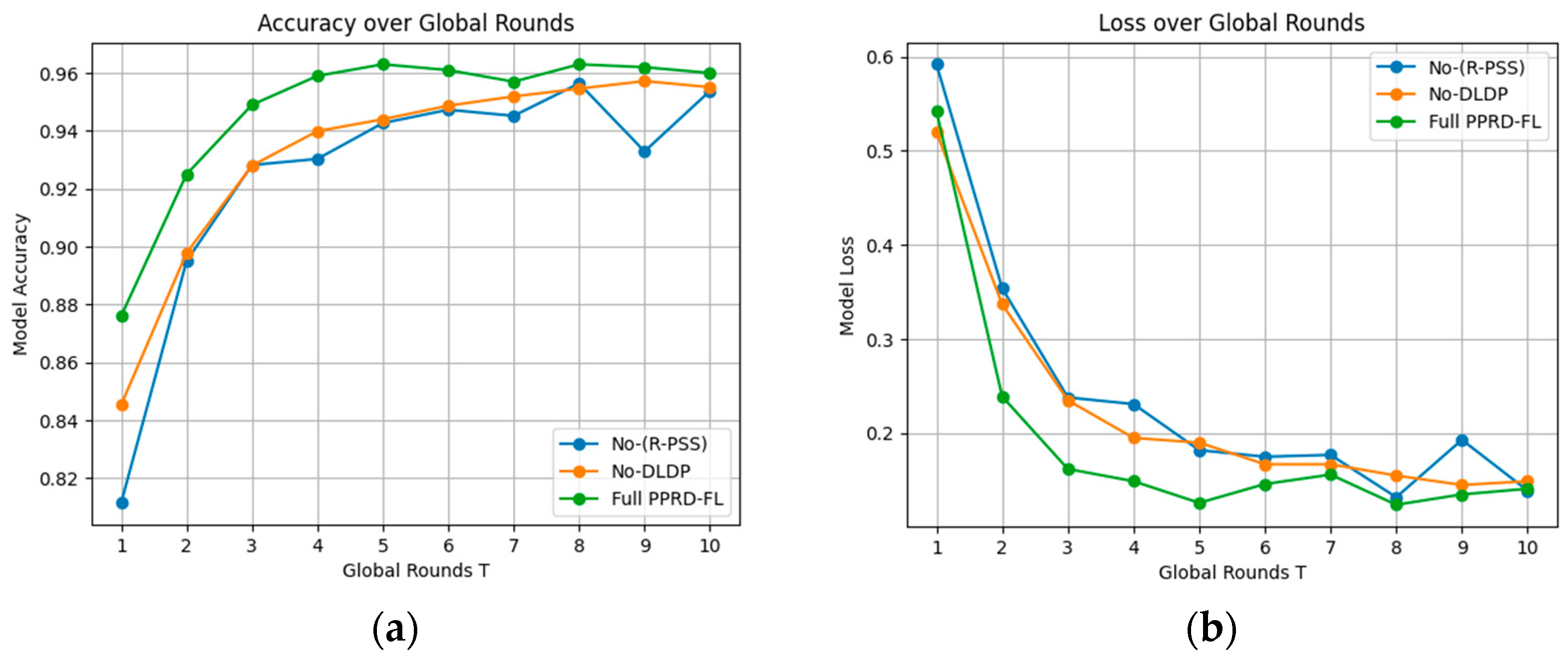
5.2.1. Component-Wise Performance Analysis of PPRD-FL
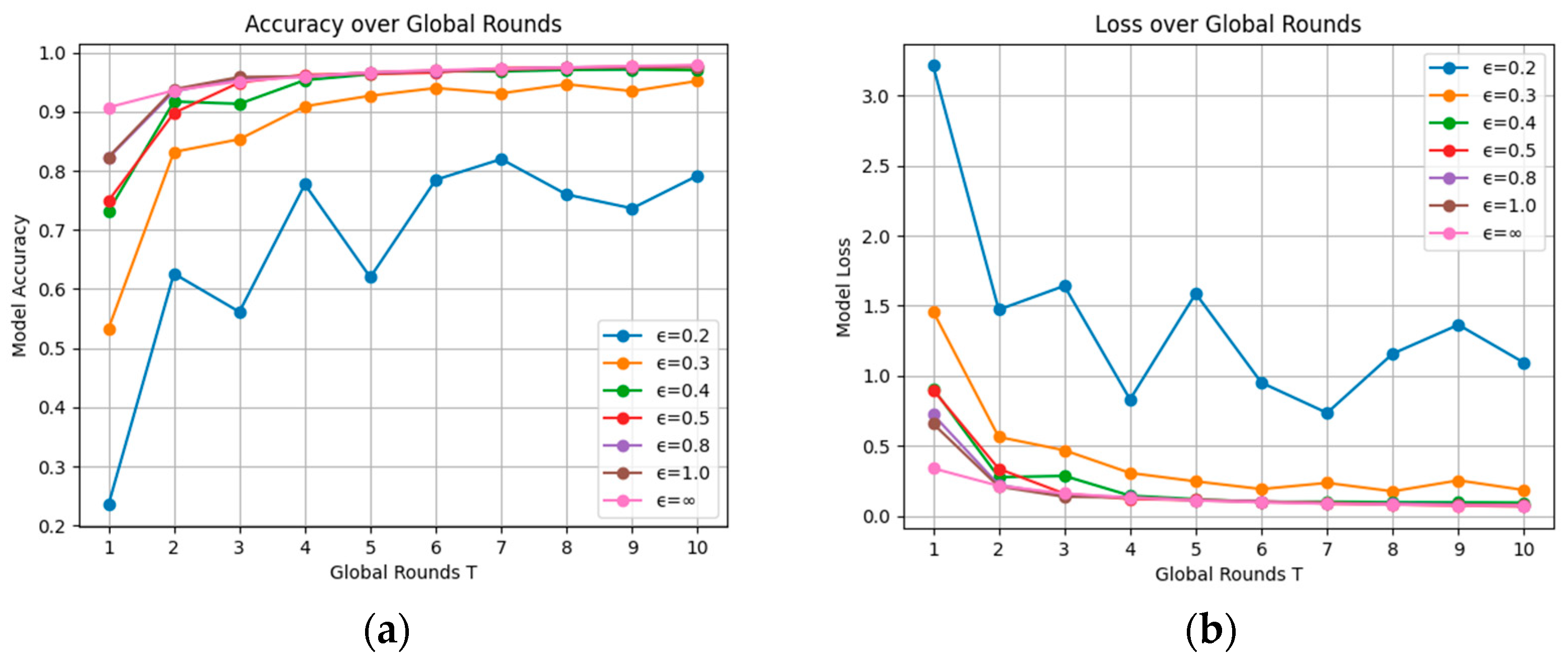
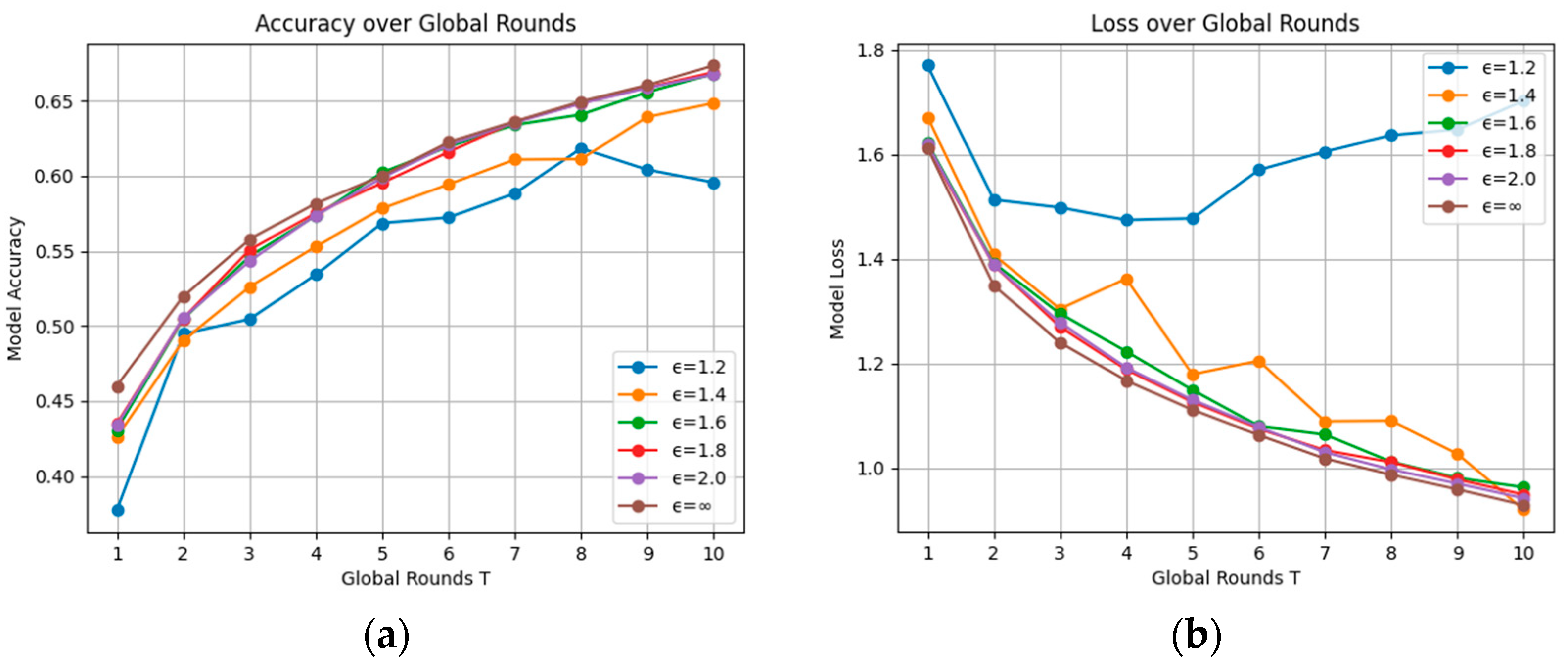
5.2.2. Evaluation on Privacy Budget
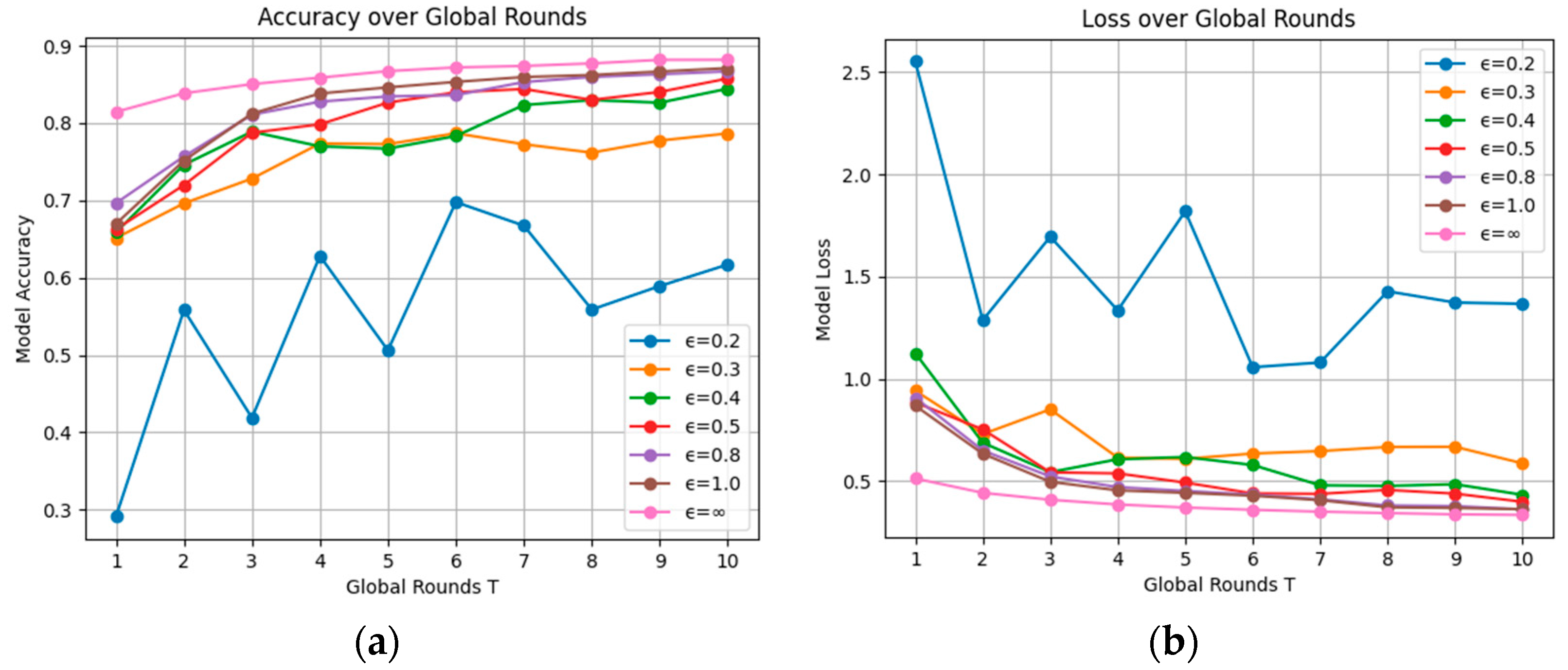
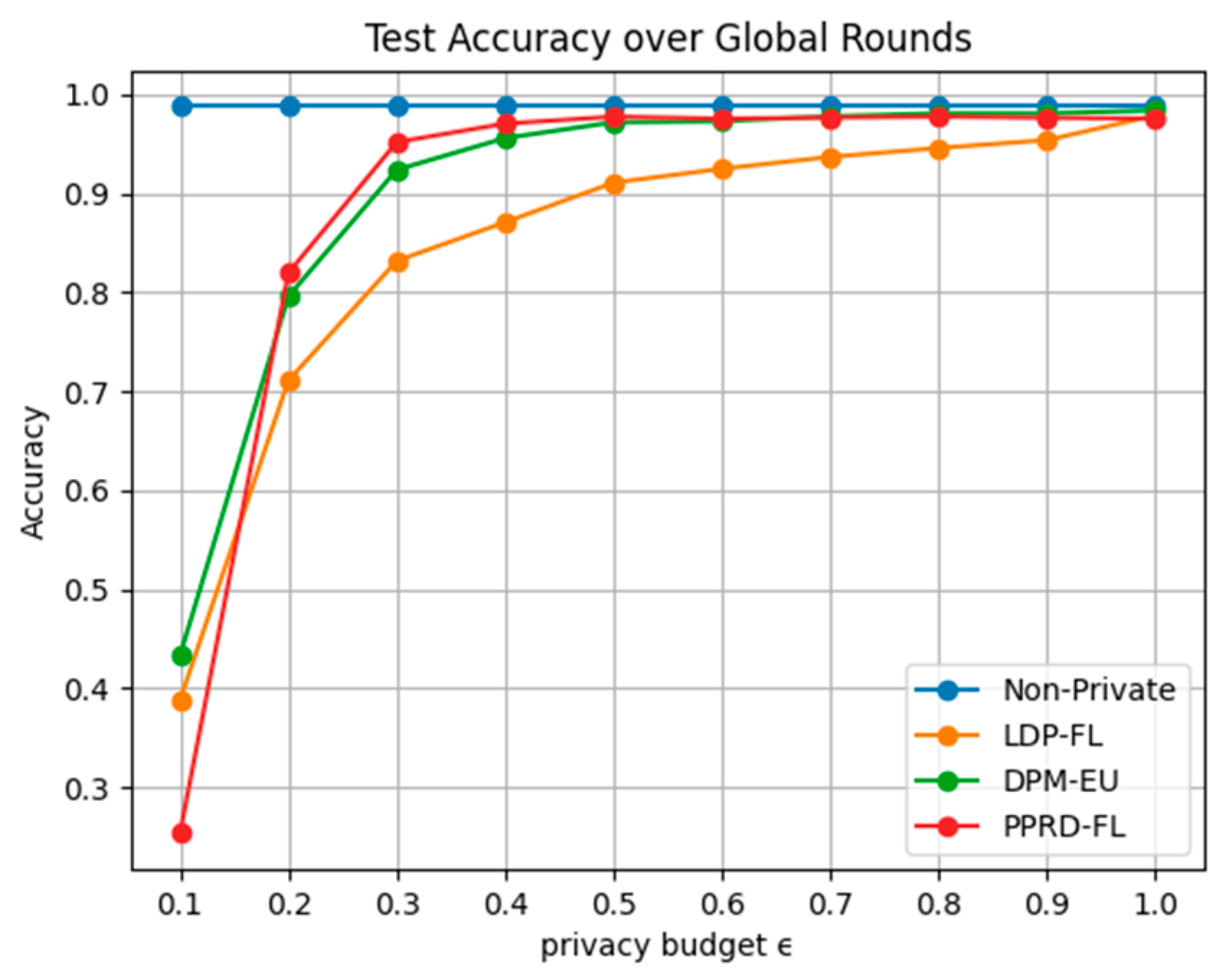
5.2.3. Model Performance Under Different Privacy Protection Schemes
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PPRD-FL | The privacy-preserving federated learning based on randomized parameter selection strategy and dynamic local differential privacy |
| FL | Federated learning |
| D-LDP | Dynamic local differential privacy |
| R-PSS | Randomized parameter selection strategy |
References
- Zhuang, Y.; Sun, X.; Li, Y.; Huai, J.; Hua, L.; Yang, X.; Cao, X.; Zhang, P.; Cao, Y.; Qi, L.; et al. Multi-sensor integrated navigation/positioning systems using data fusion: From analytics-based to learning-based approaches. Inf. Fusion 2023, 95, 62–90. [Google Scholar] [CrossRef]
- Liu, J.; Wu, G.; Luan, J.; Jiang, Z.; Liu, R.; Fan, X. HoLoCo: Holistic and local contrastive learning network for multi-exposure image fusion. Inf. Fusion 2023, 95, 237–249. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.y. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, PMLR 2017, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. Available online: https://proceedings.mlr.press/v54/mcmahan17a?ref=https://githubhelp.com (accessed on 3 March 2023).
- Phong, L.T.; Aono, Y.; Hayashi, T.; Wang, L.; Moriai, H. Privacy-preserving deep learning: Revisited and enhanced. In Proceedings of the Applications and Techniques in Information Security: 8th International Conference, ATIS 2017, Auckland, New Zealand, 6–7 July 2017; Proceedings. Springer: Singapore, 2017; pp. 100–110. Available online: https://link.springer.com/chapter/10.1007/978-981-10-5421-1_9 (accessed on 15 October 2023).
- Moshawrab, M.; Adda, M.; Bouzouane, A.; Ibrahim, H.; Raad, A. Securing Federated Learning: Approaches, Mechanisms and Opportunities. Electronics 2024, 13, 3675. [Google Scholar] [CrossRef]
- Nasr, M.; Shokri, R.; Houmansadr, A. Comprehensive privacy analysis of deep learning: Passive and active white-box inference attacks against centralized and federated learning. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP). IEEE, San Francisco, CA, USA, 19–23 May 2019; pp. 739–753. Available online: https://ieeexplore.ieee.org/abstract/document/8835245 (accessed on 2 March 2024).
- Sagar, R.; Jhaveri, R.; Borrego, C. Applications in security and evasions in machine learning: A survey. Electronics 2020, 9, 97. [Google Scholar] [CrossRef]
- Wei, W.; Liu, L.; Loper, M.; Chow, K.-H.; Gursoy, M.E.; Truex, S.; Wu, Y. A framework for evaluating gradient leakage attacks in federated learning. arXiv 2020, arXiv:2004.10397. [Google Scholar]
- Shokri, R.; Stronati, M.; Song, C.; Shmatikov, V. Membership inference attacks against machine learning models. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 3–18. Available online: https://ieeexplore.ieee.org/abstract/document/7958568 (accessed on 1 November 2023).
- Song, M.; Wang, Z.; Zhang, Z.; Song, Y.; Wang, Q.; Ren, J.; Qi, H. Analyzing user-level privacy attack against federated learning. IEEE J. Sel. Areas Commun. 2020, 38, 2430–2444. [Google Scholar] [CrossRef]
- Phong, L.T.; Aono, Y.; Hayashi, T.; Wang, L.; Moriai, S. Privacy-preserving deep learning via additively homomorphic encryption. IEEE Trans. Inf. Forensics Secur. 2017, 13, 1333–1345. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Xie, J.; Hao, T. Improved Design and Application of Security Federation Algorithm. Electronics 2023, 12, 1375. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, H. SPM-FL: A Federated Learning Privacy-Protection Mechanism Based on Local Differential Privacy. Electronics 2024, 13, 4091. [Google Scholar] [CrossRef]
- Arachchige, P.C.M.; Bertok, P.; Khalil, I.; Liu, D.; Camtepe, S.; Atiquzzaman, M. Local differential privacy for deep learning. IEEE Internet Things J. 2019, 7, 5827–5842. [Google Scholar] [CrossRef]
- Truex, S.; Liu, L.; Chow, K.-H.; Gursoy, M.E.; Wei, W. LDP-Fed: Federated learning with local differential privacy. In Proceedings of the Third ACM International Workshop on Edge Systems, Analytics and Networking, Heraklion, Greece, 27 April 2020; pp. 61–66. Available online: https://dl.acm.org/doi/abs/10.1145/3378679.3394533 (accessed on 26 September 2024).
- Frisk, O.; Dormann, F.; Lillelund, C.M.; Pedersen, C.F. Super-convergence and differential privacy: Training faster with better privacy guarantees. In Proceedings of the 2021 55th Annual Conference on Information Sciences and Systems (CISS). IEEE, Baltimore, MD, USA, 24–26 March 2021; pp. 1–6. Available online: https://ieeexplore.ieee.org/abstract/document/9400274 (accessed on 18 November 2023).
- Cheng, A.; Wang, P.; Zhang, X.S.; Cheng, J. Differentially private federated learning with local regularization and sparsification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 10122–10131. Available online: https://openaccess.thecvf.com/content/CVPR2022/html/Cheng_Differentially_Private_Federated_Learning_With_Local_Regularization_and_Sparsification_CVPR_2022_paper.html (accessed on 16 April 2024).
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3November 2017; pp. 1175–1191. Available online: https://dl.acm.org/doi/abs/10.1145/3133956.3133982 (accessed on 26 February 2023).
- Zhang, C.; Li, S.; Xia, J.; Wang, W. {BatchCrypt}: Efficient homomorphic encryption for {Cross-Silo} federated learning. In Proceedings of the 2020 USENIX Annual Technical Conference (USENIX ATC 20), Virtual, 15–17 July 2020; pp. 493–506. Available online: https://www.usenix.org/conference/atc20/presentation/zhang-chengliang (accessed on 15 August 2023).
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially private federated learning: A client level perspective. arXiv 2017, arXiv:1712.07557. [Google Scholar]
- Wang, Y.; Zhang, A.; Wu, S.; Yu, S. VOSA: Verifiable and oblivious secure aggregation for privacy-preserving federated learning. IEEE Trans. Dependable Secur. Comput. 2022, 20, 3601–3616. [Google Scholar] [CrossRef]
- Xu, G.; Li, H.; Zhang, Y.; Xu, S.; Ning, J.; Deng, R. Privacy-preserving federated deep learning with irregular users. IEEE Trans. Dependable Secur. Comput. 2020, 19, 1364–1381. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, B.; Zhang, Z. PDLHR: Privacy-preserving deep learning model with homomorphic re-encryption in robot system. IEEE Syst. J. 2021, 16, 2032–2043. [Google Scholar] [CrossRef]
- Guo, S.; Yang, J.; Long, S.; Wang, X.; Liu, G. Federated learning with differential privacy via fast Fourier transform for tighter-efficient combining. Sci. Rep. 2024, 14, 26770. [Google Scholar]
- Shen, X.; Liu, Y.; Zhang, Z. Performance-enhanced federated learning with differential privacy for internet of things. IEEE Internet Things J. 2022, 9, 24079–24094. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Yang, M.; Wang, T.; Wang, N.; Lyu, L.; Niyato, D.; Lam, K.-Y. Local differential privacy-based federated learning for internet of things. IEEE Internet Things J. 2020, 8, 8836–8853. [Google Scholar] [CrossRef]
- Liu, R.; Cao, Y.; Yoshikawa, M.; Chen, H. Fedsel: Federated sgd under local differential privacy with top-k dimension selection. In Proceedings of the Database Systems for Advanced Applications: 25th International Conference, DASFAA 2020, Jeju, Republic of Korea, 24–27 September 2020; Proceedings, Part I 25. Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 485–501. Available online: https://link.springer.com/chapter/10.1007/978-3-030-59410-7_33 (accessed on 10 July 2024).
- Chen, Q.; Wang, H.; Wang, Z.; Chen, J.; Yan, H.; Lin, X. Lldp: A layer-wise local differential privacy in federated learning. In Proceedings of the 2022 IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Wuhan, China, 9–11 December 2022; pp. 631–637. Available online: https://ieeexplore.ieee.org/abstract/document/10063630 (accessed on 22 July 2023).
- Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H.H.; Farokhi, F.; Jin, S.; Quek, T.Q.S.; Poor, H.V. Federated learning with differential privacy: Algorithms and performance analysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3454–3469. [Google Scholar] [CrossRef]
- Shin, H.; Kim, S.; Shin, J.; Xiao, X. Privacy enhanced matrix factorization for recommendation with local differential privacy. IEEE Trans. Knowl. Data Eng. 2018, 30, 1770–1782. [Google Scholar] [CrossRef]
- Sun, L.; Lyu, L. Federated model distillation with noise-free differential privacy. arXiv 2020, arXiv:2009.05537. [Google Scholar]
- Sun, L.; Qian, J.; Chen, X. LDP-FL: Practical private aggregation in federated learning with local differential privacy. arXiv 2020, arXiv:2007.15789. [Google Scholar]
- Song, S.; Du, S.; Song, Y.; Zhu, Y. Communication-Efficient and Private Federated Learning with Adaptive Sparsity-Based Pruning on Edge Computing. Electronics 2024, 13, 3435. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Y.; Jiang, H.; Zhao, Z. Ppefl: Privacy-preserving edge federated learning with local differential privacy. IEEE Internet Things J. 2023, 10, 15488–15500. [Google Scholar] [CrossRef]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy: A survey of results. In Proceedings of the International Conference on Theory and Applications of Models of Computation, Xi’an, China, 25–29 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–19. Available online: https://link.springer.com/chapter/10.1007/978-3-540-79228-4_1 (accessed on 30 June 2023).
- Bhowmick, A.; Duchi, J.; Freudiger, J.; Kapoor, G.; Rogers, R. Protection against reconstruction and its applications in private federated learning. arXiv 2018, arXiv:1812.00984. [Google Scholar]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends® Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Rashid, T. Make Your Own Neural Network. 2016. Available online: https://github.com/makeyourownneuralnetwork/makeyourownneuralnetwork?tab=readme-ov-file (accessed on 22 June 2023).
- Ross, S.M. Introduction to Probability and Statistics for Engineers and Scientists, 4th ed.; Academic Press: San Diego, CA, USA, 2009; 141p. [Google Scholar]

| Symbol | Definitions |
|---|---|
| The number of participants | |
| The i-th participant | |
| The dataset differing by one element | |
| The dataset of the i-th participant | |
| The local loss function of the i-th participant | |
| Global loss function | |
| The global model parameters at the t-th iteration | |
| The local model parameters of the i-th participant | |
| Privacy budget | |
| Maximum allowable probability of privacy leakage | |
| Sensitivity | |
| Parameter Clipping Threshold |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Guo, R.; Zhu, J. PPRD-FL: Privacy-Preserving Federated Learning Based on Randomized Parameter Selection and Dynamic Local Differential Privacy. Electronics 2025, 14, 990. https://doi.org/10.3390/electronics14050990
Feng J, Guo R, Zhu J. PPRD-FL: Privacy-Preserving Federated Learning Based on Randomized Parameter Selection and Dynamic Local Differential Privacy. Electronics. 2025; 14(5):990. https://doi.org/10.3390/electronics14050990
Chicago/Turabian StyleFeng, Jianlong, Rongxin Guo, and Jianqing Zhu. 2025. "PPRD-FL: Privacy-Preserving Federated Learning Based on Randomized Parameter Selection and Dynamic Local Differential Privacy" Electronics 14, no. 5: 990. https://doi.org/10.3390/electronics14050990
APA StyleFeng, J., Guo, R., & Zhu, J. (2025). PPRD-FL: Privacy-Preserving Federated Learning Based on Randomized Parameter Selection and Dynamic Local Differential Privacy. Electronics, 14(5), 990. https://doi.org/10.3390/electronics14050990






