Abstract
Inspired by the gender transition behavior seen in hawkfish, this paper introduces the HawkFish optimization algorithm, a nature-inspired optimization technique modeled on the unique gender transition behavior of hawkfish. By leveraging this biological phenomenon, the proposed method addresses optimization problems through dual fitness functions, combining an original and inverse fitness function to drive search space exploration while avoiding local minima. The algorithm’s performance is rigorously evaluated against benchmark problems, including the CEC/GECCO 2019 suite, and applied to real-world engineering challenges like welded beam and tension/compression spring design. The proposed method consistently outperforms existing algorithms in terms of convergence rate, accuracy, and solution quality. The results underscore the algorithm’s efficiency in exploring unknown search spaces and solving complex optimization tasks, making it a promising tool for various domains requiring high precision and optimization efficiency.
1. Introduction
The concept of “optimization” is employed in various subfields of intelligent computation, where it is known by different names such as global minimum, global maximum, least cost, high performance, and others. The specific terminology used depends on the constraints of the problem being addressed and the desired outcome derived from those constraints, which is typically represented by the objective function or fitness functions of the problem [1]. An optimization algorithm is employed to solve a problem requiring optimal solutions. Optimization issues are often distinguished by their nonlinearity and the intricate nature of their surroundings. Stochastic and deterministic approaches are the primary subdivisions within the realm of optimization algorithms [2]. Traditional deterministic algorithms include a range of subjects, including gradient-based algorithms and quadratic programming. Currently, there are heuristic, metaheuristic, and hyper-heuristic algorithms that are used in many applications. These algorithms are categorized as stochastic evolutionary algorithms, and heuristics are generally tailored to address specific problem contexts, offering efficient solutions within those constraints. Metaheuristics, on the other hand, are designed for broader applicability across a wide range of scenarios. While heuristics can be effective for particular problems, their utility often diminishes when applied to different contexts [3]. During the period spanning from 1960 to 1990, the field of stochastic techniques saw the emergence of two primary categories, namely metaheuristics and classical heuristics. One notable distinction between heuristics and metaheuristics lies in their respective scopes of applicability [4,5]. Heuristics are primarily designed to address particular circumstances, whereas metaheuristics possess the capacity to be used over a broader spectrum of scenarios, it should be noted that although heuristics may demonstrate efficacy in resolving a particular issue, their applicability may not extend to other contexts. The objective of the study conducted by [6] was to provide insight into the various methodologies used in addressing limitations, the significance of metaheuristic algorithms within this domain, and the recommended approaches for categorizing metaheuristics. This study presents a comprehensive examination of many noteworthy instances of metaheuristic algorithms and their prospective implementations [6]. In their publication, ref. [7] introduced an innovative genetic methodology for the purpose of scheduling repeated transcranial magnetic stimulation (rTMS) sessions, while metaheuristics are pivotal in solving fractional-order nonlinear systems, which are notoriously difficult to handle due to their unique memory and hereditary properties. The List Scheduling Wildcard Tournament Genetic Algorithm incorporates a unique approach for determining winners, in conjunction with a heuristic technique for initializing the population. The result yields a more accurate forecast of the victor (LSWT-GA) through the process of recombining. Metaheuristics, while effective in exploring such complex spaces, can suffer from slow convergence rates, sensitivity to parameter tuning, and potential stagnation in local optima [8]. Additionally, the initialization of populations and the stochastic nature of recombination and selection processes can introduce variability in results, making it difficult to ensure consistency and reliability in achieving global optimal solutions [9].
In their study, ref. [10] investigated the principles of chaos theory and its potential use in optimizing the Whale Optimization Algorithm (WOA) [10]. The suggested approaches of the Chaotic Whale Optimization Algorithm (CWOA), use a diverse range of chaotic maps to effectively optimize the key parameter of the WOA. This approach proves valuable in balancing the exploration and exploitation aspects of the algorithm. In their study, ref. [11] used six prominent mathematical functions, such as the rotated hyper-ellipsoid function, as test scenarios to evaluate the effectiveness of the Quantum Dolphin Swarm Algorithm (QDSA). The results indicate that the QDSA has the capability to assist in the exploration for the most favorable solution to functions of significant magnitude [11]. There are metaheuristic algorithms that are especially tailored to address issues characterized by two fitness functions or, in a broader sense, multi-objective optimization problems. The Non-Dominated Sorting Genetic Algorithm II (NSGA-II), proposed in [12], is a widely used algorithm in the field of evolutionary computation [12]. One widely used evolutionary method that has been specifically developed for addressing multi-objective optimization situations. The methodology used offers a non-dominated sorting technique to effectively manage a varied collection of solutions. Additionally, it incorporates elitism as a means of safeguarding the most optimal answers discovered during the search process. However, NSGA-II has many limitations, one of which is scalability. It may not exhibit optimal performance when dealing with situations that include a substantial number of goals. This is mostly attributed to the heightened intricacy associated with the process of non-dominated sorting. The maintenance of variety is a crucial aspect in evolutionary algorithms. While NSGA-II incorporates the usage of crowding distance as a means to preserve diversity, it may not prove to be entirely effective for situations characterized by intricate Pareto fronts. The computational difficulty of non-dominated sorting and crowding distance calculation may provide significant challenges when dealing with high population numbers [12]. Multi-Objective Particle Swarm Optimization (MOPSO) is a variant of the conventional particle swarm optimization (PSO) technique that has been developed to address multi-objective optimization issues [13]. The methodology incorporates both a global best strategy and a personal best strategy, in conjunction with an external archive, for the purpose of preserving non-dominated answers. Several limitations may be identified: The convergence of MOPSO to the genuine Pareto front may be hindered in some scenarios owing to the inherent characteristics of particle swarm optimization. The Strength Pareto Evolutionary Algorithm 2 (SPEA2) [14] is a commonly used evolutionary algorithm utilized for multi-objective optimization. It employs a fitness assignment based on strength and employs a meticulous elitism method to preserve a varied collection of non-dominated solutions [14]. The primary limitations associated with the use of the SPEA2 are as follows: The topic of discussion is computational complexity. The computational cost of the strength-based fitness assignment and the fine-grained elitism technique may be significant when applied to populations of considerable size. This limitation arises from the intricate nature of preserving a varied collection of non-dominated solutions. The Multi-Objective Evolutionary Algorithm Based on Decomposition (MOEA/D) [15] is a computational approach. The algorithm presented in this study employs a methodology that involves breaking down the multi-objective optimization issue into a collection of single-objective subproblems. These subproblems are then addressed concurrently via the use of evolutionary optimization techniques. The Tchebycheff technique is used to estimate the Pareto front. Despite the presence of some flaws, the MOEA/D may be identified as a viable approach. The decomposition strategy is a method used to break down complex problems into smaller, more manageable components. The selection of a decomposition technique may have a substantial influence on the performance of an algorithm, and its applicability may vary depending on the nature of the task at hand. The Multi-Objective Simulated Annealing (MOSA) technique, as described in [16], is a modified version of the conventional simulated annealing process that is specifically designed to address multi-objective situations. While traditional swarm intelligence algorithms, such as (PSO), (GA), and (DE), have demonstrated significant potential in solving optimization problems, they often face challenges in maintaining a balance between exploration and exploitation, as well as ensuring diversity to avoid premature convergence. Recent advancements have introduced multi-objective fitness functions and clustering mechanisms, but these are either static or lack biologically inspired adaptiveness. For example, in “Knacks of Evolutionary Mating Heuristics for Renewable Energy Source-Based Power Systems Signal Harmonics Estimation” [17], metaheuristic techniques are employed to effectively estimate harmonics in power systems driven by renewable energy sources. These systems often face challenges such as fluctuating power inputs and complex signal behaviors due to the nonlinear dynamics of renewable energy sources like solar and wind. By leveraging evolutionary heuristics, this approach ensures the accurate estimation of harmonics, thereby enhancing power quality and system stability. Similarly, in [18] the authors presented a gazelle optimization algorithm, inspired by the adaptive and evasive behaviors of gazelles in nature, provides an innovative framework for optimizing such systems. This is particularly valuable in applications like electrically stimulated muscle modeling, where precise and efficient modeling of fractional-order dynamics is essential for understanding and improving muscle stimulation technologies, Table 1 presents a comparison of the methods stated above:

Table 1.
A summary of multi-objective metaheuristic algorithms with two or more objective functions discussed above.
Conventional swarm intelligence algorithms frequently lack methods to adequately balance exploration and exploitation, resulting in difficulties in addressing complicated optimization problems with varied search areas [18]. Although several algorithms integrate multi-objective fitness functions, they infrequently amalgamate them with dynamic population clustering and adaptive behaviors [19]. Moreover, current methodologies fail to include distinct responsibilities and sensory capacities, which might greatly enhance variety and adaptation [20]. The biological phenomena of hawkfish gender change provides a convincing paradigm for overcoming these limits. Nevertheless, no existing technique completely utilizes this adaptive characteristic with dynamic grouping and fluctuating visual scopes to improve optimization efficiency; therefore, the objectives of this paper are as follows:
- To create an algorithm inspired by the adaptive gender transition behavior of hawkfish, integrating dual fitness functions, dynamic clustering, and differentiated visual scopes.
- To improve the balance between exploration and exploitation in solving complex optimization problems with diverse landscapes.
- To incorporate dynamic clustering mechanisms to maintain population diversity and prevent premature convergence.
- To utilize the distinct behaviors and visual scopes of male and female fish to optimize the search process effectively.
Despite the concerns raised in recent studies about introducing new metaphors in optimization algorithms [4], a case is made in this paper to argue that metaphors themselves are not inherently problematic. Instead, the critical determinant of a method’s value lies in the novel mechanisms, scientific contributions, and practical benefits that it brings to the field of optimization. As ref. [5] noted, natural metaphors can serve as a source of creative inspiration, provided the resulting algorithm introduces distinct, meaningful innovations and demonstrates clear advantages in solving complex optimization problems. Therefore, this article advocates for a balanced approach that values both inspiration from natural metaphors and the necessity for meaningful advancements in optimization techniques. The proposed method directly addresses some limitations of similar metaheuristic methods, based on the limitations observed in existing metaheuristic algorithms, and the proposed method seeks to directly address the following gaps:
- Several algorithms, such as MOPSO and Gazelle Optimization, exhibit convergence issues, particularly in high-dimensional or complex landscapes, leading to suboptimal solutions.
- Many approaches, including MOEA/D and SPEA2, rely on fixed or sensitive parameter settings that require extensive tuning and may not generalize well to diverse optimization scenarios.
- Algorithms like QDSA and Knacks of Evolutionary Mating face difficulties scaling to large objective spaces or adapting to highly dynamic optimization environments, limiting their effectiveness in real-world applications.
- Insufficient mechanisms for maintaining diversity in Pareto fronts, as noted in QDSA, MOPSO, and MOSA, reduce their ability to explore the solution space effectively and avoid stagnation.
This method aims to overcome these challenges by incorporating dynamic parameter adaptation, enhanced diversity preservation strategies, and scalable mechanisms tailored for complex and dynamic optimization problems. The innovative mechanisms introduced in the proposed scheme make it better suited for these challenges, as demonstrated in the experiments to follow, the proposed method emphasizes three key contributions of the proposed scheme that differentiate it from standard metaheuristic algorithms:
- Dynamic Cluster Formation and Update
The proposed HawkFish optimization algorithm introduces a dynamic clustering mechanism inspired by the hawkfish’s unique gender transition behavior. Unlike standard metaheuristic algorithms such as standard GA, where the population dynamics are fixed or static, the proposed method dynamically adjusts clusters based on real-time feedback from the fitness landscape. This ensures better exploration of the solution space and reduces premature convergence, a common limitation in metaheuristics.
- b.
- Fitness Function Bending
The dual fitness functions in the proposed method, modeled after the gender transition phases in hawkfish, provide a novel mechanism to balance exploration and exploitation. This is distinct from traditional fitness calculations in standard metaheuristic algorithms, where a single objective function often dominates. The bending mechanism adapts based on the complexity of problems, allowing the algorithm to better handle multimodal and high-dimensional optimization problems.
- c.
- Dynamic Visual Scope
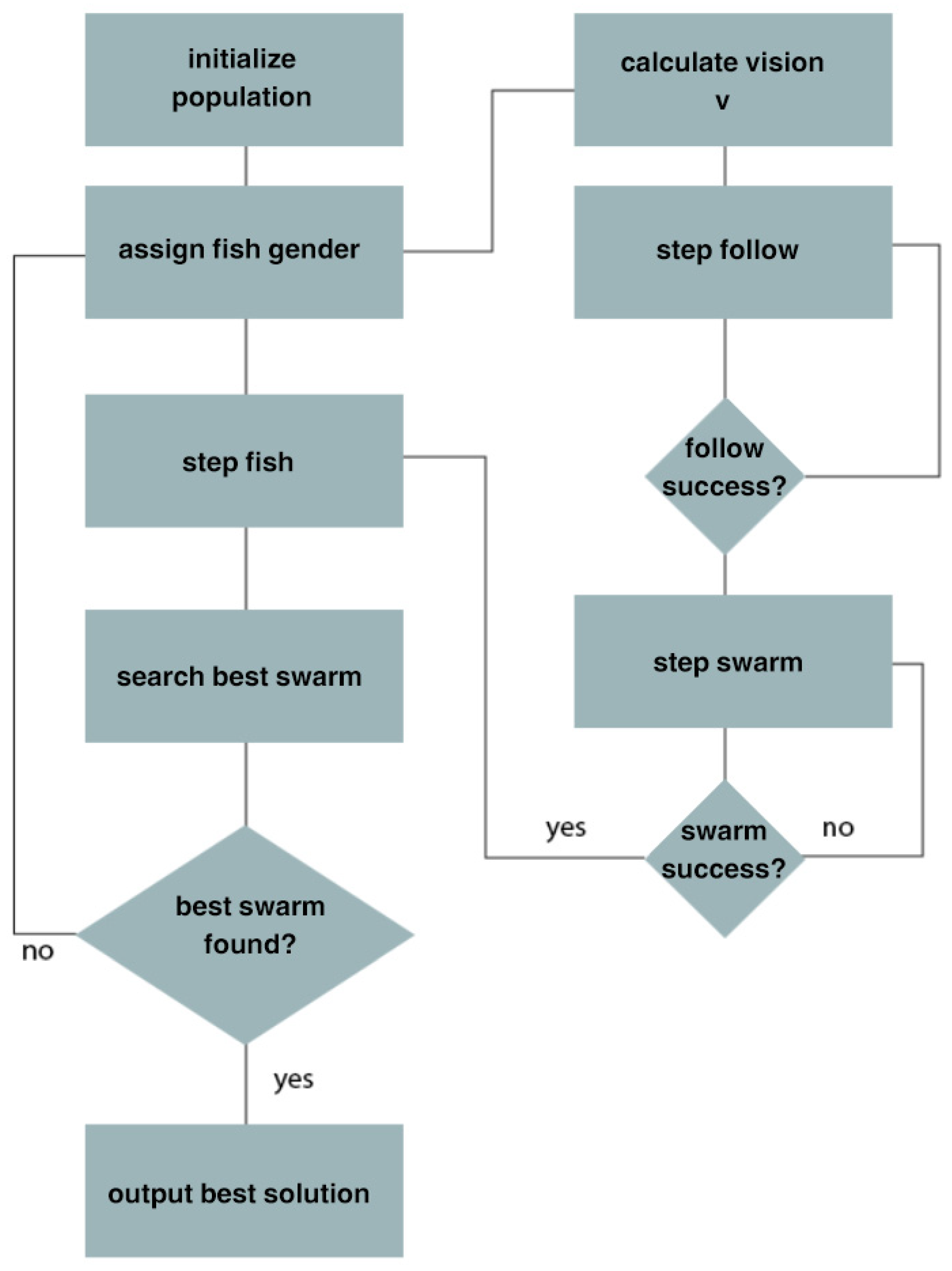
Inspired by hawkfish behavior, the algorithm incorporates a dynamic visual scope mechanism that adjusts search parameters based on proximity to local optima. This feature ensures fine-tuned exploitation near promising solutions while maintaining broad exploration in less explored areas of the search space. This research presents a unique optimization technique that draws inspiration from the phenomenon of gender bending seen in hawkfish. The issue at hand is addressed by using a dual fitness function scheme, whereby two distinct fitness functions are used (Figure 1). The combination of these two fitness functions is designed to incentivize the algorithm to explore diverse areas within the search space while simultaneously discouraging convergence towards local minima. A fitness function may be characterized as a solution that is diametrically opposed to the original solution inside the search space, hence decreasing the required search time for the original solution, Figure 1 outlines the proposed swarming action using two distinct fitness functions.
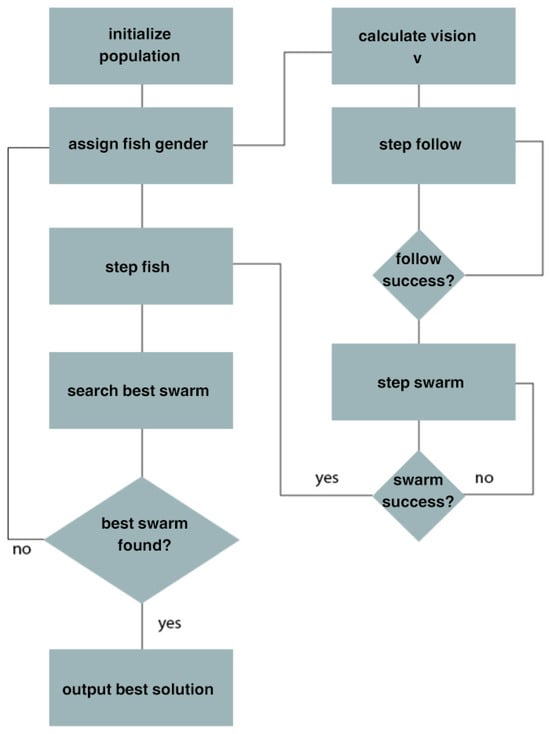
Figure 1.
Outline of the proposed swarming action.
The subsequent sections of this article are organized in the following manner: Section 2 of the document introduces the conceptual underpinnings of the proposed algorithm and presents a comprehensive overview of its procedural components. The assessment of the proposed algorithm is conducted, and the obtained experimental findings are thoroughly evaluated and contrasted in Section 3. Section 4 addresses benchmark optimization difficulties and presents a detailed review of the proposed method. Finally, Section 5 provides the conclusion and explores possible directions for further advancement.
2. Proposed Method
2.1. Hawkfish Gender Bending
Hawkfish are a collective of marine fish species that have the remarkable ability to undergo gender transformation during the course of their lifespan [21]. The organisms in question exhibit protogynous hermaphroditism, a reproductive strategy characterized by an initial female phase followed by the potential for transitioning into the male phase. The phenomenon of gender transition in hawkfish is intricately linked to their reproductive strategy. In some hawkfish species, the male population exhibits a lower frequency compared to females, hence posing challenges in their pursuit of suitable mating partners. Certain female hawkfish have the ability to undergo gender transition from female to male in situations when a male is not present or when there is an imbalance in the male-to-female ratio, hence enhancing their reproductive opportunities [22]. The phenomenon of gender transition in hawkfish is instigated by a multitude of elements, including changes in both social and environmental circumstances, such as the abundance of sustenance, the existence of predators, and the accessibility of potential mates. When a female hawkfish undergoes a gender transition, it experiences a sequence of physiological transformations, including the development of male reproductive structures and the regression of female reproductive structures [23]. Hawkfish exhibit a unique phenomenon of gender change in response to environmental stimuli, notably the presence or absence of food resources. In instances when a hawkfish experiences prolonged food scarcity, it may undergo a gender transition from female to male as a means to enhance its reproductive prospects. The mathematical equations presented below may be used to explain the process of gender transition in hawkfish.
Let the variable p(t) represent the percentage of females in the population at time t, whereas the variable q(t) represents the proportion of males:
Initially, we assume that all hawkfish are female, so p(0) = 1 and q(0) = 0.
Let d(t) be the availability of food at time t, such that d(t) > 0 represents an environment with sufficient food, and d(t) = 0 represent an environment without food.
We can model the rate of change in the proportion of females as follows:
where a is a constant that represents the rate of gender change. This equation states that the rate of change in the proportion of females is proportional to the current proportion of females, the availability of food, and a constant factor that represents the rate of gender change.
Similarly, we can model the rate of change in the proportion of males as follows:
The aforementioned equation posits that the derivative of the percentage of males is directly proportional to the current proportion of females, the availability of food, and a constant component that signifies the pace of gender transition.
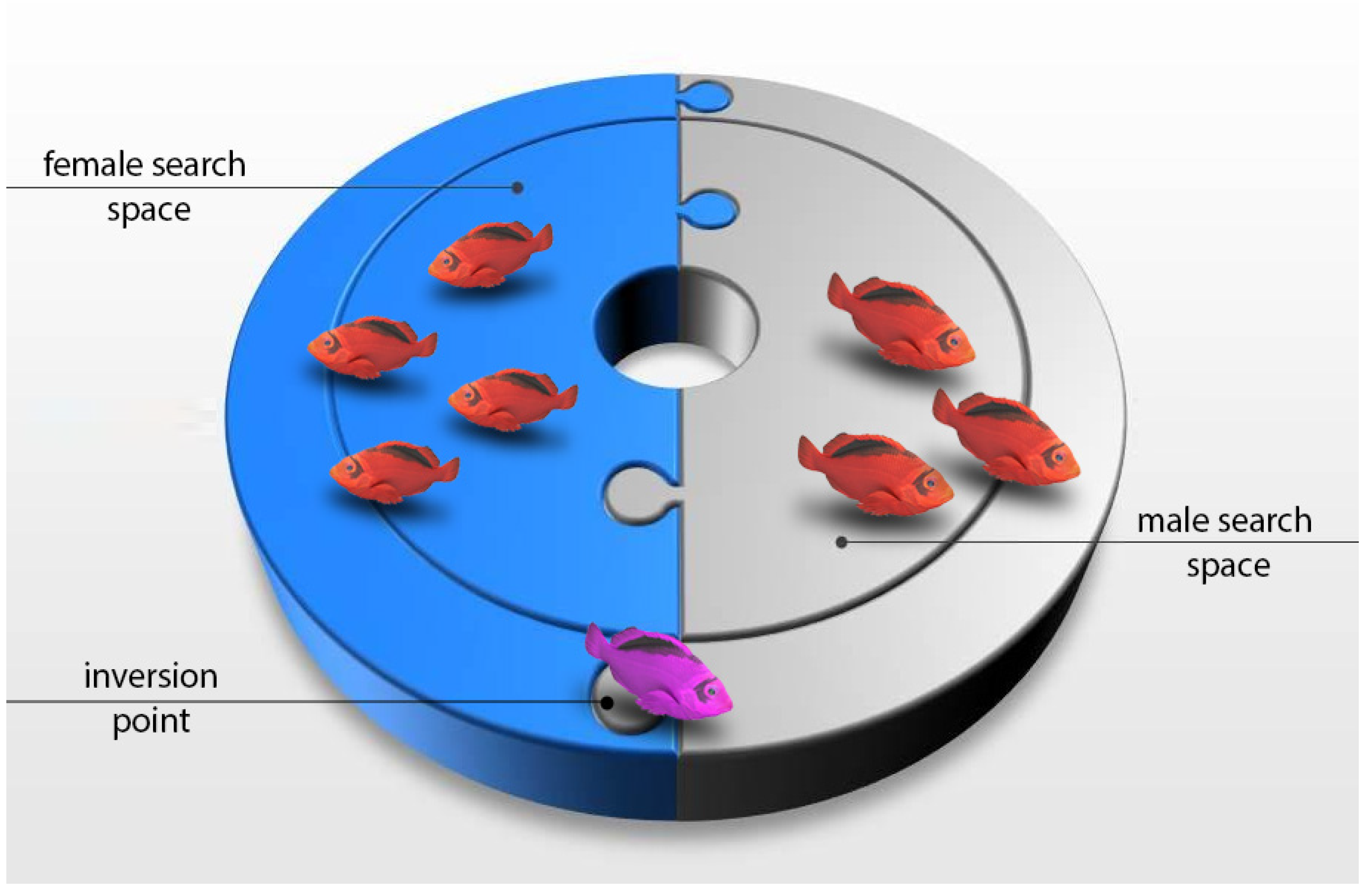
In the presence of an ample food supply (d(t) > 0), the hawkfish population will reach an equilibrium state characterized by a fixed ratio of females to males, denoted as p(t) and q(t), respectively, which remain constant throughout time. In the event of food scarcity (d(t) = 0), it is anticipated that the rate of gender change would escalate, leading to a gradual shift in the hawkfish population from mostly female to predominantly male. Figure 2 below further illustrates the process of the proposed search mechanism where f1 is the initial fitness function and f2 is the inverse of that same function as seen in Figure 2 below.
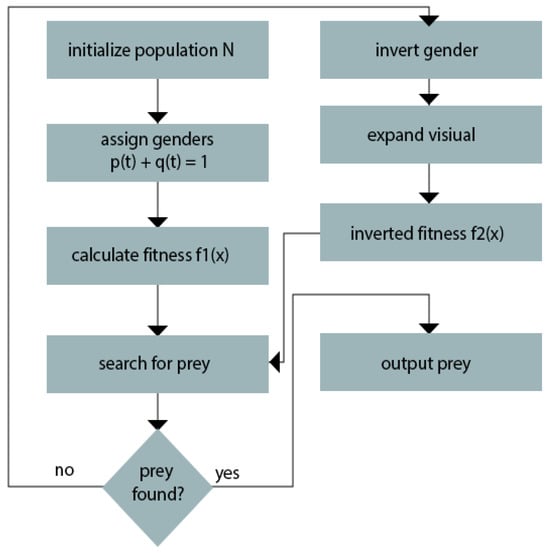
Figure 2.
Gender inversion in the proposed method.
The mathematical framework used to study gender transition in hawkfish encompasses a system of differential equations that elucidate the dynamics of the female-to-male ratio as a function of food availability. Additionally, a constant factor is included into the model to indicate the pace at which gender change occurs.
2.2. Mathematical Modeling
Hawkfish demonstrate sequential hermaphroditism, enabling females to transform into males in reaction to social and environmental stimuli, including the lack of a dominant male [22]. This adaptive behavior guarantees reproductive efficiency throughout the population, serving as an ideal paradigm for dynamic role adaptation in optimization processes. In the proposed method, this behavior is represented by two fitness functions, f1(x) and f2(x), which signify the equilibrium between exploitation (optimizing existing solutions) and exploration (pursuing new possibilities). This dichotomy reflects the hawkfish’s compromise between ensuring immediate reproductive success and evolving to enhance population stability. The algorithm encapsulates essential elements of this phenomena, including role-based adaptation, environmental feedback, and population dynamics. For example, artificial fish in the proposed method dynamically modify their roles, with some emphasizing local exploitation while others concentrate on global exploration, similar to hawkfish that adapt gender roles to optimize population equilibrium. The hawkfish’s adaptive reaction to environmental stimuli is mirrored in the algorithm’s dynamic parameter modifications, including step size, direction vectors, and cluster composition, allowing it to successfully respond to fluctuating fitness landscapes. The use of hawkfish gender transition as a model for optimization is warranted by its biological validity and its capacity to demonstrate the equilibrium between exploration and exploitation, a fundamental principle of heuristic optimization. The mathematical equations that define the fitness function in an optimization algorithm depend on the specific problem being solved. In general, the fitness function is a mathematical function that maps a candidate solution x to a fitness value, which indicates how good the solution is with respect to the problem being solved. Let us consider a simple example of a fitness function for a minimization problem. Suppose we are trying to minimize the function f(x) = x2, where x is a real number. In this case, the fitness function can be defined as follows:
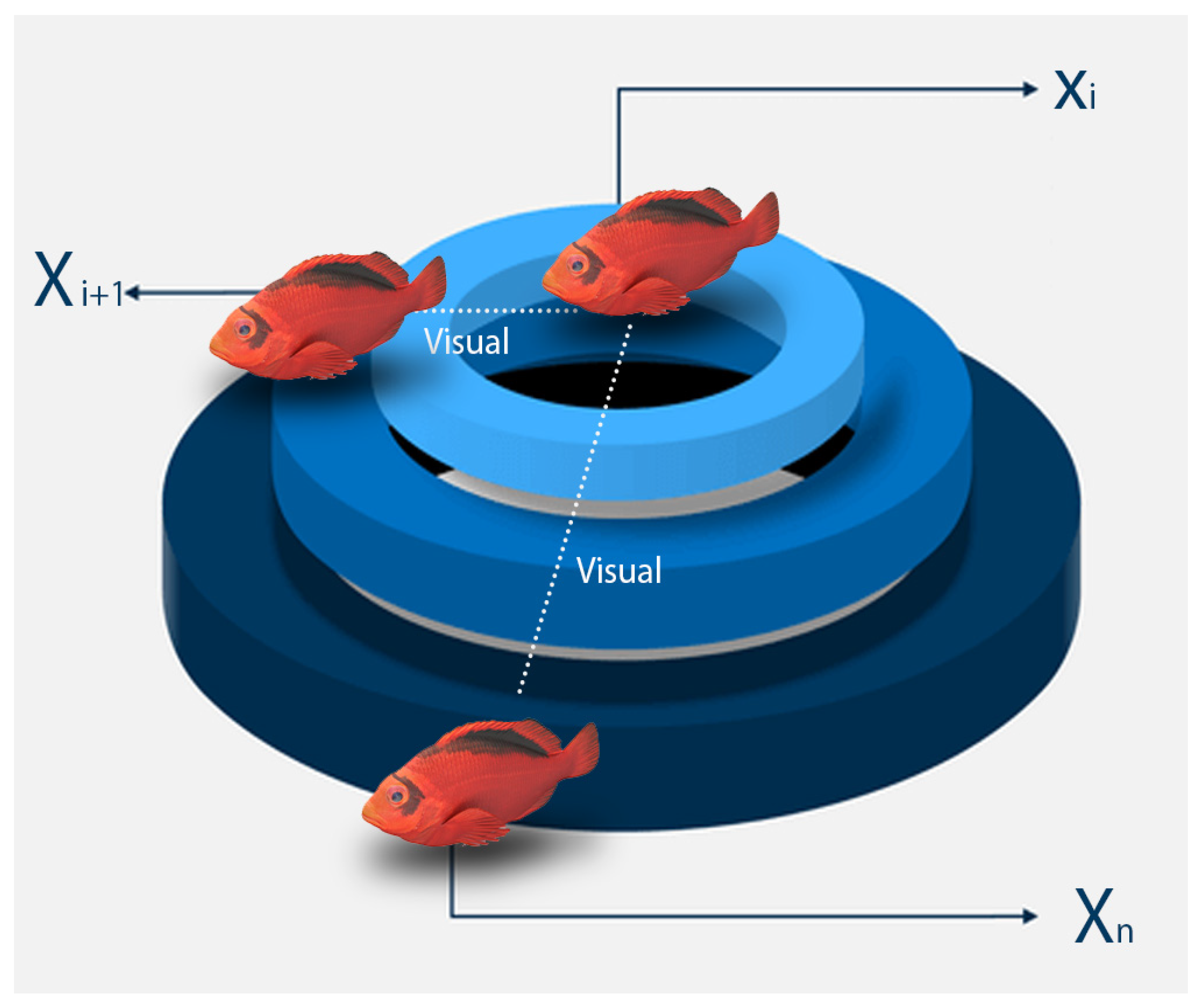
The goal of the optimization algorithm is to find the value of x that minimizes the fitness function. To do this, the algorithm generates a population of candidate solutions, which are typically represented as vectors or arrays of values [24]. For example, if we want to find the value of x that minimizes f(x) over the interval [0, 1], we might represent each candidate solution as a single real number between 0 and 1. The optimization algorithm then evaluates each candidate solution by computing its fitness value using the fitness function [25]. For example, if the candidate solution is x = 0.5, then its fitness value is f(0.5) = 0.25. The algorithm then applies selection and variation operators to the population to generate new candidate solutions [26]. The selection operator selects the best solutions from the population, while the variation operator introduces randomness and diversity into the population to help explore the search space more effectively as seen in Figure 3.
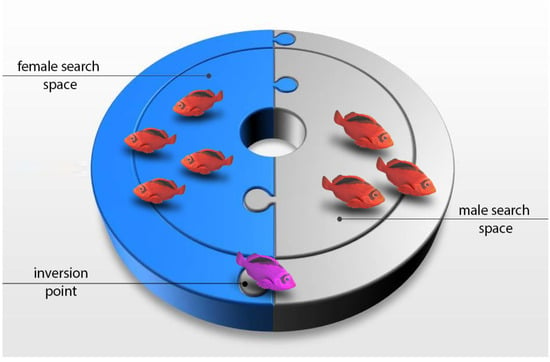
Figure 3.
Search space for males and females in the proposed HawkFish optimization algorithm.
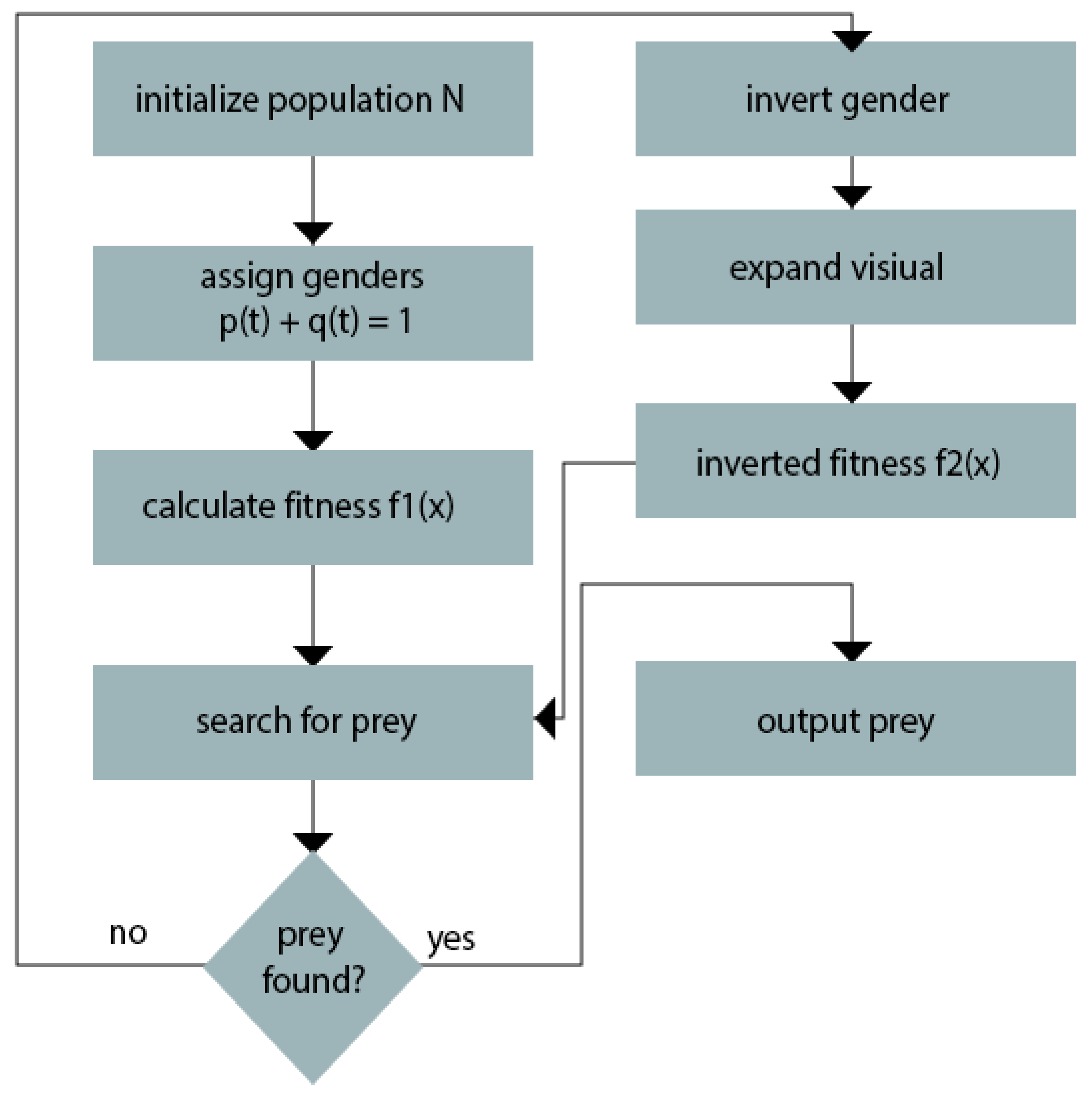
The process of generating new candidate solutions and evaluating their fitness values continues until a stopping criterion is met. The stopping criterion could be a maximum number of iterations, a maximum computation time, or a minimum acceptable fitness value. the math behind an optimization algorithm with equations of the fitness function involves defining a mathematical function that maps candidate solutions to fitness values, generating a population of candidate solutions, evaluating their fitness values, and applying selection and variation operators to generate new candidate solutions. The goal is to find the candidate solution with the best fitness value, which corresponds to the optimal solution of the problem being solved. The HawkFish optimization algorithm is a nature-inspired optimization algorithm that simulates the foraging behavior of fish in a swarm. It is a modification of the basic artificial fish swarm algorithm (AFSA) [26], introducing two opposite fitness functions instead of just one. The algorithm aims to find the optimal solution by maximizing one fitness function and minimizing the other.
The proposed algorithm can be modeled using the following mathematical equations:
- Initialize the population:The algorithm begins by initializing a population of artificial fish, where each fish is represented by a vector of n dimensions. The population size is denoted as N.
- Evaluate the fitness:The fitness of each fish is evaluated using two fitness functions, f1(x) and f2(x), where x is the position vector of the fish.
- Fish movement:The movement of each fish is determined by the following equation:where x(i, j) is the jth element of the position vector of the ith fish, s(i, j) is the step size of the ith fish, and d(i, j) is the jth element of the direction vector of the ith fish. The step size and direction vector are determined based on the fitness of the fish.
- Update the fitness:After each movement, the fitness of each fish is re-evaluated using the two fitness functions.
- Dynamic fish clustering:Let the position vectors of the fish be represented as X = {x1, x2, …, xN}, where xi is the position of the ith fish.
- Distance matrix:Calculate the pairwise distance matrix D, where D(i, j) = ||xi − xj|| represents the distance between fish i and j.
- Clustering algorithm:Use a Euclidean-based distance-based clustering to partition X into k clusters C1, C2, …, Ck, such that:
- Cluster leaders:For each cluster Cp, identify the cluster leader:xp,best = arg max f(xi), where f(xi) is the fitness function value for fish i.
- Dynamic updates:Periodically recompute the clusters to adapt to the evolving distribution of fish in the search space.
- Fish learning:Each fish in a subpopulation learns from its neighbors using the following equation:where x(jbest, j) is the jth element of the position vector of the best fish in the subpopulation, and w is the learning coefficient.
- Update the step size and direction vector:The step size and direction vector of each fish are updated using the following equations:where α and β are learning coefficients, r is a random number between 0 and 1, xglobal(j) is the jth element of the position vector of the global best fish, and xlocal(j) is the jth element of the position vector of the local best fish.
- Repeat:Steps 2–6 are repeated until a stopping criterion is met, such as a maximum number of iterations or a threshold value for the fitness function.
Below is the pseudocode for the proposed search and clustering mechanism:
The pseudocode provided in Algorithm 1 corresponds to the HawkFish optimization algorithm, as previously explained. The method commences by initializing a population of synthetic fish entities. These entities are then subjected to a fitness evaluation process, which assesses their ability to fulfill a given objective.
| Algorithm 1: Search and Clustering |
| 1. Initialize parameters: N (population size), n (number of dimensions), k (number of subpopulations), α (Global learning coefficient), β (Local learning coefficient), w (Subpopulation learning coefficient), max_iterations 2. Initialize the population of artificial fish with random positions in the search space 3. For iter in range(max_iterations): 3.1. Evaluate the fitness of each fish using f1(x) and f2(x) 3.2. Update the position of each fish based on their fitness: For i in range(N) and j = 1, 2, …, n: x(i,j) = x(i,j) + s(i,j) × d(i,j) ∀j ∈ {1, 2, …, n}. 3.3. Re-evaluate the fitness of each fish after movement 3.4. Cluster the population into k subpopulations to increase diversity xp,best = arg max f(xi), where f(xi) is the fitness function value for fish i 3.5. Perform fish learning within subpopulations: For each subpopulation: For i in range(number of fish in subpopulation): x(i,j) = x(i,j) + w × (x(jbest,j) − x(i,j)) ∀j ∈ {1, 2, …, n}. 3.6. Update the step size and direction vector of each fish: For i in range(N): s(i,j) = s(i,j) + α·random(0,1) × r × (xglobal(j) − x(i,j)) ∀j∈{1, 2, …, n} d(i,j) = d(i,j) + β random(0,1) × r × (x(i,j) − xlocal(j) ∀j∈{1, 2, …, n} 4. Return the global best solution found |
Following this, the algorithm proceeds to update the locations of the fish entities based on certain criteria. Additionally, the program clusters the population into distinct subpopulations, therefore facilitating a more focused analysis. Finally, the algorithm engages in a learning process within each subpopulation, enabling the fish entities to acquire new knowledge and improve their performance.
The aforementioned procedure is iterated until a predetermined stopping condition is satisfied, such as the attainment of the maximum allowable number of iterations. The primary concern associated with the artificial fish swarm algorithm pertains to the visual range exhibited by individual fish [27], Figure 4 below further illustrates the dynamic change in the visual scope in the fish entities:
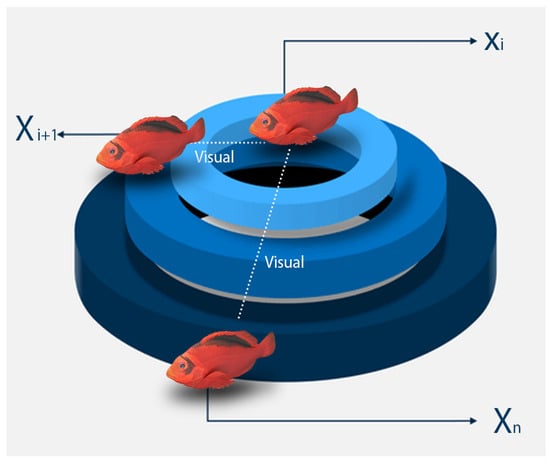
Figure 4.
Visual search scope for the proposed population.
The population is categorized into distinct genders, and each gender within the subpopulation is allocated distinct visual scopes. This methodology promotes varying degrees of investigation and exploitation within the search space, possibly resulting in a broader range of viable solutions. The approach for assigning visual acuity in a dynamic manner depending on gender may be represented by the following model:
- Divide the population P of artificial fish into 2 subpopulations: Pmale for male artificial fish and Pfemale for female artificial fish, where |Pmale| and |Pfemale| denote the sizes of the male and female subpopulations, respectively.
- Assign a unique visual scope Vmale to the male subpopulation Pmale and Vfemale to the female subpopulation Pfemale.
- Evaluate the availability of food in the search space, represented by a food metric F, which could be the average fitness of the population or another suitable measure.
- For each iteration t:
- Update the gender of each artificial fish f based on the availability of food F:If F > F_threshold, where F_threshold is a predefined threshold, change the gender of fish f. For example, if fish f is male, change it to female, and vice versa.
- For each artificial fish f in subpopulation Pmale or Pfemale, only consider other fish within the corresponding visual scope Vmale or Vfemale when evaluating the fitness and updating the position.
- The position update equation of artificial fish f in subpopulation Pmale or Pfemale can be represented as:Here, x_f(t) denotes the position of artificial fish f at iteration t, step_size is the step size, and x_center is the center of the corresponding subpopulation (Pmale or Pfemale).
- The center of the subpopulation Pmale or Pfemale can be calculated as:Here, x_j represents the position of the j-th artificial fish in the corresponding subpopulation (Pmale or Pfemale).
- When updating the position of artificial fish f in subpopulation P_dist (Pmale or Pfemale), only consider other fish within the visual scope Vmale or Vfemale:
- Find the set of neighboring fish N_f within the visual scope Vmale or Vfemale:
- Update the position of artificial fish f based on the information from neighboring fish N_f:
Here, x_nbest is the position of the best neighboring fish in N_f, based on the objective function.
By incorporating the dynamic gender-based subpopulation strategy into the artificial fish swarm algorithm, you can encourage different levels of exploration and exploitation within the search space, potentially leading to a more diverse set of candidate solutions and improved optimization performance. The dynamic gender change based on the availability of food allows the algorithm to adapt to the changing search environment more effectively. Algorithm 2 shows a pseudo-code for the dynamic gender-based subpopulation strategy with the artificial fish swarm algorithm:
| Algorithm 2: Gender Switching Sub-Strategy |
| Initialize population P with positions and genders Set Vmale and Vfemale (unique visual scopes for male and female subpopulations) Set F_threshold (predefined threshold for food availability) Set max_iterations for t = 1 to max_iterations: Calculate food metric F (e.g., average fitness of the population) for each artificial fish f in P: if F > F_threshold: Change the gender of fish f (swap between male and female) if fish f is male: Find neighboring fish N_f within visual scope Vmale else: Find neighboring fish N_f within visual scope Vfemale Determine x_nbest (position of the best neighboring fish in N_f) Update position of fish f: x_f(t+1) = x_f(t) + step_size × (x_nbest − x_f(t)) Update fitness values for all fish in the population Check stopping criteria (e.g., convergence or maximum iterations reached) |
This pseudo-code presents the main steps of the dynamic gender-based subpopulation strategy in the artificial fish swarm algorithm. The algorithm starts by initializing the population with positions and genders, and it iteratively updates the positions and genders based on the availability of food and the corresponding visual scopes. The stopping criteria can be determined by convergence or a maximum number of iterations.
3. Results and Discussion
This section begins by providing an overview of the experimental setup, including the hardware and software used, the benchmark problems, and the performance measures. The performance measures typically include objective function values, convergence rate, computational time, and any other relevant metrics [28]. The section then presents the results of the experiments. This includes tables, figures, and graphs that show the algorithm’s performance on the benchmark problems, such as the objective function values obtained, the number of function evaluations required to reach the solution, and the convergence curve. The results also be presented in terms of statistical analysis, such as Big-O notation to provide a more accurate assessment of the algorithm’s performance.
3.1. Implementation Environment
This project was implemented using MATLAB R2022a on a Dell Inspiron laptop, manufactured by Dell Inc., headquartered in Round Rock, TX, USA. The laptop is equipped with an Intel Core i7 12th generation processor, produced by Intel Corporation, based in Santa Clara, CA, USA. It also features 16 GB of RAM and a 2 GB NVIDIA GeForce dedicated GPU, developed by NVIDIA Corporation, also headquartered in Santa Clara, CA, USA.
3.2. Time of Convergence and Error Rate
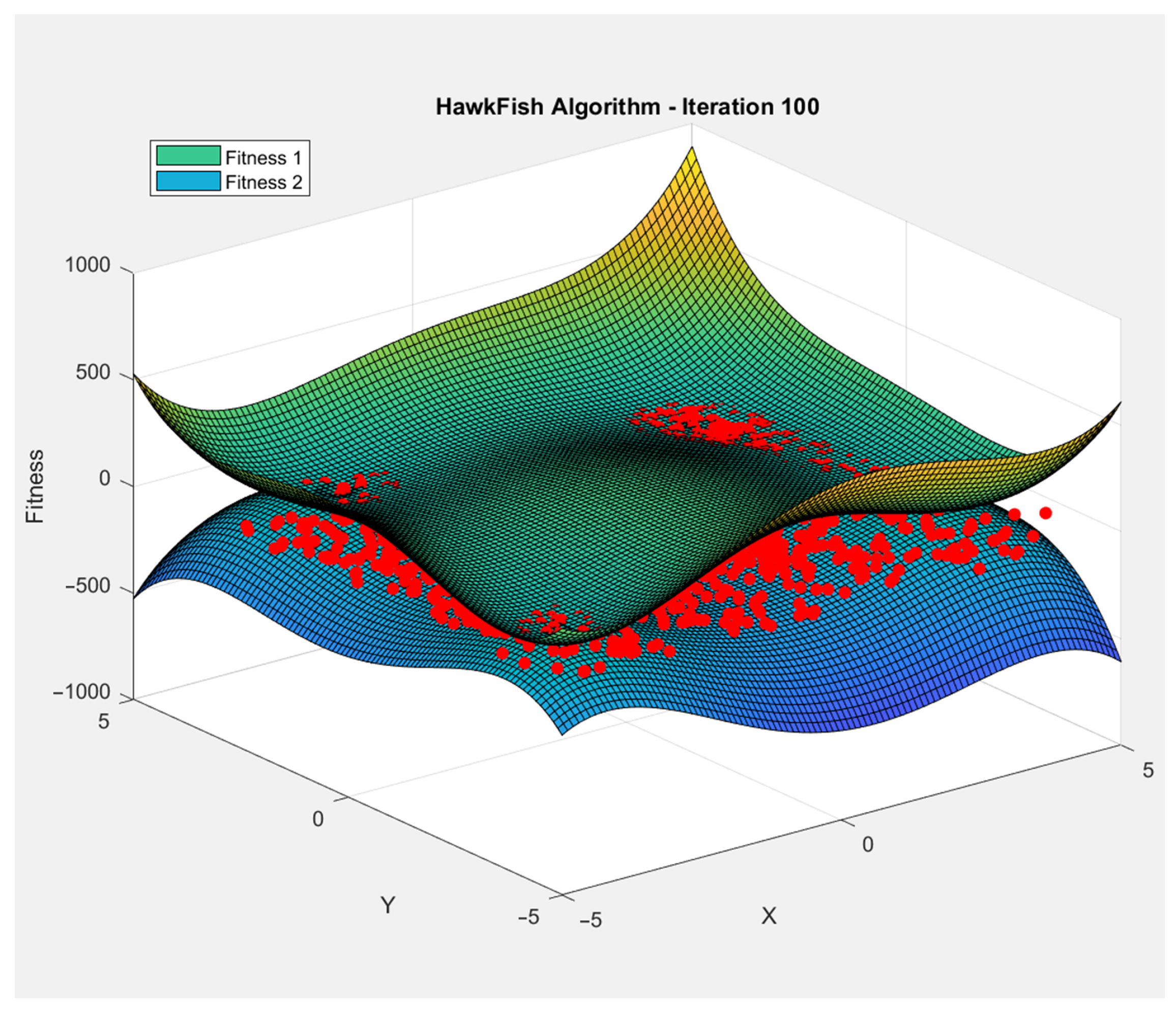
Time of convergence and error rate are two important metrics used to evaluate the performance of a metaheuristic algorithm. Time of convergence refers to the amount of time it takes for the algorithm to reach a satisfactory solution. In other words, it measures the speed of the algorithm [29]. A faster algorithm with a shorter time of convergence is generally preferred, as it can save computational resources and make the algorithm more practical for real-world applications. Error rate, on the other hand, measures the accuracy of the solution produced by the algorithm [30]. It represents the difference between the optimal solution and the solution produced by the algorithm. A lower error rate indicates that the algorithm has found a better solution, which is more accurate and closer to the optimal solution. In general, a good metaheuristic algorithm should balance the time of convergence and error rate [31]. A fast algorithm with a high error rate is not useful for practical applications, while a highly accurate algorithm with a long time of convergence is impractical and computationally expensive. Figure 5 illustrates how the proposed method explores the search space, represented by the X and Y axes, to optimize a fitness function depicted on the Z-axis which represents the fitness value (objective function value).
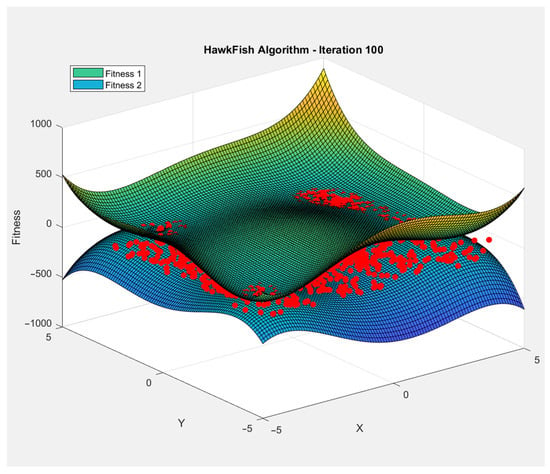
Figure 5.
Simulation of the double search spaces for both males and females in the proposed method, where the green mesh represents the fitness function, the blue mesh represents the inverse if that function, the red dots represent the population of the hawkfish, Z-axis represents the fitness value and X-, Y-axes represent the search space.
By comparing the performance of the proposed HawkFish algorithm and fish swarm algorithm (FSA), it was found that the proposed algorithm outperformed the FSA in terms of both time of convergence and error rate as presented in Table 2 and Table 3. Specifically, the proposed method was able to find better solutions in a shorter amount of time compared to the FSA. The faster convergence of the proposed method can be attributed to its double fitness scheme features, such as the use of dynamic clustering and a modified particle update equation. These features allow the algorithm to effectively explore the search space and quickly converge to a good solution. Additionally, the HawkFish optimization algorithm was found to have a lower error rate compared to the FSA. This is likely due to the fact that the proposed method is designed to handle optimization problems with multiple local optima, which can be a challenging problem for traditional optimization algorithms like the FSA. the results of this study suggest that the HawkFish optimization algorithm is a promising metaheuristic algorithm for solving optimization problems, and that it may be particularly effective in situations where time of convergence and accuracy of solutions are both important metrics.

Table 2.
Error rate by iteration and time for the fish swarm algorithm.

Table 3.
Error rate by iteration and time for the proposed algorithm.
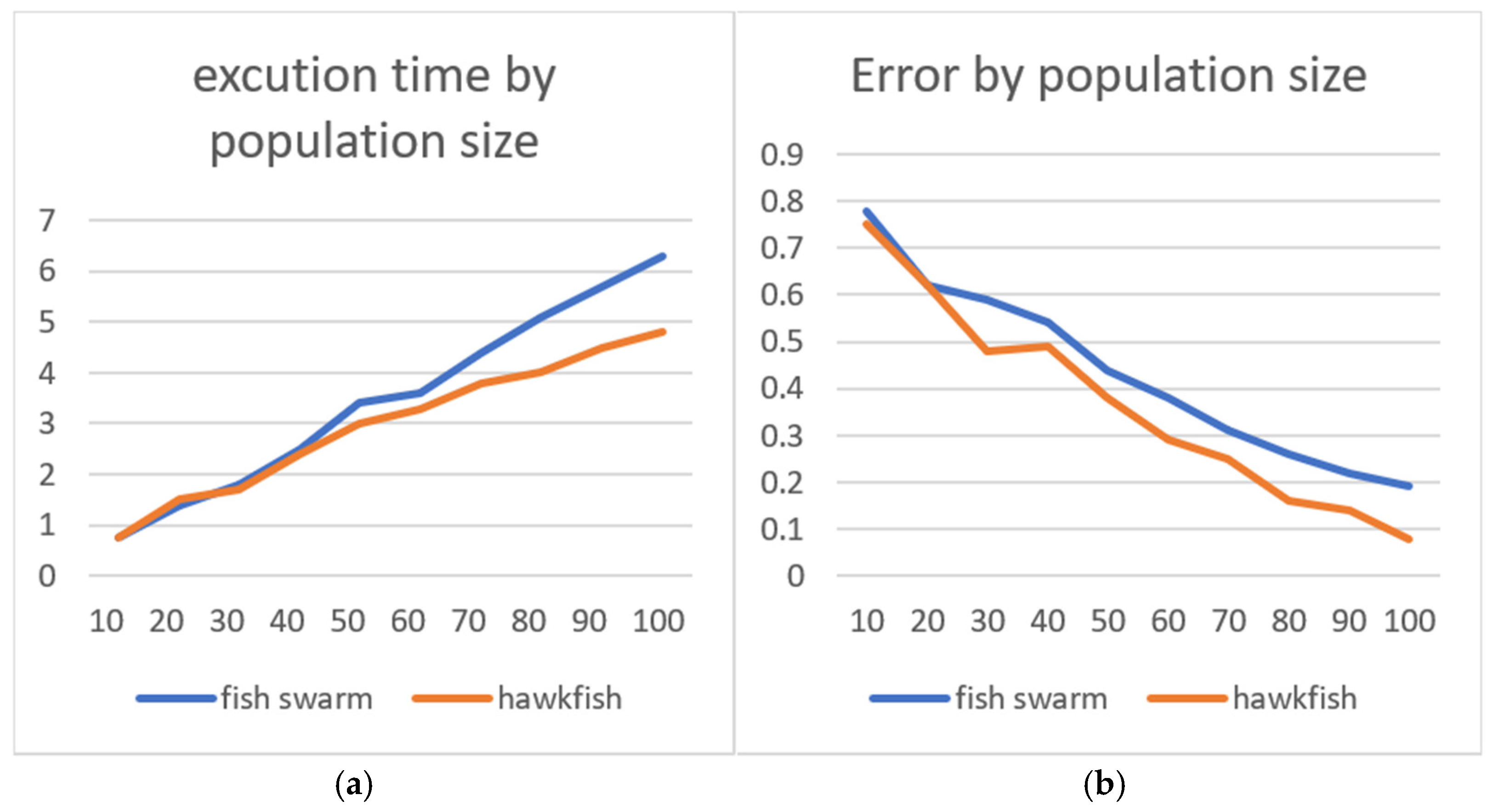
Increasing the population size can help an algorithm to explore the search space more thoroughly, which can result in better solutions. However, a larger population size also requires more computational resources, which can lead to longer computation times. Therefore, it is important to carefully select the population size for any optimization algorithm based on the specific problem being solved and the available computational resources [32]. Figure 6 compares the performance of the HawkFish optimization algorithm and the fish swarm optimization algorithm in terms of execution time (a) and error (b) as the population size increases. In subplot (a), the X-axis represents the population size, while the Y-axis represents execution time (in seconds). As the population size increases, both algorithms require more execution time due to higher computational demands. However, the proposed method (orange line) consistently demonstrates lower execution time than the fish swarm algorithm (blue line), showcasing its efficiency. In subplot (b), the X-axis again represents the population size, while the Y-axis represents error (a normalized measure). Both algorithms show decreasing error trends as the population size increases, indicating improved exploration of the solution space with larger populations. Notably, the proposed algorithm achieves lower error values compared to the fish swarm algorithm, reflecting its superior optimization performance.
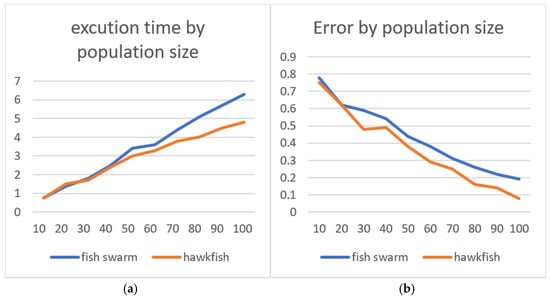
Figure 6.
Execution time (a) where the X-axis represents the iteration and the Y-axis represents the time in seconds, and error (b) where the X-axis represents the iteration and the Y-axis represents the error rate measured in MATLAB units for both the HawkFish algorithm (orange line) and the AFSA (blue line).
3.3. Benchmark Functions
The CEC/GECCO 2019 benchmark functions are a set of test functions widely used to evaluate the performance of optimization algorithms [33]. These functions were proposed as part of the Computational Intelligence and Evolutionary Computation tracks of the IEEE Congress on Evolutionary Computation (CEC) and Genetic and Evolutionary Computation Conference (GECCO) in 2019, with the aim of introducing challenging benchmarks that test the robustness and effectiveness of optimization methods. The CEC/GECCO 2019 benchmark suite comprises 30 test functions divided into two categories: unimodal and multimodal functions. Unimodal functions are designed to evaluate the ability of optimization algorithms to locate a single global optimum, while multimodal functions challenge algorithms to handle multiple local optima and identify the global optimum in such landscapes [34]. The fitness functions used in the CEC/GECCO 2019 benchmarks are mathematical models that map a set of input variables to a fitness value, representing the quality of a given solution. Depending on the specific function, the input variables may be real-valued or binary. Some notable fitness functions in the CEC/GECCO 2019 suite include [35]:
- Sphere function: a unimodal function that is commonly used to evaluate optimization algorithms. The fitness value is calculated as the sum of the squares of the input variables.
- Ackley function: a multimodal function that is designed to assess the ability of algorithms to manage problems with multiple local optima. The fitness value is calculated using a combination of trigonometric and exponential functions.
- Griewank function: a multimodal function that is designed to assess the ability of algorithms to manage problems with a large number of variables.
The fitness value is calculated as a combination of a quadratic term and a cosine term. the CEC/GECCO 2019 benchmark functions are a widely used set of test functions that provide a standard way to evaluate the performance of optimization algorithms [36].
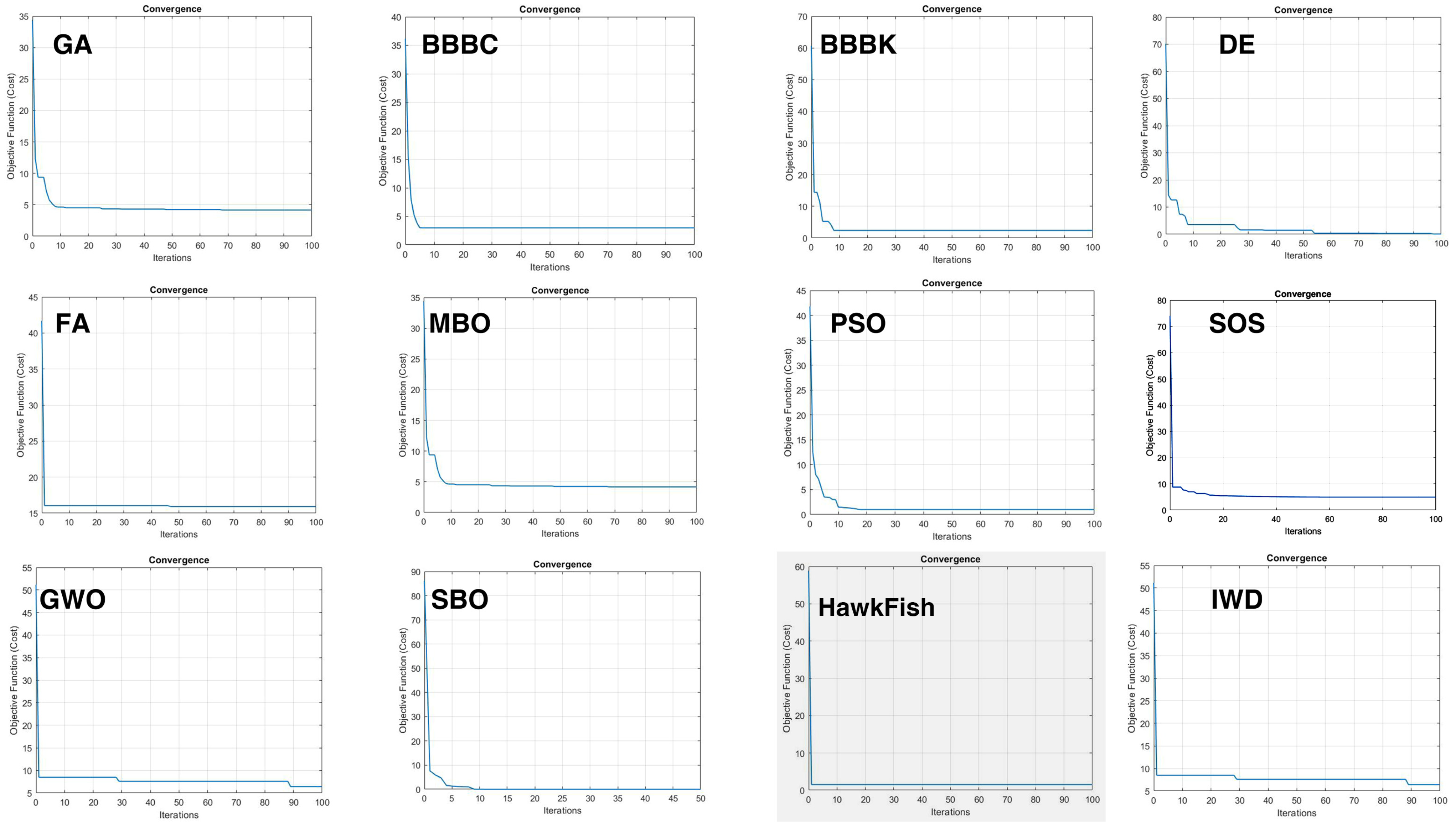
In this study, we evaluated the performance of the HawkFish optimization algorithm against several other metaheuristic algorithms such as (GA), the Firefly Algorithm (FA) and other state-of-the-art algorithms using the CEC/GECCO 2019 benchmark functions, it was found that the proposed method outperformed these algorithms in terms of convergence rate and accuracy of solutions. The study found that the HawkFish optimization algorithm achieved better convergence rates than the other algorithms, meaning that it was able to find good solutions in a shorter amount of time. Additionally, the proposed method was able to achieve higher accuracy of solutions compared to the other algorithms, indicating that it was able to find solutions that were closer to the global optimum. To ensure a fair and unbiased comparison, all the algorithms, including the proposed method and the state-of-the-art (SOTA) algorithms were executed on a local machine using their publicly available code implementations. This decision was made to guarantee that all algorithms were tested under identical conditions, such as hardware, software environments, and data. As such, the results reported in Table 4 reflect the outcomes of these consistent re-evaluations rather than the originally published results from their respective papers while Figure 7 illustrates the convergence rate of the proposed algorithm in comparison with the state-of-the-art algorithm:

Table 4.
Performance evaluation using CEC/GECCO 2019 functions for the proposed method compared to state-of-the-art optimization algorithms.
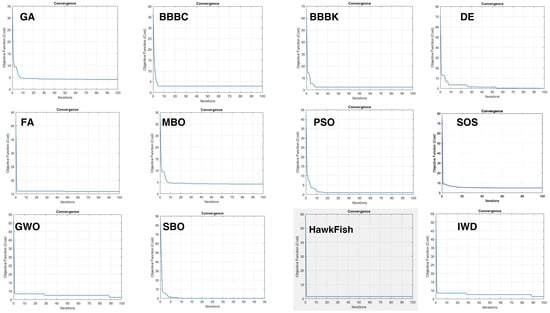
Figure 7.
Convergence graph of the proposed algorithm (highlighted in gray) compared to other state-of-the-art algorithms.
The standard deviation quantifies the variability or spread of these fitness scores, calculated as the square root of the variance of the scores around their mean [36]. A lower standard deviation indicates greater stability and consistency of the algorithm’s performance, while a higher value suggests variability across runs. The Wilcoxon p-value is derived from the Wilcoxon signed-rank test, a non-parametric statistical method used to compare the performance of two algorithms [37]. It evaluates the significance of differences in fitness values across multiple runs. A p-value less than 0.05 indicates that the performance differences are statistically significant, while a p-value greater than or equal to 0.05 suggests no significant difference [38]. Together, these metrics offer a comprehensive evaluation of the algorithms, highlighting their effectiveness, reliability, and statistical significance when compared to other methods. Table 5 presents the parameter configurations and statistical results for a comparison of various optimization algorithms, including the proposed method, BBBC, BBKH, DE, FA, GA, GWO, IWD, MBO, PSO, SBO, SOS, and WEO. The table lists the specific parameters used for each algorithm, such as learning coefficients (α, β) for the HawkFish algorithm, convergence factors for the BBBC, and mutation rates for the GA. Each algorithm’s performance is evaluated over 30 repetitions to ensure statistical reliability, with the average fitness and standard deviation reported to indicate their effectiveness and variability, respectively. The Wilcoxon p-value is provided to assess the statistical significance of differences in performance when compared to the proposed algorithm as shown in Figure 8. Notably, the proposed method achieves the best average fitness with the lowest standard deviation, demonstrating its superior balance of exploration and exploitation, while maintaining statistically significant results (p = 0.003). The implementation code for the proposed method can be accessed through the GitHub repository at [39].

Table 5.
Parameter settings and statistical results for different optimization algorithms.
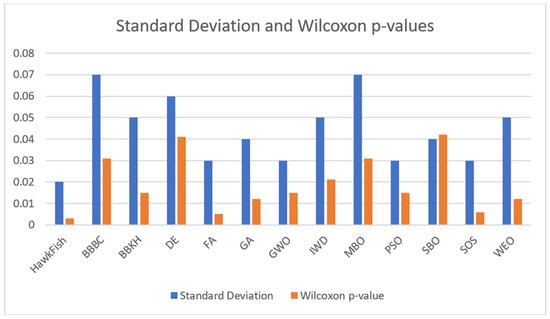
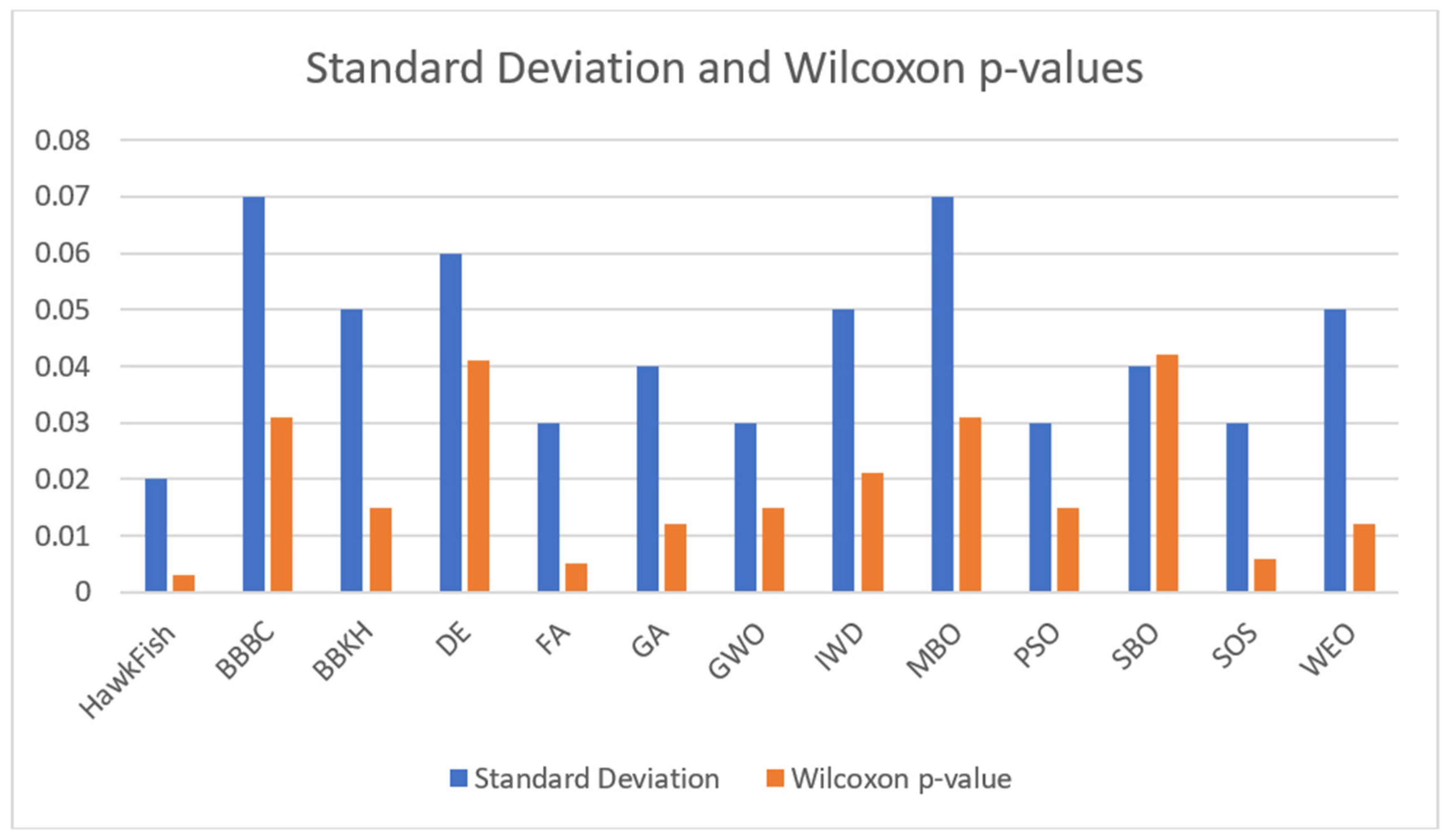
Figure 8.
Comparison of standard deviation and Wilcoxon p-values for different optimization algorithms.
The figure above, Figure 8, compares the performance of various optimization algorithms, including the proposed algorithm, BBBC, BBKH, DE, FA, GA, GWO, IWD, MBO, PSO, SBO, SOS, and WEO, based on two metrics: standard deviation (blue bars) and Wilcoxon p-values (orange bars). The standard deviation indicates the stability of an algorithm’s performance, with lower values representing more consistent results. Among the algorithms, the HawkFish algorithm shows the smallest standard deviation (0.02), demonstrating superior stability across multiple runs, while other algorithms such as BBBC, MBO, and DE exhibit higher standard deviations, suggesting greater variability in their results. The Wilcoxon p-value assesses the statistical significance of performance differences compared to a baseline or other algorithms, where smaller values (<0.05) imply significant differences. The HawkFish algorithm, with the lowest p-value (0.003), emerges as the most statistically significant performer, highlighting its superiority over competitors. While algorithms like GA and PSO also have low p-values, their higher standard deviations or slightly weaker statistical significance make them less optimal than the proposed method. Conversely, algorithms like BBBC and MBO, with higher standard deviations, demonstrate less consistent performance, even if their average fitness values are competitive.
4. Solving the Welded Beam Design Problem
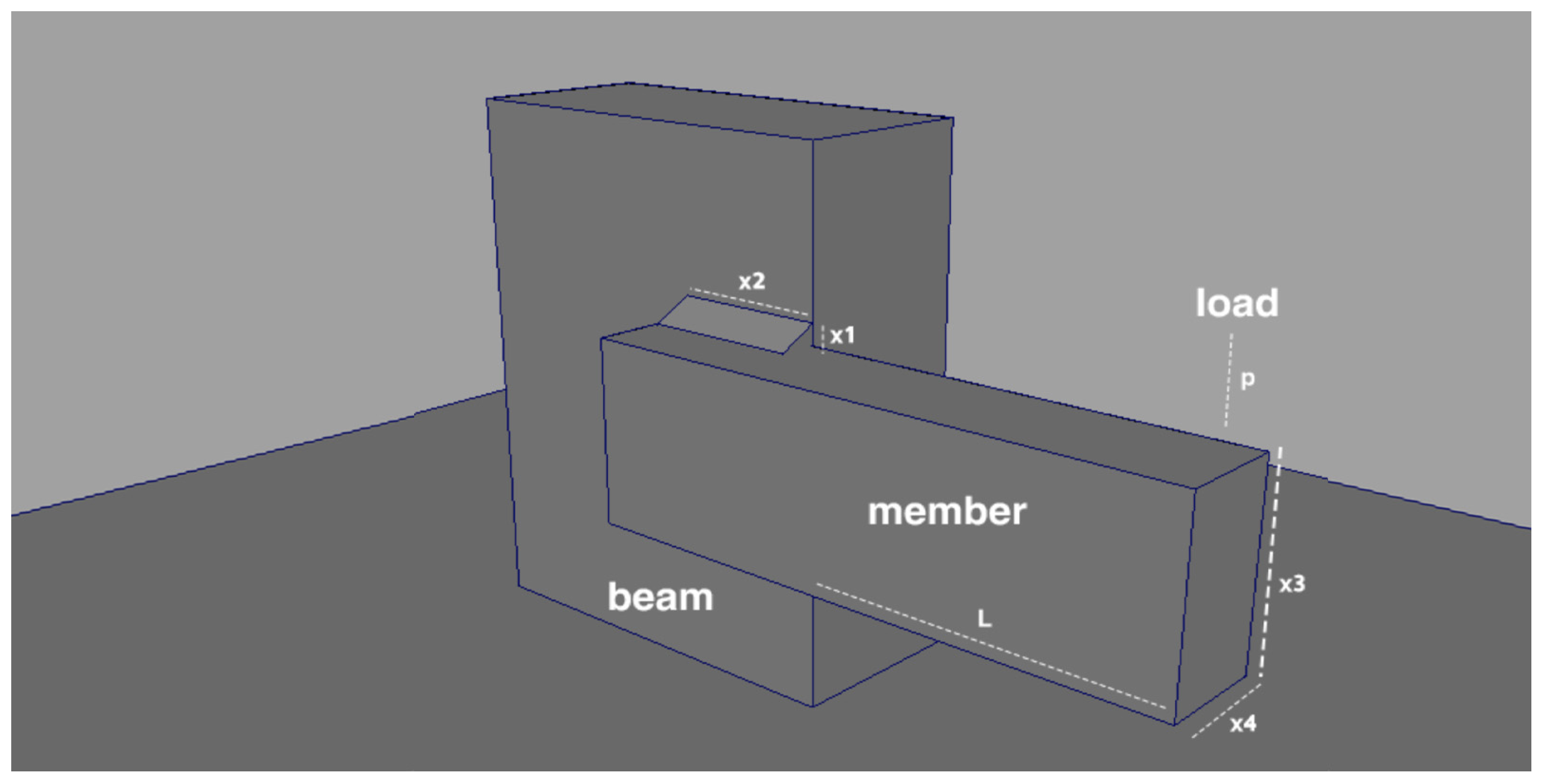
Significant computational resources are necessary to address the bulk of optimization problems that have practical relevance [40]. The element of high cost associated with optimization computer techniques may be attributed to several research constraints, including limitations in time and resources. Therefore, it is vital to ascertain techniques for expediting the optimization process while concurrently streamlining it [41]. Due to the unique process of information transmission inherent in traditional optimization algorithms, the results produced by these algorithms are often deemed satisfactory. The efficient functioning of this mechanism requires the use of many preferred solutions within a certain range of fitness evaluations, the concept of the WBD problem, which involves the consideration of various design parameters [42]. These parameters encompass the design for minimizing cost while adhering to shear stress constraints (τ), managing beams’ end deflection (δ), addressing bending stress in the beam (θ), evaluating the buckling load on the bar (Pc), and accommodating side constraints. The WDB problem, as illustrated in Figure 9, revolves around four specific design parameters, denoted as h(x), l(x2), t(x3), and b(x4). The primary objective is to devise a welded beam configuration that incurs minimal input cost. This mathematical representation succinctly captures the essence of the WDB problem [43]:
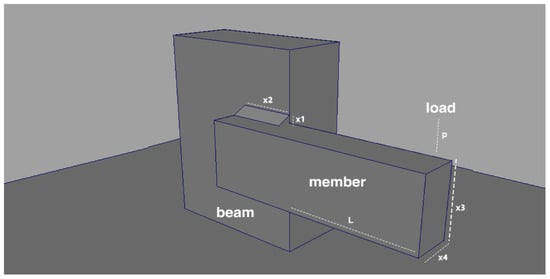
Figure 9.
Modeling of the welded beam design problem.
This constraint ensures that the shear stress, τ(x), does not exceed 13,000 units
This constraint ensures that x1 is less than or equal to x4
This constraint is a combination of various parameters x1, x2, x3, x4 ensuring that the left-hand side expression does not exceed 5.0 units.
This constraint ensures that the deflection, δ(x), does not exceed 0.25 units
By satisfying these constraints, the solution to the optimization problem will ensure that all the design criteria and limits are respected:
where τ(x) represents a stress-related measure, a combined stress calculation, accounting for different stress contributions such as primary stress (τ′), secondary stress (τ″), and R, which represents the resultant distance.
Due to the need to account for all possible resolutions, the implementation of these frameworks necessitates a substantial allocation of computational resources and effort. As a result of this phenomenon, a considerable amount of research efforts have been directed towards the creation of optimization frameworks that possess both computing efficiency and applicability for assessing a diverse array of functions [44]. In recent years, there has been a notable advancement in the creation of methodologies that, although requiring a reduced number of function evaluations, manage to achieve acceptable levels of performance [45]. In this problem, the objective is to minimize the cost and deflection of the beam while ensuring that constraints like shear stress, bending stress, and side constraints are satisfied, will provide a practical implementation of the proposed method to solve the welded beam design problem. The welded beam design problem is a well-known optimization problem in engineering design. It is a classic optimization problem that involves minimizing the cost of a welded beam subject to constraints on its dimensions and stress [46].
The problem can be defined as follows:
Minimize:
Subject to:
Bounds:
In this problem, the objective is to minimize the cost and deflection of the beam while ensuring that constraints like shear stress, bending stress, and side constraints are satisfied. To use the HawkFish optimization algorithm, first, set the initial parameters, including the population size, number of iterations, and visual scope for both male and female individuals. Then, generate an initial population of individuals, each representing a possible solution to the welded beam problem, and assign a gender (male or female) to each individual. For each individual in the population, calculate the fitness value using the appropriate gender-specific fitness function. The male fitness function might focus on minimizing cost, while the female fitness function might focus on minimizing deflection. Separate the individuals into two groups based on their gender, and each gender will perform a search within its visual scope to explore potential solutions to the problem. The search process includes a series of moves (e.g., swimming, following, or leaping) that allow individuals to update their positions in the search space. If a gender group cannot find an improved solution within its search space, individuals in that group can switch genders to adopt the other gender’s fitness function and search strategy, providing an opportunity to explore the problem space from a different perspective. After each iteration, update the population by replacing less-fit individuals with better solutions found during the search process, ensuring a mix of both male and female individuals. Continue running the algorithm for a predefined number of iterations or until a satisfactory solution is found. When the termination criterion is met, the algorithm will output the best solution it has found. Finally, analyze the best solution obtained from the proposed method and validate its feasibility based on the problem constraints. If necessary, fine-tune the algorithm’s parameters and run it again to search for improved solutions. The fitness functions for both genders should be based on the objective functions and constraints of the welded beam problem. For example, the cost equation could be expressed as:
where x1 and x2 are constants, h and t are the height and thickness of the beam, and w and l are the width and length of the weld. Similarly, the deflection equation can be expressed as
where x3 is the constant, P is the applied force, L is the length of the beam, E is the modulus of elasticity, and I is the moment of inertia. Constraints can be represented as inequality equations, such as
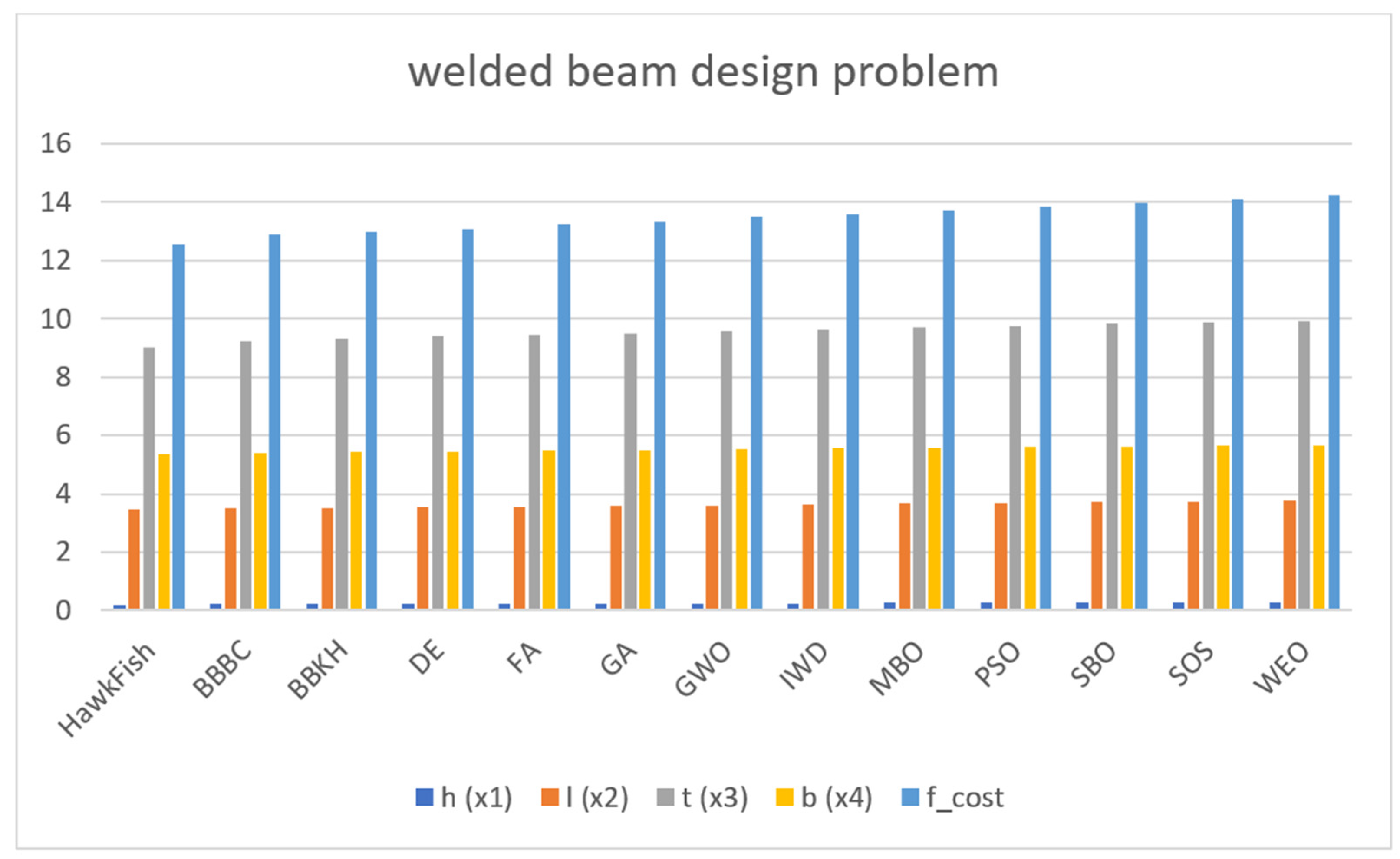
where δmax and τmax are the maximum allowable bending stress and shear stress, respectively, and hmax, hmin, tmax, and tmin are the upper and lower bounds for the height and thickness of the beam. Table 6 below presents a comparison of the HawkFish algorithm with other optimization algorithms for the welded beam design problem:

Table 6.
Comparing the cost function for the proposed method with state-of-the-art algorithms.
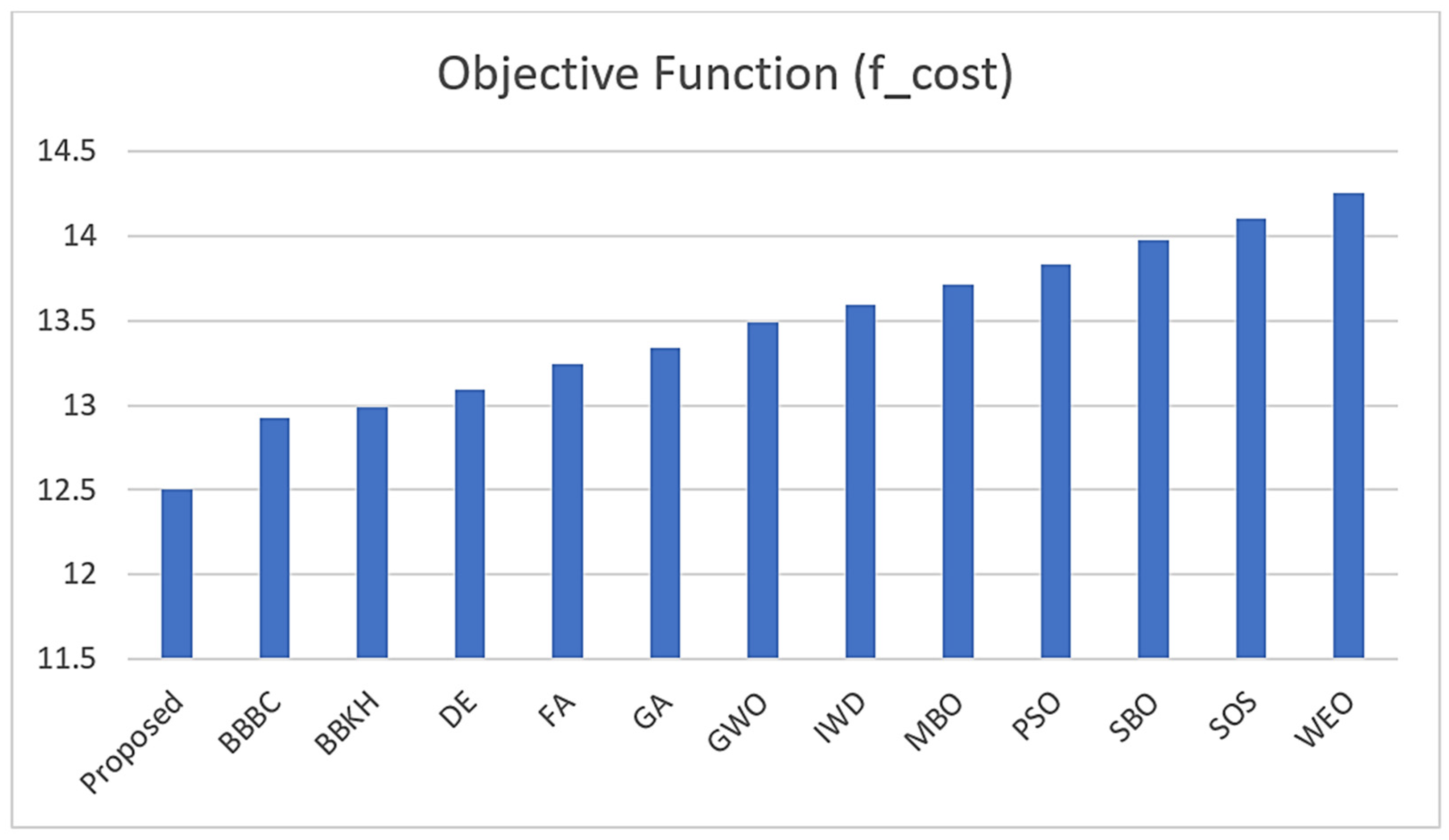
The table above and Figure 10 provide a comparison of various optimization algorithms, including the proposed algorithm in solving the welded beam design problem. Based on the values presented, it appears that the HawkFish algorithm outperforms the other algorithms with respect to the criteria of h (x1), l (x2), t (x3), b (x4), and f_cost. This suggests that the HawkFish algorithm may be a more effective method for tackling this problem, as it yields a lower f_cost, indicating a better optimized solution. The above experiments and observations support the proposed algorithm’s ability to solve complex problems with unknown search spaces.
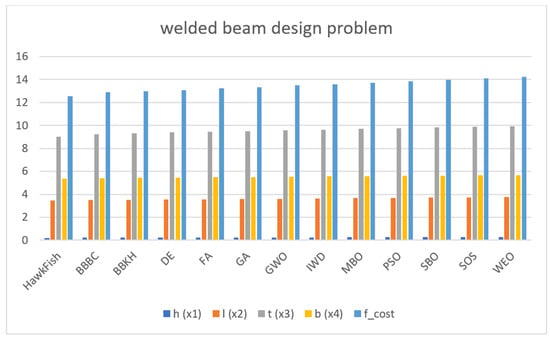
Figure 10.
Comparative performance of various optimization algorithms for welded beam design problem.
5. Solving the Tension/Compression Spring Problem
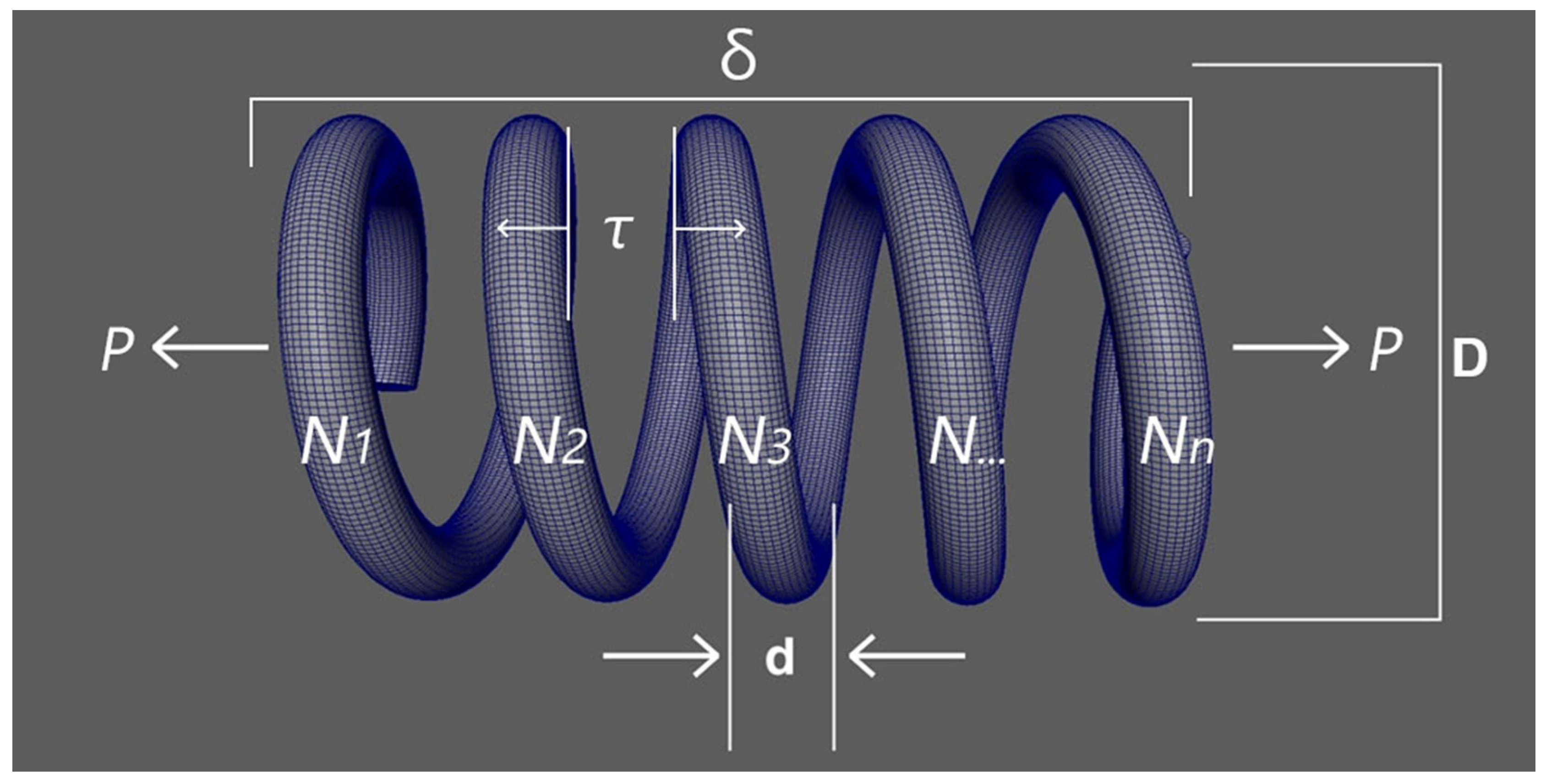
The tension/compression spring (TCS) design problem (Figure 11) is an optimization problem commonly encountered in mechanical engineering, where the goal is to design a spring that meets specific performance criteria while minimizing or maximizing certain objectives, such as weight, cost, or material usage [47]. The design involves various constraints to ensure that the spring functions correctly under the given loads and conditions [48].
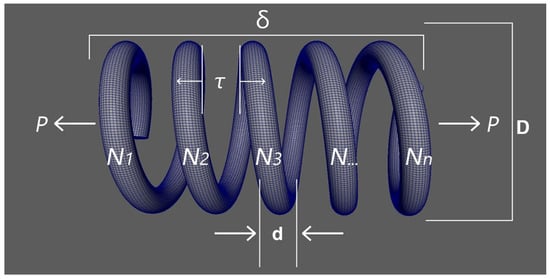
Figure 11.
Constraints of the TCS problem.
5.1. Key Parameters and Variables
The design of a spring involves several key parameters that influence its performance. The wire diameter (d) refers to the diameter of the wire used to fabricate the spring, while the mean coil diameter (D) is the average diameter of the spring’s coils. The number of active coils (N) indicates the number of coils that actively contribute to the spring’s deflection, and the modulus of rigidity (G) is a material property that reflects the rigidity of the spring’s material. Additionally, the shear stress (τ) represents the stress acting parallel to the wire’s cross-section, and the deflection (δ) denotes the displacement of the spring under an applied load. The spring index (C) is a critical ratio defined as the mean coil diameter divided by the wire diameter (C = D/dC), and the load (P) represents the force exerted on the spring. Together, these parameters determine the spring’s mechanical behavior and suitability for specific applications.
5.2. Objective Function and Constraints
The objective function for the tension/compression spring (TCS) design problem typically focuses on optimizing specific parameters to achieve the desired performance. Common objectives include minimizing weight by reducing the material used in the spring, minimizing cost by lowering manufacturing and material expenses, and maximizing efficiency to ensure the spring performs its function with minimal material while maintaining maximum durability. Several constraints ensure the spring performs correctly and safely. Typical constraints include:
- Shear stress constraint: Ensuring the shear stress in the spring does not exceed the material’s allowable stress.
τ = 8PD/(π d3) ≤ τmax
- 2.
- Deflection constraint: Ensuring the spring’s deflection under load does not exceed the permissible deflection.
δ = 8PD3N/(Gd4) ≤ δmax
- 3.
- Frequency constraint: Ensuring the spring’s natural frequency is within a desired range to avoid resonance.
f = 1/(2π) √(Gd4/(8D3N)) ≥ f_min
- 4.
- Geometric constraints: Ensuring the dimensions of the spring are within practical limits.
D_min ≤ D ≤ D_max
d_min ≤ d ≤ d_max
Given these variables, objectives, and constraints, the optimization problem can be formulated as follows:
τ − τ_max ≤ 0
δ − δ_max ≤ 0
f_min − f ≤ 0
D_min ≤ D ≤ D_max
d_min ≤ d ≤ d_max
5.3. Solving the TCS Design Problem Using HawkFish Optimization Algorithm
Using the dynamic gender-based subpopulation strategy into the proposed algorithm, we can encourage different levels of exploration and exploitation within the search space. This potentially leads to a more diverse set of candidate solutions for finding the optimal values of d, D, and N that minimize the objective function while satisfying all the constraints, the steps of the optimization are further explained below:
- Initialization:
- -
- Define the total population P of artificial fish.
- -
- Divide P into two subpopulations: Pmale and Pfemale.
- -
- Each subpopulation has a unique visual scope: Vmale for Pmale and Vfemale for Pfemale.
- Assign visual scopes Vmale and Vfemale to the male and female subpopulations, respectively.
- Evaluate the Availability of FoodWe define a food metric F representing the availability of resources in the search space. This could be the average fitness of the population or another suitable measure.
- -
- For each iteration i:
- -
- We compare the food metric F to a predefined threshold F_threshold.
- -
- If F > F_threshold, change the gender of each fish, f (e.g., male to female, and vice versa).
- -
- For each artificial fish f in Pmale or Pfemale, consider only other fish within the corresponding visual scope Vmale or Vfemale for evaluating fitness and updating positions.
- -
- Update the position of each fish f using the equation:
- -
- Here, x_f(t) is the position of fish f at iteration t, step_size is a predefined parameter, and x_center is the center of the corresponding subpopulation.
- -
- Calculate the center of subpopulation Pmale or Pfemale using:x_center = (1/|Pmale|) × Σ x_j or x_center = (1/|Pfemale|) × Σ x_j
- -
- Here, x_j represents the position of the j-th fish in the respective subpopulation.
- -
- Identify neighboring fish N_f within the visual scope:N_f = {g | g ∈ Pmale or Pfemale and dist(x_f(t), x_g(t)) ≤ Vmale or Vfemale}
- -
- Update the position of fish f based on the best neighboring fish x_nbest:
- -
- Here, x_nbest is the position of the best neighboring fish in N_f, based on the objective function.
In Table 7 below, each algorithm employs a different search strategy and heuristic to explore the solution space. As a result, they may converge to different local minima or optima, leading to different values for design parameters such as wire diameter. The wire diameter (along with other parameters) is considered a result of the optimization process. It reflects the specific design that each algorithm proposes as the best solution under the given constraints and objective function. In theory, the tension/compression spring (TCS) design problem is formulated with fixed constraints for the wire diameter (d) across all algorithms. However, in this proposed scenario the optimization algorithms are allowed to independently search for their own optimal values of d as part of the design variables, therefore variations in the wire diameter occurred.

Table 7.
Comparing the TCS design problem solving of the HawkFish algorithm with different optimization methods.
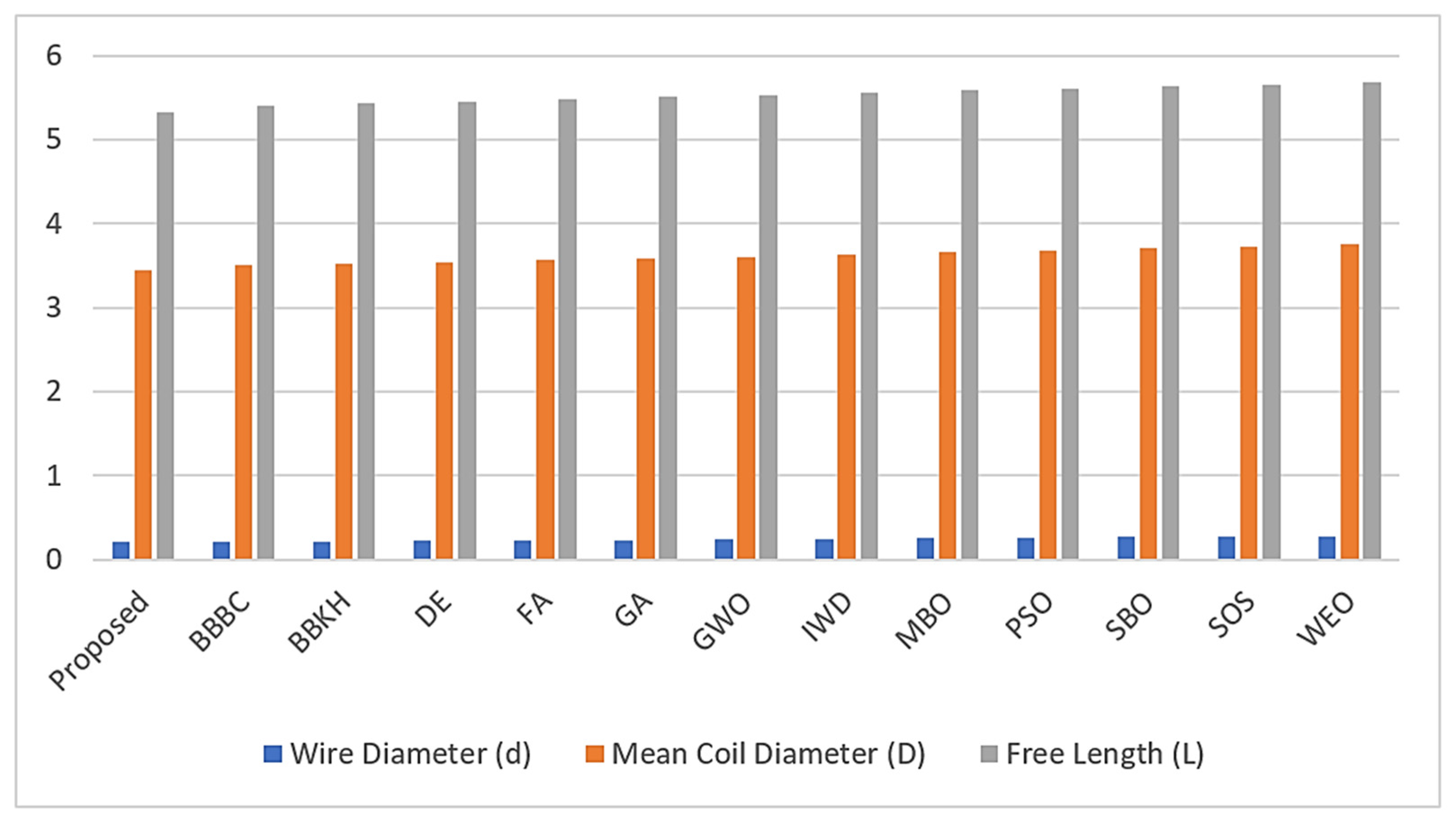
Each algorithm’s unique approach to exploring and exploiting the search space can lead to different optimized values for these parameters, demonstrating the diversity and effectiveness of each method in finding a solution to the TCS design problem. The objective is to minimize wire and coil diameters while satisfying other design constraints (cost and free length), and the proposed algorithm performed better than the other algorithms, as seen in Figure 12 and Figure 13 below:
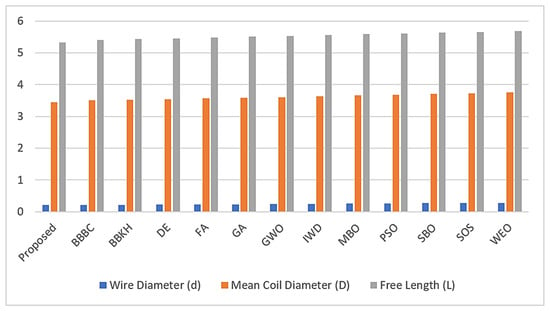
Figure 12.
Comparative performance of various optimization algorithms for tension/compression spring (tcs) design problem in terms of free length, wire diameter, and mean coil diameter, measured in mm.
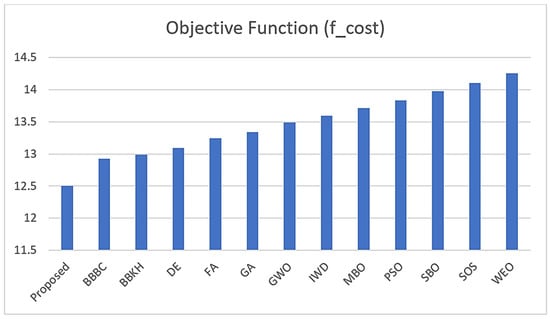
Figure 13.
Comparison of optimization algorithms for the tension/compression spring (TCS) design problem, showing objective function (f_cost) as constraints measured in MATLAB units.
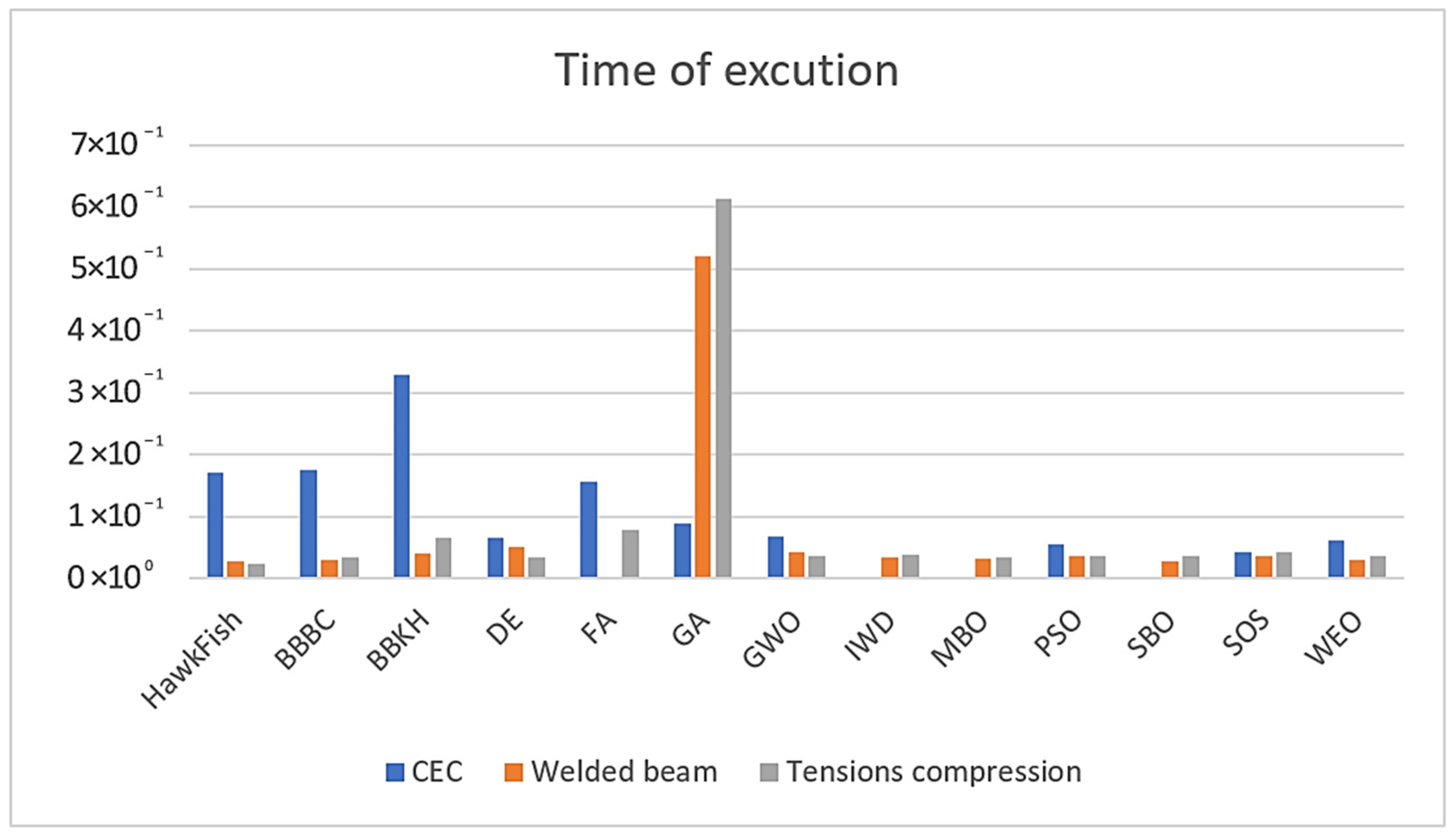
Figure 14 below illustrates the comparison of execution time for different optimization algorithms across three types of problems: CEC (2019), welded beams, and tensions compression. HawkFish proves to be a highly efficient algorithm in terms of execution time for most cases. The slight exception in the CEC case indicates room for improvement, but its better fitness performance compensates for this drawback. This suggests that HawkFish is not only computationally efficient, but also delivers high-quality solutions, which is a critical metric in optimization problems.
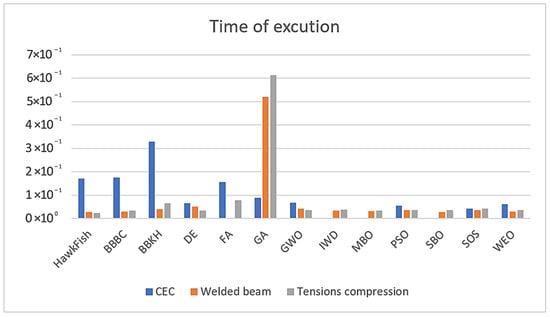
Figure 14.
Execution time comparison across SOTA algorithms.
In Figure 14, the x-axis represents the optimization algorithms, including HawkFish (the proposed algorithm), BBBC, BBKH, DE, FA, GA, GWO, IWD, MBO, PSO, SBO, SOS, and WEO. The y-axis shows the execution time in seconds, presented in scientific notation (e.g., 7.00 × 10−1 = 0.7 s) for clarity and consistency given the varying magnitudes of execution times. The HawkFish algorithm demonstrates superior efficiency with the lowest execution times across most cases (welded beam and tensions compression problems) while achieving competitive fitness in the CEC/GECCO 2019 case despite a slightly higher execution time.
6. Conclusions
The HawkFish optimization algorithm demonstrated superior performance in solving benchmark optimization problems, including the welded beam design problem and the tension/compression spring problem, when compared to state-of-the-art optimization methods such as BBBC, BBKH, DE, FA, GA, PSO, and GWO. The proposed algorithm exhibited low error rates and efficient convergence across various population sizes and iterations, as evidenced by the analysis. The algorithm maintained consistent accuracy with increasing population sizes while minimizing computation time, achieving an error rate as low as 0.31 with a population of 10 and an average error rate below 0.60 for larger populations. The proposed method outperformed other optimization techniques in optimizing both unimodal and high-dimensional CEC-06 benchmark functions. The HawkFish algorithm achieved significantly lower fitness function values compared to traditional algorithms, indicating its ability to explore and exploit the solution space effectively. The proposed algorithm also achieved the lowest cost functions in solving engineering design problems, such as the welded beam design problem and the tension/compression spring problem. The algorithm consistently provided optimal or near-optimal solutions, outperforming other algorithms across all evaluated dimensions, including beam thickness, length, and wire diameter. The success of the HawkFish algorithm can be attributed to the use of two opposing fitness functions, which allowed the algorithm to balance the exploration and exploitation of the search space. By using this approach, our algorithm was able to avoid local optima and achieve high-quality solutions in a shorter amount of time. The practical implications of our research are significant, as it has the potential to improve the efficiency and accuracy of various optimization tasks in different domains, such as engineering design, finance, and logistics, among others. The proposed method provides an effective and efficient optimization solution that can be used to address real-world optimization problems. In terms of future research, we believe that further investigation into the behavior and performance of our algorithm is necessary. This includes evaluating the algorithm’s performance on larger and more complex problems, as well as exploring the possibility of using different types of fitness functions. Additionally, more research can be conducted to determine the algorithm’s performance on mechanical problems with different characteristics and to further improve its efficiency.
Author Contributions
A.A. conceived the idea of the HawkFish Optimization Algorithm (HFOA) and designed its structure, incorporating the gender-based interaction mechanism inspired by hawkfish behavior. He implemented the algorithm in MATLAB, conducted simulations, and performed optimization experiments to evaluate its performance, as well as analyzing the results, preparing visualizations, and writing the majority of the manuscript. O.A. provided theoretical insights and feedback to refine the algorithm, contributed to the mathematical modeling and problem formulation, reviewed the experimental design, and validated the findings through comparative analysis with other optimization methods. Both authors contributed equally to the discussion of results. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rice, J.R. The Algorithm Selection Problem. Adv. Comput. 1976, 15, 65–118. [Google Scholar]
- Morales-Castañeda, B.; Zaldivar, D.; Cuevas, E.; Fausto, F.; Rodríguez, A. A better balance in metaheuristic algorithms: Does it exist? Swarm Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Kaur, K.; Kumar, Y. Swarm intelligence and its applications towards various computing: A systematic review. In Proceedings of the 2020 International Conference on Intelligent Engineering and Management (ICIEM), London, UK, 17–19 June 2020; pp. 57–62. [Google Scholar]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 74. [Google Scholar]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Mirjalili, A.S.; Saremi, M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Dafinescu, V. Review of Metaheuristics Inspired from the Animal Kingdom. Mathematics 2021, 9, 2335. [Google Scholar] [CrossRef]
- Squires, M.; Tao, X.; Elangovan, S.; Gururajan, R.; Zhou, X.; Acharya, U.R. A novel genetic algorithm-based system for the scheduling of medical treatments. Expert Syst. Appl. 2022, 195, 116464. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, D.; Shang, M.; Qi, S. Parameter Identification of Single-Phase Inverter Based on Improved Moth Flame Optimization Algorithm. Electr. Power Compon. Syst. 2019, 47, 456–469. [Google Scholar] [CrossRef]
- Kaul, S.; Kumar, Y. Nature-inspired metaheuristic algorithms for constraint handling: Challenges, issues, and research perspective. In Constraint Handling in Metaheuristics and Applications; Kulkarni, A.J., Mezura-Montes, E., Wang, Y., Gandomi, A.H., Krishnasamy, G., Eds.; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Kaur, G.; Arora, S. Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284. [Google Scholar] [CrossRef]
- Qiao, W.; Yang, Z. Solving large-scale function optimization problem by using a new metaheuristic algorithm based on quantum dolphin swarm algorithm. IEEE Access 2019, 7, 138972–138989. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2022, 6, 182–197. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, Q.; Wang, J.; Wang, Y. Application of multi-objective particle swarm optimization based on short-term memory and K-means clustering in multi-modal multi-objective optimization. Eng. Appl. Artif. Intell. 2022, 112, 104866. [Google Scholar] [CrossRef]
- Amuso, V.J.; Enslin, J. The Strength Pareto Evolutionary Algorithm 2 (SPEA2) applied to simultaneous multi-mission waveform design. In Proceedings of the 2007 International Waveform Diversity and Design Conference, Pisa, Italy, 4–8 June 2007; pp. 407–417. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, Z.; Zhang, G. A multiobjective evolutionary algorithm based on decomposition and probability model. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Cunha, M.; Marques, J. A new multiobjective simulated annealing algorithm—MOSA-GR: Application to the optimal design of water distribution networks. Water Resour. Res. 2020, 56, e2019WR025852. [Google Scholar] [CrossRef]
- Salam, M.A. Knacks of Evolutionary Mating Heuristics for Renewable Energy Source–Based Power Systems Signal Harmonics Estimation. Int. J. Energy Res. 2024, 48, 457–469. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Gazelle optimization algorithm: A novel nature-inspired metaheuristic optimizer. Neural Comput. Appl. 2023, 35, 4099–4131. [Google Scholar] [CrossRef]
- Caves, E.M.; de Busserolles, F.; Kelley, L.A. Sex differences in behavioural and anatomical estimates of visual acuity in the green swordtail, Xiphophorus helleri. J. Exp. Biol. 2021, 224, jeb243420. [Google Scholar] [CrossRef]
- Al-Janabi, S.; Kadhum, G. Synthesis Biometric Materials Based on Cooperative Among (DSA, WOA and gSpan-FBR) to Water Treatment. In Proceedings of the 12th International Conference on Soft Computing and Pattern Recognition (SoCPaR 2020), Virtual, 15–18 December 2020; Abraham, A., Ed.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Kemp, D.B.; Fox, M.J.; Coates, D.J. Distribution and abundance of four color morphs of Paracirrhites forsteri across habitats in the Red Sea. PLoS ONE 2017, 12, e0169079. [Google Scholar] [CrossRef]
- Drew, K.L.; Reece, M.; Augspurger, C.K. Genetic variation and population connectivity of Cirrhitichthys oxycephalus across geographic ranges. PeerJ 2023, 7, e18058. [Google Scholar] [CrossRef]
- Jankowski, J.A.; Walker, J.H.; White, M.E. Habitat selectivity and live coral dependence of hawkfishes (Cirrhitidae). PLoS ONE 2015, 10, e0138136. [Google Scholar] [CrossRef]
- Al-Janabi, S.; Salman, A.H. Optimization Model of Smartphone and Smart Watch Based on Multi Level of Elitism (OMSPW-MLE). In Artificial Intelligence for Cloud and Edge Computing; Misra, S., Kumar, T.A., Piuri, V., Garg, L., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Feng, Y.; Zhao, S.; Liu, H. Analysis of network coverage optimization based on feedback k-means clustering and artificial fish swarm algorithm. IEEE Access 2020, 8, 42864–42876. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, L.; Zhang, Z.; Fan, Q. Twin support vector machine based on improved artificial fish swarm algorithm with application to flame recognition. Appl. Intell. 2020, 50, 2312–2327. [Google Scholar] [CrossRef]
- Singh, S.P.; Dhiman, G.; Tiwari, P.; Jhaveri, R.H. A soft computing based multi-objective optimization approach for automatic prediction of software cost models. Appl. Soft Comput. 2021, 113, 107981. [Google Scholar] [CrossRef]
- Varga, D. Full-Reference Image Quality Assessment Based on an Optimal Linear Combination of Quality Measures Selected by Simulated Annealing. J. Imaging 2022, 8, 224. [Google Scholar] [CrossRef]
- Rosso, S.; Uriati, F.; Grigolato, L.; Meneghello, R.; Concheri, G.; Savio, G. An optimization workflow in design for additive manufacturing. Appl. Sci. 2021, 11, 2572. [Google Scholar] [CrossRef]
- Sharma, P.; Said, Z.; Kumar, A.; Nižetić, S.; Pandey, A.; Hoang, A.T.; Huang, Z.; Afzal, A.; Li, C.; Le, A.T.; et al. Recent advances in machine learning research for nanofluid-based heat transfer in renewable energy systems. Energy Fuels 2022, 36, 6626–6658. [Google Scholar] [CrossRef]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Alyasseri, Z.A.A. A novel hybrid multi-verse optimizer with K-means for text documents clustering. Neural Comput. Appl. 2020, 32, 17703–17729. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Deb, K.; Mallipeddi, R.; Pan, Q.K.; Qin, A.K. Problem Definitions and Evaluation Criteria for the CEC/GECCO 2019 Competition on Real-Parameter Single Objective Optimization, Technical Report; Nanyang Technological University: Singapore, 2019. [Google Scholar]
- Maree, S.C.; Alderliesten, T.; Bosman, P.A.N. Benchmarking HillVallEA for the GECCO 2019 Competition on Multimodal Optimization. arXiv 2019, arXiv:1907.10988. [Google Scholar]
- Abdullah, J.M.; Ahmed, T. Fitness Dependent Optimizer: Inspired by the Bee Swarming Reproductive Process. IEEE Access 2019, 7, 43473–43486. [Google Scholar] [CrossRef]
- Amin, A.A.H.; Aladdin, A.M.; Hasan, D.O.; Mohammed-Taha, S.R.; Rashid, T.A. Enhancing Algorithm Selection through Comprehensive Performance Evaluation: Statistical Analysis of Stochastic Algorithms. Computation 2023, 11, 231. [Google Scholar] [CrossRef]
- Wang, H.; Yi, J.H. An improved optimization method based on krill herd and artificial bee colony with information exchange. Memetic Comput. 2018, 10, 177–198. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Abasi, A.K. EEG signals denoising using optimal wavelet transform hybridized with efficient metaheuristic methods. IEEE Access 2019, 8, 10584–10605. [Google Scholar] [CrossRef]
- Alkharsan, A. HawkFish Optimization Algorithm, GitHub Repository. Available online: https://github.com/AliAlkharsan93/HawkFish-Optimization (accessed on 3 January 2025).
- Alomari, O.A.; Makhadmeh, S.N.; Al-Betar, M.A.; Alyasseri, Z.A.A.; Abu Doush, I.; Abasi, A.K.; Awadallah, M.A.; Abu Zitar, R. Gene selection for microarray data classification based on Gray Wolf Optimizer enhanced with TRIZ-inspired operators. Knowl.-Based Syst. 2021, 223, 107034. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Al-Betar, M.A.; Alyasseri, Z.A.A.; Abasi, A.K.; Khader, A.T.; Damaševičius, R.; Mohammed, M.A.; Abdulkareem, K.H. Smart Home Battery for the Multi-Objective Power Scheduling Problem in a Smart Home Using Grey Wolf Optimizer. Electronics 2021, 10, 447. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A. A novel hybrid grey wolf optimizer with min-conflict algorithm for power scheduling problem in a smart home. Swarm Evol. Comput. 2021, 60, 100793. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Thanh, P.D. Two levels approach based on multifactorial optimization to solve the clustered shortest path tree problem. Evol. Intell. 2020, 15, 185–213. [Google Scholar] [CrossRef]
- Hao, X.X.; Qu, R.; Liu, J. A unified framework of graph-based evolutionary multitasking hyper-heuristic. IEEE Trans. Evol. Comput. 2021, 25, 35–47. [Google Scholar] [CrossRef]
- Bali, K.K.; Gupta, A.; Ong, Y.-S.; Tan, P.S. Cognizant multitasking in multiobjective multifactorial evolution: MO-MFEA-II. IEEE Trans. Cybern. 2020, 51, 1784–1796. [Google Scholar] [CrossRef]
- Xu, Z.W.; Zhang, K.; Xu, X.; He, J.J. A fireworks algorithm based on transfer spark for evolutionary multitasking. Front. Neurorobotics 2020, 13, 109. [Google Scholar] [CrossRef]
- Lin, J.B.; Liu, H.L.; Xue, B.; Zhang, M.J.; Gu, F.Q. Multi-objective multi-tasking optimization based on incremental learning. IEEE Trans. Evol. Comput. 2020, 24, 824–838. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Wang, T.H.; Peng, X.G. MFEA-IG: A multi-task algorithm for mobile agents path planning. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 1–7 July 2020; pp. 1–7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).