Comparison of High-Frequency Circular Array Imaging Algorithms for Intravascular Ultrasound Imaging Simulations

Abstract

A circular array transducer with high frequency and small aperture size is highly desired for intravascular ultrasound (IVUS) imaging application. With the breakthrough of array transducer techniques, high-frequency circular array transducers with the advantages of high frame rate and high resolution have been developed and manufactured. Focusing on the development of a matched high-frequency imaging algorithms, this study introduces apodization functions into 55 MHz circular-array IVUS imaging, proposes a circular-array-specific apodization model, and breaks the lateral-resolution limit inherent to conventional delay-and-sum (DAS) beamforming. In the study, three typical algorithms—synthetic aperture (SA), apodized synthetic aperture (ASA), and sparse synthetic aperture (SSA)—are investigated in order to well achieve an effective imaging result for our newly derived circular array transducer with 55 MHz. In the scatterer’s simulation, at a depth of 1.5 mm, the ASA algorithm improves the lateral resolution from 260 μm for conventional SA to 175 μm (a 33% enhancement), while tripling the frame rate. Meanwhile, SSA maintains a resolution of 300 μm and reduces the data volume by 50%, laying the groundwork for real-time 3D imaging. Further phantom imaging testing shows that the SA algorithm has the best imaging effect on regional defects. The ASA algorithm has the best imaging effect on point defects while improving the imaging frame rate. This study provides insights and a foundation for optimizing circular-array intravascular ultrasound imaging, the proposed ASA model can be directly ported to existing 40–60 MHz circular-array IVUS systems, offering a new route for accurate early-plaque identification.

1. Introduction

Intravascular ultrasound (IVUS) can accurately assess the morphology of the vascular wall, optimize coronary interventional surgery, and thereby change the diagnosis and treatment of coronary artery diseases [1]. It can provide high-resolution images of the coronary artery vessel wall and is the gold standard for coronary artery wall imaging [2]. This offers significant evidence for the diagnosis of medical professionals. At present, there are two types of IVUS catheters available, namely phased-array and mechanical design [3]. The mechanical IVUS transducer achieves scanning by driving rotation through a motor [4]. Due to the mechanical binding and the inconsistent rotation of the transducers, nonuniform rotational distortion (NURD) is inevitable, which has been revealed in the existing studies [5]. Generally, a 360° rotation at a typical speed of 1800 rpm is conducted in the mechanical IVUS transducer in order to obtain the vascular cross-sectional image [6]. In this case, the corresponding frame rate of 30 frames per second is achieved, and the scanning speed of mechanical catheters is limited. Another disadvantage is that the side guidewire has a shadow effect, which leads to blurred images [7].

A solid-state IVUS transducer, which is also called a “multi-element phased array IVUS transducer” builds the image by electrical control of each element. In the solid-state catheter system, a wide range of small transducer arrays are mounted at the catheter tip around the cylinder, and a cross-sectional scan can be conducted by the ultrasonic beam [7]. Therefore, due to the narrow lateral beamwidth, it has good lateral resolution and there is no image distortion caused by rotational motion [8]. These circular array systems use synthetic aperture processing to generate images with higher lateral resolution than single-element transducers [9]. Furthermore, an IVUS array transducer can be adopted with beamforming during transmitting and receiving, which can increase the frame rates and decrease the point spread functions, thus optimizing the image quality [10].

Current commercial solid-state IVUS transducers have a center frequency of 20 MHz (Philips, Eagle Eye^®, San Diego, CA, USA), thus resulting in poor axial resolution (<170 µm) [11]. The traditional beam focusing imaging method uses multiple sub apertures to simultaneously emit multiple focused sound beams in order to improve imaging speed. However, there is crosstalk among the multiple focused sound beams, which affects the imaging quality [12]. Li et al. from North Carolina State University have developed a 40 MHz microfabrication 1–3 composite circular array for IVUS, demonstrating the broad application prospects of high-frequency circular arrays [13,14]. Especially, our research group recently innovatively prepared circular arrays based on PVDF-TrFE (polyvinylidene fluoride-trifluoroethylene) through spray coating, as shown in Figure 1. It demonstrates an extra high centra frequency of 55 MHz with wide bandwidth of 80% [15].

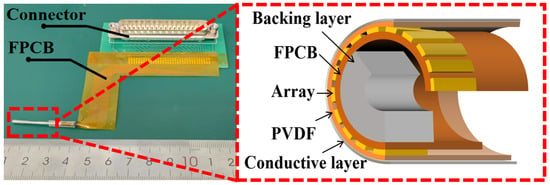
Figure 1. Structural diagram of circular array transducer.

Currently, imaging algorithms for single-element mechanical transducers are relatively mature. Yu et al. reported a method employing virtual source synthetic aperture (VSSA) and coherence factor weighting (CFW) for single-element mechanical IVUS, which improved the lateral resolution from 165 to 524 μm to 126–143 μm [16]. Lindsey et al. introduced minimum variance (MV) beamforming and the phase coherence factor (PCF) into IVUS, improving spatial resolution by 41.7% [17]. Kang et al. established a theoretical model to explore the effectiveness of synthetic aperture focusing (SAF) and coherence factor weighting (CFW) in single-element IVUS, and the results indicated that their performance was unsatisfactory [18]. With the development of these derived circular array transducers, less work however is conducted on in-depth research on imaging algorithms [19,20,21,22]. Tekes et al. employed synthetic phased-array technology to simplify the front-end electronics and improve imaging speed. However, their transducer is a forward-looking circular ring array [23]. Recently, Li et al. proposed an eccentric cylindrical wave composite imaging method, but its virtual point source is outside the circular array [24]. Tan et al. introduced three kinds of circular array endoscopic imaging algorithms, but their application scenarios are mainly for larger tissue organs [25], where transducers with proposed working frequency below 30 MHz are generally employed. Considering the application of IVUS imaging, the small aperture size of transducer and extra high centra frequency of such as above 55 MHz are generally needed in order to achieve an improved image quality of high-resolution. In this case, the algorithm for endoscopic imaging of such high-frequency circular array transducers should be well renewed considering the different processes of ultrasonic transmission.

In this work, we investigated synthetic aperture ultrasound imaging algorithms applied to intravascular high-frequency circular arrays. We firstly elaborate on the principles of synthetic aperture (SA) imaging, apodized synthetic aperture (ASA) imaging, and sparse synthetic aperture (SSA) imaging. Simulation study of circular array intravascular imaging using FOCUS fast ultrasound simulator. Analyzed the influence of the center frequency and number of elements of a circular array on imaging quality. The resolution of SA imaging algorithm, ASA algorithm, and SSA algorithm were compared, indicating that ASA imaging algorithm has certain superiority in circular arrays.

2. Materials and Methods

2.1. Synthetic Aperture Algorithm

The SA imaging algorithm originated from radar and sonar sensing, and subsequently many new algorithms were derived based on this technology [26]. Different from the traditional focused imaging, the SA algorithm achieves composite imaging by emitting non-focused waves, and at the same time, time delay compensation enables focusing at any depth [22]. Focusing is performed during the post-processing stage, allowing SA to maintain an advantage in imaging frame rates.

SA algorithms sequentially excite each array element to emit signals. All elements receive the echo signals, which are then processed and image [27]. After completing a full scan of the emitted signals, the images obtained from single-element emissions are coherently superimposed to achieve an image equivalent to that generated by a larger aperture array emission.

As shown in Figure 2a the time taken for the signal emitted by the i-th transmitting array element e_i to propagate to the point (m, n) is:

$${\mathrm{t}}_1\left(\mathrm{i},\mathrm{m},\mathrm{n}\right)={\displaystyle \frac{\left|\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right)-\left(\mathrm{m},\mathrm{n}\right)\right|}{\mathrm{c}}},$$

(1)

where c represents the speed of sound waves propagating in the medium. The time taken for the reflected echo to propagate from the point (m, n) to the j-th receiving array element e_j is:

$${\mathrm{t}}_2\left(\mathrm{j},\mathrm{m},\mathrm{n}\right)={\displaystyle \frac{\left|\left({\mathrm{x}}_{\mathrm{j}},{\mathrm{y}}_{\mathrm{j}}\right)-\left(\mathrm{m},\mathrm{n}\right)\right|}{\mathrm{c}}},$$

(2)

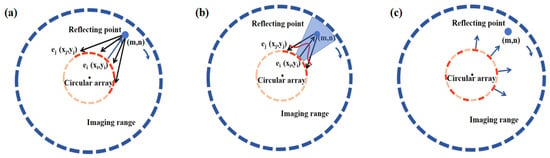
Figure 2. Schematic Diagrams of Imaging Algorithms: (a) SA Algorithm, (b) ASA Algorithm, and (c) SSA Algorithm.

Therefore, the two-way propagation time of the acoustic wave is:

$${\mathrm{t}}_{\mathrm{sa}}\left(\mathrm{i},\mathrm{j},\mathrm{m},\mathrm{n}\right)={\mathrm{t}}_1+{\mathrm{t}}_2,$$

(3)

Let RF (j, t) denote the echo signal received by the j-th receiving array element e_j. The echo signal intensity at point (m, n) can be superimposed based on the signal propagation time:

$${\mathrm{s}}_{\mathrm{s}\mathrm{a}}\left(\mathrm{i},\mathrm{m},\mathrm{n}\right)={\sum }_{\mathrm{k}={\mathrm{j}}_1}^{{\mathrm{j}}_{\mathrm{n}}}\mathrm{R}\mathrm{F}\left[\mathrm{k},{\mathrm{t}}_{\mathrm{s}\mathrm{a}}\left(\mathrm{i},\mathrm{k},\mathrm{m},\mathrm{n}\right)\right],$$

(4)

where k represents the number of all receiving transducers. After all selected transmitting array elements have emitted signals, coherent superposition of multiple image data is performed to obtain the echo intensity signal at point (m, n):

$${\mathrm{I}}_{\mathrm{s}\mathrm{a}}(\mathrm{m},\mathrm{n})={\sum }_{\mathrm{p}={\mathrm{i}}_1}^{{\mathrm{i}}_{\mathrm{N}}}{\sum }_{\mathrm{k}={\mathrm{j}}_1}^{{\mathrm{j}}_{\mathrm{n}}}\mathrm{R}\mathrm{F}\left[\mathrm{k},{\mathrm{t}}_{\mathrm{s}\mathrm{a}}\left(\mathrm{k},\mathrm{l},\mathrm{m},\mathrm{n}\right)\right],$$

(5)

Among them, the element sequences i₁, i₂, …, i_N represent the element sequences involved in SA emission.

2.2. Apodized Synthetic Aperture Algorithm

ASA imaging sequentially excites each transmitting array. Meanwhile, receiving array elements located within 1/6 of the total number of array elements around the transmitting array perform signal reception. As shown in Figure 2b, when delay-and-sum processing is applied to signals received by the array for shadow region reconstruction, an apodization function is used to process the data of the receiving array elements. The apodization function assigns greater weight to signals received by array elements closer to the transmitting array during superposition processing, while signals from elements farther away have less impact on the superposition result.

As shown in Equations (1)–(3), the two-way propagation time of the acoustic wave is denoted as t_sa. Let the apodization function be R (i, j). As illustrated in Figure 2b, the echo signal received by the j-th array element e_j is RF (j, t). The echo signal intensity at point (m, n) can be superimposed based on the signal propagation time:

$${\mathrm{s}}_{\mathrm{s}\mathrm{a}}(\mathrm{i},\mathrm{m},\mathrm{n})={\sum }_{\mathrm{k}={\mathrm{j}}_1}^{{\mathrm{j}}_{\mathrm{n}}}\mathrm{R}(\mathrm{i},\mathrm{j})\times \mathrm{R}\mathrm{F}\left[\mathrm{k},{\mathrm{t}}_{\mathrm{s}\mathrm{a}}\left(\mathrm{i},\mathrm{k},\mathrm{m},\mathrm{n}\right)\right],$$

(6)

where k represents the number of all receiving transducers. After all selected transmitting array elements have emitted signals, coherent superposition of multiple image data is performed to obtain the echo intensity signal at point (m, n):

$${\mathrm{I}}_{\mathrm{s}\mathrm{a}}(\mathrm{m},\mathrm{n})={\sum }_{\mathrm{p}={\mathrm{i}}_1}^{{\mathrm{i}}_{\mathrm{N}}}{\sum }_{\mathrm{k}={\mathrm{j}}_1}^{{\mathrm{j}}_{\mathrm{n}}}\mathrm{R}(\mathrm{i},\mathrm{j})\times \mathrm{R}\mathrm{F}\left[\mathrm{k},{\mathrm{t}}_{\mathrm{s}\mathrm{a}}\left(\mathrm{k},\mathrm{l},\mathrm{m},\mathrm{n}\right)\right],$$

(7)

Among them, the element sequences i₁, i₂, …, i_N represent the element sequences involved in SA emission.

2.3. Sparse Synthetic Aperture Algorithm

Based on SA algorithms, to further improve the imaging frame rate, every other array element is selected for transmitting signals. The sparse synthetic aperture imaging algorithm is a rapid imaging method based on non-focused wave transmission. As shown in Figure 2c, all transmitting elements are uniformly distributed. Since the emission direction of a single element is limited, the elements on both sides of each transmitting element are used for reception. Similarly, after the scanning is completed, the signals are processed using the delay-and-sum method. Based on the previously described Equations (1)–(5), the echo signal intensity at point (m, n) in the sparse synthetic aperture approach can be obtained as:

$${\mathrm{I}}_{\mathrm{s}\mathrm{a}}(\mathrm{m},\mathrm{n})={\sum }_{\mathrm{p}={\mathrm{z}}_1}^{z_{\mathrm{N}}}{\sum }_{\mathrm{k}={\mathrm{j}}_1}^{{\mathrm{j}}_{\mathrm{n}}}\mathrm{R}\mathrm{F}\left[\mathrm{k},{\mathrm{t}}_{\mathrm{s}\mathrm{a}}\left(\mathrm{k},\mathrm{l},\mathrm{m},\mathrm{n}\right)\right]$$

(8)

where the element sequence z₁, z₃, z₅, …, z_N represents the indices of the array elements that transmit acoustic waves. It should be noted that only the odd-numbered elements are selected in sequence z. Since only half of the array elements are scanned, the imaging frame rate is doubled.

3. Simulation

In the study, the FOCUS toolbox for MATLAB (R2023b; MathWorks, Natick, MA, USA) was used for theoretical simulation of ultrasound imaging. A circular array simulation model was established to analyze the impact of array element numbers and frequencies on imaging resolution. The advantages and disadvantages of SA algorithms, ASA algorithms, and SSA algorithms were also compared. The diameter of the circular array is 1.5 mm and it is placed in the middle of the blood vessel. A scatterer model was constructed, with scattering points placed at depths of 1 mm, 1.5 mm, 2 mm, and 2.5 mm from the center of the circular array, as shown in Figure 3a, to demonstrate the imaging capability near the vascular intima. Similarly, scattering points were placed at depths of 3 mm, 4 mm, 5 mm, and 6 mm from the center of the circular array, as shown in Figure 3b, and the image resolution at different depths was calculated based on the imaging results. Subsequently, the central frequency and number of the array were varied to compare resolution changes. For phantom imaging experiments simulating blood vessels, the phantom was filled with randomly distributed scatterers. It consisted of a circular ring with an inner diameter of 3 mm and an outer diameter of 5 mm. High-echo circular regions with radii of 0.2 mm, 0.3 mm, and 0.4 mm were set at a depth of 2 mm from the array center, as shown in Figure 3c. Additionally, four scatterers were added, uniformly distributed between depths of 1.8 mm and 2.1 mm, with a distance of 0.1 mm between adjacent scatterers. After acquiring the echo signals, image processing including Hilbert transformation and envelope analysis was performed to obtain the final images.

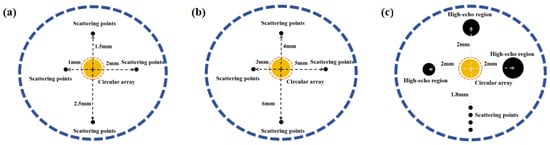
Figure 3. Schematic illustration of the simulation models: (a) scatterer distribution at depths of 1–2.5 mm, (b) scatterer distribution at depths of 3–6 mm, and (c) structure of the vascular phantom.

4. Results and Discussion

Figure 4 shows the imaging results of scattering phantoms using circular arrays with center frequencies of 20 MHz, 55 MHz, and 90 MHz. The array consists of 32 elements with a diameter of 1.5 mm. The results show that as the center frequency of the array increases, the imaging accuracy for scatterers significantly improves and artifacts are markedly reduced. However, in practical applications, 90 MHz ultrasound suffers from severe energy attenuation and limited penetration depth, making it unsuitable for IVUS [28]. In contrast, while the 20 MHz array provides sufficient penetration depth, its resolution is relatively low. Therefore, the 55 MHz transducer achieves an optimal balance between penetration depth and imaging resolution.

Figure 4. Scattering phantom imaging results using circular arrays at different frequencies: (a) 20 MHz, (b) 55 MHz and (c) 90 MHz.

We employ the −6 dB lateral resolution to evaluate imaging performance, defined as the width between the points in the lateral direction of the ultrasound beam where the signal amplitude drops to −6 dB (corresponding to the half-power level) relative to the peak value [29]. This metric is commonly characterized by the −6 dB width of the point spread function (PSF) in the lateral direction and is used to quantify the minimum resolvable distance of the system in that direction. As shown in Figure 5a,b, the −6 dB lateral and axial resolution measurements for the 20 MHz, 55 MHz, and 90 MHz arrays are presented. Compared to the 20 MHz array, the 55 MHz array exhibits significantly improved overall lateral resolution, characterized by a narrower main lobe width and lower sidelobe levels. In comparison with the 55 MHz array, the 90 MHz array shows only a marginal improvement in lateral resolution. The axial resolution in ultrasound imaging is determined by the product of the wavelength and the number of cycles in the transmitted pulse [30]. According to theoretical calculations, the axial resolution is approximately half the product of the wavelength and the number of cycles in the transmitted pulse. Taking the 55 MHz element as an example, with a pulse consisting of 2 cycles and an assumed speed of sound of 1500 m/s in the medium, the theoretical axial resolution is approximately 27 µm. Our simulation results yield an axial resolution of about 24 µm, which agrees well with the theoretical value within acceptable error margins. Similarly, the experimentally measured axial resolutions for the 20 MHz and 90 MHz arrays are 62 µm and 14 µm, respectively, closely matching their theoretical values of 75 µm and 16 µm. Furthermore, since the simulated medium was set as lossless, the axial resolution remains nearly unaffected by changes in depth.

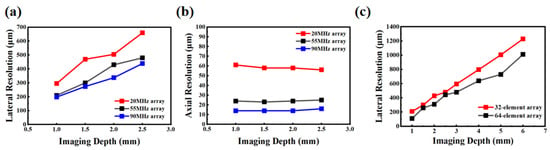
Figure 5. Resolution analysis of circular arrays: (a) lateral resolution of 20 MHz, 55 MHz, and 90 MHz; (b) axial resolution of 20 MHz, 55 MHz, and 90 MHz; (c) lateral resolution of 32-element and 64-element arrays.

The circular array has a diameter of 1.5 mm and operates at a center frequency of 55 MHz. Figure 5c and Figure 6 show the scattering phantom imaging results for 32- and 64-element arrays, respectively. It can be seen that the 64-element array provides better imaging quality with reduced side lobe effects and fewer artifacts. It also presents the lateral resolution calculations based on the −6 dB criterion. Within the depth range of 1–6 mm, the 64-element array achieves higher lateral resolution, characterized by a narrower main lobe width and superior image quality. At depths up to 3 mm, the lateral resolutions of the 64-element and 32-element arrays are comparable. Beyond 3 mm depth, the 64-element array demonstrates a significant improvement in lateral resolution.

Figure 6. Scattering phantom imaging results using circular arrays over a depth range of 1–6 mm: (a) and (b) 32-element array; (c,d) 64-element array.

Figure 7 presents the scattering phantom imaging results for SA, ASA, and SSA. Figure 8 shows the lateral resolution of the scatterers calculated at −6 dB. Figure 9 shows the phantom imaging results for SA, ASA, and SSA. As detection depth increases, lateral resolution decreases, with overall resolution ranging from 100 to 1200 μm. Within 3 mm of the array center, the ASA algorithm achieves the highest lateral resolution, while the SSA algorithm performs the worst. Compared to SA, both ASA and SSA improve imaging frame rates to varying degrees. However, beyond a depth of 3 mm, the resolutions of SA and SSA are similar, with ASA showing the poorest lateral resolution performance. Additionally, depth variation impacts the SSA algorithm the least, followed by SA, while ASA is most affected by depth changes.

Figure 7. Imaging results of scattering phantom using different algorithms: (a,d) SA algorithm, (b,e) ASA algorithm, and (c,f) SSA algorithm.

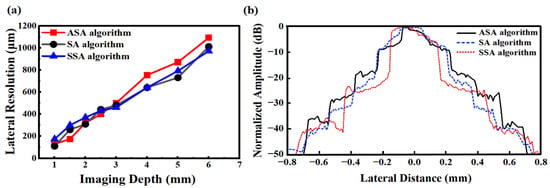
Figure 8. Comparison of SA, ASA, and SSA imaging algorithms: (a) lateral resolution and (b) normalized amplitudes from scatterers at 1.5 mm depth.

Figure 9. Phantom imaging results using SA, ASA, and SSA algorithms: (a) SA algorithm, (b) ASA algorithm, and (c) SSA algorithm.

Figure 8b presents a comparison of normalized amplitudes from scatterers at 1.5 mm depth. As shown, the SSA algorithm achieves the narrowest main lobe width while simultaneously maintaining the lowest sidelobe amplitude. In contrast, the SA and ASA techniques demonstrate comparable main lobe widths; however, the SA algorithm exhibits lower sidelobe amplitude than the ASA algorithm.

Phantom imaging shows that the SA algorithm offers the best imaging for highly reflective circular areas. The ASA algorithm produces artifacts in the defect imaging of circular areas, but it has the best effect in suppressing noise signals in defect-free areas. The SSA algorithm’s phantom imaging performance is relatively poor. However, both ASA and SSA have shortened the imaging time, with the imaging speed increasing by at least twice compared to SA. In scattering point phantom imaging, the ASA algorithm can achieve the best imaging effect with the least artifacts.

The selection of transducer frequency affects imaging resolution and penetration depth, so frequency selection must balance both aspects. Axial resolution is determined by frequency: when the transducer frequency is low, the axial resolution of the image would decrease. Lateral resolution is determined by beam width. Therefore, to achieve good imaging quality, the element frequency should not be lower than 20 MHz. For circular arrays, a higher center frequency is not always preferable. Due to current fabrication limitations, the maximum number of elements reported in the literature for such array transducers is 64. For a circular array with a diameter of 1 mm, this results in an inter-element pitch of approximately 49.1 µm. According to grating lobe theory, to avoid the formation of grating lobes, the operating wavelength must be no shorter than twice the pitch—i.e., at least 98.2 µm. Using a sound speed of 1540 m/s in water, this corresponds to a maximum allowable frequency of approximately 15.7 MHz [31]. In practice, for circular array transducers used in IVUS, the operating frequency should be even lower to effectively suppress grating lobes. Furthermore, as the center frequency increases, the achievable imaging depth correspondingly decreases. When the frequency reaches 80 MHz, the penetration depth of ultrasound in blood vessels is only 2–3 mm, making it difficult to meet practical clinical requirements [32]. The circular array designed in this study with a frequency of 55 MHz achieves good results in balancing resolution and penetration depth.

The fabrication of high-frequency arrays is challenging and involves considerations such as array dimensions, material selection, and processing techniques [33]. First, regarding array size, transducers for IVUS require a small aperture—typically less than 1.5 mm in diameter. Integrating dozens of elements within this limited aperture necessitates a very small inter-element pitch to minimize crosstalk and grating lobe artifacts [34]. However, such tight spacing can lead to variations in element bandwidth due to mutual coupling and fabrication tolerances [35]. Material selection also presents significant challenges. To fabricate a circular array, the materials must exhibit good flexibility and biocompatibility. Unlike conventional linear arrays, which are typically fabricated on flat, two-dimensional substrates, circular arrays must be integrated onto curved surfaces, introducing complications related to curvature-induced stress and mechanical strain. Moreover, the thickness of the piezoelectric layer directly affects the transducer’s frequency; achieving high-frequency elements requires precise control over the material thickness. Consequently, producing a stable, high-performance, small-aperture high-frequency circular array remains a considerable technological challenge.

The ASA algorithm only requires data from nine surrounding elements of the transmitting array during delay-and-sum processing, while most other elements remain inactive. Therefore, three sets of data can be collected simultaneously during the data acquisition phase, reducing the acquisition time by 1/3. Throughout the entire data acquisition and imaging process, a post-focus approach is adopted, concentrating the main computations on backend processing. However, with the increasing speed of computers, the backend delay-and-sum time becomes essentially fixed and short. So, the imaging time is determined by the data acquisition stage. The ASA algorithm improves the imaging frame rate while maintaining relatively low artifact levels around scatterers.

Given that target vascular diameters in practical applications typically measure approximately 3 mm with an upper limit of 5 mm, this imaging depth configuration satisfies the requirements for superficial vascular imaging. The imaging frame rate is primarily limited by the round-trip acoustic propagation time, with negligible data processing time and sound velocity set at 1540 m/s. When implementing the 64-element SA imaging algorithm, the maximum acoustic path length from transmission to reception was approximately 5 mm. Based on this path length, the calculated frame rate for the SA algorithm was approximately 4.8 kHz. Implementation of the SSA algorithm yielded a twofold increase in imaging speed relative to the SA approach, corresponding to a frame rate of approximately 10 kHz. The ASA algorithm achieved further enhancement, increasing imaging speed to three times that of the SA method.

Compared with alternative focusing imaging methods, the SA algorithm offers distinct advantages through its capability for coherent compounding at multiple focal depths, effectively reducing imaging artifacts. However, this approach typically employs a single-element transmission mode, resulting in limited transmitted energy that constrains penetration depth. Consequently, further optimization of imaging quality remains necessary. In ultrasound imaging, side-lobe interference presents an inherent limitation. In addition to the algorithmic suppression of the side lobes, the optimized array design is also a key method for improvement. For instance, employing advanced microfabrication techniques to increase element density or reduce element pitch in circular arrays can significantly enhance spatial resolution.

Balancing high resolution and high imaging frame rate is a critical challenge: resolution directly determines image quality, while frame rate dictates whether real-time imaging can be achieved. The center frequency of the transducer plays a decisive role in resolution—higher center frequencies generally yield superior resolution. However, excessively high frequencies lead to insufficient penetration depth and increased artifacts. Therefore, under the premise of meeting the clinically required imaging depth, the inter-element pitch should be minimized as much as possible to enhance spatial resolution. Furthermore, artificial intelligence (AI)-based algorithms can be integrated to effectively extract useful signals or enable automated defect detection, thereby further improving image resolution and diagnostic efficiency. Regarding frame rate, circular array transducers inherently offer a structural advantage over single-element transducers in terms of imaging speed. Additionally, techniques such as compressed sensing can achieve comparable resolution with significantly fewer sampled data points [36]. In terms of computational efficiency, beam compression methods can be employed to perform focusing in the frequency domain, substantially accelerating image reconstruction and overall imaging speed [37].

5. Conclusions

This paper delves into the imaging algorithms for circular array transducers in intravascular high-frequency ultrasound imaging. It comprehensively explores how the number of array elements and working frequency affect imaging quality, highlighting the role of high-frequency transducers in enhancing imaging resolution. Furthermore, it examines strategies to optimize imaging frame rate, leveraging the inherent high-frame-rate advantage of circular arrays. Under the intravascular imaging framework, we meticulously study three imaging algorithms—SA, ASA, and SSA—which are tailored to the key features of circular arrays and high frequency. The resolutions of 55 MHz and 20 MHz transducers were compared within the depth range of 1–2.5 mm. Results show the 55 MHz transducer triples axial resolution, matching theoretical predictions. Phantom experiments shows that an improved lateral resolution is achieved in the ASA algorithm at depths below 2 mm, while that is obtained in the SA algorithm at 2–2.5 mm depths. Observing the normalized amplitude, the main lobe width represents resolution. At a resolution of −6 dB, the main lobe width of the ASA algorithm is the narrowest. However, at around −20 dB, the SSA algorithm has the minimum main lobe width.

The theoretical and simulation work in this study lays a solid foundation for future experimental validation and algorithm optimization. By filling a key research gap, it provides a new paradigm and practical path for developing high-frequency circular array imaging technology in the field of IVUS.