Abstract
For orthogonal time–frequency space (OTFS) systems in high-mobility scenarios, traditional signal detection algorithms face challenges due to their reliance on channel state information (CSI), requiring excessive pilot overhead. Meanwhile, based on convolutional neural network (CNN) detection suffer from insufficient signal feature extraction, the message passing (MP) algorithm exhibits low efficiency in iterative signal updates. This paper proposes a signal detection method for an OTFS system based on feature fusion and a CNN (MP-WCNN), which employs wavelet decomposition to extract multi-scale signal features, combining MP enhancement for feature fusion and constructing high-dimensional feature tensors through channel-wise concatenation as CNN input to achieve signal detection. Experimental results demonstrate that the proposed MP-WCNN method achieves approximately 9 dB signal-to-noise ratio (SNR) gain compared to the MP algorithm at the same bit error rate (BER). Furthermore, the proposed method operates without requiring pilot assistance for CSI acquisition.
1. Introduction
In recent years, due to the rapid development of transportation networks such as high-speed railways and expressways, as well as the demand for emerging application scenarios like vehicle-to-vehicle communication, millimeter-wave communication, low-Earth-orbit (LEO) satellite communication, how to achieve reliable wireless communication in complex environments has become a critical research direction [1]. In high-speed mobile scenarios, the channel exhibits significant delay spread and Doppler shift characteristics, which leads to doubly selective fading. This poses severe challenges for traditional orthogonal frequency division multiplexing (OFDM) technology: the orthogonality of subcarriers is easily disrupted by Doppler spread, which causes serious inter-carrier interference (ICI). Meanwhile, the time-varying multipath effect results in time–frequency two-dimensional dispersion of signals, drastically degrading transmission performance. To address these challenges, the orthogonal time–frequency space (OTFS) technology has emerged.
Proposed by Hadani et al. [2] in 2017, this unique modulation scheme spreads the original information across the entire transmitted signal. In the delay-Doppler (DD) domain, the channel is sparse and changes slowly, while also reducing the complexity of signal detection and channel estimation and decreasing the reliance on channel state information (CSI). This enhances the system’s performance and reliability, making it highly valuable for applications. Currently, OTFS is a candidate key technology for sixth-generation (6 G) mobile communication systems [3,4,5,6].
However, OTFS technology still faces significant challenges in signal detection. Current mainstream linear detection algorithms such as Linear Minimum Mean Square Error (LMMSE) algorithms [7,8] exhibit degraded accuracy under high-SNR conditions, while theoretically optimal nonlinear algorithms like Maximum Likelihood (ML) and Maximum Ratio Combining (MRC) suffer from prohibitive computational complexity that limits practical implementation. To address these limitations, message passing (MP) algorithms have been introduced to OTFS detection due to their superior performance in sparse signal recovery [9]. Nevertheless, conventional MP algorithms and their improved variants [10,11,12,13] are inherently constrained by slow convergence rates and excessive iteration requirements. Concurrently, deep learning techniques have emerged as promising solutions for signal detection, particularly through convolutional neural network (CNN) architectures that effectively capture spatial correlations in delay-Doppler (DD) domain signals [14,15]. However, CNN model training is complex. When extracting signal features through parameter learning of multi-layer convolution kernels, its ‘‘end-to-end’‘ learning method requires a large number of data samples for training support. For the DD domain signal of OTFS, the dataset is insufficient in size, and the model is prone to overfitting, and its generalization ability is reduced. The literature [16,17] combines traditional algorithms with deep learning, using MP algorithms to enhance data to enrich the datasets and improve the performance of CNN. However, the noise in the signal will cause the algorithm to accumulate errors during MP [18] and updates; it reduces detection performance and cannot fully mine the multi-scale signal characteristics of the signal.
In order to solve the above shortcomings, wavelet analysis is introduced in this paper [19]. Through wavelet decomposition, the signal and noise can be effectively separated, the multi-scale signal characteristics can be extracted, the characteristic tensors can be constructed in combination with the MP-enhanced signal. This method not only fully utilizes the advantages of MP algorithm in sparse recovery, but also effectively improves the signal detection performance by denoising the signal. Meanwhile, it enhances the channel feature extraction capability of CNN to achieve better bit error rate performance.
To clearly present the research, the subsequent chapters of this paper are organized as follows: Section 2 “Materials and Methods”: Firstly, the OTFS system model is established, including the principles of signal modulation and demodulation, the channel characteristics in the delay-Doppler domain, and the mathematical basis of wavelet decomposition. Subsequently, the design of the proposed MP-WCNN detection method is elaborated in detail, covering the wavelet multi-scale feature extraction process, the feature fusion mechanism of the MP enhancement module, as well as the CNN structure and training parameter configuration. Section 3 “Results”: Through model training and simulation experiments, the bit error rate (BER) performance of the proposed method under signal-to-noise ratios (SNRs) ranging from 0 to 30 dB is verified, and comparative analyses are conducted with traditional MP algorithms, pure CNN detection methods, and other relevant approaches. Section 4 “Discussion”: The limitations of the MP-WCNN method are thoroughly discussed, including its adaptability to extreme channel conditions (such as ultra-dense multipath) and the optimization directions for computational complexity. Section 5 “Conclusions”: The main contributions of this paper are summarized, and future research directions in dynamic channel modeling and lightweight network design are prospected.
This paper addresses the challenges faced by signal detection in OTFS systems under high-mobility scenarios and proposes an innovative hybrid detection architecture called MP-WCNN. The main contributions of this paper can be summarized in the following three aspects:
- (1)
- A collaborative hybrid paradigm of ‘feature preprocessing–prior enhancement–deep learning’ is proposed: Unlike the existing purely model-driven or data-driven approaches, and distinct from simple algorithm concatenation, this paper pioneeringly integrates wavelet multi-scale analysis (feature preprocessing), the message passing algorithm (model-driven prior enhancement), and convolutional neural networks (data-driven feature learning) in a deeply fused manner. Through a meticulously designed three-level architecture, this paradigm achieves complementary advantages of the two methodologies, providing a new pathway for OTFS detection.
- (2)
- Systematically addressing key gaps in current research: This study directly tackles the pain points of traditional MP algorithms, such as low iterative efficiency and error accumulation, as well as the limitations of purely deep learning models, which rely on large datasets, have unclear physical feature interpretability, and are prone to overfitting. By employing a feature fusion strategy, physical priors are injected into the deep learning model in the form of multi-channel tensors, significantly enhancing feature quality and model robustness, while reducing dependency on data volume and model complexity, thereby achieving substantial performance improvements.
- (3)
- Balancing performance improvement with practicality and complexity optimization: The proposed MP-WCNN framework reduces the complexity requirements of the backend CNN model through a frontend feature enhancement module. The final solution demonstrates significant computational efficiency advantages over traditional iterative algorithms and shows great potential for application in real-time communication systems.
2. Materials and Methods
OTFS proposes a two-dimensional modulation technology in the DD domain. Through two-dimensional transformation, the two dispersion channels of time and frequency can be converted into the DD domain to become an approximately non-fading channel [20]. The block diagram of the modulation and demodulation technology of this system is shown in Figure 1.
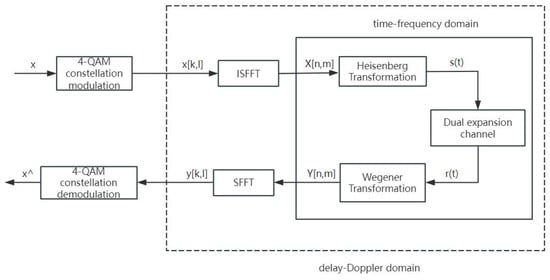
Figure 1.
OTFS modem block diagram.
2.1. Transmitter
In an OTFS system, let N be the number of subcarriers and M be the number of OTFS symbols. The generated random bits undergo 4-QAM modulation to yield an M × N matrix of data symbols, which are then mapped onto the DD domain grid x[k, l], the inverse symplectic finite Fourier transform (ISFFT). These DD domain symbols are transformed into time–frequency domain symbols X[n, m], populating the time–frequency signal grid. This transformation is mathematically formulated in (1):
After obtaining discrete time–frequency domain symbols X[n, m], the Heisenberg transformation is used to convert X[n, m] into a continuous time-domain transmission signal, as expressed by Formula (2):
represents the pulse shaping waveform at the OTFS transmitter. When is a rectangular pulse waveform, the Heisenberg transformation becomes the traditional discrete Fourier and the inverse discrete Fourier transform.
2.2. Dual Expansion Channel
In doubly dispersive channels, the channel is time-varying. The time-domain impulse response of the channel is expressed by Equation (3)
where denote the channel gain, delay, and Doppler shift, respectively, and p represents the number of paths. The channel gain is a complex random variable, which follows a Rayleigh distribution with a uniformly distributed phase. The gains of all paths are normalized, with the normalized power distribution being [1/3, 1/3, 1/3]. The delays and Doppler shifts are discretized as , where and represent integer multiples of delay taps and Doppler taps, respectively, denotes the fractional Doppler shift. To avoid inter-symbol interference, a cyclic prefix (CP) is inserted, and the CP length should be greater than the maximum delay .
2.3. Receiver
After the sending signal passes through the wireless channel, the received signal r(t) of the OTFS system is obtained, as expressed by Formula (4):
At the receiving end, the receiving end pulse shaping waveform can be used for matching filtering, then the received data can be obtained. For example, Formula (5) indicates that the time–frequency domain received signal:
Then, sample as interval to obtain discrete time–frequency domain reception signals. This step is called the Wegener transform, as expressed by Formula (6):
The time–frequency domain received signal Y[n, m] is processed using SFFT to obtain the received signal in the time-delay-Doppler domain, as expressed as Formula (7):
According to the derivation of the signal processing flow of the sending and receiving ends of the OTFS system, the input and output relationship of the signal in the DD domain is shown in Formula (8):
where , H is a multiple cycle matrix of for describing the channel, and is additive Gaussian white noise.
In order to realize signal detection based on deep learning in the OTFS system, the input–output relationship of Equation (8) is converted into a representation suitable for real-value convolution. In many deep learning methods, the imaginary part of the complex vector is often ignored, or the real part is formed by splicing the real part and the imaginary part, which may lead to the loss of the phase information of the input data and greatly hinder the signal detection performance. In this paper, we represent each OTFS frame as two real-valued matrices and stack them to form a three-dimensional tensor, as shown in (9):
where and are the real received signal and the transmitting sign tensor, respectively, and C is called the number of channels.
2.4. Feature Fusion Method Based on Wavelet Decomposition and Message Passing Enhancement
Wavelet decomposition [21] is a signal analysis method that decomposes signals into approximate components and detailed components of different scales and frequencies. Its core idea is to transform signals to achieve local analysis of signals.
Since the OTFS signal contains noise, with the noise mainly concentrated in the high-frequency part of the signal, traditional denoising is to directly remove this part. However, such a processing method will ignore the effective signal in the high-frequency part, resulting in a lower signal-to-noise ratio of the reconstructed signal after denoising. The threshold denoising [22] based on wavelet decomposition can be represented by wavelet coefficients. By performing threshold denoising on the high-frequency part, the effective signal in the high-frequency part is retained, and the signal is denoised and restored.
In order to propose X from Y in Formula (8) and effectively separate G, it is necessary to first perform wavelet decomposition of Y.
The choice of wavelet basis in this context revolves around its similarity to the signal characteristics. The effective components of OTFS signals in the delay-Doppler (DD) domain usually manifest as localized, relatively smooth pulses or edge features. The selection of the sym4 wavelet basis with a three-level decomposition depth is not arbitrary; it is a targeted optimization based on the characteristics of OTFS signals in the delay-Doppler domain under high-mobility scenarios. This choice achieves an optimal balance between feature extraction sensitivity and matching degree. The Symlet wavelet family is an improved version of the Daubechies wavelets, featuring near-symmetry that reduces distortion in signal phase analysis. Compared to DbN wavelets, Symlets maintain good vanishing moments while offering better linear phase properties. The sym4 wavelet provides an ideal compromise among support length, vanishing moments, and computational complexity. Its waveform exhibits higher similarity to the transient features of OTFS signals in the DD domain caused by Doppler shifts and delays, allowing for more precise capture of these critical changes, while avoiding potential information loss or redundancy that may arise from using Haar wavelets (too simple, poor noise resistance) or Morlet wavelets (too oscillatory, suitable for periodic oscillatory features).
The sym4 wavelet is established as the ideal choice for processing OTFS signals in this study, attributed to its exceptional phase preservation capability derived from approximate symmetry, computational efficiency ensured by compact support, and sufficient regularity that provides high matching degree with the morphological characteristics of OTFS signals. This selection ensures maximum retention of signal integrity during denoising, laying a solid foundation for subsequent accurate detection. The parameters of the sym4 wavelet basis selected in this paper are as follows:
- (1)
- Mother wavelet type: sym4 wavelet from the Symlet wavelet family (approximately symmetric wavelet with an order of 4).
- (2)
- Decomposition level: 3 layers (3-layer wavelet decomposition is performed on the real and imaginary parts of the received signal, respectively).
- (3)
- Threshold function: Hard threshold (combined with the Rigsure thresholding rule, Equation (12)).
After the above process, the corresponding wavelet coefficient will be obtained. is equal to the sum of the corresponding effective coefficient and the corresponding noise coefficient , as shown in the Formula (10):
Among them, is further divided into 1 low-frequency wavelet coefficient and 3 high-frequency wavelet coefficients horizontally , vertically , and diagonally . The three-layer wavelet decomposition is performed using the OTFS signal at the receiving end in Figure 2.
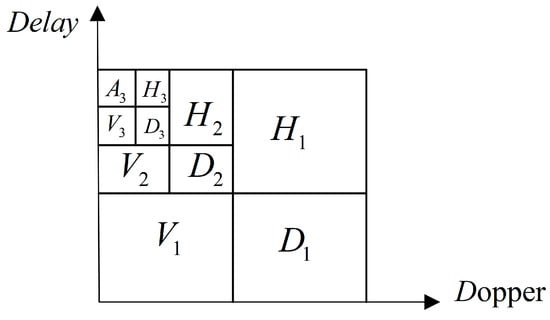
Figure 2.
Three-layer wavelet exploded diagram.
After the signal decomposition, the high- and low-frequency wavelet coefficients of each layer will be obtained. This paper uses a Rigsure threshold value to process the high-frequency wavelet coefficients under the OTFS signal of each layer as a threshold method. The Rigsure threshold mainly takes the absolute value of each coefficient after the signal decomposition, where it sorts the absolute value from small to large. Finally, after each element is squared, a new signal sequence is obtained, as shown in Formula (11):
After determining the threshold for the effect on the OTFS signal, this paper uses a hard threshold to denoise the decomposed wavelet coefficient. The expression of the hard threshold can be expressed as Equation (12):
where Y is the wavelet coefficient size after signal decomposition, s is the wavelet coefficient size that changes after the selected threshold value is applied, and T is the selected Rigsure threshold.
In high-mobility scenarios, OTFS signals exhibit a typical impulse-like sparse distribution in the DD domain, with effective information concentrated in a few multipath components of significant amplitude. The “keep or discard” nature of the hard threshold function allows it to preserve the amplitudes of all coefficients exceeding the threshold without distortion, which is crucial for accurately recovering sparse impulse signals.
It is particularly important to emphasize that the key advantage of hard thresholding lies in its ability to precisely distinguish between signal-dominant coefficients and noise-dominant coefficients. By retaining the amplitudes of all coefficients that exceed the threshold, hard thresholding not only effectively eliminates background noise but, more importantly, fully preserves the energy distribution and time–frequency characteristics of the valid signal components. This precise discrimination capability is decisive for subsequent signal detection and parameter estimation.
In contrast, soft thresholding has inherent limitations:
First, soft thresholding applies systematic shrinkage to all coefficients, causing attenuation even for strong signal components that exceed the threshold. This systematic bias leads to distortion of the signal structure, particularly weakening the amplitudes of strong coefficients representing genuine multipath components, making it difficult for subsequent detectors to accurately estimate path gains.
Second, the feature blurring effect induced by soft thresholding disrupts the sparse structure of the DD domain signal. By shrinking all coefficients, soft thresholding blurs the boundary between signal components and noise, causing the processed signal to lose its original sparse characteristics. This distortion is particularly detrimental to subsequent processing modules (such as the MP enhancement module) that rely on sparse priors.
More importantly, the non-zero coefficients after hard thresholding can more directly and faithfully reflect the underlying sparse structure of the channel. This fidelity ensures high consistency with the sparse prior assumption of the MP module, providing higher-quality and more consistent input features for the subsequent CNN.
Our choice represents a clear trade-off between “smooth denoising effects” and “sparse structure fidelity.” For the specific task of OTFS signal detection, we prioritize the accurate preservation of key signal components’ integrity, a choice entirely consistent with the sparse prior-based design philosophy of our overall method.
Finally, the low-frequency coefficient of the signal after wavelet decomposition and the high-frequency coefficient after threshold denoising under each layer are reconstructed, which has achieved the purpose of restoring the original signal.
The original received signal and the MP detected signal are enhanced to enrich the dataset. MP enhancement continuously transmits and exchanges messages between the observation node and the variable node on the factor graph model and further approximates the posterior edge probability density function of the sent signal, achieving the purpose of detecting the signal. In high-dynamic scenarios, noise can cause error accumulation during the MP (message passing) iteration process, manifesting as distortion of likelihood messages. Especially at low SNRs (<5 dB), weak path signals are easily masked by noise. Traditional MP algorithms that rely on 10 iterations can accumulate errors with each iteration, leading to an increased proportion of incorrect symbols in hard-decision symbols. Moreover, noise peaks may be misinterpreted as sparse paths, reducing path detection accuracy. This paper achieves the integration of MP and CNN through the ‘MP-enhanced multimodal feature fusion’ approach. The MP enhancement module performs lightweight processing and error control, reducing the traditional 10 MP iterations to 3, and uses an early stopping strategy to mitigate noise-induced error accumulation. The hard-decision symbols output by MP undergoes confidence evaluation, retaining only symbols with posterior probability and thereby generating a reliability-enhanced real-valued tensor. At the same time, the MP enhancement module leverages prior knowledge from sparse signal recovery to reduce CNN dependence on data samples. The CNN, through ReLU activation functions and batch normalization, learns the nonlinear boundary between noise and signals to filter residual errors. To prevent inaccuracies from propagating to the fused feature tensor, the number of MP iterations is controlled, reducing iterations from 10 to 3, and a multimodal feature tensor is formed by combining wavelet-denoised signals with raw signals. This allows the CNN, during learning, to cross-validate and correct MP errors.
The main operating flow in the MP signal detection algorithm is shown in Figure 3.
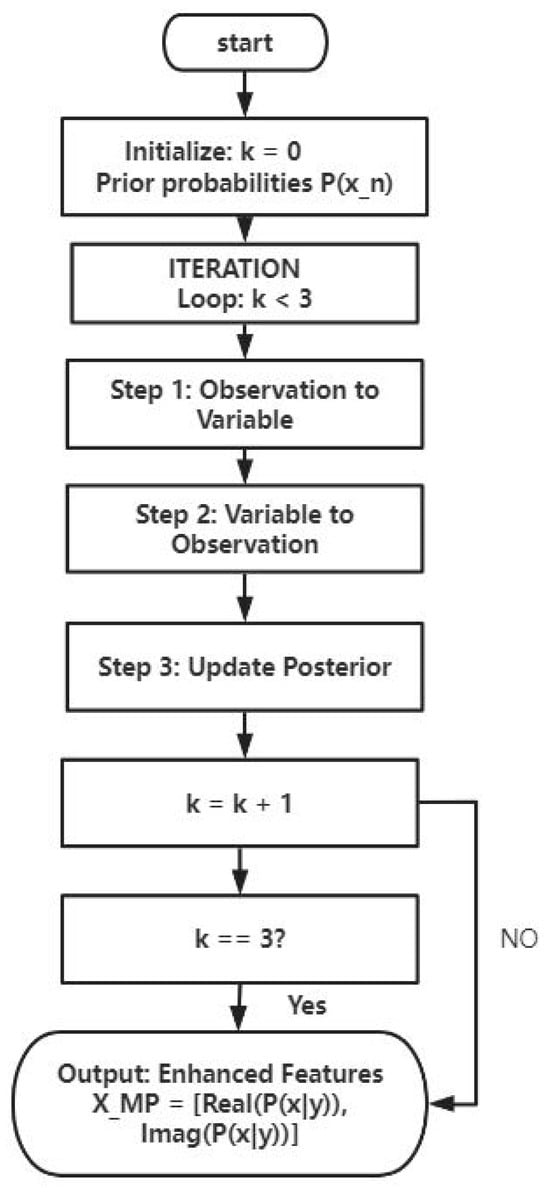
Figure 3.
MP algorithm flow chart.
Wavelet decomposition is used to denoise the receiving OTFS signal, extract multi-scale signal characteristics, combine the original received signal and the signal after the MP detector for feature fusion, splice it into a high-dimensional feature tensor according to the channel dimension as a signal input and jointly detect CNN.
2.5. OTFS System Signal Detection Model Based on MP-WCNN
2.5.1. Model Based on MP-WCN
This paper proposes the MP-WCNN joint detection method. To fully utilize the fusion information of the original signal, MP-enhanced signal, and wavelet-processed signal, this study constructs multi-source input features by concatenating along the channel dimension. The core idea of this design is to provide an information-rich high-dimensional input tensor, allowing the subsequent CNN module to autonomously learn feature importance. The trainable convolutional kernels implicitly achieve dynamic weighting of different signal channels through weight adjustments during backpropagation, thereby amplifying effective features and suppressing redundant or noisy information.
The model architecture is shown in Figure 4, which consists of three parts: the input preprocessing module, the convolution feature extraction module, and the output module.
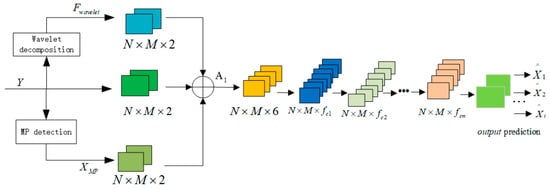
Figure 4.
Architecture diagram of MP-WCNN algorithm.
The input preprocessing module is shown in Figure 5, which includes a wavelet decomposition module, MP enhancement module, and an original received signal. The six-input channel are as follows:
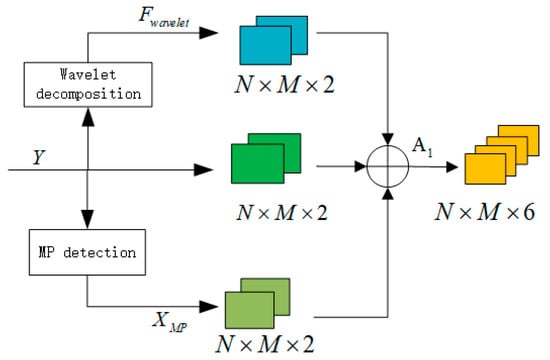
Figure 5.
Input preprocessing module.
Channel 1: Real part of the wavelet-denoised signal, Real ().
Channel 2: Imaginary part of the wavelet-denoised signal, Imag ().
Channel 3: Real part of the MP-enhanced signal, Real ().
Channel 4: Imaginary part of the MP-enhanced signal, Imag ().
Channel 5: Real part of the original received signal, Real ().
Channel 6: Imaginary part of the original received signal, Imag ().
The wavelet decomposition module is shown in Figure 6. It performs a three-layer sym4 wavelet decomposition on both the real and imaginary parts of the received complex signal . Each layer generates one low-frequency wavelet coefficient and three high-frequency wavelet coefficients horizontally , vertically , and diagonally . The low-frequency part of each layer of signal is further decomposed into the low-frequency part and high-frequency part of the next layer. The wavelet coefficients of the three-layer high-frequency part are used as threshold denoising, and the Rigsure threshold is selected to act as a hard threshold on the signal. Finally, the low-frequency coefficients obtained by wavelet decomposition and the high-frequency coefficients of each layer are denoised separately; the signal is reconstructed through these processed coefficients.
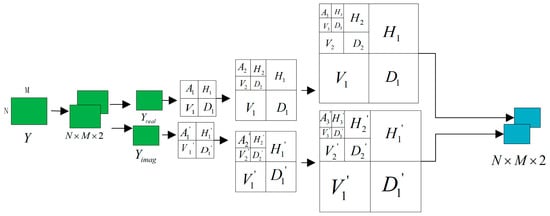
Figure 6.
Wavelet decomposition module.
MP enhancement module in Figure 7. The MP enhancement module is fixed to perform 3 iterations. This parameter was determined based on preliminary experiments: when the number of iterations exceeds 3, performance gains tend to saturate, while computational complexity and latency increase linearly. The stopping criterion is reaching the preset number of iterations. This design avoids the additional overhead of convergence detection and ensures that the module behaves deterministically and efficiently as a feature generator. First, the OTFS signal matrix at the receiving end is updated by continuously passing messages between the exchange observation node and the variable node on the factor graph model, combining messages from all observation nodes and then updating the symbol posterior probability, passing the updated probability distribution to the observation node. Finally, the MAP criterion is used to judge the output to generate detection symbol and convert it into real-value tensor .

Figure 7.
MP enhancement module.
The core function of the MP enhancement module is to provide the CNN with a data perspective different from that of the original received signal. By incorporating the prior knowledge of channel sparsity, it enriches the input feature set and provides diversified decision-making bases for subsequent detection.
Finally, the feature fusion of the three enhanced signals is carried out by stitching along the channel dimension to generate a high-dimensional input tensor , as shown in Formula (13):
The convolutional feature extraction module constitutes the core component of the proposed MP-WCNN architecture as shown in Figure 8. It adaptively learns the signal characteristics of OTFS signals through hierarchical convolutional operations. This module is formed by cascading convolution-batch normalization–activation sub-modules. Each group of subs-modules is equipped with trainable convolution kernels, which extracts the local features of the input tensor through element-wise operations. The first layer employs 7 × 7 convolution kernels. The ‘same’ padding scheme ensures consistent input–output spatial dimensions, thereby maintaining the critical spatial correlations of multipath delays and Doppler shifts in the DD domain. In subsequent layers, the number of convolution kernels is gradually reduced. The feature maps output from the previous layer are normalized using Formula (14):
where are trainable parameters, and is a small constant.
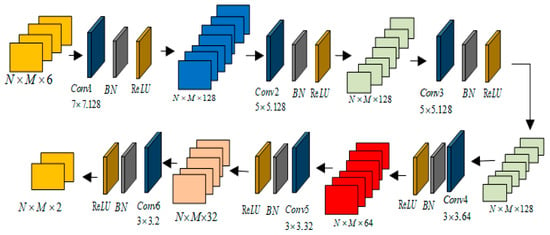
Figure 8.
Convolution feature extraction module.
The ReLU function is applied to the normalized feature maps. The “non-saturating” property of ReLU avoids the vanishing gradient problem. Meanwhile, its simple computation significantly reduces the training cost.
The output module is shown in Figure 9. The output layer uses the Tanh activation function to map the output symbols to the constellation diagram to make the optimal judgment, real and imaginary parts of the sent symbols.

Figure 9.
Output module.
2.5.2. Hyperparameter Optimization
To determine the optimal architecture of the CNN module in MP-WCNN, this study systematically searched and evaluated key hyperparameters, aiming to maintain OTFS signal detection performance while controlling model complexity to achieve efficient inference. The search process combined manual tuning and grid search, covering core parameters such as network depth, convolutional kernel sizes, channel numbers, and learning rates, and verified the robustness of the final architecture through sensitivity analysis.
The study tested convolutional structures with 4–8 layers, comparing the impact of different depths on performance; the first layer used 5 × 5, 7 × 7, and 9 × 9 kernels, while deeper layers tested 3 × 3 and 5 × 5, exploring the combination effect of “large kernels capturing global features and small kernels refining local features”; channel combinations of [64, 128, 256] and [32, 64, 128] were tested; learning rates within [0.1, 0.01, 0.001, 0.0001] were tuned, and the optimal value was ultimately determined to be 0.009 using the Adam optimizer (consistent with the training parameters in Table 1). When the network depth exceeded 6 layers or the initial number of channels exceeded 128, the BER improvement on the validation set was less than 0.5%, but the number of parameters and computational delay significantly increased, posing a risk of overfitting (consistent with the design of the 6-layer network with 128 channels in the first layer as shown in Table 1); the combination of a 7 × 7 large kernel in the first layer and 3 × 3 small kernels in deeper layers (Conv1 as 7 × 7 and Conv4–6 as 3 × 3 in Table 1) consistently outperformed the all-5 × 5 kernel scheme in capturing global interference context in the DD domain while ensuring computational efficiency. The above hyperparameter optimization process ensured a balance between detection accuracy and computational efficiency for MP-WCNN. The final CNN architecture (Table 1) consists of 6 convolutional layers, with the first layer using a 7 × 7 kernel (128 channels) and deeper layers gradually transitioning to 3 × 3 kernels (32 channels), balancing feature extraction capability with model complexity.

Table 1.
Model parameters of MP-WCNN detector.
2.6. Model Training
Although symbol detection is a classification problem during the decision phase, our CNN output layer (Tanh function) is designed to provide continuous estimates of the transmitted symbols (i.e., the constellation point coordinates), which is a regression task. On this basis, RMSE vs. MSE: RMSE is the square root of MSE. We choose RMSE because it has the same units as the target values (the real/imaginary parts of the symbols), making the loss value more physically interpretable, and during model training, the gradient magnitude is more conducive to training stability under different SNR conditions.
By learning the input–output relationship Formula (9) of the OTFS system, efficient estimation of the transmitted symbol is achieved. Specifically, MP-WCNN takes the parameter as a feature and maps the input high-dimensional fused tensor to the transmitted symbol estimate , i.e., the learning function .
To train the model, the generated OTFS dataset (where is the training data index) is used to optimize the network parameters by minimizing the expected loss , with the optimization objective being Formula (15):
E (⋅) represents the expected operator, and is the network trainable weight. When training the MP-WCNN model, the Root Mean Square Error (RMSE) is selected as the loss function to measure the difference between the real symbols and the network outputs. The formula of the loss function is defined as (16):
where is the number of batch samples and is the network trainable parameter.
Figure 10 shows the effect of feature fusion on the learning behavior of the proposed method. We can observe that when only the received signal Y is used to train the neural network, after several rounds of training, the learning process will fall into a local minimum value, with the training loss effect being extremely poor; when the received signal is enhanced by MP detection, the training loss decreases to a large extent; meanwhile, the method of fusion wavelet decomposition and MP enhancement features mentioned in this paper decreases significantly. The generalization ability of the model is significantly enhanced, and the robustness is better.
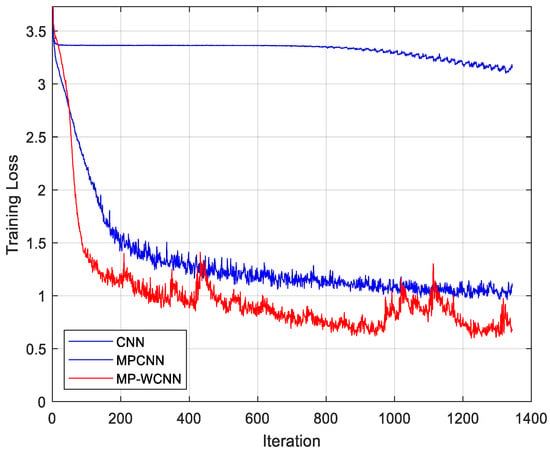
Figure 10.
Training loss graph of MP-WCNN and various methods with frame size of N = 8, M = 16.
At the same time, this paper also considers not putting the signal into the MP detector for detection but instead directly performing wavelet decomposition on the received OTFS signal, followed by threshold denoising and reconstruction, and then inputting it into the CNN for training and detection. The results are shown in Figure 11. The model training results indicate that directly performing wavelet decomposition before CNN training yields better results than traditional CNN training loss, but the training loss performance is still not ideal.
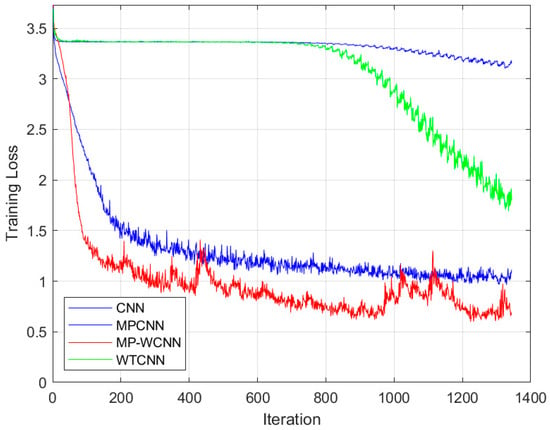
Figure 11.
Comparison of training losses of various methods when the frame size is N = 8, M = 16.
3. Results
3.1. Bit Error Rate Performance Analysis
The construction and training of convolutional neural networks are implemented based on MATLAB R2022b; the designed MP-WCNN detector model parameters is shown in Table 1.
In order to evaluate the performance of the MP-WCNN-based signal detection method proposed in this paper, this section obtains the BER of signal detection through MATLAB R2022b simulation and compares it with other methods. The channel model adopts a custom dual-scaling channel model, with the OTFS system simulation parameters shown in Table 2.

Table 2.
OTFS system simulation parameters.
This simulation experiment generates a 1000 frame dataset [23] based on the OTFS system parameters in Table 2, which completes transmission under a custom dual-scaling channel. The data is divided into 700 frames in the training set, 150 frames in the verification set, and 150 frames in the test set. The MP-WCNN model is shown in Table 1. It is implemented through a custom learning framework and is trained using the Adam optimizer, with an initial learning rate of 0.009, a batch size of 32, and a maximum training round of 64. The model input is a 6-channel tensor, and the network architecture contains a convolutional layer of 7 × 7 (128 cores) → 5 × 5 (128 cores) → 5 × 5 (128 cores) → 3 × 3 (64 cores) → 3 × 3 (32 cores) → 3 × 3 (32 cores). Finally, the output layer uses the Tanh function to achieve accurate detection of symbol values through the optimal judgment.
This section compares the performance of the MP algorithm, the CNN algorithm based on MP enhancement (MPCNN), and the proposed MP-WCNN algorithm. Figure 12 shows the BER comparison results of the proposed MP-WCNN method and the other two detection algorithms when the frame is N = 8 and M = 16.
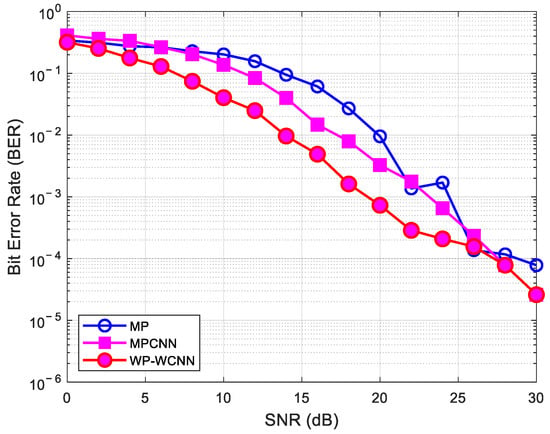
Figure 12.
The BER performance versus SNR with various methods.
To comprehensively assess the performance advantages of the MP-WCNN method, this section systematically compares it with the existing detection algorithms mentioned in the introduction. Figure 13 shows the comparison of BER performance between MP-WCNN and the aforementioned algorithms under 0–30 dB.
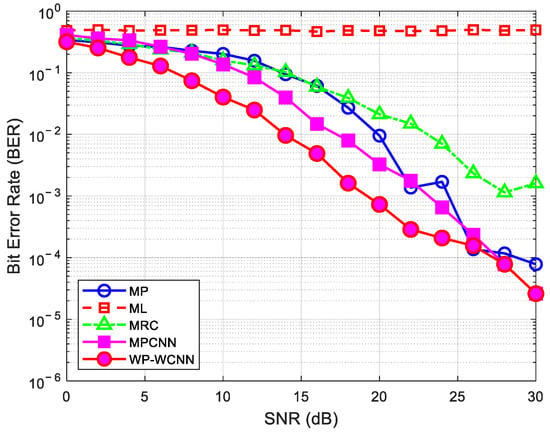
Figure 13.
The BER performance comparison between MP-WCNN and the aforementioned algorithms.
Simulation results demonstrate that the proposed MP-WCNN method significantly outperforms comparative algorithms such as ML, MRC, MP, and MPCNN in terms of bit error rate (BER) under low signal-to-noise ratio (SNR) conditions. Among these, the ML algorithm exhibits the worst performance, followed by MRC. The MP algorithm performs better than MRC, while MPCNN surpasses MP but still falls short of the proposed method. The superior performance of MP-WCNN primarily stems from its wavelet denoising of high-frequency signal coefficients to extract multi-scale features, combined with MP-based enhanced signal reconstruction, which provides the CNN with richer and more discriminative multi-dimensional input features. Experimental results show that at the same BER level, the proposed MP-WCNN method achieves approximately 9 dB of SNR gain compared to the traditional MP algorithm. Furthermore, the method operates without requiring pilot assistance for CSI acquisition.
3.2. Computational Complexity Analysis
To comprehensively evaluate the practical application value of the MP-WCNN method, this section conducts a theoretical analysis of the computational complexity of various detection algorithms. Table 3 presents a comparison of the computational complexity of different algorithms when processing a single-frame OTFS signal.

Table 3.
Comparison of the computational complexity of different detection algorithms.
The computational complexity analysis reveals a clear trade-off between detection performance and computational overhead across different algorithms. The ML [24] detector, while theoretically optimal, suffers from exponential complexity that makes it impractical for real-time applications. MRC [25] offers the lowest complexity with linear scaling but provides limited detection performance. Traditional MP [9] algorithms achieve better performance than MRC but require significant iterative processing.
The proposed MP-WCNN method introduces additional computational load compared to basic MP-CNN [16], primarily due to the wavelet decomposition and MP enhancement modules. However, this increased complexity is justified by the substantial 9 dB SNR gain demonstrated in our experiments. From a system-level perspective, this performance improvement can translate to significant reductions in transmission power requirements, potentially offsetting the additional computational costs in energy-constrained applications.
Furthermore, MP-WCNN maintains deterministic execution time through its fixed three-iteration MP enhancement and single-pass CNN processing, unlike conventional MP algorithms whose convergence time may vary with channel conditions. This characteristic makes MP-WCNN particularly suitable for real-time systems with strict latency requirements in high-mobility scenarios.
4. Discussion
This paper proposes a feature fusion and CNN detection method for dual-scaling channel detection problems faced by OTFS systems in high-dynamic scenarios. This method effectively solves the problems existing in traditional detection methods, such as low signal iterative update efficiency and insufficient feature extraction. This method employs wavelet decomposition for denoising to extract effective components from the received signal. Meanwhile, enhancing the original received signal and the signal detected by MP to enrich the dataset, before finally performing feature fusion. Signal detection is realized through CNN’s hierarchical convolution feature learning. This method does not need to rely on precise channel state information, which significantly reduces pilot overhead. At the same time, through the collaborative design of “feature fusion-deep learning”, it provides a “model-driven hybrid paradigm for OTFS signal processing.
Based on the complexity analysis in Section 3.2, we further explore the trade-off value of the MP-WCNN method in practical systems. From a system-level efficiency perspective, the 9 dB SNR gain brought by MP-WCNN has significant engineering implications: under the same bit error rate requirements, this improvement can not only significantly extend communication coverage but also compensate for the increased computational overhead at the receiver through a substantial reduction in transmit power. In practical deployment, although MP-WCNN has higher computational complexity, its fixed-latency characteristic is more conducive to meeting the real-time processing requirements in high-mobility scenarios, avoiding the additional scheduling overhead caused by the convergence uncertainty of traditional iterative algorithms. This method meets the stringent energy efficiency requirements of 6 G networks, reducing overall system energy consumption through intelligent receiver design and providing a feasible technical pathway for building green communication infrastructure.
While the channel concatenation fusion strategy employed in this study can provide multi-source information to the CNN, it lacks an explicitly designed redundancy suppression mechanism, potentially leading to overlapping features occupying model learning resources. In contrast, attention-based fusion strategies (e.g., the CBAM module) can dynamically highlight critical signal channels (such as noise-suppressed features after wavelet processing) and weaken redundant information through adaptive weight generation, which theoretically could further improve feature utilization efficiency. Due to computational resource limitations and revision cycle constraints, this study has not yet integrated such explicit fusion strategies; however, their potential merits warrant in-depth exploration.
While the proposed MP-WCNN demonstrates excellent detection performance under the custom dual-selective channel model, this study acknowledges certain limitations in channel modeling. The current evaluation primarily employs a simplified channel model to validate the core concept of feature fusion, which may not fully represent the challenges of real-world deployment scenarios. Particularly, the performance under standardized channel models with more realistic configurations, such as the 3 GPP Extended Vehicular A (EVA) and Extended Typical Urban (ETU) models that incorporate fractional Doppler shifts and richer multipath characteristics, remains to be thoroughly investigated in future work.
In addition to comparisons with algorithms such as MP and MPCNN, this study further systematically compares MP-WCNN with the Maximum Likelihood (ML) detector and the Maximal Ratio Combining (MRC) detector. Simulation results indicate that under low signal-to-noise ratio (SNR) conditions, MP-WCNN demonstrates a significant performance advantage over both the ML and MRC detectors. Specifically, the ML detector is most limited in performance under low-SNR conditions due to its insufficient utilization of channel structural features; although the MRC detector improves signal quality through coherent combining, it still encounters performance bottlenecks in complex channel environments. In contrast, MP-WCNN effectively enhances the discriminative capability of signal features through wavelet denoising and multi-scale feature extraction, while the enhanced feature tensors constructed in combination with the matching pursuit algorithm provide richer input information for the convolutional neural network, thereby achieving superior detection performance under low-SNR conditions. Moreover, we recognize that conducting an in-depth comparison of MP-WCNN with more advanced iterative detection algorithms, such as the Variational Bayesian (VB) detector and Approximate message passing (AMP), is of significant research value. Since these algorithms possess unique characteristics in terms of computational complexity and performance boundaries, incorporating them into the comparison framework will help more comprehensively evaluate the performance advantages and applicability of MP-WCNN. This will be one of the main directions for our research team’s future work.
The MP-WCNN method proposed in this paper fundamentally addresses this issue through its data-driven nature and innovative feature fusion strategy, ensuring robustness across diverse channel configurations.
First, unlike traditional algorithms that heavily rely on precise mathematical channel models (such as specific numbers of paths or fixed tap positions), MP-WCNN, as a deep learning model, leverages its core strength in automatically learning and extracting intrinsic features from data that are insensitive to channel variations. Provided the training data covers or represents key characteristics of channel variations—such as delay spread and Doppler spread—the model can learn generalized feature representations related to these variations, rather than memorizing specific configuration parameters.
Second, the core innovation of this method—multi-source feature fusion—is a key design element for enhancing generalization capability. By fusing the original received signal, the MP-enhanced signal, and multi-scale features extracted via wavelet denoising, the model is provided with multiple complementary “views” of the same signal. This fusion mechanism effectively reduces the model’s dependence on any single source of information, encouraging the network to learn more fundamental and robust features. As a result, the model maintains stable performance even when confronted with channel configurations not encountered during training.
Specifically, in the delay-Doppler domain, the essence of the channel lies in its sparsity and doubly selective characteristics. The convolutional layers in MP-WCNN learn to identify and recover original symbols from the mixed received signals by capturing universal patterns of interference between symbols, rather than memorizing specific path delays or Doppler values. Theoretically, as long as the channel maintains its sparse and doubly selective nature—a common feature in high-mobility scenarios—the interference patterns it induces in the DD domain remain macroscopically similar, even if the specific values of the number of paths, delay taps, or Doppler taps change. The convolutional kernels in the CNN inherently possess the ability to capture such similar local patterns, thereby enabling generalization to unseen channel environments.
In summary, by combining a data-driven learning paradigm with a robust feature fusion design, the MP-WCNN method reduces its dependency on specific and precise channel models, allowing it to adapt to a wider range of channel conditions. Future work will include large-scale experiments in more complex and dynamic channel scenarios to further quantitatively validate its generalization performance.
5. Conclusions
Experimental results demonstrate that the proposed MP-WCNN method effectively addresses the issues of low iteration efficiency, significant error propagation in traditional MP algorithms, and insufficient feature extraction of pure CNN models. Notably, in terms of performance, this method can achieve a bit error rate comparable to the conventional MP algorithm under a low SNR of 9 dB, highlighting its substantial advantage in power efficiency. Additionally, the method does not require pilot-assisted acquisition of channel state information, significantly reducing system overhead.
The next step of research will focus on expanding to large-scale MIMO-OTFS systems, exploring the space–time–frequency–Doppler multi-dimensional joint detection architecture, further improving spectral efficiency and transmission reliability while ensuring the bit error performance, providing a more universal solution for 6 G high-dynamic communication scenarios.
The MP-WCNN framework proposed in this paper is significant not only for providing a high-performance detector, but also for offering a new approach to the integration of model-driven and data-driven methods. Experimental results show that enhancing the quality of input data through carefully designed pre-feature engineering is far more effective than merely increasing the depth or complexity of neural networks. Future work will explore extending this integration paradigm to a broader range of communication signal processing tasks, such as channel estimation, equalization, and decoding, and will study how to further optimize the parameters of the pre-feature extraction module using neural networks.
To achieve these goals, future studies will be centered around the following key directions: (1) Comprehensive evaluation of MP-WCNN’s robustness and generalization capability under 3 GPP standardized channel models (e.g., EVA, ETU) to verify its practical application value in realistic scenarios; (2) exploring attention-based explicit feature fusion strategies by designing channel-spatial hybrid attention modules to dynamically suppress redundant information in multi-source signals and enhance feature fusion efficiency; (3) investigating the integration of the proposed MP-WCNN framework with advanced signal processing techniques to adapt to the increased complexity of large-scale MIMO-OTFS systems, aiming to balance detection accuracy and computational complexity in high-dimensional signal spaces.
6. Patents
‘A detection method for OTFS signals based on an adaptive wavelet scattering convolutional neural network’ Patent number: 202510020729.3.
Author Contributions
Conceptualization, Y.W.; Methodology, Y.W.; Investigation, M.Z.; Formal Analysis, M.Z.; Writing—Original Draft Preparation, M.Z.; Visualization, M.Z.; Resources, Y.L. and Z.L.; Funding Acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the project of Postgraduate & Practice Innovation of Jiangsu Province with project number SJCX25-2509.
Data Availability Statement
Links to publicly archived datasets that were analyzed or generated during the research period: Mengyao, Zhou (2025), “OTFS dataset”, Mendeley Data, V1, https://doi.org/10.17632/9fj27d8g32.1 (accessed on 12 October 2025) [23].
Acknowledgments
Thanks are extended to Jiangsu University of Science and Technology for the financial support of this project.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Farhang, A.; RezazadehReyhani, A.; Doyle, L.E.; Farhang-Boroujeny, B. Low Complexity Modem Structure for OFDM-Based Orthogonal Time Frequency Space Modulation. IEEE Wirel. Commun. Lett. 2018, 7, 344–347. [Google Scholar] [CrossRef]
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal Time Frequency Space Modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Bharatula, G.; Hadani, R.; Hanzo, L. Orthogonal Time-Frequency Space Modulation: A Promising Next-Generation Waveform. IEEE Wirel. Commun. 2021, 28, 136–144. [Google Scholar] [CrossRef]
- Li, S.; Yuan, W.; Wei, Z.; Schober, R.; Caire, G. Orthogonal Time Frequency Space Modulation—Part II: Transceiver Designs. IEEE Commun. Lett. 2023, 27, 9–13. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Li, S.; Schober, R.; Caire, G. Orthogonal Time Frequency Space Modulation—Part III: ISAC and Potential Applications. IEEE Commun. Lett. 2023, 27, 14–18. [Google Scholar] [CrossRef]
- Liao, Y.; Luo, Y.; Jing, Y. 6G New Time-delay Doppler Communication Paradigm: Technical Advantages, Design Challenges, Applications and Prospects of OTFS. J. Electron. Inf. Technol. 2024, 46, 1827–1842. [Google Scholar] [CrossRef]
- Feng, J.; Ngo, H.Q.; Flanagan, M.F.; Matthaiou, M. Performance Analysis of OTFS-based Uplink Massive MIMO with ZF Receivers. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Tiwari, S.; Das, S.S.; Rangamgari, V. Low complexity LMMSE Receiver for OTFS. IEEE Commun. Lett. 2019, 23, 2205–2209. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- Li, L.; Liang, Y.; Fan, P.; Guan, Y. Low Complexity Detection Algorithms for OTFS under Rapidly Time-Varying Channel. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Yuan, J.; Ng, D.W.K. A Simple Variational Bayes Detector for Orthogonal Time Frequency Space (OTFS) Modulation. IEEE Trans. Veh. Technol. 2020, 69, 7976–7980. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, M.-M.; Lei, M.; Zhao, M.-J. A Damped GAMP Detection Algorithm for OTFS System based on Deep Learning. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, F.; Yuan, W.; Guo, Q.; Wang, Z.; Yuan, J. Iterative Detection for Orthogonal Time Frequency Space Modulation With Unitary Approximate Message Passing. IEEE Trans. Wirel. Commun. 2022, 21, 714–725. [Google Scholar] [CrossRef]
- Li, Q.; Gong, Y.; Meng, F.; Xu, Z. Data-Driven Receiver for OTFS System with Deep Learning. In Proceedings of the 2021 7th IEEE International Conference on Network Intelligence and Digital Content (IC-NIDC), Beijing, China, 17–19 November 2021; pp. 172–176. [Google Scholar] [CrossRef]
- Li, Q.; Gong, Y.; Wang, J.; Meng, F.; Xu, Z. Exploring the Performance of Receiver Algorithm in OTFS Based on CNN. In Proceedings of the 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Republic of Korea, 16–20 May 2022; pp. 957–962. [Google Scholar] [CrossRef]
- Enku, Y.K.; Bai, B.; Wan, F.; Guyo, C.U.; Tiba, I.N.; Zhang, C.; Li, S. Two-Dimensional Convolutional Neural Network-Based Signal Detection for OTFS Systems. IEEE Wirel. Commun. Lett. 2021, 10, 2514–2518. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Wang, B.; Liu, Y.; Bai, W.; Shen, X. Deep Learning-Based Signal Detection for Underwater Acoustic OTFS Communication. J. Mar. Sci. Eng. 2022, 10, 1920. [Google Scholar] [CrossRef]
- Xiang, L.; Liu, Y.; Yang, L.-L.; Hanzo, L. Gaussian Approximate Message Passing Detection of Orthogonal Time Frequency Space Modulation. IEEE Trans. Veh. Technol. 2021, 70, 10999–11004. [Google Scholar] [CrossRef]
- Cheng, K.; Yi, L.; Li, L.; Zhutian, M.; Sun, G. Study of wavelet transform-based image fusion methods. J. Phys. Conf. Ser. 2021, 1757, 012049. [Google Scholar] [CrossRef]
- Pfadler; Jung, P.; Stanczak, S. Pulse-Shaped OTFS for V2X Short-Frame Communication with Tuned One-Tap Equalization. In Proceedings of the WSA 2020 24th International ITG Workshop on Smart Antennas, Hamburg, Germany, 18–20 February 2020; pp. 1–6. [Google Scholar]
- Rahim, A.A.A.; Abdullah, S.; Singh, S.S.K.; Nuawi, M. Fatigue strain signal reconstruction technique based on selected wavelet decomposition levels of an automobile coil spring. Eng. Fail. Anal. 2021, 125, 68–77. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Q.; Liu, J.; Zhang, X.; Hou, J. Noise Reduction of Steam Trap Based on SSA-VMD Improved Wavelet Threshold Function. Sensors 2025, 25, 1573. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M. “OTFS Dataset”, Mendeley Data, V1. 2025. Available online: https://data.mendeley.com/datasets/9fj27d8g32/1 (accessed on 12 October 2025).
- Surabhi, G.D.; Augustine, R.M.; Chockalingam, A. On the Diversity of Uncoded OTFS Modulation in Doubly-Dispersive Channels. IEEE Trans. Wirel. Commun. 2019, 18, 3049–3063. [Google Scholar] [CrossRef]
- Thaj, T.; Viterbo, E. Low Complexity Iterative Rake Decision Feedback Equalizer for Zero-Padded OTFS Systems. IEEE Trans. Veh. Technol. 2020, 69, 15606–15622. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).