Abstract
Accurate detection of fetal distress from cardiotocography (CTG) is clinically critical but remains subjective and error-prone. In this research, we present a leakage-safe Calibrated Global Logit Fusion (CGLF) framework that couples TabNet’s sparse, attention-based feature selection with XGBoost’s gradient-boosted rules and fuses their class probabilities through global logit blending followed by per-class vector temperature calibration. Class imbalance is addressed with SMOTE–Tomek for TabNet and one XGBoost stream (XGB–A), and class-weighted training for a second stream (XGB–B). To prevent information leakage, all preprocessing, resampling, and weighting are fitted only on the training split within each outer fold. Out-of-fold (OOF) predictions from the outer-train split are then used to optimize blend weights and fit calibration parameters, which are subsequently applied once to the corresponding held-out outer-test fold. Our calibration-guided logit fusion (CGLF) matches top-tier discrimination on the public Fetal Health dataset while producing more reliable probability estimates than strong standalone baselines. Under nested cross-validation, CGLF delivers comparable AUROC and overall accuracy to the best tree-based model, with visibly improved calibration and slightly lower balanced accuracy in some splits. We also provide interpretability and overfitting checks via TabNet sparsity, feature stability analysis, and sufficiency (k95) curves. Finally, threshold tuning under a balanced-accuracy floor preserves sensitivity to pathological cases, aligning operating points with risk-aware obstetric decision support. Overall, CGLF is a calibration-centric, leakage-controlled CTG pipeline that is interpretable and suited to threshold-based clinical deployment.
1. Introduction
The growing applications of machine learning (ML) and deep learning (DL) have significantly advanced the field of automated biomedical diagnostics. These techniques enable effective analysis of complex clinical data. Cardiotocography (CTG) is a non-invasive method that monitors fetal heart rate (FHR), fetal movements, and uterine contractions via ultrasound. It provides essential insights into maternal and fetal well-being [1]. However, clinicians still manually interpret CTG signals. This subjective process creates considerable inter-observer variability and inconsistent clinical decision-making.
Misinterpretation of CTG data is linked to preventable neonatal morbidity and mortality. This highlights the need for improvement and technological assistance in the field. False-positive diagnosis rates are as high as 60%, and clinician agreement varies by more than 30% [2]. A recent review reported that nearly 29% of adverse neonatal outcomes were directly related to CTG misinterpretation [3]. These findings underscore the need for robust automated models. Such models can help standardize and enhance the reliability of fetal health assessments.
Researchers have applied traditional ML algorithms, such as Support Vector Machines (SVMs) and logistic regression (LR), to CTG analysis. However, these methods often fail to capture the high-dimensional and non-linear characteristics of CTG signals [4]. In contrast, deep neural networks (DNNs) extract hierarchical feature representations directly from raw data. However, their susceptibility to overfitting and need for large labeled datasets limit their practical clinical utility [5].
An empirical CTG solution should therefore handle severe class imbalance without information leakage, preserve discrimination while improving probability reliability (calibration), and remain interpretable and computationally light for tabular inputs collected in real-world settings.
We address these requirements with a leakage-safe Calibrated Global Logit Fusion (CGLF) framework that couples TabNet’s sparse, attention-based feature selection [6] with XGBoost’s gradient-boosted decision rules [7]. For imbalanced CTG data, we employ two pragmatic ways to increase minority sensitivity: (1) incorporating an oversampling technique into the base models, and (2) changing the loss the learner optimizes (class weighting). Oversampling with SMOTE–Tomek (XGB–A) enriches sparse minority neighborhoods and removes borderline Tomek links, which can recover recall when pathological cases are underrepresented, but may introduce synthetic clusters if applied incautiously. Class-weighted training (XGB–B) keeps the empirical feature distribution intact while up-weighting minority errors in the objective, which often yields more stable decision boundaries and calibration, but may under-correct when minority regions are extremely thin.
Our model instantiates both streams with identical model capacity and tuning ranges, differing only in imbalance handling, and trains them inside each outer fold on the training split (no leakage). Per fold, the XGB stream deemed stronger by OOF performance is fused with TabNet via our leakage-safe logit blend and calibrated once on OOF predictions. This setup is simple to operate, easy to audit, and empirically effective, according to our results: it preserves discrimination at XGBoost levels while improving probability reliability, without adding brittle meta-parameters or violating leakage controls.
After training the base learners, we fuse their class probabilities using a dual-path strategy. The first path is a lightweight meta-learner that trains a multinomial Elastic-Net logistic regression on engineered meta-features derived solely from base predictions, including raw probabilities, Shannon entropy, top-2 class margins, and pairwise agreement indicators, and the second path is a Calibrated Global Logit Fusion that blends TabNet and the superior XGBoost stream by summing their logits with a single global weight. For probability reliability, both paths apply per-class vector–temperature calibration learned from OOF predictions; this is followed by constrained per-class reweighting, where post hoc thresholds are adjusted under a balanced-accuracy floor to ensure that sensitivity to the pathological class is not reduced relative to the best standalone base learner. Between the two fusion paths (meta and blend), the deployed path is chosen based solely on out-of-fold performance under this constraint, and the selected parameters are then applied once to the corresponding held-out outer fold.
On the public Fetal Health dataset, 10-fold outer CV shows that CGLF achieves an accuracy of , a macro-F1 of , an AUROC of , an ECE of , and a Brier of . Compared with the best standalone XGBoost baseline (accuracy of , macro-F1 of , AUROC of , ECE of , and Brier of ), CGLF offers comparable discrimination with meaningfully better calibration. Balanced accuracy is slightly lower for CGLF () vs. XGBoost (). Welch’s tests show no significant differences in macro-F1 () or balanced accuracy () across folds, while calibration consistently favors CGLF.
Furthermore, we evaluate TabNet’s feature-selection behavior by quantifying sparsity through mask entropy and assess the inner-fold stability of top-ranked features using Jaccard similarity. We also compute sufficiency curves () to estimate the number of features required to retain 95% of the full model. In our experiments, XGBoost demonstrated higher feature-ranking stability and lower (i.e., fewer features are sufficient), whereas TabNet produced sparser attention masks. These complementary signals are integrated and calibrated within the CGLF framework, resulting in reliable probability estimates that support threshold-based decision making in obstetric care.
The main contributions of our paper are summarized as follows:
- Calibration-centric fusion for CTG. We introduce a Calibrated Global Logit Fusion (CGLF) that blends TabNet and XGBoost in the log-odds domain with a single global weight chosen on OOF data and then applies per-class vector–temperature calibration, also fitted on OOF. To the best of our knowledge, this calibration-first, logit-level fusion has not previously been reported for CTG tabular classification.
- Leakage-safe path selection using probability-derived meta-features. Beyond the logit blend, we design a lightweight level-2 meta-ENet trained only on probability-derived meta-features (raw class probabilities, entropy, top-2 margin, inter-model agreement). The final path (meta vs. blend) is selected purely on OOF under a BA floor, eliminating raw-feature leakage into stacking, an uncommon safeguard in CTG ensembles.
- Clinically aligned post hoc tuning under a BA floor. We propose constrained post hoc class reweighting after calibration that optimizes performance while enforcing a balanced-accuracy floor tied to the best standalone base on that fold. This yields operating points that maintain recall for minority (pathological) cases, aligning fusion with risk-aware deployment.
- Diversity by design with dual XGBoost streams. We instantiate two complementary XGB learners XGB–A (SMOTE–Tomek) and XGB–B (class-weighted) trained in a strictly leakage-controlled manner. This pragmatic, imbalance-aware diversification, coupled with logit-level fusion and OOF-only calibration, provides a principled hedge against bias from any single imbalance remedy.
2. Literature Review
2.1. Traditional ML for CTG Interpretation
Cardiotocography (CTG) has long been analyzed with classical machine learning (ML) to assist fetal health assessment. Early studies applied Support Vector Machines (SVMs) and logistic regression (LR) to hand-crafted descriptors derived from fetal heart rate (FHR), uterine contractions, accelerations, and decelerations [4]. While these models are simple and fast, they often struggle to capture non-linear interactions and higher-order dependencies present in CTG, and performance typically degrades under class imbalance, where pathological cases are underrepresented. Tree-based ensembles mitigated some of these limitations: Random Forests (RFs) achieved up to 93% accuracy on structured CTG features in Salini et al. [8]. However, classical ensembles rarely report probability calibration and provide limited instance-wise transparency, both of which are important for clinical review and thresholding.
2.2. Deep Learning and Temporal Dynamics
Deep learning (DL) approaches reduce feature engineering by learning representations directly from signals or images. Convolutional neural networks (CNNs) have achieved competitive accuracy on CTG images or segments but typically require large, well-annotated datasets and often yield opaque decision processes that complicate clinical adoption [9]. Targeting temporal dependencies explicitly, Rao et al. proposed a multiscale LSTM on the CTU-UHB dataset (552 recordings), achieving 85.73% accuracy and 91.80% AUC [10]. This highlighted the value of modeling short- and long-range FHR dynamics but did not directly address feature selection or severe class imbalance, both of which are key issues in obstetric screening. Mushtaq and Veningston [11] improved label fidelity by training CNNs with umbilical cord blood pH as ground truth, yet questions of calibration and interpretability remained.
2.3. Real-Time CTG Processing
From a deployment perspective, Lee et al. demonstrated real-time feasibility with a ResNet-based pipeline optimized for mobile and server settings (5249 traces; 141,001 five-minute windows; ∼93% accuracy) [12]. Although this shows that low-latency inference is attainable, the study did not incorporate explicit class-imbalance controls or probability calibration, limiting risk-aware operating-point selection for pathological screening.
2.4. Calibration-Aware Fusion and Ensembles
Fusion strategies that combine deep-learning (DL) feature extractors with classical learners have proven effective in other domains. For example, Chieregato et al. fused a 3D CNN with CatBoost for COVID-19 severity prediction [13], and Wang et al. used RF/GBM voting for pulsar classification [14]. These designs typically rely on feature concatenation or fixed voting and seldom analyze probability reliability or strictly control information leakage across training stages.
Within tabular CTG settings, attention-based tabular DL is particularly relevant. TabNet performs instance-wise sparse feature selection through sequential attention, yielding compact, interpretable masks [6]. XGBoost, a gradient-boosted tree method, is well suited to structured, moderate-sized datasets and captures non-linear interactions with strong regularization [7]. Prior CTG ensembles rarely pair an attention-driven tabular network with a boosted tree under a rigorously leakage-safe protocol, nor do they emphasize calibrated probability fusion tailored to clinical thresholding.
2.5. Positioning of the Present Work
Guided by the above knowledge gaps, our study addresses three aspects that are rarely treated together in the CTG literature: (i) leakage-safe training and evaluation when combining heterogeneous learners; (ii) probability calibration to support clinically meaningful thresholds; and (iii) explicit imbalance handling that preserves sensitivity to pathological cases. Specifically, we couple TabNet [6] with XGBoost’s gradient-boosted decision rules [7] on identical CTG tabular inputs and fuse their class probabilities in the log-odds domain through global logit blending. Logit-domain fusion allows the combined scorer to emphasize whichever base learner is more informative while avoiding the over-smoothing that arises from probability averaging. All preprocessing is confined to standardization parameters learned strictly on training splits; all imbalance remedies are likewise applied only to training folds to prevent information leakage. To promote diversity under imbalance, we train two complementary XGBoost streams, one with SMOTE–Tomek resampling and another with class-weighted training, alongside a TabNet model trained on SMOTE–Tomek. Fusion parameters and calibration are estimated exclusively from out-of-fold (OOF) predictions within each outer-CV split. Specifically, we select a global logit-blend weight on OOF data, fit per-class vector–temperature calibration to improve probability reliability, and apply constrained per-class reweighting under a balanced-accuracy floor, ensuring that improvements do not come at the expense of higher false negatives.
To further safeguard against overfitting and provide flexibility, we adopt a dual-path fusion strategy: (i) a lightweight Elastic-Net logistic regression meta-learner trained on engineered meta-features derived solely from base predictions (raw probabilities, Shannon entropy, top-2 class margins, and pairwise agreement indicators), and (ii) direct global logit blending with calibrated thresholds. Between these two paths, the deployed model is selected purely on OOF performance under the balanced-accuracy floor, and the chosen parameters are applied once to the corresponding held-out fold. This leakage-safe protocol aligns with clinical needs for trustworthy probabilities and threshold-based decision support. Informed by our experiments, this design reflects what consistently works in CTG: boosted trees provide stable tabular discrimination, attention-based deep tabular networks yield sparse and interpretable feature masks, and calibrated fusion hedges model-specific biases. Our contribution is therefore a calibration-centric, leakage-controlled ensemble tailored to CTG’s data characteristics. In addition, complementary diagnostics (TabNet mask entropy, inner-fold top-feature stability (Jaccard), and sufficiency curves) connect model behavior to clinical transparency, addressing interpretability concerns that persist across ML and DL approaches in fetal monitoring.
3. Materials and Methods
3.1. Model Architecture and Design
The Calibrated Global Logit Fusion (CGLF) framework integrates complementary learners under strict leakage control. TabNet and two XGBoost variants are trained: XGB–A on SMOTE–Tomek resampled data and XGB–B with class-weighted loss. Out-of-fold (OOF) predictions from inner splits are the only inputs used for fusion and calibration, keeping all meta-level training strictly leakage-free.
Fusion is carried out in the log-odds domain, with a global blend weight tuned on OOF data. To ensure reliability and maintain sensitivity to pathological cases, per-class vector–temperature calibration and constrained reweighting under a balanced-accuracy floor are applied. To guard against overfitting, the framework compares two fusion paths (an Elastic-Net meta-learner on engineered meta-features and direct logit blending) and deploys the one with higher OOF performance under the accuracy floor. This yields calibrated probability estimates suitable for threshold-based clinical use.
3.1.1. TabNet Model
We employ TabNet [6,15] as a base learner to obtain sparse, step-wise feature selection and calibrated class probabilities on tabular data. As illustrated in Figure 1, each decision step t computes a sparse feature mask via an attentive transformer, gates the input , then transforms it into a decision vector , and the decisions are summed before passing through a linear layer and softmax [15].
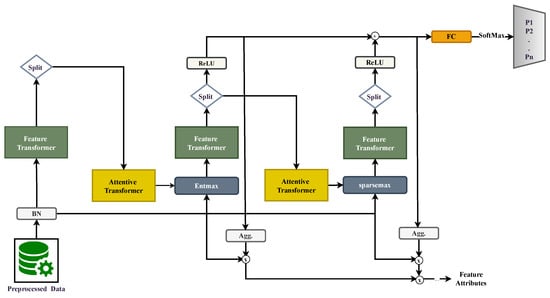
Figure 1.
TabNet encoder. As shown in the figure, each decision step t computes a sparse feature mask via an attentive transformer, gates the input , transforms it into a decision vector , and the decisions are summed before passing through a linear layer and softmax.
is a normalized input, and d is the number of covariates (features). T is the number of decision steps, K is the number of classes, and ⊙ denotes the Hadamard (elementwise) product. is the probability simplex.
At step , an attentive transformer produces unnormalized feature logits and a sparse mask (using entmax, which yields probabilities with exact zeros).
The raw input is then gated and processed by a feature transformer (shared blocks plus step-specific heads):
TabNet aggregates decisions across steps and maps the sum to class probabilities by a linear layer followed by softmax:
where and are trainable parameters.
To discourage reusing already-attended features and to encourage exploration across steps, TabNet updates a feature-usage prior multiplicatively:
which down-weights features selected at step t (Figure 1, top annotation).
We minimize the cross-entropy loss plus a sparsity regularizer on the masks:
We use decision steps, the entmax mask with , the AdamW optimizer with a step LR scheduler, and a CPU device for reproducibility.
Instance-wise sparsity and attention expose compact, clinically sensible subsets and provide a complementary decision surface to boosted trees. In our results, TabNet yields sparser masks (lower entropy), which CGLF leverages via calibrated fusion to produce reliable probabilities for threshold-based decisions.
3.1.2. XGBoost
XGBoost is a tree-boosting algorithm that builds an additive ensemble of shallow regression trees optimized with second-order gradients and Hessians [7]. For training data , with and class labels , the model maintains class margins (logits) for each round t and class k. The model is initialized from class priors,
or simply .
At each boosting round, a regression tree is fitted to the first- and second-order derivatives of the multiclass cross-entropy loss:
where is the predicted probability for class k at iteration . The tree output is added to the running margins with a learning rate :
After T boosting rounds, class probabilities are obtained by a softmax transformation:
As illustrated in Figure 2, training begins from the initial margins, the residuals (gradients and Hessians) guide each tree fit, the tree outputs update the running margins, and the final ensemble output is converted to probabilities.
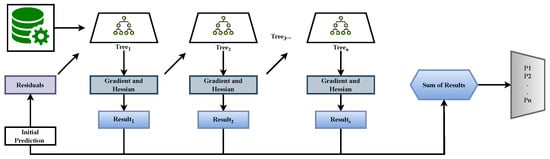
Figure 2.
XGBoost base model. Training begins from the initial class margins (6), which are updated in each round by fitting a regression tree to the residuals (gradients and Hessians ; Equation (7)). Tree outputs are added to the running margins (Equation (8)), and after T rounds, the final margins are mapped to the class probabilities by the softmax function (9). In our ensemble, two complementary streams are used: XGB–SMOTE–Tomek (resampled training) and XGB–Weighted (class-weighted training).
In our pipeline, two complementary XGBoost streams are trained in each outer-CV fold: (i) XGB–SMOTE–Tomek, trained on resampled data to reduce imbalance, and (ii) XGB–Weighted, trained on the natural distribution with a class-weighted loss. This design improves model diversity and robustness [16,17].
3.1.3. Calibrated Global Logit Fusion (CGLF)
CGLF integrates complementary base learners in a strictly leakage-safe manner, relying only on out-of-fold (OOF) predictions from inner splits within each outer fold. All fusion weights, calibration parameters, and class reweighting are estimated exclusively on OOF data and frozen before inference on the held-out outer test set. Figure 3 summarizes the workflow [18].
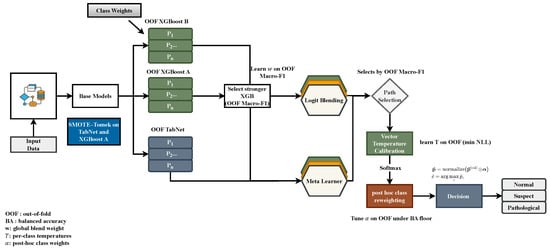
Figure 3.
Calibrated Global Logit Fusion (CGLF). The base learners (TabNet; XGBA with SMOTE–Tomek; XGBB with class weights) generate OOF probabilities across seeds. The stronger XGB stream is selected, and two fusion candidates are constructed: global logit blending and an Elastic-Net meta-learner on OOF-derived features. After vector–temperature calibration and optional reweighting under a balanced-accuracy floor, the better-performing path (based on OOF macro-F1) is frozen and applied once to the outer test split.
Seed Ensembling and OOF Probabilities
Each base learner is trained under S random seeds, and seed-level OOF probability [19,20] vectors are averaged:
where i indexes samples, K is the number of classes, and S is the number of seeds [19].
XGB Stream Selection
Between the two boosted-tree variants (SMOTE–Tomek vs. class-weighted), the stronger stream is selected based on the OOF macro-F1:
Fusion Candidates
Two complementary fusion paths are constructed:
- Global logit blend: TabNet and are fused in log-odds space with a single global weight w, tuned on OOF data:
- Meta-learner: An Elastic-Net multinomial logistic regression is trained on OOF probability-derived features (base probabilities, entropy, top-2 margin, and pairwise agreement indicators) [21].
Calibration and Reweighting
Each candidate is calibrated by per-class vector–temperature [22] scaling:
with optimized on OOF negative log-likelihood. Optionally, calibrated outputs are reweighted under a balanced-accuracy (BA) floor to ensure that improvements in macro-F1 do not degrade sensitivity to the pathological class.
To further safeguard sensitivity to the pathological class, calibrated outputs are post-processed through constrained class reweighting:
where weights are tuned on OOF data to maximize macro-F1 subject to a balanced-accuracy floor. This ensures that performance improvements are not achieved at the cost of reduced recall for pathological outcomes.
Path Selection and Inference
After calibration, the path with the higher OOF macro-F1 (subject to the BA floor) is selected:
where denotes calibration and reweighting. denotes the predicted probability for sample i and class k before calibration. At test time, the base models are retrained on the full outer-train split, and the chosen path with frozen parameters is applied once to the outer-test fold [23].
Traditional ensembles often focus on maximizing discrimination (e.g., AUROC) while overlooking two critical challenges in CTG classification: probability calibration and leakage control. In obstetric decision-making, calibrated probabilities are essential because clinical actions depend on thresholds (e.g., flagging pathological cases) rather than raw rank scores. Moreover, failure to control for information leakage during preprocessing or fusion can inflate results and undermine reproducibility. By designing CGLF around OOF-only learning and calibration, the framework directly addresses these limitations and ensures that gains are not artifacts of methodological bias but reflect generalizable improvements.
Beyond accuracy, CGLF contributes complementary benefits from its heterogeneous base models. XGBoost provides stable feature rankings and consistent class-level discrimination under imbalance, while TabNet yields sparse attentive masks that highlight instance-specific predictors, enhancing transparency in clinical interpretation. Their calibrated fusion maintains discrimination comparable to the best standalone model while consistently reducing probabilistic error (ECE, Brier). This combination of discrimination, calibration, and interpretability makes CGLF particularly suited to CTG, where robust thresholds, transparency of contributing features, and reproducibility under class imbalance are all crucial for reliable clinical deployment.
4. Experiment and Results Analysis
4.1. Dataset and Preprocessing
The original Kaggle Fetal Health dataset comprises n = 2126 cardiotocogram (CTG) records annotated by expert obstetricians into three classes: normal, suspect, and pathological. To ensure consistency and prevent information leakage during cross-validation, we applied a quality-control filtering step before training. Specifically, we removed duplicate entries that could bias fold stratification, excluded records with missing or inconsistent values across derived CTG features (e.g., accelerations, short-term variability measures), and standardized class labels. After filtering, the final dataset used in all experiments contained n = 1488 records, distributed as follows: normal = 1158, suspect = 207, and pathological = 123. This marked class imbalance, particularly in the minority pathological class, motivated our subsequent use of SMOTE–Tomek resampling and class-weighting strategies within the CGLF training pipeline.
All preprocessing was performed within the training data only to prevent leakage. We standardized features (zero mean, unit variance) using a scaler fit on the training split of each fold and applied it to the corresponding validation/held-out split.
4.2. Class Imbalance Handling
The Fetal Health dataset is markedly imbalanced (normal ≫ suspect, pathological). Class imbalance was addressed as follows: TabNet and one XGBoost stream (XGB–A) were trained on SMOTE–Tomek-augmented training data; a second XGBoost stream (XGB–B) was trained with class weights and without resampling [24]. SMOTE synthesizes minority examples by interpolation among nearest neighbors, whereas Tomek links remove borderline overlaps; together they improve minority coverage while cleaning ambiguous regions. Following recommendations in prior class-imbalance work [25,26], we coupled data-level resampling with algorithmic weighting: one XGBoost stream XGB–B was trained on class-weighted, non-resampled data; a second XGBoost stream XGB–A) and TabNet were trained on SMOTE–Tomek-augmented training data. This dual strategy increases learner diversity and supports recall for clinically critical minority cases. All resampling was performed independently inside each cross-validation (CV) training split to avoid information leakage. Besides SMOTE–Tomek, there are other sampling techniques we will navigate in future work [25,26,27].
4.3. Feature Engineering
To maintain a leakage-safe and reproducible pipeline, we introduced no hand-crafted transformations of the raw CTG covariates; all base learners consumed the 23 provided predictors without manual modification. At the meta-level, we generated principled engineered features, but only from leakage-safe out-of-fold (OOF) base predictions. Specifically, the meta-learner consumes each base’s OOF class-probability vector together with systematically derived meta-features: Shannon entropy, top-2 margin, and pairwise agreement indicators between base argmax predictions. These engineered meta-features summarize the reliability and diversity of base predictions, and no raw covariates enter level 2. All resampling and weighting strategies are confined strictly to training splits to prevent leakage [21,28].
4.4. Evaluation Metrics
We evaluated both discrimination (how well classes are separated) and calibration/reliability. Below are the discrimination metrics we report, with concise definitions and formulas. Let C be the number of classes. For each class , we calculated the following:
- Accuracy. The fraction of correctly classified samples:
- Precision/Recall/F1 (for each class i).
- Macro-F1. The unweighted average of class-wise F1 scores (treats all classes equally; helpful under imbalance):
- Balanced Accuracy. The unweighted average of recalls per class (balances sensitivity between classes):Micro AUROC (OvR). For each class i, form an OvR ROC curve using the class-i scores (e.g., predicted probabilities ). Let denote the area under that ROC. The macro-average isEquivalently, each OvR AUROC admits the ranking interpretation:We also report the Expected Calibration Error (ECE; M equal-width confidence bins) [29] and the multi-class Brier score [30]:
4.5. Baseline Models
All baselines were trained under the same leakage-safe protocol as our proposed model:
- Random Forest (RF). Bagged ensemble of decision trees with feature sub-sampling at each split; it is robust to non-linearities and interactions [30]. Settings used: 400 trees, with Gini impurity and bootstrapping enabled.
- Multi-Layer Perceptron (MLP). Feed-forward neural network trained by backpropagation [31]. Settings used: one hidden layer with 50 units, ReLU activation, cross-entropy loss, and early stopping on inner validation.
- Support Vector Machine (SVM, RBF). Maximum-margin classifier with radial-basis-function kernel to capture non-linear decision boundaries [32]. Settings used: , scale (library default), and one-vs-rest for multiclass.
- K-Nearest Neighbors (KNN). Non-parametric classifier using majority vote among the k closest samples in the feature space [33]. Settings used: and the Minkowski distance (order ).
- Logistic Regression (LR). Multinomial logistic (softmax) model optimized by maximum likelihood [34]. Settings used: multinomial loss, regularization, and inverse-class-frequency weights for imbalance.
4.6. Results Analysis
Under nested 10-fold cross-validation on CTG records (, ), the proposed CGLF framework preserved state-of-the-art discrimination and improved probability reliability.
Table 1 summarizes the head-to-head results against the strongest XGBoost baseline. CGLF attained a slightly higher accuracy ( vs. ), with the AUROC effectively tied ( vs. ). Balanced accuracy was slightly lower for CGLF ( vs. ). Welch’s t-tests (Table 1) indicated no statistically significant differences at , confirming that CGLF matched the best baseline in discrimination.

Table 1.
Performance comparison of CGLF with the base models (, , ). Means ± SD across outer folds. Welch’s t-test compares CGLF vs. best XGBoost.
Against a wider panel (Random Forest, MLP, SVM, KNN, and logistic regression), CGLF yielded the top mean balanced accuracy and accuracy, and a near-top AUROC (Table 2). This model performed better than most baseline models in both classification and calibration.

Table 2.
Performance comparison of CGLF with the baseline models. Best mean in bold; second best underlined.
It can be observed that CGLF improved absolute calibration, achieving the best Brier score () and the second-best ECE (3.54%) among all models (Table 3). Figure 4 compares the mean ECE, and Figure 5 shows that CGLF’s per-fold Brier loss was lower than XGBoost’s in 9/10 outer folds (means reported in the caption). Together, Table 3 and Figure 4 and Figure 5 indicate that CGLF delivered more reliable probabilities without sacrificing discrimination.

Table 3.
Calibration comparison (mean ± SD; lower is better). Best in bold; second best underlined.
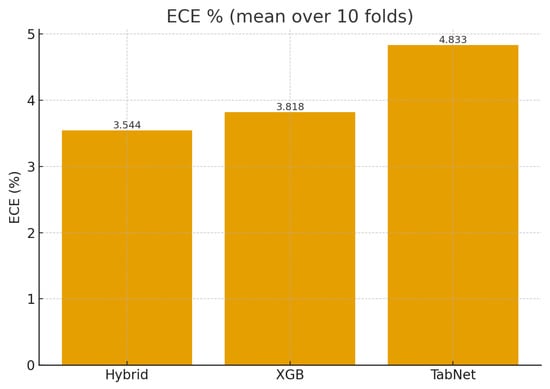
Figure 4.
Calibration comparison: ECE. CGLF 3.54%, XGB 3.82%, TabNet 4.83% (lower is better).
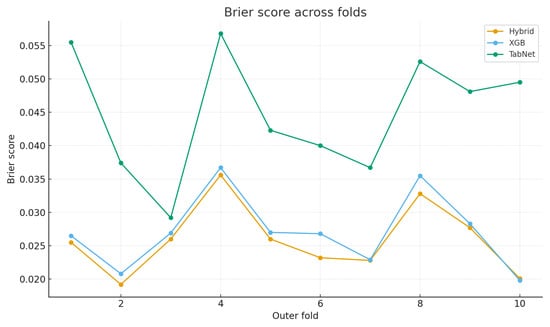
Figure 5.
Calibration comparison: per-fold Brier loss. CGLF ≤ XGB in 9/10 folds. Means ± SD: CGLF , XGB , TabNet .
As shown in Table 1, Table 2 and Table 3 and Figure 4 and Figure 5, CGLF matched the best-performing baseline on ranking (AUROC) and accuracy-type metrics while offering consistently better probability estimates, important for thresholded clinical use.
Under nested 10-fold cross-validation on 1488 CTG records, the proposed CGLF framework exhibited state-of-the-art performance by preserving discrimination while improving probability reliability. As shown in Table 1, CGLF matched the strongest XGBoost baseline on key discrimination metrics, achieving slightly higher accuracy and accuracy, nearly identical AUROC, and only a marginally lower balanced accuracy, with Welch’s t-tests confirming no significant differences at . When compared against a wider panel of baselines (Table 2), CGLF achieved the best mean scores in balanced accuracy and accuracy, and a near-top AUROC, underscoring its robustness relative to both classical and neural models. Most importantly, the calibration results in Table 3 and Figure 4 and Figure 5 highlight CGLF’s consistent advantage: it attained the best Brier score, the second-best ECE, and a lower fold-wise Brier loss than XGBoost in 9 out of 10 folds, providing more reliable probability estimates. Taken together, these findings establish that CGLF not only sustains competitive classification accuracy but also delivers superior calibration, making it particularly suitable for threshold-dependent clinical decision-making in CTG analysis.
5. Discussion
5.1. Clinical Relevance
Manual CTG interpretation suffers from inter-observer variability and inconsistent decision thresholds [35]. Under a strictly leakage-controlled, nested 10-fold protocol, our calibrated CGLF TabNet+XGBoost with global logit fusion and per-class vector–temperature calibration achieved , , and , while improving average probability quality relative to the strongest single model (best XGBoost: , , ). The calibration metrics favored CGLF (, ) over XGBoost (, ), indicating more trustworthy probabilities for thresholded clinical workflows.
5.2. Discrimination vs. Calibration Trade-Offs
Across folds, CGLF matched XGBoost’s discrimination (Welch’s t-tests: , ; balanced accuracy , ) while delivering more reliable probabilities; the ECE improved in 8/10 folds and the Brier score in 9/10 folds (with small regressions in the remaining folds). Balanced accuracy (BA) was similar overall (CGLF vs. XGBoost ), reflecting our explicit BA-floor constraint during post hoc class reweighting. Practically, this means that calibration gains were not achieved by sacrificing class-wise sensitivity, a crucial consideration for risk-aware obstetric decision support.
5.3. Where the Gains Come from
The code enforces strict leakage safety: standardization, SMOTE–Tomek, class weights, fusion (global logit blending), calibration (vector temperatures), and the optional per-class reweighting are all fitted on out-of-fold (OOF) predictions from the outer-train split and then applied once to the held-out fold. Within this framework, the global logit blend path was selected in 10/10 folds (higher OOF performance under the BA floor), suggesting that a simple, well-regularized fusion of TabNet with the stronger XGBoost stream captures complementary information without overfitting. Per-class temperature calibration further corrected probability sharpness, which is reflected in consistently lower Brier scores and reduced ECE on average.
5.4. Interpretability and Robustness Signals
Beyond scalar metrics, we examined attention sparsity, feature stability, and sufficiency. TabNet’s instance-wise attention remained sparse (mask entropy ), supporting per-sample auditability. Feature-ranking stability at top-10 (Jaccard) was higher for XGBoost than TabNet (0.813 vs. 0.570), offering complementary global interpretability. Sufficiency curves showed that XGBoost required fewer ranked features to achieve of full-model performance ( mean 5.20) than TabNet (8.70), consistent with boosted trees’ strength on tabular data. Together, these diagnostics link model behavior to familiar CTG variables and provide multiple lenses for clinical review.
5.5. Benchmarks in Context
Classical baselines confirmed the expected trends on this tabular dataset. Random Forests and an XGBoost with 500 trees were competitive in discrimination (e.g., ; ) but exhibited weaker average calibration (e.g., ). Linear and kernel methods underperformed overall, especially for minority classes. Against this backdrop, CGLF preserved top-tier discrimination while delivering the best average calibration profile, which is particularly relevant when sites tune decision thresholds to local risk tolerances.
5.6. Clinical Implications
A high AUROC (≈0.99) combined with improved calibration allows clinicians to select operating points (e.g., favoring sensitivity to the pathological class) using probability thresholds that better correspond to empirical risk. Because all components are leakage-safe and OOF-validated, the reported probabilities are more likely to transfer to prospective settings than pipelines that inadvertently leak information into the training loop. The calibration-centric design therefore addresses a central barrier to clinical adoption: reconciling strong discrimination with trustworthy risk estimates.
5.7. Limitations and Scope
A key limitation of this study is that the final training dataset, after quality-control filtering, comprised only 1488 samples (normal = 1158, suspect = 207, pathological = 123), which is relatively small for deep models such as TabNet. While multi-seed outer cross-validation and leakage-controlled resampling were designed to mitigate overfitting, external validation on independent CTG datasets is needed to confirm the generalizability of CGLF. The findings are bounded by the public dataset, its tabular featurization (23 predictors), and the specified nested CV protocol. The minority (pathological) class remains relatively small, which increases variance in sensitivity estimates. Prospective evaluations with protocolized thresholds and decision-curve analysis are needed to measure the impact of the intervention.
5.8. Deployment Considerations
Although our study prioritized methodological validity (discrimination, calibration, leakage control), the constituent models (TabNet, XGBoost) and fusion/calibration steps are amenable to efficient inference. Before operational use (e.g., bedside monitoring), engineering assessments of latency, memory/energy footprint, and fail-safe behavior are necessary, as are governance protocols for periodic recalibration and performance monitoring.
6. Conclusions
We introduced a leakage-safe Calibrated Global Logit Fusion (CGLF) framework for fetal health classification from CTG that couples TabNet’s instance-wise sparse attention with XGBoost’s gradient-boosted rules and fuses their outputs at the logit level, followed by per-class vector–temperature calibration and constrained post hoc reweighting under a balanced-accuracy (BA) floor. Every estimator in the pipeline standardization (SMOTE–Tomek, class weighting, fusion, calibration, and thresholds) is fitted strictly on out-of-fold (OOF) predictions from the training split of each outer fold and then applied once to the held-out split, eliminating information leakage by design.
In thresholded clinical workflows, calibrated probabilities are as critical as a high AUROC. By delivering XGBoost-level discrimination with measurably better average calibration under a leakage-controlled protocol, CGLF provides risk estimates that are more trustworthy for operating-point selection (e.g., prioritizing sensitivity to the pathological class). The pipeline components (TabNet, XGBoost, logit fusion, and temperature scaling) are computationally pragmatic, and their strict OOF fitting improves the likelihood of prospective reproducibility.
CGLF operationalizes a calibration-centric, leakage-safe ensemble for CTG that integrates complementary inductive biases (sparse attention and boosted rules) and emphasizes probability reliability. The resulting model is interpretable, reproducible, and well-suited to threshold-based obstetric decision support, providing a practical path toward clinically aligned AI for fetal monitoring.
Our findings are bounded by a single public dataset, a tabular feature set (23 variables), and the specified nested CV. Minority-class scarcity implies variance in sensitivity estimates; prospective studies with protocolized thresholds and decision-curve analysis are needed before implementation at the clinical level. Future directions include expanding heterogeneous bases (e.g., raw waveform encoders under the same leakage discipline), richer yet leakage-safe meta-features, uncertainty quantification, and continuous calibration monitoring under dataset shift.
Author Contributions
Conceptualization, M.E.A. and J.K.; Data curation, M.E.A.; Formal analysis, M.E.A.; Funding acquisition, J.K.; Methodology, M.E.A.; Software, M.E.A.; Supervision, J.K.; Visualization, M.E.A.; Writing—original draft, M.E.A.; Writing—review and editing, J.K. and M.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (2021R1A2C2008414); the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP2025-RS-2020-II201789); and the Artificial Intelligence Convergence Innovation Human Resources Development (IITP-2025-RS-2023-00254592), supervised by the IITP (Institute for Information and Communications Technology Planning and Evaluation).
Institutional Review Board Statement
This study utilized publicly available, anonymized data from the CTG dataset on Kaggle. According to the Bioethics and Safety Act of South Korea, research using such data is exempt from Institutional Review Board (IRB) review.
Data Availability Statement
We utilized a publicly available dataset to train our models. The datasets can be accessed at the following link: https://www.kaggle.com/code/karnikakapoor/fetal-health-classification/notebook (last accessed on 28 September 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rahmayanti, N.; Pradani, H.; Pahlawan, M.; Vinarti, R. Comparison of machine learning algorithms to classify fetal health using cardiotocogram data. Procedia Comput. Sci. 2021, 197, 162–171. [Google Scholar] [CrossRef]
- Alfirevic, Z.; Devane, D.; Gyte, G. Continuous cardiotocography (CTG) as a form of electronic fetal monitoring (EFM) for fetal assessment during labor. Cochrane Database Syst. Rev. 2017, 2, CD006066. [Google Scholar] [CrossRef]
- Ranaei-Zamani, N.; David, A.; Siassakos, D.; Dadhwal, V.; Melbourne, A.; Aughwane, R.; Russell-Buckland, J.; Tachtsidis, I.; Hillman, S.; Mitra, S. Saving babies and families from preventable harm: A review of the current state of fetoplacental monitoring and emerging opportunities. npj Womens Health 2024, 2, 10. [Google Scholar] [CrossRef]
- Mendis, L.; Palaniswami, M.; Brownfoot, F.; Keenan, E. Computerised Cardiotocography Analysis for the Automated Detection of Fetal Compromise during Labour: A Review. Bioengineering 2023, 10, 7. [Google Scholar] [CrossRef]
- Woessner, A.; Anjum, U.; Salman, H.; Lear, J.; Turner, J.T.; Campbell, R.; Beaudry, L.; Zhan, J.; Cornett, L.E.; Gauch, S.; et al. Identifying and Training Deep Learning Neural Networks on Biomedical-Related Datasets. J. Biomed. Inform. 2024, 150, 104294. [Google Scholar] [CrossRef] [PubMed]
- Arık, S.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Salini, Y.; Mohanty, S.; Ramesh, J.; Yang, M.; Chalapathi, M. Cardiotocography Data Analysis for Fetal Health Classification Using Machine Learning Models. IEEE Access 2024, 12, 26005–26022. [Google Scholar] [CrossRef]
- Mienye, I.; Swart, T. A Comprehensive Review of Deep Learning: Architectures, Recent Advances, and Applications. Information 2024, 15, 755. [Google Scholar] [CrossRef]
- Rao, H.; Karthik, S.; Gupta, R. Automatic classification of fetal heart rate based on a multi-scale LSTM network. Front. Physiol. 2024, 15, 1398735. [Google Scholar] [CrossRef] [PubMed]
- Mushtaq, G.; Veningston, K. AI driven interpretable deep learning based fetal health classification. SLAS Technol. 2024, 229, 100206. [Google Scholar] [CrossRef]
- Lee, K.; Choi, E.; Nam, Y.; Liu, N.W.; Yang, Y.S.; Kim, H.Y.; Ahn, K.H.; Hong, S.C. Real-time Classification of Fetal Status Based on Deep Learning and Cardiotocography Data. J. Med. Syst. 2023, 47, 82. [Google Scholar] [CrossRef]
- Chieregato, M.; Frangiamore, F.; Morassi, M.; Baresi, C.; Nici, S.; Bassetti, C.; Bnà, C.; Galelli, M. A hybrid machine learning/deep learning COVID-19 severity predictive model from CT images and clinical data. Sci. Rep. 2022, 12, 4329. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.; Zheng, J.; Qian, L.; Li, M. A hybrid ensemble method for pulsar candidate classification. Astrophys. Space Sci. 2019, 364, 149. [Google Scholar] [CrossRef]
- Martins, A.; Astudillo, R. From softmax to sparsemax: A sparse model of attention and multi-label classification. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1614–1623. [Google Scholar]
- Bentéjac, C.; Csőrgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on tabular data? arXiv 2022, arXiv:2207.08815. [Google Scholar] [CrossRef]
- Buddenkotte, T.; Escudero Sanchez, L.; Crispin-Ortuzar, M.; Woitek, R.; McCague, C.; Brenton, J.D.; Öktem, O.; Sala, E.; Rundo, L. Calibrating ensembles for scalable uncertainty quantification in deep learning-based medical image segmentation. Comput. Biol. Med. 2023, 163, 107096. [Google Scholar] [CrossRef]
- Silva Filho, T.; Song, H.; Perello-Nieto, M.; Santos-Rodriguez, R.; Kull, M.; Flach, P. Classifier calibration: A survey on how to assess and improve predicted class probabilities. Mach. Learn. 2023, 112, 3211–3260. [Google Scholar] [CrossRef]
- Ojeda, F.M.; Jansen, M.L.; Thiéry, A.; Blankenberg, S.; Weimar, C.; Schmid, M.; Ziegler, A. Calibrating machine learning approaches for probability estimation: A comprehensive comparison. Stat. Med. 2023, 42, 5451–5478. [Google Scholar] [CrossRef] [PubMed]
- Rivolli, A.; Garcia, L.; Soares, C. Meta-features for Meta-learning. Knowl.-Based Syst. 2022, 240, 108101. [Google Scholar] [CrossRef]
- Balanya, S.A.; Maroñas, J.; Ramos, D. Adaptive temperature scaling for robust calibration of deep neural networks. Neural Comput. Appl. 2024, 36, 8073–8095. [Google Scholar] [CrossRef]
- Jung, S.; Seo, S.; Jeong, Y.; Choi, J. Scaling of Class-wise Training Losses for Post-hoc Calibration. In Proceedings of the 40th International Conference on Machine Learning (ICML), Honolulu, HI, USA, 23–29 July 2023; Volume 202, pp. 15421–15434. [Google Scholar]
- Or, B. Improving requirements classification with SMOTE-Tomek preprocessing. arXiv 2025, arXiv:2501.06491. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks, Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Datta, D.; Mallick, P.; Reddy, A.; Mohammed, M.A.; Jaber, M.M.; Alghawli, A.S.; Al-qaness, M.A. A hybrid classification of imbalanced hyperspectral images using ADASYN and enhanced deep subsampled multi-grained cascaded forest. Remote Sens. 2022, 14, 4853. [Google Scholar] [CrossRef]
- Mujahid, M.; Kına, E.; Rustam, F.; Villar, M.G.; Alvarado, E.S.; De La Torre Diez, I.; Ashraf, I. Data oversampling and imbalanced datasets: An investigation of performance for machine learning and feature engineering. J. Big Data 2024, 11, 87. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather. Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc. Ser. B Methodol. 1958, 20, 215–242. [Google Scholar] [CrossRef]
- Taha, A.; El-Sharkawy, M. Machine learning on cardiotocography data: A systematic review. Comput. Methods Programs Biomed. 2024, 242, 107656. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).