Self-Synchronized Common-Mode Current Control Strategy for Power Rebalancing in CPS-PWM Modulated Energy-Storage Modular Multilevel Converters

Abstract

Capacitor voltage imbalance among submodules in energy storage modular multilevel converters (MMCs) can lead to current distortion, power oscillations, and even system instability. Traditional voltage control strategies, inherited from non-storage MMCs, offer limited regulation capabilities and are insufficient to address the complex balancing requirements across phases, arms, and submodules in distributed Energy-Storage MMCs (ES-MMC). This paper proposes a self-synchronized common-mode current strategy to achieve capacitor voltage rebalancing in Carrier Phase-Shifted PWM (CPS-PWM) modulated ES-MMCs. The proposed method establishes both phase-level and arm-level power rebalancing pathways by utilizing the common-mode current in the upper and lower arms. Specifically, the DC component of the common-mode current is employed to regulate common-mode power between the arms, while the fundamental-frequency component, through its interaction with the fundamental modulation voltage, is used to adjust differential-mode power. By coordinating these two power components within each phase, the method enables effective capacitor voltage rebalancing among submodules in the presence of power imbalance caused by a nonuniform distributed energy storage converter. A comprehensive analysis of differential- and common-mode voltage regulation under CPS-PWM is presented. The corresponding control algorithm is developed to inject adaptive common-mode voltage based on capacitor voltage deviations, thereby inducing self-synchronized balancing currents. Simulation and experimental results verify that the proposed strategy significantly improves power distribution uniformity and reduces capacitor voltage deviations under various load and disturbance conditions.

1. Introduction

MMC has become a key technology for high-voltage and high-power applications due to their modularity, scalability, and high-quality output waveforms. They are widely used in HVDC transmission, medium-voltage distribution networks, and flexible AC transmission systems. The modular architecture allows low-voltage power devices to share voltage, simplifying design and enhancing reliability.

Recently, the integration of energy storage into MMCs has attracted significant attention, leading to the development of ES-MMCs. Unlike conventional MMCs, ES-MMCs incorporate batteries, supercapacitors, or hybrid storage devices directly within submodules. This enables each submodule to function as both a power conversion stage and an independent energy storage unit, enhancing system flexibility and enabling bidirectional power exchange with the AC grid and DC link. ES-MMCs support grid stability, frequency regulation, peak shaving, fault tolerance, and operation under weak grid or islanded conditions, making them particularly suitable for renewable energy integration and hybrid power management.

However, energy storage integration introduces new challenges. Distributed storage alters internal power flow, often causing imbalances between upper and lower arm voltages and unequal energy utilization among phases [1,2,3,4]. Traditional voltage-balancing methods for non-storage MMCs are insufficient for ES-MMCs, especially under dynamic power exchange conditions.

Several methods have been proposed to address these issues. In [5], differential-mode fundamental-frequency components are added to the modulation voltages of the upper and lower arms, effectively regulating interphase and arm voltage differences, though this may introduce harmonic currents on the AC side. References [1,2,3,4,6,7] control the positive- and negative-sequence amplitudes of fundamental-frequency common-mode currents to balance capacitor voltages between phases and arms. However, under light-load or no-load conditions, the absence of DC in the arms eliminates the power path for phase capacitor balancing, leaving intra-arm capacitor voltages unregulated [5]. Asymmetric power distribution strategies [8] adjust output power for each phase and arm, enabling coordinated voltage balancing, but practical implementation remains complex. A generalized voltage balancing algorithm based on dynamic switching state selection is proposed, in which the switching states of the submodules are generated dynamically [9,10]. Ref. [11] analyzed the causes of capacitor voltage imbalance and proposed a control strategy based on fundamental-frequency reactive circulating current injection. Ref. [12] achieved submodule capacitor voltage balancing by introducing a regulation coefficient into the modulation. Refs. [13,14,15,16,17,18,19,20,21,22,23,24] also investigated the principles of capacitor voltage behavior and balancing control methods related to CPS-PWM, providing the theoretical foundation for this paper.

This paper proposes a self-synchronized common-mode current strategy for power rebalancing in ES-MMCs, with 2 main contributions:

• Regulation of upper and lower arm capacitor voltages through control of the phase angle between the modulation voltage and the fundamental-frequency common-mode current, while maintaining phase capacitor voltage stability via a DC common-mode offset.
• Establishment of a dedicated and controllable power-balancing pathway by maintaining a constant common-mode current amplitude, which enhances capacitor voltage balancing, operational stability, and enables flexible energy management under varying load and grid conditions.

2. Energy Storage MMC and Capacitor Voltage Deviation

2.1. Topology of Energy Storage MMC

Figure 1 illustrates the topology of the ES-MMC. The DC terminals are connected to the DC grid, while the midpoint of each phase is interfaced with the AC grid. Each submodule is derived from the conventional half-bridge configuration and extended with a bidirectional buck-boost converter connected in parallel with the capacitor, enabling the direct integration of low-voltage distributed energy storage units. An MMC arm is composed of a series connection of identical energy-storage submodules together with an arm inductor, and each phase consists of an upper and a lower arm. Compared with conventional energy-storage grid-connection schemes, this topology eliminates the need for bulky high-power DC/DC converters by utilizing the series connection of MMC arms to achieve medium-voltage operation for energy-storage units. Moreover, in the event of a failure in one or several distributed storage units, the corresponding faulty modules can be bypassed or isolated, allowing the system to continue operating reliably despite local subsystem faults.

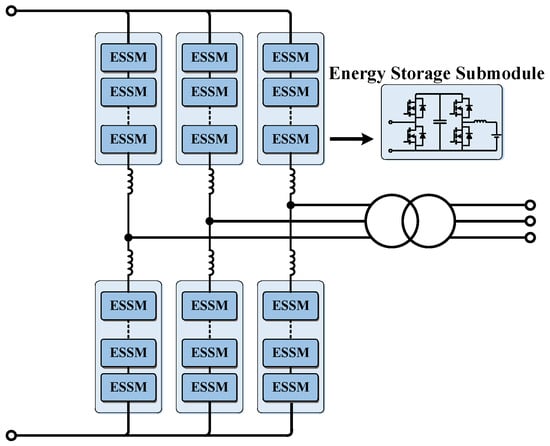
Figure 1. Topology of Energy-Storage MMC.

When the number of submodules per arm is relatively small, Nearest Level Modulation is not applicable, and conventional PWM strategies may suffer from limited voltage resolution and higher harmonics. CPS-PWM addresses this limitation by applying phase-shifted triangular carriers to each submodule, effectively increasing the apparent switching frequency at the arm level, reducing voltage ripple, and improving harmonic performance. Furthermore, with the continuous improvement of voltage ratings for power electronic devices, such as 6.5 kV IGBTs or SiC switches, only a few submodules per arm are sufficient for medium-voltage distribution grid connections.

Combined with CPS-PWM, even MMCs with a limited number of submodules can achieve stable operation and high-quality voltage waveforms, thereby simplifying system complexity and enabling efficient energy storage integration. The following section illustrates the mechanism of power imbalance in CPS-PWM-based ES-MMCs and presents the corresponding power rebalancing method.

2.2. Mechanism of Power Imbalance and Capacitor Voltage Deviation

As shown in Figure 2 and Figure 3 and reported in [7], in a conventional MMC, the AC grid-side differential-mode current is symmetrically distributed between the upper and lower arms, and the sum of the submodule voltages exhibits only fundamental-frequency pulsations without any DC bias component. Under symmetric parameter conditions, the average value of the submodule voltages in both arms of the same phase remains consistently equal to N × U_sm, where U_sm represents the nominal submodule capacitor voltage, N is the number of submodules per arm, and stable operation can be maintained by regulating the voltage distribution among submodules within each arm.

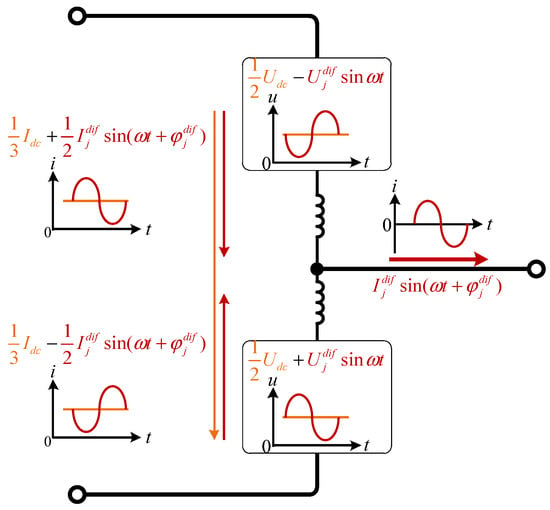
Figure 2. Schematic diagram of modulation voltages and arm currents in a non-storage MMC.

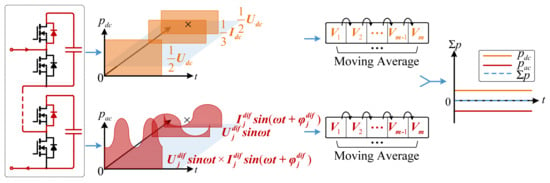
Figure 3. Illustration of power distribution in a non-storage MMC based on moving-average window analysis.

The sum of the capacitor voltages of the upper arm in phase j is denoted as $u_j^{up}$(t), and that of the lower arm is denoted as $u_j^{low}$(t), which yields

$$\left\{\begin{array}{l}{u}_j^{up}(t)={\displaystyle \frac{1}{2}}{U}_{dc}-u_{j1}^{dif}(t)\\ u_j^{low}(t)={\displaystyle \frac{1}{2}}{U}_{dc}+u_{j1}^{dif}(t)\end{array}\right.$$

(1)

U_dc represents the DC-link voltage, and $u_{j1}^{dif}$(t) denotes the fundamental modulation voltage of phase j. $U_{j1}^{dif}$ denotes the amplitude of the differential-mode modulation voltage. Thus, the relationship yields

$$u_{j1}^{dif}(t)=U_{j1}^{dif}\sin \omega t$$

(2)

$u_j^{com}$(t) denotes the common-mode voltage component of the upper and lower arms in phase j, while $u_j^{dif}$(t) represents the differential-mode voltage component. They are defined as

$$\left\{\begin{array}{l}{u}_j^{com}(t)={\displaystyle \frac{1}{2}}[u_j^{up}(t)+u_j^{low}(t)]\\ u_j^{dif}(t)={\displaystyle \frac{1}{2}}[u_j^{low}(t)-u_j^{up}(t)]\end{array}\right.$$

(3)

Correspondingly, the upper-arm current and lower-arm current of phase j are defined as $i_j^{up}$(t) and $i_j^{low}$(t), respectively, which can be expressed as

$$\left\{\begin{array}{l}{i}_j^{up}(t)={\displaystyle \frac{1}{3}}{I}_{dc}+{\displaystyle \frac{1}{2}}{i}_{j1}^{dif}(t)\\ i_j^{low}(t)={\displaystyle \frac{1}{3}}{I}_{dc}-{\displaystyle \frac{1}{2}}{i}_{j1}^{dif}(t)\end{array}\right.$$

(4)

Here, I_dc denotes the total DC-side current flowing through the three-phase DC bus, and $i_{j1}^{dif}$(t) represents the differential current component between the upper and lower arms of phase j, which also corresponds to the AC-side grid current. According to the definition,

$$i_{j1}^{dif}(t)=I_{j1}^{dif}\sin (\omega t+{\phi }_{j1}^{dif})$$

(5)

$I_{j1}^{dif}$ is the amplitude of the differential-mode current, and ${\phi }_{j1}^{dif}$ is the power factor angle.

As shown in Figure 2, the instantaneous power of the upper arm $p_j^{up}$(t) and that of the lower arm $p_j^{low}$(t) in phase j are expressed as

$$\left\{\begin{array}{l}{p}_j^{up}(t)=u_j^{up}(t)\times i_j^{up}(t)=p_{dc}(t)-p_{ac}(t)-p_{var}(t)\\ p_j^{low}(t)=u_j^{low}(t)\times i_j^{low}(t)=p_{dc}(t)-p_{ac}(t)+p_{var}(t)\end{array}\right.$$

(6)

Here, p_dc(t) denotes the power transferred from the DC side into the upper- or lower-arm capacitors, p_ac(t) represents the power delivered from the arm capacitors to the AC side, and p_var(t)corresponds to the reactive power exchanged between the upper and lower arms at the fundamental frequency (50 Hz). Their analytical expressions can be written as

$$\left\{\begin{array}{l}{p}_{dc}(t)={\displaystyle \frac{1}{6}}{U}_{dc}{I}_{dc}\\ p_{ac}(t)={\displaystyle \frac{1}{4}}{U}_{j1}^{dif}{I}_{j1}^{dif}\cos {\phi }_{j1}^{dif}-{\displaystyle \frac{1}{4}}{U}_{j1}^{dif}{I}_{j1}^{dif}\cos (2\omega t+{\phi }_{j1}^{dif})\\ p_{var}(t)={\displaystyle \frac{1}{3}}{I}_{dc}{U}_{j1}^{dif}\sin \omega t-{\displaystyle \frac{1}{4}}{U}_{dc}{I}_{j1}^{dif}\sin (\omega t+{\phi }_{j1}^{dif})\end{array}\right.$$

(7)

The instantaneous multilevel power of phase j, denoted as p_j(t), is expressed as the sum of the upper- and lower-arm instantaneous powers:

$$p_j(t)=p_j^{up}(t)+p_j^{low}(t)={\displaystyle \frac{1}{3}}{U}_{dc}{I}_{dc}-{\displaystyle \frac{1}{2}}{U}_{j1}^{dif}{I}_{j1}^{dif}\cos {\phi }_{j1}^{dif}+{\displaystyle \frac{1}{2}}{U}_{j1}^{dif}{I}_{j1}^{dif}\cos (2\omega t+{\phi }_{j1}^{dif})$$

(8)

${\displaystyle \frac{1}{3}}{U}_{dc}{I}_{dc}$ represents the active power delivered from the DC side, ${\displaystyle \frac{1}{2}}{U}_{j1}^{dif}{I}_{j1}^{dif}\cos {\phi }_{j1}^{dif}$ denotes the active power transferred to the AC side, and ${\displaystyle \frac{1}{2}}{U}_{j1}^{dif}{I}_{j1}^{dif}\cos (2\omega t+{\phi }_{j1}^{dif})$ is a second-harmonic oscillatory component associated with the AC grid-side voltage and current. For the total instantaneous power of the upper and lower arms in phase j, the power flowing into the AC side is equal to the power drawn from the DC side, while the arm capacitors in phase j are subjected to a second-harmonic power fluctuation. Consequently, the average (DC) component of the capacitor voltage remains constant, but a second-harmonic ripple is inevitably superimposed.

In conventional MMCs, the power flowing from the DC side into the upper and lower arms, as well as the power delivered to the AC side, is naturally balanced. As illustrated in Figure 3, after applying a fundamental-frequency moving-average filter, the DC components of p_dc(t) and p_ac(t) show that the arm input and output powers are equal and the total capacitor power Σp = 0. Consequently, the submodule capacitor voltages are inherently self-balanced, and only minor regulation is required to compensate for voltage deviations caused by mismatches in circuit parameters.

However, with the integration of distributed energy storage, this intrinsic balance between DC-side and AC-side powers is disrupted [1,2,3,4]. The total output power of distributed storage units alters the DC-side power flow, and power asymmetry among individual storage units further aggravates voltage imbalance within the same arm, between the upper and lower arms of the same phase, and across different phases. These multilevel asymmetries introduced by distributed storage ultimately compromise the stable operation of the MMC, highlighting the need for advanced control strategies to maintain capacitor voltage balance and overall system stability [25].

As illustrated in Figure 4, the integration of N distributed energy storage units with output powers p_es1,…, p_esN disrupts the original balance between the DC and AC sides, Σp ≠ 0. The power mismatch among the storage units leads to capacitor voltage imbalance, whereas conventional capacitor voltage regulation schemes designed for traditional MMCs lack sufficient capability to cope with the persistent imbalance in storage power.

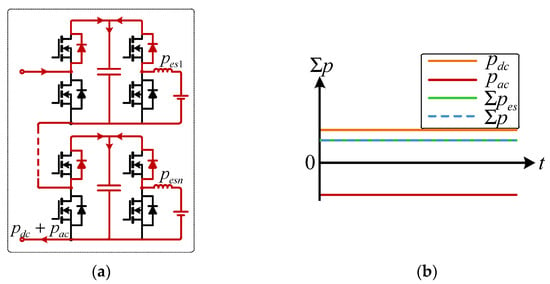
Figure 4. Power flow in an ES-MMC: (a) Current paths in an ESSM; (b) Power distribution in an ESSM.

To enhance the stability of capacitor voltage regulation under continuously unbalanced power conditions, this paper introduces a common-mode voltage, $u_{j1}^{com}$(t), into the upper and lower arms, thereby establishing a power transfer channel between the upper and lower arms at the phase level. By injecting the common-mode voltage $u_{j1}^{com}$(t), a controllable common-mode current $i_{j1}^{com}$(t) is generated, which serves as the medium for power exchange between the arms. This additional channel enables dynamic redistribution of unbalanced energy among submodules, thereby mitigating capacitor voltage deviation and enhancing the stability of the MMC under persistent storage power imbalance conditions.

3. Self-Synchronized Common-Mode Strategy

3.1. Capacitor Voltage Balancing Principle of Common-Mode Current

As shown in (9), to achieve both the average capacitor voltage regulation across all submodules in phase j and the voltage balance between the upper and lower arms, a DC common-mode component $u_{j0}^{com}$(t) and a fundamental-frequency common-mode component $u_{j1}^{com}$(t) are introduced into the modulation voltages of the upper and lower arms $u_j^{up}$(t) and $u_j^{low}$(t). The output voltage (or modulation voltage) of the upper arm can be expressed as

$$\left\{\begin{array}{l}{u}_j^{up}(t)=[{\displaystyle \frac{1}{2}}{U}_{dc}+u_{j0}^{com}(t)]-u_{j1}^{dif}(t)+u_{j1}^{com}(t)\\ u_j^{low}(t)=[{\displaystyle \frac{1}{2}}{U}_{dc}+u_{j0}^{com}(t)]+u_{j1}^{dif}(t)+u_{j1}^{com}(t)\end{array}\right.$$

(9)

The fundamental-frequency common-mode voltage component in phase j is defined as

$$u_{j1}^{com}(t)=U_{j1}^{com}\sin (\omega t+{\theta }_{j1}^{com})$$

(10)

where $U_{j1}^{com}$ denotes the amplitude of the fundamental-frequency common-mode voltage, and ${\theta }_{j1}^{com}$ represents its phase angle relative to the reference differential-mode voltage $u_{j1}^{dif}$(t).

Accordingly, in (10), the upper- and lower-arm currents $i_j^{up}$(t) and $i_j^{low}$(t) are augmented compared with (4) by the introduction of the fundamental-frequency common-mode current component:

$$\left\{\begin{array}{l}{i}_j^{up}(t)=({\displaystyle \frac{1}{3}}{I}_{dc}+I_{j0}^{com})+{\displaystyle \frac{1}{2}}{I}_{j1}^{dif}\sin (\omega t+{\phi }_{j1}^{dif})+I_{j1}^{com}\sin (\omega t+{\phi }_{j1}^{com})\\ i_j^{low}(t)=({\displaystyle \frac{1}{3}}{I}_{dc}+I_{j0}^{com})-{\displaystyle \frac{1}{2}}{I}_{j1}^{dif}\sin (\omega t+{\phi }_{j1}^{dif})+I_{j1}^{com}\sin (\omega t+{\phi }_{j1}^{com})\end{array}\right.$$

(11)

The instantaneous powers of the upper and lower arms, denoted as $p_j^{up}$(t) and $p_j^{low}$(t), are illustrated in Figure 5 and Figure 6, respectively. Figure 5 depicts the decomposition of the upper-arm power into its DC, differential-mode, and common-mode components, while Figure 6 presents the corresponding decomposition for the lower arm.

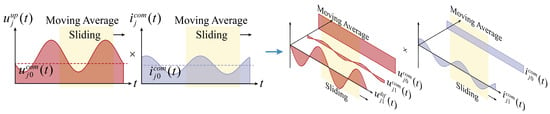
Figure 5. Frequency-domain decomposition of upper-arm power based on $u_j^{up}$(t) and $i_j^{up}$(t).

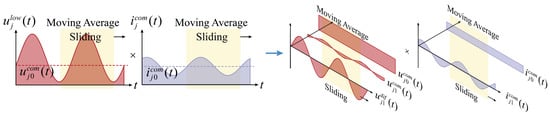
Figure 6. Frequency-domain decomposition of lower-arm power based on $u_j^{low}$(t) and $i_j^{low}$(t).

In Figure 5 and Figure 6, the product and superposition of the voltage and current components yield relatively complex expressions for instantaneous power. However, rather than focusing on the instantaneous power fluctuations, the primary concern lies in the periodic variations in the capacitor power in the upper and lower arms, namely the DC component of the power. Therefore, a moving average filter with a 0.02-s (50 Hz) time constant is applied to the output power to extract its DC component.

$$\left\{\begin{array}{l}<p_j^{up}(t){>}_{Ts}=<p_j^{com}(t){>}_{Ts}-<p_j^{dif}(t){>}_{Ts}\\ <p_j^{low}(t){>}_{Ts}=<p_j^{com}(t){>}_{Ts}+<p_j^{dif}(t){>}_{Ts}\\ <p_j(t){>}_{Ts}=2<p_j^{com}(t){>}_{Ts}\end{array}\right.$$

(12)

Then, by applying the moving average filter with an averaging interval of T_s, the DC components of the instantaneous powers in the upper and lower arms can be obtained as (12).

The DC components of the arm powers can be further decomposed into common-mode and differential-mode parts in (11). Specifically, the averaged common-mode and differential-mode power components over the window T_s are defined as

$$\left\{\begin{array}{l}<p_j^{com}(t){>}_{Ts}={\displaystyle \frac{1}{6}}{U}_{dc}{I}_{dc}-{\displaystyle \frac{1}{4}}{U}_{j1}^{dif}{I}_{j1}^{dif}\cos {\phi }_{j1}^{dif}+{\displaystyle \frac{1}{3}}{U}_{j0}^{com}{I}_{dc}+{\displaystyle \frac{1}{2}}{\mathit{U}}_{\mathit{dc}}{\mathit{I}}_{\mathit{j}0}^{\mathit{com}}+U_{j0}^{com}{I}_{j0}^{com}\\ <p_j^{dif}(t){>}_{Ts}={\displaystyle \frac{1}{2}}{\mathit{U}}_{\mathit{j}1}^{\mathit{dif}}{\mathit{I}}_{\mathit{j}1}^{\mathit{com}}\mathit{cos}{\mathit{\phi }}_{\mathit{j}1}^{\mathit{com}}-{\displaystyle \frac{1}{4}}{U}_{j1}^{com}{I}_{j1}^{dif}\cos ({\theta }_{j1}^{com}-{\phi }_{j1}^{dif})-{\displaystyle \frac{1}{2}}{U}_{j1}^{com}{I}_{j1}^{com}\cos ({\theta }_{j1}^{com}-{\phi }_{j1}^{com})\end{array}\right.$$

(13)

By regulating <$p_j^{com}$(t)>_Ts, the phase input power can be adjusted; in other words, the common-mode component of the DC power can be used to control the average capacitor voltage of the phase. Similarly, by controlling <$p_j^{dif}$(t)>_Ts, the differential power between the upper and lower arms can be modulated, allowing the differential DC component to be regulated and thereby achieving voltage balance between the upper and lower arm capacitors.

In <$p_j^{com}$(t)>_Ts, the power exchange process between the DC and AC sides is not affected by the common-mode voltage component. Among the remaining three terms, the dominant contribution arises from the DC component of ${\displaystyle \frac{1}{2}}{U}_{dc}{I}_{j0}^{com}$, which is used to regulate the average capacitor voltage of phase j. Furthermore, this DC component of the common-mode current $I_{j0}^{com}$ can be realized by controlling the DC component of the common-mode modulation voltage, $u_{j0}^{com}$(t), applied to the arm output voltage.

In <$p_j^{dif}$(t)>_Ts, the differential-mode voltage $U_{j1}^{dif}$ is typically much larger than the common-mode voltage $U_{j1}^{com}$, making it the dominant term. The power balance between the upper and lower arms can be regulated by controlling either the amplitude of the common-mode current $I_{j1}^{com}$ or the phase angle ${\phi }_{j1}^{com}$ between the common-mode current $i_{j1}^{com}$(t) and the differential-mode voltage $u_{j1}^{dif}$(t). As reported in [1,2,4,5], maintaining ${\phi }_{j1}^{com}$ = 0 and adjusting the amplitude of the common-mode modulation voltage $u_{j1}^{com}$(t) allows regulation of $i_{j1}^{com}$(t), thereby achieving voltage balance between the upper- and lower-arm capacitors.

However, amplitude-based control has a drawback under low-power operation on the AC/DC side of the MMC. Due to small power fluctuations, the resulting common-mode current is also small, and the current flowing through the arms is insufficient to redistribute power among the submodules within the arms. Consequently, although the upper- and lower-arm capacitor voltages may remain balanced, the capacitor voltages within the same arm can become unbalanced if the output powers of the submodule storage units are asymmetric.

Therefore, in this study, the arm voltage balance is achieved by regulating the phase angle ${\phi }_{j1}^{com}$. However, when ${\phi }_{j1}^{com}$ ≠ 0, the presence of the common-mode current induces fundamental-frequency reactive power exchange between the upper and lower arms. Direct control under these conditions would require frequent adjustments of the phase angle, which can degrade both control stability and performance. To mitigate this issue, a fundamental-frequency moving-average filter is applied to extract the DC component of the arm capacitor power for control, thereby avoiding the influence of reactive power. Furthermore, by superimposing a DC common-mode voltage $u_{j0}^{com}$(t) on the fundamental-frequency common-mode voltage $u_{j1}^{com}$(t), regulation of the average capacitor voltage of the phase is achieved.

This decomposition and control strategy thus establish a phase-level power transfer channel within each arm and provide an effective mechanism for capacitor power rebalancing, particularly under persistent asymmetry conditions introduced by distributed energy storage units.

3.2. Modeling and Synchronization Mechanism of Common-Mode Power

Figure 7a illustrates the phase topology of the ES-MMC, which consists of upper-arm submodules, lower-arm submodules, and arm inductors. Compared with the DC component of the arm ${\displaystyle \frac{1}{2}}{U}_{dc}$ and the differential-mode voltage $u_{j1}^{dif}$(t), both the superimposed DC common-mode voltage and the fundamental-frequency common-mode voltage can be considered as small-signal perturbations, as shown in Figure 7b.

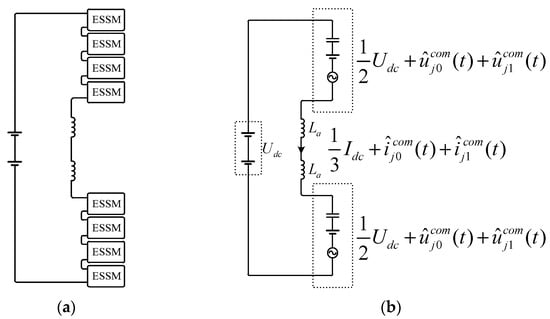
Figure 7. Small-Signal Model of the Phase-Level Common-Mode Current: (a) Original circuit topology; (b) Equivalent circuit model.

The DC common-mode voltage component $u_{j0}^{com}$(t) is denoted as ${\widehat{u}}_{j0}^{com}(t)$, and the fundamental-frequency common-mode voltage component $u_{j1}^{com}$(t) is denoted as ${\widehat{u}}_{j1}^{com}(t)$. These small-signal components are simultaneously superimposed onto the modulation signals of the upper and lower arms, generating corresponding small-signal common-mode currents in the arms, consisting of a DC component ${\widehat{i}}_{j0}^{com}(t)$ and a fundamental-frequency component ${\widehat{i}}_{j1}^{com}(t)$.

Figure 8 illustrates the small-signal circuit model derived from Figure 7 by separating the steady-state point. In this equivalent model, the arm inductance L_a and its internal resistance R_a are represented, C_eq is the equivalent capacitor from the submodule after modulation, across which a controlled DC voltage and a sinusoidal voltage are applied. Consequently, the process of generating the common-mode DC and the common-mode fundamental current can be effectively described. Figure 8 demonstrates that the amplitude of the output currents $I_{j0}^{com}$ and $I_{j1}^{com}$ can be regulated by adjusting the amplitudes of the DC and fundamental-frequency common-mode voltages. Moreover, by controlling the phase angle ${\theta }_{j1}^{com}$ of the fundamental-frequency common-mode voltage, the synchronization angle ${\phi }_{j1}^{com}$ of the common-mode current can be effectively modulated.

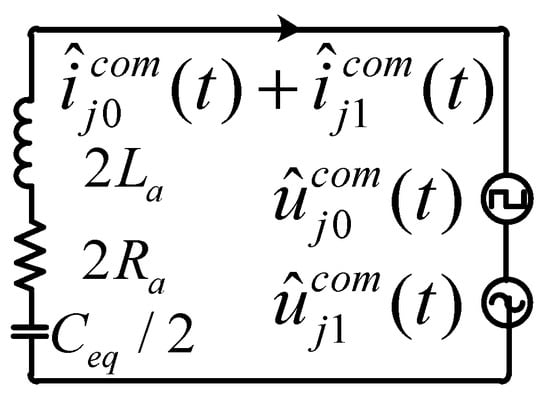
Figure 8. Frequency-domain decomposition of the small-signal common-mode current.

The periodic discrete control waveform of the common-mode current ${\widehat{i}}_j^{com}(t)$ is illustrated in Figure 9. To ensure the integrity of the synchronization-angle control process, the control angle ${\theta }_{j1}^{com}$(t) within the common-mode voltage is updated only at the end of each fundamental cycle. Accordingly, the proposed synchronization-angle control strategy adopts a discrete control scheme with a period of 0.02 s. At the beginning of each cycle, the small-signal component derived from the sum of the phase capacitor voltages ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}+{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}$ is employed to adjust the amplitude. In contrast, the small-signal component ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}-{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}$ obtained from the difference between the upper- and lower-arm voltages is used to regulate ${\theta }_{j1}^{com}$(t), thereby controlling the angle ${\phi }_{j1}^{com}$(t).

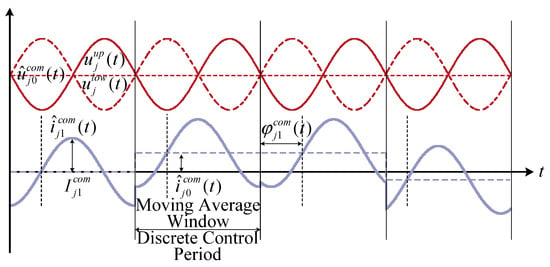
Figure 9. Operating principle of discrete common-mode current control.

The phase relationship among the fundamental common-mode voltage control angle ${\theta }_{j1}^{com}$(t), the synchronization angle of the fundamental common-mode current ${\phi }_{j1}^{com}$(t), and the differential voltage $u_{j1}^{dif}$(t) is illustrated in Figure 10. By taking the differential voltage $u_{j1}^{dif}$(t) as the reference phase, denoted as the d-axis, the control angle ${\theta }_{j1}^{com}$(t) is defined as a small-signal deviation relative to this reference. Due to the presence of the arm inductance, the inductor current lags behind the reference by ${\phi }_{j1}^{com}$(t). Its steady-state point is aligned with the q-axis, and the deviation of the synchronization angle relative to this steady-state point is denoted as a small-signal perturbation ${\widehat{\phi }}_{j1}^{com}(t)$.

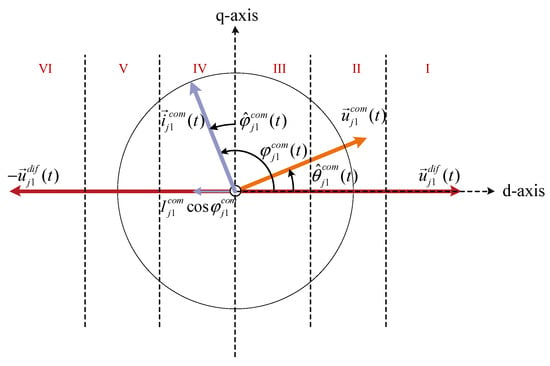
Figure 10. Phasor diagram of the fundamental common-mode balancing current under phase-angle synchronization control.

The fundamental common-mode current vector ${\overrightarrow{i}}_{j1}^{com}(t)$ can be projected onto the upper- and lower-arm differential voltages $-{\overrightarrow{u}}_j^{dif}(t)$ and ${\overrightarrow{u}}_j^{dif}(t)$ as $I_{j1}^{com}$cos${\phi }_{j1}^{com}$, which corresponds to the active power exchanged between the two arms. From the vector diagram, it is evident that, under the influence of the fundamental common-mode current, the power output directions of the upper and lower arms are always opposite. This observation is consistent with the analytical results presented in Equation (13).

The control angle ${\theta }_{j1}^{com}$(t) operates within a regulation interval centered on the d-axis, [−0.5π, 0.5π]. This interval can be further divided into six regions (I–VI), as illustrated in Figure 10. Among them, Regions III and IV represent the ideal operating zones, where the arm power difference remains below $U_{j1}^{dif}$$I_{j1}^{com}cos{\phi }_{j1}^{com}$, ensuring that the common-mode current can fully achieve power balancing between the upper and lower arms.

Regions II and V are defined as nonlinear compensation zones. In these regions, if the imbalance power falls within the feasible circular boundary, it can still be compensated by adjusting the control angle. However, once the imbalance exceeds this boundary, angle adjustment becomes ineffective, and the control angle is forced to saturate at its limits, −0.5π or 0.5π.

Finally, Regions I and VI correspond to the under-compensation zones. In these regions, even when the control angle reaches its extreme limits (−0.5π or 0.5π), capacitor power balance between the upper and lower arms cannot be achieved. Consequently, the ES-MMC inevitably loses stability. Therefore, during the design process of circuit parameters and the selection of the fundamental common-mode current amplitude $U_{j1}^{com}$, the system should be configured to avoid operation in these two regions.

3.3. Coordinated Control Under Nonuniform Energy Storage Power

3.3.1. Moving Average Filter Design and Implementation

The moving average filter is essentially a finite impulse response filter (FIR), whose transfer function in the z-domain is given by

$$H(z)={\displaystyle \frac{y(z)}{u(z)}}={\displaystyle \frac{1}{M}}{\displaystyle \sum _{k=0}^{M-1}{z}^{-k}}={\displaystyle \frac{1}{M}}{\displaystyle \frac{1-z^{-M}}{1-z^{-1}}}$$

(14)

In the practical experiment and application, the moving average filter is implemented in the controller as illustrated in Figure 11. A memory array buffer[M] of length M is allocated in the heap, and a pointer cursor tracks the oldest data u[n−M].

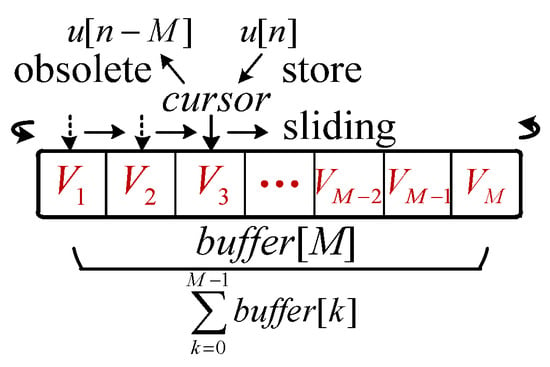
Figure 11. Implementation principle of the moving average filter.

The sum ∑buffer[k] is updated incrementally: the oldest value is replaced by the latest input u[n], and cursor is advanced to the next element. When cursor reaches the end of the array, it wraps around to form a circular buffer. The filter output is then given by ∑buffer[k]/M. During the first 200 points, the average gradually converges as the window fills. Afterward, each update requires only one addition and one subtraction, significantly improving computational efficiency compared with summing all 200 points at each step.

The frequency response of the moving average filter is given by

$$H(e^{j\omega })={\displaystyle \frac{1}{M}}{\displaystyle \frac{1-e^{-jM\omega }}{1-e^{-j\omega }}}={\displaystyle \frac{1}{M}}{e}^{-j\omega {\displaystyle \frac{M-1}{2}}}{\displaystyle \frac{\sin \frac{M\omega }{2}}{\sin \frac{\omega }{2}}}$$

(15)

As shown in Figure 12 the Bode plot, zeros appear successively at 50 Hz and its harmonics. Therefore, the moving average filter provides complete attenuation at 50 Hz and its integer multiples.

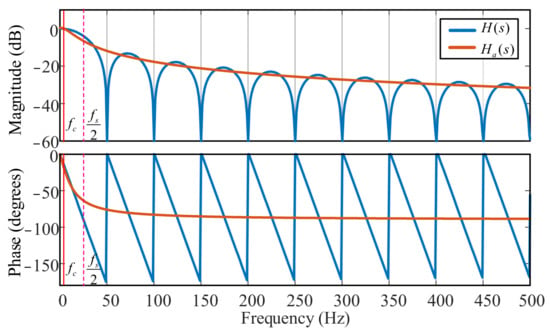
Figure 12. Bode plot of the moving average filter with T_s = 0.02 s.

In this paper, the controller design was carried out using the root locus method. However, since the frequency response of the moving average filter corresponds to a Dirichlet kernel, directly applying the root locus analysis to the z-domain transfer function in (14) is intractable. To address this problem, the moving average filter is approximated in the low-frequency range of the Nyquist frequency as a first-order inertia transfer. Specifically, yielding the following approximation:

$$H_a(s)={\displaystyle \frac{K_a}{1+T_{a}s}}\approx H(s)$$

(16)

In the low-frequency range, this first-order inertia approximation can effectively emulate the dynamic characteristics of the moving average filter as in Figure 12. Therefore, in both the experimental and simulation stages of designing phase-level capacitor voltages controller D_p(z) and arm-level capacitor voltage controller D_a(z), the approximate inertia element H_a(s) was employed in place of the moving average filter for controller parameter design.

3.3.2. Phase-Level Capacitor Voltages Control

According to the small-signal equivalent circuit of the common-mode voltage in Figure 8, a differential relationship exists between the applied common-mode voltage ${\widehat{u}}_j^{com}(t)$ and the resulting common-mode current ${\widehat{i}}_j^{com}(t)$ as

$${\widehat{u}}_j^{com}(t)=-L_a{\displaystyle \frac{d{\widehat{i}}_j^{com}(t)}{dt}}-R_a{\widehat{i}}_j^{com}(t)$$

(17)

Which can be expressed by the transfer function

$${\widehat{i}}_j^{com}(s)=-{\displaystyle \frac{1}{s{L}_a+R_a}}{\widehat{u}}_j^{com}(s)$$

(18)

Applying a zero-order-hold (ZOH) discretization to (19) with sampling period T_s = 0.02 s yields the following z-domain discrete transfer function:

$${\displaystyle \frac{{\widehat{i}}_{j0}^{com}(z)}{{\widehat{u}}_{j0}^{com}(z)}}=\mathcal{Z}\left\{{\displaystyle \frac{1-e^{-s{T}_s}}{s}}\cdot {\displaystyle \frac{1}{s{L}_a+R_a}}\right\}$$

(19)

Since the discrete sampling period coincides with the fundamental-frequency period, and the output of the controlled plant remains constant within each ZOH interval, the control input ${\widehat{u}}_j^{com}(t)$ in (20) can be regarded as its DC component ${\widehat{u}}_{j0}^{com}(z)$, while the output ${\widehat{i}}_j^{com}(t)$ can similarly be considered as its DC component ${\widehat{i}}_{j0}^{com}(z)$.

Furthermore, the sum of the modulation voltages of the upper and lower arms in the same phase equals U_dc. The product of the DC component of the common-mode current ${\widehat{i}}_{j0}^{com}(z)$ and the sum of the upper- and lower-arm output voltages U_dc corresponds to the phase-regulating power $\Sigma {\widehat{p}}_{j0}^{com}(z)$, which is used to charge the capacitors across the entire phase.

$${\displaystyle \frac{{\widehat{u}}_c(s)}{\widehat{p}(s)}}={\displaystyle \frac{1}{s{C}_{sm}{U}_{sm}}}$$

(20)

Additionally, a small-signal transfer function can be derived for the phase capacitor charging process in (20).

By applying ZOH discretization to (20) with a sampling period of T_s = 0.02 s, the discrete transfer function from the modulation voltage ${\widehat{u}}_{j0}^{com}(z)$ to the total capacitor voltage ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}+{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}$ of the upper and lower arms is established, as illustrated in Figure 13.

Figure 13. Discrete transfer function from the modulation voltage ${\widehat{u}}_{j0}^{com}(z)$ to the total capacitor voltage of the arms ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}+{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}$.

$$\left\{\begin{array}{l}{G}_{{\widehat{u}}_j^{com}\to \Sigma {\widehat{p}}_{j0}^{com}}(z)=-\mathcal{Z}\left\{{\displaystyle \frac{1-e^{-s{T}_s}}{s}}\cdot {\displaystyle \frac{U_{dc}}{2}}\cdot {\displaystyle \frac{1}{s{L}_a+R_a}}\right\}\\ G_{\Sigma {\widehat{p}}_{j0}^{com}\to \Sigma {\widehat{u}}_c}(z)=\mathcal{Z}\left\{{\displaystyle \frac{1-e^{-s{T}_s}}{s}}\cdot {\displaystyle \frac{1}{N{C}_{sm}{U}_{sm}s}}\right\}\end{array}\right.$$

(21)

In Figure 13, the discretized transfer functions are denoted as $G_{{\widehat{u}}_j^{com}\to \Sigma {\widehat{p}}_{j0}^{com}}(z)$ and $G_{\Sigma {\widehat{p}}_{j0}^{com}\to \Sigma {\widehat{u}}_c}(z)$, respectively.

As illustrated in Figure 14, a discrete controller, D_p(z), and a moving average filter, H(z), are introduced to implement closed-loop control of the plant.

Figure 14. Discrete closed-loop control of the total arm capacitor voltage ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}+{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}$.

The discrete controller D_p(z) is implemented as a PI controller and discretized using the Tustin method. Through D_p(z), the system can maintain the DC component of the common-mode current, thereby regulating the average capacitor voltage of the phase. Combined with the moving average filter H(z), the controller extracts the DC component of the arm capacitor power and provides feedback for closed-loop regulation, ensuring that the upper- and lower-arm capacitor voltages ${\displaystyle \sum _{k=1}^N{u}_{cjk}^{up}(z)}+{\displaystyle \sum _{k=1}^N{u}_{cjk}^{low}(z)}=2N{U}_{sm}$ under varying operating conditions.

The PI controller in the discrete domain is designed using the Tustin transformation, as expressed

$$D_p(z)=k_{p1}+k_{i1}{\displaystyle \frac{T_s}{2}}{\displaystyle \frac{z+1}{z-1}}=k_{p1}(1+2\pi {\displaystyle \frac{T_s}{2}}{\displaystyle \frac{z+1}{z-1}})$$

(22)

Taking the simulation parameters as an example, by substituting them into the model, the root locus under the discrete control period of T_s = 0.02 s is obtained Figure 15. It shows the root locus of the D_p(z) controller as the proportional gain kp1 varies from 0 to ∞. The discrete system is stable when the poles remain inside the unit circle.

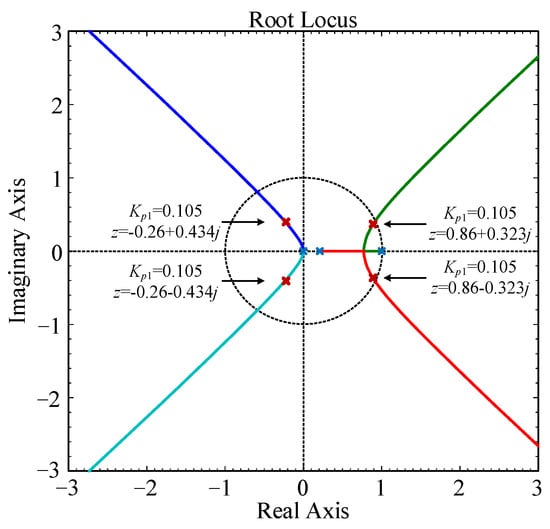
Figure 15. Root locus of the D_p(z) controller with varying k_p1.

3.3.3. Arm-Level Capacitor Voltage Control

The core of the upper- and lower-arm capacitor voltage balancing control lies in regulating the phase shift angle ${\theta }_{j1}^{com}$(t) of the fundamental common-mode voltage $u_{j1}^{com}$(t) with respect to the differential voltage $u_{j1}^{dif}$(t). This adjustment enables the synchronization angle ${\phi }_{j1}^{com}$(t) of the fundamental common-mode current $i_{j1}^{com}$(t) to be controlled. The small-signal equations of the common-mode voltage and current are expressed in (19).

$$\left\{\begin{array}{l}{u}_{j1}^{com}(t)=U_{j1}^{com}\sin [\omega t+\Theta +{\widehat{\theta }}_{j1}^{com}(t)]\\ i_{j1}^{com}(t)=I_{j1}^{com}\sin [\omega t+\Phi +{\widehat{\phi }}_{j1}^{com}(t)]\end{array}\right.$$

(23)

Evidently, the differential equation from ${\widehat{\theta }}_{j1}^{com}(t)$ to ${\widehat{\phi }}_{j1}^{com}(t)$ involves nonlinear trigonometric terms, which cannot be linearized by separating the steady-state operating point.

$${\widehat{\phi }}_{j1}^{com}(t)={\displaystyle \frac{\sqrt{{(\omega L_a)}^2+R_a^2}}{s{L}_a+R_a}}{\widehat{\theta }}_{j1}^{com}(t)$$

(24)

Considering that, under steady-state conditions in Figure 8, ${\widehat{\theta }}_{j1}^{com}(t)$ = ${\widehat{\phi }}_{j1}^{com}(t)$, the process from the voltage phase-shift angle to the current synchronization angle is simplified as an inductive inertia element with a static gain of unity, as expressed in (20).

$$\Delta {\widehat{p}}_{j1}^{com}(s)={\displaystyle \frac{1}{2}}{U}_{j1}^{dif}{I}_{j1}^{com}\cos [{\displaystyle \frac{\pi }{2}}+{\widehat{\phi }}_{j1}^{com}(t)]=-{\displaystyle \frac{1}{2}}{U}_{j1}^{dif}{I}_{j1}^{com}\sin {\widehat{\phi }}_{j1}^{com}(t)=-{\displaystyle \frac{1}{2}}{U}_{j1}^{dif}{I}_{j1}^{com}{\widehat{\phi }}_{j1}^{com}(t)$$

(25)

Furthermore, the term $\Delta {\widehat{p}}_{j1}^{com}(s)$ can be simplified at the steady-state operating point ${\phi }_{j1}^{com}={\displaystyle \frac{1}{2}}\pi$ in (25).

Applying the ZOH discretization to (20) and (24) with a sampling period of T_s = 0.02 s, the discrete transfer function from the small-signal phase-shifting angle ${\widehat{\theta }}_{j1}^{com}(t)$ to the voltage difference ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}-{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}$ between the upper and lower arms is obtained, as shown in Figure 16.

Figure 16. Discrete transfer function from the synchronization angle ${\widehat{\theta }}_{j1}^{com}(z)$ to the differential arm capacitor voltage ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}-{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}$.

$$\left\{\begin{array}{l}{G}_{{\widehat{\theta }}_{j1}^{com}\to \Delta {\widehat{p}}_{j1}^{com}}(z)=-\mathcal{Z}\left\{{\displaystyle \frac{1-e^{-s{T}_s}}{s}}\cdot {\displaystyle \frac{1}{2}}{\displaystyle \frac{U_{j1}^{dif}{I}_{j1}^{com}\sqrt{{(\omega L_0)}^2+R_0^2}}{s{L}_0+R_0}}\right\}\\ G_{\Delta {\widehat{p}}_{j0}^{com}\to \Delta {\widehat{u}}_c}(z)=\mathcal{Z}\left\{{\displaystyle \frac{1-e^{-s{T}_s}}{s}}\cdot {\displaystyle \frac{1}{N{C}_{sm}{U}_{sm}s}}\right\}\end{array}\right.$$

(26)

The discrete transfer functions in the z-domain are denoted as $G_{{\widehat{\theta }}_{j1}^{com}\to \Delta {\widehat{p}}_{j1}^{com}}(z)$ and $G_{\Delta {\widehat{p}}_{j0}^{com}\to \Delta {\widehat{u}}_c}(z)$.

Figure 17 illustrates the block diagram of the closed-loop control scheme for balancing the capacitor voltages between the upper and lower arms. D_a(z) is the PI controller for capacitor voltage balance between arms. The control objective is to suppress voltage imbalance ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}-{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}$ by regulating the phase angle ${\theta }_{j1}^{com}$(t) of the fundamental common-mode voltage $u_{j1}^{com}$(t) with respect to the differential voltage $u_{j1}^{dif}$(t). Through this mechanism, the synchronization angle of the common-mode current ${\phi }_{j1}^{com}$(t) is adjusted, thereby achieving an effective redistribution of power between the arms and maintaining capacitor voltage balance.

Figure 17. Discrete closed-loop control of the differential arm capacitor voltage ${\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{low}(z)}-{\displaystyle \sum _{k=1}^N{\widehat{u}}_{cjk}^{up}(z)}$.

Similarly, for the upper and lower arm voltage balancing control, the discrete controller is designed using a PI structure with Tustin transformation, as expressed

$$D_a(z)=k_{p2}+k_{i2}{\displaystyle \frac{T_s}{2}}{\displaystyle \frac{z+1}{z-1}}=k_{p2}(1+2\pi {\displaystyle \frac{T_s}{2}}{\displaystyle \frac{z+1}{z-1}})$$

(27)

By substituting the simulation parameters, the root locus under a discrete control period of Ts = 0.02 s is obtained in Figure 18. Figure 18 shows the root locus of the D_a(z) controller as the proportional gain k_p2 varies from 0 to ∞. The discrete system is stable when the poles remain inside the unit circle.

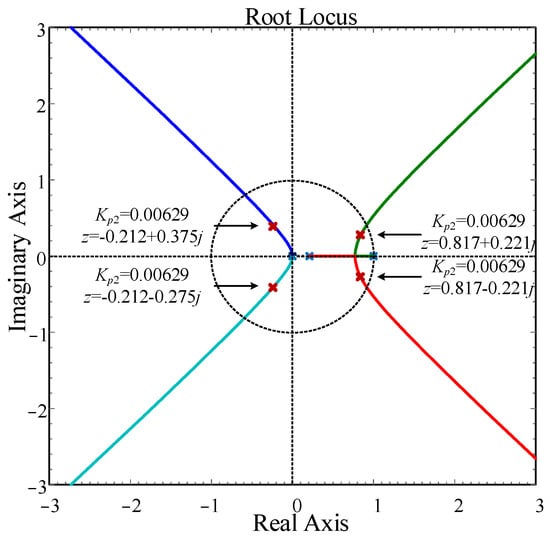
Figure 18. Root locus of the D_a(z) controller with varying k_p2.

Since Figure 15 and Figure 18 share the same type of poles but different gain values, the root locus in Figure 15 and Figure 18 exhibit similar shapes.

4. Simulation Verification

To verify the effectiveness of the proposed capacitor voltage balancing control method based on self-synchronized common-mode current, detailed simulations were conducted using the software platform.

The simulation model is established based on a 10 kV distribution network. Each arm consists of four high-voltage MMC submodules rated at 4.5 kV, with a submodule capacitance of 2000 μF. The CPS-PWM modulation strategy is applied to each submodule. The DC bus voltage is set to 18 kV. The arm inductance L_a is designed to be 10 mH with an equivalent resistance R_a of 4 Ω. The detailed simulation parameters are summarized in Table 1.

Table 1. Simulation Parameters of the Proposed ES-MMC System.

Parameters	Symbol	Value
DC Bus Voltage	Udc	18 kV
AC Grid Voltage	Uac	10 kV
Arm Inductor	La	10 mH
Equivalent Resistance of Arm Inductor	Ra	4 Ω
Submodule Number	N	4
Submodule Rated Voltage	Usm	4.5 kV
Submodule Rated Capacitor	Csm	2000 μF

Figure 19 shows the control system structure. The instantaneous reactive power control is adopted on the AC side, with the d-axis current reference set to 30 A and the q-axis current reference set to 0 A. The capacitor power rebalancing control is implemented on a per-phase basis, where the sum and difference in the upper and lower arm capacitor voltages are regulated to generate the common-mode modulation voltage $u_j^{com}$(t). This voltage is then superimposed with $u_j^{dif}$(t) and modulated using CPS-PWM, producing the phase-shifted switching signals for each submodule. The control parameters in Figure 19 are listed in Table 2.

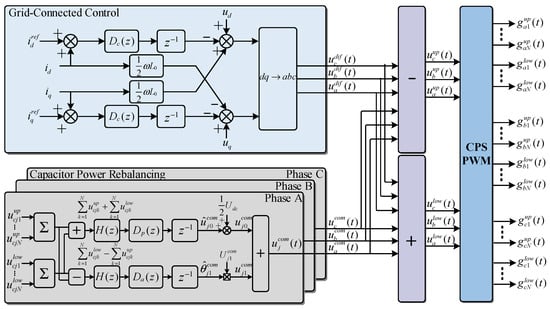
Figure 19. Control architecture of the proposed self-synchronized common-mode current strategy.

Table 2. Control Parameters.

Parameters	Symbol	Value
Active current	id	30 A
Reactive current	iq	0 A
Common-mode current	$U_{j1}^{com}$	50 V
Dc(z)	Kp	3.5812
	Ki	675.041
Dp(z)	Kp	0.468665
	Ki	2.94471
Da(z)	Kp	0.00614554
	Ki	0.0193068

The simulation results are presented in Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25. These figures illustrate the performance of the proposed control scheme in terms of grid-connected operation, capacitor voltage balancing, common-mode current synchronization, and dynamic response under different operating conditions.

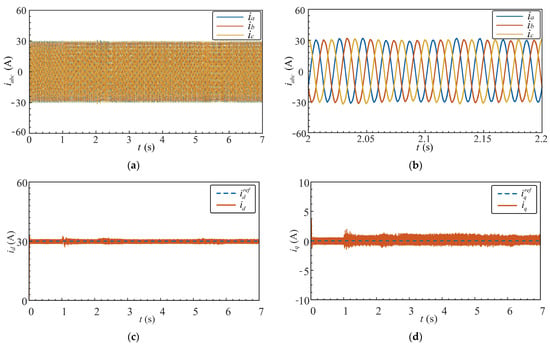
Figure 20. AC grid currents: (a) i_a, i_b, and i_c in the abc stationary reference frame; (b) zoomed waveforms of i_a, i_b, and i_c in the ABC stationary reference frame; (c) i_d in the DQ rotating reference frame; (d) i_q in the DQ rotating reference frame.

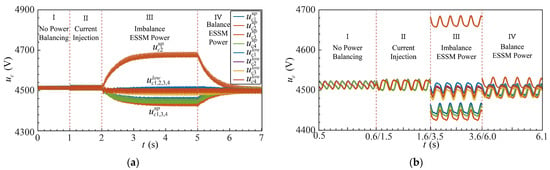
Figure 21. Submodule capacitor voltages: (a) $u_{ca1}^{up}$, $u_{ca2}^{up}$, $u_{ca1}^{low}$ and $u_{ca2}^{low}$ at different operating stages; (b) zoomed waveforms of $u_{ca1}^{up}$, $u_{ca2}^{up}$, $u_{ca1}^{low}$, and $u_{ca2}^{low}$ at different operating stages.

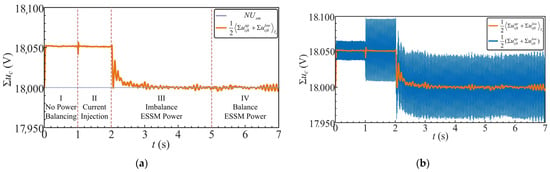
Figure 22. Average arm capacitor voltage: (a) ${\displaystyle \frac{1}{2}}{⟨{\displaystyle \sum _{k=1}^N{u}_{cjk}^{up}(z)}+{\displaystyle \sum _{k=1}^N{u}_{cjk}^{low}(z)}⟩}_{Ts}$ at different operating stages; (b) original waveform and its moving-average counterpart.

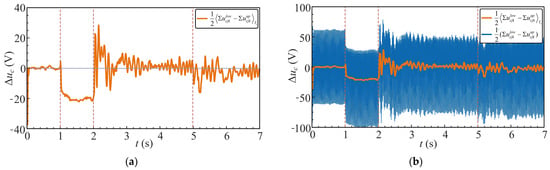
Figure 23. Differential arm capacitor voltage: (a) ${\displaystyle \frac{1}{2}}{⟨{\displaystyle \sum _{k=1}^N{u}_{cjk}^{low}(z)}-{\displaystyle \sum _{k=1}^N{u}_{cjk}^{up}(z)}⟩}_{Ts}$ at different operating stages; (b) original waveform and its moving-average counterpart.

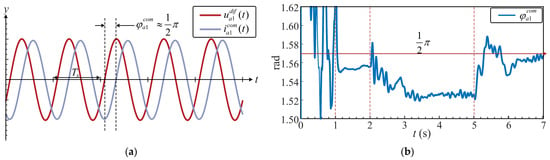
Figure 24. Synchronization angle ${\phi }_{a1}^{com}$(t): (a) time-domain waveform of ${\phi }_{a1}^{com}$(t) between $u_{a1}^{dif}$(t) and $i_{a1}^{com}$(t); (b) moving-average waveform of ${\phi }_{a1}^{com}$(t).

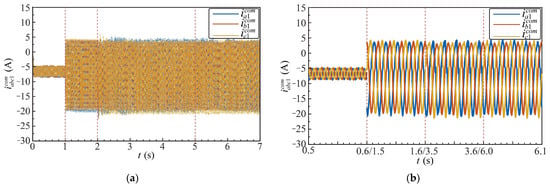
Figure 25. Common-Mode currents in the ES-MMC: (a) $i_{a1}^{com}$, $i_{b1}^{com}$, and $i_{c1}^{com}$ at different operating stages; (b) zoomed waveforms of $i_{a1}^{com}$, $i_{b1}^{com}$, and $i_{c1}^{com}$ at different operating stages.

Figure 20 illustrates the grid-side current waveforms of the ES-MMC in the three-phase stationary abc reference frame. Since the instantaneous reactive power control method is adopted with the d-axis current reference set to 30 A, the amplitude of the grid current is regulated to 30 A and remains in phase with the corresponding grid voltage. Figure 20a shows the long-term steady-state current waveform, where the grid current is stably maintained. Figure 20b presents the locally magnified waveform, confirming the sinusoidal characteristics of the CPS-PWM 10 kHz. Figure 20c illustrates the closed-loop control result of the d-axis current, which accurately tracks the 30 A reference. Figure 20d shows the closed-loop result of the q-axis current, which is effectively regulated to 0 A, demonstrating successful decoupled active and reactive current control.

Figure 21 shows the capacitor voltage waveforms of Phase A, where each upper and lower arm consists of eight submodule capacitors. Figure 21a illustrates the entire simulation process, which is divided into four stages (I–IV). In Stage I, the system operates in grid-connected mode, and the capacitor balancing control is not activated, $u_{j0}^{com}$(t) = 0, $U_{j1}^{com}$ = 0. In Stage II, $U_{j1}^{com}$ is set to 50 V, which introduces a corresponding common-mode circulating current component in the arms. As a result, the capacitor voltages exhibit larger fluctuations, as shown in Figure 21b.

In Stage III, an unbalanced power injection of 4.5 kW = 4.5 kV × 1 A is applied to the second submodule of the upper arm. Since the capacitor voltages within the same arm are regulated by the proportional control method proposed in [9], the voltages stabilize at levels proportional to the deviation in average power. Consequently, the second submodule voltage stabilizes around 4700 V due to its higher output power, while the other capacitor voltages in the upper arm are lower than the average voltage of the lower arm.

In Stage IV, when the injected power from the energy storage side is removed, the power balance among all submodules is restored, and the capacitor voltages of both upper and lower arms immediately recover to a balanced state.

Figure 22 shows the average voltage control of the upper and lower arms, which corresponds to the regulation of the DC component $u_{j0}^{com}$(t) of the common-mode voltage. Figure 22a illustrates the moving-averaged capacitor voltages of the upper and lower arms. In Stages I and II, without closed-loop control, the arm capacitor voltages slightly deviate from the rated value of 18 kV. In Stage III, after the common-mode voltage controller is activated, the average voltages of both arms are effectively compensated and stabilized at 18 kV. Figure 22b compares the moving-averaged capacitor voltage with the raw waveform. Due to the influence of the differential-mode current and common-mode current on the AC side, the raw capacitor voltage exhibits significant fluctuations. By applying a moving average filter with a sampling period of T_s = 0.02 s, the pulsating components are effectively suppressed, thereby avoiding adverse effects on the control performance.

Figure 23 illustrates the differential capacitor voltages between the upper and lower arms, which reflect the relative voltage deviation within each phase. Figure 23a shows the moving-averaged differential voltages over the simulation period. In Stages II, without closed-loop compensation but, the differential voltages exhibit noticeable deviations from zero, indicating voltage imbalance between the upper and lower arms. When the common-mode voltage controller is activated in Stage III, the differential voltages are effectively suppressed and converge close to zero, demonstrating successful balancing of the arm capacitor voltages. Figure 23b compares the moving-averaged differential voltages with the raw differential waveforms. The raw signals contain fluctuations induced by the AC-side differential-mode and common-mode currents. By applying a moving average filter with a sampling period of T_s = 0.02 s, the pulsating components are smoothed, which avoids interference with the voltage balancing control.

Figure 24 illustrates the variation in the synchronization angle between the common-mode current $i_{a1}^{com}$(t) and the differential voltage $u_{a1}^{dif}$(t) of phase a. Figure 24a presents the steady-state time-domain waveform. At steady state, the capacitor voltages of the upper and lower arms are balanced, resulting in no active power exchange between the arms. According to (13) and Figure 10, synchronization angle ${\phi }_{a1}^{com}$ equals 0.5π. Figure 24b shows the variation in the synchronization angle over different simulation stages. In Stage I, since $U_{a1}^{com}$ = 0, the common-mode current $i_{a1}^{com}$(t) = 0, and the synchronization angle exhibits random fluctuations with no practical significance. In Stage II, with $U_{a1}^{com}$ = 50 V, the synchronization angle stabilizes near the steady-state point of 0.5π. In Stage III, to compensate for the unbalanced power output between the upper and lower arms, the synchronization angle ${\phi }_{a1}^{com}$ deviates from the steady-state point. In Stage IV, after the external energy injection from all submodules is balanced, the synchronization angle returns close to the steady-state value.

The behaviors in Figure 22 and Figure 23 are mutually coupled. Through the closed-loop distribution of common-mode and differential-mode power, the control strategy compensates for the unbalanced power output of the submodule energy storage units, ensuring stable capacitor voltage regulation.

Figure 25 shows the fundamental-frequency common-mode currents $i_{a1}^{com}$, $i_{b1}^{com}$, and $i_{c1}^{com}$ in the three-phase system. Figure 25a presents the time-domain waveforms over the entire simulation. In Stage I, the fundamental common-mode currents are primarily caused by fluctuations in the submodule capacitor voltages. From Stages II to IV, after superimposing the common-mode voltage $U_{j1}^{com}$ = 50 V, the fundamental common-mode currents reach an amplitude of approximately 22 A. Figure 25b shows a locally magnified view of the waveforms, highlighting the dynamics of the common-mode currents in each stage.

These results demonstrate that the proposed common-mode voltage injection effectively generates controllable fundamental-frequency common-mode currents, which play a key role in compensating power imbalances among the arms in the same phase and maintaining capacitor voltage equilibrium.

Under rated operating conditions, the capacitor voltages of the upper and lower arms remain well balanced, demonstrating that the proposed self-synchronized common-mode current control strategy maintains steady-state performance. When unbalanced power conditions are introduced among the energy storage units, transient voltage deviations occur. However, the proposed method rapidly regulates the capacitor voltages, effectively restoring balance and ensuring system stability. These results confirm the robustness and effectiveness of the control approach under both nominal and disturbed operating scenarios.

5. Experimental Validation

To further verify the effectiveness of the proposed self-synchronized common-mode current control strategy for achieving power balancing in both upper and lower arms, a single-phase ES-MMC experimental prototype was developed. The prototype is implemented using SiC MOSFET H-bridge submodules.

An experimental platform for a single-phase ES-MMC prototype was developed, as illustrated in Figure 26. The prototype consists of four H-bridge submodules, each implemented with SiC MOSFETs, and is equipped with a 1000 µF dc-link capacitor. It is connected to distributed low-voltage storage units through bidirectional DC/DC interfaces. The system is rated at a DC bus voltage of 400 V, with an AC-side rated voltage of 110 V and an output current of 0 A. Thus, the AC-side differential voltage $u_{a1}^{dif}$ is in phase with the grid voltage. Each arm is equipped with a 4 mH inductor L_a and a series resistance R_a of approximately 0.5 Ω to suppress circulating current. Circuit parameters are listed in Table 3.

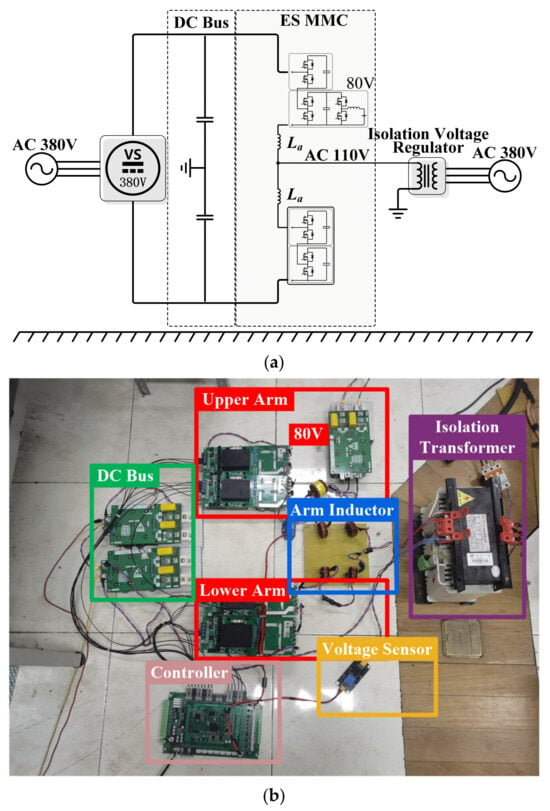
Figure 26. Experimental single-phase ES-MMC: (a) schematic diagram of the topology; (b) experimental prototype.

Table 3. Experimental Parameters of the Proposed ES-MMC System.

Parameters	Symbol	Value
DC Bus Voltage	Udc	400
AC Grid Voltage	Uac	110
Arm Inductor	La	4 mH
Equivalent Resistance of Arm Inductor	Ra	0.5 Ω
Submodule Number	N	2
Submodule Rated Voltage	Usm	200 V
Submodule Rated Capacitor	Csm	1000 μF

The control system is implemented on a digital signal processor (DSP, TMS320F28335), where the voltage and current signals are measured by Hall-effect sensors and fed into the DSP via isolated signal conditioning circuits. CPS-PWM is employed, with phase-shifted carriers generated and distributed by the DSP. This setup enables comprehensive experimental verification of the proposed self-synchronized common-mode current control strategy under various operating conditions.

Figure 27a shows the ac-side current i_a(t), which is set to 0 A. In this condition, no current flows through the arm inductors, and the voltages across the inductors are equal. Consequently, the differential modulation voltage of the upper and lower arms, $u_{a1}^{dif}$(t), is identical to the grid voltage u_a(t). Therefore, the grid voltage u_a(t) can be directly measured instead of $u_{a1}^{dif}$(t). This substitution is necessary because the differential modulation voltage is essentially a control signal that cannot be directly measured, whereas $u_{a1}^{dif}$(t) serves as the reference for the synchronization angle, which is indispensable for the study.

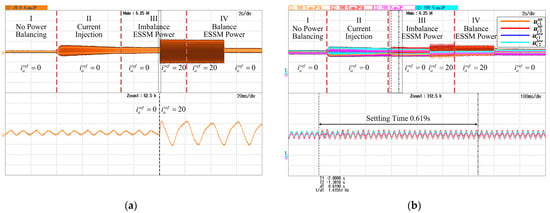
Figure 27. Submodule capacitor voltages and AC grid current: (a) AC grid current i_a; (b) capacitor voltages $u_{ca1}^{up}$, $u_{ca2}^{up}$, $u_{ca1}^{low}$, and $u_{ca2}^{low}$.

Figure 27b illustrates the waveforms of four submodule capacitor voltages, namely $u_{c1}^{up}$, $u_{c2}^{up}$, $u_{c1}^{low}$, and $u_{c2}^{low}$. In Stage I, without capacitor voltage balancing control, the capacitor voltages remain stable. In Stage II, when the common-mode current is injected, the fluctuations in capacitor voltage increase. In Stage III, an additional power of 200 W (200 V × 1 A) is injected into the second submodule of the upper arm through the buck–boost converter, leading to a higher average voltage of $u_{c2}^{up}$ compared with the others. The settling time after introducing power imbalances is about 0.619 s. The AC grid current increases from 0 to 20 A. In Stage IV, after the additional power injection is removed, the capacitor voltages of both arms recover to balance, as the grid current amplitude decreases from 20 A to 0.

Figure 28 presents the common-mode current. Since the oscilloscope cannot directly calculate the average value, the sum of the upper- and lower-arm currents, ($i_{a1}^{up}$ + $i_{a1}^{low}$)/2 = $i_{\mathrm{a}1}^{\mathrm{com}}$, is adopted as a substitute, which corresponds to twice the actual amplitude of the common-mode current. In Figure 28a, the common-mode current remains relatively small in Stage I. The common-mode voltage is injected in Stage II, and its amplitude increases. In Stage III, when additional power is injected into $u_{c2}^{up}$, the phase of $i_{a1}^{com}$ shifts accordingly. In Stage IV, as power balance is reestablished, the system reaches steady-state operation. Figure 28b depicts the steady-state common-mode current and the grid voltage u_a in Stage IV. Since the AC side current is set to 0 A, it can be approximated that $u_{a1}^{dif}$ ≈ u_a. Under this condition, the synchronization angle in the steady state is 0.5π.

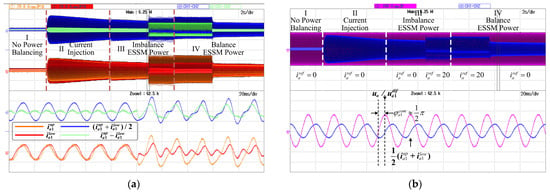
Figure 28. Common-mode current $i_{a1}^{com}$ and synchronization angle ${\phi }_{a1}^{com}$: (a) upper-arm current $i_{a1}^{up}$, lower-arm current $i_{a1}^{low}$, differential-mode current $i_{a1}^{com}$ = $i_{a1}^{up}$ − $i_{a1}^{low}$, and common-mode current $i_{a1}^{com}$ = ($i_{a1}^{up}$ + $i_{a1}^{low}$)/2; (b) synchronization angle ${\phi }_{a1}^{com}$ with respect to AC voltage u_a.

Figure 29 presents the FFT-based THD analysis of the grid current i_a = 20 A, measured by an oscilloscope. The FFT is performed with respect to the 50 Hz and its harmonics. The dominant component of the grid current is the 50 Hz, which remains nearly unchanged before and after applying the proposed capacitor voltage balancing algorithm (23.0764 dBA vs. 23.0914 dBA). In contrast, the second-order harmonic increases from 2.48735 dBA to 6.06591 dBA when the control algorithm is enabled.

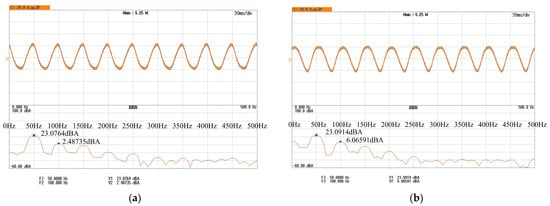
Figure 29. FFT of the grid-side AC current i_a: (a) $i_a^{ref}$ = 20 A without the proposed self-synchronized control; (b) $i_a^{ref}$ = 20 A the proposed self-synchronized control.

This increase is likely attributed to the introduced common-mode current, which induces a fundamental-frequency voltage fluctuation on the submodule capacitors. Through modulation, this fluctuation is coupled into the grid current i_a, leading to a slight rise in the second-order harmonic. Overall, the proposed capacitor voltage balancing algorithm has a negligible impact on the grid current THD.

To verify the accuracy of the experimental results, simulations were conducted based on the circuit parameters listed in Table 3. The simulated waveforms in Figure 30a–f correspond to the experimental results in Figure 27 and Figure 28.

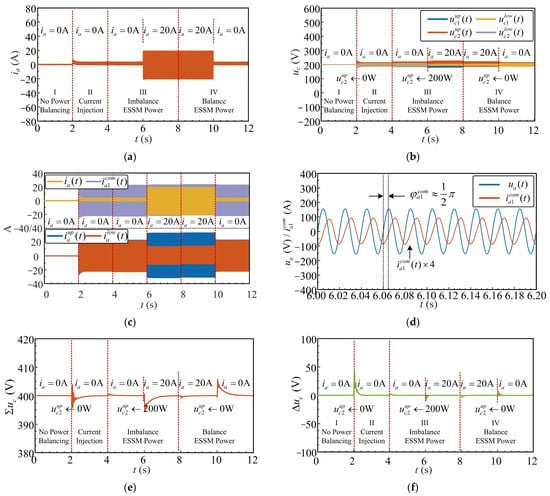
Figure 30. Simulation model with experimental parameters: (a) AC grid current i_a = 20 A; (b) capacitor voltages $u_{ca1}^{up}$, $u_{ca2}^{up}$, $u_{ca1}^{low}$, and $u_{ca2}^{low}$; (c) upper-arm current $i_{a1}^{up}$, lower-arm current $i_{a1}^{low}$, differential-mode current $i_{a1}^{com}$ = $i_{a1}^{up}$ − $i_{a1}^{low}$, and common-mode current $i_{a1}^{com}$ = ($i_{a1}^{up}$ + $i_{a1}^{low}$)/2; (d) synchronization angle ${\phi }_{a1}^{com}$ with respect to AC voltage u_a.; (e) average arm capacitor voltage ${\displaystyle \frac{1}{2}}{⟨{\displaystyle \sum _{k=1}^N{u}_{cjk}^{up}(z)}+{\displaystyle \sum _{k=1}^N{u}_{cjk}^{low}(z)}⟩}_{Ts}$; (f) differential arm capacitor voltage ${\displaystyle \frac{1}{2}}{⟨{\displaystyle \sum _{k=1}^N{u}_{cjk}^{low}(z)}-{\displaystyle \sum _{k=1}^N{u}_{cjk}^{up}(z)}⟩}_{Ts}$.

Overall, the simulation results are consistent with the experimental results I–IV. However, due to practical environmental factors and differences in controller implementation, slight discrepancies exist between the experimental and theoretical waveforms. In the experiments, the circulating current is lower than the theoretical value and is significantly affected by the grid-side AC current, resulting in waveform distortion, whereas the simulations exhibit more ideal behaviors.

6. Conclusions

The proposed method exploits the synchronization between the AC-side differential voltage and the fundamental-frequency common-mode current to achieve dynamic arm power rebalancing in ES-MMCs. Simulations and experiments on a SiC-based prototype confirm that the approach stabilizes capacitor voltages and restores power balance under unbalanced energy injection. This strategy ensures both steady-state and transient stability without additional hardware, offering promising potential for large-scale distributed energy storage integration.