Pilot Design Based on the Distribution of Inter-User Interference for Grant-Free Access

Abstract

Massive random access (MRA) involves massive devices sporadically and randomly sending short-packet messages through a shared wireless channel. It is a crucial scenario in 6G communications to support the Internet-of-Things. Grant-free access, where devices complete transmission without grants, is a promising scheme for MRA. In grant-free access, the design of pilot sequences has a significant effect on joint activity detection and channel estimation (JADCE) and, consequently, system performance. Inter-user interference (IUI), caused by non-orthogonal pilots, is random owing to the random set of active users, and existing studies on pilot design for grant-free access often attempt to reduce the mean IUI. However, the performance of JADCE is affected not only by the mean IUI but also by the tail behavior of the IUI distribution. In this paper, we propose a metric for pilot design, exploiting the distribution of IUI to reflect the impact of pilots on JADCE more precisely. We further develop a pilot design algorithm based on the proposed metric, with modified approximate message passing (AMP) adopted as the JADCE algorithm. Simulation results demonstrate that the proposed pilot design reduces the probability of missed detection of active users and channel estimation error, compared with existing pilot designs.

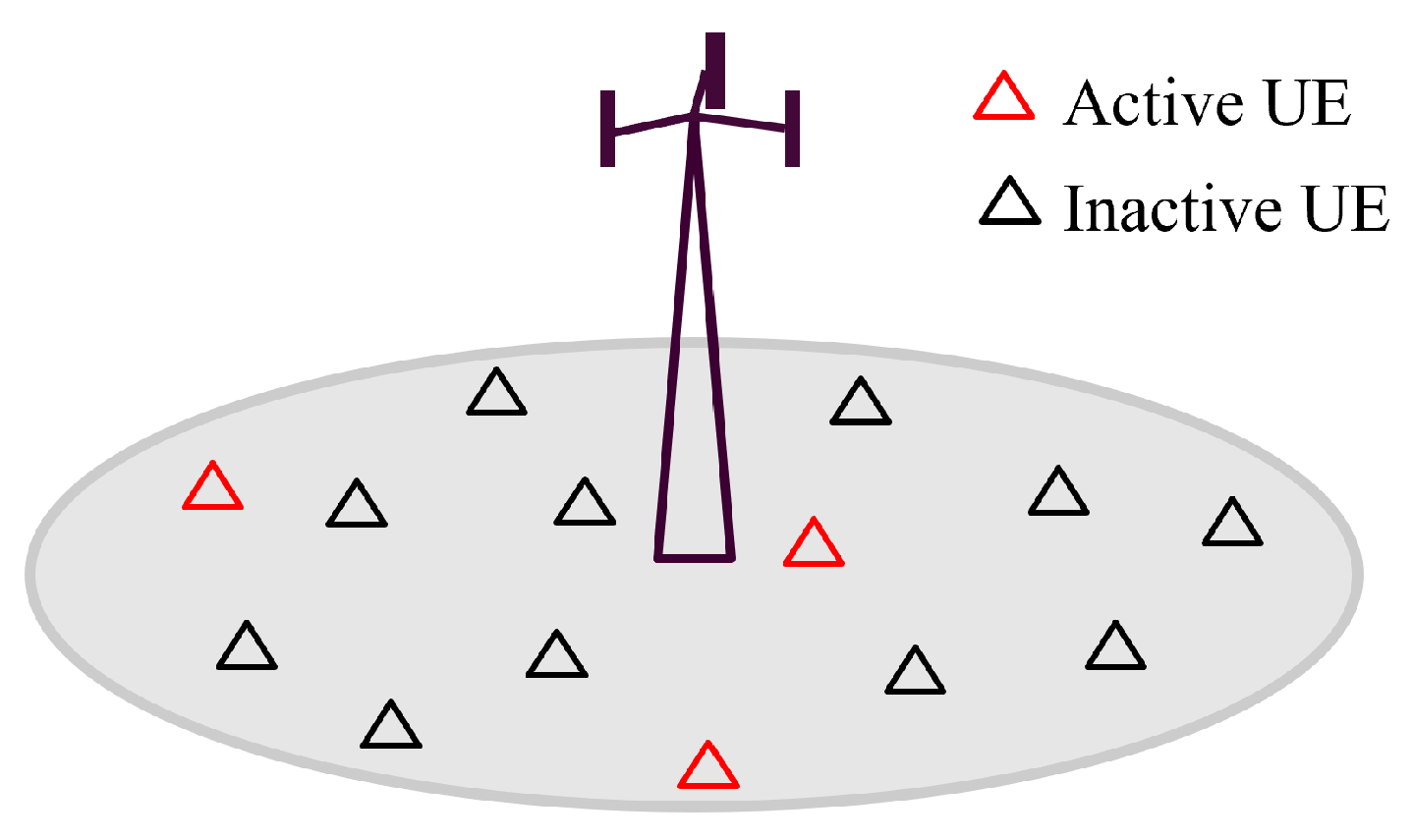
1. Introduction

Massive random access (MRA) [1] involves numerous user equipments (UEs) sporadically and randomly sending short-packet messages through a shared wireless channel. It is a crucial scenario in 6G wireless communications, supporting the Internet-of-human-machine-things (IoHMT) [2] and enabling applications based on massive devices, such as smart manufacturing and drone collaboration [3,4]. Under this circumstance, grant-free access [5], where UEs complete uplink transmission without grants, is considered a suitable scheme for MRA.

A two-phase access scheme is widely considered in grant-free access, where users send pilot sequences prior to any data transmission for user detection and channel estimation. Considering the large number of UEs and short access time, pilot sequences are non-orthogonal, bringing severe inter-user interference (IUI) and making pilot overhead the bottleneck for increasing system capacity and decreasing latency. Thus, pilot design is important in grant-free access.

This section is organized as follows: Section 1.1 introduces the two-phase grant-free access scheme. Section 1.2 reviews related studies on pilot design for grant-free access. These studies attempted to reduce the mean IUI, but the tail behavior of the IUI distribution also affects system performance. Then, Section 1.3 introduces the motivation and main contributions of our studies on pilot design exploiting IUI distribution.

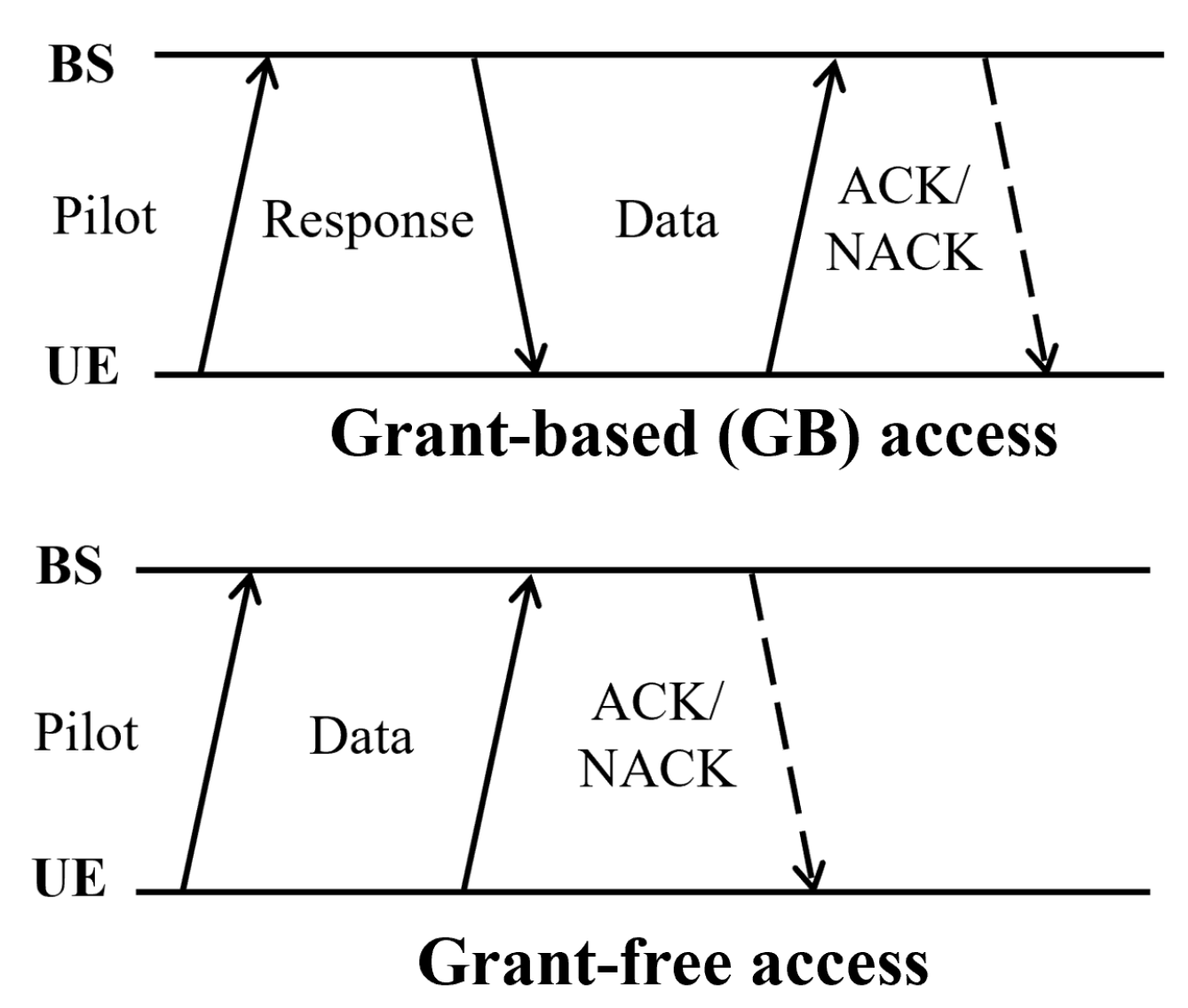
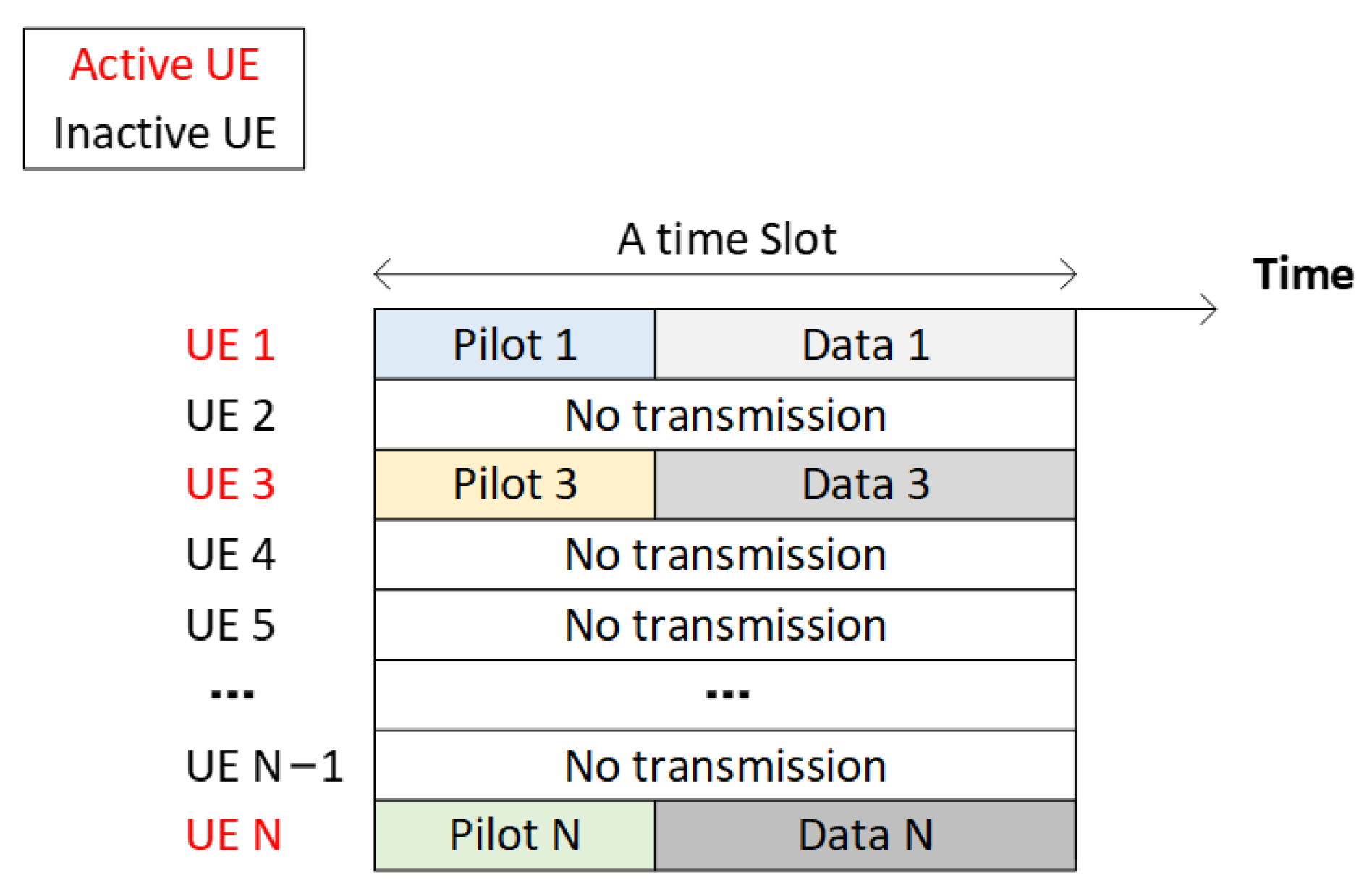
1.1. Two-Phase Grant-Free MRA Scheme

In a 6G MRA system, the device density is ${10}^6\sim {10}^8/{\mathrm{km}}^2$ and the delay is $0.1\sim 1$ ms, while the data packets sent by devices are usually smaller than 200 bytes [6,7]. Meanwhile, the arrival of packets is stochastic for each device. As a result, only a small fraction of users are active, i.e., with arriving data packets requiring uplink transmission at the same time, as shown in Figure 1.

Under this circumstance, grant-free access is widely considered. Unlike traditional grant-based access where active UEs have to obtain a grant from the base station (BS) prior to any data transmission, grant-free access allows active UEs to transmit data signals immediately after pilot sequences to reduce signaling overhead and latency, as shown in Figure 2.

Considering that the channel coefficients between UEs and the BS may be time-varying owing to changes in the scattering environment, the two-phase scheme shown in Figure 3 is applicable for grant-free access, where each active user sends a pre-allocated pilot sequence prior to data signal in a time slot. The BS implements joint activity detection and channel estimation (JADCE) based on the pilot sequences and then detects data.

In two-phase grant-free access, synchronized time slots are usually considered, where active users send user-specific pilots synchronously for JADCE, as shown in Figure 4. The duration of a two-phase slot must be shorter than the coherent time of the channel, as shown in Figure 3, which severely constrains the length of pilots. Additionally, longer slots lead to larger uplink latency for grant-free access. Therefore, it is crucial to improve JADCE performance with length-limited pilots to enhance the overall system performance.

1.2. Related Studies on Pilot Design for Grant-Free Access

To support an increasing number of users, the BSs in the grant-free access system are usually equipped with multiple-input multiple-output (MIMO) to acquire more degrees of freedom. However, the length of pilot sequences required for JADCE increases with the number of active users, according to the theory of compressed sensing [8]. Therefore, pilot overhead becomes the bottleneck of increasing system capacity, especially with an increasing number of users.

Considering this circumstance, many studies have been conducted on the design of pilot sequences. Some studies have considered orthogonal pilots, in which users assigned the same pilot will collide when activated simultaneously. The authors of [9] investigated the effect of collisions on latency and optimized the length of pilots accordingly.

On the other hand, since the number of potential users in massive access is much larger than the length of pilots, non-orthogonal pilots are more widely used to avoid frequent collisions. However, for a lot of JADCE algorithms [10,11,12,13], activity detection is implemented based on a signal energy decision, which suffers from performance degradation caused by IUI when non-orthogonal pilots are used. Thus, some studies have explored non-orthogonal pilot designs to reduce IUI and improve JADCE performance. Bernoulli sequences [14] and Zad-off Chu (ZC) sequences [15] have been validated to outperform Gaussian ones, which are adopted in many studies. In 5G new radio (NR), pilot signals for uplink transmission are generated as Gold sequences, which are actually Bernoulli pilots [16]. The authors of [17] proposed a pilot design method that minimizes the pilot coherence metric (inner product of two energy-normalized sequences) using a genetic algorithm (GA). The signal design methods in [18] based on the coherence metric can also be applied to the pilot design for grant-free access. The authors of [10] further suggest exploiting channel correlation matrices to reduce IUI and propose a pilot design algorithm that outperforms Gaussian and Bernoulli ones.

For hardware practicality, some pilot designs [14,15,17,18] satisfy element-wise constant amplitude (CA) constraints, while some other designs [10,18] do not. Some CA pilot designs further satisfy finite-phase constraints [14,15,17]. It is notable that the constraints should also be considered when comparing different pilot designs.

1.3. Motivation and Contributions

Although existing studies on pilot design have improved the system performance, they usually attempt to reduce the sum of the IUI from all potential users [10,17], which is constant when averaging over channel realizations. However, what actually influences the performance of activity detection and channel estimation is the IUI from the active users in the current time slot, which is random because the set of active users varies with different time slots. The sum of all potential IUIs, which is proportional to the mean value of the current IUI, cannot characterize the distribution of the current IUI and is inadequate for guiding pilot design.

To overcome this limitation, the IUI distribution is exploited for pilot design in this paper. Activity detection based on energy decision, which is widely used in JADCE, is analyzed in this paper. We derive that minimizing the probability $P(I_n<b_n)$, where $I_n$ is the energy of the IUI to user n and $b_n$ is a proper bound, is equivalent to minimizing the probability of missed detection with the constant false alarm rate (CFAR) [19] principle, utilizing signal hardening in the massive MIMO regime. Therefore, we propose to characterize the tail behavior of the IUI distribution using the second-order moment and derive a metric for pilot design to reduce $P(I_n<b_n)$ and enhance activity detection.

Since the proposed metric is determined by the relation between the IUI and pilots, it varies with different JADCE algorithms. In view of this, we take modified approximate message passing (mAMP) [10], a low-complexity JADCE algorithm, as an example and derive the expression of the proposed metric in this case. Building on this, we derive a pilot design algorithm which minimizes the proposed metric via projection gradient descent (PGD) [20].

The main contributions of this study are as follows:

• We propose a pilot design framework with a proposed metric exploiting the distribution of the IUI.
• We derive pilot design algorithms based on the proposed metric for different constraints on pilots. Simulation results verify that the algorithms improve the JADCE performance, which helps reduce latency and increase energy efficiency.
• Compared with the design in [10], which is also based on PGD, the proposed pilot design is more robust to iteration initialization.

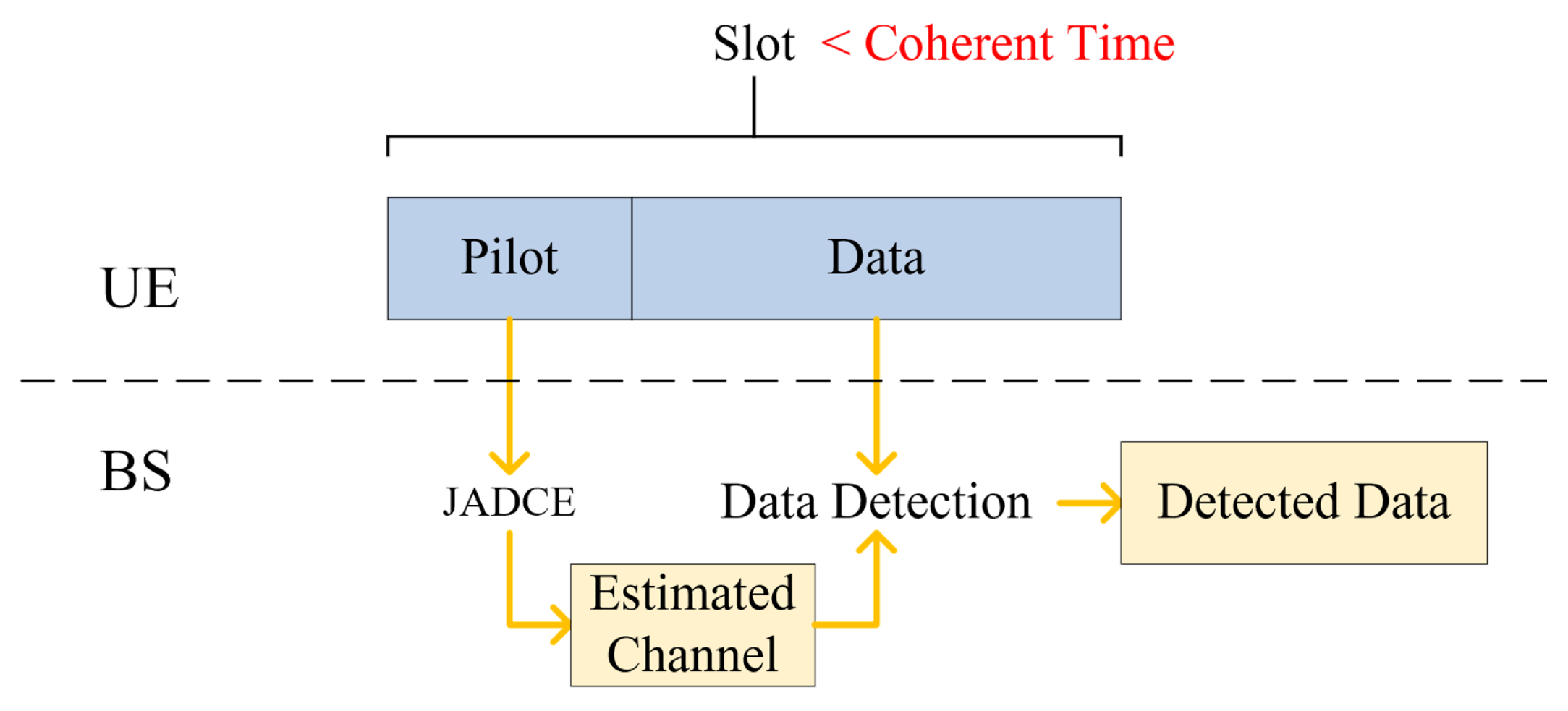
2. System Model

Consider a grant-free system with one M-antenna BS and N single-antenna users, where each user is activated independently with probability $P_a$ in each time slot. The set of all potential users is $\mathcal{N}=\{1,2,\dots ,N\}$. We use ${\alpha }_n$ to denote the activity state of user n, where ${\alpha }_n=1$ indicates that user n is active and ${\alpha }_n=0$ indicates it is not. Then, the set of active users in the current time slot is $\mathcal{K}\triangleq \{n\in \mathcal{N}|{\alpha }_n=1\}$.

Denote the complex gain vector of the channel from user n to the BS as ${\mathbf{g}}_n\in {\mathbb{C}}^M$. Assume that ${\mathbf{g}}_n\sim \mathcal{CN}(\mathbf{0},{\mathbf{R}}_n)$ and is independent among different users and different time slots. ${\mathbf{R}}_n$ is the correlation matrix of ${\mathbf{g}}_n$ and is assumed to be known for pilot design. This assumption is reasonable when correlation matrices remain stable for many time slots and can be computed according to the historical channel estimation or prior information of the physical environment [21].

User n is allocated an L-symbol pilot sequence ${\mathbf{a}}_n={[a_{n,1},\dots ,a_{n,L}]}^T\in {\mathbb{C}}^L$ in advance. It is assumed that $\parallel {\mathbf{a}}_n{\parallel }_2=1$, given that the impact of the transmit power of different users can be incorporated into the channel gain. Some pilot sequences further satisfy the constraints $|a_{n,l}{|}^2={\displaystyle \frac{1}{L}},1\le l\le L$, referred to as constant-amplitude (CA) pilots. CA pilots have the lowest peak-to-average power ratio, making them more hardware-friendly. Some CA pilots further satisfy finite-phase constraints $a_{n,l}={\displaystyle \frac{1}{\sqrt{L}}}{\mathrm{e}}^{j{\varphi }_{n,l}},{\varphi }_{n,l}\in \mathcal{P},1\le l\le L$, where $\mathcal{P}$ is a finite set containing all optional phases.

Meanwhile, the equivalent channel ${\mathbf{h}}_n={\alpha }_n{\mathbf{g}}_n$ is introduced, which needs to be estimated in JADCE. In this way, the received signal at the BS can be modeled as

$$\mathbf{Y}=\mathbf{A}\mathbf{H}+\mathbf{N}$$

(1)

where $\mathbf{A}=[{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N],\mathbf{H}={[{\mathbf{h}}_1,\dots ,{\mathbf{h}}_N]}^T$, and $\mathbf{N}$ denotes the noise, whose elements are i.i.d. and denoted by $N_{l,m}\sim \mathcal{CN}(0,{\sigma }_N^2),1\le l\le L,1\le m\le M$. The ratio of total received user signal power to noise power is $\mathrm{SNR}={\displaystyle \frac{{\mathbb{E}\parallel \mathbf{A}\mathbf{H}\parallel }_F^2}{{\mathbb{E}\parallel \mathbf{N}\parallel }_F^2}}$.

To evaluate the performance of activity detection, we use the ergodic probability of missed detection as the metric, defined as $P_M\triangleq {\displaystyle \frac{\mathbb{E}|\mathcal{K}\setminus {\mathcal{K}}^{\prime }|}{\mathbb{E}\left|\mathcal{K}\right|}}$, where ${\mathcal{K}}^{\prime }$ denotes the set of detected users. Denote activity detection as ${\mathcal{K}}^{\prime }={\mathcal{F}}_{AD}(\mathbf{Y},\mathbf{A},\mathsf{\Theta })$, where $\mathsf{\Theta }$ denotes prior information such as $P_a$ and ${\mathbf{R}}_n$. Denote the missed detection probability computation as $P_M={\mathcal{F}}_{me}(\mathcal{K},{\mathcal{K}}^{\prime })$. Then, one pilot design approach is to optimize the metric of activity detection:

$$\underset{\mathbf{A}}{min}{\mathcal{F}}_{me}(\mathcal{K},{\mathcal{F}}_{AD}(\mathbf{Y},\mathbf{A},\mathsf{\Theta })$$

(2)

3. The Proposed Pilot Design Method Exploiting the IUI Distribution

In this section, we first propose a pilot design framework exploiting the distribution of the IUI. Since different JADCE algorithms encounter different IUI expressions, we adopt a modified AMP [10] as the JADCE algorithm and derive the pilot design algorithm.

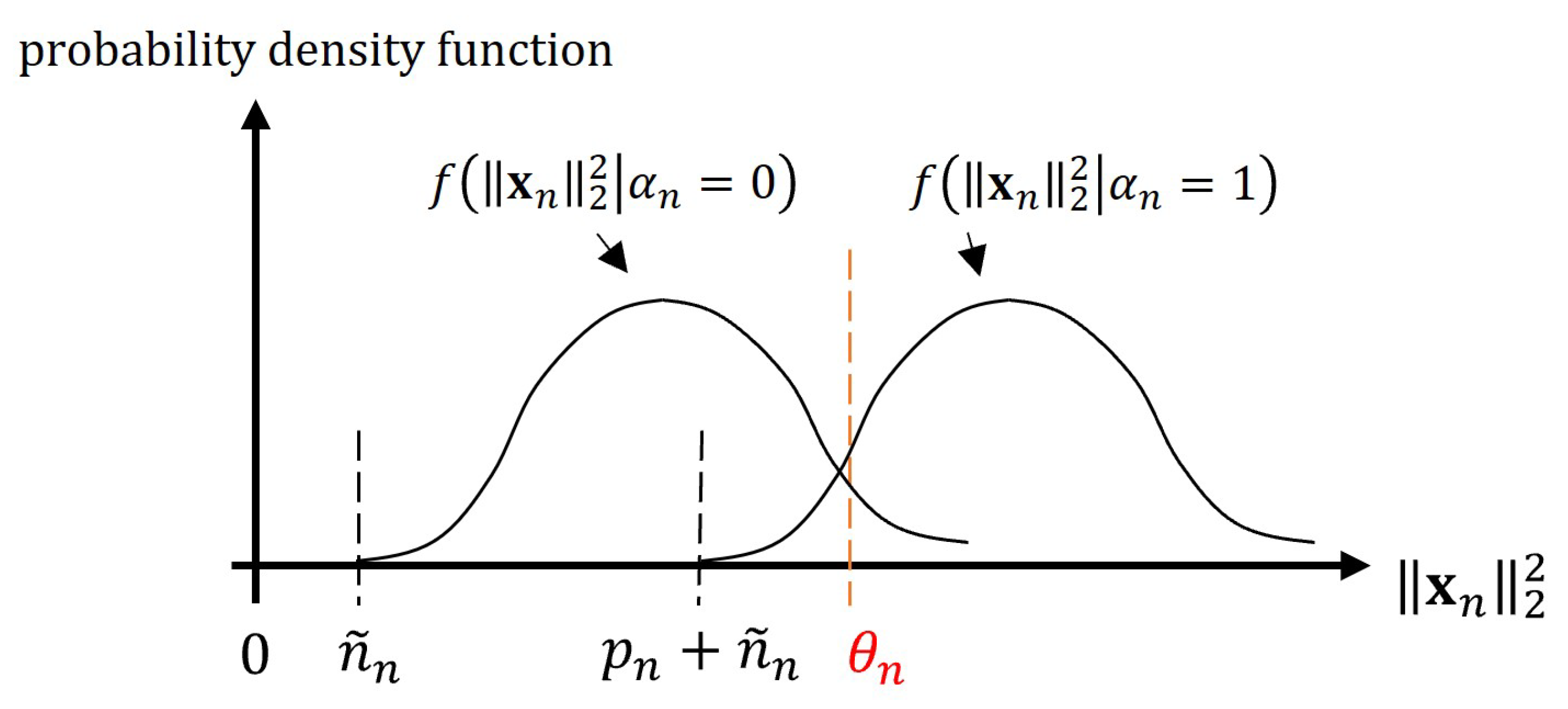
3.1. Pilot Design Framework Based on the IUI Distribution

In many JADCE algorithms [11,12,13], active users are detected through signal energy decision, i.e., user n is detected if $\parallel {\mathbf{x}}_n{\parallel }_2^2$ is larger than a proper threshold ${\theta }_n$, where ${\mathbf{x}}_n$ is the corresponding signal. For example, ${\mathbf{x}}_n$ is the estimated channel ${\widehat{\mathbf{h}}}_n$ in MAP-ADMM [12], ${\widehat{\mathbf{h}}}_n+{\mathbf{S}}^T{\mathbf{a}}_n^{*}$ in AMP-MMSE [11] (where $\mathbf{S}$ is the residual obtained by subtracting the estimated transmitting signal from $\mathbf{Y}$), and ${\mathsf{\Sigma }}_n^{1/2}{\widehat{\mathbf{h}}}_n$ in OAMP-MMV [13] (where ${\mathsf{\Sigma }}_n$ is obtained using the covariance of the estimation error of ${\mathbf{h}}_n$).

In all these cases, the signal ${\mathbf{x}}_n$ can be modeled as

$$\begin{array}{c}\hfill {\mathbf{x}}_n={\mathbf{d}}_n+{\mathbf{i}}_n+{\mathbf{e}}_n,\forall n\in \mathcal{N}\end{array}$$

(3)

where ${\mathbf{d}}_n$ denotes the ideal signal of user n without interference and ${\mathbf{d}}_n=\mathbf{0}$ if user n is nonactive. ${\mathbf{e}}_n$ denotes the effect of noise, and ${\mathbf{i}}_n$ denotes the IUI to user n, which is superposed from other active users, denoted by ${\mathbf{i}}_n={\sum }_{m\in {\mathcal{K}}_n^{-}}{\mathbf{i}}_{n,m}$, where ${\mathbf{i}}_{n,m}$ denotes the interference from user m and ${\mathcal{K}}_n^{-}\triangleq \mathcal{K}\setminus \left\{n\right\}$.

When the BS antenna number M is large enough, the variation of the signal energy $\parallel {\mathbf{x}}_n{\parallel }_2^2$ is small relative to its mean value, as a result of channel hardening [22]. Then, there is an approximation that $\parallel {\mathbf{x}}_n{\parallel }_2^2\approx \mathbb{E}{\parallel {\mathbf{x}}_n\parallel }_2^2$. Note that

$$\begin{array}{c}\hfill \mathbb{E}\parallel {\mathbf{x}}_n{\parallel }_2^2={\alpha }_n{p}_n+I_n+{\tilde{n}}_n,\forall n\in \mathcal{N}\end{array}$$

(4)

where $p_n\triangleq \mathbb{E}\left[\parallel {\mathbf{d}}_n{\parallel }_2^2{\alpha }_n=1\right]$, $I_n\triangleq \mathbb{E}{\parallel {\mathbf{i}}_n\parallel }_2^2$, and ${\tilde{n}}_n\triangleq \mathbb{E}{\parallel {\mathbf{e}}_n\parallel }_2^2$. Meanwhile, the mean energy of ${\mathbf{i}}_n$ is

$$\begin{array}{c}\hfill I_n=\sum _{m\in {\mathcal{N}}_n^{-}}{\alpha }_m{\rho }_{n,m}\end{array}$$

(5)

where ${\rho }_{n,m}\triangleq \mathbb{E}{\parallel {\mathbf{i}}_{n,m}\parallel }_2^2$. All these expectations are taken over different channel realizations; thus $p_n$, ${\tilde{n}}_n$, and ${\rho }_{n,m}$ remain constant in different time slots, whereas $I_n$ is still a random variable varying with ${\mathcal{K}}_n^{-}$.

Therefore, activity detection based on energy decision is a binary signal detection problem with a random interference $I_n$ and a threshold ${\theta }_n$, as shown in Figure 5.

Note that the probability of missed detection for user n is $P_{M,n}=P(I_n<{\theta }_n-p_n-{\tilde{n}}_n)$, and the probability of false alarm for user n is $P_{F,n}=P(I_n>{\theta }_n-{\tilde{n}}_n)$. There is a trade-off between the two rates by adjusting ${\theta }_n$. In this paper, we take a widely adopted principle, CFAR [19], with which the target of JADCE is to minimize $P_{M,n}$ with constraints $P_{F,n}\le P_F,\forall n\in \mathcal{N}$. The distribution of $I_n$, decided by ${\mathcal{K}}_n^{-}$ and ${\rho }_{n,m}$ according to (5), will influence the optimized $P_{M,n}$. Meanwhile, ${\rho }_{n,m}$, the IUI from user m to n, is influenced by the pilots ${\mathbf{a}}_n$ and ${\mathbf{a}}_m$ as well as the JADCE algorithm. Consequently, pilots $\mathbf{A}$ will influence the distribution of each $I_n$ and further influence $P_{M,n}$.

However, it is challenging to characterize the distribution of $I_n$ precisely, since the number of all potential $\mathcal{K}$ is $2^N$. Fortunately, because $I_n$ is the weighted sum of a large number of i.i.d. random variables ${\alpha }_m$, its distribution can be approximated as Gaussian $\mathcal{N}({\mu }_n,{\sigma }_n^2)$ according to the Lindeberg–Feller central limit theorem [23], where the mean value ${\mu }_n$ and the variance ${\sigma }_n^2$ are influenced by pilots.

With the approximation, $P_{F,n}=P(I_n>{\theta }_n-{\tilde{n}}_n)\approx Q\left({\displaystyle \frac{{\theta }_n-{\tilde{n}}_n-{\mu }_n}{{\sigma }_n}}\right)$. Then the constraints of CFAR are equivalent to ${\theta }_n\ge {\mu }_n+{\sigma }_n{Q}^{-1}\left(P_F\right)+{\tilde{n}}_n$. Meanwhile, the per-user missed detection rate $P_{M,n}=P(I_n<{\theta }_n-p_n-{\tilde{n}}_n)\approx 1-Q\left({\displaystyle \frac{{\theta }_n-p_n-{\tilde{n}}_n-{\mu }_n}{{\sigma }_n}}\right)$ increases with ${\theta }_n$, thus minimizing $P_{M,n}$ with CFAR by adjusting pilots is equivalent to

$$\begin{array}{cc}\hfill \mathbf{Case}\mathbf{1}:& \underset{\mathbf{A}}{min}{\mu }_n+w{\sigma }_n,\forall n\in \mathcal{N}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\parallel {\mathbf{a}}_n{\parallel }_2^2=1,\forall n\in \mathcal{N}\hfill \end{array}$$

(6)

where $w=Q^{-1}\left(P_F\right)$ is a constant for a given $P_F$. ${\tilde{\mathbf{n}}}_n$ is omitted because it is constant with different $\mathbf{A}$. Equation (6) corresponds to Case 1, where the pilots are free from element-wise constraints.

For pilots satisfying constant-amplitude (CA) constraints, denoted by Case 2, minimizing $P_{M,n}$ is equivalent to

$$\begin{array}{cc}\hfill \mathbf{Case}\mathbf{2}:& \underset{\mathbf{A}}{min}{\mu }_n+w{\sigma }_n,\forall n\in \mathcal{N}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.|a_{n,l}{|}^2={\displaystyle \frac{1}{L}},1\le l\le L,\forall n\in \mathcal{N}\hfill \end{array}$$

(7)

For CA pilots satisfying finite-phase constraints, denoted by Case 3, minimizing $P_{M,n}$ is equivalent to

$$\begin{array}{cc}\hfill \mathbf{Case}\mathbf{3}:& \underset{\mathbf{A}}{min}{\mu }_n+w{\sigma }_n,\forall n\in \mathcal{N}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.a_{n,l}={\displaystyle \frac{1}{\sqrt{L}}}{\mathrm{e}}^{j{\varphi }_{n,l}},{\varphi }_{n,l}\in \mathcal{P},1\le l\le L,\forall n\in \mathcal{N}\hfill \end{array}$$

(8)

where $\mathcal{P}$ is a finite set containing all optional phases. For example, $\mathcal{P}$ is $\{\pm {\displaystyle \frac{\pi }{4}},\pm {\displaystyle \frac{3\pi }{4}}\}$ for Bernoulli pilots.

From (5), the mean value ${\mu }_n$ and covariance ${\sigma }_n^2$ can be derived; then, the n-th objective of Problem (6), denoted by $b_n\triangleq {\mu }_n+w{\sigma }_n$, is

$$\begin{array}{c}\hfill b_n=P_a\sum _{m\in {\mathcal{N}}_n^{-}}{\rho }_{n,m}+w\sqrt{P_a(1-P_a)\sum _{m\in {\mathcal{N}}_n^{-}}{\rho }_{n,m}^2}\end{array}$$

(9)

As mentioned above, pilot design is modeled as a multi-objective optimization problem, where trade-offs among different $b_n$ are necessary because each pilot ${\mathbf{a}}_n$ will influence almost all $b_m$ through ${\rho }_{n,m}$. Because excessive IUI to any users may lead to errors in activity detection, a conservative method is

$$\begin{array}{cc}\hfill & \underset{\mathbf{A}}{min}\underset{n\in \mathcal{N}}{max}{b}_n\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill \end{array}$$

(10)

where $b_n$ is from (9), and the constraints are omitted for Cases 1–3. The objective of (10) is non-differentiable; hence, we prefer to relax it as

$$\begin{array}{cc}\hfill & \underset{\mathbf{A}}{min}{f}_p=\sum _{n\in \mathcal{N}}{b}_n^p\hfill \end{array}$$

(11)

where $p\ge 1$ is a parameter used to penalize large $b_n$ and the constraints are omitted for Cases 1–3. Problem (11) is equivalent to minimizing the l-p norm of $[b_1,\dots ,b_N]$ and tends to be equivalent to (10) when $p\to \infty$. In particular, (11) achieves Pareto optimality when $p=1$. Additionally, the method in [10] is equivalent to (11) when $p=1$ and $w=0$, concerning only the mean value of the IUI.

In this way, pilot design is modeled as an optimization problem as (11), while different constraints including Cases 1–3 may be adopted.

3.2. Pilot Design Algorithm with mAMP Adopted

With framework (11), the pilot design algorithm can be derived as long as the function of ${\rho }_{n,m}$ about pilots is known, which varies with different JADCE algorithms.

In this paper, we adopt a modified AMP (mAMP) algorithm proposed in [10] in JADCE, which exploits channel correlation and performs well with low complexity. This algorithm is one of the energy-decision-based algorithms mentioned above and applies matched filtering to the estimated channel to suppress the IUI to user n. To be specific, ${\mathbf{x}}_n={\mathbf{R}}_n^{1/2}{\widehat{\mathbf{h}}}_n$ in mAMP, where ${\mathbf{R}}_n$ is the channel correlation matrix and ${\widehat{\mathbf{h}}}_n$ is the estimated equivalent channel of user n. According to the analysis of mAMP in [10], when mAMP converges, there is an approximation that

$${\widehat{\mathbf{h}}}_n\approx {\mathbf{h}}_n+\sum _{m\in {\mathcal{K}}_n^{-}\setminus {\mathcal{K}}^{\prime }}\left({\mathbf{a}}_n^H{\mathbf{a}}_m\right){\mathbf{g}}_m+{\left({\mathbf{a}}_n^H\mathbf{N}\right)}^T$$

(12)

Then, we have the following approximation:

$${\mathbf{x}}_n={\mathbf{R}}_n^{1/2}{\mathbf{h}}_n+\sum _{m\in {\mathcal{K}}_n^{-}\setminus {\mathcal{K}}^{\prime }}\left({\mathbf{a}}_n^H{\mathbf{a}}_m\right){\mathbf{R}}_n^{1/2}{\mathbf{g}}_m+{\mathbf{R}}_n^{1/2}{\left({\mathbf{a}}_n^H\mathbf{N}\right)}^T$$

(13)

which indicates that IUI mainly comes from the undetected active users. We adopt a conservative assumption that all other active users cause IUI, leading to the following assumption:

$$\mathbb{E}\parallel {\mathbf{x}}_n{\parallel }^2={\alpha }_n\mathrm{tr}\left({\mathbf{R}}_n^2\right)+\sum _{m\in {\mathcal{K}}_n^{-}}\mathrm{tr}\left({\mathbf{R}}_n^H{\mathbf{R}}_m\right){\left|{\mathbf{a}}_n^H{\mathbf{a}}_m\right|}^2+{\sigma }_N^2\mathrm{tr}\left({\mathbf{R}}_n\right)$$

(14)

The first and second terms on the right side of (14) represent the power of ${\mathbf{d}}_n$ and ${\mathbf{e}}_{n,m}$, respectively. Thus,

$${\rho }_{n,m}=\mathrm{tr}\left({\mathbf{R}}_n^H{\mathbf{R}}_m\right){\left|{\mathbf{a}}_n^H{\mathbf{a}}_m\right|}^2$$

(15)

Combining (11) and (15), it can be noted that the objective function $f_p$ and the feasible set of $\mathbf{A}$ are both non-convex. Thus, we propose to solve the pilot design problem with constraints like Cases 1–3 via PGD [20], as shown in Algorithm 1. The gradient of $f_p$ is derived as (16):

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathsf{\partial }{f}_p}{\mathsf{\partial }{\mathbf{a}}_n^{*}}}=& p\sum _{m\in {\mathcal{N}}_n^{-}}\{P_a(b_n^{p-1}+b_m^{p-1})+k{\rho }_{n,m}\sqrt{P_a(1-P_a)}\hfill \\ \hfill & \left[b_m^{p-1}{\left(\sum _{r\in {\mathcal{N}}_m^{-}}{\rho }_{m,r}^2\right)}^{-{\displaystyle \frac{1}{2}}}+b_n^{p-1}{\left(\sum _{r\in {\mathcal{N}}_n^{-}}{\rho }_{n,r}^2\right)}^{-{\displaystyle \frac{1}{2}}}\right]\}{\displaystyle \frac{{\rho }_{n,m}}{{\mathbf{a}}_n^H{\mathbf{a}}_m}}{\mathbf{a}}_m\hfill \end{array}$$

(16)

Algorithm 1 Pilot Optimization Algorithm

Input:  Initial pilot sequences ${\mathbf{A}}^{\left(0\right)}=[{\mathbf{a}}_1^{\left(0\right)},\dots ,{\mathbf{a}}_N^{\left(0\right)}]$; channel correlation matrices ${\mathbf{R}}_n,\forall n\in \mathcal{N}$; active probability $P_a$; weight w; penalty index p; max number of iteration $t_m$; (optional symbol set $\mathcal{A}\triangleq \left\{{\displaystyle \frac{1}{\sqrt{L}}}{\mathrm{e}}^{j\varphi }\right|\varphi \in \mathcal{P}\}$, $\mathcal{P}$ is optional phase set for Case 3). Iteration of PGD:  1: for$t=1$; $t\le t_m$; $t++$do  2:     for $n=1$; $n\le N$; $n++$ do  3:         for $m=1$; $m\le N\&m\ne n$; $n++$ do  4:            ${\rho }_{n,m}=\mathrm{tr}\left({\mathbf{R}}_n^H{\mathbf{R}}_m\right){\left|{\left({\mathbf{a}}_n^{\left(t\right)}\right)}^H{\mathbf{a}}_m^{\left(t\right)}\right|}^2$  5:         end for  6:         Compute $b_n$ by (9)  7:     end for  8:     for $n=1$; $n\le N$; $n++$ do  9:         Compute ${\mathbf{d}}_n^{\left(t\right)}={\displaystyle \frac{\mathsf{\partial }{f}_p}{\mathsf{\partial }{\mathbf{a}}_n^{(t-1)*}}}$ by (16) 10:         ${\mathbf{a}}_{n,\mathrm{tmp}}={\mathbf{a}}_n^{(t-1)}-s_t{\mathbf{d}}_n^{\left(t\right)}$ 11:         if Case 1 then 12:            ${\mathbf{a}}_n^t={\mathbf{a}}_{n,\mathrm{tmp}}/{\parallel {\mathbf{a}}_{n,\mathrm{tmp}}\parallel }_2$ 13:         else if Case 2 or Case 3 then 14:            ${\left({\mathbf{a}}_n^t\right)}_l={\left({\mathbf{a}}_{n,\mathrm{tmp}}\right)}_l/\left|\sqrt{L}{\left({\mathbf{a}}_{n,\mathrm{tmp}}\right)}_l\right|,1\le l\le L$ 15:         end if 16:     end for 17: end for Phase quantization: 18: if Case 3 then 19:     ${\left(a_n^{t_m}\right)}_l={\mathrm{argmin}}_{a\in \mathcal{A}}{|{\left(a_n^{t_m}\right)}_l-a|}^2,1\le l\le L,1\le n\le N$ 20: end if Output:  Optimized pilot sequences ${\mathbf{A}}_o={\mathbf{A}}^{\left(t_m\right)}$

In Algorithm 1, $s_t$ is the step size of the gradient descent, which influences the speed and stability of the convergence. In this paper, we take $s_t=\lambda {\displaystyle \frac{\sqrt{N}}{\parallel {\mathbf{D}}^{\left(t\right)}{\parallel }_F}}$, where ${\mathbf{D}}^{\left(t\right)}=[{\mathbf{d}}_1^{\left(t\right)},\dots ,{\mathbf{d}}_N^{\left(t\right)}]$ and $\lambda \in (0,1)$. Generally speaking, when $\lambda$ increases, the speed of gradient descent increases, while the risk of divergence also increases. In the scenarios with stable channel statistics, the convergence behavior of Algorithm 1 has little impact on the overall system performance, because the pilots only need to be updated when the channel correlation matrices change.

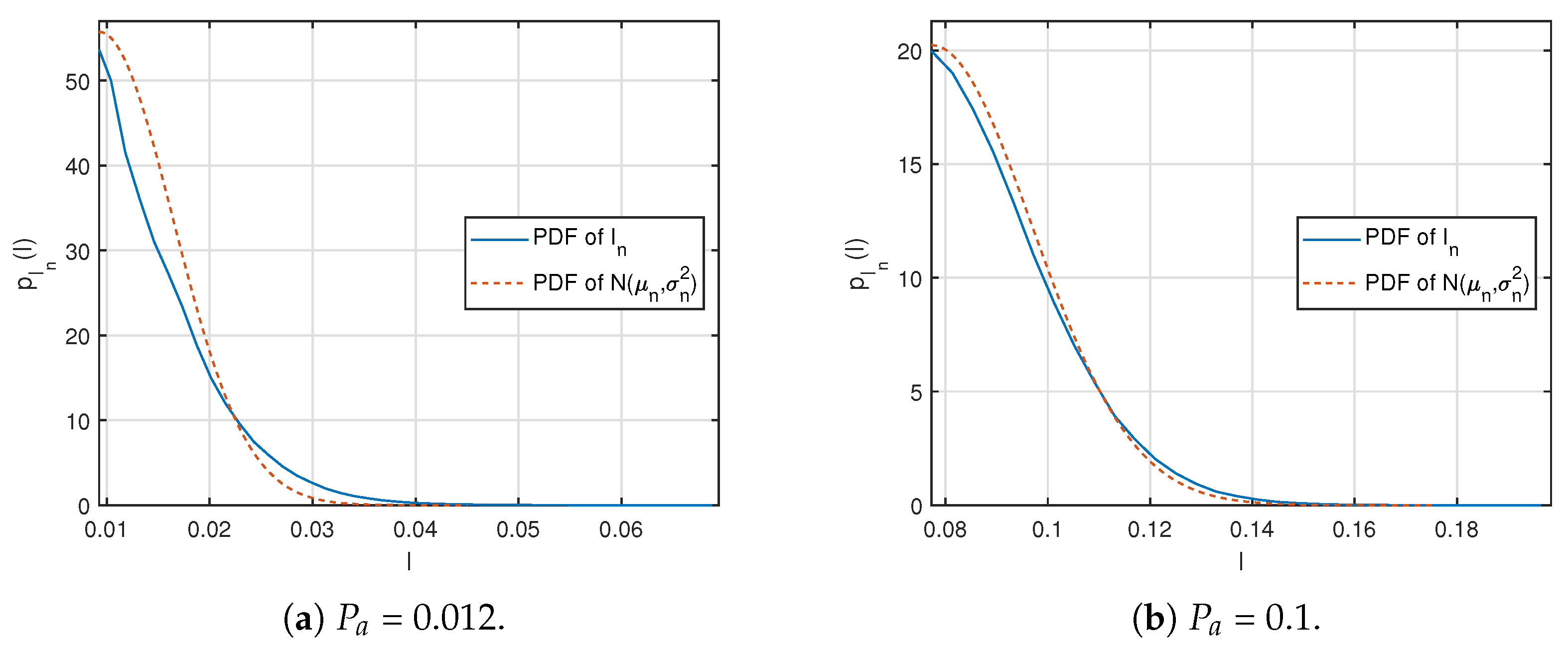
3.3. Analysis of the Proposed Pilot Design Algorithm

The computational complexity of Algorithm 1 is $\mathcal{O}(t_m{N}^{2}L+M^2{N}^2)$, whose second term comes from computing $\mathrm{tr}\left({\mathbf{R}}_n^H{\mathbf{R}}_m\right)$ before the iteration of PGD. Although the complexity grows with the numbers of users and antennas, Algorithm 1 is practical for the scenarios where the channel statistics are stable because it only needs to be executed once until the channel correlation matrices change.

The approximate expression of the per-user missed detection rate $P_{M,n}$ is exploited in the derivation of Algorithm 1. However, it is still difficult to precisely predict the actual probability of missed detection $P_M$. The inaccuracy stems from the following factors:

• The IUI approximation (14) under a certain set of active users is inaccurate;
• The Gaussian approximation of the IUI distribution is inaccurate;
• The JADCE algorithm, mAMP, uses a common threshold varying with iterations, i.e., ${\theta }_n^{\left(t\right)}={\theta }^{\left(t\right)}$. The threshold is actually determined based on the estimated equivalent channel of all users and is hard to predict.

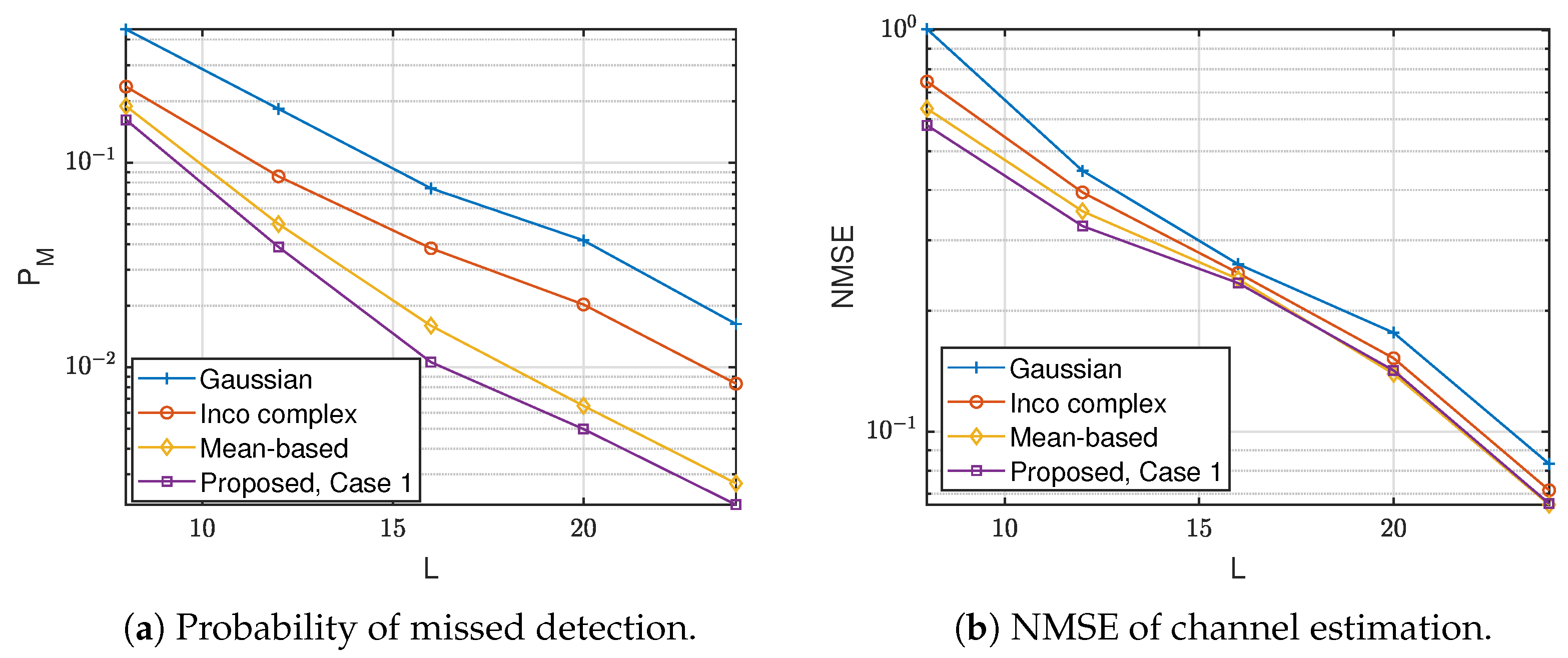
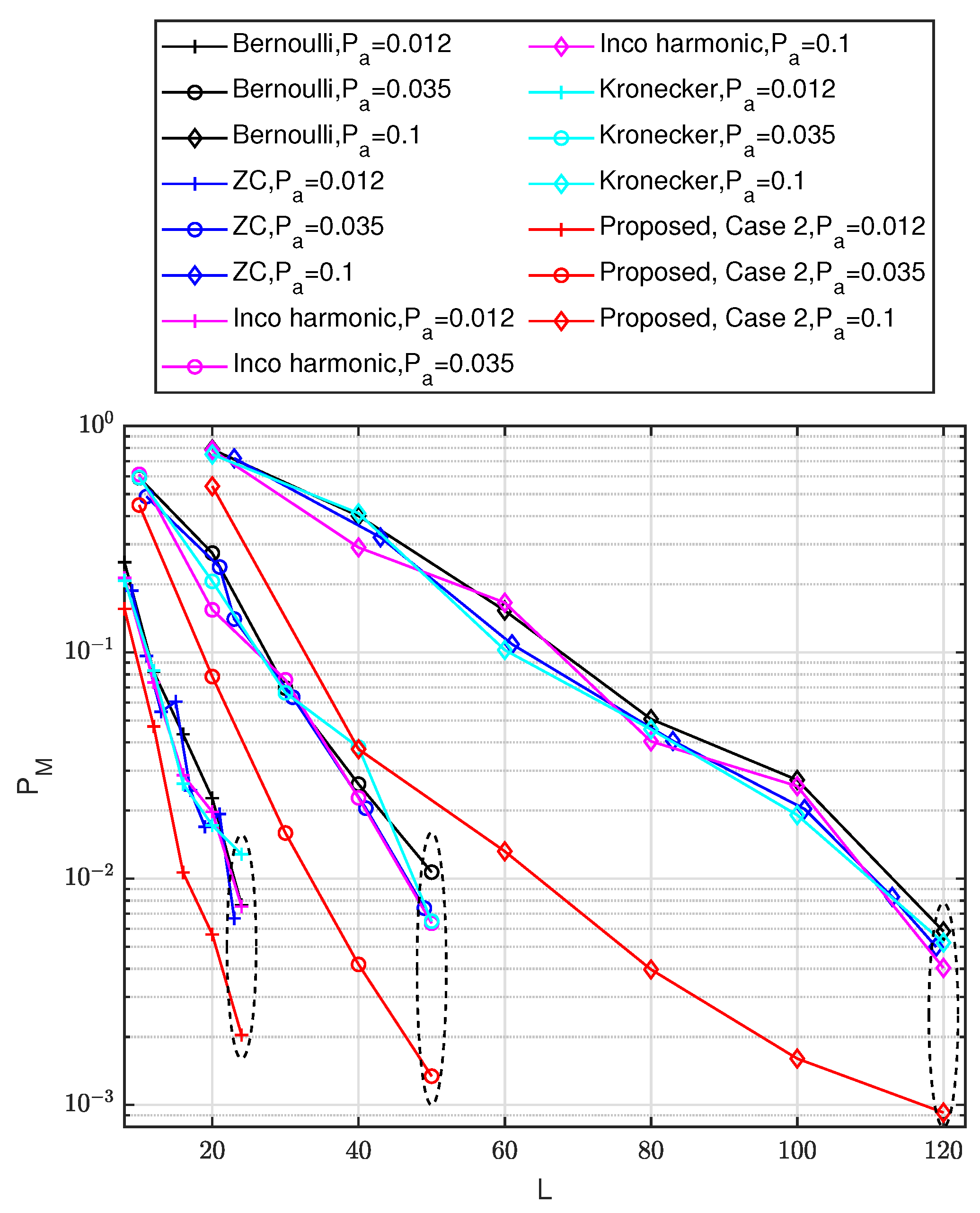
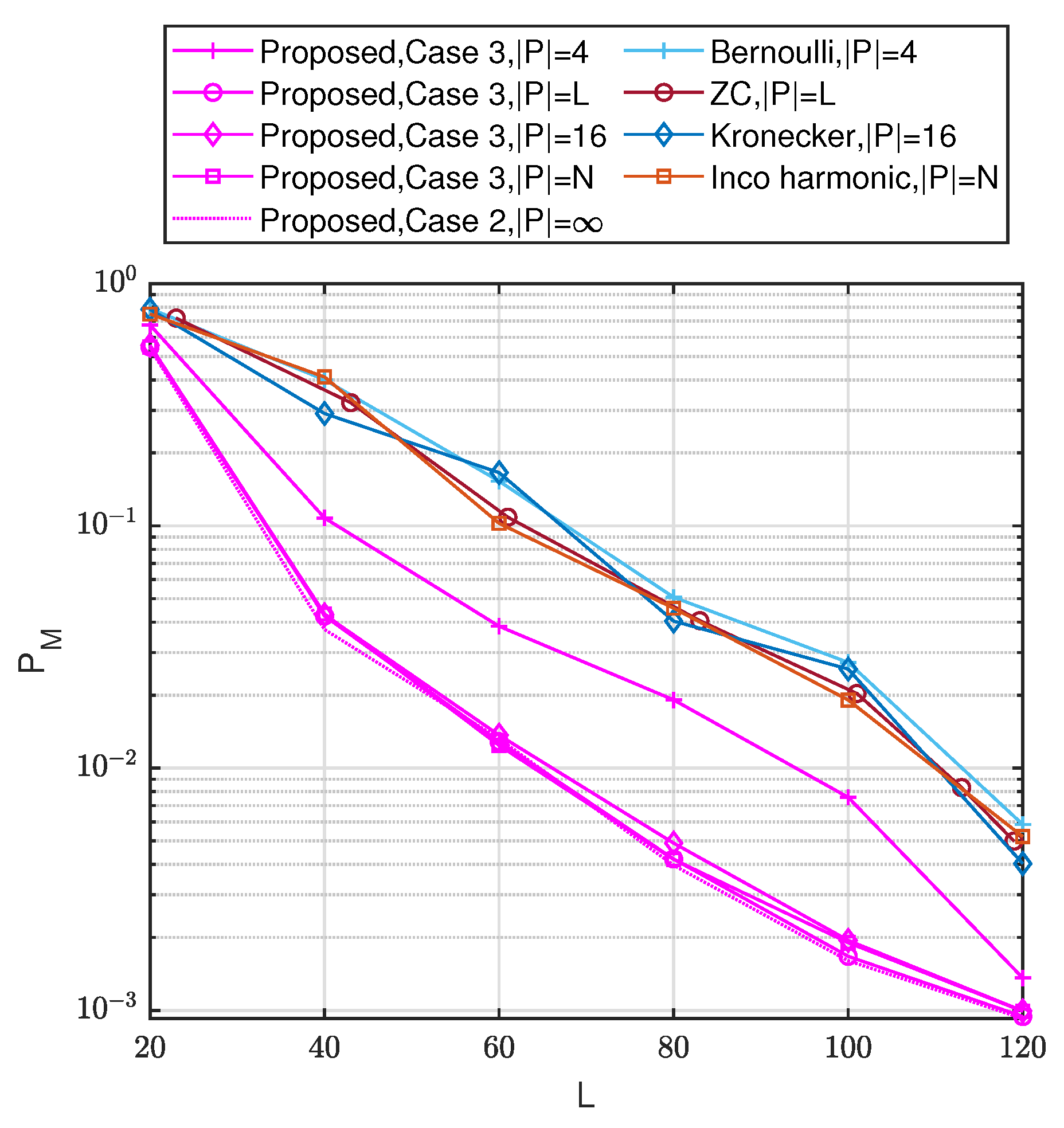
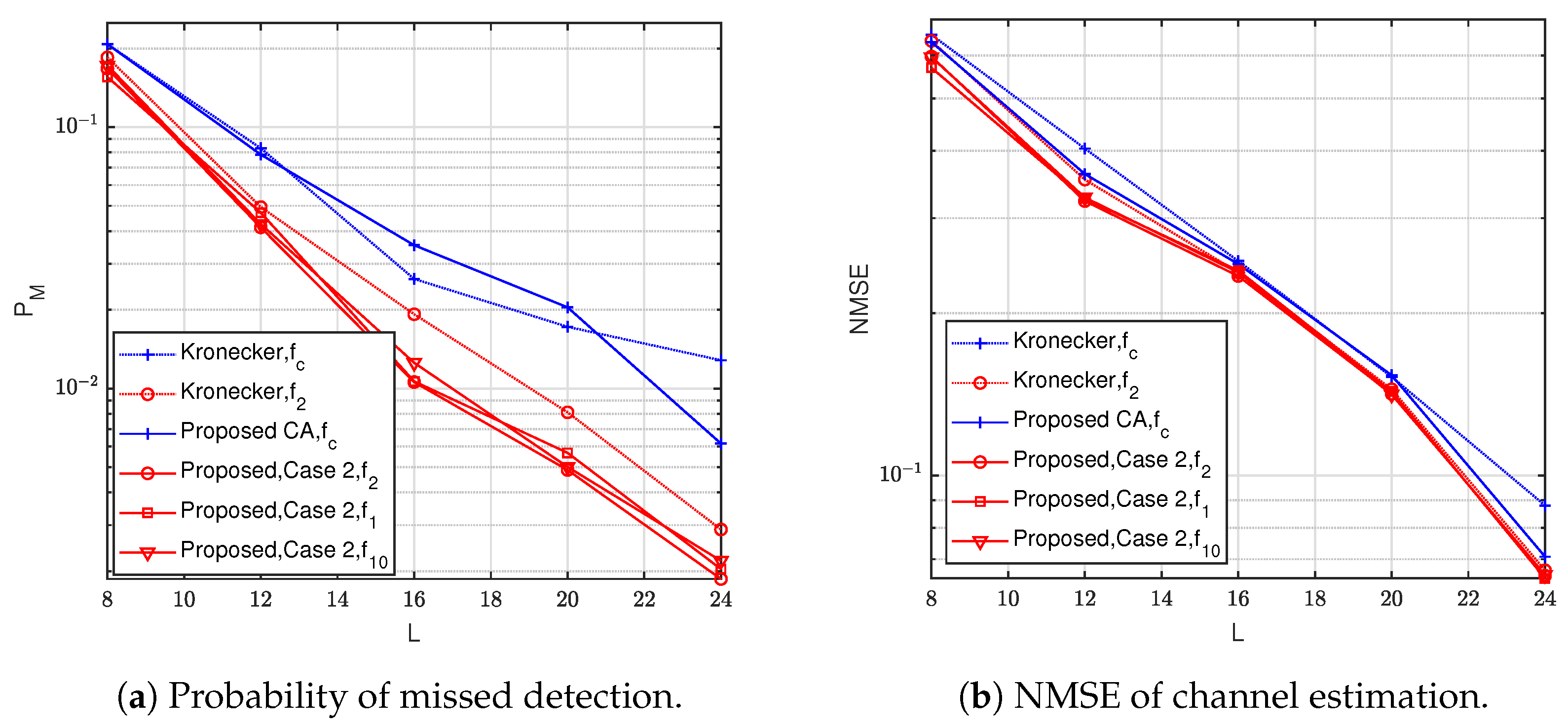
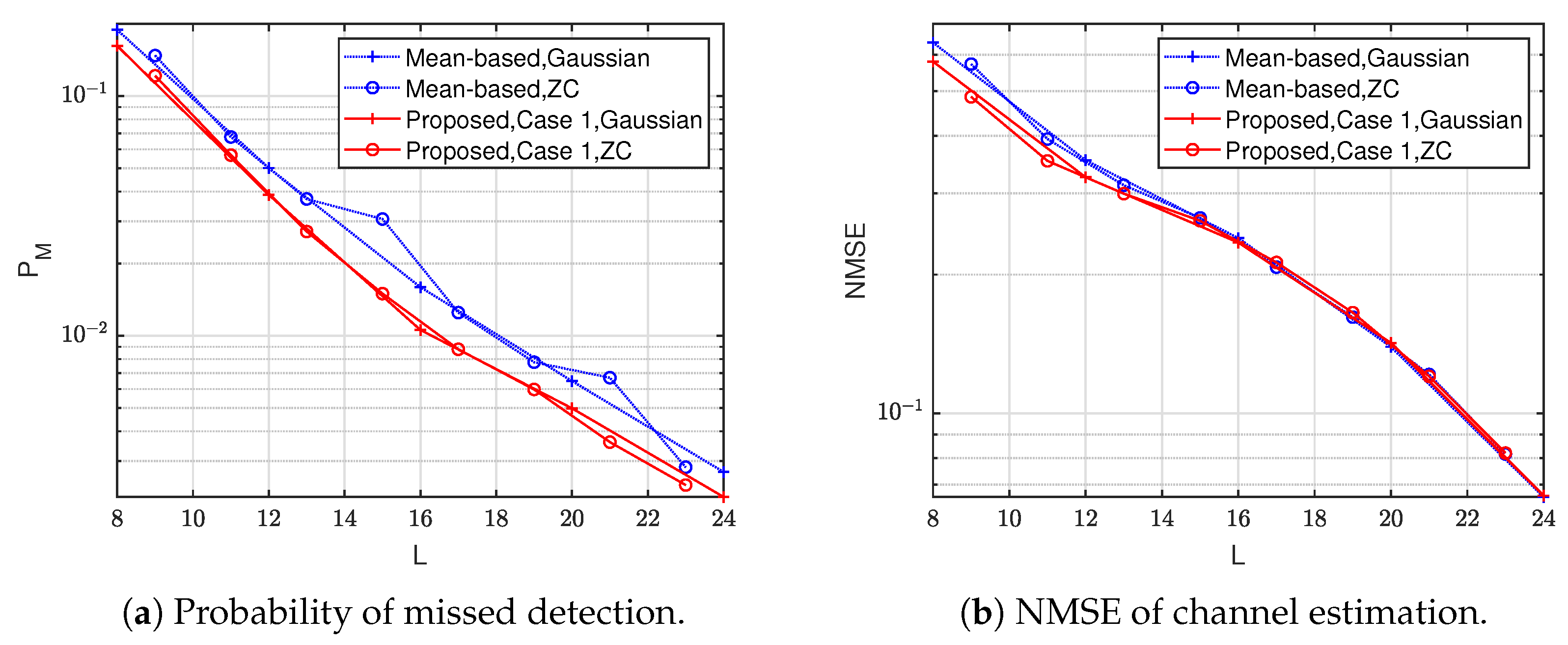
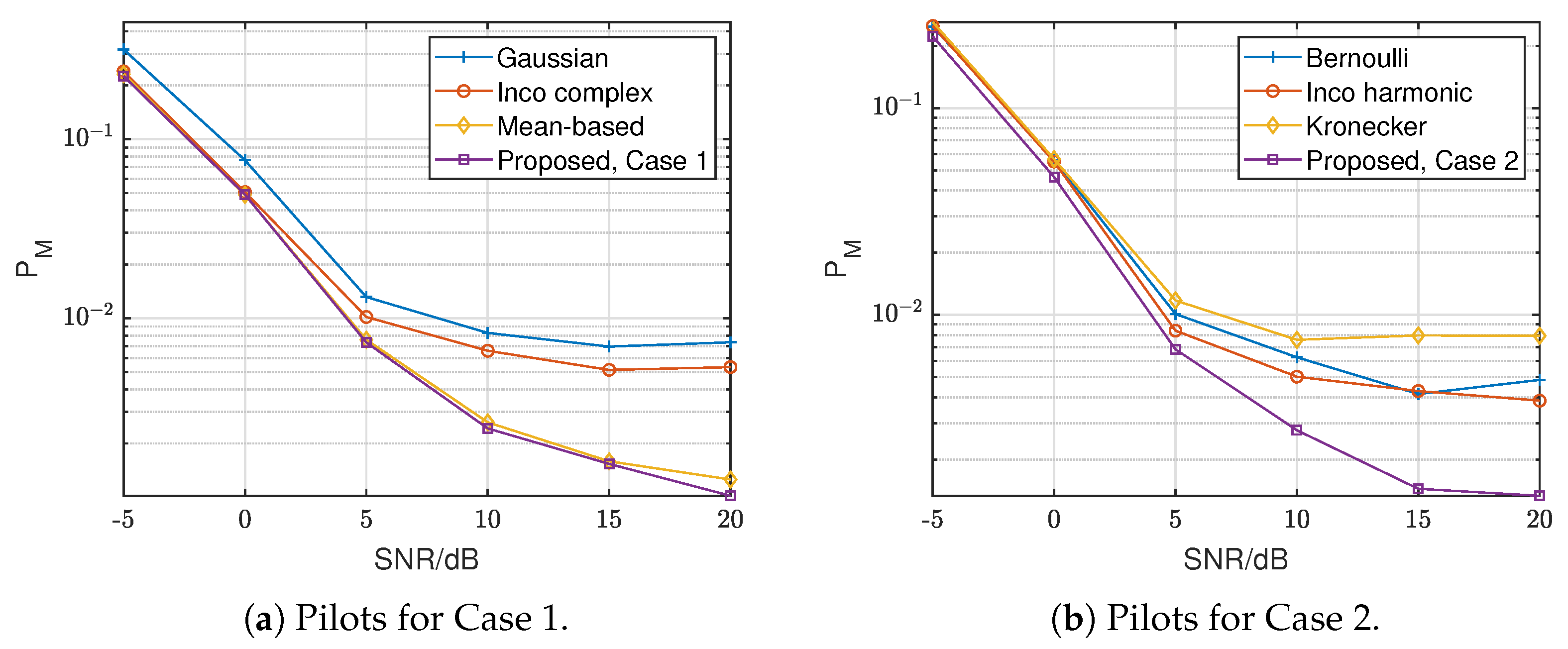
4. Numerical Experiment

In this section, we evaluate the performance of the proposed pilot design, compared with existing designs.

4.1. Simulation Setup

The channel realization is based on QuaDRiGa [24], a geometry-based stochastic channel model that simulates the statistical properties of the channel as defined in 3GPP TR 38.901 [25]. In the simulation, we set a center frequency of 6 GHz. All users are uniformly and randomly located at a distance of 100 m from the BS. Each user has a 90% probability of LOS, and the correlation distance among their LOS/NLOS states is 50 m, as defined in [25].

When implementing the proposed algorithm, we have tested the following parameters: the weight of ${\sigma }_n$ in $b_n$ is $w=3$, and the penalty index p is taken from $\{1,2,10\}$. The step size parameter $\lambda$ and the number of iterations $t_m$ are properly chosen so that the algorithm converges within $t_m$ iterations while preventing divergence. Consequently, the settings $\{\lambda =0.125,t_m=300\}$ and $\{\lambda =0.025,t_m=1500\}$ are appropriate for the cases of $p\in \{1,2\}$ and $p=10$, respectively.

The proposed pilot design and some existing ones under constraints similar to Cases 1–3 are evaluated. For the sake of fairness, the proposed pilot design for Case 1 is compared with Gaussian sequences, the complex incoherent frames in [18], and the design in [10], which are also designed for Case 1.

Other baselines include Bernoulli sequences, ZC sequences, the harmonic incoherent frames in [18], and the Kronecker-based design in [17], which satisfy the constraints for Case 3, i.e., CA pilots with finite phases, and also satisfy the constraints for Case 2, i.e., CA pilots. However, these designs have different numbers of optional phases, even with the same pilot length L. To be specific, Bernoulli pilots have 4 phases, ZC pilots have L phases, the harmonic frames in [18] have N phases, and the design in [17] has $N_h=16$ phases, where $N_h$ is a parameter.

The method in [17] represented by ‘Kronecker’ is based on the Kronecker product of Hadamard and Fourier matrices, optimized using the GA with a classic coherence metric $f_c={\sum }_{n\in \mathcal{N}}{\sum }_{m\in {\mathcal{N}}_n^{-}}\left(\right|{\mathbf{a}}_n^H{\mathbf{a}}_m{|-\sqrt{{\displaystyle \frac{N-L}{L(N-1)}}})}^2$, reducing the coherence of pilots of all users. ‘Inco complex’ and ‘Inco harmonic’, respectively, represent the pilot designs in [18] for Cases 1 and 3, which are guided by metric $f_i={max}_{1\le m<n\le N}{\left|{\mathbf{a}}_n^H{\mathbf{a}}_m\right|}^2$ and reduce the coherence of pilots as well. ‘Mean-based’ represents the method in [10], optimized via PGD with an IUI-mean-based metric $f_{\mathrm{mean}}={\sum }_{n\in \mathcal{N}}{\mu }_n$.

4.2. Results

Figure 6 compares the performance of the proposed pilot design for Case 1 (no element-wise constraint) with other pilot designs for Case 1, when active probability $P_a=0.012$ and mAMP [10] are adopted in JADCE. Figure 6a shows that the proposed design has a lower probability of missed detection, $P_M$, than the other designs for Case 1, and Figure 6b shows that the proposed design has a lower normalized mean square error (NMSE) of channel estimation than the other designs for Case 1.

Figure 7 compares the performance of the proposed pilot design for Case 2 (constant amplitude) with other designs satisfying Case 2, when active probability $P_a=0.012$ and mAMP are adopted in JADCE. Figure 7a shows that the proposed design has a lower probability of missed detection, $P_M$, than the other designs satisfying Case 2, and Figure 7b shows that the proposed design has a lower NMSE of channel estimation than the other designs satisfying Case 2.

Figure 7 also shows that the performance of ZC pilots is non-monotonic with respect to length L. This is because the number of different ZC sequences with length L is $L\mathsf{\Phi }\left(L\right)$, where $\mathsf{\Phi }\left(L\right)\triangleq \left|\right\{l\in \mathbb{Z}|1\le l<L,\gcd (l,L)=1\}|$ is non-monotonic with respect to L, and because the number of ZC sequences is smaller than N in Figure 7, leading to severe collisions.

Additionally, Figure 6 and Figure 7 show that there is a significant performance gap in activity detection among different pilot schemes, while the disparity in channel estimation performance is relatively small.

The results in Figure 6 and Figure 7 correspond to situations with active probability $P_a=0.012$. To verify whether the proposed pilot designs still perform well with higher $P_a$, the performances of pilots with higher $P_a$ and greater pilot length L are shown in Figure 8 and Figure 9.

Figure 8 compares the activity detection performance of different pilots for Case 1 (no element-wise constraint) under different $P_a$. It shows that the proposed design performs better than the other designs for Case 1 under the same active probability $P_a$ and pilot length L. Meanwhile, it can be implied that the proposed pilot design can support more active users than the other designs for Case 1 with the same pilot length and detection performance.

Figure 9 compares the activity performance of different pilots for Case 2 (constant amplitude) under different $P_a$. It shows that the proposed design performs better than other designs satisfying Case 2 under the same active probability $P_a$ and pilot length L.

Note that the baselines in Figure 9 also satisfy the constraints for Case 3 (CA and finite phase) but have different numbers of optional phases. For the sake of fairness, each baseline for Case 3 is compared with the proposed design for Case 3 with the same number of phases $\left|\mathcal{P}\right|$. Figure 10 shows the results with active probability $P_a=0.1$. According to Figure 10, the proposed pilot design for Case 3 outperforms the designs with the same constraints.

In addition, Figure 10 compares the performance of the proposed design for Case 2 (CA) and Case 3 (CA and finite phase), i.e., with different numbers of optional phases. It shows that the performance degradation caused via phase quantization is significant when $\left|\mathcal{P}\right|=4$ but is negligible when $\left|\mathcal{P}\right|\ge min\{L,16\}$. It is implied that the phase quantization of the proposed design is practical while also maintaining high performance.

According to Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the proposed pilot design can reduce the pilot length needed for a given JADCE performance guarantee, which helps to reduce latency. To be specific, the average spectral efficiency is $(1-{\displaystyle \frac{L}{L_t}})\mathbb{E}\left({\sum }_{n\in \mathcal{K}\cap {\mathcal{K}}^{\prime }}{R}_n\right)$, where $L_t$ denotes the slot duration, and $R_n$ denotes the achievable rate of detected active user n in the data phase. Therefore, to maintain certain spectral efficiency, $L_t$ should be proportional to L. The proposed pilot design reduces the L needed for certain JADCE performances, and consequently reduces uplink latency.

Figure 11 shows the probability density function (PDF) of the IUI to one user, when different pilot designs for Case 1 or 2 are adopted. It shows that the proposed pilot design effectively reduces the PDF $p_{I_n}\left(I\right)$ when I is relatively large, compared to other designs. In particular, compared to the mean-based method [10], the proposed designs reduce the variance of IUI, leading to lower $p_{I_n}\left(I\right)$ when $I>0.025$, although their mean values of IUI, ${\mu }_n$, are almost the same.

Figure 11 also shows that the proposed pilot design for Case 1 demonstrates the superior tail behavior of the IUI distribution compared to that for Case 2, owing to fewer optimization constraints.

Figure 12 shows the PDFs of the real IUI distribution and its Gaussian approximation, when the proposed pilot design is adopted. It shows that the tail behavior of the Gaussian distribution is similar to that of the real IUI distribution, especially with greater active probability.

Figure 13 compares the performance of the proposed pilot design for Case 2 (CA) with a different penalty index p in the metric, marked with ’Proposed,Case 2,$f_p$’. It shows that the choice of p has little effect on the performance of the proposed method, although $p=10$ approximates Problem (10) better.

Meanwhile, Figure 13 compares the proposed metric $f_p$ with metric $f_c$ in [17], which minimizes the coherence of all pilots. The method [17] is marked with ‘Kronecker, $f_c$’, and its modification, in which metric $f_c$ is replaced with $f_2$, is marked with ‘Kronecker, $f_2$’. Moreover, the modification of the proposed method, which replaces $f_p$ with $f_c$, is marked with ‘Proposed, Case 2, $f_c$’. Figure 13 implies that $f_p$ provides better guidance for pilot design than $f_c$, including in a discrete codebook.

Figure 14 compares the proposed pilot design for Case 1 (no element-wise constrain) and the mean-based method [10] in terms of the robustness to initialization, given that the two methods are both solved via PGD under the same constraints. In Figure 14, different initial points ${\mathbf{A}}^{\left(0\right)}$, including Gaussian and ZC sequences, are adopted for the two methods. It shows that the activity detection performance of the proposed pilot design is not sensitive to initial points, compared to the mean-based method.

Figure 15 compares the activity detection performance of different pilot schemes with different receiving SNR values at the BS. It shows that the proposed design can either achieve a lower $P_M$ at a given SNR or require a lower SNR to maintain specific $P_M$. As a result, the proposed pilot design can reduce the transmitting power of users, leading to higher energy efficiency in grant-free access.

5. Conclusions

Pilot overhead incurred by IUI becomes the bottleneck for increasing the system capacity of grant-free access. Although some pilot designs have been proposed, they neglect the randomness of IUI caused by dynamic user activity. In this paper, we propose a pilot design framework with a novel metric exploiting the distribution of the IUI to better characterize the impact of pilots on JADCE. When mAMP is adopted, we further propose to solve the pilot design problem via PGD under different constraints. It was verified by numerical experiments that the proposed method improves the tail behavior of the IUI distribution and consequently outperforms other designs in JADCE. Moreover, this study shows that applying the proposed metric can help design pilots within a given codebook. Furthermore, the proposed algorithm exhibits robustness to iteration initialization, compared with the previous method based on PGD. All in all, the proposed pilot design method can support a massive access system with lower latency and higher energy efficiency.