Research on Low-Altitude UAV Target Tracking Method Based on ISAC

Abstract

In this paper, a UAV target tracking method with 6G integrated sensing and communication (ISAC) is proposed to address the surveillance requirements for unmanned aerial vehicle (UAV) targets in the context of the rapid development of low-altitude economy. Firstly, a target tracking system model for UAVs is established based on the ISAC base station transceiver architecture. Then, an unscented Kalman filter (UKF) target tracking framework is designed to tackle the occlusion effect during UAV navigation. Specifically, the measurement position information of the UAV is obtained through a spatial rotation-based parameter estimation method. Subsequently, occlusion is detected by analyzing the Line-of-Sight (LoS) visibility between the UAV and the base station. On this basis, the problem of short-term and long-term trajectory loss under occlusion is solved by integrating cubic interpolation with a constant velocity (CV) model, which enables real-time UAV trajectory tracking. Finally, simulation results demonstrate that: (1) under no occlusion, the average estimation errors of the X/Y/Z axes are 0.82 m, 0.79 m, and 0.68 m, respectively; (2) under short-term occlusion, the average errors of the X/Y/Z axes are 1.25 m, 2.18 m, and 1.05 m, with a convergence time of 1 s after LoS recovery; (3) under long-term occlusion, the average errors of the X/Y/Z axes are 2.87 m, 3.79 m, and 1.85 m, with a convergence time of 5 s after LoS recovery; (4) the velocity estimation error can quickly converge to within 0.2 m/s after re-acquiring observations. The proposed method exhibits small trajectory and velocity estimation errors in different occlusion scenarios, effectively meeting the requirements for UAV target tracking.

1. Introduction

With the rapid development of unmanned aerial vehicle (UAV) technology and the gradual relaxation of low-altitude airspace management, the application of UAVs in various fields such as logistics delivery, disaster relief, and agricultural pest control has shown explosive growth [1]. However, with the rapid expansion of the low-altitude economy, the safety hazards posed by rogue UAVs are becoming increasingly prominent. Unauthorized flight not only threatens aviation safety but can also infringe on privacy, interfere with communication systems, and even be used for illegal activities [2], posing multi-dimensional challenges to the existing regulatory framework. On one hand, the low-altitude environment is complex and dynamic. Factors such as urban building clusters, meteorological conditions, and electromagnetic interference make conventional radar and optical sensing methods susceptible to occlusion and noise interference. On the other hand, the separate architecture of communication and sensing systems leads to low utilization efficiency of spectrum resources, making it difficult to meet the demands of multi-target real-time tracking in dense airspace [3].

With the widespread application of 5G millimeter wave/terahertz band, the spectrum overlap between communication and radar systems has intensified. Integrated sensing and communication (ISAC) addresses the problem of spectrum resource waste caused by the independent deployment of traditional communication and sensing systems through spectrum sharing and hardware platform [4,5]. ISAC demonstrates unique value in fields such as low-altitude security and intelligent transportation. It leverages the wide coverage characteristics of 5G base stations and reuses existing communication bands and massive antenna arrays. This enables a continuous monitoring range of over 1 km without new infrastructure, and allows for simultaneous tracking of multiple targets via multi-beam beamforming technology [6]. Furthermore, ISAC utilizes high-frequency beams to achieve precise positioning and real-time communication. By dynamically adapting to scenarios such as urban building obstruction and adverse weather, it can construct an all-weather, all-terrain monitoring network, thereby enhancing target detection robustness and system comprehensive efficiency [7].

Liu et al. systematically elaborated on the dual-functional architecture of ISAC in 6G networks [8], pointing out that it can significantly enhance sensing resolution and communication efficiency by sharing hardware and spectrum resources, and provided a theoretical framework for low-altitude UAV regulation, but did not address the problem of trajectory extrapolation under dynamic occlusion. To address the problem of sensing performance degradation in complex environments, Luo et al. proposed a joint beamforming algorithm based on clutter suppression [9], achieving 0.5 m level positioning accuracy in densely occluded scenarios, but it did not solve the problem of trajectory prediction deviation caused by long-term occlusion. Zhang et al. innovatively introduced channel training into terahertz ISAC systems [10], achieving sub-wavelength parameter estimation through large-scale multiple input multiple output (MIMO) arrays, but its algorithmic complexity limited real-time tracking capability. Zhao et al. proposed a multi-base station cooperative UAV target tracking mechanism that addressed the base station handover problem in cross-regional tracking [11], but it did not handle single-base station tracking under occlusion. In the context of addressing aerial threats in modern armed conflicts or terrorist actions, the literature [12], by fusing data from optical sensors and a low-probability-of-intercept radar network and employing a deep learning model based on YOLO v4, effectively achieved the distinction between drones and birds, providing a reliable source of situational awareness for a data fusion platform; however, it pointed out the necessity to enrich the dataset with images featuring more complex backgrounds and multi-scale targets to enhance model generalization. Anti-drone systems exist which combine optical and radar sensors with deep neural networks to distinguish UAVs from other targets, and that recent surveys highlight the integration of radar, RF, optical, and acoustic sensors through data fusion and AI algorithms as the main direction for improving detection accuracy [13].

Therefore, existing research in the field of UAV target tracking has limitations such as lacking an occlusion type discrimination mechanism and does not have sufficient differentiated processing strategies for short-term/long-term occlusion. To compare to existing methods, the performance improvements of this research are mainly reflected in the following aspects. Firstly, at the system model level, the innovative integration of ISAC signals with the tracking framework significantly enhances environmental adaptability. Secondly, a spatial rotation-based parameter estimation method is proposed. By introducing rotational compensation, it overcomes the resolution limitations of the DFT, thereby improving measurement accuracy. Lastly, a hierarchical occlusion processing mechanism is introduced. It determines the duration of occlusion based on prior information and geometric relationships, and employs cubic interpolation for short-term occlusion and a constant velocity model for long-term occlusion to predict trajectories, which substantially reduces trajectory estimation errors.

2. System Model

2.1. ISAC Signal Modeling and Processing Framework

This system employs a single-station integrated sensing and communication (ISAC) architecture based on large-scale multiple-input multiple-output (MIMO) uniform planar arrays (UPA). The ISAC base station utilizes a dual-functional hardware architecture, the core of which is composed of a hybrid unit (HU) and a receiving unit (RU). The HU integrates communication transceiver links and downlink sensing signal transmission functions, simultaneously generating high-gain beams towards communication users and sensing targets through digital-analog hybrid beamforming technology. Specifically, the communication submodule maps user data to antenna ports based on precoding matrices, supporting multi-user MIMO transmission; the sensing submodule generates sensing beams through predefined pilot signals, utilizing time-division multiplexing (TDM) to embed radar pulses within communication time slots, thereby achieving dynamic resource allocation for communication and sensing signals [14]. The RU is dedicated to uplink sensing signal reception, with an all-digital beamforming architecture employed to achieve high-precision echo sampling through multi-channel ADCs.

Cooperative transmission of communication and sensing signals is achieved through frame structure design and joint signal optimization. Each OFDM frame comprises a communication slot for transmitting user data and a sensing slot for transmitting radar pulses. The sensing slot employs a full-bandwidth OFDM signal, accommodating synchronization requirements under multipath channel conditions through the cyclic prefix (CP). The communication slot’s subcarrier allocation is dynamically adjusted based on user Quality of Service (QoS) [15]. At the signal level, frequency domain isolation between communication symbols and sensing pilots is achieved through orthogonal codebook design to avoid mutual interference. Simultaneously, by leveraging the spatial degrees of freedom of large-scale MIMO arrays, communication beams and sensing beams are steered towards different spatial regions, further reducing the impact of co-frequency interference on target tracking accuracy [16].

A three-dimensional Cartesian coordinate system is constructed in Figure 1 to establish the spatial geometric model of the UAV-obstacle, which intuitively presents the relative pose relationship between the UAV and the static ground obstacles. In the figure, horizontal terrain is represented by the $\mathrm{X}-\mathrm{Y}$ plane, and the $\mathrm{Z}$-axis extends vertically upward. Two types of typical obstacles are included in the figure: short-term occlusion is simulated by vegetation obstacles, and long-term occlusion is simulated by building obstacles. The spatial geometric relationship between the unmanned aerial vehicle (UAV) and obstacles is indicated by two-color path lines. The line-of-sight (LOS) propagation path is represented by a solid green line, while the path obstructed by obstacles is represented by a dashed red line.

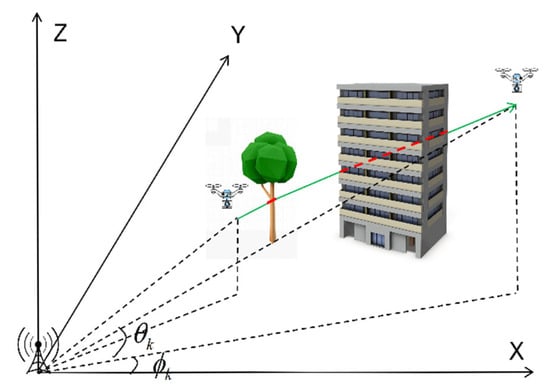
Figure 1. UAV-Obstacle Spatial Geometric Model.

The OFDM signal used by the system consists of $M$ subcarriers. Its minimum frequency is $f_0$, and the subcarrier spacing is $\Delta f$. Then, the frequency of the $\mathrm{m}$-th subcarrier can be expressed as $f_m=f_0+m\Delta f$ where $m=0,1,\dots ,M-1$. The system frame structure consists of $N$ consecutive OFDM symbols. The time interval between adjacent symbols is $T_s=T_{sym}+T_{cp}$ where $T_{sym}$ is the OFDM symbol duration, and $T_{cp}$ is the cyclic prefix guard interval [17].

Assume there are $K$ dynamic sensing targets within the base station’s coverage area, whose spherical coordinate position parameters are ${\{(r_k,{\varphi }_k,{\theta }_k)\}}_{k=1}^K$ (where $r_k$ is the distance, ${\varphi }_k$ is the azimuth angle, and ${\theta }_k$ is the elevation angle). To achieve directional sensing, beam tracking technology is employed to keep the transmit beam consistently aligned with the physical direction $\left({\theta }_k,{\phi }_k\right)$ of the $k$-th target, and the beam direction remains unchanged within a short time slot. This model focuses on the dynamic target sensing problem. In this case, the transmit signal on the $m$-th subcarrier in the $n$-th OFDM symbol can be modeled as:

$${\mathit{x}}_k\left(n,m\right)=\sqrt{P_k}{\mathit{a}}_H\left({\theta }_k,{\varphi }_k\right)s_k\left(n,m\right)$$

(1)

In Equation (1), $P_k$ is the power allocated to the sensing and tracking direction of the $k$-th target, ${\mathit{a}}_H\left({\theta }_k,{\varphi }_k\right)=a_H^x\left({\varphi }_k\right)\otimes a_H^z\left({\theta }_k,{\varphi }_k\right)\in {ℂ}^{N_H\times 1}$ is the hybrid array steering vector, and $s_k\left(n,m\right)$ the modulation symbol, satisfying $\mathbb{E}[|s_k(n,m){|}^2]=1$.

2.2. Perceived Channel Model

The three-dimensional motion state parameters of the $k$-th dynamic target during the $n$-th OFDM symbol period can be characterized as:

$$S_{k,n}={\left[r_{k,n},{\theta }_{k,n},{\varphi }_{k,n}\right]}^T\in {ℝ}^{3\times 1}$$

(2)

Based on the characteristics of narrowband OFDM systems, Doppler frequency shift and beam squint effects can be ignored [18]. In this case, the time-frequency domain echo channel matrix from the hybrid uniform planar array to the $k$-th target can be modeled as:

$${\mathit{H}}_k\left[n,m\right]={\alpha }_k{e}^{-j4\pi f_m\frac{r_k}{c}}{e}^{j4\pi f_0\frac{v_{k}n{T}_s}{c}}{a}_R({\theta }_k,{\varphi }_k)a_H^T({\theta }_k,{\varphi }_k)$$

(3)

where ${\alpha }_k=\sqrt{{\lambda }^2/{\left(4\pi \right)}^3{\left(r_k\right)}^4}{\sigma }_k$, ${\sigma }_k$ is the radar cross-sections (RCS) of the target, and $a_R\left({\theta }_k,{\varphi }_k\right)=a_R^x\left({\varphi }_k\right)\otimes a_R^z\left({\theta }_k,{\varphi }_k\right)\in {ℂ}^{N_R\times 1}$ represents the radar array steering vector, whose components in the horizontal and vertical directions are [19]:

$$a_R^x({\varphi }_k)={\left[1,e^{j{\displaystyle \frac{2\pi d}{\lambda }}\sin {\varphi }_k},\dots ,e^{j{\displaystyle \frac{2\pi d}{\lambda }}(N_R^x-1)\sin {\varphi }_k}\right]}^T$$

(4)

$$a_R^z({\theta }_k,{\varphi }_k)={\left[1,e^{j{\displaystyle \frac{2\pi d}{\lambda }}\cos {\theta }_k\sin {\varphi }_k},\dots ,e^{j{\displaystyle \frac{2\pi d}{\lambda }}(N_R^z-1)\cos {\theta }_k\sin {\varphi }_k}\right]}^T$$

(5)

Therefore, the perceived echo channel for all $K$ dynamic targets on the $n$-th subcarrier of the $m$-th OFDM symbol can be expressed as

$$H\left(n,m\right)={\displaystyle \sum _{k=1}^K{H}_k\left(n,m\right)}$$

(6)

2.3. Echo Signal Analysis

Let the measurement value of the $k$-th target be: ${\tilde{S}}_k={\left[{\tilde{r}}_k,{\tilde{\theta }}_k,{\tilde{\varphi }}_k\right]}^T$. The base station forms a sensing beam in the predicted direction $\left({\tilde{\theta }}_k,{\tilde{\varphi }}_k\right)$ using a hybrid array. Combining with the transmission signal model in Equation (1), the received echo signal can be modeled as:

$$y\left(n,m\right)=H\left(n,m\right)x_k\left(n,m\right)+n\left(n,m\right)$$

(7)

where $\mathit{n}\left(n,m\right)$ represents zero-mean additive Gaussian noise, and $\mathit{y}\left(n,m\right)$ denotes the echo signal received by all $N_R=N_R^x\times N_R^z$ receiving antennas. It is then rewritten in matrix form as:

$$\mathit{Y}\left(n,m\right)=reshape\left\{\mathit{y}\left(n,m\right),\left[N_R^z,N_R^x\right]\right\}\in {ℂ}^{N_R^z\times N_R^x}$$

(8)

To eliminate the potential impact of transmitted symbols on sensing channel estimation, transmitted symbols must be removed from the received signal to obtain the equivalent echo channel. The equivalent echo channel corresponding to $\mathit{Y}\left(n,m\right)$ can be expressed as $\tilde{\mathit{Y}}\left(n,m\right)=\mathit{Y}\left(n,m\right)/s\left(n,m\right)$. Subsequently, $\tilde{\mathit{Y}}\left(n,m\right)$ can be stacked into an equivalent echo channel tensor [20]:

$${\tilde{\mathit{Y}}}^{cube}\left[n_R^z,n_R^x,n,m\right]={\left[\tilde{\mathit{Y}}\left(n,m\right)\right]}_{n_R^z,n_R^x}\in {ℂ}^{N_R^z\times N_R^x\times N\times M}$$

(9)

The element at position $\left[n_R^z,n_R^x,n,m\right]$ in tensor ${\tilde{\mathit{Y}}}^{cube}$ can be expressed as:

$$\tilde{y}={\varsigma }_k\underset{\mathrm{distance}}{\underbrace{e^{-j4\pi f_m{\displaystyle \frac{r_k}{c}}}}}\underset{\mathrm{pitch} \mathrm{angle}}{\underbrace{e^{j{\displaystyle \frac{2\pi f_{0}d}{c}}\sin {\phi }_k}}}\underset{\mathrm{azimuth}}{\underbrace{e^{j{\displaystyle \frac{2\pi f_{0}d}{c}}\cos {\phi }_k\cos {\theta }_k{n}_R^x}}}\underset{\mathrm{radial} \mathrm{velocity}}{\underbrace{e^{j4\pi f_0{\displaystyle \frac{v_k^{r}n{T}_S}{c}}}}}+\tilde{n}\left(n,m\right)$$

(10)

Based on the theoretical model described above, the spatial information parameters of the target, including key data such as radial distance, elevation angle, and azimuth angle, can be effectively extracted from the echo signal using parameter estimation algorithms. These extracted parameters can be used as measurement inputs for the Unscented Kalman Filter for real-time estimation and tracking of the target’s motion trajectory.

3. Measurement Parameter Estimation Based on Spatial Rotation

3.1. Distance Measurement Acquisition

To estimate the distance parameter, tensor ${\tilde{\mathbf{Y}}}^{cube}\in {ℂ}^{N_R^z\times N_R^x\times N\times M}$ can be transformed into a matrix ${\mathit{Y}}^r$ with dimension $M\times N_R^z{N}_R^{x}N$, and the expression is

$${\mathit{Y}}^r={\mathit{\kappa }}^r\left(r\right)\cdot x^r+N^r\in {ℂ}^{M\times N_R^x{N}_R^{z}N}$$

(11)

where ${\mathit{\kappa }}^r\left(r\right)={\left[1,e^{-j4\pi r\Delta f/c},\dots ,e^{-j4\pi r\Delta f(M-1)/c}\right]}^T\in {ℂ}^{M\times 1}$ is the distance steering vector. First, define an $M\times M$-dimensional normalized inverse discrete Fourier transform (IDFT) matrix $\mathit{F}$, whose $\left(p^r,q^r\right)$-th element is ${\left[\mathit{F}\right]}_{p^r,q^r}=e^{j{\displaystyle \frac{2\pi }{M}}{p}^r{q}^r}/\sqrt{M^3}$.

Define the IDFT of the distance steering vector ${\mathit{\kappa }}^r\left(r\right)$ as ${\mathit{\kappa }}_{IDFT}^r\left(r\right)=\mathit{F}{\mathit{\kappa }}^r\left(r\right)$, and its $q^r$-th element is

$${\left[{\mathit{\kappa }}_{IDFT}^r\left(r\right)\right]}_{q^r}={\displaystyle \frac{1}{\sqrt{M}}}{\displaystyle \sum _{m=0}^{M-1}{e}^{j\frac{2\pi }{M}m{q}^r-j\frac{4\pi r\Delta f}{c}m}}$$

(12)

According to ${\displaystyle {\sum }_{m=0}^{M-1}{e}^{-jm\alpha }=}{e}^{-j{\displaystyle \frac{\left(M-1\right)\alpha }{2}}{\displaystyle \frac{\sin \left(\frac{M\alpha }{2}\right)}{\sin \left(\frac{\alpha }{2}\right)}}}$, assuming $\alpha ={\displaystyle \frac{4\pi rf}{c}}-{\displaystyle \frac{2\pi }{M}}{q}^r$, the above equation can be written as

$${\left[{\mathit{\kappa }}_{DFT}^r\left(r\right)\right]}_{q^r}={\displaystyle \frac{1}{\sqrt{M}}}{\displaystyle \frac{\sin \left[\frac{M}{2}\left(\frac{4\pi r\Delta f}{c}-\frac{2\pi }{M}{q}^r\right)\right]}{\sin \left[\frac{1}{2}\left(\frac{4\pi r\Delta f}{c}-\frac{2\pi }{M}{q}^r\right)\right]}}\times e^{-j\frac{M-1}{2}\left(\frac{4\pi r\Delta f}{c}-\frac{2\pi }{M}{q}^r\right)}$$

(13)

It is worth noting that when $M\to \infty$, there exists an integer $q^r=Mr\Delta f/c$ such that ${\left[{\mathit{\kappa }}_{IDFT}^r\left(r\right)\right]}_{q^r}=1/\sqrt{M}$, and elements at other positions of ${\mathit{\kappa }}_{IDFT}^r\left(r\right)$ are zero. However, in practical calculations, $Mr\Delta f/c$ is not always an integer, and channel power will leak from point $⟨Mr\Delta f/c⟩$ to surrounding points. The initial estimate $r^{ini}=q^{r,ini}c/2Mf$ of the distance can be obtained by the element $q^{r,ini}$ with the largest energy in the received signal. To improve estimation accuracy, rotation matrix $\mathit{\Phi }\left(\Delta r\right)=diag\left\{1,e^{j\Delta r},\cdots ,e^{j(M-1)\Delta r}\right\}$ can be introduced to eliminate the limitation of IDFT resolution. Where $\Delta r\in \left[-\pi /M,\pi /M\right]$ is the corresponding phase angle. The IDFT of the rotated distance steering vector is defined as ${\mathit{\kappa }}_{IDFT}^r{\left(r\right)}^{ro}=\mathit{F}\Phi \left(\Delta r\right){\mathit{\kappa }}^r\left(r\right)$, and (2) can be obtained through calculation.

$${\left[{\mathit{\kappa }}_{DFT}^r{\left(r\right)}^{ro}\right]}_{q^r}={\displaystyle \frac{1}{\sqrt{M^3}}}{\displaystyle \frac{\sin \left[\frac{M}{2}\left(\frac{4\pi r\Delta f}{c}-\Delta r-\frac{2\pi }{M}{q}^r\right)\right]}{\sin \left[\frac{1}{2}\left(\frac{4\pi r\Delta f}{c}-\Delta r-\frac{2\pi }{M}{q}^r\right)\right]}}\times e^{-j\frac{M-1}{2}\left(\frac{4\pi r\Delta f}{c}-\Delta r-\frac{2\pi }{M}{q}^r\right)}$$

(14)

Clearly, there exists $\Delta r$ such that $4\pi r\Delta f/c=\Delta r+2\pi /M{q}^{r,ini}$. At this point, ${\mathit{\kappa }}_{IDFT}^r{\left(r\right)}^{ro}$ has one and only one non-zero point. Therefore, an accurate estimate of the target distance can be obtained as:

$$\tilde{r}=\Delta r{\displaystyle \frac{c}{4\pi \Delta f}}+{\displaystyle \frac{c}{2M\Delta f}}{r}^{ini}$$

(15)

$$\Delta r=\arg \underset{\Delta r\in \left(-\frac{\pi }{M},\frac{\pi }{M}\right)}{\max }{‖f_{q^{r,ini}}\mathbf{\Phi }\left(\Delta r\right){\mathit{\kappa }}^r\left(r\right)‖}^2$$

(16)

3.2. Angular Measurement Acquisition

Initially, two Normalized DFT Matrix $F_M$ and ${\mathit{F}}_N$ are defined. Their elements are ${\left[{\mathit{F}}_M\right]}_{p^{\varphi },p^{\varphi \prime }}=e^{-j{\displaystyle \frac{2\pi }{M}}{p}^{\varphi }{p}^{\varphi \prime }}/\sqrt{M}$ and ${\left[{\mathit{F}}_N\right]}_{q^{\theta },q^{{\theta }^{\prime }}}=e^{-j{\displaystyle \frac{2\pi }{N}}{q}^{\theta }{q}^{{\theta }^{\prime }}}/\sqrt{N}$, respectively.

Similarly, for Angle Estimation, Tensor ${\tilde{\mathit{Y}}}^{cube}\in {ℂ}^{N_R^x\times N_R^z\times N\times M}$ is transformed into matrix ${\mathit{Y}}^{\varphi ,\theta }$, and the Normalized 2D DFT of this matrix is defined as ${\mathit{Y}}_{DFT}^{\varphi ,\theta }=F_M{Y}^{\varphi ,\theta }{F}_N$, whose $\left(p^{\varphi },q^{\theta }\right)$$\left(p^{\varphi }=0,1,\cdots ,M-1;q^{\theta }=0,1,\cdots ,N-1\right)$-th element is derived from Equation (17). Similarly, when the number of antenna in the array is $M\to \infty$ and $N\to \infty$, integers $p^{\varphi }=Md\cos \varphi /\lambda$ and $q^{\theta }=Nd\sin \varphi \cos \theta /\lambda$ exist, which makes ${\left[{\mathit{Y}}_{DFT}^{\varphi ,\theta }\right]}_{p^{\varphi },q^{\theta }}=1/\sqrt{MN}$. At this point, all other elements in ${\mathit{Y}}_{DFT}^{\varphi ,\theta }$ are zero, indicating that energy is concentrated on the elements at $\left(p^{\varphi },q^{\theta }\right)$. The elements of ${\mathit{Y}}_{DFT}^{\varphi ,\theta }$ exhibit Sparsity, which allows the DOA for Elevation Angle and Azimuth Angle $\left(\varphi ,\theta \right)$ to be quickly estimated using formula $\varphi ={\cos }^{-1}\left(\lambda p^{\varphi }/Md\right)$ and $\theta ={\cos }^{-1}\left(\lambda q^{\theta }/Nd\sqrt{1-{\left(\lambda p^{\varphi }/Md\right)}^2}\right)$ via the non-zero positions $\left(p^{\varphi },q^{\theta }\right)$ of ${\mathit{Y}}_{DFT}^{\varphi ,\theta }$.

$$\begin{array}{ll}{\left[Y_{DFT}^{\varphi ,\theta }\right]}_{p^{\varphi },q^{\theta }}& ={\displaystyle \frac{1}{\sqrt{MN}}}{\displaystyle \sum _{m=0}^{M-1}{\displaystyle \sum _{n=0}^{N-1}{[Y^{\varphi ,\theta }]}_{p^{\varphi },q^{\theta }}}}{e}^{-j2\pi \left({\displaystyle \frac{p^{\varphi }m}{M}}+{\displaystyle \frac{q^{\theta }n}{N}}\right)}={\displaystyle \frac{1}{\sqrt{MN}}}{e}^{-j\left(M-1\right)\left({\displaystyle \frac{\pi }{M}}{p}^{\varphi }-{\displaystyle \frac{\pi d}{\lambda }}\cos \varphi \right)}{e}^{-j\left(N-1\right)\left({\displaystyle \frac{\pi }{N}}{p}^{\varphi }-{\displaystyle \frac{\pi d}{\lambda }}\sin \varphi \cos \theta \right)}\\ & \times {\displaystyle \frac{\sin \left(\pi p^{\varphi }-\frac{M\pi d\cos \varphi }{\lambda }\right)}{\sin \left(\left(\pi p^{\varphi }-\frac{M\pi d\cos \varphi }{\lambda }\right)/M\right)}}\cdot {\displaystyle \frac{\sin \left(\pi q^{\theta }-\frac{N\pi d\sin \varphi \cos \theta }{\lambda }\right)}{\sin \left(\left(\pi q^{\theta }-\frac{N\pi d\sin \varphi \cos \theta }{\lambda }\right)/N\right)}}\end{array}$$

(17)

However, in practical operation, $Md\cos \varphi /\lambda$ and $Nd\sin \varphi \cos \theta /\lambda$ are also not always integers. The Channel power will leak to its neighboring elements. In fact, the leakage of Channel power is directly proportional to the bias, but inversely proportional to $M$ and $N$. However, ${\mathit{Y}}_{DFT}^{\varphi ,\theta }$ can still be approximated as a Sparse Matrix, with most of the power concentrated on the elements of $\left(\lceil Md\cos \varphi /\lambda ,Nd\sin \varphi \cos \theta /\lambda \rfloor \right)$. Therefore, extracting the initial DOA information using the Peak Power positions of ${\mathit{Y}}_{DFT}^{\varphi ,\theta }$ is feasible [21].

Based on the above information, the initial DOA can be expressed as

$${\widehat{\varphi }}^{ini}={\cos }^{-1}\left({\displaystyle \frac{\lambda p^{\varphi ,ini}}{Md}}\right)$$

(18)

$${\widehat{\theta }}^{ini}={\cos }^{-1}\left({\displaystyle \frac{\lambda q^{\theta ,ini}}{Nd}}/\sqrt{1-{\left({\displaystyle \frac{\lambda p^{\varphi ,ini}}{Md}}\right)}^2}\right)$$

(19)

The $\left({\widehat{\varphi }}^{ini},{\widehat{\theta }}^{ini}\right)$ resolution derived from 2D-DFT is limited by half of the DFT interval. To improve the accuracy of DOA estimation, this mismatch is compensated by employing angular rotation [22].

The angular rotation of the original channel matrix is defined as

$${\mathit{Y}}_{DFT}^{\varphi ,\theta ro}={\mathrm{\Phi }}_M\left(\Delta \varphi \right)H{\mathrm{\Phi }}_N\left(\Delta \theta \right)$$

(20)

where ${\mathit{\Phi }}_M\left(\Delta \varphi \right)=diag\left\{1,e^{j\Delta \varphi },\cdots ,e^{j\left(M-1\right)\Delta \varphi }\right\}$ ${\mathit{\Phi }}_N\left(\Delta \theta \right)=diag\left\{1,e^{j\Delta \theta },\cdots ,e^{j\left(N-1\right)\Delta \theta }\right\}$, $\Delta \varphi \in \left[-\pi /M,\pi /M\right]$, and $\Delta \theta \in \left[-\pi /N,\pi /N\right]$ are angular rotation parameters.

$$\begin{array}{l}{\left[{\mathit{Y}}_{DFT}^{\varphi ,\theta ro}\right]}_{p^{\varphi }{q}^{\theta }}={\displaystyle \frac{1}{\sqrt{MN}}}a{e}^{-j{\displaystyle \frac{M-1}{2}}\left({\displaystyle \frac{2\pi }{M}}{p}^{\varphi }-{\displaystyle \frac{2\pi d}{\lambda }}\cos \varphi -\Delta \varphi \right)}{e}^{-j{\displaystyle \frac{N-1}{2}}\left({\displaystyle \frac{2\pi }{N}}{q}^{\theta }-{\displaystyle \frac{2\pi d}{\lambda }}\sin \varphi \cos \theta -\Delta \theta \right)}\\ \times {\displaystyle \frac{\sin \left(\pi p^{\varphi }-\frac{M\pi d\cos \varphi }{\lambda }-\frac{M\Delta \varphi }{2}\right)}{\sin \left(\left(\pi p^{\varphi }-\frac{M\pi d\cos \varphi }{\lambda }-\frac{M\Delta \varphi }{2}\right)/M\right)}}\cdot {\displaystyle \frac{\sin \left(\pi q^{\theta }-\frac{N\pi d\sin \varphi \cos \theta }{\lambda }-\frac{N\Delta \theta }{2}\right)}{\sin \left(\left(\pi q^{\theta }-\frac{N\pi d\sin \varphi \cos \theta }{\lambda }-\frac{N\Delta \theta }{2}\right)/N\right)}}\end{array}$$

(21)

After the angular rotation operation, the 2D-DFT of the rotated channel matrix ${\mathit{Y}}_{DFT}^{\varphi ,\theta ro}$ is calculated by Equation (21). It can be seen that ${\mathit{Y}}_{DFT}^{\varphi ,\theta ro}$ has non-zero elements, and when the rotation angle satisfies $\Delta \varphi =2\pi p^{\varphi }/M-2\pi d\cos \varphi /\lambda$, $\Delta \theta =2\pi q^{\theta }/N-2\pi d\sin \varphi \cos \theta /\lambda$, at this point, $\left(\Delta \varphi ,\Delta \theta \right)$ is the optimal angular offset.

Based on the derived optimal angular offset, the elevation angle and azimuth angle can be estimated as:

$$\widehat{\varphi }={\cos }^{-1}\left({\displaystyle \frac{\lambda p^{\varphi }}{Md}}-{\displaystyle \frac{\lambda \Delta \varphi }{2\pi d}}\right)$$

(22)

$$\widehat{\theta }={\cos }^{-1}\left(\left({\displaystyle \frac{\lambda q^{\theta }}{Nd}}-{\displaystyle \frac{\lambda \Delta \theta }{2\pi d}}\right)/\sqrt{1-{\left({\displaystyle \frac{\lambda p^{\varphi }}{Md}}-{\displaystyle \frac{\lambda \Delta \varphi }{2\pi d}}\right)}^2}\right)$$

(23)

$$\left(\Delta \varphi ,\Delta \theta \right)=\arg \underset{\Delta \varphi \in \left[-\frac{\pi }{M},\frac{\pi }{M}\right],\Delta \theta \in \left[-\frac{\pi }{N},\frac{\pi }{N}\right]}{\max }{‖f_{M p^{\varphi ,ini}}^H{\mathit{\Phi }}_M\left(\Delta \varphi \right){\mathit{Y}}^{\varphi ,\theta }{\mathit{\Phi }}_N\left(\Delta \theta \right)f_{N{q}^{\theta ,ini}}‖}^2$$

(24)

To obtain the optimal angular offset $\left(\Delta \varphi ,\Delta \theta \right)$, a two-dimensional search is performed within a certain range. When the $\left(p^{\varphi ,ini},q^{\theta ,ini}\right)$-th element in ${\mathit{Y}}_{DFT}^{\varphi ,\theta ro}$ is reduced to its highest form, the corresponding $\left(\Delta \varphi ,\Delta \theta \right)$ can be found, represented by Equation (24), where $f_{M{p}^{\varphi ,ini}}$ is the $p^{\varphi ,ini}$-th column of ${\mathit{F}}_M$, and $f_{N{q}^{\theta ,ini}}$ is the $q^{\theta ,ini}$-th column of ${\mathit{F}}_N$. Simulation results are shown in Figure 2. With the array configuration set as $N_R^x=N_R^z=128$ half-wavelength spacing array element, spatial spectrum analysis is performed for three independent targets with angular information $\left({30}^{\circ },{120}^{\circ }\right)$, $\left(-{20}^{\circ },{60}^{\circ }\right)$ and $\left({45}^{\circ },-{30}^{\circ }\right)$, respectively. Figure 2a,b show the spatial power spectrum distribution before and after two-dimensional discrete Fourier transform (2D-DFT) processing, where the colormap range is −40 dBm to 0 dBm, and the horizontal and vertical coordinates correspond to the normalized spatial frequency components:

$$v_x={\displaystyle \frac{d}{\lambda }}\sin \theta \cos \varphi$$

(25)

$$v_y={\displaystyle \frac{d}{\lambda }}\sin \theta \sin \varphi$$

(26)

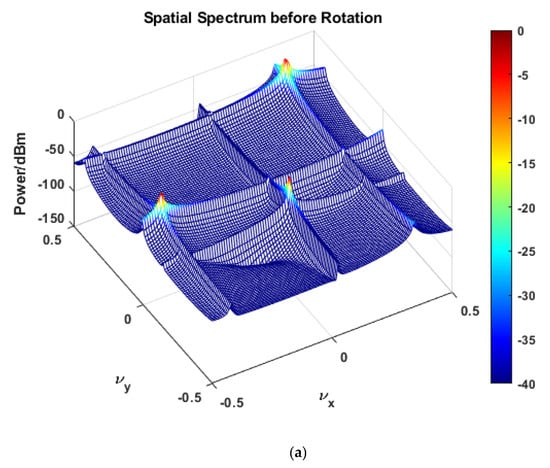
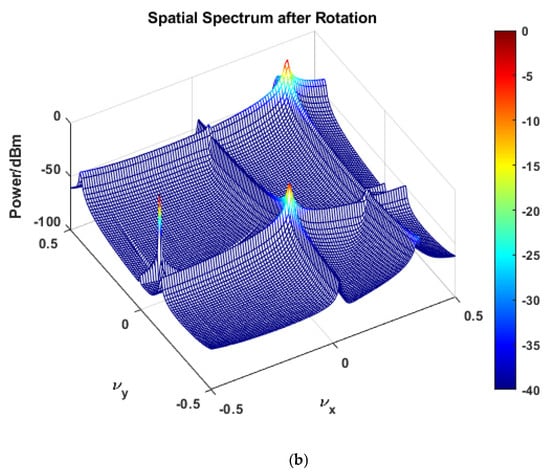
Figure 2. (a) Spatial spectrum before rotation and (b) Spatial spectrum after rotation.

As seen in the original spectrum in Figure 2a, the three targets exhibit main lobe broadening in the unprocessed spectrum. Figure 2b shows the optimized spectrum after introducing angular rotation compensation. By comparing and analyzing the changes in the spatial spectrum before and after rotation compensation, it can be concluded that the angular resolution is improved.

4. Target Tracking Algorithm for Occlusion Scenarios

4.1. Target Motion State Model and Measurement Model

The state variables of the UAV motion system are $\mathit{X}(t)=(x_k,y_k,z_k,v_{x,k},v_{y,k},v_{z,k})$, which consist of $\left(x_k,y_k,z_k\right)$, the position information of the UAV, and $\left(v_{x,k},v_{y,k},v_{z,k}\right)$, the velocity of the UAV along the three coordinate axis directions. Assuming the UAV undergoes constant velocity (CV) motion along all three coordinates axis, its system equation can be written as $X\left(t\right)=FX(t-1)+n_x(t)$. Where $\mathit{F}=\left[\begin{array}{cc}{I}_{3\times 3}& I_{3\times 3}\mathrm{T}\\ 0_{3\times 3}& I_{3\times 3}\end{array}\right]$ is the system transition matrix, and ${\mathit{n}}_x\left(t\right)$ is the process noise of the system.

The range, azimuth, and elevation information of the UAV can be estimated through the echo signal from the base station. Therefore, the observation variables of the UAV system are $\mathit{Z}(t)=({\tilde{r}}_k,{\tilde{\varphi }}_k,{\tilde{\theta }}_k)$, and the observation equation is $\mathit{Z}(t)=H\left(\mathit{X}\left(t\right)\right)+{\mathit{n}}_z(t)$.

Where the observation function H is a nonlinear function, with the form

$$H\left(\mathit{X}\left(t\right)\right)=\left[\begin{array}{c}\sqrt{x{\left(t\right)}^2+y{\left(t\right)}^2+z{\left(t\right)}^2}\\ \arctan {\displaystyle \frac{y\left(t\right)}{x\left(t\right)}}\\ \arctan {\displaystyle \frac{z\left(t\right)}{\sqrt{x{\left(t\right)}^2+y{\left(t\right)}^2}}}\end{array}\right]=\left[\begin{array}{c}{\tilde{r}}_k\left(t\right)\\ {\tilde{\varphi }}_k\left(t\right)\\ {\tilde{\theta }}_k\left(t\right)\end{array}\right]+{\mathit{n}}_z(t)$$

(27)

and ${\mathit{n}}_z\left(t\right)$ is the observation noise.

The choice of filtering algorithm was made based on the system characteristics. Due to the weak nonlinearity of the motion model and the Gaussian nature of the noise, as well as the need for real-time performance, the UKF was chosen, rather than the more advanced particle filter method.

4.2. Unscented Kalman Filter Algorithm Under Occlusion Effect

To address the nonlinear characteristics of the system, an unscented Kalman filter is employed for state estimation. Its core steps are as follows [23].

• Sigma Point Sampling. Based on the scaled unscented transform theory, $2n+1$ Sigma points $\left(n=6\right)$ are selected at state mean $\widehat{\mathit{x}}\left(t-1\right)$ and covariance $\mathit{P}\left(t-1\right)$ to cover the Gaussian characteristics of the state distribution.

  $$\left\{\begin{array}{l}{\mathit{X}}_0(t-1)=\widehat{x}\left(t-1\right)\hfill \\ {\mathit{X}}_i(t-1)=\widehat{x}\left(t-1\right)+\gamma {\sqrt{\mathit{P}\left(t-1\right)}}_i,i=1,\dots ,n\hfill \\ {\mathit{X}}_i(t-1)=\widehat{x}\left(t-1\right)-\gamma {\sqrt{\mathit{P}\left(t-1\right)}}_{i-n},i=n+1,\dots ,2n\hfill \end{array}\right.$$

  (28)

  where $\gamma =\sqrt{n+\lambda }$, $\lambda ={\alpha }^2(n+\mathit{\kappa })-n$ is the scaling factor, parameter $\alpha =0.01$ controls the distribution of sampling points, $\mathit{\kappa }=0$ is the secondary scaling factor, and $\beta =2$ is used to introduce prior information of the state distribution.
• Time Update. Sigma points are propagated through the nonlinear state transfer function: $X_i(t|t-1)=F\left(X_i(t-1)\right)+{\omega }_k, i=0,\dots ,2n$, where ${\mathit{\omega }}_k$ is process noise.
  The predicted state mean and covariance are calculated as follows.

  $$\widehat{\mathit{x}}(t|t-1)=\sum _{i=0}^{2n}{W}_i^{(m)}{\mathit{X}}_i(t|t-1)$$

  (29)

  $$\mathit{P}(t|t-1)=\sum _{i=0}^{2n}{W}_i^{(c)}\left[X_i(t|t-1)-\widehat{x}(t|t-1)\right]{\left[X_i(t|t-1)-\widehat{\mathit{x}}(t|t-1)\right]}^T+\mathit{Q}$$

  (30)

  where weighting coefficients $W_i^{(m)}$ and $W_i^{(c)}$ satisfy

  $$W_0^{(m)}=\lambda /(n+\lambda )$$

  (31)

  $$W_0^{(c)}=W_0^{(m)}+(1-{\alpha }^2+\beta )$$

  (32)

  $$W_i^{(m)}=W_i^{(c)}=1/[2(n+\lambda )], i=1,\dots ,2n$$

  (33)
• A high-precision Digital Surface Model (DSM), which encompasses elevation information of all surface features including buildings, bridges, and trees, can accurately represent the three-dimensional structures in urban environments, thereby providing a reliable environmental model for assessing potential signal blockages. After acquiring the DSM data, it is necessary to unify this data with the state vector of the UAV target into a Cartesian coordinate system originating from the base station. Once the coordinates are unified, geometric collision detection is performed to determine whether the electromagnetic wave propagation path from the base station to the UAV is obstructed by objects in the environment. To facilitate efficient geometric computation, buildings are first simplified into Axis-Aligned Bounding Boxes (AABB)—cuboids whose faces are parallel to the coordinate planes. A single building can be represented by one or multiple such cuboids, typically defined by its minimum corner point $\left(x_{min},y_{min},z_{min}\right)$ and maximum corner point $\left(x_{max},y_{max},z_{max}\right)$. The ray (signal path) is defined as the line connecting the antenna center of the base station $P_{BS}\left(x_b,y_b,z_b\right)$ to the real-time position of the UAV $P_{UAV}\left(x_k,y_k,z_k\right)$. The parametric equation of this ray is given by $R(t)=P_{BS}+t\cdot d$, where $d=P_{UAV}-P_{BS}$ is the direction vector from the base station to the UAV. The parameter $t=0$ represents the base station’s location and the parameter $t=1$ represents the UAV’s location. Subsequently, the intersection parameters between the ray and each face of the AABB are calculated. Taking the two faces perpendicular to the X-axis as an example, the intersection parameters are $t_{xmin}=(x_{min}-P_{BS,x})/d_x$ and $t_{xmax}=(x_{max}-P_{BS,x})/d_x$. Similar calculations are performed for the Y and Z axes, yielding $t_{ymin}$, $t_{ymax}$, $t_{zmin}$, $t_{zmax}$. For each dimension (e.g., X-dimension), the valid entry and exit face parameters are $t_{xenter}=min(t_{xmin},t_{xmax})$ and $t_{xexit}=max(t_{xmin},t_{xmax})$, respectively. The parameter interval during which the ray passes through the cuboid is the intersection of the intervals from all three dimensions: $t_{enter}=max(t_{xenter},t_{yenter},t_{zenter})$ and $t_{exit}=min(t_{xexit},t_{yexit},t_{zexit})$. The ray intersects the cuboid (indicating signal path occlusion) if and only if the following three conditions are simultaneously satisfied: $t_{enter}<t_{exit}$, $t_{exit}>0$, $t_{enter}<1$. Otherwise, no intersection occurs, indicating a Line-of-Sight (LoS) propagation path.
• Measurement Update. If no occlusion occurs, the Kalman gain $\mathit{K}\left(t\right)$ is calculated based on the observation variables input, and the state estimate and covariance are updated.

  $$\mathit{K}(t)=P_{xz}(t)P_{zz}^{-1}(t)$$

  (34)

  $$\widehat{\mathit{x}}(t)=\widehat{\mathit{x}}(t|t-1)+\mathit{K}(t)\left[\begin{array}{c}\mathit{z}(t)-\widehat{\mathit{z}}(t|t-1)\end{array}\right]$$

  (35)

  $$P(t)=P(t|t-1)-K(t)P_{zz}(t)K^T(t)$$

  (36)

  where ${\mathit{P}}_{xz}$ and ${\mathit{P}}_{zz}$ are the state-observation cross-covariance and observation auto-covariance Matrix, respectively.
• Short-term Occlusion. When the target trajectory experiences partial data loss due to short-term occlusion, the probability of UAV’s velocity and heading changing significantly within a short period is low. Cubic interpolation can fit a cubic polynomial using historical trajectory data to directly predict the trajectory during occlusion. For known discrete trajectory points $(x_i,y_i),i=0,1,\dots ,n$, cubic interpolation represents the path between adjacent points as a cubic polynomial function:

  $$S_k(t)=a_k{(t-t_k)}^3+b_k{(t-t_k)}^2+c_k(t-t_k)+d_k (t_k\le t\le t_{k+1})$$

  (37)

  where $t$ is the time step, and coefficients $a_k,b_k,c_k,d_k$ must satisfy the following constraints

  $$S_k(t_{k+1})=S_{k+1}(t_{k+1})=y_{k+1}$$

  (38)

  $$S_k^{\prime }(t_{k+1})=S_{k+1}^{\prime }(t_{k+1})$$

  (39)

  $$S_k^{″}(t_{k+1})=S_{k+1}^{″}(t_{k+1})$$

  (40)
  By solving the system of linear equations using a tridiagonal Matrix, the polynomial coefficients for each segment can be obtained. Subsequently, substituting the coefficients into the polynomial yields the missing target states.
• Long-term Occlusion. When the occlusion duration is long, the CV model iteratively predicts using UKF, leveraging the temporal correlation of motion states to maintain trajectory continuity in the absence of observations and continuously predict states. This assumes that UAV maintains its current velocity and heading: $x_{k+1}=x_k+v_k\cdot T$,$v_{k+1}=v_k$.

Figure 3 illustrates the basic workflow of the algorithm presented in this paper. After the system obtains the initial state through parameter estimation, UKF prediction is performed. Simultaneously, target occlusion is determined by analyzing the Line-of-Sight (LoS) visibility between the UAV and the base station. If no occlusion is detected, the system has observational input, and a UKF measurement update is performed, along with updating the system state and covariance. If the occlusion duration is short (e.g., less than 3 s), cubic interpolation is employed to maintain state continuity, and missing values are filled using historical observation data. Its error is smaller compared to using only the Unscented Kalman Filter (UKF) prediction process. However, because it assumes the trajectory remains smoothly continuous during occlusion, errors accumulate rapidly when the occlusion duration is long, and the trajectory prediction deviation significantly increases. Therefore, if the occlusion duration is long, the system switches to a Constant Velocity (CV) model for prediction, and the predicted state is finally output.

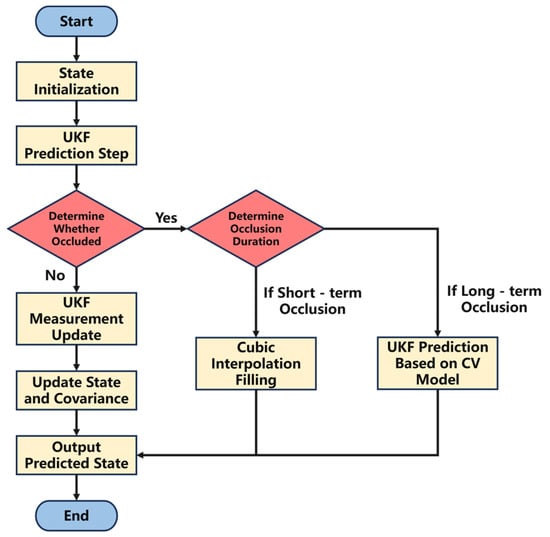
Figure 3. Tracking Algorithm Flowchart.

The algorithm presented in this paper can also be extended for use with more complex UAV motion models, such as the Uniform Acceleration (CA) model and the Constant Speed Rotating Vector (CSRV) model for helical turns, etc. By increasing the dimensionality of the system state variables, improving the system transition matrix, and keeping the measurements and measurement equations unchanged, the UAV motion state can still be tracked using Unscented Kalman Filter (UKF).

The convergence of UKF is guaranteed by the appropriateness of noise covariance matrices $Q$ and $R$. In this paper, $Q={\sigma }_v^2{I}_6$$\left({\sigma }_v=0.1 \mathrm{m}/\mathrm{s}\right)$ is set to characterize the uncertainty of UAV uniform motion, and $R=diag\left(1^2,1^2,1^2\right)$ is matched to the range measurement error. According to Lyapunov stability theory, when $Q$ and $R$ are positive definite, the mean square of the estimation error is bounded. For occlusion scenarios, although prediction errors accumulate, Kalman gain $\mathit{K}\left(t\right)$ can rapidly converge the errors after observation is restored.

5. Experimental Results and Simulation

In this section, simulation results will be provided to verify the effectiveness of the proposed method. The specific parameter settings are shown in Table 1.

Table 1. Specific Parameter Settings.

Parameter Name	Symbol	Value	Parameter Name	Symbol	Value
Carrier Frequency		$100 \mathrm{GHz}$	Number of OFDM Symbols	$N$	$32$
Subcarrier Spacing	$\Delta f$	$480 \mathrm{kHz}$	Number of $f_0$ TX Antennas (Hybrid Unit)	$N_H^x\times N_H^z$	$128\times 128$
Total Bandwidth	$B$	$30.72 \mathrm{MHz}$	Number of RX Antennas (Radar Unit)	$N_R^x\times N_R^z$	$128\times 128$
Number of Subcarriers	$M$	$64$	Antenna Spacing	$d$	$\lambda /2$

This paper considers an urban environment, as shown in Figure 4. To simplify the model, two cubes are used to simulate buildings. Through an occlusion discrimination mechanism, we can determine the periods of occlusion. As illustrated in Figure 5 the UAV is obstructed by the environment from 30 to 31 s and from 40 to 56 s, respectively. The aforementioned processing strategy is employed for trajectory estimation during these intervals.

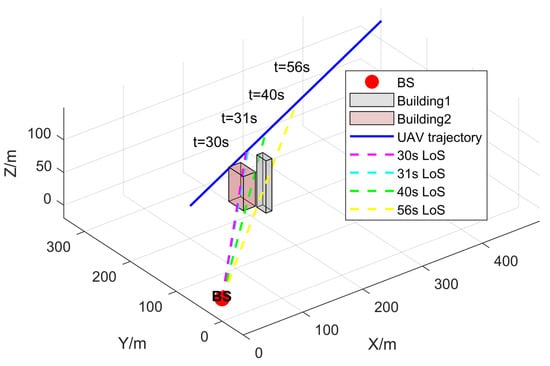
Figure 4. UAV Occlusion Detection and Tracking.

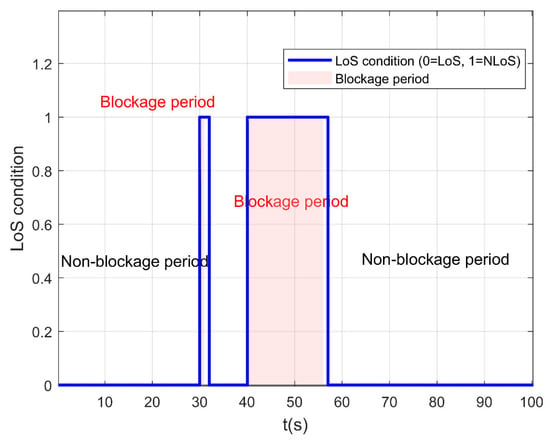
Figure 5. UAV-BS Line-of-Sight Analysis.

Figure 6 illustrates the 3D target tracking performance based on UKF and interpolation algorithm. The black solid line represents the target’s true motion trajectory, the red dashed line is the UKF estimated trajectory, the green solid line is the cubic interpolation estimated trajectory when the target experiences short-term occlusion, and the blue solid line is the estimated trajectory obtained solely using the UKF prediction process when the target experiences long-term occlusion. As can be seen from the figure, each segment of the estimated trajectory agrees well with the true trajectory, meeting the tracking requirements.

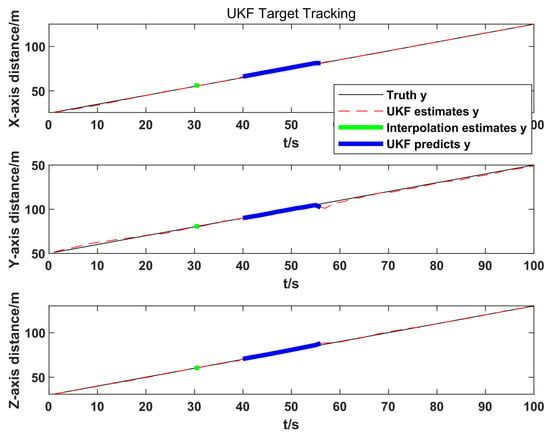
Figure 6. UKF Target Tracking.

Figure 7 and Table 2 show the estimation error of the proposed method in three dimensions. It can be seen that when the target is occluded, the error significantly increases and accumulates over time. This is because no new information is introduced to the Kalman filter by observations, which prevents the system from reducing the error through the update step, causing the error to diverge. When observations are re-introduced, the error quickly converges to within 1.5 m, verifying the feasibility of the proposed method. Additionally, it is observed that the average position error during short-term occlusion (vegetation) is significantly lower than that during long-term occlusion (buildings). This is because during short-term occlusion, the probability of target maneuver is low, and the trajectory smoothness assumption relied upon by cubic interpolation holds true. The larger errors observed during long-term occlusion indicate that the CV model has insufficient adaptability to UAV maneuvers. Maneuver models can be introduced in future research to improve tracking accuracy.

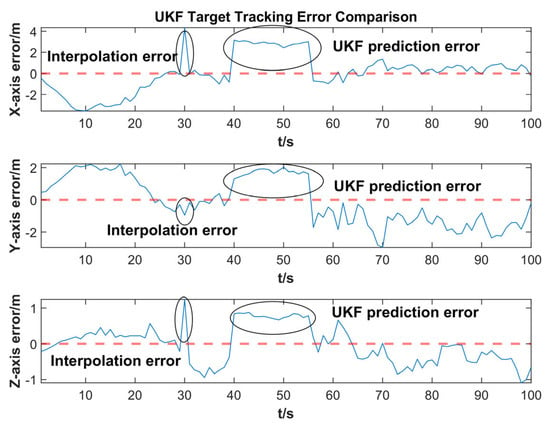
Figure 7. UKF Target Tracking Error. The blue solid line denotes the error variation curve, and the red dashed line denotes the zero-error reference line.

Table 2. Quantitative comparison of trajectory estimation errors under different blockage scenarios.

Blockage Type	Blockage Duration	Processing Method	X-Axis Average Error	Y-Axis Average Error	Z-Axis Average Error	Convergence Time
No blockage	-	UKF measurement update	0.82 m	0.79 m	0.68 m	-
Short-term blockage (vegetation)	31 s (1 s)	Cubic interpolation and UKF	1.25 m	2.18 m	1.05 m	$\le$1 s
Long-term blockage (building)	40–56 s (16 s)	CV model and UKF	2.87 m	3.79 m	1.85 m	$\le$5 s

Figure 8 and Figure 9 demonstrate the velocity estimation performance of the proposed method. Its variation trend is largely similar to that of distance estimation. When observations are missing, the error sharply increases; however, it quickly converges after reacquisition, eventually settling within 0.2 $\mathrm{m}/\mathrm{s}$. This further verifies the feasibility of the proposed method, enabling it to meet the tracking requirements for scenarios with occluded targets.

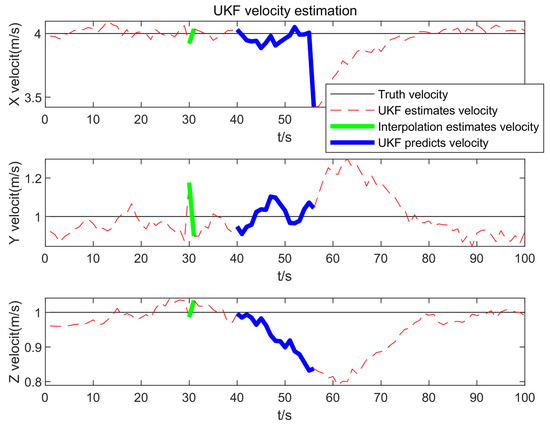
Figure 8. UKF velocity estimation.

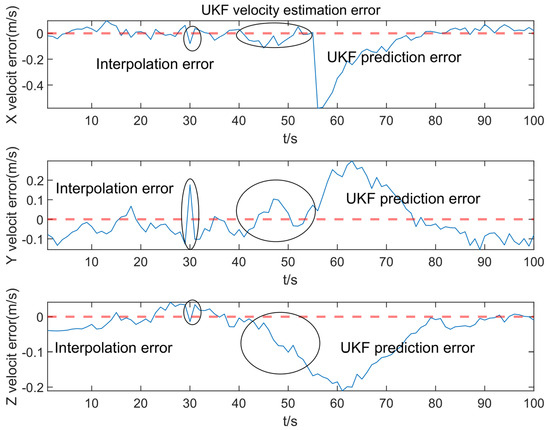
Figure 9. UKF velocity estimation error. The blue solid line denotes the error variation curve, and the red dashed line denotes the zero-error reference line.

6. Conclusions

Against the backdrop of the rapid development of the low-altitude economy, UAV target tracking technology faces significant challenges in complex occlusion environments. A 3D target tracking method based on a single-station integrated sensing and communication (ISAC) system is proposed in this paper. First, an ISAC base station transceiver system model is established. Then, using a parameter estimation method based on spatial rotation, the distance, azimuth, and elevation information of the UAV target relative to the ISAC base station is acquired as observation inputs for the Unscented Kalman Filter. During the tracking process, the Line-of-Sight (LoS) visibility between the UAV and the base station. is utilized to determine whether the target is occluded. According to different occlusion scenarios, trajectory prediction is performed using a cubic interpolation algorithm and the Unscented Kalman Filter prediction process, respectively. To verify the method’s performance, system simulation tests were conducted in a typical urban environment. Test results showed that the method exhibits excellent tracking capability in complex occluded environments. This study provides an effective solution for single-target tracking of low-altitude UAVs, serving as a crucial first step toward practical dense airspace applications.

Future work will focus on extending the research to dense multi-target scenarios, with in-depth investigation into key issues such as dynamic allocation of multi-beam resources and suppression of inter-target signal interference. The performance of the algorithm will be further validated through prototype experiments in real-world complex environments. Meanwhile, we will integrate the proposed occlusion handling framework with more advanced motion models (e.g., Constant Acceleration (CA) model, Constant Turn (CT) model) and conduct comprehensive benchmark tests on public UAV trajectory datasets to more thoroughly quantify its performance improvements across various maneuvering scenarios, ultimately providing comprehensive technical support for low-altitude security supervision. Additionally, this research still possesses certain limitations: its performance requires further validation in terms of real-world complex electromagnetic interference, the impact of adverse weather conditions on millimeter-wave signals, and the algorithm’s practical computational complexity. Future work will focus on optimizing the algorithm’s real-time performance, and integrating anti-interference and meteorological compensation models. A limitation of this study is its validation based on simulation data. Our future work will focus on implementing this algorithm on software-defined radio (SDR) platforms or similar ISAC testbeds to verify its performance with real-world data.