Abstract
The emergence of quantum computing poses significant threats to conventional public-key cryptography, driving the urgent need for quantum-resistant cryptographic solutions. While quantum key distribution addresses secure key exchange, its dependency on symmetric keys and point-to-point limitations present scalability constraints. Quantum Asymmetric Encryption (QAE) offers a promising alternative by leveraging quantum mechanical principles for security. This paper presents the first practical implementation of a QAE protocol on IBM Quantum devices, building upon the theoretical framework originally proposed by Yoon et al. We develop a generalized Grover Search Algorithm (GSA) framework that supports non-standard initial quantum states through novel diffusion operator designs, extending its applicability beyond idealized conditions. The complete QAE protocol, including key generation, encryption, and decryption stages, is translated into executable quantum circuits and evaluated on both IBM Quantum simulators and real quantum hardware. Experimental results demonstrate significant scalability challenges, with success probabilities deteriorating considerably for larger systems. The 2-qubit implementation achieves near-perfect accuracy (100% on the simulator, and 93.88% on the hardware), while performance degrades to 78.15% (simulator) and 45.84% (hardware) for 3 qubits, and declines critically to 48.08% (simulator) and 7.63% (hardware) for 4 qubits. This degradation is primarily attributed to noise and decoherence effects in current Noisy Intermediate-Scale Quantum (NISQ) devices, highlighting the limitations of single-iteration GSA approaches. Our findings underscore the critical need for enhanced hardware fidelity and algorithmic optimization to advance the practical viability of quantum cryptographic systems, providing valuable insights for bridging the gap between theoretical quantum cryptography and real-world implementations.
1. Introduction
The landscape of secure communication has been fundamentally transformed by the advent of quantum information science. The field was pioneered by quantum key distribution (QKD) protocols—most notably BB84 []—which exploit foundational quantum mechanical properties such as the no-cloning theorem and measurement-induced collapse to enable provably secure key exchange. While QKD has established itself as a cornerstone of quantum cryptography, its reliance on symmetric key schemes inherently requires secure channels for initial authentication. This dependence introduces scalability limitations, especially in multi-user and long-distance scenarios [].
1.1. Limitations of Current Quantum Cryptographic Approaches
To overcome these limitations, the concept of quantum public-key cryptography (QPKC) has garnered increasing attention. Unlike QKD, QPKC seeks to establish asymmetric cryptographic frameworks grounded in quantum principles rather than classical computational assumptions. Despite early progress, the field has developed at a slower pace due to challenges in realizing truly quantum-secure asymmetric schemes that eliminate classical dependencies.
1.2. Quantum Asymmetric Encryption: A Paradigm Shift
This quantum-mechanical foundation positions quantum coherence, measurement, and the uncertainty principle as active cryptographic resources. The quantum asymmetric encryption (QAE) protocol encodes information in coherent superposition states and achieves security through quantum interference and the exponentially large Hilbert space. The irreversible collapse of quantum states upon unauthorized measurement becomes a tamper-evident feature, while the no-cloning theorem guarantees protection against key replication attacks.
In parallel, recent developments in QPKC have expanded the theoretical and practical boundaries of quantum cryptography. Early schemes based on single-qubit rotations [,] and Bell-state configurations [,] provided foundational insights.
Recent research efforts [,] have explored the use of quantum search algorithms, particularly the Grover search algorithm (GSA) [], to design public-key infrastructures with intrinsic quantum security guarantees.
1.3. Grover Search Algorithm in Quantum Cryptography
Grover search algorithm (GSA) addresses the problem of identifying a specific target within an unsorted database containing entries []. It achieves a quadratic speedup relative to the best-known classical algorithms designed for the same task. The algorithm relies on the iterative evaluation of a function, often referred to as the “oracle,” which distinguishes the target from other database entries by assigning unique output values. While classical algorithms require oracle evaluations to locate the target, GSA reduces this complexity to , thus providing a significant computational advantage.
GSA has found significant applications in quantum cryptographic protocols such as quantum secret sharing [,], quantum encryption [,], quantum signature [], and quantum key agreement [,]. In these contexts, GSA is used to enhance efficiency by reducing the complexity of searching for specific keys or states, evaluating the strength and vulnerabilities of cryptographic methods, and testing the robustness of quantum systems against adversarial attacks.
1.4. Current Challenges and Research Gaps
Despite the theoretical promise of GSA-based quantum cryptographic schemes, several critical challenges remain unresolved. Existing GSA-based models often assume fixed initial quantum states, such as |++⟩, overlooking the performance and design implications that arise when initial states are randomly chosen from {|+⟩, |−⟩}. Moreover, while theoretical proposals have outlined the feasibility of such schemes, practical implementations on quantum hardware remain limited.
A notable advancement was proposed by Yoon et al. [], who introduced a quantum asymmetric encryption framework rooted in Grover’s amplitude amplification mechanism. In this design, public keys are generated via quantum initial states or quantum oracle constructions, while private keys correspond to Grover’s diffusion operations, forming a complete encryption–decryption cycle. Distinct from QKD, QAE enables message encryption without requiring pre-shared keys, thereby addressing scalability and multi-party communication more effectively.
1.5. Contributions and Objectives
This work makes several significant contributions to quantum public-key cryptography and its practical implementation by revisiting and enhancing Yoon et al.’s quantum asymmetric key cryptographic scheme []. This paper presents an extended version of our conference paper [], originally presented in 2025. In contrast to the conference version, the present manuscript substantially enriches the implementation details of the asymmetric quantum cryptographic protocol and provides a more comprehensive and systematic performance evaluation in both depth and breadth. Furthermore, the scope of the generalized Grover’s Search Algorithm (GSA) framework has been expanded to accommodate non-standard initial states, thereby extending its applicability beyond idealized conditions. Our contributions are fourfold:
- First, we report the initial successful implementation of an asymmetric quantum cryptographic protocol on IBM quantum computers, demonstrating the feasibility of QPKC in near-term quantum devices and establishing a crucial benchmark for practical quantum cryptographic applications.
- Second, we provide a comprehensive performance evaluation of single-iteration GSA across different qubit systems, systematically revealing scalability challenges that emerge as system size increases, and quantifying the trade-offs between theoretical quantum advantages and hardware-imposed limitations. This analysis encompasses both computational complexity assessments and experimental characterization of quantum decoherence effects on cryptographic protocol fidelity.
- Third, we introduce a generalized GSA framework specifically designed for non-standard initial states, incorporating novel diffusion operators that ensure consistent cryptographic performance across diverse quantum state preparations, thereby extending the applicability of Grover-based cryptographic schemes beyond idealized theoretical conditions.
- Fourth, this work fundamentally bridges the gap between theoretical cryptographic protocols and practical quantum implementations, providing both experimental validation and algorithmic innovations that advance the transition from proof-of-concept QPKC schemes to deployable quantum cryptographic systems. The comparative analysis of multiple quantum asymmetric encryption schemes offers a broader perspective on the unique value and positioning of the proposed approach within the current landscape of quantum cryptographic protocols. This comparative framework establishes clear performance benchmarks and identifies specific advantages of our implementation methodology over existing alternatives.
The remainder of this paper is structured as follows. Section 2 outlines the related works for quantum asymmetric encryption and the generalized GSA. Section 3 details the proposed encryption protocol, including the generalized GSA and its quantum circuit implementation. Section 4 presents experimental results and performance evaluations on IBM Quantum devices. Section 5 concludes with a discussion of findings and future research directions.
2. Preliminary
2.1. Related Works
The rapid advancement of quantum computing has fundamentally challenged the security foundations of conventional public-key systems, which rely primarily on computational complexity assumptions that are vulnerable to quantum algorithms, such as Shor’s algorithm []. This quantum threat has catalyzed intensive research into QPKC schemes that derive provable security from fundamental quantum mechanical principles rather than computational hardness assumptions.
Early pioneering work by Nikolopoulos [] introduced a QPKC scheme based on single-qubit rotations, featuring quantum states as public keys and classical bit strings as private keys. This seminal proposal demonstrated the feasibility of quantum-classical hybrid cryptographic architectures. Building upon this foundation, Zheng et al. [] later proposed an alternative QPKC construction that also employs single-qubit rotations as the fundamental encoding mechanism. Their scheme further validates the viability of such lightweight quantum operations in public-key infrastructure, reinforcing the relevance of single-qubit-based designs for scalable and implementable QPKC systems. However, subsequent analysis by Gao et al. [] revealed critical vulnerabilities to quantum state estimation attacks, where adversaries could exploit statistical inference methods to reconstruct private keys through repeated measurements of public quantum states.
Building upon these insights, Gao et al. proposed an innovative QPKC framework utilizing Bell states as both public and private keys, where both key components exist as quantum states in identical maximally mixed states . This approach represents a paradigmatic shift toward symmetric quantum keys within asymmetric cryptographic frameworks, effectively realizing quantum analogs of symmetric key concepts while maintaining the structural advantages of public-key cryptography. The security of this scheme fundamentally relies on the non-orthogonality of quantum states and the impossibility of distinguishing non-orthogonal quantum states with certainty, as governed by quantum measurement theory. Subsequently, Wu et al. [] extended the Bell state-based approach, providing rigorous security proofs for both key distribution and message transmission.
In parallel, researchers have investigated the use of GSA within QPKC schemes [,]. By leveraging amplitude amplification, these models aim to construct public keys that can encode hard-to-invert search spaces, thereby increasing resistance against both classical and quantum adversaries.
Luo and Liu [] proposed a QAE scheme grounded in the principles of one-way quantum functions and GSA. The security of the scheme is fundamentally supported by the quantum no-cloning theorem and the construction of quantum trapdoor one-way functions. The protocol architecture consists of a classical private key—comprising a Boolean function f and a random string r—and a quantum public key composed of non-orthogonal and unknown quantum states. A key feature of the design is the use of randomized logarithmic encoding, which allows a single private key to correspond to an exponential number of distinct public keys. Encryption is performed by applying unitary transformations to the receiver’s quantum public key states based on the message content. Decryption relies on Grover’s diffusion operator, using the private key to retrieve the original message. The robustness of the scheme depends critically on the reliable construction of quantum trapdoor functions. Additionally, it may be susceptible to quantum state estimation attacks if an adversary obtains a sufficiently large number of identical public key states. These aspects highlight the need for further investigation into the computational assumptions and physical security limits of such QAE constructions.
Yoon et al. [] proposed another QAE scheme, grounded in GSA, which employs amplitude amplification as its core cryptographic mechanism. In this protocol, both the public and private keys are represented as quantum operators derived from Grover’s operation. Specifically, their scheme achieves a quantum bit efficiency of 1.0, highlighting its potential viability for secure and efficient quantum public-key infrastructures.
Taken together, the evolution of QPKC demonstrates a trajectory from early proof-of-concept designs toward increasingly sophisticated models that aim to balance theoretical security with hardware feasibility. However, no existing protocol fully addresses the need for a scalable, asymmetric quantum cryptographic scheme.
2.2. Grover Search Algorithm
GSA, presented in 1996 [], is a cornerstone of quantum computing, offering a quadratic speedup over classical search algorithms for unstructured databases. It operates on a quantum register of -qubits, which represent possible states. The algorithm efficiently identifies a target state by iteratively applying two key operations: the Oracle and the Diffusion operator .
In the scenario where quantum search operates across the entire computational space , the algorithm commences with a state preparation phase that establishes an equal superposition across all possible -qubit configurations. This uniform distribution is realized through the application of Hadamard transformations to each qubit, resulting in the initial quantum state:
where for all , where is the Hadamard gate applied to each qubit, ⊗ means tensor, i.e., is equivalent to with terms.
The core mechanism of the Grover search protocol relies on an oracle function that performs conditional phase manipulation based on the target criteria. For a designated set of marked states , the oracle implements a selective sign inversion operation:
This oracle operation effectively distinguishes between solution states (marked elements) and non-solution states within the search space, applying a negative phase factor exclusively to the target configurations while preserving the amplitudes of all other states. The oracle’s ability to selectively modify phase relationships forms the foundation for the subsequent amplitude amplification process that characterizes GSA.
The amplitude amplification process in GSA concludes with the application of a diffusion operator , which can be conceptualized as a geometric reflection operation performed around the reference state . This operator is mathematically expressed as:
where is the identity matrix. This operation reflects the quantum state in terms of the average amplitude, thereby increasing the probability of the target state being measured. The diffusion operator serves as a crucial component in the iterative amplitude enhancement mechanism, systematically rotating the quantum state vector within the two-dimensional subspace defined by the superposition of marked and unmarked states.
However, it is worthwhile to note that the initial state represents the uniform superposition state over all possible computational basis states. The quantum search algorithm necessitates the sequential application of the composite operator
which incorporates both oracle and diffusion operations. This iterative process systematically enhances the probability amplitudes of target states while simultaneously diminishing those associated with non-target configurations.
After iterations of applying , the quantum state is measured, yielding the target state with high probability.
In 2020, Sadana [] addresses critical practical limitations in the implementation of the Grover quantum search algorithm for multi-target scenarios, presenting a comprehensive framework that significantly advances the field’s understanding of optimal quantum search strategies. The primary contribution lies in the development of a generalized quantum circuit construction scheme for the n-qubit Grover search algorithm GSA (, ), capable of handling arbitrary numbers of target states (1 ≤ ≤ ) with explicit implementations of both oracle functions and diffusion operators. More crucially, the work establishes a rigorous numerical procedure for determining optimal iteration counts that ensures achievement of preset success probability thresholds, thereby overcoming the inadequacies of the conventional formula in multi-target search contexts. The research demonstrates that when is not sufficiently small—particularly prevalent in multi-target search scenarios—the traditional iteration formula fails to guarantee the requisite success probability, potentially compromising algorithm efficacy. Furthermore, the study provides theoretical proof of the existence of upper bounds on achievable success probabilities for given and values, with the critical finding that the Grover search algorithm exhibits complete failure to amplify target states when . These theoretical insights are substantiated through comprehensive experimental validation using the IBM Qiskit platform, demonstrating the practical applicability of the proposed methodology across various qubit configurations and target multiplicities. The presented framework offers essential guidance for quantum algorithm deployment in finite-scale databases and multi-target environments, ensuring both effectiveness and reliability in practical quantum computing implementations.
3. The Proposed Modified Scheme with Quantum Circuit Implementation
The transition from theoretical quantum algorithms to practical quantum computing implementations necessitates careful consideration of circuit design, gate complexity, and hardware constraints. While the GSA and its application to quantum cryptographic protocols have been extensively studied from algorithmic perspectives, their efficient realization on near-term quantum devices remains a significant challenge. The preceding section utilized a mechanistic and mathematical framework to describe quantum search algorithms, while this section transitions to a quantum gate and quantum circuit model representation to facilitate practical implementation on quantum hardware platforms. This shift from abstract mathematical formulations to concrete circuit architectures enables the direct translation of theoretical quantum algorithms into executable quantum programs suitable for current quantum computing systems. We present a comprehensive framework for implementing a quantum asymmetric encryption scheme through generalized quantum circuits of GSA.
The following subsections detail two key components of our implementation framework. First, we present a generalized quantum circuit architecture for GSA that provides flexibility in oracle design and supports arbitrary search space configurations. This generalized approach enables efficient adaptation to different problem domains. Second, we demonstrate the practical application of our framework through a detailed quantum circuit implementation of Yoon et al.’s quantum asymmetric encryption protocol [], showcasing how theoretical advances can be translated into executable quantum circuits.
3.1. Generalized Quantum Circuit Architecture for Grover Search Algorithm
3.1.1. Theoretical Foundation and Circuit Design Principles
Building upon the foundational work presented in [], we propose an enhanced generalized quantum circuit framework for GSA that addresses the limitations of conventional implementations. The conventional approach restricts the initial state preparation to the uniform superposition state , which, while theoretically optimal for standard search problems, lacks the flexibility required for specialized applications such as quantum cryptography protocols.
Our generalized framework introduces parametric control over the initial state preparation, enabling the algorithm to commence from arbitrary computational basis states selected from the set . This enhancement significantly expands the applicability of GSA to domains requiring non-uniform initial distributions or specific quantum state preparations.
3.1.2. Enhanced Initial State Preparation Circuit
The initial state preparation phase represents a critical component that determines the subsequent algorithmic behavior. In our generalized implementation, the quantum state is prepared through a controlled Hadamard transformation process:
where for all , and denotes the tensor product of n Hadamard gates.
The enhanced circuit architecture, illustrated in Figure 1, incorporates conditional X-gate operations that enable selective state preparation. The components shown in black represent the original design from [], while the X-gates shown in red introduce our proposed modifications. These conditional X-gates are applied when , allowing precise control over the initial quantum state configuration.
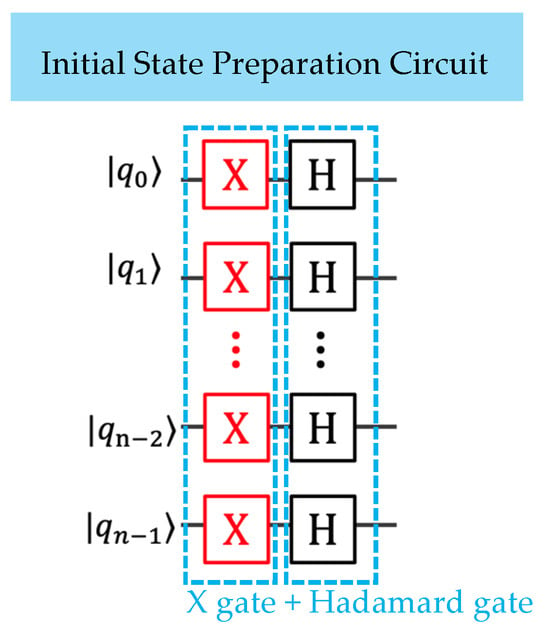
Figure 1.
The quantum circuit for generating the n-qubit Grover’s initial state in the proposed modified scheme. Red X-gates represent classically configured operations, which are statically included only when the corresponding classical bit . This generalized GSA initial state preparation subsequently serves as Alice’s initial-state configuration circuit for public-key generation.
The generalized initial state can be expressed as:
where are complex amplitudes satisfying the normalization condition . The specific values depend on the chosen basis states from .
The enhanced initial state preparation requires Hadamard gates and conditional X-gates (where represents the number of bits 1 and ≤ ), resulting in a total quantum gate count of + . The circuit implementation maintains circuit depth through parallel gate execution and requires no additional ancilla qubits, making it highly resource-efficient for practical quantum implementations.
3.1.3. Oracle Operation Implementation
The oracle operation serves as the problem-specific component that identifies target states through amplitude sign inversion. Our implementation provides a systematic construction method for arbitrary target states.
- General Oracle Construction:
For a target state , where , the oracle is defined as:
- Circuit Implementation Strategy:
A general method to achieve this is illustrated in Figure 2. The oracle construction follows a three-stage process:
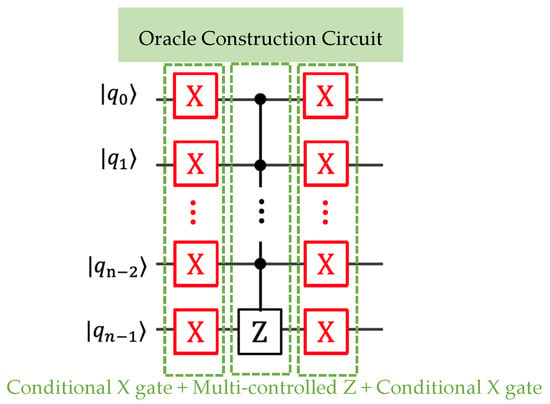
Figure 2.
The general approach for constructing a quantum circuit to implement the oracle for a specific target state. Red X-gates denote classically determined operations that are statically applied when the corresponding target bit , rather than quantum-controlled gates. This generalized oracle construction is subsequently employed as the oracle operator circuit for public-key or message encryption.
Stage 1: Conditional State Transformation. The initial bank of X gates operates under the conditional logic “if ”, where represents the i-th bit of the target state. This stage performs selective bit-flipping operations to transform the computational basis states. Specifically, X gates are applied to qubits where the target state contains a ‘0’ bit.
Stage 2: Mult-control Phase Flip. The central Z gate implements a multi-controlled phase flip operation, functioning as an (n − 1)-controlled-Z gate. This gate applies a π-phase shift exclusively when all control qubits are in the |1⟩ state. Following the conditional preparation in Stage 1, this configuration ensures that only the desired target state experiences the requisite phase inversion.
Stage 3: Conditional State Restoration. The final stage applies identical conditional X operations as Stage 1, restoring the original computational basis representation while preserving the acquired phase information on the target state.
This oracle design implements a direct phase marking mechanism that does not require ancilla qubits, leveraging the intrinsic phase manipulation capabilities of multi-controlled gates. The symmetric application of conditional X gates ensures that only the target state satisfies the condition for phase acquisition, while all other basis states remain unaffected.
The multi-controlled Z gate serves as the phase oracle’s core component, directly implementing the unitary transformation:
where if and only if corresponds to the target state , and otherwise.
Unlike ancilla-assisted implementations that rely on phase kickback from auxiliary qubits, this construction directly applies the phase shift to the target state through the multi-controlled Z operation. The conditional X gates transform the target identification problem into an all-ones detection problem, enabling the multi-controlled Z gate to directly recognize and mark the target state with a π-phase shift.
For target states, the composite oracle is constructed as follows:
where each targets a specific marked state. This composite oracle construction preserves the quadratic speedup of GSA provided that the number of marked items M remains much smaller than the total state space size N.
The single-target oracle requires X-gates and one multi-controlled Z-gate (where represents the number of zero bits in the target), while the multi-target oracle scales linearly with the number of targets. The circuit implementation exhibits circuit depth due to the multi-controlled Z-gate decomposition, where represents the number of qubits in the system.
3.1.4. Generalized Diffusion Operation
The diffusion operator represents the most significant enhancement in our generalized framework. Unlike conventional implementations that assume , our approach accommodates arbitrary initial states.
The generalized diffusion operator is defined as:
where represents the actual initial state rather than being constrained to the uniform superposition state . This generalization extends the classical Grover diffusion operator beyond the traditional assumption of equal amplitude initialization.
The operator performs a reflection on the initial state when applied to the post-oracle state , implementing the transformation:
where represents the result state of applying the oracle operation to , i.e., . This operation implements a geometric reflection within a two-dimensional subspace, where the initial state serves as the reflection axis and the post-oracle state represents the vector being reflected.
This formulation enables amplitude amplification for arbitrary initial state preparations, accommodating scenarios where the initial quantum state exhibits non-uniform amplitude distributions or specific structural properties relevant to the search problem.
Figure 3 illustrates two equivalent implementations of the n-qubit generalized diffusion operator, demonstrating systematic gate-reduced strategies for quantum hardware deployment. The proposed methodology extends conventional diffusion operator designs through conditional gate placement and circuit depth reduction techniques.
- (a)
- Modified Version: The circuit architecture in Figure 3a presents an enhanced version of the classical diffusion operator framework originally proposed by Sadana [], incorporating adaptive gate placement mechanisms based on initial state configurations. The modification principle implements a conditional X-gate insertion strategy, where additional X-gates are systematically positioned in the quantum circuit whenever the condition is satisfied for qubit .
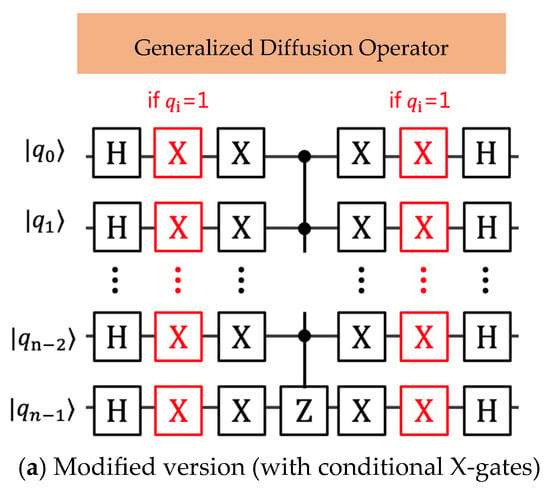
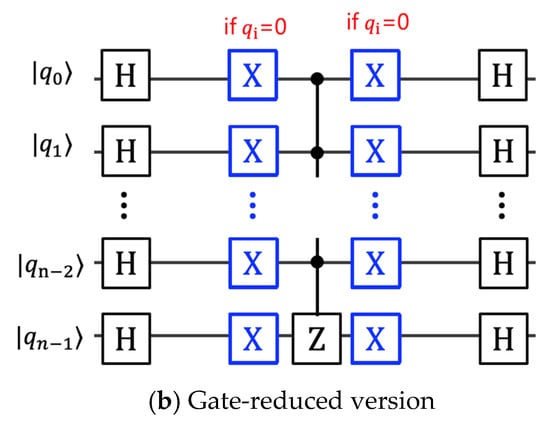
Figure 3.
The quantum circuit implementing the n-qubit Grover’s diffusion operator with a global π-phase shift: (a) the modified version and (b) an equivalent version with reduced quantum gates, i.e., the generalized GSA diffusion operator, subsequently utilized as Alice’s private-key (message decryption) diffusion operator circuit.
The circuit modification follows a structured approach: for each qubit where the initial state coefficient satisfies , an X-gate is appended both preceding and following the controlled multi-qubit Z-gate operation. This symmetric placement ensures proper state preparation and restoration while maintaining the fundamental diffusion operation properties.
The remaining structural elements of the quantum circuit, including the essential Hadamard H-gates for superposition generation and the controlled multi-qubit Z-gate for phase inversion, are preserved in accordance with the original architectural design from reference []. This preservation strategy ensures backward compatibility while enabling enhanced functionality through the conditional gate insertion mechanism.
- (b)
- Quantum Gate Reduction Version: Figure 3b demonstrates a quantum gate-reduced version of the generalized diffusion operator, achieved through strategic gate minimization and resource optimization techniques. This implementation introduces a modified gate placement design that minimizes the total number of quantum gates while preserving the mathematical equivalence of the diffusion operation.
The gate reduction process systematically identifies redundant gate operations and implements circuit simplification techniques to reduce the overall quantum gate count. The blue-highlighted X-gates represent the minimal set of conditional operations required to achieve equivalent functionality to the extended circuit in Figure 3a.
The circuit depth reduction demonstrated in Figure 3b provides significant advantages for near-term quantum device implementations, where gate fidelity and coherence time constraints impose practical limitations on circuit complexity. The gate-reduced design maintains full mathematical equivalence while reducing susceptibility to quantum decoherence and gate error accumulation.
The generalized diffusion operation maintains the same asymptotic complexity as the standard implementation, requiring gates plus additional X-gates for non-uniform initial states. The circuit depth remains due to the multi-controlled Z-gate decomposition, ensuring consistent performance scaling across different initial state configurations.
3.2. Quantum Circuit Implementation for Yoon Et Al.’S Quantum Asymmetric Encryption
3.2.1. Cryptographic Protocol Overview
The quantum asymmetric cryptographic system introduced by Yoon et al. [] represents a paradigm shift in quantum cryptography, leveraging the computational properties of GSA to establish secure communication channels. Our implementation of QAE with generalized GSA provides the first complete quantum circuit realization of this protocol, addressing both theoretical completeness and practical feasibility.
- System Architecture:
The protocol operates within a three-party framework:
- Alice: Message originator with key generation capabilities;
- Bob: Message recipient with encryption capabilities;
- Quantum Key Center (QKC): Trusted intermediary for key distribution.
- Security Foundation:
The cryptographic security relies on the quantum no-cloning theorem and the computational complexity of inverting Grover’s oracle operations without knowledge of the private key.
3.2.2. Key Generation and Distribution Protocol
- Enhanced Key Generation Process:
Alice’s key generation process has been enhanced to provide stronger security guarantees:
Step 1: Initial State Configuration. Alice selects the initial state from the expanded basis set:
This selection provides possible initial configurations, significantly expanding the key space compared to conventional approaches.
Step 2: Private Key Definition. The private key is defined as the generalized diffusion operator:
Step 3: Public Key Generation. The public key is probabilistically determined:
where is treated as a Grover’s Oracle operation based on Alice’s secret seed, denoted as of qubit size , i.e., . Alice transmits her public key to the QKC through a secure quantum channel.
Step 4: Public Key Distribution. The QKC distributes to Bob.
3.2.3. Encryption Protocol Implementation
- Enhanced Encryption Process:
Bob’s encryption process utilizes the generalized Grover framework:
Step 5: Message Encoding. Bob encodes his plaintext message into a quantum oracle:
Step 6: Ciphertext Generation. The ciphertext is generated through oracle composition:
3.2.4. Decryption Protocol and Circuit Realization
- Enhanced Decryption Process:
Alice’s decryption leverages the generalized diffusion operator:
Step 7: Diffusion Operation Application. Alice applies her private key to the received ciphertext:
Step 8: Message Extraction. The decoded quantum state is measured to extract the classical plaintext .
4. Experimental Results and Analysis
4.1. Simulation Environment
4.1.1. Quantum Computing Platform Configuration
This section presents a comprehensive experimental evaluation of the quantum asymmetric encryption scheme based on the generalized GSA for n-qubit systems. The experimental framework encompasses both theoretical validation through quantum circuit simulation and practical assessment on contemporary quantum hardware platforms.
The quantum circuit implementation was developed and executed using the IBM Quantum Platform, specifically leveraging IBM Qiskit (version 2.1.1) [] as the primary software development kit. Qiskit provides a Python-based quantum computing framework that facilitates seamless integration between quantum algorithm development and hardware deployment. The platform offers comprehensive access to IBM’s quantum computing ecosystem, including both local quantum circuit simulators and remote quantum processors.
4.1.2. Hardware and Simulation Infrastructure
The experimental infrastructure incorporates multiple quantum computing backends to ensure comprehensive performance evaluation. The experimental evaluation employed a comprehensive dual-platform approach encompassing both simulation and physical quantum hardware environments to assess the proposed quantum asymmetric encryption scheme’s performance characteristics. The simulation environment utilized the IBM Qasm Simulator to provide ideal qubit behavior modeling without noise effects, incorporating quantum hardware emulation with configurable coupling map emulation for IBM quantum processors and logical-to-physical qubit mapping through automated qubit assignment that accommodates arbitrary naming conventions. For physical quantum hardware validation, the study deployed the IBM Kyiv Quantum Processor, a 127-qubit superconducting quantum system, which features advanced quantum hardware with enhanced connectivity, enabling real-time quantum execution and direct deployment capabilities for comprehensive practical performance assessment under authentic quantum computing conditions.
The experimental methodology employs a comparative analysis approach, evaluating algorithm performance across different qubit configurations (n = 2, 3, 4) under both ideal simulation conditions and realistic hardware constraints. This dual-platform approach enables systematic characterization of the quantum asymmetric encryption protocol’s scalability and practical feasibility.
4.1.3. Measurement and Statistical Analysis Framework
All experimental trials were conducted with 10,000 measurement shots to ensure statistical significance and reliable accuracy assessment through a comprehensive measurement protocol that incorporates statistical sampling via 10,000 independent measurements per trial, accuracy calculation based on success rate for correct message recovery, and performance metrics including execution time, standard deviation, and success probability. The experimental framework further employed comparative analysis between simulator and hardware performance evaluation to quantify the impact of real quantum device limitations on cryptographic fidelity, thereby providing a robust statistical foundation for assessing the practical viability of the proposed quantum asymmetric encryption scheme across different implementation platforms.
4.2. Quantum Asymmetric Encryption Protocol Implementation
4.2.1. Protocol Execution Framework
The quantum asymmetric encryption protocol follows a one-round communication scheme between Alice and Bob, implementing a single iteration of the Grover oracle-and-diffusion process. This approach provides computational efficiency while maintaining the fundamental security properties of the quantum cryptographic system.
4.2.2. Key Generation and Distribution Phase
- Alice’s Key Generation Process:
Alice initiates the protocol by randomly selecting the starting bitstring ‘011’ to generate the initial quantum state , as illustrated in Figure 4a. This state preparation establishes the cryptographic foundation for the asymmetric encryption scheme.
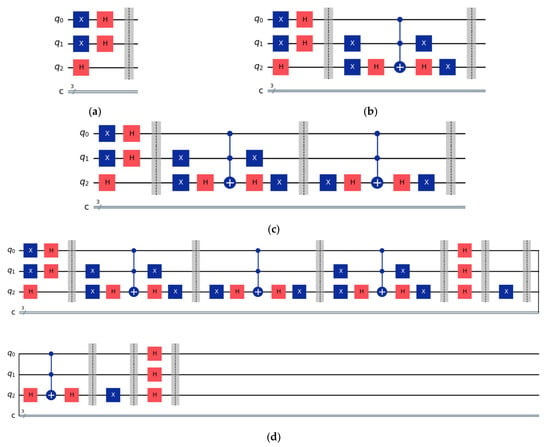
Figure 4.
Construction of the quantum circuit: (a) the initial state, (b) the public key combining the initial state and Alice’s oracle operation, (c) applying Bob’s oracle operation, and (d) the complete quantum circuit after applying Alice’s diffusion operation.
The public key generation process involves a probabilistic oracle application, where Alice computes her public key by applying the oracle operation . The oracle is constructed based on Alice’s secret seed ‘001’, ensuring cryptographic security through the computational difficulty of inverting the Grover oracle operation without knowledge of the private key, as demonstrated in Figure 4b.
- Bob’s Message Encoding:
During the encryption phase, Bob encodes his plaintext message ‘011’ as a Grover search target, implementing the quantum oracle corresponding to the message state. The encryption process applies Bob’s oracle to Alice’s public key , generating the ciphertext , as illustrated in Figure 4c.
- Ciphertext Generation:
The quantum ciphertext represents a superposition state that encodes both the message information and the cryptographic key material. The ciphertext is transmitted to Alice through a public quantum channel, maintaining security through the quantum mechanical properties of the encoded state.
4.2.3. Decryption Phase and Message Recovery
- Alice’s Decryption Process:
Alice performs message recovery using her private key, consisting of the starting bitstring ‘011’ and secret seed ‘001’. The decryption operation applies the generalized Grover diffusion operator: , where represents the generalized diffusion operator corresponding to Alice’s initial state.
- Message Extraction:
The decoded quantum state undergoes a quantum measurement to extract the classical plaintext ‘011’. The complete quantum circuit implementation for the entire protocol is presented in Figure 4d, demonstrating an integrated approach combining key generation, encryption, and decryption operations.
4.3. Experimental Results and Performance Analysis
4.3.1. Simulation Results Under Ideal Conditions
- Performance Metrics: The experimental evaluation was conducted with 10,000 measurement shots to ensure statistical reliability, as demonstrated in Figure 5. Figure 5a presents results obtained using the IBM quantum simulator under ideal conditions, while Figure 5b illustrates performance on real quantum hardware.
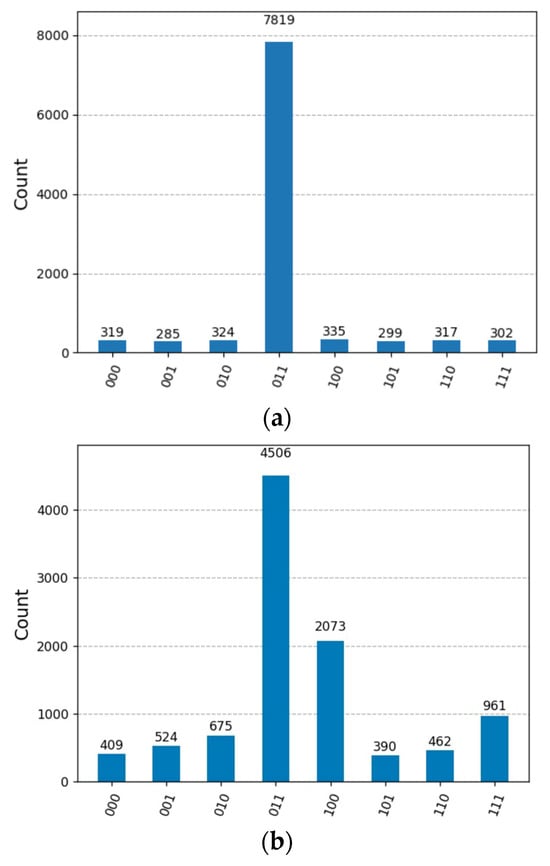 Figure 5. Comparison of results: (a) simulation using an IBM quantum simulator and (b) execution on a real IBM quantum computer.
Figure 5. Comparison of results: (a) simulation using an IBM quantum simulator and (b) execution on a real IBM quantum computer. - Scalability Analysis: The one-round quantum asymmetric encryption protocol demonstrates varying performance characteristics across different qubit configurations. For the 2-qubit implementation, the single Grover iteration maintains exceptional accuracy of 100%, as detailed in Table 1. However, systematic performance degradation occurs as the problem size increases.
 Table 1. Trials of QAE on Simulator were conducted with 10,000 shots for the 2/3/4-qubit Generalized GSA.
Table 1. Trials of QAE on Simulator were conducted with 10,000 shots for the 2/3/4-qubit Generalized GSA. - Accuracy Degradation: The experimental results demonstrate severe accuracy degradation as system size increases, with the 2-qubit system achieving perfect 100% accuracy (σ = 0.00), while the 3-qubit system exhibits a significant decline to 78.15% accuracy (σ = 0.35), and the 4-qubit system further deteriorates to 48.08% accuracy (σ = 0.51). This substantial accuracy reduction at higher qubit levels indicates fundamental limitations in the proposed single-iteration approach for quantum asymmetric encryption applications involving 4 qubits or more, suggesting that the quantum search algorithm’s effectiveness diminishes critically with increasing system complexity, thereby constraining the practical scalability of the encryption scheme.
4.3.2. Real Quantum Hardware Performance
- Hardware Implementation Results: Real quantum hardware deployment reveals additional performance challenges due to noise, decoherence, and gate error effects inherent in current quantum processors, as demonstrated by experimental results from the IBM 127-qubit Kyiv quantum processor, which show significant performance degradation compared to ideal simulation conditions. The hardware versus simulation comparison exhibits dramatic accuracy losses across all system sizes, with the 2-qubit system declining from 100% simulation accuracy to 93.88% on hardware, the 3-qubit system dropping from 78.15% to 45.84%, and the 4-qubit system experiencing a catastrophic reduction from 48.08% simulation accuracy to merely 7.63% on actual quantum hardware, as detailed in Table 2. These results underscore the critical impact of physical quantum device limitations on cryptographic fidelity, indicating that the gap between theoretical performance and practical implementation widens substantially with increasing system complexity, thereby highlighting the significant challenges facing near-term quantum cryptographic applications. The performance gap between simulation and hardware arises mainly from the multi-controlled Z gate (MCZ) rather than generic noise effects. Due to its high decomposition cost, central role in oracle and diffusion operators, and sensitivity to noise, the MCZ gate becomes the dominant source of errors, directly limiting the accuracy of encryption and decryption in current NISQ devices.
 Table 2. Trials of QAE were conducted with 10000 shots for the 2/3/4-qubit Generalized GSA on the IBM127-qubit Kyiv quantum processor.
Table 2. Trials of QAE were conducted with 10000 shots for the 2/3/4-qubit Generalized GSA on the IBM127-qubit Kyiv quantum processor. - Execution Time Analysis: Real quantum hardware exhibits significantly increased execution times due to multiple operational overhead factors, including queue processing for hardware scheduling and resource allocation, calibration overhead from real-time system calibration requirements, and communication latency arising from classical-quantum interface delays. The temporal performance impact is substantial, with average execution times ranging from 18.26 s for 2-qubit systems to 20.18 s for 4-qubit systems on quantum hardware, representing an increase by approximately a factor of 260 increase compared to the 0.07 s execution time observed in simulator-based implementations. This dramatic temporal overhead, combined with the previously demonstrated accuracy degradation, further compounds the practical limitations of current quantum hardware for cryptographic applications, highlighting the significant gap between theoretical quantum advantage and real-world implementation feasibility.
4.4. Practical Feasibility Assessment
The comprehensive evaluation of the proposed quantum asymmetric encryption scheme demonstrates significant practical limitations that constrain its immediate applicability. The experimental analysis reveals that the single-iteration Grover approach, despite its computational efficiency advantages, exhibits insufficient accuracy for reliable cryptographic implementation beyond two-qubit systems, fundamentally limiting the scheme’s scalability potential. Furthermore, the substantial accuracy degradation observed when transitioning from theoretical simulations to real quantum hardware implementations underscores the critical impact of current quantum device limitations on cryptographic fidelity. These findings collectively indicate that while the proposed quantum encryption framework presents theoretical merit, the convergence of scalability constraints and hardware readiness challenges renders near-term practical deployment infeasible, necessitating substantial advances in both algorithmic optimization and quantum hardware development before reliable large-scale cryptographic applications can be realized.
4.5. Implementation Complexity and Resource Analysis
- Quantum Resource Requirements:
The multi-controlled Z-gate introduces significantly higher circuit depth, leading to increased decoherence susceptibility and reduced fidelity on NISQ devices. This depth penalty becomes particularly problematic for quantum cryptographic applications where multiple controlled operations are required, as the cumulative circuit depth can quickly exceed the coherence limits of current quantum hardware.
The exponential complexity difference makes single X-gates significantly more practical for near-term quantum implementations compared to multi-controlled Z-gates with large control registers [,].
The circuit depth comparison between a multi-controlled Z-gate and a single X-gate reveals a fundamental difference in quantum circuit complexity, where the single X-gate maintains a constant circuit depth of 1 through direct single-qubit gate application without requiring any decomposition, while the multi-controlled Z-gate exhibits circuit depth scaling with n control qubits due to its necessary decomposition into elementary gates. This decomposition process typically involves approximately 2 CNOT gate operations, potential ancilla qubit requirements for optimization, and Toffoli gate decompositions when ≥ 2, resulting in substantially higher implementation complexity that scales linearly with the number of control qubits, thereby introducing significant overhead compared to the constant-depth single X-gate operation.
Specific implementations demonstrate the pronounced scaling differences, where a double-controlled Z-gate (CCZ, = 2) requires approximately 7–9 elementary gates through Toffoli decomposition and controlled operations, while a triple-controlled Z-gate (CCCZ, = 3) demands 15–20 elementary gates with significant decomposition overhead. This scaling behavior illustrates the stark contrast between the single X-gate’s constant depth complexity and the multi-controlled Z-gate’s linear scaling with respect to control qubit count, resulting in exponentially increasing circuit complexity that fundamentally impacts the practical feasibility of multi-controlled operations in quantum cryptographic implementations.
To quantify this overhead, Table 3 presents the implementation complexity and resource analysis of our implementation of the quantum asymmetric encryption protocol. For each major component—key generation, encryption, and decryption—we estimate the number of required qubits, gate counts, and circuit depths. The results confirm that while key generation remains efficient with constant depth , encryption and decryption incur circuit depths scaling as due to multi-controlled operations. The overall gate complexity across all components scales as , and the qubit requirements are on the order of n, where n denotes the logical qubit size of the quantum key or message.

Table 3.
Implementation Complexity and Resource Analysis of the Proposed Quantum Asymmetric Encryption Protocol.
These findings substantiate the observation that although QAE schemes based on Grover operations offer strong theoretical security, their implementation on current NISQ devices must carefully account for the non-trivial resource overhead introduced by multi-controlled gates. This analysis is crucial for guiding future optimizations in QAE protocol design, particularly in the context of hardware-constrained quantum systems.
4.6. Discussion
4.6.1. Comparative Analysis and Emerging Trends in Quantum Asymmetric Encryption
Table 4 presents a comprehensive comparison of seven quantum asymmetric encryption schemes, revealing distinct approaches to quantum cryptographic implementation and highlighting the evolutionary progression in quantum security methodologies. The comparative analysis encompasses fundamental cryptographic properties, implementation complexity, computational efficiency, and practical deployment considerations across diverse quantum resource utilization strategies.
- Quantum Resource Utilization Strategies. The examined schemes demonstrate three primary quantum resource approaches: rotation-based single qubit states employed by Nikolopoulos [] and Zheng et al. [], Bell state entanglement utilized by Gao et al. [] and Wu et al. [], and GSA implementations adopted by Luo & Liu [], Yoon et al. [], and the proposed modified scheme. This distribution indicates a research trend toward algorithmic quantum advantage exploitation rather than purely quantum state-based security mechanisms.
- Key Space and Security Architecture Analysis. The key space analysis reveals a strategic division between “Big” and “Small” key spaces, where schemes utilizing complex quantum state preparations (Nikolopoulos [], Zheng et al. [], and Luo & Liu []) maintain large key spaces, while Bell state-based approaches (Gao et al. [], Wu et al. []) and GAS-based methods (Yoon et al. [] and the proposed modified scheme) operate within smaller key spaces. Notably, all schemes maintain one-way security for private key protection, indicating consistent adherence to fundamental cryptographic security principles.
- Computational Efficiency Evaluation. Efficiency metrics reveal substantial performance disparities, with the proposed modified scheme achieving efficiency (1.0) alongside Yoon et al. [], while other approaches demonstrate reduced efficiency ranging from 50% to 2/3. The superior efficiency of GAS-based methods indicates the computational advantage of quantum search algorithms over traditional quantum state manipulation techniques for cryptographic applications.
- Quantum Memory and Public Key Infrastructure. The analysis of quantum memory storage requirements shows that only Bell state-based schemes (Gao et al. [], Wu et al. []) require quantum memory storage, while GAS-based approaches operate without this constraint, significantly reducing implementation complexity. Public key center requirements vary inconsistently across schemes, with three approaches (Gao et al. [], Luo & Liu [], and Yoon et al. [], and the proposed modified scheme) requiring centralized key management infrastructure.
- Simulation and Experimental Validation. A critical distinguishing feature of the proposed modified scheme is the inclusion of comprehensive simulation and experimental validation, uniquely positioned among the compared approaches that universally lack experimental verification. This simulation capability provides essential performance assessment and practical feasibility evaluation, addressing a significant gap in quantum cryptographic scheme validation methodologies.

Table 4.
Comparative analysis of various quantum asymmetric encryption (QAE) schemes.
The comparative analysis demonstrates that GAS-based quantum asymmetric encryption schemes represent a significant advancement in practical quantum cryptography, offering superior computational efficiency, reduced implementation complexity, and eliminated quantum memory requirements. The proposed modified scheme’s combination of efficiency and experimental validation capability positions it as a promising candidate for near-term quantum cryptographic deployment, while highlighting the ongoing progress toward practical and scalable quantum security solutions.
This study makes several important contributions to the field of quantum cryptography:
- Implementation of Quantum Asymmetric Encryption on IBM Quantum Devices: We demonstrate the first practical implementation of a quantum asymmetric encryption protocol on IBM Quantum hardware. Using Qiskit, the protocol’s key generation, encryption, and decryption stages are translated into executable quantum circuits, confirming its feasibility for real-world applications.
- Performance Analysis of One-Round GSA: Through simulations and experiments, we evaluate one-round GSA on different qubit configurations. These results highlight the impact of noise and state size on GSA performance on NISQ devices.
- Generalization of GSA: We extend GSA to handle initial states, addressing the challenge of designing diffusion operators compatible with generalized states.
- Quantum gate-reduced Diffusion Operators: We propose a specific diffusion operator design for non-standard initial states, improving algorithm performance under diverse qubit configurations and randomization scenarios.
- Quantum Cryptographic Insights: Real-device experiments reveal performance degradation in one-round GSA with increasing qubits, underscoring the need for additional iterations or higher hardware fidelity for larger systems.
It is worth noting that one limitation of this study is the concern regarding the long-term storage of quantum public keys at the QKC and their vulnerability to decoherence. While no direct storage-level solution is provided, this work mitigates the issue by emphasizing improved hardware fidelity, incorporating additional Grover iterations, and employing optimized gate-reduced diffusion operators. These strategies collectively help sustain QAE performance under the constraints of NISQ devices.
4.6.2. Security Analysis and Limitations
While this work demonstrates the practical feasibility of implementing Grover-based quantum asymmetric encryption on current quantum hardware, it is important to acknowledge that unconditional security proofs remain an open research issue. The proposed scheme inherits the security assumptions of Yoon et al.’s protocol [], relying on the computational difficulty of inverting Grover oracle operations without private key knowledge and the quantum no-cloning theorem. However, comprehensive security analysis against adaptive adversaries and sophisticated attack models has not been established. Additionally, the performance degradation observed on real quantum hardware introduces security considerations, as significant error rates and decoherence effects in NISQ devices may create vulnerabilities exploitable by adversaries familiar with specific hardware limitations. Future research should prioritize developing rigorous unconditional security proofs for Grover-based quantum asymmetric encryption schemes and analyzing security implications of hardware imperfections in practical implementations.
5. Conclusions
This study successfully addresses critical challenges in quantum cryptography by enhancing Yoon et al.’s QAE scheme and providing its first practical implementation on IBM Quantum devices. Our research translates theoretical proposals into executable quantum circuits, establishing a crucial benchmark for practical quantum cryptographic applications. Performance evaluations across two-, three-, and four-qubit configurations reveal significant scalability challenges. While two-qubit systems demonstrate near-perfect accuracy, performance degrades markedly for larger systems, highlighting fundamental limitations of single-iteration Grover operations in NISQ devices. The introduced generalized GSA framework addresses non-standard initial quantum states through novel diffusion operator designs, extending applicability beyond idealized theoretical conditions. The observed performance degradation underscores the critical need for multiple Grover iterations or improved hardware fidelity to achieve acceptable success probabilities in larger quantum systems. Our findings provide essential empirical data for future QAE protocol optimization and establish a foundation for understanding both the potential and limitations of quantum asymmetric cryptography in the NISQ era.
Author Contributions
T.-H.C. contributed to the study’s conception and design. Material preparation and data analysis were carried out by T.-H.C. and W.-H.H. The manuscript was written by T.-H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Science and Technology Council, under the grant NSTC 114-2221-E-415-013.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptol. 1992, 5, 3–28. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Wang, Q.; Zhang, J.; Ng, S.X.; Hanzo, L. The evolution of quantum key distribution networks: On the road to the qinternet. IEEE. Commun. Surv. Tutor. 2022, 24, 839–894. [Google Scholar] [CrossRef]
- Nikolopoulos, G.M. Applications of single-qubit rotations in quantum public-key cryptography. Phys. Rev. A—At. Mol. Opt. Phys. 2008, 77, 032348. [Google Scholar] [CrossRef]
- Zheng, S.; Gu, L.; Xiao, D. Bit-oriented quantum public key probabilistic encryption schemes. Int. J. Theor. Phys. 2014, 53, 116–124. [Google Scholar] [CrossRef]
- Gao, F.; Wen, Q.; Qin, S.; Zhu, F. Quantum asymmetric cryptography with symmetric keys. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 1925–1931. [Google Scholar] [CrossRef]
- Wu, W.; Cai, Q.; Zhang, H.; Liang, X. Quantum public key cryptosystem based on bell states. Int. J. Theor. Phys. 2017, 56, 3431–3440. [Google Scholar] [CrossRef]
- Luo, W.; Liu, G. Asymmetrical quantum encryption protocol based on quantum search algorithm. China Commun. 2014, 11, 104–111. [Google Scholar] [CrossRef]
- Yoon, C.S.; Hong, C.H.; Kang, M.S.; Choi, J.-W.; Yang, H.J. Quantum asymmetric key crypto scheme using Grover iteration. Sci. Rep. 2023, 13, 3810. [Google Scholar] [CrossRef] [PubMed]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Tseng, H.-Y.; Tsai, C.-W.; Hwang, T.; Li, C.-M. Quantum secret sharing based on quantum search algorithm. Int. J. Theor. Phys. 2012, 51, 3101–3108. [Google Scholar] [CrossRef]
- Rathi, D.; Musanna, F.; Kumar, S. A Four-Party Quantum Secret-Sharing Scheme based on Grover’s Search Algorithm. arXiv 2021, arXiv:2111.08932. [Google Scholar]
- Yoon, C.S.; Kang, M.S.; Lim, J.I.; Yang, H.J. Quantum signature scheme based on a quantum search algorithm. Phys. Scr. 2014, 90, 015103. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, S.-B.; Chang, Y.; Qiu, C.; Liu, D.-M.; Hou, M. Quantum key agreement protocol based on quantum search algorithm. Int. J. Theor. Phys. 2021, 60, 838–847. [Google Scholar] [CrossRef]
- Chen, T.-H.A. Grover Search-Based Quantum Key Agreement Protocol for Secure Internet of Medical Things Communication. Future Internet 2025, 17, 263. [Google Scholar] [CrossRef]
- Hung, W.-H.; Chen, T.-H. Revisiting Quantum Asymmetric Key Cryptography: Enhancing Practical Implementations with a Generalized Grover Search Algorithm. In Proceedings of the 2025 1st International Conference on Consumer Technology (ICCT-Pacific), Matsue, Japan, 29–31 March 2025; pp. 1–4. [Google Scholar]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th annual symposium on foundations of computer science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Sadana, S. Grover’s search algorithm for $ n $ qubits with optimal number of iterations. arXiv 2020, arXiv:2011.04051. [Google Scholar]
- IBM Quantum Platform. Available online: https://quantum.ibm.com/ (accessed on 11 September 2025).
- Zindorf, B.; Bose, S. Efficient implementation of multi-controlled quantum gates. arXiv 2024, arXiv:2404.02279. [Google Scholar] [CrossRef]
- Silva, J.D.; da Silva, A.J. Logarithmic Depth Decomposition of Approximate Multi-Controlled Single-Qubit Gates Without Ancilla Qubits. arXiv 2025, arXiv:2507.00400. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).