Abstract
Network anomaly detection is widely used in network analysis and security prevention, in which reconstruction-based approaches have achieved remarkable results. However, attributed networks exhibit highly nonlinear relationships and time dependence over time, which make the anomalies more complex and ambiguous, resulting in anomaly detection still facing challenges. To this end, this study proposes an adversarial reconstruction framework with spectral-augmented and graph joint embedding for anomaly detection (GAN-SAGE), which integrates an autoencoder (AE) based on the frequency feature enhanced graph transformer (GT) into the generator for generating adversarial networks (GAN), improving network representation through adversarial training. The first stage of the encoding process captures the frequency domain information of the input timing data through spectral-augmented, and the second stage enhances the modeling capability of spatial structure and graph interaction dependency through multi-attribute coupling and GTs. We conducted extensive experiments on AIOps, SWaT and WADI datasets, demonstrating the effectiveness of GAN-SAGE compared to the state-of-the-art method. The detection performance of GAN-SAGE, respectively, improved by an average of 9.64%, 18.73% and 19.79% in terms of F1-score across the three datasets.
1. Introduction
Attributed networks [] are graph structures used to store information about complex systems. In these graphs, vertices represent entities, and edges represent relationships between entities. Each node and edge is typically associated with a set of rich features. In the real world, telecommunication networks, information networks and industrial control networks can be considered as attributed networks. Taking information networks as an example, nodes can represent application devices or users, with attributes such as resource usage and security status. The edges represent the connections between different application devices, and their attributes may include performance metrics such as bandwidth and latency.
With advancing technology and the growing complexity of network environments, network security risks are rapidly evolving, becoming more intricate and diverse, thus, placing higher demands on network defense capabilities. Detecting data anomalies is crucial for many security-related applications []. Anomaly detection as a key technology for ensuring network security, involves using specific methods to identify events or observations that are inconsistent with the behavior of most data []. Anomaly detection in attributed networks can identify vulnerable nodes to prevent network attacks or failures, serving as a critical prerequisite for ensuring smooth network operations and addressing security vulnerabilities [].
The use of GANs has gradually become a new trend in anomaly detection []. When using GANs for reconstruction-based anomaly detection, the AE serves as a generator, capturing the normal data distribution and mapping it to a latent space during adversarial training, enabling it to function as an anomaly detector by encoding normal samples into latent vectors to learn feature distributions. However, attributed networks nodes not only contain their own attribute information but are also interconnected with other nodes through diverse connection relationships. Additionally, they exhibit highly nonlinear relationships and time-dependent properties over time, making the definition of anomalies more complex and ambiguous. Traditional autoencoding methods show limitations in capturing critical contextual information and complex dependencies. In networks involving complex attributes, such as information networks and industrial control networks, where network components evolve over time with high-dimensional characteristics and multi-scale fluctuations, standard AEs often overly smooth these fine-grained network features, leading to the loss of key anomaly signals []. Therefore, it is necessary to enhance learning from normal data, improve the quality of learned representations, and enhance model robustness by identifying a wide range of complex network features [,] thereby, improving the accuracy and reliability of anomaly detection.
In attributed networks where both nodes and edges play significant roles, different components interact to execute network tasks. Relying solely on single information sources is insufficient to meet the representation demands of complex scenarios []. Network embedding [] is an efficient tool for graph mining that maps large-scale complex networks to low-dimensional spaces, capturing the rich information within the network to support analysis tasks [,], where joint embedding methods for nodes and edges have garnered significant attention due to their ability to comprehensively capture network features. To address the complex interaction features present in attributed networks, joint embedding can be utilized to accurately model the graph-structured data of attributed networks, thereby enhancing their network embedding performance. However, when handling complex attributed networks with long-range dependencies, traditional graph representation paradigms such as graph convolution networks (GCNs) [,,], which rely solely on local neighborhood information for feature aggregation, struggle to capture global structural patterns, potentially leading to over-squashing [] and under-reaching []. To address their limitations in capturing long-range dependencies and adapting to complex graph structures, introducing the GT with strong relationship induction biases into graph representation enables better learning of entities, relationships and combination rules, offering an emerging perspective for graph learning [,].
Attributed networks exhibit complex graph structures characterized by strong heterogeneity and high dimensionality, whose topological properties pose significant challenges for traditional anomaly detection methods []. Meanwhile, most graph anomaly detection methods focus on extracting temporal features []. Some methods enhance the detection capabilities by combining the correlations between variables, primarily by comprehensively considering the temporal features of node neighbors [,,], but struggle to capture long-range dependencies and complex interaction features. Additionally, the temporal data in attributed networks exhibit complex joint correlations, making anomaly behavior more ambiguous []. To address this problem, this study investigates the feasibility of enhancing anomaly detection accuracy by leveraging the interactive features between nodes and edges in the network topology [,,,]. A novel adversarial reconstruction framework for anomaly detection is proposed, based on spectral-augmented and graph joint embedding. This method uses GANs as its basic framework, integrating the frequency feature enhancement GT into the AE as the GAN generator. Additionally, a synchronous encoder is introduced to adjust the generator’s learning ability in the latent space of normal data. The frequency feature enhanced GT aims to extract spectral features from time-series data to enhance the representation capability of complex interaction relationships in attributed networks. The entire anomaly detection architecture is trained using only normal samples, enabling unsupervised network anomaly detection. Through adversarial training, it enhances the learning ability of the data’s latent representation, thereby improving the accuracy of anomaly detection.
The main contributions can be summarized as follows:
(1) Adversarial detection framework with enhanced network representation: In order to achieve efficient and robust anomaly detection using only normal samples, we propose a composite framework centered on a frequency feature enhanced GT-based AE structure. We introduce synchronous encoders and generators for collaborative optimization, and use discriminators to evaluate reconstruction quality, thereby enhancing the ability to model normal data distributions.
(2) Spectral-augmented temporal dependency extraction: In order to extract temporal dependency features from attributed network, spectral decomposition is employed to transform time-series data into multi-scale time-frequency representations, followed by targeted enhancement of different frequency components, thereby enhancing the model’s capacity to represent complex dynamic behavior and improving anomaly detection accuracy.
(3) Multi-attribute graph joint embedding: In order to address the shortcomings of high dimensional and complex interaction analysis methods in attributed networks, we first unify the modeling of multi-attribute information for nodes and links in the extraction of data features. We then introduce position encoding and graph joint embedding to capture the global dependency structure, thereby effectively improving the ability to represent the network’s operating status.
2. Related Work
Deep learning methods can extract complex and high dimensional features from data. Many researchers have utilized deep learning methods for graph anomaly detection, broadly classified into two categories: graph anomaly detection based on network representation and graph anomaly detection based on reconstruction [].
2.1. Graph Anomaly Detection Based on Network Representation
The main research approach for graph anomaly detection based on network representation is to encode the graph into an embedding space and then perform anomaly detection. In time-series data with graph structure, a graph neural network (GNN) is a representative network of graph-based deep learning models, and most graph anomaly detection methods are based on GNNs to learn graph features and identify anomaly patterns [,]. In graph anomaly detection methods based on network representation, there are two types: aggregation mechanism and feature transformation.
2.1.1. Aggregation Mechanism
Feature aggregation is a simple and effective GNN representation method that learns network representations by aggregating node neighbor information in a graph.
Graph attention networks (GATs) [] as a classical feature aggregation method dynamically aggregates features through an attention mechanism that allows each node to be given different weights depending on the importance of its neighboring nodes. To address the problem of unknown anomaly patterns in attributed networks, Zhou et al. [] utilized neighbor information to determine anomaly criteria and proposed the abnormality-aware graph neural network (AAGNN), which employs subtraction aggregation to determine each node’s deviation relative to its neighbors. To enhance the ability to select appropriate neighborhood information in graph clustering mechanisms, Beid et al. [] proposed an unsupervised graph Anomaly Detection (RAND) that amplifies reliable neighbor information and reduces unreliable neighbor information through a reinforcement anomaly evaluation module and an anomaly-aware aggregator. Ma et al. [] explored the importance of inter-graph structural and attribute information, proposing a deep evolutionary graph mapping framework named GmapAD1. This framework performs adaptive mapping by considering the similarity between graphs and representative nodes, thereby learning the clear boundaries between anomalies and normal graphs. Furthermore, addressing the heterogeneity issue in graph anomaly detection, Gao et al. [] prune edges across different clusters by emphasizing high-frequency components in the spectral domain representation of graphs. To mitigate biases caused by inconsistent behavioral patterns in graphs, Wang et al. [] proposed a node representation learning method named Deep Cluster Infomax (DCI), which captures the intrinsic graph properties by clustering the entire graph into multiple parts.
2.1.2. Feature Transformation
The datasets involved in graph anomaly detection usually contain a large amount of noise information. Therefore, another method detects anomalies by transforming the graph features.
To fully exploit the nonlinear and sparse characteristics of networks, Pei et al. [] proposed a residual graph convolutional network (ResGCN), which uses attention mechanisms for deep residual modeling of networks. Liu et al. [] proposed a contrastive self-supervised learning framework based on GNNs, aiming to learn informative embedding from high-dimensional attributes and local structure. Considering that existing graph anomaly detection tends to consider only single-scale views, Jin et al. [] proposed a novel graph anomaly detection framework named ANEMONE, which can simultaneously identify anomalies across multiple graph scales. To further enhance the learning capability of complex relationships in graph structures, Ailin et al. [] encoded relationships between nodes as edges, fully learning network embedding via attention-based GNNs. To address the issue of information loss across different graph structures, Du et al. [] proposed a topology adaptive graph convolutional network (TAGCN) that uses a set of fixed-size learnable filters to capture local features of nodes in the graph, thereby avoiding the linear approximation issues associated with filters of a single size. To fully unlock the potential of edge feature topology in graph networks, Deng et al. [] constructed an interval-constrained traffic graph by considering the time correlation of traffic flows, and further learned a combined representation of statistical flow features and flow topological structure based on adaptive graph convolutions.
2.2. Graph Anomaly Detection Based on Reconstruction
However, graph anomaly detection based on network representations faces the challenge of a lack of high-quality anomaly annotation data in practice. Therefore, many research efforts have shifted to modeling the features of normal or abnormal states. Among them, anomaly detection based on reconstruction are widely used methods in deep learning, where the model is trained to learn the features of normal data and reconstruct them into an approximate representation of the original data. Common methods include reconstruction based on a graph autoencoder (GAE) and reconstruction based on adversarial learning.
2.2.1. Graph Autoencoder
A GAE [] is a commonly used method in graph reconstruction anomaly detection. They consist of a graph encoder and a graph decoder, which encode graph data into low-dimensional representations and reconstruct the original graph data through the decoder to achieve anomaly detection. The fundamental idea behind a GAE is that most normal samples can be reconstructed effectively, whereas anomalous samples, whose features differ substantially from those of normal data, are reconstructed poorly and, thus, yield large reconstruction errors. By calculating the reconstruction error for each node or graph instance, it is possible to effectively identify abnormal nodes that exhibit significant deviations from the normal pattern.
Attributed networks typically exhibit characteristics such as long-term time series, graph structures and multi-attributes. During the reconstruction phase, it is necessary to consider both their temporal features and the relational features between variables. For graph-structured data, a GAE has been proposed to leverage GNNs for encoding graph structures and node attributes, thereby enabling the detection of anomalies in graph data. To accurately obtain a low-dimensional latent representation of graph features, Park et al. [] proposed a symmetric graph convolutional autoencoder to reconstruct node features. To further account for the temporal characteristics of graph structural attributes, Zhao et al. [] used two graph attention layers to learn the complex dependencies between multivariate time series in both the temporal and feature dimensions. For system states under different temporal features, Zhang et al. [] proposed a multi-scale convolutional recurrent encoder-decoder (MSCRED) that uses multi-scale feature matrices and attention-based convolutional networks to capture multi-level system correlations and temporal patterns, followed by a convolutional decoder to reconstruct features. To further optimize network embedding performance, Fan et al. [] proposed a deep joint representation learning framework for anomaly detection through a dual autoencoder (AnomalyDAE), to capture complex interactions between network structure and node attributes. Considering the negative impact of network sparsity and data nonlinearity on detection performance, Ding et al. [] reconstructs the original data through the collaboration of GCN and AE to detect anomalies from both structural and attribute perspectives.
2.2.2. Adversarial Learning
The GAN provides an effective solution for generating realistic synthetic samples that can be used for normal pattern learning in graph anomaly detection. Specifically, the generator generates samples that are statistically indistinguishable from real data, while the discriminator learns to differentiate real from generated samples. On the other hand, GANs can be used as a reconstruction-based anomaly detection framework, mainly by continuously learning and reconstructing graph data features from normal samples through adversarial learning.
By integrating GANs on a gradient inverse mapping approach, f-AnoGAN [] uses GANs in reconstruction-based anomaly detection methods. Zhou et al. [] applied a GAN to the reconstruction of time-series data, using an AE as the generator within the GAN. To avoid the limitations of anomaly detection based on a single data attribute, Qu et al. [] integrates attention-based AE with a GAN to capture and fuse rich information from diverse data sources. Ding et al. [] introduced adversarial learning into graph anomaly detection, proposing an adversarial graph differentiation networks (AEGIS) that further employ generative adversarial learning based on graph neural layers to detect data anomalies. Guo et al. [] addressed the challenge of encoding complex graph data, proposing a graph generative adversarial network named RegraphGAN, which combines relative time encoding, diffusion-based spatial encoding and distance-based spatial encoding within the GAN framework.
3. Methodology
Attributed network nodes not only contain their own resource states as node attributes but also form complex interactive network structures with other nodes through call chains. These can be represented using the graph time-series structure , where denotes a finite set of network nodes, denotes a finite set of connections between two adjacent nodes, denotes the feature set of each node in the network over time, denotes the feature set of each edge in the network over time, n and m, respectively, represent the number of nodes/edges and the number of features, while L denotes the length of the time series. For a single node or edge, its temporal features can be represented as and .
Figure 1 shows the overall architecture of GAN-SAGE, where the generator, discriminator, and synchronous encoder undergo adversarial training to continuously learn the normal network representation. The frequency feature enhanced GT-based AE serves as the generator, consists of an encoder and a decoder. When receiving attributed network time-series data G, it first splits the data into node time-series data and edge time-series data based on the network definition, which serve as inputs to the encoder. These inputs undergo spectral-augmentation and are then fed into a multi-attribute graph joint embedding to obtain the joint embedded latent vector z of nodes and their adjacent edges in the attributed network. The decoder is responsible for reconstructing the latent vector back into the input data structure. The discriminator takes real and generated data as inputs and outputs the discrimination results. The synchronous encoder has the same structure as the encoder, takes generated data as input and outputs its latent vector . During adversarial training, the synchronous encoder interacts with the generator to enhance the learning capability of network representations.
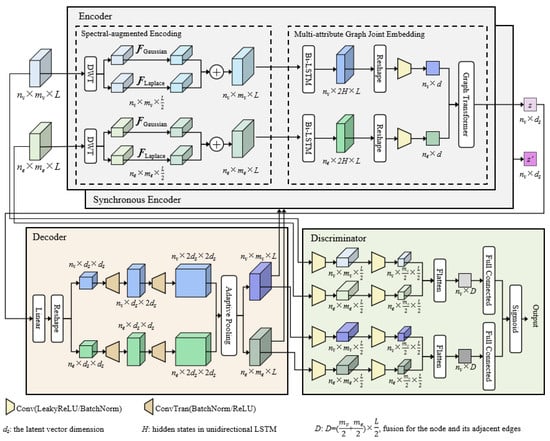
Figure 1.
Overall architecture of the GAN-SAGE.
GAN-SAGE integrates spectral-augmentation, multi-attribute graph joint embedding, and adversarial training in a complementary manner to establish a progressive learning framework. Spectral-augmentation decomposes raw time series into multi-scale sub-band signals, followed by targeted enhancement of these components to mitigate noise interference, thereby providing robust input for multi-attribute graph joint embedding. The multi-attribute graph joint embedding module explicitly models nonlinear inter-attribute dependencies and higher-order network interactions, yielding a joint latent representation that accurately captures the network’s intrinsic behavioral patterns. This latent representation serves as a semantically coherent input for the adversarial training, enabling the GAN to learn the complex distribution of normal behavior within a relatively noise-free latent space. Consequently, the learned features are more focused on critical states and interaction patterns sensitive to anomalies, thereby enhancing anomaly detection performance.
3.1. Adversarial Learning Framework
The GAN-based reconstruction framework possesses powerful feature extraction capabilities []. This framework combines the adversarial training mechanism between the generator G and discriminator D, enabling the generator G to progressively learn the deep features and latent distribution structure of the data during the reconstruction process. However, when handling complex attributed network data, it may fail to adequately capture effective network features. To address this challenge, we integrate the frequency feature enhanced GT into the AE as the generator G, which consists of an encoder GE and a decoder GD. The encoder GE consists of spectral-augmented encoding and multi-attribute graph joint embedding modules, designed to capture network features from temporal evolution dependencies and complex interactions, thus, enabling the construction of a latent space for representing normal samples. The decoder GD employs a deconvolution decoding strategy to reconstruct the input samples, generating data with a structure matching the original input. In addition, a synchronous encoder E is introduced to participate in adversarial training, aiming to enhance the GAN detection framework’s modeling capabilities for network representations under temporal evolution.
The adversarial reconstruction framework is shown in Figure 2. During the training phase, the system inputs node features Xv and edge features Xe within the time T, and the encoder GE of the generator G captures the distribution of the original real data to obtain the latent features z of the samples. Subsequently, the decoder GD in the generator G learns the distribution of the input data from the latent space, reconstructs the normal samples, and obtains the generated samples G(Xv) and G(Xe). The discriminator D receives both real samples and generated samples, respectively, evaluating them to output its judgment on the authenticity of each sample. The architecture of encoder E is the same as that of the encoder GE in the generator G. The reconstructed samples from the generator G are re-encoded by the encoder E to obtain their latent vectors z′.
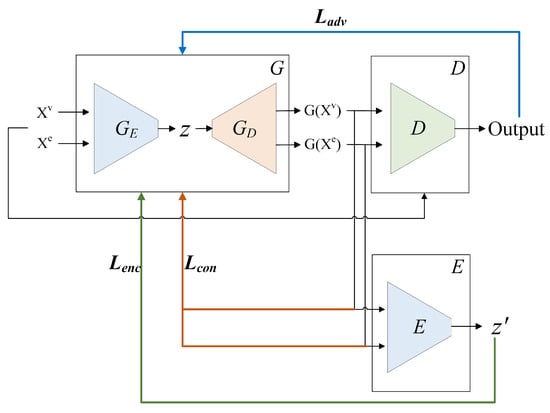
Figure 2.
The adversarial reconstruction framework.
To ensure that the distribution of the generated samples closely approximates that of the real samples, the adversarial loss Ladv guides the interplay between the discriminator D and the generator G through minimizing the difference between the distribution of actual data X and the distribution of generated data [], enabling the latent vectors z′ to learn features consistent with normal patterns:
where X represents the actual data input, consisting of node and adjacent edge data. Pr represents the distribution of actual data, implicitly learned from the training data, approximating the true data distribution as an empirical distribution [].
The synchronous encoder E encodes the latent vectors of the generated samples to calculate the encoding loss Lenc. By minimizing the difference between the latent features of the real samples and the generated samples, it guides the encoder GE to capture more critical and effective features. The representation of the latent space is optimized through the encoding loss Lenc:
To ensure the reconstruction quality of the generator G for normal samples and to ensure the similarity between the generated samples and the input samples, the content loss Lcon measures the difference between the input samples and the generated samples:
Thus, the total loss of adversarial training can be expressed as:
where adv, enc and con are weighting parameters used to adjust the impact of adversarial loss Ladv, encoding loss Lenc and content loss Lcon on the overall objective function.
The entire process continuously improves the quality of data representation through joint optimization of adversarial loss, encoding loss, and content loss, thereby enhancing the overall embedding quality of normal samples in the network.
In anomaly detection, encoding loss is used to score anomalies in samples, with the anomaly score defined as the quadratic reconstruction error:
After determining the anomaly detection threshold, the trained model is used for anomaly detection. The anomaly detection process is achieved through the joint action of the generator G and encoder E. If the anomaly score of a sample exceeds the set threshold, it is judged to be an anomaly.
3.2. Graph Joint Embedding Based on Spectral-Augmented
Network representation analysis provides a comprehensive and effective assessment of network security status. Nodes and edges in attributed networks interact and collaborate in complex ways to jointly influence network behavior. The two interact with each other in the network, and abnormal node behavior may be manifested through edge relationships, while abnormal edge characteristics may also affect the performance of connected nodes. Therefore, these potential abnormal behaviors can be captured by considering the interaction between nodes and edges in network joint embedding.
However, in network joint embedding, it is crucial to select embedding objects and construct appropriate feature representations. The feature representations of embedding objects directly determine how the model understands and distinguishes key information in the network, serving as the foundation for the model to identify and detect abnormal behavior. Accurately representing the multidimensional features of nodes and edges helps the model comprehensively understand network interactions and behavioral patterns.
In attributed networks, network behavior evolves dynamically over time, with temporal characteristics revealing distinct activity patterns during anomalies. Nodes and edges possess multidimensional attributes that not only collectively define their properties but also generate additional information through attribute interactions. This can comprehensively reflect the collaborative changes in the network’s operational process, providing more detailed clues and stronger discernment capabilities. Therefore, anomaly detection in attributed networks cannot be separated from the temporal characteristics and multidimensional attributes of the network. When constructing features for the embedding object, both temporal characteristics and multidimensional attributes should be comprehensively considered.
Therefore, the frequency feature enhanced GT is integrated into the AE of the adversarial training generator; the graph joint embedding method based on spectral-augmented is shown in Figure 3. The frequency feature enhanced GT takes graph time-series data of the attributed network as input. The spectral-augmentation is employed to extract rich temporal features by applying discrete wavelet transform (DWT) to the node time-series data and edge time-series data and performing targeted enhancement. The multi-attribute graph joint embedding receives the spectrally augmented time-series data. It first captures nonlinear state features within the data through multi-attribute coupling across different components. Then, it obtains global dependency information guided by edge features by incorporating the network structure, ultimately generating the latent vector of the network representation.
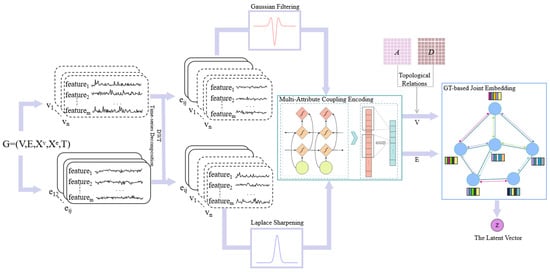
Figure 3.
The frequency feature enhanced GT.
3.2.1. Spectral-Augmented Encoding
In attributed networks, many performance metrics often exhibit complex time-varying characteristics over time, including long-term trends, periodic fluctuations and sudden anomalies. However, due to the large number of metrics, critical anomaly information is easily obscured by a large amount of unchanged time-series data, thereby hindering the timely detection of anomalies. This calls for extracting more rich features from the data to highlight anomalies and prevent information dilution, thereby addressing the issue of feature over-smoothing during the reconstruction process [].
To capture the details of performance fluctuations and rich feature information in attributed network time series data, spectral-augmented encoding is used to dig its time series features, mainly including spectral decomposition and frequency targeted enhancement. This reveals the multi-scale temporal features of attributed network time-series through a rigorous multi-resolution analysis process, while preserving the dynamic temporal structure and preventing signal features from being diluted by noise.
Spectral Decomposition
Spectral decomposition uses wavelet transforms to decompose time series into sub-sequences of different frequencies, thereby retaining the time information of the signal while revealing its frequency components, making it suitable for network time series feature learning. Given a discrete time series, we use DWT in the spectral decomposition encoder to decompose the temporal data into trend and detail components, avoiding the conflation of these two feature types when modeling at a single scale, while achieving the conversion from time domain features to multi-scale time-frequency features.
The nodes and edges of attributed networks represent different objects and their interactive relationships. Node time series reflect the behavioral patterns of individual nodes over time, manifested as changes in the nodes’ own states. Node time series typically exhibit continuity, with most nodes’ states tending to transition smoothly over time. In contrast, edge time series capture the dynamics of the relationships between nodes. Interactions between nodes can occur within short time frames, revealing the communication interactions and information flows between nodes over time, typically exhibiting instantaneity and discreteness.
Daubechies wavelets and Coiflet wavelets were selected to adapt to the temporal characteristics of nodes and edges, respectively. Daubechies wavelets can effectively capture low-frequency components, thereby better representing the continuous changes in node states over time. Coiflet wavelets have good tight support and perform well in processing local information, making them suitable for analyzing edge interaction patterns.
The DWT is implemented using the Mallat algorithm, which decomposes signals into approximate components and detail components of different frequencies through alternating operations of filter banks and downsampling. The input time series is decomposed into J layers, and the final output is the approximate coefficients of the last layer and the detail coefficients of each layer. The approximate coefficients and detail coefficients of layer J + 1 are calculated using the approximate coefficients of layer J, expressed as:
where H represents a low-pass filter and G represents a high-pass filter.
The input time series data are and . A first-order wavelet transform was performed on the input time series data to extract its trend component and detail component, represented by the approximation coefficient and detail coefficient, respectively:
where represents the DWT process, and represents the trend component and detail component of the node in the input time series data, and and represents the trend component and detail component of the link in the input time series data.
Frequency Targeted Enhancement
To further reduce noise interference and enhance the ability to distinguish frequency information, targeted feature enhancement processing was introduced for the trend component and detail component of the time series features, aiming to obtain network data with clearer temporal characteristics. Gaussian smoothing was applied to the trend component to suppress high-frequency noise and reinforce the overall trend pattern, while Laplace sharpening was applied to the detail component to highlight small changes and sudden changes.
Gaussian smoothing as a linear low-pass filter enhances the low-frequency components of a signal by computing a weighted average of data points, effectively highlighting long-term trends and global change patterns. It suppresses high-frequency noise and local fluctuations by integrating each data point with its neighbors, making it well-suited for extracting and preserving the continuity of time-series data during reconstruction. Gaussian smoothing of trend components can be expressed as:
where represents the Gaussian smoothing standard deviation, K represents the Gaussian convolution kernel radius, and l represents the discrete time step of the time series data.
Compared to smoothing, sharpening enhances high-frequency components of data signals through differential operations, emphasizing abrupt changes and local details. The Laplace sharpening operator as a second-order differential operator can effectively detect rapid signal changes by computing differences between each data point and their neighbors, identifying potential abrupt anomalies. This differential approach makes sharpening ideal for amplifying sudden anomalies during reconstruction, increasing the distinction between anomalous and normal data representations. Laplace sharpening of detail components can be expressed as:
where represents the Laplace sharpening coefficient, and represents the one-dimensional discrete Laplace operator.
To fully exploit the complementarity of the two types of features, the enhanced trend component and detail component are integrated along the feature dimension in the spectral-augmented encoder to form a fused multi-scale feature representation:
where denotes concatenation.
3.2.2. Multi-Attribute Graph Joint Embedding
The nodes and edges of attributed networks contain multiple attributes, and different attributes jointly characterize the dynamic behavior of the system during operation. The network state is often determined by the interplay of several interrelated attributes and, thus, network anomalies may manifest as a collaborative change among multiple attributes. Meanwhile, tasks in attributed networks are executed through interactions and collaborations among different components. Different nodes form global interactions with other nodes through complex invocation and transfer relationships, not only limited to directly connected neighboring nodes. Their intricate dynamic coupling relationships play an important role in identifying network anomalies. Therefore, anomaly detection should focus on the collaboration patterns and dependencies between different components.
Multi-Attribute Coupling
To capture the nonlinear interaction features of multidimensional attributes of network components under temporal evolution, we use a Bidirectional Long Short-Term Memory (Bi-LSTM) network to generate semantically rich vector for network components. BI-LSTM possesses powerful nonlinear feature extraction capabilities. Its internal memory units and gating mechanisms effectively integrate information across different attribute features. Moreover, by considering both forward and backward time dependencies, Bi-LSTM comprehensively captures patterns in time series.
When performing multi-attribute coupling on nodes and edges, a neural network containing a Bi-LSTM structure is used to extract the feature depth interaction of network features:
where represents the i-th attribute feature of a node or edge. Different attributes are passed to the bidirectional LSTM for processing. The multi-attribute coupling feature vector is obtained by averaging all potential states of the LSTM and adaptive convolution matching the input dimension of GT.
Graph Joint Embedding
Next, the GT architecture is employed to process the long-range joint interaction features of the attributed network, which can effectively capture complex global dependencies. Inspired by [], edge features are introduced into the attention mechanism of the transformer, allowing nodes to exchange information with other nodes globally and adaptively obtain collaborative dependency features with other nodes based on the actual connection edges, thereby obtaining the graph joint embedding of the attributed network.
In graph joint embedding, network structure information enhances the capture of long-distance node dependencies, improving network representation accuracy. Node and edge embedding vectors, derived from multi-attribute coupling, respectively, represent node characteristics and single connections. Therefore, it is necessary to obtain network structure information and introduce position encoding into the node embedding vectors to strengthen the global positional relationships between nodes.
In the structure of an attributed network, the adjacency matrix directly reflects the node’s connection, while the degree matrix reflects the connection strength of each node, indicating the node’s influence in the network, which helps identify nodes with higher-risk behavior in anomaly detection. Therefore, the adjacency matrix and degree matrix are used to calculate the Laplacian matrix for the network structure, comprehensively revealing the global structural relationships between nodes:
where A represents the network adjacency matrix, and D represents the network degree matrix. is the Laplacian vector of the network structure, and U, respectively, represent its eigenvalues and eigenvectors. The smallest non-trivial eigenvector k is used as the node position encoding.
After obtaining the node position encoding, add it to the node embedding vector as input to GT:
where represents the embedding vector of the node . Among them, , represents the weight matrix of the linear projection layer, and represents the bias vector.
At the same time, the edge embedding vector is used as the edge feature input for GT, representing the information features of the edge .
GT can realize the dynamic update of node features and edge features through multi-attention mechanism, and at the same time, the edge features are integrated into the process of node update, and the update process for layer l is described below:
where , , , ,, are the learned projection matrices. means the number of attention heads. is the attention head dimension.
At the end of each layer, the features will be fed into a Feed Forward Network (FFN) with two fully connected linear layers:
where denotes the FFN part, with a non-linearity [] in the between. denotes the Layer Normalization (LN) [].
After obtaining the node vectors and edge vectors that incorporate the global interaction features, the final potential vector representation is obtained by aggregating the node vectors and node proximity vectors, this is because the results of anomaly detection can ultimately be pinpointed to specific nodes through the nodes themselves or their neighboring interfaces. Attention-based aggregation is used to obtain the final potential vectors:
where is the learned projection matrix. denotes the the latent vector of .
4. Experiments and Results
All experiments used the PyTorch 2.7.1 deep learning framework and Python 3.13.2 programming language, with Linux as the operating system and an NVIDIA 4090 24GB GPU as the processor.
4.1. Datasets
GAN-SAGE is evaluated using the three open source datasets, which exhibit complex structures and dynamic interaction characteristics, aligning with the application scenarios of the proposed method.
AIOps Challenge dataset []: This dataset comes from a real open computer network system, where each system component forms a complex, heterogeneous network of interactions with other system components. It contains 15 days of network runtime metric data, during which 81 anomalies occurred, each lasting 5 min.
The Secure Water Treatment (SWaT) dataset []: The dataset comes from a real industrial water treatment test bed with multiple sensors and monitoring equipment. It contains 11 days of actual system operation data, during which 4 days were under attack.
The Water Distribution (WADI) dataset []: This dataset comes from a water distribution testbed that extends SWaT, with additional sensors and monitoring equipment installed on the testbed. It contains 16 days of data on the actual operational state of the system, during which 2 days were under attack.
To construct the graph structure from raw data, we map the network components in the dataset to a set of graph nodes V and then build the edge E set based on their connection relationships. For the AIOps dataset, the connection relationships are determined by invocation chains and component dependencies. For the SWaT and WADI datasets, the physical links between monitored entities are defined as edges. The monitoring measurements associated with nodes and edges are normalized and organized into feature vectors and , thereby transforming the data into the graph time-series structure of the attributed network. This representation preserves the temporal evolution characteristics and structural dependencies of the system, serving as input for subsequent detection tasks.
GAN-SAGE employs unsupervised learning, using only data from normal states during the training phase. In the data processing stage, data samples are constructed based on time window snapshots, with each sample containing graph structure snapshots for L consecutive time steps. If any anomalous data point exists within the time window, the sample is labeled as anomalous.
4.2. Implementation Details
In the network architecture design, there is a generator G, a discriminator D, and a synchronous encoder E, where the generator G is an AE.
The encoding part GE in generator G primarily consists of two components: spectral-augmented encoding and multi-attribute joint embedding. In the spectral-augmented encoding, the wavelet bases for node data and edge data are Daubechies wavelets and Coiflet wavelets, with a wavelet transformation order of 1. In the multi-attribute coupling, the hidden states in unidirectional LSTM is set to match the input feature dimension, and an adaptive convolution layer is used before the GT to match the input dimensions. In the GT, the number of GT layers is set to two, and the number of attention heads is four. In the synchronous encoder E, its network architecture is consistent with that of the generator GE.
The decoding part GD in generator G consists of a linear layer with learnable weight matrices, two layers of one-dimensional transposed convolutions, and an adaptive pooling layer. The weight matrix of the linear layer with learnable weight matrices is determined by the dimension of the latent vector and the number of nodes and links to be decoded. The convolution kernels of the two layers of one-dimensional transposed convolutions are two, with a stride of two and padding of zero. The output dimension of the adaptive pooling layer is determined by the temporal and feature dimensions of the nodes and links. ReLU is used as the activation function after the transposed convolution to further enhance the model’s nonlinear expression capabilities.
The discriminator D consists of two layers of one-dimensional convolutions and a fully connected layer. The convolution kernels of the two layers of one-dimensional convolutions are two, the stride is two, and the padding is zero. LeakyReLU is used as the activation function, and the fully connected layer uses Sigmoid as the activation function.
The experiments were conducted using the Adam optimizer [], with the learning rate set to . The network was trained for 500 iterations.
4.3. Evaluation Metrics
We use four standard metrics to evaluate the performance of the proposed method GAN-SAGE.
where TP, FP, TN and FN, respectively, denote true positive, false positive, true negative and false negative.
4.4. Anomaly Detection Threshold
The anomaly detection threshold is first determined experimentally, and then the performance of the model in the test set is evaluated on this basis. The threshold determination strategy is based on the histogram analysis of the distribution of anomaly scores, where the range distribution of normalized anomaly scores of normal samples is computed after obtaining them, and the anomaly detection threshold is determined by selecting a percentile of the distribution.
The histograms of anomaly score distribution on the three datasets are shown in Figure 4. The histograms of anomaly score distribution show the distribution of the percentage of anomaly scores of normal samples. In these histograms, the grey dashed lines represent the detection thresholds. Based on the data distribution, the 99th percentile is selected as the detection threshold, and the anomaly detection thresholds for AIOps, SWaT and WADi are 0.59, 0.40 and 0.38. The anomalies are judged according to the corresponding thresholds in the subsequent detection.
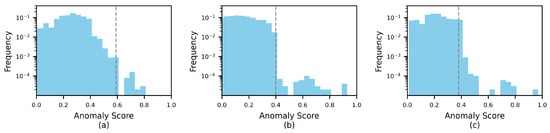
Figure 4.
The histogram of anomaly scores: (a) frequency of AIOps anomaly score distribution; (b) frequency of SWaT anomaly score distribution; (c) frequency of WADI anomaly score distribution.
We visualized the anomaly detection process for GAN-SAGE using a subset of AIOps dataset. The original samples with the reconstruction results are illustrated in Figure 5. The blue line segments in Figure 5a represent the normalized values of the original samples, while the red line segments represent the normalized values of the reconstructed samples generated by the generator from the original samples. The purple region indicates the presence of anomalies during that time period. According to the results shown, there is a regular difference between the original sample values in the anomalous region and those in the normal region, while the reconstructed samples exhibit limitations in effectively reflecting the distribution of normal samples. Figure 5b displays the anomaly scores corresponding to the same time period as Figure 5a, showing higher anomaly score values in the anomalous region compared to the normal region. Within a time window, a sample is identified as anomalous when its average anomaly score exceeds the detection threshold.
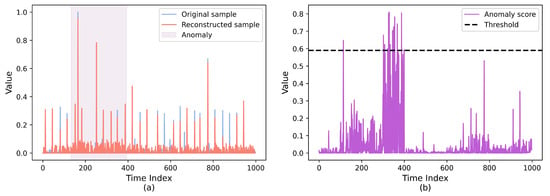
Figure 5.
Illustration of anomaly detection: (a) comparison of original and reconstructed samples; (b) showing the anomaly scores of the detected samples.
4.5. Hyperparametric Experiments
In order to test the effect of setting different hyperparameters on GAN-SAGE training, test experiments are designed for latent vector dimension and temporal sliding window size L. The latent vector dimension and the temporal sliding window size L affect the model’s ability to capture features of temporal data. The latent vector dimension determines the dimension of the latent space into which the input data is compressed, and is also related to the calculation of the detection threshold, affecting the model’s ability to represent the features. The sliding window size L determines the length of the temporal region used for reconstruction and detection, affecting the model’s ability to capture the temporal dependence of the data. Hyperparametric experiments are conducted on the AIOps, SWaT and WADI datasets, the rest of the hyperparameters other than the target parameter are kept unchanged during the experiments.
The influence of latent vector dimensions is shown in the experimental results of Figure 6. The latent vector dimension is selected, respectively. The results indicate that the comprehensive performance is best at on the AIOps and WADI datasets, and at on theSWaT dataset. The latent vector dimension for optimal performance on the AIOps and WADI dataset is higher than that on the SWaT dataset, possibly because the complex network interaction relationships in AIOps dataset and the high-dimensional characteristics of WADI dataset require a relatively larger representational space.
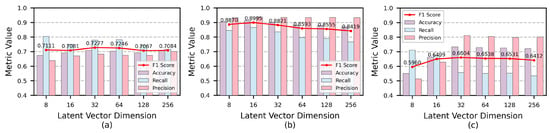
Figure 6.
Performance metrics of hyperparameter latent vector dimension : (a) experiments on AIOps; (b) experiments on SWaT; (c) experiments on WADI.
The variation in latent vector dimensions on the AIOps dataset has a minimal impact on the F1-score, with only a 0.021 difference between the best and worst performance, indicating that the GAN-SAGE exhibits strong robustness to changes in latent vector dimensions on this dataset. However, when , the recall shows a noticeable downward trend, and the F1-score experiences a slight decline, possibly due to the introduction of redundant information from excessively high dimensions, which weakens the overall ability to discriminate anomalous patterns. On the SWaT dataset, adjustments to the latent vector dimension cause fluctuations in the GAN-SAGE’s performance, but its precision remains relatively stable. On the WADI dataset, the lowest F1-score is observed when , with the model performing better at larger latent vector dimensions, possibly due to the high-dimensional of WADI dataset, which makes it difficult for the model to effectively represent complex features at lower latent vector dimensions.
The influence of sliding window sizes L is shown in the experimental results of Figure 7. The latent vector dimension is selected, respectively. GAN-SAGE achieves the best overall performance on the AIOps, SWaT and WADI datasets with sliding window sizes 100, 50 and 20, respectively. On the AIOps dataset, GAN-SAGE performs best with the largest sliding window size, possibly due to network interactions and information transfer requiring a longer time window to provide rich contextual information. In contrast, GAN-SAGE’s performance on the SWaT and WADI datasets is more sensitive to anomalies with relatively shorter time windows.
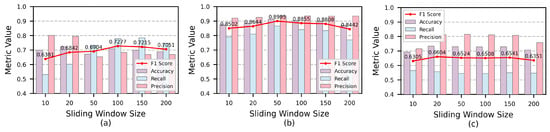
Figure 7.
Performance metrics of hyperparameter sliding window size L: (a) experiments on AIOps; (b) experiments on SWaT; (c) experiments on WADI.
GAN-SAGE on the AIOps dataset exhibits higher F1-score with larger time windows, while the recall significantly decreases when , possibly because smaller time windows limit the model’s ability to capture effective contextual information. On the SWaT dataset, GAN-SAGE’s performance declines when , possibly due to larger sliding windows introducing more noise, making smaller anomalies less detectable. On the WADI dataset, GAN-SAGE demonstrates good robustness to changes in sliding window size, with the sliding window size having minimal impact on the F1-score.
4.6. Comparative Experiments
To validate GAN-SAGE’s effectiveness, we compare it with seven existing methods, including three network representation-based methods, GAT, TAGCN and FT-GCN, and four reconstruction-based methods, AnomalyDAE, DOMINANT, BeatGAN and ConGNN:
GAT []: This model is an attention-based GNN that assigns different weights to nodes in a node’s neighborhood through an attention mechanism.
TAGCN []: This model introduces a set of filters that can adapt to different sensory field sizes to implement graph convolution, which can flexibly capture different levels of local features.
FT-GCN []: This model takes into account traffic topology and temporal correlation and learns a combinatorial representation of features based on GCN.
AnomalyDAE []: This model uses two AEs to obtain embedded representations of graph structures and attributes, and ultimately uses reconstruction errors for anomaly detection.
DOMINANT []: This model learns node embeddings based on GCN, combined with an AE to reconstruct the original data, detecting anomalies by separately calculating the reconstruction errors of attributes and structure.
BeatGAN []: This model combines AE and GAN to augment time-series data with corrected time warping to reconstruct the time series by adversarial training.
ConGNN []: This model proposes a controlled GNN with denoising diffusion, which guides the neighborhood aggregation in GNN through a graph-specific generator to compute the representation of the target node.
The results of the detection performance including accuracy, recall, precision, and F1-score are obtained after the experiments as shown in the Table 1.

Table 1.
Comparative experimental results (%).
Table 1 demonstrates the experimental data of GAN-SAGE with the other seven comparative methods, and GAN-SAGE achieves the highest F1-score on three datasets, proving the GAN-SAGE’s effectiveness.
In network representation-based methods, FT-GCN achieves a higher F1-score on the AIOps dataset compared to GAT and TAGCN, demonstrating stronger modeling capabilities for temporal correlations. This suggests that precise extraction of temporal features on the AIOps dataset significantly enhances detection performance. Compared to FT-GCN, GAN-SAGE not only precisely extracts temporal features but also considers global dependency features under complex network structures, thereby characterizing more accurate network behavior patterns and achieving better performance across three datasets. GAT exhibits the poorest performance on the AIOps dataset, likely due to its suboptimal performance in scenarios where temporal features are important. This underscores the importance of considering temporal features in the processing of graph time-series data. While both GAN-SAGE and GAT utilize attention mechanisms, GAN-SAGE more effectively extracts temporal features, resulting in superior performance compared to GAT. TAGCN outperforms GAT and FT-GCN on the SWaT dataset and shows a minimal difference in F1-score compared to GAT on the WADI dataset. This may stem from TAGCN’s filters offer stronger adaptability to the network, enabling the extraction of multi-scale local features, while its graph convolution layer’s aggregation function effectively reduces noise in node features. Both TAGCN and GAN-SAGE precisely extract network features, but GAN-SAGE emphasizes global dependencies. In attributed networks with complex structures, GAN-SAGE can more comprehensively characterize network features, thereby achieving better detection performance. Compared to the GAT, TAGCN and FT-GCN methods, the GAN-SAGE method exhibits improved performance. On the WADI dataset, TAGCN achieves a higher recall than GAN-SAGE, indicating that effective local contextual information in graphs facilitates anomaly detection. However, GAN-SAGE leverages node Laplacian positional feature vectors to represent network structural information, incorporating long-distance dependency graph information through GT without sacrificing local context, thereby providing more comprehensive graph features and achieving a higher F1 score.
In reconstruction-based methods, ConGNN outperforms AnomalyDAE, DOMINANT and BeatGAN across all three datasets. ConGNN enhances network features by leveraging controlled GNN to incorporate node neighborhood information, achieving good detection performance through learning clearer detection boundaries. However, it faces the issue of insufficient feature extraction in the temporal dimension when capturing attributed network characteristics under temporal evolution, resulting in inferior performance compared to GAN-SAGE across three datasets. AnomalyDAE and DOMINANT consider attribute and structural features through autoencoders, their performance declines in complex scenarios, underperforming compared to GAN-SAGE, which captures attribute and structural information within an adversarial framework. This highlights the capability of the adversarial framework, where incorporating adversarial training during reconstruction is increasingly valuable, as it enhances the model’s robustness across different data distributions and reducing its sensitivity to variations in data characteristics. On the AIOps dataset and the WADI dataset, BeatGAN demonstrates better recall than ConGNN, AnomalyDAE and DOMINANT, as it enhances processing for time series data, making it more sensitive to temporal anomalies. However, this may lead to more false positives, resulting in lower precision for BeatGAN. Both BeatGAN and GAN-SAGE enhance the processing of temporal information, but GAN-SAGE provides a richer perspective for temporal features through frequency-domain decomposition, thereby improving the accuracy.
Comparative analysis reveals that while reconstruction-based methods achieve more detailed and sensitive detection through precise representation and reconstruction of network features, their performance on the WADI dataset drops significantly. This is possibly due to the high-dimensional characteristics of the WADI dataset, where reconstruction-based methods are susceptible to interference in noisy and highly complex scenarios, leading to limitations and instability in maintaining accurate feature learning. Compared to ConGNN, AnomalyDAE and DOMINANT, BeatGAN and GAN-SAGE show better adaptability to dataset variations, with its performance less affected by data scenarios. This may be attributed to the adversarial training mechanisms of BeatGAN and GAN-SAGE, which improve the quality of reconstructed samples, maintaining some generalization performance in complex scenarios.
4.7. Ablation Experiments
To validate the effectiveness of GAN-SAGE’s key components, this section designs six variants of GAN-SAGE. As shown in Table 2, the full GAN-SAGE model is denoted as Scheme 1, and the six ablated variants are labeled as Schemes 2–7. By systematically removing different components and evaluating the model’s performance, the impact of each component on anomaly detection can be intuitively demonstrated.

Table 2.
Ablation experimental results (%).
Scheme 1 is the proposed complete model. It acquires time-domain information through spectral-augmentation, extracts latent vectors containing internal interactions and external long-distance dependencies in multi-attribute graph joint embedding, and further constrains the network representation through adversarial training, achieving the highest overall performance on three datasets.
Scheme 2 inadequately extracts temporal features, and struggles to effectively capture the dynamic changes in network behavior. Since network anomalies often appear over time, this leads to reduced anomaly detection performance.
Scheme 3 utilizes DWT to decompose time-series data, obtaining time-frequency components at different scales, but it does not perform frequency targeted enhancement. Compared to Scheme 2, Scheme 3 achieves higher F1-score across three datasets, indicating that the multi-scale information beneficial for anomaly detection. However, Scheme 3 shows lower performance compared to Scheme 1, demonstrating the effectiveness of frequency targeted enhancement in improving feature quality.
Scheme 1 outperforms Scheme 4 in anomaly detection by approximately 7.1%, 3.1% and 9.5% on the AIOps, SWaT and WADI datasets, indicating that relying solely on temporal features in attributed networks is insufficient to comprehensively capture network anomalies. While temporal features can reveal temporal correlations in network behavior, they are inadequate for fully capturing anomalies in complex attributed networks.
Scheme 5 removes the multi-attribute coupling from Scheme 1, directly performing graph joint embedding on the spectrally augmented time-series data. The higher F1-score of Scheme 1 indicates that the multi-attribute interaction features extracted through multi-attribute coupling can effectively indicate network anomalies.
Compared to Scheme 6 without an adversarial training framework, Scheme 1 demonstrates improved detection performance, validating the effectiveness of incorporating adversarial training in the reconstruction process. Scheme 6 can capture the latent representation of the attributed network, but it is insufficient to ensure robust characterization of normal samples. Adversarial training in Scheme 1 further guides the latent representation learning to better align with the feature distribution of normal data, thereby enhancing its effectiveness for anomaly detection.
Scheme 7 employs an adversarial training framework but does not include the synchronous encoder, leading to lower F1-score on three datasets compared to Scheme 1. This could be attributed to the absence of encoding loss and content loss guidance, which may cause semantic drift in the latent representation and, thus, diminishing its ability to detect anomalies.
Therefore, it can be concluded that the GAN-SAGE better learns temporal features in attributed networks, with contributions from its modules in extracting temporal and multi-attribute joint embedding features collectively enhancing anomaly detection performance.
5. Conclusions
Considering the limitations of existing methods in adequately capturing complex interaction features under time evolution, this paper proposes an adversarial reconstruction framework with spectral-augmented and graph joint embedding for anomaly detection. The proposed method GAN-SAGE uses DWT and frequency targeted enhancement to, respectively, decompose the time series into trend and detail components, and to extract temporal features more efficiently by decomposing the complex temporal patterns and enhancing the expansion of spectral features. In addition, the ability of the model to capture complex interaction features under the global structure is enhanced by multi-attribute graph joint embedding. We conducted extensive experiments on three public datasets, visualizing their anomaly score distributions and the detection process. We analyzed the impact of latent vector dimensions and time window size parameters to evaluate the GAN-SAGE’s performance under different conditions. The experimental results demonstrating that the GAN-SAGE outperforms seven state-of-the-art methods in attributed network scenarios, achieving average F1 score improvements of 9.64%, 18.73% and 19.79% across the three datasets, while detailed ablation studies confirmed the effectiveness of different components and overall performance. Considering the increasing complexity of network environments and the evolving tactics of attackers, future research will explore combining network feature extraction methods with other graph learning techniques to further enhance anomaly detection performance, particularly in identifying patterns of stealthy attacks.
Author Contributions
Conceptualization, L.Y. and J.W.; methodology, L.Y., J.W., Q.C. and G.Y.; software, L.Y.; validation, L.Y. and J.W.; formal analysis, L.Y., J.W. and G.Y.; investigation, L.Y., J.W. and Q.C.; resources, J.W. and Q.C.; data curation, L.Y.; writing—original draft preparation, L.Y.; writing—review and editing, L.Y., J.W., Q.C. and G.Y.; visualization, L.Y. and G.Y.; supervision, J.W. and Q.C.; project administration, J.W. and Q.C.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Institute of Next-Generation Network Intelligent Operations & Security Trusted Technology Enterprise-School Joint Innovation Center of Hubei Province and by the Technology Innovation Program (2025CDB027) funded by the Department of Science and Technology of Hubei Province.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available at https://github.com/NetManAIOps/AIOps-Challenge-2020-Data (accessed on 10 November 2024) and https://itrust.sutd.edu.sg/itrust-labs_datasets/ (accessed on 2 November 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Huang, X.; Li, J.; Hu, X. Label informed attributed network embedding. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017; pp. 731–739. [Google Scholar]
- Roshanaei, M.; Khan, M.R.; Sylvester, N.N. Enhancing cybersecurity through AI and ML: Strategies, challenges, and future directions. J. Inf. Secur. 2024, 15, 320–339. [Google Scholar] [CrossRef]
- Akoglu, L.; Tong, H.; Koutra, D. Graph based anomaly detection and description: A survey. Data Min. Knowl. Discov. 2015, 29, 626–688. [Google Scholar] [CrossRef]
- Husák, M.; Čermák, M. A graph-based representation of relations in network security alert sharing platforms. In Proceedings of the 2017 IFIP/IEEE Symposium on Integrated Network and Service Management (IM), Lisbon, Portugal, 8–12 May 2017; pp. 891–892. [Google Scholar]
- Bashar, M.A.; Nayak, R. TAnoGAN: Time series anomaly detection with generative adversarial networks. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, 1–4 December 2020; pp. 1778–1785. [Google Scholar]
- Yu, W.; Cheng, W.; Aggarwal, C.C.; Zhang, K.; Chen, H.; Wang, W. NetWalk: A flexible deep embedding approach for anomaly detection in dynamic networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; pp. 2672–2681. [Google Scholar]
- Sabuhi, M.; Zhou, M.; Bezemer, C.-P.; Musilek, P. Applications of generative adversarial networks in anomaly detection: A systematic literature review. IEEE Access 2021, 9, 161003–161029. [Google Scholar] [CrossRef]
- Lim, W.; Yong, K.S.C.; Lau, B.T.; Tan, C.C.L. Future of generative adversarial networks (GAN) for anomaly detection in network security: A review. Comput. Secur. 2024, 139, 103733. [Google Scholar] [CrossRef]
- Zhang, D.; Yin, J.; Zhu, X.; Zhang, C. Network representation learning: A survey. IEEE Trans. Big Data 2018, 6, 3–28. [Google Scholar] [CrossRef]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Li, J.; Shao, H.; Sun, D.; Wang, R.; Yan, Y.; Li, J.; Liu, S.; Tong, H.; Abdelzaher, T. Unsupervised belief representation learning with information-theoretic variational graph auto-encoders. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–14 July 2022; pp. 1728–1738. [Google Scholar]
- Wang, D.; Yan, Y.; Qiu, R.; Zhu, Y.; Guan, K.; Margenot, A.; Tong, H. Networked time series imputation via position-aware graph enhanced variational autoencoders. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 2256–2268. [Google Scholar]
- Goyal, P.; Hosseinmardi, H.; Ferrara, E.; Galstyan, A. Capturing edge attributes via network embedding. IEEE Trans. Comput. Soc. Syst. 2018, 5, 907–917. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Makarov, I.; Korovina, K.; Kiselev, D. Jonnee: Joint network nodes and edges embedding. IEEE Access 2021, 9, 144646–144659. [Google Scholar] [CrossRef]
- Di Giovanni, F.; Giusti, L.; Barbero, F.; Luise, G.; Liò, P.; Bronstein, M.M. On over-squashing in message passing neural networks: The impact of width, depth, and topology. In Proceedings of the International Conference on Machine Learning (ICML 2023), Honolulu, HI, USA, 23–29 July 2023; pp. 7865–7885. [Google Scholar]
- Barceló, P.; Kostylev, E.V.; Monet, M.; Pérez, J.; Reutter, J.; Silva, J.-P. The logical expressiveness of graph neural networks. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Ying, C.; Cai, T.; Luo, S.; Zheng, S.; Ke, G.; He, D.; Shen, Y.; Liu, T.-Y. Do transformers really perform badly for graph representation? Adv. Neural Inf. Process. Syst. 2021, 34, 28877–28888. [Google Scholar]
- Müller, L.; Galkin, M.; Morris, C.; Rampášek, L. Attending to graph transformers. arXiv 2023, arXiv:2302.04181. [Google Scholar]
- Ma, X.; Wu, J.; Xue, S.; Yang, J.; Zhou, C.; Sheng, Q.Z.; Xiong, H.; Akoglu, L. A comprehensive survey on graph anomaly detection with deep learning. IEEE Trans. Knowl. Data Eng. 2021, 35, 12012–12038. [Google Scholar] [CrossRef]
- Gupta, S.; Bedathur, S. A survey on temporal graph representation learning and generative modeling. arXiv 2022, arXiv:2208.12126. [Google Scholar] [CrossRef]
- Deng, X.; Zhu, J.; Pei, X.; Zhang, L.; Ling, Z.; Xue, K. Flow topology-based graph convolutional network for intrusion detection in label-limited IoT networks. IEEE Trans. Netw. Serv. Manag. 2022, 20, 684–696. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Duan, J.; Huang, C.; Cao, D.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; Zhang, Q. Multivariate time-series anomaly detection via graph attention network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Virtual, 17–20 November 2020; pp. 841–850. [Google Scholar]
- Zhang, C.; Song, D.; Chen, Y.; Feng, X.; Lumezanu, C.; Cheng, W.; Ni, J.; Zong, B.; Chen, H.; Chawla, N.V. A deep neural network for unsupervised anomaly detection and diagnosis in multivariate time series data. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27–28 January 2019; pp. 1409–1416. [Google Scholar]
- Ding, K.; Li, J.; Bhanushali, R.; Liu, H. Deep anomaly detection on attributed networks. In Proceedings of the 2019 SIAM International Conference on Data Mining (SDM), Calgary, AB, Canada, 2–4 May 2019; pp. 594–602. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, P.; Zhu, W. Deep learning on graphs: A survey. IEEE Trans. Knowl. Data Eng. 2020, 34, 249–270. [Google Scholar] [CrossRef]
- Zhou, S.; Tan, Q.; Xu, Z.; Huang, X.; Chung, F.-l. Subtractive aggregation for attributed network anomaly detection. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Gold Coast, QLD, Australia, 1–5 November 2021; pp. 3672–3676. [Google Scholar]
- Bei, Y.; Zhou, S.; Tan, Q.; Xu, H.; Chen, H.; Li, Z.; Bu, J. Reinforcement neighborhood selection for unsupervised graph anomaly detection. In Proceedings of the 2023 IEEE International Conference on Data Mining (ICDM), Shanghai, China, 1–4 December 2023; pp. 11–20. [Google Scholar]
- Ma, X.; Wu, J.; Yang, J.; Sheng, Q.Z. Towards graph-level anomaly detection via deep evolutionary mapping. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 1631–1642. [Google Scholar]
- Gao, Y.; Wang, X.; He, X.; Liu, Z.; Feng, H.; Zhang, Y. Addressing heterophily in graph anomaly detection: A perspective of graph spectrum. In Proceedings of the ACM Web Conference, Austin, TX, USA, 30 April–4 May 2023; pp. 1528–1538. [Google Scholar]
- Wang, Y.; Zhang, J.; Guo, S.; Yin, H.; Li, C.; Chen, H. Decoupling representation learning and classification for GNN-based anomaly detection. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 11–15 July 2021; pp. 1239–1248. [Google Scholar]
- Pei, Y.; Huang, T.; Van Ipenburg, W.; Pechenizkiy, M. ResGCN: Attention-based deep residual modeling for anomaly detection on attributed networks. Mach. Learn. 2022, 111, 519–541. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Pan, S.; Gong, C.; Zhou, C.; Karypis, G. Anomaly detection on attributed networks via contrastive self-supervised learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2378–2392. [Google Scholar] [CrossRef]
- Jin, M.; Liu, Y.; Zheng, Y.; Chi, L.; Li, Y.-F.; Pan, S. Anemone: Graph anomaly detection with multi-scale contrastive learning. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Gold Coast, QLD, Australia, 1–5 November 2021; pp. 3122–3126. [Google Scholar]
- Deng, A.; Hooi, B. Graph neural network-based anomaly detection in multivariate time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 19–21 May 2021; pp. 4027–4035. [Google Scholar]
- Du, J.; Zhang, S.; Wu, G.; Moura, J.M.; Kar, S. Topology adaptive graph convolutional networks. arXiv 2017, arXiv:1710.10370. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Park, J.; Lee, M.; Chang, H.J.; Lee, K.; Choi, J.Y. Symmetric graph convolutional autoencoder for unsupervised graph representation learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6519–6528. [Google Scholar]
- Fan, H.; Zhang, F.; Li, Z. AnomalyDAE: Dual autoencoder for anomaly detection on attributed networks. In Proceedings of the ICASSP 2020–IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Virtual, 4–9 May 2020; pp. 5685–5689. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Langs, G.; Schmidt-Erfurth, U. f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Med. Image Anal. 2019, 54, 30–44. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, S.; Hooi, B.; Cheng, X.; Ye, J. BeatGAN: Anomalous rhythm detection using adversarially generated time series. In Proceedings of the International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 4433–4439. [Google Scholar]
- Qu, X.; Liu, Z.; Wu, C.Q.; Hou, A.; Yin, X.; Chen, Z. MFGAN: Multimodal fusion for industrial anomaly detection using attention-based autoencoder and generative adversarial network. Sensors 2024, 24, 637. [Google Scholar] [CrossRef] [PubMed]
- Ding, K.; Li, J.; Agarwal, N.; Liu, H. Inductive anomaly detection on attributed networks. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 1288–1294. [Google Scholar]
- Guo, D.; Liu, Z.; Li, R. RegraphGAN: A graph generative adversarial network model for dynamic network anomaly detection. Neural Netw. 2023, 166, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.; Pan, X.; Li, N.; He, X.; Ma, L.; Zhang, X.; Ding, N. GAN-based anomaly detection: A review. Neurocomputing 2022, 493, 497–535. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 63, 139–144. [Google Scholar]
- Mohamed, S.; Lakshminarayanan, B. Learning in implicit generative models. arXiv 2016, arXiv:1610.03483. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Dwivedi, V.P.; Bresson, X. A generalization of transformer networks to graphs. arXiv 2020, arXiv:2012.09699. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- AIOps-Challenge-2020-Data. Available online: https://github.com/NetManAIOps/AIOps-Challenge-2020-Data (accessed on 10 November 2024).
- Goh, J.; Adepu, S.; Junejo, K.N.; Mathur, A. A dataset to support research in the design of secure water treatment systems. In Proceedings of the International Conference on Critical Information Infrastructures Security, Paris, France, 10–12 October 2016; pp. 88–99. [Google Scholar]
- Ahmed, C.M.; Palleti, V.R.; Mathur, A.P. WADI: A water distribution testbed for research in the design of secure cyber physical systems. In Proceedings of the 3rd International Workshop on Cyber-Physical Systems for Smart Water Networks, Pittsburgh, PA, USA, 21 April 2017; pp. 25–28. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Li, X.; Xiao, C.; Feng, Z.; Pang, S.; Tai, W.; Zhou, F. Controlled graph neural networks with denoising diffusion for anomaly detection. Expert Syst. Appl. 2024, 237, 121533. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).