Gradual Improvements in the Visual Quality of the Thin Lines Within the Random Grid Visual Cryptography Scheme

Abstract

The visual cryptography scheme (VCS) is a fundamental image encryption technique that divides a secret image into two or more shares, such that the original image can be revealed by superimposing a sufficient number of shares. A major limitation of conventional VCS methods is pixel expansion, wherein the generated shares and reconstructed image are typically at least twice the size of the original. Additionally, thin lines or curves—only one pixel wide in the original image—often appear distorted or duplicated in the reconstructed version, a distortion known as the thin-line problem (TLP). To eliminate the reliance on predefined codebooks inherent in traditional VCS, Kafri introduced the Random Grid visual cryptography scheme (RG-VCS), which eliminates the need for such codebooks. This paper introduces novel algorithms that are among the first to explicitly address the thin-line problem in the context of random grid based schemes. This paper presents novel visual cryptography algorithms specifically designed to address the thin-line preservation problem (TLP), which existing methods typically overlook. A comprehensive visual and numerical comparison was conducted against existing algorithms that do not explicitly handle the TLP. The proposed methods introduce adaptive encoding strategies that preserve fine image details, fully resolving TLP-2 and TLP-3 and partially addressing TLP-1. Experimental results show an average improvement of 18% in SSIM and 13% in contrast over existing approaches. Statistical t-tests confirm the significance of these enhancements, demonstrating the effectiveness and superiority of the proposed algorithms.

1. Introduction

The foundational principles of the deterministic visual cryptography scheme ($\mathit{D-VCS}$) were first formally introduced by Naor and Shamir [1]. As outlined in [1], the core concept of $\mathit{D-VCS}$ involves dividing a secret image into two or more random shares, each of which individually does not reveal any information about the original image. When the appropriate shares are overlaid—where “overlaying” refers to the application of the logical OR operation—the hidden image becomes visible. Given a secret image (SI) as input, a typical $VCS(k,n)$ generates n shares (images) that satisfy two key conditions: (1) any combination of k or more of the n shares can reconstruct the secret image (SI), and (2) any subset of fewer than k shares reveals no information about the secret image.

The size of the revealed image (RI) and the shares in the deterministic visual cryptography scheme ($\mathit{D-VCS}$) is typically at least twice that of the secret image (SI), athough the visual quality of the RI remains generally high. The primary limitation of $\mathit{D-VCS}$ is the pixel expansion problem. To address this issue, Yang [2] proposed a non-expansion method known as the probabilistic size-invariant visual cryptography scheme ($\mathit{P-SIVCS}$), which eliminates pixel expansion but results in RIs with reduced visual quality. Subsequently, Hou and Tu [3] introduced a multipixel size-invariant visual cryptography scheme ($\mathit{M-SIVCS}$) that incorporates both variance and contrast considerations. Consequently, the $\mathit{M-SIVCS}$ generates higher-quality RIs than the $\mathit{P-SIVCS}$.

Further advancements were made by Yan [4] and Sun [5], who improved $\mathit{M-SIVCS}$ by applying forward and backward operations between the revealed and secret images to optimize the halftoning techniques and encryption process. However, their algorithms are limited to grayscale images, specifically to $\mathit{M-SIVCS}(n,n)$, restricting their applicability to random grid VCS ($\mathit{RG-VCS}$), which is discussed later in this paper. In addition, their methods face challenges with thin lines, which are common in binary images. Wu [6] later proposed algorithms aimed at enhancing the contrast of the $\mathit{M-SIVCS}$.

Fine details, such as maps and shapes represented by thin lines, frequently appear in SIs. A thin line is defined as a line or curve that is one pixel thick, either black on a white background or white on a black background (Figure 1a–c). When $\mathit{P-SIVCS}$ is applied to such SIs, the resulting RI often suffers from ambiguity, and thin lines become difficult to discern because of low visual quality. This issue was initially termed as the thin-line problem (TLP-1). Two additional problems were later identified in the context of the $\mathit{M-SIVCS}$: TLP-2, in which certain parts of the RI lacked vertical or horizontal lines, and TLP-3, in which thin vertical or horizontal lines in the RI appeared thickened. Further details on these issues are provided in Section 3.

Figure 1. The data set used to analyze the proposed algorithms was labeled 1 to 24, starting with the top left image. The last row (a–e) contains the original image that serve as visual references to compare the proposed algorithm with other algorithms.

Liu et al. [7] evaluated four algorithms for this purpose. The third algorithm is particularly susceptible to TLP-3. On the other hand, the fourth Algorithm addresses all three problems (TLP-1, TLP-2, and TLP-3), but its security guarantees are weaker than conventional standards. Furthermore, some images produced by the fourth Algorithm lacked the visual clarity achieved by the $\mathit{D-VCS}$, partly due to residual effects of TLP-1. Despite these improvements, the algorithms still depend on codebooks.

The $\mathit{RG-VCS}$ scheme without a codebook was first proposed by Kafri [8]. However, it is subject to the same limitation as $\mathit{P-SIVCS}$, namely, the generation of low-quality reconstructed images (RIs). To address this issue, Hu [9] proposed algorithms aimed at improving the visual quality in random grids. In 2024, Wafy [10] introduced two algorithms that enhanced the visual quality of random grids; however these did not effectively resolve the thin-line problem. To the best of the author’s knowledge, the thin-line problem (TLP) has not previously been addressed within the context of random grid visual cryptography schemes ($\mathit{RG-VCS}$). This paper introduces two novel algorithms that, for the first time, explicitly address the thin-line problem (TLP) within the $\mathit{RG-VCS}$ framework. In addition to addressing this problem, the proposed algorithms offer several improvements.

• Effectively solve TLP-2 and TLP-3, and partly solve TLP-1.
• Enhance the contrast of the reconstructed images for both grayscale and binary images.
• Improve the local contrast and local pixel correlation, thus contributing to the overall visual quality and structural consistency of the generated random grids.

The remainder of this paper is organized as follows. Section 2 provides traditional definitions and background on the $\mathit{D-VCS}$, $\mathit{P-SIVCS}$, $\mathit{M-SIVCS}$, and $\mathit{RG-VCS}$. Section 3 introduces two proposed algorithms. The experimental results and analyses are presented in Section 4. Finally, Section 5 concludes the paper and offers directions for future research.

2. Background and Definitions

Algorithms in the visual cryptography scheme ($VCS$) can be broadly classified into three categories: deterministic visual cryptography schemes ($\mathit{D-VCSs}$), probabilistic size-invariant $VCSs$ ($\mathit{P-SIVCSs}$), and random grid $VCSs$ ($\mathit{RG-VCSs}$). Within the $\mathit{D-VCSs}$, we further distinguish between two types: $\mathit{D-VCSs}$ with pixel expansion ($\mathit{D-SEVCSs}$) and multipixel size-invariant $VCS$ ($\mathit{M-SIVCSs}$). Both the $\mathit{D-VCSs}$ and $\mathit{P-SIVCSs}$ rely on Boolean matrices, commonly referred to as codebooks, whereas the $\mathit{RG-VCS}$ operates without the need for codebooks. In this paper, pixel values are represented such that white is denoted by 0 and black by 1.

Definition 1 

($\mathit{D-SEVCS}(n,k)$). The two collections of Boolean matrices, for example $C_0,C_1$ (both matrices have the same dimension, $n\times m$), are $\mathit{D-SEVCS}$ if they satisfy the following two conditions:

1. 

Security: Let $f_0,f_1$ be the two functions that count the frequencies of rows $r_1,\dots ,r_l$ in $C_0$ and $C_1$, respectively. Then, $f_0\left(r_1\right)=f_1\left(r_1\right),\dots ,f_0\left(r_l\right)=f_1\left(r_l\right),l\le n$.

2. 

Contrast: Assume that $d,\alpha$ and $k,n,m$ are nonnegative integers that satisfy $1\le d\le m$ and $2\le k\le n$. $H\left(V\right)<d-\alpha \times m$ is satisfied if any k of the n rows executes the $OR$ operation for any S in $C_0$.

Example 1. 

Suppose $n=m=2$. Let $C_0$ and $C_1$ be two collections.

$$C_1=\left\{\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\right\},C_0=\left\{\left[\begin{array}{cc}0& 1\\ 0& 1\end{array}\right],\left[\begin{array}{cc}1& 0\\ 1& 0\end{array}\right]\right\}$$

(1)

• For each pixel in the secret image ($SI$), if the pixel is black (resp. white), randomly selecting matrix $a_1\in C_1$ (resp. $a_0\in C_0$).
• First row of $a_1$ (resp. $a_0$) in the first share $s{h}_1$ and the second row of $a_1$ (resp. $a_0$) on the $s{h}_2$. With two pixels representing each pixel in the image $SI$ in each share, the size of the revealed image (RI) was twice that of the secret image $SI$.
• A two-pixel (=row in matrix a) cannot determine whether it comes from $C_0$ or $C_1$, because every row in a matrix, $a\in$($C_0/C_1$) has an equal number of ones and zeros. The number of trials is $2^z$, and z is the image size to obtain the secret image from a single share. In addition, random matrix selection a ensures that we cannot distinguish between shares.

The aforementioned algorithm was designed specifically for binary images. However, subsequent algorithms, including our proposed algorithms, employ a halftoning technique to convert gray-scale images into binary format before applying the visual cryptography process. Consequently, the proposed algorithms are also applicable to gray scale images.

The pixel expansion problem in $\mathit{D-SEVCS}(k,n)$ was addressed by Yang [2], although this solution resulted in a low visual quality. Although the global contrast between the black and white pixels was statistically preserved across the entire image, the local contrast distribution exhibited a considerable variance.

To enhance the local contrast within small regions, such as a block of adjacent pixels (two pixels or more), Tu and Hou [11] proposed an algorithm that improves visual quality without introducing pixel expansion in $\mathit{D-SEVCS}(k,n)$.

Definition 2 

($\mathit{M-SIVCS}(k,n)$). Let $SI$ be a secret image, and we have shares $s{h}_1,\dots ,s{h}_n$. The block $B_{b,m}\in SI$, with size m and b is the number of black pixels in the block $B_{b,m}\in SI$, $b=0,\dots ,m.$ Matrix M is randomly selected from $C_0$ or $C_1$ according to the following rule:   

$$M\in \left\{\begin{array}{cc}{C}_1\hfill & \mathit{if}b>{\displaystyle \frac{m}{2}}\hfill \\ C_0\hfill & \mathit{if}b<{\displaystyle \frac{m}{2}}\hfill \\ \mathit{alternatively}{C}_1\mathit{or}{C}_0\hfill & \mathit{if}b={\displaystyle \frac{m}{2}}\hfill \end{array}\right.$$

(2)

Then, the matrix M is distributed on shares $s{h}_1,\dots ,s{h}_n$. m in this algorithm must be a square matrix.

Suppose that block $B_{b,2}$ consists of two pixels in the secret image (SI), one of which is black and the other white, that is $b=1$. When applying Tu’s algorithm, block $B_{b,m}$ is encoded using either $C_0$ or $C_1$, resulting in a loss of either black or white pixels. By contrast, according to Liu’s algorithm, a pixel block containing b black pixels is encrypted exactly b times using $C_0$.

Definition 3 

(Liu’s algorithm $\mathit{M-SIVCS}(k,n)$). Let $C_0$ and $C_1$, two $n\times m$ matrices, and be the basis matrices of a $\mathit{D-SEVCS}(k,n)$. The next procedure encrypts one block, $B_{b,m}$. Specify b as the number of black pixels in the block, and m as the block size and pixel expansion of the corresponding $\mathit{D-SEVCS}$. Specify the number of blocks $\left(E\right[b\left]\right)$ that have already undergone encryption and have b black pixels; $B_{b,m}$ is the block of the secret image.

• for $b=0:m$
  •   for $E\left[b\right]=0:q_1$ ($q_1$ is the total number of blocks in the secret image)
  •      Encrypt $B_{b,m}$ by $C_1$ after randomly permuting its columns if $\left(E\right[b\left]modm\right)<b$
  •      Else encrypt $B_{b,m}$ using $C_0$ after randomly rearranging its columns
  •      $E\left[b\right]=E\left[b\right]+1$
  •   end
• end

The issue with Tu’s algorithm is partially addressed by the algorithm presented above but remains unresolved.

For all algorithms discussed above, a codebook containing matrices $C_0$ and $C_1$ was employed. To overcome this limitation, Shyu [9,11,12] introduced a modified version of the Kafri [8] algorithm which is compatible with a random grid VCS ($\mathit{RG-VCS}$) and does not require a codebook.

Definition 4 

(Shyu [12] $\mathit{RG-VCS}(2,2)$). An $\mathit{RG-VCS}(2,2)$ scheme consists of two shares, constructed as follows:

1. 

The first share, denoted as $s{h}_1$, is generated using a uniform random distribution.

2. 

The second share, denoted as $s{h}_2$, is constructed based on the secret image $SI$ and the first share $s{h}_1$.

Let $x(i,j)\in SI$ represent a pixel in the secret image at position $(i,j)$, with corresponding pixels $y(i,j)\in s{h}_1$ and $z(i,j)\in s{h}_2$. All $SI$, $s{h}_1$, and $s{h}_2$ are of size $v\times w$. For all $1\le i\le v$ and $1\le j\le w$, the pixel values of $s{h}_2$ are defined as:

$$z(i,j)=\left\{\begin{array}{cc}y(i,j)\hfill & \mathit{if}x(i,j)=0(\mathit{white}\mathit{pixel})\hfill \\ \overline{y(i,j)}\hfill & \mathit{if}x(i,j)=1(\mathit{black}\mathit{pixel})\hfill \end{array}\right.$$

(3)

where $\overline{h}$ denotes the logical negation of the value h.

Shyu proved the following security condition.

Theorem 1 

(Shyu [12] $\mathit{RG-VCS}(2,2)$). Shyu’s construction satisfies the security condition for $\mathit{RG-VCS}(2,2)$, which requires that:

1. 

$Prob\left(y\right(i,j)=black)=Prob\left(y\right(i,j)=white)=0.5$;

2. 

$Prob\left(z\right(i,j)=black)=Prob\left(z\right(i,j)=white)=0.5$.

For all $1\le i\le v$ and $1\le j\le w$, where $y(i,j)\in s{h}_1$ and $z(i,j)\in s{h}_2$.

According to Shyu’s construction, if a pixel $x(i,j)\in SI$ is black and the corresponding pixel in the first share $y(i,j)\in s{h}_1$ is white (respectively, black), then based on Equation (3), the pixel $z(i,j)\in s{h}_2$ will be black (respectively, white). Consequently, the pixel $r(i,j)\in RI$ in the revealed image, computed as $r(i,j)=y(i,j)\otimes z(i,j)$ (⊗ is OR operation), will always be black. This guarantees that a black pixel in the secret image $SI$ will always appear as black in the reconstructed image $RI$, with a probability of 1.

On the other hand, if $x(i,j)\in SI$ is white, then $z(i,j)=y(i,j)$, meaning both $y(i,j)$ and $z(i,j)$ are identical. Since $y(i,j)$ is generated using a uniform random distribution, the resulting pixel $r(i,j)=y(i,j)\otimes y(i,j)$ will be white with probability $0.5$ and black with probability $0.5$. Therefore, the probability that a white pixel in $SI$ is reconstructed as white in $RI$ is ${\displaystyle \frac{1}{2}}$.

This analysis confirms that Equation (3) satisfies the contrast condition required for a valid $\mathit{RG-VCS}(2,2)$.

Shyu [12] introduced the definitions of two contrast measurements used in the $\mathit{RG-VCS}(2,2)$.

Definition 5. 

(Contrast) All white (resp. black) pixels in the SI as $G\left(0\right)$ (resp. $G\left(1\right)$) and $RI\left[G\right(0\left)\right]$ (resp. $RI\left[G\right(1\left)\right]$) is the corresponding pixels in RI. Let $Prob(.)$ be a probability function.

$$\alpha ={\displaystyle \frac{Prob\left(RI\right[G\left(0\right)\left]\right)-Prob\left(RI\right[G\left(1\right)\left]\right)}{1+Prob\left(RI\right[G\left(1\right)\left]\right)}}$$

(4)

Additionally, Shyu introduced the following practical definition of contrast, derived from experimental data.

Definition 6 

(Experimental Contrast). Let the total number of white pixels in the RI (revealed image) be $G\left(0\right)$ and z be the size of the RI. Experimental contrast (EC):

$$EC={\displaystyle \frac{G\left(0\right)}{z}}.$$

(5)

Although the white and black pixels in Shyu’s algorithm are uniformly distributed, the contrast is minimal. Although Shyu’s algorithm guarantees global contrast through a uniform distribution of black and white pixels, the local contrast varies significantly.

In 2018, Hu [13] modified Shyu’s algorithm for $\mathit{RG-VCS}(n,k)$; however, for the case of $\mathit{RG-VCS}(2,2)$, Hu’s algorithm is essentially identical to Shyu’s algorithm. By refining the share selection methods, Wafy [10] (2024) introduced two algorithms that incorporated the concept of an encrypted pixel block within a random grid for the first time. In comparison, Hu’s algorithm is less effective than Wafy’s.

Wafy’s algorithm produces the results shown in Figure 2a–c and Figure 3a–c. In these figures, parts of the horizontal and vertical lines are missing from the revealed image (RI), as shown in Figure 2a,b and Figure 3a,b, which indicates the presence of issue TLP-2. This problem affects the local correlation between the secret image (SI) and RI. Additionally, some horizontal lines in the RI are thicker than their corresponding lines in the SI, illustrating the occurrence of TLP-3.

Figure 2. The top row shows the Wafy [10] (Algorithm 1) for $\mathit{RG-VCS}(2,2)$ in (a–c). The bottom row shows the Algorithm 2 for $\mathit{RG-VCS}(2,2)-1$ in (d,e) and the Algorithm 3$\mathit{RG-VCS}(2,2)-3$ in (f).

Figure 3. (a,b) represent Wafy [10] (Algorithm 1) for $\mathit{RG-VCS}(3,5)$ and $\mathit{RG-VCS}(4,4)$ in (c). The bottom row shows Algorithm 2 for $\mathit{RG-VCS}(3,5)-1$ in (d,e) and Algorithm 3 for $\mathit{RG-VCS}(4,4)-2$ in (f).

The proposed algorithm addresses the local contrast problem with two modifications: First, a uniform distribution is applied to each block of pixels rather than to individual pixels, as in the previous approaches. In addition, both algorithms satisfy Shyu’s security condition. However, in this study, we specifically adhered to Shyu’s security condition as outlined above.

Algorithm 1 Wafy [10] $\mathit{RGV-VCS}(k,n)$

Input: An SI is $A_{v\times w}$, where a pixel $x(i,j)\in A_{v\times w}$. Output: n random grids $R_1,R_2,\dots ,R_n$. Step 1: When two adjacent pixels, denoted as $x(i,j)$ and $x(i,j+1)$, exhibit mixed    connectivity, where one pixel is black and the other is white, they are randomly    reassigned to either black or white to ensure consistency in the pixel representation. Step 2: Randomly select block size m for block $B_{b,m}$, where m can take values of 1, 2, or    4, corresponding to block sizes of one pixel ($B_{b,1}$), two pixels ($B_{b,2}$), or four pixels    ($B_{b,4}$), respectively. Step 3: A matrix a is randomly selected from the set $C_0\cup C_1$, as defined in Equation (1). Step 4: If $m=4$ pixels, then matrix a is distributed $R_1$.    In the case where $m=2$, column d is randomly selected from matrix a and is    distributed over share $R_1$.    When $m=1$, a single element is randomly selected from the matrix a and assigned     to region $R_1$. Step 5: Repeat steps 2–4 above to include all pixels in $R_1$ (first share). Step 6: Repeat steps 2–5 to generate the remaining shares $R_2,\dots ,R_{k-1}$ Step 7: For $h=0:(n-(k-1\left)\right)$. $r_{k+h}=x(i,j)\oplus r_{k+h-1}\oplus \dots \oplus r_{h+1}$, where ⊕ is XOR logical operation, end Step 8: Randomly permute pixels $r_1,\dots ,r_n$, and subsequently distribute them to $R_1,\dots ,R_n$. Step 9: Repeat steps 7–8 above to include all pixels in $A_{v\times w}$.

3. Proposed Algorithms

This section introduces the first two algorithms that address the thin-line problem in $\mathit{RG-VCS}$ while ensuring high visual quality.

Let the probabilities of selecting a block $B_{b,m}$ with $b=0,\dots ,m$ be denoted as $p_0,\dots ,p_m$, respectively. The stacking operation (OR-logical operation) ⊗ for shares $R_1,\dots ,R_k$ is defined as

$$R_{1,\dots ,k}=R_1\otimes R_2\otimes \dots \otimes R_k.$$

(6)

Algorithm 2 guarantees a high-quality visual experience by enhancing the sharpness of thin lines.

Algorithm 2$\mathit{RG-VCS}(k,n)-1$

Input: An SI is $A_{v\times w}$, where a pixel $x(i,j)\in A_{v\times w}$. Output: n shares (random grid) $R_1,R_2,\dots ,R_n$ of size $v\times w$. Step 1: Select a block $B_{b,m}$ containing b black pixels with probability $p_b$, $b=0,\dots ,m$. Step 2: Randomly select blocks $B_{b_1,m}^1,\dots ,B_{b_2,m}^{k-1}$ subject to constraints $$B_{b,m}=B_{b_1,m}^1\otimes B_{b_2,m}^2\otimes \dots \otimes B_{b_l,m}^{k-1},$$ (7) where $b_1,\dots ,b_{k-1}$ represent a distinct number of black pixels in the corresponding blocks $B_{b_1,m}^1,\dots ,B_{b_{k-1},m}^{k-1}$. Step 3: Distribute blocks $B_{b_1,m}^1,\dots ,B_{b_{k-1},m}^{k-1}$ across shares $R_1,\dots ,R_{k-1}$. Step 4: To include every pixel in $R_1,\dots ,R_{k-1}$, repeat steps 1–3 above. Step 5: For $h=0:(n-(k-1\left)\right)$ $r_{k+h}=x(i,j)\oplus r_{k+h-1}\oplus \dots \oplus r_{h+1}$, where ⊕ is XOR logical operation, end Step 6: Randomly permute the pixels $r_1,\dots ,r_n$, and assign them to shares $R_1,\dots ,R_n$. Step 7: Repeat steps 5–6 above to include all pixels in $A_{v\times w}$.

For both the illustrative example and performance analysis of this algorithm, a block size of 2 was used; that is, $B_{b,2}$ was applied. Consequently, three probabilities, $p_0$, $p_1$, and $p_2$ corresponding to blocks $B_{0,2}$, $B_{1,2}$, and $B_{2,2}$, respectively, were considered. The following example demonstrates how to determine the values of these probabilities and illustrates Steps 1–3 of Algorithm 2.

Example 2. 

This example demonstrates two scenarios: first, the encryption scheme $\mathit{RG-VCS}(3,5)-1$, and second, the encryption scheme $\mathit{RG-VCS}(4,4)-1$. Consider a two pixels block $B_{b,2}$, where b is black pixels in $B_{b,2}$. For the $\mathit{RG-VCS}(3,5)-1$ encryption scheme,

• Let $R_a$ denote the result of stacking $R_1$ and $R_2$, that is $R_a=R_1\otimes R_2$. Let $R_3$ be the third share, defined as $R_3=R_a\otimes A_{v\times w}$, where $A_{v\times w}$ represents the secret image (SI). Block $B_{b,2}^a$ in $R_a$, for $b=0,1,2$, can take one of three possible forms: $B_{0,2}^a$, $B_{1,2}^a$, or $B_{2,2}^a$, each selected randomly with probabilities $p_0$, $p_1$, and $p_2$, respectively. For each b, block $B_{b,2}^a$ can be generated from a subset of a set of 16 pairs, where each pair consists of two blocks, $B_{b,2}^1$ from $R_1$ and $B_{b,2}^2$ from $R_2$, such that $B_{b,2}^a=B_{b,2}^1\otimes B_{b,2}^2$.
• Specifically, block $B_{0,2}$ in $R_a$ can be generated by stacking block $B_{0,2}^1$ (i.e.,) from $R_1$ with block $B_{0,2}^2$ (i.e.,) from $R_2$. Among the 16 possible combinations, only one pair results in $B_{0,2}^a$. Consequently, the probability of obtaining $B_{0,2}^a$ in $R_a$ is given by $p_0={\displaystyle \frac{1}{16}}$. Thus, the pair consisting of $B_{0,2}^1$ and $B_{0,2}^2$ is assigned to shares $R_1$ and $R_2$, respectively, with a probability $p_0={\displaystyle \frac{1}{16}}$.
• Block $B_{1,2}^a$, which contain one black and one white pixel, can be generated from six possible block pairings. Two of these pairings produce $B_{1,2}^a$ directly through

  $$B_{1,2}^a=B_{1,2}^1\otimes B_{1,2}^2$$

  (8)
  namely,⊗ and ⊗.
  The remaining four pairings involve one block have one white pixel and the other block has two white pixels⊗,⊗,⊗, or ⊗.
  As there are six equally likely pairings, the probability of selecting a $B_{1,2}^a$ block is $p_1={\displaystyle \frac{6}{16}}$.
  When a $B_{1,2}^a$ block is chosen, one of these six pairings is randomly assigned to shares $R_1$ and $R_2$.
• Block $B_{2,2}$, consisting of two black pixels, is selected with probability $p_2={\displaystyle \frac{9}{16}}$, similar to the selection process for the previous blocks.

In the encryption scheme denoted as $\mathit{RG-VCS}(4,4)-1$, the generation of $k-1=3$ shares, specifically $R_1,R_2,R_3$ ($R_a=R_1\otimes R_2\otimes R_3\otimes$), is performed as follows:

• Block $B_{0,2}^a$ can be constructed exclusively from three component blocks, $B_{0,2}^1$, $B_{0,2}^2$, and $B_{0,2}^3$, similar to $\mathit{RG-VCS}(3,5)-1$, with a probability of $p_0={\displaystyle \frac{1}{60}}$.
• The block $B_{1,2}^a$ is selected with a probability of $p_1={\displaystyle \frac{14}{60}}$.
• The block $B_{2,2}^a$ is selected with probability $p_2={\displaystyle \frac{45}{60}}$.

Algorithm 2 demonstrates superior performance compared to all previously proposed algorithms, as it preserves thin lines without any loss and maintains a high visual quality, as illustrated in Figure 2d. Furthermore, Algorithm 2 achieves an enhanced local contrast relative to the other algorithms.

However, in certain scenarios, Algorithm 3 exhibits a better performance than Algorithm 2 and offers the advantage of reduced computational complexity.

Algorithm 3$\mathit{RG-VCS}(k,n)-2$

Input: An SI is $A_{v\times w}$, where pixel $x(i,j)\in A_{v\times w}$. Output: n shares (random grid) $R_1,R_2,\dots ,R_n$ of size $v\times w$. Step 1: Distribute a block $B_{b,m}$ with probability $p_b$, where $b=0,\dots ,m$ on $R_1$ subject to $$ constraint $p_b=p_{(m-b)}$. Step 2: To ensure that every pixel is included in $R_1$, repeat Step 1 as described above. Step 3: Repeat Steps 1 and 2 as outlined above to generate shares $R_2,\dots ,R_{k-1}$. Step 4: For $h=0:(n-k)$ $r_{k+h}=x(i,j)\oplus r_{k+h-1}\oplus \dots \oplus r_{h+1}$, where ⊕ is XOR logical operation, end Step 5: Randomly permute the pixels $r_1,\dots ,r_n$, and assign them to the shares $$$R_1,\dots ,R_n$. Step 6: Repeat steps 4-5 above to include all pixels in $A_{v\times w}$.

In the following example and throughout the analysis of Algorithm 3, a block size of 3 (i.e., $B_{b,3}$) is employed, whereas Algorithm 2 utilizes a block size of 2. This highlights the flexibility of the proposed algorithms in accommodating even and odd block sizes.

The probabilities used in the experimental results were $p_0=p_3=0.1$ and $p_1=p_2=0.4$; however, these values are not fixed. Readers may adjust, them for instance, by setting $p_0=p_3=0.15$ and $p_1=p_2=0.35$ to explore different outcomes.

The results corresponding to Algorithm 3 are shown in Figure 2f and Figure 3f. Steps 1–3 of Algorithm 3 are demonstrated in the following example:

Example 3. 

Consider the encryption of $\mathit{RG-VCS}(4,4)-2$ using Algorithm 3, where the block to be utilized is denoted as $B_{b,3}$. The encryption of shares $R_1,R_2,R_3$ proceeds as follows:

Step 1 

Select a block, $B_{b,3}$ from among the possible $b=0$ (representing three white pixels), $b=1,b=2,$ and $b=3$, according to the respective probabilities $p_0,p_1,p_2,p_3$ subject to constraints $p_0=p_3,p_1=p_2$.

Step 2 

Assume that the selected block is $B_{0,3}$.

Step 3 

Distribute block $B_{0,3}$ across shares $R_1,R_2,R_3$ accordingly.

The constraints $p_0=p_3,$ and $p_1=p_2$ ensure a key security property: for any pixel x in shares $R_1,R_2,R_3$, the probability that x is white is equal to the probability that it is black, that is,

$$Prob\left(aiswhite\right)=Prob\left(aisblack\right)={\displaystyle \frac{1}{2}}.$$

(9)

According to Shyu’s security condition in Theorem1, it is enough to prove that the shares $R_1,\dots ,R_k-1$ satisfy for any pixel $r_1,\dots ,r_{k-1}$ in the shares $R_1,\dots ,R_k-1$ respectively, satisfy $Prob\left(r_k\right)=black=Prob(r_k=white)=0.5$.

According to Shyu’s security condition in Theorem 1, it is sufficient to prove that the shares $R_1,\dots ,R_{k-1}$ satisfy the following: for any combination of pixels $r_1,\dots ,r_{k-1}$ in the respective shares $R_1,\dots ,R_{k-1}$, the probability that the corresponding pixel $r_l$ in share $R_l$, $l=1,\dots ,k-1$ is black or white is equal, i.e.,

$$Prob(r_l=black)=Prob(r_l=white)=0.5.$$

(10)

Theorem 2. 

Algorithm 3 satisfies the security condition in Theorem 1.

Proof. 

Let $p_0,\dots ,p_m$ denote the selection probabilities for the blocks $B_{0,m},\dots ,B_{m,m}$, where each block $B_{b,m}$ contains b black pixels and $m-b$ white pixels, for $b=0,\dots ,m$. According to Algorithm 3, the selection probabilities are symmetric such that $p_b=p_{m-b}$ for all b. This symmetry implies that for every block $B_{b,m}$ containing b black and $m-b$ white pixels, there exists a corresponding block $B_{m-b,m}$ containing $m-b$ black and b white pixels, both selected with equal probability.

The total number of black pixels across both blocks $B_{b,m}$ and $B_{m-b,m}$ is m, and similarly, the total number of white pixels is also m. Therefore, for every pixel $x\in R_l$, where $l=1,\dots ,k-1$, the probability that x is black is equal to the probability that it is white, i.e.,

$$Prob(x=black)=Prob(x=white)=0.5.$$

(11)

This guarantees that no information regarding the original pixel values $x\in SI$ ($SI$ denotes the secret image) is revealed by any individual share. Consequently, the fundamental security condition of the visual cryptography scheme was proven. □

4. Results

Figure 1a–d serve as benchmarks for the evaluation of all algorithms, including both the proposed and previous algorithms. Lines are depicted in Figure 1b,c, which consist of various geometries, including curvature lines (circles); small lines; and vertical, horizontal, and diagonal lines. Specifically, the lines in Figure 1b are uniformly one pixel thick. A further challenge arises from the contrasting nature of the image, where the lines on the right side of the figure are white on a black background, whereas the line on the left side is adjacent to the right side, thus presenting additional visual complexity. The ruler shown in Figure 1a illustrates the proximity between the vertical and horizontal lines, compounded by blurred lines. In comparison, Figure 1b shows a greater number of curved lines than Figure 1c.

4.1. Feasibility Analysis

Visual evidence supporting the security of the proposed algorithm is presented in Figure 4a–f, which displays the shares generated by Algorithm 2. Notably, none of these four shares reveal any information regarding the secret image.

Figure 4. Shares of the Algorithm 3, $R_1,R_2,R_3$, for $\mathit{RG-VCS}(3,5)-2$ are shown by (a–c), and the stack over $R_1$ and $R_2$ is shown by (d). Algorithm 2 shares for $\mathit{RG-VCS}(2,4)-1$ are shown by (e,f).

In this study, we compared the performance of our algorithm with that of Wafy’s Algorithm 1 (2024) [10], which has demonstrated superior performance compared with other algorithms in the literature.

The output of Algorithm 2, as shown in Figure 2d,e, was compared with the results of Wafy’s Algorithm 1, as depicted in Figure 2a,b. The white areas on the left side of Figure 2d,e performed better in terms of clarity than the corresponding areas in Figure 2a,b. Furthermore, the ruler in Figure 2d appears clearer than that in Figure 2a, with the numbers being more distinct.

The proposed Algorithm 2 demonstrates a successful balance in enhancing the local contrast (as shown in Figure 2d–f when compared to Wafy’s Algorithm 1 (Figure 2a–c), without necessitating the removal of specific black and white pixels, which is a step required in Wafy’s Algorithm 1. Moreover, Algorithm 2 effectively preserves the local correlations.

When evaluating the output of Algorithm 3, as shown in Figure 3f, it is evident that this method outperforms Wafy’s Algorithm 1, as shown in Figure 3c. In comparison, Wafy’s Algorithm 1, as shown in Figure 3a,b, failed to accurately depict parts of the diagonal line, right vertical line, and portions of the left vertical line, along with part of the circle on the left (with a white background). Additionally, Figure 2a from Wafy’s Algorithm 1 shows a complete loss of both the numbers and vertical lines. In contrast, the output of Algorithm 2 (Figure 2d,e) preserves all elements, leaving no parts missing. Algorithm 3, as shown in Figure 3f, also offers superior clarity compared with Wafy’s Algorithm 1 as shown in Figure 3c.

4.2. Experiment Comparison

The quality of thin lines in reconstructed images can be assessed by determining whether the line thickness matches that of the secret image, measuring the number of pixels lost in horizontal, vertical, or curved structures, and evaluating the overall clarity of the image. However, no existing metric fully captures all these criteria.

The Contrast Degradation Ratio [14] is simple to compute but ignores local structural information and is insensitive to thin-line artifacts. The Edge-Preservation Measure [14] focuses on boundary sharpness but is sensitive to noise and less effective for textured thin lines. The Pixel Error Rate (PER) [14] directly compares pixel values but penalizes small spatial shifts excessively and ignores perceptual similarity. The Structural Similarity Index (SSIM), while considering local correlation, contrast, and luminance, is generally the most effective for assessing overall image quality.

Since the proposed algorithms are specifically designed to preserve thin-line structures and enhance the quality of the reconstructed image, SSIM was selected as the primary evaluation metric in our experiments.

The Structural Similarity Index (SSIM) is a widely recognized metric for assessing the perceived quality of digital images and videos by evaluating their similarity. The SSIM is computed with reference to an assumed distortion-free, uncompressed image. This metric evaluates the image quality by combining comparisons of local correlation, local contrast, and local luminance between two images into a single value. The SSIM was calculated using a Gaussian filter applied to both the smoothed revealed image (RI) and smoothed secret image (SI). Detailed information regarding the SSIM computation can be found in [15]. Elmer [16] demonstrated that the SSIM provides the most accurate measurement for comparing original and distorted images. In addition to the SSIM, we employed experimental contrast (EC), as defined in Definition 5, to further assess the performance of our proposed algorithms.

The dataset used in this study consisted of 24 images from [17], with Figure 1 serving as the basis for comparing the performance of our proposed algorithms with that of existing algorithms. Among the algorithms tested, Wafy’s Algorithm 1 outperformed other algorithms. Consequently, we compared Algorithms 2 and 3 with Wafy’s Algorithm 1 using both the SSIM and contrast metrics on 24 datasets from [17].

Concerning the SSIM, both the proposed algorithms (Algorithms 2 and 3) outperformed Wafy’s Algorithm 1, as shown in the top row of Figure 5a–c, corresponding to $\mathit{RG-VCS}(2,2),\mathit{RG-VCS}(3,5)$, and $\mathit{RG-VCS}(4,4)$, respectively. The lower SSIM scores observed in Wafy’s Algorithm 1 are primarily attributed to the reduced local correlation, which results from the loss of image details and the presence of missing lines.

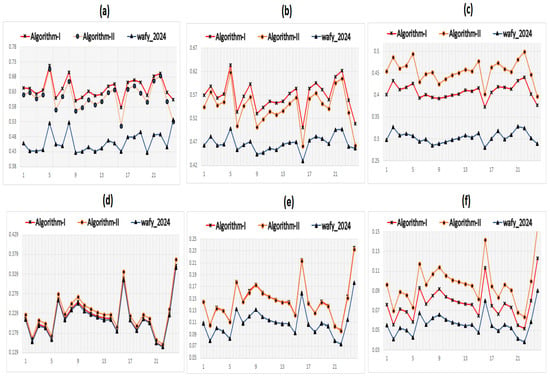
Figure 5. Comparison between the proposed algorithms and 1 [10]. The top row (subfigures (a–c)) presents the SSIM results for $\mathit{RG-VCS}(2,2)$, $\mathit{RG-VCS}(3,5)$, and $\mathit{RG-VCS}(4,4)$, respectively. The bottom row (subfigures (d–f)) shows the corresponding contrast comparisons for the same schemes.

The bottom row of Figure 5 presents a comparison, for contrast score), in which the proposed algorithms again exhibit superior performance. Although the difference in the experimental contrast (EC) for the $\mathit{RG-VCS}(2,2)$ scheme is relatively small, the SSIM difference is more pronounced, as SSIM captures both local correlation and contrast.

Overall, both the SSIM and contrast evaluations reveal that the performance gap between the proposed algorithms and Wafy’s Algorithm 1 widens as the number of stacking shares k increases. Moreover, for $\mathit{RG-VCS}(2,2)$ and $\mathit{RG-VCS}(3,5)$, Algorithm 2 achieved higher SSIM scores than Algorithm 3, despite their contrast values being nearly identical. This improvement is due to Algorithm 2’s ability to preserve more image details by maintaining white pixels after stacking $k-1$ shares ($k<n$), thus enhancing the local correlation.

However, when the number of shares is greater than three, Algorithm 2 begins to lose its local contrast and correlation. On the contrary, Algorithm 3 maintains the local contrast more effectively, leading to higher SSIM scores as the number of stacking shares increases. Specifically, in the $\mathit{RG-VCS}(4,4)$ scheme, Algorithm 3 outperformed Algorithm 2 in both the SSIM (Figure 5c) and contrast (Figure 5f). This finding is further supported by the visual comparison shown in Figure 3f (Algorithm 3) and Figure 3c (Algorithm 2), where Algorithm 3 provides a clearer and more detailed output than Algorithm 2 in the $\mathit{RG-VCS}(4,4)$.

Table 1 presents the average Structural Similarity Index Measure (SSIM) computed over a dataset of 24 images, comparing the proposed algorithms with Wafy’s Algorithm 1 [10] for the schemes $\mathit{RG-VCS}(2,2)$, $\mathit{RG-VCS}(3,5)$, and $\mathit{RG-VCS}(4,4)$. The results in the table support the conclusions drawn from Figure 5.

Table 1. Comparison between Wafy’s Algorithm 1 and the proposed algorithms based on the average SSIM and average EC values over a dataset of 24 images.

Algorithm	$\mathit{RG-VCS}(2,2)$	$\mathit{RG-VCS}(3,5)$	$\mathit{RG-VCS}(4,4)$
SSIM
Algorithm 1 [10]	0.462	0.467	0.304
Algorithm 2	0.642	0.568	0.408
Algorithm 3	0.615	0.545	0.455
EC
Algorithm 1 [10]	0.216	0.109	0.056
Algorithm 2	0.219	0.147	0.077
Algorithm 3	0.229	0.146	0.097

A t-test was conducted to determine whether there is a statistically significant difference between the SSIM scores of Algorithm 2 and Wafy’s Algorithm 1. The minimum p-value obtained across all schemes was $1.17791\times {10}^{-15}$, indicating a significant difference in SSIM scores between the two algorithms. Similarly, for contrast, the minimum p-value was $3.66584\times {10}^{-5}$, with the exception of the (2,2) scheme, where the test did not detect a significant difference. Comparable results were observed for Algorithm 3. The minimum p-value for the SSIM was $1.76645\times {10}^{-10}$, and for contrast, it was $5.0624\times {10}^{-5}$, confirming that the differences were also statistically significant.

4.3. Computational Complexity

The computational complexity is a critical factor in real-world applications. Therefore, the proposed algorithms were compared with Wafy’s Algorithm 1 [10], as presented in Table 2. All the algorithms exhibit linear time complexity ($\mathcal{O}\left(VW\right)$), where $V\times W$ represents the image dimensions. Among them, the second proposed algorithm (Algorithm 3) demonstrated the best performance in terms of execution time, as it required fewer computational steps than Algorithm 2 and Wafy’s Algorithm 1.

Table 2. Runtime comparison between Wafy’s Algorithm 1 and the two proposed algorithms. Experiments were conducted using MATLAB 2016 on a system with an Intel Core i7 processor (2.20 GHz) and 16 GB RAM.

Algorithm	$\mathit{RG-VCS}(2,2)$	$\mathit{RG-VCS}(3,5)$	$\mathit{RG-VCS}(4,4)$	$\mathcal{O}$
Algorithm 1 [10]	5.180	6.762	6.023	7VW
Algorithm 2	1.552	1.935	1.802925	3VW
Algorithm 3	1.179	1.55	1.407	2VW

Time is measured in seconds, the size of image is $V\times W$.

5. Conclusions

This paper proposes two novel algorithms for random grid visual cryptography schemes, denoted as $\mathit{RG-VCS}(k,n)-1$ and $\mathit{RG-VCS}(k,n)-2$, specifically developed to address the thin-line problem (TLP). Although the TLP has been previously examined in the context of multi-secret-image visual cryptography schemes ($\mathit{M-SIVCS}$), which are known to suffer from codebook-related issues, it has not yet been investigated within the framework of $\mathit{RG-VCS}$.

With respect to thin-line problems (TLP-1, TLP-2, and TLP-3), the proposed algorithms successfully resolved TLP-2 and TLP-3, and offered partial improvements for TLP-1. Moreover, the algorithms demonstrated enhanced visual quality for both binary and grayscale images. A comprehensive visual and quantitative evaluation was conducted to assess their performance and results were benchmarked against existing algorithms. The findings indicate that the proposed approaches outperform the previous algorithms in terms of overall performance.

Future work will aim to further enhance the visual quality of the reconstructed images, particularly by more effectively addressing TLP-1, and may focus on extending the proposed algorithms through formal parameter optimization within the framework of weak security. This would involve developing strategies to systematically tune algorithmic parameters based on quantitative measurements of share randomization. The objective would be to maximize the randomness score of the shares while simultaneously achieving optimal SSIM values, with particular attention to preserving the distribution of gray levels and maintaining fine structural details in the reconstructed image.

The author wishes to express gratitude to the reviewers for their valuable comments.