Adversarial Training for Aerial Disaster Recognition: A Curriculum-Based Defense Against PGD Attacks
Abstract
1. Introduction
- Firstly, we train a ResNet-50 model on clean aerial imagery from the AIDERV2 dataset to establish a strong baseline. This baseline references all subsequent evaluations under clean and adversarial conditions.
- Secondly, we evaluate the vulnerability of this baseline model by launching PGD attacks at varying perturbation levels. This phase quantitatively demonstrates how even small perturbations can significantly reduce classification accuracy, especially across different disaster categories.
- Thirdly, we implement adversarial training using PGD-generated images combined with clean samples, specifically employing a 50% clean and 50% adversarial data ratio. It is designed to improve the model’s ability to recognize and resist adversarial patterns. We explore multiple values, step sizes, and iteration counts to identify the most effective training configurations.
- Finally, we perform an analysis of both clean and adversarial classification results, including class-wise quality. This way, we can identify which disaster types (e.g., fire, flood, earthquake) benefit most from adversarial defense.
2. Related Works
2.1. Ensemble-Based and Training Defenses
2.2. Patch-Based Attacks and Detection
2.3. Disaster-Specific Testing and Augmentation
2.4. Autoencoders and SVM-Based Detection
2.5. Data Augmentation and Diffusion Model-Based
3. Methodology
3.1. Dataset Description
3.2. Model Architecture and Training Procedure
3.3. Adversarial Attack–PGD
3.4. Adversarial Defense–PGD-Based Adversarial Training
3.5. Evaluation Metrics
4. Results
4.1. Phase I: Baseline Training and Evaluation
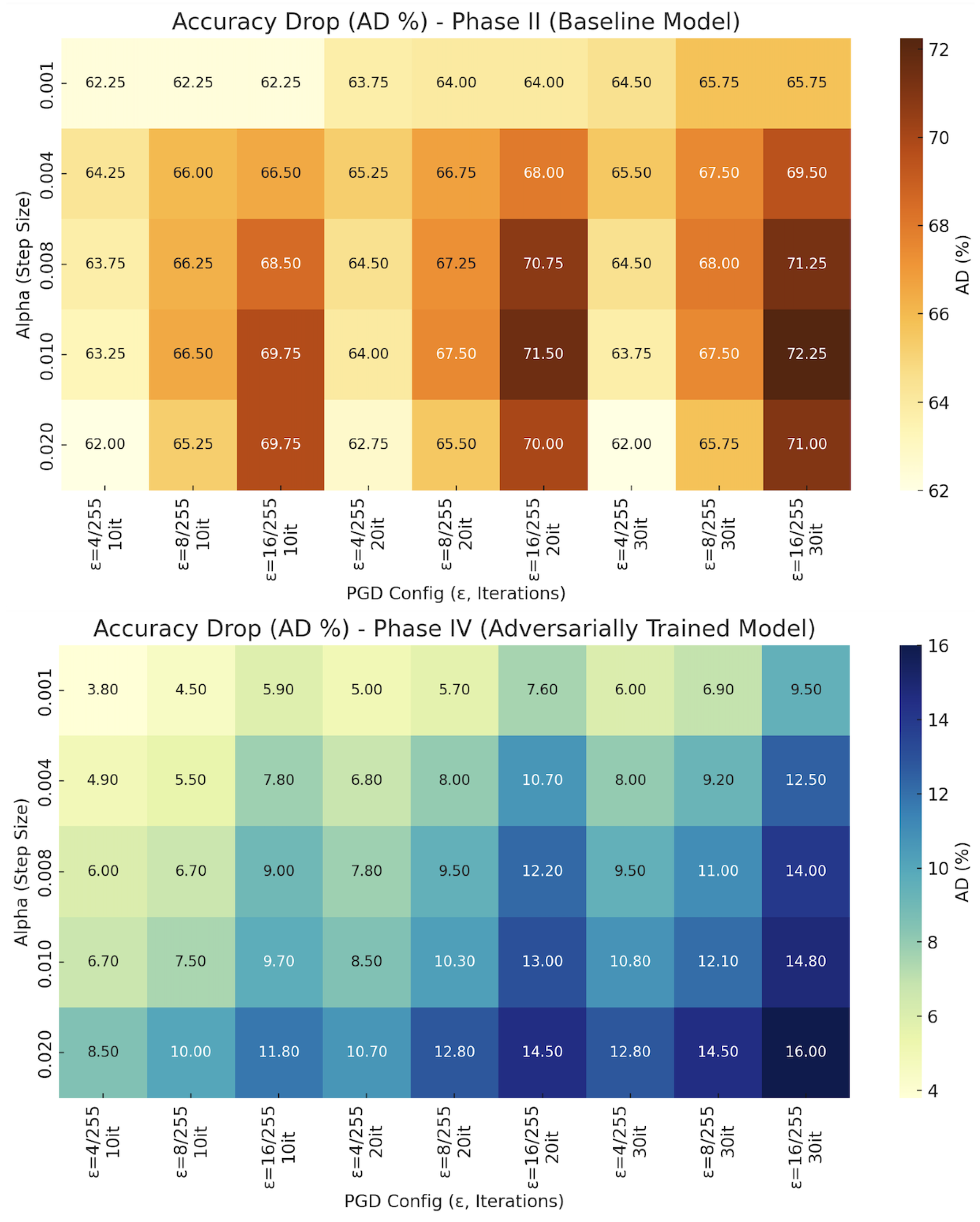
4.2. Phase II: Baseline Model Performance Under PGD Attack
4.3. Phase III: PGD-Based Adversarial Training
4.4. Phase IV: Resistance of Adversarially Trained Model Under PGD Attack
4.5. Overall Adversarial Evaluation and Comparative Metrics
- Clean Accuracy Reference
- Phase I Baseline Model: 93.25%
- Phase III Adversarially Trained Model: 91.00%
- Phase II vs. Phase IV Summary
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, J.; Guo, W.; Huang, H.; Lv, X.; Cao, H.; Li, H. Adversarial Examples for Vehicle Detection with Projection Transformation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5632418. [Google Scholar] [CrossRef]
- Lu, Z.; Sun, H.; Xu, Y. Adversarial Robustness Enhancement of UAV-Oriented Automatic Image Recognition Based on Deep Ensemble Models. Remote Sens. 2023, 15, 3007. [Google Scholar] [CrossRef]
- Lu, Z.; Sun, H.; Ji, K.; Kuang, G. Adversarial Robust Aerial Image Recognition Based on Reactive-Proactive Defense Framework with Deep Ensembles. Remote Sens. 2023, 15, 4660. [Google Scholar] [CrossRef]
- Raja, A.; Njilla, L.; Yuan, J. Adversarial Attacks and Defenses Toward AI-Assisted UAV Infrastructure Inspection. IEEE Internet Things J. 2022, 9, 23379–23389. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Qi, J.; Bin, K.; Wen, H.; Tong, X.; Zhong, P. Adversarial Patch Attack on Multi-Scale Object Detection for UAV Remote Sensing Images. Remote Sens. 2022, 14, 5298. [Google Scholar] [CrossRef]
- Pathak, S.; Shrestha, S.; AlMahmoud, A. Model Agnostic Defense against Adversarial Patch Attacks on Object Detection in Unmanned Aerial Vehicles. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 2586–2593. [Google Scholar] [CrossRef]
- Ide, R.; Yang, L. Adversarial Robustness for Deep Learning-Based Wildfire Prediction Models. Fire 2025, 8, 50. [Google Scholar] [CrossRef]
- Chen, L.; Xu, Z.; Li, Q.; Peng, J.; Wang, S.; Li, H. An Empirical Study of Adversarial Examples on Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7419–7433. [Google Scholar] [CrossRef]
- Da, Q.; Zhang, G.; Wang, W.; Zhao, Y.; Lu, D.; Li, S.; Lang, D. Adversarial Defense Method Based on Latent Representation Guidance for Remote Sensing Image Scene Classification. Entropy 2023, 25, 1306. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Li, Z.; Sun, J.; Wang, Y.; Liu, H.; Yang, J.; Gui, G. Spear and Shield: Attack and Detection for CNN-Based High Spatial Resolution Remote Sensing Images Identification. IEEE Access 2019, 7, 94583–94592. [Google Scholar] [CrossRef]
- Tasneem, S.; Islam, K.A. Improve Adversarial Robustness of AI Models in Remote Sensing via Data-Augmentation and Explainable-AI Methods. Remote Sens. 2024, 16, 3210. [Google Scholar] [CrossRef]
- Yu, W.; Xu, Y.; Ghamisi, P. Universal adversarial defense in remote sensing based on pre-trained denoising diffusion models. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104131. [Google Scholar] [CrossRef]
- Shianios, D.; Kyrkou, C.; Kolios, P.S. A Benchmark and Investigation of Deep-Learning-Based Techniques for Detecting Natural Disasters in Aerial Images. In Computer Analysis of Images and Patterns, Proceedings of the 20th International Conference, CAIP 2023, Limassol, Cyprus, 25–28 September 2023; Proceedings, Part II; Springer: Berlin/Heidelberg, Germany, 2023; pp. 244–254. [Google Scholar] [CrossRef]
- Ren, K.; Zheng, T.; Qin, Z.; Liu, X. Adversarial Attacks and Defenses in Deep Learning. Engineering 2020, 6, 346–360. [Google Scholar] [CrossRef]
- Rahman, M.; Roy, P.; Frizell, S.S.; Qian, L. Evaluating Pretrained Deep Learning Models for Image Classification Against Individual and Ensemble Adversarial Attacks. IEEE Access 2025, 13, 35230–35242. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar] [CrossRef]




| Experiment | Training Data | Testing Data | Attack Applied | Defense Applied |
|---|---|---|---|---|
| Baseline Model | Clean Images | Clean Images | No | No |
| Expected Outcome: High classification accuracy under normal conditions. | ||||
| PGD Attack on Baseline | Clean Images | Adversarial Images | Yes (PGD) | No |
| Expected Outcome: Significant drop in accuracy due to adversarial perturbations. | ||||
| Adversarially Trained Model | Clean + Adversarial Images | Clean Images | No | Yes (PGD Training) |
| Expected Outcome: Similar accuracy but improved resilience against adversarial perturbations. | ||||
| PGD Attack on Adversarially Trained Model | Clean + Adversarial Images | Adversarial Images | Yes (PGD) | Yes (PGD Training) |
| Expected Outcome: Higher accuracy than baseline under attack conditions. | ||||
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Earthquake | 0.97 | 0.96 | 0.96 | 100 |
| Fire | 0.84 | 0.98 | 0.90 | 100 |
| Flood | 0.97 | 0.98 | 0.98 | 100 |
| Normal | 0.98 | 0.81 | 0.89 | 100 |
| Accuracy | 0.93 | |||
| Macro Avg | 0.94 | 0.93 | 0.93 | 400 |
| Weighted Avg | 0.94 | 0.93 | 0.93 | 400 |
| Perturbation Bound (ϵ) | Step Size (α) | Iterations |
|---|---|---|
| 4/255, 8/255, 16/255 | 0.001, 0.004, 0.008, 0.010, 0.020 | 10, 20, 30 |
| α | 10 Iterations | 20 Iterations | 30 Iterations | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ϵ = 4/255 | ϵ = 8/255 | ϵ = 16/255 | ϵ = 4/255 | ϵ = 8/255 | ϵ = 16/255 | ϵ = 4/255 | ϵ = 8/255 | ϵ = 16/255 | |
| 0.001 | 31.00% | 31.00% | 31.00% | 29.50% | 29.25% | 29.25% | 28.75% | 27.50% | 27.50% |
| 0.004 | 29.00% | 27.25% | 26.75% | 28.00% | 26.50% | 25.25% | 27.75% | 25.75% | 23.75% |
| 0.008 | 29.50% | 27.00% | 24.75% | 28.75% | 26.00% | 22.50% | 28.75% | 25.25% | 22.00% |
| 0.010 | 30.00% | 26.75% | 23.50% | 29.25% | 25.75% | 21.75% | 29.50% | 25.75% | 21.00% |
| 0.020 | 31.25% | 28.00% | 23.50% | 30.50% | 27.75% | 23.25% | 31.25% | 27.50% | 22.25% |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Earthquake | 0.92 | 0.94 | 0.93 | 100 |
| Fire | 0.90 | 0.92 | 0.91 | 100 |
| Flood | 0.93 | 0.91 | 0.92 | 100 |
| Normal | 0.91 | 0.87 | 0.89 | 100 |
| Accuracy | 0.91 | |||
| Macro Avg | 0.92 | 0.91 | 0.91 | 400 |
| Weighted Avg | 0.92 | 0.91 | 0.91 | 400 |
| α | 10 Iterations | 20 Iterations | 30 Iterations | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ϵ = 4/255 | ϵ = 8/255 | ϵ = 16/255 | ϵ = 4/255 | ϵ = 8/255 | ϵ = 16/255 | ϵ = 4/255 | ϵ = 8/255 | ϵ = 16/255 | |
| 0.001 | 87.2% | 86.5% | 85.1% | 86.0% | 85.3% | 83.4% | 85.0% | 84.1% | 81.5% |
| 0.004 | 86.1% | 85.5% | 83.2% | 84.2% | 83.0% | 80.3% | 83.0% | 81.8% | 78.5% |
| 0.008 | 85.0% | 84.3% | 82.0% | 83.2% | 81.5% | 78.8% | 81.5% | 80.0% | 77.0% |
| 0.010 | 84.3% | 83.5% | 81.3% | 82.5% | 80.7% | 78.0% | 80.2% | 78.9% | 76.2% |
| 0.020 | 82.5% | 81.0% | 79.2% | 80.3% | 78.2% | 76.5% | 78.2% | 76.5% | 75.0% |
| Phase | Min AA | Max AA | Min ASR | Max ASR |
|---|---|---|---|---|
| Phase II (Baseline) | 21.00% | 31.25% | 68.75% | 79.00% |
| Phase IV (Adv. Trained) | 75.00% | 87.20% | 12.80% | 25.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kose, K.; Zhou, B. Adversarial Training for Aerial Disaster Recognition: A Curriculum-Based Defense Against PGD Attacks. Electronics 2025, 14, 3210. https://doi.org/10.3390/electronics14163210
Kose K, Zhou B. Adversarial Training for Aerial Disaster Recognition: A Curriculum-Based Defense Against PGD Attacks. Electronics. 2025; 14(16):3210. https://doi.org/10.3390/electronics14163210
Chicago/Turabian StyleKose, Kubra, and Bing Zhou. 2025. "Adversarial Training for Aerial Disaster Recognition: A Curriculum-Based Defense Against PGD Attacks" Electronics 14, no. 16: 3210. https://doi.org/10.3390/electronics14163210
APA StyleKose, K., & Zhou, B. (2025). Adversarial Training for Aerial Disaster Recognition: A Curriculum-Based Defense Against PGD Attacks. Electronics, 14(16), 3210. https://doi.org/10.3390/electronics14163210






