Interval-Valued Fermatean Fuzzy EDAS for Social Media Influencer Evaluation and Benchmarking

Abstract

To assist stakeholders in selecting appropriate social media influencers (SMIs), this study proposes a multi-attribute decision-making framework for influencer evaluation based on their key performance metrics and engagement characteristics. This study introduces a new modification of the Evaluation Based on Distance from Average Solution (EDAS) under an interval-valued Fermatean fuzzy (IVFF) environment, addressing the limitations of the conventional EDAS method. In addition, a conceptual framework for the static and dynamic evaluation of SMIs is developed, integrating various crisp and fuzzy multi-criteria decision-making (MCDM) approaches. Empirical validation through two practical case studies demonstrates the effectiveness and applicability of the proposed framework, resulting in recommendations for marketers seeking to optimize their influencer-based marketing strategies.

1. Introduction

The rapid expansion of digital marketing has significantly emphasized the role of social media influencers (SMIs) [1], who are instrumental in shaping consumer behaviour and brand perceptions. As businesses increasingly collaborate with social media personalities [2], identifying the most effective partners among them becomes critical for successful marketing campaigns. Although influencer marketing offers substantial opportunities, businesses frequently encounter difficulties due to ambiguous and imprecise selection criteria [3,4]. Decision-makers often rely on incomplete data, subjective opinions, and linguistic evaluations, complicating the influencer selection process. An incorrect choice may result in ineffective marketing campaigns, wasted resources, and potential damage to brand reputation [5].

In the dynamic environment of social media marketing, finding the right collaborators requires balancing numerous factors such as credibility, communication skills, domain knowledge, creative flair, and consistency with brand identity [6]. These criteria typically vary in importance based on marketing objectives and target audiences. Moreover, evaluating influencer quality often involves subjective judgments, leading to inconsistencies and biases. As the pool of potential influencers expands and decision-making contexts become more complex, there is a rising need for formalized, transparent, and systematic evaluation approaches.

The rapid expansion of digital platforms and the central role of social media in shaping consumer behaviour have made the selection of SMIs a critical component of modern marketing strategies. Poorly chosen influencers, misaligned with brand values or audience expectations, can lead to:

• Misdirected marketing budgets and low returns on investment.
• Reputational damage caused by associations with inauthentic or controversial SMIs.
• Erosion of consumer trust caused by irrelevant, misleading, or overly promotional content.

Marketers commonly encounter several challenges in SMI selection:

• The vast and diverse pool of potential candidates requires a structured evaluation across several key dimensions.
• A lack of transparency and standardization hinders objective comparisons among SMIs.
• The dynamic nature of social media trends affects influencer effectiveness over time.
• The presence of fraudulent or inflated metrics, such as fake followers or manipulated engagement, can mislead decision-makers.

Multi-criteria decision-making (MCDM) techniques have shown effectiveness in related domains, including social media and microblog user rankings [7,8] and expert opinion score estimations [9], making them applicable to influencer marketing. In particular, fuzzy-based MCDM approaches offer distinct advantages by addressing the uncertainty and vagueness commonly found in subjective evaluations from stakeholders [10]. Unlike traditional MCDM models, fuzzy extensions allow for the selection of optimal alternatives under imprecise, uncertain, or ambiguous conditions. Fuzzy logic enhances conventional decision-making by capturing real-world ambiguity more effectively, supporting more reliable rankings when expert judgments or criteria inputs are unclear [11]. These enhanced fuzzy MCDM methods, especially methods incorporating advanced fuzzy set theories, have demonstrated improved robustness and practical applicability in fast-changing social media environments characterized by incomplete or volatile data.

The primary objectives of this study are twofold: (1) to design and validate a new MCDM framework for the evaluation and benchmarking of SMIs, and (2) to develop an extended version of the Evaluation Based on Distance from Average Solution (EDAS) method within an interval-valued Fermatean fuzzy context. The proposed framework is tested under both static and dynamic conditions, enabling the comprehensive assessment of influencer effectiveness across multiple dimensions. This dual-perspective analysis provides deeper insights into influencers’ performance consistency and adaptability in real-world marketing scenarios.

The contributions of this study can be summarized as follows:

• We conduct a comprehensive review and categorization of existing multi-criteria approaches for SMI selection. These methods are classified based on the types of input data used (numeric, interval, linguistic values; crisp and fuzzy numbers), as well as by their complexity (number of integrated MCDM techniques), flexibility (degree of fuzziness), and iterativeness (single vs. repeated evaluations).
• We propose a theoretical framework for SMI ranking that incorporates both single and hybrid MCDM methods. Single methods apply a singular approach for weight assignments and ranking, while hybrid methods integrate multiple techniques. The framework includes crisp and fuzzy operations, robustness analysis, and sensitivity analysis. Furthermore, we introduce a new fuzzy Fermatean group EDAS method, enhanced with an advanced 3D distance metric to improve influencer comparisons across multiple criteria.
• We validate the proposed framework through two real-world case studies using AI-based influencer data. Static rankings are primarily based on literature reviews and expert assessments, with relatively limited incorporation of social media data. In contrast, dynamic rankings integrate real-time sentiment and emotion data extracted from social media platforms, offering more responsive and up-to-date evaluations. Comparative analyses against both traditional and fuzzy MCDM baselines demonstrate the enhanced performance and practical utility of our fuzzy framework and the extended EDAS method.

The remainder of this paper is structured as follows: Section 2 reviews the relevant literature, highlighting research motivations. Section 3 details the theoretical framework for influencer selection, including interval-valued Fermatean fuzzy (IVFF) numbers and the modified fuzzy EDAS method. Section 4 describes practical applications, presents results, and discusses implications. The final section summarizes findings, provides concluding remarks, and suggests future research directions.

2. Related Work

2.1. Applications of MCDM Methods in SMI Selection

SMIs have become central figures in contemporary marketing strategies, leading to increased attention towards effective influencer selection methods. Prior research on SMI selection using MCDM provides a foundation for understanding both how to rank influencers and which attributes contribute most to their performance. Scholars typically frame SMI selection as a complex decision-making problem that involves a mix of qualitative and quantitative factors. While some studies propose models for ranking or selecting the most appropriate influencers for specific campaigns, others concentrate on identifying and prioritizing the key criteria that define influencer effectiveness.

Wu et al. [12] integrated the Fuzzy Delphi Method (FDM), Decision-Making Trial and Evaluation Laboratory (DEMATEL), Analytic Network Process (ANP), and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) in a hybrid MCDM framework to identify optimal show hosts in a social media context. Through literature review and expert consultation, 12 key selection criteria were determined. DEMATEL revealed the interrelationships among factors, ANP computed their weights, and TOPSIS ranked candidates. The model also incorporated criteria relevant to presenter roles, demonstrating practical applicability in a real-world case study.

Tsai et al. [6] developed a hybrid importance–performance analysis (IPA)–AHP–TOPSIS model to select bloggers for hotel marketing. They gathered criteria from hotel managers and a literature review, introduced the novel “stickiness” attribute, and used IPA to filter underperforming but important criteria. AHP assigned weights, and TOPSIS finalized the rankings. This crisp MCDM approach provided a flexible, reliable decision framework aligned with stakeholder expectations.

Shukla and Dubey [13] created a group-based fuzzy MCDM framework for SMI selection, integrating perspectives from brand managers, agencies, and customers. Using a modified generalized fuzzy evaluation method (MGFEM) and the FITtradeoff mechanism, the model captured linguistic preferences and iteratively adjusted criteria weights. Applied to two hypothetical campaigns, the method yielded adaptive, context-sensitive influencer rankings while ensuring balanced stakeholder input.

Wu et al. [14] applied a hybrid MCDM model (FDM–DEMATEL–ANP–TOPSIS) to select YouTubers for hotel promotions. The model evaluated 12 criteria across four dimensions and provided both theoretical and practical insights into influencer selection for the hospitality industry.

Lam et al. [10] focused on a fuzzy hybrid MCDM framework to support key opinion leaders (KOLs) in a business-to-business (B2B) digital marketing context, addressing complex business criteria beyond engagement—such as strategic fit and brand risk. The model combined fuzzy Best–Worst Method (BWM) for weighting criteria and fuzzy TOPSIS for ranking candidates. Experts used linguistic evaluations to express subjective judgments, which were converted into fuzzy numbers. Applied in collaboration with a Hong Kong digital agency, the method proved effective in selecting the optimal influencer by translating qualitative inputs into actionable rankings. This study demonstrates how fuzzy MCDM can simplify decision-making in corporate influencer marketing.

Yang et al. [15] constructed a crisp hybrid model for evaluating fitness influencers based on professional competencies. They identified 21 criteria across six dimensions, including professional expertise, behavioural standards, and self-improvement intent. To capture uncertainty in expert assessments, Bayesian Best-Worst Method (BWM) was employed, allowing weights to be derived through probability distributions. A modified TOPSIS with Aspiration Level (TOPSIS-AL) was then used to rank five Taiwanese fitness influencers against predefined performance targets. The most influential criteria included ethical behaviour, punctuality, and creativity. The model not only produced robust rankings but also pinpointed areas for development, linking influencer evaluation to broader societal goals such as the United Nations Sustainable Development Goals (UN SDGs).

While the above six studies rank influencers based on given criteria, another stream of research focuses on determining the right criteria for evaluating SMIs. These four studies often use expert input and new analytic methods to identify which factors brands should consider when selecting influencers.

Chiu et al. [4] proposed a two-stage hybrid MCDM model to identify key criteria for evaluating SMIs by integrating both expert and consumer perspectives. In the first stage, the Delphi method was used with input from brand managers and influencers to elicit and refine selection criteria. This was complemented by survey data from consumers influenced by SMIs, ensuring alignment between brand expectations and audience perceptions. In the second stage, the DEMATEL method was applied to analyze interdependencies among criteria, revealing trustworthiness and authenticity as primary drivers of consumer engagement and platform fit. The study contributed a multidimensional framework that emphasized psychological, credibility, and platform-related factors.

Firouzkouhi et al. [16] introduced an advanced AI-enabled framework for influencer identification based on the generalized fuzzy hypergraph (GFH) methodology. This approach models social media networks by representing users and their interactions as fuzzy hyperedges, effectively capturing both the strength and uncertainty of relationships. By enabling the simultaneous evaluation of multiple influence dimensions—such as engagement levels, content diffusion, and network centrality—the model facilitates a more nuanced assessment of influencer impact. Incorporating fuzzy link prediction (FLP) and interaction scoring (SIR), the framework enhances influencer detection and link forecasting in dynamic and uncertain environments. The results demonstrate superior performance compared to traditional graph-based models, underscoring the importance of multidimensional, non-binary relationship modelling in contemporary SMI evaluation.

Çokak and Dursun [17] devised a fuzzy cognitive mapping (FCM) approach to evaluate how specific influencer marketing factors impact e-commerce performance. Drawing on expert input from the e-commerce sector, they assessed eight criteria, including product price, discount status, brand fit, follower count, product description quality, product category, number of ad shares, and commission rate. The FCM model—built using fuzzy causal links—revealed that product promotion, post frequency (shares), and price exert the strongest influence on online sales and product interest. Their analysis highlights that “soft” factors like content quality may outweigh traditional metrics such as follower count, offering practical insights for structuring influencer campaigns and selection.

Sorooshian [3] introduced a hybrid Delphi–Ordinal Priority Approach (OPA) to support structured SMI selection. The Delphi method first identified and hierarchically organized 22 influencer evaluation criteria, while OPA applied ordinal comparisons to rank influencer candidates based on these criteria. Tested in an academic event marketing case, the method helped prioritize influencers according to strategic campaign needs. This crisp MCDM approach offers a systematic, objective tool for marketers seeking transparent, criteria-based influencer selection.

To summarize the reviewed studies, Table 1 presents a comparative overview based on key aspects: study objective, dataset and data type description, MCDM methodology, and verification approach.

Table 1. Comparison of recent studies on MCDM-based SMI selection and criteria determination.

Reference	Research Objective	Dataset Characteristics	MCDM Methods	Result Evaluation
Wu et al. (2020) [12]	Assess influencer performance using multi-criteria evaluation	Literature review and expert interviews	FDM, DEMATEL, ANP, TOPSIS	Expert validation
Tsai et al. (2021) [6]	Develop a decision model to rank bloggers based on campaign efficiency	Literature review and survey data from hotel managers	IPA, AHP, TOPSIS	Ranking consistency
Shukla & Dubey (2022) [13]	Integrate MCDM methods for celebrity ranking	Secondary data on celebrity engagement metrics	MGFEM, FITtrafeoff method	Comparative performance with other MCDM methods
Wu et al. 2022 [14]	Hybrid MCDM methods	YouTube dataset, user engagement stats	FDM, DEMATEL, ANP, TOPSIS	Expert validation
Lam et al. (2024) [10]	Hybrid model for selection of KOLs based on content and interaction	B2B company data, user engagement stats	Fuzzy BWM, fuzzy TOPSIS	Sensitivity and robustness checks
Yang et al. (2024) [15]	Propose a framework for evaluating fitness influencer impacts	Literature survey and expert interviews	Bayesian BWM, TOPSIS	Fuzzy consistency and expert validation
Chiu et al. (2024) [4]	Identify essential features for influencer assessment	Survey of consumers from Taiwanese market	Delphi method, DEMATEL	Weight consistency and expert panel review
Firouzhouhi et al. (2024) [16]	Determine key criteria for SMI selection	Social media network data	Generalized fuzzy hypergraph	Consensus rate and factors influence validation
Cokak & Dursun (2025) [17]	Prioritize influencer selection factors	Literature review and structured interviews with e-commerce professionals	FCM	Comparative results with real campaigns
Sorroshian (2025) [3]	Use MCDM methods for criteria ranking	Survey data	Delphi–OPA method	Rank tests

Based on the collected data (Table 1), the reviewed literature methodologically focuses on two research directions: (1) evaluation and ranking of influencers, and (2) identification of key criteria for influencer selection. The first group, including studies by Wu et al. (2020) [12], Tsai et al. (2021) [6], Shukla and Dubey (2022) [13], Wu et al. (2022) [14], Lam et al. (2024) [10], and Yang et al. (2024) [15], aims to build decision frameworks that assess or rank SMIs based on various performance indicators. These studies typically employ hybrid MCDM methods combining ANP, ANP, DEMATEL, and TOPSIS, often enhanced with fuzzy logic, to reflect the uncertainty in subjective expert judgments and inconsistent online metrics. In contrast, the second group, represented by Chiu et al. (2024) [4], Firouzhouhi et al. (2024) [16], Cokak and Dursun (2025) [17], and Sorroshian (2025) [3], focuses on determining the most relevant evaluation criteria. These studies rely on techniques such as expert panels, systematic literature reviews, and Delphi rounds to build consensus around the key attributes of influencer effectiveness.

The data sources used across the reviewed studies vary considerably. Some rely on platform-specific information from social media channels such as Instagram, Twitter, or YouTube, while others are based on structured surveys or expert assessments. In terms of data type, a majority of the studies incorporate fuzzy data or evaluation techniques to manage uncertainty. For instance, Wu et al. (2020, 2022) [12,14] applied the FDM for criteria identification; Shukla and Dubey (2022) [13] used fuzzy group evaluation to determine criteria weights; Lam et al. (2024) [10] employed fuzzy BWM and TOPSIS; Firouzkouhi et al. (2024) [16] modelled social networks using fuzzy relations; and Çokak and Dursun (2025) [17] utilized fuzzy cognitive maps.

Conversely, several studies adopted crisp evaluation methods. Tsai et al. (2021) [6] and Yang et al. (2024) [9] collected exact scores from experts or used predefined numerical datasets. Likewise, Chiu et al. (2024) [4] and Sorooshian (2025) [3] performed analyses using precise statistical or deterministic techniques. The selection of fuzzy versus crisp methodologies often depends on the research context—for example, fuzzy approaches are more suitable when inputs are linguistic or when relationships are complex and non-binary.

Fuzzy logic is employed in the majority of ranking-focused studies (four out of six studies), whereas studies centred on criteria identification tend to favour crisp evaluations (two out of four studies). This distribution reflects a broader recognition of the ambiguity inherent in human judgement and the uncertain nature of social media data.

Evaluation practices differ, but most studies apply expert validation, comparative benchmarks, or sensitivity analysis. However, comprehensive model testing using external performance metrics remains rare. Complexity also varies: some studies build multi-stage hierarchical frameworks, while others use simpler, single-method approaches.

The literature review indicates that there is no universally adopted procedure or holistic method for selecting SMIs. Existing research provides valuable insights into influencer assessment but also reveals several limitations:

(1)

Most existing MCDM solutions address only specific aspects of the influencer selection problem, such as determining the relative importance of certain influencer characteristics or generating rankings based on a single criterion or method.

(2)

Only a limited number of studies effectively handle imprecise or subjective influencer attributes. Since the evaluation of SMIs frequently involves qualitative factors, these assessments should ideally utilize fuzzy numbers or advanced fuzzy set variants.

(3)

The majority of current fuzzy solutions typically employ only one or two MCDM methods, and notably do so without iterative procedures, which limits their robustness and reliability in dynamic environments.

However, influencer selection should be a comprehensive procedure that integrates various factors often assessed subjectively and imprecisely. To address these gaps, this study introduces a new fuzzy MCDM framework designed for evaluating and selecting SMIs. The choice of the most suitable influencer depends significantly on strategic brand goals, target audience characteristics, budget constraints, and specific campaign requirements.

2.2. Evaluation Criteria for SMI Comparison

Influencer performance can be evaluated through a set of interrelated metrics that reflect both strategic marketing effectiveness and audience perception [18,19]. A recent literature review and comparative analysis of key studies revealed several commonly cited and widely adopted criteria used in SMI evaluation systems:

• Authenticity [20] refers to the perceived sincerity, transparency, and credibility of the influencer. It is a crucial factor for building audience trust and fostering long-term engagement and brand advocacy. Genuine influencers are more likely to establish strong emotional connections with followers, which enhances persuasive effectiveness in campaigns. Authenticity is the most frequently emphasized dimension, cited in eight of ten studies, excluding only Firouzhouhi et al. [16] and Cokak and Dursun [17], and having over 19 related indicators such as trustworthiness, likability, sincerity, and familiarity.
• Innovation in social media marketing [21] captures the influencer’s use of new technologies, formats, and creative storytelling approaches. Frequent and effective innovation helps differentiate the influencer in a saturated market, increases visibility, and boosts user engagement. Innovation, mentioned in four sources [3,6,10,15], measures creative use of formats and technology.
• Content quality [22] includes the esthetic appeal, originality, clarity, and consistency of published content. High-quality content attracts attention, reinforces brand messaging, and sustains audience interest through professional standards and creative alignment. Content quality appears in six studies [4,6,13,14,15,17], encompassing attractiveness, informativeness, and entertainment value.
• Brand collaboration [23] reflects the number and reputation of brands that have partnered with the influencer. It is an indicator of commercial credibility, professional reliability, and market alignment. Strong collaboration history also signals trust and increased campaign ROI. Brand collaboration, referenced in five studies [3,4,6,10,17], signals professional credibility through past partnerships.
• Social impact [24] evaluates the influencer’s engagement with social issues and promotion of ethical or positive messaging. This attribute contributes to public trust, emotional resonance, and added brand value—especially in socially conscious consumer segments. Although this factor is explicitly highlighted in only one study [3], where it is referred to as “social responsivity and ethical consideration”, it plays a crucial role in promoting positive societal norms, encouraging responsible digital behaviour, and supporting public discourse on important social issues.
• Demographic relevance [25] assesses the alignment between an influencer’s audience and a brand’s target market in terms of demographics such as age, gender, location, income, and lifestyle. A high degree of fit enhances campaign effectiveness and conversion rates. Demographic relevance, cited in four studies [3,6,12,17], reflects audience alignment with campaign targets.
• Engagement metrics [26] measure how actively the audience interacts with the influencer’s content. Likes, comments, shares, and clicks serve as proxies for audience interest and connection, offering a more reliable indicator of influence than passive exposure alone. Engagement—likes, comments, and participatory behaviour—appears in only two studies [3,4], and social impact, such as advocacy and ethical messaging, is noted in one study [3].
• Follower count [27] represents the size of an influencer’s audience across platforms. Although often used as a reach indicator, follower numbers should be interpreted alongside engagement to assess actual influence and marketing effectiveness. Followers, as a proxy for reach and visibility, are highlighted in eight studies [3,4,6,10,12,13,14,17], linked to metrics like subscriber counts, likes rates, share rates, and click-through rates.

The factor distribution confirms a hybrid structure in SMI evaluation, where dominant dimensions like authenticity, content quality, and brand collaboration coexist with emerging factors such as innovation and social responsibility. The aforementioned criteria can be expanded further by incorporating additional indicators such as influencer consistency, historical campaign performance, brand affinity, and sentiment analysis derived from audience feedback. Each of these parameters provides deeper insights into influencer suitability and helps ensure strategic alignment with brand marketing objectives. By applying crisp or fuzzy MCDM techniques, these criteria can be quantitatively assessed to rank influencers.

2.3. SMIs and Their Defining Attributes

In this subsection, we present some of the most prominent SMIs according to the leading social media platforms. As influencer marketing evolves, a distinct category has emerged—virtual SMIs, which blur the line between technology and human engagement. Virtual SMIs are AI-generated, computer-controlled personas designed to engage audiences across digital platforms through curated content and branded interactions. Unlike traditional influencers, they do not exist physically but are developed using technologies such as 3D modelling, animation, and natural language processing [28,29,30].

They offer a distinct and timely opportunity for marketers and researchers, driven by their increasing presence in digital marketing and their technologically enabled advantages. These AI-generated personas are fully managed by their creators, allowing for consistent messaging, reduced risk of human-related controversies, and seamless alignment with brand identity. Virtual SMIs can be deployed continuously, localized for specific markets, and involved in parallel campaigns without logistical constraints or variable costs. Research highlights that virtual influencers often generate strong engagement due to their novelty and polished esthetics, which may trigger curiosity or fascination among users [31]. Their programmable nature also allows marketers to fine-tune emotional appeal and audience targeting based on demographic or psychographic data. As the virtual influencer industry grows—estimated to be valued at over USD 45 billion by 2030—studying these entities offers early insight into a transformative trend in online branding and audience interaction [32]. Beyond their novelty, virtual SMIs represent a shift toward data-driven, scalable, and controllable marketing strategies that warrant rigorous academic attention.

Given their growing prominence, it becomes essential to examine how specific virtual influencers function across diverse cultural and commercial environments. An analysis of their visual personas, engagement patterns, brand collaborations, and messaging themes uncovers the strategic functions virtual influencers fulfil within the contemporary digital communication ecosystem.

In order to explore this evolving phenomenon and its cultural, technological, and commercial impact, we present and compare five of the most prominent AI-generated SMIs, known for their high follower counts, market impact, and unique digital personas—Kenza Layli, Aitana López, Lil Miquela, Shudu Gram, and Thalasya Pov.

• Kenza Layli, Morocco, https://www.instagram.com/kenza.layli, accessed on 9 July 2025, is a winner of the inaugural Miss AI pageant. Kenza Layli is recognized for her high-quality AI-generated content and engagement in social and cultural discussions. Her image reflects inclusivity, modernity, and North African representation in virtual spaces.
• Aitana López, Spain, https://www.instagram.com/fit_aitana, accessed on 9 July 2025, is created by the Spanish company The Clueless. Aitana is a virtual model with over 370,000 Instagram followers. She generates significant income through brand collaborations and is promoted as an “ideal” influencer for the fashion and fitness industry.
• Miquela Sousa (Lil Miquela), USA, https://www.instagram.com/lilmiquela, accessed on 9 July 2025, is among the earliest and most influential virtual influencers. She has over 2.4 million Instagram followers. She is known for music releases, activism, and high-profile fashion campaigns. Created as a computer-generated imagery (CGI) persona, she has collaborated with major brands like Prada and Calvin Klein.
• Shudu Gram, UK, https://www.instagram.com/shudu.gram, accessed on 9 July 2025, is referred to as the world’s first digital supermodel. She is known for her hyper-realistic appearance. She has been featured in luxury fashion campaigns and often raises questions about diversity and the future of digital identity in modelling.
• Thalasya Pov, Indonesia, https://www.instagram.com/thalasya_, accessed on 9 July 2025, Indonesia’s first digital influencer, is recognized for her aspirational travel content and lifestyle branding. She appeals to a Southeast Asian audience and collaborates with local and regional brands.

To facilitate comparison, Table 2 summarizes key attributes of these leading virtual SMIs.

Table 2. Comparison of the selected prominent virtual SMIs.

N	Influencer	Creator	Country	Primary Domain	Features	Follower Count *
1	Kenza Layli	Miss AI Pageant Winner (N/A)	Morocco	Social advocacy	Miss AI winner, Arabic/Moroccan cultural appeal	190,000+
2	Aitana López	The Clueless (2023)	Spain	Fashion/Fitness	Revenue-focused, designed to be ideal SMI	370,000+
3	Lil Miquela	Brud (2016)	USA	Fashion/Music	Early CGI figure, activism, brand collaborations	2.4M+
4	Shudu Gram	The Diigitals (2017)	UK	Luxury fashion	Hyper-realistic, high fashion, digital diversity	230,000+
5	Thalasya Pov	Local digital agency (N/A)	Indonesia	Travel/Lifestyle	Regional branding, aspirational tone	450,000+

Note: *—Instagram follower count only; N/A—Data not available.

According to the collected data (Table 2), all the above-mentioned virtual personas represent a diverse and well-rounded sample that allows for an in-depth analysis of this trend from both global and thematic perspectives. The analysis of the main characteristics of selected influencers shows that they can be categorized by a set of classification features:

• Diversity of origin: The selected influencers come from various regions—North Africa (Kenza Layli), Europe (Aitana López), North America (Lil Miquela), Africa (Shudu Gram), and Southeast Asia (Thalasya Pov)—ensuring a geographically diverse sample that reflects the global reach and cultural relevance of AI-generated figures.
• Variety of brand engagement and purpose: Each influencer embodies a distinct commercial and narrative identity. Aitana López represents the monetization potential of virtual models through brand partnerships. Kenza Layli stands out for her activism and social messaging. Lil Miquela merges entertainment and fashion with music releases, while Shudu Gram exemplifies hyper-realism in luxury modelling. Thalasya Pov, on the other hand, highlights storytelling and travel-centric content, often tied to lifestyle branding.
• Technological and esthetic innovation: These characters illustrate different approaches to AI and CGI use, from hyper-realistic renders (Shudu Gram, Kenza Layli) to stylized and narrative-driven avatars (Lil Miquela, Thalasya Pov). This allows the study to assess the role of visual design, user engagement, and content strategy.
• Pioneering influence: Some of the selected figures, such as Lil Miquela and Shudu Gram, are pioneers in the virtual influencer space and have set industry standards. Others, like Kenza Layli and Aitana López, represent newer generations that show how the field is expanding in scope and purpose.
• Audience reach and social impact: With follower counts ranging from hundreds of thousands to millions, each influencer has demonstrated tangible audience engagement. This makes them ideal case studies for evaluating user interaction, marketing effectiveness, and emotional resonance with digital personas.

These virtual SMIs demonstrate the growing integration of synthetic personalities into influencer marketing. The presented five virtual influencers offer a representative and insightful cross-section of the AI influencer phenomenon, enabling a comparative exploration of their design, function, and impact on modern digital culture. Their diverse characteristics, creation strategies, and areas of influence offer a basis for modelling influencer effectiveness and facilitate benchmarking within MCDM frameworks.

Taken together, the reviewed studies on the application of MCDM methods, the formulation of influencer selection criteria, and the evolving characteristics of both human and virtual SMIs emphasize the multidimensional complexity of evaluating SMIs. They highlight a growing need for flexible approaches that can incorporate both crisp and fuzzy data, reflect diverse performance indicators, and adapt to the emergence of AI-generated personas. In the next section, we introduce a unified framework designed to address current methodological and practical gaps, particularly in managing uncertainty, integrating qualitative and quantitative factors, and responding to the dynamic nature of digital influence.

3. MCDM-Based Framework for SMI Assessment

This section begins by outlining the theoretical foundations of modern MCDM techniques and IVFF numbers (IVFFNs). It then presents an extended version of the EDAS method adapted to the IVFF environment. Lastly, a novel conceptual framework is proposed for the selection and evaluation of SMIs, incorporating multiple qualitative criteria.

3.1. Methodological Foundations of MCDM Methods

MCDM methods are designed to evaluate and rank alternatives based on multiple, often conflicting, criteria. These methods have evolved over the past 60 years and are now considered a cornerstone of soft computing, applicable in both crisp and fuzzy environments. Their key advantages include the following:

• Suitability for both individual and group decision-making scenarios.
• Flexible structure allowing the integration of methods for criteria weighting and alternative ranking.
• Low dependency on large datasets or high-performance computing.
• Ability to process various input data formats, such as crisp values, interval numbers, linguistic variables, or fuzzy numbers (e.g., triangular, trapezoidal, spherical, etc.), depending on the task requirements.

In recent years, the field of MCDM has witnessed the development of numerous advanced methods aimed at improving decision quality in complex and uncertain environments. As we mentioned in the previous section, these methods can be broadly classified into two groups: methods for ranking alternatives and methods designed for determining criteria weights.

The first group focuses on ranking a set of alternatives according to their performance across multiple criteria. Among the earliest in this category is COPRAS (Complex Proportional Assessment) [33], introduced in 2006, which ranks alternatives by comparing the utility of both beneficial and non-beneficial criteria. In 2012, the WASPAS (Weighted Aggregated Sum Product Assessment) method [34] was introduced, combining additive (SAW) and multiplicative (WPM) models to improve ranking stability. This was followed by MAIRCA (Multi-Attributive Ideal–Real Comparative Analysis) [35] in 2014, a method that evaluates gaps between ideal and empirical values to support ranking decisions based on proximity to ideal performance.

Later advancements include EDAS [36], developed in 2015, which ranks alternatives based on their distances—positive and negative—from the average solution across all criteria. More recently, PIV (Proportional Integral Value) [37], introduced in 2018, ranks alternatives based on proportional scores derived from normalized performance matrices, offering an effective balance between simplicity and mathematical rigour. In 2020, the RAFSI (Ranking of Alternatives through Functional mapping of criterion sub-intervals into a Single Interval) method [38] was proposed to evaluate alternatives combining radial distance concepts with fuzzy logic to enhance decision-making accuracy under uncertainty.

The second group consists of methods aimed at determining the relative importance of criteria (weighting), a fundamental step in any MCDM process. Among the earliest in this category is SWARA (Step-wise Weight Assessment Ratio Analysis) [39], introduced in 2010, which relies on expert judgement processed in a step-wise manner. In 2015, the Best–Worst Method (BWM) [40] was proposed to improve consistency and reduce the number of required pairwise comparisons by focusing only on the best and worst criteria. Then in 2018, the FUCOM (Full Consistency Method) [41] was developed to derive criteria weights with full consistency by minimizing deviation from consistency ratios, offering improved reliability over traditional pairwise comparison methods. Finally, MEREC (Method based on the Removal Effects of Criteria) [42], introduced in 2021, computes objective weights by evaluating how the exclusion of each criterion affects the overall decision outcome.

Fuzzy extensions of these methods accommodate uncertainty by employing fuzzy logic types like fuzzy sets (FSs) [43], intuitionistic fuzzy sets (IFSs) [44], Pythagorean fuzzy sets (PFSs) [45], as well as more recent types such as spherical fuzzy sets and IVFFNs. These fuzzy adaptations allow richer modelling of human judgement, making them ideal for decision contexts with qualitative or subjective evaluations.

This study focuses on the application of EDAS extended in an IVFF environment to prioritize virtual SMIs, demonstrating how modern MCDM techniques can handle uncertainty in digital marketing decisions effectively.

3.2. Core Concepts and Operations of Interval-Valued Fermatean Fuzzy Numbers

The use of interval-valued Fermatean fuzzy sets (IVFFSs) [46] in modifying the EDAS method necessitates a basic understanding of their unique structure and arithmetic rules. This subsection outlines the key concepts and operations behind IVFFNs.

IVFFSs build upon the foundation of Fermatean fuzzy sets (FFSs), introduced in 2020 [47], by incorporating interval-valued membership structures. Each IVFFS is defined by three components: Belongingness Grade (BG), Non-Belongingness Grade (NG), and Hesitation Degree, each expressed as intervals within the range [0, 1]. A fundamental condition is that the sum of the cubes of the upper bounds of the BG and NG must not exceed one. Unlike the single-point values used in traditional FFSs, IVFFSs allow for interval-valued BGs and NGs, offering a more refined approach to modelling uncertainty.

This flexibility is particularly useful in situations where it is challenging to assign precise values to BG and NG during the evaluation process. The interval representation of IVFFNs enables decision-makers to better capture and express ambiguity in their judgments, making IVFFSs a powerful tool in complex decision-making scenarios.

Definition 1.

Let $Int[0,1]$ denote the set of all closed subintervals of $[0,1]$. Then an IVFFS T in $U$ is defined by:

$$T=\left\{⟨u_i,\left[{\mu }_T^{lb}\left(u_i\right),{\mu }_T^{ub}\left(u_i\right)\right],\left[{\nu }_T^{lb}\left(u_i\right),{\nu }_T^{ub}\left(u_i\right)\right]⟩:u_i\in U\right\},$$

$$\mathrm{where}0\le {\mu }_T^{lb}\left(u_i\right)\le {\mu }_T^{ub}\left(u_i\right)\le 1,0\le {\nu }_T^{lb}\left(u_i\right)\le {\nu }_T^{ub}\left(u_i\right)\le 1\mathrm{and}{\left({\mu }_T^{ub}\left(u_i\right)\right)}^3+{\left({\nu }_T^{ub}\left(u_i\right)\right)}^3\le 1.$$

Here ${\mu }_T\left(u_i\right)=\left[{\mu }_T^{lb}\left(u_i\right),{\mu }_T^{ub}\left(u_i\right)\right]$ and ${\nu }_T\left(u_i\right)=\left[{\nu }_T^{lb}\left(u_i\right),{\nu }_T^{ub}\left(u_i\right)\right]$ represent the BG and NG of $u_i\in U$, correspondingly, in terms of interval values.

The function ${\pi }_T\left(u_i\right)=\left[{\pi }_T^{lb}\left(u_i\right),{\pi }_T^{ub}\left(u_i\right)\right]$ denotes the hesitancy (indeterminacy) degree of $u_i$ to $T$, where

$${\pi }_T^{lb}\left(u_i\right)=\sqrt[3]{{1-\left({\mu }_T^{ub}\left(u_i\right)\right)}^3-{\left({\nu }_T^{ub}\left(u_i\right)\right)}^3}\mathrm{and}{\pi }_T^{ub}\left(u_i\right)=\sqrt[3]{{1-\left({\mu }_T^{lb}\left(u_i\right)\right)}^3-{\left({\nu }_T^{lb}\left(u_i\right)\right)}^3}$$

(1)

For simplicity, an IVFFN can be represented by $F=\left(\left[{\mu }_F^{lb},{\mu }_F^{ub}\right],\left[{\nu }_F^{lb},{\nu }_F^{ub}\right]\right)$, where it satisfies the condition ${\left({\mu }_F^{ub}\right)}^3+{\left({\nu }_F^{ub}\right)}^3\le 1$.

Definition 2.

For any IVFFN $F=\left(\left[{\mu }_F^{lb},{\mu }_F^{ub}\right],\left[{\nu }_F^{lb},{\nu }_F^{ub}\right]\right)$, the score function $\mathfrak{S}$ of $F$ is given by

$$\mathfrak{S}\left(F\right)={\displaystyle \frac{1}{2}}\left({{\left({\mu }_F^{lb}\right)}^3+\left({\mu }_F^{ub}\right)}^3-{\left({\nu }_F^{lb}\right)}^3-{\left({\nu }_F^{ub}\right)}^3\right),\mathfrak{S}\left(F\right)\in \left[-1,1\right].$$

(2)

Definition 3.

For any IVFFN $F=\left(\left[{\mu }_F^{lb},{\mu }_F^{ub}\right],\left[{\nu }_F^{lb},{\nu }_F^{ub}\right]\right)$, the accuracy function $\mathfrak{E}$ of $F$ is given by

$$\mathfrak{E}\left(F\right)={\displaystyle \frac{1}{2}}\left({{\left({\mu }_F^{lb}\right)}^3+\left({\mu }_F^{ub}\right)}^3+{\left({\nu }_F^{lb}\right)}^3+{\left({\nu }_F^{ub}\right)}^3\right),\mathfrak{E}\left(F\right)\in \left[0,1\right].$$

(3)

Corresponding to the score and accuracy functions, a comparative scheme to compare any two IVFFNs $F_1$ and $F_2$ is given as:

If $\mathfrak{S}\left(F_1\right)>\mathfrak{S}\left(F_2\right)$, then $F_1\succ F_2$;

If $\mathfrak{S}\left(F_1\right)=\mathfrak{S}\left(F_2\right)$, then;

If $\mathfrak{E}\left(F_1\right)>\mathfrak{E}\left(F_2\right)$, then $F_1\succ F_2$;

If $\mathfrak{E}\left(F_1\right)<\mathfrak{E}\left(F_2\right)$, then $F_1\prec F_2$;

If $\mathfrak{E}\left(F_1\right)=\mathfrak{E}\left(F_2\right)$, then $F_1=F_2$.

Definition 4.

Let $F_1=\left(\left[{\mu }_{F_1}^{lb},{\mu }_{F_1}^{ub}\right],\left[{\nu }_{F_1}^{lb},{\nu }_{F_1}^{ub}\right]\right)$, $F_2=\left(\left[{\mu }_{F_2}^{lb},{\mu }_{F_2}^{ub}\right],\left[{\nu }_{F_2}^{lb},{\nu }_{F_2}^{ub}\right]\right)$, and $F=\left(\left[{\mu }_F^{lb},{\mu }_F^{ub}\right],\left[{\nu }_F^{lb},{\nu }_F^{ub}\right]\right)$ be three IVFFNs and $\gamma \in {\mathbb{R}}^{+}$. The operations on IVFFNs are given in the next formulas:

$$F_1\cup F_2=\left(\left[\max \left\{{\mu }_{F_1}^{lb},{\mu }_{F_2}^{lb}\right\},\max \left\{{\mu }_{F_1}^{ub},{\mu }_{F_2}^{ub}\right\}\right],\left[\min \left\{{\nu }_{F_1}^{lb},{\nu }_{F_2}^{lb}\right\},\min \left\{{\nu }_{F_1}^{ub},{\nu }_{F_2}^{ub}\right\}\right]\right)$$

(4a)

$$F_1\cap F_2=\left(\left[\min \left\{{\mu }_{F_1}^{lb},{\mu }_{F_2}^{lb}\right\},\min \left\{{\mu }_{F_1}^{ub},{\mu }_{F_2}^{ub}\right\}\right],\left[\max \left\{{\nu }_{F_1}^{lb},{\nu }_{F_2}^{lb}\right\},\max \left\{{\nu }_{F_1}^{ub},{\nu }_{F_2}^{ub}\right\}\right]\right)$$

(4b)

$$F_1\oplus F_2=\left(\left[\sqrt[3]{{\left({\mu }_{F_1}^{lb}\right)}^3+{\left({\mu }_{F_2}^{lb}\right)}^3-{\left({\mu }_{F_1}^{lb}\right)}^3{\left({\mu }_{F_2}^{lb}\right)}^3},\sqrt[3]{{\left({\mu }_{F_1}^{ub}\right)}^3+{\left({\mu }_{F_2}^{ub}\right)}^3-{\left({\mu }_{F_1}^{ub}\right)}^3{\left({\mu }_{F_2}^{ub}\right)}^3}\right],\left[{\nu }_{F_1}^{lb}{\nu }_{F_2}^{lb},{\nu }_{F_1}^{ub}{\nu }_{F_2}^{ub}\right]\right)$$

(4c)

$$F_1\otimes F_2=\left(\left[{\mu }_{F_1}^{lb}{\mu }_{F_2}^{lb},{\mu }_{F_1}^{ub}{\mu }_{F_2}^{ub}\right],\left[\sqrt[3]{{\left({\nu }_{F_1}^{lb}\right)}^3+{\left({\nu }_{F_2}^{lb}\right)}^3-{\left({\nu }_{F_1}^{lb}\right)}^3{\left({\nu }_{F_2}^{lb}\right)}^3},\sqrt[3]{{\left({\nu }_{F_1}^{ub}\right)}^3+{\left({\nu }_{F_2}^{ub}\right)}^3-{\left({\nu }_{F_1}^{ub}\right)}^3{\left({\nu }_{F_2}^{ub}\right)}^3}\right]\right)$$

(4d)

$$\gamma F=\left(\left[\sqrt[3]{1-{\left(1-{\left({\mu }^{lb}\right)}^3\right)}^{\gamma }},\sqrt[3]{1-{\left(1-{\left({\mu }^{ub}\right)}^3\right)}^{\gamma }}\right],\left[{\left({\nu }^{lb}\right)}^{\gamma },{\left({\nu }^{ub}\right)}^{\gamma }\right]\right)$$

(4e)

$$F^{\gamma }=\left(\left[{\left({\mu }^{lb}\right)}^{\gamma },{\left({\mu }^{ub}\right)}^{\gamma }\right],\left[\sqrt[3]{1-{\left(1-{\left({\nu }^{lb}\right)}^3\right)}^{\gamma }},\sqrt[3]{1-{\left(1-{\left({\nu }^{ub}\right)}^3\right)}^{\gamma }}\right]\right).$$

(4f)

In order to average IVFFNs, we employ a weighted averaging aggregation operator—the Interval-Valued Fermatean Fuzzy Weighted Averaging (IVFFWA) operator.

Definition 5.

Consider $F_j=\left(\left[{\mu }_j^{lb},{\mu }_j^{ub}\right],\left[{\nu }_j^{lb},{\nu }_j^{ub}\right]\right),$ where $j=\overline{1,n}$ is a collection of IVFFNs and $IVFFWA:{\Omega }^n\to \Omega$, then IVFFWA can be given by the formula:

$$IVFFWA\left(F_1,F_2,\dots ,F_n\right)={\oplus }_{j=1}^n{\omega }_j{F}_j,$$

where $\Omega$ is a set of all IVFFNs and ${\omega }_j$ is weight value with ${\omega }_j\in (0,1]$ and ${\sum }_{j=1}^n{\omega }_j=1$.

The IVFFWA formula [46] is as follows:

$$IVFFWA\left(F_1,F_2,\dots ,F_n\right)=\left(\left[\sqrt[3]{1-\prod _{j=1}^n{\left(1-{\left({\mu }_j^{lb}\right)}^3\right)}^{w_j}},\sqrt[3]{1-\prod _{j=1}^n{\left(1-{\left({\mu }_j^{ub}\right)}^3\right)}^{w_j}}\right],\left[\prod _{j=1}^n{\left({\nu }_j^{lb}\right)}^{w_j},\prod _{j=1}^n{\left({\nu }_j^{ub}\right)}^{w_j}\right]\right)$$

(5)

Definition 6.

Let $F_1=\left(\left[{\mu }_{F_1}^{lb},{\mu }_{F_1}^{ub}\right],\left[{\nu }_{F_1}^{lb},{\nu }_{F_1}^{ub}\right]\right)$ and $F_2=\left(\left[{\mu }_{F_2}^{lb},{\mu }_{F_2}^{ub}\right],\left[{\nu }_{F_2}^{lb},{\nu }_{F_2}^{ub}\right]\right)$ be IVFFNs. The Generalized Euclidean Distance between IVFFNs $F_1$ and $F_2$ [48] is defined as follows:

$$\begin{array}{l}{D}_{GE}\left(F_1,F_2\right)=\sqrt{{\displaystyle \frac{D_{\mu }+D_{\nu }+D_{\pi l}+D_{\pi u}}{6}}},\\ \mathrm{where}{D}_{\mu }={\left({{\mu }_{F_1}^{lb}}^3-{{\mu }_{F_2}^{lb}}^3\right)}^2+{\left({{\mu }_{F_1}^{ub}}^3-{{\mu }_{F_2}^{ub}}^3\right)}^2,D_{\nu }={\left({{\nu }_{F_1}^{lb}}^3-{{\nu }_{F_2}^{lb}}^3\right)}^2+{\left({{\nu }_{F_1}^{ub}}^3-{{\nu }_{F_2}^{ub}}^3\right)}^2,\\ D_{\pi l}={\left(\left(1-{{\mu }_{F_1}^{lb}}^3-{{\nu }_{F_1}^{lb}}^3\right)-\left(1-{{\mu }_{F_2}^{lb}}^3-{{\nu }_{F_2}^{lb}}^3\right)\right)}^2\mathrm{and}{D}_{\pi u}={\left(\left(1-{{\mu }_{F_1}^{ub}}^3-{{\nu }_{F_1}^{ub}}^3\right)-\left(1-{{\mu }_{F_2}^{ub}}^3-{{\nu }_{F_2}^{ub}}^3\right)\right)}^2.\end{array}$$

(6)

In summary, the domain of IVFFNs encompasses a broader scope than that of Interval-Valued Intuitionistic Fuzzy Numbers (IVIFNs) and Interval-Valued Pythagorean Fuzzy Numbers (IVPFNs). Owing to their more flexible constraints, IVFFSs provide enhanced capability and precision in modelling complex uncertainty, making them especially suitable for challenging MCDM scenarios.

3.3. EDAS in IVFF Environment

EDAS is a relatively recent distance-based MCDM method that evaluates alternatives based on their positive and negative distances from the average solution. One of the key advantages of the EDAS method is that it does not require the normalization of input data, unlike many other MCDM techniques such as TOPSIS or VIKOR. This is because EDAS evaluates each alternative based on its positive and negative deviations from the average value of each criterion, rather than comparing alternatives to ideal or worst-case values. By using the average as a relative reference point, EDAS preserves the original scale and meaning of the data, allowing criteria to be assessed in their natural units. This eliminates the need for rescaling and simplifies the decision-making process, making EDAS both efficient and easy to interpret, particularly in scenarios involving heterogeneous or multidimensional data.

To adapt EDAS for use within an IVFF environment, we propose calculating the deviations of alternatives from the average reference point using an appropriate IVFF distance measure. The pseudocode for the proposed IVFF-based extension of EDAS is presented in Algorithm 1.

Algorithm 1. Pseudocode of IVFF EDAS.
Step 1:	Formulation of DM problem:
	identify $A\left[i\right]$	//$A$ is the set of given alternatives
	identify $C\left[j\right]$ and $\omega \left[j\right]$	//$C$ is the set of identified criteria for $A$ evaluation //$\omega$ is the set of relative weights of criteria
	$X\left[i,j\right]\leftarrow intersec\left(A,C\right)$	//Empty matrix $X$
Step 2:	Input of decision matrix $X$
Step 2.1:	Data transformation
	$N\leftarrow length\left(A\right)$; $M\leftarrow length\left(C\right);K\leftarrow \mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{s}$	//Input of assessments of kth expert in $X^k$ matrix in linguistic variables
	for k in {1..K}
	for i in {1..N}
	for j in {1..M}
	$X^k\left[i,j\right]\leftarrow A\left[i\right],C\left[j\right]$
	${\tilde{X}}^k\left[i,j\right]\leftarrow X^k\left[i,j\right]$	//Transform X matrices in IVFF values
	endfor
	endfor
	endfor
Step 2.2:	Data processing
	for i in {1..N}	//Averaging $\tilde{X}$ for the group of experts according to Equation (5), where the experts have equal weight (1/K)
	for j in {1..M}
	$\tilde{X}\left[i,j\right]\leftarrow IVFFWA\left({\tilde{X}}^1\left[i,j\right],{\tilde{X}}^2\left[i,j\right],\dots ,{\tilde{X}}^k\left[i,j\right]\right)$
	endfor
	endfor
Step 3:	Computation of the average value for each criterion
	for i in {1..N}	//Weighted average $\tilde{X}[i,j]$ by criteria according to Equation (5)
	for j in {1..M}
	$\widetilde{AV}\left[j\right]\leftarrow IVFFWA\left(\tilde{X}\left[1,j\right],\tilde{X}\left[2,j\right],\dots ,\tilde{X}\left[N,j\right]\right)$
	endfor
	endfor
Step 4:	Calculation of the positive distance and negative distance matrices of each alternative from the average solution
	for i in {1..N}	//Computation of the positive $PDA[i,j]$ and the negative ideal $NDA[i,j]$ distance matrices for beneficial $\left(\mathbb{B}\right)$ and cost criteria $(\mathbb{C}$) according to Definition 2
	for j in {1..M}
	$DA\left[i,j\right]=\mathit{max}({0,\theta D}_{GE}\left(\tilde{X}\left[i,j\right],\widetilde{AV}\left[j\right]\right)/\mathfrak{S}\left(\widetilde{AV}\left[j\right]\right))$ $NDA\left[i,j\right]=\mathit{max}({0,-\theta D}_{GE}\left(\tilde{X}\left[i,j\right],\widetilde{AV}\left[j\right]\right)/\mathfrak{S}\left(\widetilde{AV}\left[j\right]\right))$, where $\theta =$ $\left\{\begin{array}{c}1,\mathit{if}\left[\mathfrak{S}\left(\tilde{X}\left[i,j\right]\right)>\mathfrak{S}\left(\widetilde{\mathit{AV}}\left[j\right]\right)\mathit{and\; j}\in \mathbb{B}\right]or\left[\mathfrak{S}\left(\tilde{X}\left[i,j\right]\right)<\mathfrak{S}\left(\widetilde{AV}\left[j\right]\right)andj\in \mathbb{C}\right]\\ -1,\mathit{if}\left[\mathfrak{S}\left(\tilde{X}\left[i,j\right]\right)<\mathfrak{S}\left(\widetilde{\mathit{AV}}\left[j\right]\right)\mathit{and\; j}\in \mathbb{C}\right]or\left[\mathfrak{S}\left(\tilde{X}\left[i,j\right]\right)>\mathfrak{S}\left(\widetilde{AV}\left[j\right]\right)andj\in \mathbb{B}\right]\end{array}\right.$
	endfor
	endfor
Step 5:	Calculation of the weighted forward distance and the reverse weighted distance to the average solutions for each alternative
	for i in {1..N}	//Computation of the weighted sum of PDA and NDA from each alternative to the average solution.
	$SP\left[i\right]={\sum }_{j=1}^M{w}_{j}PDA[i,j]$                  $SN\left[i\right]={\displaystyle \sum _{j=1}^M}{w}_{j}NDA[i,j]$
Step 6:	Calculation of the normalized value of the weighted distances to the average solutions for each alternative and the final evaluation score
Step 7:	for i in {1..N}         $NSP\left[i\right]={\displaystyle \frac{SP\left[i\right]}{\underset{i}{\mathit{max}}SP\left[i\right]}}$, $NSN\left[i\right]={\displaystyle \frac{SN\left[i\right]}{\underset{i}{\mathit{max}}SN\left[i\right]}}$,               $AS\left[i\right]={\displaystyle \frac{NSP\left[i\right]+NSN\left[i\right]}{2}}$	//Computation of the normalized weighted distances of each alternative to the average solution $NSP\left[i\right]$ and $NSN\left[i\right]$ and the appraisal score AS$\left[i\right]$ of alternatives
Step 8:	Output of alternatives’ ranks in descending order of their assessment

Unlike its classical fuzzy counterpart, the proposed IVFF-based extension of EDAS involves a significant computational load. However, this added complexity allows for more precise and nuanced evaluations of alternatives. The resulting rankings are derived from a more comprehensive comparison process, reflecting the full range of uncertainty inherent in expert assessments.

3.4. Conceptual Framework for SMI Selection

The framework presents a structured eight-stage decision-making process for selecting suitable SMIs (Figure 1). It supports both single-use and iterative implementation, making it adaptable to dynamic campaign contexts where influencer performance and audience sentiment may evolve over time.

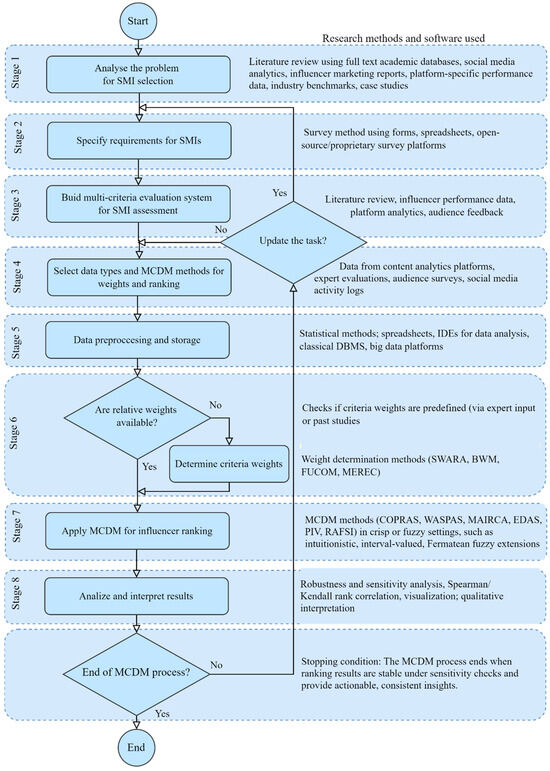
Figure 1. Flowchart of proposed framework for decision analysis of SMIs.

Stage 1. Problem definition in the context of SMI selection.

The process begins with defining the campaign goals and expectations from SMI collaboration. Decision-makers, typically marketers, consult industry reports, social platform performance data, and previous campaign evaluations to identify challenges and opportunities.

Stage 2. Specification of influencer requirements.

Key SMI attributes are specified, such as content quality, credibility, and audience fit. Input may be collected using structured surveys administered through forms, spreadsheets, or dedicated survey platforms. The outcome is a clear profile of the ideal influencer aligned with brand objectives and audience expectations.

Stage 3. Construction of a multi-criteria evaluation system.

Based on Stage 2, a multi-criteria index is developed using both quantitative and qualitative indicators. The index can include engagement rate, follower count, innovation, authenticity, and audience demographics. These criteria are derived from influencer marketing reports, social media analytics, expert opinions, and user feedback.

Stage 4. Selection of data types and MCDM methods for weighting and ranking.

Appropriate data formats (e.g., crisp, interval, fuzzy, or Fermatean fuzzy estimates) are selected based on data availability and complexity. MCDM methods for weighting (e.g., SWARA, BWM, FUCOM, MEREC) and ranking (COPRAS, EDAS, WASPAS, RAFSI, MAIRCA, PIV) are chosen accordingly. Data may come from analytics platforms, expert evaluations, or social media logs.

Stage 5. Data preprocessing and storage.

Collected data are preprocessed using standard statistical and data engineering tools (spreadsheets, IDEs, DBMS, or big data storage systems). Qualitative values are transformed into numerical formats, and data cleaning procedures address missing, duplicated, or inconsistent entries.

Stage 6. Determination of criteria weights.

The relative importance of criteria is determined through expert input or computed using weighting methods. This produces the weighted decision matrix used in the ranking phase.

Stage 7. Application of MCDM algorithms for influencer ranking.

Selected MCDM algorithms are applied to generate a prioritized list of influencers. These may operate in crisp or fuzzy environments, and hybrid configurations can be used to enhance robustness. Influencers are ranked based on how well they meet the defined multi-criteria profile.

Stage 8. Analysis and interpretation of results.

The results are interpreted using statistical and qualitative tools, including robustness and sensitivity analysis, correlation checks (e.g., Spearman/Kendall), and expert validation.

The process ends when ranking outcomes are stable under sensitivity analysis and provide consistent, actionable insights that support final decision-making.

Beyond occasional use, the proposed framework is designed for iterative use throughout an ongoing influencer marketing campaign. According to the update condition (flowchart block “Update the task?”), the process should be reactivated if stakeholder-defined criteria or evaluation objectives are found to be inaccurate, insufficient, or misaligned with the current SMI selection context. For instance, if real-time monitoring detects declining influencer performance, negative audience sentiment, or a shift in campaign priorities, decision-makers can revise the evaluation system and rerun the analysis. This adaptability ensures that influencer partnerships remain strategically aligned and responsive to the dynamic nature of social media environments. In this way, the framework not only supports initial influencer selection but also enables the continuous observation and assessment of SMIs′ performance over time. Such longitudinal monitoring helps marketers identify trends, react to sentiment- or emotion-related changes, and maintain campaign relevance through timely decision-making.

The proposed framework outlines a sequence of stages that guide decision-makers from problem definition to result interpretation, enabling a structured and data-informed approach to SMI selection in the dynamic context of social media. Its integration of MCDM techniques supports adaptability to the complexity and uncertainty inherent in digital influencer evaluation.

4. Practical Examples

4.1. Case Study: Quality-Based Evaluation of SMIs

Let M be a marketing team or decision-making authority tasked with selecting the most suitable virtual SMIs for a digital branding campaign. According to the proposed framework, in Stage 1, the team should define the problem and conduct an initial analysis. This confirms the presence of several prominent virtual SMIs suitable for campaign collaboration. For this illustrative case, the marketers focus on five well-known virtual influencers: Kenza Layli ($A_1$), Aitana López ($A_2$), Lil Miquela ($A_3$), Shudu Gram ($A_4$), and Thalasya Pov ($A_5$) (Section 2.3).

Stage 2 captures the campaign-specific requirements for influencer selection. A structured questionnaire is distributed among experts and marketing professionals to evaluate the importance of various criteria. A five-point Likert scale is used for responses, ranging from “Unimportant” (1) to “Extremely Important” (5).

Stage 3 involves constructing a multi-criteria evaluation index. The following eight criteria are selected for SMI assessment: perceived authenticity ($C_1$), innovation in content creation ($C_2$), content quality ($C_3$), brand collaboration history ($C_4$), social impact ($C_5$), demographic alignment ($C_6$), engagement rate ($C_7$), and number of followers ($C_8$) (Section 2.2).

Stage 4 determines the appropriate data format and MCDM methods. Due to the subjective and imprecise nature of some evaluations, data are represented as linguistic variables (Table 3). To ensure consistency and handle uncertainty, the proposed IVFF EDAS approach is applied for influencer ranking.

Table 3. Input decision matrix for virtual SMI selection.

Criteria Alternatives	C1	C2	C3	C4	C5	C6	C7	C8
A1	M	M	H	M	H	M	VL	L
A2	H	VH	H	H	M	H	VH	M
A3	VH	VH	VH	VH	VH	VH	L	VH
A4	M	VH	VH	H	H	H	H	M
A5	H	M	H	M	H	H	M	H
Criterion type	$\mathbb{B}$	$\mathbb{B}$	$\mathbb{B}$	$\mathbb{B}$	$\mathbb{B}$	$\mathbb{B}$	$\mathbb{B}$	$\mathbb{B}$

Stage 5 includes preprocessing steps such as aggregating expert opinions and transforming linguistic evaluations into IVFFNs, using a predefined correspondence table. Evaluations are mapped to five linguistic terms (Very Low, Low, Medium, High, Very High) and encoded accordingly using the rules from Table 4.

Table 4. Linguistic variables and their corresponding IVFF numbers.

Linguistic Term	IVFFN
Very Low (VL)	([0.05, 0.20], [0.85, 1.00])
Low (L)	([0.25, 0.40], [0.65, 0.80])
Medium (M)	([0.45, 0.60], [0.45, 0.60])
High (H)	([0.65, 0.80], [0.25, 0.40])
Very High (VH)	([0.80, 1.00], [0.05, 0.20])

Stage 6 checks for predefined relative weights. In this scenario, the weights are determined using expert assessments and normalized for use in the EDAS method.

Stage 7 applies the IVFF EDAS method to evaluate and rank the five SMIs based on the selected criteria and weighted evaluations.

Stage 8 focuses on result analysis. Sensitivity checks and the Spearman rank correlation test are conducted to ensure the robustness of the final ranking. The process concludes when rankings are consistent and provide actionable guidance for campaign planning.

Let the weights of all criteria be equal, with $w_1=w_2=w_3=w_4=w_5=w_6=w_7=w_8=0.125$. Table 5 presents the overall scores and corresponding rankings of the evaluated virtual SMIs, obtained using both the IVFF EDAS and crisp EDAS methods.

Table 5. Scores and their corresponding rankings—IVFF EDAS and crisp EDAS.

		A1	A2	A3	A4	A5
IVFF	Score	0.121	0.576	0.590	0.495	0.417
	Rank	5	2	1	3	4
Crisp	Score	0.000	0.642	0.922	0.608	0.421
	Rank	5	2	1	3	4

To demonstrate the feasibility of the IVFF EDAS solution, the resulting ranking is compared with those obtained using other methods—crisp SAW, crisp TOPSIS, and IVFF TOPSIS (Table 6).

Table 6. Overall scores and their corresponding rankings—crisp SAW, crisp TOPSIS, and IVFF TOPSIS methods.

	SAW		TOPSIS		IVFF TOPSIS
Alternative	Score	Rank	Score	Rank	Score	Rank
A1	0.575	5	0.123	5	0.057	5
A2	0.800	2	0.586	2	0.386	2
A3	0.925	1	0.650	1	0.624	1
A4	0.800	2	0.551	3	0.376	3
A5	0.725	3	0.446	4	0.156	4
Spearman’s $\rho$				0.900		0.900

The final rankings are summarized below:

SAW method: A₃ $\succ$ A₂ $\approx$ A₄ $\succ$ A₅ $\succ$ A₁.

EDAS, TOPSIS, IVFFNs TOPSIS, and IVFFNs EDAS methods: A₅$\succ$A₂$\succ$A₁$\succ$A₃$\succ$A₄.

To assess the consistency between the SAW benchmark and the outcomes of the other MCDM techniques, Spearman’s rank correlation coefficient was employed. The high correlation value, particularly for IVFF EDAS ($\rho$ = 0.900), confirms the robustness of the proposed method.

Based on the obtained rankings from the five MCDM methods, crisp SAW, crisp TOPSIS, crisp EDAS, IVFF TOPSIS, and ITFF EDAS, the results exhibit a consistent prioritization pattern, with Lil Miquela (A₃) ranked first across all methods, followed by Aitana López (A₂) and Shudu Gram (A₄). According to the obtained rankings, three groups of AI-based SMIs can be constructed:

Group 1: Top-Ranked SMI

Lil Miquela (A₃), ranked first in all methods, clearly dominates the evaluation due to a balanced combination of high performance across all eight criteria, particularly in authenticity ($C_1$), innovation ($C_2$), and content quality ($C_3$), which are crucial for digital influence.

Group 2: Mid-to-High Performers

Aitana López (A₂) and Shudu Gram (A₄) consistently occupy the second and third positions. Aitana shows strong results in engagement metrics ($C_7$), while Shudu performs well in content quality ($C_3$). Both influencers excel in innovation ($C_2$). The minor ranking variation between them (A₂ ≈ A₄ in SAW, A₂ ≻ A₄ in other methods) underscores their comparable strengths. Thalasya Pov ($A_5$) appears in fourth place in all methods, forming a transitional case between high and low performers.

Group 3: Lowest-Ranked SMI

Kenza Layli (A₁) consistently ranks last in all MCDM approaches. Despite potential visibility, her lower scores in key evaluative criteria such as authenticity (C₁), innovation (C₂), engagement rate (C₇), and number of followers (C₈) may have contributed to this outcome.

The consistency of rankings across both crisp and fuzzy MCDM methods confirms the robustness and reliability of the proposed framework for SMI selection. These results align with expected influencer performance characteristics, reinforcing the framework’s practical applicability in real-world influencer marketing scenarios, particularly for use by marketing professionals and decision-makers.

4.2. Case Study: Dynamic Attitude-Based Evaluation of SMIs

Let marketing team M be faced with the task of repeatedly selecting AI-based SMIs. The objective is to periodically rank these SMIs in order to monitor their attributes and dynamically evaluate them based on evolving user attitudes. In this illustrative example, we use a text-based emotion analysis approach grounded in Ekman’s six basic emotions: Joy, Anger, Disgust, Fear, Sadness, and Surprise [49].

The decision matrix consists of a single criterion C, representing the emotion-based assessment of user attitudes towards five AI-based SMIs (Section 2.3). The dataset used in this case study is synthetically generated to simulate realistic distributions of follower emotions at two observation points, −$t_i$ and $t_{i+1}$, representing the start and end of the evaluation period, respectively.

Evaluations of the alternatives with respect to criterion C are expressed using IVFFNs (Stage 5). In this case, the BG and NG denote the lower and upper bounds of positive and negative user attitudes, measured at $t_i$ and $t_{i+1}$. These assessments are conducted periodically over predefined time intervals $\left[t_i,t_{i+1}\right]$.

In the next stage, social media data (user comments and replies) related to each influencer’s content are collected, and emotion-based text analysis is applied. User emotions towards each influencer are quantified as percentages of total relevant posts. To convert these emotion shares into IVFFNs, the following rules are employed:

• BG is assigned the value of Joy;
• NG is calculated as the sum of Anger, Disgust, Fear, and Sadness (Table 7).
  Table 7. Social media data for virtual SMIs by time and emotion (%).

  Time	$\mathbf{Start}({\mathit{t}}_{\mathit{i}}$)					$\mathbf{End}({\mathit{t}}_{\mathit{i}+1}$)
  Alternative Emotion	A1	A2	A3	A4	A5	A1	A2	A3	A4	A5
  Joy	0.358	0.411	0.438	0.413	0.398	0.336	0.425	0.685	0.392	0.415
  Anger	0.042	0.032	0.029	0.034	0.039	0.039	0.041	0.084	0.026	0.035
  Disgust	0.021	0.029	0.031	0.019	0.025	0.025	0.025	0.046	0.013	0.018
  Fear	0.034	0.025	0.025	0.030	0.034	0.030	0.022	0.061	0.025	0.035
  Sadness	0.059	0.043	0.046	0.045	0.068	0.054	0.055	0.072	0.038	0.067
  Surprise	0.210	0.195	0.235	0.173	0.204	0.207	0.189	0.218	0.167	0.192
  BG	0.358	0.411	0.438	0.413	0.398	0.336	0.425	0.685	0.392	0.415
  NG	0.156	0.129	0.131	0.128	0.166	0.148	0.143	0.263	0.102	0.155

Note: The emotion Surprise is treated as neutral and excluded from the IVFFN calculation in this case study.

Finally, to evaluate every alternative, we implement the score function (Equation 2). The decision matrix, overall scores, and final SMI ranks can be found in Table 8.

Table 8. Evaluation scores and ranks for virtual SMIs.

Alternative	${\mathit{\mu }}^{\mathit{l}\mathit{b}}$	${\mathit{\mu }}^{\mathit{u}\mathit{b}}$	${\mathit{\nu }}^{\mathit{l}\mathit{b}}$	${\mathit{\nu }}^{\mathit{u}\mathit{b}}$	Score	Rank
A1	0.336	0.358	0.148	0.156	0.038	5
A2	0.411	0.425	0.129	0.143	0.071	2
A3	0.438	0.685	0.131	0.263	0.193	1
A4	0.392	0.413	0.102	0.128	0.064	3
A5	0.398	0.415	0.155	0.166	0.063	4

The final ranking is as follows: A₅ ≻ A₂ ≻ A₁ ≻ A₃ ≻ A₄. The comparative analysis shows that all SMIs retain their relative positions from the initial evaluation (Section 4.1). A possible reason for this strong positive sentiment towards Lil Miquela (A₁) may lie in her well-established digital presence, high-quality visual content, and her pioneering role as one of the first AI-generated influencers with global brand collaborations. Her consistent portrayal of authenticity, innovation, and creativity has earned sustained engagement from diverse online communities.

The notable performance of Aitana López (A₂) and Shudu Gram (A₄), ranked second and third, respectively, reflects their ability to maintain audience interest through niche branding and emotionally resonant content. Aitana López’s (A₂) focus on lifestyle and fitness has resonated well with younger demographics, while Shudu Gram’s (A₄) strong visual storytelling and alignment with luxury fashion have contributed to her appeal.

Thalasya Pov (A₅) maintains a mid-level ranking, indicating a relatively stable but less dominant presence, while Kenza Layli (A₁) consistently ranks last, likely due to limited content diversity and lower audience engagement in emotionally positive categories.

The task of ranking AI-based SMIs based on user attitudes can be performed periodically or in near real time using social media text analytics. Such dynamic evaluation supports marketers in tracking shifts in audience sentiment and making timely, data-informed decisions for campaign planning and influencer collaboration.

5. Conclusions

Influencer evaluation and selection tools have become increasingly relevant research topics due to the growing impact of SMIs in marketing strategies. Numerous companies across various sectors have intensified their focus on identifying effective influencers who can authentically represent their brands and engage target audiences. However, existing methods for selecting suitable SMIs frequently lack comprehensiveness and struggle with handling ambiguity inherent in subjective assessments.

In this study, we propose a new integrated framework for the selection of SMIs based on the MCDM approach, providing an objective evaluation of potential candidates. Additionally, a new IVFF-based MCDM method has been developed specifically for influencer selection. Leveraging its fuzzy logic structure, this method adeptly manages the uncertainty and imprecision often encountered in expert judgments.

The fuzzy modification proposed in this study builds upon the EDAS, acknowledged as one of the most effective distance-based multi-criteria evaluation methods. A distinctive feature of the proposed IVFF-based EDAS is the refined distance calculation formula tailored for an IVFF environment, incorporating the following:

• Interval-valued membership, non-membership, and hesitancy degrees;
• The lengths of these intervals, representing Belongingness, Non-Belongingness, and hesitancy.

These are essential components in capturing uncertainty and imprecision within the decision-making process.

The effectiveness of our framework is demonstrated through two practical applications. The first application involves selecting the most suitable influencer from a set of five candidates, evaluated across eight performance criteria. The second application involves ranking influencers according to public sentiment analysis extracted from social media content. The results highlight the robustness and practical applicability of our proposed methodology, accurately reflecting influencer performance and public perceptions.

Future enhancements to the proposed conceptual framework will integrate additional advanced MCDM methods developed in recent years. Furthermore, the influencer evaluation process will be expanded to address various types of uncertainty through the application of advanced fuzzy sets, such as hesitant interval-valued Fermatean fuzzy sets and diamond intuitionistic fuzzy sets. Future research will also focus on developing hybrid approaches that combine innovative weight determination techniques with modified MCDM algorithms to further improve the precision of alternative selection.