Time-Modifiable Chameleon Hash for Building Redactable Blockchains

Abstract

Blockchain’s immutability, while enhancing transparency and trust, presents challenges when erroneous or sensitive content must be modified. To address this, we propose a novel cryptographic primitive called Time-Modifiable Chameleon Hash (TMCH), enabling controlled and time-modifiable data redaction in blockchain systems. TMCH enhances traditional chameleon hashes by embedding a time parameter into hash generation and verification, and it supports class-adaptive collision computation via a new Update algorithm. We formally define the security model for TMCH and analyze the relationships among uniqueness, indistinguishability (IND), and collision resistance (CR). This paper presents a concrete construction based on the Boneh–Boyen signature scheme and completes its security analysis and proof. Finally, the efficiency and practicality of the proposed scheme are validated through experimental comparisons with existing algorithms. Our results show that relaxing the uniqueness requirement does not compromise overall security, while enabling traceable and time-aware redactions. The proposed TMCH achieves strong security guarantees and practical efficiency, making it well suited for applications such as compliant data redaction and time-sensitive blockchain transactions.

1. Introduction

Blockchain technology, known for its distributed ledger architecture, is widely adopted for recording cryptocurrency transactions—Bitcoin [1] being a prime example—because of its inherent transparency and openness. As the technology has evolved rapidly, its applications have expanded well beyond digital currencies to areas such as government services, healthcare, and the judiciary. Accordingly, the data recorded on the blockchain have become increasingly rich and sensitive. However, while the immutability of blockchain is designed to ensure data integrity and security, it also presents significant practical challenges: once illegal, malicious, or privacy-infringing content is recorded on-chain, it becomes virtually impossible to delete, potentially leading to long-term harm for individuals and society.

The introduction of the European Union’s General Data Protection Regulation (GDPR), which enshrines the “right to be forgotten”, has intensified this tension. Specifically, the regulation grants individuals the right to request the deletion of their personal data when certain conditions are met. However, this legal entitlement fundamentally conflicts with the immutable nature of blockchain, thereby triggering an inherent conflict between regulatory compliance and blockchain’s design principles. To address this, researchers have started investigating ways to incorporate controlled mutability into blockchains without compromising their fundamental properties. A prominent approach in this direction is the concept of redactable blockchains, which permits the modification of on-chain data under rigorous cryptographic safeguards.

In a seminal work presented at EuroS&P 2017, Ateniese et al. [2] introduced the idea of replacing traditional collision-resistant hash functions (e.g., SHA-256) in blockchain systems with a trapdoor hash function known as the chameleon hash (CH). This approach enables a block initially committed with content m and randomness r to be altered to a new block with content $m^{\prime }$ by computing new randomness $r^{\prime }$, such that the chameleon hash output remains unchanged. Fundamentally, when the modifier possesses the corresponding private trapdoor key, they can efficiently generate such collisions, ensuring that the hash value of $(m,r)$ equals that of $(m^{\prime },r^{\prime })$. This allows for controlled block modifications while preserving the integrity of the hash links.

When implementing cryptographic primitives like chameleon hashes for redactable blockchains, it is essential to address three fundamental challenges simultaneously: security, scalability, and decentralization. However, as highlighted by the well-known blockchain “Trilemma” [3], achieving all three within a single solution remains highly challenging. From a security standpoint, the redaction mechanism must withstand key exposure threats and provide semantic security comparable to that of public key encryption. At the same time, the redaction operations must be efficient enough to avoid impairing overall system performance. Moreover, in alignment with the decentralization principles of blockchain, the approach should avoid reliance on any single trusted authority. These competing demands lead to a critical question: is it possible to design a practical chameleon hash scheme that effectively balances these conflicting requirements?

To address this challenge, we propose a secure and efficient chameleon hash scheme termed TMCH. TMCH facilitates blockchain redactions with traceability and fine-grained access control, clearly defining who is authorized to modify data and the permissible time frames for such modifications. It introduces time-bound validity for redactions and enforces redaction policies via cryptographic constraints. By embedding temporal and policy conditions within the hash structure, TMCH enables authorized entities to generate valid hash collisions while preserving consistency throughout the blockchain. This design offers a practical and integrated solution that balances security, scalability, and decentralization, providing a strong foundation for the deployment of redactable blockchain systems in real-world scenarios.

Our objective is to explore whether the violation of uniqueness can be rigorously formalized and utilized without compromising overall security and whether TMCH can function as a practical cryptographic primitive for the construction of secure, time-sensitive applications. Specifically, we pose the following question:

Is it possible to construct a provably secure TMCH scheme that deliberately breaks the uniqueness property, satisfies formal IND and CR properties, and supports at least one practical application?

1.1. Contributions

The main contributions of this work are summarized as follows.

• We propose a novel Time-Modifiable Chameleon Hash (TMCH) scheme that integrates time verifiability into its core algorithms. This allows users to incorporate time parameters in hash generation and verification while preserving the ability to compute collisions akin to traditional adaptation algorithms. A key innovation in TMCH is the introduction of a new collision-finding algorithm, Update, which relaxes the conventional uniqueness constraint of chameleon hashes. This supports dynamic collision adjustments with respect to time, forming the fundamental functional extension of the scheme.
• We formalize the security requirements of TMCH and theoretically analyze the relationships among uniqueness, IND, and CR. Our proofs demonstrate how the uniqueness property can be leveraged to establish IND and CR, thereby providing a solid security foundation for the scheme.
• We validate the practicality and effectiveness of the proposed TMCH scheme through comprehensive security proofs and performance evaluations, demonstrating its efficiency and security suitability for real-world applications.

1.2. Structure

This paper is organized as follows. Section 2 provides a comparative analysis of existing research on chameleon hash applications in editable blockchains, summarizing key advancements and limitations of state-of-the-art schemes in balancing redactability and security. Section 3 introduces the necessary preliminaries, including formal definitions of algebraic groups, bilinear maps, the computational Diffie–Hellman (CDH) assumption, and other foundational cryptographic concepts. It reviews the construction of CH schemes, formalizes their required security properties, and illustrates design principles using Pedersen commitments as an example. The section concludes by introducing the construction of the TMCH scheme. Section 4 focuses on a black-box construction of TMCH, detailing its core components and formally defining its security guarantees. Through a series of game-based experiments, it rigorously proves key properties such as correctness, typical indistinguishability, new indistinguishability, typical collision resistance, and new collision resistance. Section 5 describes a concrete white-box instantiation of TMCH based on the Boneh–Boyen signature (BBS) scheme, accompanied by thorough analysis and formal proofs of five critical security properties specific to this instantiation. Section 6 evaluates the proposed scheme’s efficiency and practicality through experiments and comparative tables, demonstrating its performance advantages over existing approaches. Finally, Section 7 concludes the paper and discusses promising avenues for future research.

2. Related Works

CH functions are fundamental cryptographic primitives enabling controlled mutability in blockchain systems. In recent years, a variety of enhanced CH-based schemes have been proposed, targeting key challenges such as fine-grained access control, revocable trapdoor delegation, auditable rewriting, and decentralized trust models. These advancements have significantly improved the practical applicability of redactable blockchain frameworks by seamlessly integrating policy enforcement, accountability, and flexible deployment.

Nevertheless, despite these advances, the majority of existing CH constructions still lack time verifiability—an essential feature in enabling auditability, regulatory compliance, and time-sensitive rewriting policies. Furthermore, current schemes typically lack support for arbitrary or class-adaptive collision computation, thereby restricting their flexibility in adapting to dynamic blockchain environments.

Derler et al. [4] proposed an attribute-based chameleon hash scheme that enables fine-grained rewriting by associating trapdoor capabilities with user attributes. While it strengthens access control, it does not support temporal verifiability or flexible collision logic.

Xu et al. [5] introduced a revocable policy-based chameleon hash, enabling redaction privileges to be revoked dynamically. While improving control and forward security, this scheme still lacks the ability to verify the timing of collisions, and its collision computation remains inflexible.

Xu et al. [6] further enhanced accountability in redactable blockchains by incorporating auditable rewriting logs. This design improves traceability but still does not integrate mechanisms for time-verifiable redactions or support arbitrary, class-adaptive collisions.

Duan et al. [7] proposed a T-times chameleon hash scheme that limits the number of rewrites per trapdoor key. Despite introducing a form of temporal limitation, the number of allowed rewrites is fixed in advance and cannot be cryptographically verified in real time. Furthermore, this approach does not support arbitrary collision computation beyond a preset rewrite count.

Li et al. [8] developed a decentralized chameleon hash framework to eliminate centralized trust assumptions. However, their scheme does not address temporal verifiability or the computation of adaptive collisions, both critical for compliance and auditing in real-world blockchains.

Dong et al. [9] combined chameleon hashing with multi-authority attribute-based encryption to enable access-controlled redactable consortium blockchains. Although this enhances policy enforcement, the scheme suffers from high complexity and lacks mechanisms for time verifiability and arbitrary collision computation.

Chen et al. [10] proposed a time-verifiable policy-based chameleon hash (TPCH) for building traceable redactable blockchains. This scheme supports both private and public redaction modes, enables time traceability of redactions by introducing a time parameter, and incorporates a new Update algorithm to prevent the abuse of redaction powers. Experimental and theoretical analyses have demonstrated its feasibility and practicality. Its advantages include high efficiency in public redaction, support for fine-grained redaction, and time traceability. However, it has drawbacks: the performance of ABE-based private redaction is significantly affected by factors such as the number of attributes, resulting in insufficient efficiency, and the use of numerous cryptographic primitives increases the system complexity.

To better understand the limitations and characteristics of these existing works, we provide a comparative summary in Table 1.

Table 1. Comparison of chameleon hash schemes for blockchain applications.

Scheme	Time Verifiability	Arbitrary Collision	Revocation	Fine-Grained Control	Decentralization	Key Component
DKS+19 [4]	✕	✕	✕	✓	✕	Attribute-Based CH
XNM+21 [5]	✕	✕	✓	✓	✕	Revocable Policy-Based CH
XYL+22 [6]	✕	✕	Partial	✓	✕	Auditable Redaction Log
DWW+24 [7]	Partial (Fixed T)	✕	✕	✕	✕	T-Times CH
LSW+25 [8]	✕	✕	✕	✕	✓	Decentralized CH Functions
DLC+24 [9]	✕	✕	✓	✓	✕	CH+Multi-Authority ABE
PTCH+25 [10]	✓	✓	✕	✓	Partial	ABE+TPKE+CH

Note: ✓ indicates support; ✕ indicates no support. “Partial” indicates limited or partial support. Arbitrary collision refers to support for adaptively computing collisions using class-adaptive algorithms; revocation means dynamic revocation of modification privileges. Decentralization indicates whether the scheme avoids reliance on centralized trust entities. Key components are the core cryptographic techniques or primitives employed. ABE is attribute-based encryption. TPKE is timed-release public key encryption. CH is chameleon hash.

As illustrated in the table, most previous works lack support for time verifiability and arbitrary collision computation—two critical features that are essential for modern, auditable, and policy-driven redactable blockchain systems. Although various schemes improve certain aspects like access control or decentralization, none simultaneously offer time-bound hashing, traceable time-shifted redaction, and class-adaptive collision flexibility within a unified, provably secure framework.

To address this gap, we propose a novel TMCH scheme that directly incorporates time verifiability into the hash construction and introduces an Update algorithm supporting class-adaptive, cross-time collision computation. Our proposed TMCH offers a unified solution for controlled, accountable, and time-sensitive data redaction in blockchain systems. We provide a concrete implementation based on the Boneh–Boyen signature scheme and formally analyze its security properties and performance.

3. System Overview and Building Blocks

To facilitate an understanding of the technical details and algorithms, we summarize commonly used symbols in Table 2.

Table 2. Summary of notations and abbreviations used in this paper.

Symbol/Term	Description
TMCH	Time-modifiable chameleon hash
Hash	Algorithm for generating a hash result bound to both a message and a time parameter
Ver	Algorithm for verifying the integrity of the hash generation process
Adapt	Algorithm that maintains the original hash value while enabling message updates via collision construction
Update	Algorithm that maintains the original hash value while enabling timestamp updates via collision construction
T-IND/N-IND	Typical/New indistinguishability
T-CR/N-CR	Typical/New collision resistance
$\dot{h}$	Chameleon hash value
$\dot{r}$,${\dot{r}}^{\prime }$	Original and modified chameleon randomness parameters
m, $m^{\prime }$	Original and modified messages
t, $t^{\prime }$	Original and modified time parameters
$pk$, $sk$	Public key and secret key

$\mathsf{Hash}$ refers to the core algorithm that generates time-bound chameleon hashes, outputting both a hash value and a randomizer. $\mathsf{Ver}$ denotes the verification algorithm that validates consistency between the hash, message, randomizer, and time parameter. $\mathsf{Adapt}$ is the collision generation algorithm for updating messages under a fixed time parameter, which preserves the original hash value. $\mathsf{Update}$ represents the time adjustment algorithm that maintains hash consistency while keeping the message unchanged, enabling time traceability. KeySwitch is a cryptographic operation that transforms ciphertexts between different key contexts, enabling flexible access control in attribute-based encryption (ABE) components.

3.1. System Framework

Our system introduces a secure, time-aware redactable blockchain framework, built upon a novel cryptographic primitive: TMCH. This construction empowers authorized participants to perform verifiable redactions, while embedding time awareness and collision flexibility directly into the hash function itself.

The system involves four primary roles:

• Key Generation Center (KGC): A trusted authority responsible for initializing system parameters and issuing key pairs to users.
• User: Individuals who publish transactions on the blockchain and require hash integrity with time binding.
• Miner: Nodes that verify transaction validity and append them to the blockchain.
• Modifier: Entities granted permission (and trapdoor knowledge) to perform content redaction under predefined policies.

The lifecycle of a TMCH-based blockchain transaction proceeds through several distinct stages.

The KGC runs the Setup algorithm to generate global parameters and a master public key. Each user subsequently generates their personal key pair $(pk,sk)$ via the KeyGen algorithm.

To publish a transaction, a user uses the Hash algorithm to compute a chameleon hash bound to a specific time. Given inputs $(pk,m,t)$—the public key, message content, and a time label (e.g., block timestamp)—the algorithm outputs a hash value $\widehat{h}$ along with randomness $\widehat{r}$. This time binding ensures that any modification to m or t will alter the hash unless the trapdoor is known.

The user submits $(\dot{h},m,\dot{r},t)$ to the blockchain. The miner, serving as a validator, uses the public key $pk$ to run the Ver algorithm and checks whether the hash value $\dot{h}$ is consistent with the message m, randomness $\dot{r}$, and timestamp t. Upon successful verification, the transaction is recorded on the ledger.

If redaction is required due to regulatory compliance, error correction, or content withdrawal, an authorized modifier holding the corresponding trapdoor can invoke the Adapt algorithm to compute a collision, generating a new message $m^{\prime }$ and randomness ${\dot{r}}^{\prime }$. This process preserves the original hash value, ensuring blockchain consistency while replacing the underlying content.

To enhance auditability, TMCH introduces the Update algorithm, which enables cross-time collision generation. Unlike Adapt, Update keeps the original message m unchanged while generating a new time label $t^{″}$ and a corresponding randomizer $r^{″}$. This functionality allows the system to record when a redaction was performed or authorized and enforce time-based access control policies (e.g., “edits permitted only after 7 days” or “redactions visible only before a specified deadline”).

In summary, our system leverages TMCH to provide the following:

• Time verifiability: Every hash embeds a verifiable time component, enabling audit and delay enforcement.
• Collision flexibility: The trapdoor holder can compute both message collisions (for content updates) and time collisions (for timestamp adjustments), supporting diverse redaction policies (e.g., time-bound edits or content-specific modifications).
• Hash consistency preservation: Hash values remain unchanged across authorized redactions (whether message or time updates), ensuring the integrity of the blockchain’s chain structure.

A graphical summary of this framework and role interactions is provided in Figure 1.

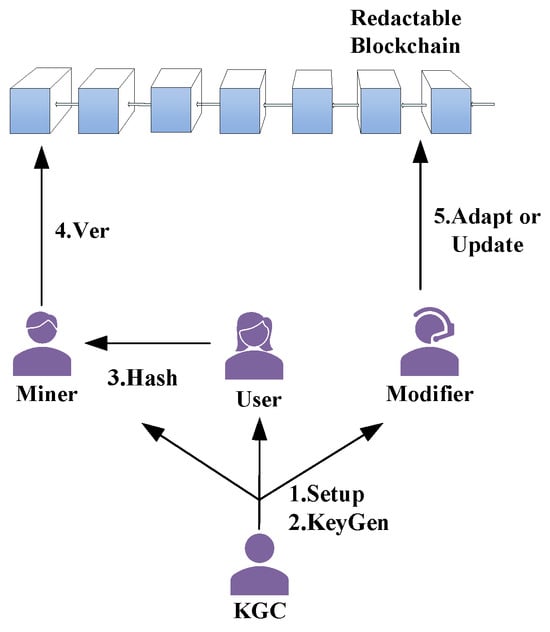
Figure 1. System framework.

3.2. Groups and Bilinear Maps

Given two multiplicative groups $\mathbb{G}$ and ${\mathbb{G}}_T$ of the same order p, and a generator g of $\mathbb{G}$, a symmetric bilinear pairing is a mapping $\widehat{e}:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$ satisfying the following properties: (1) bilinearity—for all $u,v\in \mathbb{G}$ and $a,b\in {\mathbb{Z}}_p^{*}$, it holds that $\widehat{e}(u^a,v^b)=\widehat{e}{(u,v)}^{ab}$; (2) non-degeneracy—there exists $g\in \mathbb{G}$ such that $\widehat{e}(g,g)\in {\mathbb{G}}_T$ is a generator of ${\mathbb{G}}_T$; (3) computability—for every $u,v\in \mathbb{G}$, computing $\widehat{e}(u,v)$ is efficient.

Specifically, this algebraic structure provides a rigorous mathematical framework for TMCH’s hash computation and verification algorithms, ensuring that operations like hash generation and time-shifted collision adjustment are both secure (resistant to forgery) and computationally feasible.

3.3. Intractable Problems

Definition 1. ℓ-SDH Assumption:

Introduced by Boneh and Boyen in [11], the strong Diffie–Hellman assumption states that, given inputs $g,g^x,\dots ,g^{x^{\ell }}\in \mathbb{G}$ for some $x\in {\mathbb{Z}}_p^{*}$, where $\mathbb{G}$ is a cyclic group of prime order p with generator g, it is computationally infeasible to find a pair $(g^{{\displaystyle \frac{1}{x+c}}},c)$ for any $c\in {\mathbb{Z}}_p^{*}$.

Definition 2. CDH Assumption:

Given a tuple $(g,g^A,g^B)\in {\left(\mathbb{G}\right)}^3$ with $A,B\in {\mathbb{Z}}_p^{*}$, where $\mathbb{G}$ is a cyclic group of prime order p generated by g, it is difficult to compute the element $g^{AB}$.

Definition 3. Inverse CDH Assumption:

For inputs $(g,g^A)\in {\left(\mathbb{G}\right)}^2$ with $A\in {\mathbb{Z}}_p^{*}$, in the context of a cyclic group $\mathbb{G}$ of prime order p generated by g, it is difficult to calculate $g^{A^{-1}}$.

Definition 4. DDH Assumption:

Given $(g,g^A,g^B,Z)\in {\left(\mathbb{G}\right)}^4$ for $A,B\in {\mathbb{Z}}_p^{*}$, where $\mathbb{G}$ is a cyclic group of prime order p with generator g, deciding whether Z equals $g^{AB}$ is considered computationally infeasible.

These assumptions serve as the theoretical bedrock for TMCH’s security proofs, underpinning the guarantees of indistinguishability and collision resistance and ensuring the scheme’s reliability under standard computational complexity assumptions.

3.4. Chameleon Hash

Definition 5. Chameleon Hash (CH):

Let a CH scheme be CH=Setup,KeyGen,Hash,Ver,Adapt  as follows.

• Setup$\left(1^{\lambda }\right)\to mpk$: On inputting a security parameter λ, output the public parameter $mpk$. Let $mpk$ be implicit hereafter.
• KeyGen$\left(mpk\right)\to (pk,sk)$: On inputting a public parameter $mpk$, output the public and private keys $pk$ and $sk$.
• Hash$(pk,m)\to (\dot{h},\dot{r})$: On inputting a message m and a public key $pk$, output a chameleon hash $\dot{h}$ and randomness $\dot{r}$.
• Ver$(pk,(\dot{h},m,\dot{r}))\to b$: On inputting a public key $pk$ and a triple $(m,\dot{h},\dot{r})$, output a decision $b=1$ if $(m,\dot{h},\dot{r})$ is valid. Else, output $b=0$.
• Adapt$(sk,(\dot{h},m,\dot{r}),m^{\prime })\to {\dot{r}}^{\prime }$: On inputting a private key $sk$, a message m, and a triple $(m,\dot{h},\dot{r})$, this trapdoor collision finding (denoted as typical) algorithm outputs new randomness ${\dot{r}}^{\prime }$.

Informally, a secure CH should satisfy the following properties.

Correctness:  Every output produced by properly executed  Hash  and  Adapt  procedures must successfully satisfy  Ver. More precisely, for any security parameter λ, for every $mpk\leftarrow \mathrm{Setup}\left(1^{\lambda }\right)$, for all key pairs $(sk,pk)\leftarrow \mathrm{KeyGen}\left(mpk\right)$, and for each message $m\in \mathcal{M}$ (where $\mathcal{M}$ denotes the message space), if $(\dot{h},\dot{r})\leftarrow \mathrm{Hash}(pk,m)$, then the verification algorithm yields  Ver  $(pk,(\dot{h},m,\dot{r}))=1$. Furthermore, for any $m^{\prime }\in \mathcal{M}$ and any ${\dot{r}}^{\prime }\leftarrow \mathrm{Adapt}(sk,(\dot{h},m,\dot{r}),m^{\prime })$, it holds that  Ver$(pk,(\dot{h},m^{\prime },{\dot{r}}^{\prime }))=1$. In addition to these correctness criteria, further security assurances are essential.

Indistinguishability: The randomness output ${\dot{r}}^{\prime }$ generated by Adapt is computationally indistinguishable from the randomness $\dot{r}$ produced by Hash.

Collision Resistance:  No probabilistic polynomial-time (PPT) adversary with access to the  Adapt  oracle should be able to efficiently produce two distinct tuples $(\dot{h},m,\dot{r})$ and $(\dot{h},m^{\prime },{\dot{r}}^{\prime })$ such that $1=$Ver$(pk,(\dot{h},m,\dot{r})=$Ver$(pk,(\dot{h},m^{\prime },{\dot{r}}^{\prime }))$ with any non-negligible probability. As noted by Camenisch et al. [12], key exposure freeness is a weaker security than collision resistance as it only requires that one cannot find a collision for some new “tag", while collision resistance requires finding no collision for any “tag".

Useful Property—Trapdoor Collisions:  A user with private key $sk$ should be able to find two tuples $(\dot{h},m,\dot{r})$ and $(\dot{h},m^{\prime },{\dot{r}}^{\prime })$ under a given $pk$ such that $1=$Ver$(pk,(\dot{h},m,\dot{r}))=$Ver$(pk,(\dot{h},m^{\prime },{\dot{r}}^{\prime }))$ with an overwhelming probability.

3.5. Design Insights

We exemplify the design of CH with construction based on a Pedersen commitment and show how to build a CH with time verifiability. The Pedersen commitment is a popular cryptographic primitive. In this setting, the public key $y=g^x$ is a group element in $\mathbb{G}$ associated with public key $x\in {\mathbb{Z}}_p^{*}$, and message m is a group element in ${\mathbb{Z}}_p$. We can easily use a standard (non-trapdoor) collision-resistant hash function (e.g., SHA-256) $H:{\{0,1\}}^{*}\to \mathbb{G}$ to map arbitrary-length messages to a group element m. Let $r\in {\mathbb{Z}}_p^{*}$ be randomness, and the Pedersen commitment-based chameleon hash is as follows:

$$\mathbf{Hash}(pk,m)\to \dot{h}:\dot{h}=g^m·y^r.$$

(1)

With private key x, one can compute $r^{\prime }=(m-m^{\prime }+xr)/x$ to find a hash collision for arbitrary $m^{\prime }$. However, according to Ateniese et al. [13], the above results in a key exposure problem. The reason is simple. When given a collision tuple $(m,\dot{r})$ and $(m^{\prime },{\dot{r}}^{\prime })$, anyone can compute

$$x=(m^{\prime }-m)/(r^{\prime }-r).$$

(2)

to extract the private key x. Thus, the master secret is lost. Accordingly, Chen et al. [14] proposed a CH based on a gap Diffie–Hellman group (where DDH is easy and CDH is difficult to solve). Let a be a random element over ${\mathbb{Z}}_p^{*}$. Their hashing algorithm is as follows:

$$\mathbf{Hash}(pk,m)\to (\dot{h},\dot{r})$$

(3)

where $\dot{h}={(g·\mathsf{CID})}^m·y^a,\dot{r}=(g^a,y^a)$, $\mathsf{CID}$ is an implicit parameter over $\mathbb{G}$ used to limit the key exposure problem according to Ateniese et al. [13]. To generate arbitrary collisions for $m^{\prime }\in \mathbb{G}$, compute

$$\mathbf{Adapt}(sk,(\dot{h},m,\dot{r}),m^{\prime })\to {\dot{r}}^{\prime }$$

where ${\dot{r}}^{\prime }=(g^{a^{\prime }},y^{a^{\prime }}),g^{a^{\prime }}=g^a·{(g·\mathsf{CID})}^{x^{-1}(m-m^{\prime })},y^{a^{\prime }}=y^a·{(g·\mathsf{CID})}^{(m-m^{\prime })}$. The above scheme is based on the inverse CDH assumption. If given an inverse CDH instance $(g^{\prime },g^{\prime x})$, one can deduce $g^{\prime x^{-1}}$ as

$$\begin{array}{c}\hfill g^{\prime x^{-1}}={\left({\displaystyle \frac{g^a}{g^{a^{\prime }}}}\right)}^{{(m^{\prime }-m)}^{-1}}.\end{array}$$

which is a solution to the given inverse CDH instance. Since the inverse CDH assumption is intractable, this scheme is key exposure-free. We exemplify how to break the uniqueness requirement and transform Chen et al.’s [14] CH to TMCH. Let us denote the derived construction as TMCH. Let t be a time parameter over ${\mathbb{Z}}_p^{*}$. The hashing algorithm for TMCH is

$$\mathbf{Hash}(pk,m,t)\to (\dot{h},\dot{r})$$

(4)

where $\dot{h}={(g·\mathsf{CID})}^{mt}·y^{at},\dot{r}=(g^{at},y^{at})$. To find arbitrary collisions for $m^{\prime }$, the Adapt algorithm (typical collision-finding algorithm) for TMCH is

$$\begin{array}{c}\mathbf{Adapt}(sk,(\dot{h},m,\dot{r}),m^{\prime },t)\to {\dot{r}}^{\prime }\end{array}$$

(5)

where ${\dot{r}}^{\prime }=(g^{a^{\prime }},y^{a^{\prime }t}),g^{a^{\prime }}=g^{at}·{(g·\mathsf{CID})}^{x^{-1}t(m-m^{\prime })},y^{a^{\prime }t}=y^{at}·{(g·\mathsf{CID})}^{t(m-m^{\prime })}.$ To find arbitrary collisions for $t^{″}$, the update algorithm (new collision-finding algorithm) is

$$\begin{array}{c}\mathbf{Update}(sk,(\dot{h},m,\dot{r}),t^{″})\to {\dot{r}}^{″}\hfill \end{array}$$

(6)

where ${\dot{r}}^{″}=(g^{a^{″}{t}^{″}},y^{a^{″}{t}^{″}}),g^{a^{″}{t}^{″}}=g^{at}·{(g·\mathsf{CID})}^{x^{-1}m(t-t^{″})},y^{a^{″}{t}^{″}}=y^{at}·{(g·\mathsf{CID})}^{m(t-t^{″})}$. The above Equations (4)–(6) exemplify the dominant algorithms for TMCH based on Chen et al.’s [14] CH. The correctness of Equations (5) and (6) is clear from inspection. We do not use this scheme directly in our construction. We believe that the reader will be able to complete the proof of the above construction after seeing our two different constructions and relevant security proofs.

4. Definitions of TMCH

We formalize the definition and security requirements for TMCH in this section. We focus on discussing the new collision-finding-related security.

4.1. Syntax of TMCH

Based on the CH introduced in Section 3.4, let a TMCH scheme be TMCH = {Setup, KeyGen, Hash, Ver, Adapt, Update} as follows.

• Setup$\left(1^{\lambda }\right)\to mpk$: On inputting a security parameter $\lambda$, output the public parameter $mpk$. Let $mpk$ be implicit hereafter.
• KeyGen$\left(mpk\right)\to (pk,sk)$: On inputting a public parameter $mpk$, output the public and private keys $pk$ and $sk$.
• Hash$(pk,m,t)\to (\dot{h},\dot{r})$: On inputting a message m, a public key $pk$, and a time t, output a chameleon hash $\dot{h}$ and randomness $\dot{r}$.
• Ver$(pk,(\dot{h},m,\dot{r}),t)\to b$: With $pk$ and $(\dot{h},m,\dot{r})$, additionally input a time t, and output $b\in \left\{0,1\right\}$.
• Adapt$(sk,(\dot{h},m,\dot{r}),m^{\prime },t)\to {\dot{r}}^{\prime }$: With $sk$, $(\dot{h},m,\dot{r})$, and $m^{\prime }$, additionally input a time t and output new randomness ${\dot{r}}^{\prime }$.
• Update$(sk,(\dot{h},m,\dot{r}),t,t^{″})\to {\dot{r}}^{\prime \prime }$: On inputting a private key $sk$, a triple $(\dot{h},m,\dot{r})$, and the original time period and new time period $t,t^{″}$, this new trapdoor collision-finding (denoted as new) algorithm outputs new randomness ${\dot{r}}^{″}$.

4.2. Useful Properties of TMCH

• Typical Trapdoor Collisions: A user possessing the secret key $sk$ should be capable of generating two tuples $((\dot{h},m,\dot{r}),t)$ and $((\dot{h},m^{\prime },{\dot{r}}^{\prime }),t)$ under a given public key $pk$ such that $1=$Ver$(pk,(\dot{h},m,\dot{r}),t)=$Ver$(pk,(\dot{h},m^{\prime },{\dot{r}}^{\prime }),t)$ holds with an overwhelming probability.
• New Trapdoor Collisions: A user holding the private key $sk$ should be able to construct two tuples $((\dot{h},m,\dot{r}),t)$ and $((\dot{h},m,{\dot{r}}^{″}),t^{″})$ under a specific public key $pk$ such that $1=$Ver$(pk,(\dot{h},m,\dot{r}),t)=$Ver$(pk,(\dot{h},m,{\dot{r}}^{″}),t^{″})$ with an overwhelming probability.

Definition 6. Correctness:

Every output produced by correctly executed procedures—Hash,  Adapt, and  Update—must successfully pass  Ver. Specifically, for all security parameters λ, for all $mpk\leftarrow$Setup$\left(1^{\lambda }\right)$, for all $(sk,pk)\leftarrow$KeyGen$\left(mpk\right)$, for all $m\in \mathcal{M},t\in \mathcal{T}$ ($\mathcal{T}$ as time space), and for all $(\dot{h},\dot{r})\leftarrow$Hash$(pk,m,t)$, we have  Ver$(pk,(\dot{h},m,\dot{r}),t)=1$; additionally, for all $m^{\prime }\in \mathcal{M},t^{\prime }\in \mathcal{T}$, for all ${\dot{r}}^{\prime }\leftarrow$Adapt$(sk,(\dot{h},m,\dot{r}),m^{\prime },t)$, and for ${\dot{r}}^{″}\leftarrow$Update$(sk,(\dot{h},m,\dot{r}),t,t^{″})$, we have  Ver$(pk,(\dot{h},m^{\prime },{\dot{r}}^{\prime }),t)=$Ver$(pk,(\dot{h},m,{\dot{r}}^{″}),t^{\prime \prime })=1$. Moreover, other security guarantees are needed.

Definition 7. Typical Indistinguishability (T-IND):

T-IND requires that it is computationally difficult to distinguish the distributions of chameleon randomness ${\dot{r}}^{\prime }$ generated by  Adapt  from that of $\dot{r}$ generated by  Hash, as formalized in experiment ${\mathbf{Exp}}_{\mathcal{A},\mathsf{CH}}^{\mathsf{T}-\mathsf{IND}}$ depicted below.

• Setup:  $\mathcal{C}$ runs $mp{k}_{\mathsf{ch}}\leftarrow$Setup$\left(1^{\lambda }\right)$ and $(s{k}_{\mathsf{ch}},p{k}_{\mathsf{ch}})\leftarrow$KeyGen$\left(mp{k}_{\mathsf{ch}}\right)$, and it gives $(mp{k}_{\mathsf{ch}},p{k}_{\mathsf{ch}},s{k}_{\mathsf{ch}})$ to $\mathcal{A}$.
• Query Phase:  $\mathcal{C}$ selects a random bit $b\in \left\{0,1\right\}$. The adversary $\mathcal{A}$ then proceeds to submit a series of queries to $\mathcal{C}$.

  -

  ${\mathcal{O}}_{\mathsf{HashOrUpdate}}(s{k}_{\mathsf{ch}},m,m^{\prime },t,b)$: $\mathcal{A}$ issues a query with private key $s{k}_{\mathsf{ch}}$, messages $m,m^{\prime }$ and times t, $\mathcal{C}$ runs $(\dot{h},\dot{r})\leftarrow$Hash$(p{k}_{\mathsf{ch}},m^{\prime },t)$ to get $(\dot{h},\dot{r})$ and $({\dot{h}}^{\prime },{\dot{r}}^{\prime })\leftarrow$Hash$(p{k}_{\mathsf{ch}},m,t)$ to get $({\dot{h}}^{\prime },{\dot{r}}^{\prime })$, respectively. Additionally, $\mathcal{C}$ runs ${\dot{r}}^{″}\leftarrow$Adapt$(s{k}_{\mathsf{ch}},({\dot{h}}^{\prime },m,{\dot{r}}^{\prime }),m^{\prime },t)$. $\mathcal{C}$ returns ⊥ if $\dot{r}=\perp$ or ${\dot{r}}^{″}=\perp$. Otherwise, if $b=0$, $\mathcal{C}$ returns $(\dot{h},\dot{r})$, if $b=1$, $\mathcal{C}$ returns $({\dot{h}}^{\prime },{\dot{r}}^{″})$.

• Guess:$\mathcal{A}$ makes a guess a for b.

The advantage of $\mathcal{A}$ in this game is defined as ${\mathsf{Adv}}_{\mathcal{A},\mathsf{TMCH}}^{\mathsf{T}-\mathsf{IND}}\left(1^{\lambda }\right)=\left|Pr[b^{\prime }=b]-{\displaystyle \frac{1}{2}}\right|$. A TMCH is considered T-IND-secure if any PPT adversary has at most a negligible advantage in λ.

Definition 8. New Indistinguishability (N-IND)

N-IND requires that it is computationally difficult to distinguish the distributions of ${\dot{r}}^{″}$ generated by Update from that of $\dot{r}$ from Hash, as formalized in experiment ${\mathbf{Exp}}_{\mathcal{A},\mathsf{CH}}^{\mathsf{N}-\mathsf{IND}}$, denoted as new IND. ${\mathbf{Exp}}_{\mathcal{A},\mathsf{CH}}^{\mathsf{N}-\mathsf{IND}}$ is defined through the following interaction protocol between the adversary $\mathcal{A}$ and the challenger $\mathcal{C}$.

• Setup: $\mathcal{C}$ runs $mp{k}_{\mathsf{ch}}\leftarrow$Setup$\left(1^{\lambda }\right)$ and $(p{k}_{\mathsf{ch}},s{k}_{\mathsf{ch}})\leftarrow$KeyGen$\left(mp{k}_{\mathsf{ch}}\right)$, and it gives $(p{k}_{\mathsf{ch}},s{k}_{\mathsf{ch}})$ to $\mathcal{A}$.
• Query Phase:  $\mathcal{C}$ selects a random bit $b\in \left\{0,1\right\}$. The adversary $\mathcal{A}$ then proceeds to submit a series of queries to $\mathcal{C}$.

  -

  ${\mathcal{O}}_{\mathsf{HashOrUpdate}}(s{k}_{\mathsf{ch}},m,t,t^{″})$: $\mathcal{A}$ issues hash or update query on two time $t,t^{″}\in \mathcal{T}$ and a private key $s{k}_{\mathsf{ch}}$, $\mathcal{C}$ runs $(\dot{h},\dot{r})\leftarrow$Hash$(p{k}_{\mathsf{ch}},m,t^{″})$ to get $(\dot{h},\dot{r})$ and $({\dot{h}}^{\prime },{\dot{r}}^{\prime })\leftarrow$Hash$(p{k}_{\mathsf{ch}},m,t)$ to get $({\dot{h}}^{\prime },{\dot{r}}^{\prime })$, respectively. Additionally, $\mathcal{C}$ runs ${\dot{r}}^{″}\leftarrow$Update$(sk,({\dot{h}}^{\prime },m,{\dot{r}}^{\prime }),t,t^{″})$ to get ${\dot{r}}^{″}$. $\mathcal{C}$ returns ⊥ if $\dot{r}=\perp$ or ${\dot{r}}^{″}=\perp$. Otherwise, if $b=0$, $\mathcal{C}$ returns $(\dot{h},\dot{r})$, if $b=1$, $\mathcal{C}$ returns $({\dot{h}}^{\prime },{\dot{r}}^{″})$.

• Guess:  $\mathcal{A}$ makes a guess $b^{\prime }$ for b.

The advantage of $\mathcal{A}$ in this game is defined as ${\mathsf{Adv}}_{\mathcal{A},\mathsf{TMCH}}^{\mathsf{N}-\mathsf{IND}}\left(1^{\lambda }\right)=\left|Pr[b^{\prime }=b]-{\displaystyle \frac{1}{2}}\right|$. A TMCH is considered N-IND-secure if any PPT adversary has at most a negligible advantage in λ.

Definition 9. Typical Collision Resistance: (T-CR)

T-CR requires that no probabilistic polynomial-time (PPT) adversary with access to the Adapt oracle can efficiently generate two distinct tuples $(\dot{h},m,\dot{r})$ and $(\dot{h},m^{\prime },{\dot{r}}^{\prime })$ under the same timestamp t such that $1=$Ver$(pk,(\dot{h},m,\dot{r}),t)=$Ver$(pk,(\dot{h},m^{\prime },{\dot{r}}^{\prime }),t)$ with non-negligible probability. This notion of security is formally captured by the experiment ${\mathbf{Exp}}_{\mathcal{A},\mathsf{TMCH}}^{\mathsf{T}-\mathsf{CR}}$ presented below:

• Setup:  $\mathcal{C}$ runs $\left(mp{k}_{\mathsf{ch}}\right)\leftarrow$Setup$\left(1^{\lambda }\right)$ and $(s{k}_{\mathsf{ch}},p{k}_{\mathsf{ch}})\leftarrow$KeyGen$\left(mp{k}_{\mathsf{ch}}\right)$ and gives $p{k}_{\mathsf{ch}}$ to $\mathcal{A}$, and keeps $s{k}_{\mathsf{ch}}$ secret. $\mathcal{C}$ initiates an empty list $\mathcal{Q}$.
• Query Phase:  $\mathcal{A}$ adaptively submits a sequence of the following queries to $\mathcal{C}$.:

  -

  ${\mathcal{O}}_{\mathsf{Update}}(s{k}_{\mathsf{ch}},(\dot{h},m,\dot{r}),m^{\prime },t)$: $\mathcal{A}$ issues update query on two time $t\in \mathcal{T}$ and a tuple $(\dot{h},m,\dot{r})$, $\mathcal{C}$ runs  Ver$(pk,(\dot{h},m,\dot{r}),t)$. If  Ver$(pk,(\dot{h},m,\dot{r}),t)=0$, return ⊥. Otherwise, $\mathcal{C}$ runs ${\dot{r}}^{\prime }\leftarrow \mathbf{Adapt}\left({sk}_{\mathsf{ch}},(\dot{h},m,\dot{r}),m^{\prime },t\right)$ to get ${\dot{r}}^{\prime }$. If  ${\dot{r}}^{\prime }=\perp$, return ⊥. Otherwise, update $\mathcal{Q}\leftarrow \mathcal{Q}\cup \left\{m,m^{\prime }\right\}$ and return ${\dot{r}}^{\prime }$.

• Output:  $\mathcal{A}$ outputs $\left(m^{*},{\dot{r}}^{*},m^{\prime *},{\dot{r}}^{\prime *},{\dot{h}}^{*},t\right)$, and it wins the game if: $1=$Ver$(p{k}_{\mathsf{ch}},({\dot{h}}^{*},m^{*},{\dot{r}}^{*}),t)=$Ver$(p{k}_{\mathsf{ch}},({\dot{h}}^{*},m^{\prime *},{\dot{r}}^{\prime *}),t)$, $m^{\prime *}\notin \mathcal{Q}$ and $m^{*}\ne m^{\prime *}$.

The advantage of $\mathcal{A}$ in this game is defined as ${\mathsf{Adv}}_{\mathcal{A},\mathsf{TMCH}}^{\mathsf{T}-\mathsf{CR}}\left(1^{\lambda }\right)=\left|Pr\left[\mathcal{A}wins\right]\right|$. A TMCH is considered typical collision resistant if any PPT adversary has at most a negligible advantage in λ. As it is similar to the next security, we only elaborate the latter one.

Definition 10. New Collision Resistance (N-CR):

N-CR stipulates that no probabilistic polynomial-time (PPT) adversary with access to the  Update  oracle should be able to efficiently produce a tuple $({\dot{h}}^{,}{m}^{,}{\dot{r}}^{,}{\dot{r}}^{″,}{t}^{,}{t}^{″)}$ satisfying $t^{*}\ne t^{″*}$ such that $1=$Ver$(p{k}_{\mathsf{ch}},({\dot{h}}^{*},m^{*},{\dot{r}}^{*}),t^{*})=$Ver$(p{k}_{\mathsf{ch}},({\dot{h}}^{*},m^{*},{\dot{r}}^{″*}),$$t^{\prime \prime *})$ with a non-negligible probability. This security notion is formally defined by the experiment  ${\mathbf{Exp}}_{\mathcal{A},\mathsf{TMCH}}^{\mathsf{N}-\mathsf{CR}}$, which models the interaction between the adversary $\mathcal{A}$ and the challenger $\mathcal{C}$, as described below.

• Setup:  $\mathcal{C}$ runs $\left(mp{k}_{\mathsf{ch}}\right)\leftarrow$Setup$\left(1^{\lambda }\right)$ and $(s{k}_{\mathsf{ch}},p{k}_{\mathsf{ch}})\leftarrow$KeyGen$\left(mp{k}_{\mathsf{ch}}\right)$ and gives $p{k}_{\mathsf{ch}}$ to $\mathcal{A}$ and keeps $s{k}_{\mathsf{ch}}$ secret. $\mathcal{C}$ initiates an empty list $\mathbb{T}$.
• Query Phase:  $\mathcal{A}$ adaptively submits a sequence of the following queries to $\mathcal{C}$:

  -

  ${\mathcal{O}}_{\mathsf{Update}}(s{k}_{\mathsf{ch}},(\dot{h},m,\dot{r}),t,t^{″})$: $\mathcal{A}$ issues update query at two times $t,t^{″}\in \mathcal{T}$ and a tuple $(\dot{h},m,\dot{r})$, $\mathcal{C}$ runs $b\leftarrow$Ver$(pk,(\dot{h},m,\dot{r}),t)$. If $b=0$, return ⊥. Otherwise, $\mathcal{C}$ runs ${\dot{r}}^{″}\leftarrow$Update$(s{k}_{\mathsf{ch}},(\dot{h},m,\dot{r}),t,t^{″})$ and returns ${\dot{r}}^{″}$. Update $\mathbb{T}\leftarrow \mathbb{T}\cup \{t,t^{″}\}$.

• Output:  $\mathcal{A}$ outputs $({\dot{h}}^{*},m^{*},{\dot{r}}^{*},{\dot{r}}^{″*},t^{*},t^{″*})$ and $t^{*}\ne t^{″*}$, and it wins the game if $1=$Ver$(p{k}_{\mathsf{ch}},({\dot{h}}^{*},m^{*},{\dot{r}}^{*}),t^{*})=$Ver$(p{k}_{\mathsf{ch}},({\dot{h}}^{*},m^{*},{\dot{r}}^{″*}),t^{″*})$, $t^{″}\notin \mathbb{T}$ and $t^{*}\ne t^{″*}$.

The advantage of $\mathcal{A}$ in this game is defined as ${\mathsf{Adv}}_{\mathcal{A},\mathsf{TMCH}}^{\mathsf{N}-\mathsf{CR}}\left(1^{\lambda }\right)=\left|Pr\left[\mathcal{A}wins\right]\right|$. A TMCH is considered new-collision-resistant in updates if any PPT adversary has at most a negligible advantage in λ.

Remark 1.

We do not describe uniqueness here as we intend to break the uniqueness requirement [12] to achieve the new collision algorithm  Update  . Uniqueness demands that deriving a collision for the same message and chameleon hash is computationally hard. The existence of the  Update  algorithm, as we previously exemplified in Equation (6), naturally breaks the uniqueness assumption. The correctness of Equation (6) is readily apparent upon inspection. More evidence will be provided in the forthcoming constructions.

5. Constructions for TMCH

In this section, we exemplify two concrete constructions for TMCH and provide a full security analysis.

5.1. Construction: TMCH Based on BBS

We introduce the first construction of TMCH based on Boneh and Boyen’s signature (BBS) [11] scheme.

• Setup$\left(1^{\lambda }\right)\to mpk$: Choose a multiplicative group $\mathbb{G}$ with order p and generator g. Let $H:{\{0,1\}}^{*}\to {\mathbb{Z}}_p^{*}$ be a secure collision-resistant hash function. Return public parameter $mpk=(\mathbb{G},g,p,H)$.
• KeyGen$\left(mpk\right)\to (pk,sk)$: Choose $x\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$ as the private key $sk$ and compute $y=g^x$ as the public key. Return the user’s public key and private key $(pk,sk)$.
• Hash$(pk,m,t)\to (\dot{h},\dot{r})$: Give $m\in {\{0,1\}}^{*}$ and $t\in {\mathbb{Z}}_p^{*}$ and implicitly choose a customized identity $\mathsf{CID}\stackrel{R}{\leftarrow }{\{0,1\}}^{*}$ and randomness $a\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$ to compute $e=H\left(\mathsf{CID}\right)$ and $h=g^e$. Then, compute a chameleon hash $\dot{h}=g^{H\left(m\right)t}·{(h·y)}^{at}$ and chameleon randomness $\dot{r}=(g^{at},y^{at})$. Let $\mathsf{CID}$ be implicit hereafter.
• Ver$(pk,(\dot{h},m,\dot{r}),t)\to b$: Compute $e=H\left(\mathsf{CID}\right)$ and set $h=g^e$. Then, verify whether $\dot{h}=g^{H\left(m\right)t}·{\left(g^{at}\right)}^e·y^{at}$. If the equation holds, return 1; otherwise, return 0.
• Adapt$(sk,(\dot{h},m,\dot{r}),m^{\prime },t)\to r^{\prime }$: First, run Ver$(pk,(\dot{h},m,\dot{r}),t)$ to verify the correctness. If the result is 0, output ⊥. Otherwise, compute ${\dot{r}}^{\prime }=(g^{a^{\prime }t},y^{a^{\prime }t})=(g^{at}·g^{(H\left(m\right)-H\left(m^{\prime }\right))t/(x+e)},y^{at}·y^{(H\left(m\right)-H\left(m^{\prime }\right))t/(x+e)})$.
• Update$(sk,(\dot{h},m,\dot{r}),t,t^{″})\to {\dot{r}}^{″}$: Begin by executing Ver$(pk,(\dot{h},m,\dot{r}),t)$ to confirm the validity. If the verification fails (i.e., returns 0), output ⊥. Otherwise, generate updated randomness as ${\dot{r}}^{″}=(g^{a^{″}{t}^{″}},y^{a^{″}{t}^{″}})=(g^{H\left(m\right)(t-t^{″})/(e+x)}·g^{a^{\prime }t},y^{H\left(m\right)(t-t^{″})/(e+x)}·y^{a^{\prime }t})$.

5.2. Security Analysis of TMCH

Correctness: The correctness of Adapt is as follows:

$$\begin{array}{cc}& g^{H\left(m^{\prime }\right)t}·{(h·y)}^{a^{\prime }t}\hfill \\ \hfill =& g^{H\left(m^{\prime }\right)t}·{\left(g^{a^{\prime }t}\right)}^e·y^{a^{\prime }t}\hfill \\ \hfill =& g^{H\left(m^{\prime }\right)t}·{(g^{ae}·y^a)}^t·g^{(H\left(m\right)-H\left(m^{\prime }\right))t}\hfill \\ \hfill =& g^{H\left(m\right)}·{(h·y)}^{at}=\dot{h}\hfill \end{array}$$

The correctness of Update is as follows:

$$\begin{array}{cc}& g^{H\left(m\right)t^{″}}·{(h·y)}^{a^{″}{t}^{″}}\hfill \\ \hfill =& g^{H\left(m\right)t^{″}}·h^{a^{″}{t}^{″}}·g^{H\left(m\right)(t-t^{″})}·{(h·y)}^{at}·h^{-a^{″}{t}^{″}}\hfill \\ \hfill =& g^{H\left(m\right)(t^{″}+t-t^{″})}·h^{a^{″}{t}^{″}-a^{″}{t}^{″}}·{(h·y)}^{at}\hfill \\ \hfill =& g^{H\left(m\right)}·{(h·y)}^{at}=\dot{h}\hfill \end{array}$$

Proof of T-IND for BBS-based TMCH Construction. 

Our TMCH is T-IND-secure if the DDH and ℓ-SDH assumptions are intractable. Assume that there exists a PPT adversary $\mathcal{A}$ against our T-IND security according to Definition 7; we can construct an efficient algorithm $\mathcal{B}$ to solve the DDH and ℓ-SDH assumptions. We only give a sketch of the proof.

When given a DDH instance $(g,g^A,g^B,Z)$, $\mathcal{B}$’s goal is to decide whether $(g,g^A,g^B,Z)$ is a DH-tuple, i.e., in the form of $(g,g^A,g^B,g^{AB})$. When given an ℓ-SDH instance $(g,g^x,\dots ,g^{x^{\ell }})$, $\mathcal{B}$’s goal is to find $(g^{{\displaystyle \frac{1}{x+c}}},e)$ where $x,e\in {\mathbb{Z}}_p^{*}$.

$\mathcal{B}$ simulates the challenger for $\mathcal{A}$. It runs Setup to generate $mp{k}_{\mathsf{ch}}=(\mathbb{G},g,p,H)$. $\mathcal{B}$ sets $y\leftarrow g^A$ as public key $p{k}_{\mathsf{ch}}$ and sends $(mp{k}_{\mathsf{ch}},p{k}_{\mathsf{ch}})$ to $\mathcal{A}$ where $s{k}_{\mathsf{ch}}$ is unknown. $\mathcal{A}$ selects random $t\stackrel{R}{\leftarrow }\mathcal{T}$ and $m,m^{\prime }\stackrel{R}{\leftarrow }\mathcal{M}$ and sends to $\mathcal{B}$; $\mathcal{B}$ flips a random coin $b\stackrel{R}{\leftarrow }\left\{0,1\right\}$. The analysis proceeds differently:

• If $b=0$, $\mathcal{B}$ computes $\dot{h}=g^{H\left(m^{\prime }\right)t}·{\left(g^B\right)}^e·Z$ and $\dot{r}=(g^B,Z)$. $\mathcal{B}$ returns $(\dot{h},\dot{r})$ to $\mathcal{A}$. As observed, if $(g,g^A,g^B,Z)$ is a DDH tuple, $(\dot{h},\dot{r})$ is computed exactly as in Hash.
• If $b=1$, $\mathcal{B}$ selects random $a^{\prime }\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$ and $\mathsf{CID}\stackrel{R}{\leftarrow }{\{0,1\}}^{*}$ to compute ${\dot{h}}^{\prime }=g^{H\left(m\right)t}·{(h·y)}^{a^{\prime }t}$ and ${\dot{r}}^{\prime }=(g^{a^{\prime }t},y^{a^{\prime }t})$ where $h=g^e=g^{H\left(\mathsf{CID}\right)}$. Then, $\mathcal{B}$ uses $g^B$ to replace $g^{1/(e+x)}$, and Z to replace $y^{1/(e+x)}$, respectively, in simulating the computing of Adapt. Thus, $\mathcal{B}$ computes ${\dot{r}}^{″}=(g^{a^{\prime }t}·{\left(g^B\right)}^{(H\left(m\right)-H\left(m^{\prime }\right))t},y^{a^{\prime }t}·{\left(Z\right)}^{(H\left(m\right)-H\left(m^{\prime }\right))t})$. As observed, if $(g,g^A,g^B,Z)$ is a DDH tuple and $B=1/(e+x)$, then $({\dot{h}}^{\prime },{\dot{r}}^{″})$ is computed exactly as in Adapt. Specifically, if $B=1/(e+x)$, where $e=H\left(\mathsf{CID}\right)$ and x is some unknown private key, then $g^B$ is an answer to the SDH instance.

Based on the above, we can use a sequence of games to show that we can simulate the view of the adversary without giving out any useful information at all, thus reducing our T-IND security to the intractability of the DDH and ℓ-SDH assumptions. A similar proof methodology can be found in [12]. □

Proof of N-IND for BBS-based TMCH Construction. 

Our TMCH is N-IND-secure if the DDH and ℓ-SDH assumptions are intractable. The proof is similar to that of T-IND. When given a DDH instance $(g,g^A,g^B,Z)$, we construct an algorithm $\mathcal{B}$ that simulates the challenger for adversary $\mathcal{A}$. $\mathcal{B}$ runs Setup to generate $mp{k}_{\mathsf{ch}}$ and sets $p{k}_{\mathsf{ch}}\leftarrow g^A$ and sends $(mp{k}_{\mathsf{ch}},p{k}_{\mathsf{ch}})$ to $\mathcal{A}$. $\mathcal{A}$ selects random $t,t^{″}\stackrel{R}{\leftarrow }\mathcal{T}$ and $m\stackrel{R}{\leftarrow }\mathcal{M}$ and sends to $\mathcal{B}$; $\mathcal{B}$ flips a random coin $b\stackrel{R}{\leftarrow }\left\{0,1\right\}$. The analysis proceeds differently:

• If $b=0$, $\mathcal{B}$ computes $\dot{h}=g^{H\left(m^{\prime }\right)t}·{\left(g^B\right)}^e·Z$ and $\dot{r}=(g^B,Z)$. $\mathcal{B}$ returns $(\dot{h},\dot{r})$ to $\mathcal{A}$. If $(g,g^A,g^B,Z)$ is a DDH tuple, $(\dot{h},\dot{r})$ is computed exactly as in Hash.
• If $b=1$, $\mathcal{B}$ selects random $a^{\prime }\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$ to compute ${\dot{h}}^{\prime }=g^{H\left(m\right)t}·{(h·y)}^{a^{\prime }t}$ and ${\dot{r}}^{\prime }=(g^{a^{\prime }t},y^{a^{\prime }t})$. Then, use $g^B$ to replace $g^{1/(e+x)}$, and Z to replace $y^{1/(e+x)}$, respectively, in simulating the computing of Update. Thus, $\mathcal{B}$ computes ${\dot{r}}^{″}=({\left(g^B\right)}^{H\left(m\right)(t-t^{″})}·g^{a^{\prime }t},Z^{H\left(m\right)(t-t^{″})}·y^{a^{\prime }t})$. Similarly, if $(g,g^A,g^B,Z)$ is a DDH tuple and $B=1/(e+x)$, then $({\dot{h}}^{\prime },{\dot{r}}^{″})$ are computed exactly as in Update. Accordingly, if $B=1/(e+x)$, $g^B$ is an answer to the SDH instance.

Similarly, we can use a sequence of games to show that our N-IND security holds as long as the DDH and ℓ-SDH assumptions are intractable to solve. □

Proof of T-CR for BBS-based TMCH Construction. 

Our TMCH is T-CR-secure if the ℓ-SDH assumption is intractable. Assume that $\mathcal{A}$ is an efficient adversary against our T-CR; we outline a method to construct a probabilistic polynomial-time (PPT) algorithm $\mathcal{B}$ capable of solving the ℓ-SDH problem, as defined in [11]. Given an instance of the ℓ-SDH assumption in the form $(g,g^x,\dots ,g^{x^{\ell }})$, we represent it as $(A_0,A_1,\dots ,A_{\ell })$, where each $A_i=g^{x^i}\in \mathbb{G}$ for $i\in [\ell ]$, with $A_0=g$ and $x\in {\mathbb{Z}}_p^{*}$. In order to derive ($c,g^{{\displaystyle \frac{1}{(x+c)}}}$) as the solution to SDH, where $c\in Z_q^{*}$, $\mathcal{B}$ simulates the challenger for $\mathcal{A}$ and interacts with $\mathcal{A}$ as follows.

During the Query Phase, $\mathcal{A}$ issues $q_s$ distinct queries ${\{{\mathsf{CID}}_i,({\dot{h}}_i,m_i,{\dot{r}}_i),m_i^{\prime }\}}_{i\in \left[q_s\right]}$ under the same public key $p{k}_{\mathsf{ch}}$ and $t\in {\mathbb{Z}}_p^{*}$. ${\mathsf{CID}}_i$ is an implicit parameter for each $m_i$. Assume that $q_s=\ell -1$.

To generate a response, for every $m_i$ where $i\in \left[q_s\right]$, $\mathcal{B}$ produces the corresponding reply as follows. Let $e_i=H\left({\mathsf{CID}}_i\right)$. Set polynomial $f\left(z\right)={\prod }_{i=1}^{q_s}(z+e_i)={\sum }_{i=0}^{q_s}{a}_i{z}^i$, where $a_0,\dots ,a_{q_s}$ are the coefficients of polynomial $f\left(z\right)$. Define

$$g^{\prime }=\prod _{i=0}^{q_s}{\left(A_i\right)}^{a_i}=g^{f\left(z\right)},\tilde{h}=\prod _{i=1}^{q_s}{\left(A_i\right)}^{a_{i-1}}=g^{zf\left(z\right)}={g^{\prime }}^z.$$

Next, we define polynomial $f_i\left(z\right)=f\left(z\right)/(z+e_i)={\prod }_{j=1,j\ne i}^{q_s}(z+e_j)$ and $f_i\left(z\right)={\sum }_{j=0}^{q_s-1}\left(b_j{z}^j\right)$. Expand $f_i$ and define $f_i\left(z\right)={\Sigma }_{j=0}^{q_s-1}{b}_j{z}^j$. Then, $\mathcal{B}$ computes

$${\dot{r}}_i^{\prime }=(g^{a_{i}t}·{s_i}^{(H\left(m_i\right)-H\left(m_i^{\prime }\right))t},y^{a_{i}t}·{s_i}^{xt[H\left(m_i\right)-H\left(m_i^{\prime }\right)]}),$$

$$s_i=\prod _{j=0}^{q_s-1}{\left(A_j\right)}^{b_j}={\left(g^{\prime }\right)}^{f_i\left(x\right)}={\left(g^{\prime }\right)}^{1/(x+e_i)},e_i=H\left({\mathsf{CID}}_i\right).$$

Since the above holds for $g^{H\left(m_i\right)t}{(h_i·y)}^{a_{i}t}=g^{H\left(m_i^{\prime }\right)t}{(h_i·y)}^{a_i^{\prime }t}$, where $h_i=g^{e_i}=g^{H\left({\mathsf{CID}}_i\right)}$, the value ${\dot{r}}_i^{\prime }$ represents the valid randomness, ensuring a collision for the customized identity ${\mathsf{CID}}_i$ under the given public key. The algorithm $\mathcal{B}$ responds to the adversary $\mathcal{A}$ with a collection of $q_s$ fresh randomness values, namely $({\dot{r}}^{\prime }1,\dots ,{\dot{r}}^{\prime }{q}_s)$.

Output: Adversary $\mathcal{A}$ wins by output $({\dot{h}}^{*},m^{*},{\dot{r}}^{*},m^{\prime *},{\dot{r}}^{\prime *})$, where $({\dot{h}}^{*},m^{*},{\dot{r}}^{*})$ and $({\dot{h}}^{*},m^{\prime *},{\dot{r}}^{\prime *})$ are collisions, ${{\mathsf{CID}}_i}^{*}$ is implicit, and $m^{\prime *}$ has never been queried during the Query Phase such that

$$g^{H\left(m^{*}\right)t}{(h^{*}·y)}^{a^{*}t}=g^{H\left(m^{\prime *}\right)t}{(h^{*}·y)}^{a_{*}^{\prime i}t}.$$

where $h^{*}=g^{e^{*}}=g^{H\left({\mathsf{CID}}^{*}\right)}$. We have

$${\dot{r}}^{\prime *}=(g^{a^{\prime *}t},y^{a^{\prime *}t})$$

$$=(g^{a^{*}t}·{s^{*}}^{(H\left(m^{*}\right)-H\left(m^{\prime *}\right))t},y^{a^{*}t}·{s^{*}}^{x(H\left(m^{*}\right)-H\left(m^{\prime *}\right))t}),$$

$$s^{*}={\left({\displaystyle \frac{g^{a^{\prime *}}}{g^{a^{*}}}}\right)}^{{\displaystyle \frac{1}{H(m^{*}-H\left(m^{\prime *}\right))}}}={\left(g^{\prime }\right)}^{1/(x+e^{*})}=g^{f\left(x\right)/(x+e^{*})}$$

Using polynomial long division, the polynomial f can be expressed as $f\left(z\right)=\gamma \left(z\right)(z+e^{*})+{\gamma }_{-1}$, where $\gamma \left(z\right)={\sum }_{i=0}^{q_s-1}{\gamma }_i{z}^i$ and ${\gamma }_{-1}\in {\mathbb{Z}}_p$. From this representation, we can then deduce

$$f\left(z\right)/(z+e^{*})={\displaystyle \frac{{\gamma }_{-1}}{z+e^{*}}}+\sum _{i=0}^{q_s-1}{\gamma }_i{z}^i$$

Because ${\gamma }_{-1}\ne 0$ and $\mathsf{CID}$ has not been queried previously—that is, $\mathsf{CID}\notin \mathsf{CID}1,\dots ,\mathsf{CID}{q}_s$—the polynomial $(z+e^{*})$ does not divide $f\left(z\right)$. Consequently, the algorithm $\mathcal{B}$ computes

$$\pi ={(s^{*}·\sum _{i=1}^{q_s}{\left(A_i\right)}^{-{\gamma }_i})}^{{\displaystyle \frac{1}{{\gamma }_{-1}}}}=g^{{\displaystyle \frac{1}{x+e^{*}}}}$$

The algorithm then outputs the pair $(e,\pi )$, where $e=H_1\left({\mathsf{CID}}^{*}\right)$, as the solution to the given ℓ-SDH instance $(g,g^x,\dots ,g^{x^{\ell }})$. To analyze and bound the advantage of $\mathcal{B}$ in solving the ℓ-SDH problem by leveraging $\mathcal{A}$, one can follow the approach presented in [11]; the detailed proof is omitted here. □

Proof of N-CR for BBS-based TMCH Construction. 

Our TMCH is N-CR-secure if the ℓ-SDH assumption is intractable. Similarly, assume that $\mathcal{A}$ is an efficient adversary against our N-CR; we can construct a probabilistic polynomial-time (PPT) $\mathcal{B}$ to solve the ℓ-SDH assumption. Observe that, to satisfy the winning condition of the N-IND game, we have

$$g^{H\left(m^{*}\right)t^{*}}·{(g^e·y)}^{a^{*}{t}^{*}}=g^{H\left(m^{*}\right)t^{″*}}·{(g^e·y)}^{a^{″*}{t}^{″*}}.$$

By transforming the equation, we get

$$g^{H\left(m\right)t^{*}/t^{″*}}·{(g^e·y)}^{a{t}^{*}/t^{″*}}=g^{H\left(m\right)}·{(g^e·y)}^{a^{″*}}.$$

Use $H(\Delta m)$ to represent $H\left(m\right)t^{*}/t^{\prime \prime *}$, and $\Delta a$ to represent $a(t^{*}/t^{\prime \prime *})$. We have

$${\left(g^{H(\Delta m)}·{(g^e·y)}^{\Delta a}\right)}^t={\left(g^{H\left(m\right)}·{(g^e·y)}^{a^{\prime \prime *}}\right)}^t.$$

This is exactly in the form of T-CR’s winning condition. Thus, CR is transferable to Upd. and the security analysis of T-CR applies to this part as well. □

6. Performance Evaluation

6.1. Experimental Setup

Our scheme was implemented in Java using the JPBC library and deployed on a desktop equipped with an Intel i5-13600KF processor (3.50 GHz) (manufactured by Intel Corporation, with headquarters in Santa Clara, California, United States) and 32 GB of RAM. For pairing operations, we selected a Type-I curve—specifically, a widely adopted Type-I pairing curve compatible with the PBC framework—to ensure a 96-bit security level, balancing computational efficiency and cryptographic strength [15]. The experimental and parametric environment is summarized in Table 3.

Table 3. Experimental environment configuration.

Category	Parameter
Desktop CPU	Intel i5-13600KF
Operating System	Windows 11
RAM	32 GB
GPU	Nvidia RTX 4070Ti (12 GB)
Software Environment	CUDA 12.5.78, TensorFlow 2.6.0, Conda 23.11.0
Curve Classification	Optimal Type-I Pairing Curve
Security Level	96-bit

6.2. Theoretical Complexity Comparison

Table 4 presents a systematic comparison of the computational complexity of four chameleon hash schemes, focusing on five critical operations at the user side: KeyGen, Hash, Adapt, Revoke or Update, and Verify. Both the DSS+19 and XHY+22 schemes require $\mathcal{O}\left(k\right)$ exponentiation operations in the KeyGen phase, and the Hash and Adapt operations scale linearly as $\mathcal{O}(\ell ·n)$, indicating that their computational overhead grows with attribute set size k and the dimensions of the access control matrix $\ell ·n$. In contrast, the proposed TMCH scheme maintains constant complexity $\mathcal{O}\left(1\right)$ across all operations, requiring only minimal exponentiation and group insertion steps, demonstrating significant efficiency improvements. While KXY+19 also achieves $\mathcal{O}\left(1\right)$ complexity in the KeyGen and Adapt phases, it requires more computationally expensive pairing operations during the Hash and Verify phases. Notably, TMCH stands out as the only scheme achieving constant complexity in Revoke/Update operations, whereas other schemes either do not support this feature (marked $n/a$) or lack explicit complexity specifications. This comprehensive performance advantage makes TMCH particularly suitable for large-scale applications that require frequent update operations.

Table 4. Complexity comparisons of recent CH works.

Reference	Costs (User Side)
	KeyGen	Hash	Adapt	Revoke or Update	Verify
DSS+19 [4]	$\mathcal{O}\left(k\right)\left(T_e\right)$	$\mathcal{O}(\ell ·n)T_e$	$\mathcal{O}(\ell ·n)T_e$	$\mathsf{n}/\mathsf{a}$	$\mathcal{O}\left(1\right)T_e$
XHY+22 [6]	$\mathcal{O}\left(k\right)\left(T_e\right)$	$\mathcal{O}(\ell ·n)T_e$	$\mathcal{O}(k+n)T_e$	$\mathsf{n}/\mathsf{a}$	$\mathcal{O}\left(1\right)(T_p+T_e)$
Our TMCH	$\mathcal{O}\left(1\right)T_e$	$\mathcal{O}\left(1\right)\left(T_e\right)$	$\mathcal{O}\left(1\right)(T_e+T_i)$	$\mathcal{O}\left(1\right)(T_e+T_i)$	$\mathcal{O}\left(1\right)\left(T_e\right)$
KXY+19 [16]	$\mathcal{O}\left(1\right)T_e$	$\mathcal{O}\left(1\right)(T_e+T_p)$	$\mathcal{O}\left(1\right)\left(T_e\right)$	$\mathcal{O}\left(1\right)\left(T_e\right)$	$\mathcal{O}\left(1\right)\left(T_p\right)$

$T_e$ denotes the exponentiation operation; $T_p$ denotes the pairing operation; $T_i$ represents the group insertion operation. Operations such as multiplication and one-time costs are not accounted for in the measurements. The matrix $\mathbb{M}$ refers to an access control matrix consisting of ℓ rows and n columns. The parameter k indicates the size of the attribute set linked to a user. Additionally, $\mathsf{n}/\mathsf{a}$ stands for “not applicable”, while N and R represent the total number of system users and the number of revoked users, respectively.

6.3. Runtime Performance Evaluation

For single operations of each dominant algorithm, we list the costs in Table 5. It presents the running costs of the key algorithms involved in chameleon hash operations across two schemes: the proposed TMCH and the baseline KXY-19. The operations include Hash generation, Verification, Adapt (collision under the same time), and Update (cross-time collision). TMCH consistently outperforms KXY-19 in all four operations. Specifically, the Hash computation in TMCH takes 99 ms, which is 24.4% faster than in KXY-19 (131 ms). The Verification and Adapt steps show even more pronounced improvements: 121 ms vs. 208 ms (41.8% faster) and 201 ms vs. 289 ms (30.4% faster), respectively. The Update operation—unique to TMCH for time-shifted collisions—is also executed more efficiently (205 ms vs. 273 ms). These results demonstrate that TMCH not only extends the functional capabilities (e.g., time verifiability and arbitrary collision) but also reduces the computational overhead compared to previous constructions, making it more practical for blockchain environments with frequent verification and occasional redactions.

Table 5. Running costs.

Algorithms	Hash	Verification	Adapt	Update
TMCH	99 ms	121 ms	201 ms	205 ms
KXY-19 [16]	131 ms	208 ms	289 ms	273 ms

For further quantitative analysis, we evaluated our proposed TMCH scheme in comparison with two representative baselines: the policy-based chameleon hash (PCH) scheme [4] and the KXY+19 scheme [16]. All three schemes were tested under policy set sizes ranging from 1 to 50 and from $2^1$ to $2^6$, enabling a fair and comprehensive comparison across different levels of operational complexity.

Figure 2 illustrates the relationship between the policy set size and running time for three schemes: our TMCH, KXY+19, and DSS+19. As the policy size increases from 1 to 50, TMCH maintains nearly constant performance (approximately 90–100 ms), demonstrating excellent scalability. In contrast, DSS+19 exhibits a steep increase in running time, exceeding 270 ms at the largest policy size, due to its linear complexity with respect to the policy size. KXY+19 performs better than DSS+19 but worse than TMCH, showing moderate growth with increasing policy sizes. These results confirm that TMCH is more efficient and robust under large and complex policy conditions.

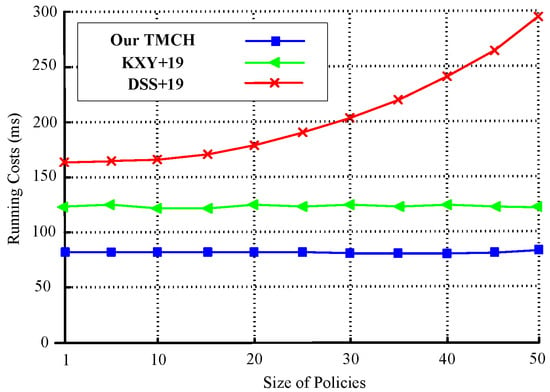
Figure 2. Hash.

Figure 3 compares the cumulative execution times of TMCH and KXY+19 over 500 runs. TMCH demonstrates significantly better performance, with a total execution time of around 40 s, compared to nearly 90 s for KXY+19. Although both schemes exhibit linear growth, the slope of KXY+19 is much steeper. This highlights TMCH’s efficiency and suitability for environments with frequent hash computations or repeated redactions, such as dynamic blockchain systems or policy auditing frameworks.

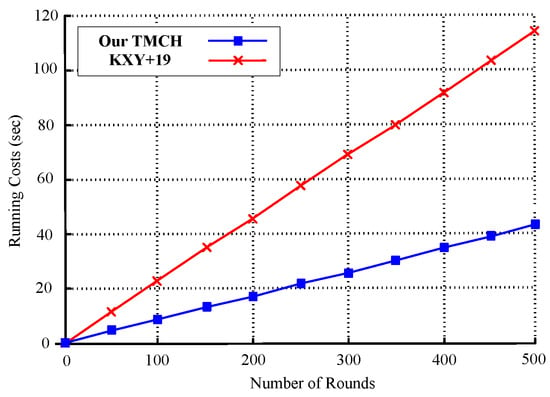
Figure 3. Ver.

Figure 4 presents the running time under exponentially growing policy sizes, ranging from 2 to 64 for TMCH, KXY+19, and DSS+19. TMCH remains nearly flat, maintaining performance within a narrow band (around 100–110 ms), indicating logarithmic or sub-linear complexity. In contrast, DSS+19 scales poorly, exceeding 450 ms at a policy size of 64. KXY+19 demonstrates moderate scalability but still lags behind TMCH. The superior performance of TMCH under growing complexity validates its design for real-world scenarios with large attribute or policy sets.

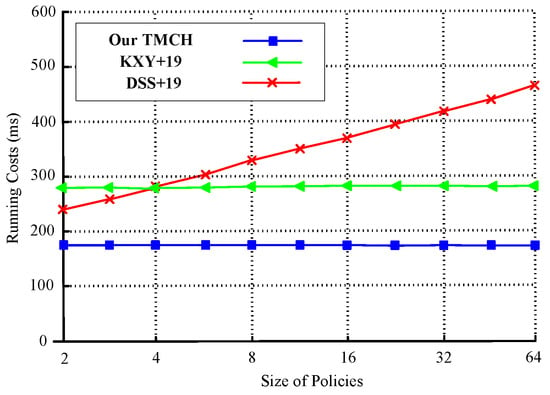
Figure 4. Adapt.

Figure 5 shows a linear comparison of the cumulative running costs for TMCH and KXY+19 as the number of executions increases from 0 to 500. Both schemes exhibit linear growth, indicating consistent time complexity per operation. TMCH demonstrates better computational efficiency, with the total running time increasing from 0 to approximately 100 s. In contrast, KXY+19 shows a steeper slope, reaching about 130 s at 500 executions. This gap becomes more pronounced as the number of rounds increases, underscoring TMCH’s superior scalability and lower per-operation cost. Such efficiency is particularly advantageous in high-frequency blockchain environments requiring repeated hash generation and verification.

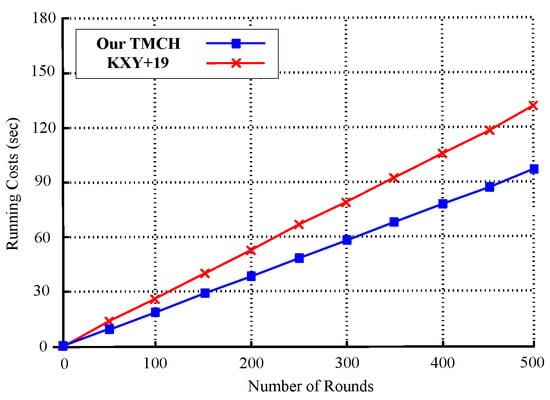
Figure 5. Update.

7. Conclusions

In this work, we formally address the open problem of non-uniqueness left unresolved by Camenisch et al. [12] and propose a novel Time-Modifiable Chameleon Hash (TMCH) scheme. TMCH introduces a novel trapdoor-based collision-finding algorithm that deliberately breaks the uniqueness property by incorporating time as an explicit parameter into key operations—hashing, verification, and adaptation. Notably, TMCH supports time-dependent arbitrary collision generation while preserving core security properties such as IND and collision resistance (CR). Our scheme achieves security and efficiency comparable to those of existing chameleon hash constructions while enabling temporal control and verifiability.

TMCH is particularly well suited for scenarios requiring time-bound data modification and strong traceability, such as regulatory-compliant blockchain redactions, short-term smart contracts, and tamper-evident log systems. For future work, we plan to explore adding verifiable update mechanisms so that every content change can be transparently audited. Another direction is the design of collaborative redaction protocols, enabling joint authorization and execution by multiple parties, enhancing both trust and security. We also aim to integrate TMCH with privacy-preserving techniques like zero-knowledge proofs, allowing controlled redaction while maintaining data confidentiality.