Prescribed Performance Control for High-Order Odd-Rational-Power Nonlinear Systems with Actuator Faults and Unknown Powers

Abstract

A global prescribed performance control method is proposed for a class of uncertain high-order odd-rational-power nonlinear systems (a chain of integrators whose power is the ratio of odd integers) with actuator faults, where the high-order odd-rational powers and the parameters of actuator faults are unknown. A new coordinate transformation on the state and tracking errors is introduced based on the tangent function and its inverse function, resulting in a global low-complexity prescribed performance controller. The proposed controller does not require any knowledge of system nonlinearities or powers, and it also does not require the time derivatives of virtual control signals without using any filters, which implies the controller is of low complexity. Finally, two simulation examples, including a practical high-maneuver flight control example, are given to demonstrate the effectiveness of our method.

1. Introduction

Over the last decade, high-order nonlinear systems have been receiving great attention. There are two reasons: first, higher-order nonlinear dynamics (with odd integer powers or odd rational powers) can be generalized to strict feedback and pure feedback dynamics; second, higher-order nonlinear dynamics appear in some practical systems, such as underactuated and weakly coupled mechanical systems [1], hydraulic systems [2], and dynamical boilers-turbine units [3]. It is widely acknowledged that high-order nonlinear systems pose greater challenges than their strict-feedback and pure-feedback counterparts, because of the ineffectiveness of feedback linearization and backstepping methods.

A control method named adding a power integrator technique has been successfully applied in stabilizing high-order nonlinear systems [1,4]. Based on this technology, scholars have studied different control problems of higher-order nonlinear systems and made some achievements [5,6,7,8]. An adaptive fuzzy control method with full-state constraints is designed in Ref. [5]. An adaptive control method for high-order systems with unknown nonlinear functions is proposed in Ref. [6]. In Ref. [8], the tracking control problem with unknown control directions is tackled. It should be noted that these approaches require the powers of the system to be known [5,6,7,8]. When the powers of the system are unknown, some control methods are proposed by combining a power integrator technique. In Ref. [9], a low-complexity tracking approach is designed for uncertain high-order nonlinear systems with unknown powers. Two different adaptive feedback control methods are presented in Ref. [10]. In Ref. [11], the stability control problem of uncertain stochastic high-order nonlinear systems is solved. An adaptive tracking control scheme was developed by combining the barrier functions in Ref. [12]. However, these schemes in [9,10,11,12] require that the upper bounds of the system powers be known and assumed to be positive odd integers and cannot be applied for higher-order nonlinear systems with odd-rational powers. To address the control challenges in high-order nonlinear systems with odd-rational powers, an adaptive fuzzy control method is introduced to handle unknown system nonlinearities, achieving semi-global stability [13]. Refs. [14,15], respectively, proposed adaptive control schemes for different control problems of higher-order nonlinear systems. However, the rational powers are required to be known in the above methods [13,14,15], and it is still an open problem to develop a tracking control method for high-order odd-rational-power systems with completely unknown odd-rational powers.

To ensure that the steady-state and transient performance of systems meet predetermined requirement, the prescribed performance control of high-order nonlinear systems has attracted widespread attention, and some outstanding research results have been reported [16,17,18]. For example, the finite time prescribed performance tracking control of stochastic high-order nonlinear systems is realized by combining fuzzy logic and adding a power integrator technique in Ref. [16]. In Ref. [17], a prescribed performance adaptive control method suitable for uncertain high-order nonlinear systems is proposed by effectively combining obstacle function with adaptive fuzzy logic control and adding the power integrator technique. For a class of uncertain high-order odd-rational-powers systems, a barrier-function-based robust funnel control method is proposed in Ref. [18]. Although the above control methods can realize great tracking performance for the system output, they all necessitate that the system’s initial values satisfy certain conditions, that is, the initial value of the system tracking error is less than the initial value of the performance function. Therefore, it is an urgent problem to realize the prescribed performance control of higher-order nonlinear systems under arbitrary initial conditions.

Actuator faults usually exist in many practical systems, which may lead to system performance degradation or even instability [19,20,21]. It is crucial to resolve such failures to ensure system safety and many fault-tolerant methods have been proposed for systems with an input power equal to 1 in references [22,23,24,25]. Subsequently, scholars conducted relevant research on high-order nonlinear systems with actuator faults [26,27,28,29]. In Ref. [26], an adaptive fuzzy fixed-time fault-tolerant tracking control scheme is proposed. To eliminate the effect of actuator failure, an adaptive elastic control technique is proposed in Ref. [27]. A prescribed-time neural network adaptive control algorithm is proposed for the consistency tracking control of high-order nonlinear multi-agent systems with actuator faults in Ref. [28]. In Ref. [29], an adaptive fuzzy controller is designed, which eliminates the effect of actuator failure and realizes the prescribed-time fault-tolerant control. However, the system power requires to be known in the above control methods [26,27,28,29]. It is well worth to further research the stability control for the high-order odd-rational-power nonlinear system in the presence of actuator fault and unknown power.

Motivated by the above discussion, this article aims to overcome the strict limitations of the traditional control methods which require the prior knowledge of odd rational powers and initial values, eliminate the influence of actuator faults, and realize the global prescribed performance control of the system. Therefore, the controller is designed for uncertain high-order odd-rational-power nonlinear systems with actuator faults and unknown powers. The main contributions are summarized as follows.

(1) The global control for a high-order odd-rational-power system with completely unknown system nonlinearities and odd-rational powers is first achieved, which suggests that the designed controller does not require any knowledge of the odd rational powers.

(2) By introducing a new coordinate transformation on the system states and tracking errors, a global low-complexity control method is proposed, which is free from the initial value of the system and does not require the knowledge of system nonlinearities.

(3) The influence of actuator faults in high-order odd-rational-power system is eliminated with the parameters of actuator faults allowed to be unknown.

2. Problem Description

Consider a class of uncertain higher-order systems with an actuator fault and unknown odd rational powers:

$$\left\{\begin{array}{c}{\dot{x}}_i=f_i({\overline{\mathit{x}}}_i)+g_i({\overline{\mathit{x}}}_i)x_{i+1}^{{\displaystyle \frac{p_i}{q_i}}}+d_i(t),\hspace{1em}i = 1, 2\dots , n-1\\ {\dot{x}}_n=f_n({\overline{\mathit{x}}}_n)+g_n({\overline{\mathit{x}}}_n)u^{{\displaystyle \frac{p_n}{q_n}}}+d_n(t)\\ y=x_1,\end{array}\right.$$

(1)

where ${\overline{\mathit{x}}}_i={[x_1,\dots ,x_i]}^T\in R^i$ indicates the system state ${\dot{x}}_i$ and ${\dot{x}}_n$ is a differentiation with respect to the time. $y\in R$ represents the output for $i = 1, \dots , n$; $p_i/q_i$ are the powers of $x_{i+1}$ in the i-th subsystem, with $p_i$ and $q_i$ being unknown positive odd integers and satisfying $p_i\ge 1,q_i\ge 1$; $f_i({\overline{\mathit{x}}}_i)$ and $g_i({\overline{\mathit{x}}}_i)$ are unknown nonlinear continuous functions; and $g_i({\overline{\mathit{x}}}_i)>0$ and $d_i(t)$ represent an unknown bounded disturbance of the system. $u\in R$ stands for the system input and the output of the actuator with fault. Along the similar idea of [30], we consider the form of actuator faults as follows

$$u=\gamma (t)u_{\mathrm{c}}+\varpi (t)$$

(2)

where $u_c$ is the actuator input, $\gamma (t)>{\gamma }_0$ represents the efficiency factor of the actuator with ${\gamma }_0$ being unknown positive constant, and $\varpi (t)$ is an unknown but bounded bias fault.

The control objective is to design a controller $u_c$ so that the output of system (1) can track the desired signal $y_r$ with preset accuracy and ensure all signals of the closed-loop system are bounded globally.

Assumption 1. 

The desired signal $y_r$ and its differential ${\dot{y}}_r$ are bounded.

Assumption 2. 

For any $i = 1, 2, \cdots , n$, $g_i(\cdot )>0$.

Assumption 3. 

The system power parameters $p_i$ and $q_i$ are unknown positive odd numbers.

Remark 1. 

In the existing control methods for high-order odd-rational-power systems, it is commonly assumed that $p_i/q_i$ is known, as in [31,32], and most previous literature assumes that $g_i(\cdot )$ has unknown upper and lower bounds, as in [15,31], while this paper only assumes that $g_i(\cdot )$ has a lower bound. Therefore, assumptions 2 and 3 are more relaxed.

Lemma 1. 

If $p/q\in R_{odd}$, then for any $x\in R$ and $y\in R$, we have

$$\left|x^{{\displaystyle \frac{p}{q}}}-y^{{\displaystyle \frac{p}{q}}}\right|\le 2^{1-{\displaystyle \frac{1}{q}}}{\left|{⌈x⌉}^p-{⌈y⌉}^p\right|}^{{\displaystyle \frac{1}{q}}}.$$

(3)

Lemma 2. 

For any $x,y\in R$ and positive odd integers $p$ and $q$, there are real-valued functions $\mu (t)$ and $\vartheta (t)$, such that

$${(x+y)}^{{\displaystyle \frac{p}{q}}}={(\vartheta (t)x^p+\mu (t)y^p)}^{{\displaystyle \frac{1}{q}}}.$$

(4)

where $0<{\epsilon }_0\le \vartheta (t)\subseteq \max \{2,2^{p-1}\}$ and $\left|\mu (t)\right|\le \overline{\mu }$. ${\epsilon }_0$ and $\overline{\mu }$ are some positive constants that are independent of $x$ and $y$.

3. Controller Design

In this section, a low-complexity controller is designed by introducing a new coordinate transformation on the system states and tracking errors. To facilitate the readers’ understanding, the overall block diagram of the control scheme is shown in Figure 1.

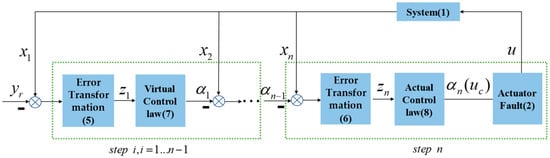
Figure 1. Block diagram of control scheme.

The following error variables are introduced based on the arctangent function and performance function:

$$z_1={\displaystyle \frac{1}{k_1(t)}}\arctan (x_1-y_r)$$

(5)

$$z_i={\displaystyle \frac{1}{k_i(t)}}\arctan (x_i-{\alpha }_{i-1}), i = 2, \cdots , n$$

(6)

where ${\alpha }_{i-1}$ are virtual control variables; $k_i(t)$ are the performance functions and $k_i(t)=(1-{\rho }_i)e^{-{\sigma }_{i}t}+{\rho }_i$ with $0<{\rho }_i<1$, ${\sigma }_i>0$, ${\rho }_i$, and ${\sigma }_i$ are some positive constants. $\left|k_i(t)\right|<k^{*}<1$, $k^{*}$ are positive constants.

Remark 2. 

When there are changes in the initial value of the system, the parameters of the barrier-function-based controller need to be adjusted [33]. However, it is not easy to obtain the initial values of the system without additional conditions, so we construct an error transformation formula (6) by using the arctangent function, which enables global control of the system even under unknown initial conditions.

Then, the virtual control law and actual control law are designed as follows

$${\alpha }_i=-{\lambda }_i\tan (z_i), i = 1, 2, \cdots , n$$

(7)

$$u_c={\alpha }_n$$

(8)

where ${\lambda }_i,i = 1, 2, \cdots , n$ represent any arbitrary positive constants.

Remark 3. 

From (7) and (8), it can be observed that the designed controller is only related to the tracking error and does not contain any information of system nonlinearities and powers, which shows that the method can be applied to other systems after simple processing.

Remark 4. 

To prevent any confusion, in the subsequent sections on stability analysis, we will use $f_i,g_i,d_i,{\vartheta }_i,{\mu }_i,k_i,\gamma ,\varpi$ instead of $f_i(\cdot ),g_i(\cdot ),d_i(t),{\vartheta }_i(t),{\mu }_i(t),k_i(t),\gamma (t),\varpi (t)$.

4. Stability Analysis

Theorem 1. 

Considering uncertain high-order nonlinear systems with unknown odd-rational-powers under Assumptions 1 to 2, the closed-loop system composed of control signals (7) and (8) can achieve the following objectives:

(1) All closed-loop system signals are globally uniformly bounded.

(2) For any time $t$, the system tracking error satisfies $\left|y-y_r\right|<Y_M=\tan (k_1(t)\pi /2)$.

Proof. 

It can be easily verified that $\left|z_i(0)\right|<\pi /2$, and there exists a positive constant $M_0$ such that $\left|z_i(0)\right|<M_0<\pi /2$. We define the error vector $z={[z_1,z_2,\cdots ,z_n]}^T$ and introduce a compact set $\mathrm{\Omega }$ as follows:

$${\mathrm{\Omega }}_0=\underset{n-times}{\underbrace{[-M^{*},M^{*}],\cdots ,[-M^{*},M^{*}]}}$$

(9)

where $M^{*}=\underset{i = 1, 2, \cdots , n}{\underbrace{\max }}\left\{M_0,\arctan \left|c_{i3}\right|\right\}$, and $c_{i3}$ is a positive constant that will be specified later.

It is obvious that $0<M^{*}<\pi /2$. If we can prove that ${\mathrm{\Omega }}_0$ is an invariant set for the error vector $z$, then Theorem 1 naturally holds.

Define $z_{\max }=\underset{i = 1, 2, \cdots , n}{\max }\left\{\left|z_i(t)\right|\right\}$, and consider the following two cases for $z_{\max }$:

Case 1: If $z_{\max }<M_0$ holds for $\forall t\in [0,\infty )$, then it is obvious that ${\mathrm{\Xi }}_0$ is an invariant set for the error vector $z$, and then $z\in {\mathrm{\Omega }}_0$ for $\forall t\ge 0$ is obtained.

Case 2: There exists a time instant $t_M>0$ such that $t_M=\inf \left\{t|z_{\max }(t)=M_0,t\ge 0\right\}$, then the proposition $z\in {\mathrm{\Omega }}_0$ naturally holds for $\forall t\in [0,t_M)$. Therefore, it is only required to prove that $z\in {\mathrm{\Omega }}_0$ for $\forall t\in [t_M,\infty )$.

According to the definition of $k_i(t)$, for $\forall t\in [t_M,\infty )$, we have

$$k_i(t)\le k_i(t_M)<1,i = 1, \cdots , n.$$

(10)

Define the following set

$${\mathrm{\Omega }}_z=\underset{n-times}{\underbrace{(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}),\cdots ,(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}})}}.$$

(11)

From the definition of ${\mathrm{\Omega }}_0$, it can be concluded that ${\mathrm{\Omega }}_0\subset {\mathrm{\Omega }}_z$ is satisfied, and $z\in {\mathrm{\Omega }}_z$ implies

$$-{\displaystyle \frac{\pi }{2}}<z_i(t)<{\displaystyle \frac{\pi }{2}}.$$

(12)

From (5) and (6), we have

$$x_1=\tan \left(k_1{z}_1\right)+y_r$$

(13)

$$x_i=tan(k_i{z}_i)+{\alpha }_{i-1}, i=2,\cdots ,n.$$

(14)

Formula (13) indicates that $x_1$ is a continuous function composed of $k_1, z_1, y_r$ and it is evident that $k_1$ and $z_1$ are bounded functions. Similar conclusions can be drawn for $x_2$ and $x_i (i=3,\cdots ,n)$.

Step $i (1\le i\le n-1)$, the time derivative of $z_i$ is

$${\dot{z}}_i=-{\displaystyle \frac{{\dot{k}}_i}{k_i^2}}\arctan (x_i-{\alpha }_{i-1})+{\displaystyle \frac{{\dot{x}}_i-{\dot{\alpha }}_{i-1}}{k_i(1+{\tan }^2(k_i{z}_i))}}.$$

(15)

A Lyapunov function candidate is chosen as

$$V_i={\displaystyle \frac{1}{2}}{\tan }^2(z_i).$$

(16)

The time derivative of $V_i$ along (6) and (15) is

$$\begin{array}{l}{\dot{V}}_i={\displaystyle \frac{\tan z_i}{{\cos }^2{z}_i}}{\dot{z}}_i\\ =-{\displaystyle \frac{{\dot{k}}_i\tan z_i}{k_i^2{\cos }^2{z}_i}}\arctan \left(x_i-{\alpha }_{i-1}\right)+{\displaystyle \frac{\tan z_i}{{\cos }^2{z}_i}}{\displaystyle \frac{{\dot{x}}_i-{\dot{\alpha }}_{i-1}}{k_i\left(1+{\tan }^2\left(k_i{z}_i\right)\right)}}\\ ={\displaystyle \frac{\tan z_i}{{\cos }^2{z}_i}}\left(-{\displaystyle \frac{{\dot{k}}_i}{k_i}}{z}_i+{\displaystyle \frac{f_i+g_i{x}_{i+1}^{\frac{p_i}{q_i}}+d_i-{\dot{\alpha }}_{i-1}}{k_i\left(1+{\tan }^2\left(k_i{z}_i\right)\right)}}\right).\end{array}$$

(17)

And applying (14) and Lemmas 2, we get

$$\begin{array}{l}{x}_{i+1}^{{\displaystyle \frac{p_i}{q_i}}}={({\alpha }_i+\tan (k_{i+1}{z}_{i+1}))}^{{\displaystyle \frac{p_i}{q_i}}}\\ ={\left[{\vartheta }_i{\alpha }_i^{p_i}+{\mu }_i{\tan }^{p_i}(k_{i+1}{z}_{i+1})\right]}^{{\displaystyle \frac{1}{q_i}}}.\end{array}$$

(18)

With the help of Lemma 1–2 and (18), one has

$$\begin{array}{l}\left|x_{i+1}^{{\displaystyle \frac{p_i}{q_i}}}-{\left({\vartheta }_i{\alpha }_i^{p_i}\right)}^{{\displaystyle \frac{1}{q_i}}}\right|=\left|{\left({\vartheta }_i{\alpha }_i^{p_i}+{\mu }_i{\tan }^{p_i}(k_{i+1}{z}_{i+1})\right)}^{{\displaystyle \frac{1}{q_i}}}-{\left({\vartheta }_i{\alpha }_i^{p_i}\right)}^{{\displaystyle \frac{1}{q_i}}}\right|\\ \le 2^{1-{\displaystyle \frac{1}{q_i}}}{\left|{\overline{\mu }}_i{\tan }^{p_i}(k_{i+1}{z}_{i+1})\right|}^{{\displaystyle \frac{1}{q_i}}},\end{array}$$

(19)

where ${\overline{\mu }}_i$ is an unknown constant that satisfies $\left|{\mu }_i\right|\le {\overline{\mu }}_i$.

Noting that

$$g_i\tan z_i{\left({\vartheta }_i{\alpha }_i^{p_i}\right)}^{{\displaystyle \frac{1}{q_i}}}=g_i{\lambda }_i^{{\displaystyle \frac{p_i}{q_i}}}{\vartheta }_i^{{\displaystyle \frac{1}{q_i}}}{\left(\tan z_i\right)}^{{\displaystyle \frac{p_i}{q_i}}+1}\ge 0.$$

(20)

In view of (17) and (19), we have

$$\begin{array}{l}{\dot{V}}_i\le {\displaystyle \frac{\tan z_i}{{\cos }^2{z}_i}}\left(-{\displaystyle \frac{{\dot{k}}_i}{k_i}}{z}_i+{\displaystyle \frac{f_i+g_i{\left({\vartheta }_i{\alpha }_i^{p_i}\right)}^{\frac{1}{q_i}}+d_i-{\dot{\alpha }}_{i-1}}{k_i\left(1+{\tan }^2\left(k_i{z}_i\right)\right)}}\right)+{\displaystyle \frac{\left|\tan z_i\right|}{{\cos }^2{z}_i}}\cdot {\displaystyle \frac{g_i{2}^{1-\frac{1}{q_i}}{\left|{\overline{\mu }}_i{\tan }^{p_i}(k_{i+1}{z}_{i+1})\right|}^{\frac{1}{q_i}}}{k_i\left(1+{\tan }^2\left(k_i{z}_i\right)\right)}}\\ \le {\displaystyle \frac{\tan z_i}{k_i{\cos }^2{z}_i}}{E}_i(t){\alpha }_i^{{\displaystyle \frac{p_i}{q_i}}}+{\displaystyle \frac{\left|\tan z_i\right|}{k_i{\cos }^2{z}_i}}{F}_i(t).\end{array}$$

(21)

where

$$E_i(t)={\displaystyle \frac{g_i{\vartheta }_i^{\frac{1}{q_i}}}{1+{\tan }^2\left(k_i{z}_i\right)}}$$

(22)

$$F_i(t)=\left|-{\dot{k}}_i{z}_i+{\displaystyle \frac{f_i+d_i-{\dot{\alpha }}_{i-1}}{1+{\tan }^2\left(k_i{z}_i\right)}}\right|+{\displaystyle \frac{g_i{2}^{1-\frac{1}{q_i}}{\left|{\overline{\mu }}_i{\tan }^{p_i}(k_{i+1}{z}_{i+1})\right|}^{\frac{1}{q_i}}}{1+{\tan }^2\left(k_i{z}_i\right)}}.$$

(23)

According to (10), (11), and (14), it is known that $x_i$, ${\alpha }_{i-1}$, $z_i$, and $z_{i+1}$ are bounded on the set ${\mathrm{\Omega }}_z$, and ${\tan }^2\left(k_i{z}_i\right)$ and $\tan \left(k_{i+1}{z}_{i+1}\right)$ are also bounded. Additionally, noting that $x_1,\cdots ,x_{i-1}$, ${\dot{\alpha }}_{i-1}$ is bounded in the first $i$ steps, and ${\vartheta }_i$, ${\dot{k}}_i$, $k_i$, $k_{i+1}$, and $d_i$ are bounded. In addition, $f_i$ and $g_i$ are continuous functions, and by the extreme value theorem, we have

$$0<c_{i1}\le {\mathrm{E}}_i(\cdot ),0\le \left|F_i(\cdot )\right|\le c_{i2}$$

(24)

where $c_{i1}$ and $c_{i2}$ are positive constants.

Due to ${\left(\tan z_i\right)}^{p_i/q_i+1}\ge 0$, substitute (24) into (21) to get

$$\begin{array}{l}{\dot{V}}_i={\displaystyle \frac{-{\lambda }_i^{\frac{p_i}{q_i}}{E}_i(t){\left(\tan z_i\right)}^{\frac{p_i}{q_i}+1}}{k_i{\cos }^2{z}_i}}+{\displaystyle \frac{F_i(t)\tan z_i}{k_i{\cos }^2{z}_i}}\\ \le {\displaystyle \frac{1}{k_i{\cos }^2{z}_i}}\left|\tan z_i\right|\left(-{\lambda }_i^{{\displaystyle \frac{p_i}{q_i}}}{c}_{i1}{\left|\tan z_i\right|}^{{\displaystyle \frac{p_i}{q_i}}}+c_{i2}\right).\end{array}$$

(25)

We can get ${\dot{V}}_i\le 0$ if $\left|\tan z_i\right|\ge {\lambda }_i^{-1}{(c_{i2}/c_{i1})}^{q_i/p_i}$, such that

$$\left|\tan z_i\right|\le c_{i3}=\max \{\left|\tan z_i(0)\right|,{\lambda }_i^{-1}{(c_{i2}/c_{i1})}^{q_i/p_i}\}.$$

(26)

Then, we have

$$\left|z_i\right|\le \arctan \left|c_{i3}\right|\le M^{*}<{\displaystyle \frac{\pi }{2}}.$$

(27)

Consequently, ${\alpha }_i$ is bounded (i.e., $\left|{\alpha }_i\right|\le {\lambda }_i\left|c_{i3}\right|$). Furthermore, using (10), (11), (13), and (14), we also conclude the boundedness of $x_{i+1}$.

In addition, the time derivative of ${\alpha }_i$ is

$${\dot{\alpha }}_i=-{\displaystyle \frac{{\lambda }_i}{{\cos }^2{e}_i}}{\dot{z}}_i=-{\displaystyle \frac{{\lambda }_i}{k_i{\cos }^2{z}_i}}\left(E_i(t){\alpha }_i+F_i(t)\right).$$

(28)

This means that ${\dot{\alpha }}_i$ is bounded.

Step $n$, the time derivative of $z_n$ is

$${\dot{z}}_n=-{\displaystyle \frac{{\dot{k}}_n}{k_n^2}}\arctan (x_n-{\alpha }_{n-1})+{\displaystyle \frac{{\dot{x}}_n-{\dot{\alpha }}_{n-1}}{k_n(1+{\tan }^2(k_n{z}_n))}}.$$

(29)

Considering the following Lyapunov function candidate

$$V_n={\displaystyle \frac{1}{2}}{\tan }^2(z_n)$$

(30)

Then, utilizing (6) and (29), ${\dot{V}}_n$ can be shown as

$$\begin{array}{l}{\dot{V}}_n={\displaystyle \frac{\tan z_n}{{\cos }^2{z}_n}}{\dot{z}}_n\\ =-{\displaystyle \frac{\tan z_n}{{\cos }^2{z}_n}}{\displaystyle \frac{{\dot{k}}_n}{k_n^2}}\arctan \left(x_n-{\alpha }_{n-1}\right)+{\displaystyle \frac{\tan z_n}{{\cos }^2{z}_n}}{\displaystyle \frac{{\dot{x}}_n-{\dot{\alpha }}_{n-1}}{k_n\left(1+{\tan }^2\left(k_n{z}_n\right)\right)}}\\ =-{\displaystyle \frac{\tan z_n}{{\cos }^2{z}_n}}{\displaystyle \frac{{\dot{k}}_n}{k_n}}{z}_n+{\displaystyle \frac{\tan z_n}{{\cos }^2{z}_n}}{\displaystyle \frac{f_n+g_n{u}^{\frac{p_n}{q_n}}+d_n-{\dot{\alpha }}_{n-1}}{k_n\left(1+{\tan }^2\left(k_n{z}_n\right)\right)}}.\end{array}$$

(31)

According to (2) and Lemma 2, one reaches

$$u^{{\displaystyle \frac{p_n}{q_n}}}={\left[{\vartheta }_n{(\gamma u_c)}^{p_n}+{\mu }_n{\varpi }^{p_n}\right]}^{{\displaystyle \frac{1}{q_n}}}.$$

(32)

And with the aid of Lemma 1–2 and (32), one has

$$\begin{array}{l}\left|u^{{\displaystyle \frac{p_n}{q_n}}}-{\left({\vartheta }_n{(\gamma u_c)}^{p_n}\right)}^{{\displaystyle \frac{1}{q_n}}}\right|\\ =\left|{\left({\vartheta }_n{(\gamma u_c)}^{p_n}+{\mu }_n{\varpi }^{p_n}\right)}^{{\displaystyle \frac{1}{q_n}}}-{\left({\vartheta }_n{(\gamma u_c)}^{p_n}\right)}^{{\displaystyle \frac{1}{q_n}}}\right|\\ \le 2^{1-{\displaystyle \frac{1}{q_n}}}{\left|{\mu }_n{\varpi }^{p_n}\right|}^{{\displaystyle \frac{1}{q_n}}},\end{array}$$

(33)

where ${\overline{\mu }}_n$ is an unknown constant that satisfies $\left|{\mu }_n\right|\le {\overline{\mu }}_n$.

Noting that

$$g_n{\left({\vartheta }_n{(\gamma u_c)}^{p_n}\right)}^{{\displaystyle \frac{1}{q_n}}}\tan z_n=g_n{(\gamma {\lambda }_n)}^{{\displaystyle \frac{p_n}{q_n}}}{\left(\tan z_n\right)}^{{\displaystyle \frac{p_n}{q_n}}+1}\ge 0$$

(34)

Using (31) and (33), we can obtain

$$\begin{array}{l}{\dot{V}}_n\le {\displaystyle \frac{\tan z_n}{k_n{\cos }^2{z}_n}}(-{\dot{k}}_n{z}_n+{\displaystyle \frac{f_n+g_n{\left({\vartheta }_n{(\gamma u_c)}^{p_n}\right)}^{\frac{1}{q_n}}+d_n-{\dot{\alpha }}_{n-1}}{\left(1+{\tan }^2\left(k_n{z}_n\right)\right)}})\\ +{\displaystyle \frac{\left|\tan z_n\right|}{{\cos }^2{z}_n}}\cdot {\displaystyle \frac{g_n{2}^{1-\frac{1}{q_n}}{\left|{\mu }_n{\varpi }^{p_n}\right|}^{\frac{1}{q_n}}}{k_n\left(1+{\tan }^2\left(k_n{z}_n\right)\right)}}\\ \le {\displaystyle \frac{\tan z_n}{k_n{\cos }^2{z}_n}}{E}_n(t)u_c^{{\displaystyle \frac{p_n}{q_n}}}+{\displaystyle \frac{\left|\tan z_n\right|}{k_n{\cos }^2{z}_n}}{F}_n(t) ,\end{array}$$

(35)

where

$$E_n(t)={\displaystyle \frac{g_n{\vartheta }^{\frac{1}{q_n}}{\gamma }^{\frac{p_n}{q_n}}}{1+{\tan }^2\left(k_n{z}_n\right)}}$$

(36)

$$F_n(t)=\left|-{\dot{k}}_n{z}_n+{\displaystyle \frac{f_n+d_n-{\dot{\alpha }}_{n-1}}{1+{\tan }^2\left(k_n{z}_n\right)}}\right|+{\displaystyle \frac{g_n{2}^{1-\frac{1}{q_n}}{\left|{\mu }_n{\varpi }^{p_n}\right|}^{\frac{1}{q_n}}}{k_n\left(1+{\tan }^2\left(k_n{z}_n\right)\right)}}.$$

(37)

According to (10) and (11), it is known that $u_c,{\tan }^2(k_n{z}_n)$ are bounded on the set ${\mathrm{\Omega }}_z$. Moreover, note that $x_1,\cdots x_{i-1}, {\dot{\alpha }}_{i-1}$ is bounded in the first $n-1$ steps, and ${\vartheta }_n, {\mu }_n, \gamma , \varpi , k_n, {\dot{k}}_n,d_n$ are also bounded. In addition, $f_n({\overline{\mathit{x}}}_n)$ and $g_n({\overline{\mathit{x}}}_n)$ are continuous functions, and by the extreme value theorem, we have

$$0<c_{n1}\le {\mathrm{E}}_n(t),0\le \left|F_n(t)\right|\le c_{n2}$$

(38)

where $c_{n1}$ and $c_{n2}$ are positive constants.

Due to ${\left(\tan z_n\right)}^{p_n/q_n+1}\ge 0$, substitute (38) into (35) to get

$$\begin{array}{l}{\dot{V}}_n={\displaystyle \frac{-{\lambda }_n^{\frac{p_n}{q_n}}{E}_n(t){\left(\tan z_n\right)}^{\frac{p_n}{q_n}+1}}{k_n{\cos }^2{z}_n}}+{\displaystyle \frac{F_n(t)\tan z_n}{k_n{\cos }^2{z}_n}}\\ \le {\displaystyle \frac{1}{k_n{\cos }^2{z}_n}}\left|\tan z_n\right|\left(-{\lambda }_n^{{\displaystyle \frac{p_n}{q_n}}}{c}_{n1}{\left|\tan z_n\right|}^{{\displaystyle \frac{p_n}{q_n}}}+c_{n2}\right).\end{array}$$

(39)

It is known from (39) that ${\dot{V}}_n\le 0$ when $\left|\tan z_n\right|\ge {\lambda }_n^{-1}{(c_{n2}/c_{n1})}^{q_n/p_n}$, so we arrive at

$$\left|\tan z_n\right|\le c_{n3}=\max \{\left|\tan z_n(0)\right|,{\lambda }_n^{-1}{(c_{n2}/c_{n1})}^{q_n/p_n}\}.$$

(40)

Then, we have

$$\left|z_n\right|\le \arctan \left|c_{n3}\right|\le M^{*}<{\displaystyle \frac{\pi }{2}}.$$

(41)

Consequently, $u_c$ is bounded (i.e., $\left|u_c\right|\le {\lambda }_n\left|c_{n3}\right|$). In view of (27) and (41), we arrive at

$$z_i(t)\in {\mathrm{\Omega }}_0,\forall t\in [t_M,\infty ),i=1,\cdots ,n.$$

(42)

Noting that $z_i(t)\in {\mathrm{\Omega }}_0$ when $0\le t\le t_M$, one gets

$$z_i(t)\in {\mathrm{\Omega }}_0,\forall t\ge 0,i=1,\cdots ,n.$$

(43)

From the proof above, we can see that ${\mathrm{\Omega }}_0$ is the invariant set of $z$, and it is also clear from previous steps that $x_1,\dots ,x_n,{\alpha }_1,\dots ,{\alpha }_{n-1},u_c$ are globally bounded. Furthermore, according to (43) one reaches

$$\left|z_i(t)\right|\le M^{*}<{\displaystyle \frac{\pi }{2}}$$

(44)

In combination with (44) and $0<k_1(t)<1$, one has

$$\left|y-y_r\right|<\tan (k_1{z}_1)<\tan ({\displaystyle \frac{k_1\pi }{2}})=Y_M$$

(45)

such that, the proof is completed. □

5. Simulation

In this section, to better demonstrate the effectiveness of the proposed method, two simulation examples are presented.

Example 1. 

Numerical example.

Consider the following high-order nonlinear system:

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2^{{\displaystyle \frac{p_1}{q_1}}}+x_1\sin (x_1)+d_1(t)\\ {\dot{x}}_2=u^{{\displaystyle \frac{p_2}{q_2}}}+x_2+d_2(t)\\ y=x_1,\end{array}\right.$$

(46)

where $p_1/q_1=1/3,p_2/q_2=5/3$. Let the desired trajectory be $y_r=0.5(\sin (t)+\sin (0.5t))$, and the initial conditions are chosen as ${[x_1(0),x_2(0)]}^T={[-1,\hspace{0.33em}1.5]}^T$. $d(t)$ represent disturbance.

To evaluate the effectiveness and robustness of the proposed method, there are three cases that we compared and simulated. Case 1 (no disturbances): $d_1(t)=d_2(t)=0$. Case 2 (with disturbances): $d_1(t)=0.5\sin (t),d_2(t)=0.5\cos (t)$. Case 3 (with output noise): $d_1(t)=0.5\sin (t)$, where $d_2(t)$ represents the band-limited white noise which is shown in Figure 2.

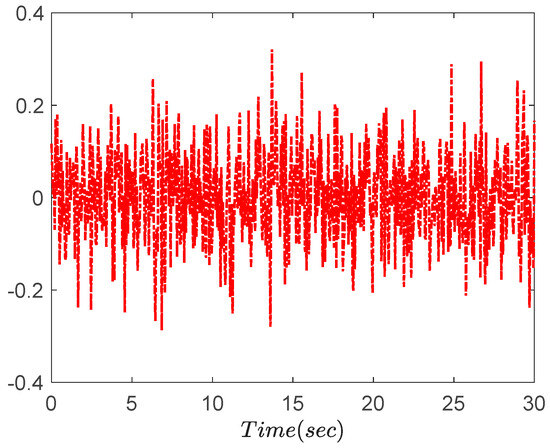
Figure 2. Band-limited white noise $d_2$.

In the given second-order uncertain high-order system (46), the virtual control signal and the actual control signal are designed according to (7) and (8), and the controller parameters and performance functions are selected as ${\lambda }_1=3, {\lambda }_2=4, k_1=0.99e^{-0.5t}+0.01$ and $k_2=0.99e^{-5t}+0.01$.

From (2), it is known that $u$ represents the system control input, and $u_c$ is the actual input. The following actuator fault parameters are provided

$$\gamma (t)=\left\{\begin{array}{c}1,\hspace{1em}0 \mathrm{s}\le t<10 \mathrm{s}\\ 0.4, 10 \mathrm{s}\le t,\end{array}\right.$$

(47)

$$\varpi =\left\{\begin{array}{c}0,\hspace{1em}0 \mathrm{s}\le \mathrm{t}<5 \mathrm{s}\\ 0.5\cos (t), 5 \mathrm{s}\le t.\end{array}\right.$$

(48)

The simulation process adopts a faster sampling time of 0.0001 s. The simulation results are shown in Figure 3, Figure 4, Figure 5 and Figure 6.

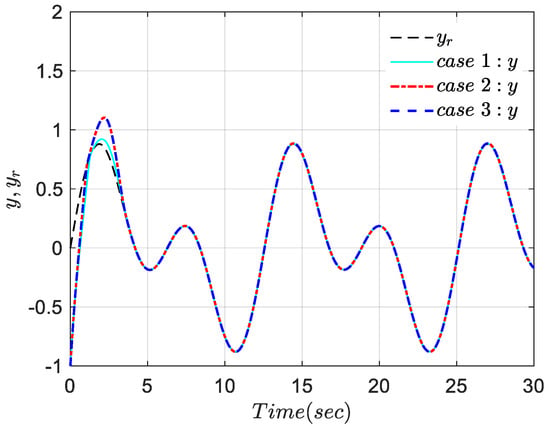
Figure 3. System output $y$ and desired trajectory $y_r$.

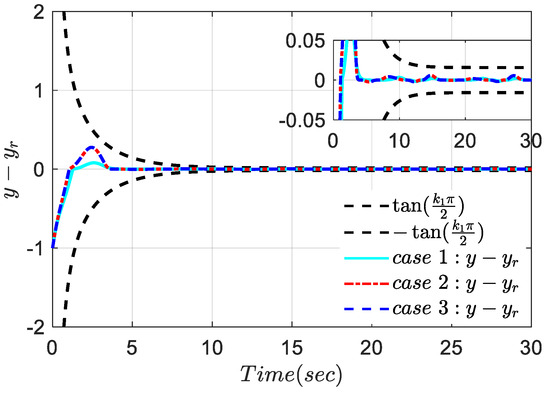
Figure 4. Tracking error $y-y_r$.

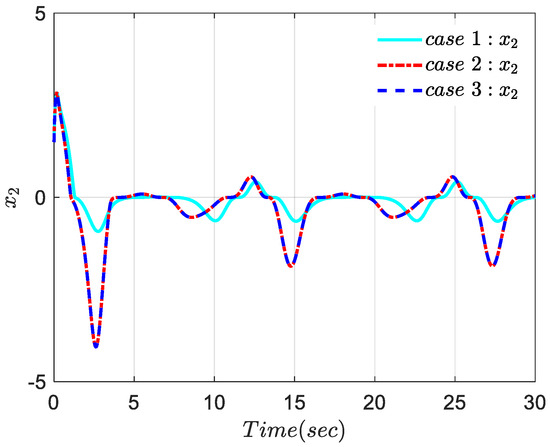
Figure 5. The system state $x_2$.

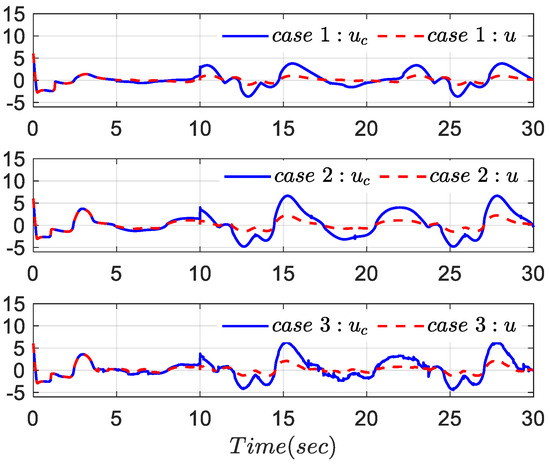
Figure 6. The system input $u$ and actual input $u_c$.

It can be seen from Figure 3 that the system’s output is capable of accurately tracking the desired trajectory signal. From Figure 4, the tracking error converges to a very small range and can adjust the tracking accuracy by selecting an appropriate value of ${\rho }_1$ in the performance function $k_1$. From the results of the three cases depicted in Figure 3 and Figure 4, it can be observed that even in the presence of disturbances and noise, the system can achieve stable control without altering the controller parameters, and the tracking error remains within the prescribed range, demonstrating excellent robustness. Additionally, Figure 5 and Figure 6 demonstrate the boundedness of the system state $x_2$ and the system inputs $u$ and $u_c$, respectively. Figure 3, Figure 4, Figure 5 and Figure 6 further confirm the boundedness of the closed-loop system signals.

Example 2. 

Practical example.

To further prove that the proposed method is not related to the system model function, but only to the system error variable, the proposed method is applied to the high-maneuver fighter (Figure 7), and its six-degree-of-freedom nonlinear mathematical model in the body coordinate system is presented as follows [34]:

$$\begin{array}{l}{\left[\begin{array}{ccccccc}\dot{\varphi }& \dot{\alpha }& \dot{\beta }& \dot{p}& \dot{q}& \dot{r}& \dot{\theta }\end{array}\right]}^{\mathrm{T}}=\\ \left[\begin{array}{c}p+q\tan \theta \sin \varphi +r\tan \theta \cos \varphi \\ q-p\beta +z_{\alpha }\Delta \alpha +(g_0/V)(\cos \theta \cos \varphi -\cos {\theta }_0)\\ y_{\beta }\beta +p(\sin {\alpha }_0+\Delta \alpha )-r\cos {\alpha }_0\\ +(g_0/V)\cos \theta \sin \varphi \\ l_{\beta }\beta +l_{p}p+l_{q}q+l_{r}r+(l_{\beta \alpha }\beta +l_{r\alpha }r)\Delta \alpha -i_{1}qr\\ m_{\alpha }\Delta \alpha +m_{q}q+i_{2}pr-{\dot{m}}_{\alpha }(g_0/V)(\cos \theta \cos \varphi -\cos {\theta }_0)\\ n_{\beta }\beta +n_{r}r+n_{p}p+n_{p\alpha }p\Delta \alpha -i_{3}pq+n_{q}q\\ q\cos \varphi -r\sin \theta \end{array}\right]\\ +\left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ l_{{\delta }_{el}}& l_{{\delta }_{er}}& l_{{\delta }_{al}}& l_{{\delta }_{ar}}& 0& 0& l_{{\delta }_r}\\ m_{{\delta }_{el}}& m_{{\delta }_{er}}& m_{{\delta }_{al}}& m_{{\delta }_{ar}}& m_{{\delta }_{lef}}& m_{{\delta }_{tef}}& m_{{\delta }_r}\\ n_{{\delta }_{el}}& n_{{\delta }_{er}}& n_{{\delta }_{al}}& n_{{\delta }_{ar}}& 0& 0& n_{{\delta }_r}\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{l}{\delta }_{\mathrm{e}\mathrm{l}}\\ {\delta }_{\mathrm{e}\mathrm{r}}\\ {\delta }_{\mathrm{a}\mathrm{l}}\\ {\delta }_{\mathrm{a}\mathrm{r}}\\ {\delta }_{\mathrm{l}\mathrm{e}\mathrm{f}}\\ {\delta }_{\mathrm{t}\mathrm{e}\mathrm{f}}\\ {\delta }_{\mathrm{r}}\end{array}\right],\end{array}$$

(49)

where $\varphi ,$ $\alpha ,$ $\beta ,$ $p,$ $q,$ $r,$ $\theta$ represents roll angle, attack angle, sideslip angle, roll angle velocity, pitch angular velocity, yaw angular velocity, and pitch angle, respectively, and ${\delta }_{\mathrm{el}},{\delta }_{\mathrm{er}},{\delta }_{\mathrm{al}},{\delta }_{\mathrm{ar}},{\delta }_{\mathrm{lef}},{\delta }_{\mathrm{tef}},{\delta }_{\mathrm{r}}$ represent the seven independent control rudder surfaces of the left and right elevators, left and right ailerons, front and rear edge flaps, and rudders. The definition of other parameters is presented in Table 1.

Figure 7. Layout of high-maneuver fighter.

Table 1. The definition of parameter.

Symbol	Unit	Definition
${\alpha }_0$	deg	trim value of attack angle
$\Delta \alpha$	deg	$\alpha -{\alpha }_0$
${\theta }_0$	deg	trim value of pitch angle
$g_0$	$m/s^2$	acceleration of gravity
$V$	$m/s$	flight speed
$l_{*}$	/	coefficient of rolling moment
$m_{*}$	/	coefficient of pitch moment
$n_{*}$	/	coefficient of yaw moment

Remark 5. 

The above model is established in the body axis coordinate system. The definition and transformation of coordinate systems can be found in Ref. [34]. Considering that the maneuvering ability of the aircraft is directly reflected by $\varphi ,\alpha ,\beta$, which serves as a basis for tracking instructions in controller design, the model has been appropriately simplified. Although it is not a full-state equation, it is sufficient for the research and design of flight controllers.

Defining ${\mathit{x}}_1={[\varphi ,\alpha ,\beta ]}^{\mathsf{{\rm T}}}$, ${\mathit{x}}_2={[p,q,r]}^{\mathrm{T}}$, and ${\mathit{x}}_3=\theta$, then the model (49) can be expressed as follows:

$$\left\{\begin{array}{l}{\dot{\mathit{x}}}_1={\mathit{f}}_1({\mathit{x}}_1,{\mathit{x}}_3)+{\mathit{G}}_1({\mathit{x}}_1,{\mathit{x}}_3){\mathit{x}}_2\\ {\dot{\mathit{x}}}_2={\mathit{f}}_2(\mathit{x})+{\mathit{G}}_2(\mathit{x})\mathit{u}\\ {\dot{\mathit{x}}}_3={\mathit{f}}_3(\mathit{x})\\ \mathit{y}={\mathit{x}}_1,\end{array}\right.$$

(50)

where $\mathit{x}={\left[{\mathit{x}}_1,{\mathit{x}}_2,{\mathit{x}}_3\right]}^{\mathrm{T}}$ are state variables and $\mathit{y}$ represents outputs of the system. ${\mathit{f}}_1({\mathit{x}}_1,{\mathit{x}}_3),{\mathit{f}}_2(\mathit{x}),{\mathit{G}}_1({\mathit{x}}_1,{\mathit{x}}_3),{\mathit{G}}_2(\mathit{x})$ are known matrix or functions for the nominal system.

The actuator fault is modeled as

$$\mathit{u}=\mathit{\gamma }(t){\mathit{u}}_c+\mathit{\varpi }(t)$$

(51)

where ${\mathit{u}}_{\mathit{c}}={\left[\begin{array}{lllllll}{\delta }_{\mathrm{cel}}\hfill & {\delta }_{\mathrm{cer}}\hfill & {\delta }_{\mathrm{cal}}\hfill & {\delta }_{\mathrm{car}}\hfill & {\delta }_{\mathrm{clef}}\hfill & {\delta }_{\mathrm{ctef}}\hfill & {\delta }_{\mathrm{cr}}\hfill \end{array}\right]}^{\mathrm{T}}$ represent the actuator control input signal to be designed; $\mathit{u}={\left[\begin{array}{lllllll}{\delta }_{\mathrm{el}}\hfill & {\delta }_{\mathrm{er}}\hfill & {\delta }_{\mathrm{al}}\hfill & {\delta }_{\mathrm{ar}}\hfill & {\delta }_{\mathrm{lef}}\hfill & {\delta }_{\mathrm{tef}}\hfill & {\delta }_{\mathrm{r}}\hfill \end{array}\right]}^{\mathrm{T}}$ are the actual deflection angle of the actuator; $\mathit{\gamma }(t)=\mathrm{diag}({\gamma }_{el}(t),\cdots ,{\gamma }_r(t))$ and $0<{\gamma }_i(t)\le 1,i=el,\cdots r$ is the time-varying performance matrix of the actuator; and $\mathit{\varpi }(t)={\left[\begin{array}{lllllll}{\varpi }_{\mathrm{el}}\hfill & {\varpi }_{\mathrm{er}}\hfill & {\varpi }_{\mathrm{al}}\hfill & {\varpi }_{\mathrm{ar}}\hfill & {\varpi }_{\mathrm{lef}}\hfill & {\varpi }_{\mathrm{tef}}\hfill & {\varpi }_{\mathrm{r}}\hfill \end{array}\right]}^{\mathrm{T}}$ is an unknown bias fault vector. Two cases of actuator bias $({\gamma }_i(t)=1,{\varpi }_i\ne 0)$ and performance degradation $(0<{\gamma }_i\left(\mathrm{t}\right)<1)$ are mainly considered in this paper. The case of complete actuator failure $({\gamma }_i\left(\mathrm{t}\right)=0)$ is not considered. The fault parameters are as follows:

$${\gamma }_{el}(t)=\left\{\begin{array}{c}0.85, 0 \mathrm{s}\le t<15 \mathrm{s}\\ 0.85+0.1\sin (t), 15 \mathrm{s}\le t\end{array}\right. ,{\varpi }_{el}=0.3e^{-t}$$

(52)

$${\gamma }_{er}(t)=\left\{\begin{array}{c}0.7, 0 \mathrm{s}\le t<10 \mathrm{s}\\ 0.5+0.3\sin (t), 10 \mathrm{s}\le t\end{array} \right.,{\varpi }_{el}=0.3\sin (t)$$

(53)

$${\gamma }_{al}(t)=0.8,{\varpi }_{al}=0.3\cos (t)$$

(54)

$${\gamma }_{ar}(t)=0.75,{\varpi }_{ar}=0$$

(55)

$${\gamma }_{lef}(t)=\left\{\begin{array}{c}0.6, 0 \mathrm{s}\le t<5 \mathrm{s}\\ 0.6+0.15e^{-0.5t}, 5 \mathrm{s}\le t\end{array} \right.,{\varpi }_{lef}=0.32\sin (t)$$

(56)

$${\gamma }_{tef}(t)=\left\{\begin{array}{c}0.5, 0 \mathrm{s}\le t<20 \mathrm{s}\\ 0.6+0.1\cos (0.5t), 20 \mathrm{s}\le t\end{array} \right.,{\varpi }_{tef}=0$$

(57)

$${\gamma }_r(t)=1 ,{\varpi }_r=0.5e^{-0.5t}.$$

(58)

The values of the relevant aerodynamic parameters of the fighter in [34] were used for simulation. The initial conditions are as follows: height $h=914.4 \mathrm{m}$, Mach $Ma=0.7$, and the angles attack and pitch in the trim state are ${\alpha }_0={3.902}^{\circ }$ and ${\theta }_0={3.902}^{\circ }$, respectively.

In the simulation, the aircraft starts with horizontal flight, rapidly increases the attack angle to 20° at 3 s, while maneuvering with a roll angle of 10°, then quickly decreases the attack angle to 2° at 8 s, and the roll angle is reduced to 0° at the same time, and the sideslip angle is maintained 0° throughout the simulation process. The simulation results are shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

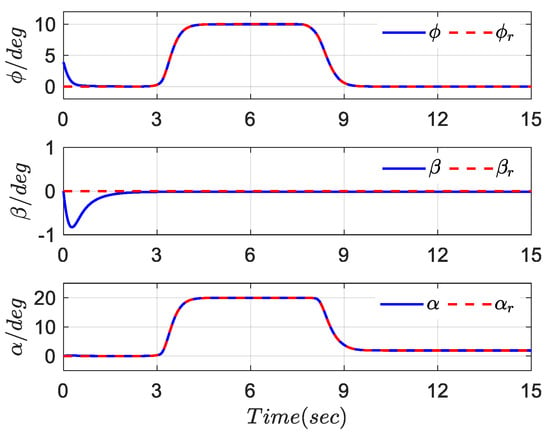
Figure 8. Response curves of $\alpha ,\beta ,\varphi$.

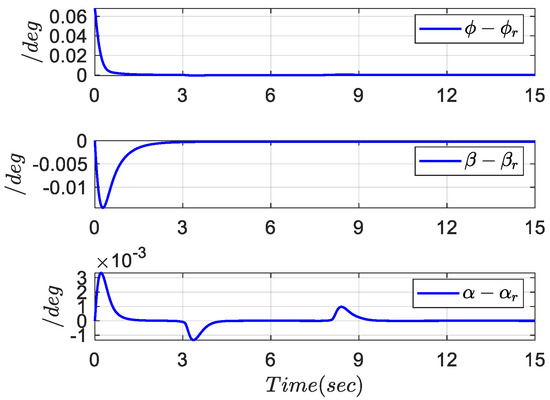
Figure 9. Tracking errors of $\alpha ,\beta ,\varphi$.

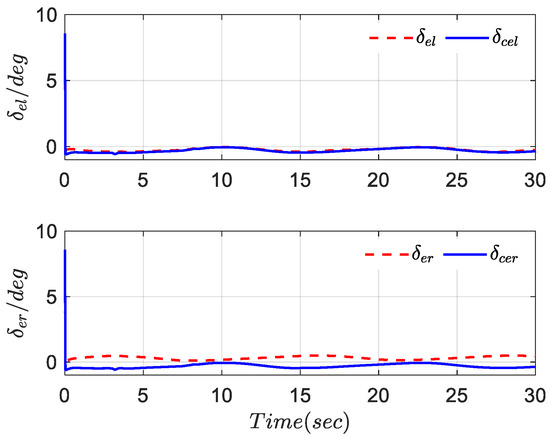
Figure 10. Deflection curves of left and right elevators.

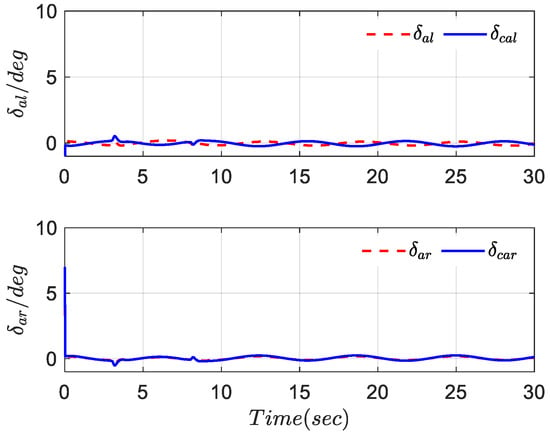
Figure 11. Deflection curves of left and right ailerons.

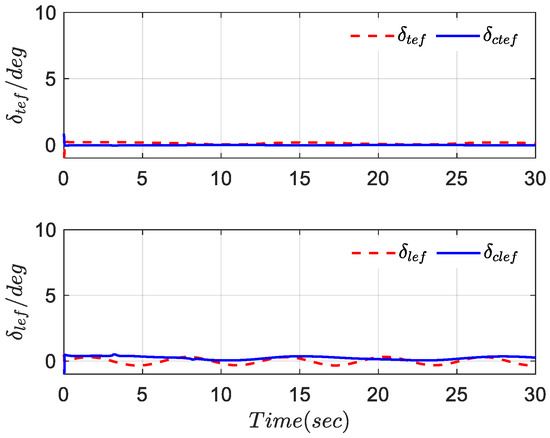
Figure 12. Deflection curves of front and rear edge flaps.

Figure 13. Deflection curves of rudders.

It can be seen from Figure 8 and Figure 9 that $\alpha ,\beta ,\varphi$ can accurately track the expected reference signal, and the tracking error can converge to the preset interval with prescribed accuracy. Figure 10, Figure 11, Figure 12 and Figure 13 show that the deflection angle of the fighter aircraft is always within the allowable range. In fact, the simulation results further demonstrate that the tracking control method proposed in this article is independent of the system model function and is only related to the error variable.

6. Conclusions

This article solved the control problem of uncertain high-order odd-rational-power nonlinear systems with actuator faults and unknown powers. By introducing the tangent function and its inverse function to perform a new coordinate transformation on the state and tracking errors, a global prescribed performance control method is proposed which does not need prior knowledge of odd rational powers, nonlinearities, and the system initial value. A global low-complexity controller is designed, which suggests that there is no need to use any filters to estimates the time derivatives of virtual control signals. Moreover, the designed controller can realize the stable control of the system even when the system suffers from actuator fault. The effectiveness of the proposed method is illustrated by the simulation of the numerical model and the practical example of high-maneuver UAV. It is underlined that the designed controller is based on full-state measurement. Working toward performing output-feedback control deserves further investigation.