A Backup Protection Based on Compensated Voltage for Transmission Lines Connected to Wind Power Plants

Abstract

Due to the influence of complex control, the short circuit current provided by wind power generation units will exhibit new characteristics, such as limited amplitude and controlled phase, affecting the performance of traditional protections. This paper analyzes the work principle and defects of one kind of multiphase compensated distance protection. Drawing on the idea of fault identification by multiphase compensated distance protection, novel pilot protection using the compensated voltage on both sides is proposed. The proposed method has a strong anti-fault resistance ability. The test results indicate that the proposed method can distinguish the internal faults and external faults reliably, unaffected by the new characteristics of short circuit current.

1. Introduction

Considering the increasingly prominent environmental problems, the development and utilization of new energy sources, such as wind power and photovoltaic power, has been accelerated around the world. However, due to the influence of complex control, the amplitude of the short circuit current provided by new energy generation units is limited and its phase angle is also controlled [1,2].

Because of the new characteristics mentioned above, it is difficult for traditional protections to meet the protection needs of the grids with high new energy source penetration. For distance protection, the measured impedance calculation will not be accurate, resulting in the mal-operation of distance protection. Furthermore, the weak feedback characteristics of short circuit current will reduce the anti-fault resistance ability of distance protection. For current differential protection, the weak feedback characteristics of the short circuit current will reduce the sensitivity of the protection.

In order to resolve the contradiction between traditional protection and new current characteristics, scholars around the world have carried out much research. In [3], a local measurement-based protection using current and voltage signals to derive accurate protection decisions was proposed. However, voltage-based protection schemes find limitations with poor protection speed and tolerance to fault resistance. Authors in [4,5] proposed the impedance differential protection scheme based on measured impedance. However, these differential protection schemes have high requirements for dual-end data synchronization. Authors in [6] applied the characteristic differences of transient high-frequency impedance to detect DC transmission line faults, which has reference significance for the protection of new energy transmission lines. References [7,8,9,10] use the current cosine similarity and waveform correlation on both sides of the line to distinguish between internal and external faults. Though these methods have good resistance to transition resistance, they have high requirements for data synchronization. A pilot protection based on the similarity and squared error of the current structure of each frequency band on both sides of the line was proposed in [11], and the proposed protection may be affected by the inverter control strategy due to the frequency band used at 10~200 Hz. Authors in [12,13] proposed a novel differential protection scheme based on inter-harmonics, which controls the inverter to inject inter-harmonics into the system, and identifies faults by using the differences in harmonic characteristics between the two sides of the line.

In this paper, drawing on the idea of fault identification by one kind of multiphase compensated distance protection, a novel pilot protection scheme is proposed. The negative sequence compensated voltages on both sides are calculated. Then, the magnitude of the ratio between the negative-sequence compensated voltage on both sides is used to distinguish internal faults and external faults. The proposed method has advantages in anti-fault resistance ability. Simulation test results show that the proposed method can distinguish the internal faults and external fault reliably, unaffected by the new characteristics of short circuit currents.

The remainder of the paper is organized as follows: the work principle and defects of the compensated distance protection are introduced in Section 2. The principles and criterion of the proposed protection method are introduced in Section 3. Simulation tests of the proposed protection method are shown in Section 4. Section 4 is the conclusion.

2. Multiphase Compensated Distance Protection

2.1. The Criterion of Multiphase Compensated Distance Protection

Multiphase compensated distance protection has been proposed and is widely used in the era of electromagnetic protection. However, most of the criteria use the ratio of different phase compensated voltages and the ratio of different phase-to-phase compensated voltages. In [14], a multiphase compensated distance protection based on the ratio between phase compensated voltage and phase-to-phase compensated voltage has been proposed. Its core criterion is as follows:

$$\{\begin{array}{c}{P}_{\mathrm{A}-\mathrm{BC}}:360°>\arg \frac{{\dot{U}}_{\mathrm{A}}^{\prime }}{{\dot{U}}_{\mathrm{BC}}^{\prime }}>180°\\ P_{\mathrm{B}-\mathrm{CA}}:360°>\arg \frac{{\dot{U}}_{\mathrm{B}}^{\prime }}{{\dot{U}}_{\mathrm{CA}}^{\prime }}>180°\\ P_{\mathrm{C}-\mathrm{AB}}:360°>\arg \frac{{\dot{U}}_{\mathrm{C}}^{\prime }}{{\dot{U}}_{\mathrm{AB}}^{\prime }}>180°\end{array}$$

(1)

where ${\dot{U}}_{\phi }^{\prime }\left(\phi =\mathrm{A},\mathrm{B},\mathrm{C}\right)$ and ${\dot{U}}_{\phi \phi }^{\prime }\left(\phi \phi =\mathrm{AB},\mathrm{BC},\mathrm{CA}\right)$ represent the phase compensated voltage and phase-to-phase compensated voltage, respectively. And they can be calculated as follows:

$$\{\begin{array}{l}{\dot{U}}_{\mathsf{\phi }}^{\prime }={\dot{U}}_{\mathsf{\phi }}-\left({\dot{I}}_{\mathsf{\phi }}+3k{\dot{I}}_0\right)Z_{\mathrm{set}}\hfill \\ {\dot{U}}_{\mathsf{\phi }\mathsf{\phi }}^{\prime }={\dot{U}}_{\mathsf{\phi }\mathsf{\phi }}-{\dot{I}}_{\mathsf{\phi }\mathsf{\phi }}{Z}_{\mathrm{set}}\hfill \end{array}$$

(2)

where ${\dot{U}}_{\mathsf{\phi }}$ and ${\dot{I}}_{\mathsf{\phi }}$ represent the phase voltage and current measured on the measuring point, ${\dot{U}}_{\mathsf{\phi }\mathsf{\phi }}$ and ${\dot{I}}_{\mathsf{\phi }\mathsf{\phi }}$ represent the phase-to-phase voltage and current measured on the measuring point, ${\dot{I}}_0$ is the zero-sequence current on the measuring point, $Z_{\mathrm{set}}$ is the setting value of the protection, and k is the zero-sequence current compensation factor and is defined as

$$k=\frac{Z_0-Z_1}{3Z_1}$$

(3)

where $Z_1$ and $Z_0$ are the positive-sequence and zero-sequence impedances of the transmission line.

2.2. The Principle of Multiphase Compensated Distance Protection

The principle of multiphase compensated distance protection is introduced using the two-end system shown in Figure 1. As Figure 1 shows, point M is the measuring point, point F is the fault point, and the action zone of the distance protection is from point M to point Y. ${\dot{E}}_{\mathrm{M}}$ and ${\dot{E}}_{\mathrm{N}}$ are the equivalent electromotive forces at both ends. $Z_{\mathrm{M}}$ and $Z_{\mathrm{N}}$ are the equivalent system impedances of the equivalent systems at both ends. $Z_{\mathrm{F}}$ represents the equivalent impedance from the point F to the Point M. $Z_{\mathrm{set}}$ represents the setting value of the distance protection. $Z_{\mathsf{\Sigma }}$ is the equivalent impedance of the two-end system.

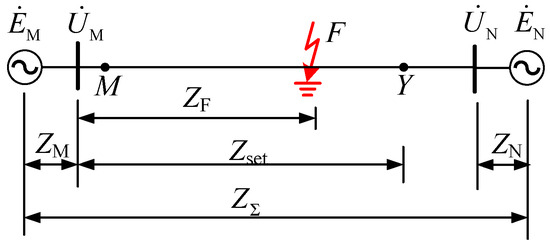
Figure 1. The sketch of the two-end system.

It is assumed that the impedance angle of all parts of the system is the same and that the structure of each sequence network is the same. Define parameters $k_{\mathrm{Y}}$ and $k_{\mathrm{F}}$ as

$$\{\begin{array}{c}{k}_{\mathrm{Y}}=\frac{Z_{\mathrm{M}}+Z_{\mathrm{set}}}{Z_{\sum }}\\ k_{\mathrm{F}}=\frac{Z_{\mathrm{M}}+Z_{\mathrm{F}}}{Z_{\sum }}\end{array}$$

(4)

Taking the criterion $P_{\mathrm{A}-\mathrm{B}\mathrm{C}}$ in Equation (1) as an example, the results of phase comparison in different situations are analyzed. When a phase A grounding fault occurs, the structure of the fault-superposed composite sequence network is shown in Figure 2. In Figure 2, ${Z^{\prime }}_{\mathrm{Nx}}=Z_{\mathrm{\Sigma x}}-Z_{\mathrm{Mx}}-Z_{\mathrm{Fx}}$, the subscript x = 1, 2, 0, and represents the sequence value of the corresponding impedance. ${\dot{U}}_{\mathrm{FA}\left[0\right]}$ is the phase A voltage at the fault point before the fault occurs, and $R_{\mathrm{g}}$ is the transition resistance. ${\dot{I}}_{\mathrm{F}1}$, ${\dot{I}}_{\mathrm{F}2}$, and ${\dot{I}}_{\mathrm{F}0}$ are the fault sequence currents at the fault point.

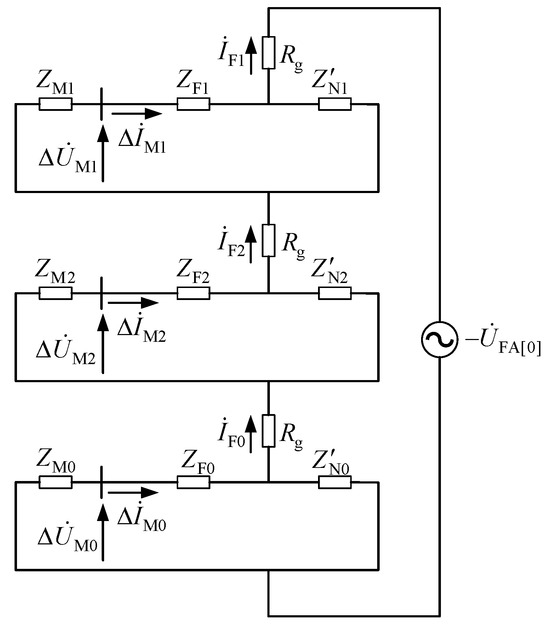
Figure 2. The structure of the fault-superposed composite sequence network.

From Figure 2, the fault sequence currents can be calculated as

$${\dot{I}}_{\mathrm{F}1}={\dot{I}}_{\mathrm{F}2}={\dot{I}}_{\mathrm{F}0}=\frac{{\dot{U}}_{\mathrm{FA}\left[0\right]}}{3R_{\mathrm{g}}+k_{\mathrm{F}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\mathsf{\Sigma }1}+Z_{\mathsf{\Sigma }0}\right)}$$

(5)

where $Z_{\mathsf{\Sigma }1}$ and $Z_{\mathsf{\Sigma }0}$ represent the positive-sequence and zero-sequence impedances of the two-end system.

Using the fault sequence currents ${\dot{I}}_{\mathsf{F}1}$, ${\dot{I}}_{\mathsf{F}2}$, and ${\dot{I}}_{\mathsf{F}0}$, the fault sequence voltages and currents at measuring point M, $\mathsf{\Delta }{\dot{U}}_{\mathsf{M}1}$, $\mathsf{\Delta }{\dot{U}}_{\mathsf{M}2}$, $\mathsf{\Delta }{\dot{U}}_{\mathsf{M}0}$, $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}$, $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}$, and $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}$ can be obtained as

$$\{\begin{array}{l}\mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}=\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}1}\hfill \\ \mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}=\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}2}\hfill \\ \mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}=\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}0}\hfill \end{array}$$

(6)

$$\{\begin{array}{l}\mathsf{\Delta }{\dot{U}}_{\mathrm{M}1}=-Z_{\mathrm{M}1}\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}1}\hfill \\ \mathsf{\Delta }{\dot{U}}_{\mathrm{M}2}=-Z_{\mathrm{M}2}\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}2}\hfill \\ \mathsf{\Delta }{\dot{U}}_{\mathrm{M}0}=-Z_{\mathrm{M}0}\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}0}\hfill \end{array}$$

(7)

After obtaining $\mathsf{\Delta }{\dot{U}}_{\mathrm{M}1}$, $\mathsf{\Delta }{\dot{U}}_{\mathrm{M}2}$, $\mathsf{\Delta }{\dot{U}}_{\mathrm{M}0}$, $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}$, $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}$, and $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}$, based on the phase-sequence transformation and superposition principle, the phase voltages and currents at M point can be calculated as:

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{A}}={\dot{U}}_{\mathrm{A}\left[0\right]}+\mathsf{\Delta }{\dot{U}}_{\mathrm{M}1}+\mathsf{\Delta }{\dot{U}}_{\mathrm{M}2}+\mathsf{\Delta }{\dot{U}}_{\mathrm{M}0}={\dot{U}}_{\mathrm{A}\left[0\right]}-\left(2Z_{\mathrm{M}1}+Z_{\mathrm{M}0}\right)\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}1}\hfill \\ {\dot{U}}_{\mathrm{B}}={\dot{U}}_{\mathrm{B}\left[0\right]}+{\alpha }^2\mathsf{\Delta }{\dot{U}}_{\mathrm{M}1}+\alpha \mathsf{\Delta }{\dot{U}}_{\mathrm{M}2}+\mathsf{\Delta }{\dot{U}}_{\mathrm{M}0}={\dot{U}}_{\mathrm{B}\left[0\right]}-\left[\left({\alpha }^2+\alpha \right)Z_{\mathrm{M}1}+Z_{\mathrm{M}0}\right]\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}1}\hfill \\ {\dot{U}}_{\mathrm{C}}={\dot{U}}_{\mathrm{C}\left[0\right]}+\alpha \mathsf{\Delta }{\dot{U}}_{\mathrm{M}1}+{\alpha }^2\mathsf{\Delta }{\dot{U}}_{\mathrm{M}2}+\mathsf{\Delta }{\dot{U}}_{\mathrm{M}0}={\dot{U}}_{\mathrm{C}\left[0\right]}-\left[\left({\alpha }^2+\alpha \right)Z_{\mathrm{M}1}+Z_{\mathrm{M}0}\right]\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}1}\hfill \end{array}$$

(8)

$$\{\begin{array}{l}{\dot{I}}_{\mathrm{A}}={\dot{I}}_{\mathrm{loadA}}+\mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}+\mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}+\mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}={\dot{I}}_{\mathrm{loadA}}+3\left(1-k_{\mathrm{F}}\right){\dot{I}}_{\mathrm{F}1}\hfill \\ {\dot{I}}_{\mathrm{B}}={\dot{I}}_{\mathrm{loadB}}+{\alpha }^2\mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}+\alpha \mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}+\mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}={\dot{I}}_{\mathrm{loadB}}\hfill \\ {\dot{I}}_{\mathrm{C}}={\dot{I}}_{\mathrm{loadC}}+\alpha \mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}+{\alpha }^2\mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}+\mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}={\dot{I}}_{\mathrm{loadC}}\hfill \end{array}$$

(9)

In (8), ${\dot{U}}_{\mathrm{A}\left[0\right]}$, ${\dot{U}}_{\mathrm{B}\left[0\right]}$, and ${\dot{U}}_{\mathrm{C}\left[0\right]}$ are the three phase voltages at point M before the fault occurs, $\alpha =e^{j\frac{2\pi }{3}}$. In (9), ${\dot{I}}_{\mathrm{loadA}}$, ${\dot{I}}_{\mathrm{loadB}}$, and ${\dot{I}}_{\mathrm{loadC}}$ are the three phase currents at point M before the fault occurs. Substituting (5), (8), and (9) into (2), the compensated voltages of three phases are calculated as

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{A}}^{\prime }={\dot{U}}_{\mathrm{YA}\left[0\right]}-\frac{k_{\mathrm{Y}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\sum 1}+Z_{\sum 0}\right)}{3R_{\mathrm{g}}+k_{\mathrm{F}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\sum 1}+Z_{\sum 0}\right)}{\dot{U}}_{\mathrm{FA}\left[0\right]}\hfill \\ {\dot{U}}_{\mathrm{B}}^{\prime }={\alpha }^2{\dot{U}}_{\mathrm{YA}\left[0\right]}-\frac{k_{\mathrm{Y}}\left(1-k_{\mathrm{F}}\right)\left(Z_{\sum 0}-Z_{\sum 1}\right)}{3R_{\mathrm{g}}+k_{\mathrm{F}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\sum 1}+Z_{\sum 0}\right)}{\dot{U}}_{\mathrm{FA}\left[0\right]}\hfill \\ {\dot{U}}_{\mathrm{C}}^{\prime }=\alpha {\dot{U}}_{\mathrm{YA}\left[0\right]}-\frac{k_{\mathrm{Y}}\left(1-k_{\mathrm{F}}\right)\left(Z_{\sum 0}-Z_{\sum 1}\right)}{3R_{\mathrm{g}}+k_{\mathrm{F}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\sum 1}+Z_{\sum 0}\right)}{\dot{U}}_{\mathrm{FA}\left[0\right]}\hfill \end{array}$$

(10)

where ${\dot{U}}_{\mathrm{YA}\left[0\right]}$ is the phase A voltage at the setting point before the fault occurs.

Substituting (10) into $P_{\mathrm{A}-\mathrm{BC}}$ gives

$$\arg \frac{{\dot{U}}_{\mathrm{A}}^{\prime }}{{\dot{U}}_{\mathrm{BC}}^{\prime }}=\arg \frac{1}{{\alpha }^2-\alpha }+\arg \frac{{\dot{U}}_{\mathrm{YA}\left[0\right]}-\frac{k_{\mathrm{Y}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\mathsf{\Sigma }1}+Z_{\mathsf{\Sigma }0}\right)}{3R_{\mathrm{g}}^{\left(1\right)}+k_{\mathrm{F}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\mathsf{\Sigma }1}+Z_{\mathsf{\Sigma }0}\right)}{\dot{U}}_{\mathrm{FA}\left[0\right]}}{{\dot{U}}_{\mathrm{YA}\left[0\right]}}$$

(11)

Considering that ${\dot{U}}_{\mathrm{YA}[0]}$ and ${\dot{U}}_{\mathrm{FA}[0]}$ are approximately equal, (11) can be written approximately as

$$\arg \frac{{\dot{U}}_{\mathrm{A}}^{\prime }}{{\dot{U}}_{\mathrm{BC}}^{\prime }}\approx 90°+\arg \left(1-\frac{k_{\mathrm{Y}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\mathsf{\Sigma }1}+Z_{\mathsf{\Sigma }0}\right)}{3R_{\mathrm{g}}^{\left(1\right)}+k_{\mathrm{F}}\left(1-k_{\mathrm{F}}\right)\left(2Z_{\mathsf{\Sigma }1}+Z_{\mathsf{\Sigma }0}\right)}\right)$$

(12)

Ignoring the transition resistance, (12) can be rewritten as

$$\arg \frac{{\dot{U}}_{\mathrm{A}}^{\prime }}{{\dot{U}}_{\mathrm{BC}}^{\prime }}\approx 90°+\arg \left(1-\frac{k_{\mathrm{Y}}}{k_{\mathrm{F}}}\right)$$

(13)

According to (13), the criterion is actually to distinguish between external faults and internal faults by judging the magnitude relationship between $k_{\mathrm{Y}}/k_{\mathrm{F}}$ and 1. Based on the definitions of $k_{\mathrm{Y}}$ and $k_{\mathrm{F}}$, $k_{\mathrm{Y}}/k_{\mathrm{F}}$ actually reflects the location relationship between the fault point and the action zone of the protection. If $k_{\mathrm{Y}}/k_{\mathrm{F}}$ is greater than 1, the fault point will be within the action zone of the protection, and vice versa if the fault point is outside the action zone of the protection. Similar conclusions can be drawn in the case of two-phase short-circuit faults and two-phase ground short-circuit faults.

However, from (12), the transition resistance can affect the value of $k_{\mathrm{Y}}/k_{\mathrm{F}}$, which may cause protection refusal. In addition, the assumption that the impedance angle of all parts of the system is the same and that the structure of each sequence network is the same is hard to meet in practice. The performance of the criterion shown in (1) is affected by the structure and parameters of the system.

3. Distance Protection Based on Compensated Sequence Voltage

3.1. The Principle of Distance Protection

As mentioned in Section 2, the multiphase compensated distance protection introduced in Section 2 has a weak ability to resist transition resistance, and its performance is also affected by the system structure and parameters. When the protection is applied to the transmission line connected to the new energy resource, the above defects of the method will be further amplified, since the response of new energy resource control strategies to the fault will make the difference between the positive and negative equivalent impedances of the system quite large. On the other hand, from the analysis in Section 2, it can be seen that the compensated voltage contains information about the fault position and the action zone of the protection. Therefore, distance protection based on compensated sequence voltage is proposed for the transmission line connected to the wind power plant, here. The principle of distance protection is introduced as follows.

When a fault occurs on the transmission line connected to the wind power plant, the fault current and voltage can be divided into three stages. In the first stage, the characteristics of the fault current and voltage are mainly influenced by the topology of the grid. In the second stage, the control system of the wind power plant begins to intervene, and it is difficult to describe the fault characteristics. In the third stage, the control system response process ends, the control strategy remains unchanged, and the characteristics of the fault current and voltage become stable.

The proposed protection method is based on the characteristics of the third stage, since the fault current and voltage are stable in the third stage. In addition, as mentioned above, the impedance angle of all parts of the system is the same and the structure of each sequence network is the same, which is hard to meet in practice, and several parameters are re-defined as

$$\{\begin{array}{c}{k}_{\mathrm{Y}1}=\frac{Z_{\mathrm{Mx}}+Z_{\mathrm{setx}}}{Z_{\sum \mathrm{x}}}\\ k_{\mathrm{F}1}=\frac{Z_{\mathrm{Mx}}+Z_{\mathrm{Fx}}}{Z_{\sum \mathrm{x}}}\end{array}$$

(14)

where the subscript x is 1, 2, 0, which represents the positive, negative, and zero sequence components. And the compensated voltages for different fault types are deduced as follows.

3.1.1. Single-Phase Grounding Fault

Taking the phase A grounding fault as an example, the corresponding three-phase compensated voltage on the M side can be calculated by using the three-phase current voltage measured on the M side, and the expressions is

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{MA}}^{\prime }={\dot{U}}_{\mathrm{YA}[0]}^{\prime }-k_{\mathrm{F}1}\left(1-k_{\mathrm{F}1}\right)Z_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(1\right)}-k_{\mathrm{F}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(1\right)}-k_{\mathrm{F}0}\left(1-k_{\mathrm{F}0}\right)Z_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{\left(1\right)}\hfill \\ {\dot{U}}_{\mathrm{MB}}^{\prime }={\dot{U}}_{\mathrm{YB}[0]}^{\prime }-{\alpha }^2{k}_{\mathrm{F}1}\left(1-k_{\mathrm{F}1}\right)Z_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(1\right)}-\alpha k_{\mathrm{F}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(1\right)}-k_{\mathrm{F}0}\left(1-k_{\mathrm{F}0}\right)Z_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{\left(1\right)}\hfill \\ {\dot{U}}_{\mathrm{MC}}^{\prime }={\dot{U}}_{\mathrm{YC}[0]}^{\prime }-\alpha k_{\mathrm{F}1}\left(1-k_{\mathrm{F}1}\right)Z_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(1\right)}-{\alpha }^2{k}_{\mathrm{F}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(1\right)}-k_{\mathrm{F}0}\left(1-k_{\mathrm{F}0}\right)Z_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{\left(1\right)}\hfill \end{array}$$

(15)

where ${\dot{U}}_{\mathrm{YA}\left[0\right]}^{\prime }$, ${\dot{U}}_{\mathrm{YB}\left[0\right]}^{\prime }$, and ${\dot{U}}_{\mathrm{YC}\left[0\right]}^{\prime }$ are the voltages at the setting point before the fault, and ${\dot{I}}_{\mathrm{F}1}^{\left(1\right)}$, ${\dot{I}}_{\mathrm{F}2}^{\left(1\right)}$, and ${\dot{I}}_{\mathrm{F}0}^{\left(1\right)}$ are the three-sequence currents at fault point.

After obtaining the three-phase compensated voltage on the M side, based on the phase-sequence transformation, the negative sequence and zero sequence compensated voltages on the M side can be calculated as:

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{M}2}^{\prime }=\frac{1}{3}\left({\dot{U}}_{\mathrm{MA}}^{\prime }+{\alpha }^2{\dot{U}}_{\mathrm{MB}}^{\prime }+\alpha {\dot{U}}_{\mathrm{MC}}^{\prime }\right)=-k_{\mathrm{F}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{(1)}\hfill \\ {\dot{U}}_{\mathrm{M}0}^{\prime }=\frac{1}{3}\left({\dot{U}}_{\mathrm{MA}}^{\prime }+{\dot{U}}_{\mathrm{MB}}^{\prime }+{\dot{U}}_{\mathrm{MC}}^{\prime }\right)=-k_{\mathrm{F}0}\left(1-k_{\mathrm{F}0}\right)Z_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{(1)}\hfill \end{array}$$

(16)

If $Z_{\mathrm{L}}-Z_{\mathrm{set}}$ is taken as the setting value of the protection on the N side, for the same fault, the corresponding three-phase compensated voltage on the N side can be calculated as:

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{NA}}^{\prime }={\dot{U}}_{\mathrm{YA}[0]}^{\prime }-\left(1-k_{\mathrm{Y}1}\right)k_{\mathrm{F}1}{Z}_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(1\right)}-\left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(1\right)}-\left(1-k_{\mathrm{Y}0}\right)k_{\mathrm{F}0}{Z}_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{\left(1\right)}\hfill \\ {\dot{U}}_{\mathrm{NB}}^{\prime }={\dot{U}}_{\mathrm{YB}[0]}^{\prime }-{\alpha }^2\left(1-k_{\mathrm{Y}1}\right)k_{\mathrm{F}1}{Z}_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(1\right)}-\alpha \left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(1\right)}-\left(1-k_{\mathrm{Y}0}\right)k_{\mathrm{F}0}{Z}_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{\left(1\right)}\hfill \\ {\dot{U}}_{\mathrm{NC}}^{\prime }={\dot{U}}_{\mathrm{YC}[0]}^{\prime }-\alpha \left(1-k_{\mathrm{Y}1}\right)k_{\mathrm{F}1}{Z}_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(1\right)}-{\alpha }^2\left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(1\right)}-\left(1-k_{\mathrm{Y}0}\right)k_{\mathrm{F}0}{Z}_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{\left(1\right)}\hfill \end{array}$$

(17)

From (17), negative sequence and zero sequence compensated voltages on the N side can be calculated as:

$$\{\begin{array}{c}{\dot{U}}_{\mathrm{N}2}^{\prime }=-\left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{(1)}\\ {\dot{U}}_{\mathrm{N}0}^{\prime }=-\left(1-k_{\mathrm{Y}0}\right)k_{\mathrm{F}0}{Z}_{\sum 0}{\dot{I}}_{\mathrm{F}0}^{(1)}\end{array}$$

(18)

According to (16) and (18), the ratio of the negative sequence compensated voltage on the M side and the negative sequence compensated voltage on the N side can be calculated as:

$$\frac{{\dot{U}}_{\mathrm{M}2}^{\prime }}{{\dot{U}}_{\mathrm{N}2}^{\prime }}=\frac{k_{\mathrm{Y}2}\left(1-k_{\mathrm{F}2}\right)}{k_{\mathrm{F}2}\left(1-k_{\mathrm{Y}2}\right)}=\frac{Z_{\mathrm{M}2}+Z_{\mathrm{set}2}}{Z_{\mathrm{M}2}+Z_{\mathrm{F}2}}\cdot \frac{Z_{\sum 2}-Z_{\mathrm{M}2}-Z_{\mathrm{F}2}}{Z_{\sum 2}-Z_{\mathrm{M}2}-Z_{\mathrm{set}2}}$$

(19)

At the same time, the ratio of the zero-sequence compensated voltage on the M side and the zero-sequence compensated voltage on the N-side can be calculated as:

$$\frac{{\dot{U}}_{\mathrm{M}0}^{\prime }}{{\dot{U}}_{\mathrm{N}0}^{\prime }}=\frac{k_{\mathrm{Y}0}\left(1-k_{\mathrm{F}0}\right)}{k_{\mathrm{F}0}\left(1-k_{\mathrm{Y}0}\right)}=\frac{Z_{\mathrm{M}0}+Z_{\mathrm{set}0}}{Z_{\mathrm{M}0}+Z_{\mathrm{F}0}}\cdot \frac{Z_{\sum 0}-Z_{\mathrm{M}0}-Z_{\mathrm{F}0}}{Z_{\sum 0}-Z_{\mathrm{M}0}-Z_{\mathrm{set}0}}$$

(20)

From (19) and (20), it can be seen that the relationship between the fault location and the protection action zone can be reflected in both the ratio of the negative sequence compensated voltages on the M and N sides and the ratio of the zero sequence compensated voltages on the M and N sides. When a single-phase grounding fault occurs within the protection action zone, the amplitude of their ratios is greater than 1; when faults occur outside the protection action zone, the amplitude of their ratios is less than 1.

3.1.2. Two-Phase Short-Circuit Fault

Taking the BC phase short-circuit fault as an example, the corresponding three-phase compensated voltage on the M side can be calculated as

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{MA}}^{\prime }={\dot{U}}_{\mathrm{YA}[0]}^{\prime }-k_{\mathrm{F}1}\left(1-k_{\mathrm{F}1}\right)Z_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(2\right)}-k_{\mathrm{F}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(2\right)}\hfill \\ {\dot{U}}_{\mathrm{MB}}^{\prime }={\dot{U}}_{\mathrm{YB}[0]}^{\prime }-{\alpha }^2{k}_{\mathrm{F}1}\left(1-k_{\mathrm{F}1}\right)Z_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(2\right)}-\alpha k_{\mathrm{F}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(2\right)}\hfill \\ {\dot{U}}_{\mathrm{MC}}^{\prime }={\dot{U}}_{\mathrm{YC}[0]}^{\prime }-\alpha k_{\mathrm{F}1}\left(1-k_{\mathrm{F}1}\right)Z_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(2\right)}-{\alpha }^2{k}_{\mathrm{F}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(2\right)}\hfill \end{array}$$

(21)

where ${\dot{I}}_{F1}^{\left(2\right)}$ and ${\dot{I}}_{F2}^{\left(2\right)}$ are the positive-sequence current and negative-sequence current at the fault point, respectively.

From (21), it can be seen that, unlike a single-phase ground fault, there is no zero-sequence compensated voltage for a two-phase short-circuit fault. Now the corresponding negative sequence compensated voltage on the M side can be calculated as

$${\dot{U}}_{\mathrm{M}2}^{\prime }=-k_{\mathrm{Y}2}\left(1-k_{\mathrm{F}2}\right)Z_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{(2)}$$

(22)

Similar to the single-phase grounding fault, if $Z_L-Z_{\mathrm{set}}$ is used as the protection setting value on the N-side, the corresponding three-phase compensated voltage on the N side can be expressed as

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{NA}}^{\prime }={\dot{U}}_{\mathrm{YA}[0]}^{\prime }-\left(1-k_{\mathrm{Y}1}\right)k_{\mathrm{F}1}{Z}_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(2\right)}-\left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(2\right)}\hfill \\ {\dot{U}}_{\mathrm{NB}}^{\prime }={\dot{U}}_{\mathrm{YB}[0]}^{\prime }-{\alpha }^2\left(1-k_{\mathrm{Y}1}\right)k_{\mathrm{F}1}{Z}_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(2\right)}-\alpha \left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(2\right)}\hfill \\ {\dot{U}}_{\mathrm{NC}}^{\prime }={\dot{U}}_{\mathrm{YC}[0]}^{\prime }-\alpha \left(1-k_{\mathrm{Y}1}\right)k_{\mathrm{F}1}{Z}_{\sum 1}{\dot{I}}_{\mathrm{F}1}^{\left(2\right)}-{\alpha }^2\left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{\left(2\right)}\hfill \end{array}$$

(23)

From (23), the corresponding negative sequence compensated voltage on the N side can also be calculated as

$${\dot{U}}_{\mathrm{N}0}^{\prime }=-\left(1-k_{\mathrm{Y}2}\right)k_{\mathrm{F}2}{Z}_{\sum 2}{\dot{I}}_{\mathrm{F}2}^{(2)}$$

(24)

According to (22) and (24), the ratio of the negative sequence compensated voltage on the M side and the negative sequence compensated voltage on the N side can be calculated as

$$\frac{{\dot{U}}_{\mathrm{M}2}^{\prime }}{{\dot{U}}_{\mathrm{N}2}^{\prime }}=\frac{k_{\mathrm{Y}2}\left(1-k_{\mathrm{F}2}\right)}{k_{\mathrm{F}2}\left(1-k_{\mathrm{Y}2}\right)}=\frac{Z_{\mathrm{M}2}+Z_{\mathrm{set}2}}{Z_{\mathrm{M}2}+Z_{\mathrm{F}2}}\cdot \frac{Z_{\sum 2}-Z_{\mathrm{M}2}-Z_{\mathrm{F}2}}{Z_{\sum 2}-Z_{\mathrm{M}2}-Z_{\mathrm{set}2}}$$

(25)

From (25), it can be concluded that the ratio of the negative sequence compensated voltages on the M and N side reflects the relationship between the fault location and the protection action zone. When the fault occurs within the protection action zone, the amplitude of its ratio is greater than 1; When a no-fault occurs outside the protection action zone, the amplitude of the ratio is less than 1.

For the two-phase short-circuit grounding fault, the expressions of the three-phase sequence compensated voltage on the M side and the N side are basically the same as those of (15) and (17), except that the fault sequence current at the fault point is different. Therefore, the same conclusion can be drawn as in the case of single-phase grounding faults; that is, the ratio of the negative sequence compensated voltage on the M side to the negative sequence compensated voltage on the N side, or the ratio of the zero-sequence compensated voltage on the M side to the zero-sequence compensated voltage on the N side, reflects the relationship between the fault location and the protection action zone. When the fault occurs within the protection action zone, the amplitude of their ratio is greater than 1; when the fault occurs outside the protection action zone, the amplitude of their ratio is less than 1.

3.1.3. Backward Fault

For the measurement points, the faults discussed in Section 3.1.1 and Section 3.1.2 are forward faults, regardless of whether they are internal faults or external faults. In fact, there is also a backward fault, which is a kind of external fault for measuring points. Taking the measuring point M in Figure 1 as an example, the relative position relationship between the fault point and point M is shown in Figure 3. In the figure, point F is the fault point.

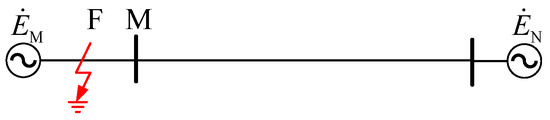
Figure 3. The relative position relationship between the fault point and the measuring point.

Under the fault situation shown in Figure 3, still taking the phase A grounding fault as an example, the structure of the fault superposed composite sequence network is shown in Figure 4. In the figure, $Z_{\mathrm{L}}$ is the equivalent impedance of the transmission line, and subscripts 1, 2, and 0 represent the positive sequence value, negative sequence value, and zero sequence value of $Z_{\mathrm{L}}$, respectively. Considering the fault point, the equivalent system impedance $Z_{\mathrm{M}}$ is divided into two parts, which are represented as $Z_{\mathrm{M}\alpha }$ and $Z_{\mathrm{M}\beta }$ in Figure 4.

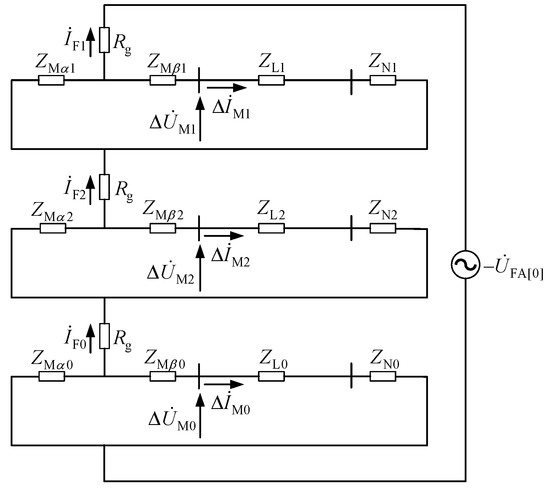
Figure 4. The structure of the fault-superposed composite sequence network under the backward phase A grounding fault.

Similar to the derivation in Section 2, when a backward phase A grounding fault occurs, the fault sequence currents and voltages $\mathsf{\Delta }{\dot{U}}_{\mathrm{M}1}$, $\mathsf{\Delta }{\dot{U}}_{\mathrm{M}2}$, $\mathsf{\Delta }{\dot{U}}_{\mathrm{M}0}$, $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}$, $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}$, and $\mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}$ can be calculated as

$$\{\begin{array}{l}\mathsf{\Delta }{\dot{I}}_{\mathrm{M}1}=-\frac{Z_{\mathrm{M}\alpha 1}}{Z_{\mathsf{\Sigma }1}}{\dot{I}}_{\mathrm{F}1}\hfill \\ \mathsf{\Delta }{\dot{I}}_{\mathrm{M}2}=-\frac{Z_{\mathrm{M}\alpha 2}}{Z_{\mathsf{\Sigma }2}}{\dot{I}}_{\mathrm{F}2}\hfill \\ \mathsf{\Delta }{\dot{I}}_{\mathrm{M}0}=-\frac{Z_{\mathrm{M}\alpha 1}}{Z_{\mathsf{\Sigma }0}}{\dot{I}}_{\mathrm{F}0}\hfill \end{array}$$

(26)

$$\{\begin{array}{l}\mathsf{\Delta }{\dot{U}}_{\mathrm{M}1}=-\left(Z_{\mathrm{N}1}+Z_{\mathrm{L}1}\right)\frac{Z_{\mathrm{M}\alpha 1}}{Z_{\mathsf{\Sigma }1}}{\dot{I}}_{\mathrm{F}1}\hfill \\ \mathsf{\Delta }{\dot{U}}_{\mathrm{M}2}=-\left(Z_{\mathrm{N}2}+Z_{\mathrm{L}2}\right)\frac{Z_{\mathrm{M}\alpha 2}}{Z_{\mathsf{\Sigma }1}}{\dot{I}}_{\mathrm{F}2}\hfill \\ \mathsf{\Delta }{\dot{U}}_{\mathrm{M}0}=-\left(Z_{\mathrm{N}0}+Z_{\mathrm{L}0}\right)\frac{Z_{\mathrm{M}\alpha 0}}{Z_{\mathsf{\Sigma }0}}{\dot{I}}_{\mathrm{F}0}\hfill \end{array}$$

(27)

And the corresponding compensated voltages on the M side can be calculated as

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{MA}}^{\prime }={\dot{U}}_{\mathrm{YA}[0]}^{\prime }+\left(1-k_{\mathrm{Y}1}\right)Z_{\mathrm{M}\alpha 1}{\dot{I}}_{\mathrm{F}1}+\left(1-k_{\mathrm{Y}2}\right)Z_{\mathrm{M}\alpha 2}{\dot{I}}_{\mathrm{F}2}+\left(1-k_{\mathrm{Y}1}\right)Z_{\mathrm{M}\alpha 0}{\dot{I}}_{\mathrm{F}0}\hfill \\ {\dot{U}}_{\mathrm{MB}}^{\prime }={\dot{U}}_{\mathrm{YB}[0]}^{\prime }+{\alpha }^2\left(1-k_{\mathrm{Y}1}\right)Z_{\mathrm{M}\alpha 1}{\dot{I}}_{\mathrm{F}1}+\alpha \left(1-k_{\mathrm{Y}2}\right)Z_{\mathrm{M}\alpha 2}{\dot{I}}_{\mathrm{F}2}+\left(1-k_{\mathrm{Y}1}\right)Z_{\mathrm{M}\alpha 0}{\dot{I}}_{\mathrm{F}0}\hfill \\ {\dot{U}}_{\mathrm{MC}}^{\prime }={\dot{U}}_{\mathrm{YC}[0]}^{\prime }+\alpha \left(1-k_{\mathrm{Y}1}\right)Z_{\mathrm{M}\alpha 1}{\dot{I}}_{\mathrm{F}1}+{\alpha }^2\left(1-k_{\mathrm{Y}2}\right)Z_{\mathrm{M}\alpha 2}{\dot{I}}_{\mathrm{F}2}+\left(1-k_{\mathrm{Y}1}\right)Z_{\mathrm{M}\alpha 0}{\dot{I}}_{\mathrm{F}0}\hfill \end{array}$$

(28)

Based on (28), the negative sequence and zero sequence compensated voltages on the M side can be calculated as

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{M}2}^{\prime }=\frac{1}{3}\left({\dot{U}}_{\mathrm{MA}}^{\prime }+{\alpha }^2{\dot{U}}_{\mathrm{MB}}^{\prime }+\alpha {\dot{U}}_{\mathrm{MC}}^{\prime }\right)=\left(1-k_{\mathrm{Y}2}\right)Z_{\mathrm{M}\alpha 2}{\dot{I}}_{\mathrm{F}2}\hfill \\ {\dot{U}}_{\mathrm{M}0}^{\prime }=\frac{1}{3}\left({\dot{U}}_{\mathrm{MA}}^{\prime }+{\dot{U}}_{\mathrm{MB}}^{\prime }+{\dot{U}}_{\mathrm{MC}}^{\prime }\right)=\left(1-k_{\mathrm{Y}0}\right)Z_{\mathrm{M}\alpha 0}{\dot{I}}_{\mathrm{F}0}\hfill \end{array}$$

(29)

Then, using $Z_{\mathrm{L}}-Z_{\mathrm{set}}$ as the protection setting value on the N side, after a similar derivation, the expressions of the negative sequence and zero sequence compensated voltages on the N side are

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{N}2}^{\prime }=-\left(1-k_{\mathrm{Y}2}\right)Z_{\mathrm{M}\alpha 2}{\dot{I}}_{\mathrm{F}2}\hfill \\ {\dot{U}}_{\mathrm{N}0}^{\prime }=-\left(1-k_{\mathrm{Y}0}\right)Z_{\mathrm{M}\alpha 0}{\dot{I}}_{\mathrm{F}0}\hfill \end{array}$$

(30)

From (29) and (30), the ratio of the negative sequence compensated voltage on the M side and the negative sequence compensated voltage on the N side can be calculated as:

$$\frac{{\dot{U}}_{\mathrm{M}2}^{\prime }}{{\dot{U}}_{\mathrm{N}2}^{\prime }}=\frac{\left(1-k_{\mathrm{Y}2}\right)Z_{\mathrm{M}\alpha 2}}{-\left(1-k_{\mathrm{Y}2}\right)Z_{\mathrm{M}\alpha 2}}=-1$$

(31)

And the ratio of the zero-sequence compensated voltage on the M side and the zero sequence compensated voltage on the N side can be calculated as:

$$\frac{{\dot{U}}_{\mathrm{M}0}^{\prime }}{{\dot{U}}_{\mathrm{N}0}^{\prime }}=\frac{\left(1-k_{\mathrm{Y}0}\right)Z_{\mathrm{M}\alpha 0}}{-\left(1-k_{\mathrm{Y}0}\right)Z_{\mathrm{M}\alpha 0}}=-1$$

(32)

From (31) and (32), the ratio of the negative sequence compensated voltage on the M side to the negative sequence compensated voltage on the N side, or the ratio of the zero-sequence compensated voltage on the M side to the zero-sequence compensated voltage on the N side, is equal to −1 and the amplitude is equal to 1 after a backward single-phase grounding fault occurs.

Also, the amplitude of the ratio of the negative sequence compensated voltage on the M side to the negative sequence compensated voltage on the N side under the backward two-phase short-circuit fault is equal to 1. The derivation process is similar and will not be repeated here.

3.2. The Protection Criterion and Flow Chart

Based on the above analysis, considering that there is only a negative sequence compensated voltage under the two-phase short-circuit fault situation, the ratio of the negative sequence compensated voltage on the M side and the N side can be used to distinguish the internal faults from the external faults by using the ratio result of the negative sequence compensated voltage on the M side and the N side. The corresponding criterion can be written as

$$K_2=\left|\frac{{\dot{U}}_{2\mathrm{M}}^{\prime }}{{\dot{U}}_{2\mathrm{N}}^{\prime }}\right|>K_{\mathrm{set}}$$

(33)

where $K_{\mathrm{set}}$ is the threshold of the criterion. Considering the value of $K_2$ analyzed above, $K_{\mathrm{set}}$ can be set to 1.05.

The flow chart of the protection is shown in Figure 5. As the flow chart shows, the corresponding negative sequence and zero sequence compensated voltages are calculated using the current and voltage measured on the local side after the protection is activated. Once the negative compensated voltage information from the opposite side is accepted, the negative sequence compensated voltage is compared with a threshold. If it is greater than the threshold value, the amplitude of ${\dot{U}}_{2\mathrm{M}}^{\prime }/{\dot{U}}_{2\mathrm{N}}^{\prime }$ is calculated and compared with the threshold $K_{\mathrm{set}}$. If the amplitude is greater than $K_{\mathrm{set}}$, then the protection operates, and if vice versa, the protection will not operate.

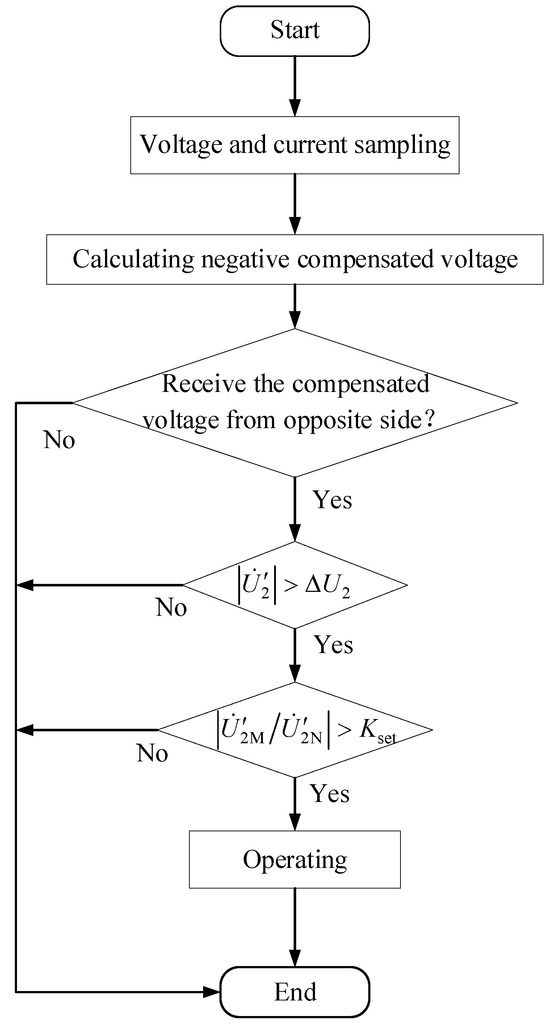
Figure 5. The flow chart of the protection.

4. Simulation Tests

In order to test the performance of the proposed method, a simulation system shown in Figure 6 was built in PSCAD/EMTDC.

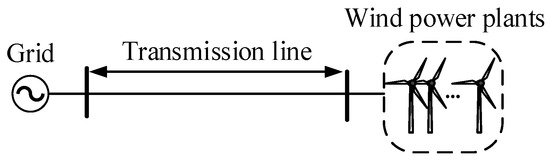
Figure 6. The structure of the simulation system.

In the Figure, the left side is the AC grid and the right side is the wind power plants. The length of the transmission line is 250 km, the detail parameters of the transmission line are shown in Table 1 [15].

Table 1. Parameters of the transmission line.

Parameter	R (Ω/km)	L (mH/km)	C (μF/km)
Positive sequence	0.0705	1.274	0.0086
Negative sequence	0.323	3.822	0.00605

4.1. Tests for Different Fault Types

Using the simulation system, different fault types are simulated to test the effectiveness of the proposed method. The protection action zone is set to 200 km, $K_{\mathrm{set}}$ is set to 1.05, and the test results are shown in Table 2. In the table, “AG”, “BC”, and “CAG” represent the phase A grounding fault, BC phase short-circuit fault, and CA phase short-circuit grounding fault, respectively. Fault distance refers to the distance from the fault point to the wind power plant side, and “Backward” represents the fault that occurs on the dorsal side of the measuring point. “I.F.” and “E.F.” represent the internal fault and external fault, respectively. From Table 2, the proposed protection method can distinguish between different types of internal fault and external fault reliably.

Table 2. Tests results of different fault types.

Fault Types	Fault Distance (km)	K2	Result
AG	20	6.97	I.F.
	50	5.31	I.F.
	80	4.02	I.F.
	125	2.55	I.F.
	170	1.50	I.F.
	190	1.21	I.F.
	210	0.82	E.F.
	225	0.51	E.F.
	240	0.28	E.F.
	Backward	0.98	E.F.
BC	20	7.08	I.F.
	50	3.43	I.F.
	80	4.13	I.F.
	125	2.66	I.F.
	170	1.56	I.F.
	190	1.17	I.F.
	210	0.79	E.F.
	225	0.59	E.F.
	240	0.30	E.F.
	Backward	0.94	E.F.
CAG	20	7.34	I.F.
	50	5.72	I.F.
	80	4.42	I.F.
	125	2.89	I.F.
	170	1.71	I.F.
	190	1.27	I.F.
	210	0.86	E.F.
	225	0.58	E.F.
	240	0.32	E.F.
	Backward	0.88	E.F.

4.2. The Influence of Transition Resistance

Considering the fact that the transition resistance between phases is mostly arc resistance, which is generally small, only the influence of the transition resistance on the proposed method in the case of grounding faults is discussed here. Table 3 shows the test results of the proposed method for grounding faults with different transition resistances. The fault distances of the phase A grounding fault and the CA phase short-circuit grounding fault are both set to 125 km.

Table 3. The test results considering different transition resistance values.

Fault Types	Transition Resistance	K2	Result
AG	5	2.58	I.F.
	25	2.63	I.F.
	50	2.65	I.F.
	75	2.65	I.F.
	100	2.68	I.F.
CAG	5	2.92	I.F.
	25	2.84	I.F.
	50	2.75	I.F.
	75	2.78	I.F.
	100	2.79	I.F.

Actually, from the expression of the negative sequence compensated voltage in Section 3, for the negative sequence compensated voltage, the transition resistance mainly affects the denominator. When the negative sequence compensated voltages on both sides are used to calculate K₂, the denominators cancel each other out, and the influence of transition resistance is theoretically eliminated. Therefore, the proposed method has a strong anti-resistance ability. And this is also confirmed by the test results shown in Table 3.

4.3. The Influence of Fault Time

For AC transmission lines, the fault characteristics are affected by fault time. Considering different fault times, various asymmetric fault scenarios are simulated to test the performance of the proposed method. The test results are shown in Table 4. From the results in Table 4, it can be seen that when faults occur at different times, the proposed method is not affected by the time of fault occurrence and can reliably distinguish between internal and external faults.

Table 4. The test results considering different fault times.

Fault Types	Fault Distance (km)	Fault Time (s)	K2	Result
AG	125	3.005	2.82	I.F.
		3.010	2.56	I.F.
		3.015	2.80	I.F.
	225	3.005	0.58	E.F.
		3.010	0.51	E.F.
		3.015	0.58	E.F.

5. Conclusions

Large-scale new energy power supply systems are connected to the power grid, and due to the response of the control of the new energy power supply itself to the fault, the characteristics of the change in each electrical quantity after the fault of the line appear new, and the performance of traditional AC line protection is affected. In this paper, a distance protection method for the transmission line connected to wind power plant is proposed. The proposed method is based on the negative sequence compensated voltage on both sides of the line and distinguishes internal and external faults by the amplitude of the ratio of the negative sequence compensated voltage at both ends of the line. Simulation results show that the proposed method is not affected by the time of fault occurrence and has strong anti-transition resistance ability. The proposed method can be used as a reliable backup protection.