A Multi-View Temporal Knowledge Graph Reasoning Framework with Interpretable Logic Rules and Feature Fusion

Abstract

A temporal knowledge graph represents temporal information between entities in a multi-relational graph. Its reasoning aims to infer and predict potential links among entities. Predicting time-aware entities is a challenging task due to significant differences in entity appearances over time, such as different timestamps and frequencies. Current embedding-based similarity-matching methods have been introduced for predicting temporal facts. However, they lack deterministic logical explainability and cannot model the dynamic evolution of entities over time. To address these challenges, we propose a novel framework for temporal knowledge graph reasoning based on multi-view feature fusion (MVFF). First, MVFF extracts logical rules and uses the Gumbel-Softmax trick to sample high-quality rules. Second, it integrates logical rules, temporal quadruples, and factual triples to capture semantic features, temporal information, and structural information to solve link prediction tasks. Through experiments on four benchmark datasets, we show that MVFF outperforms state-of-the-art methods, providing not only better performance but also interpretable results.

1. Introduction

Knowledge graphs (KGs) contain facts/triples that indicate relationships between entities, such as (South Korea, Accuse, and North Korea). However, in the real world, many entities and relations are time-dependent. To capture the evolution of information over time, temporal knowledge graphs (TKGs) have been developed. In TKGs, triples (s, p, o) are expanded into quadruples (s, p, o, t), where the time t denotes the validity of the fact. For example, (South Korea, Accuse, North Korea, 17 October 2014) indicates that South Korea accused North Korea on 17 October 2014.

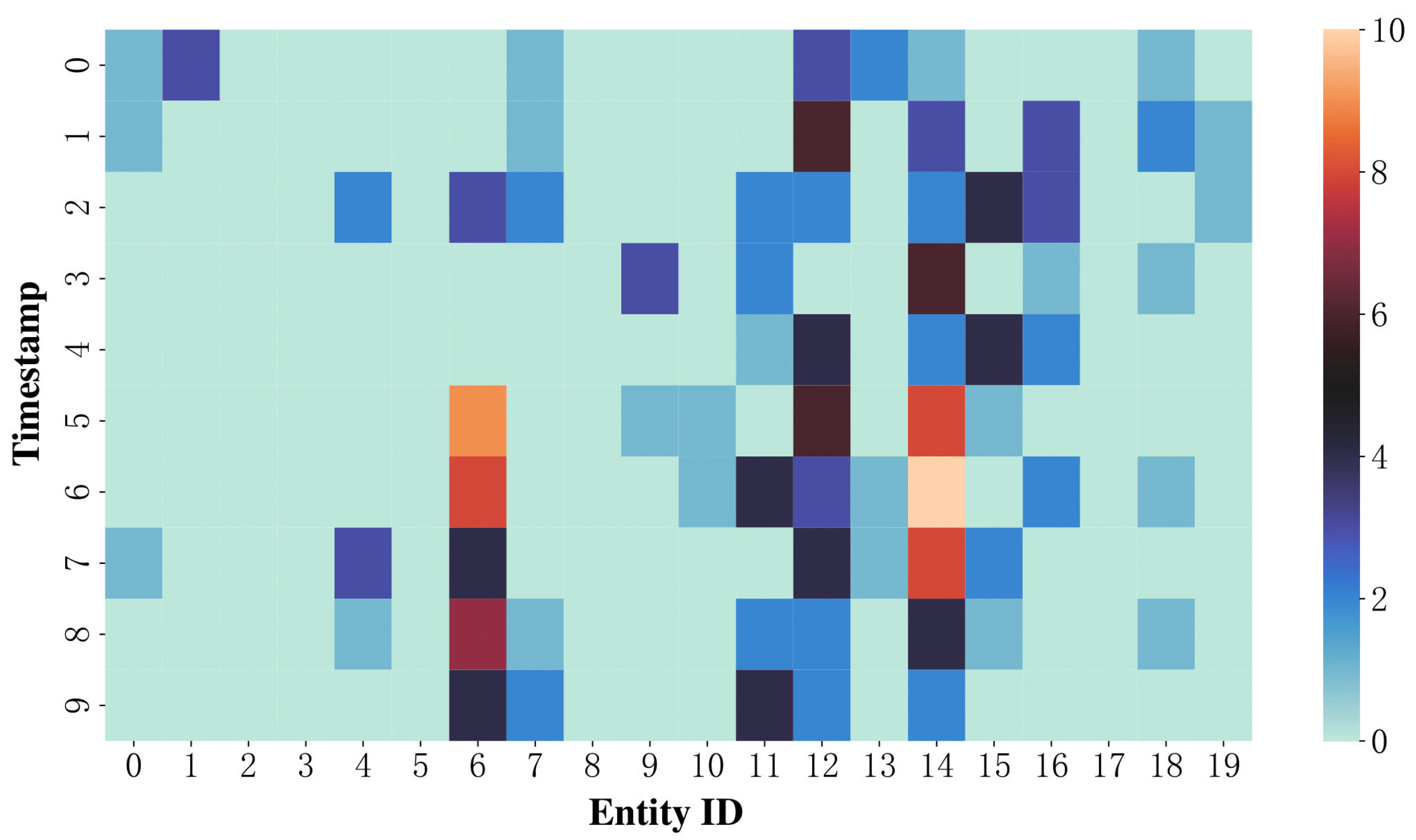
While the TKGs provide a comprehensive description of the dynamics of real-world relationships, specific complexities are introduced when dealing with such structures. Temporal knowledge graph reasoning is realized through a link prediction task that focuses on identifying candidates that are most likely to complete a timestamped query of the form (s, p, ?, t), where s represents the head entity, p represents the relationship, and t represents the timestamp. Traditional learning techniques for static KGs are unable to capture the dynamic interactions between entities. To address this issue, various temporal knowledge graph embedding (KGE) models are proposed to encode entities and relations in a low-dimensional space using translation-based functions [1,2], a deep neural network-based method [3,4], and a tensor decomposition method [5,6]. As these methodologies have progressed, numerous strategies for TKG completion have been proposed, including geometric methods (ChronoR [7], BoxTE [8], TLT-KGE [9], RotateQVS [10], HTTR [11], PTKE [12]); tensor decomposition methods (QDN [13], TBDRI [14]); deep learning and embedding-based methods (TASTER [15], TeAST [16], RoAN [17], BiQCap [18]); and graph neural network-based reasoning methods (TARGCN [19], T-GAP [20], TAL-TKGC [21]). Interpolation is a statistical method that utilizes the relevant known values to estimate an unknown value or set [19]. The goal of extrapolation is to infer “future” unknown values from the current information [22]. These models employ time-dependent embedding of entities and relations to enhance the KG reasoning process. While effective, these methods lack interpretability. As shown in Figure 1, the color shades in the heatmap indicate how often the entity appears at different timestamps. Temporal information can be regarded as perturbations to the representations of entities or relations. As a result, it can be challenging for current models to accurately represent their temporal dynamics over time.

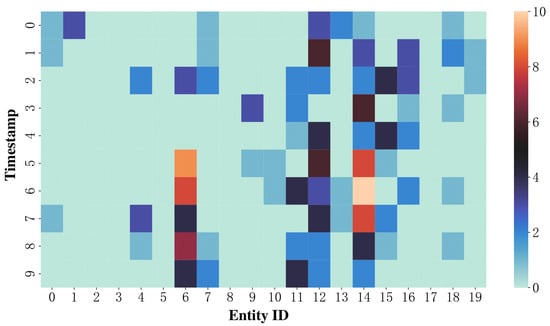
Figure 1. Differences in periods and frequencies of entity appearances over time on ICEWS14.

To overcome this issue, logic rule-based symbolic techniques have been proposed as a substitute for embedding-based models. One advantage of these methods is that they produce transparent and comprehensible inference results. However, the subtleties of event complexities can make the manual rule formulation process challenging, which might impede the acquisition of knowledge. Recent works, such as TLogic [23] and LCGE [24], propose methods for temporal KG reasoning and automatically extract knowledge rules. However, there are still several challenges that need to be addressed. First, these techniques used to determine confidence in individual rules sometimes ignore the interaction between several rules, resulting in an oversight of certain rules. Second, temporal rule selection with high-confidence metrics may include inconsistencies and irrelevant facts.

To overcome the limitations of both embedding-based and rule-based methods, we propose the MVFF framework that integrates temporal logical rules, tensor decomposition, time-encoding module, and GNN-based method. MVFF employs closed-loop restrictions and the temporal random walk algorithm [25] to produce a set of candidate rules based on sample entity sequences. The rules obtained after Gumbel sampling are combined with tensor decomposition embedding, time-encoding, and relationship-aware graph neural networks [26] for both scalability and interpretability.

The main contributions of our work include:

• The proposed rule sampling method is differentiable, which aids in network backpropagation and weight updates. Additionally, it allows for the exploration of rule diversity or the utilization of rules with high confidence through temperature parameters.
• To capture semantic, structural, and temporal information about temporal knowledge graphs, MVFF combines temporal coding techniques, relation-aware graph neural networks, and tensor decomposition.
• Experimental results on four benchmark temporal knowledge graph datasets show that our model significantly outperforms many state-of-the-art baseline methods. Our framework improves 2.98%/4.96%/23.97%/6.78% on the MRR evaluation metrics, and 5.03%/3.29%/26.0%/7.82% on the Hit@1 evaluation metrics for datasets ICEWS14/ICEWS05-15/Wikidata12k/GDELT, respectively.

The rest of this paper is organized as follows. Section 2 briefly reviews the related work of temporal knowledge graph reasoning. In Section 3, we introduce the proposed method (MVFF), including the temporal logical rule learning module, temporal logical rule learning module, and multi-view feature fusion module. Afterward, we discuss experiments of temporal knowledge graph reasoning in Section 4. Section 5 delineates the limitations of our method. Section 6 concludes this paper and discusses the future research directions.

2. Related Work

2.1. Embedding-Based Methods

Embedding-based methods mainly include translation-based models, tensor factorization-based models, and neural network-based models. The translation-based models originate from the TransE [27] series of methods, which are extended in TKG by embedding timestamps as a vector. Leblay et al. [1] proposed the TTransE model. Jiang et al. [28] capture the temporal relationship between relationships using the temporal evolution matrix. García-Durán et al. [29] learn the time-aware representation of relationship types. The above methods consider entities and relationships in the same semantic space. However, in different timestamps, entities and relationships may correspond to different tail entities. To solve this problem, Dasgupta et al. [2] borrow the idea of TransH [30] and represent time as a hyperplane. Xu et al. [31] propose the TeRo model to solve the limitations. Yuan et al. [32] proposed the TRHyTE model, which represents temporal relations through a series of hyperplane combinations. The tensor decomposition-based model views TKG as a fourth-order tensor and represents entities, relations, and timestamps as low-dimensional matrices through tensor decomposition. Lacroix et al. [6] decomposed the tensor into a complex space. Goel et al. [4] proposed a time-entity embedding method based on temporal embeddings of entities. Shao et al. [33] used the Tucker decomposition to represent entities, relations, and timestamps by viewing TKG as a fourth-order tensor. A model for the polar temporal knowledge graph reasoning method (PTKE) is proposed by [12]. It is a member of the translation-based model family and integrates time-aware facts into a polar coordinate system. TASTER is a new and efficient TKG reasoning technique that offers a framework for leveraging both global and local information [15]. A relation-oriented attention network (RoAN) is constructed to model temporal embeddings of relations in accordance with the attention mechanism [17]. In order to fully capture the semantics, Wang et al. [13] propose a novel TKG reasoning method called the quadruplet distributor network (QDN), which builds the QDN to facilitate the information aggregation and distribution among items. In the first section on multi-view feature fusion, we employ a fourth-order tensor decomposition method that can effectively encode the basic information of quadruples in a temporal knowledge graph.

2.2. Graph Neural Network-Based Reasoning Methods

Graph reasoning techniques, which represent the correlations in graph structures to accomplish the task of reasoning about temporal knowledge graphs, have been consistently proposed as temporal knowledge graphs and include rich information about graph structures. Wu et al. [3] divided the entity representation into structural and temporal representations. Jin et al. [34] proposed a recursive event network (RE-NET), which uses a neighborhood aggregator to model facts. He et al. [35] proposed a historical information propagation model (HIP). Li et al. [36] proposed a time-directed recurrent graph network (TiRGN) with local–global historical patterns. Jung et al. [20] proposed a new graph neural network encoder that can effectively capture query-related information from TKGs. Nie et al. [21] presented TAL-TKGC, a temporal attention learning-based TKG reasoning approach that consists of an importance-weighted GCN and a temporal attention module. Zhu et al. [37] proposed employing the WinGNN framework to model dynamic graphs. It is based on a straightforward GNN model that incorporates a novel random gradient aggregation mechanism and a meta-learning technique. In the second part of multi-view feature fusion, we utilize a relation-aware graph neural network to encode the structural information of static knowledge graphs, effectively mining the structural associations between entities.

2.3. Temporal Rule-Based Methods

Currently, the use of temporal logic rules in TKGs is relatively underexplored due to three reasons. Firstly, there is a lack of fast and accurate rule extraction methods that do not require manual correction in TKGs. Secondly, logic rule-based methods mostly have a large search space. Additionally, when rules cannot cover all relationships, rule-based systems may not provide answers. A temporal graph encoder and a logical decoder are the two fundamental components of the explainable extrapolation reasoning framework called Temporal LogiCal Graph Networks (TECHS), which was proposed by Lin et al. [38]. Bai et al. [39] proposed a temporal logic-based reasoning model to generate a set of candidate rules and select the optimal rule through pruning strategies. Liu et al. [23] used a random walk method to extract rules. However, this method only considers rules where atomic propositions increase over time and does not consider rules with other time patterns. In the methods section, we propose a method for the extraction and learning of temporal logic rules.

Unlike embedding-based and graph neural network-based methods, our MVFF framework integrates multiple feature representations, offering a more nuanced understanding of temporal dynamics in TKGs. While embedding-based methods focus on static representations and graph neural networks emphasize structural relationships, MVFF captures both static and dynamic features, providing a holistic view of temporal entities and relations. Additionally, while embedding methods and graph neural network approaches lack the ability to explain their reasoning results, our differentiable rule selection method offers interpretability of the reasoning process.

3. Approach

3.1. Overview of MVFF

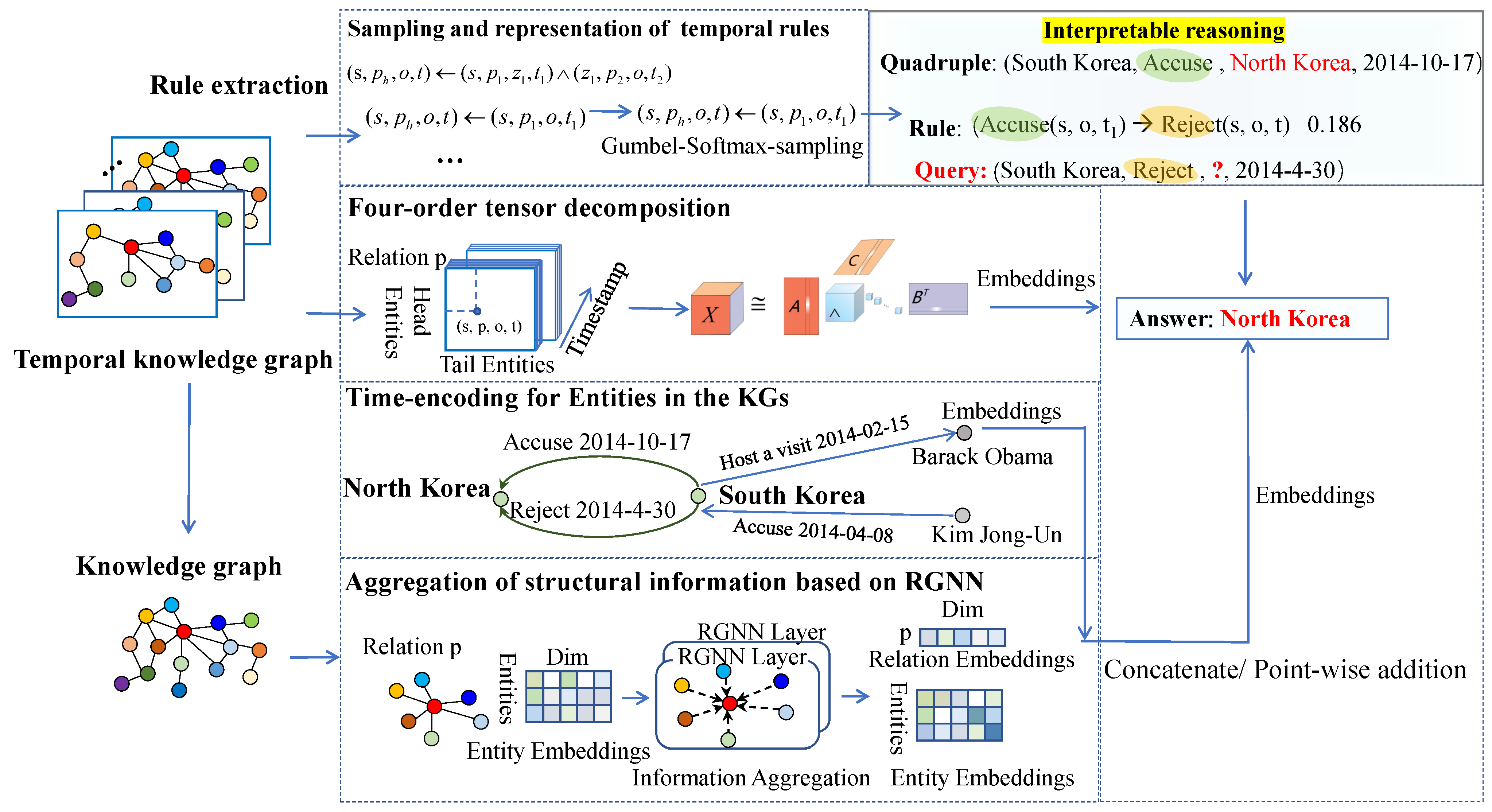
MVFF can be divided into four modules: (1) the temporal rule module, which conducts explainable reasoning; (2) the four-order tensor decomposition module, which captures both temporal evolution and semantic dependence simultaneously; (3) the RGNN module, which effectively captures structural information; and (4) the time-encoding module, which represents the temporarily valid entities. Figure 2 illustrates an example of interpretable reasoning for temporal rules at the top, and the multi-view feature encoding process is depicted in the subsequent three rectangles.

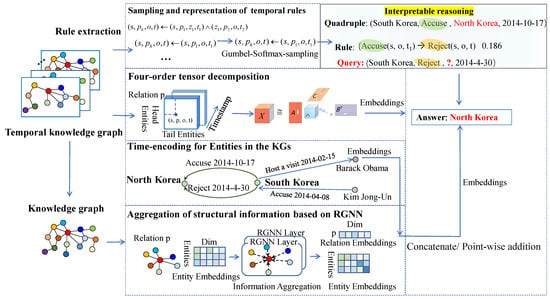
Figure 2. Framework of MVFF. Rule-based reasoning is illustrated by explainable reasoning.

3.2. Temporal Logical Rule Learning

3.2.1. Temporal Logical Rules

Given the symbolic nature of knowledge graphs (KGs), logic rules are ideally suited for tasks involving temporal knowledge graph link prediction. In rule-based TKG reasoning, temporal logic rules are generally expressed using Horn clauses. They consist of a head and a body, where the head is a single atomic proposition and the body is a conjunction of several atomic propositions. Horn clauses can be represented as Equation (1).

$$u\leftarrow p\wedge q\wedge \cdots \wedge v,$$

(1)

where u denotes the head of the rule, and $p\wedge q\wedge \cdots \wedge v$ refers to the body of the rule. The validity of facts is time-sensitive. Thus, Horn clauses can be used for temporal relationships between facts, as shown in Equation (2).

$$\left(s,p_h,o,t\right)\leftarrow \left(s,p_1,z_1,t_1\right)\wedge \cdots \wedge \left(z_n,r_n,o,t_n\right),$$

(2)

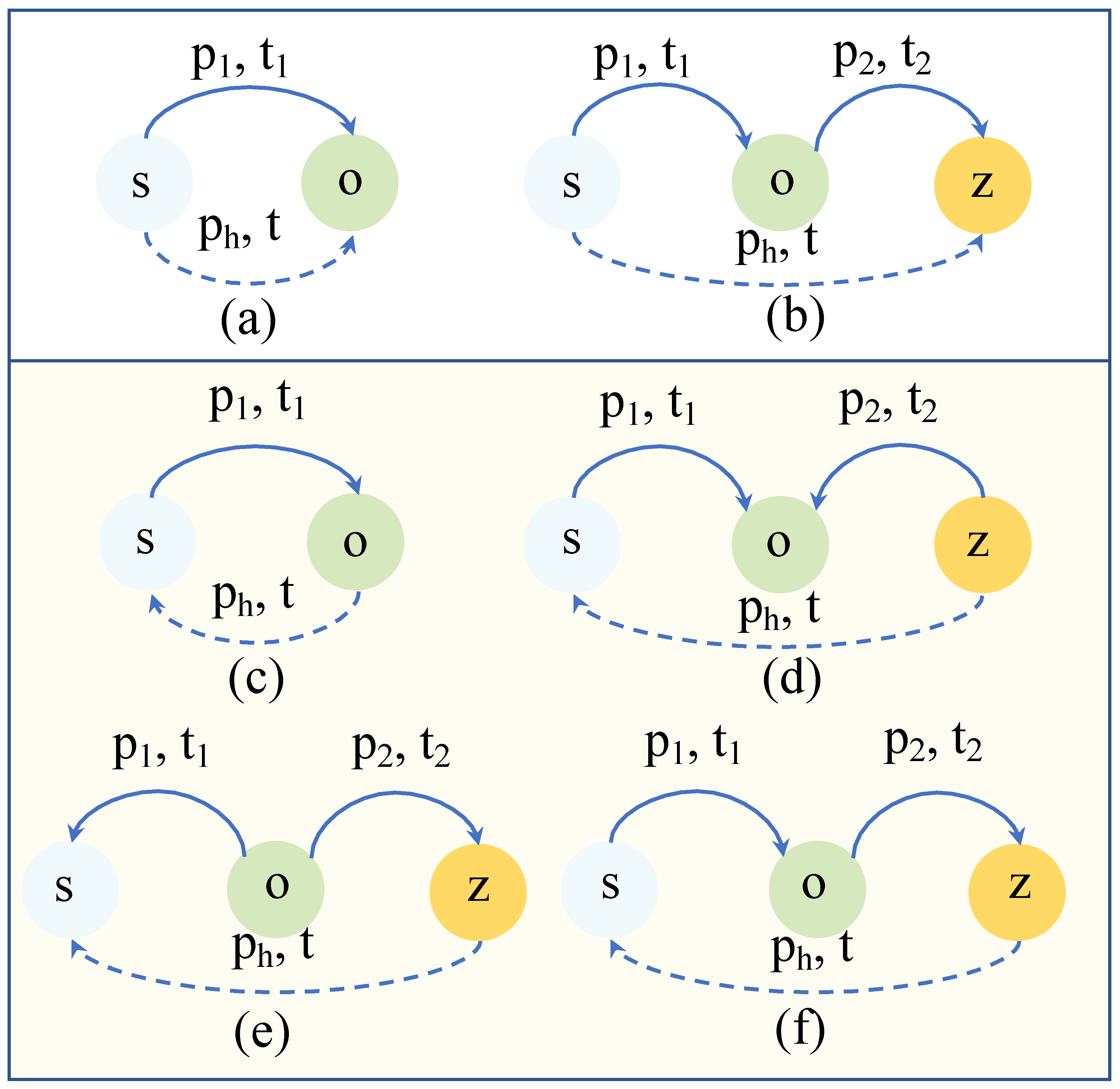
where $p_i(i=1,\dots ,h)$ denotes the relationships between head and tail entities; s, o, and $z_j(j=1,\dots ,n)$ refer to different entities; and $t_k(k=1,\dots ,m)$ means timestamp. To enable horn clauses to represent temporal relationships between quadruple propositions, the temporal information needs to satisfy the constraint $t_1\le t_2\le \cdots t_n⩽t$. Based on the length of the temporal logic rule’s body and the temporal relationships, the rules can be divided into different forms. Table 1 shows all temporal logic rules with lengths of 1 and 2.

Table 1. Representation of different temporal rule patterns.

Rule Patterns	Temporal Rules	Temporal Constraint	Temporal Rule Representation
Pattern 1	$(s,p_h,o,t)$←$(s,p_1,o,t_1)$	$t_1=t$	$\parallel p_{r_1}-p_{r_h}\parallel$
Pattern 2	$(s,p_h,o,t)$←$(s,p_1,o,t_1)$	$t_1$ < t	$\parallel (W_t\circ p_{r_1})-p_{r_h}\parallel$
Pattern 3	$(s,p_h,o,t)$←$(s,p_1,o,t_1)$∧$(z_1,p_2,o,t_2)$	$t_1$ < $t_2$ < t	$\parallel (W_t\circ W_t\circ p_{r_1})+(W_t\circ p_{r_2})-p_{r_h}\parallel$
Pattern 4	$(s,p_h,o,t)$←$(s,p_1,z_1,t_1)$∧$(z_1,p_2,o,t_2)$	$t_1=t_2$ < t	$\parallel (W_t\circ p_{r_1})+(W_t\circ p_{r_2})-p_{r_h}\parallel$
Pattern 5	$(s,p_h,o,t)$←$(s,p_1,z_1,t_1)$∧$(z_1,p_2,o,t_2)$	$t_1$ < $t_2=t$	$\parallel \left(W_t\circ p_{r_1}\right)+p_{r_2}-p_{r_h}\parallel$
Pattern 6	$(s,p_h,o,t)$←$(s,p_1,z_1,t_1)$∧$(z_1,p_2,o,t_2)$	$t_1=t_2=t$	$\parallel p_{r_1}+p_{r_2}-p_{r_h}\parallel$

Figure 3a,b show the general pattern of rules with a length of 1 and 2, respectively, which can be inferred through chain propagation. Figure 3c–f show other patterns of links. To mine temporal logic rules using such links, we add inverse relations to mine potential temporal logic patterns.

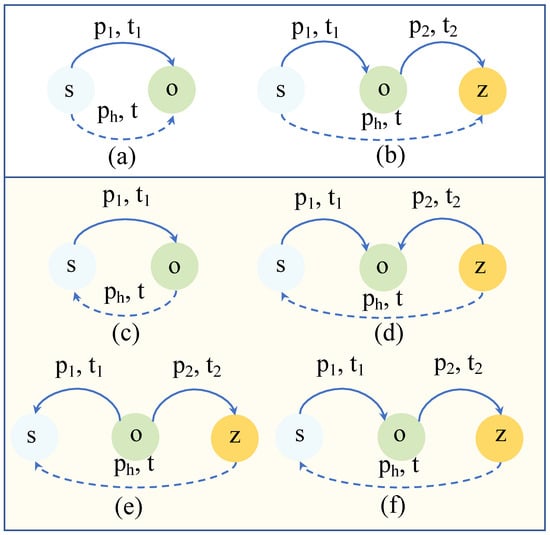
Figure 3. Different patterns of linking between entities. (a,b) show the general pattern of rules with a length of 1 and 2. (c–f) are four compositions of temporal logic rules.

We utilize the temporal random walk to extract temporal sequences from TKGs. By adding constraints from cycles during the random walk, circular sequences like those in Figure 3c,d can be obtained by the following Equations (3) and (4). In our environment conditions, the number of tuples impacted by the temporal order is typically rather significant. Stated differently, it is challenging for a single formulation of the temporal logical rule to address them to the greatest extent feasible. We define three compositions of different patterns of linking between entities. When o and s are linked by relation $p_1$ at timestamp $t_1$, and o and z are linked by relation $p_2$ at $t_2$, we can infer that z and s will be linked by relation $p_h$ at timestamp $t_1$, as shown in Figure 3d. The differences between the three subgraphs, namely Figure 3d–f, lie in the orientation of the arrows. When ‘s’, ‘o’, and ‘z’ are in different directions, they serve as distinct starting and ending entities for the links, resulting in different temporal logical rules being generated.

$$\left(\left(s,p_1,o,t_1\right),\left(o,p_h,s,t\right)\right)t_1\le t,$$

(3)

$$\left(\left(s,p_1,o,t_1\right),\left(o,p_2,z,t_2\right),\left(z,p_h,s,t\right)\right)t_1\le t_2\le t,$$

(4)

To extract temporal logic rules from circular sequences of entities, we introduce inverse relationships between connected entities, which are expressed in Equations (5) and (6).

$$\left(s,p_h^{-1},o,t\right)\leftarrow \left(s,p_1,o,t_1\right)t_1\le t,$$

(5)

$$\left(s,p_h^{-1},z,t\right)\leftarrow \left(s,p_1,o,t_1\right)\wedge \left(o,p_2,z,t_2\right)t_1\le t_2\le t,$$

(6)

For a rule head relationship, multiple rules may be generated during temporal random walks, which may overlap or conflict with each other. Therefore, it is necessary to determine the confidence of a rule to evaluate the likelihood of its correctness. Using Equation (6) as an example, s, o, and z in the equation represent entity variables, which are replaced with actual entities. The number of specific sequences that satisfy the rule body in the TKGs is referred to as body support, and the number of sequences that satisfy the rule grounding is referred to as rule support. Rule confidence is defined as the ratio of rule support to body support.

3.2.2. Representation of Temporal Logic Rules

To embed temporal logical rules, we represent the relationships as atomic propositions and adopt a linear layer as a time transition operator (W), which maps the relationships in the rule body to the same time as the rule head relationship for correlation calculation via the Hadamard product, as shown in Table 1. We obtain different patterns of rules by setting different time constraints of temporal random walks and then translate the relationships of different times involved in the rules into the same vector space for representation learning, using an approach similar to TransR [40].

By performing temporal random walks, a large number of temporal logical rules can be obtained. Existing methods for applying rules to specific queries directly select the rule with the maximum confidence [23] or use all the rules [24]. The method of selecting the rule with the maximum confidence does not take into account the diversity of the rules. Using all the rules may lead to conflicting rules and cause a significant increase in computational complexity. In this paper, we employ the Gumbel-softmax [41] to sample temporal rules, which address the issues of resource scarcity and slow reasoning that arise from using all rules, as well as the problem of always selecting the rule with the maximum confidence using Argmax. Furthermore, this method retains gradient information during the sampling process and can be optimized using backpropagation.

Suppose there are k rules under the relation $p_h$ in a certain pattern, we sample k random numbers ${\epsilon }_1,\cdots ,{\epsilon }_k$ from a uniform distribution and use the Gumbel distribution to transform these random numbers. The resulting values are added to the original probability of each rule. The Gumbel distribution is expressed as follows:

$$\begin{array}{cc}\hfill & g_i\sim Gumbel(0,1)=-log(-log{u}_i),\hfill \\ \hfill & u_i\sim Uniform(0,1),\hfill \end{array}$$

(7)

By using the Gumbel-Softmax method, we transfer the randomness of rule sampling to the sampling of the uniform distribution, which has no unknown parameters. This completes the reparameterization process of discrete rules. To maintain differentiability, we apply the softmax function to smooth the approximate result of Argmax. The final rule is obtained as follows:

$$rule=softmax{\left(\frac{g_i+log{a}_i}{\tau }\right)}_{i-1}^k={\left(\frac{exp\left(\frac{g_i+log{a}_i}{\tau }\right)}{{\sum }_{j=1}^{k}exp\left(\frac{g_i+log{a}_i}{\tau }\right)}\right)}_{i-1}^k,$$

(8)

where $a_i$ is the probability corresponding to the rule; $g_i$ is the Gumbel noise added to the rule; $\tau$ is the temperature coefficient, and the smaller its value, the closer the result is to Argmax; k represents the number of temporal logical rules under the patterns with the head relation $p_h$.

3.3. Multi-View Feature Fusion

3.3.1. Tensor Decomposition

In this paper, we utilize a four-order tensor decomposition method (e.g., [6]) that incorporates temporal information to represent entities and relations. Specifically, some relations in the TKG are influenced by timestamps, while others are not. Therefore, we represent the relationship in the four-tuple as a time-constrained representation and a time-independent representation. The tensor decomposition is defined as follows:

$$\widehat{X}=Re\left((S,P^t,\overline{O},T)+(S,P,\overline{O},1)\right)\iff {\widehat{X}}_{i,j,k,l}=Re\left(⟨s_i,p_j^t\circ t_l+p_j,\overline{o_k}⟩\right),$$

(9)

where Re denotes the real part of the complex numbers; S denotes the tensor matrix of the head entity; $P^t$ denotes the time-dependent relational tensor matrix; $\overline{O}$ denotes the conjugate of the tensor matrix of the tail entity; T denotes the tensor matrix of time; P denotes the time-independent relational tensor matrix; and $i,j,k,l$ denote the tensor indexes in the corresponding matrices, respectively. The time-independent relation $p_i$ is embedded using the embedding obtained by learning the temporal logic rules.

In TKGs, some facts will never occur because there is no possible connection between certain types of entities, as shown in Figure 1. At the same time, the method based on tensor decomposition can obtain representations of entities, relationships, and time but does not sufficiently model the structural information in TKGs. Based on these considerations, this paper converts TKG into a static graph by removing the time and then uses RGNN to encode the static knowledge graph.

3.3.2. RGNN Module and Time-Encoding Module

The RGNN model (e.g., [26]) is trained on a static knowledge graph to obtain the static constraints between entities and relations. In a relational multi-graph propagation model, the entity s embedding is updated as follows:

$$h_s^{(l+1)}=\sigma \left(\sum _{p\in \mathcal{P}}\sum _{j\in {\mathcal{N}}_s^p}\frac{1}{c_{s,p}}{W}_p^{\left(l\right)}{h}_j^{\left(l\right)}+W_0^{\left(l\right)}{h}_s^{\left(l\right)}\right),$$

(10)

where a set of neighbor entities with a p-relationship to entity s is represented by the symbol $N_s^p$. $c_{s,p}$ is a regularization constant, the value of $c_{s,p}$ is $\left|N_i^r\right|$, $W_p^{\left(l\right)}$ is a linear transformation function.

To enable “knowledge” and entities to keep pace with time and update automatically, the time coding module (TE) encodes the temporal information through a neural network and concatenates it with the entity features encoded by the relation-aware graph neural network to complete the coding of the temporal information, as shown in Figure 2.

3.3.3. Learning

For a given quadruple, the rationality of the quadruple is evaluated using the scoring function in Equation (11). Similarly, the triple is scored using the function in Equation (12).

$$f_1(s,p,o,t)=Re\left(\sum _{i=1}^d{\left[s\right]}_i·{\left[p\circ t+p_r\right]}_i·{\left[\overline{o}\right]}_i\right),$$

(11)

where $Re(·)$ represents the real part of a complex number; ${\left[s\right]}_i$ represents the ith dimension of the complex vector of the head entity; $p\circ t$ represents the relationship representation related to timestamp t; $p_r$ represents the relationship representation; $\overline{o}$ represents the conjugate of the vector of the tail entity.

$$f_2(s,p,o)=\sum _{i=1}^k{\left[s\right]}_i·{\left[p\right]}_i·{\left[o\right]}_i,$$

(12)

During model optimization, the cross-entropy function is used to calculate the loss of positive and negative samples of quadruples and triples. N3 regularization is used for the embedding representation of entities and relationships based on tensor decomposition. The following displays the objective functions.

$$L_1=-log\left(\frac{exp\left(f_1(s,p,o,t)\right)}{{\sum }_{s^{\prime }\in \epsilon }exp\left(f_1\left(s^{\prime },p,o,t\right)\right)}\right)-log\left(\frac{exp\left(f_1(s,p,o,t)\right)}{{\sum }_{o^{\prime }\in \epsilon }exp\left(f_1\left(s,p,o^{\prime },t\right)\right)}\right),$$

(13)

$$L_2=-log\left(\frac{exp\left(f_2(s,p,o)\right)}{{\sum }_{s^{\prime }\in \epsilon }exp\left(f_2\left(s^{\prime },p,o\right)\right)}\right)-log\left(\frac{exp\left(f_2(s,p,o)\right)}{{\sum }_{o^{\prime }\in \epsilon }exp\left(f_2\left(s,p,o^{\prime }\right)\right)}\right),$$

(14)

$$\left.\left.L=\sum _{(s,p,o,t)\in \tau }\left[\left(L_1+\alpha ·\left({\parallel s\parallel }_3^3+{∥p_t∥}_3^3+{∥p_r∥}_3^3+{\parallel o\parallel }_3^3\right)\right)+\lambda ·L_2\right)\right)\right],$$

(15)

where $\alpha$ represents the weight of the regularization term, and $\lambda$ controls the proportion of static embeddings.

4. Experiments

4.1. Datasets

In this paper, we utilized four datasets to validate the effectiveness of the proposed model, including ICEWS14 [10], ICEWS0515 [10], Wikidata12k [2], and GDELT [10]. Dataset statistics are shown in Table 2. The following explains the selection of the above datasets in this paper: First, training distinct time sets can satisfy the variable time intervals in these datasets. Second, the temporal representation of Wikidata12k is similar to that of ICEWS. Third, to give a more precise comparison of the experimental results, we chose the same dataset as the benchmark model.

Table 2. The datasets used in experiments.

Dataset	Entities	Relations	Time Span	Granularity	Train	Valid	Test
ICEWS14	7128	230	1 year	Daily	72,826	8941	8963
ICEWS05-15	10,488	251	11 year	Daily	368,962	46,275	46,092
Wikidata12k	12,554	24	539 year	Year	32,497	4062	4062
GDELT	500	20	1 year	Daily	2,735,685	341,961	341,961

4.2. Experimental Setup

RGNN was first trained on static knowledge graphs without temporal information. The embedding dimensions of entities and relations ranged from 100, 150, 200, 250, and the learning rate was optimized within 0.01, 0.05, 0.1, 0.2. The batch size of each training data set was set to 30,000. The rule confidence threshold range used was 0.1, 0.2, 0.3, 0.4, 0.5. The range of embedding dimensions of entities and relations in the tensor decomposition is 500, 1000, 1500, 2000, 2500. The learning rate was set within 0.01, 0.05, 0.1, 0.5, and the weight range of N3 regularization was set to 0.01. The ratio of static knowledge features in the loss calculation was set to 2.5, and the batch size was set to 1000. The maximum number of iterations for the model was set to 500. During model training, early stopping was used.

4.3. Baseline Models

We compare MVFF with static knowledge graph methods and temporal knowledge graph methods. Static knowledge graph methods include TransE [27], DisMult [42], ComplEx [5], SimplE [43]. TKG methods are divided into geometric methods (TTransE [1], HyTE [2], TeRo [31], ChronoR [7], BoxTE [8], TLT-KGE [9], RotateQVS [10], HTTR [11], PTKE [12], TGeomE [44]); tensor decomposition methods (TNTComplEx [6], TuckERTNT [33], QDN [13], TBDRI [14]); deep learning and embedding-based methods (TeMP-SA [3], DE-Simple [4], TeLM [45], TASTER [15], TeAST [16], RoAN [17], BiQCap [18]); and graph neural network based-reasoning methods (TARGCN [19], T-GAP [20], TAL-TKGC [21]).

4.4. Measures

We evaluate MVFF using mean reciprocal rank (MRR) and Hits@{1, 3, 10}(H@1, 3, 10).

$$MRR=\frac{1}{N}·\sum _i^N\frac{1}{{rank}_i},$$

(16)

where N is the total amount of test data.

$$Hits@n=\frac{1}{N}·\sum _i^{N}f\left({rank}_i\le n\right),$$

(17)

If $ran{k}_i<n$ is true, the value of function f is 1. Typically, n is usually set as 1, 3, or 10. Keep in mind that better performance is indicated by higher MRR and Hits@n.

4.5. Overall Results

In this section, we compare the MVFF model with other TKG reasoning models, including traditional static knowledge graph-based reasoning models, embedding-based TKG reasoning models, and GNN-based TKG reasoning models. The comparison results on the ICEWS2014 and ICEWS05-15 datasets are shown in Table 3, and the comparison results on the Wikidata12k and GDELT datasets are shown in Table 4.

Table 3. Temporal knowledge graph link prediction results on datasets ICEWS14 and ICEWS05-15. The highest score is in the bold, and the second highest score is underlined.

Models	ICEWS14				ICEWS05-15
	MRR	H@1	H@3	H@10	MRR	H@1	H@3	H@10
		The static KG methods
TransE 1	0.280	0.094	-	0.637	0.294	0.090	-	0.663
DisMult 1	0.439	0.323	-	0.672	0.456	0.337	-	0.691
ComplEx 2	0.470	0.350	0.540	0.710	0.490	0.370	0.550	0.730
SimplE 2	0.458	0.341	0.516	0.687	0.478	0.359	0.539	0.708
		The temporal KG methods
Geometric methods
TTransE 1	0.255	0.074	-	0.601	0.271	0.084	-	0.616
HyTE 1	0.297	0.108	0.416	0.655	0.316	0.116	0.445	0.681
TeRo	0.562	0.468	0.621	0.732	0.586	0.469	0.668	0.795
ChronoR	0.625	0.547	0.669	0.773	0.675	0.596	0.723	0.820
BoxTE	0.613	0.528	0.664	0.763	0.667	0.582	0.719	0.820
TLT-KGE	0.634	0.551	0.684	0.786	0.690	0.609	0.741	0.835
RotateQVS	0.591	0.507	0.642	0.754	0.633	0.529	0.709	0.813
PTKE	0.554	0.444	0.624	0.760	0.572	0.454	0.649	0.789
TGeomE	0.629	0.546	0.680	0.780	0.686	0.605	0.736	0.833
HTTR	0.616	0.544	0.666	0.770	0.663	0.581	0.717	0.815
Tensor decomposition methods
TNTComplEx	0.560	0.520	0.660	0.760	0.670	0.590	0.710	0.810
TuckERTNT	0.625	0.544	0.673	0.733	0.675	0.593	0.725	0.819
QDN	0.643	0.567	0.688	0.784	0.692	0.611	0.743	0.838
TBDRI	0.652	0.552	0.697	0.785	0.709	0.646	0.757	0.821
Deep learning and embedding-based methods
TA-DisMult 1	0.477	0.363	-	0.686	0.474	0.346	-	0.728
DE-SimplE 1	0.526	0.418	0.592	0.725	0.513	0.392	0.578	0.748
TeLM	0.625	0.545	0.673	0.774	0.678	0.599	0.728	0.823
TASTER	0.611	0.527	-	0.767	0.654	0.562	-	0.818
TeAST	0.637	0.560	0.682	0.782	0.683	0.604	0.732	0.829
RoAN	0.588	0.476	0.661	0.788	0.599	0.479	0.679	0.823
BiQCap	0.643	0.563	0.687	0.798	0.691	0.621	0.738	0.837
Graph neural network-based reasoning methods
TARGCN	0.636	0.576	0.672	0.746	0.702	0.635	0.743	0.823
T-GAP	0.610	0.509	0.677	0.790	0.670	0.568	0.743	0.845
TAL-TKGC	0.312	0.215	0.490	0.690	0.354	0.226	0.493	0.692
MVFF (ours)	0.672	0.597	0.731	0.840	0.746	0.668	0.789	0.873

¹ The Results from RotateQVS [10]. ² The Results from ChronoR [7]. The other results are from the published paper.

Table 4. Temporal knowledge graph link prediction results on datasets Wikidata12k and GDELT.

Models	Wikidata12k				GDELT
	MRR	H@1	H@3	H@10	MRR	H@1	H@3	H@10
TeRo	0.299	0.198	0.329	0.507	0.245	0.154		0.420
TeLM	0.333	0.231	0.360	0.542	-	-	-	-
RotateQVS	-	-	-	-	0.270	0.175	0.293	0.458
TLT-KGE	-	-	-	-	0.248	0.165	0.268	0.407
PTKE	0.280	0.179	0.300	0.482	-	-	-	-
TeAST	-	-	-	-	0.371	0.283	0.401	0.544
RoAN	-	-	-	-	0.290	0.187	0.315	0.496
TGeomE	0.333	0.232	0.362	0.546	-	-	-	-
BiQCap	0.312	0.216	0.343	0.517	0.273	0.183	0.308	0.469
MVFF (ours)	0.438	0.317	0.506	0.685	0.398	0.307	0.456	0.573

The highest score is in the bold, and the second highest score is underlined.

As shown in the tables, the MVFF model achieved the best experimental results in all evaluation metrics. We notice that, across all datasets, the MVFF model consistently and significantly outperforms all baselines. Our technique achieves significant performance increases, particularly when compared to the baselines that perform the best overall. Compared to the state-of-the-art approach, our framework improves 2.98%/4.96%/ 23.97%/6.78% on the MRR evaluation metrics and 5.03%/3.29%/26.0%/7.82% on the Hit@1 evaluation metrics for datasets ICEWS14/ICEWS05-15/Wikidata12k/GDELT, respectively.

4.6. The Impact of Different Hyperparameters

This section investigates the impact of different hyperparameters on model performance.

4.6.1. Comparison of Different Rule Confidence

Based on the knowledge graph reasoning algorithm that uses temporal logical rules, the quality of the rules plays a crucial role in the algorithm’s performance. The rule confidence threshold is a metric utilized to measure the minimum probability value at which a rule is considered to be correct. In this study, we conducted experiments to determine the optimal range of rule confidence thresholds, which include values of 0.1, 0.2, 0.3, 0.4, 0.5. We specified a minimum body support of 20 for the experiment to prevent small body support from leading to high overall rule confidence. Moreover, we held all other parameters constant to disentangle the influence of the rule confidence threshold from other factors. The results, which are displayed in Table 5, illustrate how various rule confidence criteria affect the algorithm’s performance for the ICEWS14 and ICEWS05-15 datasets.

Table 5. Results of link prediction on ICEWS14 and ICEWS05-15 with different levels of confidence.

Models	ICEWS14				ICEWS05-15
	MRR	H@1	H@3	H@10	MRR	H@1	H@3	H@10
0.1	0.664	0.582	0.723	0.835	0.733	0.654	0.776	0.863
0.2	0.672	0.597	0.731	0.840	0.746	0.668	0.789	0.873
0.3	0.666	0.588	0.727	0.836	0.735	0.657	0.778	0.865
0.4	0.668	0.591	0.727	0.835	0.735	0.657	0.782	0.865
0.5	0.670	0.593	0.734	0.837	0.743	0.659	0.780	0.870

4.6.2. Comparison of Embedding Dimensions

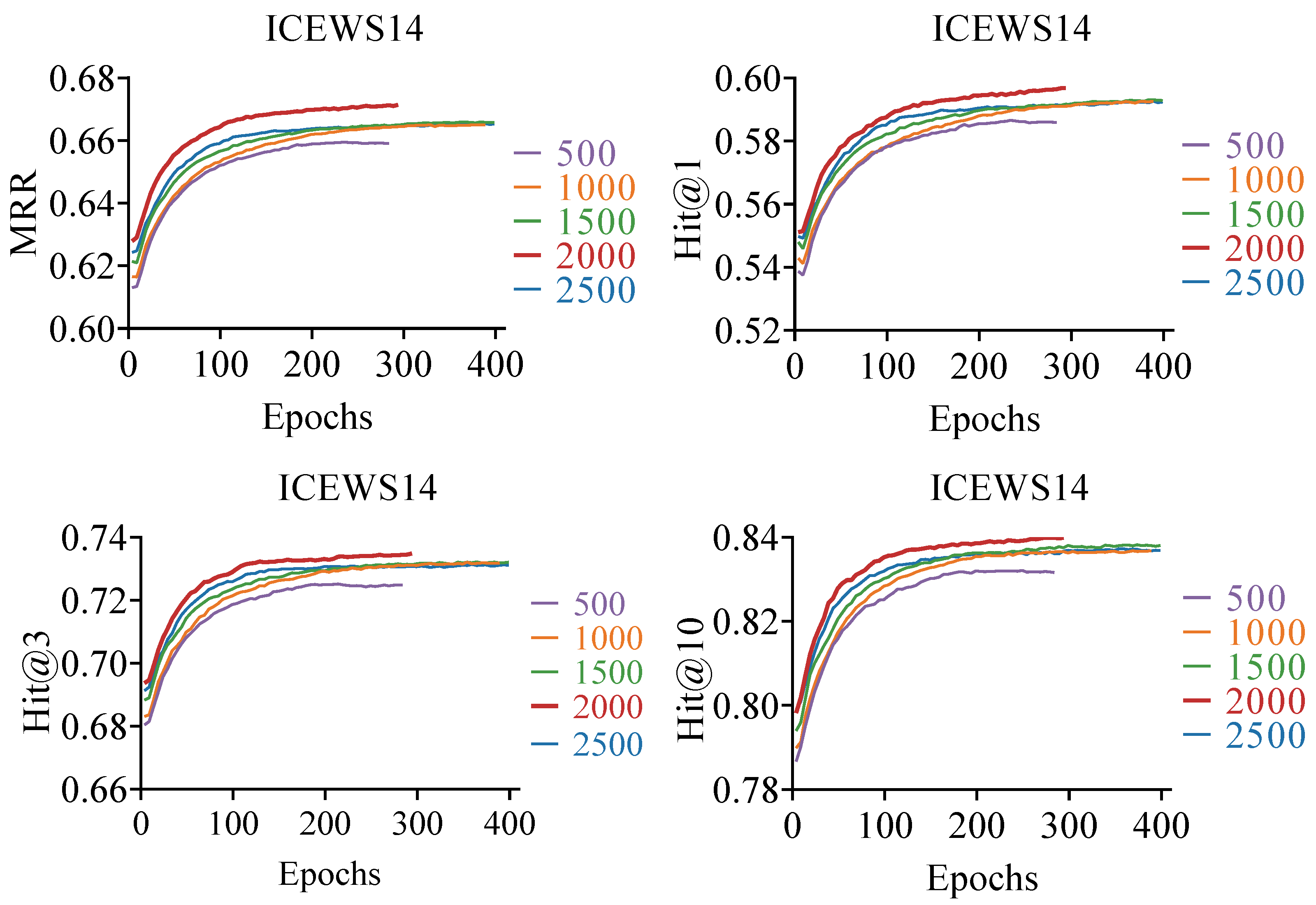
In this study, we investigated the impact of embedding dimensions on the TKG reasoning method based on embedding representation, where entities, relations, and timestamps are embedded into a low-dimensional vector space for link prediction tasks. While higher embedding dimensions can improve model performance, excessively high dimensions can also increase the computational cost. To examine the influence of embedding dimensions, with a batch size of 1000, an RGNN embedding dimension of 250, a learning rate of 0.1, and a rule confidence threshold of 0.2, we conducted comparison analyses on the ICEWS14 dataset. Except for the embedding dimension, all other parameters remained unchanged. According to the experimental results, as illustrated in Figure 4, the model’s performance increases with increasing embedding dimensions—that is, until a certain point, at which point it begins to decrease. As Figure 4 shows, the embedding dimension is fixed at 2000.

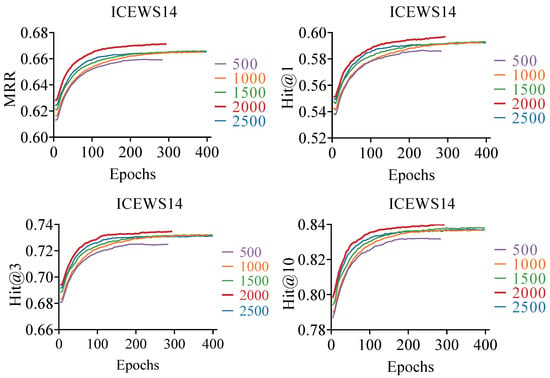
Figure 4. Training curves on ICEWS14 for various embedding dimensions.

4.6.3. The Impact of Rule Sampling Methods

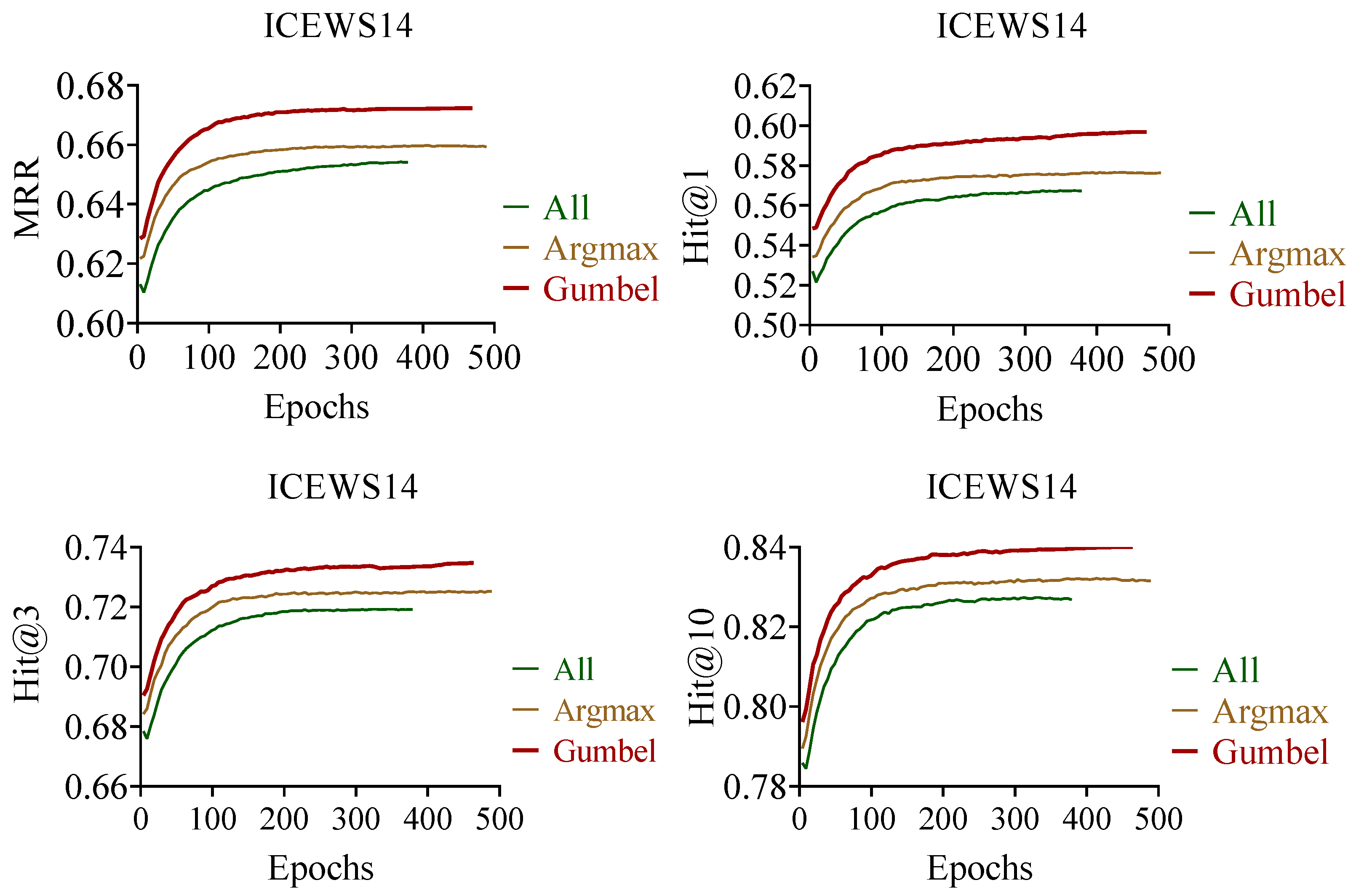
The experiment used a Gumbel-Softmax method to sample rules that meet the conditions for specific relationships. Other methods utilized Argmax to select the rule with the highest confidence score and used all the rules that meet the conditions without sampling. Comparative experiments were conducted on the ICEWS14 dataset while keeping other model parameters constant. The experimental results, as shown in Figure 5, demonstrated that the Gumbel-Softmax method yielded the best performance.

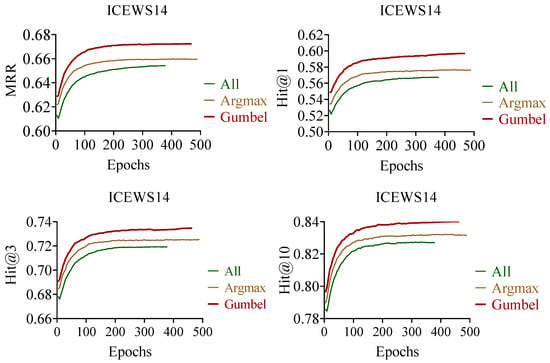
Figure 5. Training curves on ICEWS14 for different sample methods.

In the comparative analysis of temporal rule sampling methods, the Gumbel-softmax method can flexibly sample the appropriate rules, the Argmax method selects the rules with maximum confidence, and the third method uses all the rules; the experiment was performed on the ICEWS14 dataset. As can be seen in Figure 5, the training evaluation curve of the Gumbel-softmax method has been kept the highest, and as a result, it can be confirmed that this study utilizes differentiable sampling effectively.

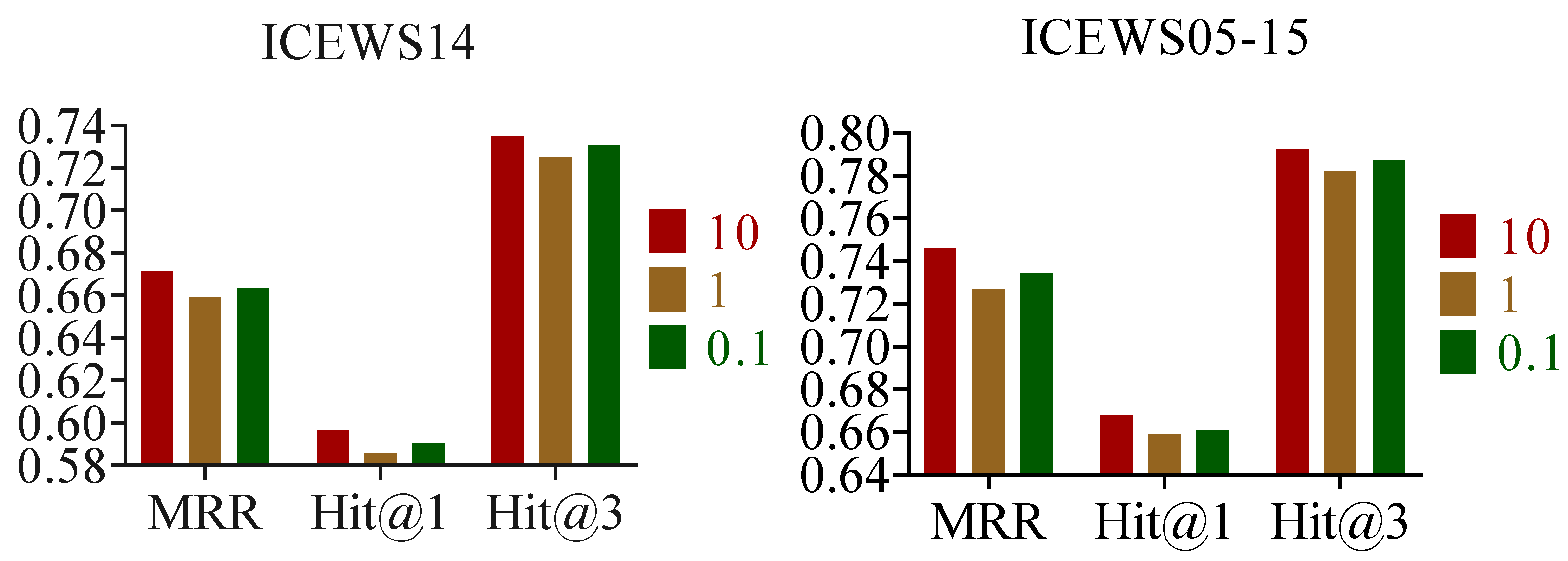
4.6.4. Comparison of Different Temperature Coefficients

To explore the impact of the Gumbel-Softmax method on rule sampling, we conducted experiments using different temperature coefficients ($\tau$). A higher $\tau$ value means more new rules are explored during the sampling process, while a lower $\tau$ value means more rules with higher probabilities are exploited. It can be seen from Figure 6 that $\tau$ is set to 10, and the result is the best. This implies that the model prefers to explore diverse temporal logic rules.

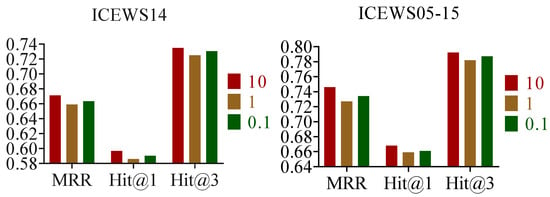
Figure 6. Results of link prediction using different $\tau$ (10, 1, 0.1) temperature coefficients.

4.7. Statistics of Extracted Temporal Logic Rules

Table 6 displays the statistics of the rules collected from the ICEWS14 dataset. The number of excursions across each relation was set to 200, and the sequence lengths of the excursions were 2 and 3, corresponding to rules of lengths 1 and 2. Table 7 includes the number of rule instances and the number of rules for various rule confidence levels. Our study presents six distinct temporal reasoning patterns, each with its own confidence level, reflecting the likelihood of one event leading to another within temporal knowledge graphs. These patterns range from direct actions such as accusations leading to rejections (Pattern 1, confidence 0.186) to more complex interactions involving multiple parties and actions, like the influence of making statements and hosting visits on subsequent consultations (Pattern 3, confidence 0.143). Notably, Pattern 2 (confidence 0.506) underscores a significant likelihood of property confiscation following investigations, highlighting a strong predictive relationship in legal or regulatory contexts. By synthesizing these examples, we gain insights into the reasoning power and practical implications of these patterns. This not only validates the effectiveness of our method in capturing complex temporal relationships but also opens avenues for further exploration into the impact of various rule extraction methods on reasoning accuracy.

Table 6. Statistical information on rules in the ICEWS14 dataset.

	Pattern 1	Pattern 2	Pattern 3	Pattern 4	Pattern 5	Pattern 6
Rule length	1	1	2	2	2	2
Number of walks per relationship	200	200	200	200	200	200
Time relationship	$t_1=t$	$t_1<t$	$t_1<t_2<t$	$t_1=t_2<t$	$t_1<t_2=t$	$t_1=t_2=t$
Relationship number	376	412	378	321	335	250
Number of rules	4077	7956	7105	2061	2148	1203

Table 7. Examples of rules in ICEWS14.

Pattern	Case	Confidence
Pattern 1	$Reject(s,o,t)\leftarrow Accuse(s,o,t)$	0.186
Pattern 2	$Confiscate\_property(s,o,t)\leftarrow Investigate(s,o,t_1)$	0.506
Pattern 3	$Consult(s,o,t)\leftarrow Make\_statement(s,z,t_1)\wedge Host\_a\_visit(z,o,t_2)$	0.143
Pattern 4	$Consult(s,o,t)\leftarrow Make\_statement(s,z,t_1)\wedge Accuse(z,o,t_2)$	0.141
Pattern 5	$Investigate(s,o,t)\leftarrow \_Make\_statement(s,z,t_1)\wedge Demand(z,o,t_2)$	0.124
Pattern 6	$Accuse(s,o,t)\leftarrow Make\_statement(s,z,t_1)\wedge Threaten(z,o,t_2)$	0.150

4.8. Ablation Study

To further analyze the contribution of model components (logic rules, RGNN, and TE), we perform a set of ablation studies. In the MVFF model, the temporal logic rule models the causal relationship using extracted rules, the RGNN encodes structural information for the static knowledge graph, and TE learns the temporal information. To ensure the comparability of the results, the same parameters were used in the experiments. The embedding dimension of RGNN was set to 250, the embedding dimension of tensor decomposition was set to 2000, and the rule confidence threshold was set to 0.2. The experimental results are shown in Table 8. As shown in the table, the performance of MVFF decreases no matter which module is removed, especially after the removal of the RGNN module, the performance of MVFF decreases the most, thus verifying the importance of a static knowledge graph in temporal knowledge graph reasoning.

Table 8. Ablation study of removing the rule module, RGNN, and TE from the whole model MVFF.

Models	ICEWS14				ICEWS05-15
	MRR	H@1	H@3	H@10	MRR	H@1	H@3	H@10
w/o Rule	0.635	0.588	0.720	0.827	0.699	0.615	0.744	0.841
w/o RGNN	0.631	0.577	0.706	0.821	0.687	0.626	0.739	0.840
w/o TE	0.662	0.584	0.723	0.833	0.740	0.655	0.776	0.862
MVFF	0.672	0.597	0.731	0.840	0.746	0.668	0.789	0.873

4.9. Case Study

Our framework provides interpretable reasoning processes, as can be seen in the explainable reasoning module in the top right corner of Figure 2; for the query (South Korea, Reject, ?, 30 April 2024), based on the temporal rules $Reject(s,o,t)\leftarrow Accuse(s,o,t_1)$ and the existing quadruple (South Korea, Accuse, North Korea, 17 October 2024), we can interpretably answer the query as to where the answer (North Korea) is located.

5. Limitation

Our proposed method integrates logic rules and multi-view feature encoding modules for the task of temporal knowledge graph reasoning. However, the rules extracted under different settings may vary, potentially impacting the final reasoning outcomes. In subsequent research, we will further explore and study the effects of different rule extraction methods on temporal knowledge graph reasoning. Although our multi-view feature fusion approach has already achieved optimal results in reasoning tasks, it lacks mathematical theoretical proof. In future studies, we will continue to investigate how to theoretically explain the advanced nature of our proposed method.

6. Conclusions and Future Work

In this paper, we propose a novel framework that combines logic rule-based and embedding-based methods for temporal knowledge graphs (TKG). The proposed framework provides both the interpretability of logic rule-based methods and the scalability of embedding-based methods. We introduced the pattern of temporal logic rules and demonstrated how they can be automatically extracted in TKG. Additionally, we introduced the Gumbel-Softmax sampling method used in rule sampling and the multi-view representation of TKG, where entities and relations are embedded separately in the static knowledge graph and TKG. Our experimental results demonstrate that the MVFF performs well on the link prediction task. This provides strong evidence that the combination of rule-based and embedding-based methods improves the performance of TKG reasoning.

In the future, we will learn how entities and relations in quaternions evolve as time goes on, transitioning from interpolative to extrapolative reasoning. Additionally, we will theoretically investigate the contribution of static knowledge graph representations to temporal knowledge graph reasoning. Due to the powerful understanding capabilities of large models, we further explore the task of temporal knowledge graph reasoning by integrating it with symbolic reasoning in large models [46].