Optimizing Privacy in Set-Valued Data: Comparing Certainty Penalty and Information Gain

Abstract

The increase in set-valued data such as transaction records and medical histories has introduced new challenges in data anonymization. Traditional anonymization techniques targeting structured microdata comprising single-attribute- rather than set-valued records are often insufficient to ensure privacy protection in complex datasets, particularly when re-identification attacks leverage partial background knowledge. To address these limitations, this study proposed the Local Generalization and Reallocation (LGR) + algorithm to replace the Normalized Certainty Penalty loss measure (hereafter, NCP) used in traditional LGR algorithms with the Information Gain Heuristic metric (hereafter, IGH). IGH, an entropy-based metric, evaluates information loss based on uncertainty and provides users with the advantage of balancing privacy protection and data utility. For instance, when IGH causes greater information-scale data annotation loss than NCP, it ensures stronger privacy protection for datasets that contain sensitive or high-risk information. Conversely, when IGH induces less information loss, it provides better data utility for less sensitive or low-risk datasets. The experimental results based on using the BMS-WebView-2 and BMS-POS datasets showed that the IGH-based LGR + algorithm caused up to 100 times greater information loss than NCP, indicating significantly improved privacy protection. Although the opposite case also exists, the use of IGH introduces the issue of increased computational complexity. Future research will focus on optimizing efficiency through parallel processing and sampling techniques. Ultimately, LGR+ provides the only viable solution for improving the balance between data utility and privacy protection, particularly in scenarios that prioritize strong privacy or utility guarantees.

1. Introduction

1.1. Necessity and Purpose of the Study

To protect information related to individual records, traditional data anonymization methods primarily focus on structured microdata. These records typically comprise attributes in the form of single numerical or textual values such as age or address. However, there is an increasing trend toward set-valued data, which include multiple items within a single record, such as purchase histories from large marketplaces or medical records. Set-valued data pose challenges for existing anonymization techniques because such datasets afford limited privacy protection and may be vulnerable to re-identification attacks, particularly when quasi-identifiers are involved. For instance, if a large marketplace discloses customers’ purchase histories, even if the k-anonymity model is applied, an attacker with background knowledge (e.g., knowing some of the items in the target’s shopping cart) could easily infer specific items purchased by the target. This demonstrates the need for additional anonymization techniques specifically designed for set-valued data.

This paper presents the Local Generalization and Reallocation (LGR) + algorithm, which addresses the anonymization challenges of set-valued transaction data. This algorithm incorporates the Information Gain Heuristic (IGH) metric to overcome the limitations of the traditional NCP (Normalized Certainty Penalty) loss measure. The entropy-based IGH metric enables a more precise evaluation of information loss and provides a better balance between privacy protection and data utility, particularly when dealing with sensitive data. In the following sections, we review various studies that have addressed set-valued data anonymization and discuss the strengths and limitations of the NCP metric.

1.2. Research Background

Data privacy models such as k-anonymity [1], l-diversity [2], and t-closeness [3] have been proposed for structured data anonymization. These models have been well documented in international standards such as ISO/IEC 20889 [4,5]. Significant research efforts have been made regarding the anonymization of set-valued microtransaction data, as summarized in Table 1 below.

Table 1. Approaches that address the anonymization challenges in set-valued transaction data.

Author Name/Reference	Algorithm	Key Features
Manolis Terrovitis and Nikos Mamoulis [6,7,8]	km-anonymity	Ensures at least k transactions exist for any given transaction where an attacker knows up to m items, preventing the attacker from inferring an individual’s identity.
Y. Xu et al. [9,10]	(h, k, p)-consistency	Ensures that a database containing a combination of p non-sensitive items includes at least k transactions, while up to h% of transactions contain some sensitive items. It models the attacker’s prior knowledge of the p parameter, providing flexibility in anonymization.
Yeye He and Jeffrey F. Naughton [11]	k-anonymity (LG, Local Generalization)	To address issues raised in [6,8,9,10], this method draws on the “local recording” technique defined in the anonymization taxonomy proposed by Agrawal R. and Srikant R. [12]. It defines k-anonymity as being satisfied when each transaction is identical to at least k-1 other transactions.
Junqiang Liu and Ke Wang [13]	HgHs (Heuristic generalization with Heuristic suppression)	Improves on the limitations of [13] by applying heuristic methods to find optimal cut points in a generalization tree structure, where both generalization and suppression techniques are used. While it results in less information loss compared to the k-anonymity method, it has the drawback of significantly longer CPU execution times.
Cao et al. [14]	ρ-uncertainty	Limits the probability that an individual is associated with a specific sensitive item to below a threshold ρ, thereby protecting privacy from attribute disclosure.
Loukides. G and Gkoulalas-Divanis [15]	Clustering-based anonymization	Aims to achieve km-anonymity by utilizing generalization and suppression techniques through a clustering-based anonymization mechanism.
Jia et al. [16]	partial suppression	Proposed partial suppression algorithm using divide-and-conquer.
Nakagawa et al. [17]	Personalized ρm- and (ε, σ)-ρm-uncertainty	Proposed to relax privacy guarantees in transaction datasets by offering personalized privacy protection.
Puri et al. [18]	Top-down strategy based on global generalization	Utilizes a top-down approach with global generalization to further enhance the security of km-anonymity.
Vartika et al. [19]	(k, m, t)-anonymity	Clusters k records based on combinations of m items, with an additional threshold t for the distance between sensitive attribute distributions within the cluster. This approach effectively prevents distortion attacks and the exposure of identities and attributes in transactions.
Yao. L et al. [20]	Bucketization by dividing datasets into non-overlapping subsets	Proposes dividing the dataset into non-overlapping subsets to separate relationships between attributes without modifying the published data. Commonly referred to as anatomization [21] and slicing [22], this technique is frequently used to anonymize a fixed number of attributes in relational databases.
Andrew et al. [23]	Greedy heuristic protection method	Proposes a greedy heuristic protection method where elected representatives, in communication with data owners and collectors, collaborate to prevent attacks through clustering-based techniques.
Soonseok Kim [24]	LGR (Local Generalization and Reallocation)	Offers the same level of privacy protection as existing methods like k-anonymity (local generalization) [11] and HgHs [13] while achieving minimal information loss. This makes it highly useful for real-world applications where data analysis is required. Its performance has been validated through practical experiments.

Recent studies have explored various methods for protecting privacy, including data anonymization through disassociation and local suppression [25,26,27,28,29,30,31,32,33,34] and evaluating big data anonymization in IoT environments [35,36]. Certain studies have focused on anonymizing electronic health records (EHR) [26,27] and improving horizontal partitioning algorithms [25,31]. Additionally, vertical partitioning algorithms for applying k^m-anonymity have been enhanced [33], and methods to prevent attribute disclosure risks in datasets with disassociated attribute links have been proposed [28,29,30]. Andrew et al. [34] proposed a fixed-interval approach and l-diversity slicing technique to protect sensitive medical data. Although several studies allow analysis using reconstructed datasets by disassociating cell links that contain set values, this process can be highly time-consuming [25]. In particular, some studies have introduced the lρ-suppression technique [37] to improve privacy protection in transactional datasets while maintaining data utility. Research that combines AI and machine learning to anonymize quasi-identifiers suggests the potential to achieve better privacy protection and data utility balance compared with existing techniques [38]. Other notable studies include data anonymization in edge-storage environments [39] and the protection of medical data using a cluster-based anonymity model [40]. Additionally, ARX tools have been utilized to minimize information loss in traditional k-anonymity-based anonymization [41], and new models have been proposed for the real-time anonymization of big data streams [42,43]. These studies aimed to prevent information leakage and minimize information loss in big-data-processing environments. Notably, studies on secure re-identification frameworks [44] and large-scale data anonymization using Spark distributed computing [45] have presented efficient privacy protection methods for modern big data environments. Furthermore, research on the performance evaluation and scalability of anonymization algorithms [46] continues to advance this field.

Several studies have addressed privacy issues and the linkage re-identification risks in complex networks. For instance, ref. [47] emphasizes the risks associated with re-identification through data matching and linkage, providing an important context for how the IGH metric proposed in this study can mitigate such risks. Furthermore, ref. [48] discusses the threat of privacy leakage due to de-anonymization in multiple social networks, illustrating how the IGH metric could potentially contribute to reducing these de-anonymization risks. Last, ref. [49] proposes a data-publishing algorithm utilizing connectivity-based outlier detection and Mondrian techniques, offering a valuable benchmark for comparative analysis with the IGH metric.

The anonymization problem must balance privacy protection with data utility. As anonymized data must still be useful for analysis, the balance between security and utility is crucial. Utility, which is associated with information loss, refers to the extent to which useful information is preserved. The lower the information loss, the higher the utility. These two aspects— privacy and utility—are always in a tradeoff relationship, and achieving a balance between them is critical. For set-valued microtransaction data, privacy is typically measured using probabilistic re-identification risks, similar to traditional structured data models such as k-anonymity, with a 1/k probability of re-identification. However, most algorithms proposed to measure the utility (as listed in Table 2), including [9,10,12,14,16,17,19,20,21,23,24], use the Normalized Certainty Penalty (NCP) metric [50,51]. NCP measures the extent of generalization or suppression applied to the anonymized data compared to its original state. Higher levels of generalization indicate a greater loss of information. Table 2 summarizes the strengths and weaknesses of the anonymization algorithms based on metrics.

Table 2. Comparison of strengths and weaknesses of NCP-based anonymization algorithm strengths.

Strengths		Weaknesses
Simple and intuitive calculation	-The calculation is based on data ranges, making the process simple and intuitive. -It clearly measures the difference between generalized values and the original values.	Does not reflect the data’s meaning	-For example, even if important information is generalized, the significance of that information is not reflected, which can lead to underestimating the loss of critical information.
Fast processing	-Since it does not require complex mathematical calculations, it can be processed quickly even with large datasets. -It has the advantage of being able to quickly assess information loss during the anonymization process.	Does not consider the data distribution	-Even if the data values within an anonymized group are uniformly distributed, NCP calculates based on the same range of generalization. -This can be a limitation, as it fails to reflect the data’s actual distribution and characteristics.
Evaluation of the degree of generalization	-When data are anonymized, the extent of generalization can be numerically evaluated, allowing for the determination of whether anonymization can be performed while maintaining the specificity of the data.	Applies the same weight to all items	-Some attributes may contain more important information than others, but this is not reflected, which can result in underestimating the information loss for specific attributes.
Comparable across anonymization methods	-NCP allows for the relative comparison of information loss across different anonymization techniques, making it useful for evaluating which method is more efficient.	Low information loss does not necessarily imply high utility	-Since NCP is a simple numerical comparison of data ranges, it does not assess whether essential information required for data analysis has been lost.

1.3. Contributions of This Study

This paper presents the LGR + algorithm, which addresses the anonymization challenges of set-valued transaction data, and makes several major research contributions. The LGR+ algorithm replaces the traditional loss measure based on NCP used in the LGR algorithm with the IGH [52,53,54] metric. The IGH metric is entropy-based and allows for a more precise evaluation of information loss, thereby better balancing data utility and privacy protection. The LGR+ algorithm addresses the limitations of the NCP-based approach by enhancing privacy protection through the entropy-based evaluation of information loss. Using IGH also offers researchers more flexibility in balancing privacy and utility because it reflects both the distribution and the significance of the data.

The traditional NCP-based approach is simple and computationally fast, but has limitations in reflecting the meaning of data or considering the importance of attributes. In particular, this approach fails to capture data uncertainty and distribution adequately, which can result in limited protection for sensitive data. This study points out these limitations in existing research and emphasizes how the IGH metric contributes to addressing this issue. By utilizing entropy to assess information loss, IGH reflects data uncertainty and distribution, enabling a more precise and meaningful evaluation of information loss. This allows for strong privacy protection for sensitive information while preserving data utility. The study highlights the limitations of existing research by comparing the strengths and weaknesses of NCP and IGH, emphasizing the accuracy of information loss evaluation using IGH. Hereby, researchers can enhance their understanding of information loss assessment methods and reinforce the significance of their research findings.

The experimental evaluation used the BMS-WebView-2 and BMS-POS datasets [55]. BMS-WebView-2 comprises 77,512 records of clickstream data from an e-commerce website containing 3340 items, whereas BMS-POS contains 515,597 records of electronic retail transaction logs representing 1657 items. These datasets were used to compare the performance of the LGR+ algorithm with that of the traditional NCP-based LGR algorithm. This study employed an experimental approach to evaluate the proposed LGR+ algorithm’s performance. The levels of information loss and privacy protection were measured for different k-anonymity values. To compare with the NCP, normalized differences were calculated to assess the relative information loss between the two algorithms. In conclusion, this study provided a novel approach for enhancing the balance between data utility and privacy protection, particularly for the secure use of sensitive datasets. The proposed LGR+ algorithm offers a practical and effective solution for improving privacy protection while maintaining data utility, thereby addressing significant challenges in data anonymization.

Section 2 of this paper defines the existing NCP metric and the newly proposed IGH metric and provides examples, followed by a comparison of their strengths and weaknesses. Thereafter, we propose a metric that is more suitable for specific applications. Chapter 3 presents and analyzes the results of experiments using the same datasets from [24], comparing the average information loss values of NCP and IGH as measured by applying the LGR+ algorithm, where IGH replaces NCP. Section 4 concludes the paper.

2. The NCP and IGH Metrics

This section introduces the definitions and differences between the traditional NCP information loss measurement method and the proposed IGH metric. Both measure the information loss that occurs during data anonymization. NCP focuses primarily on the generalized data range, whereas IGH evaluates the loss based on entropy, which reflects the uncertainty of the information. In this section, we present the definitions and calculation methods of both metrics and explain, using concrete examples, how they assess information loss differently in actual datasets.

2.1. NCP Metric

The NCP metric evaluates information loss based on the level of generalization of specific attributes. It was first introduced in [54] and subsequently used in various algorithms [6,7,8,9,10,11,12,13,14,15,16,17,18,19,23,24,35,36]. It is defined as the proportion of generalized items to the total data items, with higher generalization resulting in greater information loss. For example, if the original value “Seoul” is generalized to “South Korea”, information loss occurs within the group containing that value because the specific information necessary for data analysis is lost. NCP is calculated by defining the ratio of generalized items relative to the total |I|, where p represents an item in I, and |u_p| represents the number of nodes below the generalized node when p is generalized (i.e., nodes at the same level as p). This is defined as follows:

$$NCP\left(p\right)=\left\{\begin{array}{c}0, \\ {\displaystyle \frac{\left|u_p\right|}{I}},\end{array}{\displaystyle \genfrac{}{}{0pt}{}{\left|u_p\right|=1}{Otherwise}}\right.$$

(1)

When the total occurrence of item p in database D is denoted as C_p, the overall information loss NCP(D) in dataset D is defined as follows:

$$NCP\left(D\right)={\displaystyle \frac{{\sum }_{p\in I}{C}_p·NCP\left(p\right)}{\sum _{p\in I}{C}_p}}$$

(2)

For example, in Figure 1, when a₁ is generalized to A in transaction T, NCP(a₁) = 2/4.

Figure 1. Example of NCP-based anonymization for the original dataset (when {a₁, a₂} are generalized to A).

When {a₁, a₂} are generalized to A, and the information loss is 2.5/11 (=20.5 + 30.5 + 0 + 0/11). In Figure 1a, there are two occurrences of a₁, three of a₂, three of b₁, and three of b₂. Therefore, the total C_p is 11. Additionally, the NCP values were 2/4, 2/4, 0, and 0 because b₁ and b₂ were not generalized, resulting in an NCP of 0.

However, NCP is limited by only evaluating the extent of range expansion without reflecting the actual distribution or importance of the data. For example, even if sensitive information is generalized, its significance is not considered, which could limit the assessment of critical information loss.

2.2. The IGH Metric

The IGH metric [37,38,39] evaluates information loss based on entropy, which represents uncertainty in the data, with higher values indicating greater uncertainty. IGH assesses the extent to which a particular attribute reduces the uncertainty of the data and allows information loss in generalized data to be measured more precisely. First, the entropy metric measures the uncertainty in the data, where higher entropy values indicate greater uncertainty and lower values indicate less uncertainty. When P(x_i) is the probability of item x_i in dataset D, the entropy H(D) is calculated as follows:

$$H\left(D\right)=-{\sum }_{i}P\left(x_i\right){\log }_{2}P\left(x_i\right)$$

(3)

Next, given a specific attribute, the conditional entropy H(D|A) measures the uncertainty of the data. Here, P(A_j) is the probability of value A_j for attribute A, and H(D|A) represents the entropy when attribute A takes value A_j. The conditional entropy H(D|A) is calculated as follows:

Finally, IGH indicates the extent to which the entropy of the data is reduced when a specific attribute A is given. It evaluates the extent to which an attribute contributes to reducing data uncertainty and is calculated as follows:

$$H\left(D|A\right)={\sum }_{j}P\left(A_j\right)H\left(D\right|A_j)$$

(4)

$$IGH\left(D,A\right)=H\left(D\right)-H\left(D\right|A)$$

(5)

For example, if two values, ‘apple’ and ‘banana’, are generalized to ‘fruit,’ the uncertainty within this category is reduced. This is because an attacker would only know the generalized category ‘fruit,’ making it difficult to infer specific values. In this manner, IGH calculates the extent to which the generalized data reduce the uncertainty of the original data, thereby evaluating the information loss. Additionally, the entropy decreasing from 0.9 to 0.4 indicates that the information loss is minimal and privacy protection has been significantly strengthened. Unlike NCP, the IGH method can reflect the data distribution and importance of the information.

2.3. Comparison Between NCP and the Proposed IGH Metric

For example, as shown in Table 3, when comparing the information loss between NCP and IGH applied to five transaction datasets, the former simply calculates the information loss based on the range expansion of each attribute, whereas the latter calculates the information loss more precisely by considering the data distribution and entropy. Consequently, NCP and IGH, respectively, record information losses of 3.8 and 2.3, demonstrating that IGH better preserves data utility through a more detailed information loss evaluation. In Table 3, the frequencies of each item were a₁ (five occurrences), a₂ (four occurrences), b₁ (two occurrences), and b₂ (two occurrences). Thus, the probabilities for each item were $P\left(a_1\right)=5/13, p\left(a_2\right)=4/13, p\left(b_1\right)=2/13, p\left(b_2\right)=2/13$. The entropy $H\left(D\right)$ of the entire dataset was calculated as follows:

$$H\left(D\right)=-\left(P\right(a_1\left){\mathit{log}}_{2}P\left(a_1\right)+\right(P\left(a_2\right){\mathit{log}}_{2}P\left(a_2\right)+\left(P\right(b_1\left){\mathit{log}}_{2}P\left(b_1\right)+\right(P\left(b_2\right)=1.8852$$

Table 3. Comparison of information loss values between NCP- and IGH-based anonymization (2-Anonymity) in transaction datasets.

Transaction	Original Data	NCP-Based Anonymization [24]		Proposed IGH-Based Anonymization
		2-Anonymity Results	Information Loss Value	2-Anonymity Results	Information Loss Value
T1	{a1}	{A}	1.0	{A}	0
T2	{a1,b1}	{A,b1}	0.5	{A,b1}	0
T3	{a2,b1}	{A,b1}	0.5	{A,b1}	0
T4	{a1,a2,b2}	{A,B}	0.6667	{A,b2}	0.667
T5	{a1,a2,b2}	{A,B}	0.6667	{A,b2}	0.667
T6	{a1,a2}	{A}	0.5	{A}	1.0
Total Information Loss			3.8334		2.334

Next, the information loss for each transaction was calculated as follows: For T1–T3, the original and generalized entropies were the same, resulting in a difference of 0. For T4 and T5, the original entropies $H\left(\left\{a_1, a_2, b_2\right\}\right)$ were:

$$H\left(\left\{a_1, a_2, b_2\right\}\right)=-({\displaystyle \frac{1}{3}}{\mathit{log}}_2{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{3}}{\mathit{log}}_2{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{3}}{\mathit{log}}_{2}1/3)=1.585$$

and the generalized entropy was:

$$H\left(\left\{A, b_2\right\}\right) \mathrm{is}: H\left(\left\{A, b_2\right\}\right)=-({\displaystyle \frac{2}{3}}{\mathit{log}}_2{\displaystyle \frac{2}{3}}+{\displaystyle \frac{1}{3}}{\mathit{log}}_2{\displaystyle \frac{1}{3}})=0.918$$

resulting in an information loss of 0.667 (1.585–0.918).

For T6, the original entropy was:

$$H\left(\left\{a_1, a_2\right\}\right) \mathrm{is}: H\left(\left\{a_1, a_2\right\}\right)=-({\displaystyle \frac{1}{2}}{\mathit{log}}_2{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\mathit{log}}_2{\displaystyle \frac{1}{2}})=1$$

and the generalized entropy $H\left(\left\{A\right\}\right)$ was 0, resulting in an information loss of 1 (=1-0).

Therefore, the total information loss using the IGH method was 2.334 (=0 + 0 + 0 + 0.667 + 0.667 + 1).

Conversely, the information loss using the NCP method was calculated as follows:

T1 is 1.0 (=1/1), T2 is 0.5 (=1/2), T3 is 0.5 (=1/2), T4 is 0.6667 (=2/3), T5 is 0.6667 (=2/3), and T6 is 0.5 (=1/2).

Therefore, the total information loss using the NCP method was:

3.8334 (=1.0 + 0.5 + 0.5 + 0.6667 + 0.6667 + 0.5)

Table 3 highlights the distinct differences in how NCP and IGH measure information loss, reflecting the strengths and weaknesses of each approach. The simplicity of the NCP method, which calculates the information loss based on the range generalization of each attribute, has the advantage of low computational complexity. However, this simplification often fails to capture the actual impact on data utility, particularly when important data attributes are generalized without considering their significance. By contrast, the IGH method provides a more detailed approach. By utilizing entropy, IGH considers both generalization and the inherent uncertainty and distribution of the data. For example, although the results for T4 and T5 show similar values for both IGH and NCP, the IGH approach evaluates information loss more precisely, offering better insights into how data utility is preserved. This is particularly evident because IGH-based anonymization induces a lower total information loss (2.334), whereas NCP records a higher total information loss (3.8334).

This comparison is elucidated in more detail in Table 4, explaining how the two metrics play complementary roles in optimizing privacy protection and data utility. Specifically, NCP focuses on simple range expansion, allowing for low computational complexity and fast evaluation, but is limited by not reflecting the meaning or distribution of the data. Conversely, being based on entropy, IGH evaluates data uncertainty and importance, enabling information loss to be measured more precisely. This demonstrates that IGH can contribute to preserving data utility more effectively and goes beyond simple information loss assessment by considering the distribution of the data and the relative importance of attributes.

Table 4. Comparison of strengths and weaknesses: NCP and the proposed IGH metric (+ represents strengths, and − represents weaknesses).

Functionality	NCP Metric	IGH Metric
Reflects Data Meaning	(−) Does not reflect the meaning or importance of the data. It is difficult to assess the loss of important information.	(+) Reflects the meaning and amount of information, allowing for a more accurate evaluation of information loss. Suitable for assessing data utility.
Considers Data Distribution	(−) Does not consider data distribution. It only evaluates range expansion, making it difficult to assess properly when the distribution is uneven.	(+) Considers data distribution, allowing for a more accurate evaluation of information loss even with an uneven distribution.
Evaluates Data Utility	(−) Focuses solely on range expansion, making it difficult to accurately evaluate data utility. Even if information loss is low, the actual utility may be reduced.	(+) Allows for a more accurate evaluation by reflecting the impact of information loss on data utility.
Precisely Measures Information Loss	(−) Evaluates information loss roughly based on simple range expansion, failing to reflect fine-grained information loss accurately.	(+) Allows for precise measurement of information loss through entropy, reflecting the diversity and uncertainty of the information.
Reflects Importance Between Attributes	(−) Applies the same weight to all attributes, failing to distinguish between important and less important attributes when evaluating information loss.	(+) Can more accurately reflect information loss based on the importance and amount of information in each attribute, allowing for detailed assessments of information loss in important attributes.
Computational Complexity	(+) Simple and fast calculations. Since only ranges are compared, no complex calculations are required. Performs well even with large datasets.	(−) The calculations are complex, and processing time is particularly long for large datasets due to entropy calculations.
Suitability for Large Datasets	(+) Simple and fast calculations. Since only ranges are compared, no complex calculations are required. Performs well even with large datasets.	(−) The calculations are complex and time-consuming, which can make it inefficient for processing large datasets.
Scope of Application	Applicable to all data types where range expansion is evaluated and can be used for simple generalization or suppressed data.	More suitable when data distribution and uncertainty need to be reflected. It may be overly complex for simple data.

Although the examples in Table 3 show that, compared with NCP, the IGH value results in 1.5 times less information loss, in some cases, the IGH value is even greater. This is because IGH provides a more detailed assessment by reflecting the meaning, uncertainty (entropy), and data distribution compared to NCP. Therefore, if IGH induces a higher information loss, it implies that privacy has been strengthened through a more refined evaluation, whereas a lower value indicates that data utility has improved. However, data anonymization requires a balance between privacy and utility, as these two factors are in a tradeoff relationship and ultimately demand a choice. This is illustrated in Table 4 and Table 5.

Table 5. Considerations when using the IGH metric.

Item	Considerations When Using the IGH Metric
Data Sensitivity	-IGH is suitable when dealing with sensitive data, such as personal, financial, or medical information. -Since IGH evaluates information loss based on entropy, it allows for a more precise assessment of how the loss of sensitive information impacts utility.
Maintaining Data Utility	-IGH is effective for evaluating the utility of data. -For example, when certain information must be retained for data analysis, IGH helps assess how much information loss affects the meaning of the data. -If the ability to analyze data needs to be maintained after anonymization, IGH can be used to evaluate utility and pursue the minimum necessary information loss.
Data Diversity and Distribution	-IGH reflects the data distribution, an advantage in evaluating the information loss in unevenly distributed data. -When data diversity is important, IGH can precisely measure information loss across various items. -Conversely, if the data distribution is uniform, IGH’s complex evaluation method could enhance simpler methods’ efficiency.
Computational Complexity	-In cases requiring large datasets or real-time processing, IGH may involve complex calculations, so considerations for computation time and resource consumption are essential. -When processing speed is critical, sampling techniques or approximation calculations can be utilized to reduce computational complexity.
Detailed Evaluation of Data Loss	-Since IGH calculates information loss based on entropy, it allows for a detailed assessment of the loss for each attribute. -When a specific attribute of the data is critical, IGH enables accurate analysis of the information loss associated with that attribute.

Table 4 compares the strengths and weaknesses of the NCP and proposed IGH metrics. Both NCP and IGH measure information loss in data anonymization, but their methods and purposes differ significantly. NCP calculates the information loss based on the range of data generalization, and the calculation process is simple and intuitive. However, it fails to reflect the loss of important information and does not consider data distribution. By contrast, IGH evaluates data uncertainty using entropy, considering both the importance and distribution of data to measure information loss more precisely.

When using the IGH metric, as shown in Table 5, certain factors, such as the characteristics and purpose of the data, must be considered. Setting thresholds for the measurement results is crucial in balancing data protection and utility, considering the data’s sensitivity, legal obligations, and intended use. If data utility is important or the amount of sensitive information is relatively low, a low IGH value (e.g., 0 <= IGH <= 1) should be chosen as the threshold. In cases where a balance between privacy protection and data utility is required, a moderate IGH value (e.g., 1 <= IGH <= 5) is appropriate. Conversely, if privacy protection is the top priority, particularly in high-risk data leakage scenarios, a relatively high IGH value (e.g., IGH > 5) should be set.

We next examine how the NCP and IGH metrics are applied to the proposed LGR+ algorithm and its experimental results.

3. The Proposed LGR+ Algorithm (Micro-Transaction Data Anonymization Using the IGH Metric)

We previously proposed a new LGR algorithm that maintains the same level of privacy protection as existing methods, e.g., k-anonymity (local generalization) [11] and HgH [13], while exhibiting the least amount of NCP information loss [24]. This section introduces our LGR algorithm and then presents the differences and advantages of the improved algorithm based on IGH as an information loss metric, replacing the previously used NCP.

3.1. Existing LGR Algorithm

The existing LGR algorithm [24] for anonymizing transaction data comprises the following steps:

[STEP 1] Anonymize(partition): Begin partitioning the transaction data to satisfy k-anonymity. This initial procedure constructs a generalization tree and partitions the transaction items. Next, the Pick_node() function is used to select the first partition, which then expands to the lower nodes. Each transaction is assigned to an expanded partition, and the Distribute_data() procedure processes the partitioned transactions. The Balance_partition() routine ensures that the partitions are balanced and checks whether k-anonymity is satisfied. If k-anonymity is met, the transactions move to Final_partition(); otherwise, a rollback occurs, and the Expand_node() procedure is called again.

[STEP 2] Pick_node() and Expand_node(): The optimal node is sequentially selected from the partition. In Expand_node(), the selected partition is expanded to the lower nodes in the tree structure. To minimize information loss during transaction distribution, the NCP values are calculated in order to choose the node that causes the least information loss among the expanded partitions.

[STEP 3] Distribute_data() and Balance_partition(): Transactions are distributed to the partitions, maintaining a balance between them. In Distribute_ Data (), transactions are assigned to each expanded partition. Balance_partition() checks whether each partition satisfies k-anonymity. Otherwise, transactions are stored in a waiting queue.

[STEP 4] WaitForQ_data() and FinalQ_data: Partitions not satisfying k-anonymity are stored in a waiting queue (WFQ), and transactions that satisfy k-anonymity are ultimately saved in FinalQ. In WaitForQ_data(), the partitions and transactions not satisfying k-anonymity are stored in WFQ, whereas FinalQ_data stores those that do.

[STEP 5] Final_partition(): The transactions and partitions not satisfying k-anonymity are reassigned via an upward search. We explore the remaining partitions in the waiting queue (WFQ) and match them with the partitions in FinalQ. If a matched partition satisfies k-anonymity, it moves to FinalQ; otherwise, the generalization occurs upward until k-anonymity is satisfied. Reallocation starts with the partition with the least information loss (NCP).

[STEP 6] Results Publication: After assigning all transactions to the partitions, transactions that satisfy k-anonymity are published. Once all the transactions in the waiting queue are processed, the transactions in FinalQ are publicly released, and the algorithm concludes.

3.2. Proposed LGR+ Algorithm

The proposed LGR+ algorithm’s overall flow is identical to that of the original algorithm, with the main difference being that IGH instead of NCP is used as the information loss metric. Algorithm 1 shows the proposed LGR+ algorithm’s pseudocode, and the key differences between the proposed IGH-based LGR+ algorithm and the existing NCP-based LGR algorithm are given in Table 6:

Table 6. Comparison of differences between the existing LGR algorithm [24] and the proposed LGR+.

Algorithm Steps	NCP-Based LGR [24]	Our IGH-Based LGR+	Differences
1. Anonymize(partition)	Partitions are divided based on NCP values, and transactions are assigned to partitions with minimal information loss.	Partitions are divided based on IGH values, and transactions are assigned in a way that minimizes entropy, considering the uncertainty of the information.	NCP evaluates information loss based on range expansion, whereas IGH assesses information loss by considering entropy-based data uncertainty, thus providing a more precise evaluation that helps achieve a better balance between privacy and utility.
2. Pick_node() and Expand_node()	Calculate NCP values to expand partitions and select nodes in a way that minimizes information loss.	Calculate IGH values to expand and select nodes in a way that reduces information uncertainty.	NCP considers the range of generalization for each item during node expansion, while IGH selects nodes based on probabilistic information loss, which allows for a more sophisticated approach to preserving data utility.
3. Distribute_data() and Balance_partition()	Distribute transactions to the partitions based on NCP and assess whether k-anonymity is satisfied.	Distribute transactions based on IGH values and adjust partitions to minimize entropy-based information loss.	NCP calculates information loss by expanding the range of each transaction, whereas IGH reduces information loss by measuring the uncertainty of the transactions, offering better insights into data utility preservation.
4. WaitForQ_data() and FinalQ_data()	Transactions that do not find suitable partitions based on NCP are stored in the waiting queue (WFQ).	Transactions that do not find suitable partitions based on IGH values are stored in the waiting queue (WFQ).	If a suitable partition cannot be found with a low IGH value, the transactions are held in the waiting queue, and those evaluated based on IGH are processed in a state of high uncertainty, ensuring more accurate control over data sensitivity.
5. Final_partition()	Roll back transactions upward and reassign partitions to satisfy k-anonymity based on NCP values.	Roll back transactions upward and reassign partitions to satisfy k-anonymity based on IGH values.	NCP calculates information loss based on range expansion, while IGH measures uncertainty based on entropy, enabling a more refined method of minimizing information loss.
6. Publish the Results	Publish the transactions that satisfy k-anonymity based on the NCP values.	Publish the transactions that satisfy k-anonymity based on the IGH values.	IGH publishes the final data in a way that reduces information uncertainty (entropy), thereby better balancing privacy protection and data utility.

Information Loss Calculation Scheme: NCP evaluates information loss based on range expansion, whereas IGH measures information loss by assessing data uncertainty using entropy.

Transaction Assignment Criteria: NCP aims to minimize the loss due to range expansion within each partition, whereas IGH assigns transactions in a way that minimizes uncertainty.

Upward Rollback Process: In the upward rollback process, NCP considers losses due to range expansion, whereas IGH reduces information loss by minimizing probabilistic information loss (entropy). Thus, replacing NCP with IGH shifts the information loss evaluation criterion of the LGR algorithm to a more sophisticated entropy-based assessment.

Algorithm 1. Pseudocode of our proposed LGR+ Algorithm.

1. Algorithm LGR+_Algorithm(Partition, IGH_metric): List of Partitions 2. Input: 3.  Partition—The initial data partition to be processed. 4.  IGH_metric—The entropy-based metric used for evaluating information loss and guiding partitioning decisions. 5. Output: 6.  List of Partitions—The resulting partitions after the anonymization process, where each partition satisfies k-anonymity. 7. Steps: 8. if (no further drill down possible for Partition) then    // If no further drill-down is possible for the given partition 9.   return and add Partition to the global list of returned partitions     // Return the partition and add it to the global list 10. else 11.   expandedNode <- pickNode(Partition, IGH_metric)     // Pick a node from the partition based on the IGH metric 12.    for each transaction in Partition do 13.      resultPartitions <- distributeData(transaction, expandedNode, IGH_metric)         // Distribute the data to the expanded nodes with IGH metric consideration 14.    end for 15.     balancePartitions(resultPartitions, IGH_metric)         // Balance the partitions to ensure k-anonymity and minimize entropy-based information loss 16.    for each transaction in resultPartitions do 17.      WFQ <- addToWaitForQueue(transaction, resultPartitions)       // Add to waiting queue if k-anonymity is not satisfied 18.      FinalQ <- addToFinalQueue(transaction, resultPartitions)         // Add to the final queue if k-anonymity is satisfied 19.    end for 20.    for each subPartition in resultPartitions do 21.      LGR+_Algorithm(subPartition, IGH_metric)         // Recursively anonymize the sub-partition 22.    end for 23.  end if 24.  Final_partition(WFQ, FinalQ, IGH_metric)   // Final reallocation of transactions in the waiting queue and publish results once k-anonymity is achieved

Our LGR+ algorithm primarily uses IGH to evaluate information loss. IGH is entropy-based and calculates loss by considering data uncertainty, reflecting the inherent distribution and significance of the data. This algorithm assigns transactions to partitions and maintains balanced partitions to satisfy k-anonymity. By providing a more precise evaluation of information loss than the traditional NCP-based method, the proposed LGR+ algorithm achieves a better balance between privacy protection and data utility. Using the IGH allows the evaluation of information loss to reflect the meaning and uncertainty of data, providing stronger privacy protection for more sensitive datasets.

3.3. Algorithm Analysis and Experimental Results

The most significant difference between the LGR and LGR+ algorithms is the method used to measure information loss. Based on NCP, the LGR algorithm supports relatively simple and fast calculations for data range expansion, whereas the LGR+ algorithm requires more complex computations owing to the inclusion of entropy calculations based on IGH. In particular, the computational complexity of IGH can significantly affect processing time when dealing with large datasets.

The next section compares the time complexities of the two algorithms and proposes optimization strategies to address this issue.

3.3.1. Time Complexity of the LGR Algorithm

In the LGR algorithm, information loss calculated using the NCP metric depends primarily on each transaction’s generalization range. The specific steps for computing the time complexity are: (a) exploration of the transaction dataset: The main task of the LGR algorithm is to explore the transaction dataset. Let n be the number of transactions and h be the height of the generalization tree. Each transaction is processed to determine the appropriate partition and proceeds recursively to the depth of the tree. (b) Generalization range calculation: During exploration, the information loss is calculated based on the extent to which each item’s attributes in the transaction are generalized to satisfy k-anonymity. Thus, the generalization range expansion is calculated at each level and repeated until a leaf node is reached or k-anonymity is satisfied. (c) Time complexity calculation: When calculating information loss using the NCP metric, the worst-case time complexity occurs when each transaction processes all the levels of the tree. Since n transactions are processed through h levels, the time complexity is given by $O(n·h)$, where n is the number of transactions and h is the height of the generalization tree.

3.3.2. Time Complexity of the LGR+ Algorithm

The LGR+ algorithm increases the complexity compared to the existing LGR algorithm by adding the entropy calculation. The specific steps for computing the time complexity are as follows: (a) Entropy calculation for each transaction: In addition to exploring the dataset, the LGR+ algorithm calculates the entropy $H\left(D\right)$ for each transaction. It is based on the distribution and frequency of items, represented by $f\left(i\right)$ for item $i$, and involves logarithmic operations, denoted as $log\left(n\right)$. Entropy is calculated by traversing the dataset to evaluate each partition’s uncertainty using the IGH metric. (b) Recursive processing through tree levels: Similarly to the LGR algorithm, the LGR+ algorithm processes each transaction recursively through the levels of the generalization tree, but with the added entropy calculation. However, the depth of the recursive exploration remains h. (c) Time complexity calculation: In the LGR+ algorithm, the computational complexity of each transaction includes both tree traversal and entropy calculations. Thus, complexity is given by $O(nh\mathit{log}\left(n\right))$, where n is the number of transactions, h is the height of the generalization tree, and $\mathit{log}\left(n\right)$ represents the complexity of the logarithmic operations involved in the entropy calculation. This logarithmic operation $log\left(n\right)$ reflects the complexity of the entropy calculation, increasing the overall computational cost compared with the LGR algorithm. This time complexity represents the worst-case scenario, in which each transaction is recursively processed through all levels of the tree and the entropy is calculated for each item in the transaction.

3.3.3. Optimization Strategies for Time Complexity

The IGH-based LGR+ algorithm offers a more precise evaluation of information loss than the NCP-based algorithm, but has higher computational complexity, leading to increased processing time for large datasets. To address this, the following optimization strategies can be introduced:

(a) Parallel Processing: Parallel processing distributes the entropy calculations across multiple processors, reducing the overall processing time. When optimized, computational complexity can be reduced to $O({\displaystyle \frac{p}{n}}hlog\left(n\right))$, where n is the number of transactions, h is the height of the generalization tree, and p is the number of processors.

(b) Sampling Techniques: By calculating entropy using only a portion of the dataset, the computational load can be reduced. For example, using a 10% sample of the data can decrease overall computational complexity from $O(nhlog\left(n\right))$ to $O(0.1nh\log \left(n\right))$.

(c) Data Structure Optimization: Utilizing efficient data structures (e.g., B-trees, hash tables) can improve data retrieval and entropy calculation speeds, thus reducing the time complexity. Implementing such structures can boost data access and calculation efficiency, improving algorithm performance.

(d) Approximation Methods: Approximation methods can simplify calculations, thus reducing time complexity. This approach can further lower computational costs and improve performance in real-time processing.

(e) Memory Optimization: Dynamic memory allocation and caching strategies can reduce memory usage during entropy calculations, improving the time complexity. These strategies help alleviate memory bottlenecks and maintain efficiency depending on the dataset size.

These optimization strategies enhance the computational efficiency of the IGH-based LGR+ algorithm, particularly for large datasets, making real-time processing more feasible.

3.3.4. Performance Comparison of LGR and LGR+ Algorithms: Analysis of Information Loss and Data Utility

In this study, we compared the performance of the traditional LGR algorithm and the IGH-based LGR+ algorithm using the BMS-POS and BMS-WebView-2 datasets [24,55], which were also utilized in previous experiments for the original LGR [24]. The BMS-POS dataset consists of 515,597 electronic retail transaction logs containing up to 1657 items, with each record potentially including up to 164 items. Each item is represented by a four-digit product code purchased by customers, ranging from 0 to 1404. For example, if the product code is ‘1302’, the major category is ‘1’, the subcategory is ‘3’, the minor category is ‘0’, and the detailed category is ‘2’. Based on this structure, we constructed a generalization tree with a maximum depth of 5. The experiment was conducted using the 345,204 data points remaining after data preprocessing and cleaning, which involved correcting data errors and removing unnecessary or inconsistent records.

The BMS-WebView-2 dataset includes 77,512 records, representing up to 3340 items. This dataset comprises clickstream data collected over several months from an e-commerce website. Similar to the BMS-POS dataset, product codes ranging from 55,267 to 330,285 represent individual items purchased. Based on this structure, a generalization tree with a maximum depth of 7 was constructed, and each record could contain up to 161 items. This tree was designed to accommodate various levels of generalization, enabling the effective classification of complex set-valued data.

The main specifications of the experimental data are summarized in Table 7, and Table 8 shows a sample of the data used in the experiments, where each item is delimited by the ‘|’ symbol.

Table 7. Main specifications of the data used in the experiments.

Data Name	Number of Transactions	Maximum Transaction Size	Total Number of Leaf Nodes in the Generalization Tree	Maximum Depth of Generalization Tree
BMS-WebView-2	77,512	161	3340	7
BMS-POS	345,204	86	1657	5

Table 8. Sample of original data used in the experiments.

BMS-POS	BMS-WebView-2
166|167	84,475|84,211|86,919|86,927|86,943
168|169	56,109|22,699
166|175|179|180|181|182|183|184|185	55,455
194	91,759|81,991
185|192|193|197|198|199	84,947|84,999

To implement the LGR and LGR+ algorithms, we used Python along with the pandas library for reading and processing the CSV files. The generalization tree, which is a core data structure for both algorithms, was defined and constructed to support the hierarchical generalization of data attributes. This tree structure was implemented to allow multiple child nodes to be connected to a parent node, thereby supporting flexible and precise data generalization processes. The data were input and partitioned using this tree, with the transaction data stored in the generalization tree class for efficient processing.

The LGR+ algorithm employed an additional entropy calculation to evaluate information loss, analyzing the distribution and frequency of items within the generalization tree class to compute entropy effectively. This allowed the IGH-based algorithm to consider data uncertainty and distribution during the anonymization process. Additionally, the LGR+ algorithm introduced a recursive rollback process, generalizing data to higher nodes when k-anonymity was not met, ensuring compliance with privacy constraints.

The experiments were conducted on a Windows 10 system equipped with a 12th Gen Intel(R) Core(TM) i9-12900KS 3.40 GHz PC and 64 GB of memory. The k-anonymity values were set to 3, 5, 10, 25, and 50, and the average NCP and IGH values for each dataset were measured and compared. The experimental results are summarized in Table 9 and illustrated in Figure 2.

Table 9. Experimental results: comparison of average NCP, IGH values, and their normalized differences.

	BMS-Webview-2					BMS-POS
k(-anonymity)	3	5	10	25	50	3	5	10	25	50
Average NCP value	0.17	0.16	0.17	0.31	0.65	0.02	0.02	0.02	0.02	0.02
Average IGH value	0.90	3.56	6.14	7.89	9.40	2.55	5.61	7.48	7.52	7.52
normalized differences	0.81	0.96	0.97	0.96	0.93	0.992	0.996	0.997	0.997	0.997

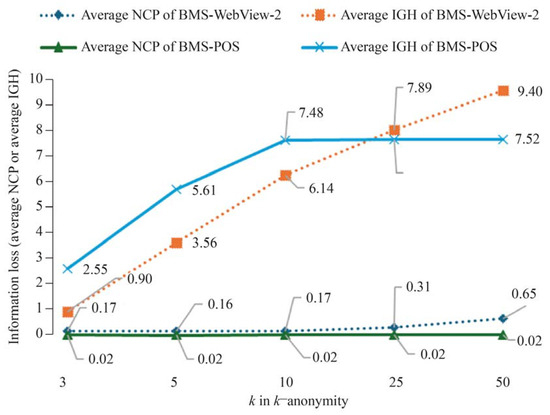
Figure 2. Comparison of information loss between the BMS-WebView-2 and BMS-POS datasets using the NCP and IGH metrics under different k-anonymity values.

Figure 2 compares the BMS-WebView-2 and BMS-POS datasets using different metrics (NCP and IGH) under varying k-anonymity values. The y-axis represents “information loss”, measured as either an average NCP or average IGH value. NCP measures information loss based on range generalization, whereas IGH evaluates information considering data uncertainty (entropy). The dashed lines represent the average NCP and IGH values for BMS-WebView-2, providing a clear distinction from the values corresponding to the BMS-POS data. The metrics were derived by calculating the loss for each anonymized transaction, with higher values indicating greater generalization and potentially lower utility.

(a) Analysis of Information Loss and Data Utility: As described in Section 2.1, NCP measured information loss based on the range of generalization and showed relatively low values across both datasets. Figure 2 compares information loss for the BMS-WebView-2 and BMS-POS datasets under varying k-anonymity values. Specifically, the NCP value for the BMS-POS dataset was <0.02, indicating minimal information loss. Conversely, IGH generally resulted in higher information loss. For example, in the BMS-POS dataset at k = 3, the IGH value was 2.55, approximately 100 times higher than the NCP value of 0.02. This suggests that while IGH enhances the protection of sensitive data, it may reduce data utility.

(b) Impact of Information Loss on Data Utility: Higher information loss can generalize data characteristics, limiting the accuracy and insights arising from analysis. For instance, when analyzing customer purchase patterns to develop targeted marketing strategies, substantial information loss can reduce the reliability of the analysis. Conversely, lower information loss retains more specific data, enhancing the utility of subsequent analyses but potentially compromising privacy. The normalized differences shown in Table 7 highlight the variance in information loss between NCP and IGH. Specifically, at k = 3 for the BMS-POS dataset, the normalized difference was 0.9924, confirming that IGH induced significantly higher information loss than NCP. This indicates that, while IGH is effective for scenarios requiring robust privacy protection, it may limit utility in data analysis.

(c) Scenario-Based Analysis of Information Loss: The impact of information loss on data utility can vary depending on the analytical scenario. For instance, in real-time financial data analysis, where quick processing and utility are paramount, the NCP-based approach with lower information loss may be more suitable. In contrast, for scenarios prioritizing privacy, such as medical data or sensitive personal information, the IGH-based LGR+ algorithm may be more effective in safeguarding sensitive data.

As such, while IGH provides strong privacy protection with higher information loss, its effect on data utility must be strategically considered based on the analytical objective and the scenario. Ultimately, the choice between IGH and NCP should be made by comprehensively reviewing the data’s sensitivity, analysis goals, and legal requirements.

4. Discussion

This study compared the LGR+ algorithm using the IGH metric with the traditional NCP-based LGR algorithm to analyze the differences in information loss and privacy protection. The experimental results clearly demonstrate how IGH improves the balance between data utility and privacy protection. Furthermore, in this section, we discuss the advantages and disadvantages of LGR+ compared to other metrics, the impact of information loss on data utility, various optimization strategies, and the observed variations in information loss among the metrics from the experiments.

4.1. Research Contributions and Significance

This paper introduces the entropy-based IGH metric to address the limitations of NCP, which fails to account adequately for data uncertainty and distribution, as identified in previous studies. For instance, prior research [6,7,8,14] has emphasized that methods such as k^m-anonymity and global suppression can only provide limited data protection. In contrast, IGH enhances privacy protection for sensitive data by evaluating data uncertainty more effectively. This approach expands upon the issues discussed in previous studies and enables stronger privacy protection, particularly for sensitive datasets.

The main contribution of this study lies in identifying the limitations of NCP-based methods and demonstrating that an IGH-based approach can improve the balance between data utility and privacy protection by more precisely evaluating data uncertainty and importance. IGH measures information loss by considering the inherent data distribution and entropy rather than relying solely on range expansion. This characteristic allows for a more accurate reflection of the information’s significance and utility, providing a robust foundation for researchers to effectively employ IGH in privacy protection strategies.

As presented in Table 4 of Section 2.3, this study highlights the limitations of existing research by comparing NCP and IGH and underscores the precision of information loss assessment when using IGH. This enhances the understanding of information loss evaluation methods and strengthens the significance of the study’s findings. The IGH-based LGR+ algorithm, which was experimentally validated under various k-anonymity levels, demonstrated its ability to provide stronger privacy protection for sensitive datasets compared to the traditional NCP-based methods.

Moreover, this study addresses the shortcomings of NCP-based methods, which maintain data utility but fail to adequately reflect significant information loss [9,23,24]. By incorporating entropy, IGH more accurately reflects data distribution and uncertainty, thus enhancing the precision of information loss assessment and filling gaps in existing research. This contribution marks a significant advancement in data anonymization and privacy protection, assisting researchers in understanding and applying more sophisticated information loss evaluation methods.

4.2. The Comparative Analysis of LGR+ and Other Entropy-Based Metrics

The IGH-based LGR+ algorithm is described in terms of its differences from the traditional NCP-based approach concerning information loss, data utility, computational complexity, and privacy protection levels. To highlight the strengths and limitations of LGR+, this analysis particularly focuses on comparing LGR+ with other entropy-based metrics, such as Shannon entropy and conditional entropy. The comparative performance analysis is summarized in Table 10.

Table 10. Comparative performance analysis of LGR+ and other entropy-based metrics.

Metric	Information Loss	Data Utility	Computational Complexity	Privacy Protection Level
LGR+ (IGH-based)	High (more precise due to entropy)	Moderate (depends on application)	High (due to complex entropy calculations)	High (effective for sensitive data)
Shannon Entropy [56,57]	Moderate	High	Moderate	Moderate
Conditional Entropy [58,59]	Low to Moderate	High	Low to Moderate	Low to Moderate

The LGR+ algorithm using the IGH metric evaluates information loss based on entropy, which accurately reflects data uncertainty and distribution. While LGR+ results in higher information loss, it is more precisely assessed using entropy calculations. This increased information loss enhances sensitive data protection but comes at the cost of greater computational complexity, necessitating optimization strategies for real-time data processing. The data utility of LGR+ varies depending on the application and analysis objectives, making it particularly effective for scenarios where privacy protection is paramount.

Shannon entropy [56,57] is an efficient metric known for evaluating the information content of data. It generally results in moderate information loss and high data utility. The computational complexity is relatively low, making it effective even for large datasets. Shannon entropy is widely used in various data analysis applications due to its simplicity, which makes it suitable for real-time processing. However, its level of privacy protection is lower compared to LGR+, which may make it less effective in protecting sensitive data.

Conditional entropy [58,59] measures the information loss given specific attributes, maintaining high data utility with relatively low computational complexity, which is ideal for real-time processing. However, its privacy protection level is lower compared to LGR+, making it more suitable for scenarios where privacy protection is not a priority. Conditional entropy can be advantageous in applications where analyzing the relationships between data attributes is essential.

In conclusion, while LGR+ incurs higher information loss, it is highly beneficial in situations where protecting sensitive data is crucial. The IGH-based evaluation more precisely reflects data uncertainty and importance, providing robust privacy protection, especially for sensitive datasets. However, the increased computational complexity may hinder performance in real-time data processing, necessitating optimization strategies. Conversely, Shannon entropy and conditional entropy provide lower computational complexity and higher data utility, making them more suitable for real-time analysis and data use, although their privacy protection levels are more limited.

4.3. Information Loss and Privacy Protection

Experiments using the BMS-WebView-2 and BMS-POS datasets showed that the IGH-based LGR+ algorithm tended to cause greater information loss than the NCP-based algorithm. IGH allows for a more precise evaluation of information loss by assessing data uncertainty through entropy, thereby enhancing privacy protection. For example, on the BMS-POS dataset with k = 3, IGH recorded approximately 100 times more information loss than NCP, indicating a higher level of privacy protection. Conversely, NCP maintained lower information loss and preserved data utility better.

These results suggest that IGH provides stronger privacy protection for datasets that contain sensitive information. High information loss implies more generalized data, making it more difficult for an attacker to infer specific personal information. Conversely, lower information loss indicates that more specific information is retained, ensuring higher utility for subsequent data analysis.

4.4. Balancing Data Utility and Privacy Protection

In this study, IGH and NCP exhibited contrasting performances regarding privacy protection and data utility. IGH enhances privacy protection by providing a more detailed measurement of information loss, although it can also reduce utility. While maintaining relatively low information loss, NCP exhibited a weaker privacy protection performance than IGH. This highlights the importance of balancing privacy and utility in data anonymization and selecting an appropriate metric based on data characteristics and purposes.

For example, when privacy is prioritized for sensitive information, IGH may be more suitable. In contrast, when maintaining utility for data analysis, NCP could be a better choice. Thus, the choice between IGH and NCP should comprehensively consider factors such as data sensitivity, analytical purpose, and legal requirements.

4.5. Computational Complexity and Optimization Strategies

The high computational complexity of the IGH-based LGR+ algorithm can impact performance in real-time applications. While IGH’s entropy-based approach accurately evaluates data uncertainty and distribution, it can reduce processing efficiency due to its complex calculations. To address this, various optimization strategies, including parallel processing and sampling techniques, are proposed in Section 3.3.3. This section discusses additional measures to enhance the algorithm’s applicability in real-time scenarios:

(a) Impact on Real-Time Applications: The computational load of the IGH-based LGR+ algorithm can affect response times in real-time data processing. The complexity of entropy calculations can be particularly challenging for large datasets, requiring additional optimization to ensure real-time performance. Effective memory management and caching strategies are crucial for maintaining speed and efficiency. The pre-computation and caching of frequently used entropy values can reduce repetitive calculations and improve processing speed, significantly enhancing real-time responsiveness.

(b) Dynamic Algorithm Adjustment: Another approach is to dynamically adjust the algorithm’s complexity based on data characteristics and analysis goals during real-time processing. Adjusting the precision of entropy calculations as needed can optimize processing speed and performance, balancing speed and accuracy in real-time analysis.

(c) Lightweight Approximation Methods: Approximation methods can simplify entropy calculations, helping to maintain real-time processing performance. These techniques reduce computational complexity while ensuring the adequate accuracy of information loss, making them beneficial for real-time applications.

(d) Entropy Calculation Optimization: Minimizing unnecessary operations or improving the mathematical processes involved in entropy calculations can boost processing speed. Such optimizations are vital for reducing computational overhead and maintaining performance in real-time scenarios.

When applying the IGH-based LGR+ algorithm in real-time applications, high computational complexity can pose challenges. However, employing techniques such as memory management, caching, dynamic algorithm adjustment, and approximation methods can effectively address these issues. This enables the IGH-based LGR+ algorithm to maintain strong privacy protection and efficiency in real-time environments.

4.6. Limitations of the Study

Although this study demonstrates the effectiveness of IGH in enhancing privacy protection, further validation with diverse datasets is required to generalize the findings. Additionally, the effectiveness of optimization techniques to address the computational complexity of IGH should be further explored.

5. Conclusions

This study proposed a novel LGR+ algorithm incorporating the information gain heuristic (IGH) to address the limitations of normalized certainty penalty (NCP)-based methods in anonymizing set-valued transaction data. By providing a more precise assessment of data uncertainty, this algorithm improves the balance between privacy protection and data utility.

The primary goal is to overcome NCP’s limitations in evaluating information loss through simple range expansion and to propose a more sophisticated method that better protects sensitive data. The experimental results show that the IGH-based LGR+ algorithm offers stronger privacy protection for sensitive datasets, essential in sectors like e-commerce, finance, and healthcare.

The findings demonstrate that IGH more accurately reflects the data distribution and uncertainty, enhancing privacy protection compared to NCP. However, the increased computational complexity poses efficiency challenges for large datasets.

Future research will focus on improving the computational efficiency of the LGR+ algorithm through parallel processing and sampling techniques to enable real-time processing. Additionally, integrating other privacy models, such as l-diversity and t-closeness, will be explored to meet diverse privacy requirements.