A Two-Phase Deep Learning Approach to Link Quality Estimation for Multiple-Beam Transmission

Abstract

In the multi-user multiple-input-multiple-output (MU-MIMO) beamforming (BF) training defined by the 802.11ay standard, since a single initiator transmits a significant number of action frames to multiple responders, inefficient configuration of the transmit antenna arrays when sending these action frames increases the signaling and latency overheads of MU-MIMO BF training. To configure appropriate transmit antenna arrays for transmitting action frames, the initiator needs to accurately estimate the signal to noise ratios (SNRs) measured at the responders for each configuration of the transmit antenna arrays. In this paper, we propose a two-phase deep learning approach to improve the accuracy of SNR estimation for multiple concurrent beams by reducing the measurement errors of the SNRs for individual single beams when each action frame is transmitted through multiple concurrent beams. Through simulations, we demonstrated that our proposed scheme enabled more responders to successfully receive action frames during MU-MIMO BF training compared to existing schemes.

1. Introduction

Various applications, such as AR/VR, mobile offloading, high-bandwidth connectivity to multiple TV and monitor displays, and wireless backhaul, demand new technologies for wireless local area networks (WLANs) [1]. Recently, the 802.11ay standard, which enables WLAN devices to achieve data rates of up to hundreds of Gbps in millimeter waves (mmWaves), was established [2]. However, communication in the mmWave band suffers from increased severe path loss, blockage by common materials, and Doppler spread compared to the microwave band [3]. To improve the quality of the mmWave link, the 802.11ay standard defines beamforming (BF) training protocols that determine the proper antenna weight vectors (AWVs) for the transmitter and receiver to establish highly directional communications [2,4].

Numerous studies have been conducted to reduce the overhead of BF training for 802.11ay WLANs. Studies [1,5,6,7] investigated the BF training procedures specified in the 802.11ay standard and discussed the impact of BF training design [2]. In [8,9,10,11], algorithms were proposed to enhance the performance of BF training, such as beam selection and reducing BF training latency. Studies [12,13,14] have proposed methods for applying the BF training of 802.11ay to fixed wireless access and virtual reality applications. Recent studies have used deep learning models to develop efficient BF training in the mmWave band. Algorithms utilizing deep learning approaches have mainly addressed the challenges of beam selection and channel estimation in BF training [15,16,17,18]. Other studies [19,20] have used deep learning approaches to propose efficient BF training in specific scenarios, such as massive multiple-input-multiple-output (MIMO) and linear movable antenna arrays.

Given that one of the major advancements of 802.11ay is downlink multi-user multiple-input-multiple-output (MU-MIMO) transmission, many studies have also been conducted on the BF training of MU-MIMO. Studies [21,22] have tackled the challenges of BF training for uplink MU-MIMO transmissions, which is not defined in the 802.11ay standard [2]. On the other hand, our prior studies [23,24,25] proposed algorithms to reduce the latency and failure probability of MU-MIMO BF training within the framework of the 802.11ay standard [2]. Specifically, in the MIMO phase of MU-MIMO BF training defined by the 802.11ay standard, the access point (AP) transmits numerous action frames to multiple stations (STAs) in the multi-user (MU) group [2]; our previous studies proposed methods to determine the appropriate transmit sectors (TSs), i.e., precomputed AWVs, for transmitting these action frames. Action frames should be transmitted though multiple concurrent beams using multiple antenna arrays [2]. Therefore, to determine the appropriate transmit sectors, the AP is required to accurately estimate the SNRs measured at the STAs when multiple concurrent beams are transmitted through candidate transmit sectors. The scheme in [23] estimates the signal to noise ratio (SNR) for multiple concurrent beams by selecting the highest SNR among the respective single beams. In [24], the proposed scheme measures the channel information for respective single beams and uses this information to estimate the SNR for multiple concurrent beams. The scheme in [25] uses the SNRs of respective single beams as input to a deep learning model and estimates the SNR for multiple concurrent beams as the output of the deep learning model. However, the scheme in [24] has the overhead of requiring an additional process not defined in the 802.11ay standard, where the AP must collect channel information from the STAs [2]. The schemes in [23,25] estimate the SNR for multiple concurrent beams based on the SNRs of individual single beams obtained from a single measurement, leading to significant estimation errors.

In the mmWave band, because each single beam is transmitted through multiple paths, multiple concurrent beams can cause inter-symbol interference [26]. To reduce the effects of inter-symbol interference, the 802.11ay standard applies a transmit diversity technique, cyclic shift diversity (CSD), to the transmission of multiple concurrent beams [2]. Moreover, the SNR of each single beam can vary significantly with each measurement, even in the same propagation environment, due to diffuse reflections scattered randomly from irregular surfaces. Therefore, using the SNRs of single beams measured once to estimate the SNR for multiple concurrent beams can lead to significant errors. This make the AP uncertain whether the STAs has successfully received the action frame transmitted through multiple concurrent beams during the MIMO phase of MU-MIMO BF training. The AP may send additional unnecessary action frames, and the STAs may fail to receive the action frames. Consequently, the latency of MU-MIMO BF training increases.

To address the aforementioned issues, in this paper, we propose a two-phase deep learning based multiple-beam transmission (TDMT) scheme for MU-MIMO BF training. In the first-phase deep learning model of our TDMT scheme, the SNRs of the respective single beams are calibrated to improve the accuracy of the SNR estimation for multiple concurrent beams. Then, in the proposed second-phase deep learning model, the calibrated SNRs are used to estimate the SNRs that will be measured at the STA when multiple concurrent beams are received. The main contributions of the study are summarized as follows:

• We use an autoencoder to calibrate the SNRs of single beams transmitted through each of the AP’s transmit sectors during the SISO phase of MU-MIMO BF training. To achieve this, we propose a method for training the autoencoder to reduce the measurement errors of the SNRs for single beams.
• We also provide a deep learning model that accurately estimates the SNR for multiple concurrent beams based on the calibrated SNRs for single beams.
• Using a deep learning model that accurately estimates the SNR of multiple concurrent beams, we propose an algorithm to configure the transmit antenna arrays for transmitting action frames through multiple concurrent beams during the MIMO phase of MU-MIMO BF training.
• For a realistic performance evaluation, we extend the open-source code of [27], which implements a sparse multipath environment based on the Q-D channel model. Additionally, we implement a transceiver for transmitting action frames as defined in the 802.11ay standard using the MATLAB WLAN toolbox [2].

The rest of this article is structured as follows. In Section 2, we describe the signaling procedure of MU-MIMO BF training and discuss related studies on BF training in the mmWave band. Section 3 presents a system model for transmitting action frames during the MIMO phase of MU-MIMO BF training. Section 4 details our proposed TDMT scheme. In Section 5, we discuss the simulation results. Finally, Section 6 concludes the paper.

2. Background and Contributions

In this section, we first describe the procedure of MU-MIMO BF training, the main topic of this paper, as specified in the 802.11ay standard [2]. We then introduce recent studies on the performance improvement, performance evaluation, and applications of BF training in 802.11ay. Finally, we present studies that utilized deep learning approaches to enhance the performance of BF training, similarly to the method proposed in this paper.

2.1. MU-MIMO Beamforming

In addition to the IEEE 802.11ay standard [2], many recent studies, such as [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], have detailed the procedure of MU-MIMO BFT. The MU-MIMO BF training in IEEE 802.11ay consists of a single-input-single-output (SISO) phase and a MIMO phase.

The SISO phase can be divided into a transmit sector sweep subphase and a feedback subphase, as shown in Figure 1. In the transmit sector sweep subphase, the AP transmits short sector sweep (SSW) frames to STAs in the MU group across all transmit sectors. In the feedback subphase, each STA sends a feedback frame to the AP containing the SNRs measured when receiving the SSW frames and the transmit sector identifiers included in the SSW frames.

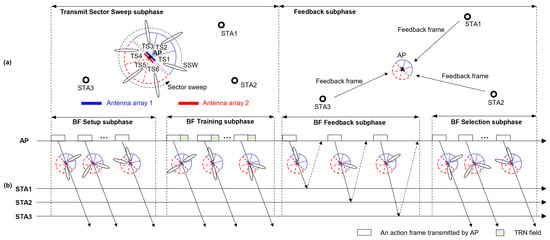
Figure 1. The (a) SISO phase and (b) MIMO phase of MU-MIMO BF training specified in the 802.11ay standard.

The MIMO phase is divided into a BF setup subphase, BF training subphase, BF feedback subphase, and BF selection subphase. During the BF setup subphase, the AP transmits action frames named BF setup, which include a list of STAs participating in the MIMO phase. In the BF training subphase, the AP transmits action frames named BRP-RX/TX, which contain TRN fields used to test candidate AWVs for downlink MU-MIMO transmission. During the BF feedback subphase, each STA sends an action frame named BF feedback to the AP, including the results of tests on candidate AWVs conducted during the BF training subphase. Finally, in the BF selection subphase, the AP transmits action frames named BF selection, which include information on the receive AWVs that the STAs should use during downlink MU-MIMO transmission.

2.2. BF Training Schemes for mmWave WLAN

The 802.11ay standard for mmWave WLAN defines protocols for BF training and the format of related frames but does not provide specific details such as the configuration of the transmitter’s antenna array. The authors of [7] described the beamforming training field defined in the standard and evaluated the impact of beamforming on the frame error rate and channel statistics. The authors of [6] introduced a beam refinement protocol and asymmetric beamforming training for 802.11ay WLAN. Studies [8,9] have proposed algorithms for determining beam patterns to reduce inter-stream interference during the simultaneous transmission of multiple spatial streams. Fixed wireless access using 802.11ay was proposed in  [12,13]. The authors of [10,11] proposed algorithms for efficient beamforming training in dense 802.11ay WLAN environments. Studies [23,24,25] have proposed algorithms for configuring the transmitter’s antenna array to transmit action frames in MU-MIMO BF training as specified in the 802.11ay standard. Another study [14] designed MU-MIMO BF training to support virtual reality applications. A recent study [21] proposed a BF training algorithm for realizing uplink MU-MIMO communication. The authors of [22,28] designed BF training frameworks for MU-MIMO transmissions using a single RF chain.

2.3. Deep Learning Approaches for BF Training

Many recent studies have employed deep learning approaches to tackle issues such as beamforming design, beam selection, and channel estimation.

The authors of [15] proposed a deep-learning-based algorithm for the concurrent transmission of multiple beams in dense mmWave networks, utilizing beam management and interference coordination. In [16], the authors proposed a low-overhead analog beam selection scheme for mmWave communications using deep learning. The authors of [29] utilized a deep CNN model to dynamically adjust the number of training beams. The authors of [17] tackled the challenges of beamforming and maximizing phased array gain for practical phase shifters using a deep learning approach. In [18], a model-driven deep learning approach was utilized to address the problems of beamforming design and channel estimation. The authors of [19] studied the problems of antenna selection and beamforming design for massive MIMO using deep self-supervised learning. In [20], the authors proposed a novel deep learning model for multicast beamforming with a linear movable antenna array.

3. System Model

Since this paper addresses the configuration of transmit antenna arrays for transmitting action frames during the MIMO phase of MU-MIMO BF training, this section describes the transmitter architecture when an action frame is transmitted as multiple concurrent beams, and presents a channel model for calculating the SNR measured at each STA for these multiple concurrent beams.

3.1. Transmitter Architecture

In MU-MIMO BF training, each action frame is transmitted using a control mode over a 2.16 GHz channel; the control mode is based on BPSK modulation with a spreading factor of 32, enabling the AP and the STAs to communicate with a low SNR [1,2]. As depicted in Figure 2, the transmitter, i.e., the AP, scrambles, encodes, and modulates the bit stream of an action frame. Then, the AP maps the encoded and modulated bit stream to all radio frequency (RF) chains by applying a spatial expansion with cyclic shift diversity. Finally, each antenna array transmits the bit stream, which is mapped to each RF chain, through a transmit sector.

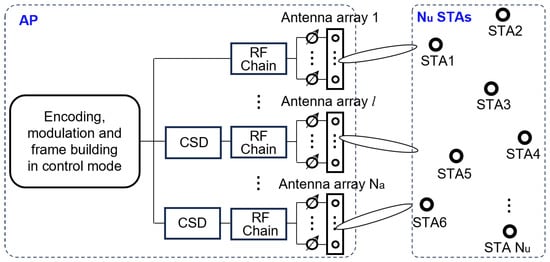
Figure 2. Control mode transmitter block diagram for transmission of action frames during the MIMO phase of MU-MIMO BF training.

3.2. Channel Model

In the mmWave bands, most of the transmission power is propagated from the transmitter to the receiver through the direct path and reflected paths. Each reflected path can be characterized by the clustering of a strong specular reflection from a flat surface and weak diffuse reflections scattered from irregular surfaces.

Let $N_C$ represent the total number of multipath component clusters, including the direct path and all reflected paths. Then, let $N_M$ denote the number of all direct, specular reflection, and diffuse reflection paths within these clusters. Referring to [25,30,31], the channel impulse response of the beamformed channel at time t between the l-th antenna array and the receive antenna array is given by

$$\begin{array}{c}\hfill h_l^{BF}\left(t\right)={\displaystyle \frac{1}{\sqrt{N_C}}}\sum _{m=1}^{N_M}\left({10}^{P{G}_m/20}·e^{j(-2\pi f_c{t}_m+{\mathrm{\Psi }}_m)}·\delta (t-t_m)·{\mathbf{w}}_r·{\mathbf{a}}_r({\varphi }_m^a,{\theta }_m^a)·{\mathbf{a}}_t{({\varphi }_m^d,{\theta }_m^d)}^{\ast }·{\mathbf{w}}_t\right),\end{array}$$

(1)

where $f_c$ is the carrier frequency; $P{G}_m$ is the path gain; $t_m$ is the delay time for the ray to arrive at the receive antenna array via the m-th path; ${\mathrm{\Psi }}_m$ is the phase shift; $\delta (·)$ is the Dirac delta function; ${\mathbf{w}}_t$ is the weight vectors of the transmit antenna array; ${\mathbf{w}}_r$ is the weight vectors of the receive antenna array; ${\mathbf{a}}_t({\varphi }_m^d,{\theta }_m^d)$ is the steering vector when ${\varphi }_m^d$ and ${\theta }_m^d$ are given as the azimuth and elevation angles of departure for the ray departing from the transmit antenna array via the m-th path; ${\mathbf{a}}_r({\varphi }_m^a,{\theta }_m^a)$ is the steering vector when ${\varphi }_m^a$ and ${\theta }_m^a$ are given as the azimuth and elevation angles of arrival for the ray to arrive at the receive antenna array via the m-th path.

Let ${\mathbf{h}}_l$ denote the channel vector for an antenna array l using an equivalent uniformly spaced tapped delay line. Then, the channel vector ${\mathbf{h}}_l$ can be represented from the channel impulse response $h_l^{BF}\left(t\right)$ by applying interpolation filtering [32]. We assume a frequency-selective channel and adopt a block-fading model where the channel remains constant over each transmission block [26]. Given a transmission block containing L symbols, the channel vector ${\mathbf{h}}_l$ with L elements can be represented as follows:

$$\begin{array}{c}\hfill {\mathbf{h}}_l=[h_{l,1},\cdots ,h_{l,d},\cdots ,h_{l,\nu }\cdots 0],\end{array}$$

(2)

where $h_{l,d}$ is the channel coefficient for the delay of the d-th tap, measured in units of single carrier chip time, and $\nu$ is the number of delay taps of the channel.

As explained in Section 3.1, the AP simultaneously transmits the bit stream of a single action frame through multiple antenna arrays by applying cyclic shift diversity to each antenna array. Let ${\mathbf{h}}_{csd}$ be the channel vector used to obtain the signal when receiving this multiple concurrent transmission. Then, the channel vector ${\mathbf{h}}_{csd}$ is given by

$$\begin{array}{c}\hfill {\mathbf{h}}_{csd}=\sum _{l=1}^{N_a}{f}_{csd}({\mathbf{h}}_l,{\delta }_l),\end{array}$$

(3)

where ${\delta }_l$ is the number of shifts applied to antenna array l for cyclic shift diversity, and $f_{csd}(·)$ is a function that shifts the channel vector ${\mathbf{h}}_l$ to the right by ${\delta }_l$.

Let $\mathbf{x}$ denote the encoded and modulated bit stream of the action frame with length L before applying cyclic shift diversity. Then, the equalized received signal can be obtained as follows:

$$\begin{array}{c}\hfill \mathbf{y}=\sqrt{\rho }·\mathbf{E}·{\mathbf{H}}_{csd}·\mathbf{x}+\mathbf{E}·\mathbf{n},\end{array}$$

(4)

where $\rho$ is the transmit power, $\mathbf{E}$ is an equalizer, $\mathbf{n}$ is a noise vector, and ${\mathbf{H}}_{csd}$ is an $L\times L$ truncated Toeplitz matrix whose first row is the channel vector ${\mathbf{h}}_{csd}$.

Let ${\mathbf{e}}_k$ be the k-th row of matrix $\mathbf{E}$, and let ${\mathbf{h}}_{csd}^{\left(k\right)}$ be the k-th column of matrix ${\mathbf{H}}_{csd}$. The SNR for the equalized received signal $\mathbf{y}$ with length L can be calculated as follows:

$$\begin{array}{c}\hfill \gamma ={\displaystyle \frac{1}{L}}\sum _{k=1}^L{\displaystyle \frac{\rho (||{\mathbf{e}}_k{\mathbf{h}}_{csd}^{\left(k\right)}{\left|\right|}_2{)}^2}{\rho ·{\sum }_{k^{\prime }\ne k}^L\left(\right||{\mathbf{e}}_k{\mathbf{h}}_{csd}^{\left(k^{\prime }\right)}{\left|\right|}_2{)}^2)+{\rho }_n·{\mathbf{e}}_k{\mathbf{e}}_k^{\ast }}},\end{array}$$

(5)

where ${\rho }_n$ is the noise power, $\left|\right|·{\left|\right|}_2$ represents the Euclidean norm, and ${\mathbf{e}}_k^{\ast }$ represents the transpose of the vector ${\mathbf{e}}_k$.

4. Two-Phase Deep Learning Approach to Link Quality Estimation

In the MIMO phase of MU-MIMO BF training, action frames should be transmitted through multiple concurrent beams to reduce the required number of transmissions [2]. The AP should select appropriate transmit sectors to transmit the multiple concurrent beams. To this end, the AP should estimate the accurate link quality, i.e., the SNR, that will be measured at the STAs when a set of transmit sectors are used concurrently to transmit multiple beams.

To estimate the SNR of an action frame transmitted through multiple concurrent beams in the MIMO phase, the SNR of each single beam measured in the SISO phase is used. However, the SNR for multiple concurrent beams cannot be simply estimated from the SNRs of individual single beams. Since each individual single beam is transmitted via multiple paths, simultaneous transmission of multiple single beams can cause inter-symbol interference. Moreover, even if the position and receive pattern of the STA are the same, the SNR of each beam can vary significantly with each measurement at the STA, due to diffuse reflections randomly scattered from irregular surfaces. Therefore, using the SNRs of single beams measured once during the SISO phase to estimate the SNR for multiple concurrent beams can lead to significant errors. To accurately estimate the SNR of multiple concurrent beams, our proposed scheme employs a two-phase deep learning approach.

In this section, we first describe how our proposed first-phase deep learning model calibrates the SNRs of single beams measured once during the SISO phase. Next, we explain how our proposed second-phase deep learning model uses these calibrated SNRs to estimate the SNR for multiple concurrent beams. Finally, we detail how the MU-MIMO BF training operates with our two-phase deep learning approach.

Figure 3 illustrates the overall procedure of our TDMT scheme, and Table 1 presents the notations used to describe our TDMT scheme.

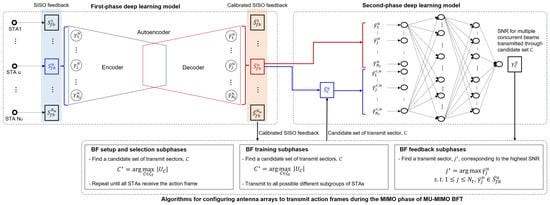
Figure 3. Overall procedure of our TDMT scheme.

Table 1. Notations used to describe our proposed TDMT scheme.

Notation	Description
$N_t$	Number of transmit sectors of the AP
$N_a$	Number of antenna arrays of the AP
$S_{fb}^u$	Set of SNRs measured at the STA u for SSW frames transmitted across all transmit sectors of the AP
${\gamma }_j^u$	SNR measured at the STA u for the SSW frame transmitted through the j-th transmit sector
${\overline{S}}_{fb}^u$	Set of SNRs calibrated from $S_{fb}^u$
${\overline{\gamma }}_j^u$	SNR calibrated from ${\gamma }_j^u$
${\overline{S}}_C^u$	Set of SNRs corresponding to the transmit sectors of the candidate set of transmit sectors C
${\overline{\gamma }}_j^{c,u}$	j-th SNR of the set ${\overline{S}}_C^u$
${\zeta }_t$	Collection comprising all candidate sets of transmit sectors
$U_C$	Subgroups of STAs within the MU group that are reachable by transmission through the candidate set of transmit sectors C
${\delta }_r$	SNR threshold for the successful transmission of an action frame to the STA

4.1. Calibration of Link Qualities Measured with Single Beams

The SNR of multiple concurrent beams is estimated from the SNRs measured from the respective single beams. Therefore, our proposed first-phase deep learning model calibrates the SNRs of the respective single beams to improve the accuracy of the SNR estimation for multiple concurrent beams.

For the first-phase deep learning model, we use an autoencoder consisting of an encoder, a latent space, and a decoder. The encoder includes a single input layer, with the number of nodes being equal to the number of transmit sectors of the AP. The input data comprise SNR values measured at the STA for single beams transmitted through each respective transmit sector of the AP. The latent space is a compressed representation that captures the essential features of the input data. The decoder, which includes an output layer, reconstructs the input data from the latent space representation.

Our first-phase deep learning model should be pre-trained before MU-MIMO BF training is conducted. For training, a dataset must be collected that includes SNR values for single beams transmitted through each transmit sector of the AP, with the AP’s position fixed in a designated propagation environment. To this end, the STA measures the SNRs for the single beams at each possible position within the designated propagation environment using the same receive antenna pattern. To capture the variations in SNR values measured for each single beam, the AP transmits single beams multiple times through each transmit sector, and the STA includes the corresponding SNR measurements in the dataset.

Let ${\mathcal{S}}^p=\{S_1^p,\cdots ,S_i^p,\cdots ,S_{N_m}^p\}$ denote a collection of $N_m$ sets of SNRs measured when the position of the STA is p. Here, $S_i^p$ is the i-th set of SNRs, and $S_i^p=\{{\gamma }_{i,1},\cdots ,{\gamma }_{i,j},\cdots ,$${\gamma }_{i,N_t}\}$, where $N_t$ is the total number of transmit sectors of the AP, and ${\gamma }_{i,j}$ is the SNR measured when the STA receives a single beam transmitted through the j-th transmit sector. To train our first-phase deep learning model when the position of the STA is p, we use the set of SNRs, $\forall S_i^p\in {\mathcal{S}}^p$, as the input data. We then use the average of all SNRs contained in the collection ${\mathcal{S}}^p$ for each transmit sector, denoted by ${\overline{S}}_p$, as the target output. The target output ${\overline{S}}_p$ can be obtained as follows:

$$\begin{array}{c}\hfill {\overline{S}}_p=\{{\overline{\gamma }}_1^p,\cdots ,{\overline{\gamma }}_j^p,\cdots ,{\overline{\gamma }}_{N_t}^p\}\end{array}$$

(6)

where

$$\begin{array}{c}\hfill {\overline{\gamma }}_j^p=\sum _{i=1}^{N_m}{\displaystyle \frac{{\gamma }_{i,j}}{N_m}}.\end{array}$$

(7)

4.2. Estimation of Link Quality for Multiple Concurrent Beams

Our proposed second-phase deep learning model is utilized to estimate the SNR to be measured at the STA when multiple concurrent beams are received. For the second-phase deep learning model, we use a multilayer perceptron neural network consisting of one input layer, one output layer, and multiple hidden layers. Each layer contains a set of nodes that are fully connected to the nodes in the next layer; however, the nodes within a layer are not connected to each other.

Let $S_{fb}^u$ denote the set of SNRs measured at the STA u for SSW frames transmitted across all transmit sectors of the AP. Here, $S_{fb}^u=\{{\gamma }_1^u,\cdots ,{\gamma }_j^u,\cdots ,{\gamma }_{N_t}^u\}$, where ${\gamma }_j^u$ is the SNR measured at the STA u for the SSW frame transmitted through the j-th transmit sector. In the MU-MIMO BF training, the set $S_{fb}^u$ can be obtained from the STA u during the feedback subphase of the SISO phase.

Let ${\overline{S}}_{fb}^u=\{{\overline{\gamma }}_1^u,\cdots ,{\overline{\gamma }}_j^u,\cdots ,{\overline{\gamma }}_{N_t}^u\}$ be the output of our first-phase deep learning model when the set $S_{fb}^u$ is used as an input; that is, ${\overline{S}}_{fb}^u$ represents the set of SNRs calibrated from $S_{fb}^u$. Let C be a candidate set of multiple transmit sectors that can be used simultaneously to transmit multiple concurrent beams. Then, ${\overline{S}}_C^u=\{{\overline{\gamma }}_1^{c,u},\cdots ,{\overline{\gamma }}_j^{c,u},\cdots ,{\overline{\gamma }}_{N_t}^{c,u}\}$ denotes a set of SNRs corresponding to the transmit sectors of the candidate set C. If the candidate set C includes the j-th transmit sector of the AP, the j-th SNR of the set ${\overline{S}}_C^u$, ${\overline{\gamma }}_j^{c,u}$, is set to the j-th SNR of the set ${\overline{S}}_{fb}^u$; otherwise, ${\overline{\gamma }}_j^{c,u}$ is zero. Therefore, the input to our second-phase deep learning model can be presented as the tuple $({\overline{S}}_{fb}^u,{\overline{S}}_C^u)$, while the output, denoted as ${\gamma }_C^u$, is the SNR to be measured at STA u when all transmit sectors in the candidate set C are used simultaneously to transmit an action frame in the MIMO phase of MU-MIMO BF training.

4.3. MU-MIMO BF Training with Two-Phase Deep Learning

In the MIMO phase of MU-MIMO BF training, the AP transmits each action frame through multiple transmit sectors of multiple antenna arrays; thus, the action frame is transmitted through multiple beams, and this enables multiple STAs to receive the action frame at the same time. The SNRs corresponding to the respective transmit sectors of the AP, which are included in the SISO feedback, are considered to determine the set of transmit sectors to be used to transmit the action frame.

BF setup and selection subphases: In the BF setup or selection subphase of the MIMO phase, the AP should transmit the same action frame to all STAs within the MU group. To this end, the AP repeats the transmission until all STAs have received the action frame; each transmission is performed through a different set of transmit sectors to reduce unnecessary transmissions. Then, our proposed scheme determines a set of transmit sectors to be used to perform each transmission of the action frame, as follows (Algorithm 1):

Algorithm 1 Transmit antenna configuration during the BF setup and selection subphases

(1) Our proposed scheme finds a candidate set of transmit sectors, C, such that, when the AP transmits the action frame through the candidate set C, the transmission reaches the largest number of STAs that have not received the action frame. Let $N_a$ be the number of antenna arrays of the AP; then, $C=\{{\alpha }_1,\cdots ,{\alpha }_l,\cdots ,{\alpha }_{N_a}\}$ where ${\alpha }_l$ is the selected transmit sector among the transmit sectors of the l-th antenna array. Our proposed scheme utilizes ${\gamma }_C^u$, which is obtained as described in Section 4.2, to determine if the transmission through the candidate set C reaches STA u. Let ${\delta }_r$ denote the threshold for the SNR to be measured at a STA, ensuring successful transmission to the STA; then, if ${\gamma }_C^u>{\delta }_r$, our proposed scheme determines that the transmission through the candidate set C can reach the STA u. (2) The AP transmits the action frame through the candidate set C, and our proposed scheme assumes that the transmission has successfully reached all STAs u satisfying ${\gamma }_C^u>{\delta }_r$. Then, steps 1 and 2 are repeated until all STAs have received the action frame.

However, in the first step of the above procedure, if the SNRs corresponding to all candidate sets of transmit sectors need to be estimated, our scheme will have a high computational complexity. Thus, our proposed scheme reduces the complexity as follows (Algorithm 2):

Algorithm 2 Transmit antenna configuration to reduce complexity

(1) Our proposed scheme eliminates candidate sets that have at least one transmit sector not included in the SISO feedbacks received from the STAs. (2) For each remaining candidate set C, the SNR measured at the STA u when the action frame is transmitted through the transmit sectors of the candidate set C, i.e., ${\gamma }_C^u$, is estimated by simply summing the SNRs corresponding to the respective transmit sectors in the candidate set C. The SNRs corresponding to the respective transmit sectors in the candidate set C can be obtained from the SISO feedback received from the STA u, i.e., $S_{fb}^u$. (3) Our proposed scheme, similarly to the first step of Algorithm 1, finds a candidate set of transmit sectors, $C^{\ast }$, such that the transmission through the candidate set $C^{\ast }$ reaches the largest number of STAs. (4) For each STA u, our scheme obtains ${\left({\gamma }_{C^{\ast }}^u\right)}^{\prime }$, as described in Section 4.2; then, if the existing ${\gamma }_{C^{\ast }}^u$ is not equal to ${\left({\gamma }_{C^{\ast }}^u\right)}^{\prime }$, ${\gamma }_{C^{\ast }}^u$ is updated to ${\left({\gamma }_{C^{\ast }}^u\right)}^{\prime }$. (5) Our proposed scheme iterates steps 3, 4, and 5 until ${\gamma }_{C^{\ast }}^u$ is not updated for all STAs u. (6) The AP, similarly to the second step of Algorithm 1, transmits the action frame through the candidate set $C^{\ast }$. Then, steps 3 to 6 are repeated until all STAs have received the action frame.

BF training subphase: In the BF training subphase of the MIMO phase, we assume that the AP determines appropriate directional antenna patterns for all possible different subgroups of STAs within the MU group. Then, action frames, i.e., BRP-RX/TX, should be transmitted to all possible different subgroups of STAs within the MU group, as follows:

(1)

Let ${\zeta }_t$ represent a collection comprising all candidate sets of transmit sectors; then, for each candidate set C, our proposed scheme identifies the subgroups of STAs within the MU group, denoted as $U_C$, that are reachable by transmission through the candidate set C.

(2)

Our proposed scheme finds a candidate set of transmit sectors, $C^{\ast }$, that corresponds to the subgroup, $U_{C^{\ast }}$, containing the maximum number of STAs, as follows:

$$\begin{array}{c}\hfill C^{\ast }=arg\underset{C\in {\zeta }_t}{max}|U_C|\end{array}$$

(8)

where $|U_C|$ is the number of STAs in the subgroup $U_C$.

(3)

The AP transmits the action frame, i.e., BRP-RX/TX, through the candidate set $C^{\ast }$.

(4)

Our proposed scheme excludes a candidate set C from the collection ${\zeta }_t$ when its corresponding subgroup $U_C$ falls within the subgroup $U_{C^{\ast }}$.

(5)

Steps 2 to 5 are repeated until the collection ${\zeta }_t$ is empty.

The above procedure can be transformed in a manner similarly to Algorithm 2 to reduce the computational complexity.

BF feedback subphase: In the BF feedback subphase of the MIMO phase, our proposed scheme transmits the action frame through a single transmit sector corresponding to the highest SNR included in the SISO feedback. To this end, for the STA u, our scheme employs the set of SNRs, ${\overline{S}}_{fb}^u$, calibrated through our first-phase deep learning model from the SISO feedback of the STA u, $S_{fb}^u$, as follows:

$$\begin{array}{c}{j}^{\ast }=argmax{\overline{\gamma }}_j^u\hfill \\ \mathrm{s}.\mathrm{t}.1\le j\le N_t,{\overline{\gamma }}_j^u\in {\overline{S}}_{fb}^u\hfill \end{array}$$

(9)

Then, the AP transmits the action frame to the STA u through the $j^{\ast }$-th transmit sector.

5. Performance Evaluation

We evaluated the performance of our proposed TDMT scheme through simulations, in terms of the estimation error of the SNRs measured at the STAs for the action frames transmitted during MU-MIMO BF training and the latency of the MIMO phase in MU-MIMO BF training. The performance of our proposed TDMT scheme was compared to that of the DTAC scheme, proposed in [25], which uses a deep learning model in a similar manner. Additionally, we compared the performance of our proposed scheme with the SSBE scheme, which estimates the SNR of multiple concurrent beams by summing the SNRs of individual single beams [24]. Figure 4 illustrates the implementation of the simulation programs used to evaluate the performance of our proposed scheme.

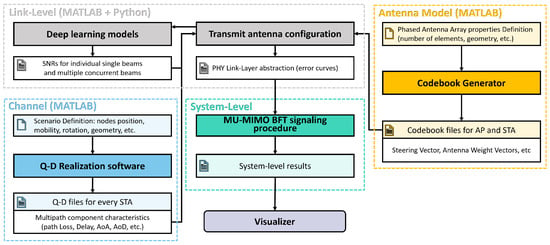
Figure 4. Implementation of simulation programs with MATLAB and python 3.10 [27].

5.1. Simulation Setup

To evaluate the performance over realistic mmWave channels, we used the Q-D channel realization software developed as open-source by NIST. As shown in Figure 5, we used the propagation scenarios of a lecture room and an L-shaped room, with the AP fixed at the coordinates (1,3,1) and (9,3,1) m, respectively. The MU group consisted of 11 STAs, each randomly positioned within the designated propagation scenario. The AP used three phased antenna arrays (PAAs), i.e., $N_a=3$, to transmit action frames during MU-MIMO BF training, while each STA used one PAA to receive the action frames. Each PAA of the AP consisted of 16 elements and was associated with nine predefined transmit sectors, making the total number of transmit sectors for the AP, i.e., $N_t$, equal to 27. We defined the transmit sectors of the AP using the codebook generator provided in [27]. The Q-D realization software provided the path loss, angle of arrival, angle of departure, delay, and phase shift for each path when multiple concurrent beams were transmitted through multiple paths in the mmWave band. These multiple paths included the direct ray and first-order reflected rays, with the reflected rays comprising strong deterministic rays and weaker diffuse rays. The reflection loss for the diffuse rays was stochastically calculated based on the NIST measurement campaign. We applied the encoding and modulation schemes of the control mode implemented in the MATLAB WLAN toolbox for transmitting action frames during MU-MIMO BF training.

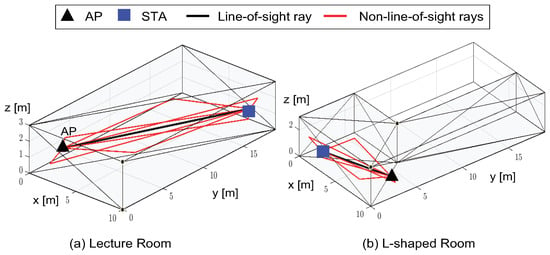
Figure 5. Visualization of our evaluation scenarios.

We implemented an encoder and a decoder, each consisting of five layers, for the autoencoder in our first-phase deep learning model. The five layers of the encoder had 27, 25, 23, and 19 nodes, respectively, while the layers of the decoder had the same number of nodes in reverse order. We used ReLU as the activation function for each node. The multilayer perceptron neural network for our second-phase deep learning model had three hidden layers, with 128, 64, and 32 nodes, respectively. We collected 29,700 input–output sample pairs to train and validate our first-phase deep learning model for each propagation scenario, and 801,900 input–output sample pairs for the second-phase model. We implemented our first-phase and second-phase deep learning models using the Adam optimizer and the mean squared error loss function. To train our first-phase and second-phase deep learning models, given a fixed position p of an STA in the designated propagation scenario, we first trained our first-phase model as described in Section 4.1. Then, using the target output ${\overline{S}}_p$ of our first-phase deep learning model at position p as the input, we trained our second-phase deep learning model as described in Section 4.2.

The parameters for calculating the SNRs of the action frames transmitted during the MIMO phase of MU-MIMO BF training were set as follows: $f_c=60$ GHz, $\rho =10$ dBm, ${\rho }_n=-90$ dBm, and ${\delta }_l=4$. In addition, the length and duration of each action frame used to calculate the duration of the MIMO phase were set according to the values provided in [24].

5.2. Discussion on the Simulation Results

We measured the duration of the MIMO phase while performing MU-MIMO BF training using the proposed TDMT scheme and compared the results with those of the DTAC and SSBE schemes. Figure 6 shows the duration of the MIMO phase, and Table 2 presents the duration of each subphase in the MIMO phase when the SNR threshold ${\delta }_r=7$. As shown in Figure 6, the duration of the MIMO phase increased as the SNR threshold increased. This was because, as the SNR threshold increased, more action frames needed to be transmitted to ensure that the SNRs measured at the STAs exceeded the required threshold. We can also observe from Figure 6 that the latency performance of our proposed TDMT scheme surpassed that of both the DTAC and SSBE schemes. The latency of the MIMO phase is analyzed numerically in [24]. As shown in Table 2, the latency of our proposed TDMT scheme during the BF feedback subphase of the MIMO phase was lower than that of the DTAC and SSBE schemes. This was because, as depicted in Figure 7, the TDMT scheme had a lower failure probability in the BF feedback subphase compared to the DTAC and SSBE schemes. Referring to [24] and Figure 1, if the STA u does not send a feedback frame containing BF training information to the AP after receiving an action frame from the AP during the BF feedback subphase, we define this as a BF feedback failure. A BF feedback failure occurs when the STA u either fails to receive the action frames during the BF setup subphase or successfully receives the action frames during the BF setup subphase but fails to receive the action frames during the BF training subphase. Our proposed TDMT scheme enhanced the accuracy of predicting the SNR of multiple concurrent beams in the MIMO phase by using the first-phase deep learning model to calibrate the SNRs of individual single beams measured during the SISO phase, thereby mitigating the impact of SNR measurement errors. As a result, as shown in Figure 7, the probability of BF feedback failure was lower compared to the other two schemes and, as indicated in Table 2, the latency in the BF feedback subphase was also reduced. However, in order to ensure the successful reception of action frames by the STAs, our proposed TDMT scheme had to transmit more action frames than the DTAC and SSBE schemes during the BF setup, BF training, and BF selection subphases. Consequently, as shown in Table 2, the latency of our TDMT scheme in these subphases was higher than that of the DTAC and SSBE schemes. Both the lecture room and L-shaped room propagation scenarios showed similar patterns in terms of the MIMO phase latency and BF feedback failure probability.

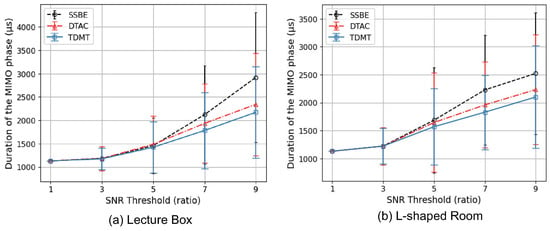
Figure 6. Duration of the MIMO phase in the scenarios (a) lecture room and (b) L-shaped room.

Table 2. Performance of each subphase in the MIMO phase by setting the SNR threshold to 7 (${\delta }_{mu}=7$).

Scenario	Scheme	Duration of Each Subphase in MIMO Phase (μs)
		BF Setup	BF Training	BF Feedback	BF Selection
	SSBE	27.14	204.49	1763.08	99.59
Lecture Room	DTAC	32.21	295.93	1461.43	116.85
	TDMT	33.06	290.66	1311.2	119.72
	SSBE	29.12	248.45	1817.63	106.3
L-shaped Room	DTAC	37.85	426.06	1332.43	136.02
	TDMT	41.79	501.67	1109.08	149.45

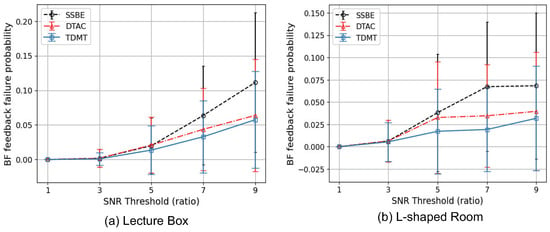
Figure 7. Probability of an STA being unable to transmit the BF feedback frame for the scenarios (a) lecture room and (b) L-shaped room.

Our proposed TDMT scheme and one of the comparison schemes, DTAC, used a deep learning model that took the SNRs of individual single beams as input and output the SNR for multiple concurrent beams. Figure 8a,b show the root mean squared error between the SNRs measured for individual single beams during the SISO phase, used as input for the deep learning models in our proposed TDMT scheme and the DTAC scheme, and their mean, for the lecture room and L-shaped room scenarios, respectively. We can observe that the SNRs for the single beams used as input for the deep learning model in the DTAC scheme exhibited significant measurement errors, even when the position of the STA and the configuration of the transmit antenna arrays remained the same. In contrast, our proposed TDMT scheme used calibrated SNRs, resulting in smaller measurement errors. As a result, as shown in Figure 9, which depicts the root mean squared error between the SNRs estimated for multiple concurrent beams during the MIMO phase by the deep learning model and the actual measured SNRs, our proposed TDMT scheme estimated the SNRs more accurately than the DTAC scheme.

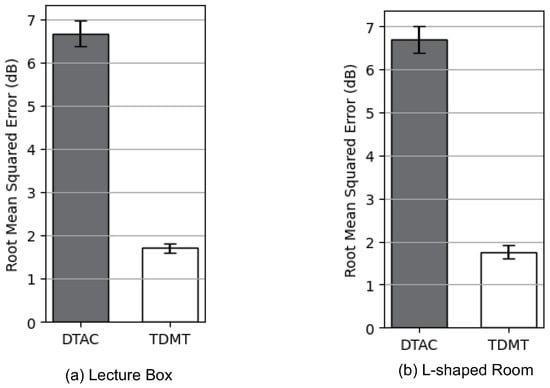
Figure 8. Root mean squared error for the SNRs measured during the SISO phase in the scenarios (a) lecture room and (b) L-shaped room.

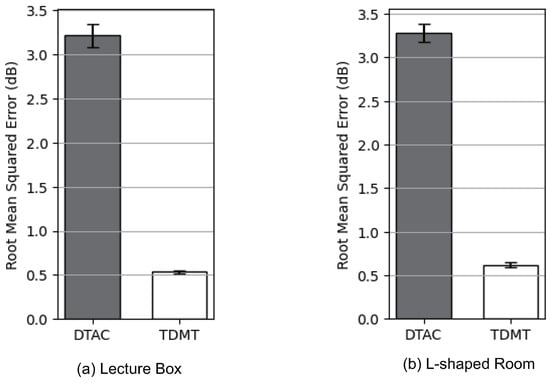
Figure 9. Root mean squared error between the SNRs estimated during the MIMO phase and the actual measured SNRs in the two propagation scenarios.

6. Conclusions

The 802.11ay standard does not specify how the AP should configure its transmit antenna arrays for transmitting action frames when performing MU-MIMO BF training with multiple STAs. Specifically, in the MU-MIMO phase of MU-MIMO BF training, since action frames should be transmitted using multiple concurrent beams, an accurate estimation of the SNRs measured at the STAs for each configuration of the transmit antenna arrays for the multiple concurrent beams is required. However, existing studies estimated the SNR for multiple concurrent beams based on the SNRs of individual single beams measured during the SISO phase, leading to reduced estimation accuracy. In this paper, we employed an autoencoder-based first-phase deep learning model to calibrate the SNRs of individual single beams measured during the SISO phase and used a multilayer perceptron neural-network-based second-phase deep learning model to estimate the SNR of multiple concurrent beams. The simulation results demonstrated that our proposed TDMT scheme reduced the latency of the MIMO phase by allowing more STAs to successfully receive action frames in each subphase compared to existing schemes.