Abstract
Reclaiming–loading operations in dry bulk terminals often face conflicts and delays due to limitations in equipment processing capacity and operational line accessibility, which significantly compromise the safety and efficiency of these operations. This paper aims to optimize the reclaiming–loading schedule for each incoming vessel by considering parallel equipment operations and potential conflicts, with the goal of enhancing both the safety and efficiency of the loading processes. Through a detailed analysis of bulk reclaiming and reclaiming–loading mechanisms, we formulate the dry bulk terminal loading scheduling problem to minimize the total operational time for all loading tasks, taking into account constraints such as parallel reclaiming, collaborative loading, operational conflicts, and line accessibility. In order to obtain a good solution, including task execution sequences and allocation of reclaimers and shiploaders, a knowledge-driven memetic algorithm is developed by integrating knowledge-driven mechanisms with problem-specific operators within a memetic computing framework. Finally, numerical experiments for various scales are conducted using the layout and operational data from the Huanghua Port’s coal port area. The experimental results demonstrate the effectiveness of the proposed optimization algorithm.
1. Introduction
Dry bulk ports and terminals are critical components of the global economy, facilitating approximately 50% of the world’s seaborne trade []. These facilities, either dedicated or multipurpose, handle a variety of dry bulk commodities, including bulk minerals, agricultural products, fertilizers, and biomass, and serve as essential nodes in the logistics supply chain. In China, coal plays a dominant role in the national energy structure. Due to geographical imbalances between coal supply and demand, large-scale coal transportation from the west to the east and north to the south is essential. Ports, as vital hubs in this network, ensure the efficient operation of the coal transport system. With increasing demand for coal transport, enhancing the dispatching capacity and scheduling efficiency of dry bulk coal terminals has become a pressing need.
The coal loading process at export terminals is highly specialized. It involves reclaimers positioned along reclaimer lines to retrieve coal from stockpiles, transporting it via conveyors to the shiploading line, and completing the loading onto the vessel by a shiploader. Terminal productivity and efficiency are directly influenced by infrastructure, handling equipment, and operational practices. Given the discrepancy between vessel demands and stockpile arrangements, a single vessel often requires coal from multiple stockpiles. To meet blending requirements, terminals typically configure “dual reclaimers on a single line”, wherein two reclaimers retrieve coal from different stockpiles in specified proportions, blending them before loading. Additionally, mobile shiploaders, when feasible, load coal to adjacent berths, either individually or cooperatively.
Effective planning is crucial for improving the efficiency of reclaiming and loading operations. In the context of shiploading operations at container terminals, Ref. [] provides a comprehensive literature review on the shiploading problem, emphasizing the integration of stowage planning with loading sequencing and scheduling to enhance ship handling efficiency. Iris et al. [] further advance this integration by combining operational stowage planning with transport vehicle assignment and scheduling, and propose a GRASP heuristic based on greedy randomized adaptive search to obtain efficient, near-optimal solutions for complex terminal operations. To address the integrated berth allocation and quay crane assignment problem in container terminals, Iris et al. [] propose novel set partitioning models and variable reduction techniques, while Iris et al. [] introduce an Adaptive Large Neighborhood Search (ALNS) heuristic that improves known bounds and outperforms state-of-the-art heuristics on larger benchmarks. Although research related to container terminals provides valuable insights for optimizing shiploading [], transportation operations [], and storage yard management [], bulk cargo terminals present unique characteristics. These include variable stockpile sizes, the limitation of bucket-wheel reclaimers to linear tracks, and greater flexibility in the movement of container carriers []. For bulk cargo terminals, the production department must devise appropriate loading schemes based on the vessel demand schedule and the stockpile distribution within the yard. Ships require varying coal types for different cabins, with products stored across multiple stockpile locations. This increases the number of potential loading schemes and could result in operational conflicts between reclaimers or shiploaders, leading to interruptions and delays. Such disruptions not only extend loading times but also negatively affect subsequent vessel schedules.
The complexity of bulk cargo port operations and the critical need for efficient scheduling have attracted substantial research interest. To address the comprehensive scheduling challenges in dry bulk ports, several methods have been proposed, including meta-heuristic algorithms [,], mixed-integer programming (MIP) with rule-based heuristics [], MIP with Benders decomposition [], MIP with meta-heuristics [], as well as constraint programming enhanced by meta-heuristics []. De Paula et al. [] introduced an integrated scheduling strategy for the Hunter Valley coal export system, utilizing a parallel genetic algorithm to concurrently schedule train and vessel arrivals, stockpile buildup, and reclaim periods across three coal export terminals. To tackle the integrated problem of planning, scheduling, yard allocation, and berth assignment in dry bulk terminals, De Andrade et al. [] proposed a solution based on column generation, which accounted for conflicts in equipment usage. In the context of dry bulk terminals handling fertilizers, Cheimanoff et al. [] developed a mixed-integer linear programming model incorporating production scheduling, berth allocation, and yard storage. This model was solved using a multi-start GRASP-ILS meta-heuristic algorithm. Lu et al. [] focused on coal blending operations and proposed an integrated scheduling solution for coal port inbound and outbound operations. This solution employed a two-stage method that combined constraint programming with adaptive local search. Unsal et al. [] addressed berth allocation, reclaimer scheduling, and stockyard allocation at export dry bulk terminals by proposing a logic-driven Benders decomposition algorithm. Improving energy efficiency and reducing carbon emissions in ports have become critical focus areas for the port industry. Ref. [] conducts a systematic literature review to analyze operational strategies, technology usage, renewable energy, alternative fuels, and more, aimed at enhancing the energy efficiency of ports and terminals. To minimize total scheduling time, maximize berth allocation efficiency, and reduce carbon emissions, Jiang et al. [] developed a multi-objective optimization model integrating channel vessel scheduling, berth loading, and yard unloading, solved using the NSGA-II-DPGR algorithm.
Recently, integrated challenges within dry bulk terminals and coal export supply chains have attracted significant research attention [,,,]. However, several of these studies simplify key aspects of reclaimer operations by assuming, for instance, that each rail track is served by a single reclaimer [,]. In practice, most dry bulk terminals enable more flexible configurations where shiploaders can move to adjacent berths for collaborative loading, and two reclaimers operating on the same track can perform parallel reclaiming or blending operations simultaneously. Collaborative loading [] and parallel reclaiming [] significantly enhance operational efficiency and reduce vessel berthing wait times. To address the scheduling of collaborative shiploader operations, an optimization problem was formulated in [] to minimize both the energy consumption of operational lines and the berthing times of vessels at coal export terminals, utilizing a mixed-integer programming (MIP) model and a simulation-based decoding scheme. Additionally, Wang et al. [] demonstrated that deploying two reclaimers for simultaneous material reclaiming from the same stockpile notably boosts efficiency, although this introduces potential collision risks between reclaimers.
In practice, while multiple reclaimers might operate on the same rail track, they cannot pass each other. Avoiding equipment conflicts during collaborative loading and parallel reclaiming thus becomes a critical research issue. Recognizing the presence of multiple reclaimers on a single track, recent studies [,,] have incorporated reclaimer cross-operational conflict constraints into the scheduling optimization problem at dry bulk terminals. However, these studies assume that each vessel only loads a single type of bulk material, overlooking the complexity of reclaiming from multiple stockpiles and the potential for parallel reclaiming to further enhance efficiency. Burdett et al. [] addressed reclaimer conflicts by adapting a collision detection strategy from the train scheduling domain, dividing each reclaiming line into smaller regions and applying a penalty to the objective function when conflicts were detected. Lu et al. [] accounted for reclaimer conflicts in blending operations to meet ship demands. While Li et al. [] introduced stockyard scheduling into the reclaiming–loading process, they restricted operations to single-machine modes for both reclaimers and shiploaders, significantly reducing operational efficiency.
The reclaiming–loading scheduling (RLS) problems in dry bulk ports are unequivocally classified as NP-hard problems since they contain multiple subproblems, including task sequencing, reclaimer selection, and shiploader selection []. Due to the exponential growth in the number of variables and constraints of the proposed mathematical models, the model-based exact algorithms are unable to yield optimal solutions within an acceptable time. When attempting to address this issue within a reasonable duration, traditional heuristics often fail to produce satisfactory scheduling solutions. In this context, the memetic algorithm (MA), a robust optimization technique that integrates evolutionary mechanisms with problem-specific local intensification, holds promise for effectively solving complex scheduling problems.
Inspired by Darwinian principles of natural evolution and Dawkins’ concept of the meme, the algorithm incorporates both evolutionary search and local refinements, constituting what is termed a memetic algorithm [,]. As a versatile optimization framework, MAs have been successfully applied for various problem domains, including the traveling salesman problem and the shop scheduling problem [], as well as the graph bipartition problem []. A review of the literature on MAs applied to scheduling problems reveals that the specially designed problem-specific algorithms in the memetic computing framework can solve complex problems effectively. Specifically, the analysis of problem characteristics, the extraction and application of knowledge, and the adoption of a reasonable cooperative approach are fundamental to successfully addressing intricate scheduling challenges. Consequently, it is anticipated that a superior performance can be achieved by merging knowledge-driven mechanisms with problem-specific operators within the memetic computing framework.
This paper addresses the RLS problem within real-world coal port operations using a memetic algorithm framework that incorporates factors such as parallel reclaiming, collaborative loading, and equipment conflicts. To minimize the total operational time across all loading tasks, we developed a calculation model that accounts for key operational constraints, including task sequencing, reclaimer selection, and shiploader selection. Based on this model, we propose an innovative knowledge-driven memetic algorithm (KDMA), which integrates domain-specific knowledge with problem-specific operators within a memetic computing framework. A comprehensive series of multi-scale and multi-parameter experimental analyses demonstrates the effectiveness of the KDMA in solving the RLS problem. Comparisons with a genetic algorithm and a non-parallel operation strategy reveal the distinct advantages of the KDMA, underscoring the potential of knowledge-driven memetic algorithms to enhance scheduling efficiency in coal port operations.
The remainder of this paper is organized as follows. Section 2 analyzes the characteristics of scheduling in dry bulk ports. Section 3 formulates the reclaiming–loading scheduling problem. The design of the knowledge-driven memetic algorithm is detailed in Section 4. Section 5 presents and analyzes the results of multi-scale experimental studies. Finally, Section 6 concludes the paper with a summary of key findings.
2. Characteristics of Dry Bulk Port Reclaiming–Loading Scheduling
In the context of a specialized dry bulk port for coal exports, such a facility exhibits a high degree of specialization. Figure 1 illustrates the layout of a dry bulk port in northern China, which includes three berths: #1, #2, and #3. The reclaiming–loading operation consists of three types of operational lines and two types of equipment: reclaiming lines (BQ1, BQ2, and BQ3), conveyor lines (BC1 and BC2), ship conveyor lines (BM1, BM2, and BM3), as well as reclaimers (R1 to R5) and shiploaders (BL1, BL2, and BL3). Typically, vessels have multiple cabins, each corresponding to one product type. The definition of each cabin’s material requirements—both types and quantities—is referred to as a loading task. Each loading task utilizes a set of operational lines, including one reclaiming line, one conveyor line, and one shiploading line, for continuous operations. Based on the vessel’s task requirements and the distribution of material types within the stockyard, the reclaimer performs material reclaiming operations at the designated stockpile positions. The conveyor lines use a belt conveyor system to transport dry bulk cargo from the reclaiming lines to the shiploading lines. On the shiploading lines, the shiploaders execute the loading operations according to the specific tasks assigned to each cabin position on the vessel.
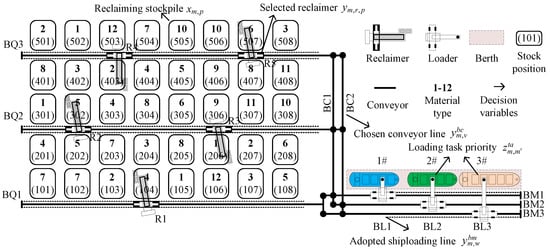
Figure 1.
Layout of the reclaiming–loading operation in a dry bulk port.
2.1. Parallel Operation of Reclaimers and Operational Conflicts
For a specific shiploading task, the reclaimer scheduling involves stockpile selection and reclaimer selection. As shown in Figure 1, the stockyard contains 40 stockpiles, each designated for storing a specific type of dry bulk cargo. With a total of 12 types of dry bulk cargo, one or more stockpiles can be used for material reclaiming for each specific shiploading task. On the reclaiming lines, there may be one or two reclaimers that can reclaim from different stockpiles. To enhance loading efficiency, a “dual-reclaimers single-loader” operational mode is implemented, where two reclaimers operate in parallel on the same line. Specifically, for each loading task, either a single reclaimer or both reclaimers may be used to perform the material reclaiming, while one shiploader executes the loading operation.
In optimizing the reclaiming–loading operation planning, the primary principle is to avoid operational conflicts. When multiple reclaimers are present on the same track, and each reclaimer can only perform reclaiming operations on one side of the track, it is crucial to consider the potential for conflicts between these reclaimers. For instance, as illustrated in Figure 2, when material reclaiming is being conducted for material 8, reclaimer R2 reclaims from stockpile position 205, while reclaimer R3 reclaims from stockpile position 304. In this scenario, R2 and R3 experience cross-side operational conflicts. Similarly, when reclaiming material 10, reclaimer R4 performs reclaiming from stockpile position 506, and reclaimer R5 reclaims from stockpile position 505. Here, R4 and R5 face same-side operational conflicts. Meanwhile, to ensure safety, it is common practice not to use two reclaimers to extract material from the same stockpile simultaneously. Avoiding reclaimer conflicts is essential to ensure efficient and uninterrupted operations.
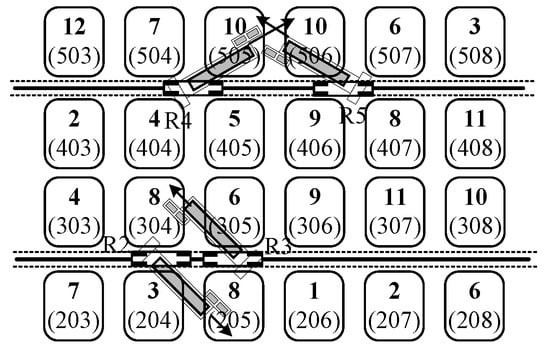
Figure 2.
Crossing operation conflicts of reclaimers.
2.2. Collaborative Operations of Shiploaders and Operational Conflicts
To improve operational efficiency, the port is equipped with mobile shiploaders, which, under suitable conditions, can load ships at adjacent berths. These loaders can operate both independently and in a collaborative manner.
When multiple shiploaders are situated on the same track near a berth, and each loader can only perform loading operations on the seaside, it is essential to consider potential crossing operation conflicts among these loaders. As illustrated in Figure 3, when shiploader SL2 is engaged in loading operations for a ship at berth 2# and shiploader SL3 is engaged in loading operations for a ship at berth 1#, conflicts arise due to the crossing operations of SL2 and SL3. This crossing operation conflict of shiploaders must be managed to ensure smooth and efficient loading processes.
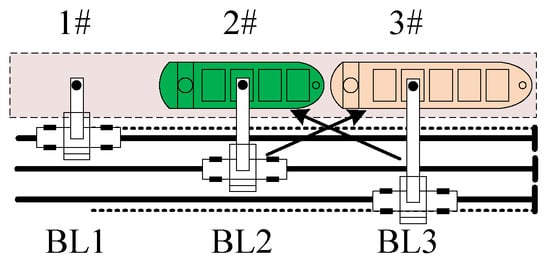
Figure 3.
Crossing operation conflicts among shiploaders.
The objective of developing a reclaiming–loading plan is to ensure that the cargo loading process is efficient and orderly by appropriately allocating the existing storage resources and loading equipment at dry bulk port ports. For dry bulk port ports, reclaimers and shiploaders are the primary loading equipment. When preparing the reclaiming–loading plan, the following principles should be considered:
(1) Safety: the primary principle is to avoid conflicts between loading equipment during operation, ensuring that cross-operation conflicts do not occur.
(2) Efficiency: aim to maximize the loading efficiency per unit time while ensuring that the loading process remains uninterrupted.
In the context of parallel operation of reclaimers and collaborative operation of shiploaders, the key to optimizing the loading plan is to allocate a rational reclaiming–loading scheme and equipment to all ships waiting at the berth during the planning period. The goal is to minimize the total loading completion time for all ships.
3. Reclaiming–Loading Scheduling Problem Formulation
3.1. Problem Formulation
According to Section 2, each loading task can be accomplished by selecting from various stockpiles that meet the material type requirements and by choosing among different reclaimers and shiploaders, which utilize different reclaiming lines, conveyor lines, and shiploading lines to perform the loading operations. The objective of optimizing the loading operation schedule is to enhance loading efficiency and minimize vessel berthing time, while accounting for parallel reclaiming operations of reclaimers, collaborative loading operations of shiploaders, and potential equipment conflicts during these operations.
The problem definition is based on the following assumptions:
- –
- The arrival time and corresponding berth of each vessel are known in advance.
- –
- The vessel’s time in port is measured from the vessel’s arrival in port to the completion of untying and disembarkation.
- –
- The loading task requirements are predefined, with each task corresponding to a specific material type present in the stockpile, eliminating the need for blending operations.
- –
- The operating efficiency of the reclaimer and the rate of the belt conveyor system are known, and the loading rate of the shiploader matches the parallel reclaiming rate of the reclaimer.
- –
- No other loading tasks can be performed on the rail track occupied by a ongoing loading task until that task is completed.
- –
- Equipment failures related to the reclaiming–loading process are not considered.
Additionally, notations for sets, parameters, intermediate variables, and decision variables are illustrated in Table 1.

Table 1.
Notations.
3.2. Optimization Objective and Constraints
Using the notations provided in Table 1, the optimization problem for loading operations in dry bulk ports, considering various constraints, is formulated as follows.
Subject to:
The objective function (1) aims to minimize the total port stay time, which can also be considered as the total loading time, for all vessels.
For parallel reclaiming, Constraint (2) specifies that each shiploading task m involves either a single reclaiming operation from one stockpile or a parallel reclaiming operation from two stockpiles. Constraints (3) and (4) state that, for each reclaimer performing task m, it can only reclaim from one stockpile; likewise, for each stockpile occupied by the task, only one reclaimer can perform the reclaiming operation. Constraint (5) indicates that the reclaiming line used by the reclaimer is occupied.
To prevent operational conflicts between parallel reclaimers, stockpile positions in the stockyard are renumbered from top to bottom and from left to right, as shown in Figure 4. Constraints (6) and (7) describe that when two reclaimers operate in parallel on the same reclaiming line, their sequence aligns with the sequence of the corresponding stockpile positions. This alignment helps avoid conflicts between the two reclaimers operating in parallel on the same reclaiming line.
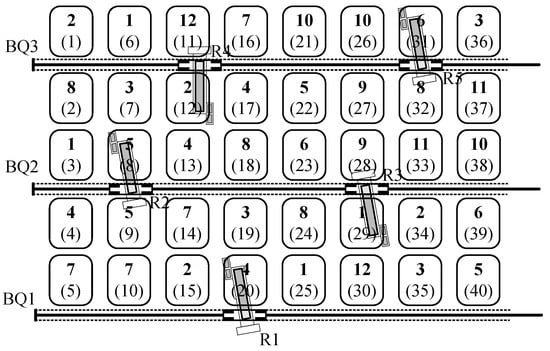
Figure 4.
Renumbered stockpile position in stockyard.
Time constraints are crucial for the smooth and efficient execution of shiploading tasks. For any loading operation task, the total loading duration consists of two key components: the material reclaiming time and the transportation operation time, as defined by Constraints (8–10). Constraint (11) indicates that the berthing time of any vessel is scheduled after the later of two times: the departure time of the preceding vessel at the same berth and the turnaround time required after this vessel arrives in port. Constraint (12) states that the vessel begins its operations only after completing auxiliary tasks, and Constraint (13) calculates the vessel’s departure time. For two loading tasks that occupy the same stockpile position, reclaiming line, conveyor line, or shiploading line, Constraint (14) defines the priority constraint. Constraint (15) explains that for two loading tasks with priority constraints, the task with the lower priority can only start after the higher-priority task has been completed. Additionally, if both tasks use the same shiploader and are at different berths, Constraint (16) clarifies that the shiploader has completed the travel between the two berths. Constraints (17–19) describe that the operational process of the same loading task is uninterrupted.
Regarding the use of operation lines, Constraint (20) describes that a loading task requires only one reclaiming line, one conveyor line, and one shiploading line. Constraints (21)–(23) represent the accessibility constraints between the stockpile position, reclaiming line, conveyor line, shiploading line, and berth occupied by the loading task.
To prevent operational conflicts between collaborative loaders, Constraints (24) and (25) impose constraints on the shiploading lines, where Constraint (24) states that loaders cannot perform cross-line operations, and Constraint (25) describes that collaborative operation is allowed only between adjacent loaders.
Since this calculation model is nonlinear and non-convex, it is challenging and time-consuming to obtain the optimal solution by model solvers such as Gurobi and CPLEX for the extensive and complex scheduling problems. Consequently, based on the calculation model, the next section will present the development of a heuristic algorithm to obtain an approximate optimal solution within a reasonable computation time.
4. Knowledge-Driven Memetic Algorithm
In this section, a knowledge-driven memetic algorithm is proposed, featuring components such as encoding and decoding, population initialization, a knowledge-driven evolutionary mechanism, and local intensification.
4.1. Encoding and Initialization
Effective encoding and decoding methods can directly influence the search space and search efficiency. For the operation scheduling in a dry bulk port, the task sequence of each vessel, stockpile selection, reclaimer selection, and shiploader selection for each task should be determined together. Thus, a four-layer string is used to represent an encoded solution. The length of each of the four strings is the number of the tasks . The first string with task sequence is used to represent the task sequence of each vessel, where represents the task sequence belonging to vessel s, . The second string is represented by , where denotes the assigned stockpiles for task . The third string is represented by , where denotes the assigned reclaimer for task . The fourth string is represented by , where denotes the assigned shiploader/shiploading lines for task . Considering the task constraints, each task occurs once and only once in the and each task must belong to the corresponding vessel. Meanwhile, due to the constraints of different operation lines, the stockpiles should be selected in the available set of each task . Furthermore, the reclaimer and shiploader should be selected in the available set, considering accessibility. Therefore, the solution can be ensured to be feasible according the the above rules.
To obtain high-quality schedules based on the encoded solutions, the decoding method is designed considering parallel reclaiming, collaborative operation between adjacent loaders, and conflicts between reclaimers and loaders. To improve reclaiming efficiency, if there is more than one reclaimer on the assigned reclaiming lines and multiple available stockpiles, parallel reclaiming can be performed. To ensure the parallel reclaiming can reduce the task operation time, the available time of the parallel reclaimers should also be taken into account. If the completion time of parallel reclaimers is more than that of one reclaimer, parallel reclaiming will not be executed. To speed up the operation time, collaborative operation between adjacent loaders is also incorporated into the decoding process. If the adjacent loader is idle, the task assigned to it can be operated simultaneously. In addition, the conflicts between reclaimers and loaders are also considered during the decoding process to satisfying the constraints developed in the calculation model.
In the initialization phase, the population with solutions is generated randomly, considering the various constraints and decoded to the schedules. During the search process, the best solution is retained.
4.2. Knowledge-Driven Evolutionary Mechanism
To improve search efficiency, a knowledge-driven evolutionary mechanism is designed to enable inferior solutions to learn from elite solutions. First, two solutions in the population are selected randomly. Second, the inferior solution learns from elite solution based on their performance. Specifically, the difference in operation time for each vessel between solutions and is calculated, and the vessel with largest time difference is selected due to the huge space improvement. Third, the task schedule of the selected vessel of solution is transplanted to the corresponding vessel of solution . Thus, solution can be improved by learning from the better solution.
To enhance the population diversity, a mutation operator is developed for the improved solution with a mutation probability . The mutation operator is implemented by randomly selecting a vessel and regenerating its task sequence, stockpile, reclaimer, and shiploader. Consequently, the KDMA can improve convergence while mitigating the risk of local optima.
4.3. Local Intensification
To enhance the exploitation capability, a knowledge-driven local intensification is designed to further refine promising solutions. To reduce the total loading time for all vessels, three local search operators with prior knowledge are designed for adjusting the task sequence, reclaimer selection, and loader selection, including critical task swap (TS), task insertion (TI), reclaimer selection (CS), and loader selection (LS). Suppose the vessel s is selected to adjust the three subproblems:
TS: For the tasks belonging to the vessel s, select two tasks randomly and then swap them.
TI: For the tasks belonging to the vessel s, select two tasks randomly and then insert one task before another one.
CS: For all tasks belonging to the vessel s, select two stockpiles with two available reclaimers. If there are no stockpiles satisfying the condition, then randomly select one stockpile and reclaimer.
LS: For all tasks belonging to the vessel s, select a different available and adjacent loader from the loaders of previous task to improve the possibility of collaborative operation.
The procedure of local intensification is shown as Algorithm 1, where denotes the depth of local intensification.
| Algorithm 1 Local Intensification |
|
4.4. Algorithm Framework
The pseudo-code of the knowledge-driven memetic algorithm (KDMA) is delineated in Algorithm 2, including the population initialization, knowledge-driven evolutionary mechanism, and local intensification scheme. Through the several problem-specific designs, it is expected to achieve a superior performance via a balance of exploration and exploitation.
| Algorithm 2 Knowledge-driven Memetic Algorithm |
|
5. Experimental Results and Analysis
As a case study, this paper compares and analyzes the scheduling plan derived from the proposed optimization problem with the results obtained from genetic algorithm optimization at a coal export terminal in China, thereby validating the effectiveness of the proposed optimization algorithm. The layout of the entire shiploading operation is illustrated in Figure 1. Without considering the collaborative operation of shiploaders, the accessibility between the designated berth and the three conveyor lines—the reclaiming line, horizontal line, and shiploading line—is detailed in Table 2. Additionally, the reclaiming speeds of reclaimers R1 to R5 are 6000, 6000, 3000, 6000, and 3000 t per hour, respectively. The distances from berths 1# to 3# to the stockyard are 450, 750, and 1000 m, respectively.

Table 2.
Accessibility among berths and reclaiming line, conveyor line, and shiploading line.
This experiment considers the optimization of the shiploading tasks for 60 vessels during the planning period. Table 3 provides detailed information on vessel arrival times, dock assignments, and the types and quantities of bulk cargo required.

Table 3.
Basic information about arrival vessels and corresponding tasks.
For the scheduling optimization of 30 vessels and their corresponding 185 tasks over a 15-day period, Figure 5 and Figure 6 present the results obtained using the KDMA proposed in this paper. Due to space constraints, only the optimization results for the first six days are shown, with each subplot displaying results for two days or 48 h. Figure 5 illustrates the outcomes under a conventional single reclaimer operation, while Figure 6 demonstrates the performance of the proposed parallel reclaiming operation, where two reclaimers can simultaneously handle the same type of bulk cargo from different stockpiles. For each loading task, Table 4 details the utilization of the stockpiles, reclaimers, and the three operational lines under both conditions: with and without the reclaimer parallel strategy.
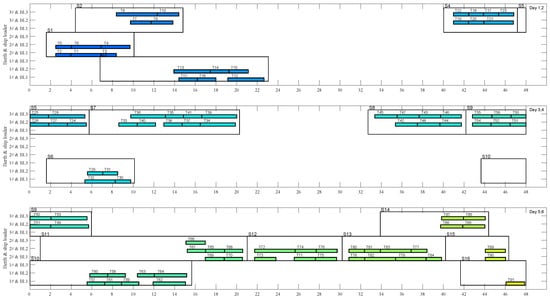
Figure 5.
Scheduling optimization plan using the proposed KDMA without parallel reclaiming.
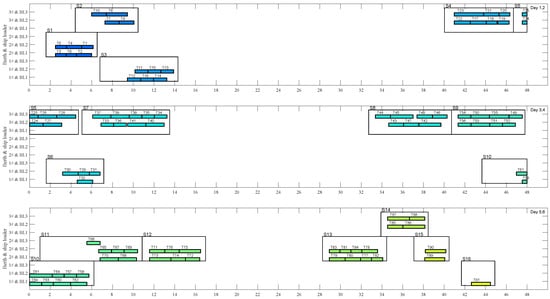
Figure 6.
Scheduling optimization plan using the proposed KDMA with parallel reclaiming.

Table 4.
Comparison of stockpile, reclaimer, and operational line utilization with and without parallel reclaiming by KDMA.
Taking vessel S1 as an example, we illustrate the scheduling result adopting the traditional approach of using a single reclaimer for a loading task, as shown in Figure 5. The vertical lines on either side of the unfilled rectangular box represent the vessel’s docking and departure times. The vessel S1 docks at berth 2# at 01:15 on day 1. After completing the turnaround operations, it sequentially performs its six loading tasks (T5, T2, T6, T1, T3, T4) during the following time intervals: T5 from 02:30 to 04:01, T2 from 02:30 to 03:58, T6 from 04:01 to 06:54, T1 from 03:58 to 06:52, T3 from 06:52 to 08:21, and T4 from 06:54 to 09:41. Once the final task, T4, and the auxiliary operations are completed, the vessel departs at 10:04. It is important to note that due to the collaborative loading mechanism, shiploader BL1 executes the loading tasks (T2, T1, T3), while shiploader BL2 executes the tasks (T5, T6, T4) simultaneously.
Using the parallel reclaiming strategy, as shown in Table 4 and Figure 6, vessel S1 performs its six reclaiming tasks as follows: Task T3 is reclaimed from stockpile 2 by reclaimer R4 and from stockpile 32 by reclaimer R5 in parallel between 02:30 and 03:31. Task T5 is reclaimed from stockpile 18 by reclaimer R2 and from stockpile 24 by reclaimer R3 in parallel between 02:30 and 03:31. Tasks T6, T4, T2, and T1 are reclaimed in a similar manner, either in parallel or individually. Finally, Task T1 is reclaimed from stockpile 2 by reclaimer R4 and from stockpile 32 by reclaimer R5 in parallel between 05:01 and 06:08. After completing the final task T1, vessel S1 is unfastened and departs at 06:31.
Due to the implementation of the parallel reclaiming operation mechanism, the docking duration of vessel S1 was reduced by 40.36%, from 8.824 h to 5.263 h. As a result of the expedited completion of tasks for vessel S1, the waiting time for vessel S2 decreased by 60.03%, from 3.959 h to 1.581 h. This improvement is clearly illustrated on day 4 to day 6 in Figure 5, where inefficient completion of earlier shiploading tasks caused delays and accumulations for subsequent vessels S10 to S15—at least six consecutive ships. However, by adopting the parallel strategy, as shown in Figure 6, only the loading tasks for vessels S10 and S11 were affected, while operations for S12 and those following were restored to normal. Overall, for all 30 vessels, the total loading time F was reduced by 33.3%, from 329.64 h to 219.66 h, significantly enhancing the efficiency of port loading operations. Meanwhile, ship-based emissions—particularly during port stay time—constitute a significant portion of the total energy consumption in container and dry bulk terminals [,]. By converting energy consumption into monetary terms, the analysis shows that the unit port stay cost is RMB 1416 per hour, as reported by Tian []. Following optimization, the port stay cost for 30 vessels decreased from RMB 466,770 to RMB 311,038, achieving a savings of RMB 155,731.
On the other hand, Table 4 illustrates that, when employing the parallel reclaiming strategy, the number orders of the adopted reclaimers and the stockpiles are consistent, indicating that the proposed algorithm can effectively avoid conflicts in parallel reclaiming operations. Meanwhile, as shown in Figure 6, on the third day, shiploader BL3 is assigned to perform the T28 loading task for the vessel S5 docked at berth 3#, while shiploader BL2 is assigned to perform the T30 loading task for the vessel S6 docked at berth 1#. The consistency in the number order of the selected shiploaders and the berths indicates that the proposed scheme can effectively avoid conflicts of shiploaders in the collaborative loading operations.
To further validate the effectiveness of the proposed KDMA, the genetic algorithm (GA) was used to solve the bulk cargo terminal loading scheduling optimization problem. For the scheduling of 30 vessels, the convergence effects of the algorithms are compared as shown in Figure 7. Although the GA converges after only 42 iterations, its optimal solution of 299.05 h is significantly worse than the KDMA’s optimal solution of 218.20 h. Additionally, the GA’s computation time of 416.52 s is notably longer than the KDMA’s 244.6 s.
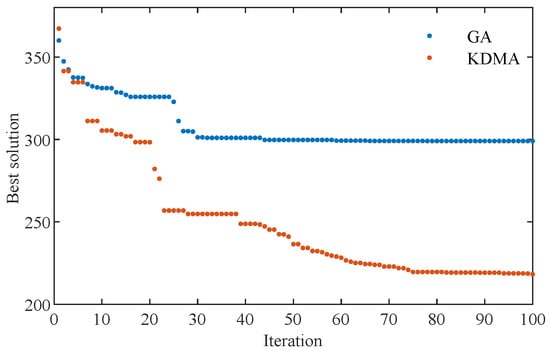
Figure 7.
Comparison of convergence trends across different algorithms.
As shown in Table 5, extensive experiments with scheduling tasks ranging from 5 to 60 vessels clearly demonstrate the consistent advantages of the KDMA, achieving an average reduction in optimal loading time of 20.3% and a reduction in computation time of 45.84%.

Table 5.
Comparison of GA and KDMA associated with different numbers of vessels.
ANOVA (two-way analysis of variance) was conducted to evaluate the impact of two factors: (depth of local intensification) and (population size) on the best solution in the proposed KDMA. Five different settings of were selected: 60, 80, 100, 120, and 140. Similarly, five different settings for were chosen: 30, 40, 50, 60, and 70. Each combination of factors was repeated 50 times to ensure data reliability and stability. The ANOVA results are presented in Table 6.

Table 6.
ANOVA results regarding parameters in KDMA.
The p-values for both and , and their interaction, are all greater than 0.05, indicating that neither the single factors nor their interaction significantly influence the best solution, thereby demonstrating the robustness of the proposed KDMA.
Overall, by formulating the RLS problem to incorporate parallel reclaiming, collaborative loading, and operational conflicts, we have significantly enhanced loading efficiency. Additionally, the proposed KDMA not only delivers superior solutions but also requires less computation time compared to the traditional GA. The robustness of the parameters within this algorithm has also been effectively demonstrated. Notably, this approach is adaptable beyond the specific port setup described in this study, making it suitable for a wide range of bulk cargo terminal layouts and operational requirements.
6. Conclusions
Through an in-depth analysis of the dry bulk terminal loading process, focusing on practical constraints such as loading plans, parallel reclaiming, collaborative loading, and equipment conflict, we formulated an optimization problem aimed at minimizing total loading time. Within a memetic computing framework, we designed a novel knowledge-driven memory algorithm that combines knowledge-based mechanisms with problem-specific operators to effectively optimize the calculation model. Analysis of the loading schedule obtained for 30 vessels reveals that the proposed parallel reclaiming and collaborative loading mechanisms significantly enhance loading efficiency. Compared to the traditional single-reclaimer approach, the total loading time was reduced by approximately 33.3%, with no operational conflicts between reclaimers or shiploaders, validating the effectiveness of the optimization algorithm. Simulations conducted across 12 different scales of vessel numbers show that the proposed algorithm reduces total loading time by 20.3% compared to the GA, along with a computational efficiency gain of approximately 45.84%. The loading scheduling method proposed in this paper offers terminal managers valuable decision support for loading operations, enhancing operational efficiency and service quality at bulk cargo ports. In the future, we will focus on studying the mathematical model of reclaiming–loading scheduling in dry bulk terminals and developing efficient exact solution algorithms. Additionally, future research will explore loading tasks that involve blending operations, as well as the integrated optimization of equipment maintenance and loading schedules, with the goal of further improving loading efficiency at dry bulk terminals.
Author Contributions
Conceptualization, Q.L., X.N., H.L., J.W. and K.W.; validation, J.W.; formal analysis, Q.L., X.N. and H.L.; writing—original draft preparation, K.W. and J.W.; writing—review and editing, K.W.; supervision, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original data presented in the study are openly available at https://github.com/DaniuWong/KMA.git, accessed on 25 October 2024.
Conflicts of Interest
Authors Q.L., X.N., and H.L. were employed by the company Hebei Bulk Port Technology Innovation Center, CHN Energy Huanghua Port Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MIP | mixed-integer programming |
| RLS | reclaiming–loading scheduling |
| MA | memetic algorithm |
| KDMA | knowledge-driven memetic algorithm |
| TS | task swap |
| TI | task insertion |
| CS | reclaimer selection |
| LS | loader selection |
| GA | genetic algorithm |
References
- Sirimanne, S.N.; Hoffman, J.; Juan, W.; Asariotis, R.; Assaf, M.; Bacrot, C.; Benamara, H.; Hansen, P.; Kulaga, T.; Premti, A.; et al. Review of Maritime Transport 2023; United Nations Conference on Trade and Development: Geneva, Switzerland, 2023; Available online: https://unctad.org/publication/review-maritime-transport-2023 (accessed on 14 August 2024).
- Iris, C.; Pacino, D. A Survey on the Ship Loading Problem. In Computational Logistics; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Iris, Ç.; Christensen, J.; Pacino, D.; Ropke, S. Flexible ship loading problem with transfer vehicle assignment and scheduling. Transp. Res. Part B Methodol. 2018, 111, 113–134. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated Berth Allocation and Quay Crane Assignment Problem: Set partitioning models and computational results. Transp. Res. Part E Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S. Improved formulations and an Adaptive Large Neighborhood Search heuristic for the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 123–147. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A.; Roodbergen, K.J. Transport operations in container terminals: Literature overview, trends, research directions and classification scheme. Eur. J. Oper. Res. 2014, 236, 1–13. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A.; Roodbergen, K.J. Storage yard operations in container terminals: Literature overview, trends, and research directions. Eur. J. Oper. Res. 2014, 235, 412–430. [Google Scholar] [CrossRef]
- Wang, C.; Lu, X.W.; Sitters, R. Scheduling reclaimer operations in the stockyard to minimize makespan. Acta Math. Appl. Sin.-Engl. Ser. 2018, 34, 597–609. [Google Scholar] [CrossRef]
- De Paula, M.R.; Boland, N.; Ernst, A.T.; Mendes, A.; Savelsbergh, M. Throughput optimisation in a coal export system with multiple terminals and shared resources. Comput. Ind. Eng. 2019, 134, 37–51. [Google Scholar] [CrossRef]
- Jiang, X.; Zhong, M.; Shi, J.; Li, W. Optimization of integrated scheduling of restricted channels, berths, and yards in bulk cargo ports considering carbon emissions. Expert Syst. Appl. 2024, 255, 124604. [Google Scholar] [CrossRef]
- Cheimanoff, N.; Féniès, P.; Kitri, M.N.; Tchernev, N. Exact and metaheuristic approaches to solve the integrated production scheduling, berth allocation and storage yard allocation problem. Comput. Oper. Res. 2023, 153, 106174. [Google Scholar] [CrossRef]
- Unsal, O.; Oguz, C. An exact algorithm for integrated planning of operations in dry bulk terminals. Transp. Res. Part E-Logist. Transp. Rev. 2019, 126, 103–121. [Google Scholar] [CrossRef]
- De Andrade, J.L.M.; Menezes, G.C. A column generation-based heuristic to solve the integrated planning, scheduling, yard allocation and berth allocation problem in bulk ports. J. Heuris. 2023, 29, 39–76. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, Y.; Zheng, L.; Yang, C.; Wang, J. Integrated inbound and outbound scheduling for coal port: Constraint programming and adaptive local search. J. Mar. Sci. Eng. 2024, 12, 124. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Hu, D.; Yao, Z. Stacker-reclaimer scheduling in a dry bulk terminal. Int. J. Comput. Integr. Manuf. 2012, 25, 1047–1058. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P.; Yarlagadda, P.K.D.V.; Eustace, C.; Smith, S. A flexible job shop scheduling approach with operators for coal export terminals. Comput. Oper. Res. 2019, 104, 15–36. [Google Scholar] [CrossRef]
- Menezes, G.C.; Mateus, G.R.; Ravetti, M.G. A branch and price algorithm to solve the integrated production planning and scheduling in bulk ports. Eur. J. Oper. Res. 2017, 258, 926–937. [Google Scholar] [CrossRef]
- Bouzekri, H.; Alpan, G.; Giard, V. Integrated laycan and berth allocation problem with ship stability and conveyor routing constraints in bulk ports. Comput. Ind. Eng. 2023, 181, 109341. [Google Scholar] [CrossRef]
- Feng, P.; Guo, Z.; Jiang, Y.; Cao, Z.; Xu, X. Scheduling optimization of loading operation in coal export terminals considering union operation of ship loaders. J. Shanghai Marit. Univ. 2021, 42, 26–33. [Google Scholar] [CrossRef]
- Ünsal, Ö. Reclaimer scheduling in dry bulk terminals. IEEE Access 2020, 8, 96294–96303. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Wang, J.; Yan, J. Ship loading operation scheduling optimization in bulk cargo export terminals considering operation conflicts of loading equipments. J. Dalian Marit. Univ. 2022, 48, 66–74. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Yang, Z.; Wang, X. Collaborative optimization for loading operation planning and vessel traffic scheduling in dry bulk ports. Adv. Eng. Inform. 2022, 51, 101489. [Google Scholar] [CrossRef]
- Ong, Y.S.; Lim, M.H.; Chen, X. Research frontier-memetic computation—past, present & future. IEEE Comput. Intell. Mag. 2010, 5, 24. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Jin, Y.H. An effective PSO-based memetic algorithm for flow shop scheduling. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2007, 37, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Merz, P. Memetic Algorithms for Combinatorial Optimization Problems: Fitness Landscapes and Effective Search Strategies. Ph.D. Thesis, Universität Siegen, Siegen, Germany, 2000. Available online: https://dspace.ub.uni-siegen.de/handle/ubsi/181 (accessed on 17 November 2024).
- Tian, Q. Collaborative Optimization of Maintenance and Scheduling for Shiploading Operation System in Dry Bulk Port. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).