Analysis of Optimal Diversity Combining with Imperfect Channel State Information for Cooperative Jamming-Aided Internet of Things Security

Abstract

Cooperative jamming (CJ) combined with single-input multiple-output (SIMO) technology can effectively improve the security and reliability of Internet of Things (IoT) systems. However, imperfect main channel state information (CSI) leads to incomplete CJ cancellation, which degrades the performance after combining. In this paper, by considering channel estimation errors and residual CJ at each receiving antenna, the residual CJ power after jamming suppression is analyzed, and the optimal combining coefficient for maximizing the signal-to-jamming-noise ratio (SJNR) is derived. The output SJNR of optimal diversity combining is given, and the achievable secrecy rate is analyzed on this basis. The theoretical and simulation results verify the combined effect of channel estimation errors and residual CJ on the combining performance. Moreover, it is worth noting that the combining performance is closely related to the spatial correlation of residual CJ.

1. Introduction

In recent years, Internet of Things (IoT) technology has developed rapidly, and various smart devices have gradually entered the public field of vision, widely used in home, medical, manufacturing, and other fields. In particular, the vision of the Internet of Everything (IoE) will be further advanced by the sixth-generation mobile (6G) network, which will be a fully connected world with integrated terrestrial wireless and satellite communications. However, with the number and types of nodes in wireless networks having shown explosive growth, the problem of network security has become increasingly prominent. Due to the broadcast nature of wireless communication, any node can receive the signal sent by the transmitter within the signal-receiving range in free space [1]. In IoT-oriented 6G systems, physical layer security technology can improve the security of information transmission in wireless communication to ensure efficient and reliable system operation.

Unlike the traditional encryption mechanism, physical layer security does not depend on the computing power of the device but makes full use of the inherent randomness and complexity of the wireless channel to achieve secure communication [2]. Cooperative jamming (CJ) is an effective physical layer security technique used to improve the secrecy rate [3]. Different from artificial noise, in CJ, the independent sender adds random signals to the channel, and the licensed and eavesdropping channels simultaneously interfered with the random signals. However, the licensed receiver can utilize the prior information of CJ to separate the desired signal.

1.1. Background Study of CJ Performance

CJ technology has been widely used in security systems [4,5,6,7,8]. Specifically, ref. [4] presents a robust security study for a two-unmanned aerial vehicle scenario with an intelligent reflecting surface, in which one drone is used to transmit CJ to interfere with eavesdroppers. The authors in [5] analyze the feasibility of using an intermittent jamming strategy to achieve physical layer security in IoT security systems, and a matching precision optimization algorithm is designed to achieve the optimal time-slot-free security transmission. A multi-leader single-follower Stackelberg game is proposed in [6] to maximize the benefits of jamming nodes. The authors in [7] investigate the use of CJ to improve transmission confidentiality and provide a secure transmission design to maximize the confidentiality of the secrecy outage probability (SOP) constraints secrecy rate. For scenarios where legitimate and non-legitimate channels are highly correlated, ref. [8] proposes a CJ-aided beamforming design scheme that maximizes the secrecy rate under SOP constraints.

The above papers are based on the assumption that the main channel’s channel state information (CSI) is perfect. In practice, it is difficult to cancel all the CJ due to non-ideal factors, even at the licensed receiver. Further, the residual CJ caused by incomplete jamming cancellation will worsen the licensed receiver’s signal-to-jamming-noise ratio (SJNR), thereby affecting the safety of the systems. For this problem, ref. [9] analyzes the influence of non-ideal factors on CJ suppression performance. Different from the theoretical analysis of the above literature, ref. [10] explicitly proposes a CJ cancellation architecture for point-to-point communication systems, and a test bench is designed to implement the proposed architecture. In the experimental results, the architecture can provide about 51dB CJ cancellation capability, which provides the experimental basis for CJ cancellation in the receiver. Unfortunately, it does not discuss reducing the system deterioration caused by residual CJ.

For the deterioration of security performance caused by these non-ideal factors, most studies optimize the SJNR from the power allocation between CJ and desired signals, e.g., ref. [11] optimizes the transmit power ratio between CJ and desired signals for signal distortion caused by transceiver in-phase and quadrature imbalance. In [12], the secrecy performance is jointly optimized from two perspectives of transmitter power allocation and receiver reconstruction CJ compensation with frequency mismatch. In addition, ref. [13] proposes the use of the frequency offset least mean squares (FO-LMSs) algorithm to improve the influence of carrier and sampling frequency offset on CJ cancellation.

The optimization studies of the above literature are all based on single-input, single-output (SISO) systems. For single-input multi-output (SIMO) systems, N independent branch signals can be obtained at the licensed receiver, and the signal output of each branch can be combined with appropriate combining technology, which can reduce the influence of residual CJ on the systems and achieve diversity gain. The traditional maximum ratio combining (MRC) [14] can achieve the best performance in terms of improvement under the condition that CSI is completely known and the CJ can be perfectly suppressed. However, when CSI is not perfect, the optimal coefficient of MRC cannot be accurately achieved, e.g., the influence of time migration on the MRC coefficient and the output signal-to-noise ratio (SNR) is analyzed in [15]. On the other hand, refs. [16,17] point out that the traditional MRC is not an optimal combining method when the received signal has interference other than Gaussian white noise. Specifically, ref. [16] studies the performance of MRC applied to SIMO systems with Poisson field of interferers. In [17], the SNR of the received signal with pulse noise is derived and compared under different combination schemes.

1.2. Contributions

Although literature [15,16,17] analyze the influence of non-ideal factors on diversity combining schemes, they are all based on communication scenarios, and their purpose is to maximize the communication rate, which is quite different from our research background and objectives; in these studies, the effects of residual CJ on the merging coefficient and security performance are not considered. In this paper, for the CJ-aided single-input multiple-output multiple-eavesdropper (SIMOME) systems, we analyze the influence of channel estimation error on CJ suppression and then derive the optimal combining coefficient and the security performance after combining them. To the best of the authors’ knowledge, we are the first to analyze the effects of incomplete CSI and the resulting residual CJ on diversity combining performance in CJ-aided SIMOME systems. Our key contributions are summarized as follows:

• The CJ-aided physical layer security model for SIMOME systems is presented.
• The effects of licensed receiver’s incomplete CSI and the resulting residual CJ on the signal-to-jamming-plus-noise ratio (SJNR) are analyzed, and the closed-form expression of the combined output SJNR is given.
• The optimal combining coefficient is derived for maximizing the combined output SJNR, and the achievable secrecy rate is analyzed to evaluate the security performance of the systems.

Bold uppercase and lowercase letters are used to represent matrices and vectors, respectively. The notation $C_a$ denotes the auto-covariance matrix of $a$, and $R_{ab}$ denotes the cross-correlation matrix between a and b. Function $\mathrm{E}[\cdot ]$ denotes mathematic expectation.

2. System Model

Consider the system model shown in Figure 1, which includes a desired signal transmitter (Alice), CJ transmitter (Jammer), licensed receiver (Bob), and eavesdropper (Eve). Alice and Jammer each have a single antenna, and Bob and Eve are equipped with N antennas. Assume that the channel matrices of Alice to Bob and Eve are $h_s$ and $g_s$, and the channel matrices of Jammer to Bob and Eve are $h_j$ and $g_j$, respectively.

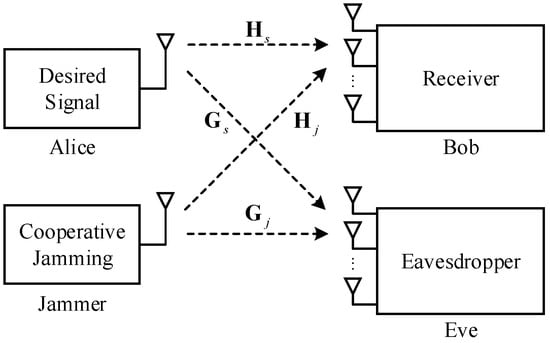
Figure 1. Model of SIMOME system.

2.1. Signal Transmission

$h_s={\left[h_s^{\left(1\right)},h_s^{\left(2\right)},\cdots ,h_s^{\left(N\right)}\right]}^T$ is defined as a complex Gaussian random vector and $h_s~CN\left(0,C_{h_s}\right)$, where $C_{h_s}$ is the auto-covariance matrix of $h_s$, which is given by

$$C_{h_s}=\mathrm{E}\left[h_s{h}_s^H\right]$$

(1)

Similarly, $h_j={\left[h_j^{\left(1\right)},h_j^{\left(2\right)},\cdots ,h_j^{\left(N\right)}\right]}^T$ is also a complex Gaussian random vector and $h_j~CN\left(0,C_{h_j}\right)$, where $C_{h_j}$ is the auto-covariance matrix of $h_j$, which is given by

$$C_{h_j}=\mathrm{E}\left[h_j{h}_j^H\right]$$

(2)

Suppose that the transmitted signal of Alice and Jammer obeys the complex Gaussian distribution, and $j$ is uncorrelated with $s$. $E_s$ and $E_j$ are the variances of desired signal and CJ, i.e., $s~CN\left(0,E_s\right)$ and $j~CN\left(0,E_j\right)$. Bob’s received signal is a mixed signal consisting of desired signal, CJ, and additive Gaussian white noise (AWGN), which can be expressed in vector form as

$$r=h_{s}s+h_{j}j+n,$$

(3)

where $n={\left[n_1,n_2,\cdots ,n_N\right]}^H$ denotes AWGN. Assume that the noise power on each branch is $N_0$, then $n~CN\left(0,N_{0}I\right)$.

At Bob, the jamming is separated from the mixed signal, and the residual signal is then combined according to a certain weight (see Figure 2). In this paper, CJ cancellation and combining are carried out in Bob. The original jamming is used for CJ reconstruction by using the estimated channel coefficient, and the reconstructed CJ is subtracted from the received signal. After jamming cancellation, the combined coefficient is estimated, and the combined signal is obtained according to the weight of each branch phase.

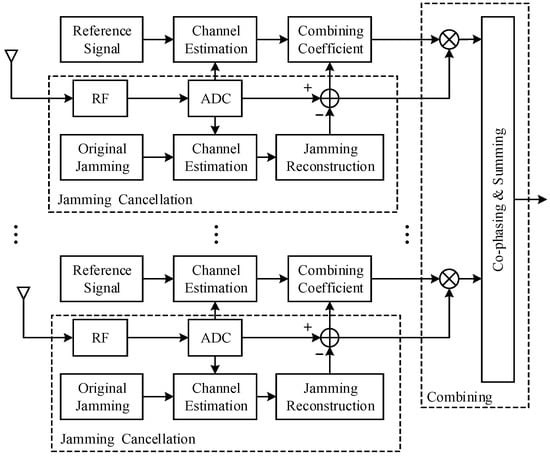
Figure 2. Combining in CJ-aided SIMOME system (Bob).

2.2. Jamming Cancellation

Since the priori information of CJ is known to Bob, the CJ can be reconstructed and cancellated by utilizing the original jamming. However, even Bob cannot accurately reconstruct CJ due to imperfect CSI, which will result in incomplete jamming cancellation.

${\widehat{h}}_j~CN\left(0,C_{{\widehat{h}}_j}\right)$ is the channel observation for $h_j$, where the auto-covariance matrix $C_{{\widehat{h}}_j}=\mathrm{E}\left[{\widehat{h}}_j{\widehat{h}}_j^H\right]$. In this paper, the minimum mean square error (MMSE) algorithm is used to optimize ${\widehat{h}}_j$; thus, the estimated channel value ${\tilde{h}}_j$ is given by

$${\tilde{h}}_j=R_{h_j{\widehat{h}}_j}{C}_{{\widehat{h}}_j}^{-1}{\widehat{h}}_j.$$

(4)

${\tilde{h}}_j$ is the zero-mean complex Gaussian vector with the auto-covariance matrix

$$C_{{\tilde{h}}_j}=R_{h_j{\widehat{h}}_j}{C}_{{\widehat{h}}_j}^{-1}{R}_{h_j{\widehat{h}}_j}^H.$$

(5)

The auto-covariance matrix of CJ’s channel estimation error is defined as $C_{e_j}$, and then the channel estimation error is defined as $e_j~CN\left(0,C_{e_j}\right)$, which is uncorrelated with ${\tilde{h}}_j$, and

$$e_j=h_j-{\tilde{h}}_j,$$

(6)

$$C_{e_j}=C_{h_j}-C_{{\tilde{h}}_j}.$$

(7)

The reconstructed jamming can be expressed as

$$\tilde{j}={\tilde{h}}_{j}j.$$

(8)

Thus, the residual signal after jamming cancellation is the combination of the desired signal, residual CJ, and AWGN, which is given by

$$r_m=r-\tilde{j}=h_{s}s+e_{j}j+n.$$

(9)

2.3. Diversity Combining

Similarly with jamming cancellation, the estimated channel coefficient vector ${\tilde{h}}_s$ can be obtained by MMSE estimation for $h_s$, and

$${\tilde{h}}_s=R_{h_s{\widehat{h}}_s}{C}_{{\widehat{h}}_s}^{-1}{\widehat{h}}_s,$$

(10)

where the auto-covariance matrix $C_{{\widehat{h}}_s}=\mathrm{E}\left[{\widehat{h}}_s{\widehat{h}}_s^H\right]$ and ${\widehat{h}}_s~CN\left(0,C_{{\widehat{h}}_s}\right)$ denote the channel observation vector for $h_s$. ${\tilde{h}}_s$ is also a zero-mean complex Gaussian vector with the auto-covariance matrix

$$C_{{\tilde{h}}_s}=R_{h_s{\widehat{h}}_s}{C}_{{\widehat{h}}_s}^{-1}{R}_{h_s{\widehat{h}}_s}^H.$$

(11)

The auto-covariance matrix of the desired signal’s channel estimation error is defined as $C_{e_s}$, and then the channel estimation errors $e_s~CN\left(0,C_{e_s}\right)$ and $e_s$ are given by

$$e_s=h_s-{\tilde{h}}_s,$$

(12)

$$C_{e_s}=C_{h_s}-C_{{\tilde{h}}_s}.$$

(13)

To achieve diversity gain, we use the weight vector $w={\left[w_1,w_2,\cdots w_N\right]}^T$ to combine the signals after jamming cancellation, where $w_k$ is the weight coefficient of the k-th signal branch. By multiplying each signal branch by the complex coefficient $w_k$ and then accumulating all branches, the combined variable $d$ can be expresses as

$$d=w^H{r}_m=w^H\left({\tilde{h}}_{s}s+e_{s}s+e_{j}j+n\right).$$

(14)

It can be seen from (14) that in addition to noise, the combined signal also contains residual jamming due to channel estimation error, which will worsen the combined SJNR. Selecting the appropriate weight can maximize the output SJNR and reduce the influence of residual jamming on the system safety performance. Thus, the problem of the determination of the weight vector $w$ is key and proves difficult for diversity combining.

3. Optimal Combining in SIMOME Systems

Traditional MRC is an optimal method under the assumption that CSI is perfectly known, and the signal does not contain any jamming other than white noise. In this method, the system can achieve the maximum diversity gain when $w=h_s$ [18].

However, since CSI is always unperfect, $h_s$ cannot be obtained accurately. Besides the desired signal and AWGN, residual CJ is also included in $r_m$, and residual CJ between each branch is not necessarily independent. Thus, the result of the traditional MRC in [14] cannot be used directly in our system. In this scenario, both residual CJ and the channel estimation error of the desired signal need to be taken into account to achieve the maximum output SJNR. To solve this problem, this section deduces the optimal combining coefficient and combining performance based on residual CJ and the desired signal’s channel estimation error analyzed in Section 2.

3.1. Combining Coefficient

Equation (14) presents the output signal after diversity combining. For block-fading channels [19], the channel statistics change much more slowly than the channel state. Therefore, we do assume that perfect channel statistics can be obtained from the receiver. Moreover, both $e_{s}s$ and $e_{j}j$ are regarded as jamming due to $e_s$ and $e_j$ but are not observable. Equation (14) can be rewritten as

$$d=w^H{\tilde{h}}_{s}s+w^H\left(e_{s}s+e_{j}j+n\right)=d_s+d_n$$

(15)

where $d_s=w^H{\tilde{h}}_{s}s$ and $d_n=w^H\left(e_{s}s+e_{j}j+n\right)$. The power of the combined signal is

$$\mathrm{P}\left[d_s\right]={\left|w^H{\tilde{h}}_s\right|}^2{E}_s,$$

(16)

and the power of $d_n$ is calculated as

$$\mathrm{P}\left[d_n\right]=w^H\left(C_{e_s}{E}_s+C_{e_j}{E}_j+N_{0}I\right)w.$$

(17)

Thus, the output SJNR of the combiner is defined as

$${\gamma }_o={\displaystyle \frac{\mathrm{P}\left[d_s\right]}{\mathrm{P}\left[d_n\right]}}={\displaystyle \frac{{\left|w^H{\tilde{h}}_s\right|}^2{E}_s}{w^H\left(C_{e_s}{E}_s+C_{e_j}{E}_j+N_{0}I\right)w}}.$$

(18)

Proposition 1.

The maximum SJNR can be obtained when

$$w={\left(C_{e_s}{E}_s+C_{e_j}{E}_j+N_{0}I\right)}^{-1}{\tilde{h}}_s.$$

(19)

Proof of Proposition 1

. Please see Appendix A.

By substituting (19) to (18), the output SJNR ${\gamma }_o$ can be expressed as

$$\begin{array}{l}{\gamma }_o={\displaystyle \frac{\left\{{\left[{\left(C_{e_s}{E}_s+C_{e_j}{E}_j+N_{0}I\right)}^{-1}{\tilde{h}}_s\right]}^H{\tilde{h}}_s\right\}\left\{{\tilde{h}}_s^H\left[{\left(C_{e_s}{E}_s+C_{e_j}{E}_j+N_{0}I\right)}^{-1}{\tilde{h}}_s\right]\right\}{E}_s}{{\left[{\left(C_{e_s}{E}_s+C_{e_j}{E}_j+N_{0}I\right)}^{-1}{\tilde{h}}_s\right]}^H{\tilde{h}}_s}}\\ ={\tilde{h}}_s^H{\left(C_{e_s}{E}_s+C_{e_j}{E}_j+N_{0}I\right)}^{-1}{\tilde{h}}_s{E}_s\end{array}$$

(20)

□

Remark 1.

Consider the ideal scenario, where ${\tilde{h}}_s=h_s$ and ${\tilde{h}}_j=h_j$, i.e., $e_s=0$ and $e_j=0$. In this case, the special form of output SJNR  ${\gamma }_o$  can be obtained as

$${\gamma }_o={\left|h_s\right|}^2{E}_s\cdot N_0^{-1},$$

(21)

and the optimal combining coefficient can be expressed as

$$w=h_s.$$

(22)

It can be seen that this result is consistent with that of MRC. Thus, the traditional MRC can be regarded as an ideal case for this paper.

Remark 2.

At one extreme, if the channel errors between branches are independent of each other, i.e.,  $C_{e_s}$ and $C_{e_j}$ are diagonal matrices, ${\gamma }_o$  takes on the largest value, which can be expressed as

$${\gamma }_o={\displaystyle {\sum }_{i=0}^N\frac{{\left|{\tilde{h}}_s^{\left(i\right)}\right|}^2{E}_s}{E_s{C}_{e_s}^{\left(i,i\right)}+E_j{C}_{e_j}^{\left(i,i\right)}+N_0}}.$$

(23)

Remark 3.

At the other extreme, if the channel errors between branches are complete correlated, i.e., $C_{e_s}=C_{e_s}\cdot e{e}^H$, $C_{e_j}=C_{e_j}\cdot e{e}^H$, where e = [1, 1, 1, …]^T, ${\gamma }_o$ takes on the smallest value, which can be expressed as

$${\gamma }_o={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N{\left|{\tilde{h}}_s^{\left(i\right)}\right|}^2{E}_s}}{{\displaystyle {\sum }_{i=1}^N{E}_s{C}_{e_s}}+{\displaystyle {\sum }_{i=1}^N{E}_j{C}_{e_j}}+N_0}}.$$

(24)

3.2. Achievable Secrecy Rate

In the system model in Figure 1, Eve is also equipped with multiple antennas. The mixed signal received by Eve can be expressed as

$$r_e=g_{s}s+g_{j}j+n_e,$$

(25)

where $g_s~CN\left(0,C_{g_s}\right)$ and $g_j~CN\left(0,C_{g_j}\right)$ are channel coefficient matrices with Alice and Jammer to Eve, respectively. $n_e$ denotes Gaussian white noise and $n_e~CN\left(0,N_{e}I\right)$.

Since Eve cannot obtain prior information about CJ, it cannot separate the desired signal from the received mix signal. Assuming that the combining weight vector of Eve is $w_e={\left[w_e^{\left(1\right)},w_e^{\left(2\right)},\cdots w_e^{\left(N\right)}\right]}^T$, then the combined signal of Eve is

$$d_e=w_e{r}_e.$$

(26)

In order to more conservatively evaluate the security performance of the system, we assume that Eve can perform the ideal MRC and $w_e=g_s$, and then the output SJNR ${\gamma }_e$ can be expressed as

$${\gamma }_e={\displaystyle \frac{{\left|w_e^H{g}_s\right|}^2{E}_s}{{\left|w_e^H{g}_j\right|}^2{E}_j+w_e^H\left(N_{e}I\right)w_e}}.$$

(27)

In this paper, the achievable secrecy rate [2] is used to evaluate the security performance of the SIMOME system. The achievable secrecy rate denotes the difference between the mutual information of Alice–Bob and Alice–Eve, which can be expressed as

$$R_s={\left[{\log }_2\left(1+{\gamma }_o\right)-{\log }_2\left(1+{\gamma }_e\right)\right]}^{+},$$

(28)

where ${\left[x\right]}^{+}:=\max \left\{x,0\right\}$. It can be seen that when ${\gamma }_o>{\gamma }_e$, $R_s>0$, the system has secrecy capability.

Further, ref. [20] proposes that the thermal noise at Eve can be assumed to be 0 to determine the secrecy rate more conservatively. Under this assumption, ${\gamma }_e$ can be rewritten as

$${\gamma }_e={\displaystyle \frac{{\left|w_e^H{g}_s\right|}^2{E}_s}{{\left|w_e^H{g}_j\right|}^2{E}_j}}={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N{\left|g_s^{\left(i\right)}\right|}^2{E}_s}}{{\displaystyle {\sum }_{i=1}^N{g}_s^{\left(i\right)}{g}_j^{\left(i\right)}{E}_j}}}.$$

(29)

4. Simulation Results

In this section, we simulate and verify the combining performance under the imperfect CSI analyzed in this paper and compare the proposed scheme with other traditional schemes that do not consider the imperfect CSI and the resulting residual CJ. In simulations, the power of CJ is equal to that of the desired signal, and $E_s /N_0=100 \mathrm{dB}$. The normalized channel estimation error variances of the desired signal and the CJ at the i-th branch are $C_{e_s}^{\left(i,i\right)} /{\left|h_s^{\left(i\right)}\right|}^2$ and $C_{e_j}^{\left(i,i\right)} /{\left|h_j^{\left(i\right)}\right|}^2$, respectively. Both ${\left|h_s^{\left(i\right)}\right|}^2$ and ${\left|h_j^{\left(i\right)}\right|}^2$ are random values of $-66 \mathrm{dB}~-100 \mathrm{dB}$. The specific simulation parameters are shown in Table 1.

Table 1. Simulation Conditions.

Parameter	Value
CJ type	Cyclic PN sequence
Channel type	Block-fading channel
Bandwidth	10 MHz
Carrier frequency	2.4 GHz
Sampling	100 ns
Estimated period	1024 symbols

Firstly, Figure 3 shows the output SJNR under different normalized channel estimation errors, where the errors of each branch are uncorrelated. Let the normalized channel estimation error variance of the desired signal and CJ on each branch be equalized; this applies in the following simulations. When the channel estimation error is small, the output SJNR of the proposed optimal combining scheme and MRC schemes are both close to the ideal MRC. When the channel estimation error is large, the residual jamming is large; thus, the output SJNR of the three schemes deteriorates. Still, the performance of the optimal combining scheme is always better than that of MRC schemes, and the greater the channel estimation error, the more obvious the advantage of the optimal combining scheme over MRC schemes. Among them, the performance of the optimized MRC scheme is better than that of the traditional MRC scheme because the channel estimation error of the communication signal is considered. Moreover, compared with equal-gain combining, the optimal combining scheme can obtain a higher output SJNR, especially when the channel estimation error is small.

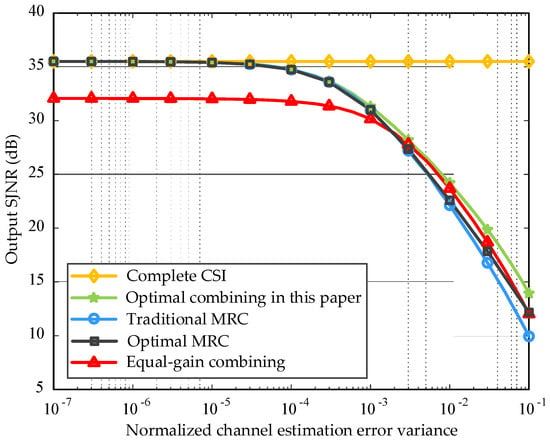
Figure 3. Comparison of combining performance under different channel estimation errors, where traditional MRC is proposed in [21] and optimal MRC is proposed in [22].

Next, Figure 4 compares the effect of antenna number on the output SJNR when the channel errors of each branch are correlated and not correlated. When the channel estimation errors between branches are not correlated, the growth trend in the SJNR in optimal combining is similar to that of ideal MRC, which increases with the increase in antenna number. In this case, the residual jamming can be regarded as noise, and its influence on performance can be reduced by increasing the number of antennas. On the contrary, when the channel estimation errors among branches are completely correlated, increasing the antenna numbers cannot reduce the influence of residual jamming on the output SJNR. In particular, the larger the normalized channel estimation error, the more limited the optimization of the SJNR by combining. These phenomena are consistent with remark 2 and remark 3.

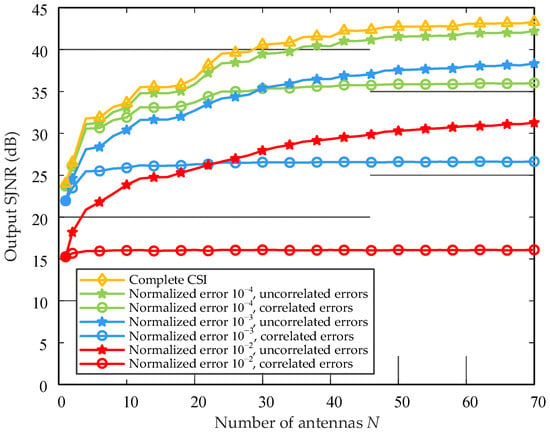
Figure 4. Comparison of combining performance under different antenna numbers.

Suppose Bob and Eve are close to each other, and ${\left|h_s^{\left(i\right)}\right|}^2={\left|g_s^{\left(i\right)}\right|}^2=-66 \mathrm{dB}$, ${\left|h_j^{\left(i\right)}\right|}^2={\left|g_j^{\left(i\right)}\right|}^2=-66 \mathrm{dB}$ [23]. Figure 5 further proves that the optimization effect of increasing the number of antennas decreases as the error correlation increases. Compared with the curve for the same number of antennas, the achievable secrecy rate decreases with the increase in the normalized channel estimation error, regardless of whether the channel estimation errors are correlated. It is worth noting that for the perfectly correlated channel estimation errors, when the normalized channel estimation errors are large, the achievable secrecy rate cannot be improved, even if the number of antennas is increased.

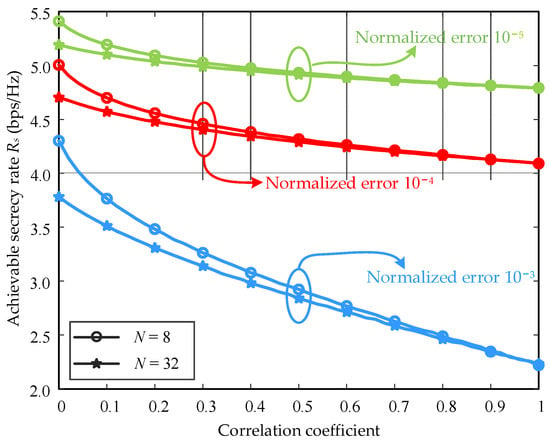
Figure 5. Effect of channel estimation errors correlation on achievable secrecy rate.

5. Conclusions

This paper investigates the effect of imperfect CSI and the resulting residual CJ on diversity combining and security performance in IoT systems and analyzes the optimal combining scheme considering imperfect CSI. To improve the security of IoT systems, a CJ cancellation model combined with the diversity combining technique at licensed receivers is proposed. Considering the imperfect CSI, the optimal diversity combining coefficient is derived to maximize the output SJNR, and the achievable secrecy rate is given to evaluate the security performance. The theoretical and simulation results show that the proposed scheme is superior to other combining schemes, especially when the channel estimation error is large. In the follow-up study, we will not only focus on the channel estimation error but also consider the influence of non-ideal factors such as phase noise, delay, and frequency offset on jamming cancellation and combining performance.