Efficient Electronic Voting System Based on Homomorphic Encryption

Abstract

In the last decade, E-voting has received great attention due to its advantages in efficiency and accuracy. Fan et al. presented a novel E-voting system named HSE-Voting by utilizing homomorphic signcryption. The HSE-Voting system was claimed to gain a provable security goal under the standard proof. In this paper, we illustrate that their scheme may suffer from some potential security issues. On the one hand, the voting information could be recovered by the authentication center (AC). On the other hand, any malicious voter could disrupt the voting system undetected by locally modifying his ballot. In order to increase the resilience of the voting system to risks, an improvement of the HSE-Voting system is developed. Our improved system fixes the above security weaknesses but increases the computation cost on the AC side by a small amount. In addition, the proposed scheme satisfies voter anonymity, ballot privacy, and verifiability of election results.

1. Introduction

E-voting refers to voting that allows voters to cast their votes through the internet. Compared with traditional elections, E-voting not only saves a lot of ballot printing, transportation, and manual counting costs but also improves voting efficiency and convenience. For example, the 2020 US presidential election coincides with the national public health security problem. If the traditional voting method is adopted, it will inevitably cause a large number of people to gather, while electronic voting can solve this problem well. Many countries, including India and Brazil, have used electronic voting technology in many different electoral fields [1].

In 2020, Fan et al. [2] proposed a homomorphic signcryption scheme to construct an E-voting system named HSE-Voting in order to improve the efficiency of E-voting. Due to the integrated design of signcryption, its efficiency has been greatly optimized compared with Yang et al.’s system [3] on the agency side. Furthermore, it gives a comparative security analysis. However, there are some security issues in Fan et al.’s system, such as voter privacy being leaked, and the E-voting system may not properly being completed.

In this paper, we propose two cryptanalytic attacks on Fan et al.’s system [2]. In the first attack algorithm, we show that an honest-but-curious authentication center (AC) can recover the voter’s voting information from the corresponding ballot. In the second attack algorithm, we reveal that malicious voters can disrupt the election process by sending special incorrect ballots. Moreover, in order to enhance the security of the HSE-Voting system, we propose an improved HSE-Voting system by combining the signature and the proof of partial-knowledge protocol (PPK). While avoiding the above security risks, our system also reduces the computation cost on the agency-side compared to the existing work.

1.1. Related Work

Electronic voting [4,5,6] has been one of the key areas of focus for researchers. Over the past decade, many E-voting schemes have been proposed [7,8,9,10]. Most efficient E-voting protocols can be categorized by their approaches into the following types: blind signature [11,12,13], mix-nets [14], and homomorphic encryption [3,11,12,14,15,16,17]. In this subsection, we focus on the homomorphic encryption-based E-voting system.

Homomorphic encryption has been utilized in E-voting systems. The benefit of its homomorphic property is that ballots can be tallied without accessing the content of any ballot [18]. The ElGamal scheme [19] is one of the most widely used homomorphic encryption schemes in electronic voting. For instance, Refs. [3,11,12,14,15,16] exploit ElGamal to encrypt the ballots, thereby constructing an E-voting system with some existing cryptography tools, such as the proof of zero-knowledge [20] and the proof of partial knowledge [21].

In [14], Adida proposed a web-based E-voting system named Helios, which achieved open-audit voting using ElGamal encryption. Helios has strong security. Assuming that there are enough auditors, even if all the authorities collaborate to corrupt the system, there is a high probability of being exposed. Nevertheless, the security of Helios is closely related to the shuffling mechanism. It follows that if the Helios server is corrupted, then the submitted votes may be shuffled incorrectly, or the encrypted votes may be decrypted incorrectly. Furthermore, the performance results reported in [14] demonstrate that there is a large time overhead in the actual application. In an election with only two options in each vote and 500 voters, the Helios program takes more than 8 h.

In [12], the Helios system made several dramatic improvements to form the Helios 2.0 program, which was applied to support a real-world election. Specifically, Helios 2.0 updated the open audit mechanism. However, the key generation and decryption codes of Helios 2.0 are required to be completed by several trusted election committees. In fact, it is difficult to guarantee that the trustees are trusted in real environments. In addition, Helios 2.0 does not optimize its efficiency.

In [3], Yang et al. proposed a ranked choice E-voting system based on homomorphic encryption. Compared with the similar previous work, this system greatly improves the computation efficiency on the voter side. However, in this system, signature and encryption exist independently; the computation cost of the election agency increases rapidly as the number of voters grows. In addition, it also lacks the standardized proof of security.

Yuan et al. proposed an E-Voting scheme [7] based on Paillier homomorphic encryption and decentralization. The scheme utilizes signatures and double-encrypted technologies to secure the ballot information during transmission. In addition, the decentralization character avoids the risks associated with the corruption of a single institution and increases the openness and transparency of the system.

Qu et al. proposed an electronic voting protocol [8] based on the homomorphic signcryption. This protocol utilizes blockchain to make the election procedure public. Benefiting from the decentralized nature of blockchain, their protocol eliminates the requirement for trusted institutions.

In addition, Sheela et al. [9] and Saproo et al. [10] developed E-voting software based on homomorphic encryption, which further promotes the application of E-voting technology in practice.

E-voting represents a complex practical application scenario that necessitates the comprehensive consideration of multiple factors. Beyond safeguarding the privacy of voters’ ballot information as a fundamental requirement, it is imperative to ensure eligibility, accuracy, non-repeatability, reliability, verifiability and so on. Consequently, existing schemes enrich the functionality of the voting system to align with practical demands. On the other hand, there is a need to strike a balance between functionality and efficiency to ensure the practicality of the voting system.

1.2. Organization

Section 2 and Section 3 describe cryptographic tools and Fan et al.’s HSE-Voting system, respectively. Section 4 presents the cryptanalytic algorithm, and Section 5 proposes our improved HSE-Voting system. Section 6 provides the characteristic analysis of our system. The performance analysis is shown in Section 7. Section 8 concludes this paper.

2. Preliminaries

In this section, we introduce the notations and the basics of cryptography used in this paper. In the content described, the Diffie–Hellman problem is the intractability problem on which the security of the improvement scheme is based. We use the ElGamal scheme to protect ballot privacy and use its additive homomorphism to count ballot information. The proof of partial knowledge and proof of zero-knowledge (PZK) are adopted to provide the verifiability of election results. These concepts are important in enhancing the security of the HSE-Voting system.

2.1. Diffie–Hellman Problem

The Diffie–Hellman problem is a difficult problem of cryptography proposed by Whitfield Diffie and Martin Hellman in [22].

Definition 1 

(Computational Diffie–Hellman Assumption, CDH). Considering $\mathbb{G}$ is a cyclic group of order q, g is a generator of $\mathbb{G}$ and two elements $a,b\leftarrow {\mathbb{Z}}_q$. Given $g^a$ and $g^b$, it is computationally intractable to compute the value $g^{ab}$.

Definition 2 

(Decisional Diffie–Hellman Assumption, DDH). Considering $\mathbb{G}$ is a cyclic group of order q, g is a generator of $\mathbb{G}$, three elements $a,b,c\leftarrow {\mathbb{Z}}_q$. The DDH tuple $D=\left(g,g^a,g^b,g^{ab}\right)$ and random tuple $R=\left(g,g^a,g^b,g^c\right)$ are computationally indistinguishable.

2.2. Elgamal Cryptography

ElGamal cryptography [19] is a well-known homomorphic encryption scheme. We select a safe-prime p of the form $p=2q+1$, where q is also a prime. In the remainder of this paper, we consider $\mathbb{G}$ is a cyclic group of quadratic residues modulo p. The ElGamal scheme consists of the following three algorithms.

KeyGen: Let g be a generator of $\mathbb{G}$. Randomly choose $x\leftarrow {\mathbb{Z}}_q$, then compute $y=g^x$. Output the key pair $(SK,PK)$ as follows.

$$(SK,PK)=(x,y).$$

Enc: Given a message $m\in {\mathbb{Z}}_q$, randomly choose element $r\leftarrow {\mathbb{Z}}_q$, and encrypt m as follows.

$$\mathrm{Enc}\left(m\right)=c=(c_0,c_1)=(g^r,g^m{y}^r).$$

Dec: Given the ciphertext c, decrypt the ciphertext as follows.

$$\mathrm{Dec}\left(c\right)=c_1/c_0^x=g^m,$$

where m can be revealed by computing a discrete algorithm.

Homomorphism: We show that the multiplication of $\mathrm{Enc}\left(m_1\right)$ and $\mathrm{Enc}\left(m_2\right)$ is a ciphertext corresponding to $m_1+m_2$. Note that

$$\begin{array}{cc}\hfill \mathrm{Enc}\left(m_1\right)·\mathrm{Enc}\left(m_2\right)& =\left(g^{r_1},g^{m_1}{y}^{r_1}\right)·\left(g^{r_2},g^{m_2}{y}^{r_2}\right)\hfill \\ \hfill & =\left(g^{r_1+r_2},g^{m_1+m_2}{y}^{r_1+r_2}\right)\hfill \\ \hfill & =\mathrm{Enc}\left(m_1+m_2\right).\hfill \end{array}$$

2.3. Proof of Partial Knowledge

In an ElGamal cryptography system, there is a cyclic group of quadratic residues $\mathbb{G}$ of order q with a generator g, the public key $y=g^x$, and the secret key is x. Randomly select two plaintexts $m_1,m_2\in {\mathbb{Z}}_q$, compute $\mathrm{Enc}\left(m_1\right)=\left(c_0,c_1\right)=\left(g^r,g^{m_1}{y}^r\right)$. Then, we describe the process of proof of partial knowledge based on the ElGamal scheme [21], in which the prover P can prove to the verifier V that the provided ciphertext is one of $\mathrm{Enc}\left(m_1\right)$ and $\mathrm{Enc}\left(m_2\right)$, but the verifier V cannot determine which plaintext corresponds to the ciphertext.

Firstly, the prover P generates the PPK parameters $PPK$ as Algorithm 1.

Algorithm 1 Generating the PPK verification parameters

Input:     $c_0$, $c_1$, $m_1$, $m_2$, y Output:     $PPK=(c_0,c_1,T_0,T_1,T_2,v_1,v_2,s_1,s_2)$ 1: Prover P: 2:  Generate $e,v_2\leftarrow {\mathbb{Z}}_q$. 3:  Compute $s_2=r·v_2+emodq$. 4:  Compute $T_0=g^e$. 5:  Compute $T_1=y^e$. 6:  Compute $T_2=\left(g^{m_2{v}_2}{y}^{s_2}\right)/c_1^{v_2}$. 7:  Compute $v=\mathrm{hash}\left(T_0\left|\right|T_1\left|\right|T_2\left|\right|c_0\left|\right|c_1\right)$. 8:  Compute $v_1=v_2\oplus v$. 9:  Compute $s_1=r·v_1+emodq$. 10: $PPK=(c_0,c_1,T_0,T_1,T_2,v_1,v_2,s_1,s_2)$ 11: return  $PPK$

Then, the prover P sends $PPK$ to the verifier V. After that, the verifier V verifies the correctness of the PPK parameters as Algorithm 2.

If Algorithm 2 outputs true, verifier V believes that the ciphertext is either $\mathrm{Enc}\left(m_1\right)$ or $\mathrm{Enc}\left(m_2\right)$, but the exact value of the plaintext cannot be determined. If the $m_2$ is chosen to be encrypted, let step 6 in Algorithm 1 be $T_2=\left(g^{m_1{v}_2}{y}^{s_2}/c_1^{v_2}\right)$, and set $m_1=m_2,m_2=m_1$ for Algorithm 2. More details can be seen in [21].

Algorithm 2 Verifying the PPK parameters

Input:     $PPK$, $m_1$, $m_2$ Output:     true or false 1: Verifier V: 2:  Verify $v_1\oplus v_2=hash\left(T_0∥T_1∥T_2∥c_0∥c_1\right)$. 3:  Verify $g^{s_1}=T_0·c_0^{v_1}$. 4:  Verify $g^{s_2}=T_0·c_0^{v_2}$. 5:  Verify $y^{s_1}=T_1·{\left(c_1/g^{m_1}\right)}^{v_1}$. 6:  Verify $y^{s_2}=T_2·{\left(c_1/g^{m_2}\right)}^{v_2}$. 7: If all equations hold, return true; otherwise, return false.

2.4. Proof of Zero-Knowledge

This subsection introduces the preliminary knowledge related to proof of zero-knowledge [20]. As in the previous subsection, this part is still based on the ElGamal cryptography system definition. The process of PZK [20] is described as follows in which the prover P can prove to the verifier V that the return value t and the prover’s public key $h=g^x$ have the same exponentiation, i.e., x. However, the verifier V cannot obtain any information about the prover’s secret key $sk=x$.

Firstly, the verifier V generates and discloses a random parameter $a\leftarrow {\mathbb{Z}}_q$. Then, the prover P generates the PZK parameters as Algorithm 3.

Algorithm 3 Generating the verification parameters

Input:     a, h, x Output:     $PZK=(t,s,v,T_0,T_1)$ 1: Prover P: 2:  Generate $e\leftarrow {\mathbb{Z}}_q$. 3:  Compute $t=a^x$. 4:  Compute $T_0=g^e$. 5:  Compute $T_1=a^e$. 6:  Compute $v=\mathrm{hash}\left(t\left|\right|a\left|\right|T_0\left|\right|T_1\right)$. 7:  Compute $s=x·v+e\mathrm{mod}q$. 8: $PZK=(t,s,v,T_0,T_1)$ 9: return  $PZK$

After that, the prover P sends PZK parameters $PZK$ to the verifier V. Then, the verifier V verifies the correctness of the PZK protocol with the parameters.

If Algorithm 4 outputs true, the verifier V trusts the statement of the prover P.

Algorithm 4 Verifying the PZK parameters

Input:     a, $PZK$ Output:     true or false 1: Verifier V: 2:  Verify $v=\mathrm{hash}\left(t\left|\right|a\left|\right|T_0\left|\right|T_1\right)$. 3:  Verify $g^s=T_0·h^v$. 4:  Verify $a^s=T_1·t^v$. 5: If all equations hold, return true; otherwise, return false.

3. HSE-Voting System Overview

In this section, we briefly introduce the entities and election processes included in the HSE-Voting system [2].

3.1. Entities in the HSE-Voting System

Here, we list all entities involved in the HSE-Voting system.

• Voters: People who are authorized to vote.
• Authentication Center: AC takes responsibility for verifying the identification of voters, tallying and other related work in an election. Especially, AC is honest-but-curious.
• Bulletin Board (B Board): An insert-only bulletin board, which displays all information about the election.
• Auditors: Auditors are responsible for supervising the voting process and verifying the election result. Furthermore, the auditors are credible.

3.2. Initialization and Registration

In the initialization phase, AC applies the safe parameter $\lambda$ to generate the parameters $params=(\mathbb{G},g,q)$ and a key pair $(SK,PK)$, where $SK=\left(x_0,x_1,x_2\right)\leftarrow {\mathbb{Z}}_q^3$, $PK=\left(y_0,y_1,y_2\right)=\left(g^{x_0},g^{x_1},g^{x_2}\right)$, then publishes $params$ and $PK$ on the B Board.

In order to register with the HSE-Voting system, every voter has to provide valid identification. Once a voter’s identity has been verified, AC sends a random $ID$ number to them through a secure channel. In the subsequent election process, the HSE-Voting system requires voters to identify themselves using an $ID$ number. Obviously, AC can easily determine the voter identity corresponding to the allocated $ID$ number.

3.3. Ballot Generation

The voter $V_i$ generates plaintext votes $b_{i,j}\in \{0,1\}$ for each candidate, where $i\in \left\{1,\dots ,N_v\right\}$, $j\in \left\{1,\dots ,N_c\right\}$ (1 means support the candidate, 0 means do not support the candidate). The voter $V_i$ computes the signcryption of plaintext vote $b_{i,j}$, the corresponding PPK parameters $PP{K}_i$ and their public key $p{k}_i$ as Algorithm 5, and sends $c_i$, $PP{K}_i$, $I{D}_i$ as well as $p{k}_i$ to AC.

Algorithm 5 Computing Signcrypt and PPK

Input:      $b_{i,1},\dots ,b_{i,N_c}$, $PK$, $params$, Output:  $V_i$’s signcryption ballots: $c_i=\left(c_{i,1},\dots ,c_{i,N_c}\right)$                 Corresponding PPK: $PP{K}_i=\left(PP{K}_{i,1},\dots ,PP{K}_{i,N_c}\right)$ 1: Set $s{k}_i=w_i\leftarrow {\mathbb{Z}}_q$, $p{k}_i=g^{w_i}$. 2: while  $j=1,\dots ,N_c$do 3:     Signcrypt: 4:     Set $r_{i,j}\leftarrow {\mathbb{Z}}_q$. 5:     Compute: $c_{i,j}=\left(c_{i,j,0},c_{i,j,1},c_{i,j,2}\right)$   $=\left(g^{r_{i,j}},g^{b_{i,j}}{y}_0{}^{r_i},y_1{}^{w_i}{y}_1^{b_{i,j}}{y}_2{}^{r_i}\right)$ 6:     PPK: 7:     Set $t^{i,j},{a_1}^{i,j},{d_1}^{i,j}\leftarrow {\mathbb{Z}}_q$. 8:     Set $b_{i,j}^{\prime }\in \{0,1\}\mathrm{and}{b}_{i,j}^{\prime }\ne b^{i,j}$. 9:     Compute ${P_0}^{i,j}=g^{t^{i,j}}$. 10:    Compute ${P_1}^{i,j}={y_0}^{t^{i,j}}$. 11:    Compute ${P_2}^{i,j}=g^{b_{i,j}^{\prime }·{a_1}^{i,j}}·{y_0}^{{d_1}^{i,j}}/{c_{i,j,1}}^{{a_1}^{i,j}}$. 12:    Set $P^{i,j}=\left({P_0}^{i,j},{P_1}^{i,j},{P_2}^{i,j}\right)$. 13:    Compute $a^{i,j}=\mathrm{hash}\left(c_{i,j,0}\left|\right|c_{i,j,1}\left|\right|{P_0}^{i,j}\left|\right|{P_1}^{i,j}\left|\right|{P_2}^{i,j}\right)$. 14:    Compute ${a_0}^{i,j}={a_1}^{i,j}\oplus a^{i,j}$. 15:    Compute $d_0^{i,j}=r_{i,j}·{a_0}^{i,j}+t^{i,j}$. 16:    Set $PP{K}_{i,j}=\left(c_{i,j},P^{i,j},{a_0}^{i,j},{a_1}^{i,j},{d_0}^{i,j},{d_1}^{i,j}\right)$. 17: end while 18: Set $PP{K}_i=\left(PP{K}_{i,1},\dots ,PP{K}_{i,N_c}\right)$. 19: Set $c_i=\left(c_{i,1},\dots ,c_{i,N_c}\right)$. 20: return $c_i$ and $PP{K}_i$

3.4. Vote Tallying

AC performs the verifications as follows.

• Verifying the legitimacy of each $I{D}_i$.
• Verifying the eligibility of each ballot $c_i$ through $PP{K}_i$.

AC tallies all eligibility ballots (i.e., $fla{g}_i=1$) as follows.

$$\begin{array}{cc}\hfill C_j& =\left(C_{j,0},C_{j,1},C_{j,2}\right)=\left(\prod _{i=1}^{N_v}{c}_{i,j,0},\prod _{i=1}^{N_v}{c}_{i,j,1},\prod _{i=1}^{N_v}{c}_{i,j,2}\right).\hfill \end{array}$$

Then, AC decrypts the tallied ballot and computes the voters’ joint public key as follows.

$$\begin{array}{c}\hfill b_j={log}_g\frac{C_{j,1}}{C_{j,0}^{x_0}},pk=\prod _{i=1}^{N_v}p{k}_i.\end{array}$$

After that, AC verifies whether the following equation holds.

$$C_{j,2}=p{k}^{x_1}{y}_1^{b_j}{C}_{j,0}^{x_2}.$$

If the above equation holds, AC publishes the election results $B=(b_1,\dots ,b_{N_c})$, where $b_j$ is the total number of votes received by the j-candidate.

3.5. Vote Audit

The auditor firstly asks the AC for secret key $x_0$ and then verifies

• $g^{x_0}=y_0$,
• $C_{j,1}={C_{j,0}}^{x_0}·g^{b_j},j\in \{1,\dots ,N_c\}$.

If both equations hold, the auditor believes that the election result is fair, impartial, and credible.

4. Cryptanalysis of the HSE-Voting System

In this section, we describe our attack algorithms about recovering electoral preference from the ballot and sabotaging the election with the wrong signcryption in detail.

4.1. Recovering Electoral Preference from the Ballot

Theorem 1. 

In the HSE-Voting system, the AC can recover every voter’s electoral preference from his ballot.

Proof. 

As shown in the Section 3.1, the AC generates $(PK,SK)$, and the voters send their ballots to the AC. Through the components of the ballots, the AC can resume the electoral preference in two ways. The first method is as follows.

• The AC computes $C{T}_{i,j}=p{k}_i^{x_1}{c}_{i,j,0}^{x_2}=y_1^{{\omega }_i}{y}_2^{r_{i,j}}$.
• With the voter’s ballot $c_{i,j}=\left(c_{i,j,0},c_{i,j,1},c_{i,j,2}\right)$, the AC computes $C{T}_{i,j}^{\prime }=c_{i,j,2}/C{T}_{i,j}=y_1^{b_{i,j}}$.
• If $C{T}_{i,j}^{\prime }=1$, the plaintext vote is 0; otherwise, the plaintext vote is 1.

In the second method, since all ballots are posted on the B Board, the adversary can obtain the signcryption and corresponding PPK of the voter $V_i$. According to the generation method of $PP{K}_{i,j}$, the parameters ${a_1}^{i,j}$ and ${d_1}^{i,j}$ are two random elements in ${\mathbb{Z}}_q$. Therefore, the probability of the following equation is $\frac{1}{q}$.

$$g^{{d_1}^{i,j}}={P_0}^{i,j}·{c_{i,j,0}}^{a_1^{i,j}}.$$

According to the verification equations in Algorithm 6, there is

$$g^{{d_0}^{i,j}}={P_0}^{i,j}·{c_{i,j,0}}^{a_0^{i,j}}.$$

As a consequence, the adversary can easily distinguish between ${d_0}^{i,j}$ and ${d_1}^{i,j}$. Obviously, the vote $b_{i,j}$ satisfies the following equation.

$$y_0^{{d_0}^{i,j}}={P_1}^{i,j}·{\left(c_{i,j,1}/g^{b_{i,j}}\right)}^{a_0^{i,j}}.$$

Because of $b_{i,j}\in \{0,1\}$, we can retrieve the voting preference easily.

As voters register with the AC, the AC can confirm the real identity of the voter by $I{D}_i$. In summary, the AC can recover every voter’s electoral preference from his ballot. The reason for this security risk is that the AC has all the private keys $SK=(x_0,x_1,x_2)$. One potential solution is to encrypt the ballot using a collaborative public key approach, thereby circumventing the issue where the AC could decrypt a single ballot.   □

Algorithm 6 Verifying PPK

Input:      $c_1,\dots ,c_{N_v}$, $PP{K}_1,\dots ,PP{K}_{N_v}$, $PK$, $params$ Output:  $fla{g}_i$ = 0 or 1 1:  Set $fla{g}_i=1$. 2:  while  $j=1,\dots ,N_c$do 3:     if ${a_0}^{i,j}\oplus {a_1}^{i,j}\ne \mathrm{hash}\left(c_{i,j,0}\left|\right|c_{i,j,1}\left|\right|{P_0}^{i,j}\left|\right|{P_1}^{i,j}\left|\right|{P_2}^{i,j}\right)$ then 4:       Set $fla{g}_i=fla{g}_i\times 0$. 5:     end if 6:     if $g^{{d_0}^{i,j}}\ne {P_0}^{i,j}·{c_{i,j,0}}^{a_0^{i,j}}$ then 7:       Set $fla{g}_i=fla{g}_i\times 0$. 8:     end if 9:     if $y_0^{{d_0}^{i,j}}\ne {P_1}^{i,j}·{\left(c_{i,j,1}/g^{m_0}\right)}^{a_0^{i,j}}$ then 10:      Set $fla{g}_i=fla{g}_i\times 0$. 11:    end if 12:    if $y_0^{{d_1}^{i,j}}\ne {P_2}^{i,j}·{\left(c_{i,j,1}/g^{m_1}\right)}^{a_1^{i,j}}$ then 13:      Set $fla{g}_i=fla{g}_i\times 0$. 14:    end if 15: end while 16: return  $fla{g}_i$

4.2. Sabotaging the Election with the Wrong Signcryption

Theorem 2. 

Malicious voters can disrupt the election process by sending the wrong signcryption.

Proof. 

In the phase of ballot generation, the adversary can choose a random element $R\leftarrow {\mathbb{Z}}_q$ and generate a partially incorrect signcryption for ballot $b_{i,j}$.

$$c_{i,j}^{\prime }=(c_{i,j,0}^{\prime },c_{i,j,1}^{\prime },c_{i,j,2}^{\prime })=\left(g^{r_i},g^{b_{i,j}}{y}_0{}^{r_i},R\right).$$

After that, the adversary generates a $PP{K}_{i,j}^{\prime }$ corresponding to $c_{i,j}^{\prime }$ and sends the signcryption $c_{i,j}^{\prime }$, the PPK parameters $PP{K}_{i,j}^{\prime }$, the identity number $I{D}_i$, and $p{k}_i$ to the AC. According to the validation rules in the phase of vote tallying, the adversary’s identity number $I{D}_i$ is legitimate, and the verification of $PP{K}_i^{\prime }$ does not involve R. Therefore, the erroneous ballot can pass the verification.

Therefore, the tallied ballot is

$$\begin{array}{cc}\hfill C_j^{\prime }& =\left(C_{j,0}^{\prime },C_{j,1}^{\prime },C_{j,2}^{\prime }\right)\hfill \\ \hfill & =\left(\prod _{t=1}^{N_v}{c}_{t,j,0}^{\prime },\prod _{t=1}^{N_v}{c}_{t,j,1}^{\prime },R·\prod _{t=1}^{i-1}{c}_{t,j,2}^{\prime }·\prod _{t=i+1}^{N_v}{c}_{t,j,2}^{\prime }\right).\hfill \end{array}$$

The AC computes the voters’ joint public key and the election result as follows.

$$\begin{array}{cc}\hfill pk& =\prod _{i=1}^{N_v}p{k}_i,{b^{\prime }}_j={log}_g\frac{{C^{\prime }}_{j,1}}{{C^{\prime }}_{j,0}^{x_0}}.\hfill \end{array}$$

At this point, it is clear that the following inequality holds.

$${C^{\prime }}_{j,2}\ne p{k}^{x_1}{y}_1^{{b^{\prime }}_j}{C^{\prime }}_{j,0}^{x_2}.$$

In this case, even if the election process is restarted, the adversary can still cause the election process to fail in the same way. This means that the adversary can achieve the purpose of disrupting the election process through the above steps. This occurred because the voting system was unable to precisely identify the questionable ballots, necessitating a re-initiation of the election. Furthermore, the verification procedure omits the involvement of the third component from the ciphertext. To address this limitation, it would be advisable to enhance the system’s verifiability.   □

5. Improved HSE-Voting System

This section describes the details of our improved HSE-Voting system, which applies the same entities as in [2] but makes some minor changes to their specific functions. While retaining the advantages of the HSE-Voting system, we solve the security problem described in Section 4.

5.1. Entities of Our System

In our system, we modify the functions of entities AC and auditor as follows and leave the definitions of the other unchanged entities.

• Authentication Center: As a voting institution, the AC is still responsible for verifying the identification of voters, tallying, and other related work. However, voters no longer only use the AC’s public key to encrypt their ballots. Similarly, we assume that the AC is honest-but-curious.
• Auditor: As a voting institution, the auditor is added with a new function to generate a part of the election public key. In our system, the auditor is no longer credible.

5.2. Initialization of Election

At the beginning of an election, the AC generates the election public parameters $params$ and its public key $P{K}_a$. Then, the AC posts the $params$ and $P{K}_a$ on the B Board. Then, the auditor creates its own key pair $(P{K}_r,S{K}_r)$ and uploads its public key on the B Board.

• The AC generates public $params$$(\mathbb{G},g,q)$.
• The AC uses $params$ to generate its key pair $(P{K}_a,S{K}_a)$, where $S{K}_a=\left(x_0,x_1\right)\leftarrow {\mathbb{Z}}_q$, $P{K}_a=\left(y_0,y_1\right)=\left(g^{x_0},g^{x_1}\right)$.
• The auditor generates its own key pair, where $S{K}_r=x_2\leftarrow {\mathbb{Z}}_q$, $P{K}_r=y_2=g^{x_2}$.
• The AC and auditor calculate the joint public key $PK=y=y_0^{x_2}=y_2^{x_0}=g^{x_0{x}_2}$ and make it public.

5.3. Registration of Voters

In the registration phase, each voter $V_i$ should generate an ElGamal key pair $(p{k}_{v_i},s{k}_{v_i})=(g^{w_i},w_i)$. Then, every voter provides the AC with his real valid identification (e.g., identification card) and public key $p{k}_{v_i}$. Once a voter’s identity has been verified, its corresponding voter public key will be added to the registration list, which will be posted on the B Board.

5.4. Generate Ballot

The voter $V_i$ generates the binary plaintext votes $b_i=(b_{i,1},\dots ,b_{i,N_c})$ (where $b_{i,j}=$ 0 or 1) for all candidates. Then, $V_i$ computes his own encrypted vote as Algorithm 7.   

Algorithm 7 Generating an encrypted vote

Input:     $b_{i,1},\dots ,b_{i,N_c}$, $PK$, $params$ Output:     $c_i=\left(c_{i,1},c_{i,2},\dots ,c_{i,N_c}\right)$ 1: while  $j=1,\dots ,N_c$do 2:    Set $r_{i,j}\leftarrow {\mathbb{Z}}_q$. 3:    Compute $c_{i,j}=\left(c_{i,j,0},c_{i,j,1}\right)=\left(g^{r_{i,j}},g^{b_{i,j}}{y}^{r_{i,j}}\right)$. 4: end while 5: Set $c_i=\left(c_{i,1},c_{i,2},\dots ,c_{i,N_c}\right)$. 6: return $c_i$

After obtaining the encrypted vote $c_i$, $V_i$ generates the PPK parameters $PP{K}_i$ corresponding to the $c_i$ using his secret key $s{k}_{v_i}$, the random parameters $r_1,\dots r_{N_c}$, the AC’s public key $P{K}_a$, and the auditor’s public key $P{K}_r$. The details are described in Algorithm 8.

Algorithm 8 Generating a PPK of an encrypted vote

Input:     $b_{i,1},\dots ,b_{i,N_c}$, $r_{i,1},\dots ,r_{i,N_c}$, $c_i$, ${PK}_a$, $P{K}_r$, $PK$, $s{k}_{v_i}$, $params$ Output:     $PP{K}_i=\left(PP{K}_{i,1},PP{K}_{i,2},\dots ,PP{K}_{i,N_c}\right)$ 1:  Set $si{g}_i=y_1^{{\omega }_i}$ 2:  while  $j=1,\dots ,N_c$do 3:     Set $a_{i,j}\leftarrow \{0,1\}$ and $a_{i,j}\ne b_{i,j}$. 4:     Set $e_{i,j},u_{i,j,2}\leftarrow {\mathbb{Z}}_q$. 5:     Compute $l_{i,j,2}=r_{i,j}·u_{i,j,2}+e_{i,j}modq$. 6:     Compute $T_{i,j,0}=g^{e_{i,j}}$. 7:     Compute $L_{i,j,1}=y^{e_{i,j}}$. 8:     Compute $L_{i,j,2}=\left[g^{a_{i,j}{u}_{i,j,2}}{y}^{l_{i,j,2}}\right]/{\left(c_{i,j,1}\right)}^{u_{i,j,2}}$. 9:     if $b_{i,j}=0$ then 10:      Set $(T_{i,j,1},T_{i,j,2})=(L_{i,j,1},L_{i,j,2})$. 11:    else 12:      Set $(T_{i,j,1},T_{i,j,2})=(L_{i,j,2},L_{i,j,1})$. 13:    end if 14:    Compute $u_{i,j}=hash\left(T_{i,j,0}\left|\right|T_{i,j,1}\left|\right|T_{i,j,2}\left|\right|c_{i,j,0}\left|\right|c_{i,j,1}\right)$. 15:    Compute $u_{i,j,1}=u_{i,j,2}\oplus u_{i,j}$. 16:    Compute $l_{i,j,1}=r_{i,j}·u_{i,j,1}+e_{i,j}modq$. 17:    if $b_{i,j}=0$ then 18:      Set $(s_{i,j,1},s_{i,j,2})=(l_{i,j,1},l_{i,j,2})$. 19:      Set $(v_{i,j,1},v_{i,j,2})=(u_{i,j,1},u_{i,j,2})$. 20:    else 21:      Set $(s_{i,j,1},s_{i,j,2})=(l_{i,j,2},l_{i,j,1})$. 22:      Set $(v_{i,j,1},v_{i,j,2})=(u_{i,j,2},u_{i,j,1})$. 23:    end if 24:    Compute $V_{i,j,1}=v_{i,j,1}\oplus si{g}_i$. 25:    Compute $V_{i,j,2}=v_{i,j,2}\oplus si{g}_i$. 26:    Set $PP{K}_{i,j}=\left(T_{i,j,0},T_{i,j,1},T_{i,j,2},V_{i,j,1},V_{i,j,2},s_{i,j,1},s_{i,j,2}\right)$. 27: end while 28: Set $PP{K}_i=\left(PP{K}_{i,1},PP{K}_{i,2},\dots ,PP{K}_{i,N_c}\right)$. 29: return $PP{K}_i$

The voter $V_i$ posts $c_i$, $PP{K}_i$, and $p{k}_{v_i}$ on the B Board as their ballot.

5.5. Verifications of Each Submission

As shown in the previous subsection, the contents of all ballots are posted on the B Board, including the encrypted votes, the PPK parameters, and the public key of voters. However, in order to avoid tallying any illegal ballots to the final result, the verification of each submission is an essential and crucial part of the election process. It contains the following three verification steps.

• Verifying whether the sender is authorized: in order to prevent unauthorized people from illegally voting, each voter is required to send a ballot with their public key $p{k}_{v_i}$. The $p{k}_{v_i}$ of each authorized voter is added to the registration list once they successfully register, and the AC posts a registration list on the B Board. Thus, anyone can verify whether a subsequent submission is sent by an authorized voter or not. For example, if $p{k}_{v_i}$ belongs to the registration list, the sender is an authorized person. Otherwise, the submission will be discarded.
• Verifying whether the public key has not been accepted: in order to prevent unauthorized people from using authorized voters’ information posted on the B Board and prevent authorized voters from repeating voting, the AC is required to check whether it has accepted another submission that contains the same public key. If not, this submission is legal. Otherwise, the submission will be discarded.
• Verifying the eligibility of the encrypted ballot: our system stipulates that each vote of a valid submitted encrypted ballot must be either $\mathrm{Enc}\left(1\right)$ or $\mathrm{Enc}\left(0\right)$. The proof of each voter’s submission is based on the well-known PPK protocol [21]. Specific details are described in Algorithm 9.

Algorithm 9 Verifying the eligibility of encrypted ballot $c_i$

Input:     $c_i$, $PP{K}_i$, $P{K}_a$, $S{K}_a$, $P{K}_r$, $p{k}_{v_i}$, $params$ Output:     $Fla{g}_{v_i}$=1 (means true) or 0 (means false). 1:  Set $Fla{g}_{v_i}=1,m_0=0,m_1=1,si{g}_i=p{k}_{v_i}^{x_1}$. 2:  Compute $v_{i,j,1}=V_{i,j,1}\oplus p{k}_{v_i}^{x_1}$. 3:  Compute $v_{i,j,2}=V_{i,j,1}\oplus p{k}_{v_i}^{x_1}$. 4:  while  $j=1,\dots ,N_c$do 5:     if $v_{i,j,1}\oplus v_{i,j,2}\ne hash\left(T_{i,j,0}\left|\right|T_{i,j,1}\left|\right|T_{i,j,2}\left|\right|c_{i,j,0}\left|\right|c_{i,j,1}\right)$ then 6:       Set $fla{g}_{v_{i,1}}=fla{g}_{v_i}\times 0$. 7:     end if 8:     if $g^{s_{i,j,1}}\ne T_{i,j,0}·C_{i,j,0}^{v_{i,j,1}}$ then 9:       Set $fla{g}_{v_{i,1}}=fla{g}_{v_i}\times 0$. 10:    end if 11:    if $g^{s_{i,j,2}}\ne T_{i,j,0}·C_{i,j,0}^{v_{i,j,2}}$ then 12:      Set $fla{g}_{v_{i,1}}=fla{g}_{v_i}\times 0$. 13:    end if 14:    if $y^{s_{i,j,1}}\ne T_{i,j,1}·{(C_{i,j,1}/g^{m_0})}^{v_{i,j,1}}$ then 15:      Set $fla{g}_{v_{i,1}}=fla{g}_{v_i}\times 0$. 16:    end if 17:    if $y^{s_{i,j,2}}\ne T_{i,j,2}·{(C_{i,j,1}/g^{m_1})}^{v_{i,j,2}}$ then 18:      Set $fla{g}_{v_{i,1}}=fla{g}_{v_i}\times 0$. 19:    end if 20: end while 21: return  $Fla{g}_{v_i}$

If $Fla{g}_{v_i}=1$, the ballot meets the eligibility criteria. Otherwise, the submission is discarded. The submissions that pass all the verification processes will be posted on the B Board. Then, the AC accepts these ballots as valid ballots.

5.6. Tallying All Valid Ballots and Decryption

After the voting process, the AC counts all valid ballots $c_1,\dots ,c_{N_v}$, which is described in Algorithm 10.

Algorithm 10 Tallying all valid ballots

Input:     $c_1,\dots ,c_{N_v}$, $params$ Output:     $TC=\left(T{C}_1,T{C}_2,\dots ,T{C}_{N_c}\right)$ 1: while  $j=1,\dots ,N_c$do 2:    Compute $T{C}_{j,0}={\prod }_{i=1}^{N_v}{c}_{i,j,0}$. 3:    Compute $T{C}_{j,1}={\prod }_{i=1}^{N_v}{c}_{i,j,1}$. 4:    Set $T{C}_j=\left(T{C}_{j,0},T{C}_{j,1}\right)$ 5: end while 6: Set $TC=\left(T{C}_1,T{C}_2,\dots ,T{C}_{N_c}\right)$. 7: return $TC$

Then, the AC announces the valid ballot-ciphertext $TC$ and the secret key $x_1$ on the B Board. After that, every entity can verify the legitimacy of each ballot.

Afterward, the auditor generates the intermediate parameter $key$ and its corresponding PZK parameters $PZK$ as Algorithm 11.

Algorithm 11 Generating intermediate parameter and PZK

Input:     $TC$, $s{k}_r$, $params$ Output:     Intermediate parameter: $key=(ke{y}_1,\dots ,ke{y}_{N_c})$     PZK of $key$: $PZK=\left(PZ{K}_1,\dots ,PZ{K}_{N_c}\right)$ 1:  while  $j=1,\dots ,N_c$do 2:     Compute $ke{y}_j=T{C}_{j,0}^{x_2}$. 3:     Set $e{z}_j\leftarrow {\mathbb{Z}}_q$. 4:     Compute $T{Z}_{j,0}=g^{e{z}_j}$. 5:     Compute $T{Z}_{j,1}=T{C}_{j,0}^{e{z}_j}$. 6:     Compute $v{z}_j=\mathrm{hash}\left(T{Z}_{j,0}\left|\right|T{Z}_{j,1}\left|\right|T{C}_{j,0}\right)$. 7:     Compute $s{z}_j=x_2·v{z}_j+e{z}_{j}modq$. 8:     Set $PZ{K}_j=\left(T{Z}_{j,0},T{Z}_{j,1},v{z}_j,s{z}_j\right)$. 9:  end while 10: Set $key=\left(ke{y}_1,\dots ,ke{y}_{N_c}\right)$. 11: Set $PZK=\left(PZ{K}_1,\dots ,PZ{K}_{N_c}\right)$. 12: return $key$ and $PZK$

AC verifies the correctness of intermediate parameter $key$ through the PZK parameters $PZK$ as Algorithm 12.  

Algorithm 12 Verifying the $PZK$ of $TC$

Input:     $key$, $TC$, $P{K}_r$, $PZK$, $params$ Output:     $FlagZ=$ 1 (means true) or 0 (means false) 1:  Set $FlagZ=1$. 2:  while  $j=1,\dots ,N_c$do 3:     if $v{z}_j\ne \mathrm{hash}\left(T{Z}_{j,0}\left|\right|T{Z}_{j,1}\left|\right|T{C}_{j,1}\right)$ then 4:       Set $FlagZ=Flag{Z}_j\times 0$. 5:     end if 6:     if $g^{s{z}_j}\ne T{Z}_{j,0}·{y_2}^{v{z}_j}$ then 7:       Set $FlagZ=Flag{Z}_j\times 0$. 8:     end if 9:     if $T{C}_{j,0}^{s{z}_j}\ne T{Z}_{j,1}·{ke{y}_j}^{v{z}_j}$ then 10:      Set $FlagZ=Flag{Z}_j\times 0$. 11:    end if 12: end while 13: return  $FlagZ$

After that, AC decrypts the valid ballot-ciphertext $TC$ using its secret key $S{K}_a$ and intermediate parameter $key$ as Algorithm 13. Finally, the AC publishes the election results on the B Board.  

Algorithm 13 Decrypting the valid ballot-ciphertext

Input:     $TC$, $S{K}_a$, $key$, $params$ Output:     Final result: $B=\left(B_1,B_2,\dots ,B_{N_c}\right)$ 1: while  $j=1,\dots ,N_c$do 2:    Compute $b_j={log}_g(T{C}_{j,1}/ke{y}_j^{x_0})$. 3: end while 4: Set $B=\left(B_1,B_2,\dots ,B_{N_c}\right)$  5: return B

5.7. Results Auditing

During the results auditing phase, the auditor (or any voter) verifies the correctness of the final result as follows.

• The AC computes and publishes $T{C}_{j,0}^{x_0}$ and its corresponding PZK parameters.
• The auditor verifies the PZK parameters (the details are omitted here since the procedure is similar to Algorithm 12) and verifies the following equation.

  $$\begin{array}{c}\hfill T{C}_{j,1}={\left(T{C}_{j,0}^{x_0}\right)}^{x_2}·g^{b_j}.\end{array}$$

If the verifications pass, the election result is believed to be credible. The auditor accepts the result and posts it on the B Board.

6. Characteristic Analysis

This section is devoted to giving a detailed security analysis of our improved HSE-Voting system, including the privacy of voters, the correctness of the final election result, and the voting verifiability.

6.1. Privacy of Voters

It is very necessary to protect the voters’ voting preferences. We argue for voter privacy from the following two points: (i) any probabilistic polynomial time adversary cannot distinguish whether a ballot is encrypted by 0 or 1 based on the information on the B Board; (ii) when using the PPK protocol, voters’ voting preferences of ballots will not be revealed during ballot verification.

Theorem 3. 

If the ElGamal cryptosystem is semantically secure, any probabilistic polynomial time adversary cannot obtain the voters’ voting preferences from the B Board.

Proof. 

Every cast ballot has been encrypted using the ElGamal cryptosystem (cf. Section 2.2) before submitting. ElGamal has homomorphic properties and semantic security. Thus, in our system, there is no probabilistic polynomial time adversary that can distinguish whether a ballot-ciphertext is $\mathrm{Enc}\left(0\right)$ or $\mathrm{Enc}\left(1\right)$ from the information published on the B Board. As mentioned above, the voting preferences of ballots remain secure. □

Theorem 4. 

When using the PPK protocol and PZK protocol, the voting preferences and the information of the auditor’s secret key will not be revealed during verification.

Proof. 

The PPK parameters $PP{K}_{i,j}$ are generated by using the PPK protocol, which consists of $T_{i,j,0}$, $T_{i,j,1}$, $T_{i,j,2}$, $V_{i,j,1}$, $V_{i,j,2}$, $s_{i,j,1}$, and $s_{i,j,2}$, where $v_{i,j,2}$ and $s_{i,j,1}$ are random integers, $T_{i,j,0}$, $T_{i,j,1}$, $T_{i,j,2}$, $v_{i,j,1}$ are computed by using random numbers $v_{i,j,2}$, $s_{i,j,2}$, $e_{i,j}$, and $V_{i,j,1}$, $V_{i,j,2}$ are computes by $si{g}_{i,j}$, $v_{i,j,1}$, as well as $v_{i,j,2}$. The parameter $si{g}_{i,j}$ is the Diffie–Hellman signature between the AC and the voter $V_i$. The PPK protocol is given in [21], which shows the details of proof that PPK will not reveal the original message. By using the PPK protocol, the verifier can verify all the elements without decryption. The verifier could only know whether an element is encrypted by 0 or 1, but cannot determine the exact value of plaintext.

The PZK parameters $PZ{K}_j$ are computed by the PZK protocol, which consists of $T{Z}_{j,0}$, $T{Z}_{j,1}$, $v{z}_j$, and $s{z}_j$, where $v{z}_j$ is a random number, $T{Z}_{j,0}$, $T{Z}_{j,1}$ are computed by random number $e_{i,j}$, and $s{z}_j$ is computed by random numbers $e_{i,j}$ as well as $v{z}_j$. The PZK protocol is given in [20], which shows the PZK protocol has zero-knowledge and will not reveal any additional information.

Based on the security of the PPK and PZK protocols, the relevant parameters are not considered to readily reveal private information about voters’ electoral preferences. □

6.2. Correctness of the Election Result

In this subsection, we analyze the correctness of the election results from two aspects: the correctness of ballot delivery and the correctness of ballot integration and decryption.

Theorem 5. 

Only authorized voters can vote, and no one can vote repeatedly.

Proof. 

Suppose an unauthorized adversary attempts to use the i-th voter’s public key $p{k}_{v_i}$ to participate in the election. For the PPK parameter $V_{i,j,1}=v_{i,j,1}\oplus y_1^{{\omega }_i}$ in $PP{K}_{i,j}$, due to Definition 1, the difficulty of the CDH problem shows the probability of the adversary successfully forging $y_1^{{\omega }_i}=g^{{\omega }_i·x_1}$ when they only know g, $g^{{\omega }_i}$ and $g^{x_1}$ is negligible. Therefore, the probability of the adversary successfully forging a valid PPK parameter $V_{i,j,1}^{\prime }$ that satisfies $V_{i,j,1}^{\prime }=v_{i,j,1}\oplus y_1^{{\omega }_i}$ is negligible. In addition, our system ensures that each voter can vote only once by verifying whether their public key is included in other accepted ballots. □

Theorem 6. 

The election process during ballot tallying and valid ballot-ciphertext decrypting is correct.

Proof. 

In Section 2.2, we introduced the additive homomorphism of the ElGamal scheme. Therefore, the AC can count all the ballots on the B Board according to the correct steps.

$$T{C}_{j,0}=\prod _{i=1}^{N_v}{C}_{i,j,0}=\prod _{i=1}^{N_v}{g}^{r_{i,j}}=g^{{\sum }_{i=1}^{N_v}{r}_{i,j}},$$

$$T{C}_{j,1}=\prod _{i=1}^{N_v}{C}_{i,j,1}=\prod _{i=1}^{N_v}{g}^{b_{i,j}}{y}^{r_{i,j}}=g^{{\sum }_{i=1}^{N_v}{b}_{i,j}}{g}^{x_0{x}_2{\sum }_{i=1}^{N_v}{r}_{i,j}}.$$

Then, the AC uploads all accepted ballots to the B Board. At this time, everyone can check if their ballot is lost. In the end, the AC and auditors jointly decrypt valid ballot-ciphertext to obtain the election result.

Auditors compute

$$ke{y}_j=T{C}_{j,0}^{x_2}=g^{x_2{\sum }_{i=1}^{N_v}{r}_{i,j}}.$$

Then, the AC computes

$${log}_g(T{C}_{j,1}/ke{y}_j^{x_0})={log}_g(g^{{\sum }_{i=1}^{N_v}{b}_{i,j}}{y}^{{\sum }_{i=1}^{N_v}{r}_{i,j}}/{\left(g^{x_2{\sum }_{i=1}^{N_v}{r}_{i,j}}\right)}^{x_0})={log}_g\left(g^{{\sum }_{i=1}^{N_v}{b}_{i,j}}\right)=\sum _{i=1}^{N_v}{b}_{i,j}=b_j.$$

Since $b_{i,j}\in \{0,1\}$, $b_j={\sum }_{i=1}^{N_v}{b}_{i,j}\le N_v$ is small in practice. It is feasible to compute the discrete logarithm ${log}_g\left(g^{b_j}\right)$. Therefore, the election process of ballot tallying and valid ballot-ciphertext decryption is correct. □

Theorem 7. 

The AC can check $PPK$ and $PZK$ in order to ensure the legality of the contents.

Proof. 

According to the properties of PPK outlined in Section 2.3, the AC can utilize the voter’s public key $p{k}_{v_i}$ to ascertain whether the plaintext corresponding to an encrypted ballot represents 0 or 1, thereby confirming the legitimacy and validity of this ballot. Similarly, in accordance with the PZK properties delineated in Section 2.4, the AC can confirm that the auditor has provided the correct decryption information $key$, thus ensuring the accurate decryption of the election results. □

6.3. Voting Verifiability

In this section, we divide the verifiability requirements into two parts: universal verifiability and individual verifiability.

Universal verifiability: the B Board in our E-voting system is public, so everyone can check the accepted ballots and the election result on the B Board. In addition, since all accepted ballots are disclosed, voters can check the correctness of their ballots and prevent their ballots from being forged or tampered with.

Individual verifiability: the auditor (as well as each voter) can verify the final result of the election. The legality of verification is proved in Theorem 8.

Theorem 8. 

The auditor (or each voter) can correctly verify the final election result.

Proof. 

The auditor first verifies the $PZK$ to prove that the correctness of $T{C}_{j,0}^{x_0}$. Then, he checks the correctness of the final election result by verifying the equation. The correctness of the verification equation is as follows.

$$\begin{array}{c}\hfill {\left(T{C}_{j,0}^{x_0}\right)}^{x_2}·g^{{\sum }_{i=1}^{N_v}{b}_{i,j}}=g^{x_0{x}_2{\sum }_{i=1}^{N_v}{r}_{i,j}}·g^{{\sum }_{i=1}^{N_v}{b}_{i,j}}=T{C}_{j,1}.\end{array}$$

□

6.4. Comparison of Characteristics with Related Work

In order to provide a clearer indication of the contribution of the proposed scheme, we compared the characteristics of the proposed scheme with related work, and the results are shown in Table 1. In Yuan et al.’s scheme [7], the RSA signature scheme is employed to guarantee the integrity of ballots. However, there is no consideration of validating the legality of the ballot, i.e., the ciphertext is $Enc\left(0\right)$ or $Enc\left(1\right)$. In Qu et al.’s scheme [8], the smart contract with the decryption key is able to decrypt the ciphertext of each ballot and verify its legality. Therefore, this scheme lacks the public verifiability. In Fan et al.’s HSE-Voting system [2], only the trusted auditor can verify the election results.

Table 1. Characteristic comparison.

System	Eligibility	Uniqueness	Single Ballot Privacy	Public Verification of Ballot Legality	Public Verification of Electoral Correctness
Yuan et al.’s system [7]	✓	✓	✓	×	✓
Qu et al.’s system [8]	✓	✓	×	×	×
Yang et al.’s system [3]	✓	✓	✓	✓	✓
HSE-Voting system [2]	✓	✓	×	✓	×
Our system	✓	✓	✓	✓	✓

The symbol ✓ represents that the characteristic is supported by the system and the symbol × indicates that it is not supported.

7. Performance Analysis

This section presents the performance analysis of our improved HSE-Voting system. We use $cos{t}_t$ to denote the computation time of one exponentiation. Meanwhile, we separately analyze the computation cost on the voter side and the AC side. Due to the small computation cost and little use of the auditor side, no detailed analysis is performed here. Furthermore, the comparison of our improved HSE-Voting system with the HSE-Voting system [2] and Yang et al.’s system [3] is given below.

7.1. Performance of the Voter Side

On the voter side, every voter should generate their ballot and submit it to AC. According to Section 5.4, the total computation cost for a voter can be present as the sum of the time of computing the encrypted vote $c_i$ and the corresponding $PPK$s, which can be expressed as follows.

$$2\times cos{t}_t\times N_c+5\times cos{t}_t\times N_c+cos{t}_t.$$

See Table 2 for a detailed comparison.

Table 2. Performance comparison.

System	Computational Cost of Voter	Computational Cost of AC
Yang et al.’s system [3]	$7\times cos{t}_t\times N_c+3\times cos{t}_t$	$8\times cos{t}_t\times N_c\times N_v+6\times cos{t}_t\times N_v+cos{t}_t\times N_c$
HSE-Voting system [2]	$9\times cos{t}_t\times N_c$	$6\times cos{t}_t\times N_c\times N_v+4\times cos{t}_t$
Our system	$7\times cos{t}_t\times N_c+cos{t}_t$	$8\times cos{t}_t\times N_c\times N_v+5\times cos{t}_t\times N_c+N_v\times cos{t}_t$

7.2. Performance of the AC Side

The performance of the AC side can be summarized in three parts: verifying the $PPK$s of ballots, checking the $PZK$s of intermediate parameters, and decrypting the valid ballot-ciphertext. The total computation time of the AC side is as follows; see Table 2 for a detailed comparison.

$$8\times cos{t}_t\times N_c\times N_v+cos{t}_t\times N_v+4\times cos{t}_t\times N_c+cos{t}_t\times N_c.$$

7.3. Experimental Simulation

In this subsection, all tests were performed on a laptop with the following specifications: 2.4 GHz quad-core Intel Core i7 with 16 GB of 1600 MHz DDR3L onboard memory. We used a high-performance implementation from libgmp via the gmpy2 Python module (https://gmpy2.readthedocs.io/en/latest/ (accessed on 4 January 2024)).

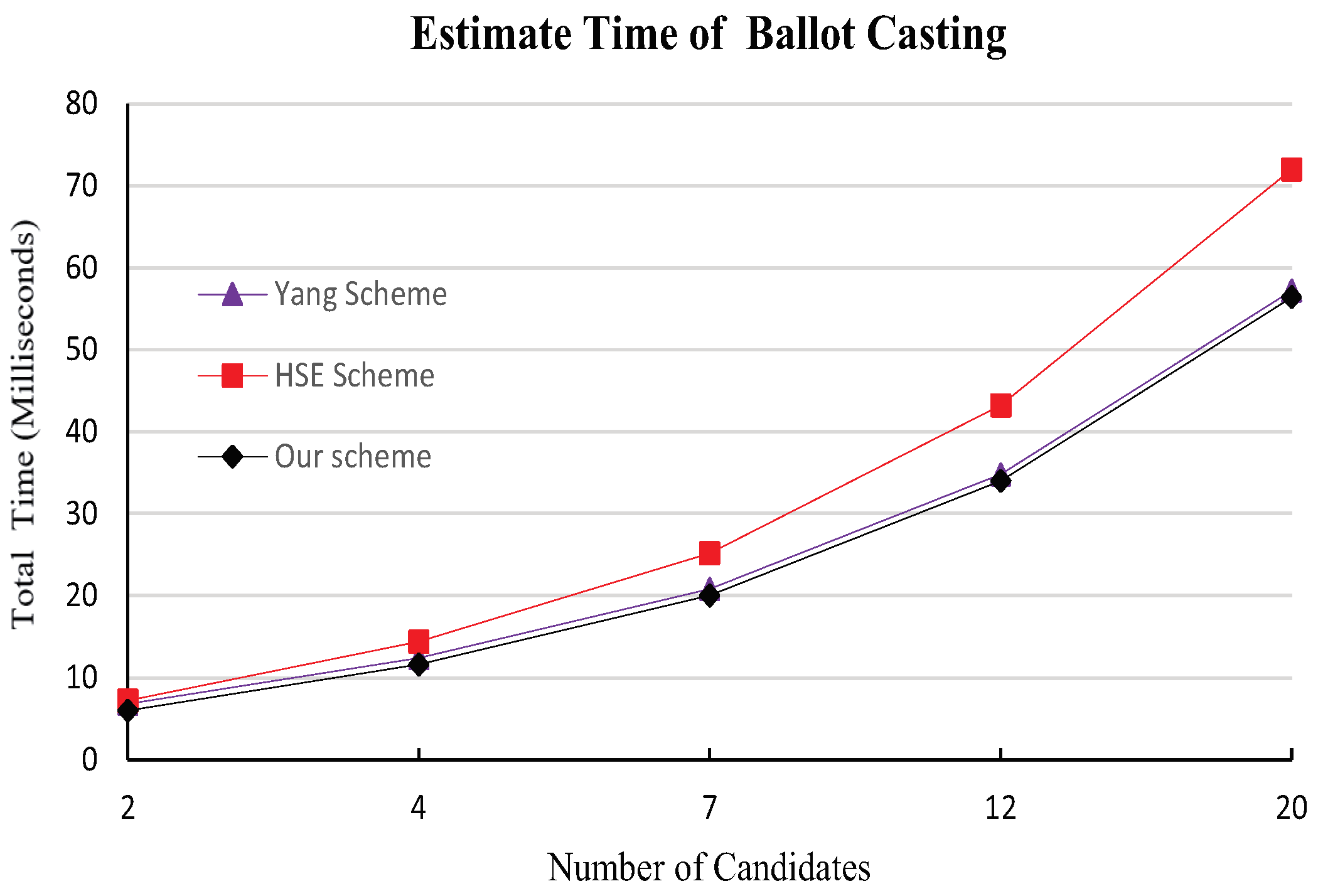
As depicted in Figure 1 and based on our experimental findings, it appears that our scheme may exhibit some efficiency benefits over the HSE-Voting system [2] in ballot casting, while the computational overhead seems to align closely with that of Yang et al.’s scheme [3].

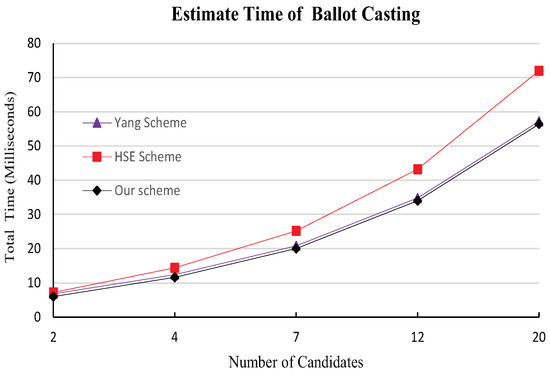
Figure 1. Estimate total time comparison for a voter of the three systems.

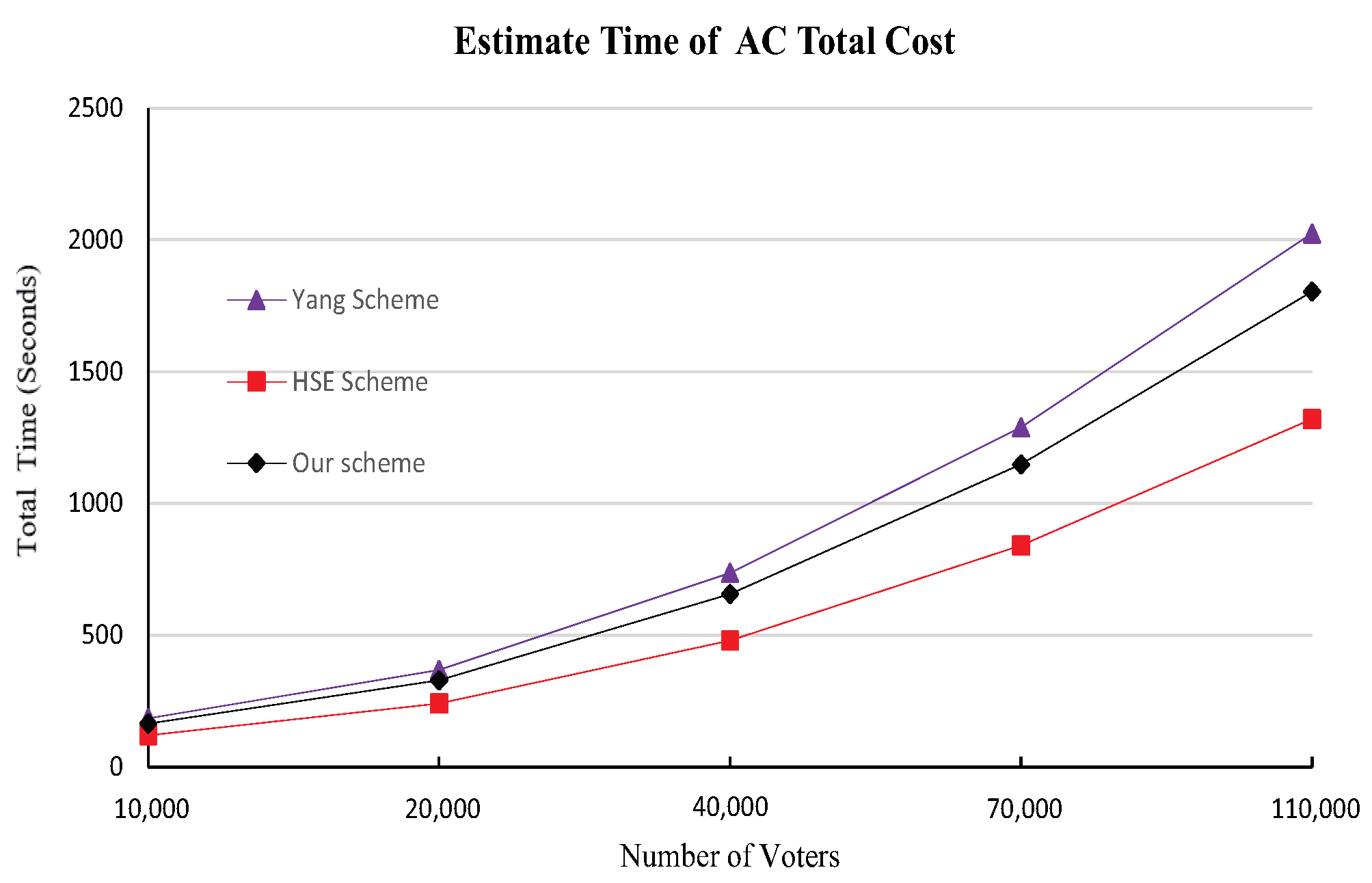
As shown in Figure 2, the computational overhead for the AC side in our enhanced scheme is slightly higher than that of the HSE-Voting system [2]. This increase can be attributed to the integration of additional computational components aimed at bolstering security. In addition, the computational overhead of our AC side is slightly smaller than Yang et al.’s scheme [3], which is one of the design goals of the HSE system.

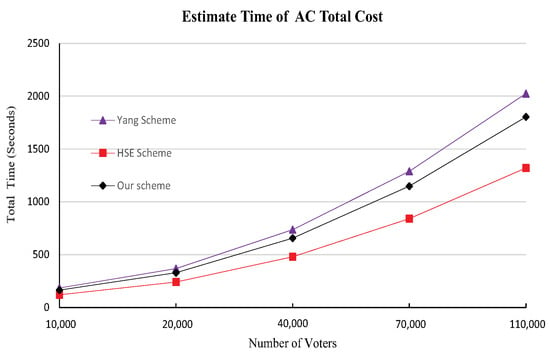
Figure 2. Estimate total time comparison for AC of 5 candidates.

Combining the comparison results of characteristics and efficiency, the contribution of our scheme is to support the public verification of the ballot legality as well as the validity of election results, and the overall efficiency is slightly higher than Yang et al.’s scheme [3].

8. Conclusions

In this paper, we indicated two potential security threats to the HSE-Voting system and proposed a security-enhanced system based on Fan et al.’s scheme. Firstly, we pointed out that the content of each voter’s ballot could be obtained by the AC. Then, we discovered that malicious voters could create illegitimate ballots to disrupt the election process without being detected. Further, we proposed an improved scheme to avoid the above security risks. In addition, we showed a detailed analysis and demonstration of the characteristics of the improved HSE-Voting system. Comparison results of theoretical analyses and experimental tests suggest that our proposed scheme might offer some insights or benefits when compared to related schemes.