A Hybrid Approach to Modeling Heart Rate Response for Personalized Fitness Recommendations Using Wearable Data

Abstract

Heart rate (HR) is a key indicator of fitness and cardiovascular health, and accurate HR monitoring and prediction are essential for enhancing personalized fitness experiences. The rise of wearable technology has significantly improved the ability to track personal health, including HR metrics. Accurate modeling of HR response during workouts is crucial for providing effective fitness recommendations, which help users achieve their goals while maintaining safe workout intensities. Although several HR monitoring and prediction models have been developed for personalized fitness recommendations, many remain impractical for real-world applications, and the domain of personalization in fitness applications still lacks sufficient research and innovation. This paper presents a hybrid approach to modeling HR response to workout intensity for personalized fitness recommendations. The proposed approach integrates a physiological model using Dynamic Bayesian Networks (DBNs) to capture heart rate dynamics during workout sessions. DBNs, combined with Long Short-Term Memory (LSTM) networks, model the evolution of HR over time based on workout intensity and individual fitness characteristics. The DBN parameters are dynamically derived from flexible neural networks that account for each user’s personalized health state, enabling the prediction of a full HR profile for each workout, while incorporating factors such as workout history and environmental factors. An adaptive feature selection module further enhances the model’s performance by focusing on relevant data and ensuring responsiveness to new data. We validated the proposed approach on the FitRec dataset, and experimental results show that our model can accurately predict HR responses to workout intensity in future sessions, achieving an average mean absolute error of 5.2 BPM per workout—significantly improving upon existing models. In addition to HR prediction, the model provides real-time fitness personalized recommendations based on individual’s observed workout intensity to an exercise. These findings demonstrate the model’s effectiveness in delivering precise, user personalized heart response to exercise with potential applications in fitness apps for personalized training and health monitoring.

1. Introduction

It is well understood that physical activity provides major health benefits for the heart, body, and mind, playing a vital role in preventing and treating many chronic diseases, such as heart disease and diabetes [1]. This is why the World Health Organization (WHO), and other health organizations emphasize the importance of daily physical activity and have issued public health guidelines to prevent and manage chronic illnesses associated with physical inactivity [2].

The rapid growth and popularity of wearable technologies have significantly impacted how individuals engage with their health practices. Wearable devices and mobile health (mHealth) apps have empowered users to monitor and track their physiological data and daily exercise activities [3]. These technologies not only allow users to track their physical fitness but also serve as motivational tools, helping individuals tailor their fitness plans toward achieving results and fostering safer training environments. For instance, previous research has shown that data from wearables are a data-rich resource, which can provide valuable insights into an individual’s overall health—crucial for developing personalized fitness recommendation systems [4,5,6].

Personalization plays an essential role in many modern applications, from enhancing user engagement to improving overall satisfaction. However, modeling an individual’s fitness in fitness tracking apps for personalization presents a significant challenge, as user behavior and workout preferences can vary and evolve over time. Factors such as differences in fitness levels, workout plans, exercise intensity, heart rate zones, and environmental conditions highlight the need for robust modeling techniques that capture dynamic changes in user features and account for substantial individual variation.

Ensuring accuracy and relevance in personalized fitness applications is challenging. While personalization has been a core focus for fitness recommendations, and some studies have shown notable improvements, a significant gap remains in most algorithms’ ability to adapt to dynamic changes in user data over time, which limits their practicality in real-world recommendation systems. Furthermore, transforming noisy wearable data into transparent and actionable insights for personalization adds another layer of complexity to this task [4].

Additionally, wearable data often lack critical implicit user behavior data, such as clicks, likes, and views, which are essential for understanding behavior patterns making recommendations. This gap presents another challenge in building effective personalized fitness models. Despite these challenges, personalization remains vital for effective fitness recommendations. Heart rate is a fundamental physiological feature that reflects an individual’s response to workout intensity, serving as an indicator of both exercise intensity and overall health in daily workout routines [7]. Accurately monitoring and predicting heart rate response during exercise are crucial steps for developing effective, personalized recommendations algorithms. Wearables offer an innovative approach to monitoring heart rate and other significant metrics during various fitness activities, providing valuable data to understand individual health [8]. However, interpreting and leveraging these data for personalized fitness recommendations present several challenges:

• Individual Variability: The response of heart rate to exercise varies greatly among individuals based on age, current fitness levels, genetic factors, and other factors including overall health conditions [9,10].
• Temporal Dynamics: An individual’s heart rate response may vary depending on their fitness level over time, so models must capture and adapt to these temporal changes [11,12].
• Environmental Factors: External conditions like temperature, humidity, and altitude can affect the heart’s response to exercise, making accurate prediction and personalization more challenging [4].
• Data Quality: Despite advancements in wearable technology, data from these devices can still be noisy or inconsistent, especially during high-intensity activities or when the device fit is suboptimal.
• Contextual Information: The heart rate metric alone may not provide a complete understanding of an exercise session. Integrating other contextual data, such as perceived exertion, workout type, and recovery status, is crucial for building a comprehensive fitness model [5].

To address these challenges and improve the accuracy of personalized fitness recommendations, we proposed a scalable algorithm, physiological Hybrid DBN model, which combines a physiological model with flexible machine learning techniques to learn an individual’s personalized, multidimensional representation of fitness. The model describes heart rate dynamics during exercise using Dynamic Bayesian Networks (DBNs). We derived DBN parameters using neural networks that connect a personalized representation based on the user’s workout history and immediate workout intensity, augmented with additional features through the use of LSTM networks. Our approach integrates wearable data measurements such as speed, elevation gain, distance covered, speed variability, and time elapsed to enhance fitness recommendation algorithms in health applications. This enables the delivery of personalized recommendations tailored to individual physiological responses to varying workout intensities.

Related literature explores the development of physiological models combined with machine learning techniques and other inference methods [4,13,14] for heart rate prediction. Our algorithm monitors heart rate evolution and estimates user-specific parameters over time, learning to map an individual’s recent workout history to a personalized representation that predict heart rate response over time. We employed DBNs to address the limitations of existing algorithms in making long-term predictions, as DBNs are well suited for capturing the temporal relationships in how heart rate evolves over time in response to exercise intensity. Additionally, DBNs handle the inherited uncertainty in prediction by considering the probabilistic nature of HR changes alongside additional factors, such as environmental conditions and other external influences.

The Hybrid DBN model is further enhanced to predict personalized heart rates by adjusting user-specific parameters over time, allowing the model to reflect individual’s unique physiological responses. We incorporated an adaptive feature selection module that tunes feature weights based on their relevance, considering that in real-world scenarios, user behavior and experiences vary and change. This ensures that the model remains responsive and adaptive in user behavior and exercise patterns.

The remainder of the paper is structured as follows: Section 2 provides a literature review of existing work related to physiological modeling, heart rate prediction, and fitness personalization. Section 3 presents materials and methods. Section 4 details our methodology, including the design of our model architecture. Section 5 presents the results of our experiments. Section 6 discusses the implications of our model for personalized fitness recommendations. Finally, Section 7 concludes the paper.

2. Related Work

This section reviews the existing literature on wearable data technologies, heart rate prediction models, the integration of physiological models with machine learning, the use of Dynamic Bayesian Networks (DBNs), and the development of recommender systems for personalized fitness recommendations:

Wearable Data Technologies: Wearable devices, such as fitness trackers and smartwatches, have empowered individuals to continuously monitor their health metrics, providing a rich data source that can be leveraged in machine learning models to uncover causal relationships between human health and device signals [15,16]. Ferguson [15] highlights how data mining from wearables can play a crucial role in personalized health interventions. Numerous studies have shown the value of wearable data in predicting health outcomes, ranging from clinical monitoring tools to fitness and activity planners [17,18,19]. These applications include machine learning models for cardiovascular fitness and disease surveillance [20,21,22]. Nazaret [4] discusses the utilization of wearable technology in monitoring heart rate (HR) and other physiological signals to model personalized heart rate responses to exercise and environmental factors. The study uses data from wearable devices, specifically Apple Watches, to capture detailed workout information such as step count, speed, elevation change, and environmental factors like temperature and humidity. These data are collected in real-time during various activities, allowing for a comprehensive analysis of an individual’s HR dynamics in uncontrolled, real-world environments. Jiamo [5] discusses the utilizing wearable devices, such as smartwatches and fitness trackers, to collect extensive data for modeling heart rate and activity patterns. These devices continuously capture various types of data types, including heart rate, GPS location, altitude, and other contextual information like weather and user demographics [5]. This data can be used to create personalized fitness and exercise behavior models, specifically focusing on heart rate dynamics and prediction.

Heart Rate Prediction Models: Heart rate is a critical physiological parameter used to assess cardiovascular health, exercise intensity, and other physiological states. Several models have been developed to predict heart rate, ranging from simple regression-based models to more scalable algorithms. Oyeleye [23] conducted a review of heart rate prediction using various machine learning techniques, including Autoregressive Integrated Moving Average (ARIMA) and linear regression, as well as Long Short-Term Memory (LSTM) models. Their results highlighted the potential of heart rate prediction in various areas of health monitoring. Kuano Tao [24] utilized linear regression and artificial intelligence networks to estimate heart rate and assess cardiovascular fitness in middle-aged adults. Hybrid approaches have also been developed; for instance, Lin [25] proposed a new method for heart rate prediction using LSTM-BILSTM-Att, which improved accuracy compared to baseline model. Zetao [7] introduced a study using LSTM to predict heart rate during different activities as part of a fitness training optimization system. Additionally, scalable algorithms for personalized heart rate response to exercise and environmental factors using wearables data have been developed [4] with the aim is to monitor heart rate evolution in response to workout intensity.

Integration of Physiological Models with machine learning techniques: Numerous studies have focused on integrating physiological models with machine learning techniques, particularly on heart rate parameters for various health outcomes. These models aim to overcome the limitations of traditional methods and standalone machine learning models, offering more accurate heart rate predictions. Recent research has explored combining physiological models with flexible neural networks to leverage both physiological understanding and data-driven models, enhancing prediction accuracy and adaptability in personalized interventions. For example, Nazaret [4] developed a physiological model using Ordinary Differential Equations (ODE) combined with flexible neural networks to monitor heart rate evolution during workout sessions, enabling personalized heart rate profiling. Signorini [26] integrated machine learning techniques and physiological heart rate features for antepartum fetal monitoring, helping identify potential pathologies early in pregnancy management. Another model, proposed by [27], predicts fitness levels by focusing on physiological features such as heart rate, step count data, and total oxygen consumption. Milan [28] emphasized the importance of dynamic models that capture physiological parameters, such as heart rate, in response to exercise, aiming to better understand the relationship between physiological responses and exercise.

Dynamic Bayesian Networks (DBNs): Dynamic Bayesian Networks have emerged as powerful tools for modeling time-series data due to their ability to capture temporal dependencies and handle uncertainty in dynamic environments. DBNs are particularly well suited for modeling physiological data, such as heart rate (HR), where responses can be highly variable and influenced by numerous factors. While there are not many studies specifically applying DBNs to heart rate modeling, DBNs have shown their strength in healthcare. For instance, Fernando [29] proposed a framework that uses Bayesian networks to describe heart rate dynamics and estimate the autoregulation of the autonomic nervous system. Zhang [30] introduced a heart prediction model using Bayesian networks to overcome the limitations of short-term models, enabling multiple predictions to enhance heart rate prediction accuracy during running activities. Ladyzynski [31] demonstrated DBNs’ capabilities in health monitoring and treatment of chronic lymphocytic leukemia, validating the use of DBNs in predicting health changes over time. Qi chen [32] applied DBNs to model complicated relationships among physiological variables across time slices for predicting physiological changes, organ dysfunction and mortality risk in critical trauma patients. Their results indicated that DBNs can serve as effective real-time tools for predict physiological changes. Marshall [33] introduced a dynamic Bayesian network to investigate the relationship between patient variables, cardiovascular disease and survival rates in heart disease patients. To our knowledge, limited research has applied DBNs as physiological inference methods to model heart rate in fitness environment for personalized fitness recommendations. In our work, we demonstrated the potential of DBNs in physiological modeling for fitness personalization.

Recurrent Neural Networks (RNNs): RNNs, particularly Long Short-Term Memory (LSTM) networks, have been widely used in recent years to analyze time-series data for sequential modeling tasks, such as speech recognition and machine translation [34]. In heart rate prediction, Oyeleye [22] investigated advanced deep learning models, including LSTM, for time-series modeling to overcome the limitations of traditional models such as ARIMA. Their work demonstrated improved results across multiple metrics compared to baseline models. Their work demonstrated improved results across multiple metrics compared to baseline models. Lin [25] proposed a method for predicting heart rate using LSTM-BILSTM-Att technique. Additionally, Jiamo [5] proposed FitRec, which utilizes LSTM networks to model heart rate by estimating heart rate profiles during ongoing exercise. Similarly, Xia Liu [35] proposed a multi-level deep learning approach using LSTM for heart rate prediction, which was later used to provide personalized recommendations.

Adaptive Feature Selection: In the realm of personalized recommender systems, Lin [35] highlights the importance of feature selection, shedding valuable insights on how each variable influences recommendation tasks. This analysis not only indicates the transparency of recommendation systems but also provides a deeper understanding of users’ preferences. Building on this, AdaFS [36] introduces an adaptive feature selection framework designed to optimize recommendation performance by selecting the most predictive features. AdaFS employs a novel controller network that automatically adapts to the dynamic nature of recommendation environments, ensuring that relevant features are selected as the system evolves. Similarly, Kayange [37] proposed the ProAdaFS framework, a probabilistic and adaptive feature selection approach for recommendation systems. This framework accounts for the fact that features in user-item interactions may vary over time, continually updating recommendation models to adapt to changes in user behavior and new data. We applied a similar concept in our physiological hybrid DBN model, recognizing that user behavior and preferences in practical recommendation systems fluctuate over time. This adaptive module dynamically enhances our model by incorporating evolving user exercise patterns, thereby improving performance.

Personalized Fitness recommendations: Several studies have focused on personalized fitness recommendations, utilizing approaches ranging from recurrent neural networks to physiological models and machine learning techniques. Jiamo [5] proposed a personalized fitness recommendation system FitRec, which models sequential fitness data, such as heart rate sequences, during ongoing workout sessions. Later Xia Liu [35] introduced a multi-level deep learning approach for fitness recommendations, focusing on personalizing workout distance and speed sequences in response to user activity. Additionally, as mentioned earlier, Nazaret [4] proposed a physiological model to personalize heart response to a workout intensity. Their model can also be applied to personal activity planning and predicting future workouts.

Despite the progress in wearable technology and fitness personalization, there remains a research gap in ensuring the accuracy and relevance of personalized fitness recommendations. The field lacks sufficient innovation and comprehensive research. From our review of existing literature, we found that most models focus on short-term predictions, which makes it difficult to maintain accuracy in long-term fitness environments. Additionally, many models are static and fail to adapt to the dynamic nature of user data over time. Utilizing fitness data for recommendations is also challenging, as these data often lack behavioral indicators like clicks or likes, which are crucial in understanding user behavior in traditional recommendation models. To address these gaps, we proposed a hybrid physiological model using Dynamic Bayesian Networks (DBNs) to model the evolution of heart rate over time in response to exercise. This approach also incorporates LSTM networks and an adaptive feature selection module, allowing the system to dynamically adapt to new data. Our proposed method aims to overcome the limitations of existing models and provide more accurate, personalized fitness recommendations by combining physiological modeling with machine learning techniques.

3. Materials and Methods

3.1. Dataset

We used the FitRec dataset from [5], which is collected from Endomondo fitness tracking applications and is a collection of workout data from wearables. The dataset provides rich insights into various physical activities performed by users, including different types of sports workouts such as running, biking, and other fitness routines, along with physiological data like heart rate. The dataset is sourced as a JSON format containing multiple entries for different individual’s workout sessions. Each entry contains timestamps, duration, distance covered, heart rate, speed, and GPS coordinates, making it an ideal dataset for studies focused on user behavior and predicting workout sessions for enhanced personalized fitness recommendations. The key variables used in this work, including heart rate, speed, distance, altitude and other derived variables are summarized in Table 1. For our study, we filtered the dataset to include only running workout sessions, with additional contextual information such as user ID, workout ID, and gender. A detailed summary of the dataset statistics, including the number of users and total workouts, is provided in Table 2. The JSON entries were parsed and converted into a Pandas DataFrame for efficient data manipulation and analysis.

Table 1. Description of workout data variables.

Variable	Unit
Measurement
Heart rate	Beats per Minute (BPM)
Time Grid	Seconds
Distance	Meters
Speed (Horizontal)	Meters per Second (m/s)
Speed (Vertical)	Meters per Second (m/s)
Contextual
UserID
WorkoutID
Sport
Gender	Male (1), Female (0)
Altitude	Meters (m)
Longitude	Degrees
Latitude	Degrees
Derived
Elevation Gain	Meters (m)
Average Speed	Kilometers per Hour (KMPH)
Speed Variability	Meters per Second (m/s)
Max Heart Rate	Beats per Minute (BPM)
Total Distance	Meters (m)

Table 2. Statics of the FitRec dataset on running sport.

Statistics	Value
Total number of users	665 (590 male, 65 female)
Total number of workouts	38,323
Average workout speed	3.7 km/h
Workout frequency per User	68
Average workout duration	48.54 Min

3.2. Data Processing

3.2.1. Temporal Data Alignment

We converted the timestamps into Python datetime objects to easily calculate the duration of each individual’s workout session, from start to finish. We retained workouts with durations between 10 min and 2 h 20 min, removing sessions that were either too short or excessively long. This filtering step ensures that our results reflect typical real-world workout sessions.

3.2.2. Interpolation and Grid Alignment

We applied a uniform grid at a 10-s interval for each workout to standardize the temporal resolution, resulting in a heart rate time series, $\widehat{HR }\in$ ${\mathbb{R}}^d$ [4] and workout intensity time series, I $\in$ ${\mathbb{R}}^d$, for each session. GPS coordinates, altitude, and heart rate were interpolated to ensure it aligns with the applied time grid. This approach minimizes the issue arising from irregular sampling intervals, ensuring a continuous representation of each workout’s dynamics.

3.2.3. Feature Engineering

To process the distance covered, we used the Haversine formula [37], which calculates the distance between two data points based on their latitude and longitude. For speed, we derived horizontal and vertical speeds from the interpolated distance and altitude, respectively. Additionally, we engineered features such as elevation gain, average speed, speed variability, maximum heart rate, and gender encodings to enrich the model inputs for better performance. We also applied normalization and standardization, particularly for heart rate, to ensure that the input data are consistent for model training, enhancing both the model’s performance and stability. Specifically, heart rate values were normalized by subtracting the mean heart rate and dividing by the average standard deviation, thereby centering the data and scaling them for uniformity across users.

3.2.4. Personalized Heart Rate Model

Following the approach from [4], we developed a personalized heart rate model by assigning each individual personalized parameters (A, B, including a drive function f and ${HR}_{\min }$, ${HR}_{\max }$), These parameters help capture the dynamic response to exercise. As mentioned by [4], learning each individual’s parameter health representation is computationally expensive. To address this, we assumed that a low-dimensional latent vector z $\in$ ${\mathbb{R}}^{\mathit{d}\mathit{i}}$ can represent an individual’s health status at a given time, where di is the dimensionality of the latent space.

4. Proposed Model

Our physiological DBN model integrates LSTM and flexible neural networks to predict personalized heart rate responses to exercise intensity during workout sessions. The architecture of our model consists of several key components, as illustrated in Figure 1.

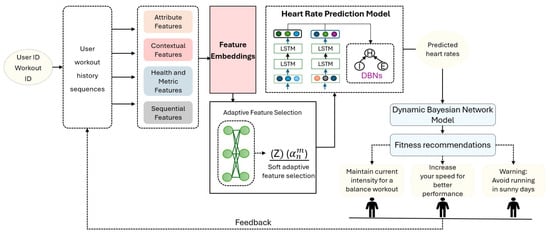
Figure 1. Model architecture of the proposed approach for personalized heart rate prediction to enhance fitness recommendations.

4.1. Dynamic Bayesian Network

Dynamic Bayesian Networks (DBNs) are an extension of Bayesian networks, designed to handle time-dependent data and capture the relationships between different features over time. This makes DBNs well suited for modeling sequences of variables where temporal dependencies are key. Moreover, DBNs are particularly effective in modeling time-series data due to their ability to capture both temporal dynamics and probabilistic relationships among variables. In this research, we applied DBNs to model heart rate changes in response to varying exercise intensities over time. Figure 2 provides a graphical representation of DBNs, where $z_t$represents the individual health status at time t and $E_t$ represent the observed heart rate. DBNs allow the model to capture temporal correlations and non-linear relationships in heart rate variations, which is essential given the noisy nature of wearable data. Additionally, DBNs enable the model to adapt its predictions based on changes in user behavior. Our model development focused on two core components of DBNs.

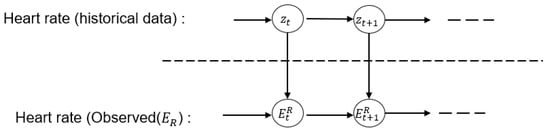
Figure 2. A graphical representation of DBNs where $z_t$ is an individual health status at time t and E is the observed heart rate.

State Transition: The state transition probability describes how the system evolves from one state to another over time. In the context of heart rate prediction, it captures how heart rate changes in response to variations in exercise intensity and duration. Figure 3 illustrates a graphical representation of our DBN model for heart rate prediction based on exercise workout intensity, where $y_t$ represents variables influencing heart rate and $x_t$ represents heart rate frequencies at time t. In our study, the state transition is modeled using the following equation:

$$P\left(x_t∣x_{t-1},S_t\right)=\left(x_t∣f_{\mathrm{trans}}\left(x_{t-1},S_t\right),{\sigma }^2\right),$$

(1)

where $x_t$ is the heart rate at time step t, $x_{t-1}$ is the heart rate at the previous time step t − 1, and $S_t$ is the state of influencing factors at time t, such as exercise intensity, speed, distance, elevation gain, and environmental conditions like temperature. The function $f_{trans}$ ($x_{t-1}$, $S_t$) is a transition function that models the expected heart rate at time t, based on the previous heart rate $x_{t-1}$ and the influencing factors, and $S_t$. ${\sigma }^2$ represents the variance of the transition noise, indicating uncertainty in the prediction. We assume that $x_t$ follows a normal distribution with mean $\mu$ = $f_{trans }(x_{t-1}$, $S_t$), and variance ${\sigma }^2$.

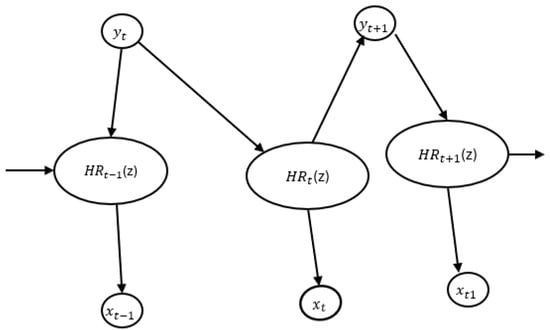
Figure 3. Graphical representation of the DBN model for heart rate prediction ${HR}_t$ based on exercise workout intensity, $y_t$ are variables influencing HR at state t and $x_t$ are heart rate frequencies at time t.

Equation (1) expresses that the heart rate at the current time step is normally distributed around a mean value $f_{trans}$ ($x_{t-1}$, $S_t$), which is a function of the previous heart rate and the current influencing factors. The noise term ${\sigma }^2$ accounts for uncertainties in heart rate transition. Incorporating state transition in our model captures temporal dependencies in heart rate dynamics, where the heart rate depends on both the previous state and contextual factors. This approach is crucial for monitoring user behavior changes over time.

Emission Modeling: The emission equation models how the latent physiological state relates to the observed heart rate at each time step. The emission equation is modeled as follows:

$$Y_t=f_{\mathrm{em}}\left(X_t\right)+{\mathsf{ϵ}}_t,\hspace{1em}{\mathsf{ϵ}}_t\sim N\left(0,{\mathsf{\sigma }}^2\right),$$

(2)

where $Y_t$ is the observed heart rate at time t, $X_t$ is the latent state at time t. The function $f_{em}(X_t$) is the function that estimates the observed heart rate from the latent state, and ${ϵ}_t$ represents prediction error, which follows a normal distribution with mean 0 and variance ${\sigma }^2$. The function $f_{em}(X_t$) maps the latent physiological state to the actual observed heart rate, capturing complex non-linear relationships.

Combining Equations (1) and (2), we can model the evolution of heart rate during workout sessions using our DBN model. The model is formulated as follows:

$$H{R}_{t+1}=H{R}_t\left(z\right)+f\left(H{R}_t\left(z\right),S_t\left(z\right)\right)+{\mathsf{\epsilon }}_t.$$

(3)

${HR}_{t+1}$ is the predicted heart rate at time t + 1, and ${HR}_t$(z) is the current heart rate at time t where z is the individual’s health status. The function $f$(${HR}_t$(z), $S_t$(z) estimates the change in heart rate based on individual’s current health state, considering both the current heart rate ${HR}_t$(z) and influencing factors $S_t\left(z\right)$, such as exercise intensity, speed, and environmental conditions. Lastly, ${\epsilon }_t$ is the noise accounting prediction error, representing random fluctuations.

4.2. Long Short-Term Memory (LSTM) Networks

LSTMs are a type of recurrent neural network (RNN) designed to model time-series data and capture long-range dependencies. Unlike traditional RNNs, LSTMs use memory cells to retain information over extended periods, enabling them to learn patterns and relationships in sequences that may not have been visible before. In our model, we used LSTM networks to process users’ workout histories and create personalized health representations through flexible neural networks. These representations are critical for informing the parameters of the Dynamic Bayesian Network (DBN) model, enhancing its ability to make accurate personalized predictions about heart rate responses.

We introduced an LSTM encoder that considers historical workout data, including features such as past heart rate data, exercise intensity, duration, speed, elevation gain, and other relevant physiological and contextual information. The LSTM processes this sequence data and learns a latent representation, z, which captures the user’s unique physiological characteristics and exercise patterns over time. This latent representation allows the model to personalize its predictions based on the user’s specific physiological state and workout history.

The LSTM network consists of a series of gates, as depicted in Figure 4: input, forget, and output gates, which regulate the flow of information through the memory cell. In our model, for a given step t, the LSTM calculates $h_t$, the output of the LSTM, which is subsequently fed into the DBN model. The $h_t$ is computed as follows:

$$f_t=\mathsf{\sigma }\left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right),$$

(4)

$$i_t=\mathsf{\sigma }\left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right),$$

(5)

$$o_t=\mathsf{\sigma }\left(W_o\cdot \left[h_{t-1},x_t\right]+b_o\right),$$

(6)

$$\widetilde{C_t}=\tanh \left(W_C\cdot \left[h_{t-1},x_t\right]+b_C\right),$$

(7)

$$C_t=f_t\cdot C_{t-1}+i_t\cdot \widetilde{C_t},\hspace{1em}{h}_t=o_t\cdot \tanh \left(C_t\right),$$

(8)

where $f_t$, $i_t$, $o_t$ represent the forget gate, input, and output gates, respectively, $C_t$ is the cell state at time step t, and $\widetilde{C_t}$ is the candidate cell state, $h_t$ is the hidden state output at time step t, σ denotes the sigmoid activation function, tanh denotes the hyperbolic tangent activation function, and W and b are weight matrices and bias vectors, respectively.

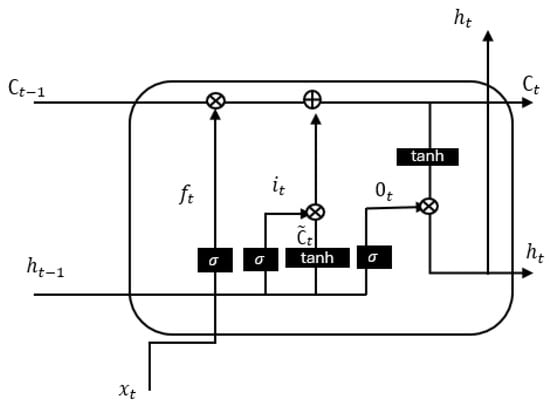
Figure 4. Structure of an LSTM cell.

4.3. Personalized Heart Rate Prediction

To accurately predict heart rate over time t during a workout session, our physiological model uses the following equation:

$$HR\left(t\right)=H{R}_{\min }+\left(H{R}_{\max }-H{R}_{\min }\right)\cdot \left(1-e^{-A\left(z\right)-B\left(z\right)\cdot I\left(t\right)}\right),$$

(9)

where $HR\left(t\right)$ is the predicted heart rate at time t, ${HR}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is the resting heart rate of the individual before a workout session, and ${HR}_{\max }$ is the maximum heart rate reached during an exercise session. $A\left(z\right)$ is the decay constant that controls how quickly the heart rate approaches its maximum, personalized through latent vector z. B(z) is the intensity coefficient that modulates the heart rate response based on exercise intensity I(t), also personalized through latent vector z, which represent the exercise intensity at time t.

This equation captures the dynamic heart rate behavior as it responds to exercise. It combines physiological aspects (resting and maximum heart rate) and exercise-specific factors (intensity and duration) to provide a comprehensive prediction model that adapts dynamically to exercise intensity through the decay function. The term $e^{-A\left(z\right)-B\left(z\right)\cdot I\left(t\right)}$ models the physiological response to exercise, where the rate of change in heart rate is controlled by both the duration and intensity of an exercise, modulated by personalized parameters. This formulation allows the model to account for physiological constraints and dynamic responses to exercise over time. It provides a transparent prediction that adapts to each individual’s unique characteristics and workout history, improving the precision of fitness recommendations.

4.4. Adaptive Feature Selection

We employed an adaptive feature selection module as an attention mechanism within the LSTM encoder, which assigns weights to different features based on their relevance at time t. This module illustrated in Figure 5, takes the latent vector z and assigns a weight of ${\alpha }_n^m$ where n is the $n^{th}$ feature and m is the $m^{th}$ data point in the input latent vector z. To achieve this, we designed a multi-layer perceptron (MLP) network controller that dynamically assigns weights to the latent vector z based on each feature’s predictive power. This enables the model to prioritize the most relevant features for heart rate prediction, ensuring more accurate and personalized recommendations.

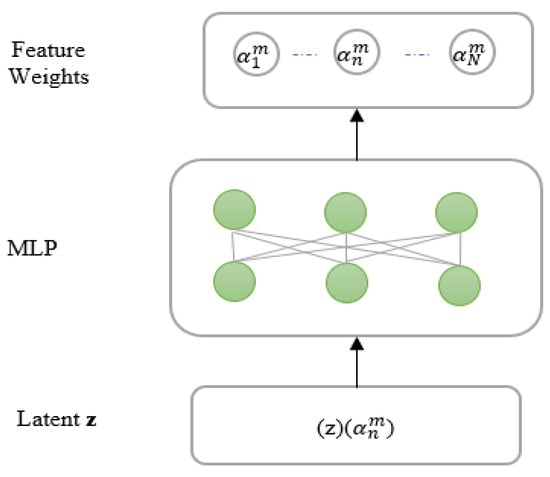
Figure 5. Adaptive feature selection module.

5. Experiments

This section focuses on evaluating the proposed model’s performance in predicting heart rate (HR) responses and its effectiveness in providing personalized fitness recommendations. We will outline the experimental setup, describe the evaluation metrics used, and present the results of our experiments, highlighting the model’s accuracy and adaptability.

5.1. Experimental Setup

We conducted our experiments using the FitRec dataset, which contains 38,323 logged workout sessions of running workouts across 665 individuals. The dataset includes various workout types such as running, cycling, and walking, alongside wearable data (e.g., heart rate), speed/pace, elevation gain, and GPS coordinates. To focus on the most relevant information, we filtered the dataset to include only workouts lasting between 10 min and 2 h and 20 min. Several additional features were derived from the raw data including speed variability, calculated as the standard deviation of speed, elevation gain computed as the sum of positive altitude changes, normalized heart rate. We created a time grid for each workout session to facilitate interpolation and alignment of features.

For training and validation, the dataset was split into two subsets: 80% for training and 20% for validation, ensuring that workouts from the same user were not split across subsets. This split was necessary to evaluate the model’s generalization capability to unseen data.

DBN parameters were configured to model the state transitions and emission probabilities, capturing the dynamics of heart rate response during exercise. The LSTM encoder was set up with two layers, a hidden dimension of 128, and a dropout rate of 0.2 to prevent overfitting. We also utilized flexible neural networks, specifically the PersonalizedScalerNN [4], to dynamically adjust the DBN parameters based on the latent representations generated by the LSTM encoder.

For the training procedure, we used the Adam optimizer with a learning rate of 1 × ${10}^{-3}$. The model was trained by minimizing the mean squared error (MSE) between the predicted and actual heart rate values. To prevent exploding gradients, gradient clipping was employed

5.2. Evaluation Metrics

To evaluate the performance of our model in both heart rate prediction and personalized fitness recommendation, we used the following metrics:

• Mean Absolute Error (MAE): This metric measures the average absolute difference between predicted and actual heart rate values. It provides a straightforward measure of prediction accuracy by calculating the magnitude of errors.

  $$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-\widehat{y_i}\right|$$

  (10)
• Root Mean Squared Error [RMSE]: measures the square root of the average squared differences between actual and predicted values. It gives higher weight to larger errors, making it sensitive to large deviations.

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(11)

where n is the total number of data points, $y_i$ is the actual heart rate data and, $\widehat{y_i}$ is the predicted heart rate data.

5.3. Results and Analysis

5.3.1. Heart Rate Prediction Performance

The proposed hybrid DBN model achieved an average Mean Absolute Error (MAE) of 5.2 BPM and a Root Mean Square Error (RMSE) of 8.1 BPM across all validation workouts. These results demonstrate the model’s ability to accurately predict heart rate responses to exercise intensity during workout sessions, indicating its effectiveness in capturing dynamic physiological changes.

Figure 6 illustrates the model’s performance in predicting heart rate during workout sessions. The x-axis represents the time from the start of the workout session, while the y-axis shows the instantaneous heart rate in beats per minute (BPM). The solid blue line indicates the actual heart rate measured during the workout, and the dashed orange line represents the predicted heart rates generated by the model. The shaded region around the predicted values represents uncertainty bands of ±5 BPM, accounting for variability in heart rate measurements.

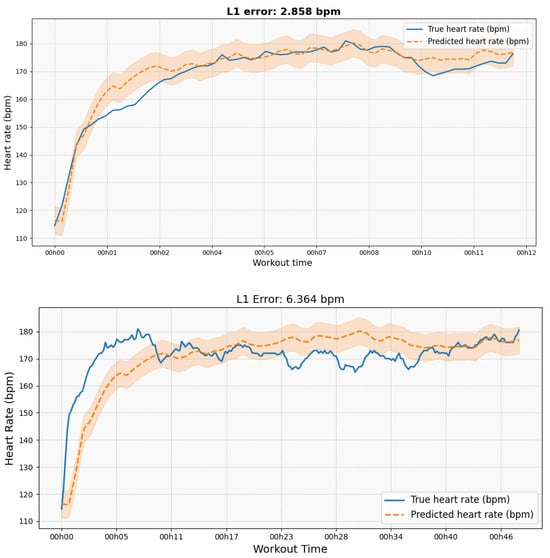
Figure 6. True vs. predicted heart rates for the specific session.

5.3.2. Performance Analysis

We demonstrated visualizations of the predicted heart rate versus actual heart rate for a variety of workout sessions, as a measure for the model proposed in this paper.

Figure 7 shows the difference between the predicted and actual heart rates across all workout sessions, plotted against the average of those heart rates. The plot has a mean bias of 0.42 BPM, indicating that, on average, the model slightly overestimates heart rates. The limits of agreement, set at ±1.96 times the standard deviation from the mean bias, range from −15.53 BPM to 16.38 BPM. These relatively tight limits suggest that most predictions are close to the actual heart rates, highlighting the model’s accuracy across various heart rate ranges. The points on the plot are evenly distributed around the mean bias line, with no clear patterns or systematic errors, indicating that the errors are random and not biased toward any particular heart rate level. The narrow range of the limits further supports the notion that our DBN model provides reliable heart rate predictions with minimal error. Such consistent performance is critical in real-world applications, where accurate heart rate monitoring is essential for making personalized fitness recommendations.

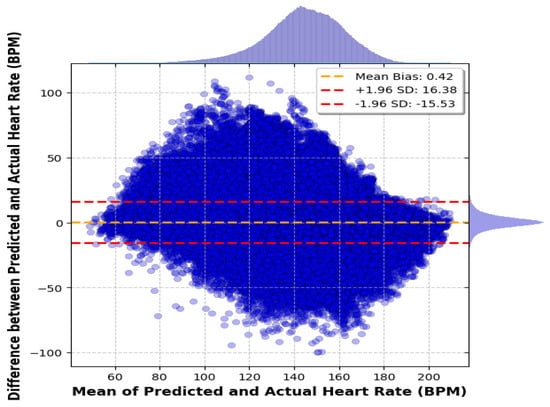
Figure 7. The Bland–Altman plot.

For further insights, Figure 8 demonstrates the model’s performance on true vs predicted heart rates for a specific session.

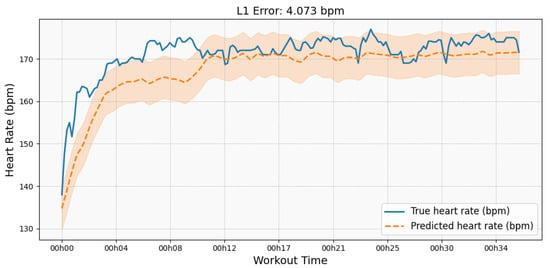
Figure 8. True vs. predicted heart rates for the specific session.

Figure 9 illustrates the model’s ability to predict heart rate evolution across different individuals during workout sessions. The solid blue lines represent the actual heart rate evolution, while the dashed orange lines depict the model’s predictions. Across all individuals, the model closely follows the heart rate trends, demonstrating its capacity to generalize well across varying users and workout intensities. The model accurately predicts heart rate responses to different exercise intensities, capturing rapid increases during high-intensity intervals and smooth declines during recovery periods. For most individuals, the predicted heart rate closely aligns with the actual heart rate, particularly during steady-state phases of the workout. However, minor discrepancies can be seen during rapid heart rate fluctuations, which may be attributed to physiological differences between individuals or noise in the sensor data. Overall, the model’s performance across multiple individuals highlights its robustness in handling varying user profiles and workout conditions, making it effective for personalized heart rate prediction and health tracking applications, as well as for delivering personalized fitness recommendations in real-world scenario.

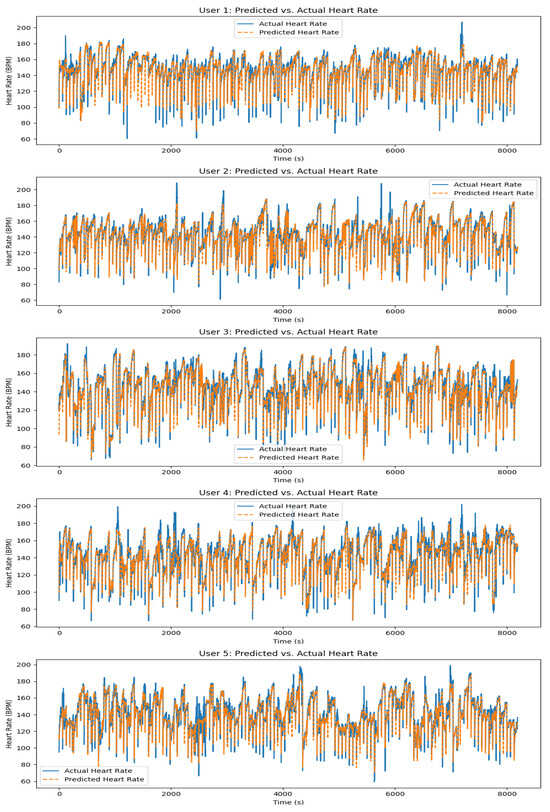
Figure 9. Model performance on actual and predicted heart rate evolution for different individuals.

Table 3 presents a comparison of Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) between the proposed hybrid DBN model and two state-of-the-art models, hybrid ODE [4] and FitRec [5]. All models were evaluated on the same dataset for consistency. The Hybrid DBN model achieves a significantly lower MAE of 5.2 BPM and RMSE of 8.1 BPM, demonstrating its effectiveness in capturing the complex dynamics of heart rate response during exercise.

Table 3. DBN Model comparison against state-the-of art.

Model	MAE (BPM)	RMSE (BPM)
Hybrid ODE Model	6.1	-
FitRec (U/S/C)	7.0	17.1
Hybrid DBN Model	5.2	8.1

This improved performance highlights the Hybrid DBN model’s ability to model personalized heart rate predictions more accurately, making it a reliable tool for understanding user behavior and providing personalized fitness recommendations. Compared to the FitRec model, which has an MAE of 7.0 BPM and an RMSE of 17.1 BPM, the Hybrid DBN model offers a substantial improvement in both error metrics.

5.3.3. Ablation Study

The ablation study in Table 4 illustrates the contributions of different components to the overall performance of the Hybrid DBN model. The table shows that removing the LSTM encoder increases the MAE, highlighting the critical role of the individual’s health status representation (i.e., past workout data) in ensuring precise predictions.

Table 4. Ablation study on components contribution.

Model	MAE (BPM)
Hybrid DBN Model	5.2
Without LSTM Encoder	21.3
Without Adaptive Feature Selection	12.5
Without Personalized Parameters	11.7

Furthermore, omitting the adaptive feature selection module results in a significant decline in model performance, emphasizing the module’s function in dynamically selecting the most relevant features. Lastly, the elimination of personalized parameters also negatively affects prediction accuracy, demonstrating the importance of personalization for adapting the model to individual users.

6. Personalized Recommendations

In addition to predicting heart rate responses to exercise, our model demonstrates the ability to offer personalized fitness recommendations tailored to individual behavior patterns. In this section, we explore recommendation tasks that showcase the model’s practical utility in real-world fitness environments:

• Workout Optimization Recommendation: Based on a user’s predicted heart rate profile and specific workout goals, we suggest adjusting workout parameters, such as speed or intensity, to optimize performance and achieve desired outcomes. For instance, if a user aims to maintain a particular heart rate zone (e.g., fat-burning or aerobic zone), our model can dynamically adjust recommendations during the workout, advising users to increase or decrease their pace accordingly. This functionality is particularly beneficial for users who aim to meet specific heart rate targets or improve cardiovascular endurance. Additionally, the system can suggest variations in exercise routines to prevent fitness plateaus, recommending different workout intensities or durations based on historical performance data.
  Scenari: A user who frequently runs on a flat course might receive a suggestion to try a hilly route that provides a similar heart rate response due to its variability in incline. This approach helps users diversify their workouts, potentially enhancing overall fitness by exposing them to different physical demands while keeping the exercise routine engaging.
• Real-Time Workout Guidance: Our model serves as a real-time personal trainer, predicting the short-term fluctuations in heart rate based on the current user pace and environmental conditions. If the model predicts that the person’s heart rate will go above some threshold (e.g., 85% of maximum heart rate), the system can proactively alert the user to adjust their pace, ensuring a safer and more effective workout. It helps avoid overexertion, making exercise much safer and far more effective, especially for novices or people with specific health concerns.
  Scenario: During a high-intensity interval training (HIIT) session, the system monitors the user’s heart rate in real-time. If the heart rate approaches a critical level, the system suggests a brief recovery period or a reduction in intensity to avoid excessive strain.
• Workout route and Activity Suggestion: The model can recommend specific workout routes or activities that align with the user’s fitness goals and preferences by analyzing historical workout data and heart rate responses. This is especially beneficial for users who wish to explore new routes or maintain their regular exercise routine while traveling. The recommendation system can identify routes that match a user’s preferred heart rate profile or suggest new routes that offer similar physiological challenges, such as maintaining a steady heart rate or achieving specific exertion levels.
  Scenario: A user who frequently runs on a flat course might receive a suggestion to try a hilly route that provides a similar heart rate response due to its variability in incline. This approach helps users diversify their workouts, potentially enhancing overall fitness by exposing them to different physical demands while keeping the exercise routine engaging.

7. Conclusions

In this study, we developed a novel hybrid physiological model using Dynamic Bayesian Networks (DBNs). The integration of DBNs enables robust modeling of heart rate dynamics over time, capturing both the physiological aspects of heart rate response and the influence of external factors, such as workout intensity and environmental conditions. The incorporation of LSTM networks further enhances the model’s ability to learn from sequential data, providing a personalized health representation that adapts to each user’s specific physiological state and exercise patterns.

However, there are some limitations to our study. The model was trained and validated on the FitRec dataset, which may not fully represent the diversity of real-world users, and the data are skewed toward male individuals. Testing our model with data from a broader range of sources, such as those collected from Apple Fitness or Samsung Health platforms, could offer a more comprehensive evaluation of its performance across different devices and user demographics. Access to such data would also allow us to better explore the model’s generalization and adaptability.

Despite these limitations, our results demonstrate that the proposed model not only predicts heart rate with improved accuracy but also provides valuable insights into individual fitness levels and responses to exercise. This capability can be applied to developing personalized fitness recommendations, offering real-time guidance based on predicted heart rate zones and exercise intensity.

Future work will focus on extending the model to other types of exercises and further improving its interpretability by incorporating more extensive data from wearables. Additionally, exploring the model’s potential to predict long-term health outcomes and integrating it into comprehensive health monitoring systems could lead to more personalized and effective fitness and health recommendations.

Overall, this work represents a significant step forward in leveraging machine learning and physiological modeling to provide personalized fitness insights, demonstrating the potential of hybrid models in health and fitness applications.