Quantum-Dot CA-Based Fredkin Gate and Conservative D-Latch for Reliability-Based Information Transmission on Reversible Computing

Abstract

Reversible computation is very important to minimize energy dissipation and prevent information loss not only in quantum computing but also in digital computing. Therefore, interest in designing efficient universal logic gates has recently increased. In this study, we efficiently design the Fredkin gate (FRG), a well-known conservative reversible operation gate, using quantum-dot cellular automata (QCA), and propose a D-latch using it. The proposed FRG structure can be designed efficiently using the structure of a QCA multiplexer using cell interaction, and a symmetric structure was designed. The proposed structure was simulated using QCADesigner 2.0.3 and QCADesigner-E for accurate comparison of various performance metrics, and the proposed structure clearly shows superiority in most performances and two representative design costs. Therefore, the lightweight design of an efficient reversible gate prevents data loss and increases information reliability.

1. Introduction

Reversible computation was proposed in the 1970s by Bennett, who was inspired by Landauer’s discovery that information deletion requires entropy [1,2]. Landauer demonstrated that the loss of 1 bit of information results in a loss of energy of k_BTln2 joules where k_B = 1.38 × 10⁻²³ JK⁻¹ is the Boltzmann constant and T is the temperature in Kelvin, and Bennett demonstrated the feasibility of this energy loss in an irreversible circuit being recoverable in a reversible circuit [3]. This showed a direct connection between information loss, energy dissipation, and reversible circuits. The most famous example of reversible computing is the billiard ball computer developed by Fredkin and Toffoli, which calculates the collision function of a billiard ball using reversible logic [4]. Afterwards, Bruce et al. designed a reversible carry-ripple adder and carry-skip adder using Fredkin gates [5].

Quantum-dot cellular automata (QCA) proposed by Lent and Tougaw is attracting attention as an alternative that can overcome the problems of high-power loss and information loss in existing irreversible CMOS-VLSI circuits [6,7]. The dissipated energy is measured based on the Hamiltonian matrix using the HartreeFock approximation in relation to the Coulomb repulsion between QCA cells as shown in Equation (1) [8].

$$H=\left[\begin{array}{cc}{\displaystyle \frac{-E_k}{2}}{\sum }_i{C}_i{f}_{i,j}& -\gamma \\ -\gamma & {\displaystyle \frac{E_k}{2}}{\sum }_i{C}_i{f}_{i,j}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{-E_k}{2}}\left(C_{j-1}+C_{j+1}\right)& -\gamma \\ -\gamma & {\displaystyle \frac{E_k}{2}}\left(C_{j-1}+C_{j+1}\right)\end{array}\right]$$

(1)

where $E_k$ is the energy cost of two neighboring cells with opposite polarization, called kink energy, and $C_i$ denotes the polarization of the i-th neighboring cell and, $f_{i,j}$ denotes the geometrical factor identifying the electrostatic interaction between cells i and j due to the geometrical distance. The kink energy is a value related to the cost of energy in two cells with different polarizations. γ refers to the electron tunneling energy that changes depending on the clock. The nonadiabatic power estimation model was used to estimate the power loss or energy dissipation of the cell [9,10]. ${(C}_{j-1}+C_{j+1}$) means the sum of the kink energy of polarized neighbors.

The power dissipation using the Hamiltonian matrix shown in Equation (1) can be summarized in terms of energy per clock cycle as shown in Equation (2) [10].

$$P_{diss}={\displaystyle \frac{E_{diss}}{T_c}}⟨{\displaystyle \frac{\hslash }{2T_c}}{\overrightarrow{\Gamma }}_{+}\times \left[-{\displaystyle \frac{{\overrightarrow{\Gamma }}_{+}}{\left|{\overrightarrow{\Gamma }}_{+}\right|}}\tanh \left({\displaystyle \frac{\mathrm{\hslash }\left|{\overrightarrow{\Gamma }}_{+}\right|}{k_{B}T}}\right)+{\displaystyle \frac{{\overrightarrow{\Gamma }}_{-}}{\left|{\overrightarrow{\Gamma }}_{-}\right|}}\tanh \left({\displaystyle \frac{\mathrm{\hslash }\left|{\overrightarrow{\Gamma }}_{-}\right|}{k_{B}T}}\right)\right]⟩$$

(2)

where $T_c$ is the clock period and ${\overrightarrow{\Gamma }}_{+}$ and ${\overrightarrow{\Gamma }}_{-}$ are the Hamiltonian values before and after the transaction.

Recently, with the rapid development of the quantum computing environment, interest in reversible computing is increasing, and much interest continues in the implementation of reversible gates using QCA in the digital computing environment. QCA-based Feynman gate [11,12,13,14], QCA-based Toffoli gate [15,16,17], and QCA-based Peres gate [18,19,20] have XOR as the main operation, so the design of an efficient QCA-based XOR gate can have a significant impact on the performance of the circuit. After the Fredkin gate appeared, interest in the development of conservative gates increased [21]. However, since the QCA-based Fredkin gate [22,23,24,25,26,27,28,29,30] includes the operation of a multiplexer (MUX), the design of a QCA-based MUX can be an important issue. One of the most common applications using Mux is D-latch. This is because a D-latch can be easily designed by reusing the output of the Mux as an input. Therefore, various studies are in progress on the design of D-latches using reversible gates [30,31,32,33]. In the proposed study, the Fredkin gate (FRG), which can be used as a universal reversible gate, is efficiently designed using QCA, and an efficient D-latch is designed using the FRG. The key contributions of this study are summarized as follows.

• FRGs, which are universal reversible gates, are designed using QCA.
• Conservative reversible D-latches using the proposed FRGs are designed.
• The proposed study analyzes the performance of cell count, area, delay, and energy dissipation required for implementation, calculates two representative standard design costs, and compares them with existing studies.
• The proposed QCA-based circuits showed significant improvement in most performances and design costs compared to existing excellent circuits.

The paper is structured as follows. Section 2 describes the basic knowledge of FRG, QCA, and QCA circuits. Section 3 shows the proposed QCA-based FRGs and D-latches. In Section 4, the proposed structures are compared with existing circuits in terms of performances and design costs. Finally, Section 5 summarizes the study and presents conclusions.

2. Related Works

This section briefly reviews the basic knowledge about FRG, QCA, QCA-based MUX, and D-latches.

2.1. Fredkin Gate

Reversible computation makes it possible to completely restore the initial state in a system with a single final state value. For example, a NOT gate can be returned to its initial state without any information loss by performing two NOT gate operations. However, it is impossible to return the result of an AND or OR gate to the initial state. This is because one result value was created with two inputs, but it is logically impossible to create two input values with one result value. Therefore, a reversible gate must have the same number of inputs and outputs.

Controlled SWAP (CSWAP) gate is a 3 × 3 reversible gate introduced by Fredkin. It has one control bit A and two target bits B and C, and is called Fredkin gate (FRG) as shown in Figure 1a with its truth table in Table 1. This is a conservative logic gate that operates by exchanging two target bits only when A is 1, as shown in Figure 1c, and does not operate otherwise, as shown in Figure 1b [4]. FRG is a universal gate that can express all Boolean functions. Figure 1d–f show the logical expressions of AND, OR, and NOT using FRG, respectively.

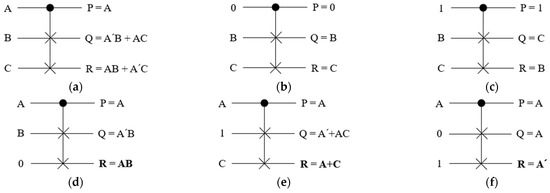
Figure 1. Quantum circuit diagram of FRG: (a) CSWAP: F(A, B, C); (b) No operation: F(0, B, C); (c) Swap: F(1, B, C); (d) AND operation: F(A, B, 0); (e) OR operation: F(A, 1, C); (f) NOT operation: F(A, 0, 1).

Table 1. Truth table of Fredkin gate (P is a garbage output, and Q and R output the multiplexer operation results of inputs B and C for the selected input A or A′).

Inputs			Outputs
A	B	C	P = A	Q = A′B + AC	R = AB + A′C
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	1	0
1	1	0	1	0	1
1	1	1	1	1	1

2.2. Basics of QCA

A QCA cell consists of four quantum dots and is located at each corner of a square cell. Two electrons are located on two diagonals due to Coulomb repulsion, and this is expressed as P = +1 or P = −1 as shown in Figure 2a,b. These become 1 or 0 in binary operations. Figure 2c shows the QCA wiring with one input cell and one output cell. Wiring can be easily obtained by arranging the QCA cells in succession, and the QCA clock cycle consists of four clock phases displayed in different colors from clock0 to clock3 [8,34].

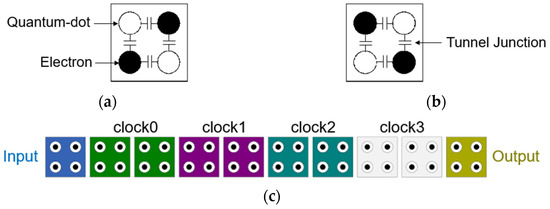
Figure 2. QCA cell: (a) P = +1; (b) P = −1; (c) QCA wire with four clock phases.

In QCA, values are transmitted as the barrier height between quantum dots changes over time, as shown in Figure 3. A QCA cell has four states: switch, hold, release, and relax. Switch is a state in which the barrier between quantum dots is increasing, and hold is a state in which the barrier between quantum dots has become sufficiently high that electrons cannot move between quantum dots. At this time, the potential energy of the electrons is at its strongest and has a clear polarization. Release refers to a state in which the barrier between quantum dots is gradually lowering, and relax refers to a state in which the barrier between quantum dots is sufficiently lowered so that the potential energy of electrons is lowered and tunneling is possible freely [8].

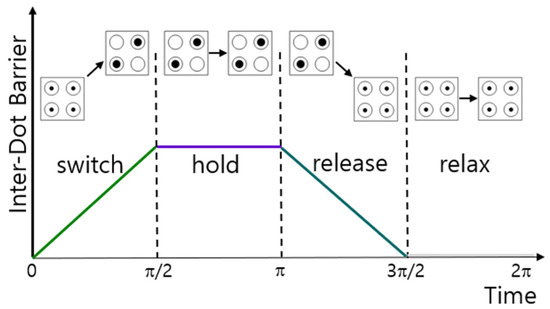
Figure 3. Four different states of the QCA clock depending on the barrier height between quantum dots and changes in time. (switch: a state in which the barrier between quantum dots gradually increases; hold: a state in which the barrier becomes sufficiently high that electrons cannot move; release: a state in which the barrier gradually decreases; relax: a state in which the barrier becomes sufficiently low that electrons are free to move).

2.3. QCA-Based Multiplexer and D-Latch

A 2-to-1 MUX is a combination circuit that receives two inputs and uses a selector to select one of the input values and output it. When the two inputs are B and C and the selector is A, the output F is as follows.

$$F=A^{\prime }B+AC=MG\left(MG\left(B,A^{\prime },-1\right),MG\left(C,A,-1\right),1\right)$$

(3)

As shown in Equation (3), the logic expression of the 2-to-1 MUX can be expressed with three majority gates, and is the same as the output Q of the Fredkin gate shown in Table 1. Also, if the order of the two inputs and B and C is changed, the result of Equation (3) is the same with the output R of the Fredkin gate. Therefore, a well-made 2-to-1 MUX can determine the performance of the Fredkin gate.

Existing QCA-based MUX is divided into a majority gate-based circuit [35,36,37,38] and cell interaction-based circuit [39,40,41,42,43]. Circuits based on majority gates are easy to design and read, are structurally simple, and have low-energy consumption. However, there are limits to minimizing the number and area of cells. On the other hand, circuits based on cell interaction are difficult to design and read, and the number and area of cells, as well as delay, can be minimized. Additionally, the noise of the output signal can be relatively reduced.

Meanwhile, the D-latch is a very important design element applied to various sequential circuits. It can be expanded to D-flip-flops and shift registers and is used as a basic element in various memory structures. Various studies have shown that the design of a D-latch is possible by returning the output of a 2-to-1 MUX circuit back to the input value [44,45,46]. Additionally, research was conducted on D-latch design using reversible gates. Chabi et al. designed an FRG using an XOR gate and a 2-to-1 MUX, Bhoi et al. proposed a new parity-preserving reversible gate, and in two cases, Mohammadi et al. and Naz et al. designed an FRG based on majority voting gates. They all designed D-latches using the proposed reversible gates [30,31,32,33].

3. Proposed QCA-Based Fredkin Gate

As shown in Figure 1a, the output of FRG, Q = A′B + AC, is the same as the output of a 2-to-1 multiplexer (MUX) with a selection input A and two inputs B and C. By the same principle, R = AB + A′C is the same as the output of a 2-to-1 MUX with only the order of the two inputs changed. Therefore, the FRG in Figure 1a can be expressed as two facing 2-to-1 MUXs as in Figure 4a. The MUX that best matches the structure is the symmetrical MUX proposed by Jeon in [39], and it is possible to obtain a square-shaped FRG with a completely symmetrical structure as shown in Figure 4b. A, the selector, is input to two MUXes on both sides of the circuit, and B and C are also input to both the left and right from the center of the circuit. At this time, the garbage output P is obtained immediately on the first clock phase. The other two effective outputs Q and R are obtained very stably outside the circuit on the second clock phase, and 33 cells and an area of 24,564 nm² were used for the QCA-based FRG (QFRG). Figure 4c shows an improved QFRG (IQFRG) with the three cells indicated by the red dotted line in Figure 4b deleted, while still maintaining vertical symmetry, and 30 cells and an area of 21,804 nm² were used. Both proposed structures have the same simulation results as shown in Figure 4d. The results of Q and R are output to CLOCK1, the second clock phase, and the result value is also confirmed to be the same as the truth table in Table 1.

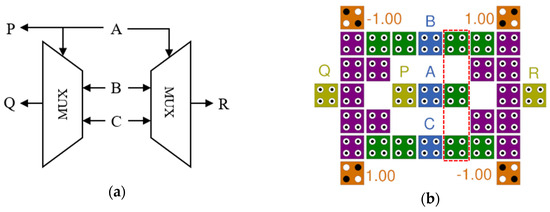
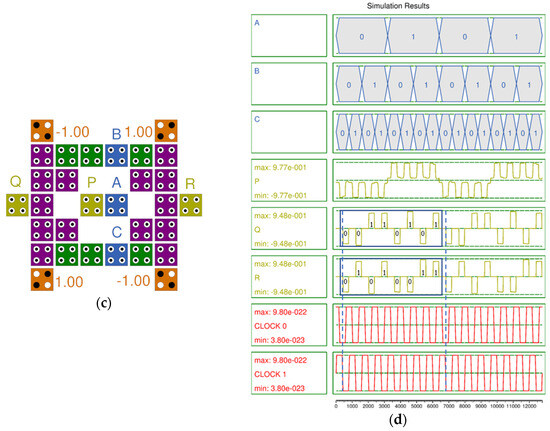
Figure 4. Proposed FRG structures: (a) A logic diagram of FRG using two 2-to-1MUX; (b) QCA implementation of FRG (QFRG); (c) Improved QFRG (IQFRG); (d) Simulation result of QFRG and IQFRG.

FRG can be used as a reversible D-latch by adjusting the input and output and adding wires, as shown in Figure 5a. The three inputs are as follows. The first is the clock of the latch, the second is the value to be stored in the D-latch, and the third is the output value of the nth D-latch. As a result, garbage output values of G1 = CLK and G2 = CLK′·D + CLK·Q_n are generated, and Q_n+1 = CLK·D + CLK′·Q_n, the current storage value of the D-latch, is output. Figure 5b completes the D-latch based on QFRG (DQFRG) by returning the output value, Q_n+1, back to the position of the input value to make a loop, and requires 46 cells and an area of 35,244 nm². Since two clock phases are used for the internal operation of the FRG gate, the loop also used two clock phases. Therefore, the value of the D-latch is updated every two clock phases. Figure 5c shows the D-latch with IQFRG (DIQFRG) applied, which can greatly reduce cells and area, and requires 42 cells and an area of 31,684 nm². Figure 5d shows the simulation results of the proposed two FRG-based reversible D-latches. The simulation result shows that the value of the D-latch is updated every two clock phases according to Table 2, and shows very high output polarization and a stable, noise-free output signal.

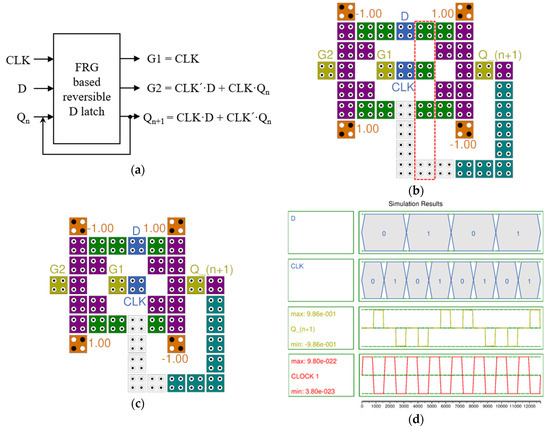
Figure 5. Proposed D-latch structures: (a) A block diagram of reversible D-latch based on FRG; (b) QCA implementation of D-latch based on QFRG (DQFRG); (c) D-latch with improved DQFRG (DIQFRG); (d) Simulation result of DQFRG and DIQFRG.

Table 2. Truth table of Fredkin gate-based reversible D-latch.

Inputs			Output
CLK	D	Qn	Qn+1
0	x	0	0
0	x	1	1
1	0	x	0
1	1	x	1

Table 2 shows the truth table of the proposed Fredkin gate-based reversible D-latch. When CLK is 0, the existing value of Q_n is output as Q_n+1 regardless of the value of the D-input to the latch, and when CLK is 1, it shows that Q_n+1 is output according to the value of the D-input to the latch.

4. Performance Analysis and Comparison

In this section, in order to measure the performance of the circuits, area and delay were obtained using QCADesigner 2.0.3, and energy dissipation was measured using QCADesinger-E 2.2 [47,48]. The simulation engine and parameters used are shown in Table 3.

Table 3. Simulation engines and parameters on QCADesinger2.0.3 and QCADesigner-E.

	QCADesigner 2.0.3	QCADesigner-E
Parameters	Bistable Approximation	Coherence Vector with Energy
Cell size (nm)	18	18
Dot diameter (nm)	5	5
Cell separation (nm)	2	2
Layer separation (nm)	11.5	11.5
Clock high (J)	9.8 × 10−22	9.8 × 10−22
Clock low (J)	3.8 × 10−23	3.8 × 10−23
Clock shift	0	0
Clock amplitude factor	2.0	2.0
Relative permittivity	12.9	12.9
Radius of effect (nm)	65	80
Number of samples	12,800	-
Convergence tolerance	1.0 × 10−3	-
Maximum iterations per sample	100	-
Temperature (K)	-	1
Relaxation time (s)	-	1.0 × 10−15
Clock slope (s)	-	1.0 × 10−12
Time step (s)	-	1.0 × 10−16
Clock/input period (s)	-	4.0 × 10−12

The metrics to be used as indicators for performance analysis are as follows. Cell count is the number of QCA cells used for design, area means cutting the plane space required for design into a rectangle, and delay indicates the clock phase at which the first output for all inputs occurs. Energy dissipation indicates the total energy loss required to operate the entire circuit. $Cos{t}_{AD}$ is a standard design cost indicator expressed as the product of the square of area and delay, as shown in Equation (4). This is because the importance of delay is evaluated more highly due to the recent rapid development of hardware. $Cos{t}_{ED}$ is a standard design cost indicator defined as Equation (5) by calculating energy dissipation and delay [49].

$$Cos{t}_{AD}=A\times D^2$$

(4)

$$Cos{t}_{ED}=E^2\times D^2$$

(5)

where A, D, and E refer to the area, delay, and energy dissipation required in circuit design.

Table 4 shows a comparison of the performances and design costs of QCA-based Fredkin gates. The proposed IQFRG showed excellent results in most performance metrics but energy dissipation. The proposed circuit is slightly larger in energy dissipation than the circuit in [29], however, since this indicator has a trade-off relationship with delay, it was confirmed that the proposed circuit was reduced by at least two times compared to the existing circuit in $Cos{t}_{ED}$, which is the design cost of the circuit calculated by considering delay as well. The improvement rate for each metric is shown in Figure 6 and Figure 7.

Table 4. Performance and design cost comparison of Fredkin gates.

FRG Circuit	Cell Count	Area (µm2)	Delay (Clock Phase)	Ener. Diss. (10−2 eV)	$\mathit{C}\mathit{o}\mathit{s}{\mathit{t}}_{\mathit{A}\mathit{D}}$	$\mathit{C}\mathit{o}\mathit{s}{\mathit{t}}_{\mathit{E}\mathit{D}}$
[22]	108	0.094	6	3.31	3.383	394.4
[23]	109	0.150	4	3.71	2.407	220.2
[24]	83	0.096	3	4.33	0.861	168.7
[25]	94	0.091	3	3.95	0.820	140.4
[26]	68	0.065	3	2.75	0.585	68.1
[27]	68	0.064	3	2.34	0.578	49.3
[28]	57	0.048	3	4.02	0.431	145.4
[29]	42	0.042	3	1.23	0.381	13.6
[30]	48	0.048	4	3.67	0.760	215.5
QFRG	33	0.025	2	1.96	0.098	15.4
IQFRG	30	0.022	2	1.29	0.087	6.7

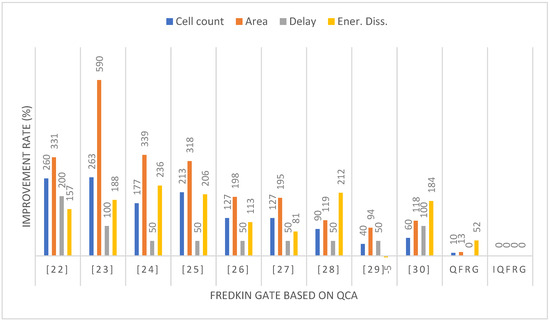
Figure 6. Performance improvement of proposed QFRG and IQFRG compared with typical FRG based on QCA.

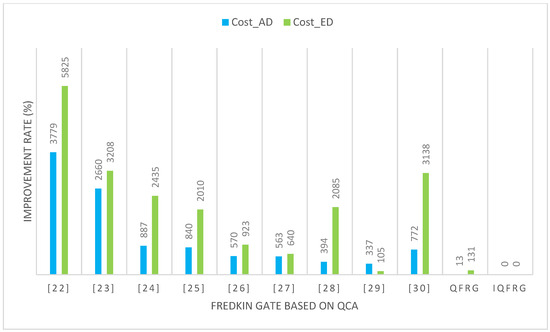
Figure 7. Improvement of design costs of proposed QFRG and IQFRG compared with typical FRG based on QCA.

Figure 6 shows a comparison of various performances, and the proposed IQFRG showed improvement rates of at least 40%, 94%, and 50% in cell count, area, and delay, respectively. Energy dissipation was also found to be the best except for one circuit. However, considering the trade-off between energy dissipation and delay, the results seem to be good enough. This becomes clear when checking the design cost, $Cos{t}_{ED}$, in Figure 7.

The IQFRG proposed in $Cos{t}_{AD}$ and $Cos{t}_{ED}$, the two representative design costs in Figure 7, was confirmed to require the lowest design costs while showing remarkable improvement rates of 337% and 105%, respectively, compared to the best existing research.

Table 5 compares the performances and design costs of reversible gate-based D-latches. The proposed DQFRG and DIQFRG were found to be the best in all metrics and brought about great progress in design costs by significantly improving delay. The improvement rate for each metric is shown in Figure 8 and Figure 9.

Table 5. Performance and design cost comparison of reversible gate-based D-latches.

D-Latch Circuit	Cell Count	Area (µm2)	Delay (Clock Phase)	Ener. Diss. (10−2 eV)	$\mathit{C}\mathit{o}\mathit{s}{\mathit{t}}_{\mathit{A}\mathit{D}}$	$\mathit{C}\mathit{o}\mathit{s}{\mathit{t}}_{\mathit{E}\mathit{D}}$
[33]	137	0.128	4	3.29	2.04	173
[32]	133	0.114	4	4.26	1.82	290
[31]	106	0.107	4	2.77	1.72	123
[30]	59	0.056	4	2.76	0.90	122
DQFRG	46	0.035	2	2.07	0.14	17
DIQFRG	42	0.032	2	1.42	0.13	8

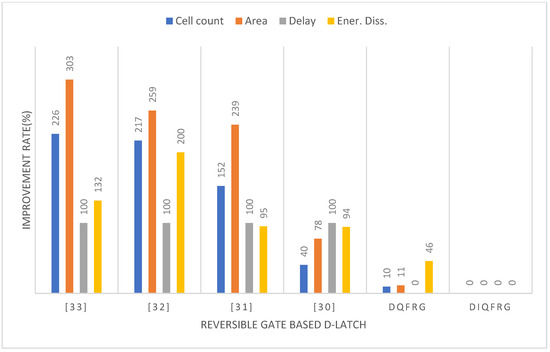
Figure 8. Performance improvement of proposed DQFRG and DIQFRG compared with typical reversible gate-based D-latches.

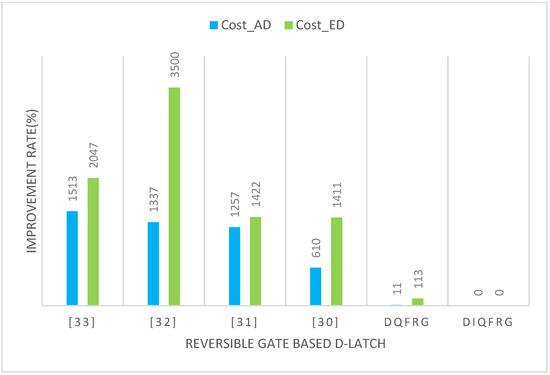
Figure 9. Improvement of design costs of proposed DQFRG and DIQFRG compared with typical reversible gate-based D-latches.

As shown in Figure 8, the proposed DIQFRG showed significant improvement rates of at least 40%, 78%, 100%, and 94% in cell count, area, delay, and energy dissipation. In addition, the proposed DIQFRG clearly demonstrated the superiority of the proposed structures by showing incredible improvement rates of 610% and 1411% in $Cos{t}_{AD}$ and $Cos{t}_{ED}$ compared to the best existing circuits.

5. Conclusions

The proposed research sought to efficiently design a Fredkin gate, a well-known reversible and universal logic gate. QCA was used to minimize design costs through fast switching speed and minimal use of area. For the first time, a perfectly symmetrical QFRG based on QCA MUX was proposed and then a modified vertically symmetrical IQFRG was proposed. All circuits were tested by well-known simulators, and the proposed IQFRG showed significant improvement rates of 337% and 105% in two design cost indices. Additionally, a D-latch was proposed using the structural characteristics of the proposed structures. The proposed DIQFRG demonstrated the superiority of the proposed structures by showing incredible improvement rates of 610% and 1411% in two design cost indices. In the modern digital computing era, the problem of power or energy dissipation is directly related to information loss and requires continuous research, and much attention is needed on the efficient design of QCA-based reversible gates and their applications to solve these problems.