Abstract
In continuous neural modeling, memristor coupling has been investigated widely. Yet, there is little research on discrete neural networks in the field. Discrete models with synaptic crosstalk are even less common. In this paper, two locally active discrete memristors are used to couple two discrete Aihara neurons to form a map called DMCAN. Then, the synapse is modeled using a discrete memristor and the DMCAN map with crosstalk is constructed. The DMCAN map is investigated using phase diagram, chaotic sequence, Lyapunov exponent spectrum (LEs) and bifurcation diagrams (BD). Its rich and complex dynamical behavior, which includes attractor coexistence, state transfer, Feigenbaum trees, and complexity, is systematically analyzed. In addition, the DMCAN map is implemented in hardware on a DSP platform. Numerical simulations are further validated for correctness. Numerical and experimental findings show that the synaptic connections of neurons can be modeled by discrete memristor coupling which leads to the construction of more complicated discrete neural networks.
1. Introduction
Neurons are the basic components of the nervous system and which form neural networks through complex connections [1,2]. Research has illustrated that neural networks composed of simulated neurons can be used to simulate many of the basic states of the human brain [3]. Therefore, it is highly meaningful that in-depth analysis and study of neuron simulation can provide insights into the operating mechanisms of the human brain [4]. Discrete and continuous systems are the main mathematical models used to describe the complex dynamical behavior of neurons [5,6]. Recently, chaotic systems have gained extensive interest [7,8]. Many researchers have made in-depth studies of continuous neurons by utilizing these systems [9]. Guo et al. [10] established a memristor-coupled HR and FHN neural network to analyze various discharge modes of the system. The numerical simulation results were verified by circuit simulation. Njitacke et al. [11] investigated a 4D Hopfield network of nerves with nonlinear synapse weights. A variety of complex dynamical behaviors were analyzed. These include the interesting Feigenbaum tree phenomenon [12,13]. Discrete neuron models, such as the Izhikevich model [14], the Rulkov model [15], and the Aihara model, have also been extensively studied. Ma et al. [16] analyzed complex phenomena such as multi-stability and multi-transient states by using two magnetically controlled memristors coupled to the Rulkov neuron model. Cao et al. [17] used discrete memristors to couple discrete Chialvo and Rulkov neurons to form a simple neural network. The equilibrium of this discrete map was studied, and its dynamical behavior was investigated by multiple methods with different parameters. Wang et al. [18] constructed a discrete memristor-coupled heterogeneous neural network by coupling KTz neurons and taboo learning neurons with locally active discrete memristors. The rich dynamical behaviors as well as multiple bursting patterns were analyzed, and multiple stability was demonstrated. Nobukawa et al. [19] introduced an extended Izhikevich neuron model that considered weakly periodic signals and analyzed their chaotic properties in detail. A large number of studies have shown that the discrete neuron model can simulate real biological neurons and even various states of certain pathological diseases [20]. It has become a research hotspot in recent years. Therefore, it is important to study the various dynamical behaviors of discrete neurons.
Memristors possess memory properties and synaptic plasticity [21,22,23,24,25,26], among other inherent properties [27,28,29,30]. Due to these unique electrical properties, they are well suited for modeling neuronal synapses [31,32,33]. In their latest research, Yang et al. [34] constructed a neural circuit model of sensorimotor control consisting of three memory HH neurons using a memristor, and applied it to robotic obstacle avoidance. Youn et al. [35] investigated the implementation of programmable threshold logic in the cross-gate array of a memristor. The internal logic of the memristor was better studied, which helped the next research on memristors. Lai et al. [36] used optoelectronic artificial synaptic devices with a ferroelectric Bi2FeCrO6 diode effect for neuromorphic computation by inducing synaptic plasticity through light signal activation. Obviously, their work has great significance. However, it was found that the synaptic plasticity of the memristor was much stronger. It could even simulate the information-processing patterns of the human brain [37,38]. This is very helpful in studying the various rich behaviors of neural networks. It is significant to construct a model of a memristor-coupled neural network. Therefore, many researchers have studied the complex dynamical behavior of memristor-coupled neural networks [39,40]. The majority of the research in recent years has been focused on the continuous type of memristor [41,42,43,44,45,46]. There are relatively few studies on discrete memristors [47]. Ren et al. [48] proposed a new discrete memristor model, built a new 3D hyperchaotic map by coupling, and investigated its dynamical behavior. Lu et al. [49] built a discrete memristor with sinusoidal conductance to apply it to a coupled Rulkov neuron map. The effects of coupling strength and control parameters on synchronization were investigated. Ma et al. [50] proposed a local active discrete memristor model and performed a series of dynamical analyses. It provided a good basis for further analyzing discrete memristors. Therefore, the research of discrete memristors and their application to discrete neural networks is very attractive and valuable [51,52].
Aihara neurons were first proposed in 1990 [53], and the model exhibits several very distinct nonlinear phenomena such as doubly periodic bifurcation and chaos. Tanaka et al. [54] proposed a new single-neuron model by extending Aihara’s model and observed the rupture phenomenon. Li et al. [55] considered a network of Aihara neurons coupled via electrical synapses. These efforts facilitated the study of discrete neurons. However, most studies have only considered the effects of individual Aihara neurons as well as electrical synapses. This is not sufficient to observe more dynamical behavior. Synaptic crosstalk is an important phenomenon in neural networks [56]. It is caused by the spillover of certain chemicals that carry information from one synapse to another [57,58,59,60]. In neural networks, the synaptic crosstalk effect makes its dynamical behavior extraordinarily complex [61]. Because the composition of one synapse affects the strength of neighboring synapses [62], existing research on this aspect is also not very extensive. Considering the above two problems, this paper introduces two memristors that have crosstalk with each other. The intention is to examine the complicated dynamical behavior of locally active discrete memristor-coupled neural networks. The internal mechanisms of neural networks are revealed. This is of vital relevance to the study of their complex dynamical behavior. Most of the current memristor-coupled neural network models only consider a single biological function and rarely take into account ubiquitous factors such as light, sound, and temperature [63]. This indicates that the study of neural network models and their chaotic dynamics is still in its infancy and needs to be further explored. However, the results of the study can provide a reference for the application of chaotic systems in biomedicine, image encryption, and confidential communication in the future [64,65,66,67,68]. This indicates that the research is of great significance. To this end, this paper is a relevant discussion. In this paper, the two-dimensional Aihara neuron is used as the object of study, and the related research work is carried out by using methods such as LEs, [69], BD, and phase diagrams. The innovations of this study are as follows:
(a) A DMCAN map for investigating chaotic dynamical behavior is constructed using two memristors as synapses coupling two neurons.
(b) The rich dynamical behavior demonstrated in DMCAN maps is studied by considering coefficients such as crosstalk intensity.
(c) A DSP platform is built which demonstrates the hardware circuit of the DMCAN map.
The rest of the paper is organized as follows. Section 2 discusses the Aihara neurons as well as the memristor and establishes the DMCAN map. Section 3 analyzes the multi-stability of the map. The state transfer phenomenon and complexity of the map are studied in Section 4. Section 5 describes the hardware implementation. The conclusion is presented in the final section.
2. Mathematical Model
2.1. Model of the Memristor
A model of the discrete memristor can be expressed below:
where W(φn) is the memductance, which is the reciprocal of the memristance; φn is the state flux of the memristor, which is the magnetic flux, and its relation to charge is included in the definition of the memristor; vn denotes the input voltage; and in denotes the output current. The internal state function is denoted by F(φ,v), which is a Lipschitz function. a, b, and c are the three constant parameters of the memristor, which are used to regulate the performance of the memristor in this research. The values of the three constant parameters were set after a lot of experiments to achieve a better performance of the memristor. The parameters are set as a = 0.1, b = 1, and c = 9.
A three-fingerprint characterization of the local active discrete memristor model was investigated using sinusoidal discrete voltage signals vn = Asin(ωn). A = 0.11, ω = 0.06, and φ0 = 0; the characteristic curve of vn and in with the number of iterations is presented in Figure 1a. The vn-in curves of the local active discrete memristor model are illustrated in Figure 1b–d. A = 0.11, f = 0 in Figure 1b. A = 0.11 and ω = 0.06 in Figure 1c. ω = 0.06 and f = 0 in Figure 1d. It can be seen that the curve shows a contraction of the pinch loop through the origin. When the frequency ω grows from 0.06 to 0.12, the hysteresis loop monotonically decreases in area. It gradually shrinks to a single-valued function with increasing frequency. As the amplitude A grows from 0.09 to 0.11, the hysteresis loop area monotonically enlarges. Obviously, the presented model satisfies the conditions of the generalized memristor.
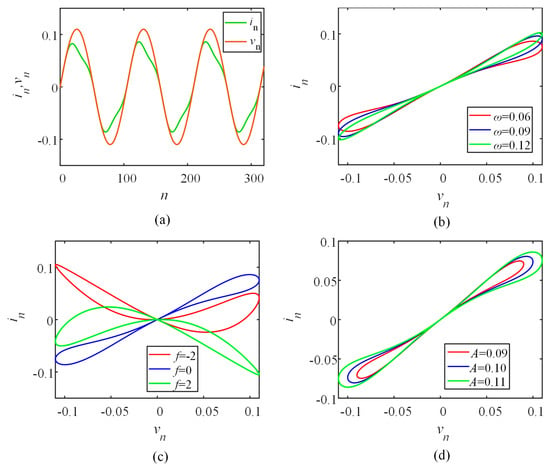
Figure 1.
(a) Chaotic sequence; (b–d) the pinch hysteresis loop.
Local active memristors have the advantages of simulating neuronal function, generating complex dynamical behaviors, and having a simple structure. Thus, localized active memristors have a greater potential for application in the field of brain-like computing. In order to verify that the proposed discrete memristor is locally active, the value of the variable φ was allowed to vary in the range (−2, 2). The DC V-I diagram is presented in Figure 2a. Obviously, it has three negative-slope areas and one positive-slope area and is, therefore, a localized active memristor.
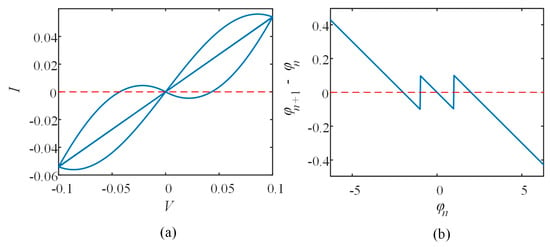
Figure 2.
(a) DC V-I plot over the region −2 < φ < 2; (b) the memristor POP plot with five balancing points.
The non-volatile nature of memristors gives them many advantages. These include fast read and write speeds, low power consumption, high density, durability, and stability, as well as value in applications such as neural networks and image processing. To demonstrate the non-volatile nature of the memristor, we drew a power-off plot (POP) as illustrated in Figure 2b. As can be seen from the figure, the POP curve of the local active discrete memristor has three negative slopes intersecting the x-axis. Five points crossing the x-axis, which indicates that the memristor has five equilibrium points. Among the asymptotically stable are the three negative slope equilibrium points, and the two positive slope equilibrium points are unstable. If its stabilization point is greater than two, then the proposed memristor is a non-volatile memristor.
2.2. DMCAN Map
The Aihara neuron is a common discrete neuron that is able to simulate many behaviors of neuronal systems. The chaotic discrete neuron model considered is as follows:
where x can be considered as the membrane potential of the neuron. y represents the cell membrane level of ions. n is the number of iterations. k1 and k2 are damping factors for neuronal refractoriness. The parameters a and b are positive constants, and f(u) = (1 + exp(−u/c)) − 1 is a logarithmic function for the steepness parameter c > 0.
The parameters k1 = 0.65, k2 = 0.11, a = 1, b = 0.8, and c = 0.05 and the initial values x0 = 0.2, y0 = −0.12 were set. The phase diagram shown in Figure 3a was plotted. k1 ranges from 0.2 to 1.8 and other values remain constant, the BD of which is shown in Figure 3b and the LEs of which is shown in Figure 3d. k1 = 0.62, and the chaotic sequence of the model is shown in Figure 3c.
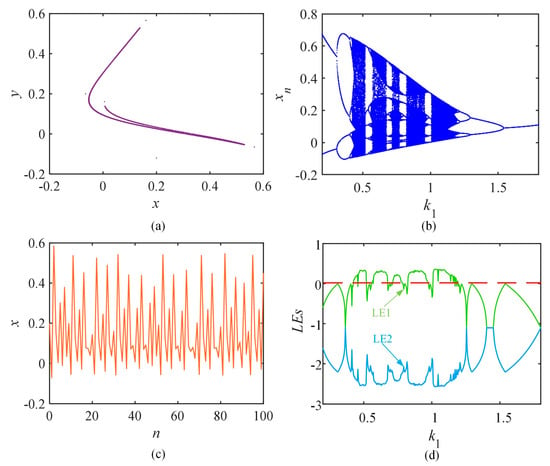
Figure 3.
Dynamical analysis of Aihara neuron simulation plots: (a) phase diagram; (b) BD; (c) chaotic sequence; and (d) LEs.
In a neural network, information is conveyed and switched by synaptic connections between neurons. Therefore, two local active discrete memristors were introduced between two 2D Aihara neurons to simulate synapses. Crosstalk existed between the two memristors. The model is shown in Figure 4, which constitutes the DMCAN map, and the map is formulated as follows:
where x, y, z, and m are the neuronal state variables, and f and g are the effects of the memristor. k is the coupling parameter between neurons. b1 and b2 are the crosstalk between the two memristors.
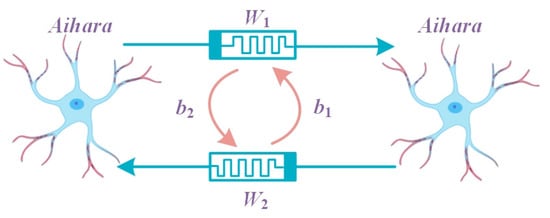
Figure 4.
Discrete memristor-coupled Aihara neuron topology.
2.3. Fixed-Point Characterization
Computing some stationary points may describe the stability of a discrete map that returns to itself after repeated iterations. Equation (3) is given as S = (x*, y*, z*, m*, f*, g*) for the stationary point, which leads to Equation (4).
The corresponding Jacobian matrix is given as follows:
where,
The DMCAN map parameters were set to (a, b, c, d, e, h, k, b1, b2) = (1.045, 0.8, 0.05, 0.62, 0.28, 0.11, 0.1, 0.1, 0.1). The equilibrium point calculated from the above equation and the given parameters is (8, 8, 8, 8, 8, 0, 0). The equilibrium equations are as follows:
The six eigenvalues obtained from the solution are as follows:
According to Equation (8), it can be seen that all eigenvalues satisfy |λ| < 1, and thus the map is unstable at this point.
3. Hidden Dynamical Analysis of DMCAN with Multi-Stability
In traditional continuous-time dynamical systems, attractor coexistence is often closely associated with chaotic states. In discrete-time systems, the phenomenon is much richer and more complex. A dynamical system is multi-stable if it is capable of producing more than one attractor with varying starting values. This kind of multi-stability is very common in nonlinear systems.
The study of the variation of map parameters is crucial for investigating the dynamical behavior of the map. During the course of this study, the system was found to have multiple stabilization phenomena in different ranges of different parameters. This chapter will analyze the hidden behavior of the system dynamics under different parameter variations by means of phase diagrams, BD, LEs, and chaotic sequences. Because the initial conditions and parameter settings have an important influence on the results, a large number of experiments and repeated validations were conducted. Eventually, it was found that several sets of parameters can make the whole memristor-coupled neural network system achieve more desirable results with richer dynamical behaviors and higher complexity, which is very helpful for subsequent neural network research.
3.1. Variation of the Crosstalk Strength b2
Assume that the two sets of initial conditions are (x0, y0, z0, m0, f0, g0) = (0.1, 0.1, 0, 0.1, 0, 0) and (x0, y0, z0, m0, f0, g0) = (0.1, −0.1, 0, −0.1, 0, 0). The parameters are specified as (a, b, c, d, e, h, k, b1) = (1.18, 0.8, 0.05, 0.62, 0.4, 0.11, 0.1, 0.1). b2 takes values in the range (0, 0.8). The corresponding BD and LEs are shown in Figure 5.
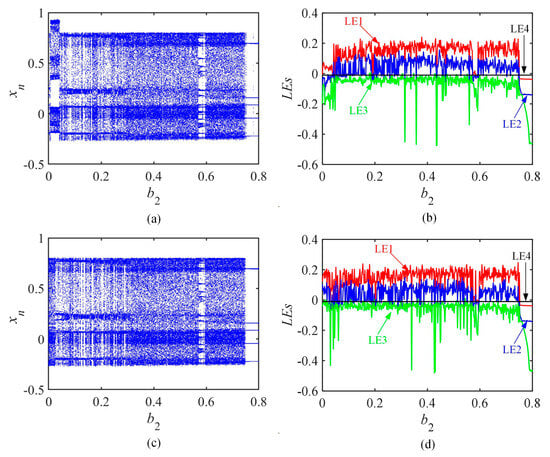
Figure 5.
The BD and LEs for different initial values when the crosstalk coefficient b2 changes. (a,b) values are (0.1, 0.1, 0, 0.1, 0, 0); (c,d) values are (0.1, −0.1, 0, −0.1, 0, 0).
As shown in Figure 5a,b, under the first set of parameters, it changes from chaos to hyperchaos. After a short period, it continues to be hyperchaos until it becomes periodic. As shown in Figure 5c,d, under the second set of parameters, there is not much difference from the first set. The difference is almost always in hyperchaos. It is easy to see that there are coexisting attractors under the two sets of parameters, which are next verified using the phase diagram. As shown in Figure 6, when the parameters b2 are 0.01, 0.456, and 0.779, the phase diagrams and the chaotic sequences of the coexisting attractors of different topologies can be obtained. There is still good correspondence. Figure 6a,b shows the coexistence of a chaotic attractor and a chaotic attractor. Figure 6c,d shows the coexistence of a chaotic attractor and a multi-periodic attractor. Figure 6e,f shows the coexistence of a multi-periodic attractor and a multi-periodic attractor. The three groups of coexisting phenomena nicely demonstrate the system’s complex dynamical behavior. The multiple stability is verified for the system.
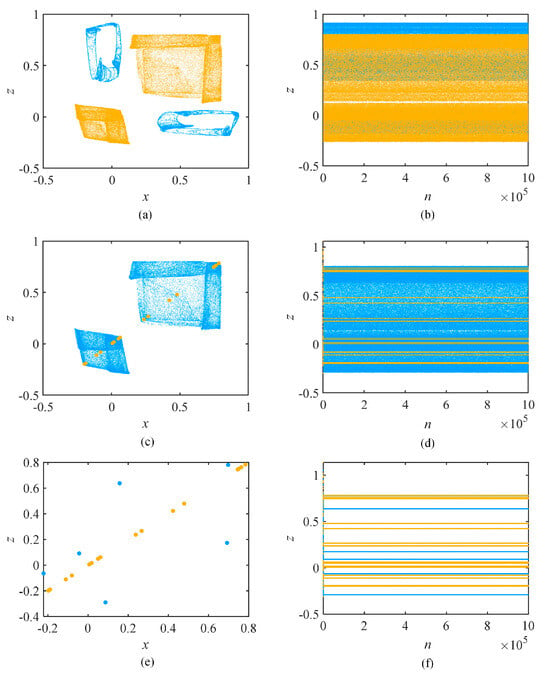
Figure 6.
Phase diagram and chaotic sequences of attractor coexistence. (a,b) b2 = 0.01; (c,d) b2 = 0.456; and (e,f) b2 = 0.779.
3.2. Variation of the Coupling Coefficient k between Neurons
Consider that the two sets of initial conditions are (x0, y0, z0, m0, f0, g0) = (0.1, 0.1, 0, 0.1, 0, 0) and (x0, y0, z0, m0, f0, g0) = (0.1, −0.1, 0, −0.1, 0, 0). The parameters are specified as (a, b, c, d, e, h, b1, b2) = (1.18, 0.8, 0.05, 0.62, 0.75, 0.11, 0.1, 0.1). The range of k is taken to be (0, 0.25). Then, the corresponding BD and LEs are shown in Figure 7.
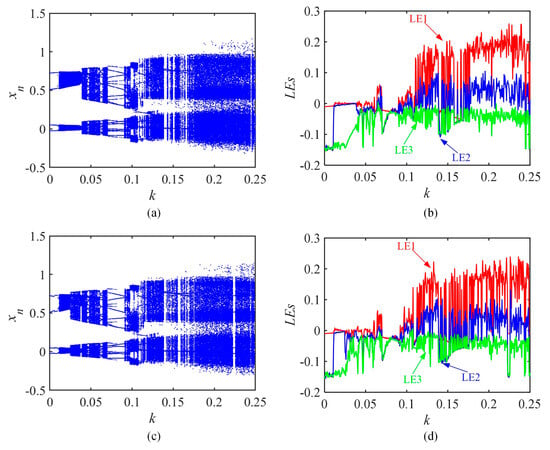
Figure 7.
The BD and LEs for different initial values for variations in the coupling parameter k. (a,b) values are (0.1, 0.1, 0, 0.1, 0, 0); (c,d) values are (0.1, −0.1, 0, −0.1, 0, 0).
As shown in Figure 7, under both sets of parameters, the early phase is less chaotic and relatively insignificant. The late phase remains almost always hyperchaotic except for a few cycles. Next, the phase diagram is used to verify the existence of coexisting attractors under both sets of parameters. In Figure 8, the value of parameter k is set to 0.025, 0.16, and 0.1149, correspondingly. Chaotic sequences of phase diagrams can be obtained for different topological structures as well as coexisting attractors. Still, the system is well presented by the study of k.
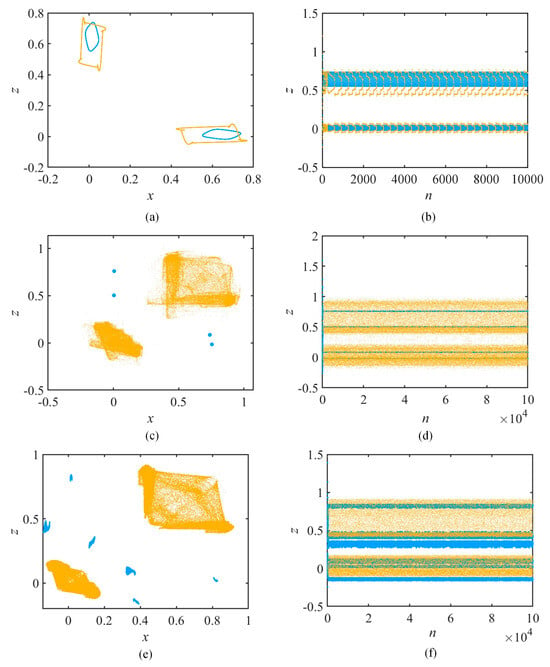
Figure 8.
Phase diagram and chaotic sequences of attractor coexistence. (a,b) k = 0.025; (c,d) k = 0.16; (e,f) k = 0.1149.
3.3. Variation of Neural Network System Parameter e
Suppose the two sets of initial conditions are (x0, y0, z0, m0, f0, g0) = (0.2, 0.2, 0.3, 0.3, 0.1, 0.1) and (x0, y0, z0, m0, f0, g0) = (0.2, 0.2, −0.3, 0.3, 0.1, 0.1) separately. The parameters are set to (a, b, c, d, h, k, b1, b2) = (1.045, 0.8, 0.05, 0.62, 0.11, 0.1, 0.1, 0.1). The value of e ranges from (0, 0.8). The corresponding BD and LEs are depicted in Figure 9.
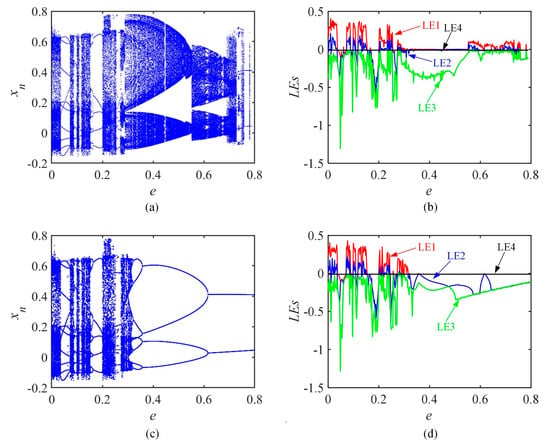
Figure 9.
BD and LEs for different initial values when the coefficient e varies. (a,b) values are (0.2, 0.2, 0.3, 0.3, 0.1, 0.1); (c,d) values are (0.2, 0.2, −0.3, 0.3, 0.1, 0.1).
As shown in Figure 9a,b, chaos, hyperchaos, and cycles alternate under the first set of parameters. Additionally, as shown in Figure 9c,d, under the second set of parameters, the three phenomena continue to alternate in the early stage, while the cycle is maintained afterward. The BD shows an interesting inverse doubling cycle bifurcation phenomenon. Coexisting attractors still exist under these two sets of parameters.
As shown in Figure 10, when the parameter e is 0.28, the phase diagram and the chaotic sequences for the coexistence of chaotic attractors and chaotic attractors can still be derived. Multi-stability is well reflected in these phenomena of the system.
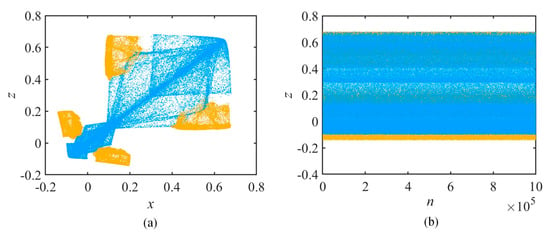
Figure 10.
(a) Phase diagram and (b)chaotic sequences of attractor coexistence for e = 0.28.
The Feigenbaum tree is a graphical method for describing the bifurcation structure of nonlinear maps with changing parameters. It depicts the transition of a system from simple through complex to chaotic, as well as the path to chaos. Its significance is to provide a tool to understand the phenomenon of chaos, revealing that even in seemingly chaotic and disordered systems, there exists a certain regularity and self-similarity. In the study of BD, the range of values of e remain at (0, 0.8) and the value of the system parameter a should be changed. Then the BD of e will show the interesting phenomenon of the Feigenbaum tree.
As shown in Figure 11, when the system parameter a = 1.145, there is a bubble with primary period 4. Then, the bubble keeps expanding until it bifurcates into a bubble with secondary period 8. As the system parameter a gradually increases, the bubble develops further until finally an infinite branching tree appears at a = 1.19 and grows into a fully mature tree. The evolutionary process of a complete Feigenbaum tree is perfectly presented. Consider the inverse multiplicative period bifurcation of Figure 9. The whole process consists of entering the periodic orbit through the reverse multiplicative period bifurcation path. As the control parameter a increases from the positive multiplicative cycle bifurcation path into chaos, it finally comes out of chaos through the inverse doubling period bifurcation path. The phenomenon enriches the dynamical behavior of the DMCAN map.
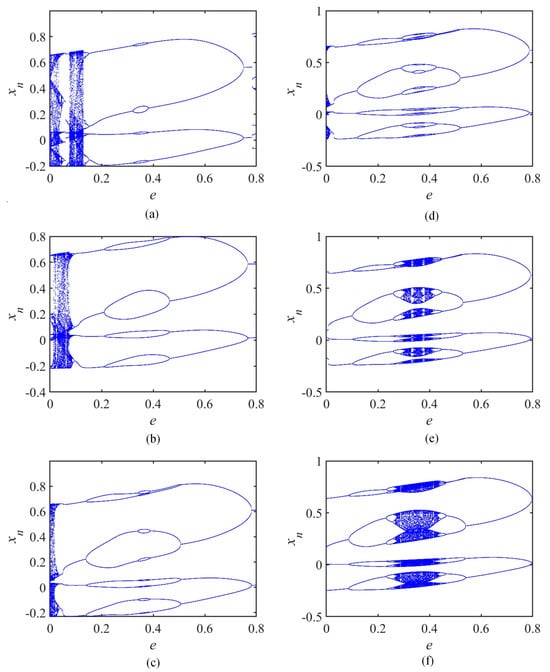
Figure 11.
The change of the value of the system parameter a; the BD of e shows the Feigenbaum tree phenomenon. (a) a = 1.145; (b) a = 1.16; (c) a = 1.175; (d) a = 1.18; (e) a = 1.185; and (f) a = 1.19.
4. State Transfer and Complexity
4.1. State Transfer
In chaotic systems, state transfer usually refers to the process of transitioning the system from one state of motion to another. At this time, the parameters are fixed as well as the initial values. The state may degenerate from a chaotic into a periodic state or change from a periodic into a chaotic state. The transitions between them can be abrupt and unpredictable. The phenomenon enriches the complex dynamical properties of the system. Suppose the initial condition is (x0, y0, z0, m0, f0, g0) = (0.1, 0.1, 0, 0.1, 0, 0) and the parameters are set to (a, b, c, d, e, h, k, b1, b2) = (1.18, 0.8, 0.05, 0.62, 0.4, 0.11, 0.1, 0.1, 0.584). The chaotic sequence is shown in Figure 12a, where it can be seen that the system realizes the transition between chaotic and periodic states in a small range. Figure 12b,c is the phase diagram of the corresponding state.
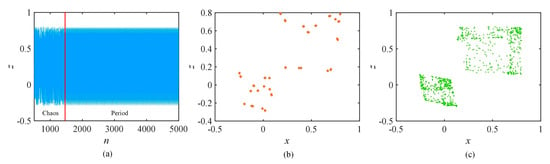
Figure 12.
The state transfer in the DMCAN map. (a) the chaotic sequence map; (b,c) the corresponding attractor phase maps.
4.2. SE Complexity Analysis
Chaotic system complexity is determined by the degree of proximity between sequences of chaos and sequences of randomness by means of an algorithm of correlation. The chaotic state corresponds to the brain’s regular working state in a neural network system, while the periodic state corresponds to the brain’s pathological behavior. Therefore, the increasing complexity denotes the approach to the mechanism of regular operation. At this time, chaotic sequences are closer to random sequences and have good resistance to interference and interception. The sequence corresponds to a high-security level. The system of entropic complexity (SE) of the spectrum is used for the analysis. SE utilizes the distribution of energy in the Fourier transform field to capture the entropy value of the spectrum. A high SE value indicates a relatively complex sequence.
With the initial value fixed at (0.1, 0.1, 0, 0.1, 0, 0), the parameters are specified as (a, b, c, d, e, h, k) = (1.18, 0.8, 0.05, 0.62, 0.4, 0.11, 0.1). The set complexity varies with parameters in the horizontal and vertical range (−2, 2). As illustrated in Figure 13a, the complexity varies with the variation of parameters b1 and b2. The largest value of SE is 0.9 when parameters b1 and b2 are varied, and an improved chaotic performance of the system is achieved. The above initial values as well as the parameters remain unchanged. With b1 = 0.1 and b2 = 0.1 set, the complexity SE with initial values x0 and z0 is shown in Figure 13b. The complexity varying with initial values x0 and f0 is shown in Figure 13c. It can be seen that the maximum value of SE is still around 0.9, and the complexity is high in most regions. The red region with high parameter interval complexity should be chosen as much as possible in the figure. The system may generate chaotic attractors in this region when taking the relevant parameters, while the blue region has lower parameter interval complexity. The analysis shows that the system is more complex.
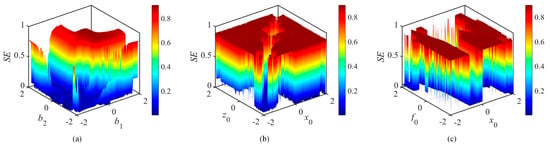
Figure 13.
Three-dimensional SE complexity images of the system, (a) varying with crosstalk coefficients b1, b2; (b) varying with initial values x0 and z0; and (c) varying with initial values x0 and f0.
5. DSP Implementation
Hardware realization of chaotic systems is very critical for putting them into engineering applications. DSP is simple and strongly programmable. It is utilized to achieve a DMCAN map using TMS320F28335 as the central controlling unit.
The digital signals are converted to analog signals by applying the relevant program by means of a two-channel D/A translator and feeding this into an oscilloscope. This proves that a practical stage can be used to realize the complicated chaotic phenomena produced. The DSP hardware map is depicted in Figure 14, with a set of initial values (0.2, 0.2, 0.3, 0.3, 0.1, −0.1) and with parameters set to (e, b2) = (0.1, 0.01). The remaining parameters are the same as in Section 3.3. The phase diagram in Figure 15a can be obtained. Figure 15b then shows its corresponding final experimental result realized by the DSP oscilloscope. The DSP hardware realization is described in Figure 16.
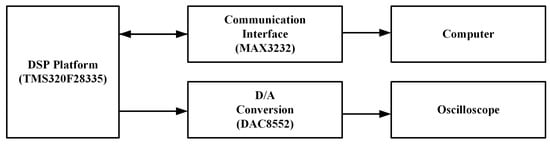
Figure 14.
DSP hardware diagram.
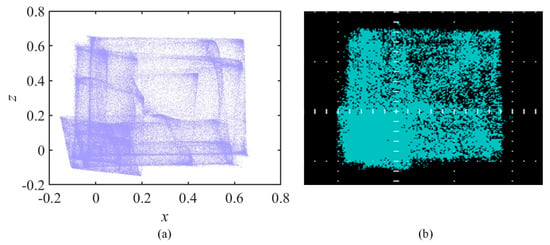
Figure 15.
(a) phase diagram. (b) corresponding hardware realization results.

Figure 16.
DSP implementation platform.
6. Conclusions
It is demonstrated that the map of discrete memristor-coupled Aihara neurons built in this paper has a diverse range of complex behaviors. Synaptic crosstalk in neural networks is realized by memristor synaptic coupling. It is observed that different crosstalk strengths and coupling coefficients lead to different attractor coexistences in the system. These include the coexistence of chaotic attractors, the coexistence of periodic attractors, and the coexistence of chaotic and periodic attractors. These findings highlight the multi-stability behavior of the DMCAN map. The discussion of the multiplicative period bifurcation and the Feigenbaum tree phenomenon found for parameter e further enriches the dynamical behavior of the DMCAN map. In addition, the state transfer phenomenon and SE complexity of the system reflect the better complexity of the system. Finally, these attractors have been successfully achieved on the DSP stage for better application of the research in biomedical and other fields. Next will be to advance the application of DMCAN maps in various fields such as biomedicine and other practical applications.
Author Contributions
Conceptualization, D.L. and Y.C.; methodology, D.L. and Y.C.; software, D.L. and Y.C.; validation, D.L. and Y.C.; formal analysis, D.L. and Y.C.; investigation, J.L. and K.W.; resources, D.L., Y.C., J.L. and K.W.; data curation, D.L. and Y.C.; writing—original draft preparation, D.L.; writing—review and editing, Y.C.; visualization, J.L. and K.W.; supervision, Y.C.; project administration, J.L. and K.W.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Research on an Electronic Component Assembly Robot (Grant Nos. 2022JJ12GX018), Research on a Small Electronic Component Assembly Robot (Grant Nos. LJKZ0524), and technological innovation projects in the field of artificial intelligence in Liaoning province (Grant Nos. 2023JH26/10300011).
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The authors thank the referees for their detailed reading and comments that were both helpful and insightful.
Conflicts of Interest
There are no conflicts of interest about the publication from all of the authors.
References
- Sun, J.; Li, C.; Wang, Z.; Wang, Y. A memristive fully connect neural network and application of medical image encryption based on central diffusion algorithm. IEEE Trans. Ind. Inform. 2023, 20, 3778–3788. [Google Scholar] [CrossRef]
- Mou, J.; Ma, T.; Banerjee, S.; Zhang, Y. A novel memcapacitive-synapse neuron: Bionic modeling, complex dynamics analysis and circuit implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1771–1780. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Sun, J.; Du, S.; Deng, Z.; Deng, Q. A review of chaotic systems based on memristive Hopfield neural networks. Mathematics 2023, 11, 1369. [Google Scholar] [CrossRef]
- Lv, M.; Ma, J. Multiple modes of electrical activities in a new neuron model under electromagnetic radiation. Neurocomputing 2016, 205, 375–381. [Google Scholar] [CrossRef]
- Han, X.; Mou, J.; Lu, J.; Banerjee, S.; Cao, Y. Two discrete memristive chaotic maps and its DSP implementation. Fractals 2023, 31, 2340104. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Wang, J.; Banerjee, S.; Li, P. Dynamical analysis of a novel fractional-order chaotic system based on memcapacitor and meminductor. Fractal Fract. 2022, 6, 671. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Sun, Y. A universal variable extension method for designing multiscroll/wing chaotic systems. IEEE Trans. Ind. Electron. 2023, 71, 7806–7818. [Google Scholar] [CrossRef]
- Ma, Y.; Mou, J.; Banerjee, S.; Miao, M. A quartic nonlinear flux-controlled memristor model and its application in chaotic system. Appl. Comput. Math. 2023, 22, 317–337. [Google Scholar]
- Han, Z.; Sun, B.; Banerjee, S.; Mou, J. Biological neuron modeling based on bifunctional memristor and its application in secure communication. Chaos Solitons Fractals 2024, 184, 115020. [Google Scholar] [CrossRef]
- Guo, Z.-H.; Li, Z.-J.; Wang, M.-J.; Ma, M.-L. Hopf bifurcation and phase synchronization in memristor-coupled Hindmarsh–Rose and FitzHugh–Nagumo neurons with two time delays. Chin. Phys. B 2023, 32, 038701. [Google Scholar] [CrossRef]
- Njitacke, Z.; Kengne, J. Communications. Complex dynamics of a 4D Hopfield neural networks (HNNs) with a nonlinear synaptic weight: Coexistence of multiple attractors and remerging Feigenbaum trees. AEU Int. J. Electron. Commun. 2018, 93, 242–252. [Google Scholar]
- Zhang, S.; Zeng, Y. A simple Jerk-like system without equilibrium: Asymmetric coexisting hidden attractors, bursting oscillation and double full Feigenbaum remerging trees. Chaos Solitons Fractals 2019, 120, 25–40. [Google Scholar] [CrossRef]
- Bier, M.; Bountis, T.C. Remerging Feigenbaum trees in dynamical systems. Phys. Lett. A 1984, 104, 239–244. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [PubMed]
- Rulkov, N.F. Regularization of synchronized chaotic bursts. Phys. Rev. Lett. 2001, 86, 183. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Mou, J.; Al-Barakati, A.A.; Jahanshahi, H.; Miao, M. Hidden dynamics of memristor-coupled neurons with multi-stability and multi-transient hyperchaotic behavior. Phys. Scr. 2023, 98, 105202. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Banerjee, S.; Cao, Y.; Mou, J. A discrete Chialvo–Rulkov neuron network coupled with a novel memristor model: Design, Dynamical analysis, DSP implementation and its application. Chaos Solitons Fractals 2024, 179, 114466. [Google Scholar] [CrossRef]
- Wang, M.; Mou, J.; Qin, L.; Jahanshahi, H. A memristor-coupled heterogeneous discrete neural networks with infinite multi-structure hyperchaotic attractors. Eur. Phys. J. Plus 2023, 138, 1137. [Google Scholar] [CrossRef]
- Nobukawa, S.; Nishimura, H.; Yamanishi, T.; Liu, J.-Q. Analysis of chaotic resonance in Izhikevich neuron model. PLoS ONE 2015, 10, e0138919. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Hu, G.; Guan, Z.-H.; Iu, H.H.-C. Constructing multiscroll memristive neural network with local activity memristor and application in image encryption. IEEE Trans. Cybern. 2024, 54, 4039–4048. [Google Scholar] [CrossRef]
- Kong, X.; Yu, F.; Yao, W.; Cai, S.; Zhang, J.; Lin, H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: Image encryption and FPGA implementation. Neural Netw. 2024, 171, 85–103. [Google Scholar] [CrossRef]
- Yu, F.; Kong, X.; Yao, W.; Zhang, J.; Cai, S.; Lin, H.; Jin, J. Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor. Chaos Solitons Fractals 2024, 179, 114440. [Google Scholar] [CrossRef]
- Tang, D.; Wang, C.; Lin, H.; Yu, F. Dynamics analysis and hardware implementation of multi-scroll hyperchaotic hidden attractors based on locally active memristive Hopfield neural network. Nonlinear Dyn. 2024, 112, 1511–1527. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Y.; Iu, H.H.-C.; Wang, N.; Bao, H.J. Locally active memristor-based neuromorphic circuit: Firing pattern and hardware experiment. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3130–3141. [Google Scholar] [CrossRef]
- Ji, X.; Dong, Z.; Han, Y.; Lai, C.S.; Zhou, G.; Qi, D. EMSN: An energy-efficient memristive sequencer network for human emotion classification in mental health monitoring. IEEE Trans. Consum. Electron. 2023, 69, 1005–1016. [Google Scholar] [CrossRef]
- Ji, X.; Dong, Z.; Han, Y.; Lai, C.S.; Qi, D. A brain-inspired hierarchical interactive in-memory computing system and its application in video sentiment analysis. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 7928–7942. [Google Scholar] [CrossRef]
- Ma, Y.; Mou, J.; Jahanshahi, H.; Alkhateeb, A.F.; Bi, X. Design and DSP implementation of a hyperchaotic map with infinite coexisting attractors and intermittent chaos based on a novel locally active memcapacitor. Chaos Solitons Fractals 2023, 173, 113708. [Google Scholar] [CrossRef]
- Wang, X.; Cao, Y.; Li, H.; Li, B. A chaos-enhanced fractional-order chaotic system with self-reproduction based on a memcapacitor and meminductor. Fractal Fract. 2023, 7, 582. [Google Scholar] [CrossRef]
- Mou, J.; Han, Z.; Cao, Y.; Banerjee, S. Discrete second-order memristor and its application to chaotic map. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2824–2828. [Google Scholar] [CrossRef]
- Han, Z.; Al-Barakati, A.A.; Jahanshahi, H.; Mou, J. A novel circuit based on memristor-memcapacitor with extreme multistability. Nonlinear Dyn. 2024, 112, 4863–4877. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Lin, H.J. Memristive Hopfield neural network dynamics with heterogeneous activation functions and its application. Chaos Solitons Fractals 2024, 178, 114387. [Google Scholar] [CrossRef]
- Wang, C.; Tang, D.; Lin, H.; Yu, F.; Sun, Y. High-dimensional memristive neural network and its application in commercial data encryption communication. Expert Syst. Appl. 2024, 242, 122513. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Chen, G. Design and performance analysis of discrete memristive hyperchaotic systems with stuffed cube attractors and ultraboosting behaviors. IEEE Trans. Ind. Electron. 2023, 71, 7819–7828. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, F.; Zhang, X.; Chen, P.; Wang, Y.; Zhu, J.; Ding, Y.; Cheng, L.; Li, C.; Jiang, H. Firing feature-driven neural circuits with scalable memristive neurons for robotic obstacle avoidance. Nat. Commun. 2024, 15, 4318. [Google Scholar] [CrossRef] [PubMed]
- Youn, S.; Lee, J.; Kim, S.; Park, J.; Kim, K.; Kim, H.J. Programmable threshold logic implementations in a memristor crossbar array. Nano Lett. 2024, 24, 3581–3589. [Google Scholar] [CrossRef] [PubMed]
- Lai, X.-C.; Tang, Z.; Fang, J.; Feng, L.; Yao, D.-J.; Zhang, L.; Jiang, Y.-P.; Liu, Q.-X.; Tang, X.-G.; Zhou, Y.-C. An adjustable multistage resistance switching behavior of a photoelectric artificial synaptic device with a ferroelectric diode effect for neuromorphic computing. Mater. Horizons 2024, 11, 2886–2897. [Google Scholar] [CrossRef]
- Qi, A.-X.; Zhu, B.-D.; Wang, G.-Y. Complex dynamic behaviors in hyperbolic-type memristor-based cellular neural network. Chin. Phys. B 2022, 31, 020502. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Banerjee, S.; Cao, Y. Analysis of the functional behavior of fractional-order discrete neuron under electromagnetic radiation. Chaos Solitons Fractals 2023, 176, 114113. [Google Scholar] [CrossRef]
- Ma, M.-L.; Xie, X.-H.; Yang, Y.; Li, Z.-J.; Sun, Y.-C. Synchronization coexistence in a Rulkov neural network based on locally active discrete memristor. Chin. Phys. B 2023, 32, 058701. [Google Scholar] [CrossRef]
- Zhang, J.; Liao, X. Synchronization and chaos in coupled memristor-based FitzHugh-Nagumo circuits with memristor synapse. AEU-Int. J. Electron. Commun. 2017, 75, 82–90. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Yang, X.; Zi, X.; Xiao, F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn. 2022, 108, 1697–1717. [Google Scholar] [CrossRef]
- Li, C.; Li, H.; Xie, W.; Du, J. A S-type bistable locally active memristor model and its analog implementation in an oscillator circuit. Nonlinear Dyn. 2021, 106, 1041–1058. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, C.; Zhou, L. A novel no-equilibrium hyperchaotic multi-wing system via introducing memristor. Int. J. Circuit Theory Appl. 2018, 46, 84–98. [Google Scholar] [CrossRef]
- Guo, M.; Zhu, Y.; Yang, R.; Zhang, M.; Zhao, K.; Yang, H.; Dou, G. A single-T chaotic circuit based on a physical memristor. Eur. Phys. J. Spéc. Top. 2022, 231, 3163–3170. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zheng, J.; Wang, X.; Zeng, Z.; Chen, G. Generating any number of diversified hidden attractors via memristor coupling. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4945–4956. [Google Scholar] [CrossRef]
- Fu, H.; Hong, Q.; Wang, C.; Sun, J.; Li, Y. Solving non-homogeneous linear ordinary differential equations using memristor-capacitor circuit. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4495–4507. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, X.; Wu, H.; Iu, H.H.-C.; Parastesh, F.; Wang, N. ReLU Function-Based Locally Active Memristor and Its Application in Generating Spiking Behaviors. IEEE Trans. Circuits Syst. II Express Briefs 2024. [Google Scholar] [CrossRef]
- Ren, L.; Mou, J.; Banerjee, S.; Zhang, Y. A hyperchaotic map with a new discrete memristor model: Design, dynamical analysis, implementation and application. Chaos Solitons Fractals 2023, 167, 113024. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, C.; Deng, Q. Rulkov neural network coupled with discrete memristors. Netw. Comput. Neural Syst. 2022, 33, 214–232. [Google Scholar] [CrossRef]
- Ma, M.; Yang, Y.; Qiu, Z.; Peng, Y.; Sun, Y.; Li, Z.; Wang, M. A locally active discrete memristor model and its application in a hyperchaotic map. Nonlinear Dyn. 2022, 107, 2935–2949. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Zhang, Y.; Cao, Y. A new hyperchaotic map based on discrete memristor and meminductor: Dynamics analysis, encryption application, and DSP implementation. IEEE Trans. Ind. Electron. 2023, 71, 5094–5104. [Google Scholar] [CrossRef]
- Ren, L.; Qin, L.; Jahanshahi, H.; Mou, J. Infinitely many coexisting attractors and scrolls in a fractional-order discrete neuron map. Int. J. Bifurc. Chaos 2023, 33, 2350197. [Google Scholar] [CrossRef]
- Aihara, K.; Takabe, T.; Toyoda, M. Chaotic neural networks. Phys. Lett. A 1990, 144, 333–340. [Google Scholar] [CrossRef]
- Tanaka, H.; Ushio, T.; Kawanami, S. A high-dimensional chaotic discrete-time neuron model and bursting phenomena. Phys. Lett. A 2003, 308, 41–46. [Google Scholar] [CrossRef]
- Li, S.; He, Y.; Cao, H. Necessary conditions for complete synchronization of a coupled chaotic Aihara neuron network with electrical synapses. Int. J. Bifurc. Chaos 2019, 29, 1950063. [Google Scholar] [CrossRef]
- Leng, Y.; Yu, D.; Hu, Y.; Yu, S.S.; Ye, Z. Dynamic behaviors of hyperbolic-type memristor-based Hopfield neural network considering synaptic crosstalk. J. Nonlinear Sci. 2020, 30, 033108. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Xiong, K.; Li, Z.; He, S. Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk. Chin. Phys. B 2024, 33, 028706. [Google Scholar] [CrossRef]
- Kloek, T. The Effect of Dendritic Spine Morphology on Synaptic Crosstalk: Two Multisynapse Models, Integrating Diffusion on Curved Surfaces. Master’s Thesis, The Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Kawahara, M.; Kato-Negishi, M.; Tanaka, K. Cross talk between neurometals and amyloidogenic proteins at the synapse and the pathogenesis of neurodegenerative diseases. Metallomics 2017, 9, 619–633. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, A.N.; Triller, A.; Sieghart, W. GABAA receptors: Post-synaptic co-localization and cross-talk with other receptors. Front. Cell. Neurosci. 2011, 5, 7. [Google Scholar] [CrossRef] [PubMed]
- Qiu, R.; Dong, Y.; Jiang, X.; Wang, G. Two-neuron based memristive hopfield neural network with synaptic crosstalk. Electronics 2022, 11, 3034. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Wang, M.; Ma, M. Dynamic behavior in memristor coupled Hindmarsh–Rose and Fitzhugh–Nagumo neurons with synaptic crosstalk. Indian J. Phys. 2023, 98, 1043–1059. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Deng, Q.; Xu, C.; Deng, Z.; Zhou, C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn. 2021, 106, 959–973. [Google Scholar] [CrossRef]
- Sha, Y.; Mou, J.; Banerjee, S.; Zhang, Y. Exploiting flexible and secure cryptographic technique for multi-dimensional image based on graph data structure and three-input majority gate. IEEE Trans. Ind. Inform. 2023, 20, 3835–3846. [Google Scholar] [CrossRef]
- Zhang, Z.; Mou, J.; Banerjee, S.; Cao, Y. A chaotic hierarchical encryption/watermark embedding scheme for multi-medical images based on row–column confusion and closed-loop bi-directional diffusion. Chin. Phys. B 2024, 33, 020503. [Google Scholar] [CrossRef]
- Chen, X.; Mou, J.; Cao, Y.; Banerjee, S. Chaotic multiple-image encryption algorithm based on block scrambling and dynamic DNA coding. Int. J. Bifurc. Chaos 2023, 33, 2350190. [Google Scholar] [CrossRef]
- Wang, L.; Banerjee, S.; Cao, Y.; Mou, J.; Sun, B. A new self-embedding digital watermarking encryption scheme. Nonlinear Dyn. 2024, 112, 8637–8652. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, N.; Sun, B.; Cao, Y.; Mou, J. Novel self-embedding holographic watermarking image encryption protection scheme. Chin. Phys. B 2024, 33, 050501. [Google Scholar] [CrossRef]
- Shimada, I.; Nagashima, T. A numerical approach to ergodic problem of dissipative dynamical systems. Prog. Theor. Phys. 1979, 61, 1605–1616. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).