Abstract
The swift advancement in communication technology alongside the rise of the Medical Internet of Things (IoT) has spurred the extensive adoption of diverse sensor-driven healthcare and monitoring systems. While the rapid development of healthcare systems is underway, concerns about the privacy leakage of medical data have also attracted attention. Federated learning plays a certain protective role in data, but studies have shown that gradient transmission under federated learning environments still leads to privacy leakage. Therefore, we proposed secure and efficient federated learning schemes for smart healthcare systems. In this scheme, we used Paillier encryption technology to encrypt the shared training models on the client side, ensuring the security and privacy of the training models. Meanwhile, we designed a zero-knowledge identity authentication module to verify the authenticity of clients participating in the training process. Second, we designed a gradient filtering compression algorithm to eliminate locally updated gradients that were irrelevant to the convergence trend and used computationally negligible compression operators to quantize updates, thereby improving communication efficiency while ensuring model accuracy. The experimental results demonstrated that the proposed scheme not only had high model accuracy but also had significant advantages in communication overhead compared with existing schemes.
1. Introduction
The rapid development of the Internet of Things (IOT) has made smart life a reality. At the same time, the development of smart devices also brings more convenience to people’s lives as these devices have more advanced sensors and computing and communication capabilities. As a result, they can enable a variety of IoT applications, such as smart healthcare [], smart transportation [], and smart cities []. Alongside the emergence of machine learning (ML) [], the abundant data collected from end devices presents a multitude of opportunities for valuable research and practical applications.
Secure use of personal healthcare data is critical in the current healthcare system. In traditional machine learning methods, data collected by mobile devices are first uploaded to cloud servers or data processing centers before being processed. For example, smart wearable devices and smartphones can continuously detect a user’s heart rate, blood pressure, etc., and can send these data to a medical center for further diagnosis. However, due to the explosive growth of IoT data on the web, transferring large volumes of IoT data to remote servers may not be feasible due to the network resources required and the latency incurred. The substantial volume of health monitoring data stored in cloud centers presents a significant risk of privacy breaches, given its sensitive nature involving personal privacy. Addressing these challenges, distributed machine learning [] has emerged as a prominent research area. Compared with traditional machine learning methods, distributed machine learning enables training of larger models on massive data but is still vulnerable to security and privacy leakage. Secure and open access to these isolated data centers becomes the biggest challenge when managing a central global model. The proposal of federated learning (FL) [] has marked a new paradigm for machine learning, where multiple data holders (such as cell phones, IoT devices, or healthcare organizations) collaborate to train a model without sharing the data, exchanging only the training parameters at intermediate stages. Chen et al. [] designed a migrating federated learning framework for wearable medical device healthcare with good scalability. In Wu et al. [], a federated learning framework for home health monitoring was designed to enable personalized monitoring. Although the feature of uploading only the gradient without uploading the raw data makes federated learning naturally protective of users’ private data, there is still a risk of privacy leakage in federated learning scenarios []. First, untrustworthy servers have the right to access a large amount of auxiliary knowledge (e.g., model structure, initialization parameters, etc.) of each participant’s locally trained model, as Zhu et al. [] found that a malicious attacker was able to steal the raw training data based on the partially updated gradient information. Second, federated learning participants themselves are untrustworthy, and malicious participants colluding with untrustworthy servers can reveal more precise private information about other users or tamper with computational results []. Also, due to limited broadband costs and other communication constraints, some edge nodes may not be able to connect directly to the global learning model, especially in large-scale and complex mobile edge networks. The global model is exclusively distributed to the clients engaged in the network []. Mobile devices frequently operate offline, posing challenges for maintaining direct connectivity between the global model and the client model []. Unreliable servers can attempt to infer personal information from users’ local updates, posing a threat to users’ privacy.
For this reason, we proposed a secure and efficient federated learning scheme for smart healthcare systems. We used homomorphic encryption to process uploaded gradients, ensuring the security and privacy of the shared model without sacrificing model training accuracy. Second, we constructed an identity authentication module to reduce the possibility of malicious clients joining the training. Simultaneously, we designed a gradient selection filtering algorithm to filter out locally updated gradients that were irrelevant to the convergence trend and adopted computationally negligible compression operators to quantize update parameters to reduce the communication overhead.
The main contributions of this paper are as follows:
- Enhancing the security of federated learning while reducing the likelihood of malicious clients joining the training process. This paper proposes a secure and efficient federated learning scheme for smart healthcare systems. The scheme introduces homomorphic encryption to ensure the security of gradient updates at each node and to prevent the server from accessing the privacy of the model after aggregation. Combining with the Schnorr zero-knowledge proof (ZKP) identity authentication module ensures the authenticity and reliability of the clients participating in the training.
- Reducing communication overhead. This paper designs a gradient selection filtering algorithm to filter out parameters that are irrelevant to local convergence and uses computationally negligible compression operators to quantitatively update the parameters, which reduces the number of communications while lowering the communication overhead.
- The experimental results on commonly used datasets show that the algorithm in the paper achieves an effective balance between communication efficiency, privacy protection, and model accuracy.
2. Related Work
Healthcare data sharing serves as the foundation for collaboration among diverse healthcare organizations, yet its privacy implications also stand as a primary barrier to data sharing among these entities. Therefore, addressing the issue of information leakage in federated learning is crucial. For the privacy leakage risk faced by federated attacks, existing schemes are mainly based on the following three techniques: differential privacy, secure multiparty computation, and homomorphic encryption.
2.1. Differential Privacy
Differential privacy [] is a rigorously provable mathematical framework that makes it impossible for an attacker to infer privacy data by analyzing the output by adding well-designed noise to the parameters that need to be preserved during the federated learning training process. Huang et al. [] proposed a differential privacy federated learning framework, DP-FL, to address the issue of imbalanced data among clients. This framework sets different differential privacy budgets for each user’s data and shows certain advantages in imbalanced datasets. Wei et al. [] designed a staged differential privacy preservation model, NbAFL, where at the end of the local model training and parameter uploading stage, each terminal adds a noise to satisfy the centered differential privacy preservation noise for its own update parameters, which can achieve the optimal convergence performance at a fixed privacy preservation level. Li et al. [] proposed a federated learning scheme for solving the multi-point fmri problem, and the scheme uses differential privacy to solve the privacy leakage problem. Choudhury et al. [] also proposed a scheme for healthcare data preservation in conjunction with differential privacy. However, the noise added in the above scheme impacts both the accuracy of the model and the convergence speed, resulting in increased model convergence time and reduced accuracy.
2.2. Secure Multiparty Computation
Secure multiparty computation facilitates federated learning, allowing mutually untrusted parties to collaborate securely without revealing their raw data, even in the absence of a trusted third party. Bonawitz et al. [] proposed a secure aggregation scheme for federated learning, which uses dual masking and secret sharing to protect model parameters. However, in this scheme, the server cannot detect malicious participants uploading incorrect parameters, thus failing to ensure the availability of the federated learning model. The federated learning scheme combined with secure multi-party computing requires multiple rounds of interactions between participants to achieve secure aggregation, and it cannot bear the huge computational and communication pressure for resource-constrained participants. Fang et al. [] proposed an efficient federated learning framework in conjunction with secure multi-party computation, and the scheme developed a streamlined encryption protocol to protect privacy while designing optimization policies to improve efficiency. However, secure multi-party computation relies on a large number of ciphertext computations and security proofs, which severely restricts the computational efficiency and fails to provide privacy preservation during the model release phase.
2.3. Homomorphic Encryption
Homomorphic encryption [] not only provides strong privacy protection for data transmission but also ensures that the accuracy of the model training is consistent with that of centralized training. Based on this, Phong et al. [] proposed a federated learning privacy protection scheme PPDL based on additive homomorphic encryption mechanism. The scheme consists of any terminal generating a key pair and sharing it with other terminals; the terminal encrypts and uploads the local gradient with a public key, the central server computes the ciphertext additive homomorphic and sends it downstream, and the terminal decrypts the ciphertext using the private key to obtain the updated global gradient. However, since all terminals share the private key, once a terminal obtains the ciphertext sent by other terminals, it is able to decrypt it to obtain the corresponding plaintext information. Ren et al. [] introduced an advanced security protocol aimed at enhancing the security and privacy of IoT systems. Due to the higher computational cost of homomorphic encryption, the computational efficiency of the above schemes is significantly lower, while the communication overhead is relatively increased. Lee et al. [] proposed a federated learning framework for patient similarity in conjunction with homomorphic encryption.
2.4. Communication
In FL, devices are trained on local datasets and then aggregated on cloud servers. But in large networks, FL suffers from huge propagation delays. Devices that are far away from the cloud server will face a communication bottleneck []. To solve this problem, Caldas et al. [] uses a lightweight lossy compression technique to reduce the communication overhead from server to client. Wang et al. [] choose to filter out local updates that are not relevant to the convergence trend, achieving high performance in communication while ensuring learning convergence. Asad et al. [] proposed a communication-efficient homomorphic encryption federated learning scheme CEEP-FL by combining the gradient selection mechanism from CMFL [] with the homomorphic encryption system NIZKP-HC based on non-interactive zero-knowledge proofs to minimize communication costs. Although the scheme significantly reduces the number of communication rounds, the selected clients still upload complete model update parameters, so the communication volume remains unchanged. Asad et al. [] use a sparse compression algorithm to improve the communication efficiency, while combining homomorphic encryption and differential privacy ensures security.
In general, these three techniques are commonly used in federated learning frameworks. Each of these techniques has its own advantages and disadvantages, and different privacy preservation schemes have to be designed according to specific scenarios. In order to address security concerns in healthcare systems, we designed a new federated learning scheme to balance model accuracy, communication efficiency, and privacy preservation.
3. Preliminary
3.1. Federated Learning
The main idea of federated learning is that the client directly uses local data for training, and the trained model is uploaded to the central server, which performs an aggregation operation on all the collected client models to generate a global model, after which the global model is sent down to the client. The above training pattern is repeated until the model converges.
Federated learning enables decentralized machine learning services by distributing the training phase across participants. Localized model training allows users to avoid exposing their data to enterprises or other participants, giving federated learning a clear advantage in client data privacy protection. The federated learning architecture is shown in Figure 1. In a complete training process, the central server initially transmits the initial global model to multiple clients. Upon receiving the global model, clients utilize their local training datasets to train local models. Subsequently, clients upload their local update parameters to the central server. Finally, the central server further aggregates and averages these parameters to obtain a new global model.
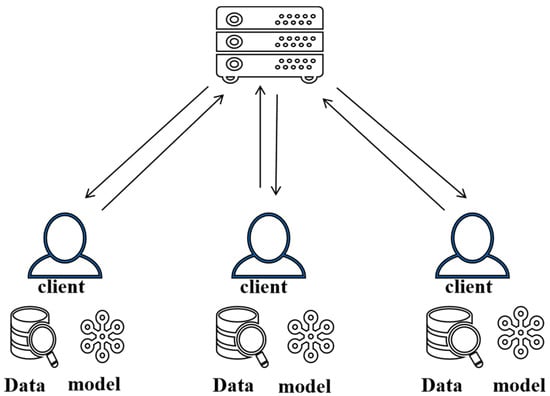
Figure 1.
Federated learning framework.
3.2. Paillier Homomorphic Encryption
The Paillier homomorphic encryption algorithm is a public key encryption scheme that allows homomorphic computations to be performed on the encrypted domain, i.e., performing mathematical operations on the ciphertext without decryption. This makes it possible to perform a series of operations, including addition and multiplication, in the encrypted state and decrypt the result correctly to obtain a result that matches the plaintext operation. The Paillier cryptosystem is described as follows:
KenGen: Choose two large prime numbers and that satisfy . Compute , , randomly selecting that satisfy . Defining Functions , then compute . The public and private key pairs can be expressed as .
ENC: For any plaintext , randomly generate a number that satisfies , computing plaintext .
DEC: Given that the aggregated ciphertext corresponds to an aggregated plaintext of .
3.3. Natural Compression
Natural compression [] is a function based on random logarithmic rounding , . When , suppose that satisfies , then
where probability . The IEEE 754 standard binary32 (single-precision floating-point format) or binary64 (double-precision floating-point format) is the most commonly used format for 32- or 64-bit computers; this includes the 1-bit sign bit , 8-bit (or 11-bit) index bit , and remaining 23-bit (or 52-bit) trailing bits . Any one can be expressed as , where is bit 0 or 1, count . When , we can obtain , . If x is represented by binary32, we can obtain . Clearly, can be obtained from x without any computation, i.e., by deleting the tail m and exponentiating according to the probability, and according to the probability to the exponent e + 1. x is the unbiased estimate of natural compression operator that satisfies .
4. Problem Definition
4.1. System Model
The system model of this program is shown in Figure 2.
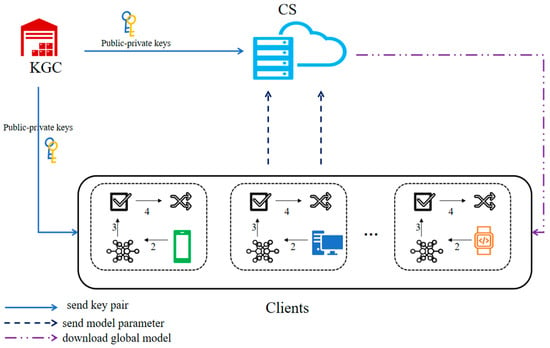
Figure 2.
Overview of system model.
KGC (key generation center): Independent and trusted, responsible for generating, distributing, and managing all keys in the system.
CS (cloud server): Responsible for providing privacy computation services to clients, collecting gradients submitted by clients, and aggregating them to obtain an optimized global model.
Clients: Train local models using their respective local data under the coordination of CS and encrypt the parameters to upload them to CS; receive the parameters sent by CS and decrypt them.
4.2. Threat Model
Both the server and clients are untrustworthy (honest and curious) entities. Centralized servers and devices involved in federated learning will faithfully adhere to the designed training protocol and will not actively inject false messages into the training process. However, they are curious about the private data of the target device and may infer private information from the shared data during the training process. Access to shared model updates allows an adversary to launch a reconstruction attack to reconstruct the original training data or use an inference attack to obtain whether data records exist in the original training dataset. Therefore, strict privacy guarantees need to be provided to defend against the above privacy attacks. An external adversary can eavesdrop on messages transmitted during training and attempt to infer the data privacy of each participant but cannot interrupt the message transmission process or inject toxic data.
4.3. Design Goal
Confidentiality: Since the model constructed by each participant contains its own private information, it should be guaranteed that the server cannot obtain this data privacy from the data it receives, i.e., the server is allowed to train the global model without revealing the local gradients of the participants, while the participants are not able to infer the data of other participants from the global model. In addition, an external adversary cannot infer data from eavesdropping messages.
Verifiability: Dishonest clients may share invalid or harmful data, and it is important to verify the identity of clients. Therefore, the verifiability design should be able to verify the client identity and ensure the legitimacy of clients participating in the training
Efficiency: The core of federated learning is to train models on distributed devices, so it is crucial to ensure the communication efficiency of transferring data between devices. And federated learning usually faces challenges such as uneven data distribution and differences in device performance, so the efficient design should be able to quickly adapt to different data distributions and device conditions to achieve fast model convergence.
5. Proposed Scheme
The main steps of the program are as follows:
- (1)
- Client selection phase: The server sets the authenticated user as the client participating in the training.
- (2)
- Key distribution phase: The KGC broadcasts the public key pk and publishes the private key sk and the system parameters v to the client over a secure channel.
- (3)
- Client computing phase: The client runs the SGD (stochastic gradient descent) algorithm to train the local model and runs the gradient filtering compression algorithm to update the local model. The clients encrypt the local models before uploading them to the server.
- (4)
- Aggregation phase: The server computes the aggregation result after receiving encrypted updates from all clients, then performs the federated averaging process on the aggregation result to obtain the updated global model.
- (5)
- Global model update phase: The server broadcasts the global model to all clients.
The entire federated learning process iterates until the global model converges.
5.1. Model Parameter Encryption
Federated learning exposes model parameters to the server during model transfer, and global model parameters issued by the server are also available to each client. An attacker can launch a reconstruction attack to invert the original data through the shared parameters.
To solve this problem, our scheme invokes Paillier homomorphic encryption against untrustworthy servers. The public and private keys are generated by the KGC (Key Generation Center) and distributed to each client before the start of training; each client encrypts the local gradient and uploads it after the start of training, and the server receives the ciphertext and then aggregates all the received ciphertexts. The server can have the ciphertext decrypted to obtain the plaintext after aggregation, but the plaintext is the aggregated information, and the server cannot determine the gradient information of local individuals. Therefore, the scheme not only prevents the leakage of user training set information but also effectively protects the privacy preservation of gradient vectors of each participant.
5.2. Schnorr Zero-Knowledge Proof Identity Authentication
If the user’s public key is obtained maliciously and random perturbation noise is added to the decrypted data, it will result in meaningless computations or make it impossible for the server to distinguish the correctness of the received results. Therefore, it is also important to verify the authenticity of the client’s identity.
The traditional authentication mechanism consists of two entities, the user and the server. The server has all the user’s identity information, and hence, it is easy to obtain the user’s information. At the same time, the signature information that the user sends to the server for authentication may be intercepted by the attacker to compute the user’s identity information, resulting in the leakage of the user’s information. Our proposed Schnorr zero-knowledge-based authentication mechanism can better solve the above problems. Zero-knowledge proof [] refers to the ability of a prover to convince an authenticator that an assertion is correct without presenting any useful information to the authenticator. The Schnorr mechanism [] is a zero-knowledge proof mechanism based on the discrete logarithm puzzle. In the authentication module of this paper, the client C is required to prove to the server S that it possesses a digital signature ( and ) on the identity information without revealing any useful information about and to prove the authenticity of the identity. The public parameters are as follows: is any prime number, the generating element is , the public key is , and the possessed private key is . The authentication process is shown in Figure 3 and described as follows.

Figure 3.
The authentication process.
- (1)
- Client C signature: First, C encrypts a message using , chooses a random number and computes ; second, hash operation is performed on (, ) to obtain the corresponding hash value ; then, is computed; and finally, the signature (, ) is generated and sent to the verifier S.
- (2)
- Server S verification: Calculate and verify . If equal, the authentication passes; otherwise, it fails.
The verification process is to prove . First, prove that . Bringing into yields
And because of , we obtain . Substituting into Equation (2) yields , so .
5.3. Gradient Filtering Compression Algorithm
The correlation between the global update and local update parameters is first calculated. The gradient correlation formula is
The higher the correlation, the more local updates follow the global optimization direction; the lower the correlation, the fewer local updates affect the global optimization. By setting a threshold to prevent clients from uploading irrelevant local updates, unnecessary communication overhead is reduced, while the impact on model accuracy is minimized. To further reduce communication costs, a natural compression operator is used to perform compression on the filtered gradient. The gradient filtering compression algorithm is implemented as follows (Algorithm 1).
| Algorithm 1 Gradient filtering compression algorithm |
| Inputs: client index , update gradient , original gradient , correlation threshold |
| Output: updated gradient after client filter compression |
| 1. Calculated according to Equation (3) |
| 2. If |
| 3. return null |
| 4. else |
| 5. Compute the local model update to be used in the next round of communication |
| 6. Quantize using the natural compression operator |
| 7. Return |
Scheme [] demonstrates that the variance of the natural compression operator is only and therefore hardly affects the model convergence speed. The gradient filtering compression algorithm improves the model convergence speed by selecting only strongly correlated gradient updates, and each gradient update is then quantized by the natural compression operator, thus reducing the communication overhead.
After the training starts, the client runs the stochastic gradient descent algorithm to train the local model based on the local dataset and runs the gradient filtering compression algorithm at the same time in the following steps:
Step 1: Client computes the gradient in a given communication round , where is the minimization loss function of the SGD algorithm, is the training sample of participant , and is the global model weight.
Step 2: Client performs a gradient filtering compression algorithm to compute the next round of communication local model update correlation . If , return to step 1; otherwise, perform step 3.
Step 3: Calculate local update parameters where is the local model weight of client in the round of communication and is the learning rate.
Step 4: Client computes local model updates , then quantizes the local model update, as .
6. Experiments
The experimental environment was Ubuntu 18.04 system, Intel(R) Core (TM) i7-7700HQ CPU @ 2.80 GHz, GTX 1050Ti GPU, 16 GB RAM; the federated learning model was trained using the Pytorch 1.10.0 framework; and the gmpy2 python extension module was used to implement the Paillier encryption.
The experimental dataset used the MNIST dataset and the CIFAR10 dataset. MNIST was a handwritten dataset containing 60,000 training samples and 10,000 test samples, each of which was a 28 × 28 grayscale digital image; the CIFAR10 dataset contained 50,000 training samples and 10,000 test samples, each of which consisted of a 32 × 32 pixel image with three different RGB channels. The network structure used a conventional neural network (CNN) consisting of three 3 × 3 convolutional layers and two fully connected layers. Its specific structure is shown in Table 1. The hyperparameters settings in federated learning are shown in Table 2.

Table 1.
Specific structure of the network model.

Table 2.
Federated learning hyperparameters configuration.
Comparison Experiments: The proposed scheme used FedAvg [], PPDL [], CEEP-FL [], and SEFL [] as comparison experiments. Among them, FedAvg is the original federated learning scheme without adding privacy preservation, PPDL is the classical scheme that provides privacy preservation to federated learning frameworks using homomorphic encryption, and CEEP-FL and SEFL are the most recent schemes that currently improve the efficiency on the basis of considering privacy preservation in federated learning scenarios.
6.1. Accuracy
Model accuracy is one of the important indicators of model performance. In order to test the advantage of the scheme of this paper on the impact of the accuracy of the calculation results, the accuracy of the proposed scheme was compared with that of the contrast experiments on different datasets under the same parameter settings as shown in Table 1. The comparison is illustrated in Figure 4 and Figure 5.
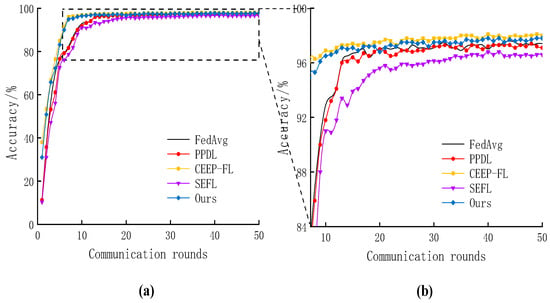
Figure 4.
Comparison of accuracy among different approaches on MNIST. (a) Accuracy comparison. (b) Enlarged view of local details.
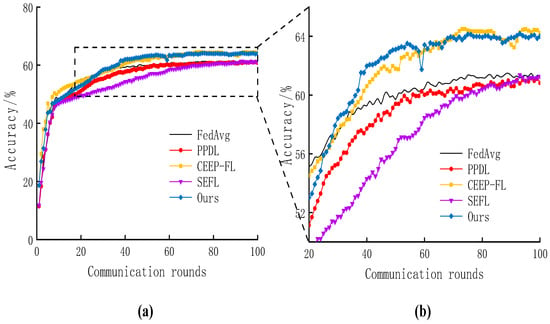
Figure 5.
Comparison of accuracy among different approaches on CIFAR10. (a) Accuracy comparison. (b) Enlarged view of local details.
On MNIST, FedAvg achieved an accuracy of 97.4%; PPDL, utilizing Paillier homomorphic encryption to protect model parameters, achieved an accuracy of 97.3%; CEEP-FL, employing non-interactive zero-knowledge proof homomorphic encryption mechanism NIZKP-HC and gradient update filtering mechanism, achieved an accuracy of 98.1%; and the SEFL algorithm utilized the gradient pruning technique, reducing parameters and floating-point operation, but incurred a loss of some weights, resulting in an accuracy drop to 96.5%. Our algorithm adopted an improved Paillier homomorphic encryption for protecting update parameters and designed a gradient filtering compression algorithm, achieving an accuracy of 97.8%.
On CIFAR10, the accuracy of FedAvg was 61.3%, SEFL dropped to 61.1% on the CIFAR10 dataset, PPDL reached 61% on the CIFAR10 dataset, CEEP-FL reached 64.2% on the CIFAR10 dataset, and our algorithm had an accuracy of set with an accuracy of 64%. Although our algorithm was slightly inferior to CEEP-FL in terms of accuracy, our algorithm achieved a significant improvement in model convergence speed, which also highlights our algorithm’s advantage in balancing accuracy and model convergence speed.
6.2. Communication Overhead
Communication overhead is a major challenge in federated learning. Employing encryption schemes during training increases both communication and computation overhead, thereby affecting training efficiency. To evaluate the advantage of our approach in terms of communication overhead, experiments compared the communication overhead of different approaches under the same number of client environments. The experiments selected encryption-based federated learning schemes PPDL, CEEP-FL, and SEFL as comparative experiments, with model update parameters represented in double-precision floating-point format. As shown in Figure 6, in a round of global updates, the increase in model weights resulted in higher communication overhead due to the PPDL and CEEP-FL algorithms encrypting all plaintext parameters using Paillier homomorphic encryption before uploading them to the server. On the other hand, the SEFL algorithm reduced the number of parameters that needed to be uploaded by approximately 40% through pruning techniques, thus reducing communication overhead. In contrast, our scheme compressed the parameter volume by quantizing them naturally before uploading them to the server, reducing communication overhead by up to approximately 70%, demonstrating significant advantages.
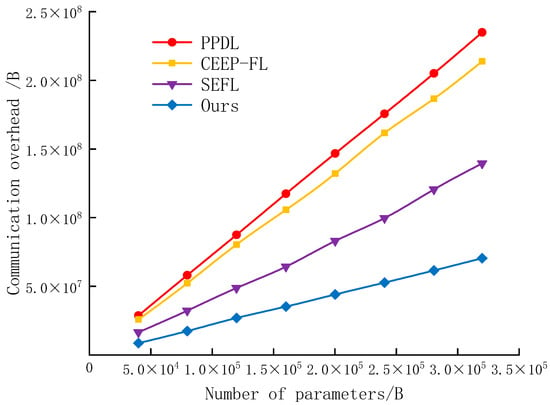
Figure 6.
Comparison of communication overhead.
Table 3 provides the specific communication overhead of different approaches given a certain model accuracy and dataset. On MNIST, when the accuracy reached 95%, PPDL incurred a communication overhead of 276.48 MB per client, while CEEP-FL reduced the communication overhead to 224.64 MB due to a reduction in the number of communications. SEFL required a communication cost of 259.19 MB. On CIFAR10, when the model accuracy reached 60%, PPDL incurred a communication overhead of 2519.5 MB per client, while CEEP-FL reduced the communication overhead to 174.6 MB. SEFL reduced the parameter volume through model pruning, resulting in a communication overhead of 2318.48 MB. Our scheme not only filtered irrelevant gradient updates to reduce the number of communications but also used natural compression operators to quantize ciphertexts, resulting in a communication overhead of only 172.84 MB on MNIST and 1274.1 MB on CIFAR10. In summary, our scheme effectively improved communication efficiency.

Table 3.
Communication overhead required to achieve the target accuracy of the global model (MB).
7. Conclusions
This paper proposed secure and efficient federated learning schemes for smart healthcare systems. In this scheme, we used Paillier encryption technology to encrypt the shared training models on the client side, ensuring the security and privacy of the training models. Meanwhile, we designed a zero-knowledge identity authentication module to ensure the authenticity of the client’s identity participating in the training. Second, we designed a gradient filtering compression algorithm to filter out locally updated gradients that were irrelevant to the convergence trend and used computationally negligible compression operators to quantize updates, thereby improving communication efficiency while ensuring model accuracy. The experimental results demonstrated that the solution achieved high accuracy and also exhibited significant advantages in terms of communication overhead. Wearable devices, as the largest consumer product type in the current IoT industry, supported by technologies like artificial intelligence, bring significant convenience to users’ daily lives. Their functionalities extend beyond simple daily management to include real-time health monitoring and provision of informed medical advice. Users are increasingly aware of the high sensitivity of data such as physiological indicators monitored by wearable devices, making it increasingly challenging for manufacturers and medical institutions to access these data. Additionally, there exists a data silo phenomenon among different institutions. The proposed scheme trains higher-quality health risk prediction models for wearable devices without compromising user privacy. This leads to more accurate health assessments for users, thereby further improving the service quality of wearable devices.
However, homomorphic encryption suffers from the problems of too large secret key and inefficient operation, and in practical applications, resource-constrained devices can hardly afford the extra computational overhead brought by encryption operations. In future work, more efficient privacy preservation federated learning architectures will be further designed.
Author Contributions
Conceptualization, C.S. and W.P.; methodology, C.S.; validation, Z.W.; formal analysis, C.S. and N.Y.; investigation, C.S. and W.P.; resources, W.P. and N.Y.; data curation, Z.W. and N.Y.; writing—original draft preparation, Z.W.; writing—review and editing, Z.W.; supervision, C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Fundamental Research Funds for the Universities of Henan Province NSFRF240310.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rauniyar, A.; Hagos, D.H.; Jha, D.; Håkegård, J.E.; Bagci, U.; Rawat, D.B.; Vlassov, V. Federated Learning for Medical Applications: A Taxonomy, Current Trends, Challenges, and Future Research Directions. IEEE Internet Things J. 2024, 11, 7374–7398. [Google Scholar] [CrossRef]
- Aggarwal, M.; Khullar, V.; Rani, S.; Prola, T.A.; Bhattacharjee, S.B.; Shawon, S.M.; Goyal, N. Federated Learning on Internet of Things: Extensive and Systematic Review. Comput. Mater. Contin. 2024, 79, 1795–1834. [Google Scholar] [CrossRef]
- Mohammadi, M.; Al-Fuqaha, A. Enabling Cognitive Smart Cities Using Big Data and Machine Learning: Approaches and Challenges. IEEE Commun. Mag. 2018, 56, 94–101. [Google Scholar] [CrossRef]
- Thomas, R.N.; Gupta, R. A Survey on Machine Learning Approaches and Its Techniques. In Proceedings of the 2020 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 22–23 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Klymash, M.; Kyryk, M.; Demydov, I.; Hordiichuk-Bublivska, O.; Kopets, H.; Pleskanka, N. Research on Distributed Machine Learning Methods in Databases. In Proceedings of the 2021 IEEE 4th International Conference on Advanced Information and Communication Technologies (AICT), Lviv, Ukraine, 21–25 September 2021; pp. 128–131. [Google Scholar] [CrossRef]
- Mcmahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Artificial Intelligence and Statistics; PMLR: New York, NY, USA, 2017; pp. 1273–1282. [Google Scholar]
- Chen, Y.; Qin, X.; Wang, J.; Yu, C.; Gao, W. FedHealth: A Federated Transfer Learning Framework for Wearable Healthcare. IEEE Intell. Syst. 2020, 35, 83–93. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, X.; Zhou, Z.; Zhang, J. FedHome: Cloud-Edge Based Personalized Federated Learning for In-Home Health Monitoring. IEEE Trans. Mob. Comput. 2022, 21, 2818–2832. [Google Scholar] [CrossRef]
- Kairouz, P.; Mcmahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and Open Problems in Federated Learning. Found. Trends Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Zhu, L.G.; Liu, Z.J.; Han, S. Deep Leakage from Gradients. Adv. Neural Inf. Process. Syst. 2019, 32, 14774–14784. [Google Scholar]
- Liu, Y.; Chen, H.; Liu, Y.; Li, C. Privacy-Preserving Techniques in Federated Learning. J. Softw. 2022, 33, 1057–1092. [Google Scholar]
- Niknam, S.; Dhillon, H.S.; Reed, J.H. Federated Learning for Wireless Communications: Motivation, Opportunities, and Challenges. IEEE Commun. Mag. 2020, 58, 46–51. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, B.; Sun, W.; Liu, Y.; Yu, Z. Cross-FCL: Toward a Cross-Edge Federated Continual Learning Framework in Mobile Edge Computing Systems. IEEE Trans. Mob. Comput. 2024, 23, 313–326. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep Learning with Differential Privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Huang, X.X.; Ding, Y.; Jiang, Z.L.; Qi, S.; Wang, X.; Liao, Q. DP-FL: A Novel Differentially Private Federated Learning Framework for the Unbalanced Data. World Wide Web 2020, 23, 2529–2545. [Google Scholar] [CrossRef]
- Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H.H.; Farokhi, F.; Jin, S.; Quek, T.Q.S.; Poor, H.V. Federated Learning with Differential Privacy: Algorithms and Performance Analysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3454–3469. [Google Scholar] [CrossRef]
- Li, X.; Gu, Y.; Dvornek, N.; Staib, L.H.; Ventola, P.; Duncan, J.S. Multi-site fMRI analysis using privacy-preserving federated learning and domain adaptation: ABIDE results. Med. Image Anal. 2020, 65, 101765. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, O.; Gkoulalas-Divanis, A.; Salonidis, T.; Sylla, I.; Park, Y.; Hsu, G.; Das, A. Differential privacy-enabled federated learning for sensitive health data. arXiv 2019, arXiv:1910.02578. [Google Scholar]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical Secure Aggregation for Privacy-Preserving Machine Learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar]
- Fang, C.; Guo, Y.; Wang, N.; Ju, A. Highly efficient federated learning with strong privacy preservation in cloud computing. Comput. Secur. 2020, 96, 101889. [Google Scholar] [CrossRef]
- Che, X.L.; Zhou, H.N.; Yang, X.Y. Efficient Multi-Key Fully Homomorphic Encryption Scheme from RLWE. J. Xidian Univ. 2021, 48, 87–95. [Google Scholar]
- Phong, L.T.; Aono, Y.; Hayashi, T.; Wang, L.; Moriai, S. Privacy-Preserving Deep Learning via Additively Homomorphic Encryption. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1333–1345. [Google Scholar] [CrossRef]
- Ren, W.; Tong, X.; Du, J.; Wang, N.; Li, S.C.; Min, G.; Zhao, Z.; Bashir, A.K. Privacy-Preserving using Homomorphic Encryption in Mobile IoT Systems. Comput. Commun. 2021, 165, 105–111. [Google Scholar] [CrossRef]
- Lee, J.; Sun, J.; Wang, F.; Wang, S.; Jun, C.; Jiang, X. Privacy-Preserving Patient Similarity Learning in a Federated Environment: Development and Analysis. JMIR Med. Inf. 2018, 6, e20. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Vincent, H. Poor Federated Learning for Internet of Things: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 1622–1658. [Google Scholar] [CrossRef]
- Caldas, S.; Konečny, J.; McMahan, H.B.; Talwalkar, A. Expanding the reach of federated learning by reducing client resource requirements. arXiv 2018, arXiv:1812.07210. [Google Scholar]
- Wang, L.; Wang, W.; Li, B. CMFL: Mitigating Communication Overhead for Federated Learning. In Proceedings of the 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, TX, USA, 7–10 July 2019; pp. 954–964. [Google Scholar] [CrossRef]
- Asad, M.; Moustafa, A.; Aslam, M. CEEP-FL: A Comprehensive Approach for Communication Efficiency and Enhanced Privacy in Federated Learning. Appl. Soft Comput. 2021, 104, 107235. [Google Scholar] [CrossRef]
- Asad, M.; Moustafa, A.; Ito, T. FedOpt: Towards Communication Efficiency and Privacy Preservation in Federated Learning. Appl. Sci. 2020, 10, 2864. [Google Scholar] [CrossRef]
- Horvóth, S.; Ho, C.Y.; Horvath, L.; Sahu, A.N.; Canini, M.; Richtárik, P. Natural compression for distributed deep learning. In Mathematical and Scientific Machine Learning; PMLR: New York, NY, USA, 2022; pp. 129–141. [Google Scholar]
- Dwivedi, A.D.; Singh, R.; Ghosh, U.; Mukkamala, R.R.; Tolba, A.; Said, O. Privacy preserving authentication system based on non-interactive zero knowledge proof suitable for Internet of Things. J. Ambient Intell. Hum. Comput. 2022, 13, 4639–4649. [Google Scholar] [CrossRef]
- Major, W.; Buchanan, W.J.; Ahmad, J. An authentication protocol based on chaos and zero knowledge proof. Nonlinear Dyn. 2020, 99, 3065–3087. [Google Scholar] [CrossRef]
- Mohammadi, S.; Sinaei, S.; Balador, A.; Flammini, F. Secure and efficient federated learning by combining homomorphic encryption and gradient pruning in speech emotion recognition. In Proceedings of the International Conference on Information Security Practice and Experience, Copenhagen, Denmark, 24–25 August 2023; Springer: Berlin, Heidelberg, 2023; pp. 1–16. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).