Safety-Critical Control for Control Affine Systems under Spatio-Temporal and Input Constraints

Abstract

Safety-critical control is a type of modern control task where potentially conflicting stability, safety, and input constraints coexist. In this paper, the Prescribed-Time Zeroing Control Barrier Function (PT-ZCBF) is introduced, which can be applied as a prescribed-time stability constraint in safety-critical control tasks. Furthermore, we formulate a PT-ZCBF-based Quadratic Program (QP), which is able to mediate the potentially conflicting constraints of safety-critical control. The solution of the newly designed QP, acting as the control input of a safety-critical system, can drive the closed-loop trajectories to converge in a user-defined prescribed time period while observing the safety and input constraints. Finally, we use the Adaptive Cruise Control (ACC) problem as an example of numerical simulation to evaluate the performance of the QP-based method.

1. Introduction

Safety-critical control is one of the most critical tasks in the research field of modern control theory. A safety-critical control problem often consists of spatio-temporal constraints and input constraints that are potentially conflicting [1]. Spatio-temporal constraints can be understood as the combination of spatial and temporal constraints [2]. Spatial constraints require the system states to converge in a surface or a point (stability constraint) while maintaining in a safe set (safety constraint). In addition, temporal constraints require the trajectories of the states to converge within a prescribed time period. Moreover, input constraints, e.g., saturation of actuators, are also unavoidable in reality.

In practice, an effective and efficient method in solving safety-critical control problems is to use Control Barrier Functions (CBFs) to describe spatio-temporal constraints [1]. The Zeroing Control Barrier Function (ZCBF) is a type of CBF that drives the value of a function to zero when the states approach the boundary of its predefined desired set. Using ZCBF-based methods, the system states can be rendered forward-invariant [2], which is a significant criterion for safety in control theory. Furthermore, ZCBFs can also be applied to describe stability constraints. In [3], it is shown that ZCBFs can guarantee asymptotic convergence to desired sets. Despite the advantages of ZCBF, it cannot fulfill the temporal specifications of safety-critical systems. As an alternative, the Finite-Time (convergence) Control Barrier Function (FCBF) [4] is proposed to ensure finite-time stability (FTS). Furthermore, fixed-time stability (FxTS) [5] control methods are also proposed, where the time of convergence is determined by various parameters and is independent of the initial condition [2]. Nevertheless, in the research field of safety-critical control, it is necessary to design control inputs that drive the system state to converge within a prescribed time period defined by the user, namely to achieve prescribed-time stability (PTS) [6,7,8,9] instead of FTS or FxTS. For instance, the space robot is required to catch the expired inhabited spacecraft within a prescribed time period [10]. Inspired by the advantages of ZCBF, we can extend its property of asymptotic stability (AS) to PTS via time transformation techniques. Hence, it is necessary to propose the Prescribed-Time (convergence) ZCBF (PT-ZCBF), which can be applied as a stability constraint function for a safety-critical control system.

From another perspective, it is a challenging problem to describe and solve a safety-critical control task under the coexistence of the prescribed-time stability constraint, safety constraint, and input constraints [2]. For example, the proposed methods in [1,2,4] only achieved exponential stability (ES), FTS, and FxTS, respectively, instead of PTS. In addition, although the authors of [11] designed a PTS controller, it failed to take the input constraints into consideration. A crucial approach of the current research is the application of a Quadratic Program (QP) to describe these constraints, which could be conflicting since a QP can find the optimal solutions to constrained optimization problems efficiently [1,12]. Therefore, in this paper, we aim at proposing a PT-ZCBF-based QP under safety and input constraints to address safety-critical control tasks.

Take the trajectory planning of a robot as an example [13,14]. A finite amount of goal sets with intersections are set up to constrain the trajectory of the robot. This is shown in Figure 1. The robot goes from the point Start into the circle $G_1$ within time $T_1$. Then, it goes from $G_1$ into $G_2$ within time $T_2$, and so on. Thus, the robot follows this trajectory with a prescribed time limit.

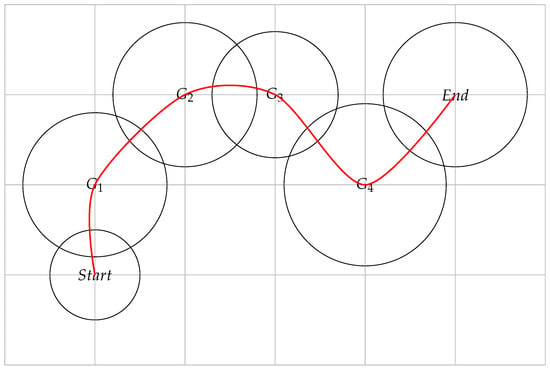
Figure 1. Trajectory planning sketch.

In this paper, we propose the PT-ZCBF to characterize the practical requirement that the system states converge within a prescribed time period, and obtain the control strategy via PT-ZCBF-based Quadratic Programs. To the best of the authors’ knowledge, the prescribed-time stability is realized in safety-critical control systems under safety and input constraints for the first time. Specifically, a time transformation technique is utilized to convert the normal ZCBF into the newly designed PT-ZCBF. This PT-ZCBF is incorporated as the prescribed-time stability constraint in QP. By introducing slack variables, we ensure the solvability of the QP such that the feasible control input always exists.

The remainder of the paper is organized as follows. The notations, preliminaries, and the main problem of the paper are demonstrated in Section 2. Then, the main results and the related proofs are illustrated in Section 3. Afterward, the Adaptive Cruise Control (ACC) problem is applied as an example of numerical simulation to evaluate the performance of the newly designed QP-based method in Section 4. Finally, the paper is concluded with possibilities for future research in Section 5.

2. Preliminaries and Problem Formulation

2.1. Notations

Let $\mathbb{R}$ denote the set of real numbers and ${\mathbb{R}}_{\ge 0}$ denote the set of non-negative real numbers. Let $∥·∥$ denote the Euclidean norm. We denote ${\left|x\right|}_{\mathcal{S}}={inf}_{y\in \mathcal{S}}∥x-y∥$ as the distance of a point $x\in {\mathbb{R}}^n\backslash \mathcal{S}$ from a set $\mathcal{S}$. Let ${\mathcal{C}}^k$ denote the set of k times continuously differentiable functions. We denote the Lie derivative of a ${\mathcal{C}}^1$ function $h:{\mathbb{R}}^n\to \mathbb{R}$ in a vector field direction $f:{\mathbb{R}}^n\to \mathbb{R}$ at $x\in {\mathbb{R}}^n$ as $L_{f}h\left(x\right):=\frac{\partial h}{\partial x}f\left(x\right)$. We define the following classes of functions [15].

Definition 1.

A continuous function $\alpha :[0,a)\to [0,\infty )$ belongs to class $\mathcal{K}$ if $\alpha \left(0\right)=0$ and it is strictly increasing.

Definition 2.

The class $\mathcal{K}$ function α belongs to class ${\mathcal{K}}_{\infty }$ if $a=\infty$ and $\alpha \left(r\right)\to \infty$ when $r\to \infty$.

Definition 3.

A continuous function $\beta :[0,a)\times [0,\infty )\to [0,\infty )$ belongs to class $\mathcal{K}\mathcal{L}$, if $\beta (r,s)$ belongs to class $\mathcal{K}$ in relation to r for each s and $\beta (r,s)$ is decreasing in relation to s for each r and $\beta (r,s)\to 0$ when $s\to \infty$.

Definition 4.

A continuous function $\alpha :(-b,a)\to (-\infty ,\infty )$ belongs to the extended class $\mathcal{K}$ for $a,b>0$ if $\alpha \left(0\right)=0$ and it is strictly increasing.

2.2. Preliminaries

2.2.1. Dynamic System

Consider a control affine system given by the differential equation

$$\dot{x}\left(t\right)=f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)u,x\left(t_0\right)=x_0$$

(1)

with the state vector $x\in {\mathbb{R}}^n$, and the input vector $u\in {\mathbb{R}}^m$. The system vector fields $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ and $g:{\mathbb{R}}^n\to {\mathbb{R}}^{n\times m}$ are assumed Lipschitz continuous. We denote $x\left(0\right)$ as the initial values of the states at $t=0$.

2.2.2. Goal Set and Safe Set

Define a set $\mathcal{S}\subset {\mathbb{R}}^n$, and its boundary and interior as

$$\begin{array}{c}\hfill \mathcal{S}=\left\{x\in {\mathbb{R}}^n:h\left(x\right)\le 0\right\},\end{array}$$

(2a)

$$\begin{array}{c}\hfill \mathrm{Int}\left(\mathcal{S}\right)=\left\{x\in {\mathbb{R}}^n:h\left(x\right)<0\right\},\end{array}$$

(2b)

$$\begin{array}{c}\hfill \partial \mathcal{S}=\left\{x\in {\mathbb{R}}^n:h\left(x\right)=0\right\}\end{array}$$

(2c)

with the continuously differentiable function $h:{\mathbb{R}}^n\to \mathbb{R}$.

We define the goal set

$$S_g=\left\{x\right|h_g\left(x\right)\le 0\}$$

(3)

and the safe set

$$S_s=\left\{x\right|h_s\left(x\right)\le 0\},$$

(4)

where the functions $h_g,h_s:{\mathbb{R}}^n\to \mathbb{R}$ are defined by the user. We need the following assumption for the theoretical analysis in Section 3.

Assumption 1

([2] (Assumption 1)). The sets $S_s\cap S_g\ne \varnothing$, and the functions $h_g,h_s\in {\mathcal{C}}^1$. The goal set $S_g$ is assumed to be compact. For the safe set $S_s$ and goal set $S_g$, it is assumed that their interiors are not empty. In addition, the function $h_g$ is proper in relation to the set $S_g$, i.e., a class ${\mathcal{K}}_{\infty }$ function ${\alpha }_g$ exists, which satisfies $h_g\left(x\right)\ge {\alpha }_g{\left(\right|x|}_{S_g}),\forall x\notin S_g$.

2.3. ZCBF and Its Properties

Garg et al. [2] use Nagumo’s Theorem on set invariance [16] to prove the safety (forward invariance) of $S_s$ for (1), where the following assumption in combination with the conditions of ZCBF is required.

Assumption 2

([2] (Assumption 2)). Consider the system (1). A control input u exists for all $x\in \partial S_s$, which satisfies

$$L_f{h}_s\left(x\right)+L_g{h}_s\left(x\right)u<0.$$

(5)

Assumption 2 appears in [1,17]. Its rationality can be obtained in [2] (Section III).

Next, the definition of ZCBF is presented.

Definition 5

([2] (Definition 1)). Consider the system (1) and a set $\mathcal{S}$, which is defined in (2) with a ${\mathcal{C}}^1$ function h. The function h is defined as a ZCBF on set $\mathcal{E}$ with $\mathcal{S}\subseteq \mathcal{E}\subset {\mathbb{R}}^n$, if an extended class $\mathcal{K}$ function α exists, which satisfies

$$\underset{u\in U}{inf}\left[L_{f}h\left(x\right)+L_{g}h\left(x\right)u\right]\le -\alpha \left(h\left(x\right)\right),\forall x\in \mathcal{E}$$

(6)

Note that the function $h_s$ satisfies (5) if it is a ZCBF with respect to the system (1). A special case of (6) is

$$\underset{u\in U}{inf}\left[L_{f}h\left(x\right)+L_{g}h\left(x\right)u\right]\le -\rho h\left(x\right),$$

(7)

where $\rho \ge 0$, as discussed in [1] (Remark 6). We need (7) for the QP formulation in Section 3.

In addition to forward invariance [1], another important property of ZCBF-based control is the ability to render the system states asymptotically stable. We now introduce a lemma that summarizes both important characteristics of ZCBFs.

Lemma 1

([3] (Theorem S5)). Consider the control affine system (1). The set $\mathcal{S}$ with a ${\mathcal{C}}^1$ function h is defined in (2). Then, any Lipschitz continuous controller u satisfying (6) for all $x\in \mathcal{E}$ will cause the set $\mathcal{S}$ to become asymptotically stable and forward-invariant, namely

• if $x\left(0\right)\notin \mathcal{S}$, then $x\left(t\right)$ converges to $\mathcal{S}$ when $t\to \infty$ (asymptotic stability);
• if $x\left(0\right)\in \mathcal{S}$, then $x\left(t\right)\in \mathcal{S},\forall t\ge 0$ (forward invariance).

Both properties are essential for the theoretical analysis in Section 3.

2.4. Prescribed-Time Stability and Time Transformation

Definition 6

([11] (Definition 1)). The dynamical system (1) is called prescribed-time stable if the states of (1) converge to a bounded set or a point in finite prescribed time $T\in (0,\infty )$ defined by the user.

In order to analyze prescribed-time stability, a commonly used technique is time transformation, where a finite-time interval $t\in [0,T)$ in domain t is converted into an infinite-time interval $s\in [0,\infty )$ in domain s [6,18,19]. We define the function $\lambda :{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{\ge 0}$ as

$$t=\lambda \left(s\right)$$

(8)

with $s\in [0,\infty )$, $t\in [0,T)$ such that

$$\begin{array}{c}\lambda \left(0\right)=0,\end{array}$$

(9a)

$$\begin{array}{c}{\lambda }^{\prime }\left(0\right)=1,\end{array}$$

(9b)

$$\begin{array}{c}{s}_1>s_2\ge 0\Rightarrow \lambda \left(s_1\right)>\lambda \left(s_2\right),\end{array}$$

(9c)

$$\begin{array}{c}\underset{s\to \infty }{lim}\lambda (s)=T,\end{array}$$

(9d)

$$\begin{array}{c}\underset{s\to \infty }{lim}{\lambda }^{\prime }(s)=0,\end{array}$$

(9e)

where ${\lambda }^{\prime }\left(s\right):=\frac{\mathrm{d}\lambda \left(s\right)}{\mathrm{d}s}$. With (9a) and (9b), the mapping from the set $s\in [0,\infty )$ to the set $t\in [0,T)$ is feasible. It can be implied from (9c) that the function $\lambda$ is strictly increasing. According to (9d) and (9e), we can conclude that the system (1) is prescribed-time stable in domain t if it is asymptotically stable in domain s.

2.5. Problem Formulation

We define the main problem as follows.

Problem 1.

Design a control input

$$u\left(t\right)\in \mathcal{U}=\{u\in {\mathbb{R}}^m|u_{mi{n}_i}\le u_i\le u_{ma{x}_i},i=1,2,\dots ,m\}$$

(10)

of the system (1), such that the trajectories of the closed-loop system converge to the goal set $S_g$ in user-defined prescribed time T. Meanwhile, the states $x\left(t\right)$ should always remain in the safe set $S_s$ for all $x_0\in S_s$ and $t\ge 0$.

3. Main Results

We present the main results of this paper and the related proofs in this section. First, we introduce our design of the Prescribed-Time (convergence) ZCBF (PT-ZCBF) via the time transformation technique. Afterward, we propose the QP-based formulation, using PT-ZCBF as a constraint function. We prove the feasibility of the QP and the continuity of its solution under certain conditions, which are necessary to prove that Problem 1 can be solved by the QP solution under certain conditions. All the main results in this section are demonstrated under Assumptions 1 and 2.

3.1. PT-ZCBF and Its Properties

In this subsection, we propose the definition of PT-ZCBF, showing its property of prescribed-time stability.

We define PT-ZCBF as follows.

Definition 7.

Consider the system (1). Consider a set $\mathcal{S}$ with a ${\mathcal{C}}^1$ function h defined as in (2). The function h is a PT-ZCBF on set $\mathcal{E}$ with $\mathcal{S}\subseteq \mathcal{E}\subset {\mathbb{R}}^n$, if an extended class $\mathcal{K}$ function α exists, which satisfies

$$\begin{array}{cc}\hfill \underset{u\in \mathcal{U}}{inf}\left[L_{f}h\left(x\right)+L_{g}h\left(x\right)u\right]& \le -\alpha \left(h\left(x\right)\right)\frac{T}{T-t},\forall t\in [0,T),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \underset{u\in \mathcal{U}}{inf}\left[L_{f}h\left(x\right)+L_{g}h\left(x\right)u\right]& \le -\alpha \left(h\right(x\left)\right),\forall t\in [T,\infty ).\hfill \end{array}$$

(12)

Furthermore, we introduce the Comparison Lemma, which is essential for the proof of Theorem 1.

Lemma 2

([20] (Lemma 4.4)). Consider the following scalar differential equation:

$$\dot{z}=-\alpha \left(z\right),z\left(t_0\right)=z_0,$$

(13)

with the locally Lipschitz class $\mathcal{K}$ function α defined on $[0,a)$. The solution $z\left(t\right)$ of this differential equation in time interval $t\in [t_0,\infty )$ is unique for all $0\le z_0<a$. In addition, the solution can be described as

$$z\left(t\right)=\sigma (z_0,t-t_0)$$

(14)

with a class $\mathcal{KL}$ function σ defined on $[0,a)\times [0,\infty )$.

Now, we are ready to present our first main result.

Theorem 1.

Consider the system (1). The set $\mathcal{S}$ with a ${\mathcal{C}}^1$ function h is defined as in (2). If there exists an extended class $\mathcal{K}$ function α, such that the function h is a PT-ZCBF on set $\mathcal{E}$ with $\mathcal{S}\subseteq \mathcal{E}\subset {\mathbb{R}}^n$ satisfying (11) and (12), then there exists a function $\sigma (h_0,t)$ such that

$$\begin{array}{c}h\left(x\right(t\left)\right)\le \sigma (h_0,t),\forall t\in [0,T),\end{array}$$

(15)

$$\begin{array}{c}h\left(x\right(t\left)\right)\le 0,\forall t\in [T,\infty )\end{array}$$

(16)

for any given time limit $T>0$, where the initial value $h_0=h\left(x\left(0\right)\right)$, $\sigma (h_0,t)$ decreases strictly in t for $t\in [0,T)$, and $\underset{t\to T}{lim}\sigma (h_0,t)=0$ holds. Specifically, any Lipschitz continuous controller $u\in \mathcal{U}$ of the system (1) satisfying (11) and (12) renders the trajectories of the closed-loop system (1) to converge to the set $\mathcal{S}$ in user-defined prescribed time T, and then remain forward-invariant.

Using the time transformation technique and the Comparison Lemma, Theorem 1 can be proven.

Proof. 

First, $t\in [0,T)$ is considered.

From (11) and (1), we can derive

$$\dot{h}\left(x\left(t\right)\right):=\frac{\mathrm{d}h\left(x\right(t\left)\right)}{\mathrm{d}t}\le -\alpha \left(h\left(x\left(t\right)\right)\right)\frac{T}{T-t},\forall t\in [0,T).$$

(17)

We use the time transformation candidate function

$$t=\lambda \left(s\right)\triangleq T(1-e^{-s/T})$$

(18)

with the time constant $T>0$ defined by the user. It is easy to prove that (18) satisfies (9). The back-transformation of (18) is

$$s={\lambda }^{-1}\left(t\right)=Tlog\frac{T}{T-t}.$$

(19)

It can be derived that

$$\frac{\mathrm{d}s}{\mathrm{d}t}=\frac{T}{T-t}.$$

(20)

Inserting (20) into (17), we can derive

$$\dot{h}\left(x\left(t\right)\right):=\frac{\mathrm{d}h\left(x\right(t\left)\right)}{\mathrm{d}t}\le -\alpha \left(h\left(x\left(t\right)\right)\right)\frac{\mathrm{d}s}{\mathrm{d}t},\forall t\in [0,T).$$

(21)

Since we have

$$h_s^{\prime }\left(x\left(s\right)\right):=\frac{\mathrm{d}{h}_s\left(x\left(s\right)\right)}{\mathrm{d}s}=\frac{\mathrm{d}h\left(x\right(t\left)\right)}{\mathrm{d}t}\frac{\mathrm{d}t}{\mathrm{d}s},$$

(22)

where we denote $h_s\left(x\left(s\right)\right)$ as the value of the function $h\left(x\right(t\left)\right)$ in domain s, we can derive

$$h_s^{\prime }\left(x\left(s\right)\right):=\frac{\mathrm{d}{h}_s\left(x\left(s\right)\right)}{\mathrm{d}s}\le -\alpha \left(h_s\left(x\left(s\right)\right)\right),\forall s\in [0,\infty ).$$

(23)

Next, we apply Lemma 2. In Lemma 2, let y denote $h_s\left(x\left(s\right)\right)$, and let t denote s with $t_0=s_0=0$. It can be concluded that a class $\mathcal{K}\mathcal{L}$ function ${\sigma }_s(h_0,s)$ with

$$h_s\left(x\left(s\right)\right)\le {\sigma }_s(h_0,s),\forall s\in [0,\infty )$$

(24)

exists, where $h_0$ is the initial value of the function h at $t=s=0$. Applying the back-transformation (19) to (24), we can prove (15). Based on the definition of the class $\mathcal{K}\mathcal{L}$ function, it can be concluded that $\sigma (h_0,t)$ decreases strictly with t for $t\in [0,T)$, and

$$\underset{t\to T}{lim}\sigma (h_0,t)=0$$

(25)

holds. According to (6) in Definition 5, it is evident that $h_s\left(x\right)$ is a ZCBF in the s domain. Thus, we can conclude according to Lemma 1 that any Lipschitz continuous controller $u\in \mathcal{U}$ of (1) forces the closed-loop trajectories to converge in the set $\mathcal{S}$ in user-defined time T.

Then, $t\in [T,\infty )$ is considered. At $t=T$, we can conclude from (15) that

$$h\left(x\right(t=T\left)\right)\le 0$$

(26)

holds. According to (12), we can conclude that h is a ZCBF for $t\in [T,\infty )$. Therefore, the set $\mathcal{S}$ is forward-invariant for $t\in [T,\infty )$. Hence, (16) is proven.

Thus, Theorem 1 is proven.    □

3.2. PT-ZCBF-Based QP

In this subsection, the PT-ZCBF-based QP and its feasibility are demonstrated, and it is proven that Problem 1 can be solved by the QP solution under certain conditions. Define

$$z=\left(\begin{array}{c}u\\ {\delta }_1\\ {\delta }_2\end{array}\right)\in {\mathbb{R}}^{m+2},$$

(27)

and the PT-ZCBF-based QP is defined as follows:

$$\begin{array}{cc}\hfill \underset{u,{\delta }_1,{\delta }_2}{min}\frac{1}{2}{z}^{T}Hz& \end{array}$$

(28a)

$$\begin{array}{cc}\hfill s.t.A_{u}u\le b_u& \hfill \end{array}$$

(28b)

$$\begin{array}{cc}\hfill L_f{h}_g\left(x\right)+L_g{h}_g\left(x\right)u+{\gamma }_1{h}_g\left(x\right)\frac{T}{T-t}\le {\delta }_1,t<T& \end{array}$$

(28c)

$$\begin{array}{cc}\hfill L_f{h}_g\left(x\right)+L_g{h}_g\left(x\right)u+{\gamma }_2{h}_g\left(x\right)\le {\delta }_1,t\ge T& \end{array}$$

(28d)

$$\begin{array}{cc}\hfill L_f{h}_s\left(x\right)+L_g{h}_s\left(x\right)u\le -{\delta }_2{h}_s\left(x\right).& \end{array}$$

(28e)

The matrix $H=\mathrm{diag}\left\{w_{u1},\dots ,w_{um},w_1,w_2\right\}$ is diagonal with weights $w_{u1},\dots ,w_{um},w_1,$ $w_2>0$. The matrix $A_u\in {\mathbb{R}}^{2m\times m}$ and the vector $b_u\in {\mathbb{R}}^{2m}$ define the input constraints. $T>0$ is the user-defined prescribed time of convergence, and the hyperparameters ${\gamma }_1,{\gamma }_2>0$. According to Theorem 1, the constraints (28c) and (28d) are designed according to the PT-ZCBF, which aim to ensure prescribed-time convergence. According to Lemma 1, the constraint (28e) guarantees safety.

Parameters ${\delta }_1,{\delta }_2$ are relaxation parameters. With the relaxation parameters, the feasibility of the QP (28) is guaranteed.

We can rewrite the constraints (28b)–(28e) in the form of

$$A\left(x\right)z\le b\left(x\right),$$

(29)

where

$$A\left(x\right)=\left(\begin{array}{ccc}{A}_u& 0_{2m}& 0_{2m}\\ L_g{h}_g\left(x\right)& -1& 0\\ L_g{h}_s\left(x\right)& 0& h_s\left(x\right)\end{array}\right),$$

(30)

$$b\left(x\right)=\left\{\begin{array}{c}\left(\begin{array}{c}{b}_u\\ -L_f{h}_g\left(x\right)-{\gamma }_1{h}_g\left(x\right)\frac{T}{T-t}\\ -L_f{h}_s\left(x\right)\end{array}\right),t<T\hfill \\ \left(\begin{array}{c}{b}_u\\ -L_f{h}_g\left(x\right)-{\gamma }_2{h}_g\left(x\right)\\ -L_f{h}_s\left(x\right)\end{array}\right),t\le T\hfill \end{array}\right..$$

(31)

The elements of the column vector $0_{2m}\in {\mathbb{R}}^{2m}$ are zeros. Furthermore, we define the functions

$$G_j(x,z)=A_j\left(x\right)z-b_j\left(x\right)$$

(32)

where $A_j,b_j$ denote the j-th row of A and b. Then, we can express the constraints of the QP (28) as

$$G_j(x,z)\le 0,\forall j\le 2m+2,j\in {\mathbb{N}}^{+}.$$

(33)

Lemma 3.

Parameters $(u,{\delta }_1,{\delta }_2)$, which satisfy (28b)–(28e), always exist for all x. In other words, the QP (28) is always feasible for all x.

Proof. 

Consider the cases of $h_s\left(x\right)<0$ and $h_s\left(x\right)=0$ separately.

First, the case $h_s\left(x\right)<0$ ($x\in \mathrm{Int}\left({\mathrm{S}}_{\mathrm{s}}\right)$) is to be considered. Because the set $\mathcal{U}$ is not empty, there exists $u=\overline{u}\in \mathcal{U}$, which satisfies (28b). We define

$$\overline{{\delta }_2}=-\frac{L_f{h}_S\left(x\right)+L_g{h}_S\left(x\right)\overline{u}}{h_s\left(x\right)},$$

(34)

which satisfies (28e) with equality. Finally, we choose

$$\overline{{\delta }_1}=L_f{h}_G\left(x\right)+L_g{h}_G\left(x\right)\overline{u}+{\gamma }_1{h}_g\left(x\right)\frac{T}{T-t},t\in [0,T),$$

(35)

and

$$\overline{{\delta }_1}=L_f{h}_G\left(x\right)+L_g{h}_G\left(x\right)\overline{u}+{\gamma }_1{h}_g\left(x\right),t\in [T,\infty ),$$

(36)

so that (28c) and (28d) are satisfied with equality. Therefore, in the first case, parameters $(\overline{u},\overline{{\delta }_1},\overline{{\delta }_2})$ exist, which satisfy (28b)–(28e).

Then, the case $h_s\left(x\right)=0$ ($x\in \partial S_s$) is to be considered. According to Assumption 2, it can be concluded that $u=\overline{u}\in \mathcal{U}$ satisfying (28b) exists. Because $h_s\left(x\right)=0$, any value of ${\delta }_2$ is possible. Therefore, ${\delta }_2=0$ can be chosen. As a result, we can choose

$$z=\left(\begin{array}{c}u\\ {\delta }_1\\ {\delta }_2\end{array}\right)=\left(\begin{array}{c}\overline{u}\\ \overline{{\delta }_1}\\ 0\end{array}\right),$$

(37)

which satisfies (28b)–(28e).

Therefore, the QP (28) is always feasible.    □

Remark 1.

Due to the coexistence of multiple constraints that are potentially conflicting, we must add slack variables (relaxation parameters) ${\delta }_1$ and ${\delta }_2$ to ensure the feasibility of the QP (28). However, due to the slack variables ${\delta }_1$, the stability constraint, i.e., prescribed-time stability, may not be perfectly guaranteed. When the input, stability, and safety constraints are not conflicting, the solution of the QP will result in ${\delta }_1\approx 0$ if a weight $w_1$ is chosen appropriately. As a result, a sufficiently large weight $w_1$ will result in a negligible value of ${\delta }_1$, which ensures the effectiveness of the stability constraint. In short, the stability objective is a soft constraint because of the existence of the relaxation parameter, and it is still effective if a sufficiently large weight $w_1$ is chosen. Setting ${\delta }_1=0$ will make the stability constraint a hard constraint, but the feasibility of the QP cannot be guaranteed [21,22].

In contrast, the safety constraint (28e) implies that the forward invariance of the safe set $S_s$ can never be violated according to Definition 5 and Assumption 2. Therefore, the safety constraint (28e) is a hard constraint.

Next, we would like to prove that under certain assumptions, the solution of the QP (28) solves Problem 1. That is, the solution of the QP (28) can render the trajectories of the system (1) forward-invariant in the safe set $S_s$, and the system states will converge to the goal set $S_g$ in user-defined prescribed time T while satisfying the input constraints (28b).

According to [2], the authors’ idea to ensure safety is a combination of Nagumo’s theorem [16] and Assumption 2. As the prerequisite for safety and stability, the continuity of the solution $z^{*}\left(x\right)$ of the QP (28) has to be ensured. Thus, we make the following assumptions to prove that the solution $z^{*}\left(x\right)$ of the QP (28) is continuous.

Assumption 3.

At $t=T$, the solution $z^{*}\left(x\right)$ of the QP (28) is continuous.

Let $z^{*}$ and ${\lambda }^{*}\in {\mathbb{R}}_{+}^{2m+2}$ denote the optimal solution of the QP (28) and the corresponding Lagrange multiplier.

Assumption 4

([2] (Assumption 3)). The constraints (28b)–(28e) of the QP (28) satisfy strict complementary slackness, which means that either ${\lambda }_j^{*}>0$ or $G_j(x,z^{*})<0$ holds for all $x\in \mathrm{Int}\left(S_s\right)\backslash S_g$ and for each $j\le 2m+2,j\in {\mathbb{N}}^{+}$.

Remark 2.

For an explanation of complementary slackness, please refer to [2] (Section IV).

Assumption 5.

The functions $h_g\left(x\right),h_s\left(x\right)$ are at least three times continuously differentiable in x.

Theorem 2.

Under Assumptions 3–5, the solution $z^{*}(·)$ of the QP (28) is continuous on $\mathrm{Int}\left(S_s\right)\backslash S_g$.

Proof. 

According to [2] (Theorem 5), the QP (28) solution $z^{*}(·)$ is continuous under the assumptions above. Note that the Lie derivatives $L_f{h}_g\left(x\right)$, $L_g{h}_g\left(x\right)$, $L_f{h}_s\left(x\right)$, $L_g{h}_s\left(x\right)$ should be at least twice continuously differentiable in x [23] (Theorem 2.1). Therefore, $h_s$, $h_g$ should be at least three times continuously differentiable in x, which corresponds to Assumption 5.    □

Now, we are ready to show that the solution of the QP (28) solves Problem 1 under the aforementioned assumptions.

Theorem 3.

Under Assumptions 1–5, if the solution $z^{*}\left(x\right)$ of the QP (28) given as

$$z^{*}\left(x\right)=\left(\begin{array}{c}{u}^{*}\left(x\right)\\ {\delta }_1^{*}\left(x\right)\\ {\delta }_2^{*}\left(x\right)\end{array}\right)$$

(38)

satisfies ${\delta }_1^{*}\left(x\right)\le 0,\forall x\in S_s$, then $u\left(x\right)=u^{*}\left(x\right)$ solves Problem 1 for all $x\left(0\right)\in S_s$.

Proof. 

This proof is based on [2] (Theorem 6).

First, we show that the closed-loop trajectories of (1) have the property of prescribed-time stability with respect to $S_g$. From Theorem 2, it can be concluded that the closed-loop system dynamics are continuous when we choose $u\left(x\right)=u^{*}\left(x\right)$. Applying [24] (Theorem 3.15.1) and using a Lyapunov function candidate

$$V\left(w\right)=\frac{1}{2}{\left|w\right|}^2,$$

(39)

we can prove that $w\equiv 0$ is the unique solution of the equation

$$\dot{w}=\varphi \left(w\right):=\left\{\begin{array}{c}-{\gamma }_1\frac{T}{T-t}w,t<T\hfill \\ -{\gamma }_{2}w,t\ge T\hfill \end{array}\right.$$

(40)

for $w\left(0\right)=0$ under Assumption 3. From the properties of the goal set function $h_g\left(x\right)$, we have that

$$h_g\left(x\right)=0,\forall x\in \partial S_g,$$

(41)

and that

$$h_g\left(x\right)>0,\forall x\notin S_g,$$

(42)

i.e., the goal set function $h_g\left(x\right)$ is positive definite with respect to the goal set $S_g$. Therefore, per [24] (Theorem 3.18.1), with the function g defined as $\varphi$ and the fact that

$$\dot{h_g}\left(x\right)\le \varphi \left(h_g\left(x\right)\right),x\notin S_g$$

(43)

holds since ${\delta }_1^{*}\left(x\right)\le 0$, the closed-loop system (1) has a unique solution. According to Theorem 1, it can be concluded that the closed-loop trajectories of (1) with $u\left(x\right)=u^{*}\left(x\right)$ converge to the goal set $S_g$ within user-defined prescribed time T for all $x\left(0\right)\in S_s$, and then remain forward-invariant with respect to the goal set $S_g$.

Then, we show that the closed-loop trajectories have the property of safety, i.e., $x\left(t\right)\in S_s$ for all $t>0$ when we choose $u\left(x\right)=u^{*}\left(x\right)$. Since the solution $z^{*}(·)$ is continuous under the assumptions above, the optimal control input $u\left(x\right)=u^{*}\left(x\right)$ is also continuous. Furthermore, a bounded safe set $S_s$ results in bounded closed-loop trajectories. Thus, the solution of the closed-loop system (1) is well-defined and unique [24] (Chapter 3). Since $h_s$ is a ZCBF, it satisfies (5). Therefore, by Nagumo’s Theorem on set invariance [16], we directly obtain the forward invariance (safety) of the safe set $S_s$.

Additionally, according to the input constraints (28b) and the solvability of the QP (28) from Theorem 3, it can be concluded that the control input $u\left(x\right)=u^{*}\left(x\right)$ satisfies the linear input constraints (28b).

Therefore, the optimal control input $u\left(x\right)=u^{*}\left(x\right)$ solves Problem 1 for all $x\left(0\right)\in S_s$ under the aforementioned assumptions.    □

In many engineering problems, the system vector fields and the control input are assumed to be Lipschitz continuous. Next, we will show that under the following technical assumption, Problem 1 can be solved by the solution of QP (28) [1,3].

Assumption 6.

The system vector fields f, g in (1) and the solution $z^{*}\left(x\right)$ of the QP (28) are (locally) Lipschitz continuous.

Theorem 4.

Denote

$$z^{*}\left(x\right)=\left(\begin{array}{c}{u}^{*}\left(x\right)\\ {\delta }_1^{*}\left(x\right)\\ {\delta }_2^{*}\left(x\right)\end{array}\right)$$

(44)

as the solution of the QP (28). Under Assumptions 1, 2, 3 and 6, Problem 1 can be solved by $u\left(x\right)=u^{*}\left(x\right)$ for all $x\left(0\right)\in S_s$.

Proof. 

According to Lemma 1, if the solution of the QP (28) is Lipschitz continuous for all $x\left(0\right)\in S_s$, then the trajectory of the closed-loop system (1) will be forward-invariant in safe set $S_s$ under the safety constraint (28e). Furthermore, according to Theorem 1, under the condition that the QP solution is Lipschitz continuous for all $x\left(0\right)\in S_s$, the system states will be driven into the goal set $S_g$ within user-defined prescribed time period T under the stability constraint (28c), and then remain forward-invariant under the stability constraint (28d). Moreover, the input constraint (28b) specifies the upper and lower bounds of control inputs as described in Problem 1. In addition, the QP (28) is always feasible according to Lemma 3. Hence, Problem 1 can be solved by $u^{*}$ for all $x\left(0\right)\in S_s$.    □

Remark 3.

According to [1] (Theorem 3), if we ignore the input constraints (28b), we can prove the Lipschitz continuity of the solution of QP (28) for $x\in \mathrm{Int}\left(S_s\right)$ under the assumptions that the QP solution is locally Lipschitz continuous at $t=T$, and that the functions f, g in (1), the gradients of $h_s$, $h_g$ are locally Lipschitz continuous, and that the relative degree one condition holds. However, the Lipschitz continuity of the QP solution with input constraints (28b) is not currently guaranteed.

Remark 4.

The newly designed QP (28) can find the optimal control input of a control affine system (1) under the prescribed-time stability constraint, safety constraint, and input constraints of a typical safety-critical system, which is different from the function of the controllers designed in [1,2]. We learn from the ideas of proofs in [1,2], but for our newly designed QP (28), it is proven that the control goal of PTS is achieved. Although we are inspired by the ideas in previous research, the prescribed-time stability constraint in our QP (28) is based on PT-ZCBF, which is different from the stability constraints in [1,2]. Then, the resulted closed-loop trajectories of the safety-critical system will be prescribed-time stable under safety and input constraints.

4. A Numerical Case Study

In this section, the Adaptive Cruise Control (ACC) problem [1] (Section V.A) is adopted to show the effectiveness of the designed method. The objective of our problem is to track the expected speed of the following vehicle while keeping a safe distance from the leading vehicle. QP (28) is applied to find the control input that solves the ACC problem. The Matlab solver ode4 with a fixed step size is applied in our program. The Matlab function quadprog is applied to find the QP solution at every time step.

4.1. Introduction of the ACC Problem

The ACC problem contains a following vehicle and a leading vehicle. The following vehicle possesses the ACC system, which aims to converge to a prescribed driving speed (stability constraint, soft constraint). Furthermore, the following vehicle needs to keep a safe distance behind the leading vehicle (safety constraint, hard constraint). Therefore, the following vehicle’s speed has to be reduced to observe the safety constraint when the distance between the two vehicles decreases. We assume that both vehicles are modeled as mass points, and they travel in a one-dimensional coordinate.

The system equation of the ACC problem is [1]

$$\dot{x}=f\left(x\right)+g\left(x\right)u.$$

(45)

By choosing the system vector fields properly, we can derive

$$\dot{x}=\underset{f\left(x\right)}{\underbrace{\left(\begin{array}{c}-F_r/M\\ a_L\\ x_2-x_1\end{array}\right)}}+\underset{g\left(x\right)}{\underbrace{\left(\begin{array}{c}1/M\\ 0\\ 0\end{array}\right)}}u.$$

(46)

In the system equations,

$$x=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)=\left(\begin{array}{c}{v}_f\\ v_l\\ D\end{array}\right)$$

(47)

are the system states, where we define $v_f$ as the following vehicle speed (in m/s), $v_l$ as the leading vehicle speed (in m/s), and D as the space between both vehicles (in m). $u\in [-u_{max},u_{max}]$ is the control input, whose physical significance is the driving wheel force (in N) of the following vehicle supplied from the powertrain system. M is defined as the mass of the following vehicle (in kg); $F_r\left(x\right)=f_0+f_{1}v+f_2{v}_f^2$ is the resistance (in N), where the constants $f_0$, $f_1$, and $f_2$ are chosen empirically. We define $a_L\in [-a_{l}g,a_{l}g]$ as the acceleration (or deceleration) of the leading vehicle (in m/s²).

Furthermore, we have to define the goal set function $h_g\left(x\right)$ and safe set function $h_s\left(x\right)$ in our QP (28). We set

$$h_g\left(x\right)={(x_1-v_d)}^2,$$

(48)

and

$$h_s\left(x\right)={\tau }_d{x}_1-x_3,$$

(49)

with $v_d$ being the prescribed velocity defined by the user and ${\tau }_d$ the desired time headway.

Next, we choose the model parameters according to the physical systems in reality. We set the desired velocity $v_d=22$ m/s, the desired time headway ${\tau }_d=1.82$ s, the mass of the following vehicle $M=1650$ kg, the gravitational acceleration $g=9.81$ m/s², the maximum available control effort (driving wheel force) $u_{max}=0.25Mg$, the constants in the expression of aerodynamic drag force $f_0=0.1$ N, $f_1=5$ Ns/m, $f_2=0.25$ Ns²/m², and the leading vehicle acceleration parameter $a_l=0.3$. Then, we define the initial condition of the dynamic system: $v_l\left(0\right)=10$ m/s, $v_f\left(0\right)\in [14,30]$ m/s, $D\left(0\right)=150$ m. We choose $T=5$ s.

To achieve better performance for our control system in the ACC problem, we slightly change the QP (28) such that the stability constraints are forced to be invalid when the value of the safe set function $h_s\left(x\left(t\right)\right)$ approximates zero (when $h_s\left(x\left(t\right)\right)>-10$), which can result in better obedience to the safety constraints. We implement the QP (28) with $H=\mathrm{diag}\left\{\frac{2}{M^2},100,400\right\}$, $A_u=\left(\begin{array}{ccc}1& 0& 0\\ -1& 0& 0\end{array}\right)$, $b_u=\left(\begin{array}{c}{u}_{max}\\ u_{max}\end{array}\right)$, ${\gamma }_1=1000$, ${\gamma }_2=1000$, $T=5$, and $h_g\left(x\right)$, $h_s\left(x\right)$ defined in (48), (49).

4.2. Simulation Results without Disturbances

Now, we are ready to present the simulation results. Figure 2 shows the tracking performance of the following vehicle with the control input computed from QP (28). The solid lines in different colors represent the following vehicle speeds for different initial conditions $v_f\left(0\right)\in [14,30]$ m/s. Figure 3 illustrates the dynamics of the safe set function $h_s\left(x\left(t\right)\right)$ with the same initial conditions. Figure 4 shows the dynamics of the computed control input $u\left(t\right)$ (driving wheel force of the following vehicle supplied from the powertrain system).

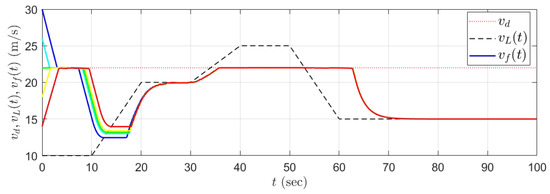
Figure 2. Tracking performance for different initial following speeds $v_f\left(0\right)\in [14,30]$ m/s with $T=5$ s.

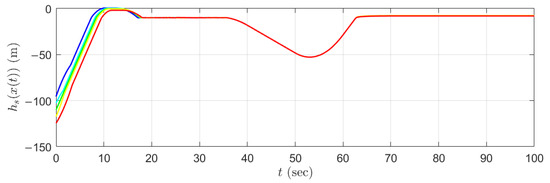
Figure 3. Dynamics of the safe set function $h_s\left(x\left(t\right)\right)$ for different initial following speeds $v_f\left(0\right)\in [14,30]$ m/s with $T=5$ s.

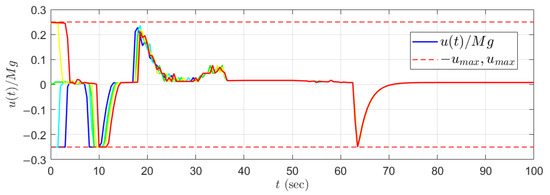
Figure 4. Dynamics of the computed $u\left(t\right)$ for different initial following speeds $v_f\left(0\right)\in [14,30]$ m/s with $T=5$ s.

4.3. Simulation Results with Disturbances

We now examine the robustness of the proposed approach against disturbances. Suppose that the system equations with disturbances can be written as

$$\dot{x}=f\left(x\right)+gu+z\left(x\right),$$

(50)

where $f\left(x\right)$ and g are given in (46), and we consider the Lipschitz continuous disturbance

$$z\left(x\right)=\left(\begin{array}{c}\frac{C_{\delta }}{M}\left|v_f-v_d\right|\\ 0\\ 0\end{array}\right),$$

(51)

where $C_{\delta }$ is the disturbance constant. In our simulation program, we set $C_{\delta }\in [0,40]$ kg/s, the initial velocity of the following vehicle $v_f\left(0\right)=30$ m/s, and we slightly modify the proposed QP (28) such that the stability constraints are set to be invalid when the value of the safe set function $h_s\left(x\left(t\right)\right)$ approximates zero (when $h_s\left(x\left(t\right)\right)>-20$). Figure 5, Figure 6 and Figure 7 illustrate the tracking performance, dynamics of the safe set function $h_s\left(x\left(t\right)\right)$, and control input $u\left(t\right)$, respectively.

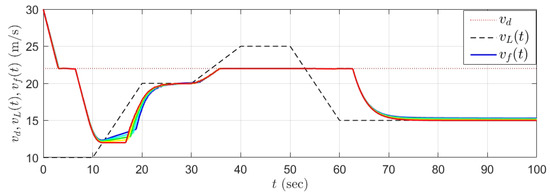
Figure 5. Tracking performance with disturbances for $C_{\delta }\in [0,40]$ kg/s (red to blue) and $v_f\left(0\right)=30$ m/s.

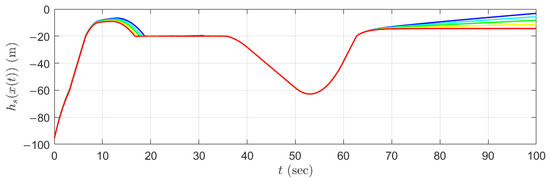
Figure 6. Dynamics of the safe set function $h_s\left(x\left(t\right)\right)$ with disturbances for $C_{\delta }\in [0,40]$ kg/s (red to blue) and $v_f\left(0\right)=30$ m/s.

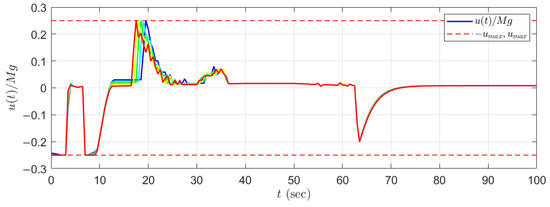
Figure 7. Dynamics of the control input $u\left(t\right)$ with disturbances for $C_{\delta }\in [0,40]$ kg/s (red to blue) and $v_f\left(0\right)=30$ m/s.

4.4. Conclusions of Simulation Results

It can be concluded that the desired velocity $v_d$ of the following vehicle can be reached in a user-defined prescribed time $T=5$ s without violating the input constraints when the trajectories of the system states are away from the boundaries of the safe set, namely when the value of the function $h_s\left(x\left(t\right)\right)$ is much smaller than zero. Furthermore, the velocity of the following vehicle will be decreased to satisfy the safety constraint if the system states are near the safe set boundaries, namely if $h_s\left(x\left(t\right)\right)$ approaches zero.

We can see that there are slight oscillations in our simulation results, especially in Figure 4. One of the reasons lies in the fact that the computed control input varies when the value of the safe set function $h_s\left(x\left(t\right)\right)$ approaches the predefined value from above and below. Furthermore, there are small simulation errors in the solver ode4. For example, in Figure 2, the speed of the following vehicle oscillates between 21.95 m/s and 22.05 m/s in a steady state. Theoretically, many control techniques can be applied to reduce the oscillation (e.g., a dead-zone controller [25]). However, the oscillation of the vehicle speed with an amplitude of 0.1 m/s may not cause any serious problems in reality.

5. Conclusions

We presented the definition and properties of PT-ZCBF, which can describe the prescribed-time stability constraint of safety-critical systems. We combined the input, safety, and stability constraints of safety-critical systems in a PT-ZCBF-based QP formulation, which is able to find the optimal control input under the designated constraints. We discussed its feasibility and how it can solve the main problem under certain mild assumptions. Finally, we applied the proposed QP to the ACC problem as a numerical simulation example. The simulation results showed that the proposed approach can solve the ACC problem with satisfaction. Compared to previous works, a QP-based method combining the prescribed-time stability constraint, safety constraint, and input constraints is proposed in this paper for the first time.

In the future, we would like to search for a method to reduce the oscillation behaviors of the proposed method in numerical case studies. In addition, we are interested in different methods to solve the prescribed-time stability problem, e.g., the Control Lyapunov Function method introduced in [11]. We want to modify the stability constraints of the proposed QP according to different PTS methods, use the modified QP in numerical case studies, and compare the results using the QP with different PTS methods. Furthermore, we would like to study the applicability of the proposed approach to more numerical examples and large-scale systems [26,27], and then apply the methods to practical experimental studies.