Three-Way Selection Random Forest Optimization Model for Anomaly Traffic Detection

Abstract

With the application and development of Internet technology, network traffic is growing rapidly, and the situation of network security is becoming more and more serious. As an important way to protect network security, abnormal traffic detection has been paid more and more attention. In this paper, the uncertainty of the samples in the abnormal traffic detection dataset is studied. Combining the three-way decision idea with the random forest algorithm, a three-way selection random forest optimization model for abnormal traffic detection is proposed. Firstly, the three-way decision idea is integrated into the random selection process of feature attributes, and the attribute importance based on decision boundary entropy is calculated. The feature attributes are divided into the normal domain, abnormal domain, and uncertain domain, and the three-way attribute random selection rules are designed to randomly select the feature attributes that conform to the rules from different domains. Secondly, the classifier evaluation function is constructed by combining pure accuracy and diversity, and the anomaly traffic detection base classifier with a high evaluation value is selected for integration to eliminate the unstable factors caused by randomness in the process of base classifier generation. Thirdly, the optimal node weight combination of the base classifier is obtained by iterative calculation of the gray wolf optimization algorithm to further improve the prediction effect and robustness of the model. Finally, the model is applied to the abnormal traffic detection dataset. The experimental results show that the prediction accuracy of the three-way selection random forest optimization model on CIC-IDS2017, KDDCUP99, and NSLKDD datasets is 96.1%, 95.2%, and 95.3%, respectively, which has a better detection effect than other machine learning algorithms.

1. Introduction

Network intrusion detection has become an increasingly critical area of research in light of the explosive growth of computer business and the surge of network information traffic. Anomalous traffic identification, in particular, has emerged as a key component of cybersecurity. With the proliferation of mobile devices and the construction of network infrastructure, daily data access and traffic acquisition in cyberspace have become increasingly accessible. As network traffic often contains valuable data content and user privacy information, the ability to detect and identify abnormal traffic has significant theoretical and practical implications for maintaining cyberspace security. By studying network traffic data, researchers can discover network anomalies and take timely warning measures to protect private information. As such, the development of effective abnormal traffic detection methods is of great significance and practical value for the cybersecurity community.

Traditional detection methods for abnormal network traffic include misuse-based [1] and signature-based [2] detection. However, these methods lack robustness and cannot adapt well to the variability and concealment of abnormal network traffic in complex environments. Deep learning-based methods have shown promise in this field. For instance, Akarsh et al. [3] used a long- and short-term memory (LSTM) network to detect abnormal data traffic, while Liu et al. designed convolutional kernels of different sizes to improve the accuracy and robustness of detection. Huang et al. [4] introduced the self-attention mechanism for multi-feature learning of network traffic data, while Dai et al. converted network traffic samples into grayscale images and achieved high detection performance using residual networks for classification. Dong et al. [5] proposed a deep neural network model based on stack convolution attention to detect abnormal network traffic, which can learn the sample distribution rules in network traffic data and represent key information in the sample, as well as the correlation between multiple feature attributes. However, deep learning-based methods have two major limitations. First, a large amount of labeled data and hardware computing resources are required for training, which makes the training and application costs very high. Second, the internal calculation and feature extraction process of these methods is difficult to understand, making it hard to explain the decision-making process of the model. Therefore, it is essential to investigate effective and practical methods for detecting network traffic anomalies.

Ensemble learning, a technique that integrates multiple weak learners to improve performance, has gained widespread popularity in the field of anomaly traffic detection. Among various methods, random forest has emerged as a preferred approach due to its high accuracy and fast learning speed. For instance, L et al. [6] proposed a novel detection method that combines information entropy of detection flow and random forest classification to enhance system network security detection. By leveraging key feature groups, this approach effectively improves the reliability and early warning capability of the system. In another study, Zhang et al. [7] applied a random forest classification algorithm to distributed systems and proposed a network intrusion detection method based on distributed random forest. The proposed high-speed traffic data detection processing method offers a new solution to network intrusion detection. Similarly, S. Bagu et al. [8] used binary and random forests to detect attacks in network traffic in distributed big data environments. They also introduced information gain and principal component analysis to preprocess the UNSW-NB15 dataset, which significantly improved the prediction performance of the model. Furthermore, Li et al. [9] developed an intrusion detection system based on random forest feature selection to construct an automatic encoder. By constructing the training set of the model through feature selection and grouping, the proposed approach effectively improved the prediction accuracy. After training, the model can use the automatic encoder to predict the test sample, which significantly enhances the overall performance of the system. In summary, ensemble learning, particularly the random forest algorithm, has become an increasingly popular method in the field of anomaly traffic detection. The studies discussed above demonstrate the effectiveness of this approach and offer new solutions to enhance system network security detection and improve prediction performance.

Random forest [10] is a popular ensemble learning method for classifying abnormal traffic due to its resistance to overfitting and strong anti-interference properties. However, the inherent randomness in the attribute selection process during the construction of a random forest can result in suboptimal decision tree performance. To address this issue, document [11] proposes a novel approach based on decision boundary entropy, which selects three branches for each attribute during decision tree construction. This method improves the accuracy of individual decision trees and subsequently, the overall classification performance of the forest. Building on this, literature [12] applies this approach to intrusion detection and achieves favorable results. However, the final integration stage of these methods does not take into account the quality of individual decision trees. In this paper, we propose a novel three-branch selection random forest optimization model that integrates three-branch decision-making ideas into traditional random forest classification models. Our approach brings the classifier’s decision-making process closer to human decision-making methods, thereby enhancing the classification and processing ability of uncertain samples in datasets. We achieve this by using a classifier evaluation method that combines pure accuracy and diversity to optimize the integration method of classifiers, solving the problem of low-quality decision trees in the classifier set. Moreover, we introduce the gray wolf optimization algorithm to automatically, quickly, and conveniently obtain the leaf node weight coefficients of a set of base classifiers. This enhancement enhances the voting proportion of the leaf node classification results of key classifiers in the classifier set and further improves the detection performance of the classifier. The contributions of our proposed model are threefold: First, it effectively addresses the problem of large hardware resource requirements, high training and application costs, and the difficult-to-understand decision-making process. Second, it integrates decision-making ideas from multiple branches, improving the classifier’s decision-making process. Third, it enhances the detection performance of the classifier, making it more effective in classifying uncertain samples. Overall, our proposed model demonstrates promising results and has the potential to be applied in real-world scenarios.

The article is structured as follows: The Introduction to Basic Theories section outlines three-branch decision-making and three-branch attribute selection rules based on attribute importance, establishing the theoretical foundation for subsequent detection models. The Framework of the Three-Branch Selection Random Forest Optimization Model section explains in detail the preprocessing of abnormal traffic data, the three-branch attribute random selection, the evaluation of the classifier’s three-branch selection, the process of the random forest node weighting algorithm based on GWO optimization, and the algorithm’s detailed steps. The Parameter Analysis and Experimental Comparison section includes an analysis of three selected random forest optimization models and a comparison of three abnormal flow datasets with traditional algorithms. Finally, the Conclusion section provides a summary of the findings.

2. Related Work

2.1. Three-Way Decision Theory

Rough set theory [13] is a powerful mathematical tool that addresses incomplete and inaccurate data with up to 90% accuracy and provides a framework for handling uncertainty. The main idea is to derive decision or classification rules from the data via knowledge reduction [14] while retaining classification ability, attribute reduction, and attribute importance measurement. In the context of real-world abnormal traffic detection, the importance of attributes in abnormal traffic data samples may vary across different application scenarios. To capture this variability, we employ the rough set method of attribute importance to measure attribute importance [15] and dependence.

In the field of decision-making under uncertainty, Professor Yao Yiyu has proposed a novel approach called the three-way decision theory [16], which combines principles from probability rough set and decision rough set. This approach offers a significant improvement over the traditional two-way decision model, providing a valuable tool for dealing with data uncertainty [17]. By building upon the foundations of rough set theory and the two-way decision model, the three-way decision theory introduces a new level of sophistication into the decision-making process. At its core, the three-way decision theory involves incorporating the concept of uncertainty into the decision-making process, specifically when dealing with abnormal traffic samples. To achieve this, the theory employs a decision evaluation function to construct three distinct and independent domains: the normal domain (ND), the abnormal domain (AD), and the uncertain domain (UD).

$$\mathit{ND}(X)=\{x\in X|F(x)\ge \beta \}$$

(1)

$$\mathit{UD}(X)=\{x\in X|\alpha <F(x)<\beta \}$$

(2)

$$\mathit{AD}(X)=\{x\in X|F(x)\le \alpha \}$$

(3)

Construct a decision table $\mathit{DT}=(U,C,D,V,f)$, where $U$ is the domain of discussion, including all data instances; $C$ is a non-empty set containing conditional attributes of anomaly traffic data samples; $D$ is the decision attribute of abnormal traffic data; $V$ is the abnormal traffic data attribute value; $f$ is the mapping relationship between attributes and attribute values. The dependence ${\gamma }_B(D)$ of $\forall B\subseteq C$, $\forall C^{\prime }\subseteq C-B$, $D$ on B and the attribute importance $\mathit{Sig}(C^{\prime },B,D)$ of attribute subset $C^{\prime }$ on B and D are defined as:

$${\gamma }_B(D)=\frac{\left|{\mathit{ND}}_B(D)\right|}{\left|U\right|}$$

(4)

$$\mathit{Sig}(C^{\prime },B,D)={\gamma }_B(D)-{\gamma }_{B-C^{\prime }}(D)$$

(5)

$\left|{\mathit{ND}}_B(D)\right|$ represents the normal domain of decision attribute D to condition attribute B.

Machine learning algorithms have proven effective in detecting abnormal traffic due to their powerful feature extraction and nonlinear fitting capabilities [18]. However, these algorithms are limited by their assumption that data can be categorized as either normal or abnormal. In reality, there exist uncertain states in between, which require additional decision-making information to accurately classify. To address this issue, we propose the use of a three-branch decision-making approach, which extends traditional two-branch decision-making by providing an uncertain choice when decision information is insufficient. This approach improves the decision-making efficiency of abnormal traffic detection tasks and enhances the adaptability and decision-making ability in complex network scenarios. By incorporating the three-branch decision-making idea, we can obtain more rational and feasible results in detecting abnormal traffic samples.

2.2. Three-Way Attribute Selection Rules Based on Attribute Importance

In the process of constructing random forests, randomly selecting attributes from the dataset [19] can improve the model’s robustness and generalization ability by up to 20%, but it is not guaranteed to improve prediction accuracy. Directly deleting attributes may also negatively impact the model’s classification effect due to uncertainty regarding attribute importance. To ensure optimal results, it is essential to collect sample information from diverse perspectives when forming the dataset. The quality of the dataset significantly affects model training outcomes. To prioritize important attributes while maintaining randomness in attribute selection, we propose a three-way decision approach based on decision boundary entropy to further divide and process the dataset’s attributes. This method improves model accuracy and retains the randomness of attribute selection.

Approximate classification accuracy is a method used to assess the relationship between conditional attributes and decision attributes by analyzing the description of target concepts using existing information [20]. However, this approach has its limitations, as it only considers attribute information within the normal domain, while ignoring attributes that fall into the uncertain domain. These attributes are just as important as those in the normal domain, as they are divided into the uncertain domain due to the uncertainty surrounding their attribute importance. To address this limitation, the decision boundary entropy model has been redesigned by incorporating information from the attribute uncertainty domain and the approximate classification accuracy. This new approach allows for a more comprehensive analysis of the data, providing a more accurate and nuanced understanding of the relationships between attributes and decision outcomes.

$$\mathit{DBE}(D,B)=(1-{\alpha }_B(D))·{\displaystyle \sum _{i=1}^n{P}_i{\mathit{log}}_2(P_i+1)}$$

(6)

$$P_i=\frac{|U{D}_B(D_i)|}{\left|U\right|},i=1,2\dots ,n$$

(7)

${\alpha }_B\left(D\right)$ represents the approximate classification accuracy of condition attribute B to decision attribute D, and ${\mathit{UD}}_B\left(D_i\right)$ represents the uncertainty region of condition attribute B. The redesigned decision boundary entropy provides a new attribute measure, which considers the attribute information in both normal and uncertain domains. There are $\forall B\subset C$, $a\in C-B$, attribute a about condition attribute B to decision attribute D based on decision boundary entropy attribute importance calculation formula is as follows:

$$\mathit{Sig}(a,B,D)=DBE(D,B-\{a\})-DBE(D,B)$$

(8)

The attribute importance based on decision boundary entropy is used as the evaluation function $F(x)=\mathit{Sig}(a,C,D)$ of the three-way decision attribute division, and the threshold pair $({\alpha }_1,{\beta }_1)$ is introduced. After evaluating the importance of the feature attributes in turn, the normal domain, abnormal domain, and uncertain domain of the random three-way decision are constructed.

The dataset’s feature attributes were computed and categorized into three domains. During the feature selection process, three attribute selection rules were implemented by the base classifier, introducing an element of randomness to the selection process. The three attribute selection rules are defined as follows:

• If $\left|\mathit{ND}\right|>(1+\delta )\sqrt{k}$, $\sqrt{k}$ attributes are randomly selected from the normal domain as attribute subsets;
• If $\left|\mathit{ND}\right|+\left|\mathit{UD}\right|>(1+\delta )\sqrt{k}$, $\sqrt{k}$ attributes are randomly selected from normal and uncertain domains as attribute subsets;
• If $\left|\mathit{ND}\right|+\left|\mathit{UD}\right|\le (1+\delta )\sqrt{k}$, $\frac{\left|\mathit{ND}\right|+\left|\mathit{UD}\right|}{\sqrt{k}}$ attributes are randomly selected from the normal and uncertain domains, and $(1-\frac{\left|\mathit{ND}\right|+\left|\mathit{UD}\right|}{k})\cdot \sqrt{k}$ attributes are randomly selected from the abnormal domain to form a subset of attributes.

$k=\left|\mathit{ND}\right|+\left|\mathit{UD}\right|+\left|\mathit{AD}\right|$ represents the total number of feature attributes of the abnormal traffic dataset, the feature attribute randomness variable $\delta \in (0,\sqrt{k}-1)$, $|•|$ represents the number of feature attributes in the domain where the feature attributes of the abnormal traffic dataset are divided.

The use of three-branch decision-making allows for the prioritization of important attributes while maintaining the randomness of attribute selection. To further refine the selection process, we propose a novel approach based on decision boundary entropy to divide and process attributes within a given dataset. Through this approach, we are able to improve model accuracy during the training process without sacrificing the randomness of attribute selection, ultimately leading to greater efficiency in constructing abnormal traffic detection models.

2.3. Gray Wolf Optimization Algorithm

The gray wolf optimization (GWO) algorithm is a swarm intelligence optimization algorithm proposed by Seyedali M et al. [21], which obtains the optimal solution by simulating the hierarchy and hunting behavior between gray wolf groups in nature. The main process is shown in Figure 1. In the GWO algorithm, the gray wolves are divided into four layers according to their status: layer $\alpha ,\beta ,\delta ,\omega$, where layer $\alpha$ is the optimal wolf, layer $\beta$ is the suboptimal wolf, layer $\delta$ is the third optimal wolf, and layer $\omega$ is the remaining wolf group. The algorithm is to hunt and hunt the prey by $\alpha ,\beta ,\delta$ wolf leading subordinate wolf $\omega$. Assuming the population $X=[X_1,X_2,\dots ,X_N]$ is composed of N gray wolves, the search space of the optimal solution is k-dimensional, and the i-th gray wolf is expressed as $X_i=[X_i^1,X_i^2,\dots ,X_i^k]$, and the wolves move their positions in the following way.

$$X_i^{}(t+1)=X_p^{}(t)-A\cdot |C\cdot X_p^{}(t)-X_i^{}(t)|$$

(9)

$$A=2a\cdot r_1-a$$

(10)

$$C=2\cdot r_2$$

(11)

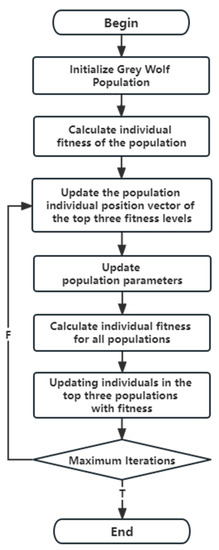
Figure 1. GWO algorithm flow chart.

$t$ is the current number of iterations, $X_p$ is the position vector of prey, $X_i$ is the position vector of the i-th gray wolf, A and C are coefficients, $r_1$ and $r_2$ are random numbers in the range of [0,1].

Although the true position of the prey in the wolves’ pursuit of the prey is unknown, the $\alpha ,\beta ,\delta$ wolf’s position is closer to the prey, by updating the $\alpha ,\beta ,\delta$ wolf’s position vector and then updating the gray wolf $\omega$‘s position with the average of the three wolves’ position vectors. The updated formula is:

$$X_{i,\alpha }^{}(t)=X_{\alpha }^{}(t)-A_1\cdot |C_1\cdot X_{\alpha }^{}-X_i^{}(t)|$$

(12)

$$X_{i,\beta }^{}(t)=X_{\beta }^{}(t)-A_2\cdot |C_2\cdot X_{\beta }^{}-X_i^{}(t)|$$

(13)

$$X_{i,\delta }^{}(t)=X_{\delta }^{}(t)-A_3\cdot |C_3\cdot X_{\delta }^{}-X_i^{}(t)|$$

(14)

$$X_i^{}(t+1)=\{X_{i,\delta }^{}(t)+X_{i,\beta }^{}(t)+X_{i,\delta }^{}(t)\}/3$$

(15)

$X_{\alpha },X_{\beta },X_{\delta }$ is the top three gray wolf positions in the t-th iteration process, $A_1,A_2,A_3$ and $C_1,C_2,C_3$ are the coefficients used in the iteration process, and $X_{i,\alpha },X_{i,\beta },X_{i,\delta }$ is the position updated after the t-th iteration.

Random forests are popular machine-learning models that use ensemble methods to improve classification accuracy. However, the randomization processes used in training and feature selection may lead to suboptimal performance of individual classifiers and affect the overall prediction accuracy. We propose using the gray wolf optimization algorithm, a metaheuristic optimization technique inspired by wolf hunting behavior, to optimize the leaf node weight coefficients of a set of base classifiers. This approach enhances the voting proportion of the leaf node classification results of key classifiers and improves the overall model detection performance. Compared to other optimization algorithms such as genetic algorithm and particle swarm optimization, the gray wolf algorithm has faster convergence speed and simpler parameter settings, making it a more efficient and practical choice for optimizing random forest models. Experimental results on multiple datasets demonstrate the effectiveness of our proposed method in improving classification accuracy.

3. Three-Way Selection Random Forest Optimization Model

3.1. Model Framework

In this paper, we propose a novel approach for detecting abnormal traffic using a three-way selection random forest optimization model. This model combines the principles of three-way decision-making and node-weighted optimization to enhance the classical random forest model and address the uncertainty inherent in abnormal traffic samples. Our model comprises three key components: three-way attribute random selection, three-way selection classifier evaluation, and random forest node weighting. The model structure is shown in Figure 2.

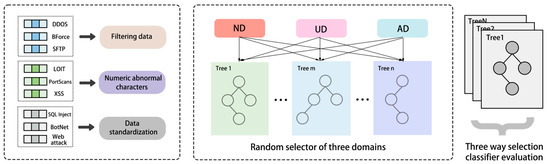
Figure 2. Overall framework of three-way selection random forest optimization model.

To detect abnormal traffic, we first preprocess the dataset and calculate the importance of each feature using decision boundary entropy. We use this information to divide the dataset into three domains based on attribute importance and domain thresholds: normal, abnormal, and uncertain. Using a set of decision trees generated from attributes that meet three random selection rules, we apply a pure accuracy and diversity evaluation method to each base classifier and retain the best-performing combinations. Finally, we use a random forest node weighting algorithm based on GWO optimization to iteratively calculate the best combination of node coefficients, improving the prediction accuracy of the integrated base classifier for abnormal traffic detection.

3.2. Anomaly Flow Data Preprocessing

The abnormal traffic samples obtained from the abnormal traffic dataset often contain special characters, null values, invalid features, marking errors, etc. In order to be able to smoothly input the data into the abnormal traffic detection model for training, it is necessary to preprocess the abnormal traffic data. The main process is shown in Figure 3.

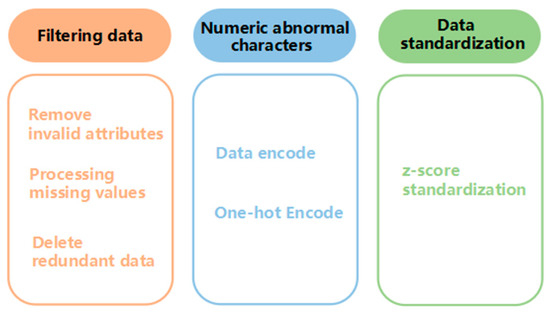
Figure 3. Abnormal flow data preprocessing method.

The data preprocessing method is mainly divided into three steps: data screening, abnormal character numericalization, and data standardization. The data samples processed by the above steps are convenient for model training, improve the calculation speed of the model training process, and accelerate the convergence of the anomaly traffic detection model.

3.3. Three-Attribute Random Selection Algorithm

Random forest is a widely used ensemble learning model that employs decision trees as base classifiers [22]. During the construction process, random sampling of abnormal traffic data and features helps ensure diversity and prevent overfitting. To further enhance the importance of feature attributes in abnormal traffic datasets, we propose a three-way attribute random selection approach that categorizes attributes into three domains based on their importance and randomly selects attributes from each domain to generate decision trees. This approach is designed to introduce the concept of three-way decision-making into the feature selection process of random forest. Figure 4 illustrates the algorithm for the three-way attribute random selection. By incorporating this method into the random forest model, we can better evaluate and utilize the important feature attributes in abnormal traffic datasets.

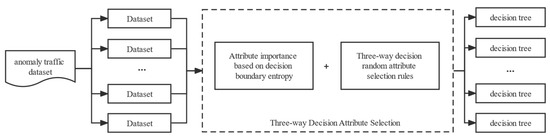
Figure 4. Three attributes random selection algorithm.

To improve the performance of random forest models in detecting abnormal traffic data, we propose a three-way decision attribute selection approach. This approach involves self-sampling of the original dataset to generate N sub-datasets, followed by the calculation of the importance of each feature attribute using decision boundary entropy as the evaluation function. Based on the attribute importance and threshold comparison results, each attribute of the abnormal traffic sample is categorized into normal, abnormal, or uncertain domains. To maintain the randomness of random forest in feature selection, we define selection rules for three-way decision random attributes and randomly select feature attributes that meet the selection criteria and are distributed across different domains. The decision tree classifier is then trained with the new attribute sets to generate an integrated decision tree combination. Experimental results show that our proposed method can effectively improve the detection performance of random forest models for abnormal traffic data.

According to the attribute importance evaluation function based on decision boundary entropy, the attributes are divided into the normal domain, abnormal domain, and uncertain domain. Constant $k=\left|\mathit{ND}\right|+\left|\mathit{UD}\right|+\left|\mathit{AD}\right|$ and attribute randomness variable $\delta \in (0,\sqrt{k}-1)$ are defined, and three-way attribute random selection rules in different domains are designed. For algorithm rule design, see Algorithm 1.

Algorithm 1: Random selection of three attributes

Input: three attribute division threshold $(\alpha ,\beta )$, attribute random variable $\delta$ Output: random attribute set N

$1:\mathbf{If}\left|\mathit{ND}\right|>(1+\delta )\sqrt{k}$ then

$2:\mathrm{Randomly}\mathrm{select}\sqrt{k}$ attributes in the normal domain

3:     Else

4:          If $\left|\mathit{ND}\right|+\left|\mathit{UD}\right|>(1+\delta )\sqrt{k}$ then

$5:\mathrm{Random}\mathrm{selection}\mathrm{of}\sqrt{k}$ attributes in normal and uncertain domains

6:          Else

$7:\mathrm{Randomly}\mathrm{select}\frac{\left|\mathit{ND}\right|+\left|\mathit{UD}\right|}{k}\sqrt{k}$ $\mathrm{attributes}\mathrm{in}\mathrm{normal}\mathrm{domain}\mathrm{and}\mathrm{uncertain}\mathrm{domain}.\mathrm{Randomly}\mathrm{select}\frac{\left|\mathit{AD}\right|}{k}\cdot \sqrt{k}$ attributes in the exception field

8:          End if

9:      End if

10: return N

3.4. Three-Way Selection Classifier Evaluation Algorithm

Accuracy is a crucial performance index for evaluating anomaly traffic detection classifiers. Dai et al. [23] developed a selective classifier ensemble that prioritizes diversity to improve generalization ability and considers accuracy when evaluating model performance. While accuracy is an important metric, it is affected by factors like data distribution, leading to instability and room for improvement. To address this issue, we propose constructing an evaluation function for anomaly traffic detection classifiers that combines pure accuracy [24] with diversity metrics to account for randomness and stabilize performance. Incorporating additional metrics that capture the performance of the classifier under different data distributions could further enhance the evaluation function.

In the classical binary classification problem, it is assumed that $X=\{x_1,x_2,\dots ,x_n\}$ is an n-dimensional feature space and $Y=\{0,1\}$ is the label result of the binary classification. The dataset composed of X and Y is used to train the classifier $h(X)$, and the confusion matrix is introduced to describe the classification result. As shown in Table 1.

Table 1. Confusion matrix.

Y/h(X)	h(X) = 1	h(X) = 0	Total (Y)
Y = 1	TP	FN	p
Y = 0	FP	TN	1 − p
Total (h)	q(h)	1 − q(h)	1

p represents the proportion of positive samples in the data sample of Y = 1, and q(h) represents the proportion of positive samples in the classification result of 1. The random accuracy of classifier h(X) is calculated by:

$$\mathit{RA}(h)=p\cdot q(h)+(1-p)\cdot (1-q(h))$$

(16)

The efficacy of a classifier trained on various datasets can vary significantly. Therefore, evaluating the classifier’s performance based solely on its accuracy is not always sufficient. Instead, it is more appropriate to utilize the pure accuracy index, which eliminates the effects of random accuracy and normalizes the data. The pure accuracy of a classifier h(X) can be defined as follows:

$$\mathit{PA}(h)=\frac{Acc(h)-RA(h)}{1-RA(h)}$$

(17)

The definition of pure accuracy describes the relationship between pure accuracy and accuracy, where the accuracy resulting from random consistency is termed random accuracy [25]. Pure accuracy represents the accuracy of a model after eliminating the effects of random consistency and is a relative indicator. On the other hand, accuracy is an absolute index that measures the algorithm’s performance, which comprises the sum of random accuracy and pure accuracy. During machine learning training tasks, the classifier may produce varying degrees of random consistency due to differences in datasets, operating environments, and algorithm implementations. Hence, evaluating the classifier’s performance using pure accuracy, which removes the effects of random consistency, is a more accurate and reasonable approach. A higher calculated pure accuracy indicates better performance of the abnormal traffic detection classifier.

The calculation method of the classifier evaluation index combined with pure accuracy and diversity design is:

$$\mathit{PAD}(h_t)=\frac{h_t^D-\mathit{min}(h_t^D)}{\mathit{max}(h_t^D)-\mathit{min}(h_t^D)}+\frac{h_t^p-\mathit{min}(h_t^p)}{\mathit{max}(h_t^p)-\mathit{min}(h_t^p)}$$

(18)

$h_t^D$ represents the DFTwo value of the anomaly traffic detection classifier $h_t$, $\mathit{min}\left(h_t^D\right)$ represents the minimum value of DFTwo in all anomaly traffic detection classifiers, and $\mathit{max}\left(h_t^D\right)$ represents the maximum value of DFTwo in all anomaly traffic detection classifiers. $h_t^p$ represents the PA value of the anomaly traffic detection classifier $h_t$, $\mathit{min}\left(h_t^p\right)$ represents the minimum value of all anomaly traffic detection classifiers PA, and $\mathit{max}\left(h_t^p\right)$ represents the maximum value of all anomaly traffic detection classifiers PA.

In order to further improve the performance of the decision tree in the ensemble model, a three-way selection classifier evaluation method is introduced into the base classifier set generated by the random selection of three attributes. The basic idea is shown in Figure 5. Set the pure accuracy and diversity as the classifier evaluation index, $({\alpha }_2,{\beta }_2)$ as the division threshold of the normal domain, abnormal domain, and uncertain domain, when the $PAD(h_t)$ value is larger, the base classifier $h_t$ should be left.

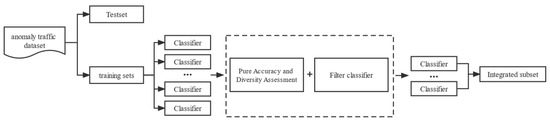
Figure 5. Three-way selection classifier evaluation ideas.

Thus, when the $PAD(h_t)$ value of the base classifier is greater than ${\beta }_2$, the base classifier $h_t$ is divided into the normal domain; when the $PAD(h_t)$ value of the base classifier is less than ${\alpha }_2$, the base classifier $h_t$ is divided into the anomaly domain, and the classifier is divided into the anomaly domain is deleted directly. When the $PAD(h_t)$ value of the base classifier is greater than ${\alpha }_2$ and less than ${\beta }_2$, the base classifier $h_t$ is divided into an uncertain domain. If the accuracy of the ensemble subset of the base classifier $h_t$ is increased, the base classifier $h_t$ in the uncertain domain is deleted, otherwise, the base classifier $h_t$ is retained.

Three-way selection classifier evaluation is a selection method of ensemble learning classifier. The base classifier set $H=\{h_1,h_2,\dots ,h_n\}$ generated by dataset training is screened to find the base classifier combination with the best pure accuracy and diversity evaluation index, and further eliminate the instability caused by randomness. The three-way selection classifier evaluation steps are shown in Algorithm 2.

Algorithm 2: Three-Way Selection Classifier Evaluation Algorithm

Input: Base classifier set $H=\left\{h_1,h_2,\dots ,h_N\right\}$, threshold parameter $({\alpha }_2,{\beta }_2)$, confidence $\mathsf{\theta }$ Output: BestEnsemble

$1:\mathbf{Initialize}\mathrm{S}=\mathrm{H},\mathrm{BestEnsemble}=\varnothing ,\mathrm{MaxDiv}=0,\mathrm{POS}=\mathrm{BND}=\mathrm{NEG}=\varnothing$

$2:\mathbf{while}\mathrm{S} \ne \varnothing$ do

$3:\mathbf{For}{h}_tϵ\mathrm{S}$ do

$4:\mathrm{compute}\mathrm{PAD}(h_1$)

$5:\mathbf{If}\mathrm{PAD}\left(h_t\right)>\mathsf{\alpha }$ then

$6:\mathrm{POS}\leftarrow h_t$

7:           Else

$8:\mathbf{If}\mathsf{\beta }<P$$\mathrm{AD}(h_t$$)<\mathsf{\alpha }$ then

$9:\mathrm{BND}\leftarrow h_t$

$10:\mathbf{If}A(S-\{h_t$}) > A(S) then

$11: S_t$ = $S$ − {$h_t$}

12:                     End if

13:               Else

14:                 NEG $\leftarrow h_t$

15:                $S_t$ = S − {$h_t$}

16:           End if

17:           If A($S_t$) >$\mathsf{\theta }$ then

18:              If Diversty($S_t$) > MaxDiv then

19:                    MaxDiv = Diversty($S_t$)

20:                    BestEnsemble =$S_t$

21:               End if

22:            Else

23:               S = $S_t$

24:            End if

25:        End for

26:   End While

27:   Return BestEnsemble

3.5. Random Forest Node Weighting Algorithm Based on GWO Optimization

As an ensemble learning method consisting of N decision tree combinations, random forest utilizes random extraction to generate a subset of abnormal traffic data for training. Additionally, the random selection of abnormal traffic sample features is used to calculate split nodes, which effectively enhances the generalization ability of the model and reduces overfitting. However, due to the random selections involved in the process of generating the decision tree classifiers, there may be significant differences in classification accuracy between these classifiers and different nodes within the same decision tree. Consequently, the integrated random forest model may be negatively impacted by decision tree classifiers with poor performance, resulting in suboptimal overall abnormal traffic prediction accuracy.

To address this issue, we propose a random forest node weighting algorithm based on GWO optimization, using the random selection of three attributes and the evaluation of a three-way selection classifier. The algorithm assigns different weight coefficients to the leaf nodes of each tree in the final integrated base classifier set, with the swarm intelligence GWO algorithm used for adaptive optimization to identify the best coefficient combination for improving the prediction accuracy of the random forest classifier in detecting abnormal traffic data. For details on the algorithm flow, please refer to Algorithm 3.

Algorithm 3: Random forest node weighting algorithm based on GWO optimization

Input: Sample set $S=\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\},\mathrm{classifier}\mathrm{number}k,\mathrm{iteration}\mathrm{number}d$ Output: Node weighted decision tree set T

$1:\mathbf{Initialize}\mathrm{S}=\mathrm{H},\mathrm{BestEnsemble}=\varnothing ,\mathrm{MaxDiv}=0,\mathrm{POS}=\mathrm{BND}=\mathrm{NEG}=\varnothing$

$2:\mathbf{Initializate}P=[p_1^l,p_2^l,\dots ,p_L^l],l\in \{1,2,\dots ,k\}$, $fitness=\frac{1}{n}{\displaystyle \sum _{u=1}^n|\underset{i=1,2,\dots ,s}{\arg \max }{\displaystyle \sum _{j=1}^{N}F[(f_j(x)=i)\cdot P_j^{}]}-y|}$

$3:\mathbf{For}u\leftarrow 1$$\mathrm{to}k\mathbf{then}$

$4:\mathrm{Obtaining}{\mathrm{Group}}^u\mathrm{Training}\mathrm{Set}\mathrm{to}{\mathrm{Train}}^u$ Decision Tree Classifier

$5:\mathbf{For}v\leftarrow 1$$\mathrm{to}d\mathbf{then}$

$6:\mathrm{Initializate}\mathrm{gray}\mathrm{wolf}\mathrm{populations}{\mathrm{X}}_{\mathrm{L}},a,\mathrm{A},\mathrm{C}$

$7:\mathrm{Calculate}\mathrm{the}fitness$ of individuals in the population

$8:\mathrm{Save}\mathrm{the}\mathrm{first}\mathrm{three}\mathrm{wolves}\alpha ,\beta ,\delta \mathrm{with}\mathrm{the}\mathrm{smallest}fitness$

$9:\mathrm{Update}\mathrm{the}\mathrm{position}\mathrm{of}\mathrm{the}\mathrm{wolves}\mathrm{in}\mathrm{population}{\mathrm{X}}_{\mathrm{L}}$

$10:\mathrm{Update}\mathrm{parameters}a,\mathrm{A},\mathrm{C}$

$11:\mathrm{Calculate}\mathrm{the}fitness$ of all gray wolves

$12:\mathrm{Update}\alpha ,\beta ,\delta$ locations

13:       End

$14:\mathrm{Get}\mathrm{the}\mathrm{best}\mathrm{weighted}\mathrm{coefficient}\mathrm{combination}{p}^u$

15:     End

16:     Return T

In the fitness function $fitness=\frac{1}{n}{\displaystyle \sum _{u=1}^n|\underset{i=1,2,\dots ,s}{\mathit{arg}\mathit{max}}{\displaystyle \sum _{j=1}^{N}F[(f_j(x)=i)\cdot P_j^{}]}-y|}$, $x,y$ is the data and label of the test set, $N$ is the number of classifiers,$s$ is the number of categories classified, $f_j(x)$ represents the classification result of the $j$ classifier, and $F(\cdot )$ function is used to determine whether the parameters meet the output conditions.

4. Experiment and Result Analysis

4.1. Experimental Environment and Dataset

(1) Hardware and software environment

The CPU model of the device selected in this experiment is Intel (R) Xeon (R) W-1390 P (3.50 GHz), the memory is 16 GB, and the software environment for running the algorithm is Python 3.8.

(2) Selected datasets

The experimental data used in this paper are CIC-IDS-2017, KDDCUP99, and NSLKDD.

The CIC-IDS-2017 dataset is a collaboration project between the Communications Security Agency (CSE) and the Canadian Cybersecurity Institute (CIC). It contains the latest 14 types of network attack traffic and normal traffic. A total of 78 attribute features were extracted, including 14 types of network abnormal traffic attacks. The dataset contains traffic data for a total of 5 days.

The KDDCUP99 dataset comes from the DARPA intrusion detection evaluation project. All network data traffic comes from the simulated Air Force LAN, which contains nearly 5 million network connections. The dataset contains 41 feature attributes and a category identifier.

The NSLKDD dataset is an improved version of the KDDCUP99 dataset, which has no redundant data. The dataset contains four different types of attacks: denial of service, detection, U2R, and R2L. There are 125,973 data in the KDDTrain + training set and 22,544 data in the test set. Each of the data contains 41 features.

In order to improve the efficiency of the experiment, the above three experimental datasets were stratified random sampling, and random samples to generate datasets, a total of 19,832 data.

4.2. Evaluation Indicators

Different machine learning tasks require different evaluation criteria, which are selected based on the priorities of the task. For instance, in medical aid diagnosis systems, accurate and reliable diagnoses are critical for patient outcomes, and the recall rate (i.e., the probability of illness in the aid diagnosis results after combining medical information) is a key factor in achieving this goal. In recommendation systems based on large-scale data analysis, the focus is on whether the system comprehensively pushes content of interest based on user usage habits, making the recall rate a more reasonable indicator. In this article, we select several evaluation indicators, including the precision rate, recall rate, F1 score, and accuracy, to observe the performance of abnormal traffic detection models. The confusion matrix is defined in Table 2.

Table 2. Model index evaluation criteria.

	Truth Value
predicted value	TP (True Positive)	FN (False Positive)
	FP (False Negative)	TN (True Negative)

The evaluation of classification results and model performance often relies on measures of precision and recall. Precision, for instance, reflects the probability that the predicted abnormal samples actually correspond to abnormalities in the data, thereby capturing the precision of model abnormal samples. Recall rate, on the other hand, quantifies the proportion of actual abnormal samples that the model successfully detects, thus revealing the model’s ability to identify such instances. Both precision and recall are critical to assessing the overall detection ability of a model and are commonly used to evaluate its performance. Additionally, F1-Score provides a useful means of evaluating classification accuracy, accounting for both precision and recall rates. Finally, accuracy serves as a crucial measure of model performance, capturing the ratio of true positives and true negatives to all predictions and samples. This value is calculated according to the following formula:

$$\mathrm{Precision}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}$$

(19)

$$\mathrm{Recall}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$$

(20)

$$\mathrm{F}1\_\mathrm{score}=\frac{2\times \mathrm{precision}\times \mathrm{recall}}{\mathrm{precision}+\mathrm{recall}}$$

(21)

$$\mathrm{Accuracy}=\frac{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}}$$

(22)

4.3. Data Pre-Processing

The original samples extracted from the dataset need to be preprocessed. The content of data preprocessing includes data filtering, abnormal character numericalization, and numerical data standardization.

(1) Data filtering

The training and test sets of the CIC-IDS-2017 dataset, the KDDCUP99 dataset, and the NSLKDD dataset are merged to filter the combined new dataset. Remove invalid features in the dataset; takes the value in the dataset column to two decimal places; delete samples with the wrong label or invalid label values; delete redundant data samples with the same value. After the above data filtering processing, the dataset contains 16,683 data samples. The distribution of data samples is as Table 3:

Table 3. Sample information after experimental dataset screening.

	CIC-IDS-2017	KDDCUP99	NSLKDD
feature dimension	65	41	41
category number	13	19	5
Test set data	6521	5583	4579

(2) Numericalization of abnormal characters

Because there are abnormal characters in the feature attribute values of the datasets used in the experiment, one-hot encoding is used to re-encode them. In order to avoid a large number of redundant features generated by using one-hot encoding for the attribute columns with a large number of eigenvalues, the categorical feature attribute values of the CIC-IDS-2017 dataset, KDDCUP99 dataset and NSLKDD dataset are labeled, and encoded, respectively. The label category selects the one-hot encoding to convert the dataset into numerical feature attributes.

(3) Numerical data standardization

In order to eliminate the difference between different column attribute data, shorten the calculation time of the model and accelerate the convergence speed of the algorithm, it is necessary to standardize the numerical data. The Z-Score standardization method is used to make the data obey the distribution with a mean of 0 and a variance of 1. The standardized Z-Score calculation is as follows:

$$\tilde{x}=\frac{x-\mu }{\sigma }$$

(23)

$x$ is the value in the attribute column of the original dataset, $\mu$ is the mean value of the column feature attribute of the dataset, $\sigma$ is the standard deviation of the column feature attribute of the dataset, and $\tilde{x}$ is the result of the standardization of the original data.

4.4. Influence Analysis of Experimental Parameters

(1) Analysis of Three-Way Decision Attribute Random Selection Parameter

In the dataset, 80% of the samples are randomly selected as the training set and 20% of the samples are used as the test set. The three-way attributes of the model randomly select the hyperparameter $({\alpha }_1,{\beta }_1)$ in the 0.0001~0.1 value interval according to the gradient. Set to 0.0001~0.001, 0.001~0.01, 0.01~0.1 three groups of experimental intervals for comparison, and named interval 1, interval 2, and interval 3. The value range of parameter $\delta$ is set between 0 and 2.34 according to the experience of parameter adjustment. The precision and recall rate changing with $\delta$ are shown in Figure 6, where the horizontal axis is the value of parameter $\delta$ and the vertical axis is the precision/recall rate.

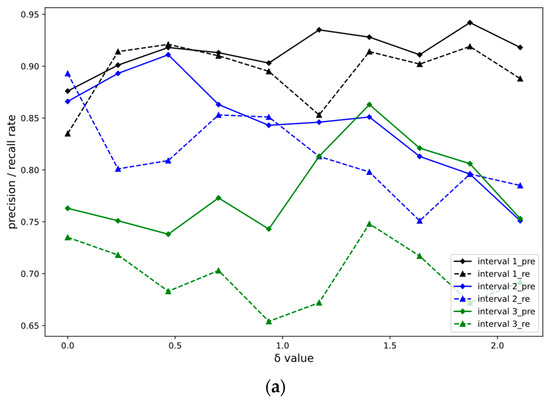
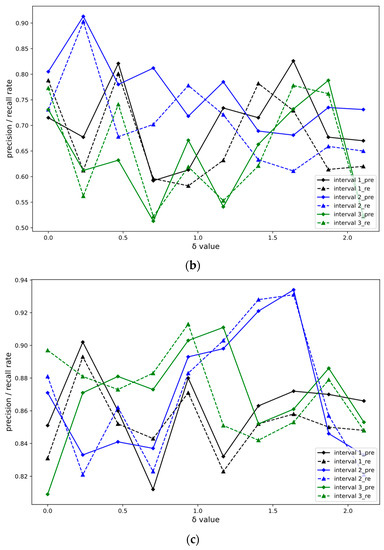
Figure 6. Curves of experimental dataset changing with parameter $\delta$ in different $({\alpha }_1,{\beta }_1)$ intervals. (a) CIC-IDS-2017 Dataset Experimental Results. (b) KDDCUP99 Dataset Experiment Results. (c) Experimental results of NSLKDD dataset.

Compare the change curves of accuracy and recall rate with parameter $\delta$ under three attribute random selection hyperparameters $({\alpha }_1,{\beta }_1)$ in three different value intervals. Taking the three experimental datasets selected in this paper as an example, when the hyperparameter $\delta$ is calculated with 0.26 as the step size in the range of (0, 2.34), the results of accuracy and recall rate are calculated. The repeated experiments compare the accuracy and recall rate indicators to determine the $\delta$ optimal values of the three experimental datasets, as shown in Table 4.

Table 4. Optimal Values of A and B Parameters for Three Datasets.

Dataset	$\mathit{(}{\mathit{\alpha }}_1,{\mathit{\beta }}_1\mathit{)}$	$\mathit{\delta }$	Optimal Value
CIC-IDS-2017	0.0001~0.001	(0, 2.34)	2.08
KDDCUP99	0.001~0.01	(0, 2.34)	0.26
NSLKDD	0.001~0.01	(0, 2.34)	1.82

In Section 3.3, we propose a three-attribute random selection algorithm and introduce three attribute partition thresholds $({\alpha }_1,{\beta }_1)$ and a hyperparameter $\delta$ to improve the rules for random forest attribute selection. By optimizing the hyperparameter $\delta$ across different gradient intervals and using experimental results to compare Precision and Recall indicators for varying values of the hyperparameter under different gradients, we identify the optimal threshold values $({\alpha }_1,{\beta }_1)$ and hyperparameter $\delta$ based on the experimental comparison results. Our approach offers a novel solution for selecting attributes in random forests and has the potential for improving accuracy in a variety of applications.

(2) Three-way selection classifier evaluation parameter analysis.

The value range of different ${\alpha }_1$ and ${\beta }_1$ ultrasound parameters will affect the proportion of datasets in different domains after attribute division. The value of hyperparameter $\delta$ determines the selection of attributes in the positive domain, negative domain, and boundary domain of the base classifier. It can be seen from the experimental results that there are still many fluctuations in the indicators of the experimental results under the combination of different hyperparameters. It may be that the reconstruction errors of some abnormal samples in the dataset are latent in the normal error level, resulting in fluctuations in the model detection results. After determining the optimal value of the hyper-parameters $\delta$ in the experimental dataset, the parameter grid search method and the five-fold cross-validation method are used to compare the three-way selection classifiers of the three experimental datasets to evaluate the relationship between the hyper-parameters ${\alpha }_2$ and ${\beta }_2$ and the accuracy, and further determine the value range of the hyper-parameters ${\alpha }_2$ and ${\beta }_2$. The experimental results are shown in Figure 7, where the horizontal axis represents the hyper-parameter ${\alpha }_2$ and the vertical axis represents the hyper-parameter ${\beta }_2$.

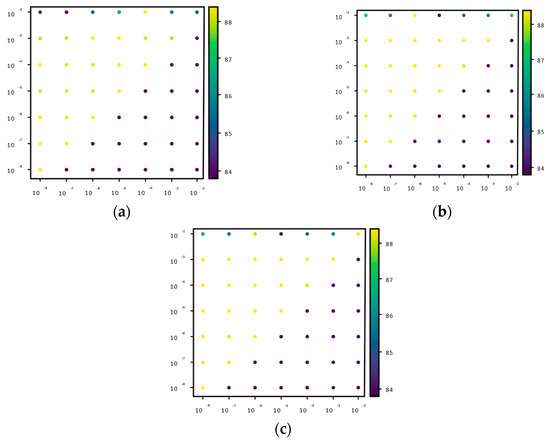
Figure 7. Model hyperparameter grid search results. (a) CIC-IDS-2017 Dataset Experimental Results. (b) KDDCUP99 Dataset Experiment Results. (c) Experimental results of NSLKDD dataset.

According to the experimental results of the parameter grid search in Figure 7, the three-way selection classifier of the three-way selection random forest optimization model for abnormal traffic detection is determined. The results of the evaluation of the hyperparameters ${\alpha }_2$ and ${\beta }_2$ are shown in Table 5, and the corresponding accuracy and recall rate are the effect of the selective integration of the decision tree with parameters ${\alpha }_2$ and ${\beta }_2$.

Table 5. Model hyperparameters.

Dataset	${\mathit{\alpha }}_2$	${\mathit{\beta }}_2$	Precision Rate	Recall Rate
CIC-IDS-2017	1.23 × 10−7	1.14 × 10−4	0.9532	0.9344
KDDCUP99	1.18 × 10−5	1.21 × 10−3	0.9463	0.9122
NSLKDD	1.06 × 10−7	1.45 × 10−3	0.9481	0.9255

Building upon the optimal parameter combination identified in Section 4.3, we have devised three branch selection classifiers to assess the efficacy of various base classifiers for subsequent screening. The experimental results obtained from the grid search demonstrate that the hyperparameter value plays a crucial role in determining the final set of retained base classifiers, thus affecting the accuracy of prediction outcomes significantly.

4.5. Weighted Coefficient Optimization of GWO Algorithm

The optimized random forest model can be prone to overfitting, but the use of three-way attribute random selection and three-way selection classifiers effectively address this issue. However, despite these randomization processes, there may still be variations in performance among classifiers and leaf nodes. As such, some classifiers with poor performance can negatively impact the accuracy of the overall model.

To improve the classification ability of the optimized model, we employed the Gray Wolf Optimization (GWO) algorithm. This algorithm is known for its strong optimization ability, fast calculation speed, and ability to avoid local optima. The GWO algorithm optimized the node coefficients of the model evaluated by the three-way attribute random selection and three-way selection classifiers and determined a set of weighting coefficients. The GWO algorithm was initialized with 20 populations and run for a maximum of 100 iterations. The range of weighting coefficients was set to [0.1, 10], and the initial values were generated randomly. The results of the optimization iteration are shown in Figure 8.

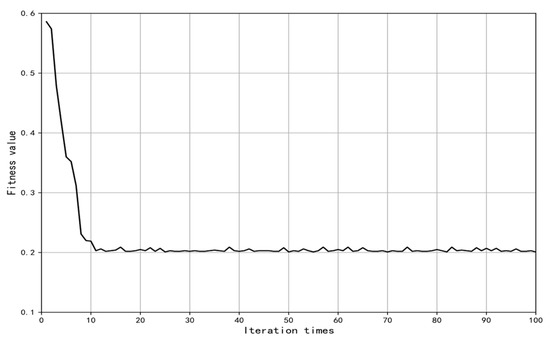
Figure 8. GWO optimization iterative curve.

The GWO algorithm weighted coefficient optimization throughout the iterative process of fitness value changes is shown in Figure 8. It can be seen that the fitness value reaches the minimum around the 10th time and the subsequent iteration values fluctuate around the minimum value. The results of the minimum fitness value are brought into the three-way attribute random selection and three-way selection classifier to evaluate the optimized random forest model. The accuracy comparison results before and after model optimization are shown in Table 6. It can be seen that the introduction of the optimization algorithm improves the performance of different datasets.

Table 6. Algorithm optimization experiment accuracy comparison results.

Dataset	Before	Optimized
CIC-IDS-2017	0.9532	0.9614
KDDCUP99	0.9464	0.9523
NSLKDD	0.9481	0.9536

4.6. Model Comparison Experiment

We conducted comparative experiments using SVM, GBDT, CNN, a three-branch decision random forest optimization model, a three-branch decision random forest model, and a random forest model. For each model, we calculated the precision, recall, and F1 scores for the abnormal network traffic datasets CIC-ISD-2017, KDDCUP99, and NSLKDD. Our proposed model was compared to the other five models in terms of F1 score, and the results are presented in Figure 9.

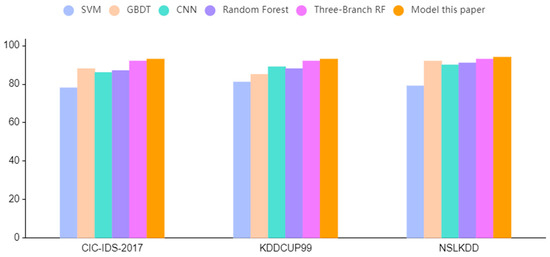
Figure 9. Comparison of F1 score indicators of models on the experimental dataset.

Based on the findings in Figure 9, our proposed three-branch random forest optimization model for detecting abnormal traffic outperforms both traditional machine learning algorithms and convolutional neural networks in terms of the F1 score performance index. The model achieved the best results on all three datasets, with an improvement ranging from 0.02% to 0.18% when compared to traditional machine learning detection models. Compared to the CNN model, the F1 score index increased by 0.08%, suggesting that our proposed model outperforms other comparative models in detecting abnormal traffic. In summary, the results of this study demonstrate that our model can achieve superior detection performance in abnormal traffic detection tasks. We further compared the performance differences of different models in Precision, Recall, and Accuracy, as shown in Figure 10.

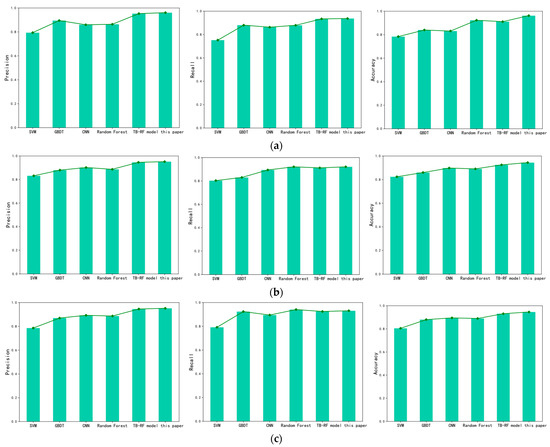
Figure 10. Comp Comparative results of indicators from different models on the experimental dataset. (a) Comparison Results of Model Indicators on CIC-ISD2017 Dataset. (b) Comparison Results of Model Indicators on KDDCUP99 Dataset. (c) Comparison results of model indicators on the NSLKDD dataset.

Based on the data presented, the proposed model in this article outperforms traditional machine learning algorithms, such as SVM, GBDT, and Random Forest, in detecting abnormal traffic on the CIC-ISD2017, KDDCUP99, and NSLKDD datasets. Specifically, on the CIC-ISD2017 dataset, the proposed model achieves a 6.6% to 16.7% increase in accuracy and a 5.7% to 18.5% increase in recall, as well as a 3.9% to 17.8% increase in precision. On the KDDCUP99 dataset, the precision index is improved by 5% to 12%, the recall index is improved by 0% to 11.8%, and the accuracy index is improved by 4.6% to 12%. Finally, on the NSLKDD dataset, the precision index is improved by 6% to 16.7%, the recall index is improved by 0% to 13.9%, and the accuracy index is improved by 5.1% to 14.1%. These results demonstrate that the proposed model performs better than traditional machine learning algorithms on different datasets in terms of detection performance.

The present study compares the accuracy, recall, and precision of three different datasets, namely CIC-ISD-2017, KDDCUP99, and NSLKDD, using various algorithms. As shown in Table 7 and Table 8. To improve the process of feature attribute selection and classifier construction of random forests, the authors introduce a novel approach that combines the weighted coefficient method with the three-branch decision-making idea. Despite increasing the computational complexity of the algorithm and sacrificing the training time, the proposed weighted three-branch decision-making random forest model exhibits improved accuracy in abnormal network traffic prediction tasks. Table 9 presents a comparison of the training times of the proposed model with those of other approaches.

Table 7. F1 score index of the model on the experimental dataset.

Dataset	SVM	GBDT	CNN	Random Forest	Three_Branch RF	Model This Paper
CIC-IDS-2017	0.7823	0.8851	0.8631	0.8747	0.9241	0.9448
KDDCUP99	0.8114	0.8532	0.8972	0.8831	0.9237	0.9331
NSLKDD	0.7962	0.9253	0.9031	0.9147	0.9362	0.9439

Table 8. Summary of experimental results for the model on the experimental dataset.

	CIC-IDS2017			KDDCUP99			NSLKDD
	Precision	Recall	Accuracy	Precision	Recall	Accuracy	Precision	Recall	Accuracy
SVM	0.7942	0.7524	0.7846	0.8328	0.8036	0.8247	0.7864	0.7929	0.8055
GBDT	0.8954	0.8802	0.8411	0.8806	0.8311	0.8605	0.8702	0.9716	0.8803
CNN	0.8605	0.8534	0.8305	0.9021	0.8943	0.8982	0.8935	0.8987	0.8955
Random Forest	0.8646	0.8797	0.9237	0.8873	0.9214	0.8914	0.8937	0.9416	0.8907
Three_Branch RF	0.9538	0.9346	0.9113	0.9465	0.9125	0.9255	0.9488	0.9255	0.9318
Model this paper	0.9614	0.9375	0.9625	0.9527	0.9216	0.9443	0.9531	0.9314	0.9464

Table 9. Model training time comparison.

Dataset	Random Forest	Three-Way Decision Random Forest	Model in This Paper
CIC-IDS-2017	62.36 s	4931.21 s	5063.42 s
KDDCUP99	56.21 s	4321.73 s	4401.87 s
NSLKDD	44.83 s	3922.14 s	4029.56 s

5. Conclusions

This article addresses the challenge of uncertain samples in abnormal traffic detection datasets. We present a novel approach to abnormal traffic detection using a three-branch selection random forest optimization model. Our model leverages three-attribute random selection, three-selection classifier evaluation, and random forest node weighting based on GWO optimization to overcome issues related to the prediction performance of the final model due to differences in attribute selection and classifier performance during construction. To comprehensively consider characteristic attributes in abnormal traffic samples, we adopt a delayed decision method. We avoid dimensionality reduction techniques to provide decision-makers with as much feature information as possible, further improving model performance. Our experimental analysis demonstrates superior detection results compared to traditional machine learning methods. Future work will focus on optimizing the model training cost, streamlining the model structure, and exploring detection performance under real network traffic data.