Chebyshev Polynomial-Based Fog Computing Scheme Supporting Pseudonym Revocation for 5G-Enabled Vehicular Networks

Abstract

The privacy and security of the information exchanged between automobiles in 5G-enabled vehicular networks is at risk. Several academics have offered a solution to these problems in the form of an authentication technique that uses an elliptic curve or bilinear pair to sign messages and verify the signature. The problem is that these tasks are lengthy and difficult to execute effectively. Further, the needs for revoking a pseudonym in a vehicular network are not met by these approaches. Thus, this research offers a fog computing strategy for 5G-enabled automotive networks that is based on the Chebyshev polynomial and allows for the revocation of pseudonyms. Our solution eliminates the threat of an insider attack by making use of fog computing. In particular, the fog server does not renew the signature key when the validity period of a pseudonym-ID is about to end. In addition to meeting privacy and security requirements, our proposal is also resistant to a wide range of potential security breaches. Finally, the Chebyshev polynomial is used in our work to sign the message and verify the signature, resulting in a greater performance cost efficiency than would otherwise be possible if an elliptic curve or bilinear pair operation had been employed.

1. Introduction

The wide deployment of wireless technologies is rapidly and continuously growing, and the fifth-generation (5G)-enabled vehicular networks have paid attention to and interest in providing intelligent vehicles to communicate with other vehicles for improving the driving experience and enhancing traffic safety [1,2].

Safer road conditions for drivers and passengers are made possible by 5G-enabled vehicular networks [3]. The latest trend in the evolution of wireless communication technologies is the use and evolution of 5G cellular systems, which is supported by significant government development in many countries [4,5]. As a result of 5G’s features, which increase the node information per unit region by a factor of ten thousand with a broadcast rate as high as 10 Gbps, a 5G network satisfies a speed boost that is orders of magnitude greater than that of the current 4G systems [6,7]. The five-fold decrease in latency and the doubling of battery life brought about by 5G open up numerous possibilities for transportation-based networks [8,9].

There are security and privacy concerns for vehicular networks because of the information provided by automobiles [10,11,12]. Intruders can alter the vehicle’s transmitted message. In order to solve these problems, various researchers have developed an authentication strategy for vehicular networks [13,14].

The existing schemes are vulnerable to support pseudonym revocation requirements and the massive overhead costs of networks. The insider attacker should be revoked from the use of services for vehicular networks. In addition, in high traffic density, the vehicle should be signed and verified very fast, which requires a lightweight operation to achieve a good efficiency performance. The main question of this paper is “does Chebyshev polynomial satisfy pseudonym revocation and reduce the overhead of the system in terms of communication and computational costs”. Therefore, this paper proposes a Chebyshev polynomial-based fog computing scheme supporting pseudonym revocation for 5G-enabled vehicular networks. The important contributions are listed as follows.

• We present a fog computing technique for 5G-enabled vehicle networks, which is based on the Chebyshev polynomial and allows for the revocation of pseudonyms.
• We adapt fog computing in the proposed scheme to generate security parameters and check the validity of vehicles.
• We adapt the 5G technology to increase the communication range among vehicles and the system, which avoid the expensive RSU used.
• In order to stop an insider attack, we use fog computing. As soon as the fog server detects that a pseudonym-timestamp ID is about to expire, it will not renew the signature key.
• Our solutions not only pass all privacy and security tests but are also resistant to a wide range of common security assaults.
• In our study, we use the Chebyshev polynomial to sign messages and verify the signature, which results in lower overall performance costs.

The remaining sections of this paper are laid out as follows. We discuss the relevant work conducted on vehicle networks in Section 2. In Section 3, we present the context of this paper. Our proposed method of removing pseudonyms is described in the cited Section 4. In Section 5, we detail the findings of our work’s security analysis and performance evaluation. Lastly, Section 6 is the conclusion.

2. Related Work

Here, we take a look back at the research that relates to vehicle networks. To address the privacy and security concerns inherent in vehicle networks, numerous authentication systems have been developed recently.

Wang et al. [15] described a multiple-strategies differential privacy framework on sparse tensor factorization for the analysis of HOHDST network traffic data. The MDPSTF has three differential privacy (DP) mechanisms: DP, concentrated DP, and local DP.

In 5G-enabled vehicle networks, Al-Shareeda et al. [16] presented a lightweight quantum-resistant strategy based on the lattice approach. In order to produce and verify the signatures of the messages exchanged between cars, the solution leverages matrix multiplication in place of operations-based bilinear pair cryptography or operations-based elliptic curve encryption. Despite its reduced performance, our solution is still lightweight enough to withstand quantum attacks. The plan relies only on 5G technology and makes no reference to RSUs in any way. According to the results of the security research, the solution does not only satisfy the privacy and security qualities, but it also is resistant to quantum attacks.

Pu et al. [17] proposed a deep-learning-based automatic fetal ultrasound standard plane recognition (FUSPR) model for the IIoT setting, with the goal of creating a distributed ultrasound data processing and forecasting platform. This would make use of both IIoT and HPC technologies.

For this reason, Cui et al. [18] created the IoAV paradigm to deal with the issues that arise due to these constraints. Authentication schemes that are both trustworthy and applicable in the IoAV are necessary for ensuring the safe remote control of AVs. A secure remote control system for AVs is proposed using our suggested chaotic map-based authenticated key agreement (CMAKA) mechanism. Users, data centers, and the AV all negotiate their own unique session keys to create a safe channel of communication. In addition, during the authentication process, a physical unclonable function (PUF) is used to generate a secure private key. Game hopping and the popular Real-or-Random (ROR) model are used to assess our scheme’s security.

The 5G-enabled vehicular fog computing may collect and analyze the relevant vehicle data, paving the way for non-contact autonomous healthcare monitoring while also improving the driving experience and safety on the road. Al-Shareeda et al. [5] offered a COVID-19 vehicle with a mutual authentication method for 5G-enabled vehicular fog computing as a means of controlling the spread of the auto epidemic. Two versions of the special flag are used in the proposed scheme: SF = 0 for regular vehicles and SF = 1 for COVID-19 vehicles. In addition to achieving COVID-19 and healthcare goals, the proposed scheme also adheres to stringent privacy and security standards.

In the context of fifth-generation (5G) wireless communications, Wang et al. [19] described a network architecture in which unmanned aerial vehicles (UAVs) are used as an aerial radio access platform to intelligently develop a system strategy and allow for the offloading of tasks and the harvesting of energy by ground-based devices.

Abassi et al. [20] proposed a proposition of a trust-based security scheme by presenting a VANET Grouping Technique (VGA), a suitable clustering algorithm that divides the network into sections led by volunteers. Next, it is based on the Video Graphics Array (VGA).

Zhang et al. [21] proposed a dual blockchain-assisted conditional privacy-preserving authentication framework and protocol for VANETs. The identity authentication and privacy preservation of vehicles in VANETs can be realized without relying on a centralized trusted third party. The proposed scheme also allows for the conditional tracking of illegal vehicles. The decentralized dynamic revocation of illegal vehicles can be realized through smart contracts, rendering the scheme efficient and scalable.

To prevent unauthorized access, Bayat et al. [22] developed an authentication mechanism in which the system’s master key is stored in advance in all participating vehicles. The vehicle generates its own pseudonym-ID and signature key using the system’s master key throughout the message signing procedure of Bayat et al. [22].

Li et al. [23] presented an authentication approach in which groups of pseudonym-IDs and their matching signature keys are preloaded into each participating vehicle. When signing a message using the approach proposed by Li et al.’s scheme [23], the vehicle chooses a pseudonym-ID and signature key at random from sets sent by the TA.

Using a 5G-enabled vehicular network, Cui et al. [24] developed a content-sharing method in which the master key is preloaded to each registered car.

Al-Shareeda et al. [25] suggested a Chinese remainder theorem-based password-guessing attack-aware authentication technique, with the security parameters supplied by the trusted authority (TA) at the registration process.

Additionally, we summarize the security comparison between the related work and our proposal in Table 1. In this paper, we propose a new Chebyshev polynomial-based fog computing scheme supporting pseudonym revocation for a 5G-enabled car system. However, as we can see from Table 1, the schemes of Bayat et al. [22], Li et al. [23], Cui et al. [24], and Al-Shareeda et al. [25] are vulnerable to support revocation requirements. Since applying the elliptic curve and bilinear pair operations, these schemes are not efficient in terms of performance costs. Unlike the existing schemes, this paper applies the Chebyshev polynomial-based fog computing scheme to sign the message and verify the signature. This is because the existing schemes used elliptic curve and bilinear pairing operations to sign and verify messages. These operations are considered time-consuming and complexity operations.

Table 1. Assessment of Present Authentication Systems’ Security. Look to Section 3.2 for explanation of the seven criteria of comparison.

	Bayat et al. [22]	Li et al. [23]	Cui et al. [24]	Al-Shareeda et al. [25]	Our Work
Authentication and Integrity	Yes	Yes	Yes	Yes	Yes
Identity Privacy	Yes	Yes	Yes	Yes	Yes
Traceability	Yes	Yes	Yes	Yes	Yes
Unlinkability	Yes	Yes	Yes	Yes	Yes
Resistance to Attacks	Yes	Yes	Yes	Yes	Yes
Pseudonyms Revocation	NO	NO	NO	NO	Yes
Efficient	NO	NO	NO	NO	Yes

3. Background

In this section, the architecture and design goals of our work are described as follows.

3.1. Architecture

As described in Figure 1, our work’s architecture consists of the following four components: the trusted authority (TA), the 5G-base station (5G-BS), the fog server, and the onboard unit (OBU).

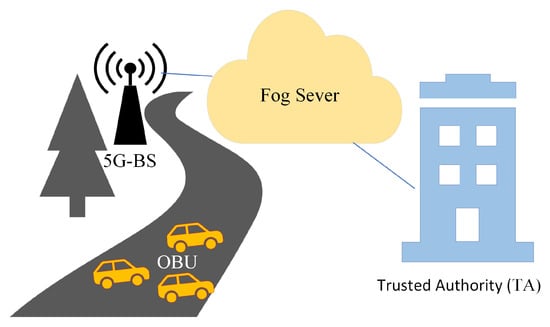
Figure 1. Architecture of Our Work.

• TA: TA is in charge of providing a valid computation and storage capacity for the main parameter of fog servers and OBUs within its authority. If the system contains incorrect or malicious information, the TA can trace and revoke the pseudonym-ID of the information source. In the vehicular network, all entities hold TA in high regard, and it is impossible to compromise TA.
• 5G-BS: A 5G-BS is a piece of roadway infrastructure that is permanently installed. Through the 5G protocol and secure wired connections, the 5G-BS can communicate with the vehicle’s OBU and the TA within a large range of communication.
• Fog Server: The fog server is in charge of providing the signature key of participating vehicles during joining through 5G-BS. The fog server saves the system’s master key to validate and authenticate the vehicle. We trust the fog server implicitly to help TA reveal the signers’ identities.
• OBU: The vehicle is equipped with an OBU that supports the dedicated short-range communication (DSRC) protocol and 5G protocol. The OBU sends a traffic-related message to the other OBUs or fog servers on a regular basis, informing them of traffic statuses, such as speed, location, and danger warnings.

3.2. Design Goals

Our solution should be secure and private for use in vehicle networks in the following criteria of comparison:

• Authentication and Integrity: The authenticity of the owner and validity of the message must be fulfilled to avoid any modification from the attacker.
• Identity Privacy: The true identity of the vehicle should be hidden in pseudonym-ID of the message.
• Traceability: The TA can trace any insider attacker by revealing the true identity of the vehicle.
• Pseudonym Revocation: The TA has the ability to revoke insider attackers to use services.
• Unlinkability: The attacker cannot link several signatures sent by the same owner.
• Resistance to Security Attacks: Our proposal must resist the security attacks, such as replay, forgery, modify, and man-in-the-middle attacks.
• Efficient: Our proposal must lower performances costs in terms of communication and computational overheads.

3.3. Proposed Framework

In this section, the proposed phases have the following phases.

• System Initialization (Phase 1): In our work, the TA is in charge of setting up the security parameters and registering vehicles and fog servers.
• Vehicle Joining to Fog Server (Phase 2): When a vehicle joins the covered area of the fog server through 5G-BS, it should be validated and authenticated to that fog server to share messages according to the parameters of the fog server. When a vehicle enters the covered area of the new fog server or its pseudonym-ID is expired, it should be joined to the fog server area and obtains the signature key and pseudonym-ID from the fog server.
• Message Signing (Phase 3): Before messages can be transmitted between vehicles on 5G-enabled networks, the linked vehicle must sign them using its signature key.
• Signature Verification (Phase 4): Before proceeding with the message $M_i$, the receiver-enrolled vehicle must verify the authenticity of the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$}.
• Pseudonym Revocation (Phase 5): Prior to the adversary broadcasting counterfeit messages to disrupt the 5G-enabled vehicular networks, we are able to track down the fraudulently registered car and revoke its pseudonym-ID during the pseudonym revocation phase.

3.4. Mathematics Used

In this section, we explain the following algorithms:

• Chebyshev Polynomial: Cosine and sine polynomials are represented by the Chebyshev polynomials and the Chebyshev polynomials, respectively. Some studies [26,27,28] based on Chebyshev polynomial.
• Elliptic Curve: Number theorists place a premium on elliptic curves, and this topic is currently a hotspot for study, for instance, Andrew Wiles’s demonstration of Fermat’s Last Theorem relied on elliptic curves. Elliptic curve cryptography (ECC) and integer factorization are two other areas where they are useful. Some studies [29,30] based on elliptic curve.
• Bilinear Pair: Ingenious systems for one-round three-party key negotiation, identity-based encryption, and aggregate signatures have all been developed using bilinear pairings. For certain selected elliptic curves, the Tate pairing can be used to generate appropriate bilinear pairings. Some studies [31,32,33] based on bilinear pair.

4. Proposed Scheme

As shown in Figure 2, our process entails the subsequent five phases. The notation used in the following phases of the proposal is described in Table 2.

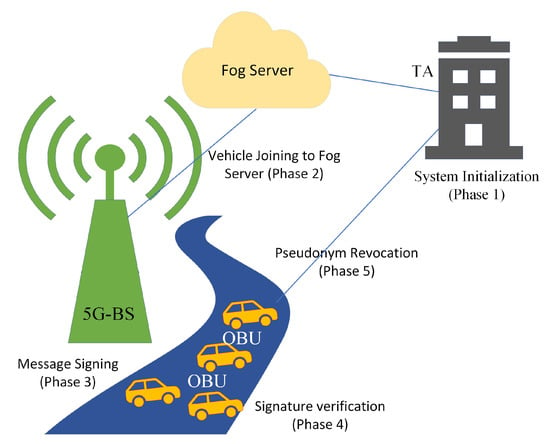
Figure 2. Five Phases of Our Work.

Table 2. Math Symbols Used and Their Definition.

Math Symbol	Definition
TA	Trusted Authority
5G-BS	Fifth-Generation Base Station
$P,k_S^{TA},x$	Chebyshev Polynomial Parameters
$PI{D}_{v_i}$	Pseudonym-IDs of Vehicle
$S{k}_{v_i}$	Signature Key
h	One-Way Hash Function
$S_{TA}$	Master’s Private Key
$\psi$	Security Parameter
$A{C}_{v_i}$	Authentication Code
$TI{D}_{v_i}$	Vehicle’s True Identity
$T_i$	Current Timestamp
||	Operations of Concatenation
⊕	Operation of X-OR

4.1. System Initialization (Phase 1)

We explain the following steps in detail.

• Let P and $k_S^{TA},x$ be the large prime and generated values regarding Chebyshev polynomial, respectively.
• TA chooses a random number $S_{TA}\in Z_q^{*}$ as its master secret key.
• Let $h:$${[-0,1]}^{*}\to$${[-0,1]}^l$ be one-way hash function according to Chebyshev polynomial.
• Let $\psi =$ {$k_{S}TA$, x, P, h} be the security parameters.
• TA chooses a random number $e{v}_i\in Z_q^{*}$ as secret parameter.
• Let $A{C}_{v_i}$ = $h\left(S_{TA}\right|\left|e{v}_i\right)$ be an authentication code.
• TA preloads an authentication code $A{C}_{v_i}$ and the security parameters $\psi =$ { $k_S^{TA}$, x, P, h} in each vehicle.
• TA preloads the master key $S_{TA}$ and the security parameters $\psi =$ { $k_S^{TA}$, x, P, h} in each fog server.

4.2. Vehicle Joining to Fog Server (Phase 2)

After entering the covered area of the new fog server through 5G-BS, the vehicle runs the following steps.

• The vehicle chooses random number $r\in Z_q^{*}$ and computes parameter $\alpha ={\mathcal{T}}_r\left(x\right)$ mod P and calculates pseudonym-ID $PI{D}_{v_i}=TI{D}_{v_i}\oplus h(A{C}_{v_i}\left|\right|T_1)$, where $TI{D}_{v_i}$ is a vehicle’s true identity and $T_1$ is a newness timestamp.
• The vehicle sends the first-tuple $\{\alpha ,PI{D}_{v_i},T_1{\delta }_{V-TA}\}$ to TA through 5G-BS by assisting fog server, where ${\delta }_{V-TA}=h\left(\alpha \right||PI{D}_{v_i}\left|\right|T_1\left|\right|A{C}_{v_i})$.
• Upon receiving the first-tuple $\{\alpha ,PI{D}_{v_i},T_1{\delta }_{V-TA}\}$, the TA tests the latest timestamp $T_1$ as Equation (1). If Equation (1) holds, $T_1$ is freshness. Otherwise, the first-tuple $\{\alpha ,PI{D}_{v_i},T_1{\delta }_{V-TA}\}$ is rejected.

  $$T_{▿}>T_r-T_1$$

  (1)

  where $T_{▿}$ is the predefined delay and $T_r$ is the received delay.
• The TA then reveals vehicle’s true identity $TI{D}_{v_i}$ by computing $TI{D}_{v_i}=PI{D}_{v_i}\oplus h(A{C}_{v_i}\left|\right|T_1)$, where $A{C}_{v_i}$ is an authentication code.
• Once checking the validity and authenticity of the vehicle’s true identity $TI{D}_{v_i}$, the TA sends $\{TI{D}_{v_i},A{C}_{v_i}\}$ to the fog server via the secure channel.
• The fog server selects the signature key $S{k}_{v_i}$ as the following Equation.

  $$S{k}_{v_i}={\mathcal{T}}_{PI{D}_{v_i}.S_{TA}}\left(x\right)modP$$

  (2)
• The fog server encrypts the signature key $S{k}_{v_i}$ as the following Equation.

  $$S{k}_{v_i}^{enc}=S{k}_{v_i}\oplus h(A{C}_{v_i}\left|\right|T_1)$$

  (3)
• The fog server sends the second-tuple $\{S{k}_{v_i}^{enc},V{T}_i,T_2,{\delta }_{f2v}\}$ to vehicle, where ${\delta }_{f2v}=h(V{T}_i\left|\right|S{k}_{v_i}^{enc}\left|\right|PI{D}_{v_i}\left|\right|T_2)$ and $V{T}_i$ is a valid timestamp obtained from fog server.
• After checking the freshness of timestamp $T_2$, the vehicle decrypts the signature key $S{k}_{v_i}$ as the following Equation.

  $$S{k}_{v_i}=S{k}_{v_i}^{enc}\oplus h(A{C}_{v_i}\left|\right|T_1)$$

  (4)

Note that when the valid timestamp $V{T}_i$ is close to expiring, the vehicle in our work renews the above process to receive a new signature key encrypted by the fog server via 5G-BS to join in 5G-enabled vehicular networks.

4.3. Message Signing (Phase 3)

Here is the procedure:

• The vehicle signs the message ${\sigma }_{m_i}=h(M_i\left|\right|V{T}_i\left|\right|PI{D}_{v_i}\left|\right|T_i)$, where $T_i$ is current timestamp.
• A signature of the communication is calculated by the vehicle as ${\delta }_{m_i}=$${\mathcal{T}}_{{\sigma }_{m_i}}\left(S{k}_{v_i}\right)modP$.
• The vehicle then uses V2V communication on 5G-enabled vehicular networks to broadcast the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} to other cars.

4.4. Signature Verification (Phase 4)

Here is how the procedure goes down.

• Upon receiving the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$}, the checker initially tests the newness of timestamp $T_i$ as Equation (1).
• The checker then computes the parameter ${\sigma }_{m_i}^{-}=h(M_i\left|\right|V{T}_i\left|\right|PI{D}_{v_i}\left|\right|T_i)$.
• The checker then uses the signature ${\delta }_{m_i}$ of the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} to validate the message $M_i$, where ${\delta }_{m_i}=$${\mathcal{T}}_{{\sigma }_{m_i}}\left(S{k}_{v_i}\right)modP$. The checker accepts the message $M_i$ when Equation (5) holds. If the message does not meet these requirements, it will be rejected

$$\begin{array}{c}\hfill {\mathcal{T}}_{PI{D}_{v_i}.{{\sigma }_{m_i}}^{-}}\left(S{k}_{v_i}\right)\stackrel{?}{=}{\mathcal{T}}_{PI{D}_{v_i}}\left({\delta }_{m_i}\right)\end{array}$$

(5)

4.5. Pseudonym Revocation (Phase 5)

The following is the description of this phase.

• Upon the malicious registered vehicle broadcasting the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$}, the fog server computes the vehicle’s true identity $TI{D}_{v_i}$ as Equation (6).

  $$TI{D}_{v_i}=PI{D}_{v_i}\oplus h(A{C}_{v_i}\left|\right|T_1)$$

  (6)
• The fog server then sends $TI{D}_{v_i}$ to the TA through a secure channel.
• The TA checks the data stored about it in the vehicle registration list and deletes it.
• The TA sends $\{Acknowledgment Message\}$ to all fog servers for revoking process.
• Once the valid timestamp $V{T}_i$ is close to expiring, the malicious vehicle requests a new signature key from the fog server.
• After checking the $TI{D}_{v_i}$ in the revocation list, the fog server rejects the request because it is revoked.

5. Result

This section provides the security analysis and performance evaluation of our work as follows.

5.1. Security Analysis

This subsection demonstrates that our work can meet the privacy and security criteria for the 5G-enabled vehicular network outlined in the design goals part (Section 3.2).

• Authentication and Integrity: The checker in our work can verify the legality and integrity of the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} by verifying whether Equation (5) holds. Thus, the legality and integrity of our work are satisfied.
• Identity Privacy: In a 5G-enabled vehicular network, the vehicle’s true identity of $TI{D}_{v_i}$ is involved in the pseudonym-ID of the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} generated by the vehicle. Hence, no attacker can obtain the true identity $TI{D}_{v_i}$ of the vehicle through the $TI{D}_{v_i}$. Thus, our work satisfies the identity privacy requirement.
• Traceability: The true identity of the vehicle $TI{D}_{v_i}$ is hidden in the $PI{D}_{v_i}$ generated by the vehicle, where $PI{D}_{v_i}=TI{D}_{v_i}\oplus h(A{C}_{v_i}\left|\right|T_1)$. By using an authentication code $A{C}_{v_i}$, the TA or fog server computes $TI{D}_{v_i}$ by calculating $TI{D}_{v_i}=PI{D}_{v_i}\oplus h(A{C}_{v_i}\left|\right|T_1)$. Hence, our work provides a traceability requirement.
• Pseudonym Revocation: Once the process of traceability is done, the TA has the ability to revoke the pseudonym of the vehicle as shown in Section 4.5. Hence, our work provides a pseudonym revocation requirement.
• Unlinkability: The vehicle uses a pseudonym-ID to create the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$}. Once the valid timestamp $V{T}_i$ is close to expiring, the vehicle creates a new pseudonym-ID to request a new signature for completing the joining process. Our work also utilizes the freshness timestamp $T_i$ to compute the signature ${\delta }_{m_i}$. Any attacker who tries to link multiple final-tuples {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} may not succeed because of changes in their pseudonym-ID and timestamp. Nevertheless, no linkability issue arises in our work.
• Resistance to Replay Attacks: The newness timestamp $T_i$ is included in the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$}. Before accepting the message $M_i$, the verifier checks whether the inequality $(T_{▿}>T_r-T_1)$ holds. If it is valid, the verifier accepts the message $M_i$ to be checked further; otherwise, the message $M_i$ is rejected. Therefore, the resistance to replay attacks is satisfied in our work.
• Resistance to Forgery Attacks: The attacker cannot forge a valid final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} in our work. This is because the checker can verify the authenticity of the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} by computing whether the equation ${\mathcal{T}}_{PI{D}_{v_i}.{{\sigma }_{m_i}}^{-}}\left(S{k}_{v_i}\right)\stackrel{?}{=}{\mathcal{T}}_{PI{D}_{v_i}}\left({\delta }_{m_i}\right)$ holds. If it is valid, the checker accepts the message $M_i$; otherwise, it is rejected. Therefore, the resistance to forgery attacks is satisfied in our work.
• Resistance to Modify Attacks: The attacker cannot easily modify a valid final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$}, where ${\delta }_{m_i}=$${\mathcal{T}}_{{\sigma }_{m_i}}\left(S{k}_{v_i}\right)modP$. The checker can check the validity of the final-tuple {$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$} by computing whether the equation ${\mathcal{T}}_{PI{D}_{v_i}.{{\sigma }_{m_i}}^{-}}\left(S{k}_{v_i}\right)\stackrel{?}{=}{\mathcal{T}}_{PI{D}_{v_i}}\left({\delta }_{m_i}\right)$ holds. If it is so, the checker accepts the message $M_i$; otherwise, it is rejected. Therefore, the resistance to modify attacks is satisfied in our work.
• Resistance to Man-In-The-Middle Attacks: The investigation of the node authenticity and message validity above proves that it is necessary to verify that the relation between the signer and the checker should be verified and that a real message cannot be modified and fabricated. Therefore, the resistance to man-in-the-middle attacks is satisfied in our work.

5.2. Performance Evaluation

In order to prove that our proposal is efficient compared to the existing schemes, this section provides the evaluation of the performance in terms of the communication and computation overheads. For your convenience, Table 3 describes the runtime of a few common cryptographic operations. The main reason for using the Chebyshev polynomial instead of other security algorithms is the efficient and lightweight operations used to sign and verify the messages. Based on Table 3, the operation of $T_{chev}$ is very low compared with $T_{pair}^{bp}$ and $T_{mul}^{ecc}$. Our work was written on the 3.2 GH platform using the Java Cryptography library to determine the execution time of various cryptographic procedures; the details of the machine’s configuration are provided in [34].

Table 3. Time Required for Various Cryptographic Operations.

Operations	Definition	Times (ms)
$T_{pair}^{bp}$	The duration of the bilinear pairing cryptography (BPC) operation’s runtime.	1.537
$T_{mul}^{bp}$	The scale multiplication operation’s runtime for the BPC.	0.137
$T_{mul}^{ecc}$	The scale multiplication operation’s runtime for the elliptic curve cryptography (ECC).	0.063075
$T_{chev}$	Chebyshev’s polynomial mapping operation’s runtime.	0.021025

5.2.1. Overhead of Computational

The scheme’s cryptographic operations of Bayat et al. [22] are built on a bilinear pair, while the schemes of Li et al. [23], Cui et al. [24], and Al-Shareeda et al. [25] use an elliptic curve. On the other hand, our proposed solution implements a Chebyshev polynomial-based fog computing technique that allows for the pseudonym revocation in 5G-enabled vehicle networks. The differences between the message signing and signature verification are listed in Table 4.

Table 4. An Analysis of Signature Verification and Message Signing.

Schemes	Message Signing	Signature Verification
Bayat et al. [22]	$5T_{mul}^{bp}\approx 0.685$	$3T_{pair}^{bp}+1T_{mul}^{bp}\approx 4.748$
Li et al. [23]	$1T_{mul}^{ecc}\approx 0.063075$	$4T_{mul}^{ecc}\approx 0.2523$
Cui et al. [24]	$3T_{mul}^{ecc}\approx 0.18921$	$3T_{mul}^{ecc}\approx 0.18921$
Al-Shareeda et al. [25]	$1T_{mul}^{ecc}\approx 0.06307$	$2T_{mul}^{ecc}\approx 0.12614$
Our Proposal	$1T_{chev}\approx 0.021025$	$2T_{chev}\approx 0.04205$

The efficiency of our work in signing messages and verifying signatures is compared to other relevant systems in Table 4. Figure 3 compares the computational costs for the proposal with other schemes.

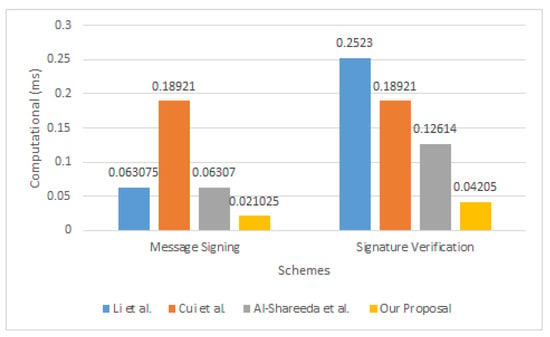
Figure 3. Comparison Computational Costs for Proposal and Other Schemes.

5.2.2. Overhead of Communication

In this section, we present the authentication methods by comparing the relative overhead and transmission costs of the various methods of Bayat et al. [22], Li et al. [23], Cui et al. [24], and Al-Shareeda et al. [25] along with our proposed system of vehicular networks. Given that, this study makes the following assumptions: the product of a hash function is 20 bytes, the product of a timestamp is 4 bytes, the product of a bilinear pair point $P=(P_x,P_y)$ is 128 bytes, and the product of a point on an elliptic curve is 40 bytes. The message’s end result is not involved in this procedure. Table 5 displays a comparison of the communication costs.

Table 5. Costs of Different Methods of Contact Compared.

Schemes	Final-Tuple	Size of Tuple (bytes)	Size of n Tuples (bytes)
Bayat et al. [22]	$\{PI{D}_i,M,V,r,T_{i1},T_{i2},T_{i3},t{s}_i\}$	$4+20+5·128\approx 664$	664 n
Li et al. [23]	$\{M_j,RI{D}_j,Y_j,W_j,T_j,Rsi{g}_j\}$	$64·2+4+20\approx 152$	152 n
Cui et al. [24]	$\{D{T}_{ij},D_j,PI{D}_j,{\delta }_j,T_j\}$	$4+2·20+2·64\approx 172$	172 n
Al-Shareeda et al. [25]	$\{M_i,R_i,AI{D}_i,T_i,{\sigma }_i\}$	$4+20+2·64\approx 152$	152 n
Our Proposal	{$PI{D}_{v_i}$, $M_i$, $T_i$, $T_1$, $V{T}_i$, ${\delta }_{m_i}$}	$4·3+20+64\approx 96$	96 n

Our solution has a lower communication overhead than similar techniques, as illustrated in Table 5. Figure 4 compares the communication costs for the proposal with other schemes.

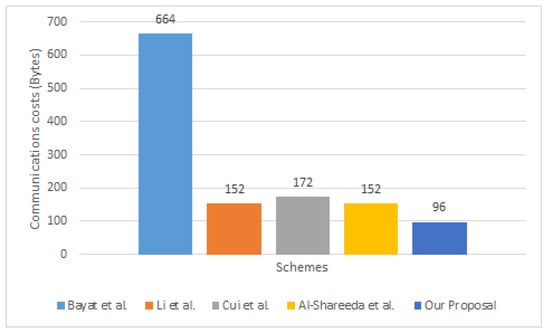
Figure 4. Comparison Communication Costs for Proposal and Other Schemes.

6. Conclusions and Future Work

For 5G-enabled vehicle networks, this research proposes a fog computing technique based on the Chebyshev polynomial that allows for the revocation of pseudonyms. When a pseudonym-ID with a valid timestamp is about to expire, our solution exploits the fog computing idea to revoke the insider attacker by not renewing the signature key. Our approach not only protects against common security threats such as replay, forgery, modification, and man-in-the-middle attacks, but it also satisfies privacy requirements, such as unlinkability and identity privacy. The signing process and verifying process of the computational costs of the proposed one is 0.021025 ms and 0.04205 ms, receptively. Finally, our solution uses the Chebyshev polynomial to sign messages and verify signatures, which is more efficient than the elliptic curve and bilinear pair procedures.

For further research, the experiment might be run on simulation platforms such as OMNET++ and SUMO to model the VANET networks and vehicular traffic, respectively, to test and ensure the efficacy of the proposed work and the 6G technologies used in the suggested system.