Dispersive Optical Solitons with Differential Group Delay Having Multiplicative White Noise by Itô Calculus

Abstract

The current paper recovers dispersive optical solitons in birefringent fibers that are modeled by the Schrödinger–Hirota equation with differential group delay and white noise. Itô Calculus conducts the preliminary analysis. The $\left(G^{\prime }/G\right)$-expansion approach and the enhanced Kudryashov’s scheme gave way to a wide spectrum of soliton solutions with the white noise component reflected in the phase of the soliton.

1. Introduction

One of the major issues that arise in soliton propagation through optical fibers across inter-continental distances [1,2,3,4,5,6,7,8,9,10,11] is the depletion of the chromatic dispersion (CD) count. There are several countermeasures that have been adopted in the telecommunications industry to circumvent this situation. These would include the consideration of the gratings structure in these waveguides that are known as Bragg gratings that would introduce dispersive reflectivity. Many other measures have been adopted with time. Another popular method to arrest this low count of CD is to introduce third order dispersion (3OD) and that would lead to the Schrödinger–Hirota equation (SHE) that can be obtained from the nonlinear Schrödinger equation (NLSE) via Lie transform analysis. The current paper includes the spatio-temporal dispersion (STD) in addition to CD just to supplement a possible low CD count.

The current paper is an analysis of SHE but in birefringent fibers. These are the familiar erbium-doped fibers with the presence of third-order dispersion effect, in addition to CD and STD. This is an effect of differential group delay (DGD) after the occurrence of pulse splitting. The accumulation of such DGD leads to the effect of birefringence [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Thus, SHE in birefringent fibers would be the focus of attention in this work. However, a multiplicative noise is also included in the model because no optoelectronic device is perfectly deterministic and consequently noise would naturally creep in. This paper therefore considers the multiplicative white noise that emerges from the standard Weiner process. The Itô Calculus would be applied to carry out the preliminary mathematical analysis. Thereafter, the $G^{\prime }/G$-expansion scheme and the enhanced Kudryashov’s algorithm would be applied to secure solitons with the model. It must be noted that additive noise has been studied in the past for soliton propagation [15,16,17]. In those cases, it is the Langevin equation that led to the mean free velocity of the soliton. The details of the current work are addressed after an overview of the model.

It is worth mentioning that the model is addressed in a single channel but in birefringent fibers to address additive stochasticity in the form of white noise by Itô Calculus. While the next stage is to address such a study to a further generalization of the model with DWDM topology, it is therefore imperative to obtain preliminary results in birefringent fibers and also in birefringence-free fibers. Another feature that needs to be noted is that SHE is an approximate model with the radiation component ignored. In fact, SHE is derived from the perturbed NLSE with the application of Lie transform where higher order terms are discarded to retain SHE which is integrated by the aid of Inverse Scattering Transform. Thus, the model is a far cry from actuality in real life scenarios although it is a starting point.

Governing Model

The Schrödinger–Hirota equation with differential group delay and white noise that governs dispersive optical solitons in birefringent fibers is presented as below

$$\begin{array}{c}i{q}_t+a_1{q}_{xx}+b_1{q}_{xt}+\left(c_1{\left|q\right|}^2+d_1{\left|r\right|}^2\right)q\\ \\ +i\left[{\alpha }_1{q}_x+{\lambda }_1{\left({\left|q\right|}^{2}q\right)}_x+{\upsilon }_1{\left({\left|q\right|}^2\right)}_{x}q+{\theta }_1{\left|q\right|}^2{q}_x+{\gamma }_1{q}_{xxx}\right]+{\sigma }_1\left(q-i{b}_1{q}_x\right)\frac{d{W}_1\left(t\right)}{dt}=0,\end{array}$$

(1)

and

$$\begin{array}{c}i{r}_t+a_2{r}_{xx}+b_2{r}_{xt}+\left(c_2{\left|r\right|}^2+d_2{\left|q\right|}^2\right)r\\ \\ +i\left[{\alpha }_2{r}_x+{\lambda }_2{\left({\left|r\right|}^{2}r\right)}_x+{\upsilon }_2{\left({\left|r\right|}^2\right)}_{x}r+{\theta }_2{\left|r\right|}^2{r}_x+{\gamma }_2{r}_{xxx}\right]+{\sigma }_2\left(r-i{b}_2{r}_x\right)\frac{d{W}_2\left(t\right)}{dt}=0,\end{array}$$

(2)

where ${\sigma }_j$$\left(j=1,2\right)$ come from the noise strength. Setting ${\sigma }_j=0$ decrease systems (1) and (2) to the familiar SHE in birefringent fibers. $W_j\left(t\right)$ arise from the standard Wiener processes and $d{W}_j\left(t\right)/dt$ give the white noises. ${\lambda }_j$ denote the self-steepening, while ${\alpha }_j$ depict the inter-modal dispersion. $c_j$ arise from the self-phase modulation, while ${\gamma }_j$ stem from the 3OD. $q(x,t)$ and $r(x,t)$ stand as the soliton profiles, while ${\upsilon }_j$ and ${\theta }_j$ stick out as the nonlinear dispersions. $d_j$ come out as the cross-phase modulation, while $a_j$ read as the CD. Next, $b_j$ account for the STD that is from the spatio-temporal dispersive effect. The first terms signify the temporal evolution with $i=\sqrt{-1}$.

2. Mathematical Analysis

Equations (1) and (2) represent the propagation of dispersive optical soliton through a birefringent fiber. This happens when pulses propagating through an optical fiber split into two pulses, occasionally three, thus leading to differential group delay (DGD). It is the cumulative effect of DGD that leads to birefringence. The fundamental causes for pulse splitting come from the rough handling of long fibers while laying underground as well as undersea for global cable connection, which could lead to squeezing, bending and other rough issues. Thus, birefringence is unavoidable. Hence, it is imperative to address the model that studies dispersive solitons, namely SHE, with the effect of birefringence included. It must be note that the model for birefringence with dispersive solitons was first proposed during 2011 [14]. The current paper extends the model with the effects of perturbation terms included [37]. To give it a complete and flavorful taste, both deterministic as well as stochastic perturbative effects are taken into consideration. The stochastic perturbative effect [38,39,40,41,42] is additive and comes from white noise. However, the effect of the multiplicative perturbation term, for the scalar SHE, was studied almost two decades ago and was addressed using the derived Langevin equation [38]. This extends the study of the current paper, and makes it generalized and truly novel.

The soliton profiles shapes up as

$$\begin{array}{c}q(x,t)={\Phi }_1\left(\xi \right)expi\left[{\psi }_1\left(x,t\right)+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],\\ \\ r(x,t)={\Phi }_2\left(\xi \right)expi\left[{\psi }_2\left(x,t\right)+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right],\end{array}$$

(3)

and

$$\xi =x-vt,{\psi }_j\left(x,t\right)=-{\kappa }_{j}x+{\omega }_{j}t+{\theta }_j,$$

(4)

where ${\Phi }_j\left(\xi \right)$ comes from the soliton amplitude components, while v emerges from the soliton velocity. ${\theta }_j$ arise from the phase constants, while ${\kappa }_j$ arise from the soliton frequencies. ${\psi }_j\left(x,t\right)$ evolve from the soliton phase components, while ${\omega }_j$ stand as the soliton wave numbers.

Equations (3) and (4) are the decomposed versions of models (1) and (2) into phase–amplitude format. This is significant. This way, the soliton amplitude, inverse width, velocity as well as the soliton wave number can easily be recovered. Such a form of phase–amplitude style decomposition is preferred to retrieve these essential physical features. The other form of decomposition of Equations (1) and (2) into real and imaginary parts is normally applicable when Lie symmetry analysis is taken up. However, the current paper will implement the G’/G-expansion method and the enhanced Kudryashov’s scheme that would give the soliton solutions with the essential physical features in it as indicated.

Putting (3) and (4) into (1) and (2) and then decomposing into real and imaginary parts yields a few relations. The real parts are presented as below

$$\begin{array}{c}\left(a_1-b_{1}v+3{\kappa }_1{\gamma }_1\right){\Phi }_1^{″}\left(\xi \right)-\left[a_1{\kappa }_1^2-{\kappa }_1{\alpha }_1+{\gamma }_1{\kappa }_1^3+\left({\omega }_1-{\sigma }_1^2\right)\left(1-b_1{\kappa }_1\right)\right]{\Phi }_1\left(\xi \right)\\ \\ +d_1{\Phi }_1\left(\xi \right){\Phi }_2^2\left(\xi \right)+\left(c_1+{\lambda }_1{\kappa }_1+{\theta }_1{\kappa }_1\right){\Phi }_1^3\left(\xi \right)=0,\end{array}$$

(5)

and

$$\begin{array}{c}\left(a_2-b_{2}v+3{\kappa }_2{\gamma }_2\right){\Phi }_2^{″}\left(\xi \right)-\left[a_2{\kappa }_2^2-{\kappa }_2{\alpha }_2+{\gamma }_2{\kappa }_2^3+\left({\omega }_2-{\sigma }_2^2\right)\left(1-b_2{\kappa }_2\right)\right]{\Phi }_2\left(\xi \right)\\ \\ +d_2{\Phi }_2\left(\xi \right){\Phi }_1^2\left(\xi \right)+\left(c_2+{\lambda }_2{\kappa }_2+{\theta }_2{\kappa }_2\right){\Phi }_2^3\left(\xi \right)=0,\end{array}$$

(6)

while the imaginary parts are given by

$$\begin{array}{c}{\gamma }_1{\Phi }_1^{‴}\left(\xi \right)-\left[2a_1{\kappa }_1-b_1\left({\omega }_1-{\sigma }_1^2\right)-{\alpha }_1+3{\gamma }_1{\kappa }_1^2+\left(1-b_1{\kappa }_1\right)v\right]{\Phi }_1^{\prime }\left(\xi \right)\\ \\ +\left(3{\lambda }_1+2{\mu }_1+{\theta }_1\right){\Phi }_1^2\left(\xi \right){\Phi }_1^{\prime }\left(\xi \right)=0,\end{array}$$

(7)

and

$$\begin{array}{c}{\gamma }_2{\Phi }_2^{‴}\left(\xi \right)-\left[2a_2{\kappa }_2-b_2\left({\omega }_2-{\sigma }_2^2\right)-{\alpha }_2+3{\gamma }_2{\kappa }_2^2+\left(1-b_2{\kappa }_2\right)v\right]{\Phi }_2^{\prime }\left(\xi \right)\\ \\ +\left(3{\lambda }_2+2{\mu }_2+{\theta }_2\right){\Phi }_2^2\left(\xi \right){\Phi }_2^{\prime }\left(\xi \right)=0.\end{array}$$

(8)

Setting

$${\Phi }_2\left(\xi \right)=\chi {\Phi }_1\left(\xi \right),\chi \ne 0\mathrm{or}1,$$

(9)

the real and imaginary parts (5)–(8) stick out as

$$\begin{array}{c}\left(a_1-b_{1}v+3{\kappa }_1{\gamma }_1\right){\Phi }_1^{″}\left(\xi \right)-\left[a_1{\kappa }_1^2-{\kappa }_1{\alpha }_1+{\gamma }_1{\kappa }_1^3+\left({\omega }_1-{\sigma }_1^2\right)\left(1-b_1{\kappa }_1\right)\right]{\Phi }_1\left(\xi \right)\\ \\ +\left(d_1{\chi }^2+c_1+{\lambda }_1{\kappa }_1+{\theta }_1{\kappa }_1\right){\Phi }_1^3\left(\xi \right)=0,\end{array}$$

(10)

$$\begin{array}{c}\left(a_2-b_{2}v+3{\kappa }_2{\gamma }_2\right){\Phi }_1^{″}\left(\xi \right)-\left[a_2{\kappa }_2^2-{\kappa }_2{\alpha }_2+{\gamma }_2{\kappa }_2^3+\left({\omega }_2-{\sigma }_2^2\right)\left(1-b_2{\kappa }_2\right)\right]{\Phi }_1\left(\xi \right)\\ \\ +\left[d_2+{\chi }^2\left(c_2+{\lambda }_2{\kappa }_2+{\theta }_2{\kappa }_2\right)\right]{\Phi }_1^3\left(\xi \right)=0,\end{array}$$

(11)

and

$$\begin{array}{c}{\gamma }_1{\Phi }_1^{‴}\left(\xi \right)-\left[2a_1{\kappa }_1-b_1\left({\omega }_1-{\sigma }_1^2\right)-{\alpha }_1+3{\gamma }_1{\kappa }_1^2+\left(1-b_1{\kappa }_1\right)v\right]{\Phi }_1^{\prime }\left(\xi \right)\\ \\ +\left(3{\lambda }_1+2{\mu }_1+{\theta }_1\right)B_1^2\left(\xi \right)B_1^{\prime }\left(\xi \right)=0,\end{array}$$

(12)

$$\begin{array}{c}{\gamma }_2{\Phi }_1^{‴}\left(\xi \right)-\left[2a_2{\kappa }_2-b_2\left({\omega }_2-{\sigma }_2^2\right)-{\alpha }_2+3{\gamma }_2{\kappa }_2^2+\left(1-b_2{\kappa }_2\right)v\right]{\Phi }_1^{\prime }\left(\xi \right)\\ \\ +{\chi }^2\left(3{\lambda }_2+2{\mu }_2+{\theta }_2\right){\Phi }_1^2\left(\xi \right){\Phi }_1^{\prime }\left(\xi \right)=0,\end{array}$$

(13)

respectively. Integrating (12) and (13) with zero-integration constants produces

$$\begin{array}{c}{\gamma }_1{\Phi }_1^{″}\left(\xi \right)-\left[2a_1{\kappa }_1-b_1\left({\omega }_1-{\sigma }_1^2\right)-{\alpha }_1+3{\gamma }_1{\kappa }_1^2+\left(1-b_1{\kappa }_1\right)v\right]{\Phi }_1\left(\xi \right)\\ \\ +\frac{1}{3}\left(3{\lambda }_1+2{\mu }_1+{\theta }_1\right){\Phi }_1^3\left(\xi \right)=0,\end{array}$$

(14)

$$\begin{array}{c}{\gamma }_2{\Phi }_1^{″}\left(\xi \right)-\left[2a_2{\kappa }_2-b_2\left({\omega }_2-{\sigma }_2^2\right)-{\alpha }_2+3{\gamma }_2{\kappa }_2^2+\left(1-b_2{\kappa }_2\right)v\right]{\Phi }_1\left(\xi \right)\\ \\ +\frac{1}{3}{\chi }^2\left(3{\lambda }_2+2{\mu }_2+{\theta }_2\right){\Phi }_1^3\left(\xi \right)=0.\end{array}$$

(15)

Setting the coeffcients of the linearly independent functions of Equations (10) and (11), we arrive at the soliton velocity

$$v=\frac{a_j+3{\gamma }_j{\kappa }_j}{b_j},b_j\ne 0,$$

(16)

the wave numbers

$${\omega }_j={\displaystyle \frac{a_j{\kappa }_j^2-{\kappa }_j{\alpha }_j+{\gamma }_j{\kappa }_j^3-{\sigma }_j^2+{\sigma }_j^2{b}_j{\kappa }_j}{b_j{\kappa }_j-1}},b_j{\kappa }_j\ne 1,$$

(17)

and the constraint conditions

$$d_1{\chi }^2+c_1+{\lambda }_1{\kappa }_1+{\theta }_1{\kappa }_1=0,$$

(18)

$$d_2+{\chi }^2\left(c_2+{\lambda }_2{\kappa }_2+{\theta }_2{\kappa }_2\right)=0.$$

(19)

To secure optical solitons with the model in the current paper, one of Equations (14) and (15) can be addressed with the aid of the relations

$$\frac{{\gamma }_1}{{\gamma }_2}=\frac{2a_1{\kappa }_1-b_1\left({\omega }_1-{\sigma }_1^2\right)-{\alpha }_1+3{\gamma }_1{\kappa }_1^2+\left(1-b_1{\kappa }_1\right)v}{2a_2{\kappa }_2-b_2\left({\omega }_2-{\sigma }_2^2\right)-{\alpha }_2+3{\gamma }_2{\kappa }_2^2+\left(1-b_2{\kappa }_2\right)v}=\frac{3{\lambda }_1+2{\mu }_1+{\theta }_1}{{\chi }^2\left(3{\lambda }_2+2{\mu }_2+{\theta }_2\right)},$$

(20)

which satisfies the real-valued parametric restrictions

$${\alpha }_2=\frac{\left[\left(b_1{\kappa }_1-1\right)v-2a_1{\kappa }_1+b_1\left({\omega }_1-{\sigma }_1^2\right)+{\alpha }_1\right]{\gamma }_2-\left[\left(b_2{\kappa }_2-1\right)v-2a_2{\kappa }_2+b_2\left({\omega }_2-{\sigma }_2^2\right)-\left(3{\kappa }_2^2-3{\kappa }_1^2\right){\gamma }_2\right]{\gamma }_1}{{\gamma }_1},$$

(21)

and

$${\lambda }_2={\displaystyle \frac{{\gamma }_2\left(2{\mu }_1+3{\lambda }_1+{\theta }_1\right)-{\gamma }_1{\chi }^2\left(2{\mu }_2+{\theta }_2\right)}{3{\gamma }_1{\chi }^2}},{\gamma }_1\ne 0.$$

(22)

The present paper considers the fundamental Equation (14) which is also presented as below

$$\begin{array}{c}{\Phi }_1^{″}\left(\xi \right)+{\Delta }_1{\Phi }_1\left(\xi \right)+{\Delta }_3{\Phi }_1^3\left(\xi \right)=0,\end{array}$$

(23)

where

$${\Delta }_1=\frac{\left(b_1{\kappa }_1-1\right)v+b_1\left({\omega }_1-{\sigma }_1^2\right)-2a_1{\kappa }_1+{\alpha }_1-3{\gamma }_1{\kappa }_1^2}{{\gamma }_1},{\Delta }_3=\frac{3{\lambda }_1+2{\mu }_1+{\theta }_1}{3{\gamma }_1}.$$

(24)

3. $\left({\mathit{G}}^{\prime }/\mathit{G}\right)$-Expansion Algorithm

In this integration tool, the fundamental governing Equation (23) admits the explicit solution

$${\Phi }_1\left(\xi \right)=\sum _{J=0}^N{\delta }_J{F}^J\left(\xi \right),F\left(\xi \right)=\frac{G^{\prime }\left(\xi \right)}{G\left(\xi \right)},{\delta }_N\ne 0,$$

(25)

along with the ancillary equations

$$G^{″}+\lambda G^{\prime }+\mu G=0,$$

(26)

and

$$F^{\prime }=-\left(F^2+\lambda F+\mu \right),$$

(27)

which ensures the analytical solutions

$$F\left(\xi \right)=-\frac{\lambda }{2}+\frac{1}{2}\sqrt{{\lambda }^2-4\mu }\left[\frac{{\epsilon }_{1}sinh\left(\frac{1}{2}\xi \sqrt{{\lambda }^2-4\mu }\right)+{\epsilon }_{2}cosh\left(\frac{1}{2}\xi \sqrt{{\lambda }^2-4\mu }\right)}{{\epsilon }_{1}cosh\left(\frac{1}{2}\xi \sqrt{{\lambda }^2-4\mu }\right)+{\epsilon }_{2}sinh\left(\frac{1}{2}\xi \sqrt{{\lambda }^2-4\mu }\right)}\right],{\lambda }^2-4\mu >0,$$

(28)

$$F\left(\xi \right)=-\frac{\lambda }{2}+\frac{1}{2}\sqrt{-\left({\lambda }^2-4\mu \right)}\left[\frac{{\epsilon }_{1}cos\left(\frac{1}{2}\xi \sqrt{-\left({\lambda }^2-4\mu \right)}\right)-{\epsilon }_{2}sin\left(\frac{1}{2}\xi \sqrt{-\left({\lambda }^2-4\mu \right)}\right)}{{\epsilon }_{1}sin\left(\frac{1}{2}\xi \sqrt{-\left({\lambda }^2-4\mu \right)}\right)+{\epsilon }_{2}cos\left(\frac{1}{2}\xi \sqrt{-\left({\lambda }^2-4\mu \right)}\right)}\right],{\lambda }^2-4\mu <0,$$

(29)

$$F\left(\xi \right)=-\frac{\lambda }{2}+\frac{{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2\xi },{\lambda }^2-4\mu =0,$$

(30)

where ${\delta }_J(J=0-N)$, $\lambda$, $\mu$, ${\epsilon }_1$ and ${\epsilon }_2$ are constants. Balancing ${\Phi }_1^{″}\left(\xi \right)$ and ${\Phi }_1^3\left(\xi \right)$ in (23) simplifies (25) to

$${\Phi }_1\left(\xi \right)={\delta }_0+{\delta }_{1}F\left(\xi \right),{\delta }_1\ne 0.$$

(31)

Putting (31) along with (27) into (23) paves the way to the simplest equations

$$\left.\begin{array}{c}2{\delta }_1+{\Delta }_3{\delta }_1^3=0,\hfill \\ 3{\delta }_1\lambda +3{\Delta }_3{\delta }_0{\delta }_1^2=0,\hfill \\ {\delta }_1\mu \lambda +{\Delta }_1{\delta }_0+{\Delta }_3{\delta }_0^3=0,\hfill \\ {\delta }_1{\lambda }^2+3{\Delta }_3{\delta }_0^2{\delta }_1+{\Delta }_1{\delta }_1+2{\delta }_1\mu =0,\hfill \end{array}\right\}$$

(32)

which secure the results:

$${\delta }_0=\pm \sqrt{-\frac{{\Delta }_1+2\mu }{{\Delta }_3}},{\delta }_1=\pm \sqrt{-\frac{2}{{\Delta }_3}},\lambda =\pm \sqrt{2\left({\Delta }_1+2\mu \right)},\mu =\mu ,{\Delta }_3<0,{\Delta }_1+2\mu >0.$$

(33)

Type-1: Plugging (33) along with (28) into (31) leaves us with the straddled solitons

$$q(x,t)=\pm \sqrt{-\frac{{\Delta }_1}{{\Delta }_3}}\left\{\frac{{\epsilon }_{1}sinh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]+{\epsilon }_{2}cosh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]}{{\epsilon }_{1}cosh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]+{\epsilon }_{2}sinh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]}\right\}expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(34)

and

$$r(x,t)=\pm \chi \sqrt{-\frac{{\Delta }_1}{{\Delta }_3}}\left\{\frac{{\epsilon }_{1}sinh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]+{\epsilon }_{2}cosh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]}{{\epsilon }_{1}cosh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]+{\epsilon }_{2}sinh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]}\right\}expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(35)

Taking ${\epsilon }_1\ne 0$ and ${\epsilon }_2=0$ changes (34) and (35) to the dark solitons

$$q(x,t)=\pm \sqrt{-\frac{{\Delta }_1}{{\Delta }_3}}tanh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(36)

and

$$r(x,t)=\pm \chi \sqrt{-\frac{{\Delta }_1}{{\Delta }_3}}tanh\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(37)

The surface plots of solitons (36) and (37) are depicted in Figure 1. The parameter values chosen are: $a_{1,2}=1,{\alpha }_1=1,b_{1,2}=3,{\gamma }_{1,2}=1,{\kappa }_{1,2}=1,{\lambda }_1=1,{\mu }_1=-3,{\sigma }_1=1,{\theta }_1=1$ and $\chi =3$.

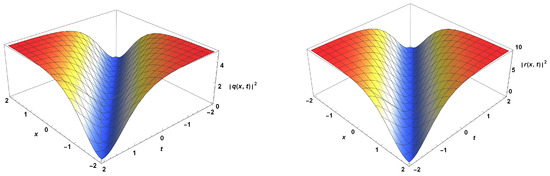
Figure 1. Profiles of dark solitons in birefringent fibers.

Setting ${\epsilon }_1=0$ and ${\epsilon }_2\ne 0$ also transforms (34) and (35) to the singular solitons

$$q(x,t)=\pm \sqrt{-\frac{{\Delta }_1}{{\Delta }_3}}coth\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(38)

and

$$r(x,t)=\pm \chi \sqrt{-\frac{{\Delta }_1}{{\Delta }_3}}coth\left[\frac{1}{2}\sqrt{2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(39)

Type-2: Putting (33) along with (29) into (31) paves way to the singular periodic waves

$$q(x,t)=\pm \sqrt{\frac{{\Delta }_1}{{\Delta }_3}}\left\{\frac{{\epsilon }_{1}sin\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]-{\epsilon }_{2}cos\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]}{{\epsilon }_{1}cos\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]+{\epsilon }_{2}sin\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]}\right\}expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(40)

and

$$r(x,t)=\pm \chi \sqrt{\frac{{\Delta }_1}{{\Delta }_3}}\left\{\frac{{\epsilon }_{1}sin\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]-{\epsilon }_{2}cos\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]}{{\epsilon }_{1}cos\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]+{\epsilon }_{2}sin\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]}\right\}expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(41)

Setting ${\epsilon }_1\ne 0$ and ${\epsilon }_2=0$ turns (40) and (41) into the singular periodic waves

$$q(x,t)=\pm \sqrt{\frac{{\Delta }_1}{{\Delta }_3}}tan\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(42)

and

$$r(x,t)=\pm \chi \sqrt{\frac{{\Delta }_1}{{\Delta }_3}}tan\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(43)

Taking ${\epsilon }_1=0$ and ${\epsilon }_2\ne 0$ also transforms (40) and (41) to the singular periodic waves

$$q(x,t)=\pm \sqrt{\frac{{\Delta }_1}{{\Delta }_3}}cot\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(44)

and

$$r(x,t)=\pm \chi \sqrt{\frac{{\Delta }_1}{{\Delta }_3}}cot\left[\frac{1}{2}\sqrt{-2{\Delta }_1}\left(x-vt\right)\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(45)

Type-3: Inserting $\mu =\frac{1}{4}{\lambda }^2$ into (32) provides us the results:

$${\delta }_0=\pm \frac{\lambda }{2}\sqrt{-\frac{2}{{\Delta }_3}},{\delta }_1=\pm \sqrt{-\frac{2}{{\Delta }_3}},\lambda =\lambda ,$$

(46)

and

$${\Delta }_1=0,{\Delta }_3<0.$$

(47)

Substituting (46) along with (30) into (31) causes the rational waves

$$q(x,t)=\pm \sqrt{-\frac{2}{{\Delta }_3}}\left[{\displaystyle \frac{{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2\left(x-vt\right)}}\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(48)

and

$$r(x,t)=\pm \chi \sqrt{-\frac{2}{{\Delta }_3}}\left[{\displaystyle \frac{{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2\left(x-vt\right)}}\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(49)

4. Enhanced Kudryashov’s Algorithm

In this case, the fundamental governing Equation (23) satisfies the explicit solution

$${\Phi }_1\left(\xi \right)=\sum _{J=0}^N{H}_J{R}^J\left(\xi \right),H_N\ne 0,$$

(50)

along with the auxiliary equation

$$R^{{}^{\prime }2}\left(\xi \right)=R^2\left(\xi \right)[1-A{R}^{2p}\left(\xi \right)]{ln}^{2}a,0<a\ne 1,$$

(51)

which admits the combo bright-singular soliton

$$R\left(\xi \right)={\left[\frac{4B}{\left(4B^2+A\right)cosh\left(p\xi lna\right)+\left(4B^2-A\right)sinh\left(p\xi lna\right)}\right]}^{\frac{1}{p}},$$

(52)

where $H_J(J=0-N)$, A, p, B are constants. Balancing ${\Phi }_1^{″}\left(\xi \right)$ and ${\Phi }_1^3\left(\xi \right)$ in (23) leaves us with

$$N+2p=3N⟹N=p.$$

(53)

Case-1: Taking $p=1$ transforms (50) to

$${\Phi }_1\left(\xi \right)=H_0+H_{1}R\left(\xi \right),H_1\ne 0.$$

(54)

Inserting (54) along with (51) into (23) paves way to the simplest equations

$$\left.\begin{array}{c}3{\Delta }_3{H}_0{H}_1^2=0,\hfill \\ {\Delta }_3{H}_0^3+{\Delta }_1{H}_0=0,\hfill \\ {\Delta }_3{H}_1^3-2H_{1}A{ln}^{2}a=0,\hfill \\ 3{\Delta }_3{H}_0^2{H}_1+{\Delta }_1{H}_1+H_1{ln}^{2}a=0,\hfill \end{array}\right\}$$

(55)

which admit the results:

$$H_0=0,H_1=\sqrt{\frac{2A}{{\Delta }_3}}lna,$$

(56)

and

$${\Delta }_1=-{ln}^{2}a,A{\Delta }_3>0.$$

(57)

Putting (56) along with (52) into (54) gives way to the straddled solitons

$$q(x,t)=\pm \sqrt{\frac{2A}{{\Delta }_3}}\left[\frac{4Blna}{\left(4B^2+A\right)cosh\left[\left(x-vt\right)lna\right]+\left(4B^2-A\right)sinh\left[\left(x-vt\right)lna\right]}\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(58)

and

$$r(x,t)=\pm \chi \sqrt{\frac{2A}{{\Delta }_3}}\left[\frac{4Blna}{\left(4B^2+A\right)cosh\left[\left(x-vt\right)lna\right]+\left(4B^2-A\right)sinh\left[\left(x-vt\right)lna\right]}\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(59)

Setting $A=4B^2$ changes (58) and (59) to the bright solitons

$$q(x,t)=\pm \sqrt{\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{sech}\left[\left(x-vt\right)lna\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(60)

and

$$r(x,t)=\pm \chi \sqrt{\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{sech}\left[\left(x-vt\right)lna\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(61)

The surface plots of solitons (60) and (61) are depicted in Figure 2. The parameter values chosen are: ${\gamma }_{1,2}=1,{\kappa }_{1,2}=1,{\lambda }_1=1,{\mu }_1=1,{\theta }_1=1,a_{1,2}=1,b_{1,2}=1,a=e$ and $\chi =3$.

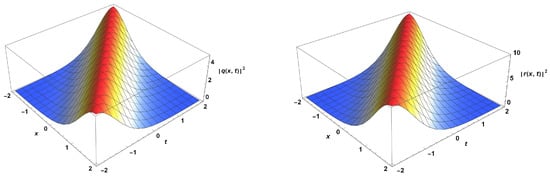
Figure 2. Profiles of bright solitons in birefringent fibers.

Taking $A=-4B^2$ also condenses (58) and (59) to the singular solitons

$$q(x,t)=\pm \sqrt{-\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{csch}\left[\left(x-vt\right)lna\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(62)

and

$$r(x,t)=\pm \chi \sqrt{-\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{csch}\left[\left(x-vt\right)lna\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(63)

Case-2: Setting $p=2$ simplifies (50) to

$${\Phi }_1\left(\xi \right)=H_0+H_{1}R\left(\xi \right)+H_2{R}^2\left(\xi \right),H_2\ne 0.$$

(64)

Putting (64) along with (51) into (23) provides us the simplest equations

$$\left.\begin{array}{c}{\Delta }_3{H}_0^3+{\Delta }_1{H}_0=0,\hfill \\ 3{\Delta }_3{H}_0{H}_2^2+3{\Delta }_3{H}_1^2{H}_2=0,\hfill \\ 3{\Delta }_3{H}_1{H}_2^2-3H_{1}A{ln}^{2}a=0,\hfill \\ {\Delta }_3{H}_2^3-8H_{2}A{ln}^{2}a=0,\hfill \\ 6{\Delta }_3{H}_0{H}_1{H}_2+{\Delta }_3{H}_1^3=0,\hfill \\ 3{\Delta }_3{H}_0^2{H}_1+{\Delta }_1{H}_1+H_1{ln}^{2}a=0,\hfill \\ 3{\Delta }_3{H}_0^2{H}_2+{\Delta }_1{H}_2+3{\Delta }_3{H}_0{H}_1^{2}4H_2{ln}^{2}a=0.\hfill \end{array}\right\}$$

(65)

which permit the results:

$$H_0=0,H_1=0,H_2=2\sqrt{\frac{2A}{{\Delta }_3}}lna,$$

(66)

and

$${\Delta }_1=-4{ln}^{2}a,A{\Delta }_3>0.$$

(67)

The two Figure 1 and Figure 2 represent the surface plots of dark and bright 1-soliton solutions, respectively. The parameter choices are also indicated. For each of the two plots, the solitons along the two components of the fiber are color coded as indicated in the legend. It must be noted that these being dispersive solitons with the presence of 3OD substantial radiation must be present and consequently the slowdown of solitons must also occur [43]. These effects are discarded as the focus of the current paper is on the cire soliton regime, namely the region with bound states. Once again, the analysis of the continuous regime is not studied in the current paper.

Inserting (66) along with (52) into (64) gives the straddled solitons

$$q(x,t)=\pm 2\sqrt{\frac{2A}{{\Delta }_3}}\left[\frac{4Blna}{\left(4B^2+A\right)cosh\left[2\left(x-vt\right)lna\right]+\left(4B^2-A\right)sinh\left[2\left(x-vt\right)lna\right]}\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(68)

and

$$r(x,t)=\pm 2\chi \sqrt{\frac{2A}{{\Delta }_3}}\left[\frac{4Blna}{\left(4B^2+A\right)cosh\left[2\left(x-vt\right)lna\right]+\left(4B^2-A\right)sinh\left[2\left(x-vt\right)lna\right]}\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(69)

Setting $A=4B^2$ translates (68) and (69) to the bright solitons

$$q(x,t)=\pm 2\sqrt{\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{sech}\left[2\left(x-vt\right)lna\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(70)

and

$$r(x,t)=\pm 2\chi \sqrt{\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{sech}\left[2\left(x-vt\right)lna\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(71)

Taking $A=-4B^2$ also changes (68) and (69) to the singular solitons

$$q(x,t)=\pm 2\sqrt{-\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{csch}\left[2\left(x-vt\right)lna\right]expi\left[-{\kappa }_{1}x+{\omega }_{1}t+{\theta }_1+{\sigma }_1{W}_1\left(t\right)-{\sigma }_1^{2}t\right],$$

(72)

and

$$r(x,t)=\pm 2\chi \sqrt{-\frac{2}{{\Delta }_3}}\left(lna\right)\mathrm{csch}\left[2\left(x-vt\right)lna\right]expi\left[-{\kappa }_{2}x+{\omega }_{2}t+{\theta }_2+{\sigma }_2{W}_2\left(t\right)-{\sigma }_2^{2}t\right].$$

(73)

These relations (68)–(73) represent the solutions of the models (1) and (2) that were the main equations and that were the goal of this paper. These soliton solution structures are now subjected to their classification. The solutions (68) and (69) are straddled solitons since they remain straddled between purely bright and purely dark solitons. Next, upon choosing convenient parameter combinations, namely $A=4B^2$ or $A=-4B^2$, it is the pure bright or pure singular soliton solutions that emerge. These are represented by the pairs (70)–(71) and (72)–(73), respectively. Thus, the mathematical scheme that is adopted here to address the governing equations, namely the enhanced Kudryashov approach, reveals three forms of solitons, which are straddled solitons and pure bright and pure singular solitons although the bright and singular solitons are a byproduct of the straddled solitons with a subtle choice of the free parameters.

These results have some interesting features that are being reported for the first time in the paper. Firstly, all of the solitons (68)–(73) contain the white noise component confined to the respective phase component of the solitons for both $q(x,t)$ as well as $r(x,t)$. Thus, it is safe to say from these relations that the soliton amplitude and their inverse widths are not affected in the presence of white noise. Moreover, the structure of the soliton phase along the two components also shows that the velocity of the soliton also remain unchanged. It is only the wave number of the solitons that is affected with the inclusion of the white noise. This is an interesting observation, namely the key features of the solitons along the two components in a birefringent fiber do not change the amplitude, inverse width and velocity. This is true for all kinds of solitons that are displayed in (68)–(73).

5. Conclusions

The current paper addressed the multiplicative white noise effect in birefringent fibers that is addressed with SHE for the study of dispersive optical solitons. It has been established that the bright, dark and singular solitons that stem from the model carry the white noise effect in their phase components only and not in the amplitude portion. This is an interesting observation. These bright solitons with the stochastic phase component are visible on an oscilloscope by means of eye diagrams, while this is the case for the dark solitons only when a defined background wave is in place. The third category of solitons, namely the singular solitons, is a viable alternative terminology for optical rogons. Thus, these are unwanted features and are nevertheless listed just so that the formation of such solitons must be avoided at all costs.

One of the most interesting observations is that the soliton solutions that are derived in the work, namely the bright, dark and singular solitons, carry the effect of white noise only in their phase components. This means that the presence of white noise does not affect the key features of the bright solitons, namely their amplitude, inverse width and velocity. Moreover, for dark and singular solitons, the free parameters and the soliton velocity are not at all affected. This is an interesting and a novel observation.

The paper focuses on the mathematical implications of the effect of birefringence in dispersive soliton transmittal across intercontinental distances. Various additional engineering aspects are tacitly ignored in this mathematically flavored paper. These include the effect of artificially increasing birefringence artificially, which could lead to the departure of the fiber core from cylindrical symmetry to an elliptical core. This typically occurs when the birefringence parameter is at O(${10}^{-6}$). Stress-induced elements can also lead to awkward shaped optical fibers that are also referred to as “panda” fibers or “bow-tie” fibers. This typically happens when the birefringence parameter is at O(${10}^{-4}$). Another effect is that for hi-bi fibers, with fiber length much bigger than 1 cm, the effect of four wave mixing can be neglected and, in contrast, for weakly birefringent fibers, this effect must be retained. Such physical and engineering effects are ignored in the current work and are to be addressed separately in future papers.

Later, this model would be extended to cover DWDM topology and other such optoelectronic devices such as magneto-optic waveguides, Bragg grating metamaterials and metasurfaces. Those research activities are underway and are to appear shortly.