Abstract
In order to enhance the performance of disturbance rejection in AUV’s path tracking, this paper proposes a novel tube-based event-triggered path-tracking strategy. The proposed tracking strategy consists of a speed control law and an event-triggered tube model predictive control (tube MPC) scheme. Firstly, the speed control law using linear model predictive control (LMPC) technology is obtained to converge the nominal path-tracking deviation. Secondly, the event-triggered tube MPC scheme is used to calculate the optimal control input, which can enhance the performance of disturbance rejection. Considering the nonlinear hydrodynamic characteristics of AUV, a linear matrix inequality (LMI) is formulated to obtain tight constraints on the AUV and the feedback matrix. Moreover, to enhance real-time performance, tight constraints and the feedback matrix are all calculated offline. An event-triggering mechanism is used. When the surge speed change command does not exceed the upper bound, adaptive tight constraints are obtained. Finally, numerical simulation results show that the proposed tube-based event-triggered path-tracking strategy can enhance the performance of disturbance rejection and ensure good real-time performance.
1. Introduction
Autonomous underwater vehicles (AUVs) have been widely used in marine scientific research, underwater resource exploration, underwater oil and gas pipeline and structure overhaul, seabed hydrothermal research, and military fields [1,2]. When AUVs perform underwater tasks, they usually need to complete path-tracking tasks [3].
The 6-DOF motion of AUV in three-dimensional underwater space is coupled and nonlinear, and the parameters of the model are often difficult to obtain precisely. In model-based control methods, the control performance will suffer from parametric uncertainties [4]. Moreover, external disturbances caused by ocean currents will also degrade the control performance [5,6]. Therefore, it is a challenge to enhance the robustness against external disturbances and parametric uncertainties in model-based control methods [7]. Until now, researchers have applied strategies for improving the robustness of model-based control methods such as the model predictive control (MPC) technique [8,9] and sliding mode control (SMC) technology [10] in the path-tracking control of AUVs. Note that MPC can easily handle the physical constraints of the AUV when formulating the optimal control problem. It is also well-known that MPC technology can provide some assistance for the disturbance rejection [11]. In other words, the MPC technology itself is robust against disturbance. Therefore, MPC is widely used in the path-tracking control of AUVs [12,13].
Zhang proposed a 3D path-tracking control method for AUVs using a linear model predictive control (LMPC) [13]. The LMPC controller is used to calculate the speed control law. Then, the control inputs of the AUV were directly calculated based on the dynamics model, where the physical constraints on the control input failed to be considered. In [14,15], the speed control law was generated by the kinematics LMPC, and the control inputs were generated by the dynamic LMPC. These physical constraints on the control input can be considered when formulating the optimal control problem. Compared with [13], the method in [14,15] can also enhance the robust performance against disturbances, by the robustness of the nominal MPC technology itself. However, there is no direct disturbance rejection strategy, such as disturbance estimation [16,17] or robust MPC technology [18]. The robustness of the nominal MPC technology itself is limited. These disturbance rejection strategies can significantly improve the robustness performance, compared with the nominal MPC technology. Therefore, a direct disturbance rejection strategy can be introduced in the nominal MPC technology to improve the tracking control performance.
The extended Kalman filter technology is used to estimate external current disturbances [17]. Based on the 12-dimensional kinematic model and kinetic model, a NMPC controller is proposed to calculate the optimal control law using these results of disturbance estimation. However, the disturbance estimation will bring extra dimensions, which may lead to poor real-time performance. To overcome the challenge, disturbance estimation is only based on the 5-dimensional kinematic model using MPC, which can save online optimization computing time [10]. Note that control inputs are calculated using adaptive sliding mode control technology, which is sensitive to the noise in the actual control system. The control performance may suffer from the chattering problem in the practical application [19].
Tube MPC, as a disturbance rejection strategy, was first proposed by Blanchini [20]. Compared with the disturbance estimation, the robustness improvement is achieved by its own relatively stable mechanism. Suffering from external disturbance and parametric uncertainties, there is a model mismatch between the nominal model and the actual model. A robust positively invariant (RPI) set is proposed to measure the boundedness of the mismatch [21]. In the tube MPC scheme, the tight constraint is calculated by tightening the constraints of the actual system by an RPI set. The control law of the tube MPC scheme consists of a nominal optimal control law and a feedback control law. The nominal control law is obtained by solving a receding horizon optimal control problem with a tight constraint. The feedback control law is used to address the deviation of the nominal and actual states due to the model mismatch. The traditional tube MPC scheme [21,22] is proposed for AUV’s path tracking [18]. Note that the RPI set is obtained based on the assumed disturbance upper bound. Hence, the corresponding tight constraints may become too conservative to degrade the path-tracking performance. Based on the coupled 6-dimensional AUV model, both the RPI set and the terminal feasible set are easy to have no solution. Moreover, online calculating tight constraints of the nominal model brings too much computing time, which will also lead to poor real-time performance.
Since the inherent robustness of the nominal MPC to address the model mismatch is limited, the tube MPC has the potential to improve robustness against model mismatches. However, the control performance suffers from poor real-time performance and no solution for the RPI set. Our motivation is to apply the tube MPC to enhance the robustness of AUV’s path tracking, with these issues addressed. This study proposes a tube-based event-triggered path-tracking strategy, which consists of a kinematics LMPC controller and a tube MPC controller. To converge the nominal path-tracking deviation, the kinematics LMPC controller is used to calculate the optimal speed control law. The tube MPC controller is used to compute the control input of the AUV to track the speed control law. Compared with the tube MPC technology used in [18], to avoid no solution to the RPI, the coupled kinetic model is decoupled into three Lipschitz nonlinear models [23]: a surge speed control model, a heading control model, and a depth control model. With the corresponding Lipschitz constant obtained, nonlinear properties of these models when formulating a linear matrix inequality (LMI) are used to calculate the RPI set and the feedback matrix. The terminal feasible set is obtained based on linear differential inclusion (LDI) technology. In order to achieve good real-time performance, constraints on the nominal model and the feedback matrix are all calculated offline. Note that the hydrodynamic force of the AUV is related to the surge speed. The mismatch may depend on the surge speed change command. These offline calculated invariant constraints are too conservative to achieve better control performance. Then, an event-triggering mechanism is used. When the surge speed change command does not exceed the upper bound, two decision variables are introduced to formulate a flexible tube. Then, adaptive constraints on the nominal model are obtained to address the mismatch. When the surge speed change command exceeds the upper bound, the offline tight constraints will be used. The main contributions of this work are as follows:
- A tube-based event-triggered path-tracking strategy, which consists of a LMPC controller and a tube MPC controller, is proposed to enhance the robustness against disturbances and parametric uncertainties. The LMPC controller is used to calculate the speed control law to converge the path-tracking deviation, and the tube MPC controller is used to track the speed control law.
- In the tube MPC controller, with nonlinear characteristics of AUV hydrodynamic force considered, tight constraints in the nominal control law and the feedback matrix in the feedback control law are obtained by formulating two LMIs. To achieve real-time performance, these linear matrix inequalities are all calculated offline.
- To overcome control performance degradation brought by conservative tight constraints calculated offline, an event-triggering mechanism is used to dynamically adjust these constraints in the nominal control law according to the surge speed change command. Compared with conservative tight constraints, better path tracking can be achieved, and the real-time performance is also satisfied.
The remainder of this paper is organized as follows. In Section 2, preliminaries are given. In Section 3, the AUV’s motion model and the path-tracking problem are given. In Section 4, the detail design of the tube-based event-triggered path-tracking strategy is given. In Section 5, the numerical simulation analysis is shown.
2. Preliminaries
The actual nonlinear continuous-time dynamics is described as a Lipschitz nonlinear system [23]:
with and . denotes the bounded external disturbance. Positive constant is the disturbance upper bound. System (1) is also subject to state and control input constraints:
where is a compact set and is bounded. Here is a Lipschitz nonlinear function with a Lipschitz constant such that:
The overline format of a variable denotes its nominal value, e.g., denotes the nominal value of . The continuous-time nominal model is given by:
and the corresponding discrete-time system models are given by:
Define . The nominal cost function of predicted state sequence, , , and control input sequence, , , is given as:
where is the predictive horizon. is the positive definite stage cost and is the terminal cost:
The state deviation between the actual system and the nominal actual is denoted by . The deviation system is given as:
In a tube MPC controller, the control law consists of a nominal MPC control law and a state feedback control law :
where is obtained by solving an optimal control problem, and is used to converge the state deviation .
Definition 1.
(Robust positively invariant (RPI) set): A set is the RPI set of deviation system (9), if there exists a feedback control law
, such that for all and
, it holds that
for all .
Then the constraints of nominal system (6) are given with an RPI set as:
where and are tight constraint sets, which can be expressed as:
Considering linear constraints, these constraints can also be expressed as a polytope:
Considering tight constraints (11) and nominal system dynamics (6), the following optimal control problem is formulated to calculate the nominal MPC control law:
where is the terminal feasible set. The optimal control input sequence , , is the solution to optimal control problem (14), and the nominal optimal MPC control law is obtained by:
3. AUV Motion Model and Problem Formulation
In this section, the kinematics model and kinetic model of the AUV are given, where both external disturbances and parametric uncertainty are considered in the kinetic model. In the proposed tube-based event-triggered path-tracking strategy, described in Section 4, based on the kinematics model, a speed control law is designed to converge the nominal path-tracking deviation. Then, based on the kinetic model, the control input of the AUV is calculated to track the speed control law. Correspondingly, two problems treated in this study are formalized.
3.1. AUV Motion Model
The global coordinate and the local coordinate frame are defined, and the coordinate transformation relationship is shown in Figure 1. Here denotes the global coordinate system, and denotes the local coordinate system [24].
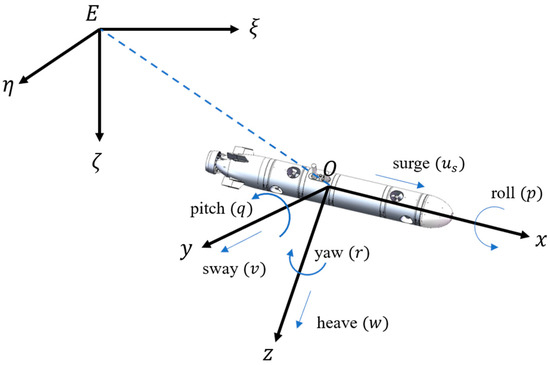
Figure 1.
AUV coordinate system [24].
Note that the roll motion is self-stable, and the roll motion attitude is also small, meaning that the roll angle and the roll speed can all be regarded as 0. Therefore, the roll motion is not considered in this paper. The speed vector is denoted by in the motion coordinate , where , , , , and are respectively surge speed, sway speed, heave speed, pitch speed, and yaw speed. The position and attitude angle (pitch and yaw angles) vector is denoted by in global coordinate system . The kinematics model is given as:
where is a transformation matrix from to :
The kinetic model is given as:
where is the inertial matrix, is the Coriolis and centripetal matrix, is the hydrodynamic damping matrix, and is the hydrostatic force and moment. is the AUV’s control vector, where is the stern thruster force, is the vertical plane deflection, and is the translational plane deflection. is the active control force in the AUV’s motion coordinate system . is the external disturbance. represents the disturbance brought by parametric uncertainties [10].
3.2. Model Decoupling
Note that the degrees of freedom of the AUV are coupled in nonlinear model (18). In order to simplify the design of the controller, the 5 DOF nonlinear dynamic model (18) of the AUV is decoupled for surge speed control, heading control, and depth control. Considering that the AUV always maintains a constant surge speed for path tracking, the nominal surge speed in the heading nominal control model and depth nominal control model above is set as a constant. Then, these decoupled models can all be described as a Lipschitz nonlinear system. The hydrodynamic coefficients in these models are given in our previous research [24].
- 1.
- Surge speed nominal control model:
- 2.
- Heading nominal control model:
- 3.
- Depth nominal control model:
3.3. Problem Statement
Problem 1.
Given a vector that stands for the reference position and attitude angle and a vector that stands for the reference speed, the nominal path-tracking deviation vector is denoted by and the surge speed deviation vector is denoted by . The speed control law needs to be obtained to converge the nominal path-tracking deviation:.
Problem 2.
The speed control law deviation vector is denoted by and the actual path-tracking deviation is denoted by . Based on decoupling models (19), (20), and (22), AUV’s control vector needs to be obtained to respond to the speed control law:. Finally, the actual path-tracking deviation can be converged: .
4. Methodology
In order to address the external ocean current disturbance and parametric uncertainties of the Coriolis and centripetal matrix and the hydrodynamic damping matrix, a tube-based event-triggered path-tracking strategy consisting of a LMPC controller and a tube MPC controller is developed. The scheme of the proposed path-tracking strategy is shown in Figure 2.
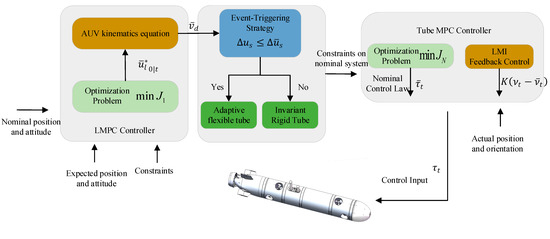
Figure 2.
Scheme of the proposed path-tracking strategy.
Based on the kinematics model, the LMPC controller is used to address Problem 1, whose inputs are the reference waypoint and real-time nominal states of the AUV, and outputs are the speed control law.
Based on decoupled models (19), (20), and (22), according to the speed control law and real-time states of the AUV, the tube MPC controller is used to compute optimal control inputs of the AUV. The nominal control law is obtained by solving a constrained optimal control problem. According to these decoupled models, the surge speed will have a great effect on the AUV’s state, and the mismatch of these decoupled models may depend on the surge speed. These offline calculated invariable constraints on the nominal system may be too conservative. According to the change in the surge speed command, an event-triggering strategy is used to formulate an adaptive flexible tube to deal with the mismatch.
4.1. LMPC Controller
First, nominal kinematics model (1) is discretized as:
where is the sampling time.
Limited by the AUV’s kinetics characteristics, sharp changes in speed are not allowed. Then, the increment of speed is used as the control input:
To minimize the path-tracking deviation and avoid sharp changes in speed, the objective function is designed as follows:
where is the predictive horizon in the LMPC controller.
The constraints of the control input and speed are given as:
where and are the control input’s upper bound and low bound, which satisfy, and and are the speed’s upper bound and low bound.
Then an optimal control problem is designed to calculate the nominal speed control law :
where is the solution to the optimal control problem. Then the speed control law is obtained as:
where is the increment of speed in the present moment.
4.2. Tube MPC Controller
Like the tube MPC scheme given in (10)–(14), the nominal control law is used to track the speed control law, which is obtained by solving an optimal control problem. The nonlinear hydrodynamic characteristics are considered in the state transition constraint, , which are decoupled in (19), (20), and (22). Moreover, the terminal feasible set and the RPI set also need to be obtained when formulating the optimal control problem. The state feedback control law, which considers the nonlinear characteristics of the AUV, is used to converge the deviation of the actual state and the nominal state . In a Lipschitz nonlinear system, the Lipschitz constant can be used to describe the nonlinear characteristics. Following [23], with the Lipschitz constant set, a feedback matrix used to calculate the stated feedback control law and the (RPI) set can be obtained by formulating an LMI. Following [25], another optimal control problem is formulated to obtain the terminal feasible set considering the linear differential inclusion characteristics of the AUV. To ensure real-time performance, they are calculated offline. A brief derivation of the LMI and the optimal control problem is given as follows.
Assumption 1.
In these decoupling models, there always exists a corresponding constant to satisfy the condition of the Lipschitz nonlinear function (3).
Lemma 1
[23]. For a Lipschitz nonlinear system (1), there exists a positive definite matrix , a matrix , and scalars and such that:
with and the feedback matrix.
With parameters and set, LMI (31) is solved to obtain the matrices and the parameter . Matrices and are used to calculate the feedback matrix . With disturbance upper bound set, together with and , the RPI set and the feedback control law can be obtained:
where the RPI set and the feedback matrix are all invariant. With the RPI set calculated, the constraint on the nominal state is obtained, which is equivalent to constraints on the nominal control input using the Minkowski Operation [26]. Then, constraints of nominal system (11) can be obtained.
With the RPI set obtained, the constraints of nominal system (6) are invariant, which are treated as an invariant rigid tube. The LDI of nominal system (6) is defined:
The minimum convex polytope is denoted by :
where is the extreme matrix of the minimum convex polytope , and is the number of the extreme matrix.
The terminal feasible set is obtained as follows:
Lemma 2
[25]. Suppose the LDI of nominal system (6) is given by (33), and the constraints of nominal system (6) are obtained by (11) and (31). There exist matrices and such that:
and
are satisfied with . The terminal weighting matrix is set as . and are positive definite diagonal matrices.
Note that the determinant, , represents the volume of the terminal region , and a too-small terminal region will easily lead to the infeasibility of nominal optimal control problem (14). To enlarge the terminal region, another optimal control problem is formulated as:
According to speed control law (30), surge speed step signal can be obtained. When the surge speed step signal exceeds the upper bound, i.e., , the constraints of nominal system (6) will be used. When the surge speed step signal does not exceed the upper bound, i.e., , an adaptive flexible tube, treated in the form of inequalities, is introduced.
The variable, which represents the size of the adaptive flexible tube, is calculated by decision variable to change offline calculated constraints (11). The decision variable is subject to nonlinear function . Then, optimal control problem (14) becomes:
where constant is a decay factor, and is a positive constant. Constraint upper bound and are all positive constants.
The nonlinear constraint is given by:
where is a polynomial with . and are positive constants.
4.3. Implementation of the Proposed Strategy
To conclude, the proposed tube-based event-triggered path-tracking strategy consists of an offline strategy and an online strategy. To achieve good real-time performance, the offline strategy is introduced in Algorithm 1. LMI (31) is used to calculate the tight constraint and the feedback matrix . Optimal control problem (37) is used to calculate the terminal feasible set . The online strategy is introduced in Algorithm 2. The optimal control problem (29) in the LMPC controller is first solved to obtain the speed control law. Then, the control law of the tube MPC controller (10), which consists of a nominal control law and a feedback control law, is respectively calculated to track the speed control law based on these decoupled models (19), (20), and (22). According to the surge speed step signal , optimal control problem (38) or optimal control problem (14) is solved to obtain the nominal control law based on the offline calculated tight constraint and terminal feasible set . Then, the offline calculated feedback control matrix is used to calculate the feedback control law to converge the deviation of the nominal and actual states.
| Algorithm 1 Offline strategy |
| 1. Define nominal cost function (7); choose state and control input constraints (2) |
| 2. Choose appropriate parameters and to solve LMI (31) |
| 3. Obtain feedback matrix and RPI set (32) |
| 4. Calculate invariant rigid tube (11) |
| 5. Choose appropriate weight matrices to solve optimal control problem (37) 6. Obtain terminal feasible set |
| Algorithm 2 Online AUV path-tracking algorithm |
| 1. Measure AUV’s actual state , and nominal state |
| 2. Solve optimal control problem (29) to obtain the speed control law |
| 3. If : 4. Based on these decoupling models (19–20,22), separately formulate optimal control problem (38) to obtain nominal control vector 5. Otherwise: 6. Based on these decoupling models (19–20,22), separately formulate optimal control problem (14) to obtain nominal control vector 7. End |
| 8. Calculate the AUV’s control vector |
| 9. Set , and go back to 1 |
5. Numerical Simulation
Numerical simulations are conducted to demonstrate the control performance of the proposed tube-based event-triggered path-tracking strategy. Path-tracking deviation, control input smoothness, and real-time performance are used to evaluate the control performance. In order to show the variation trend of the path-tracking deviation intuitively, the path-tracking integral deviation index is introduced, e.g., denotes the integral deviation of in global coordinate system :
Problem 1 is always solved by the proposed LMPC controller. These contrasting simulations differ in the method for solving Problem 2: “MPC” denotes simulation results using a nominal MPC controller from [15]. “RTMPC” denotes the simulation results using the tube MPC scheme (10)–(14) [23]. “ATMPC” denotes simulation results using the proposed tube-based event-triggered path-tracking strategy. To verify the superiority of the proposed path-tracking strategy, three real-time simulations were carried out, where “ATMPC” is compared with “RTMPC” and “MPC”.
Numerical simulations were carried out using Simulink/Matlab, with AMD Ryzen Threadripper PRO 3995WX 64-Cores 2.70Ghz CPU and 256 GB RAM running Windows 10. Following this, optimal control problem (29) can be converted to a standard quadratic programming (QP) problem [22]. Then, the ‘quadprog’ function in Matlab can be used to solve the QP problem. When formulating the general optimal control problem (38), we refer to the open-source code, gitlab.ethz.ch/ics/RAMPC-CCM.
5.1. Parameters Set
Note that the influence of parameters on control performance in the optimal control problem is significant. To focus on evaluating the control performance of the proposed path-tracking strategy, in the contrasting simulations, these same parameters in different methods are all set to the same value. Then, the parameters in the numerical simulation are given as follows. Following [10], the external sinusoidal disturbance term is set as . The upper bound of the surge speed step signal is set as . Following [10], the parametric uncertainties are reflected by the percentage of the hydrodynamic term. Then, is set as .
Note that the proposed path-tracking strategy consists of a LMPC controller and a tube MPC controller. The LMPC controller is used to calculate the speed control law to converge the path-tracking deviation, and the tube MPC controller is used to track the speed control law.
For the LMPC controller, these parameters in (24–29) are listed in Table 1. In the LMPC controller, weighting matrix and are for minimizing the path-tracking deviation . The weight matrix is for the smooth change in AUV’s speed. With these weight matrices set appropriately, the speed control law can efficiently converge the path-tracking deviation, avoiding abrupt changes in AUV’s speed.

Table 1.
Parameter value in the LMPC controller.
Note that the tube MPC controller is used for surge speed control, heading control, and depth control, respectively, based on these decoupled models (19), (20), and (22). These corresponding parameters of each controller in (24)–(29) and (38) are listed in Table 2, Table 3 and Table 4. is the increment of the stern thruster force. is the increment of the vertical plane deflection. is increment of the translation plane deflection. In the tube MPC controller, the weighting matrices play a similar role. With the appropriate and set, the control input of the AUV can change smoothly to track the nonmail speed control law. The RPI set in Definition 1 is used to obtain the tight constraint in nominal system dynamics to ensure that the deviation (9) also contained in the RPI set. The feedback matrix is used to converge the deviation. As mentioned in Section 4.2, with appropriate parameters and obtained, the tube MPC controller can efficiently track the speed control law.

Table 2.
Parameter value in the tube MPC controller for surge speed control.

Table 3.
Parameter value in the tube MPC controller for heading control.

Table 4.
Parameter value in the tube MPC controller for depth control.
When the adaptive flexible tube is used, two decision variables are used to dynamically adjust these tight constraints. Parameter represents the upper bound of the tight constraints. Parameters , , and nonlinear function are used to represent the variation in the tight constraint.
5.2. Analysis and Discussion
The reference path of the AUV is generated by tracking the sinusoidal shape trajectory, and the initial state of the AUV is set as:.
To visually compare the control performance of “MPC”, “RTMPC”, and “ATMPC”, AUV’s trajectories during path tracking are shown in Figure 3.
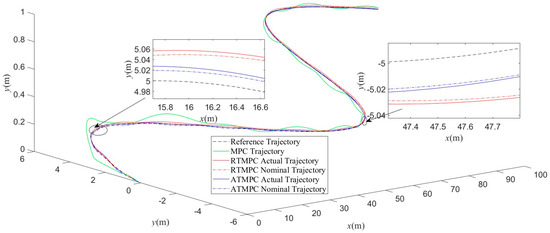
Figure 3.
AUV trajectory during path tracking.
Intuitive path-tracking performance can be visualized in the trajectory of AUV during path tracking, which is the position of the AUV given in Section 3.1. Figure 3 shows a three-dimensional view of the AUV’s path-tracking control performance of “MPC”, “RTMPC”, and “ATMPC”. The trajectory of “MPC” fails to track the reference trajectory well. Although the path-tracking deviation of “MPC” tends to converge, there are still several obvious position offsets, especially at the beginning of path tracking. Actual trajectories of both “RTMPC” and “ATMPC” can separately track the nominal trajectory. Note that the nominal trajectory of “ATMPC” tracks the reference trajectory better, compared with that of “RTMPC”.
where , , and are the reference positions. is the reference surge speed.
To compare the path-tracking deviation in detail, the path-tracking deviation and path-tracking integral deviation are respectively shown in Figure 4 and Figure 5. The maximum deviations in position and attitude angles are given in Table 5. Section 3.3 introduced the path-tracking deviation, whose absolute value is used. The definition of path-tracking integral deviation is given in (41). As shown in Figure 4, under sinusoidal external disturbances and parametric uncertainties, position and attitude angle deviations of three methods all have a bounded and convergent tendency over time. Compared with the position and attitude deviations of “MPC”, that of “RTMPC” has been all effectively reduced in every moment. As shown in Figure 5, the growth trend of the integral deviation is also much slower. In addition, the maximum position deviation of “RTMPC” can be reduced from 0.38 m to 0.12 m. That is a reduction of about 68%. The maximum pitch angle deviation of “RTMPC” can be reduced from 3.45° to 0.58°. That is a reduction of about 83%. The maximum yaw angle deviation of “RTMPC” can be reduced from 3.45° to 1.07°. That is a reduction of about 69%. It can be seen the “RTMPC” has good robustness against external disturbances and parametric uncertainties.
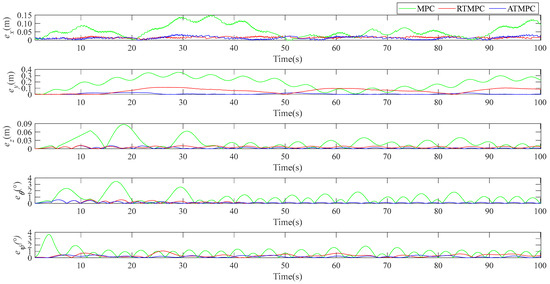
Figure 4.
Deviation of position and attitude angle.
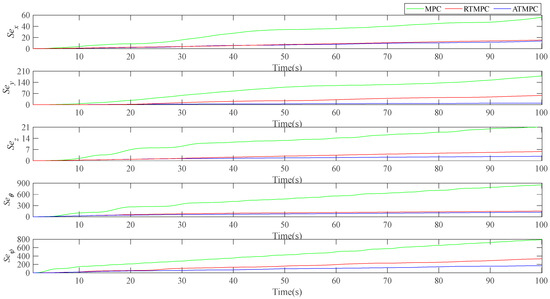
Figure 5.
Integral deviation of position and attitude angle.

Table 5.
Maximum deviation of position and attitude angles.
Compared with “RTMPC”, the proposed tube-based event-triggered path-tracking strategy has a smaller position and attitude angle deviations. The maximum position deviation of “ATMPC” can be reduced from 0.12 m to 0.04 m. That is a reduction of about 67%. As shown in Figure 4, compared with the position deviation in the direction and of “RTMPC”, that of “ATMPC” is almost the same in every moment. However, after about 20 s, the position deviation of is much smaller in every moment. In addition, the maximum yaw angle deviation can be reduced from 1.07° to 0.45°. That is a reduction of about 58%. As shown in Figure 4, after about 10 s, the yaw angle deviation is almost smaller in every moment. Integral deviations can intuitively show the variation trend of these position and attitude deviations in Figure 5.
To compare control input smoothness, the range of the AUV’s speed and the control input are respectively shown in Figure 6 and Figure 7. AUV’s speed and the control input have been given in Section 3.1. As shown in Figure 6, the surge speed of “ATMPC” and “RTMPC” tracks the desired surge speed well. The sway speed, heave speed, pitch speed, and yaw speed changes in “ATMPC” and “RTMPC” occur more smoothly, compared with those of “MPC”.
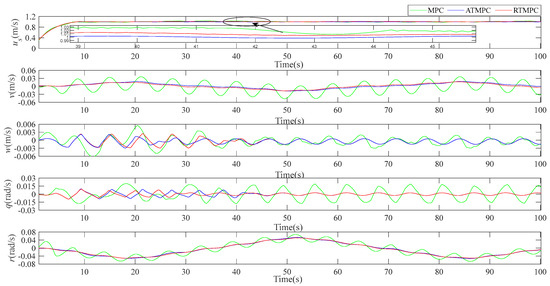
Figure 6.
Range of the AUV’s speed.
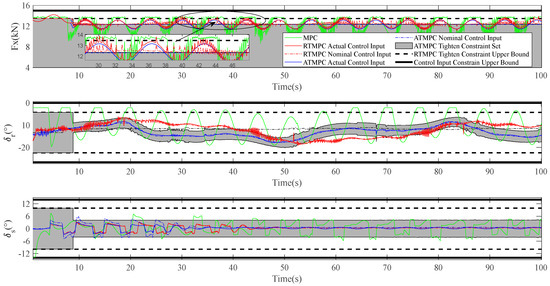
Figure 7.
Range of the AUV’s control input.
As shown in Figure 7, compared with the stern thruster force of “MPC”, that of “ATMPC” and “RTMPC” have better smoothness, avoiding the high-frequency oscillation phenomenon. As shown in the local zoom-in of Figure 7, the smoothness of the stern thruster force of “ATMPC” is enhanced, compared with that of “RTMPC”. It can be seen that the nominal control input of the “ATMPC” is within the upper bound of the tight constraint, and the output value of “ATMPC” is almost the lowest, which may be consistent with the purpose of energy conservation in real-world application.
Like the vertical plane deflection shown in Figure 7, those of “RTMPC” and “ATMPC” can all avoid large periodic changes, compared with that of “MPC”. At the beginning of the simulation, the range of the vertical plane deflection of “MPC” has a tendency to be unstable. With the adaptive tight constrain introduced, the vertical plane deflection of “ATMPC” changes more smoothly. As the simulation time goes on, there is almost no oscillation phenomenon. As shown in Figure 7, the blue line is contained within the gray area, and the trend of the upper and lower limits in the gray area is consistent with the trend of the blue line.
Like the translational plane deflection shown in Figure 7, that of “RTMPC” and “ATMPC” can also avoid large periodic changes, compared with that of “MPC”. With the adaptive tight constraint introduced, the translational plane deflection of “ATMPC” changes more smoothly, and tends to stabilize more quickly.
To analyze the real-time performance, the time consumption of different methods is recorded in Table 6. Note that the tightened constraint set of “RTMPC” is calculated offline. It can be explained that the average time consumption and the maximal time consumption of “RTMPC” are almost the same as those of “MPC”. The average time consumption and the maximal time consumption of “ATMPC” will not increase by much: the average time consumption increases by 2.91 ms, and the maximal time consumption increases by 3.47 ms.

Table 6.
Time consumption of different methods.
6. Conclusions
In this paper, a novel tube-based event-triggered path-tracking strategy against disturbance is proposed, which consists of an LMPC controller and a tube MPC controller. In the LMPC controller, based on the nominal kinematics model of the AUV, a nominal optimal speed control law is obtained to converge the nominal path-tracking deviation. In the tube MPC controller, AUV’s available control inputs are separately calculated based on a decoupled model. Considering the nonlinear hydrodynamic characteristics of the AUV, an LMI is formulated to calculate the feedback matrix and tight constraints offline. The terminal region in the tube MPC controller is obtained offline using linear differential inclusion technology. When the surge speed step signal does not exceed the upper bound, the tight constraints become adaptive. Numerical simulation results show that the feedback matrix is successfully used to match the actual trajectory and the nominal trajectory. With the adaptive constraints introduced, the nominal trajectory tracks the reference better. Note that the online computing time of the tube MPC is acceptable, and these corresponding control inputs are also smooth. Therefore, the proposed tube-based event-triggered path-tracking strategy can enhance the path-tracking performance and ensure good real-time performance.
In the MPC controller, the disturbance upper bound needs to be set appropriately. If the bound is too small, the robustness is weak; otherwise, the tube will be too conservative. The RPI set may not be obtained, or the optimal control problem is easy to be infeasible. In numerical simulation, the disturbance upper bound is still easy to set appropriately. In the application of a real-world system, it may be a challenge. The disturbance bound is different for different real-time scenarios, which may be difficult to accurately set. This may lead to degradation of the control performance. In future research, the work will be extended to predict the model mismatches due to parametric uncertainties and external disturbances to improve the accuracy of the nominal model, based on data-driven technology, such as machine learning. The RPI set is used to address the bounded prediction deviation. If the prediction deviation is convergent and bounded, it can effectively solve the problem of setting the disturbance upper bound in real-world applications.
Author Contributions
Conceptualization, Y.C. and Y.B.; methodology, Y.C. and Y.B.; software, Y.C.; validation, Y.C. and Y.B.; formal analysis, Y.C. and Y.B.; investigation, Y.C. and Y.B.; resources, Y.C. and Y.B.; data curation, Y.C. and Y.B.; writing—original draft preparation, Y.C.; writing—review and editing, Y.C. and Y.B.; visualization, Y.C. and Y.B.; supervision, Y.B.; project administration, Y.B.; funding acquisition, Y.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Hunan Provincial Natural Science Foundation of China (2021JC0010), and Defense Industrial Technology Development Program (JCKY2021110B024, JCKY2022110C072).
Data Availability Statement
Data is unavailable due to privacy or ethical restrictions.
Acknowledgments
Haicheng Zhang (Hunan University) and Weisheng Zou (Hunan University) were acknowledged to provide careful guidance.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Pontryagin difference, | n-dimensional identity matrix | ||
| () | the smallest (largest) real part of eigenvalues of a matrix | A matrix with m rows and n columns | |
| bounded external disturbance | disturbance upper bound | ||
| positive weight matrix | quadratic norm of a vector with positive weight matrix | ||
| Lipschitz nonlinear function | Lipschitz constant | ||
| nominal state and control input | actual state and control input | ||
| cost function | feedback matrix | ||
| terminal feasible set | robust positively invariant (RPI) set | ||
| inequality constraint | constraint set | ||
| state transition function | predictive horizon | ||
| linear differential inclusion function | minimum convex polytope | ||
| determinant calculation | polynomial function | ||
| set |
References
- Bibuli, M.; Zereik, E.; De Palma, D.; Ingrosso, R.; Indiveri, G. Analysis of an Unmanned Underwater Vehicle Propulsion Model for Motion Control. J. Guid. Control Dyn. 2022, 45, 1046–1059. [Google Scholar] [CrossRef]
- Guerrero, J.; Torres, J.; Creuze, V.; Chemori, A.; Campos, E. Saturation based nonlinear PID control for underwater vehicles: Design, stability analysis and experiments. Mechatronics 2019, 61, 96–105. [Google Scholar] [CrossRef]
- Petritoli, E.; Bartoletti, C.; Leccese, F. Preliminary Study for AUV: Longitudinal Stabilization Method Based on Takagi-Sugeno Fuzzy Inference System. Sensors 2021, 21, 1866. [Google Scholar] [CrossRef] [PubMed]
- Sedghi, F.; Arefi, M.M.; Abooee, A.; Kaynak, O. Adaptive Robust Finite-Time Nonlinear Control of a Typical Autonomous Underwater Vehicle with Saturated Inputs and Uncertainties. IEEE/ASME Trans. Mechatron. 2021, 26, 2517–2527. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Hua, C.C.; Guan, X.P. Trajectory Tracking Control of Autonomous Underwater Vehicle with Unknown Parameters and External Disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1054–1063. [Google Scholar] [CrossRef]
- Jia, Z.; Qiao, L.; Zhang, W. Adaptive tracking control of unmanned underwater vehicles with compensation for external perturbations and uncertainties using Port-Hamiltonian theory. Ocean Eng. 2020, 209, 107402. [Google Scholar] [CrossRef]
- Kou, L.; He, S.; Li, Y.; Xiang, J. Constrained Control Allocation of a Quadrotor-Like Autonomous Underwater Vehicle. J. Guid. Control Dyn. 2021, 44, 659–666. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Trajectory Tracking Control of an Autonomous Underwater Vehicle Using Lyapunov-Based Model Predictive Control. IEEE Trans. Ind. Electron. 2018, 65, 5796–5805. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Yu, Z.; Zhang, B.; Zhang, N. Dynamic Trajectory Planning and Tracking for Autonomous Vehicle with Obstacle Avoidance Based on Model Predictive Control. IEEE Access 2019, 7, 132074–132086. [Google Scholar] [CrossRef]
- Long, C.; Hu, M.; Qin, X.; Bian, Y. Hierarchical trajectory tracking control for ROVs subject to disturbances and parametric uncertainties. Ocean Eng. 2022, 266, 112733. [Google Scholar] [CrossRef]
- Li, H.; Swartz, C.L.E. Robust model predictive control via multi-scenario reference trajectory optimization with closed-loop prediction. J. Process Control 2021, 100, 80–92. [Google Scholar] [CrossRef]
- Wang, W.; Yan, J.; Wang, H.; Ge, H.; Zhu, Z.; Yang, G. Adaptive MPC trajectory tracking for AUV based on Laguerre function. Ocean Eng. 2022, 261, 111870. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Luo, M.; Yang, C. MPC-based 3-D trajectory tracking for an autonomous underwater vehicle with constraints in complex ocean environments. Ocean Eng. 2019, 189, 106309. [Google Scholar] [CrossRef]
- Yan, Z.; Gong, P.; Zhang, W.; Wu, W. Model predictive control of autonomous underwater vehicles for trajectory tracking with external disturbances. Ocean Eng. 2020, 217, 107884. [Google Scholar] [CrossRef]
- Gong, P.; Yan, Z.; Zhang, W.; Tang, J. Trajectory tracking control for autonomous underwater vehicles based on dual closed-loop of MPC with uncertain dynamics. Ocean Eng. 2022, 265, 112697. [Google Scholar] [CrossRef]
- Dai, L.; Lu, Y.; Xie, H.; Sun, Z.; Xia, Y. Robust Tracking Model Predictive Control with Quadratic Robustness Constraint for Mobile Robots with Incremental Input Constraints. IEEE Trans. Ind. Electron. 2021, 68, 9789–9799. [Google Scholar] [CrossRef]
- Long, C.Q.; Qin, X.H.; Bian, Y.G.; Hu, M.J. Trajectory tracking control of ROVs considering external disturbances and measurement noises using ESKF-based MPC. Ocean Eng. 2021, 241, 109991. [Google Scholar] [CrossRef]
- Nikou, A.; Verginis, C.K.; Heshmati-alamdari, S.; Dimarogonas, D.V. A robust non-linear MPC framework for control of underwater vehicle manipulator systems under high-level tasks. Iet Control Theory Appl. 2021, 15, 323–337. [Google Scholar] [CrossRef]
- Vu, Q.V.; Dinh, T.A.; Nguyen, T.V.; Tran, H.V.; Le, H.X.; Pham, H.V.; Nguyen, L. An Adaptive Hierarchical Sliding Mode Controller for Autonomous Underwater Vehicles. Electronics 2021, 10, 2316. [Google Scholar] [CrossRef]
- Blanchini, F. Control synthesis for discrete time systems with control and state bounds in the presence of disturbances. J. Optim. Theory Appl. 1990, 65, 29–40. [Google Scholar] [CrossRef]
- Rakovic, S.V.; Kerrigan, E.C.; Kouramas, K.I.; Mayne, D.Q. Invariant approximations of the minimal robust positively Invariant set. IEEE Trans. Autom. Control 2005, 50, 406–410. [Google Scholar] [CrossRef]
- Chryssochoos, I.; Raković, S.; Mayne, D.Q. Robust model predictive control using tubes. Automatica 2004, 40, 125–133. [Google Scholar]
- Yu, S.; Maier, C.; Chen, H.; Allgöwer, F. Tube MPC scheme based on robust control invariant set with application to Lipschitz nonlinear systems. Syst. Control Lett. 2013, 62, 194–200. [Google Scholar] [CrossRef]
- Chen, Y.; Bian, Y.; Cui, Q.; Dong, L.; Xu, B.; Hu, M. LTVMPC for Dynamic Positioning of An Autonomous Underwater Vehicle. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), Tianjin, China, 29–31 October 2021; pp. 1–5. [Google Scholar]
- Chen, W.H.; O’Reilly, J.; Ballance, D.J. On the terminal region of model predictive control for non-linear systems with input/state constraints. Int. J. Adapt. Control Signal Process. 2003, 17, 195–207. [Google Scholar] [CrossRef]
- Cox, W.; While, L.; Reynolds, M. A Review of Methods to Compute Minkowski Operations for Geometric Overlap Detection. IEEE Trans. Vis. Comput. Graph. 2021, 27, 3377–3396. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).