Abstract
This paper focuses on embedded system modeling, proposing a solution to obtain a refined net via the refinement operation of an extended Petri net. Object-oriented technology and Petri net with inhibitor-arcs-based representation for embedded systems (PIRES+) are combined to obtain an object-oriented PIRES+ (OOPIRES+). A gateway refinement method of OOPIRES+ is proposed, and the preservation of the liveness, boundedness, reachability, functionality, and timing of the refined net system is investigated. The modeling analysis of a smart home system is taken as an example to verify the effectiveness of the refinement method. The results can provide an effective way for the investigation of the refined properties of a Petri net system and a favorable means for large-scale complex embedded system modeling, which has broad application prospects.
1. Introduction
Embedded systems are the driving force behind the rapid development of the information technology industry and have widely penetrated and been integrated into every corner of the national economic and social development. As an industry leading the future economic boom, the research of the Internet of Things is also inseparable from embedded systems. Roberto et al. [1] introduced an event network SCIFI-II system, which can separate application components from the event brokers that connect components and realize the deployment of components in any environment. The design and manufacturing of embedded systems has become a hot research topic internationally. In order to improve the design and manufacturing efficiency of embedded systems, formal modeling and verification of the system are very important.
For embedded system modeling, there are usually two methods: the non-formal modeling method and the formal modeling method. Non-formal modeling methods can express certain functional characteristics of a system, but they cannot be validated using rigorous mathematical methods. Formal methods use symbols and mathematical language to describe the properties of a system, which can systematically describe and validate the system [2]. Common formal modeling methods mainly include the extended finite-state machine method [3], data flow diagram method [4], communication process method [5], Petri net method [6], entity relationship diagram method, object-oriented UML method [7], etc. These modeling methods describe the characteristics of embedded systems from different perspectives but do not form a unified standard. Due to their intuitive graphical expression ability and rigorous mathematical expression, Petri nets have a wide range of applications in the behavioral analysis of concurrent systems [8]. However, classical Petri nets lack a hierarchical structure, cannot fully describe data flows, and lack the concept of time [9], making it impossible to fully describe embedded systems.
In order to improve the modeling ability of Petri nets on embedded systems, domestic and foreign scholars have improved the classical Petri nets and proposed a variety of extension forms, such as colored Petri nets (CPNs) [10], time Petri nets [11], fuzzy Petri nets [12], logical delay Petri nets, PRES+ [13], etc. These extended forms of Petri nets enhance the ability to model and analyze embedded systems based on different application requirements, where PRES+ can capture real-time information and describe the hierarchical structure of the system.
In the field of embedded system modeling and analysis, research on the theory and application of PRES+ has achieved some results. Cortés et al. [13] proposed the concept of PRES+ and analyzed two embedded system PRES+ models. Karlsson et al. used PRES+ to accurately model and validate mobile phone systems and represented the embedded systems that need to be validated as PRES+ models [14]. They provided a model validation method for analyzing the system’s coverage and decidability [15]. By using the PRES+ and model transformation method, Bandyopadhyay et al. [16,17] verified the Very Large Scale Integrated (VLSI) system model. In order to improve the efficiency of PRES+ model verification, Xia et al. [18] modeled and analyzed the subsystem sharing system.
Although PRES+ has significantly improved the accuracy of embedded system modeling compared to classical Petri nets, there are still issues with the inability to describe event priorities and fully express complex program control and data flow. Adding inhibitor arcs to Petri nets can be used to control event sequences, adjust priority relationships between sequences, improve model analysis capabilities, and, to some extent, affect the expression of control flow and data flow. Therefore, adding inhibitor arcs to PRES+ can generate a PRES+ with inhibitor arcs (PIRES+, Petri net with inhibitor-arcs-based representation for embedded systems). Xia et al. [19] analyzed the refinement operation of the PIRES+ and applied it to the modeling and verification of the mobile communication systems.
As a system model, the PIRES+ can consider the system and behavior uniformly, but it is not easy to reflect the division of functional modules. The outstanding advantage of object-oriented technology lies in the use of object-oriented technology to divide the system into functional modules, effectively dividing the entire complex system into multiple simple subsystems and conducting corresponding modeling research. By combining object-oriented technology with Petri nets, an object-oriented Petri net (OOPN) can be obtained, which divides the entire system into multiple subsystem modules based on functional implementation, which is beneficial for modeling large-scale complex systems. There have been some research achievements in the analysis and modeling of the object-oriented Petri nets. Zhao et al. [20] proposed an extended-object-oriented petri net (EOOPN), supporting the description and evolution of components in the context of intelligent and cloud computing. Hu et al. [21] worked on a compression algorithm to convert an object-oriented generalized stochastic Petri net (OGSPN) into a generalized stochastic Petri net (GSPN).
However, as the complexity and scale of embedded systems increase, the number of system states will increase exponentially, highlighting the problem of “state space explosion”. Since the “state space explosion” problem of OOPIRES+ is NP-hard, it cannot be completely solved, but it can be alleviated through property preserving transformations. The commonly used Petri net transformation methods include refinement, synthesis, and reduction. Among them, refinement is a “top-down” modeling method. In the modeling of complex system modules, an abstract model is first established; then, it is refined layer by layer; and, finally, a refined model is obtained. When the refinement condition is satisfied, some important properties of the original Petri net system are preserved when the Petri net system is extended without the analysis of the reachable space. Therefore, refinement can alleviate the problem of “state space explosion”.
In recent years, extensive research has been conducted on the refinement and application of Petri nets. Padberg et al. [22] provided an overview of refinement methods for place/transition Petri net systems. Wang et al. [23] proposed a Petri net refinement method without reachability analysis. Based on the basic net system, Bernardinello et al. [24] proposed a refinement method for distributed systems. For the refinement operation of the place/transition net, Huang et al. [25] provided the conditions to keep the original net system’s liveness, boundedness, fairness, and other properties. Lakos et al. [26] provided three types of refinement operations for the colored Petri net (CPN). Based on the workflow net, Van Hee et al. [27] presented several refinement rules for preserving system reliability. For extended-time Petri nets, Mejia et al. [28] proposed a refinement operation mode.
Cortes et al. [13] extended PRES+ by introducing the definition of hierarchical structure and proposed some equivalent concepts of PRES+ and refinement methods to preserve complete equivalence. Xia et al. [19] proposed a PIRES+ refinement method and applied it to modeling network communication systems.
This paper proposes an object-oriented PIRES+ (OOPIRES+) and a gateway refinement operation for the formal modeling and analysis of the large-scale complex embedded systems. So far, there has been little research on the gateway refinement operations. Due to the crucial role of gateway refinement in the transmission and control of system data and information flows, it is necessary to conduct in-depth research on it. For the refinement operation of the OOPIRES+’s gateway, we studied the preservation of liveness, boundedness, reachability, functionality, and timing. This can greatly alleviate the “state space explosion” problem encountered in the modeling process of complex embedded systems. We applied this refinement operation to the modeling of smart home control systems, and we found that it has great guiding significance for the research of embedded system modeling.
The structure of this paper is as follows: Section 2 proposes the related concepts of OOPIRES+. Section 3 presents the gateway refinement operation of OOPIRES+ and investigates the preservation of liveness, boundedness, reachability, functionality, and timing. In Section 4, a smart home remote control system is modeled and analyzed by using the OOPIRES+ gateway refinement operation. Section 5 summarizes the contributions of the refinement method.
2. Relevant Concepts of OOPIRES+
This section provides the relevant concepts of OOPIRES+.
Definition 1 ([19]).
is said to be a PIRES+ model, where is the place set, is the transition set, is the input arc set, is the output arc set, is the inhibitor arc set, and M is the marking.
Definition 2 ([19]).
For , there exists a transition function, , where , . For , there exists a minimum transition delay, , and a maximum transition delay, , both of which are non-negative real numbers.
Figure 1 shows an example of the PIRES+ model.
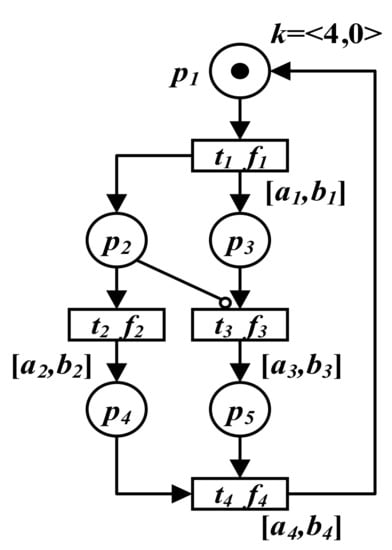
Figure 1.
An example of the PIRES+ model.
Here, , and ; ; ; ; and is the initial marking, where and . The transition functions of transitions , , , and are , , , and , respectively. The transition delays of transitions , , , and are , , , and , respectively.
Definition 3.
An OOPIRES+ object subnet is a six-tuple , where is the place set of , represented by ; is the transition set of , represented by ; represents the flow relationship of , including and , where is the set of input arcs and is the set of output arcs; is the inhibitor arc set of ; and is the message place set of , represented by , including input place and output place .
For each transition (), there are a transition function () and a transition delay ( and ) associated with it. Object subnets are connected by the gateway, . Gateways are classified into input gateways and output gateways according to their positions relative to subnets. As the gateway can be used to preprocess data before flowing into the next object subnet, here, the gateway () is also assigned the attributes of the gateway function, , and the gateway delay, .
Figure 2 shows an example of the OOPIRES+ object subnet.
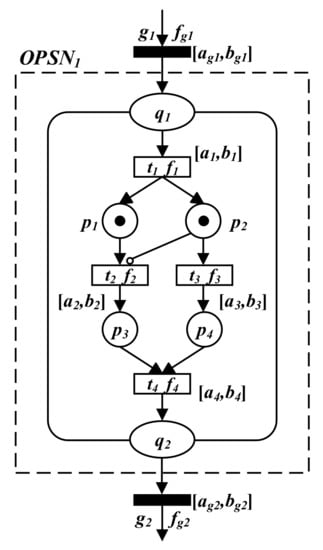
Figure 2.
An example of the OOPIRES+ object subnet.
Here, , and ; ; ; ; , where is the input message place, and is the output message place; and and are the input gateway and the output gateway of the object subnet . Moreover, , , , and are transition functions of transitions , , , and , respectively. Their corresponding transition delays are , , , and , respectively. In addition, and are the gateway functions of gateways and , and their corresponding gateway delays are and .
Definition 4.
An OOPIRES+ net system is a four-tuple , where is the object subnet set of OOPIRES+; is the set of all gateways; includes and , where , ; is the marking; and the initial marking is .
Definition 5.
Suppose that is an OOPIRES+ net system, , and is the inhibitor place set of transition, .
- (i)
- If and, then is called enabled under if , , and ;
- (ii)
- If and , then is called enabled under if and ;
- (iii)
- If and and, then is called enabled under if , ;
- (iv)
- If and , then is called enabled under if ;
- (v)
- The system marking changes after the firing of transition :, where
Definition 6.
Suppose an OOPIRES+ net system is , where is the initial marking, , and . Then, we have the following:
- (i)
- If , , , then is said to be live. If , , , then is said to be live.
- (ii)
- If ,, , and are live, then the OOPIRES+ net system OPN is said to be live.
Definition 7.
Suppose an OOPIRES+ net system is , where is the initial marking, , and . Then, we have the following:
- (i)
- Place is said to be bounded if , . Message place is said to be bounded if , .
- (ii)
- If ,,, and are bounded, then the OOPIRES+ net system is said to be bounded.
Definition 8.
Assuming that and are two OOPIRES+ object subnets, then and are said to have the same reachability if and only if the following takes place:
- (i)
- The pre-set place’s number of input gateway and the post-set place’s number of output gateway of are the same as those of .
- (ii)
- If the number of tokens in pre-set places of the input gateway of is equal to that of , then the number of tokens in post-set place of the output gateway of is equal to that of .
Definition 9.
Assuming that and are two OOPIRES+ object subnets, then and are said to have the same functionality if and only if the following takes place:
- (i)
- and have the same reachability.
- (ii)
- If the token type of tokens in pre-set places of the input gateway of is equal to that of , then the token type of tokens in the post-set place of output gateway of is equal to that of .
Definition 10.
Assuming that and are two OOPIRES+ object subnets, and are said to have the same timing if and only if the following takes place:
- (i)
- and have the same reachability.
- (ii)
- If the token time of tokens in pre-set places of the input gateway of is equal to that of , then the token time of tokens in the post-set place of output gateway of is equal to that of .
3. OOPIRES+ Gateway Refinement Operation and Property Analysis
In this section, the gateway refinement operation of OOPIRES+ is proposed, and the preservation of liveness, boundedness, reachability, functionality, and timing of the original net system by this refinement operation is investigated.
Figure 3 is a schematic diagram of the gateway refinement operation of the OOPIRES+ net system.
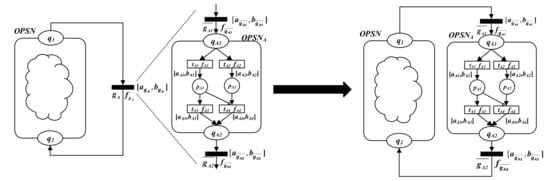
Figure 3.
Gateway refinement operation schematic diagram of the OOPIRES+ net system.
Definition 11.
Gateway refinement operation of the OOPIRES+ net system : The gateway, , of the OOPIRES+ net system is refined into a subnet and a gateway set, ; that is, is replaced by the subnet, , and the gateway set . Then, a new OOPIRES + net system, , is obtained, where we have the following:
- (i)
- ;
- (ii)
- ;
- (iii)
- (here, is the function composition operator), where , , and are the gateway functions of , , and , respectively; , , and .
- (iv)
- , and , where , , and are the minimum gateway delays of , , and , respectively; , , and are the maximum gateway delays of , , , respectively; and and are the minimum and the maximum transition delays of .
- (v)
- includes and , where , and ;
- (vi)
- .
Definition 12.
The closed net system of the OOPIRES+ subnet is defined as a three-tuple ; that is, the gateway set, , and message place, , are added to , where is the input gateway of , is the output gateway of , and .
Definition 13.
The extended subnet of the gateway, , is a three-tuple ; that is, a message place set, , and a flow relationship, , are added to the gateway, , where includes and , and .
In the following, we investigate the preservation of liveness, boundedness, reachability, functionality, and timing of the gateway refinement operation of the OOPIRES+ net system.
It is assumed that the OOPIRES+ net system is obtained from the OOPIRES+ net system by using the gateway refinement operation .
Theorem 1.
is live if and only if and the closed net system of are live.
Proof.
() For the net system , since is live, according to Definition 6, and , for , there exists , such that and , and then and are live. For the closed net system , since is live, according to Definition 6, and , and for , there exists , such that and ; then, and are live. Since is obtained from by using and to replace , , . According to Definition 12, for , , , , such that , , , and are live. Therefore, the net system is live.
() Suppose that is live. Without loss of generality, assume that is not live, and then or , , , such that or . Since and , then or , , , or , so is not live. This contradicts the hypothesis. Therefore, and are live. □
Theorem 2.
is bounded if and only if and the closed net system of are bounded.
Proof.
() Since the net system is bounded, according to Definition 7, , , , such that . Since the closed net system is bounded, according to Definition 7, , , , such that . Let and then ,, such that . Thus, is bounded.
() Suppose that is bounded. Without loss of generality, assume that is not bounded, and then, for , or , for , or . Since and , for , or , , or , so is not bounded. This contradicts the hypothesis. Therefore, and are both bounded. □
Theorem 3.
and have the same reachability.
Proof.
According to gateway refinement operation, , of the OOPIRES + system, in and , the number of pre-set places and post-set places of and is the same, and the number of tokens in the pre-set places of is equal to that of . According to Definition 11, the tokens’ number in the post -set places of is equal to that of . According to Definition 8, the reachability of and is the same. Since , the reachability of and is the same. □
Theorem 4.
and have the same functionality.
Proof.
According to Theorem 3, net system and have the same reachability. In and , the token type of tokens in the pre-set places of is the same as that of . According to Definition 11, ; therefore, the token type of tokens in post-set places of is the same as that of . By Definition 9, and have the same functionality. Since , and have the same functionality. □
Theorem 5.
and have the same timing.
Proof.
According to Theorem 3, net systems and have the same reachability. In and , the token time of tokens in the pre-set places of is the same as that of . According to Definition 11, , ; therefore, the token time of tokens in post-set places of is the same as that of . By Definition 10, and have the same timing. Since , then and have the same timing. □
4. Applications
This section applies the gateway refinement method of the object-oriented PIRES+ (OOPIRES+) to the modeling and analysis of smart home remote control systems.
The smart home remote control system is mainly composed of five functional modules: mobile control module, PC control module, instruction data transmission module, function echo feedback module, and system function control module. When users want to manage their smart homes, they can give instructions to the smart home devices connected to the network, one by one, through the mobile phones or PC terminals. Instructions are summarized by the mobile control module or PC control module and uploaded to the cloud for storage. The instructions are transmitted to the system function control module through the instruction data transmission module, achieving management and control of the smart home, and ultimately completing the feedback of the instructions.
4.1. Construct OOPIRES+ Model for Smart Home Remote Control System
In this subsection, the smart home remote control system’s OOPIRES+ model is constructed. We first provide the OOPIRES+ abstract model and then apply the above refinement operation method to obtain its refined OOPIRES+ model.
As shown in Figure 4, the abstract OOPIRES+ net system model of the smart home remote control system is proposed, which includes instructions transmission module , function feedback module , and gateways and . The meaning of the internal transition of and is as follows: , receive current instructions; , remote transmission of instructions; , instruction transmission completed; , receive functional feedback; , functional feedback transmission; and , screen status display.
Figure 4.
Abstract model of the system.
Figure 5 shows the object subnet model , which includes system function control module and gateways and . According to the received instructions, completes the control of subsystems. The meaning of the internal transition is as follows: , apply for control permission; , confirm system status; , confirm control permission; and , complete instruction execution. Moreover, ~ corresponds to control systems, which include the lighting control system, monitoring control system, and electrical control system, and realizes corresponding instruction functions.
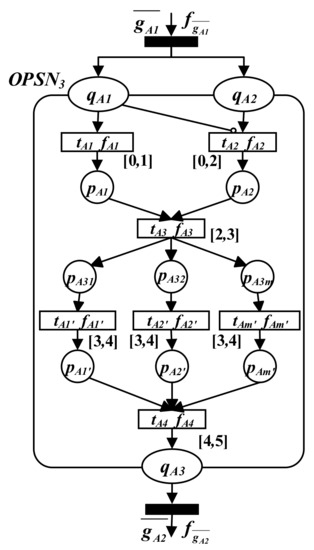
Figure 5.
The object subnet .
Figure 6 shows the object subnet , including mobile terminal control module , PC control module , and the gateways and . According to the operator’s intention, this module sends instructions to the functional control terminal through different devices. The meaning of the internal transitions of and is as follows: , apply to activate mobile devices; , summarize current instructions; , check network connectivity; , upload instructions to the cloud; , complete cloud upload; , apply to enable PC devices; , check synchronization on PC devices; , confirm synchronization on PC devices; , summarize current instructions; and , instruction cloud synchronization. Moreover, ~ and ~ are used to realize the collection of system instructions on a mobile phone and PC terminal.
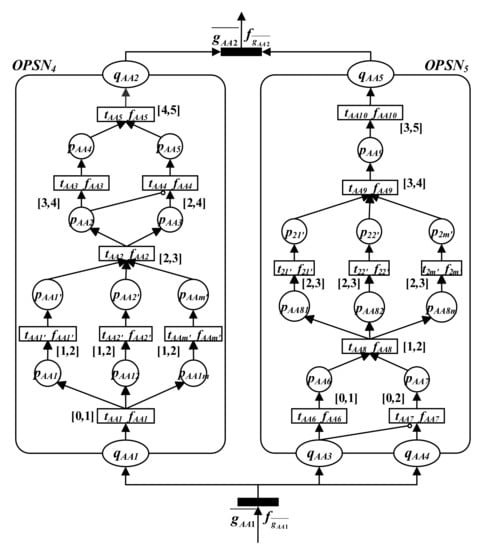
Figure 6.
The object subnet .
Next, the object subnets and are used to carry out refinement operations on and in the net system abstract model , and the smart home remote control system is obtained (as shown in Figure 7). The system begins to issue control instructions to smart home devices from or . receives the instructions and transmits them remotely to . receives the instructions and executes them. is used to control the screen display and remind the users of their smart home status.
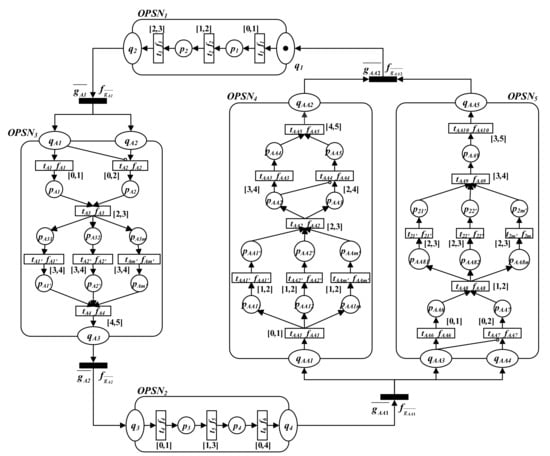
Figure 7.
The refined smart home remote control system .
4.2. Property Preservation Analysis of the OOPIRES+ Model
In this subsection, the property preservations of the smart home remote control system’s OOPIRES+ model are analyzed.
4.2.1. Liveness and Boundedness Preservation
As can be seen from Figure 5, the net system is live and bounded, and the corresponding closed net systems can be obtained by adding message places on the basis of the models of and in Figure 5 and Figure 6. It is easy to see that the closed net systems are also live and bounded. The net system is obtained from the net system by using and to replace and , respectively. Therefore, according to Theorems 1 and 2, the net system is also live and bounded. As can be seen from Figure 4 and Figure 7, and are both live and bounded. In addition, the liveness and boundedness of (Figure 4) and (Figure 7) can also be verified by the modeling tool Tina 3.7.0, and the verification results are shown in Figure 8 and Figure 9.
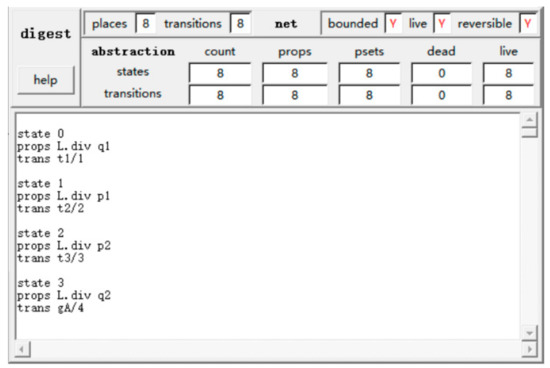
Figure 8.
Verification result of liveness and boundedness of .
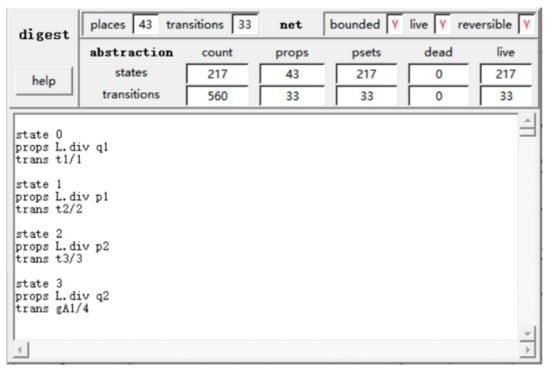
Figure 9.
Verification result of liveness and boundedness of .
4.2.2. Reachability, Functionality, and Timing Preservation
In Figure 4 and Figure 7, the pre-set places of and are , and the post-set places of and are . Since and have the same number of pre-set places and the same number of tokens, and after the refinement operation, and have the same number of post-set places and the same number of tokens, ’s extended subnet has the same reachability as subnet . Since the token type of tokens in the pre-set places of and is the same; the gateway function of is equal to the function of ; and, after the refinement operation, the token type of tokens in the post-set places of and is the same, ’s extended subnet has the same functionality as subnet . Since the token time of tokens in the pre-set places of and is the same; the gateway delay of is equal to the delay of ; and, after the refinement operation, the token time of tokens in the post-set places of and is the same, ’s extended subnet has the same timing as subnet . Similarly, the extended subnet of and the subnet have the same reachability, functionality, and timing. Thus, by Theorems 3, 4, and 5, and have the same reachability, functionality, and timing. According to Figure 4 and Figure 7, it is easy to see that and have the same reachability, functionality, and timing.
Note that the gateway refinement method can be used for the modeling and validation of various embedded-system instances, such as intelligent transportation, smart cities, smart homes, etc. The modeling and verification of the smart home remote control system is only one of many system examples. The application of the refinement method to model and validate different system instances may vary, and a specific analysis should be conducted on specific issues. However, the basic modeling and validation process is similar.
5. Conclusions
For embedded system modeling, common formal modeling methods, such as the extended finite-state machine method, data flow diagram method, communication process method, etc., can describe the characteristics of embedded systems from different perspectives but do not form a unified standard. Classical Petri nets lack a hierarchical structure and the concept of time, making it impossible to fully describe embedded systems. PRES+ improved the accuracy of embedded system modeling, but there are still issues with the inability to describe event priorities and fully express complex program control and data flow. PIRES+ can consider the system and behavior uniformly, but it is not easy to reflect the division of functional modules.
In response to the problem of formal modeling and analysis of large-scale complex embedded systems, object-oriented technology is combined with PIRES+, and an object-oriented PIRES+ (OOPIRES+) and a gateway refinement operation method are proposed. This paper investigates the preservation of the liveness, boundedness, reachability, functionality, and timing of the original net system by the gateway refinement operation and presents the preservation conditions for the above important properties of the refinement operation, which can effectively alleviate the “state space explosion” problem of OOPIRES+. The application in the refined modeling and analysis of smart home remote control systems also demonstrates the effectiveness and practicality of the proposed refinement method. The research results of this paper will also provide a new method for modeling and analysis of large complex embedded systems.
The limitation of the gateway refinement approach is that the operation must meet the constraints of gateway replacement, gateway function, gateway delay, and so on. The next research work may consider proposing a wider range of conditions for the study of OOPIRES+ gateway refinement operations or other refinement operations (such as a subnet refinement operation).
Author Contributions
Conceptualization, C.X.; methodology, C.X.; validation, C.X., M.Q. and Y.S.; formal analysis, C.X. and M.Q.; investigation, C.X.; resources, C.X.; writing—original draft preparation, C.X.; writing—review and editing, M.Q., Y.S. and M.G.; supervision, C.X.; project administration, C.X.; funding acquisition, C.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Shandong Province (Grant No. ZR2022MF348).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roberto, B.; Montserrat, M.; María, E.B.G.; Ana, F.G. An Event Mesh for Event Driven IoT Applications. Int. J. Interact. Multimed. Artif. Intell. 2022, 7, 54–59. [Google Scholar]
- Marwedel, P. Embedded System Design—Embedded Systems Foundations of Cyber-Physical Systems, and the Internet of Things, 4th ed.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Tausan, N.; Markkula, J.; Kuvaja, P.; Oivo, M. Choreography in the embedded systems domain: A systematic literature review. Inf. Softw. Technol. 2017, 91, 82–101. [Google Scholar] [CrossRef][Green Version]
- Stoutchini, A.; Benini, L. StreamDrive: A dynamic dataflow framework for clustered embedded architectures. J. Signal Process. Syst. 2019, 91, 630–640. [Google Scholar]
- Firdaus, A.F.; Meribout, M. A new parallel VLSI architecture for real-time electrical capacitance tomography. IEEE Trans. Comput. 2016, 65, 30–41. [Google Scholar] [CrossRef]
- Ding, Z.; Yang, R.; Cui, P.; Zhou, M.C.; Jiang, C. Variable Petri nets for mobility. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4784–4797. [Google Scholar] [CrossRef]
- Ciccozzi, F.; Malavolta, I.; Selic, B. Execution of UML models: A systematic review of research and practice. Softw. Syst. Model. 2019, 18, 2313–2360. [Google Scholar] [CrossRef]
- Moutinho, F.; Gomes, L. Asynchronous-channels within Petri net-based GALS distributed embedded systems modeling. IEEE Transections Ind. Inform. 2014, 10, 2024–2033. [Google Scholar] [CrossRef]
- Andrzej, B.; Tomasz, R.; Dariusz, R. Timed colored Petri net-based event generators for web systems simulation. Appl. Sci. 2022, 12, 12385. [Google Scholar]
- Borstel, F.D.V.; Villa-Medina, J.F.; Gutiérrez, J. Development of mobile robots based on wireless robotic components using UML and hierarchical colored Petri nets. J. Intell. Robot. Syst. 2022, 104, 70. [Google Scholar] [CrossRef]
- Gutierrez, A.; Bressan, M.; Jimenez, J.F.; Alonso, C. Real-time emulation of boost inverter using the systems modeling language and Petri nets. Math. Comput. Simul. 2019, 158, 216–234. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, K.-Q.; Sarkheyli-Hägele, A.M.; Zain, A. Modeling, reasoning, and application of fuzzy Petri net model: A survey. Artif. Intell. Rev. 2022, 55, 6567–6605. [Google Scholar] [CrossRef]
- Cortés, L.A.; Eles, P.; Peng, Z. Modeling and formal verification of embedded systems based on a Petri net representation. J. Syst. Archit. 2003, 49, 571–598. [Google Scholar] [CrossRef]
- Karlsson, D.; Eles, P.; Peng, Z. Formal verification of component-based designs. J. Des. Autom. Embed. Syst. 2007, 11, 49–90. [Google Scholar] [CrossRef]
- Karlsson, D.; Eles, P.; Peng, Z. Model validation for embedded systems using formal method-aided simulation. LET Comput. Digit. Tech. 2008, 2, 413–433. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Sarkar, S.; Sarkar, D.; Mandal, C. SamaTulyata: An efficient path based equivalence checking Tool. In Automated Technology for Verification and Analysis, Proceedings of the 15th International Symposium, ATVA 2017, Pune, India, 3–6 October 2017; D’Souza, D., Narayan Kumar, K., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10482, pp. 109–116. [Google Scholar]
- Bandyopadhyay, S.; Sarkar, D.; Mandal, C. Equivalence checking of petri net models of programs using static and dynamic cut-points. Acta Inform. 2019, 56, 321–383. [Google Scholar] [CrossRef]
- Xia, C.; Li, C. Property preservation of Petri synthesis net based representation for embedded systems. IEEE/CAA J. Autom. Sin. 2021, 8, 905–915. [Google Scholar] [CrossRef]
- Xia, C.; Wang, Z.; Wang, Z. The refinement of Petri net with inhibitor arcs based representation for embedded systems. Electronics 2022, 11, 1389. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, Y.; Wang, J.; Xie, Z.W.; Yang, Z.D.; Cheng, L. An extended object-oriented Petri net supporting the description and evolution of components: EOOPN. Clust. Comput. 2019, 22, 2701–2708. [Google Scholar] [CrossRef]
- Hu, H.; Yu, J.; Li, Z.; Chen, J.; Hu, H. Modeling and analysis of cyber–physical system based on object-oriented generalized stochastic Petri net. IEEE Trans. Reliab. 2021, 70, 1271–1285. [Google Scholar] [CrossRef]
- Padberg, J.; Urášek, M. Rule-based refinement of Petri nets: A Survey. In Petri Net Technology for Communication-Based SystemsEhrig; Reisig, H., Rozenberg, W., Weber, G.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 161–196. [Google Scholar]
- Wang, S.; You, D.; Zhou, M.; Seatzu, C. Characterization of admissible marking sets in Petri nets with uncontrollable transitions. IEEE Trans. Autom. Control. 2016, 61, 1953–1958. [Google Scholar] [CrossRef]
- Bernardinello, L.; Kılınç, G.; Mangioni, E.; Pomello, L. Modeling distributed private key generation by composing Petri nets. In Transactions on Petri Nets and Other Models of Concurrency IX; Koutny, M., Haddad, S., Yakovlev, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 19–40. [Google Scholar]
- Huang, H.; Cheung, T.-y.; Mak, W.M. Structure and behavior preservation by Petri-net-based refinements in system design. Theor. Comput. Sci. 2004, 328, 245–269. [Google Scholar] [CrossRef][Green Version]
- Lakos, C.; Lewis, G. Incremental state space construction of colored Petri nets. In Proceedings of the International Conference on Application and Theory of Petri Nets, Virtual Event, 23–25 June 2021; Colom, J.-M., Koutny, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 263–282. [Google Scholar]
- Van Hee, K.M.; Sidorova, N.; van der Werf, J.M. Business process modeling using Petri nets. In Transactions on Petri Nets and Other Models of Concurrency VII; Jensen, K., Koutny, M., Balbo, G., Wolf, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 116–161. [Google Scholar]
- Mejía, G.; Niño, K.; Montoya, C.; Sánchez, M.A.; Palacios, J.; Amodeo, L. A Petri net based framework for realistic project management and scheduling: An application in animation and videogames. Comput. Oper. Res. 2016, 66, 190–198. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).