Improved LSTM Neural Network-Assisted Combined Vehicle-Mounted GNSS/SINS Navigation and Positioning Algorithm

Abstract

Aiming at the problem of the combined navigation system of on-board GNSS (global navigation satellite system)/SINS (strapdown inertial navigation system), the accuracy of the combined navigation system decreases due to the dispersion of the SINS over time and under the condition of No GNSS signals. An improved LSTM (long short-term memory) neural network in No GNSS signal conditions is proposed to assist the combination of navigation data and the positioning algorithm. When the GNSS signal is normal input, the current on-board combination of the navigation module’s output sensor data information is used for training to improve the LSTM algorithm and to establish the incremental output of the GNSS position of the mapping of the different weights. In No GNSS signal conditions, using the improved LSTM algorithm can improve the combination of navigation and positioning algorithms. Under No GNSS signal conditions, the improved LSTM training model is used to predict the dynamics of SINS information component data. Under No GNSS signal conditions, the combined navigation filtering design is completed, and the error correction of SINS navigation and positioning information is carried out to obtain a more accurate combination of navigation and positioning system accuracy. It can be seen through the actual test experiment using a sports car in the two trajectories under the conditions of No GNSS signals that the proposed algorithm can be compared with the LSTM algorithm. In testing road sections, the proposed algorithm, when compared with the LSTM algorithm to obtain the northward position that the mean square errors were improved by 55.63% and 76.64%, and the eastward position mean square errors were improved by 43.42% and 54.67%. In a straight-line trajectory, improving the effect’s navigation and positioning accuracy and reliability is significant.

1. Introduction

In recent years, with the rapid development of science and technology, means of communication, as well as geographic information, continue to mature, vehicle navigation applications are gradually improving, and vehicle high-precision navigation and positioning have become one of the basic needs of modern human life, with vehicle navigation systems reducing the impact of external environmental factors to reduce the occurrence of traffic accidents [1,2]. Vehicle position information is a key type of information in navigation and in the development of technical means such as in-vehicle navigation, driver assistance, autonomous driving, and intelligent transportation. High-precision vehicle positioning is the basis for vehicles to achieve path planning and motion-track tracking [3]. The use of GNSS and SINS sensors is currently a basic method of vehicle positioning; however, if used in a variety of complex driving environments such as buildings and tunnels, GNSS is prone to signal loss, which can lead to positioning being inaccurate or vehicles even being unable to receive positioning information. As a result, the positioning performance of in-vehicle GNSS navigation is unreliable in densely populated urban areas. In particular, the increasing number of elevated roads, tunnels, and other multi-layered traffic road structures make precise vehicle positioning even more difficult. Mis-matching of road layers often occurs in GNSS navigation systems, which can lead to irrational navigation commands, which can be a potential hazard and even a safety issue for drivers and pedestrians.

The random and integration errors of the inertial sensors and the onboard conditions of highly complex environmental information can lead to errors in the positioning accuracy of the combined GNSS/SINS navigation due to limited time. GNSS signals are easily affected by complex environments such as buildings and tunnels, and in this case, the lack of position and velocity information provided by GNSS in the combined navigation system leads to missing measurement information in the Kalman filter and the lack of measurement corrections. The combined navigation system then becomes a pure SINS solution under No GNSS signal conditions. This leads to rapid dispersion of navigation and positioning accuracy. Therefore, many scholars in China and abroad have conducted extensive research on combined navigation systems under No GNSS conditions, building models to assist combined navigation through neural networks and providing pseudo-GNSS information to suppress the dispersion of SINS navigation results.

Li X.Y et al. [4] proposed a BP neural network-assisted combined navigation algorithm to improve the performance of a combined navigation system by using a BP neural network for online training to improve the position and velocity estimation accuracy of the combined navigation system and to enter the training mode under No GNSS signals to predict the position and velocity in real-time to obtain the position and velocity estimates to improve the performance and accuracy of combined navigation. This has been proven to be effective in terms of improving navigation accuracy under pure inertial navigation through in-vehicle measurements. Zhi et al. [5] proposed a convolutional neural network-long and short time (CNN-LSTM)-based performance compensation method for GPS signal loss by building a CNN-LSTM network model and a wavelet. The LSTM network model and a wavelet threshold denoising algorithm were combined with the model algorithm. The improved model can effectively improve the performance of the combined navigation system when GPS is interrupted. Xu B et al. [6] used a radial basis function-based neural network model (RBF) combined with volumetric Kalman filtering to assist the combined navigation and positioning system under No GNSS signals. The predictive model was used to correct the pure inertial guidance solution results under No GNSS signals to improve the navigation and positioning accuracy of their combined navigation system under No GNSS signals. Similarly, Sun W et al. [7] modeled a radial basis function neural network. An improved K-means algorithm and a genetic algorithm were used to optimize the weight parameters of RBF neurons to improve the navigation positioning accuracy of their combined navigation system under No GNSS signals. However, the radial-based neural network model is prone to data sickness during the training process due to insufficient data work, which can lead to a sudden degradation in the performance of the predicted combined navigation results. Bai X et al. [8] proposed an Elman neural network-assisted combined navigation federal filtering algorithm to ensure the stability and accuracy of combined navigation by correcting the position and velocity of the combined navigation system through Elman training when the satellite navigation signal is No or even out of range. The method uses the navigation results of inertial navigation as the network input and the position information of GNSS as the desired output for predictive corrections. A methodology for modelling the relationship between carrier attitude, velocity, MEMS sensor measurements and carrier position increments using multilayer perceptron neural network (MLPNN) to support combinatorial navigation [9]. In order to solve the problem that the pure inertial derivation diverges strongly when the GPS is out of lock, the gated recurrent unit (GRU)-assisted INS/GPS method is adopted [10,11]. A nonlinear autoregressive with external input (NARX) neural network assisted combinatorial navigation method is proposed [12]. A new Extreme Learning Machine (ELM) based GPS/INS intelligent structure for INS position error prediction and correction is proposed [13]. Modelling and prediction of GNSS accuracy from GNSS time series using machine learning techniques such as LSTM [14]. A recursive wavelet neural network (RWNN)-based algorithm is developed for data fusion in mobile SINS/GNSS systems, which significantly improves the overall navigation accuracy of low-cost SINS/GNSS systems [15]. Adaptive error damping coefficient based INS gives reliable navigation parameters during time intervals when GPS data is not available [16]. Fang Wei et al. [17] proposed the use of a long short-term memory neural network (LSTM) to correct the error of navigation results relying on INS solutions under No GNSS signals so as to circumvent the problem of suppressing the performance accuracy of combined navigation due to pure INS divergence. In order to improve the positioning accuracy and performance of the combined navigation and positioning system in the time dimension, this paper adopts the LSTM neural network for the prediction processing, which makes good use of the advantages of this neural network in terms of real-time and correlation in the time dimension.

To address the training effect of the various neural network-assisted combined navigation algorithms mentioned above, this paper proposes an improved LSTM algorithm-assisted combined navigation method under No GNSS signals, which simulates the relationship between the dynamic information of the vehicle and navigation and positioning through an improved LSTM neural network-assisted combined GNSS/SINS navigation system modeling method under No GNSS signal conditions to improve the accuracy and reliability of combined navigation and positioning effects.

2. Relevant Basic Theory

2.1. Kalman Filtering

The Kalman filter algorithm is an optimization data processing algorithm proposed by mathematician Kalman [18] and is widely used in many fields. The Kalman filter algorithm combines the current moment’s observations with the previous moment’s state update values by constructing a mathematical model to derive the current moment’s state update values.

Assume that the discretized equation of state for the system is

$$X_{k+1}={\Phi }_{(k+1)/k}{X}_k+W_k$$

(1)

where $X_k$ and $X_{k+1}$ are the state vectors at moment k and k + 1, respectively; ${\Phi }_{(k+1)/k}$ is the state transfer matrix of the system; $W_k$ is the system noise of the system at moment k.

The observation equation for the system is

$$Z_{k+1}=H_{k+1}{X}_{k+1}+V_{k+1}$$

(2)

where ${{\rm Z}}_{k+1}$ represents the system measurements at moment k + 1; $H_{k+1}$ is the observation matrix of the system at moment k + 1; $V_{k+1}$ is the measurement noise of the system at moment k + 1.

Denote by ${\widehat{X}}_k$ the optimal estimate at k moments $X_k$.${\widehat{X}}_{(k+1)/k}$ denote the optimal predicted value at k moments $X_{k+1}$. Then, the Kalman filter recursive algorithm is as follows:

State prediction equation:

$${\widehat{X}}_{k+1}={\Phi }_{(k+1)/k}{\widehat{X}}_k$$

(3)

Covariance prediction equation:

$$P_{k+1}={\Phi }_{(k+1)/k}{P}_k{\Phi }_{(k+1)/k}^T+Q_k$$

(4)

Filter gain equation:

$$K_{k+1}=P_{(k+1)/k}{H}_{k+1}^T{\left(H_{k+1}{P}_{(k+1)/k}{H}_{k+1}^T+R_{k+1}\right)}^{-1}$$

(5)

State estimating equation:

$${\widehat{X}}_{k+1}={\widehat{X}}_{(k+1)/k}+K_{k+1}\left(Z_{k+1}-H_{k+1}{\widehat{X}}_{(k+1)/k}\right)$$

(6)

Filtered covariance update equation:

$$P_{k+1}=\left(I-K_{k+1}{H}_{k+1}\right)P_{(k+1)/k}$$

(7)

where $P_{(k+1)/k}$ is the covariance matrix of the forecast error estimates at moment k for moment k + 1.

By building a Kalman model, the Kalman filtering algorithm is used to iterate the system to achieve the estimation of the overall state information of the system.

2.2. Long- and Short-Term Memory Network LSTM Model

Long- and short-term memory networks are a type of recurrent neural network (RNN) [19].

For a standard RNN neuron, the output equation is

$$h_t=\tanh \left(W_x\cdot x_t+W_h\cdot h_{t-1}+b\right)$$

(8)

where W_x is the weight of the input sampled at the current moment, W_h is the network output weight sampled at the previous moment, and b is a constant. To solve the problems of gradient loss and gradient explosion in traditional recurrent neural networks when dealing with long data sequences, LSTM proposes to introduce new concepts such as cells, input gates, forgetting gates, and output gates to solve the dependence of recurrent neural networks on long data sequences [19].

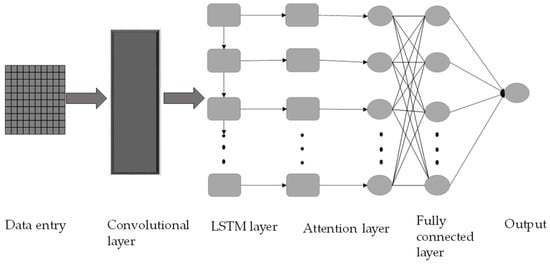
The neurons in the LSTM neural network consist of “forgetting gates” $f_t$, “input gates” $i_t$ and “output gates” $o_t$, where the “forgetting gates” $f_t$ qualifies the input information from the previous point in time and forget it. The “input gate” $i_t$ selects a new input, while the “output gate” $o_t$ calculates the current output based on the new input and the previous output. The structure is shown in Figure 1.

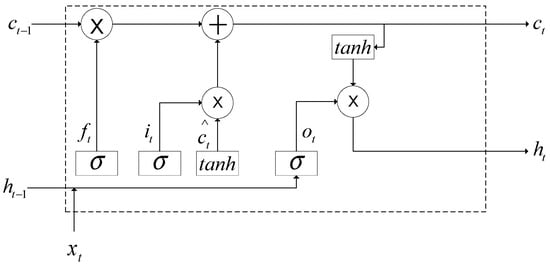
Figure 1. LSTM structure diagram.

3. Design of GNSS/SINS Combined Navigation Algorithm Scheme with Improved LSTM

This method is aimed at the GNSS/SINS combination navigation system in the No GNSS signal SINS system over time easy to dispersion leads to the combination of navigation system accuracy degradation problem, put forward an improved LSTM model in the No GNSS signal to provide pseudo-GNSS information to assist the combination of navigation methods, the overall process is shown in Figure 2, first of all, through the host computer data acquisition system through the use of the serial communications protocol to solve to get the Inertial sensor IMU and global navigation and positioning system GNSS output information, in the IMU output data preprocessing to get the current body of the specific force information and angular velocity information, when the GNSS signal is normal through the SINS navigation solution to get the current body of the speed and position information and the GNSS speed and position information received through the iterative update of the Kalman filter for error correction The accurate combined navigation and positioning accuracy information is obtained. When under No GNSS signal conditions, the acceleration, attitude angle, angular velocity, and speed information of the current vehicle-mounted SINS are input through the GNSS signal when it is normal to establish the mapping relationship with different weights between the current vehicle-mounted SINS and the incremental outputs of the GNSS position under the LSTM-Attention model; and secondly, under the No GNSS signal conditions, the LSTM-Attention training model is used to evaluate the Secondly, under the No GNSS signal condition, the LSTM-Attention training model is used to predict the pseudo GNSS position increment information by using the dynamics of SINS in each information component data; finally, the predicted position increment information is combined with the position information solved by SINS after integral solving, and then the difference is calculated by the iterative updating of Kalman filtering to obtain a more accurate accuracy of the combined navigation and positioning system.

Figure 2. The general flow of the improved LSTM algorithm.

3.1. Improved LSTM Model

When LSTM neural network models are prone to irrelevant information in the process of processing multi-dimensional input information by introducing an attention mechanism layer, it can be achieved to increase the weight of some key input information, thus improving the processing efficiency of the neural network. For the LSTM model with the introduction of the attention mechanism, the input information such as acceleration, attitude angle, angular velocity, and velocity, as well as the output information features of GNSS position increments, are extracted from the long-term dependencies and then built as the improved LSTM model studied in this paper. The attention mechanism can be simply interpreted as a weighted sum. It first calculates the importance of the input multidimensional features; a softmax function is then applied to ensure that the sum of the weights of all the input features is 1. The weights and the input features are multiplied accordingly, and they are eventually summed to obtain the output. Given a task-related vector q, its attention weights are calculated as follows:

$$b_i=\mathrm{softmax}(s(x_i,q))=\frac{\exp \left(s(x_i,q)\right)}{{{\displaystyle \sum }}_{j=1}^N\exp \left(s(x_j,q)\right)}$$

(9)

where $b_i$ is the attention weight of the ith input sequence, $s(x_i,q)$ denotes the attention scoring function, and $x_i$ denotes the ith input information from the LSTM layer to the attention layer. The LSTM-Attention model can be constructed based on the above, and the structure is shown in Figure 3.

Figure 3. Schematic diagram of the improved LSTM structure.

This improved model uses optimization of the LSTM neural network through the introduction of an attention mechanism, using multidimensional features of data input through the convolutional layer for learning. Then, each element is processed through the LSTM layer for input sequence, and multidimensional features are learned for the input layer through desired output value, through learning mapping of input on-vehicle SINS dynamics data and desired output GNSS position increment, using attention layer for scientific assignment of different weights. Finally, the vehicle dynamics component data of the vehicle-mounted SINS system and the target value of the GNSS position increment are obtained through the fully connected layer for output.

3.2. Improved LSTM-Assisted Combined Navigation and Positioning Model

The combined GNSS/SINS navigation system modeling approach assisted by LSTM neural networks under No GNSS signal conditions focuses on modeling the relationship between the dynamical information of the vehicle and the navigation and positioning position. In conventional modeling, the position error values between GNSS and SINS are used as true values for neural network training, i.e., $O_{\mathit{SINS}}-\delta {\mathit{P}}_{\mathit{SINS}}$. In the $O_{\mathit{SINS}}-\delta {\mathit{P}}_{\mathit{SINS}}$ relationship, the position error information $\delta P_{SINS-GNSS}$ between GNSS and SINS is shown in the following equation:

$$\begin{array}{l}\delta {\widehat{\mathit{P}}}_{SINS-GNSS}={\widehat{\mathit{P}}}_{SINS}-{\widehat{\mathit{P}}}_{GNSS}\\ ={\mathit{P}}_{SINS}+\delta {\mathit{P}}_{SINS}-({\mathit{P}}_{GNSS}+\delta {\mathit{P}}_{GNSS})=\delta {\mathit{P}}_{SINS-GNSS}+\left(\delta {\mathit{P}}_{SINS}-\delta {\mathit{P}}_{GNSS}\right)\end{array}$$

(10)

This includes not only GNSS errors but also SINS errors. The problem of cumulative errors due to the dispersion of the navigation system solution over time due to SINS is a shortcoming. And in $O_{\mathit{SINS}}-\Delta {\mathit{P}}_{\mathit{GNSS}}$ the model relationship is shown below:

$$\begin{array}{l}\mathsf{\Delta }{\widehat{\mathit{P}}}_{GNSS}(k)={\widehat{\mathit{P}}}_{GNSS}(k)-{\widehat{\mathit{P}}}_{GNSS}(k-1)\\ ={\mathit{P}}_{GNSS}(k)+\delta {\mathit{P}}_{GNSS}(k)-\left({\mathit{P}}_{GNSS}(k-1)+\delta {\mathit{P}}_{GNSS}(k-1)\right)\\ =\mathsf{\Delta }{\mathit{P}}_{GNSS}(k)+\left(\delta {\mathit{P}}_{GNSS}(k)-\delta {\mathit{P}}_{GNSS}(k-1)\right)\end{array}$$

(11)

The position increment $\Delta {\widehat{\mathit{P}}}_{GNSS}$ in the GNSS adjacent period contains only the GNSS position measurement noise $\delta {\mathit{P}}_{GNSS}\left(t_k\right)-\delta {\mathit{P}}_{GNSS}\left(t_{k-1}\right)$ at the adjacent moment, so the additional error is considered to be very small for the adjacent position noise. Therefore, the choice $O_{\mathit{SINS}}-\Delta {\mathit{P}}_{\mathit{GNSS}}$ model accuracy will be higher.

In the $O_{\mathit{SINS}}-\Delta {\mathit{P}}_{\mathit{GNSS}}$ model relationship, over a short period $\Delta {\mathit{P}}_{\mathit{SINS}}\approx \Delta {\mathit{P}}_{\mathit{GNSS}}$. From the specific force equation, the position increment $\Delta {\mathit{P}}_{\mathit{SINS}}$ of the inertial solution under the SINS system over the time interval t is:

$$\begin{array}{c}\Delta {\mathit{P}}_{\mathit{SINS}}={\displaystyle \iint {\dot{\mathit{v}}}_{}^{\mathrm{n}}\mathrm{d}tdt}=\\ {\displaystyle \iint \left({\mathit{C}}_{\mathit{b}}^{\mathit{n}}{\mathit{f}}^b-\left(2{\mathit{\omega }}_{ie}^n+{\mathit{\omega }}_{en}^n\right)\times {\mathit{v}}_{}^n+{\mathit{g}}^n\right)dtdt}\end{array}$$

(12)

where $C_{\mathrm{b}}^{\mathrm{n}}$ is the directional cosine matrix for the angular change of attitude, $f^b$ is the on-board specific force information, i.e., the data collected by the accelerometer of the IMU; ${\omega }_{ie}^n$ is the projection of the angular velocity of the Earth’s rotation in the n-system; ${\omega }_{\mathit{en}}^n$ is the projection of the angular velocity of the rotation of the n-system for the Earth system (e-system) in the n-system; ${\omega }_{\mathit{en}}^n$ and ${\omega }_{ie}^n$ are related only to the latitude $\phi$ and the radius of the meridian circle of the Earth $R_M$ and the radius of the U-ring $R_N$, as shown in the following equation:

$$\begin{array}{l}{\mathit{\omega }}_{ie}^n={\left[{\omega }_{e}cos\phi ,0,-{\omega }_{e}sin\phi \right]}^T\hfill \\ {\mathit{\omega }}_{en}^n={\left[\frac{V^E}{R_N+h},\frac{-V^N}{R_M+h},\frac{-V^{E}tan\phi }{R_N+h}\right]}^T\hfill \end{array}$$

(13)

$v^n$ is the velocity vector and $g^n$ is the gravity vector. Moreover, in the on-board motion, the gravity vector is mainly related to the latitude and longitude. And $C_b^n$ is related to the traverse and pitch angles of the attitude angle as well as the heading angle. Therefore, to improve the training capability and computational efficiency of the neural network model, the $O_{\mathit{SINS}}-\Delta {\mathit{P}}_{\mathit{GNSS}}$ model is chosen as the model relationship between the vehicle dynamics component data and the GNSS position increment output from the on-board SINS system, and the input values of the neural network in this paper are chosen as the 3-axis angular velocity $\omega$, 3-axis acceleration $f$ velocity $\mathit{v}$ and attitude angle A information.

When the GNSS signal is available, the three-axis angular velocity $\omega$, three-axis acceleration $f$, velocity $v$, and attitude angle A information is used as input layer information for the LSTM-Attention module, and the GNSS position increment is used as the desired output information for the LSTM-Attention model. The relationship between the GNSS increment and the acceleration, angular velocity information, and velocity and attitude angle of the vehicle dynamics data is found through the training mapping of the LSTM-Attention model; Figure 4 shows the flowchart of the GNSS signal availability algorithm

Figure 4. Schematic of the GNSS signal availability algorithm.

When the GNSS signal is not available, the GNSS position increments are not available, but the acceleration, angular velocity information, and velocity and attitude angle information can still be fed to the LSTM-Attention module for navigation. This information is assigned weight coefficients by the trained LSTM-Attention module, and the GNSS position increments are predicted $\Delta {\mathit{P}}_{\mathit{GNSS}}$. The pseudo-GNSS position information for the current moment is then integrated over the prediction period $\Delta {\mathit{P}}_{\mathit{GNSS}}$, which instead becomes the position information for positioning when the GNSS signal is normal. The flowchart of the algorithm for the no GNSS signal condition is shown in Figure 5.

Figure 5. Flowchart of the algorithm in the absence of GNSS signals.

3.3. Combined Navigation Filtering Design under No GNSS Signal Conditions

This paper adopts an indirect method for filtering design based on the pine combination navigation, firstly converting the error parameters between SINS and GNSS into the state vector of the system and then using this state vector to correct the navigation parameters of the SINS system to obtain the best navigation parameters and, thus, improve the state estimation accuracy of the system.

3.3.1. Equation of State for Combined GNSS/SINS Navigation Systems

The equation of state for a combined GNSS/SINS navigation system is

$${\dot{X}}_t=F_t{X}_t+G_t{W}_t$$

(14)

$$X_t={\left[\begin{array}{l}{\phi }_E,{\phi }_N,{\phi }_U,\delta v_E,\delta v_N,\delta v_U,\delta L,\delta \lambda ,\\ \delta h,{\epsilon }_{bx,}{\epsilon }_{by,},{\epsilon }_{b\mathrm{z}},{\epsilon }_{rx,}{\epsilon }_{ry},{\epsilon }_{rz},{\mathsf{\nabla }}_{ax,}{\mathsf{\nabla }}_{ay,}{\mathsf{\nabla }}_{az}\end{array}\right]}^T$$

where ${\phi }_E,{\phi }_N,{\phi }_U$ is the attitude angle error, $\delta v_E,\delta v_N,\delta v_U$ is the eastward, northward, and skyward velocity error, $\delta L,\delta \lambda ,\delta h$ is the longitude, latitude, and altitude error, ${\epsilon }_{bx,}{\epsilon }_{by,},{\epsilon }_{b\mathrm{z}}$ is the gyroscope random constant error, ${\epsilon }_{rx,}{\epsilon }_{ry},{\epsilon }_{rz}$ is the first order Markov process of the gyroscope and ${\mathsf{\nabla }}_{ax,}{\mathsf{\nabla }}_{ay,}{\mathsf{\nabla }}_{az}$ is the zero bias error of the accelerometer.

System noise is

$$\mathit{W}(t)={\left[\begin{array}{ccccccccc}{\omega }_{gx}& {\omega }_{gy}& {\omega }_{gz}& {\omega }_{rx}& {\omega }_{ry}& {\omega }_{rz}& {\omega }_{ax}& {\omega }_{ay}& {\omega }_{az}\end{array}\right]}^T$$

The state transfer matrix and noise factor matrix of the system are

$$F_t=\left[\begin{array}{cc}{F}_N& F_S\\ 0& I\end{array}\right]$$

$$G(t)=\left[\begin{array}{ccc}-C_b^n& 0_{3\times 3}& 0_{3\times 3}\\ 0_{9\times 3}& 0_{9\times 3}& 0_{9\times 3}\\ 0_{3\times 3}& {\mathrm{{\rm I}}}_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& {\mathrm{{\rm I}}}_{3\times 3}\end{array}\right]$$

3.3.2. Measurement Equations for Combined GNSS/SINS Navigation Systems

The combined SINS/GNSS navigation system designed in this paper is a loose combined position and velocity-based navigation system, which consists of the latitude, longitude, and altitude information obtained by the Jetlink inertial SINS and the longitude, latitude, and altitude information obtained by the GNSS receiver, by solving the Northeast sky velocity information obtained by the Jetlink inertial SINS and the Northeast sky velocity information obtained by the GNSS receiver. The error value is used as the velocity observation data. However, the No GNSS signal conditions currently only provide predicted pseudo-position information but not velocity information through the improved LSTM algorithm, and therefore, only constitute a combined navigation algorithm measurement equation based on the position information.

The SINS location information is shown below:

$$\begin{array}{l}{L}_I=L+\delta L\\ {\lambda }_I=\lambda +\delta \lambda \end{array}$$

(15)

The pseudo-GNSS predicted location information is shown below:

$$\begin{array}{l}{L}_G=L+\delta L_G\\ {\lambda }_G=\lambda +\delta {\lambda }_G\end{array}$$

(16)

where $(L,\lambda )$ is the true position of the vehicle, $\left(L_I,{\lambda }_I\right)$ is the longitude and latitude information from the SINS, and $(\delta L,\delta \lambda )$ is the latitude and longitude error from the SINS. $\left(L_G,{\lambda }_G\right)$ is the pseudo-GNSS latitude and longitude information predicted by the improved LSTM algorithm and $\left(\delta L_G,\delta {\lambda }_G\right)$ is the latitude and longitude error output when the GNSS signal is good.

$$Z_t=\left[\begin{array}{c}\left(L_I-L_G\right)R\\ \left({\lambda }_I-{\lambda }_G\right)R\cos L\end{array}\right]=\left[\begin{array}{c}R\delta L\\ R\cos L\delta \lambda \end{array}\right]=H_t{X}_t+V_t$$

(17)

The system equations and measurement equations for the combined navigation error state under No GNSS signal conditions are obtained by constructing the Kalman filter properties in the navigation coordinate system. The Kalman filter algorithm is applied to the SINS/GNSS combined navigation in-vehicle real-world experiments to verify the accuracy difference between the experimental results of the combined navigation algorithm and further illustrate the superiority of the improved LSTM algorithm in assisting the filtering algorithm under No GNSS signal conditions.

4. Algorithm Validation

4.1. Overview of On-Board Experiments

The combined navigation unit consists of an Inertial Measurement Unit (IMU) and an RTK antenna for the GNSS receiver. The combined navigation module is connected to the host PC (Personal Computer) through an RS232-to-USB serial data cable so that the IMU of the combined navigation module can receive acceleration and angular velocity information while the GNSS can output position and velocity information. Table 1 shows the performance parameters of the IMU, and Figure 6 shows the hardware environment of the combined navigation vehicle experiment and the vehicle experiment.

Table 1. IMU equipment performance parameters.

Parameters	Numerical Values	Unit
Gyroscope constant zero offset	10	°/h
Gyroscope range	250	°/s
Accelerometer constant zero offset	0.1	mg
Accelerometer range	4	g

Figure 6. As shown in the picture above. The left figure (a) shows the vehicle combination navigation sports car environment setup, and the right figure (b) shows the vehicle combination navigation actual test sports car experiment.

Using the combined navigation device, after making sure the wiring is correct, power up the system and make sure the operating voltage and current of all devices are within normal range; when the vehicle is at a standstill, first detect the working of GNSS receiving signal, then transmit the valid speed and position information to the inertial guidance system and use it as the initial value. Based on this, the inertial device at rest for 30 s is used to obtain its position information and achieve the initial alignment. The test vehicle is started up, and its navigation parameters are observed in real-time so that it is in maximum smooth motion. After the sports car has been tested, the output values of the combined navigation system IMU and GNSS in the case of real-time vehicle movement are stored via the upper computer data acquisition system to analyze the onboard data for positioning accuracy through an offline algorithm.

4.2. Onboard Offline Data Processing

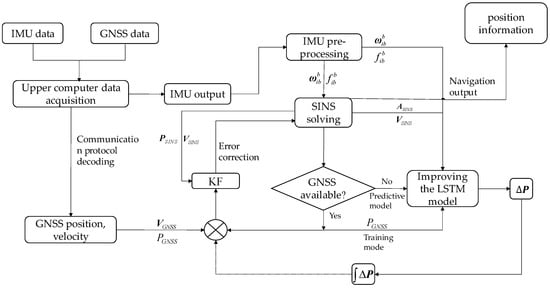
The onboard offline data processing is carried out through an upper computer data acquisition system for the combined navigation system. The upper computer data acquisition system is connected to the PC through the RS232 and RS422 serial to USB serial communication data line from the combined navigation device. The general flow of the upper computer data acquisition system is shown in Figure 7.

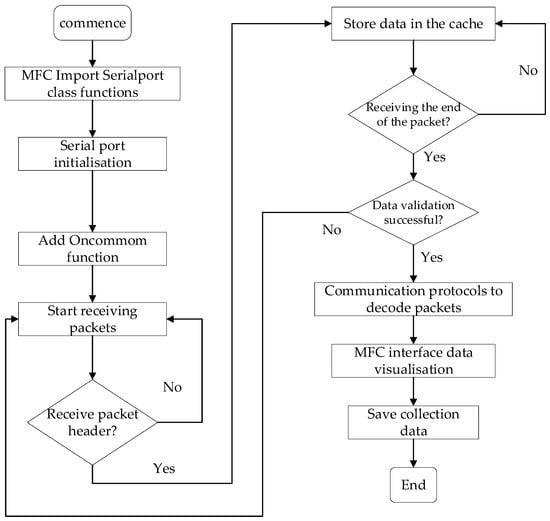
Figure 7. General flowchart of the upper computer data acquisition system.

Considering the effect of real-time full-duplex communication, the serial port class function is introduced in the MFC (Microsoft Foundation Classes) interface to complete the upper computer acquisition system of the PC side and the in-vehicle combined navigation system, firstly to initialize the serial port and then to receive and solve the raw data output by the combined navigation system through the On-common function. As the data is transmitted in real-time, it is necessary to collect a complete set of data packets. After receiving the packet header of a set of data packets, the subsequent data of this set of data packets will be stored in the buffer until the end of the completely received packet tail data, after which the data put into the buffer will be checked, and if the check passes the communication protocol to decode the data packets, the data will be displayed visually in the MFC interface and then saved. Real-time data collection. This lays the foundation for subsequent research into the positioning algorithms of in-vehicle combined navigation systems.

4.3. Analysis of the Results of the On-Board Experiments

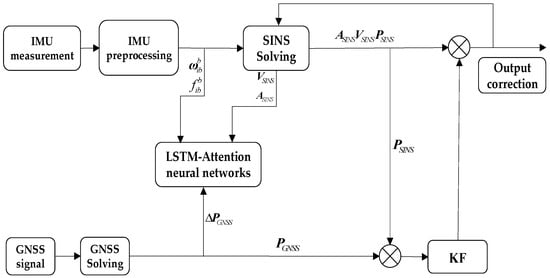
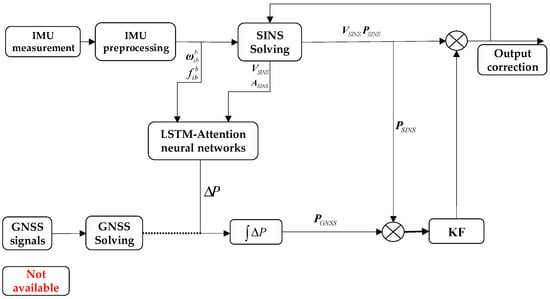
The pseudo-position information is predicted by the improved LSTM model algorithm in the case of signal loss within a short period, replacing the GNSS position information in the case of good signal, inputting it into the Kalman filter for optimal estimation, and correcting the SINS navigation error by the loose combination navigation algorithm to improve the performance of loose combination navigation under No GNSS conditions. The validity of the algorithm is verified by comparing the predicted values with the actual values through real experiments in a sports car.

The specific parameters of the improved LSTM algorithm are set:

By modeling the improved LSTM algorithm, it is determined that its input layers are set to 12 layers, 3-axis angular velocity, 3-axis acceleration, 3-axis velocity, and attitude angle a total of 12-dimensional feature vectors. Set up 2 layers of convolutional layer, activation function using RELU function, set up 1 layer of LSTM network layer; the initial learning rate is 0.006, learning rate descent factor is 0.1, add the attention layer, highlighting the impact of the key input dimensional feature vectors on the output, and finally carry out the dot-multiplication fully-connected layer for the output, the maximum number of training times is set to 300, the optimization algorithm adopts the learning rate adaptive Adam gradient descent algorithm [20,21,22].

In Xi’an University of Architecture and Technology (XUAST) Cao Tang campus for 800 s of sports car measurement experiments, sports car trajectory as shown in Figure 8, the red trajectory for the vehicle measured trajectory, the black trajectory for the IMU sensor solved trajectory, due to the SINS solved trajectory error is too large, so the use of the combination of SINS/GNSS navigation trajectory and the vehicle measured trajectory for comparison, the comparison of trajectory as shown in Figure 9. There are two sections in Figure 9 for GNSS signal shielding processing, experimental Section 1 and experimental Section 2 are the 60 s and 42 s, respectively, for two time periods on the GNSS information collected by the host computer data acquisition system, to achieve the effect of the existence of a No GNSS signal condition in the period.

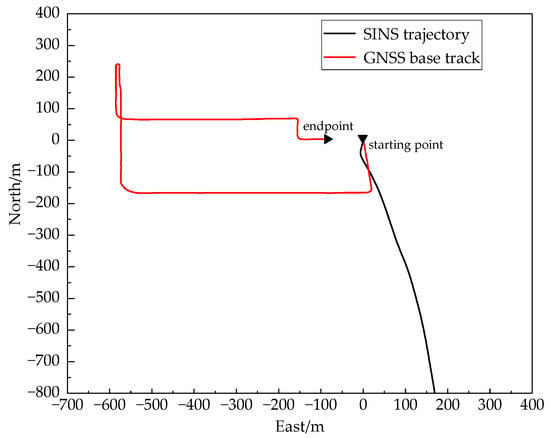
Figure 8. GNSS reference trajectory and SINS trajectory.

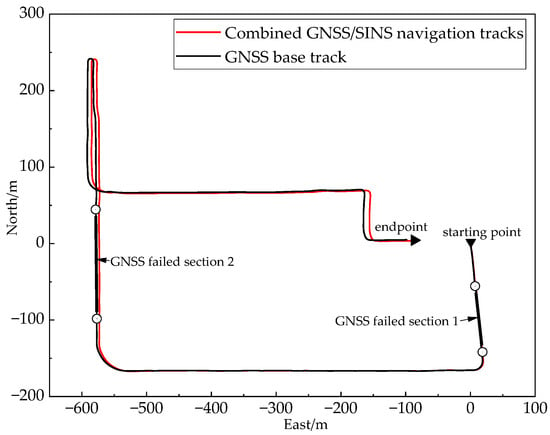
Figure 9. Combined GNSS/SINS navigation trajectory and GNSS reference trajectory.

GNSS Failure Section 1: No GNSS signal processing is carried out in the track Section 1. This experimental Section 1 is used to simulate the No GNSS signal conditions in the onboard complex environment by using the data acquisition system of the upper computer to process the data collected by the GNSS receiver offline in the time from 50 s to 110 s.

Figure 10 shows the comparison between the trajectories of the three different algorithms and the benchmark trajectory under the No GNSS signal conditions in the experimental road Section 1, and it can be seen from Figure 10 that under the No GNSS signal conditions in road Section 1, the predicted trajectory of the improved LSTM algorithm proposed in this paper is closer to the real benchmark trajectory, To make a clear comparison, this paper also carries out the eastward position error comparison and northward position error comparison analysis of three different algorithms, and the position error comparison analysis is shown in Figure 11 and Figure 12. The position error values are analyzed through the data of different algorithm comparison experiments to further verify the feasibility of the algorithm in this paper.

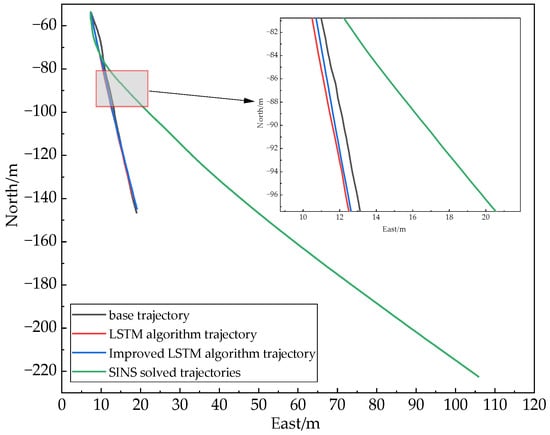
Figure 10. Comparison of trajectories of each algorithm under 60 s No GNSS signal condition.

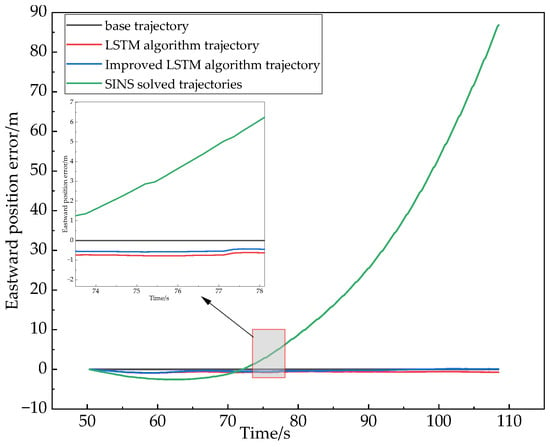
Figure 11. Comparison of eastward position error of each algorithm under 60 s No GNSS signal condition.

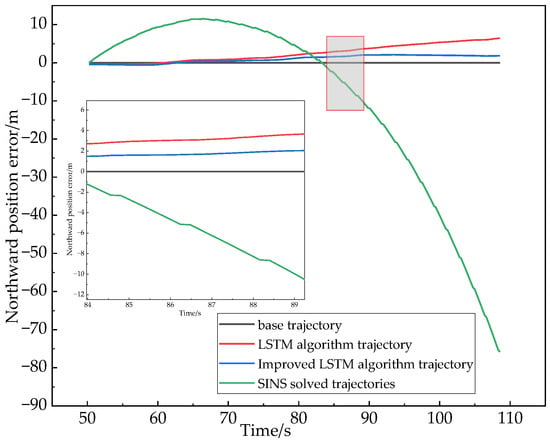
Figure 12. Comparison of northward position error of each algorithm under 60 s No GNSS signal condition.

In experimental Section 1, in the time from 50 s to 110 s, the use of the host computer data acquisition system on the GNSS receiver collected data offline processing to achieve the simulation of the vehicle complex environment of No GNSS signal conditions, Figure 11 and Figure 12 show the position error comparison of the three algorithms in 60 s No GNSS signal conditions, the results show in the first experimental section of the No GNSS signal process, the positioning accuracy of the three positioning methods will have different errors, and the improved LSTM neural network assisted combined navigation algorithm used in this paper has a higher positioning accuracy than that of LSTM with SINS. In the whole movement state, the maximum error absolute value, the root mean square error, is selected for data analysis to reflect the change of data before and after the improved algorithm. From Figure 11 and Figure 12, we can see that the improved LSTM algorithm is better than the other algorithms in terms of the root mean square error and the maximum absolute error under the whole motion state.

From the position error analysis table derived from Table 2, we can obtain the comparative analysis of the maximum error of the eastward position; the accuracy of the improved LSTM algorithm is improved by 5.03% over the LSTM algorithm and 98.91% over the pure SINS solution. Comparative analysis of the root mean square error of the eastward position, the accuracy of the improved LSTM algorithm is improved by 43.42% over the LSTM algorithm and 98.88% over the pure SINS solution. For the comparative analysis of the maximum error of the northward position, the accuracy of the improved LSTM algorithm is improved by 66.64% over the LSTM algorithm and 98.29% over the pure SINS solution. Comparative analysis of the root mean square error of the northward position, the accuracy of the improved LSTM algorithm is improved by 55.63% over the LSTM algorithm and 95.98% over the pure SINS solution.

Table 2. Comparison of statistical parameters of different neural networks under 60 s No GNSS signal conditions.

Algorithm Comparison	Maximum Absolute Value of Error/m	Root Mean Square Error/m
Eastward position SINS error	86.931	25.914
Eastward position LSTM assisted prediction error	0.933	0.288
Eastward position improvement LSTM-aided prediction error	0.886	0.163
Northward position SINS error	75.821	24.146
Northward position LSTM assisted prediction error	6.295	2.201
Northward position improvement LSTM-aided prediction error	2.099	0.976

GNSS Failure Section 2: No GNSS signal processing is carried out in the track Section 2. In experiment Section 2, the data collected by the GNSS receiver is processed offline by using the data acquisition system of the upper computer in the time from 380 s to 422 s to achieve the simulation of the No GNSS signal conditions in the onboard complex environment.

Figure 13 shows the comparison between the trajectories of the three different algorithms and the benchmark trajectory under the No GNSS signal conditions in the experimental Section 2. It can be seen from Figure 13 that the trajectories predicted by the improved LSTM algorithm proposed in this paper are closer to the real benchmark trajectory under the No GNSS signal conditions in Section 2. To make a clear comparison, this paper also carries out the position error comparison of three different algorithms in the east direction and the position error comparison in the north direction, and the position error comparison analysis is shown in Figure 14 and Figure 15. The position error values are analyzed through the data of different algorithm comparison experiments to further verify the feasibility of the algorithm in this paper.

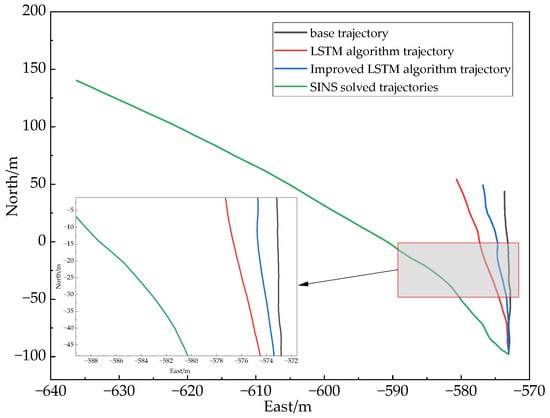
Figure 13. Comparison of trajectories of each algorithm under 42 s No GNSS signal condition.

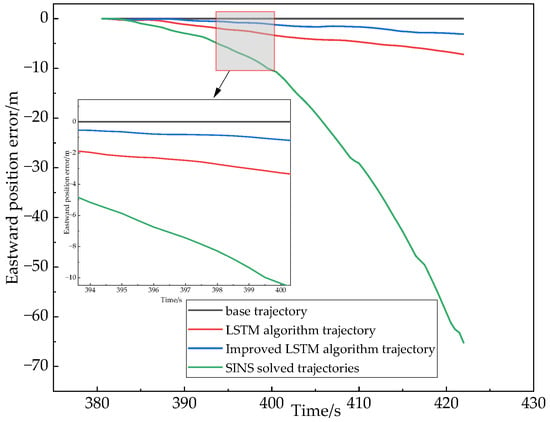
Figure 14. Comparison of the eastward position errors of the algorithms under 42 s No GNSS signal conditions.

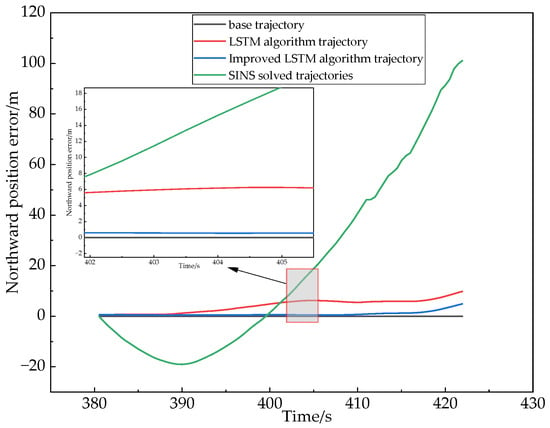
Figure 15. Comparison of the northward position errors of the algorithms under 42 s No GNSS signal conditions.

In this experimental Section 2 in the time from 380 s to 422 s, the use of the host computer data acquisition system on the GNSS receiver collected data for offline processing to achieve the simulation of the vehicle’s complex environment under the conditions of No GNSS signals, Figure 14 and Figure 15 show the position error comparison of the three algorithms in the 42 s No GNSS signal conditions, the results show that in the second experimental section of No GNSS signals process, the positioning accuracy of the three positioning methods will have different errors, and the improved LSTM neural network-assisted combined navigation algorithm used in this paper has a higher positioning accuracy than that of LSTM with SINS. In the whole movement state, the maximum error absolute value and the root mean square error are selected for data analysis to reflect the change of data before and after the improved algorithm. From Figure 14 and Figure 15, we can see that the improved LSTM algorithm is better than the other algorithms in terms of the root mean square error and the maximum absolute error under the whole motion state.

From the position error analysis table derived from Table 3, we can obtain the comparative analysis of the maximum error of the eastward position; the accuracy of the improved LSTM algorithm is improved by 56.82% over the LSTM algorithm and 95.21% over the pure SINS solution. Comparative analysis of the root mean square error of the eastward position, the accuracy of the improved LSTM algorithm is improved by 54.67% over the LSTM algorithm and 95.01% over the pure SINS solution. Comparative analysis of the maximum error of the northward position, the accuracy of the improved LSTM algorithm is improved by 48.15% over the LSTM algorithm and 94.72% over the pure SINS solution. For the comparative analysis of the root mean square error of the northward position, the accuracy of the improved LSTM algorithm is improved by 76.64% over the LSTM algorithm and 97.26% over the pure SINS solution.

Table 3. Comparison of statistical parameters of different neural networks under 42 s No GNSS signal conditions.

Algorithm Comparison	Maximum Absolute Value of Error/m	Root Mean Square Error/m
Eastward position SINS error	65.319	19.611
Eastward position LSTM assisted prediction error	7.192	2.159
Eastward position improvement LSTM-aided prediction error	3.105	0.977
Northward position SINS error	102.055	37.472
Northward position LSTM assisted prediction error	10.354	2.608
Northward position improvement LSTM-aided prediction error	5.368	1.023

The reliability and superiority of the improved LSTM algorithm-assisted GNSS/SINS loose-combination navigation algorithm under No GNSS signals for a short period is verified by 2 in a smooth, straight-line driving trajectory section.

5. Conclusions

Aiming at the problem that GNSS signals are easily lost, or No GNSS signals exist due to the complex in-vehicle navigation road environment under the algorithm research of combined in-vehicle GNSS/SINS navigation system, an improved LSTM algorithm is proposed to assist the combined in-vehicle GNSS/SINS navigation and positioning algorithm. The method solves the problem that navigation information can affect the accuracy and precision of in-vehicle navigation when it is provided by the SINS system only, which can easily cause excessive position deviation and improve the accuracy and performance of combined navigation under No GNSS conditions.

The experiments in a real environment of a sports car show that in two No GNSS signal conditions, the root mean square error of the eastbound position is improved by 43.42% and 54.67% compared with the LSTM algorithm, and the root mean square error of the northbound position is improved by 55.63% and 76.64% compared with the LSTM algorithm, respectively, which verifies the effectiveness and feasibility of the algorithm.

Shortcomings: This article is only GNSS/SINS loose combination navigation mode research, can only be in the No GNSS signal conditions of a short period through the improved LSTM algorithm to assist the combination of navigation algorithms for offline vehicle navigation and positioning research, and the algorithm is currently the research situation only applies to the smooth straight-line trajectory. The real-time positioning of high-precision vehicle navigation in complex environments still requires further research and analysis and can be used in the way of multi-sensor fusion to carry out long-time positioning research of vehicle navigation.