Lightweight Tunnel Defect Detection Algorithm Based on Knowledge Distillation

Abstract

One of the greatest engineering feats in history is the construction of tunnels, and the management of tunnel safety depends heavily on the detection of tunnel defects. However, the real-time, portability, and accuracy issues with the present tunnel defect detection technique still exist. The study improves the traditional defect detection technology based on the knowledge distillation algorithm, the depth pooling residual structure is designed in the teacher network to enhance the ability to extract target features. Next, the MobileNetv3 lightweight network is built into the student network to reduce the number and volume of model parameters. The lightweight model is then trained in terms of both features and outputs using a multidimensional knowledge distillation approach. By processing the tunnel radar detection photos, the dataset is created. The experimental findings demonstrate that the multidimensional knowledge distillation approach greatly increases the detection efficiency: the number of parameters is decreased by 81.4%, from 16.03 MB to 2.98 MB, while the accuracy is improved by 2.5%, from 83.4% to 85.9%.

1. Introduce

Road tunnels of 24,698,900 long meters had been constructed nationwide by the end of 2021, according to the Statistical Bulletin of Transport Industry Development 2021. However, there are several flaws in tunnels, including uncompacted, empty, and water-filled tunnels, because of the circumstances surrounding tunnel construction and the surrounding environment. Tunnel defect detection is the cornerstone of ensuring the safe operation of tunnels because these flaws can significantly impair the service life and safety of tunnels.

Traditional tunnel defect detection methods include visual inspection methods, acoustic inspection methods, and multi-sensor inspection methods. For instance, Minardo and Monsberger [1,2] highlighted the shortcomings of conventional structural monitoring techniques. Infrared thermal imaging was employed by Afshani et al. [3] for tunnel inspection. It is challenging to satisfy the demands of large-scale, effective, and high-precision defect detection using these conventional methods, which are not only susceptible to missing parts and leakage detection but also use a lot of human and material resources. Researchers’ focus has steadily shifted to developing inspection techniques based on deep learning that can automatically identify and locate tunnel flaws. The issue of small size and damage overlap in defect identification was successfully resolved by Dong et al. [4] by combining the SegNet model with the focused loss function. A full convolutional network model (FCN) based on classification was utilized by Xue et al. [5], which significantly increased detection efficiency and accuracy while consuming fewer processing resources. By training and testing photos with various backdrop complexity levels, Zhou [6] and coworkers considerably increased the detection speed and accuracy of the Yolov4 network. Three-dimensional ground-penetrating radar data and the Yolo model were merged by Liu et al. [7] to quickly identify road problems and accomplish automated defect detection. The project team enhanced the SGD network [8] to increase model accuracy and added an adversarial network [9] to increase the dataset. Researchers’ attention is now focused on finding ways to ensure lightweight deployment in the context of the development of edge-enabled devices. To address the issue of data learning rate during training, Liu et al. [10] created variable convolutional layers as well as joint learning methodologies. In order to improve interference countermeasures and transfer the knowledge obtained by the model to other recognition models using transfer learning approaches, Liu et al. [11] created a network based on two-layer adversarial. This significantly increases training efficiency and model accuracy. In order to implement the deployment on the robot side, Huang [12] et al. employed a weight quantization approach, which compressed the memory by 22.5 times but required continual parameter adjustment and a lot of labor. Class-aware tracking ratio optimization (CATRO) was utilized by Hu [13] and others to minimize computation, which considerably boosted calculation performance but also increased model sparsity, increased hardware needs, and made it challenging to deploy at the edge devices. Zhang [14] et al. used a knowledge distillation method for human posture prediction to enable lightweight deployment without altering the model’s structure. A similar information distillation technique was applied by Zhao [15] et al. to produce a lightweight fusion of infrared and visible pictures. Hinton [16], Romero [17], and Zagoruyko [18] have each put forth a variety of knowledge distillation-based methodologies.

Based on conventional tunnel defect detection methods, deep learning methods, and knowledge migration methods, the study enhances the knowledge distillation methodology. The following are the research’s main contributions:

(1)

Create a deep pooling residual structure to pool and weight feature information deeply

(2)

Use MobileNetv3 to optimize the network backbone for improved model lightweight

(3)

Construct a method for multidimensional knowledge extraction that can extract information from both the feature layer and the output layer.

2. Related Work

Deep learning is one of the most popular methods in the field of computer vision, which typically uses deep neural networks to extract features from images. These neural network models often have several layers of neurons, each of which can separate higher-level, more abstract properties from the input data. A back-propagation technique optimizes the models during deep learning training by progressively changing the network parameters and enhancing model performance. Computer vision systems can learn to extract helpful features from input photos for a range of different vision programs by employing deep learning models for training.

2.1. YOLO Method

A highly popular real-time target identification technique, the YOLO (You Only Look Once) [19,20,21] algorithm offers very quick target recognition at the tradeoff of very little accuracy. As seen in Figure 1, the YOLO algorithm divides the entire image into numerous grids and forecasts bounding boxes and class probabilities for each grid. This method is extremely quick and enables the YOLO algorithm to detect several targets in a single forward pass, which is ideal for the real-time demands of tunnel detection.

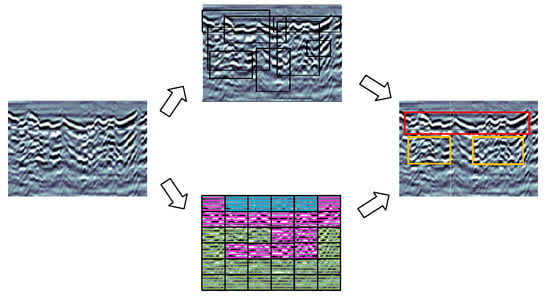
Figure 1. Process of yolo detection in a grid. Each fixed-size cell must identify one object in the image before a confidence score determines which prediction frame is the best.

The relationship between the network input x and output $\hat{\mathrm{y}}$ is as in Equation (1). The loss function in Equation (2) is used to characterize the error between the model output $\hat{\mathrm{y}}$ and the desired output y. For the regression problem, the output of the model h(x) and the sample labeling are real numbers, and the common method to evaluate its performance on the sample set is the mean square error, i.e., Equation (3).

$$\hat{\mathrm{y}}=\mathrm{h}\left({\mathrm{x}}_{\mathrm{i}}\right)$$

(1)

$$\mathrm{L}\left(\hat{\mathrm{y}},\mathrm{y}\right)=\mathrm{L}\left(\mathrm{h}\left({\mathrm{x}}_{\mathrm{i}}\right),\mathrm{y}\right)$$

(2)

$$\mathrm{E}\left(\mathrm{h}\right)=\frac{1}{\mathrm{N}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\left(\mathrm{h}\left({\mathrm{x}}_{\mathrm{i}}\right)-{\mathrm{y}}_{\mathrm{i}}\right)}^2$$

(3)

As shown in Figure 1, in the YOLO algorithm the input image is divided into S × S grids, each grid contains five pieces of information: (x, y, w, h, c), where x and y represent the horizontal and vertical coordinates of the prediction frame, w and h represent is the width and height of the prediction frame, c represents the confidence level, and the formula is calculated as in Equation (4):

$$\mathrm{c}={\mathrm{p}}_0\times {\mathrm{P}}_{\mathrm{IOU}}$$

(4)

where ${\mathrm{p}}_0$ denotes the probability that the prediction frame contains a detection object, if it does, then ${\mathrm{p}}_0$ = 1, and vice versa ${\mathrm{p}}_0$ = 0; ${\mathrm{P}}_{\mathrm{IOU}}$ denotes the area of overlap between the prediction frame and the real detection object area. Then the YOLO algorithm loss function can be expressed as Equation (5):

$$\begin{array}{c}\mathrm{L}={\mathrm{L}}_{\mathrm{I}\mathrm{O}\mathrm{U}}+{\mathrm{L}}_{\mathrm{obj}}+{\mathrm{L}}_{\mathrm{class}}\\ ={\lambda }_{\mathrm{coord}}\sum _{\mathrm{i}=0}^{{\mathrm{S}}^2}\sum _{\mathrm{j}=0}^{\mathrm{B}}{\mathrm{l}}_{\mathrm{i}\mathrm{j}}^{\mathrm{obj}}[{({\mathrm{x}}_{\mathrm{i}}-{\hat{\mathrm{x}}}_{\mathrm{i}})}^2+{({\mathrm{y}}_{\mathrm{i}}-{\hat{\mathrm{y}}}_{\mathrm{i}})}^2]+{\lambda }_{\mathrm{coord}}\sum _{\mathrm{i}=0}^{{\mathrm{S}}^2}\sum _{\mathrm{j}=0}^{\mathrm{B}}{1}_{\mathrm{i}\mathrm{j}}^{\mathrm{obj}}[{(\sqrt{{\omega }_{\mathrm{i}}}-\sqrt{{\hat{\omega }}_{\mathrm{i}}})}^2+{(\sqrt{{\mathrm{h}}_{\mathrm{i}}}-\sqrt{{\hat{\mathrm{h}}}_{\mathrm{i}}})}^2]\hfill \\ +\sum _{\mathrm{i}=0}^{{\mathrm{S}}^2}\sum _{\mathrm{j}=0}^{\mathrm{B}}{1}_{\mathrm{i}\mathrm{j}}^{\mathrm{obj}}{({\mathrm{c}}_{\mathrm{i}}-{\hat{\mathrm{c}}}_{\mathrm{i}})}^2+{\lambda }_{\mathrm{noobj}}\sum _{\mathrm{i}=0}^{{\mathrm{S}}^2}\sum _{\mathrm{j}=0}^{\mathrm{B}}{1}_{\mathrm{i}\mathrm{j}}^{\mathrm{no}}{({\mathrm{c}}_{\mathrm{i}}-{\hat{\mathrm{c}}}_{\mathrm{i}})}^2+{\lambda }_{\mathrm{obj}}\sum _{\mathrm{i}=0}^{{\mathrm{S}}^2}{1}_{\mathrm{i}\mathrm{j}}^{\mathrm{obj}}\sum _{\mathrm{c} \in \mathrm{c}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{s}}{({\mathrm{p}}_{\mathrm{i}}(\mathrm{c})-{\hat{\mathrm{p}}}_{\mathrm{i}}(\mathrm{c}))}^2\hfill \end{array}$$

(5)

where ${\mathrm{L}}_{\mathrm{IOU}}$ denotes the regression loss, which measures the match between the prediction frame and the true frame, and is calculated as the intersection ratio of the prediction frame and the true frame, and ${\mathrm{L}}_{\mathrm{obj}}$ denotes confidence loss, which measures the presence or absence of a target in the prediction frame, i.e., the probability that a target exists in the prediction frame; ${\mathrm{L}}_{\mathrm{class}}$ denotes classification loss, which is used to measure the accuracy of the model in predicting the target class, and is calculated as the multivariate cross-entropy loss. ${\mathrm{x}}_{\mathrm{i}}$, and ${\mathrm{y}}_{\mathrm{i}}$ denote the true frame coordinates, the ${\hat{\mathrm{x}}}_{\mathrm{i}}$, and ${\hat{\mathrm{y}}}_{\mathrm{i}}$ denote the prediction frame coordinates; ${\mathsf{\omega }}_{\mathrm{i}}$ and ${\mathrm{h}}_{\mathrm{i}}$ denote the true frame width and height, and ${\hat{\mathsf{\omega }}}_{\mathrm{i}}$ and ${\hat{\mathrm{h}}}_{\mathrm{i}}$ denotes the predicted frame width and height; ${\mathrm{l}}_{\mathrm{ij}}^{\mathrm{obj}}$ denotes the part with loss of detection target, and ${\mathrm{l}}_{\mathrm{ij}}^{\mathrm{noobj}}$ denotes the part without detection target loss, and ${\mathrm{c}}_{\mathrm{i}}$ is the confidence label, and ${\hat{\mathrm{c}}}_{\mathrm{i}}$ is the prediction confidence label; ${\mathrm{p}}_{\mathrm{i}}\left(\mathrm{c}\right)$ indicates the current category true value (0, 1), and ${\hat{\mathrm{p}}}_{\mathrm{i}}\left(\mathrm{c}\right)$ denotes the current category probability obtained by the activation function.

2.2. Knowledge Distillation

Deep learning models often require large amounts of computational resources for training and inference, which limits their use in many practical applications. To address this problem, model compression, and acceleration techniques have become popular areas of research.

Among these, the knowledge distillation algorithm [16,22,23,24,25] is a very effective model compression and acceleration technique that extracts knowledge from large, complex deep teacher models and passes it on to small, simple student models. This approach can significantly reduce the complexity and computational cost of student models, while still maintaining model performance.

The loss function of the knowledge distillation algorithm utilizes the generalized softmax function defined in Equation (6):

$${\mathrm{q}}_{\mathrm{i}}=\frac{\exp \left({\mathrm{z}}_{\mathrm{i}}\right)}{{{\displaystyle \sum }}_{\mathrm{j}}\exp \left({\mathrm{z}}_{\mathrm{j}}\right)}$$

(6)

where ${\mathrm{z}}_{\mathrm{i}}$ denotes the output of the teacher model and ${\mathrm{q}}_{\mathrm{i}}$ is the output of using the softmax function, the dark knowledge of the teacher’s network can be better extracted to guide the learning of the student model. To solve the problem of prediction results converging to the zero phenomena in the case of multiple classifications, the cross-entropy loss function is constructed as in Equation (7):

$${\mathrm{L}}_{\mathrm{i}}=-{\mathrm{logq}}_{\mathrm{i}}=-\log \frac{\exp \left({\mathrm{z}}_{\mathrm{i}}\right)}{{{\displaystyle \sum }}_{\mathrm{j}}\exp \left({\mathrm{z}}_{\mathrm{j}}\right)}$$

(7)

where ${\mathrm{L}}_{\mathrm{i}}$ denotes the cross-entropy loss function for the ith sample, and ${\mathrm{q}}_{\mathrm{i}}$ denotes the model output of the ith sample. By minimizing the cross-entropy loss function, the student model output can be made closer to the teacher model output. The final target loss function for the teacher model and the student model is obtained as in Equation (8):

$$\mathrm{L}={\mathsf{\alpha }\mathrm{L}}_{\mathrm{soft}}+{\mathsf{\beta }\mathrm{L}}_{\mathrm{hard}}$$

(8)

where ${\mathrm{L}}_{\mathrm{soft}}$ denotes the teacher model with a soft loss of cross-entropy to the student model, ${\mathrm{L}}_{\mathrm{hard}}$ denotes the student model with a hard loss of cross-entropy to the true value, and $\mathsf{\alpha }$ and $\mathsf{\beta }$ denote the weights of the two loss components.

3. Improving the Model

The multidimensional distillation model demonstrated in this section is shown in Figure 2 and consists of three main components: the teacher network, the student network, and the distillation architecture, where rectangles indicate the neural network layers and arrows indicate the direction of information flow. During the training process, the input data were first fed into the teacher network for feature extraction, resulting in a series of complex feature representations. These feature representations are then fed into the distillation architecture, which is transformed by temperature parameters and soft targets to obtain an intermediate representation suitable for learning by the student network. Finally, the student network is trained based on the intermediate representation to learn the knowledge in the teacher network and obtain the final output.

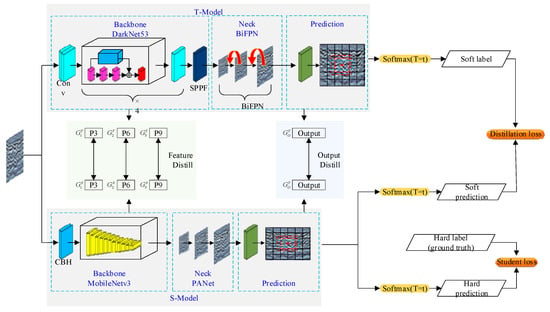
Figure 2. The multidimensional knowledge distillation structure flow, where T-Model is a complicated teacher model with high detection accuracy and S-Model is the soft loss function and the hard loss function connects these two models. Section, feature layer feature information is distilled, and in the Output Distill part, output image information is distilled.

3.1. Deep Pooling of Residual Structures

In the knowledge distillation process, a teacher model is often a high-performance, high-complexity model. The teacher model helps the student model learn a more accurate and generalized representation of knowledge by "teaching" what it has learned from the training data. Improving the teacher model can improve knowledge transfer efficiency and knowledge generalization, reduce overfitting, and improve the interpretability of the model, leading to better knowledge distillation and better applications.

The YOLO algorithm introduces the concept of residual blocks in the training process to avoid problems such as gradient disappearance and low training efficiency due to the depth of the network [26] as shown in Figure 3. The introduction of the residual structure allows YOLO to achieve deeper and easier training while improving classification accuracy [27,28].

Figure 3. The most basic residual structure, with jump connections shown by red arrows.

The improved residual structure is applied to the C3 module of the YOLO algorithm, as shown in Figure 4. Two simultaneous pooling layers are added to the jump connection section, namely average pooling and maximum pooling, where average pooling can preserve the spatial information of the feature map and smooth the feature map to improve robustness; maximum pooling can smooth the input feature map noise; and maximum pooling can smooth out the noise of the input feature map and extract the most significant feature information from the feature map. In summary, the pooling layer can reduce the size of the input feature map, reduce the number of parameters in the network, and further learn the feature information.

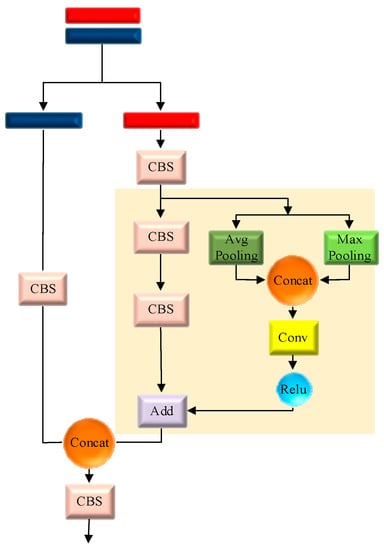
Figure 4. Improved deep pooling residual structure, where the improved portion is the yellow background region and is primarily connected by two pooling weights. The improved activation function is Relu, which enhances the capability of feature extraction.

The new feature information is obtained by normalizing the output of the two pooling layers by giving weights to the weights, which are fed into the convolution layer as an intermediate layer feature, and the deflated low-resolution feature map is mapped to the original feature map in higher space, thus restoring the expressiveness of the feature information, after which the non-linear expressiveness of the feature is enhanced by the Relu activation function.

3.2. Multidimensional Knowledge Distillation

Deep neural networks excel at learning multi-level feature representations of increasing abstraction, so both the image output of the final layer and the feature output of the middle layer can be used as knowledge for supervised student model training. In this study, a multidimensional knowledge distillation algorithm fusing the feature and output layers is designed to transfer pre-trained dark knowledge of complex teacher models to lightweight student models for better control of the compression performance trade-offs. Researchers have created thin network topologies including SqueezeNet, ShuffleNet, and MobileNet for the lightweight student model. The employment of the Fire module, which lowers the number of network parameters while raising the nonlinear transformations, is the key component of the SqueezeNet network. The Fire module combines a Squeeze layer, which reduces the number of channels, with an Expand layer, which increases the number of channels. This significantly reduces the number of convolution kernels but at the expense of a deeper network architecture, which prolongs detection times and significantly lowers detection accuracy. ShuffleNet networks are most notable for their use of channel shuffle operations, which involve first segmenting the input channel into a number of groups and then rearranging each group’s channels to improve inter-group communication. However, because the operation is so complex, it is more challenging to implement at the device’s edge. The foundation of the MobileNet network is the division of convolution into Depthwise Conv and Poingwise Conv. It has been upgraded to the v3 version, which adds new technologies such as SE Attention Module, h-swish activation function, etc., and further reduces network size and computation amount in comparison to SqueezeNet and ShuffleNet networks and enhances precision without lengthening consumption time.

The knowledge transfer process is shown in the Figure 5. In the training process, the original data were first trained using a complex teacher model, which records the feature representations of the intermediate and output layers. These feature representations are then passed on to the lightweight student model for training as dark knowledge. During the training of the student model, a multidimensional knowledge distillation algorithm is used to transfer the dark knowledge from the teacher model to the student model and to train it in conjunction with the student model’s feature representations. The multidimensional knowledge distillation algorithm fuses the intermediate and output layer feature representations from the teacher model with the corresponding layer feature representations from the student model in a weighted manner, thus better guiding the learning of the student model.

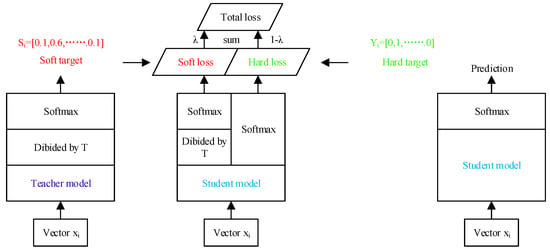
Figure 5. The multidimensional knowledge distillation process, where the leftmost component is the teacher model learning process, is connected to the middle student model through the distillation parameter “T” to form Soft loss, and the rightmost component is the real label with parameter “T” of 1, connected to The rightmost component is the real label with parameter “T” of 1, connected to the student model to form Hard loss, and the two losses are combined to form the full multidimensional knowledge distillation loss.

To help train the student network in depth, the outputs of the intermediate layers of the teacher network were introduced, and then each intermediate and output layer parameter was optimized by a loss function as in Equation (9):

$$L_{FeaD}\left(f_t\left(x\right),f_s\left(x\right)\right)={ℒ}_F\left({\varphi }_t\left(f_t\left(x\right)\right),{\varphi }_s\left(f_s\left(x\right)\right)\right)$$

(9)

Of these, the $f_t\left(x\right)$ and $f_s\left(x\right)$ are the feature maps of the middle layer of the teacher and student models respectively. When the feature maps of the teacher and student models are not in the same shape, it is common to apply the transformation functions ${\varphi }_t\left(f_t\left(x\right)\right)$ and ${\varphi }_s\left(f_s\left(x\right)\right)$. ${ℒ}_F( )$ denotes the similarity function used to match the feature maps of the teacher and student models, and in this study ${ℒ}_F( )$ denotes the cross-entropy loss function.

The training process is distilled by distilling the output with the high-temperature match to obtain a hard loss ${\mathrm{L}}_{\mathrm{hard}}$ defined as the cross-entropy loss between the ground truth label and the student model as in Equation (10):

$$\begin{array}{c}{\mathrm{L}}_{\mathrm{hard}}=-{\displaystyle {\displaystyle \sum }_{\mathrm{i}}^{\mathrm{N}}}{\mathrm{c}}_{\mathrm{i}}\log \left({\mathrm{q}}_{\mathrm{i}}^{\mathrm{T}}\right)\\ {\mathrm{q}}_{\mathrm{i}}^{\mathrm{T}}=\frac{\exp \left({\mathrm{z}}_{\mathrm{i}}\right)}{{{\displaystyle \sum }}_{\mathrm{i}}^{\mathrm{N}}\left({\mathrm{z}}_{\mathrm{i}}\right)}\end{array}$$

(10)

Soft loss ${\mathrm{L}}_{\mathrm{soft}}$ is defined as the cross-entropy between the teacher model and the student model as in Equation (11):

$$\begin{array}{c}{\mathrm{L}}_{\mathrm{soft}}=-{\displaystyle {\displaystyle \sum }_{\mathrm{i}}^{\mathrm{N}}}{\mathrm{p}}_{\mathrm{i}}^{\mathrm{T}}\log \left({\mathrm{q}}_{\mathrm{i}}^{\mathrm{T}}\right)\\ {\mathrm{p}}_{\mathrm{i}}^{\mathrm{T}}=\frac{\exp \left(\frac{{\mathrm{v}}_{\mathrm{i}}}{\mathrm{T}}\right)}{{{\displaystyle \sum }}_{\mathrm{k}}^{\mathrm{N}}\left(\frac{{\mathrm{v}}_{\mathrm{k}}}{\mathrm{T}}\right)}\\ {\mathrm{q}}_{\mathrm{i}}^{\mathrm{T}}=\frac{\exp \left(\frac{{\mathrm{z}}_{\mathrm{i}}}{\mathrm{T}}\right)}{{{\displaystyle \sum }}_{\mathrm{k}}^{\mathrm{N}}\left(\frac{{\mathrm{z}}_{\mathrm{k}}}{\mathrm{T}}\right)}\end{array}$$

(11)

where ${\mathrm{v}}_{\mathrm{i}}$ denotes the output of the teacher network, ${\mathrm{z}}_{\mathrm{i}}$ denotes the output of the student network and ${\mathrm{p}}_{\mathrm{i}}^{\mathrm{T}}$, and ${\mathrm{q}}_{\mathrm{i}}^{\mathrm{T}}$ denotes the value of the softmax output of the teacher network and the student network at temperature T for class i, respectively. ${\mathrm{c}}_{\mathrm{i}}$ denotes the value of ground truth at class i. ${\mathrm{c}}_{\mathrm{j}}\in \left\{0,1\right\}$ N denotes the total number of samples.

The total loss in the output layer is obtained through Equation (8) as Equation (12):

$$\mathrm{L}=\mathsf{\alpha }{\displaystyle \sum }_{\mathrm{i}}^{\mathrm{N}}{\mathrm{p}}_{\mathrm{i}}^{\mathrm{T}}\log \left({\mathrm{q}}_{\mathrm{i}}^{\mathrm{T}}\right)+\mathsf{\beta }{\displaystyle \sum }_{\mathrm{i}}^{\mathrm{N}}{\mathrm{c}}_{\mathrm{i}}\log \left({\mathrm{q}}_{\mathrm{i}}^{\mathrm{T}}\right)$$

(12)

Through a multidimensional knowledge distillation approach, the dark knowledge of a pre-trained complex teacher model is successfully transferred to a lightweight student model, and model compression and acceleration are achieved while maintaining model performance. The experimental results show that the multidimensional knowledge distillation algorithm in this study, which fuses the feature and output layers, can better maintain the performance and robustness of the model while achieving higher compression rates and faster inference than direct pruning or distillation of the student model.

4. Experimental Studies

4.1. Data Processing

To construct the dataset required for this study, we collected multiple segments of tunnel defect radar data and performed post-processing operations such as uncompacted, hollow, and water-filling on these data, which mainly include types of defects such as uncompacted, emptying, hollow, and water-filled. Specifically, image enhancement algorithms were used to enhance the quality and usability of the data, and manual annotation of the data was carried out to obtain accurate annotation information. Some typical examples of defects are illustrated in the Figure 6.

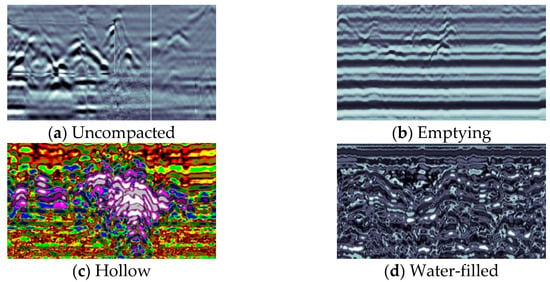
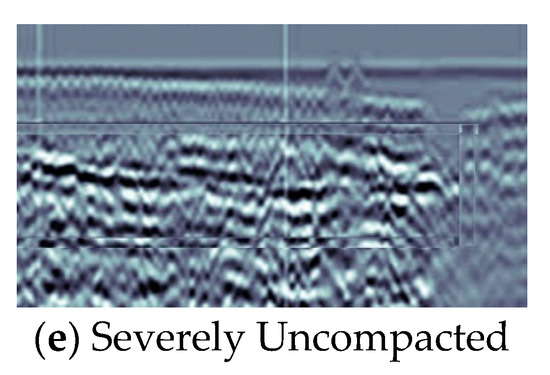
Figure 6. Examples of defects include those where (a) denotes an uncompacted defect, (b) an emptying defect, (c) a hollow defect, (d) a water-filled flaw, and (e) a serious uncompacted defect.

The group increased the data samples by mosaic data enhancement and cropping and stitching methods in previous studies, while the final data set of more than 5700 images was obtained by labeling with LabelImg software (v1.8.6.) to form the data set for this study. The defect images were classified into five categories, such as BM, TK, KD, CS, and YBM, which represent the five types of defects: uncompact, dehollowed, hollow, water-filled, and severely uncompacted defects. Table 1 shows the distribution of the defect images in the dataset.

Table 1. Distribution of Tunnel Defect Dataset.

Defect Type	Training Set	Validation Set	Test Set	Tags
BM	1301	114	76	0
TK	1815	127	139	1
KD	904	78	254	2
CS	1136	80	197	3
YBM	1175	111	107	4

4.2. Experimental Procedure

4.2.1. Experimental Configuration

The ground-penetrating radar vehicle is equipped with ground-penetrating radar equipment that emits radar waves into the ground and then receives the bounced signals to obtain information about underground objects or terrain with the relevant parameters shown in Table 2.

Table 2. Radar rover related parameters.

Name	Configure
Equipment Model	TGRI-GPR200
Center Frequency	200 MHz
Operating Bandwidth	100 MHz–500 MHz
Depth of detection	10 m
Dynamic Range	40 dB

The deep learning simulation experiments were built on a Linux system (20.04.1), using Python (3.8) and PyTorch (1.10.2) to build the deep learning framework. The hardware setup shown in Table 3 includes components such as CPU, GPU, memory, and storage.

Table 3. Experimental hardware configuration.

Name	Configure
Operating System	Linux
Video Card	NVIDIA RTX3090
Video Memory	24G
Processor	Intel(R) Core i3-8100
Programming Language	Python
Deep training framework	PyTorch
Programming Platforms	Pycharm

Table 4 shows some of the trainable parameters in the deep learning model, including weights and biases, which are obtained by back-propagation and optimization of the training data to minimize the loss function of the model.

Table 4. Experimental model parameters.

Name	Value
Pixel	640 × 640
Epoch	100
Batch size	32

4.2.2. Evaluation Indicators

To accurately assess the effectiveness of the target detection algorithm in detecting tunnel defects, the experiments in this study use the mean accuracy (mAP) and the number of parameters to measure the optimization effect. mAP can be calculated by Precision and Recall, which are calculated as follows in Equation (13).

$$\begin{gathered} \mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} \\ \mathrm{Recall}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} \\ \mathrm{AP}={{\displaystyle \int }}_0^1\mathrm{P}\left(\mathrm{R}\right)\mathrm{dR} \\ \mathrm{mAP}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{AP}}_{\mathrm{i}}}{\mathrm{N}} \\ {\mathrm{mAP}}_{\left[@0.5,@0.95\right]} =\frac{{{\displaystyle \sum }}_{i=0.5}^{0.95}{\mathrm{mAP}}_{@0.5}}{10} \end{gathered}$$

(13)

where TP represents the number of positive examples correctly classified, TN represents the number of negative examples correctly classified, FP represents the number of positive examples incorrectly classified, and FN represents the number of negative examples incorrectly classified.

5. Experimental Results

The study used the distillation model for tunnel defect detection and successfully detected a wide range of defect types and sizes, with some of the defect detection results shown in Figure 7.

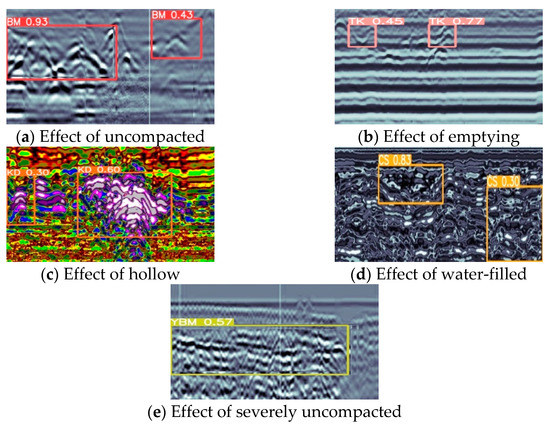
Figure 7. Detection of five different types of defects. (a) Effect of uncompacted; (b) Effect of emptying; (c) Effect of hollow; (d) Effect of water-filled; (e) Effect of severely uncompacted.

The loss function data during the training of the YOLO model, teacher model, student model, and multidimensional knowledge distillation model were represented as scatter plots, and the loss function curves shown in Figure 8 were obtained. By observing the images, it can be seen that in the 20th round, the loss function starts to converge and then tends to stabilize. The convergence and stabilization of the loss function values indicate that the model gradually reaches an optimal state.

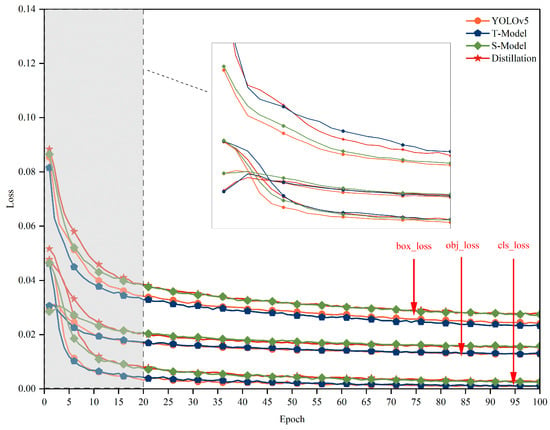
Figure 8. Comparison of the loss function curves of the four models, where orange is the original model, purple is the improved teacher model, green is the student model and red is the multidimensional knowledge distillation model.

To assess the model classification performance and compare the model prediction results with the actual label differences, the original model was compared with the confusion matrix of the multidimensional distillation model as shown in Figure 9. It can be seen that the improved model has improved the prediction accuracy for all types of defects, the most obvious of which is the case of uncompacted defect prediction, which has improved from 48% to 94%.

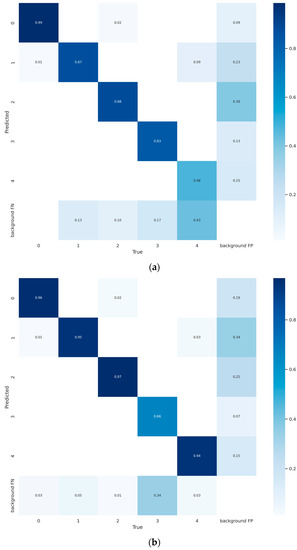
Figure 9. Confusion_matrix, where (a) denotes the original model confusion matrix and (b) denotes the improved model confusion matrix.

Also, to verify the effectiveness of each model for various defects and highlight the importance of each module, the study tallied the detection results of each model on different defect types, as shown in Figure 10 and Table 5. The results showed that the multidimensional distillation model proposed in this study outperformed the original model for various tunnel roadbed defect types, which further validated the effectiveness of the model in tunnel roadbed defect detection.

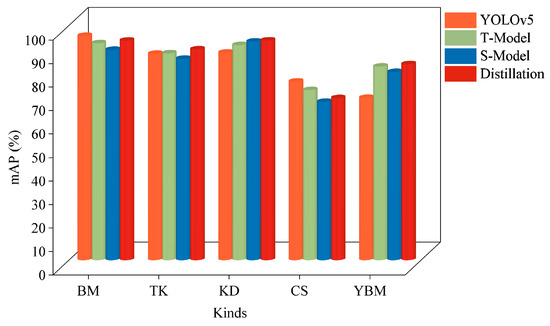
Figure 10. Comparison of different models for different categories of detection.

Table 5. Comparison of experimental results of the models in different categories of defects.

Type	Average Accuracy Rate/%
Models	BM	TK	KD	CS	YBM
Yolov5	95.6	87.9	88.4	76.1	69.1
T-Model	92.4	88.1	91.6	72.4	82.5
S-Model	89.6	85.8	93.1	67.4	80.2
Distillation	93.5	89.8	93.6	69.0	83.5

To more accurately assess the performance of the multidimensional distillation model proposed in this study, further ablation tests were conducted, and experimental results were obtained as shown in Figure 11 and Table 6. The results show that with the improved distillation technique, an accuracy of 87.1% of the parameter file size was achieved. These results show that the distillation model can significantly improve the lightweight and accuracy of the model in complex tunnel roadbed defect detection scenarios.

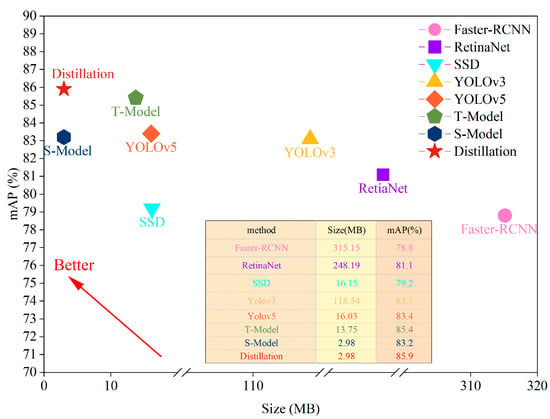
Figure 11. Comparison of model accuracy and number of parameters.

Table 6. Model performance comparison.

Model	mAP@0.5 (%)	mAP@0.5:0.95 (%)	Precision (%)	Recall (%)	GFLOPS (G)	Size (MB)
Faster-RCNN	78.8	48.8	78.6	80.2	88.2	315.15
RetinaNet	81.1	49.8	79.7	81.3	70.3	248.19
SSD	79.2	47.0	75.2	82.1	15.2	16.15
Yolov3	83.1	49.1	80.3	81.6	154.6	118.54
Yolov5	83.4	47.9	75.4	82.4	16.8	16.03
T-Model	85.4	49.6	76.3	80.3	15.8	13.75
S-Model	83.2	46.7	74.8	80.9	2.3	2.98
Distillation	85.9	50.3	77.4	83.1	2.3	2.98

The loss function and prediction correctness, recall, and accuracy data during the training of the distilled model are recorded as shown in Figure 12, which shows that the model converges very quickly.

Figure 12. Performance of a multidimensional knowledge distillation compression model, with the red portions representing accuracy, recall, and prediction rates; the higher they are, the better, and the green portions representing loss functions; the lower they are, the better.

The dataset was tested in this study, and the test results are presented through a visual display in Figure 13. An in-depth analysis of Table 5 and Table 6 and Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 reveals that the detection efficiency of the improved algorithm relative to the original algorithm has been significantly improved, with the number of its references reduced by 81.4%, from 16.03 MB to 2.98 MB, while the accuracy has been improved by 2.5%, from 83.4% to 85.9%; the prediction accuracy for various types of defects has also been significantly improved, and the matching between the detection frame and the target to be detected has also been significantly improved; at the same time, the algorithm proposed in this study can detect small targets that were missed or wrongly detected by the original algorithm. These improvements highlight the superiority and effectiveness of the proposed algorithm compared to existing algorithms.

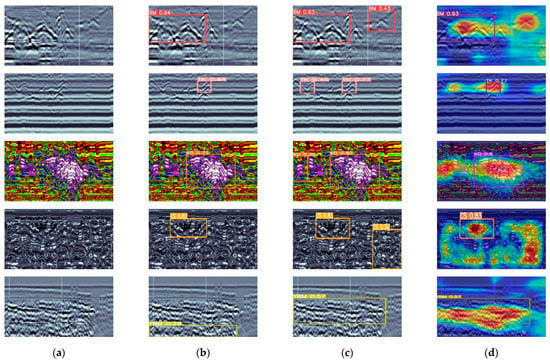
Figure 13. Detection result graphs where (a) is the original defect map, (b) is the original model detection result map, (c) is the improved multi-dimensional knowledge distillation model detection result map, and (d) is the result visualization map.

Figure 14 depicts the experimental findings from this study’s use of the publicly available VOC data set, which demonstrated that the improved model is In the VOC data set, the multi-location knowledge distillation model’s detection accuracy In the VOC data set, the multi-location knowledge distillation model’s detection accuracy increased by 3.6% from the original model’s 59.9% to 63.5%.

Figure 14. Performance results of the multidimensional knowledge distillation model and the Yolo model on the VOC dataset Where (a,c) are the original model detection results map and (b,d) are the multidimensional knowledge distillation results map.

6. Conclusions

In this study, we suggest a multidimensional knowledge distillation and detection approach. First, we increase the detection accuracy of the teacher model using pooling and weighting operations using a deep pooling residual structure; next, we introduce the MovileNetv3 lightweight backbone network into the student model; and finally, we learn how to extract feature information from the feature layer and the output layer in order to transfer the teacher model. The experimental results show that the improved model achieves 85.9% accuracy in tunnel defect detection, an improvement of 2.5%, and the model size is 2.98 MB, a volume compression of 83.2%, which meets the current demand for lightweight tunnel defect detection engineering. This accuracy improvement was achieved by testing the model on the radar detection dataset.

In order to further improve the detection efficiency and robustness of the algorithms, future work will explore how to combine transfer learning with knowledge distillation techniques to achieve simultaneous migration across domains and models, and combining these two techniques can effectively improve the generalization ability and robustness of the models while reducing the training time and computational cost; in terms of lightweight, we will continue to investigate how to combine pruning quantization techniques with knowledge distillation techniques to further reduce the number of parameters and computation of the model, such as quantization-aware training, weight clustering, etc.; in terms of accuracy, we will focus on designing more effective model structures to improve model performance and loss functions.