Enabling Efficient and Privacy-Preserving Task Allocation with Temporal Access Control for Mobile Crowdsensing

Abstract

The increasing proliferation of GPS-enabled mobile devices, including Unmanned Aerial Vehicles (UAVs), smartphones, and laptops, has resulted in a significant upsurge in the outsourcing of spatial data to cloud servers for storage and computation purposes, such as task allocation and location-based services. However, the reliance on untrusted cloud servers introduces the risk of privacy breaches, as these servers possess the ability to deduce and access users’ private information based on task content and query requirements. Existing privacy-preserving task-allocation schemes offer only coarse-grained and non-temporal access control, which restricts their applicability in scenarios involving multiple users and time-series data, such as trajectory and time-related routes. To overcome these challenges, this paper proposes an Efficient and Privacy-Preserving Task Allocation with Temporal Access Control (EPTA-T) scheme for mobile crowdsensing. By leveraging the techniques of Gray code and randomizable matrix multiplication, EPTA-T achieves efficient and privacy-preserving task allocation in mobile crowdsensing. Specifically, EPTA-T supports fine-grained and temporal access control through the utilization of an attribute-based access tree and function integration. The formal security analysis demonstrated that EPTA-T effectively guarantees data privacy and query privacy throughout the task allocation process. Extensive experiments conducted using a real-world dataset indicated that the EPTA-T scheme surpassed the performance of the state-of-the-art scheme.

1. Introduction

Recently, with the increasing proliferation of task allocation in mobile crowdsensing, it notably enhances the crowdsensing paradigm capability of helping requesters find workers to complete location-aware tasks. This enables requesters to specify task requirements that can be matched with workers based on their respective locations. However, in the mobile crowdsensing environment, the crowdsensing paradigm is inherently untrusted, creating the potential for the capture or inference of task information and workers’ locations [1,2]. A prevailing method is to encrypt the spatial data and task content before outsourcing to the crowdsensing paradigm [3], which alleviates the privacy concerns, but incurs limited query functionality and query performance. In addition, the presence of time-related spatial data necessitates the implementation of Temporal Access Control (TAC) in task allocation. For instance, in a Didi Chuxing-based task allocation scenario, if a driver is situated near a requester between the hours of 9:00 and 10:00, the requester can find the driver at any time within that time range, such as 9:30; otherwise, he/she cannot match the driver. Theoretically speaking, a worker’s spatial data can only be accessed at the current time $t_c$ if and only if $t_c$ falls within the worker’s time constraint interval $[t_1,t_2]$. Unfortunately, existing task-allocation schemes do not support temporal access control.

Challenge 1: How to design an Efficient and Privacy-Preserving Task Allocation (EPTA) scheme that supports Temporal Access Control (TAC). In mobile crowdsensing, workers’ spatial data are typically associated with time-series objects, while requesters’ attributes also contain timestamps. To achieve effective and accurate task allocation, TAC needs to be considered and integrated into the mobile crowdsensing system. However, directly combining existing EPTA schemes [1,2,4] with TAC schemes [5,6] may result in privacy breaches and an excessive burden of key management. EPTA and TAC are performed separately. To this end, the cloud server knows which worker meets the task requirements regardless of whether he/she can be accessed, which reveals the worker’s timestamp and the worker’s location. Moreover, the crowdsensing paradigm can deduce which workers satisfy the task requirements by observing the accessed spatial data, thereby leaking the access pattern. Unfortunately, access pattern leakage can lead to significant privacy issues, such as the disclosure of home addresses, preferences, and behaviors. Additionally, existing approaches have employed attribute-based encryption to enable fine-grained data sharing with access control [7]. However, this introduces computational overhead in terms of data encryption and task allocation. To improve search performance, some symmetric-encryption-based task-allocation schemes [1,8] have been designed. Nevertheless, in multi-user task allocation models, clients are required to share the same secret key, which may lead to key privacy leakage and key management concerns.

Challenge 2: How to provide an arbitrary geometric range query while achieving a fast search. In task allocation, requesters often submit irregular geometric query ranges to find suitable workers located within specific areas for task assignments. However, existing schemes [9,10] only support single or limited geometric ranges, such as circular, rectangular, or triangular ranges. While homomorphic encryption offers a viable approach for secure geometric range queries [11], the computational overhead associated with it is often unacceptable in practical scenarios. To achieve a fast search, Searchable Symmetric Encryption (SSE) [12,13,14] is commonly employed to enable secure and efficient retrieval of ciphertexts. Unfortunately, SSE fails to support complex query functions such as geometric range queries and lacks flexible key management for multi-user task allocation scenarios. In particular, some works have explored schemes for k-Nearest Neighbor (kNN) queries [15] and skyline queries [16] with privacy guarantees. However, these schemes cannot be directly applied to geometric range queries.

In this paper, we aimed to address the above challenging issues. Specifically, we propose an Efficient and Privacy-Preserving Task Allocation with Temporal Access Control (EPTA-T) scheme for mobile crowdsensing, which efficiently allocates tasks while preserving privacy and incorporating temporal access control. EPTA-T is specifically designed to address the limitations of existing schemes in supporting both task allocation and temporal access control. The main contributions are summarized as follows:

• We utilized Gray code to encode spatial data into vectors. These encoded vectors were then encrypted using randomizable matrix multiplication, enabling us to achieve efficient and privacy-preserving task allocation. This approach significantly reduced the computational overhead associated with data encryption and task allocation, while eliminating the need for key sharing among users.
• To support temporal access control, we leveraged the techniques of function differentiation and function integration. By incorporating these techniques into ciphertext-policy Attribute-Based Encryption (ABE), we constructed an access-tree-based policy. This policy enables precise control over temporal access to the encrypted data. Additionally, the secret involved in the data encryption is treated as the secret of the access policy, ensuring access pattern privacy protection.
• Formal security analysis proves that EPTA-T ensures the confidentiality of data and queries under an Indistinguishability under Selective Chosen-Plaintext Attacks (IND-SCPA) model. The experimental results over a real-world dataset indicated that the running time of EPTA-T outperformed the state-of-the-art scheme in terms of index encryption, trapdoor generation, and task allocation.

The remainder of this paper is organized as follows. Section 2 presents an overview of related works on privacy-preserving task-allocation schemes. In Section 3, we outline the system model, threat model, design goals, and problem definition of EPTA-T. In Section 4, we provide the necessary background knowledge. Then, in Section 5, we present the detailed construction and technical aspects of the proposed scheme. In Section 6, we prove the security of the proposed scheme. In Section 7, we evaluate and analyze the performance of EPTA-T via experiments. Finally, we conclude our work in Section 8.

2. Related Work

In this section, we mainly focus on the related works on secure task allocation for mobile crowdsensing, including privacy-preserving task allocation and privacy-preserving range query.

2.1. Privacy-Preserving Task Allocation

Currently, privacy-preserving task allocation has received great attention in academia and industry [1,2,4,17,18]. To address the problem of privacy preservation in task allocation, Song et al. [1] proposed an efficient and privacy-preserving task-recommendation scheme by utilizing predicate encryption and randomizable matrix multiplication. Different from randomizable-matrix-based task allocation, Wang et al. [18] utilized a planar Laplace distribution to perturb tasks and workers’ locations to protect their location privacy. However, using perturbed locations for task allocation can lead to a decrease in the effectiveness of the task assignments. Thus, Xia et al. [19] presented a probabilistic method to quantify the accessibility between workers and requesters and reduced the effect of the perturbed location on task allocation. To achieve task privacy protection, Zhou et al. [20] designed a tree-based privacy-preserving task-allocation system that addresses the task-allocation problem based on the combinatorial multi-armed slot machine problem. To the balance of user privacy and the usability of task allocation, Wang et al. [18] employed differential privacy to protect location privacy and proposed a multi-task assignment scheme for perturbing the available location information. Xu et al. [21] proposed a privacy-preserving task-allocation scheme using inner-product-based encryption to protect the privacy of task information and workers’ locations. However, the schemes in [18,19,20,21] do not support temporal access control, i.e., deciding whether the requesters’ temporal attributes satisfy a designed time-based access policy.

In summary, how to design an efficient and privacy-preserving task-allocation scheme that supports temporal access control is a crucial issue that needs to be addressed in mobile crowdsensing.

2.2. Privacy-Preserving Range Query

Searchable Symmetric Encryption (SSE) [12,13,14,22,23,24] is an effective cryptographic method for secure range query. Based on SSE, Li et al. [25] proposed a tree-aid indistinguishable index structure, which can only support one-dimensional range query. To achieve multi-dimensional range query, several works [1,8] employed an asymmetric scalar-product-preserving encryption approach. For strong security in range query, homomorphic encryption [11,15,26,27,28,29] is applied to realize the direct operations over ciphertext, but the computational cost is heavy and unacceptable. Furthermore, Several schemes have explored the limitations and weaknesses of SSE, which significantly balances security and efficiency effectively. Moreover, Wang et al. [9,10] proposed SSE-based schemes for geometric range query, but these schemes have some limitations such as a single geometric query type, inefficient search performance, and a low-dimensional space. To address these issues, Wang et al. [30] proposed a DSSE-based spatial keyword query scheme for dynamic updates. It is worth noting that the above schemes failed to support accurate and efficient geometric range query and temporal access control.

In a word, how to design an efficient and privacy-preserving geometric range query scheme that achieves an arbitrary geometric range query with a fast search is a significant problem that needs to be solved in the spatial data query.

Compared with the existing works, our proposed EPTA-T has three strong aspects: (1) our EPTA-T scheme achieves efficient and privacy-preserving task allocation with temporal access control in mobile crowdsensing; (2) our EPTA-T scheme supports an efficient and privacy-preserving geometric range query with a fast search in a multi-user setting; (3) our EPTA-T scheme guarantees the confidentiality of the data and queries under the IND-SCPA model.

3. Problem Formulation

In this section, we introduce the system model, threat model, design goals, and problem definition of EPTA-T.

3.1. System Model

As shown in Figure 1, the architecture of our mobile crowdsensing system consists of four entities, i.e., a trusted authority ($\mathcal{TA}$), a service provider ($\mathcal{SP}$), multiple workers ($\mathcal{W}$s), and multiple data requesters ($\mathcal{DR}$s).

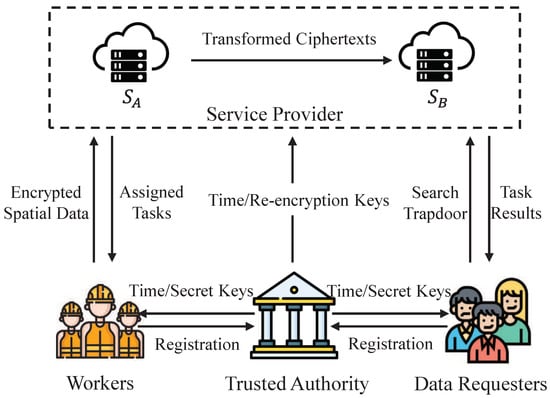
Figure 1. System model.

• Trusted Authority ($\mathcal{TA}$): The $\mathcal{TA}$ is responsible for initializing the system and distributing the secret keys. Initially, the $\mathcal{TA}$ sets up the system to provide registration services for both workers and data requesters and generates encryption keys and re-encryption keys for participating entities.
• Service Provider ($\mathcal{SP}$): The $\mathcal{SP}$ is a crowdsourcing service provider that receives and stores the task content from data requesters. Additionally, the $\mathcal{SP}$ allocates the task requirements to suitable workers. In this model, two non-colluding cloud servers $S_A$ and $S_B$ are introduced to serve as the service provider.
• Workers ($\mathcal{W}s$): Workers encrypt their locations and send the ciphertexts to the service provider. Based on the locations of the workers, the $\mathcal{SP}$ allocates the task requirements to the proper workers. After that, the workers accomplish the task and return the task results to the service provider.
• Data Requesters ($\mathcal{DR}s$): Before publishing the tasks, data requesters encrypt their task requirements. To find suitable workers who satisfy the query constraints, the $\mathcal{DR}s$ generate search trapdoors for their task requirements and submit the search trapdoors along with the encrypted task content to the $\mathcal{SP}$.

In our task allocation model, the $\mathcal{W}$ encrypts his/her spatial data according to the designated access policies, constructs encrypted indexes for task allocation, and transmits both the encrypted spatial data and indexes to the $\mathcal{SP}$. Prior to the $\mathcal{DR}$ releasing a task to the $\mathcal{SP}$, the $\mathcal{DR}$ generates a search trapdoor based on the task requirements and submits it to the $\mathcal{SP}$. Upon receiving the search trapdoor from the $\mathcal{DR}$, the $\mathcal{SP}$ initially converts the $\mathcal{DR}$’s privileged time trapdoor into the trapdoor associated with the current time $t_c$, but only if the $t_c$ falls within the $\mathcal{DR}$’s privileged time range. Subsequently, the $\mathcal{SP}$ employs EPTA and TAC for task allocation, concurrently verifying whether the $\mathcal{DR}$’s attributes satisfy the access policy and if the search trapdoor corresponds to the appropriate worker index. If these conditions are met, the $\mathcal{SP}$ dispatches the task requirements to the suitable worker. Following the reception of the task results from the selected worker, the $\mathcal{SP}$ returns the results to the $\mathcal{DR}$.

3.2. Threat Model

In our task recommendation, the $\mathcal{TA}$ is fully trusted in the system, and all communications between the $\mathcal{TA}$ and other entities are secure. The $\mathcal{W}$ and $\mathcal{DR}$ are considered to be fully trusted, which means they keep their private keys secret. They would not leak or sell their keys to the $\mathcal{SP}$ for profits. The $\mathcal{SP}$ is considered as semi-honest (i.e., honest-but-curious), which means the $\mathcal{SP}$ will honestly perform the designed protocols to provide the task recommendation services, but the $\mathcal{SP}$ may try to derive private information from encrypted locations and search trapdoors. Based on the information that $\mathcal{SP}$ may derive, we considered the following two attacks:

• Ciphertext-only attack: The $\mathcal{SP}$ observes a number of ciphertexts including encrypted locations, encrypted tasks, and search trapdoors, but the $\mathcal{SP}$ cannot obtain their corresponding plaintexts.
• Chosen-plaintext attack: Except knowing the encrypted locations and trapdoors, the $\mathcal{SP}$ can oracle access the task recommendation protocols to obtain some plaintext–ciphertext pairs.

Generally, we assumed that there is no collusion between two cloud servers. This assumption is reasonable, as cloud servers are expected to maintain their reputations and protect their own interests [8]. It is worth noting that the no-collusion assumption has been widely adopted in numerous research works within the security community, particularly in the context of the two-server model [8,15,31].

3.3. Design Goals

The design goals of EPTA-T are summarized as follows:

• Privacy protection: The privacy of workers and data requesters should be protected in our EPTA-T scheme. It is not difficult to see that, in task allocation applications that involve more sensitive user data such as workers’ locations, requesters’ queries, and task results, revealing these data can easily violate user privacy.
• Temporal access control: The EPTA-T scheme should achieve temporal access control for the time-series data (e.g., trajectory data, validity period, and hours of services) in task allocation.
• Efficiency: The computational overhead and communication overhead on the worker and publisher side should be minimized, since the mobile devices are resource-limited. The proposed EPTA-T scheme should achieve efficient data encryption and task allocation.

3.4. Problem Definition

In this paper, our objective was to achieve Efficient and Privacy-Preserving Task Allocation (EPTA) with Temporal Access Control (TAC) for handling massive spatial data comprising temporal and non-temporal attributes. Each spatial datum $L_i$ is encoded as spatial point ${\mathsf{p}}_i$ with a private identity of the worker $i{d}_{\varrho }$. The worker’s identity $i{d}_{\varrho }$ is encrypted using a secret key s under an access policy $\mathcal{T}\varrho$, which encompasses both temporal and non-temporal access attributes. Specifically, the spatial data can only be accessed within the valid time period defined by $at[t_1,t_2]\in \mathcal{T}\varrho$. Let IndexEnc be the index encryption algorithm executed by $\mathcal{W}$. Based on the IndexEnc algorithm, each spatial datum $L_i$ is encrypted as $\widehat{C_{I_i}}$ by using the $\mathcal{W}$’s secret key $s{k}_i$, i.e., $\mathsf{IndexEnc}(L_i,s{k}_i)\to \widehat{C_{I_i}}$. Let $\mathsf{IndexTran}$ be the index transformation algorithm executed by the $\mathcal{SP}$. In the IndexTran algorithm, the $\mathcal{SP}$ utilizes the corresponding re-encryption keys $R{K}_A$ and $R{K}_B$ to transform the encrypted ciphertext, i.e., $\mathsf{IndexTran}(\widehat{C_{I_i}},R{K}_A,R{K}_B)\to C_{I_i}$. Let TrapGen be the trapdoor-generation algorithm executed by $\mathcal{DR}$. When the $\mathcal{DR}$ with an attribute set $S=\{a{t}_1,a{t}_2,\cdots ,a{t}_i[t_1^{\prime },t_2^{\prime }],\cdots ,a{t}_{\left|S\right|}\}$ submits a geometric range $R_q$ of task requirements to the $\mathcal{SP}$ at the current time $t_c$, the search trapdoor $\widehat{T_Q}$ is generated for the geometric range by using the $\mathcal{DR}$’s secret key $s{k}_q$, i.e., $\mathsf{TrapGen}(R_q,s{k}_q)\to \widehat{T_Q}$. When the $\mathcal{SP}$ receives the search trapdoor $\widehat{T_Q}$ from the $\mathcal{DR}$, using the $\mathsf{TrapTran}$ algorithm, the $\mathcal{SP}$ transforms the $\mathcal{DR}$’s privileged time trapdoor into the search trapdoor linked to the current time $t_c$ when the $t_c$ falls within the privileged time range of $\mathcal{DR}$, i.e., $\mathsf{TrapTran}(\widehat{T_Q},R{K}_A,R{K}_B)\to T_Q$. Upon receiving the transformed trapdoor $T_Q$, the $\mathcal{SP}$ performs the task allocation to search the proper workers who satisfy the access policy ${\mathcal{T}}_{\varrho }(S,t_c)=1$ and the geometric range query condition simultaneously. Here, ${\mathcal{T}}_{\varrho }(S,t_c)=1$ means the current time $t_c$ belongs to a valid time period of access policy and the access attribute set, and the $\mathcal{DR}$’s attributes satisfy the designed access policy ${\mathcal{T}}_{\varrho }$, i.e., $(t_c\in [t_1,t_2]\cap [t_1^{\prime },t_2^{\prime }])\bigwedge ({\mathcal{T}}_{\varrho }\left(S\right)=1)$. Let $\mathsf{TAC}(·)$ be the temporal access control function; we have

$$\mathsf{TAC}({\mathcal{T}}_{\varrho },S,t_c)=\left\{\begin{array}{c}\left[\left[s\right]\right],if{\mathcal{T}}_{\varrho }(S,t_c)=1;\hfill \\ 0,otherwise,\hfill \end{array}\right.$$

(1)

where $\left[\right[s\left]\right]$ denotes the encrypted secret. Let $\mathsf{EPTA}(·)$ be the efficient and privacy-preserving task allocation primitive function; we have

$$\mathsf{EPTA}(C_{I_i},T_Q,t_c,\left[\left[s\right]\right])=\left\{\begin{array}{c}1,iftr\left(C_{I_i}{T}_Q\right)=0;\hfill \\ 0,otherwise.\hfill \end{array}\right.$$

(2)

Based on the above problem statement, we give the definition of EPTA-T as follows.

Definition 1

(EPTA-T). For a worker with the spatial data $L_i$ encrypted under the access policy $\mathcal{T}\varrho$, the worker is considered as an accessible and suitable one for a $\mathcal{DR}$ who possesses an attribute set S and submits a geometric range $R_q$ of task requirements at the current time $t_c$, if and only if both conditions $\mathsf{TAC}(\mathcal{T}\varrho ,S,t_c)=\left[\left[s\right]\right]$ and $\mathsf{EPTA}(C_{I_i},T_Q,t_c,\left[\left[s\right]\right])=1$ are met.

4. Preliminaries

In this section, we review some building blocks that are used in our proposed scheme, including Gray code [6], the access tree [22], and polynomial functions [4].

4.1. Gray Code

The process of converting a binary number $d_1{d}_2\cdots d_n$ into its corresponding binary reflected Gray code involves iterating from right to left. Starting with the rightmost digit $d_n$, if the preceding digit $d_{n-1}$ is 1, we replace $d_n$ with $1-d_{n-1}$. If $d_{n-1}$ is 0, we leave $d_n$ unchanged. We then proceed to the next digit $d_{n-1}$ and repeat the process until we reach the first digit $d_1$, which remains the same as $d_0$ was assumed to be 0. The resulting sequence $g_1{g}_2\cdots g_n$ represents the binary reflected Gray code. To convert a binary reflected Gray code $g_1{g}_2\cdots g_n$ back to a binary number, we start with the n-th digit and compute the equation as follows:

$${\Sigma }_n=\sum _{i=1}^{n-1}{g}_i\left(mod2\right).$$

(3)

If ${\Sigma }_n=1$, replace $g_n$ by $1-g_n$; otherwise, leave it unchanged. Next, we compute

$${\Sigma }_{n-1}=\sum _{i=1}^{n-2}{g}_i\left(mod2\right).$$

(4)

By applying the above calculation, we obtain that the binary number $d_1{d}_2\cdots d_n$ corresponds to the initial binary reflected Gray code.

Therefore, the Gray code for $d+1$ bits can be represented as

$$G_{d+1}=\left(0\right||g_1,\cdots ,0\left|\right|g_{2^d},1\left|\right|g_{2^d},\cdots ,1\left|\right|g_1),$$

where || denotes the concatenation operator. For example, $G_1=(0,1)$, $G_2=(00,01,11,10)$. When using Gray code to encode a $d\times d$ grid, the length of each binary code representing a cell is $2·2^{\lceil {log}_{2}d\rceil }$.

4.2. Access Tree

Consider a tree $\mathcal{T}$ that represents an access policy. In this tree, each non-leaf node represents a threshold gate. The node is defined by its children and a threshold value. The threshold value $k_x$ of a node x is such that $0<k_x\le {\mathrm{num}}_x$, where ${\mathrm{num}}_x$ represents the number of children of node x. On the other hand, each leaf node x in $\mathcal{T}$ represents an attribute $a{t}_x$, where the threshold value $k_x$ is set to 1.

Let ${\mathcal{T}}_x$ denote the subtree of $\mathcal{T}$ rooted at node x. If x is a non-leaf node, ${\mathcal{T}}_x\left(S\right)=1$ if and only if it contains at least $k_x$ children $x_{i}i\in [1,k_x]$ for which ${\mathcal{T}}_{x_i}\left(S\right)=1$. In other words, ${\mathcal{T}}_x\left(S\right)$ is true if there are enough child nodes satisfying ${\mathcal{T}}_{x_i}\left(S\right)=1$ according to the threshold value $k_x$.

If x is a leaf node, ${\mathcal{T}}_x\left(S\right)=1$ if and only if the attribute $a{t}_x$ is present in the attribute set S. In other words, ${\mathcal{T}}_x\left(S\right)$ is true if the attribute $a{t}_x$ is a member of S.

4.3. Polynomial Function

The polynomial function relates the coefficients of a polynomial to the sums and products of its roots. Let $f\left(x\right)$ be a polynomial function of degree n, i.e., $f\left(x\right)=a_n{x}^n+\cdots +a_{1}x+a_0$, where the coefficient of $x^i$ is $a_i$, and $a_n\ne 0$. Based on the property of the polynomial function, we have

$$f\left(x\right)=a_n{x}^n+\cdots +a_{1}x+a_0=a_n(x-x_n)\cdots (x-x_1),$$

where $x_1,\cdots ,x_n$ are the roots of $f\left(x\right)$. According to the construction of the polynomial function $f\left(x\right)$, we can calculate any subproducts of the roots. For any $i\in [0,n]$, the $(n-i)$-th coefficient $a_{n-i}$ is associated with a signed sum of all possible subproducts of the roots, as shown in Equation (5).

$$\sum _{1\le k_1\le \cdots \le k_i\le n}{x}_{k_1}{x}_{k_2}\cdots x_{k_i}={(-1)}^i\frac{a_{n-i}}{a_n}.$$

(5)

5. The Proposed Scheme

In this section, we first introduce the overview of EPTA-T. After that, we give the detailed construction of EPTA-T. In our EPTA-T, it mainly consists of seven algorithms: System Setup (SystSetup), Key Generation (KeyGen), Index Encryption (IndexEnc), Index Transformation (IndexTran), Trapdoor Generation (TrapGen), Trapdoor Transformation (TrapTran), and task allocation (Query). Finally, we analyzed the correctness of EPTA-T.

5.1. Overview

Since EPTA-T supports secure task allocation in multi-worker multi-requester settings without key sharing, the main idea of EPTA-T is to encode and encrypt the index of the spatial data and the search trapdoor of the task requirement into a matrix-trace-based matching operation, such that TAC can be implemented by the same encryption mechanism without involving additional computational overhead.

Transforming the geometric-range-based task allocation into the inner-product-based matching operation. To enable task allocation based on the geometric ranges of the task requirements, the space is divided into uniform cells with dimensions $L\times L$. The task allocation conditions, specifying the spatial data of workers located within the geometric range defined by the data requester, are encoded using Gray code, where 0 and 1 are represented by two positive integers, X and Y, respectively. Each spatial datum $L_i$ is encoded as spatial point ${\mathsf{p}}_i$ by using Gray code and further expanded into a spatial vector $\overrightarrow{{\mathsf{p}}_i}$ by padding it with additional entries, including $-1$. The geometric query range $R_q$ is encoded as the aggregated query code ${\mathsf{q}}_i$, which represents the combination of the codes for the cells encompassed by the geometric range $R_q$. Subsequently, the aggregated range query vector $\overrightarrow{{\mathsf{q}}_i}$ is generated by padding the query code with additional entries, including the sum of the squares of the code values. Specifically, the aggregated query code is generated by replacing the different entries with 0 to reduce the scale of codes in the query range. Consequently, if the inner product between the spatial vector $\overrightarrow{{\mathsf{p}}_i}$ and the query vector $\overrightarrow{{\mathsf{q}}_i}$ is 0 (i.e., $\overrightarrow{{\mathsf{p}}_i}\circ \overrightarrow{{\mathsf{q}}_i}=0$), this indicates that the spatial data $L_i$ of the worker are located within the geometric query range $R_q$. Otherwise, if the inner product is non-zero, this signifies that the spatial data are located outside the query range.

As shown in Figure 2, we give an example of the encoding procedure and geometric range query. In Figure 2, the spatial space is uniformly split into $4\times 4$ cells. The spatial point ${\mathsf{p}}_i$ is encoded as $g_{{\mathsf{p}}_i}=YYXX$ and further extended as spatial vector $\overrightarrow{{\mathsf{p}}_i}=(Y,Y,X,X,-1)$. In addition, the geometric query range (green domain) is encoded as $g_{{\mathsf{q}}_1}=XYXX\vee XYXY\vee YYXX\vee YYXY=0YX0$ and $g_{{\mathsf{q}}_2}=YYYY$. After that, the corresponding query vectors are further extended as $\overrightarrow{{\mathsf{q}}_1}=(0,Y,X,0,Y^2+X^2)$ and $\overrightarrow{{\mathsf{q}}_2}=(Y,Y,Y,Y,4Y^2)$, respectively. Therefore, the inner product between $\overrightarrow{{\mathsf{p}}_i}$ and $\overrightarrow{{\mathsf{q}}_1}$ is 0, which means that the spatial point ${\mathsf{p}}_i$ is located in the geometric query range $R_{{\mathsf{q}}_1}$.

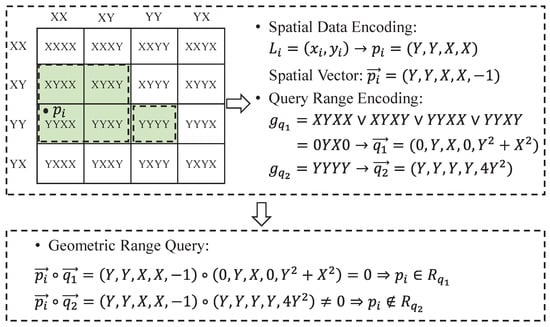
Figure 2. An Encoding Example of Spatial Data and Query Range and Geometric Range Query.

Secure matrix-trace-based task allocation mechanism. In EPTA-T, we encrypt the spatial data $L_i$ as $\widehat{C_{I_i}}$ and transform them as $C_{I_i}$ by calling IndexEnc and IndexTran, respectively. In addition, we encrypt the geometric query range $R_q$ of task allocation as $\widehat{T_Q}$ and transform it as $T_Q$ by calling TrapGen and TrapTran, respectively. After that, we call the Query protocol to calculate the matrix trace (i.e., $tr\left(C_{I_i}{T}_Q\right)$) to retrieve proper workers for task allocation. If the worker ${\mathcal{W}}_i$ is the proper one, his/her spatial data are located in the geometric range of the task requirement, i.e., $L_i\in R_q$, then $tr\left(C_{I_i}{T}_Q\right)=0$.

Secure temporal access control. To achieve EPTA with TAC, the key idea is to perturb the search results of EPTA with the access policy by employing a secret used in IndexEnc as the secret of the access policy to encrypt the corresponding spatial data. To this end, privacy-preserving task allocation is correctly performed only when the spatial data are accessible.

To achieve temporal access control, we add time validity to a secret associated with the spatial data and correlate the encrypted secret with an access time period. Only when a data requester has attributes that satisfy the defined access policy and a secret that corresponds to the accessible time period can the data requester access the spatial data.

For TAC, we constructed a hierarchical temporal access tree $\mathcal{T}$ and utilized its leaf nodes to denote different time attributes $at[t_1,t_2]$. In addition, when the $\mathcal{DR}$ can access the spatial data, the $\mathcal{DR}$’s privileged time period $at[t_1^{\prime },t_2^{\prime }]\in S$ should be satisfied. If the current time $t_c$ satisfies $t_c\in [t_1,t_2]\cap [t_1^{\prime },t_2^{\prime }]$, we utilize the polynomial function property to transform the time-related derivation function $f\left(t\right)$ associated with $[t_1,t_2]$ and $[t_1^{\prime },t_2^{\prime }]$ into the original function $F\left(t\right)$ related to $t_c$. If $a{t}_x\in S$, we calculate the original function $F_x\left(t\right)$ as shown in Equation (6).

$$F_x{\left(t\right)|}_{t=t_c}=a{\int }_{t_1}^{t_2}{\int }_{t_1^{\prime }}^{t_2^{\prime }}{f}_x\left(t\right)dtd{t}^{\prime }=e{(g_p,H)}^{a{y}_x\left(0\right)},$$

(6)

where a represents a unique entry used to differentiate between different data requesters ($\mathcal{DR}$) selected by the $\mathcal{TA}$, x is a leaf node of the hierarchical temporal access tree, and $y_x\left(0\right)$ is the secret share of s for the leaf node x. The entry s is regarded as the secret of the hierarchical temporal access tree $\mathcal{T}$’s root node, which is used to encrypt the private identity of the worker $i{d}_i$. When the $\mathcal{DR}$’s attributes satisfy the defined access policy at the current time $t_c$, we have $F_{root}=e{(g_p,H)}^{as}$.

In our EPTA-T, $\mathcal{SP}$ should first execute TAC by checking whether the $\mathcal{DR}$’s attributes satisfy the defined access policy tree $\mathcal{T}$ at the current time $t_c$. If the $\mathcal{SP}$ calculates that $F_{root}=e{(g_p,H)}^{as}$ holds, this indicates that the $\mathcal{DR}$ can access the spatial data. After that, the $\mathcal{SP}$ performs EPTA to calculate $tr\left(C_{I_i}{T}_Q\right)$. If $tr\left(C_{I_i}{T}_Q\right)=0$ holds, the accessible spatial data satisfy the geometric query range, and the $\mathcal{SP}$ selects the worker identity $i{d}_{\varrho }$ as the proper worker and sends the task to this target one.

Remark 1.

To the best of our knowledge, EPTA-T is the first work to support fine-grained and temporal access control in privacy-preserving task allocation, which achieves efficient geometric range query and IND-SCPA security in the multi-worker multi-requester setting without key sharing.

5.2. The Detailed Construction of EPTA-T

Based on the above overview, we describe the detailed construction of EPTA-T:

(1)

SystSetup $\left(1^{\lambda }\right)\to (pp,msk)$. Given a security parameter $\lambda$, the $\mathcal{TA}$ generates the master key $msk$, which consists of two $(n+1)\times (n+1)$ random invertible matrices $\{M_1,M_2\}$, a hash function $h:{\{0,1\}}^{*}\to {\mathbb{Z}}_p^{*}$, which hashes any spatial vector and query vector to positive values in ${\mathbb{Z}}_p^{*}$ and converts the attribute string to a group element, respectively, a random symmetric key K, and a random permutation $\pi :{\mathbb{Z}}_p^{n+1}\to {\mathbb{Z}}_p^{n+1}$. In addition, $\mathcal{TA}$ generates a composite order bilinear system $\mathbb{S}=(\mathbb{G},{\mathbb{G}}_T,e)$ of order $n=p\times r$ and generators $g_p\in {\mathbb{G}}_p$, $g_r\in {\mathbb{G}}_r$. Additionally, the $\mathcal{TA}$ randomly selects an entry $\theta \in {\mathbb{Z}}_p$ and calculates $H=g_p^{\theta }{g}_r^{\theta }$. Namely, the masker secret key can be denoted as $msk=\{M_1,M_2,\pi ,h\}$, and the public parameters are generated as $pp=\{\mathbb{S},g_p,g_r,h,H\}$.

(2)

KeyGen $(msk,{\mathcal{W}}_i,{\mathcal{DR}}_q)\to (s{k}_i,s{k}_q,R{K}_A,R{K}_B)$. For a worker ${\mathcal{W}}_i$, the $\mathcal{TA}$ first chooses two random $(n+1)\times (n+1)$ matrices $\{M_{i,1},M_{i,2}\}$. Then, $\mathcal{TA}$ computes $M_{i,1}^{\prime }=M_1{M}_{i,1}^{-1}$ and $M_{i,2}^{\prime }=M_1{M}_{i,2}^{-1}$. For a data requester ${\mathcal{DR}}_q$, the $\mathcal{TA}$ randomly selects two $(n+1)\times (n+1)$ $\{M_{q,1},M_{q,2}\}$, and then, the $\mathcal{TA}$ computes $M_{q,1}^{\prime }=M_{q,1}^{-1}{M}_1^{-1}$ and $M_{q,2}^{\prime }=M_2^{-1}{M}_{q,2}^{-1}$. Finally, the $\mathcal{TA}$ sends the secret key $s{k}_i=\{M_{i,1},M_{i,2},\pi ,h\}$ to the worker ${\mathcal{W}}_i$ and the secret key $s{k}_q=\{M_{q,1},M_{q,2},\pi ,h,K\}$ to the data requester ${\mathcal{DR}}_q$, and the $\mathcal{TA}$ distributes the re-encryption key $R{K}_A=\{M_{i,1}^{\prime },M_{q,2}^{\prime }\}$ to $S_A$ and the re-encryption key $R{K}_B=\{M_{i,2}^{\prime },M_{q,1}^{\prime }\}$ to $S_B$. To distinguish different $\mathcal{DR}$s, the $\mathcal{TA}$ chooses a unique element $a\in {\mathbb{Z}}_p$ for a certain $\mathcal{DR}$’s attribute set S.

(3)

IndexEnc $(L_i,s{k}_i)\to \widehat{C_{I_i}}$. Given a worker ${\mathcal{W}}_i$’s spatial data $L_i=(x_i,y_i)$, ${\mathcal{W}}_i$ encrypts his/her spatial data and outsources it to $\mathcal{SP}$ as follows:

Step 1: Firstly, the ${\mathcal{W}}_i$ encodes the spatial data $L_i$ as a spatial vector $\overrightarrow{{\mathsf{p}}_i}=(b_1,b_2,\cdots ,b_d)\leftarrow Gray\left(L_i\right)$, where $b_i(i\in [1,d-1])$ is a value of X or Y, and $b_d=-1$.

Step 2: For the spatial vector $\overrightarrow{{\mathsf{p}}_i}=(b_1,b_2,\cdots ,b_d)$, the ${\mathcal{W}}_i$ transforms $\overrightarrow{{\mathsf{p}}_i}$ to a positive integer $v_i={\sum }_{l=1}^d{b}_l·2^{d-l}$. After that, the workers have a collection of integers, i.e., $\{v_1,v_2,\cdots ,v_m\}$, where m denotes the number of workers in the mobile crowdsensing system.

Step 3: To protect the privacy of the transformative integer $v_i$, the ${\mathcal{W}}_i$ maps the integer with the one-way hash function h and obtains the hash value $h\left(v_i\right)$. Then, the ${\mathcal{W}}_i$ calculates different powers for the hash value $h\left(v_i\right)$ to generate an $(n+1)$-dimensional vector $I_i=(h{\left(v_i\right)}^0,h{\left(v_i\right)}^1,\cdots ,h{\left(v_i\right)}^n)$.

Step 4: Next, the ${\mathcal{W}}_i$ generates a one-time random positive number $\alpha$ and embeds it into the vector $I_i$. That is, the ${\mathcal{W}}_i$ obtains the random vector $\overline{I_i}=(\alpha h{\left(v_i\right)}^0,\alpha h{\left(v_i\right)}^1,\cdots ,\alpha h{\left(v_i\right)}^n)$.

Step 5: After that, the ${\mathcal{W}}_i$ permutes the random vector $\overline{I_i}$ to another vector $\widehat{I_i}$ by using the permutation $\pi$, i.e., $\widehat{I_i}=\pi \left(\overline{I_i}\right)$. Then, the ${\mathcal{W}}_i$ transforms the permuted vector $\widehat{I_i}$ to a corresponding diagonal matrix $\widehat{D_{I_i}}$ with the diagonal being $\widehat{I_i}$.

Step 6: Finally, the ${\mathcal{W}}_i$ generates a random $(n+1)\times (n+1)$ upper triangular matrix ${\mathcal{U}}_i$, where the main diagonal entries are 1, and the remainder of the non-zero entries are one-time random values. Then, the ${\mathcal{W}}_i$ uses his/her secret key $s{k}_i$ to encrypt $\widehat{D_{I_i}}$ as shown in Equation (7). After this operation, the ${\mathcal{W}}_i$ sends the encrypted location $\widehat{C_{I_i}}$ to $S_A$.

$$\widehat{C_{I_i}}=M_{i,1}{\mathcal{U}}_i\widehat{D_{I_i}}{M}_{i,2}$$

(7)

Specifically, to protect identity privacy, the worker ${\mathcal{W}}_i$ encrypts the identity $i{d}_{\varrho }$ as ${\mathsf{c}}_{\varrho }$ via the standard encryption algorithm (e.g., AES) and encrypts the hierarchical temporal access tree as follows:

• Firstly, the worker ${\mathcal{W}}_i$ selects the entry s as the secret of the root node of the hierarchical temporal access tree ${\mathcal{T}}_{\varrho }$.
• Then, the worker ${\mathcal{W}}_i$ calculates the secret shares of s for each leaf node x as $y_x\left(0\right)$.
• Finally, for each leaf node x, if x is represented as a temporal attribute $a{t}_x[t_1,t_2]$, the ${\mathcal{W}}_i$ splits $y_x\left(0\right)$ into $y_x{\left(0\right)}^{\prime },y_x{\left(0\right)}^{″}$, which should guarantee that $y_x\left(0\right)=y_x{\left(0\right)}^{\prime }+y_x{\left(0\right)}^{″}$ holds. Thus, ${\mathcal{W}}_i$ encrypts the leaf node x as $C_x=(H^{y_x{\left(0\right)}^{\prime }},h{\left(a{t}_x\right)}^{y_x{\left(0\right)}^{\prime }},H^{y_x{\left(0\right)}^{″}},$ $h{\left(a{t}_x\right)}^{y_x{\left(0\right)}^{″}})$; otherwise, ${\mathcal{W}}_i$ encrypts it as $C_x=(g_p^{y_x\left(0\right)},h{\left(a{t}_x\right)}^{y_x\left(0\right)})$.

To achieve secure task allocation, ${\mathcal{W}}_i$ outsources the ciphertexts $(c_{\varrho },\widehat{C_{I_i}},C_x)$ to $S_A$.

(4)

IndexTran $(c_{\varrho },\widehat{C_{I_i}},C_x,R{K}_A,R{K}_B)\to C_{I_i}$. Upon receiving the encrypted index $\widehat{C_{I_i}}$, $S_A$ uses the corresponding re-encryption key $M_{i,1}^{\prime }$ to re-encrypt $\widehat{C_{I_i}}$ as shown in Equation (8).

$$\begin{array}{cc}\hfill \widetilde{C_{I_i}}& =M_{i,1}^{\prime }\widehat{C_{I_i}}\hfill \\ \hfill & =M_{i,1}^{\prime }{M}_{i,1}{\mathcal{U}}_i\widehat{D_{I_i}}{M}_{i,2}\hfill \\ \hfill & =M_1{\mathcal{U}}_i\widehat{D_{I_i}}{M}_{i,2}.\hfill \end{array}$$

(8)

Then, $S_A$ sends $\widetilde{C_{I_i}}$ to $S_B$. After receiving converted ciphertext $\widetilde{C_{I_i}}$, $S_B$ re-encrypts it with the re-encryption key $M_{i,2}^{\prime }$ as shown in Equation (9).

$$\begin{array}{cc}\hfill C_{I_i}& =\widetilde{C_{I_i}}{M}_{I,2}^{\prime }\hfill \\ \hfill & =M_1{\mathcal{U}}_i\widehat{D_{I_i}}{M}_{i,2}{M}_{i,2}^{\prime }\hfill \\ \hfill & =M_1{\mathcal{U}}_i\widehat{D_{I_i}}{M}_2.\hfill \end{array}$$

(9)

Finally, $S_B$ stores the converted ciphertext $C_{I_i}$, the encrypted identity $c_{\varrho }$, and the encrypted access tree $C_x$:

(5)

TrapGen $(R_q,s{k}_q)\to \widehat{T_Q}$. The data requester ${\mathcal{DR}}_q$ designated the geometric range of the task requirement as $R_q=(R_{q,ll},R_{q,lu},R_{q,rl},R_{q,ru})$, where $ll,lu,rl,ru$ denote left-lower, left-upper, right-lower, and right-upper of the geometric range bound, respectively. Then, the ${\mathcal{DR}}_q$ encodes geometric query range $R_q$ into the query vector $\overrightarrow{q}$ based on the Gray code. After that, the data requester ${\mathcal{DR}}_q$ performs the following operations to generate the search trapdoor:

Step 1: Firstly, ${\mathcal{DR}}_q$ encodes the geometric range $R_q$ of the task requirement to query vector $\overrightarrow{q}$ as shown in Equation (10) by using the Gray code method.

$$\overrightarrow{q}=(q_1,q_2,\cdots ,q_d),$$

(10)

where $q_i(i\in [1,d-1])$ is one of X, Y, or 0 and $q_d={\sum }_{i=1}^{d-1}{q}_i^2$.

Step 2: Secondly, to protect the privacy of the query vector, the ${\mathcal{DR}}_q$ transforms the query vector $\overrightarrow{q}$ into an n-dimensional vector $v_q=(v_{q,1},v_{q,2},\cdots ,v_{q,n})$ by using the same transformation $v_{q,i}={\sum }_{i=1}^d{q}_i·2^{d-i}$ as mentioned in IndexEnc, where each entry $v_{q,i}$ $(i\in [1,n\left]\right)$ is a positive integer value.

Step 3: After that, the ${\mathcal{DR}}_q$ hashes the integer vector $v_q$ as shown in Equation (11) by using the hash function h.

$$h\left(v_q\right)=(h\left(v_{q,1}\right),h\left(v_{q,2}\right),\cdots ,h\left(v_{q,n}\right)).$$

(11)

Step 4: To further protect the privacy of the mapping-based task requirement, the ${\mathcal{DR}}_q$ constructs a polynomial function $f\left(q\right)$ of the task requirement with the degree being n, as shown in Equation (12).

$$\begin{array}{cc}\hfill f\left(q\right)& =\prod _{i=1}^n(q-h\left(v_{q,i}\right))\hfill \\ \hfill & =a_0+a_{1}q+\cdots +a_n{q}^n.\hfill \end{array}$$

(12)

Step 5: Subsequently, the ${\mathcal{DR}}_q$ extracts the coefficients of the task function to construct the coefficient vector as $Q=(a_o,a_1,\cdots ,a_n)$. Then, the ${\mathcal{DR}}_q$ embeds a one-time random positive number $\beta$ into the coefficient vector Q and generates the random vector $\overline{Q}=(\beta a_0,\beta a_1,\cdots ,\beta a_n)$.

Step 6: Next, the ${\mathcal{DR}}_q$ permutes the random vector $\overline{Q}$ as $\widehat{Q}=\pi \left(\overline{Q}\right)$, and then, the ${\mathcal{DR}}_q$ transforms $\widehat{Q}$ into the corresponding diagonal matrix $\widehat{D_Q}$ with the diagonal being $\widehat{Q}$.

Step 7: Finally, the ${\mathcal{DR}}_q$ generates a random $(n+1)\times (n+1)$ upper triangular matrix ${\mathcal{P}}_q$ with the main diagonal being $(1,1,\cdots ,1)$ and encrypts the diagonal matrix $\widehat{D_Q}$ by using the secret key $s{k}_q$ and the ${\mathcal{DR}}_q$ as shown in Equation (13). After that, the ${\mathcal{DR}}_q$ sends the encrypted task $En{c}_K\left(\mathcal{T}\right)$ and search trapdoor $\widehat{T_Q}$ to $S_A$, where $Enc$ denotes symmetric encryption (e.g., AES), and $\mathcal{T}$ is the plaintext of ${\mathcal{DR}}_q$’s task.

$$\widehat{T_Q}=M_{q,2}\widehat{D_Q}{\mathcal{P}}_q{M}_{q,1}.$$

(13)

(6)

TrapTran $(\widehat{T_Q},R{K}_A,R{K}_B)\to T_Q$. Upon receiving the search trapdoor $\widehat{T_Q}$, $S_A$ utilizes the corresponding re-encryption key $M_{q,2}^{\prime }$ to re-encrypt $\widehat{T_Q}$, as shown in Equation (14).

$$\begin{array}{cc}\hfill \widetilde{T_Q}& =M_{q,2}^{\prime }\widehat{T_Q}\hfill \\ \hfill & =M_{q,2}^{\prime }{M}_{q,2}\widehat{D_Q}{\mathcal{P}}_q{M}_{q,1}\hfill \\ \hfill & =M_2^{-1}\widehat{D_Q}{\mathcal{P}}_q{M}_{q,1}.\hfill \end{array}$$

(14)

After that, $S_A$ sends $\widetilde{T_Q}$ to $S_B$. Subsequently, $S_B$ finds the requester ${\mathcal{DR}}_q$’s re-encryption key $M_{q,1}^{\prime }$ and re-encrypts $\widetilde{T_Q}$ to $T_Q$ as shown in Equation (15).

$$\begin{array}{cc}\hfill T_Q& =\widetilde{T_Q}{M}_{q,1}^{\prime }\hfill \\ \hfill & =M_2^{-1}\widehat{D_Q}{\mathcal{P}}_q{M}_{q,1}{M}_{q,1}^{\prime }\hfill \\ \hfill & =M_2^{-1}\widehat{D_Q}{\mathcal{P}}_q{M}_1^{-1}.\hfill \end{array}$$

(15)

(7)

Query $(c_{\varrho },C_x,t_c,C_{I_i},T_Q)\to {\mathcal{R}}_i$. Upon receiving the search trapdoor $T_Q$, for each encrypted object $\mathsf{EO}=(c_{\varrho },C_x,C_{I_i})$, $S_B$ first checks whether the ${\mathcal{DR}}_q$’s attribute set S satisfies the defined access policy ${\mathcal{T}}_{\varrho }$ based on Definition 1. If not, $S_B$ outputs ⊥; otherwise, $S_B$ executes the following Query procedure for task allocation.

Step 1: For each leaf node x in hierarchical temporal access tree ${\mathcal{T}}_{\varrho }$, if $a{t}_x\notin S$, $S_B$ outputs ⊥. If $a{t}_x\in S$ and $t_c\in [t_1,t_2]\cap [t_1^{\prime },t_2^{\prime }])\bigwedge ({\mathcal{T}}_{\varrho }\left(S\right)=1)$, $S_B$ utilizes the ciphertext $C_x$ and time-related derivation function to calculate $F_x=a{\int }_{t_1}^{t_2}{\int }_{t_1^{\prime }}^{t_2^{\prime }}{f}_x\left(t\right)dtd{t}^{\prime }=e{(g_p,H)}^{a{y}_x\left(0\right)}$; otherwise, $S_B$ outputs $\mathsf{TAC}({\mathcal{T}}_{\varrho },S,t_c)=0$. By doing this, we have $F_{root}=e{(g_p,H)}^{as}$ in the root node of the temporal access tree.

Step 2: Then, $S_B$ checks whether the worker ${\mathcal{W}}_i$ is a suitable one via the corresponding matrix trace between the ${\mathcal{W}}_i$’s index $C_{I_i}$ and ${\mathcal{DR}}_q$’s search trapdoor $T_Q$, which is equivalent to checking whether the inner product of spatial vector $\overrightarrow{{\mathsf{p}}_i}$ and query vector $\overrightarrow{\mathsf{q}}$ is equal to 0. By doing this, $S_B$ can determine whether the spatial data $L_i$ of the ${\mathcal{W}}_i$ are located in the geometric query range $R_q$ of the task requirement by calculating the trace $tr\left(C_{I_i}{T}_Q\right)$ as shown in Equation (16).

$$\begin{array}{cc}\hfill tr\left(C_{I_i}{T}_Q\right)& =tr\left(M_1{\mathcal{U}}_i\widehat{D_{I_i}}{M}_2{M}_2^{-1}\widehat{D_Q}{\mathcal{P}}_q{M}_1^{-1}\right)\hfill \\ \hfill & =tr\left(M_1{\mathcal{U}}_i\widehat{D_{I_i}}\widehat{D_Q}{\mathcal{P}}_q{M}_1^{-1}\right)\hfill \\ \hfill & =\overline{I_i}\circ \overline{Q}\hfill \\ \hfill & =\alpha \beta \left(a_{0}h{\left(v_i\right)}^0+a_{1}h{\left(v_i\right)}^1+\cdots +a_{n}h{\left(v_i\right)}^n\right).\hfill \end{array}$$

(16)

If $tr\left(C_{I_i}{T}_Q\right)=0$ holds, the worker ${\mathcal{W}}_i$’s spatial data $L_i$ are located in the geometric query range $R_q$ of the task requirement. Thus, $\mathsf{EPTA}(C_{I_i},T_Q,t_c,C_x,c_{\varrho })={\mathcal{R}}_i=1$ holds, which means the ${\mathcal{W}}_i$ is an accessible and proper worker at the current time $t_c$ and adds $\{c_{\varrho },F_{root}\}$ to the search result $\mathcal{R}$. Otherwise, $S_B$ chooses another re-encrypted spatial datum and performs the above secure task allocation procedure until all encrypted spatial data are searched.

5.3. Correctness Analysis

From linear algebra, we have the following theorem about the correctness of EPTA-T.

Theorem 1

(Correctness of EPTA-T). In EPTA-T, EPTA-T.Query$(C_{I_i},T_Q,t_c,C_x,c_{\varrho })\to {\mathcal{R}}_i=1$ is correct if and only if both $F_{root}=e{(g_p,H)}^{as}$ and $tr\left(C_{I_i}{T}_Q\right)=0$ are satisfied.

Proof. 

To demonstrate the correctness of EPTA-T, we should prove that both the data requester ${\mathcal{DR}}_q$’s attribute set S satisfies the temporal access policy ${\mathcal{T}}_{\varrho }$ at the current time $t_c$ and the worker ${\mathcal{W}}_i$’s location $L_i$ is located in the geometric range $R_q$ of the task requirement when $tr\left(C_{I_i}{T}_Q\right)=0$ are satisfied.

For the temporal access control constraint, since $y_x\left(0\right)=y_x{\left(0\right)}^{\prime }+y_x{\left(0\right)}^{″}$ and $C_x=(H^{y_x{\left(0\right)}^{\prime }},$ $h{\left(a{t}_x\right)}^{y_x{\left(0\right)}^{\prime }},H^{y_x{\left(0\right)}^{″}},h{\left(a{t}_x\right)}^{y_x{\left(0\right)}^{″}})$, we have Equations (17) and (18).

$$F_x^{\prime }=\frac{e(g_p^{a}h{\left(a{t}_x\right)}^a,H^{y_x{\left(0\right)}^{\prime }})}{e(H^a,h{\left(a{t}_x\right)}^{y_x{\left(0\right)}^{\prime }})}=e{(g_p,H)}^{a{y}_x{\left(0\right)}^{\prime }}.$$

(17)

$$F_x^{″}=\frac{e(g_p^{a}h{\left(a{t}_x\right)}^a,H^{y_x\left(0\right)″})}{e(H^a,h{\left(a{t}_x\right)}^{y_x{\left(0\right)}^{″}})}=e{(g_p,H)}^{a{y}_x{\left(0\right)}^{″}}.$$

(18)

Based on Equations (17) and (18), we can calculate that $F_x=F_x^{\prime }·F_x^{″}=e{(g_p,H)}^{a{y}_x\left(0\right)}$. Similarly, for the non-leaf node x in ${\mathcal{T}}_{\varrho }$, we also can calculate $F_x$ in a recursive way. To this end, we have $F_{r}oot=e{(g_p,H)}^{as}$, which means the ${\mathcal{DR}}_q$’s attribute set S satisfies the defined access policy ${\mathcal{T}}_{\varrho }$ at the current time $t_c$. Therefore, the correctness of TAC is demonstrated.

For the EPTA constraint, note that $C_{I_i}{T}_Q=M_1{\mathcal{U}}_i\widehat{D_{I_i}}\widehat{D_Q}{\mathcal{P}}_q{M}_1^{-1}$. According to the similarity transformation in linear algebra, we have $tr\left(C_{I_i}{T}_Q\right)=tr\left({\mathcal{U}}_i\widehat{D_{I_i}}\widehat{D_Q}{\mathcal{P}}_q\right)$. Since ${\mathcal{U}}_i$ and ${\mathcal{P}}_q$ are upper triangular matrices with the main diagonals being $(1,1,\cdots ,1)$, both ${\mathcal{U}}_i\widehat{D_{I_i}}$ and $\widehat{D_Q}{\mathcal{P}}_q$ are upper triangular matrices with the main diagonals being $\widehat{I_i}$ and $\widehat{Q}$. Additionally, by using the same permutation $\pi$, $\overline{I_i}$ and $\overline{Q}$ are permuted to $\widehat{I_i}$ and $\widehat{Q}$, respectively. Therefore, we have

$$\begin{array}{cc}\hfill tr\left(C_{I_i}{T}_Q\right)& =\widehat{I_i}\circ \widehat{Q}\hfill \\ \hfill & =\overline{I_i}\circ \overline{Q}\hfill \\ \hfill & =\alpha \beta \left(a_{0}h{\left(v_i\right)}^0+a_{1}h{\left(v_i\right)}^1+\cdots +a_{n}h{\left(v_i\right)}^n\right),\hfill \end{array}$$

(19)

where $\widehat{I_i}\circ \widehat{Q}$ denotes the inner product between $\widehat{I_i}$ and $\widehat{Q}$. In Equation (19), since both $\alpha$ and $\beta$ are two one-time positive values, if $tr\left(C_{I_i}{T}_Q\right)=0$ holds, the equation $a_{0}h{\left(v_i\right)}^0+a_{1}h{\left(v_i\right)}^1+\cdots +a_{n}h{\left(v_i\right)}^n=0$ is satisfied, which means the hash value $h\left(v_i\right)$ is the root of the polynomial function $f\left(q\right)$ constructed by the requester ${\mathcal{DR}}_q$. Since $h\left(v_i\right)$ and $h\left(v_q\right)$ are derived from the spatial vector $\overrightarrow{{\mathsf{p}}_i}$ and $\overrightarrow{\mathsf{q}}$, we have $\overrightarrow{{\mathsf{p}}_i}\circ \overrightarrow{\mathsf{q}}=0$. That is, the ${\mathcal{W}}_i$’s spatial data $L_i$ are located in the geometric query range $R_q$ of the task requirement, i.e., ${\mathcal{R}}_i=1$. Therefore, the correctness of EPTA-T is demonstrated. □

Discussion: Our EPTA-T achieves secure task allocation and temporal access control simultaneously. By using randomizable matrix multiplication, EPTA-T can resist the IND-SCPA in multi-user setting. In addition, EPTA-T supports temporal access control by leveraging function differentiation and integration, along with CP-ABE, to regulate access to tasks over time. Our EPTA-T considers the locations of the workers, which is not sufficient for accurate task allocation. In practical task allocation scenarios, workers’ keywords are also significant for task matching. To provide a detailed discussion on the advantages and challenges of EPTA-T, we discuss both the functionality and efficiency of EPTA-T as follows:

• Functionality: Our EPTA-T scheme can support task allocation in multi-user settings without key sharing. This is made possible by leveraging proxy re-encryption, which allows the transformation of ciphertexts from an asymmetric key environment to re-encrypted ciphertexts in a symmetric key setting. As a result, even when workers and requesters employ different keys, secure task allocation can still be achieved by utilizing different types of ciphertexts.
• Efficiency: Our EPTA-T scheme provides significant reductions in computational overhead for both the data encryption and task allocation processes. By utilizing randomizable matrix multiplication and matrix decomposition techniques, our EPTA-T scheme avoids heavy cryptographic operations such as fully homomorphic encryption, Paillier encryption, exponential operations, and secure circuits. This design choice leads to a notable improvement in the performance of data encryption and task allocation, as the computational burden is reduced.

6. Security Analysis

Since CPA is stronger than COA, if EPTA-T can resist CPA, it logically follows that it can also provide resistance against COA. Therefore, in this section, we mainly analyzed how EPTA-T can protect the confidentiality of spatial data, workers’ identity, the geometric query of the task requirements, and the task results under an Indistinguishability under Selective Chosen-Plaintext Attacks (IND-SCPA) model. Before demonstrating the security of EPTA-T under the IND-SCPA model, we give the definitions of the secure simulation-based experiment between a computationally bounded adversary $\mathcal{A}$ and a challenger $\mathcal{C}$ as follows.

Definition 2

(IND-SCPA data privacy of EPTA-T). Let ∏ be a privacy-preserving task-allocation scheme with temporal access control over a security parameter λ. A security game of data privacy between a challenger $\mathcal{C}$ and an adversary $\mathcal{A}$ is defined as follows:

• Initialization: Given a security parameter λ, $\mathcal{A}$ generates two spatial databases ${\mathsf{DB}}_0=\{L_{0,1},L_{0,2},\cdots ,L_{0,m}\}$, and ${\mathsf{DB}}_1=\{L_{1,1},L_{1,2},\cdots ,L_{1,m}\}$, and sends them to $\mathcal{C}$.
• Setup: $\mathcal{C}$ performs the Setup algorithm and the KeyGen algorithm to generate a master key, public parameter, secret key, and re-encryption key and sends the public parameter to $\mathcal{A}$
• Phase 1: $\mathcal{A}$ adaptively submits several encrypted data and trapdoor requests, where each request is one of the following types:
  • Encrypted data request: Upon the j-th encrypted data request, $\mathcal{A}$ outputs a spatial dataset $L_j^{\prime }=\{L_{j,1}^{\prime },L_{j,2}^{\prime },\cdots ,L_{j,m}^{\prime }\}$. $\mathcal{C}$ responds with encrypted spatial data $\widehat{C_{I_i}^{\prime }}\leftarrow \mathsf{IndexEnc}(L_j^{\prime },s{k}_i)$.
  • Search trapdoor request: Upon the j-th search trapdoor request, $\mathcal{A}$ generates a geometric range query $R_q$ and sends it to $\mathcal{C}$. After that, $\mathcal{C}$ responds with a search trapdoor $T_{Q_j}=\mathsf{TrapGen}(R_{q_j},s{k}_q)$. Here, $R_{q_j}$ is subject to $\mathcal{L}({\mathsf{DB}}_0,R_{q_j})=\mathcal{L}({\mathsf{DB}}_1,R_{q_j})$, where $\mathcal{L}$ is a leakage function obtaining all the information leaked during the task allocation process:
• Challenge: With ${\mathsf{DB}}_0$ and ${\mathsf{DB}}_1$ selected from the initialization, $\mathcal{C}$ flips a coin $b\in \{0,1\}$, executes IndexEnc to calculate the encrypted spatial data $\widehat{C_{I_i}^{\prime }}$, and sends them to $\mathcal{A}$.
• Phase 2: $\mathcal{A}$ runs Phase 1 again and adaptively selects several spatial data, then issues them to $\mathcal{C}$.
• Guess: $\mathcal{A}$ outputs his/her guess $b^{\prime }$ of b. If $b^{\prime }=b$ holds, $\mathcal{A}$ wins the security game; otherwise, $\mathcal{A}$ fails.

∏ is secure against IND-SCPA on data privacy if, for any polynomial-time adversary $\mathcal{A}$ in the above security game, $\mathcal{A}$ has at most a negligible advantage as follows:

$$Ad{v}_{\prod ,\mathcal{A}}^{IND-SCPA,Data}=|Pr(b^{\prime }=b)-\frac{1}{2}|\le negl\left(\lambda \right),$$

where $negl\left(\lambda \right)$ is a negligible function.

Definition 3

(IND-SCPA query privacy of EPTA-T). Let ∏ be a privacy-preserving task-allocation scheme with temporal access control over a security parameter λ. A security game of query privacy between a challenger $\mathcal{C}$ and an adversary $\mathcal{A}$ is defined as follows:

• Initialization: $\mathcal{A}$ submits two geometric range queries $R_{q_0}$ and $R_{q_1}$ with the same dimensional space to $\mathcal{C}$.
• Setup: $\mathcal{C}$ runs the KeyGen algorithm to generate a secret key for trapdoor encryption.
• Phase 1: $\mathcal{A}$ adaptively submits a series of requests to $\mathcal{C}$. After that, $\mathcal{C}$ responds with encrypted spatial data and trapdoor. Each request is one of the following two types:
  • Encrypted data request: Upon the j-th encrypted data request, $\mathcal{A}$ outputs a spatial dataset $L_j^{\prime }=\{L_{j,1}^{\prime },L_{j,2}^{\prime },\cdots ,L_{j,m}^{\prime }\}$. Then, $\mathcal{C}$ responds with encrypted spatial data $\widehat{C_{I_i}^{\prime }}=\mathsf{IndexEnc}(L_j^{\prime },s{k}_i)$, where $\widehat{C_{I_i}^{\prime }}$ is subject to $\mathcal{L}(\widehat{C_{I_i}^{\prime }},R_{q_0})=\mathcal{L}(\widehat{C_{I_i}^{\prime }},R_{q_1})$.
  • Search trapdoor request: Upon the j-th trapdoor request, $\mathcal{A}$ outputs a geometric query request $R_{q_j}$. Then, $\mathcal{C}$ responds with a search trapdoor $\widehat{T_{Q_j}}\leftarrow \mathsf{TrapGen}(R_{q_j},s{k}_q)$:
• Challenge: With $R_{q_0}$ and $R_{q_1}$ selected in the initialization, $\mathcal{C}$ flips a coin $b\in \{0,1\}$ and calculates $\widehat{T_{Q_{b,j}}}$. After that, $\mathcal{C}$ sends it back to $\mathcal{A}$.
• Phase 2: $\mathcal{A}$ adaptively selects a series of trapdoor requests and sends them to $\mathcal{C}$, which are still subject to the same restrictions in Phase 1.
• Guess: $\mathcal{A}$ outputs his/her guess $b^{\prime }$ of b. If $b^{\prime }=b$ holds, $\mathcal{A}$ wins the security game; otherwise, $\mathcal{A}$ fails.

∏ is secure against IND-SCPA regarding query privacy if, for any polynomial-time adversary $\mathcal{A}$ in the above security game, $\mathcal{A}$ has at most a negligible advantage:

$$Ad{v}_{\prod ,\mathcal{A}}^{IND-SCPA,Query}=|Pr(b^{\prime }=b)-\frac{1}{2}|\le negl\left(\lambda \right).$$

6.1. Data Privacy and Identity Privacy

Theorem 2.

Our EPTA-T scheme guarantees IND-SCPA data privacy and identity privacy.

Proof. 

To prove the IND-SCPA data privacy of EPTA-T, we should demonstrate that $\mathcal{A}$ cannot distinguish the ciphertext $\widehat{C_{I_{0,j}}}$ and $\widehat{C_{I_{1,j}}}$ based on the security game defined in Definition 2, even though $\mathcal{A}$ has oracle access to $\mathsf{IndexEnc}$.

Considering that the ${\mathcal{W}}_i$’s spatial data $L_i$ are firstly encoded as spatial vector $\overrightarrow{{\mathsf{p}}_i}$ by using Gray code, then ${\mathcal{W}}_i$ transforms $\overrightarrow{{\mathsf{p}}_i}$ into a positive integer $v_i$ and obtains a hash value by using the hash function h. After that, the ${\mathcal{W}}_i$ calculates an $(n+1)$-dimensional vector $I_i$ based on the hash value $h\left(v_i\right)$. In addition, the ${\mathcal{W}}_i$ permutes the random vector $\overline{I_i}$ to $\widehat{I_i}$ with the random permutation $\pi$. Following this, the permuted vector $\widehat{I_i}$ is transformed into a corresponding diagonal matrix $\widehat{D_{I_i}}$. Finally, the spatial data $L_i$ are encrypted as $\widehat{C_{I_i}}=M_{i,1}{\mathcal{U}}_i\widehat{D_{I_i}}{M}_{i,2}$. Since $\mathcal{A}$ has no idea about the one-time random value $\alpha$, the random permutation $\pi$, and the random triangular matrix ${\mathcal{U}}_i$, it is hard to recover the secret key $s{k}_i$. Additionally, $\mathcal{A}$ can obtain several plaintext–ciphertext pairs, but it is difficult for $\mathcal{A}$ to launch a linear analysis attack.

In Phase 1 and Phase 2 of Definition 2, $\mathcal{A}$ can adaptively select different spatial data ${\left\{L_j^{\prime }\right\}}_{j=1}^m$ and obtain the corresponding ciphertexts ${\left\{\widehat{C_{I_j}}\right\}}_{j=1}^m$. Unfortunately, both $\overline{I_i}$ and ${\mathcal{U}}_i$ are a one-time random vector and matrix determined by $\mathcal{C}$, and the ciphertexts ${\left\{\widehat{C_{I_j}}\right\}}_{j=1}^m$ are random according to $\mathcal{A}$. That is, for the given ciphertexts $\widehat{C_{I_{0,j}}}$ and $\widehat{C_{I_{1,j}}}$ selected by $\mathcal{A}$, $\mathcal{A}$ cannot distinguish which spatial data are actually encrypted. Therefore, even though $\mathcal{A}$ has oracle access to IndexEnc, it has a random guess $b^{\prime }$ of b with a negligible advantage:

$$Ad{v}_{\prod ,\mathcal{A}}^{IND-SCPA,Data}=|Pr(b^{\prime }=b)-\frac{1}{2}|\le negl\left(\lambda \right).$$

For the identity privacy in EPTA-T, since the worker’s identity $i{d}_{\varrho }$ is encrypted as $c_{\varrho }$ by using AES and the secret key of AES is kept private to $\mathcal{A}$, the identity privacy can be well protected. □

6.2. Query Privacy and Result Privacy

Theorem 3.

Our EPTA-T scheme guarantees IND-SCPA query privacy and result privacy.

Proof. 

Based on Definition 3, to prove the query privacy, we should demonstrate that $\mathcal{A}$ cannot obtain any sensitive information from the encrypted trapdoor $\widehat{T_Q}$, encrypted attribute set $C_x$, and matrix trace $tr\left(C_{I_i}{T}_Q\right)$. Similar to the operation in IndexEnc, $\mathcal{A}$ can adaptively select different geometric query range ${\left\{R_{q_j}\right\}}_{j=1}^m$ and observe the corresponding trapdoor ${\left\{\widehat{T_{Q_j}}\right\}}_{j=1}^m$. However, both $\overline{Q}$ and ${\mathcal{P}}_q$ are a one-time random vector and matrix determined by $\mathcal{C}$, and the encrypted trapdoor ${\left\{\widehat{T_{Q_j}}\right\}}_{j=1}^m$ is random according to $\mathcal{A}$. Therefore, for the given trapdoors $\widehat{T_{Q_{0,j}}}$ and $\widehat{T_{Q_{1,j}}}$ selected by $\mathcal{A}$, even though $\mathcal{A}$ has oracle access to TrapGen, $\mathcal{A}$ only has a random guess $b^{\prime }$ of b for the geometric query range with a negligible advantage:

$$Ad{v}_{\prod ,\mathcal{A}}^{IND-SCPA,Query}=|Pr(b^{\prime }=b)-\frac{1}{2}|\le negl\left(\lambda \right).$$

In addition, $\mathcal{A}$ can obtain $F_{root}=e(g_p,H)$ and $tr\left(C_{I_i}{T}_Q\right)$ for temporal access control and task allocation, respectively. However, the privacy of the temporal access tree can be well guaranteed by using Bilinear Diffie–Hellman Assumption (DBDH). Furthermore, the query result only reveals whether $tr\left(C_{I_i}{T}_Q\right)$ is equal to 0 or not, and no more sensitive information of the geometric query can be obtained by $\mathcal{A}$. Therefore, our EPTA-T scheme can well guarantee IND-SCPA query privacy and result privacy. □

7. Performance Evaluation

In this section, we provide a thorough experimental evaluation of the EPTA-T scheme. We first depict the configuration of the experimental environment and selection of parameters. Since our EPTA-T scheme is the first work to support fine-grained and temporal access control in privacy-preserving task allocation, we present the comparison of EPTA-T with Privacy-Preserving Boolean Range Query with Temporal Access Control (PBRQ-T) [6] in terms of the computational overhead on IndexEnc, TrapGen, and Query.

7.1. Implementation Settings

Experimental environment. We implemented our EPTA-T scheme and PBRQ-T with JAVA and utilized the JDK library to implement cryptographic primitives such as AES. We conducted experiments on a laptop with a 2.8 GHz, Intel Core i7, 16 GB RAM as $\mathcal{SP}$ and an Android phone with 8G RAM and Octa-core Processors as $\mathcal{W}$ and $\mathcal{DR}$. In order to precisely measure the computational cost of the $\mathcal{SP}$, $\mathcal{W}$, and $\mathcal{DR}$, all experiments were performed on the same devices. Furthermore, all the reported running times were the average of 100 experiments.

Dataset. We randomly selected 10,000 spatial data from the Yelp dataset (https://www.yelp.com/dataset (accessed on 19 May 2023)) as the test dataset, where each spatial datum included the spatial location and attributes. The number of attributes was 44 in the test dataset.

Parameter setting. To compare with PBRQ-T, all primes were set as 60 bits. In addition, we divided the space into $1000\times 1000$ cells; the dimension of the spatial vector was 100; the geometric query range $R_q$ was set as a $64\times 64$ square. In our experimental evaluation, we set the number of the $\mathcal{DR}$’s attributes and system attributes as 10, and we assumed that there was only one temporal attribute in the task allocation system.

We compared our EPTA-T scheme with the state-of-the-art PBRQ-T scheme [6]. Note that the PBRQ-T scheme does not support task recommendation in mobile crowdsensing systems. To test the cost domination of our EPTA-T over different database sizes m and dimension vectors n, we mainly evaluated the complexity of index encryption, index transformation, trapdoor generation, trapdoor transformation, and query between $\mathcal{W}$, $\mathcal{DR}$, and $\mathcal{SP}$, respectively.

7.2. Evaluation and Comparison

Performance evaluation of IndexEnc and IndexTran. The cost of IndexEnc was dominated by the database size m. As shown in Figure 3a, when the database size was 10,000, the index encryption time of EPTA-T was about 3 s, while that of PBRQ-T was more than 2500 s. The reason is that our EPTA-T scheme only executes randomizable matrix multiplication for data privacy protection, while PBRQ-T conducts bilinear mapping and exponentiation operations, which have a more-expensive computational cost than our scheme. Therefore, with the increase of the database’s size, EPTA-T can save more computational costs on the worker side. Since PBRQ-T does not involve the index transformation operation, we only evaluated our EPTA-T on IndexTran with varying vector dimensions (i.e., n). As shown in Figure 3b, we noticed that our proposed EPTA-T increased linearly with the variable vector dimension n. In addition, the IndexTran costs over different database sizes m were almost close in the lower-dimensional setting.

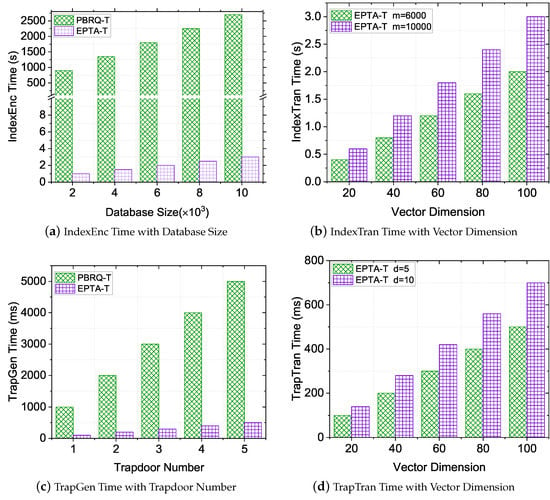
Figure 3. Performance Evaluation of IndexEnc, IndexTran, TrapGen, and TrapTran.

Performance evaluation of TrapGen and TrapTran. From Figure 3c, we can notice that our EPTA-T had less computational cost for TrapGen and slightly increased with the variable number d of trapdoors, and it was at least $10\times$ faster than PBRQ-T. The underlying reason is that the number of trapdoors had little effect on the calculation of the matrix multiplication. As shown in Figure 3d, we can notice that the TrapTran computational cost of EPTA-T linearly grew with the variable n. Specifically, when the vector dimension achieved 100, the time cost of TrapTran was only 0.7 s, even though the $\mathcal{DR}$ submitted 10 geometric queries at one time.

Performance evaluation of Query. To comprehensively evaluate the query cost, we ran the experiments on the database with different sizes and vectors with different dimensions. As shown in Figure 4, the query overhead was scarcely influenced by the database size and the vector dimension. From Figure 4a, we can notice that the query time of both EPTA-T and PBRQ-T increased linearly with m, and the query performance of EPTA-T outperformed that of PBRQ-T. The query time of EPTA-T was about $500\times$ faster than that of PBRQ-T, which indicates that the calculation operations of matrix trace and functional integration were more efficient than those of exponent arithmetic and bilinear mapping. From Figure 4b, we can notice that a higher vector dimension had a greater query time cost with EPTA-T. The underlying logic is that the increase of the vector dimension d caused the number of matrix dimensions to grow and the computational cost of the matrix-trace-based operation to increase.

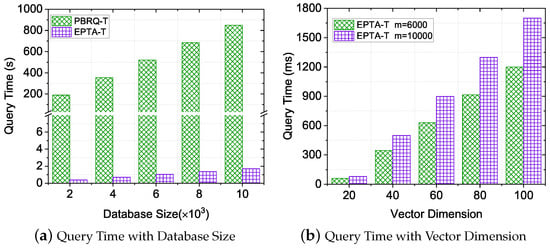
Figure 4. Performance Evaluation of Query.

8. Conclusions

In this paper, we investigated and studied the problem of privacy-preserving task allocation with temporal access control for mobile crowdsensing. Specifically, we proposed an Efficient and Privacy-Preserving Task Allocation with Temporal Access Control (EPTA-T) scheme that efficiently achieved secure task allocation in multi-user settings by using Gray code and randomizable matrix multiplication. Moreover, EPTA-T incorporates temporal access control by leveraging function differentiation and integration, along with CP-ABE, to regulate access to tasks over time. Furthermore, formal security analysis and experimental evaluations demonstrated that EPTA-T protects data privacy and query privacy and achieves efficient task allocation compared with the state-of-the-art scheme. Regarding open problems, privacy-preserving spatial-keyword-based task allocation is still a challenging issue that needs to be resolved. For future work, we will further consider additional constraints in privacy-preserving task allocation, such as workers’ interests and incentives.