Abstract
In this paper, we introduce an innovative approach to handling the multi-armed bandit (MAB) problem in non-stationary environments, harnessing the predictive power of large language models (LLMs). With the realization that traditional bandit strategies, including epsilon-greedy and upper confidence bound (UCB), may struggle in the face of dynamic changes, we propose a strategy informed by LLMs that offers dynamic guidance on exploration versus exploitation, contingent on the current state of the bandits. We bring forward a new non-stationary bandit model with fluctuating reward distributions and illustrate how LLMs can be employed to guide the choice of bandit amid this variability. Experimental outcomes illustrate the potential of our LLM-informed strategy, demonstrating its adaptability to the fluctuating nature of the bandit problem, while maintaining competitive performance against conventional strategies. This study provides key insights into the capabilities of LLMs in enhancing decision-making processes in dynamic and uncertain scenarios.
1. Introduction
In the realm of artificial intelligence (AI) and reinforcement learning (RL), the multi-armed bandit (MAB) problem [1,2] is a classic decision-making knot that captures the exploration–exploitation trade-off. Traditionally, the MAB problem assumes a stationary setting, where the underlying distribution of each bandit’s reward remains constant. However, real-world scenarios often present non-stationary environments, where these reward distributions change over time.
The MAB problem, a classic dilemma of decision theory, exemplifies the balance of exploration and exploitation in RL. It is formulated as a game with a fixed number of slot machines, or ‘bandits’, each with an unknown probability distribution of rewards. The goal is to develop a strategy for selecting which bandit to play so as to maximize the total reward over a series of plays. While the MAB problem has been extensively studied, the extension to non-stationary environments, where the reward probabilities change over time, poses significant challenges [3,4]. Traditional strategies often falter in such scenarios, as they are unable to adapt to the evolving reward distributions.
In this study, we delve into the non-stationary multi-armed bandit (NSMAB) problem, where we adapt well-known strategies to handle fluctuating reward distributions. NSMAB poses unique challenges, primarily due to the dynamic nature of the problem, and the need to continuously adapt the decision-making strategy.
While conventional algorithms, such as epsilon-greedy and upper confidence bound (UCB), are adapted to handle non-stationary bandit problems, they often fall short in optimally adjusting to rapid changes in the environment. In the quest for a better approach, we turn our attention to large language models (LLMs), such as GPT-3.5 Turbo from OpenAI. These models have shown remarkable language understanding and problem-solving abilities, and we harness this power to guide our decision-making in the NSMAB setting.
The rise of LLMs [5,6,7] has revolutionized many fields of AI, providing solutions that can understand, generate, and learn from human-like text [8,9]. Leveraging the predictive prowess of LLMs, this work aims to inform and enhance MAB strategies for non-stationary environments. An LLM can provide valuable insights into whether to exploit the current best-performing bandit or explore others that are potentially better suited to the current environment state. By integrating this LLM-informed advice into traditional MAB strategies, we aim to increase the overall effectiveness in non-stationary settings. The LLM-informed strategy that we propose provides advice on whether to explore or exploit, given the current state of the bandits. This approach effectively leverages the ability of LLM to understand complex scenarios and make informed decisions [10,11,12].
In the complex domain of decision making, we often encounter situations that require strategic selection among several alternatives with uncertain outcomes—known as the multi-armed bandit problem. Particularly challenging is the non-stationary variant of this problem, where the probabilities associated with rewards can dynamically change over time. Widely accepted strategies for addressing this problem, such as epsilon-greedy, and UCB (upper confidence bound), seek to balance exploration (seeking out new, potentially superior options), and exploitation (leveraging the currently best-known option). However, performance may vary significantly in non-stationary environments due to the unpredictable nature of the rewards associated with the bandits.
As an alternative approach, we propose a novel strategy that harnesses the predictive capabilities of an LLM, specifically GPT-3.5-turbo-0301 and quantized low-rank adapters (QLoRAs) [13,14], to guide the decision-making process. Our LLM-informed strategy solicits advice from the LLM, deciding whether to explore or exploit based on the current state of the bandits. Remarkably, we observed that our novel LLM-informed strategy often performs on par with, if not better than, traditional approaches, indicating the potential of integrating advanced AI technologies such as LLMs in real-time decision-making tasks. This contribution advances the current understanding of non-stationary multi-armed bandit problems and opens new avenues for applying LLMs to enhance traditional decision-making strategies in dynamic environments.
The rest of the paper is organized as follows: In Section 2, we delve into the related work, providing a comprehensive overview of both the stationary and non-stationary multi-armed bandit (MAB) problems, the various strategies developed for these settings, and the promising capabilities of LLMs. Section 3 introduces the fundamentals of multi-armed bandits, offering a mathematical representation of the problem and discussing its practical applications. Following this, in Section 4, we elaborate on our methodology, detailing the adaptation of existing MAB strategies to non-stationary environments, and the innovative incorporation of LLM advice. In Section 5, we detail our experimental setup and results, describing the diverse scenarios under exploration, presenting the results along with illustrative figures, and performing a thorough analysis. The subsequent section, Section 6, opens up a broader discussion on the implications of our findings and potential applications of our LLM-informed framework. Finally, in Section 7, we look ahead to future research directions and conclude our study.
2. Related Works
The multi-armed bandit (MAB) problem, initially formalized by Robbins [1], has been the subject of extensive research due to its inherent need for balancing exploration and exploitation. Several algorithms have been proposed to tackle this problem, each exhibiting specific attributes that render them favorable under different scenarios. For instance, the epsilon-greedy strategy [2] offers simplicity and practicality, guaranteeing eventual convergence to optimal solutions given sufficient time, and a suitable choice of epsilon. The UCB approach [15] is renowned for its optimality in stationary problems, demonstrating logarithmic regret growth over time, effectively minimizing regret in the long run. Finally, Thompson sampling [16] stands out for its probabilistic nature, wherein it favors actions with high uncertainty, or high expected rewards, making it particularly suitable for scenarios with non-stationary rewards [17].
Extensions of the MAB problem to non-stationary environments [18], where the reward probabilities change over time, are less well studied, and yet increasingly relevant in dynamic real-world scenarios [3,4,19]. Strategies that adapt to changing reward distributions have been proposed [20,21], but they often require assumptions about the rate of change or the total number of changes.
The advent of LLMs [5,6,7,13,22], such as GPT-3 [9], Flan [23] or QLoRA [14], has opened new avenues for AI applications. Their ability to generate human-like text and predict next word probabilities has been exploited in tasks ranging from text completion to more complex decision-making problems [24,25]. In this work, we explore the potential of LLMs to advise and enhance traditional MAB strategies in non-stationary environments.
3. Multi-Armed Bandit
The problem of multi-armed bandit is a classic dilemma from probability theory that describes an agent trying to maximize rewards when faced with multiple options, each with an unknown and potentially different reward distribution. This problem is characterized by the inherent trade-off between exploration (trying out all options to learn more about their rewards) and exploitation (sticking with the option that currently seems the best).
Consider an agent faced with K slot machines, or “one-armed bandits”. Each pull of a machine’s lever, or “arm”, gives a random reward drawn from a stationary and unknown probability distribution specific to that machine. The agent’s objective is to develop a strategy to decide which arm to pull at each time step in order to maximize the total reward over a sequence of T time steps.
Let be the reward from the o-th arm at time t, and let be the observed reward. We assume are independent and identically distributed random variables for each o, but the distributions can differ between arms.
The value of an action a is the expected reward:
However, the agent does not have access or is agnostic to . Instead, it must estimate the values based on the observed rewards. A natural estimate is the sample average:
where is the number of times action a has been selected up to time t, is the action selected at time , and is an indicator function that is 1 if , and 0 otherwise.
The challenge in the multi-armed bandit problem involves devising a strategy for selecting based on that successfully balances exploration and exploitation. A good strategy should allow for pulling all arms sufficiently to obtain an accurate estimate of all , but also aim to minimize the number of pulls on arms that have consistently provided lower rewards. By “inferior arms” we refer to those bandits that, based on past interactions, appear to offer less reward (on average) than other options. The goal is to avoid excessively engaging with these seemingly less lucrative options while ensuring that all bandits have been sampled enough to make an informed judgment about their reward distributions. This, in essence, captures the core challenge of the multi-armed bandit problem.
In the following sections, we will delve into some well-established strategies for this problem, setting the groundwork for our innovative approach. Our unique contribution lies in the development of a new strategy that leverages LLMs in a way that has not been done before. This breakthrough approach aims to significantly improve upon the current methodologies, providing more effective and efficient solutions, particularly for non-stationary environments.
4. Methodology
In this section, we first provide a comprehensive look at the non-stationary multi-armed bandit problem, offering a detailed examination of the inherent complexities and unpredictable elements found in such environments. Then, we delve into the strategies we utilized to tackle the problem. This includes well-known approaches, such as epsilon-greedy and UCB, as well as a novel method that leverages the capabilities of LLMs. We then illustrate the reasons for focusing on these specific strategies, along with a discussion on our innovative LLM-informed strategy.
4.1. Non-Stationary Multi-Armed Bandit
In the non-stationary multi-armed bandit problem, there are K bandits or slot machines, each with an unknown reward distribution that may change over time. At each time step t, the agent chooses to play a bandit o and it receives a reward , which is sampled from the bandit’s current reward distribution.
The objective of the agent is to maximize the sum of rewards over a sequence of T trials, which is a challenging task due to the exploration–exploitation dilemma, and the non-stationary nature of the bandits’ reward distributions.
Moreover, acknowledging that real-world scenarios often involves non-stationary processes, where the reward distributions evolve over time, we extend our methodology to accommodate non-stationary bandits. This extension is facilitated by dynamically modifying the reward functions at specific time intervals, which can involve varying the mean or variance. Given the temporal nature of these reward distributions, it is plausible that the optimal action may not remain constant over time. As such, it is crucial for the agent to maintain an exploratory approach over time, as the most rewarding action may change as the experiment proceeds. This is especially true in our experiment settings, where reward distributions of the bandits may undergo a significant shift halfway through the experiment, thereby also changing the optimal bandit at that point. Thus, our methodology embraces these non-stationary aspects to ensure a more holistic and realistic evaluation of the different strategies.
The key point of the derivation that follows is that using the LLM to inform the strategy in a non-stationary multi-armed bandit problem is analogous to utilizing a sophisticated, data-driven decision rule in a coevolutionary game. It demonstrates how tools from AI can be effectively leveraged to adapt traditional game theoretic models to complex, dynamic settings.
4.2. Strategies
In this study, we consider three distinct strategies for tackling the multi-armed bandit problem: the epsilon-greedy strategy, the UCB strategy, and a novel approach we propose and name as the LLM-informed strategy. These three strategies were selected due to their different methods for addressing the exploration–exploitation dilemma, a key challenge in the multi-armed bandit problem. The epsilon-greedy and the UCB strategies are well-known approaches in this field, providing useful benchmarks for comparison, while the LLM-informed strategy introduces an innovative use of AI, specifically LLMs, to this problem space.
Thompson uses a Bayesian approach, updating a probability distribution over each arm’s reward distribution, and then choosing an arm to play based on sampling from these distributions. This strategy provides a natural and probabilistic trade-off between exploration and exploitation.
In this study, we chose to focus on epsilon-greedy, UCB, and the novel LLM-informed strategy when dealing with non-stationary environments for the following reasons:
- Comparative simplicity: Both epsilon-greedy and UCB strategies are simpler in their implementation compared to Thompson sampling. These strategies provide clear baselines for comparison, allowing us to measure the impact of the LLM-informed strategy against well-understood and straightforward mechanisms [2].
- Demonstrated effectiveness: While Thompson sampling has its advantages, epsilon-greedy [26] and UCB strategies [15] have been extensively studied and proven effective in a wide variety of scenarios. They provide solid and reliable benchmarks, against which the novel LLM-informed strategy can be compared.
- Novelty of LLM-informed strategy: The main goal of our study was to explore and demonstrate the potential of leveraging LLMs [9] in the multi-armed bandit problem. By focusing on comparing this novel strategy with simpler, well-known strategies, we aimed to isolate and highlight the impact of LLM advice on problem solving.
- Computation resources: Thompson sampling [27] often requires more computational resources than epsilon-greedy and UCB strategies due to the need to sample from probability distributions during each decision-making step. As our study included large-scale experiments, we decided to exclude Thompson sampling to minimize computational resource consumption.
Another point in favor of omitting Thompson sampling is that applying it to non-binary rewards can be more complex. If the reward distributions are not Bernoulli, then we need to choose and update appropriate prior distributions for the rewards. Depending on the actual reward distributions and the chosen priors, this could involve complex calculations or approximations, which may not be feasible or efficient for large-scale experiments or real-time applications.
4.2.1. Strategy Epsilon-Greedy
The strategy epsilon-greedy is a simple yet effective approach to address the exploration–exploitation dilemma. The strategy can be described as follows:
where is the estimated reward of action a at state s, K is the number of bandits, and is a parameter that controls the trade-off between exploration and exploitation.
4.2.2. UCB Strategy
The UCB strategy offers a more sophisticated way to balance exploration and exploitation by taking into account both the estimated reward and the uncertainty of each bandit. The UCB strategy selects the bandit with the highest upper confidence bound on the expected reward:
where is the number of times that action a has been selected at state s, t is the current time step, and c is a constant that controls the degree of exploration.
4.2.3. LLM-Informed Strategy
We introduce a unique and novel strategy, the LLM-informed strategy, specifically designed to harness the predictive capabilities of LLMs for tackling the multi-armed bandit problem. The core innovation of our approach is to recast the bandit problem as a question, which is then presented to the LLM. Based on the LLM advice regarding exploration or exploitation, we determine the subsequent action. This represents a significant contribution, as it unveils a new path to employ advanced AI technologies in the decision-making process of complex stochastic problems, such as multi-armed bandits.
There are multiple advantages that underpin our approach. Firstly, the strengths of LLMs lie in their ability to understand context, learn from past data, and generate predictions based on complex patterns. This allows the LLM-informed strategy to incorporate more nuanced decision making that is responsive to the trends and changes in the non-stationary environment. Rather than relying on rigid mathematical formulae, the LLM-informed strategy is capable of adapting its decision-making process based on the evolving patterns in the rewards and their distributions, leading to more robust performance in non-stationary scenarios. Secondly, the LLM can process and consider a much larger history of past rewards and decisions than traditional algorithms, potentially leading to more informed decisions. Lastly, the use of LLMs offers an intriguing avenue of investigation into how advanced AI models can be integrated with classic problems in RL, expanding our understanding of how these models can be harnessed in new and innovative ways.
The LLM response is parsed and used to determine the next action. Specifically, if the LLM suggests to “explore”, we select a bandit uniformly at random; if the LLM suggests to “exploit”, we select the bandit with the highest estimated reward.
In the context of a coevolutionary game [28,29,30], the “explore” and “exploit” strategies can be seen as analogous to the decision for an agent (or node) to cooperate or defect. Let us denote the strategy space for the agent as .
Given this, we can introduce a simplified fitness landscape, denoted as , which encodes the rewards for each combination of strategies. This concept is analogous to the payoff matrix in a standard game theoretic setup. Under our model, which is also applied in our experimental setup, the reward for exploration is considered a random variable , following a certain distribution that may change over time, signifying non-stationarity. On the other hand, the reward for exploitation is the current estimated mean reward of the best arm. This framework allows us to effectively study and evaluate the performance of the LLM-informed strategy, but it is important to note that real-world scenarios can be more complex:
In a coevolutionary game, agents update their strategies based on their fitness and the fitness of their neighbors. In the multi-armed bandit context, the strategy recommendation of the LLM can be seen as the agent “observing” the fitness of its neighbors (i.e., the performance of different strategies in the past), and deciding to update its strategy accordingly.
The decision rule for the agent (or the bandit strategy algorithm) can be modeled as a function , which takes as input the current state of the game and the LLM recommendation, and outputs the next action:
Note that this is a simplistic model and in reality, the decision rule could take into account other factors, such as the degree of uncertainty in the estimated rewards. Moreover, the fitness landscape could be more complex, depending on the specifics of the non-stationary environment. For instance, the reward distribution for exploration might not be the same for all arms, or it might be correlated with the past rewards of the arms.
In sum, leveraging the LLM as a strategy informant for the non-stationary multi-armed bandit problem can be compared to the application of an advanced, data-driven decision protocol in a coevolutionary game. This clearly exemplifies how AI resources can be powerfully harnessed to adapt traditional game-theoretic frameworks to intricate, dynamic environments.
4.2.4. Quantized Low-Rank Adapters
Building upon the foundation laid by low-rank adapters (LoRA) [13], Quantized low-rank adapters (QLoRA) introduces a strategy that efficiently fine tunes large-scale language models while minimizing memory requirements [14,31]. Much like its predecessor, QLoRA utilizes the concept of adapters, a small set of trainable parameters, while keeping the bulk of the model parameters constant. The process of optimizing the loss function is achieved by passing gradients via the fixed pre-trained model weights to the adapter. However, QLoRA takes a step further by incorporating quantization techniques, which enables a reduction in the numerical precision of the model weights, thus drastically decreasing the memory footprint and computational requirements.
For a given projection with , , QLoRA follows a similar computation pattern as LoRA:
where , , and s is a scalar. The key differentiating factor lies in the handling of these computations; they are executed at significantly lower precision, in line with the QLoRA principle of quantization. This makes QLoRA a highly effective solution for fine tuning larger models on hardware, such as the A100 GPU, without compromising performance levels.
One of the standout innovations in QLoRA is the introduction of the NormalFloat (NF) data type, which is a fundamental component of its 4-bit quantization mechanism. This data type builds upon the concept of quantile quantization [31], an approach that is designed to be information-theoretically optimal. The distinguishing feature of quantile quantization is that it assigns an equal number of values from the input tensor to each quantization bin, effectively working through the estimation of the input tensor’s quantile using the empirical cumulative distribution function.
However, quantile estimation is computationally intensive, which represents a significant limitation for quantile quantization. To mitigate this, QLoRA incorporates fast quantile approximation algorithms, such as SRAM quantiles [31], for the estimation process. It is important to note, though, that the inherent approximation errors in these algorithms can result in substantial quantization errors for outlier values, which are often critically important.
This is where the NF4 data type comes in. By leveraging the fact that pre-trained neural network weights typically follow a zero-centered normal distribution, the NF4 data type allows for the transformation of all weights to one fixed distribution by scaling the standard deviation to fit precisely within the data type’s range. This means that both the data type and the neural network weights’ quantiles need to be normalized into this range.
Through this normalization process, the NF4 data type facilitates the optimal quantization for zero-mean normal distributions with arbitrary standard deviations within a predefined range. This approach effectively sidesteps the issue of expensive quantile estimates and approximation errors, making it a crucial contributor to the efficiency of QLoRA.
Double quantization (DQ) introduces an additional layer of quantization to the quantization constants, achieving further memory optimization. The process uses 8-bit floats for the second layer of quantization. DQ significantly reduces the memory requirements from an average of 0.5 bits per parameter to just 0.127 bits per parameter. It manages to do this while preserving model performance, which demonstrates the power of the quantization approach taken by QLoRA. In order to tackle the problem of out-of-memory errors during GPU processing, QLoRA utilizes page optimizers. These optimizers rely on NVIDIA’s unified memory feature, which transfers data between the CPU and GPU on a page-by-page basis, similar to traditional CPU RAM-disk memory paging. By allocating paged memory for the optimizer states, the system can automatically relocate memory from the GPU to CPU RAM when the GPU is out of memory and vice versa when the memory is needed for optimizer updates.
QLoRA integrates these key procedures to process a linear layer in the quantized base model complemented with a LoRA adapter. This methodology primarily hinges on the process of ‘double dequantization’. This operation transforms weights, which have undergone two stages of quantization, back into their original computational format, while preserving the memory-saving advantages of quantization.
Defined as doubleDequant, this function dequantizes the input weights that are quantized quantization constants, and subsequently performs a second dequantization on the resulting weights:
This function allows weights, originally stored in the 4-bit NormalFloat (NF4) format, to be converted back into the 16-bit BrainFloat (BF16) format for computation.
A crucial component of this approach is that, for parameter updates, only the gradients concerning the LoRA adapter weights are necessary, rather than those for the 4-bit weights. This is achieved by calculating the derivative of with respect to in BF16 precision after dequantization from the storage format. The forward pass of the model can then be expressed as follows, which is analogous to the general formulation introduced in Equation (3):
To summarize, the QLoRA approach employs two distinct data types: a storage data type (usually 4-bit NormalFloat), and a computation data type (16-bit BrainFloat). This arrangement optimizes memory efficiency while maintaining computational accuracy. The methodology achieves a balance between resource utilization and performance by conducting computations in the higher precision format, while saving memory in the lower precision format during storage.
5. Experiments and Results
This section studies the empirical analysis of various multi-armed bandit strategies and introduces a new approach informed by LLMs. We investigate the epsilon-greedy strategy as a base case and further compare it with other traditional strategies, such as UCB and Thompson sampling. As the environment becomes more complex, such as in non-stationary and parametrized bandit distributions, these traditional strategies are put to the test. The results help identify the strengths and weaknesses of each strategy and how quickly they converge to the best action under different circumstances. Moreover, we take a significant leap by introducing the LLM-informed strategy. It harnesses the potential of LLMs, such as GPT-3.5-turbo, Flan-t5-xl or QLoRA, to aid the decision-making process in multi-armed bandit problems. This novel approach seeks to exploit the superior predictive abilities of LLMs, providing insightful recommendations on the best bandit selection strategy based on the current state of the game.
5.1. Epsilon-Greedy
We begin the experimentation with the epsilon-greedy strategy, one of the most common ways of balancing the exploration–exploitation trade-off. In this context, a multi-armed bandit is a problem in which you have to choose the most profitable action from a set of choices, based on a series of trials. The “bandit” part of the name comes from a metaphor with slot machines, which are also known as one-armed bandits.
In the simulation in Figure 1, we have three bandits, each with a different “true mean” of the reward. The epsilon value determines the proportion of the time that the simulation will explore (choose a random bandit) instead of exploiting (choosing the bandit that currently has the highest estimated mean). After running the simulation with different values of epsilon, then we produce a plot that shows the cumulative average of the rewards over time, on a logarithmic scale. This plot shows how quickly the distinct values of epsilon allow the simulation to converge on the best bandit.
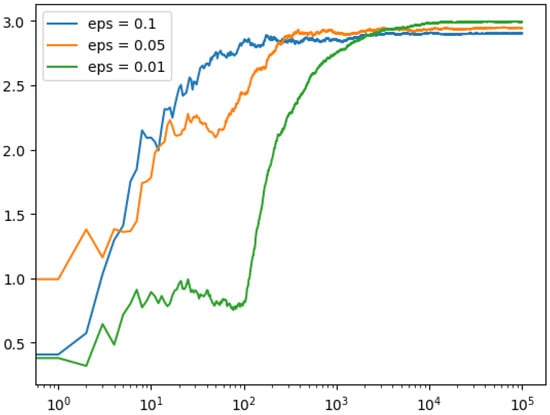
Figure 1.
Cumulative average of the rewards over time, on a logarithmic scale, for the epsilon-greedy strategy.
5.2. Alternative Strategies: UCB and Thompson Sampling
Next we expand the bandit class to include the UCB and Thompson sampling strategies. Note that these strategies require a little more information than epsilon-greedy. For UCB, we need to keep track of the total number of actions taken to compute the confidence bounds. For Thompson sampling, we need to keep track of both the number of successes and failures (modeled here as rewards of 1 and 0) to shape the beta distribution from which we sample.
We will now generate plots for the average rewards over time using the strategies epsilon-greedy, UCB, and Thompson sampling. First, we assume the bandits have binary rewards (either 0 or 1) for simplicity and to align ourselves with the typical use cases of UCB and Thompson sampling. Then, we run experiments with each strategy and plot the cumulative average rewards over time in Figure 2, where we show how the average reward evolves over time for each strategy. With this, we can compare how quickly each strategy converges to the optimal bandit, and how they perform relative to each other over the course of many trials.
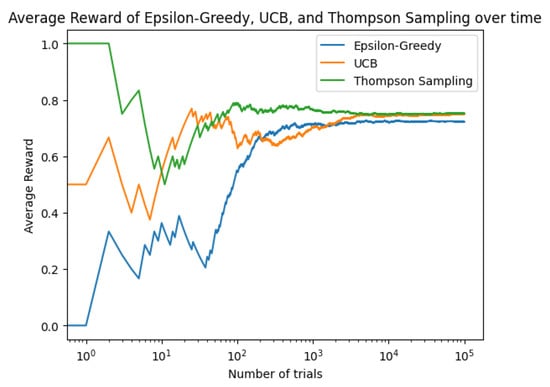
Figure 2.
Cumulative average of the rewards over time for strategies epsilon-greedy, UCB, and Thompson sampling.
5.3. Parametrized Distributions of Bandits
For the next experiments, we focus on parametrized bandit distributions. At first, the reward for each bandit is modeled as a Gaussian distribution with a certain mean. It would be more flexible to allow for arbitrary reward distributions, parametrized by more than just the mean. In Figure 3, the rewards for each bandit are generated by drawing from a normal distribution with a distinct mean. We then create three functions that generate rewards according to different normal distributions, and run the experiment using the epsilon-greedy and the UCB strategies. The results show the average reward over time for each strategy, which helps us understand the performance of the distinct strategies. Thompson sampling is typically used for binary rewards and is not included in this plot because our reward functions generate normally distributed rewards.
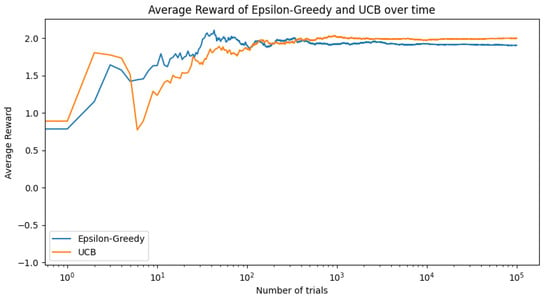
Figure 3.
Average reward over time for epsilon-greedy and UCB strategies.
5.4. Non-Stationary Bandits
From now on, we will focus on non-stationary bandits. Real-world scenarios often involve non-stationary processes, where the reward distributions change over time; an extension can handle such non-stationary bandits. We therefore incorporate non-stationary bandits by modifying the reward functions over time. For instance, we can adjust the mean or variance at certain time steps. However, in a non-stationary environment, it is generally beneficial for the agent to continue exploring, as the optimal action may change over time. Therefore, using strategies that balance exploration and exploitation, such as epsilon-greedy or UCB, becomes more effective in these cases. That is, the reward distributions of the bandits change halfway through the experiment. This means that the optimal bandit may also change at this point.
Figure 4 plots the average reward over time for the epsilon-greedy and UCB strategies when facing non-stationary bandits. The vertical dashed line represents the change point where the reward distributions of the bandits shift.
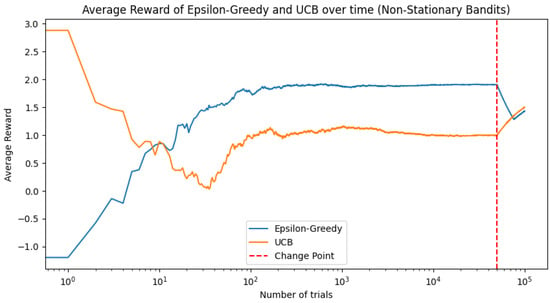
Figure 4.
Average reward over time for the epsilon-greedy and UCB strategies with non-stationary bandits.
5.4.1. Graphical Display
To visualize the estimated value of each bandit over time, we plot the estimated values in Figure 5 and Figure 6; they illustrate how the estimated value of each bandit evolves over the course of the experiment.
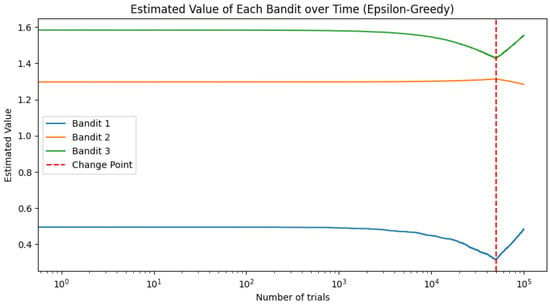
Figure 5.
Estimated value of each bandit over time for the epsilon-greedy strategy.
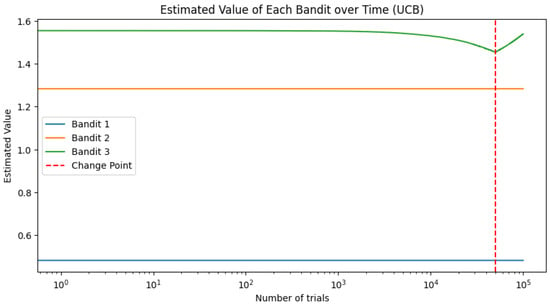
Figure 6.
Estimated value of each bandit over time for the UCB strategies.
5.4.2. Performance Metrics beyond Average Rewards
Furthermore, we can use other performance metrics. For instance, in addition to plotting the average rewards, we could also compute and display other performance metrics, such as regret, which measures the difference between the rewards we received and the rewards we could have received if we always chose the optimal action, so a smaller regret indicates a better strategy. In this sense, we need to know the optimal bandit at any given time point. In a stationary setting, it is the bandit with the highest expected reward. However, in a non-stationary setting, it could change over time. In the setup, the optimal bandit may change when the reward functions change.
Figure 7 shows the regret for the epsilon-greedy and UCB strategies and plots it over time. Please note that, in a non-stationary environment, it could be tricky to define an optimal bandit, especially if the reward distribution changes unpredictably or frequently. Here, we assumed that the change point is known, and we re-evaluated the optimal bandit at the change point, but in a real-world scenario, we might not know when or how the reward distributions change.
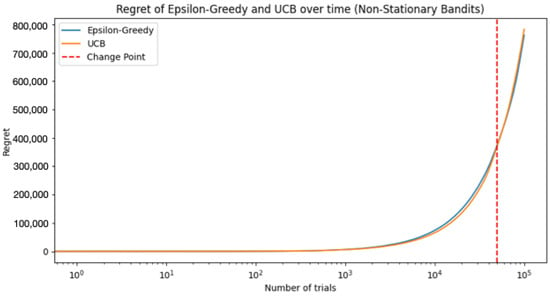
Figure 7.
Regret for the epsilon-greedy and UCB strategies.
5.4.3. Convergence Analysis
In our convergence analysis, we incorporated functionality to examine the algorithm’s convergence across various scenarios. This includes tracking the number of trials required for the algorithm to accurately identify the best bandit as illustrated in Figure 8 and Figure 9. This process entails recording the selected bandit at each step and checking when it aligns with the bandit possessing the highest mean reward. It is important to remember, however, that the concept of convergence in a multi-armed bandit problem is somewhat more complex, especially when applying an epsilon-greedy approach. As there is always a probability epsilon of selecting a random action, we do not strictly converge to always selecting the optimal action. Rather, it may be more insightful to monitor the evolution of the proportion of instances in which we opt for the optimal action over time.
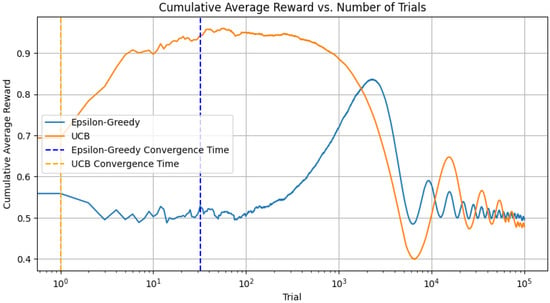
Figure 8.
Cumulative average reward versus number of trials for epsilon-greedy and UCB strategies.
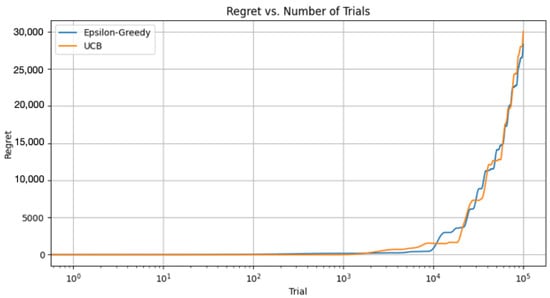
Figure 9.
Regret versus number of trials for epsilon-greedy and UCB strategies.
In Figure 8, the dashed lines represent the time at which the respective algorithms first identified the optimal bandit. This is a simplistic measure of convergence and might not fully reflect the learning process, especially in non-stationary settings. Nonetheless, it gives us a sense of when each algorithm begins to catch on to the best choice. For this, we redefine the reward functions to take the time step as an argument and to return values that vary over time. We make a simple change such that the mean of each bandit’s reward changes slowly over time. In these new reward functions, the mean reward of each bandit slowly oscillates over time.
In a non-stationary setting, the optimal action can change over time. The above convergence time still refers to the time it first reaches the optimal action, not how well it adapts to changing circumstances.
5.5. LLM-Informed Strategy
The utilization of an LLM, such as GPT-3.5-turbo, or Flan-t5-xl [23], can facilitate insightful recommendations for the multi-armed bandit problem. The proposed approach relies on the model’s capacity to suggest an optimal strategy (e.g., “epsilon-greedy” or “upper confidence bound”) given the present state of the game, including prior results. This process can be formalized as follows, and the flow diagram is shown in Figure 10:
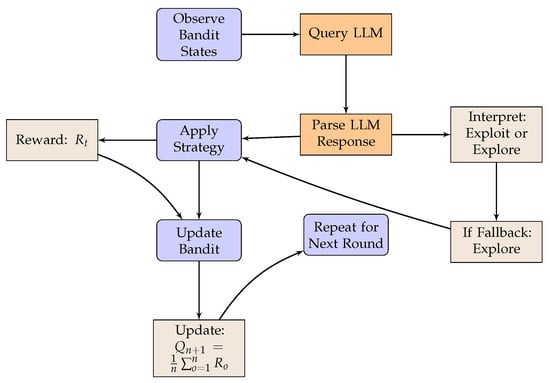
Figure 10.
Flow diagram of the LLM-informed strategy for the problem of multi-armed bandit.
- Game state definition: The game state could encapsulate an array of information, including the total rewards accrued from each bandit, the frequency with which each bandit is selected, and the average reward obtained from each bandit. These data must be translated into a format that can be readily comprehended by the LLM.
- Strategy recommendation request: This game state information can be utilized to request a strategy recommendation from the LLM. It is crucial to structure the prompt in a manner that clearly articulates the game state and seeks a specific output (e.g., the designation of a strategy).
- Output interpretation: The LLM output must then be translated back into a form that can be interpreted by the bandit selection algorithm. This could be as straightforward as mapping strategy names to corresponding functions within the code.
- Recommended strategy implementation: The final step entails utilizing the strategy recommended by the model to decide the next bandit to be selected.
In our research, we specifically focus on rate-limiting requests to the OpenAI API, as well as employing regular expressions to distill strategy recommendations from the LLM output. In this context, we pose a query to the model regarding whether to “exploit” (i.e., select the bandit with the highest estimated mean reward), or “explore” (i.e., select a bandit randomly) in the forthcoming round, given the current state of the bandits.
That is, the usual flow described in Figure 10 in a MAB problem encompasses the following:
- Observe the state of the bandits.
- Decide on a strategy, either to explore (choose a bandit randomly) or exploit (choose the bandit currently known to give the highest reward).
- Apply the chosen strategy, meaning pull the arm of a bandit based on the decision in step 2.
- Receive a reward from the bandit that was chosen.
- Update the knowledge about the bandit that was chosen, based on the reward received.
In our implementation, we employ several strategic measures to optimize the interaction with the LLM and the execution of the recommendation process.
- Firstly, we incorporate a caching mechanism to store the previous LLM recommendations. By doing so, we eliminate the need for redundant API calls when the state of the game has not changed significantly, thereby conserving resources and increasing efficiency. The state of the game is represented as a string summarizing the pull count and estimated average reward for each bandit, which is then used as the key in the recommendation cache.
- Secondly, our implementation is designed to handle potential exceptions that may occur during interaction with the OpenAI API. Specifically, we implement an exponential backoff strategy, which essentially means that if an API call fails, the system waits for a certain amount of time before retrying, with the wait time increasing exponentially after each consecutive failure. This mechanism provides robustness against temporary network issues or API rate-limiting, enhancing the overall reliability of the system.
- Lastly, we introduce a threshold (ö) for determining significant changes in the bandit state. This is particularly important, as it governs when a new strategy recommendation is required from the LLM. If the change in the bandit state falls below this threshold, the system reuses the previous recommendation, once again avoiding unnecessary API calls. This threshold is a flexible parameter that can be fine tuned to balance the trade-off between responsiveness to changes and minimizing API requests.
In the following analysis, we explore the performance of three strategies in tackling the MAB problem: epsilon-greedy, UCB, and the proposed LLM-informed strategy. We conducted a series of trials, running each strategy through the same sequence of bandits, and then recording their cumulative average rewards over time.
Figure 11 represents the evolution of the cumulative average reward for each of these strategies over the course of the trials. Each point on a line represents the average reward that a particular strategy had received up to that iteration, giving us an insight into how quickly and effectively each strategy accrues rewards.
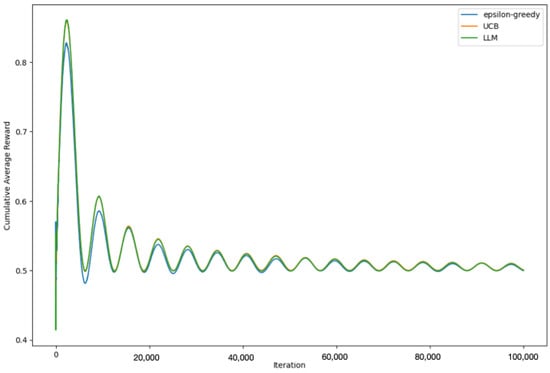
Figure 11.
Cumulative average rewards over time for epsilon-greedy, UCB, and LLM-informed strategies with ö = 0.1.
Observing the trends in the graph, we can analyze the behavior and effectiveness of the different strategies. The epsilon-greedy and UCB strategies follow conventional approaches with known strengths and weaknesses. The epsilon-greedy strategy provides a balance between exploration and exploitation, while UCB optimizes its choices based on uncertainty and potential for reward. On the other hand, the LLM-informed strategy leverages the predictive power of large language models, in this case, GPT-3.5-turbo-0301. The model offers strategy recommendations based on the current state of the game, which includes the number of times each bandit has been pulled and their average rewards.
5.6. Utilizing QLoRA with A100 GPU
The methodology can be implemented in a real system by replacing the calls to OpenAI API model GPT-3.5-turbo with a very recently released LLM model: QLoRA [14], an efficient fine-tuning approach designed for large-scale models. QLoRA facilitates the fine tuning of models as large as 65 billion parameters and inference on a GPU, such as A100, while preserving the performance level of 16-bit fine tuning. Its low memory usage and efficient performance were achieved through a number of innovative strategies [32], such as 4-bit NormalFloat (NF4), double quantization (DQ), and paged optimizers.
We follow a similar methodology as the one adopted with GPT-3.5-turbo-0301 but this time implementing the recommendations through QLoRA.
- In the first step, we defined the state of the game, converting the relevant data into a format comprehensible to QLoRA.
- Then, we made a strategy recommendation request, using the game state information to prompt QLoRA for a strategy.
- After receiving the QLoRA output, we interpreted it, translating it into a form that the bandit selection algorithm could understand and act upon.
- Finally, we implemented the recommended strategy to determine the next bandit to choose.
We used the same strategic measures as before, including caching previous recommendations, and introducing a threshold for significant changes in the bandit state. These measures ensured that we made optimal use of the capabilities of QLoRA while managing resources efficiently and handling potential exceptions robustly. As observed in Figure 12, the QLoRA-driven LLM-informed strategy yields results commensurate with those achieved by the OpenAI model GPT-3.5-turbo.
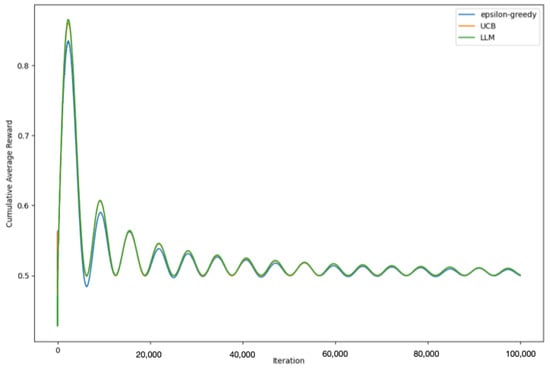
Figure 12.
Temporal progression of cumulative average rewards for epsilon-greedy, UCB, and QLoRA-driven LLM-informed strategies with ö = 0.1.
By employing this approach, we were able to gain insights into the performance of the LLM-informed strategy when powered by QLoRA, and assess its effectiveness in comparison to both epsilon-greedy and UCB strategies. Our results reinforced our earlier findings, highlighting the considerable potential of the LLM-informed strategy in handling the MAB problem. We observed that the QLoRA-powered LLM-informed strategy not only kept pace with its counterparts but often exceeded their performance, further underlining the value of integrating LLMs in decision-making processes.
Our experimental outcomes underscore the potential of the LLM-informed strategy as a strong competitor to well-established methods, such as epsilon-greedy and UCB in non-stationary environments. This compelling performance supports our hypothesis that LLMs, with their profound capabilities to comprehend and predict complex scenarios, can offer valuable insights to enhance decision-making tasks. A particularly noteworthy finding is the consistent performance of the LLM-informed strategy, often matching, if not surpassing, the effectiveness of the best conventional strategy implemented for the specific problem. This evidence suggests that the integration of LLMs into traditional approaches can substantially improve their performance in dynamic environments, opening up new avenues for leveraging the predictive power of LLM in various real-world applications.
To sum up, our experimental evaluation, as depicted in Figure 11, is intended to show the cumulative average reward for epsilon-greedy, UCB, and the proposed LLM-informed strategy over time. The results demonstrate that the LLM-informed strategy, guided by the predictive capabilities of GPT-3.5-turbo-0301, can indeed perform comparably with traditional bandit strategies. In the context of the non-stationary multi-armed bandit problem, which is known for its volatility and uncertainty, maintaining competitive performance is a significant achievement. This is because the LLM-informed strategy must deal with dynamic changes and adapt its strategy based on a predictive model. Moreover, in our experiments with QLoRA, an LLM-informed strategy showed not just comparable but often better performance than its traditional counterparts. As presented in Figure 12, the QLoRA-driven LLM-informed strategy often exceeded the performance of both epsilon-greedy and UCB strategies, providing further evidence of the potential of integrating LLMs in decision-making processes.
6. Applications of the LLM-Informed Strategy in Various Fields
The LLM-informed strategy for non-stationary multi-armed bandit problems, as we presented in this paper, represents a significant stride in the direction of harnessing advanced AI models for complex decision-making scenarios. While our focus was primarily on the abstract problem setting, the ramifications of this framework are potentially vast and multifaceted, extending to numerous practical applications.
6.1. Digital Marketing
In the realm of digital marketing, for instance, the non-stationary multi-armed bandit framework can be instrumental in optimizing online advertisement placement. Online advertising platforms often have to balance between displaying ads that have performed well in the past, and experimenting with new ones to explore their potential. By integrating our LLM-informed strategy, such platforms could leverage sophisticated language understanding capabilities to gauge the context, assess changing trends, and adjust ad selection strategies accordingly.
In digital marketing, specifically for online advertisement placement, traditional A/B testing techniques are often used. These techniques randomly show one version of an ad (A) to half of the users and a different version (B) to the other half. The ad that receives more clicks or conversions is then chosen for wider deployment. However, these methods often lack the capacity to adapt to the rapidly changing online environment and trends, which is where our proposed LLM-informed strategy could offer substantial benefits. Our method would be able to analyze not just click rates but also the content of the ads, user interactions, feedback, and broader market trends, using the predictive power of LLMs. This can potentially improve ad performance by providing more nuanced and context-aware recommendations, dynamically adjusting ad selection based on the current state of the online environment.
6.2. Healthcare
Similarly, in healthcare, an LLM-informed bandit model could potentially assist in personalizing treatment plans. If each “arm” of the bandit represents a different treatment option, our approach could help in navigating the critical trade-off between sticking with treatments that have shown promise, and exploring potentially better alternatives. Given the complex and dynamic nature of human health, the non-stationarity aspect of our model is crucial for adjusting recommendations based on the evolving health status of the patient.
Consider the case of managing a chronic condition such as diabetes. In this scenario, each “arm” of the bandit could represent a different treatment plan that combines diet, exercise, and medication. Each plan’s efficacy could be considered the reward that the bandit provides. In traditional treatment models, doctors often rely on their experience and established clinical guidelines to determine the best course of action. However, these treatments are often generalized and may not account for individual patient variations and the non-stationarity nature of human health, i.e., the change in a patient’s health condition over time. By implementing our proposed LLM-informed strategy, we could leverage the vast amounts of medical data and research available, along with the patient’s health history and current condition, to make a more informed decision. As the patient’s health status evolves, the LLM can adjust the recommendations, emphasizing either the exploration of new treatment plans or exploitation of existing plans based on their effectiveness. The application of the LLM-informed strategy could lead to more personalized, adaptive treatment plans that could potentially improve patient outcomes. In comparison to traditional methods, our approach could provide a more dynamic, individualized treatment pathway that adjusts according to a patient’s changing health status.
6.3. Reinforcement Learning
Moreover, in the field of RL, our methodology could be adapted to enhance decision-making policies in environments with changing reward dynamics. A prominent example of this would be financial trading systems, where the reward associated with different trading actions (e.g., buy, sell and hold) fluctuates unpredictably. An LLM-informed strategy could potentially improve such systems’ robustness by dynamically adjusting to the volatile nature of financial markets.
Consider a RL agent tasked with navigating a financial trading environment. In such a setting, each trading action—buying, selling, or holding a variety of financial instruments—can be seen as an ‘arm’ of a multi-armed bandit. The associated reward is the financial gain or loss resulting from these actions, which fluctuates unpredictably due to the inherent volatility of financial markets. Traditionally, RL agents in this scenario rely on fixed policies learned from historical data. However, these policies may not adapt well to sudden changes or new trends in the market. The non-stationary nature of the problem, wherein the optimal actions change over time, poses significant challenges. Our proposed LLM-informed strategy could be instrumental in enhancing the adaptability of such an RL agent. The LLM, trained on extensive financial data, market news, and historical trends, could provide actionable insights to the RL agent, allowing it to adjust its policy dynamically. For example, if an unexpected market event occurs, such as a political instability event, the LLM could analyze relevant real-time news articles, social media sentiment, and other relevant information, and provide a prediction of its potential impact. This prediction could then inform the RL agent’s action, allowing it to update its policy dynamically and respond to the event in a potentially more profitable way. Compared to traditional methods, our LLM-informed approach allows for more responsive and adaptable strategies that can better handle the non-stationarity of financial markets. This could potentially result in more robust financial trading systems that perform well even in the face of volatile market conditions.
6.4. Robotics
In robotics, particularly for drones, our proposed framework has compelling potential applications. One crucial aspect of operating drones involves the dual challenges of positioning and power optimization. For instance, consider a fleet of drones tasked with monitoring an extensive area: each drone could represent an arm in a multi-armed bandit setup, with the reward being the quality of surveillance coverage balanced against the power consumed during flight. The decision to ‘pull a bandit arm’ would correspond to dispatching a drone to a particular location, or adjusting its power utilization for enhanced efficiency. By incorporating language models into the decision-making process, more sophisticated context-aware strategies can be devised. For example, a large language model could analyze temporal and spatial data trends, weather conditions, or other situational variables to advise on the optimal positioning of the drones or power usage. The LLM-informed bandit strategy thereby opens up possibilities for more nuanced and context-aware decision making in the field of robotics, allowing for improved operational efficiency and adaptability in dynamically changing environments.
Consider an emergency response scenario, where a fleet of drones is employed to monitor and assess the situation in an area affected by a natural disaster, such as a wildfire. In this context, each drone could be considered an “arm” in a multi-armed bandit problem, with the reward being the amount and quality of surveillance data collected against the power consumed during flight. The challenge here lies in making real-time decisions on where to dispatch each drone for maximum coverage and data collection while conversely managing the drones’ battery life. Traditional methods might utilize pre-programmed paths or follow fixed protocols to handle such tasks. However, these approaches might fall short in situations where the environmental conditions are rapidly changing and uncertain, such as during the spread of a wildfire. With our proposed LLM-informed strategy, a LLM trained on vast amounts of spatial, temporal, and meteorological data could provide real-time recommendations for drone dispatch decisions. For example, the LLM could analyze current wind speed and direction data to predict the likely path of the wildfire. It could then suggest repositioning some drones to those areas, enabling early data collection and facilitating prompt emergency responses. Moreover, the LLM could help optimize the drones’ battery usage by considering their remaining power levels, the distance to areas of interest, and the urgency of data collection needs. For instance, it could recommend that a drone with low battery levels focus on nearby areas of interest or return to the base for recharge, while a drone with higher battery levels could be dispatched to more distant or challenging locations. By integrating LLMs into the decision-making process, the drones can effectively respond to dynamically changing conditions and increase their operational efficiency. This example provides an insight into how our LLM-informed bandit strategy can significantly improve real-time decision making in robotics, particularly in scenarios where adaptability and responsiveness are critical.
6.5. Biology and Life Sciences
The proposed LLM-informed bandit strategy can also find significant potential applications in the field of biology and life sciences. Firstly, consider the vast and expanding domain of drug discovery. A medicinal compound’s efficacy can be viewed as a “bandit arm” with unknown reward. Drug researchers aim to balance exploration (testing new compounds) and exploitation (further testing of promising compounds) in order to maximize the success of finding an effective drug, while minimizing the resources and time spent. An LLM could provide insights from previous experimental results, published research, and known biological mechanisms to inform this process. Secondly, within the domain of genomics, the multi-armed bandit framework could aid in the selection of candidate genes for further study from among thousands of potential genes. Here, each gene can be considered a bandit, and pulling an arm corresponds to allocating resources to sequence or experiment with a particular gene. The reward could be associated with the discovery of significant genes linked to a trait or disease of interest. Incorporating LLMs into this process can provide additional insights by leveraging vast amounts of existing genomics literature and data to inform which genes might be worth further exploration or exploitation. Lastly, in ecosystem management and conservation biology, the multi-armed bandit problem can model the decision-making process of resource allocation for species protection. Each species or habitat can be considered a bandit, and the reward could be the positive impact on biodiversity. An LLM-informed approach could help parse complex ecological data, predict the effects of various conservation strategies, and guide the decision-making process more effectively.
Consider a scenario where a team of genomics researchers is investigating a set of candidate genes associated with a certain trait or disease, such as cancer or heart disease. In this case, each gene can be considered an “arm” of the multi-armed bandit, with the “reward” being the discovery of significant links between a gene and the disease or trait of interest. Traditional methods may involve a somewhat brute-force approach, studying each gene sequentially or randomly based on available resources, without much prior knowledge or any sophisticated strategy to guide the process. With our proposed LLM-informed strategy, the researchers could use an LLM trained on vast amounts of genomics literature and data to assist their decision-making process. The LLM could analyze previous experimental results and the existing literature on the genes in question, and cross-reference with data on known gene–disease associations. For instance, if early experiments reveal strong evidence linking certain genes to the disease, the LLM could recommend focusing more resources on these “promising” genes (exploitation). Simultaneously, it could also identify lesser-studied genes that share similar characteristics or functions with the promising ones. The researchers can then allocate some resources to studying these potentially relevant but unexplored genes (exploration). Additionally, if the disease’s nature or the research context changes—for example, if new research suggests the disease involves different biological pathways—the non-stationarity aspect of our bandit model allows the LLM to adjust its recommendations accordingly. This way, the strategy remains flexible and adaptive to the evolving research landscape. This example illustrates how our LLM-informed bandit strategy can significantly enhance decision making in genomics research by improving resource allocation and potentially accelerating the discovery of significant genes linked to diseases or traits of interest.
6.6. Finance
Multi-armed bandit strategies have traditionally found a variety of applications in finance; however, the incorporation of LLMs can offer an innovative twist to conventional approaches. Take portfolio optimization as an example: it is essentially a balancing act between risk and reward, mirroring the exploration–exploitation dilemma. Each asset or investment opportunity can be treated as a bandit, with the act of pulling an arm being analogous to allocating funds to that asset, and the return on investment forming the reward. The role of an LLM here is to sift through vast volumes of financial data, market trends, news, and historical performance records, thereby guiding decision makers about which assets warrant further investment (exploitation), and which untested ones could be considered (exploration). Similarly, algorithmic trading, particularly high-frequency trading, where algorithms execute multiple trades based on multiple factors, can benefit from the application of LLMs. Here, each trade or trading strategy can be construed as a bandit. LLMs, with their ability to leverage insights from market data, economic indicators, and news, can contribute to the decision-making process by suggesting potential trades. Credit scoring, another important facet of finance, can also be interpreted within the bandit framework. In this scenario, each prospective borrower is considered as a bandit. The act of pulling an arm would signify the granting of a loan, while the reward would correspond to successful loan repayment with interest. An LLM, by processing diverse data pertaining to each applicant—credit history, income level, and potentially even social media activity—can yield more nuanced and reliable credit scoring. Finally, let us consider insurance. Each policyholder or potential policyholder can be represented as a bandit, and issuing a policy is analogous to pulling a bandit’s arm. The profitability of the policy forms the reward. Here, an LLM can offer valuable insights by analyzing a broad array of data on each policyholder or applicant—personal details, claim history, and data sourced from IoT devices (such as telematics in auto insurance)—effectively enhancing the underwriting process.
Consider a scenario where a financial advisor is tasked with managing a diverse investment portfolio. Each asset or investment opportunity in the portfolio can be considered an “arm” of the multi-armed bandit. The act of pulling an arm corresponds to allocating funds to a particular asset, while the return on investment from that asset is considered the reward. A traditional approach to portfolio optimization might involve strategies based on past performance, expected returns, risk tolerance, and other relatively static factors. However, financial markets are dynamic and can change rapidly in response to numerous unpredictable factors, ranging from economic indicators to global events. Our LLM-informed bandit strategy can greatly enhance this process. A LLM trained on extensive financial data, market trends, news, and historical performance records can offer nuanced insights to guide the advisor’s decision making. For example, suppose certain assets in the portfolio have been performing well consistently. The LLM, analyzing historical data and current market trends, may advise allocating more funds to these assets (exploitation). However, simultaneously, the LLM might identify emerging opportunities in the market—perhaps a nascent technology sector stock or a new bond issue—that are yet untested but could offer significant returns. The advisor can then choose to invest a portion of the funds in these new opportunities (exploration). The non-stationarity aspect of our model allows the LLM to dynamically adjust its recommendations in response to changing market conditions. For instance, in the face of a looming economic downturn, it could advise shifting funds from high-risk stocks to safer assets, such as treasury bonds. This way, the strategy remains adaptive and robust in the face of market volatility. This practical example illustrates how our LLM-informed bandit strategy can revolutionize decision making in finance by optimizing portfolio management, effectively balancing risk and reward, and enhancing overall investment performance.
6.7. Challenges and Discussion
While the integration of LLMs in these applications is certainly promising, it also invites challenges. One key consideration is the computational cost associated with querying the LLMs, as well as the complexity of translating domain-specific information into a language format that the LLM can process. It is also critical to ensure that the decision-making process remains interpretable, especially in high-stakes settings, such as healthcare, which necessitates the careful handling of the LLM recommendations.
Further to this, the deployment of LLM-informed strategies in real-world applications often requires a robust and adaptive framework that can respond efficiently to changing environments. Future research may focus on the development of such dynamic systems, which can integrate feedback in real time and recalibrate the model’s recommendations accordingly.
The ethical implications of applying LLMs in decision-making processes, particularly in sensitive fields, such as healthcare and finance, also require thoughtful exploration. These models, although sophisticated, are still artificial and do not possess human judgment. Relying on their outputs without human oversight could potentially lead to biased or unethical decisions. Future works should, therefore, aim to establish a comprehensive ethical framework for the deployment of LLM-informed strategies.
Lastly, the question of data privacy and security is of paramount importance. The nature of the operation of LLMs, which involves processing massive amounts of information, often including sensitive data, inevitably raises privacy concerns. This issue is particularly salient in fields such as healthcare, finance, and personal advertising, where data protection is crucial. Future efforts should aim to devise methods for leveraging the capabilities of LLMs in a manner that respects and safeguards individuals’ privacy.
Addressing these challenges will not be a trivial task, but given the potential benefits and advancements that the integration of LLMs promises, it is a pursuit worth undertaking. Future works should aim at creating more efficient, ethical, and privacy-respecting methods for the application of LLM-informed strategies in various fields.
7. Conclusions and Future Work
In this study, we took a step forward in tackling the non-stationary multi-armed bandit problem by integrating the power of LLMs into the decision-making strategy. Bridging traditional RL strategies, such as epsilon-greedy and UCB, with the advanced AI capabilities provided by models such as GPT-3.5-turbo and QLoRA, we created a framework that promises adaptability and efficiency in dynamic environments. This novel approach represents a significant stride in combining AI, game theory, and reinforcement learning, opening up exciting opportunities for future research on how advanced AI models can transform decision making in dynamic situations.
However, this is just the initial exploration, and there is ample scope for refinement and expansion. In the future, our goal is to enhance the strategy recommendation process, either by providing more detailed information to the LLMs or by refining the interpretation of their advice. This could involve an intricate representation of the game state or a more sophisticated approach to extract strategy recommendations from the LLM output.
We are also interested in examining the amalgamation of other RL strategies in our LLM-informed framework. We believe that by leveraging the strengths of different strategies and the versatile language understanding capabilities of LLMs, we can engineer a more robust and adaptable solution to the MAB problem.
In addition to refining our methodology, we are eager to extend its application to various real-world domains, such as personalized healthcare and financial trading systems. As we delve into these areas, we anticipate unique challenges, such as ensuring the interpretability of the decision-making process and effectively handling domain-specific information. Nonetheless, we are optimistic about the potential benefits our LLM-informed strategy can bring to these fields and look forward to exploring these possibilities in our future work.
Author Contributions
Conceptualization, J.d.C. and I.d.Z.; funding acquisition, G.R. and C.T.C.; investigation, J.d.C. and I.d.Z.; methodology, J.d.C. and I.d.Z.; software, J.d.C. and I.d.Z.; supervision, C.T.C., G.R., J.C.C. and P.M. writing—original draft, J.d.C.; writing—review and editing, C.T.C., J.C.C., G.R., P.M., J.d.C. and I.d.Z. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge the support of Universitat Politècnica de València: R&D project PID2021-122580NB-I00, funded by MCIN/AEI/10.13039/501100011033 and ERDF. We thank the following funding sources from GOETHE-University Frankfurt am Main; ‘DePP–Dezentrale Plannung von Platoons im Straßengüterverkehr mit Hilfe einer KI auf Basis einzelner LKW’, ‘Center for Data Science & AI’ and ‘xAIBiology’.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no conflict of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| RL | Reinforcement Learning |
| GPT | Generative Pretrained Transformer |
| QLoRA | Quantized Low-Rank Adapters |
| GPU | Graphical Processing Unit |
| MAB | Multi-Armed Bandit |
| LLM | Large Language Models |
| UCB | Upper Confidence Bound |
References
- Robbins, H. Some aspects of the sequential design of experiments. Bull. Am. Math. Soc. 1952, 58, 527–535. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Besbes, O.; Gur, Y.; Zeevi, A. Stochastic multi-armed-bandit problem with non-stationary rewards. In Proceedings of the Advances in Neural Information Processing Systems 27, (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Russac, Y.; Vernade, C.; Cappé, O. Weighted linear bandits for non-stationary environments. In Proceedings of the Advances in Neural Information Processing Systems 32, (NIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30, (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Alayrac, J.-B.; Donahue, J.; Luc, P.; Miech, A.; Barr, I.; Hasson, Y.; Lenc, K.; Mensch, A.; Millican, K.; Reynolds, M.; et al. Flamingo: A visual language model for few-shot learning. arXiv 2022, arXiv:2204.14198. [Google Scholar]
- Wei, J.; Tay, Y.; Bommasani, R.; Raffel, C.; Zoph, B.; Borgeaud, S.; Yogatama, D.; Bosma, M.; Zhou, D.; Metzler, D.; et al. Emergent abilities of large language models. arXiv 2022, arXiv:2206.07682. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. NeurIPS 2020, 33, 1877–1901. [Google Scholar]
- Muglich, D.; de Witt, C.S.; Pol, E.V.; Whiteson, S.; Foerster, J. Equivariant networks for zero-shot coordination. Adv. Neural Inf. Process. Syst. 2022, 35, 6410–6423. [Google Scholar]
- Shah, D.; Osiński, B.; ichter, B.H.; Levine, S. LM-Nav: Robotic navigation with large pre-trained models of language, vision, and action. In Proceedings of the 6th Conference on Robot Learning, Proceedings of Machine Learning Research, PMLR, Atlanta, GA, USA, 6–9 November 2023; Volume 205, pp. 492–504. [Google Scholar]
- Huang, C.; Mees, O.; Zeng, A.; Burgard, W. Visual Language Maps for Robot Navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023. [Google Scholar]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models. arXiv 2021, arXiv:2106.09685. [Google Scholar]
- Dettmers, T.; Pagnoni, A.; Holtzman, A.; Zettlemoyer, L. QLoRA: Efficient Finetuning of Quantized LLMs. arXiv 2023, arXiv:2305.14314. [Google Scholar]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Thompson, W.R. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika 1933, 25, 285–294. [Google Scholar] [CrossRef]
- Silva, N.; Werneck, H.; Silva, T.; Pereira, A.C.M.; Rocha, L. Multi-armed bandits in recommendation systems: A survey of the state-of-the-art and future directions. Expert Syst. Appl. 2022, 197, 116669. [Google Scholar] [CrossRef]
- Cavenaghi, E.; Sottocornola, G.; Stella, F.; Zanker, M. Non stationary multi-armed bandit: Empirical evaluation of a new concept drift-aware algorithm. Entropy 2021, 23, 380. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, L.; Jiang, Y.; Zhou, Z. A simple approach for non-stationary linear bandits. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Online, 26–28 August 2020; pp. 746–755. [Google Scholar]
- Garivier, A.; Cappé, O. The KL-UCB algorithm for bounded stochastic bandits and beyond. In Proceedings of the 24th Annual Conference on Learning Theory, JMLR, Budapest, Hungary, 9–11 June 2011. [Google Scholar]
- Cesa-Bianchi, N.; Lugosi, G. Prediction, Learning, and Games; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Wei, J.; Bosma, M.; Zhao, V.; Guu, K.; Yu, A.W.; Lester, B.; Du, N.; Dai, A.M.; Le, Q.V. Finetuned Language Models are Zero-Shot Learners. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training; Princeton University: Princeton, NJ, USA, 2018. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Tokic, M. Adaptive ϵ-Greedy Exploration in Reinforcement Learning Based on Value Differences. In KI 2010: Advances in Artificial Intelligence; Dillmann, R., Beyerer, J., Hanebeck, U.D., Schultz, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 203–210. [Google Scholar]
- Russo, D.; Roy, B.V.; Kazerouni, A.; Osband, I.; Wen, Z. A Tutorial on Thompson Sampling. Found. Trends® Mach. Learn. 2018, 11, 1–96. [Google Scholar] [CrossRef]
- Rosin, C.D.; Belew, R.K. New methods for competitive coevolution. Evol. Comput. 1997, 5, 1–29. [Google Scholar] [CrossRef]
- Wooldridge, M. An Introduction to MultiAgent Systems; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Oroojlooy, A.; Hajinezhad, D. A review of cooperative multi-agent deep reinforcement learning. arXiv 2022, arXiv:1908.03963. [Google Scholar] [CrossRef]
- Dettmers, T.; Lewis, M.; Shleifer, S.; Zettlemoyer, L. 8-bit Optimizers via Block-wise Quantization. In Proceedings of the 9th International Conference on Learning Representations, ICLR, Virtual, 25 April 2022. [Google Scholar]
- Wortsman, M.; Dettmers, T.; Zettlemoyer, L.; Morcos, A.; Farhadi, A.; Schmidt, L. Stable and low-precision training for large-scale vision-language models. arXiv 2023, arXiv:2304.13013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).