Abstract
As sensor nodes communicate via wireless channels, information security is essential for wireless sensor networks. Efficient protection mechanisms to ensure data security among nodes are critical. This study developed the bi-directed grouping (top-down grouping (TDG) and bottom-up grouping (BUG)) methods. In this study, we propose a group-based key distribution method, “aggregator-based grouping” (ABG), which combines the advantages of TDG and BUG to address the security issues of nodes. It employs horizontal and vertical searches, which are based on breadth-first and aggregator searches, respectively. A node performs encryption and decryption only when it requires either data aggregation or inter-group communication. The secure aggregation method can be applied to key-grouping management. We compared the proposed method with TDG and BUG using the same number of groups and network structure. For a network with maximum group members of 50 (total sensor nodes = 1000), compared with TDG and BUG, ABG reduced the number of encryption and decryption operations by ~36%. ABG avoids unnecessary encryption and decryption in the network.
1. Introduction
According to a report on the Internet of Things (IoT) analytics, the number of connected devices will increase to ~27 billion by 2025 [1]. The increasing number of devices needs to be integrated and communicated; thus, network technologies are essential for the connectivity of several devices. Various network technologies are used to connect devices. The wireless sensor network (WSN) is a major network technology. It comprises a group of sensor nodes with tiny shapes and limited power resources. It is used to measure the physical conditions of an environment, and the collected data are forwarded to data storage. Since WSNs can easily deploy a local network at a low cost, they can be employed in many domains for different novel applications [2,3,4,5]. WSN is essential to the IoT evolution, which will become a mainstream part of the Internet in the future [6]. In WSNs, each sensor node collects data from the environment and then delivers them to the base station (BS) by multi-hops via other nodes. As wireless communication in WSN is power consuming, some specific nodes on the multi-hops path are “data aggregators,” aggregating data received from children nodes to reduce the data volume and the number of transmissions to the parent node [7]. Notably, communication in WSN is conducted through wireless channels. It is more vulnerable to malicious attacks, such as eavesdropping, camouflage, and modification. Thus, there is a need for a protection mechanism to ensure data security between nodes [8,9].
As the keys used for encryption and decryption are different in the asymmetric encryption approach, heavy computation is required, which is unsuitable for WSN [10,11]. The symmetric encryption approach, where encryption and decryption operations use the same key, is more favorable to WSN. However, an efficient key management mechanism to distribute keys to nodes is vital in such an approach. Herein, we propose an implicit security scheme [12] for key distribution as it is easy to implement and requires only linear complexity. This scheme employs a group-based key management framework [13], where, based on the grouping algorithm applied, a WSN is divided into several groups. Then, it generates and delivers correspondent encryption parameters for each group to calculate its key for later encryption and decryption operations. Each group uses a unique key to encrypt data. Designing a good grouping algorithm is vital because the group topology determines the number of encryption and decryption operations needed. Unfortunately, existing key management techniques demand high computation, a large amount of memory, and complex communication rounds. However, the secure aggregation method has good management efficiency in WSNs. In our previous study [14], we proposed an online query scheme (OBEQ) with a tree topology of WSN, which uses aggregators between BS and sensors for communication processes. Further, we developed two intuitive grouping strategies: top-down grouping (TDG) and bottom-up grouping (BUG). In this study, we propose aggregator-based grouping (ABG), a generic design for efficient private key management, which protects sensor node data using a group aggregation scheme. It combines TDG and BUG and executes horizontal and vertical searches separately based on the breadth-first and aggregator-based searches from TDG and BUG, respectively. It is adaptable to the efficiency and security requirements of various sensor node distributions.
Furthermore, we developed a group-based key distribution strategy to address the security issues of nodes. Using the proposed ABG, a node executes encryption and decryption operations if and only if it must do either data aggregation or inter-group communication. Thus, the proposed algorithm can minimize unnecessary encryption and decryption operations. The remainder of this study is organized as follows: Section 2 presents typical key distribution approaches and protection schemes for data aggregators in WSN; Section 3 introduces the details of the proposed method; an experiment and a performance evaluation are presented in Section 4; Section 5 presents the conclusion and significance of the study.
2. Related Work
Data security for wireless communication between nodes is a crucial issue in WSNs. Considering data security, data have been protected using keys while they are communicated among different sensor nodes [13,14,15,16,17,18,19,20]. However, efficient and lightweight security mechanisms are needed because each sensor node has limited power computation and storage capacities. The matrix-based structure and group key set-up protocols are used in key management to secure multicast communications in heterogeneous WSNs, but it has high energy consumption [21]. Key distribution and management approaches are categorized into four types: single master key (SMK), all pair wise key (APWK), random pair wise key (RPWK), and group-based key (GBK) [13,14,16]. SMK is the simplest for distributing keys [22,23,24], where all sensor nodes use the same encryption key to protect their communications. Despite its simplicity, the entire protection mechanism is broken when a hacker breaks and captures one of the sensor nodes. In APWK, a unique encryption key protects communication between any two nodes [17]. A break in any communication does not proliferate to other communications, but this approach is not energy efficient, especially during calculations [25]. In RPWK, a key pool is created, from which each node randomly chooses some keys to make its key ring [18,19,20,21,22,23,24,25,26]. Nodes broadcast their key ring identities (ID) to other nodes. A secure channel is established if either of the two nodes within the wireless communication coverage has the same ID. For GBK [19,20], an entire WSN is divided into several groups. Sensor nodes’ connections are of two types: in group and inter-group. All sensor nodes in the same group use the same key to protect their communications. One node (or some nodes) has the key of its neighboring group to ensure secure communication between the two groups. Hereafter, such a node is called a “boundary node.” Among these four approaches, GBK has good security and resilience since cracking one node will not endanger the entire network. Moreover, GBK is scalable since each node needs to store only one or two keys. In addition, the entire network is more difficult to crack because the damage caused by any single attack will only be confined to its group nodes. An algorithm based on the implicit certificate has been proposed to solve the security problem among the access points in a dynamic access point group and between the users’ equipment [27]. The hybrid-session key management scheme for WSN was proposed to reduce power consumption by minimizing public key cryptography [28]. The uneven clustering approach improves the energy efficiency load balance in WSN [29]. In summary, group- and matrix-based management approaches have quick reaction times and high connectivity with networks, respectively. However, they have high computation overhead time and memory consumption [30]. To address these challenges, herein, we use the aggregating method to solve the large memory consumption and constrained computation performance of the existing key management methods.
In WSNs, secure aggregation methods are widely employed in inference attack protection [31] and smart grids [32]. Secure aggregation has been employed in federated learning systems, and the results show that the method needs fewer training iterations and is flexible [31]. Regarding data aggregation, Secure Information Aggregation (SIA) [33,34] targets a flatter WSN hierarchy with only one data aggregator to which all sensor nodes send data. In addition to aggregating the received data, the aggregator uses the hash tree [35,36,37] to convert individual data to an authentication code. As SIA considers only one data aggregator, it is unsuitable for large-scale network deployment. Some studies have been conducted to improve the computation efficiency of aggregation methods [12,37,38,39,40,41]. The turbo-aggregate method achieves O(nLogn) for a secure aggregation in a network with n users, and it can speed up the network’s dispatching efficiency [37].
Energy consumption is another issue in data aggregation. The facility derived from data aggregation is not fully utilized, and much power is consumed during communication. For energy efficiency in WSN, a fuzzy-based node arrangement is used to select the parent node and format the tree topology. Secure Reference-based Data Aggregation (SRDA), in which each sensor node compares its sensed data with the averaged value of previous sensed data (“reference value”), has been proposed [39]. Each node transmits and encrypts only the differential value between the sensed data and the reference value to reduce bandwidth and power consumption. The main disadvantage of this scheme is that only the cluster root can aggregate sensed data; thus, the aggregation effectiveness is reduced. In [40], the authors proposed “Concealed Data Aggregation” to build upon privacy homomorphism, which can directly perform calculations on encrypted data. Thus, all encrypted data are directly fed into the aggregation function, and the aggregated result is delivered to the BS. However, this scheme cannot render high-level security. The logical key hierarchy is used to speed up the encryption and decryption for implementing an effective key-numbering approach [41,42]. In Ref. [43], the logic operations are used to develop the lightweight authenticated group-key distribution scheme to speed up the encryption and decryption operation. In Ref. [12], a promising scheme called implicit security was proposed. The term “implicit security” implies that data protection comes from the partitioning of data d into pieces using mathematical polynomial operations (instead of relying on cryptography). The time complexity for this implicit security scheme is only O(n) for data partitioning or recovery. In this study, we used this scheme to partition and reconstruct our encryption key.
Compared with existing key management approaches, the algorithm proposed herein employs the aggregating method to group keys, and the bi-directed search improves the computation performance. In contrast to previous studies, we account for data aggregation and develop clustering algorithms with the minimum number of encryption/decryption operations to generate a group key. This enables secure communication among nodes within a group and increases scalability.
3. The Proposed Methods
The sensing nodes are safe before deployment, and their positions cannot be changed afterward. Moreover, after deployment, the position of the nodes cannot be predicted in advance. We divided the sensor nodes into three roles: the BS, aggregation node (Aggregator), and general sensor node. Therefore, it can store information for each node. It also controls the selection of aggregation nodes. Unless a replacement instruction is issued, the aggregation node that performs the aggregation function is fixed every time a user makes a request. Generally, the sensing node senses parameters in the environment or serves as an intermediate node that transmits data received from its child nodes to the aggregation node. Each node generates a group key, which is shared between a single node and all nodes in the group to which it belongs for secure data communication.
The proposed network approach undergoes six stages to ensure data security between nodes, namely, “network deployment,” “key partitioning and distribution,” “network grouping,” “group key generation,” “key and node management,” and “data encryption, transmission, and aggregation,” in that order. The aggregation nodes are generated by random selection. In network deployment, the algorithm proposed in [44] is used to construct the tree topology for the WSN. First, BS broadcasts a request to build up tree topology for all sensor nodes. The request contains a BS ID and a parameter depth indicating how many levels the tree topology should have. When node i receives this request from node j, it adds one to the parameter depth, sets node j as a parent node, and broadcasts the request to other nodes. This step constructs a tree topology for “all” network nodes in a normal case. Thus, the process continues until all nodes have received the request. This constraint can be refined to ensure the process does not terminate. Figure 1 shows a schematic of the network deployment.
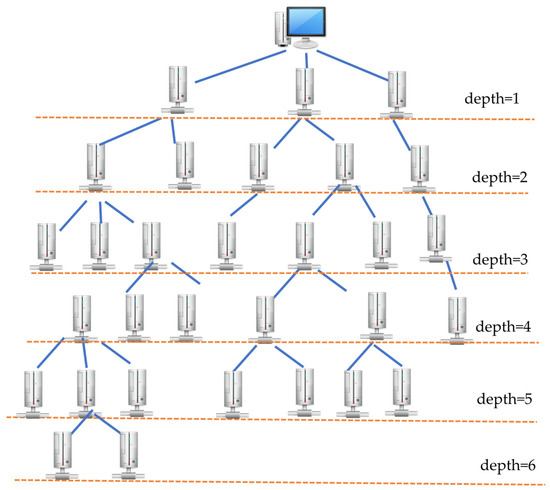
Figure 1.
Architecture of the network.
After the network accomplishes deployment, keys need to be added to the network to secure the data. The key partition is a critical element in creating a group key in the next stage. When WSN deployment is completed, the BS produces a specific key partition for each sensor node following the framework in Figure 2 [12]. As expressed in Equations (1) and (2), we assume there are k roots, r1, r2,…, and rk, and p is a large prime.
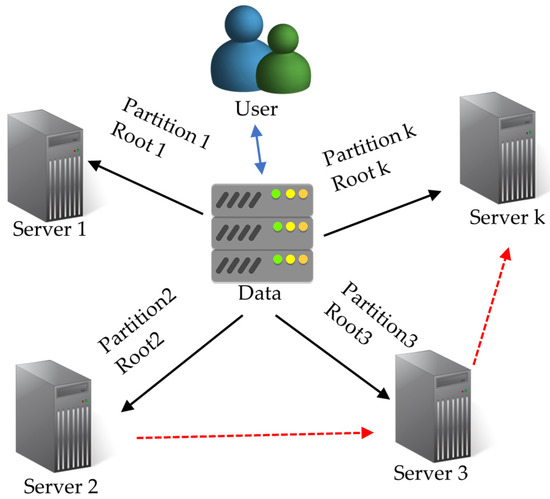
Figure 2.
Framework of the key partitioning and distribution.
In this study, we adopt implicit security techniques to handle keys and to construct a tree-based network that dynamically adjusts its topology. With our mechanism, the network is divided into several subtrees, with each subtree being a group of multiple nodes. Each node within a subtree uses key partitioning to generate a group key, which is used for data transmission between group nodes. Additionally, we use symmetric encryption algorithms and hash functions to achieve secure data aggregation with reduced computational overhead. Notably, the leaking of any piece or partition of information will not expose the original data since its reconstruction requires access to each server and the knowledge about the servers that store data partitions. Accordingly, every partition is implicitly secure without the need for encryption.
Each root in Equation (2) represents a partition. Based on [12], all partitions must be acquired to perform the calculation in Equation (3) to recover the original data (key). Parakh [12] found the roots in polynomials over a finite field (which was a large prime number), as presented in Equation (1), where there are a total of n roots. To utilize it in encryption algorithms, transformation to a finite field is carried out based on Equation (2). Subsequently, the data is substituted in Equation (1), and k roots (r1…rk) are obtained. Each root is referred to as a partition, and the partitions are randomly distributed among various network servers. Only the owner is aware of the storage locations of the partitions, and to access them, one must know the server’s password (the password for accessing the server and not the data password). Notably, all partitions are required to recover the original data. Figure 2 illustrates the concept of data partitions. To recover the original data, the partitions are multiplied as presented in Equation (3). Thus, these pieces can be stored randomly on different network servers.
The BS delineates the production of key partitions. It randomly generates a key d and a large prime p. For N sensor nodes, BS randomly generates N-1 integers (i.e., r1, r2,…, and rN-1) smaller than p and uses them to perform an inverse multiplication operation. Then, the kth key partition can be obtained from Equation (4). Finally, the BS distributes the N key partitions to the corresponding N nodes. Each node receives one key partition.
The key is arranged in the network. We employed the group key management approach as described in the previous section to improve the network scalability and reduce the memory space. In the network grouping phase, our tree network is further divided into several subtrees. Each subtree represents a group, and all nodes in a group use a shared group key to protect their in group communications. We propose two intuitive strategies, TDG and BUG, to divide a network into groups, with MN_G being the maximum group size.
In TDG, a breadth-first search starts from BS (Figure 3). If the number of nodes joining the group equals the maximum number of group members, the search stops, and the group is completed. The node with the lowest depth in a group is delegated as the root of the group, and the search restarts from the deepest node to its child node. The above process continues until all sensor nodes are assigned to a group, and all groups can connect with other groups via a shared node. Considering the tree topology in Figure 4 as an example, we assume a maximum number of group members of six. With TDG, the entire network can be divided into eight groups.

Figure 3.
Pseudocode of the top-down grouping (TDG) algorithm.
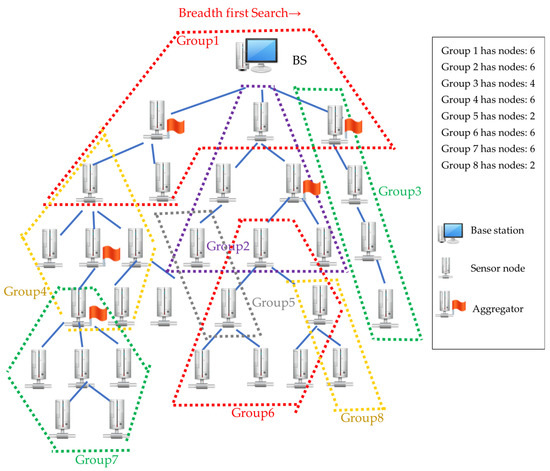
Figure 4.
Grouping results of the TDG algorithm.
In BUG, the search starts from the deepest node to its parent node (Figure 5). If the number of nodes joining the group is smaller than MN_G, other child nodes of parent node y are searched for and added to the group. If the parent node y has no child nodes, it will conduct the breadth-first search from its parent node to find other child nodes. When the number of group sizes equals MN_G, the search stops, and the group is completed. The node with the lowest depth is delegated as the root of the group, and the search restarts from its parent node to create another group. This process continues until all sensor nodes are assigned to a group, and all groups can connect with other groups via a shared node. Similarly to the previous example, with BUG, the whole network can be divided into nine groups, and the grouping results are shown in Figure 6.

Figure 5.
Pseudocode of the bottom-up grouping (BUG) algorithm.
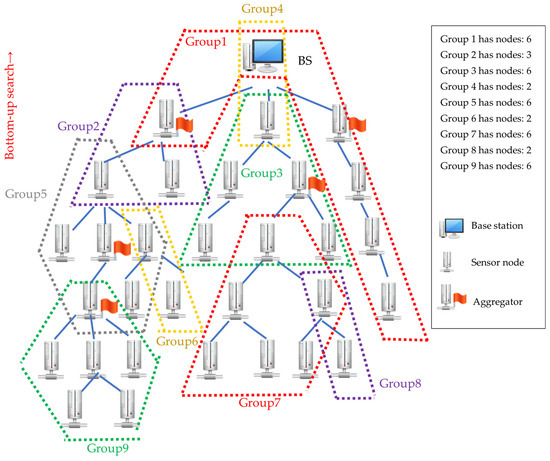
Figure 6.
Grouping results of the BUG algorithm.
To integrate the aggregation and encryption functions more effectively, we propose an alternative grouping algorithm, ABG (Figure 7). The breadth- and left-first searches start from BS to its child node x. If the number of nodes added to the group is smaller than MN_G, it continues searching for other child nodes of node x. When the aggregator is met, the search is targeted at other child nodes, which are non-aggregators. If the number of nodes added to the group is smaller than MN_G, the search stops, and the group is completed. The node with the lowest depth is delegated as the root of the group, and the search restarts from the deepest node to its child node. This process continues until all sensor nodes are assigned to a group, and all groups can connect with other groups via a shared node. For the previous example, ABG can divide the entire network into nine groups. The grouping results are shown in Figure 8.

Figure 7.
Pseudocode of the aggregator-based grouping (ABG) algorithm.
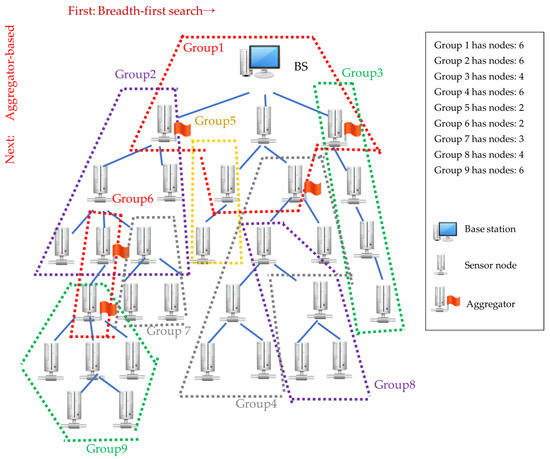
Figure 8.
Grouping results of the ABG algorithm.
According to the grouping results obtained in the earlier phase, each node in each group is assigned to a corresponding group key parameter by BS. The group key parameter of each node is composed of the key partitions of other nodes in the same group. Specifically, the group key parameter gpi for node i is calculated from Equation (5), where kpj represents the key partition of the node, and m and N are the total number of sensor nodes in the group and the entire network, respectively. Then, the group key GK is calculated from Equation (6).
GK = kpi • gpi • r mod p.
Since the group key parameters and partitions may not be altered frequently, the last random number r is generated and used in each user request to change the group key, thus enhancing the security level for the entire system. Therefore, nodes residing in the same group will obtain the same GK by referencing the corresponding key partitions, group key parameters, and a random number. To sustain the WSN operation, the actions of removing and inserting some sensor nodes in the network are unavoidable. For example, a node must be replaced when it runs out of power. This alters the network topology; thus, the network grouping and group key parameters must be adjusted. This phase is out of the scope of this study; thus, no further details are provided.
When completing the above grouping processes, secure communication channels are established for the entire WSN. Each sensor node senses, encrypts, and transmits data to its parent nodes. The data aggregator decrypts all received data, performs the data aggregation function, re-encrypts the aggregation result, and delivers it to the parent nodes. The boundary node in charge of inter-group communications decrypts the received data using the same group key and encrypts them using the key of the group to which the data are delivered. We can change only the random number and leave the rest unchanged to relieve the work on the generation of key partitions and group key parameters for BS to update or alter group keys. If higher security is required, changing the random number during a shorter period is a convenient way to update group keys frequently.
We propose a group-based key distribution mechanism, symmetric encryption systems, and hash functions for encryption and the verification of transmitted data. We summarize the common security requirements and explain how these requirements are met by our mechanisms:
- (1)
- Confidentiality: Provide a secure and confidential channel for wireless network communication to prevent eavesdropping. We use secret-sharing techniques to divide the group key into “n” shares, which also corresponds to the number of nodes. These shares are used to generate a group key required for symmetric data encryption.
- (2)
- Integrity: Verify that the message has not been altered during transmission. Each node and base station stores a one-way hash function. Before data transmission, the node hashes the data, and the receiving end verifies data integrity using the same hash function. If the node loses a message, it can send a request to the base station to retransmit the message.
- (3)
- Availability and authentication: Ensure that the entire wireless sensor network, or even individual sensor nodes, can provide service. In addition, authenticate the primary nodes in a cluster or the base station. The base station periodically broadcasts a random number.
When a node receives a random number broadcast from the base station, it combines the number with its key share and encrypts the number using the group key before sending it back to the base station. Since the base station has the key shares of all nodes, it can compare the received value with its calculation to verify the legitimacy of a node and to detect malicious nodes in the network. A non-authenticated node must be confirmed by the user before being allowed to join the network. The base station allocates a share to the added node and redistributes the group key parameters to the nodes within the group.
- (4)
- Scalability: The system must be able to support large-scale network architectures, particularly considering the key distribution mechanism for large networks.
We adopt a group key distribution mechanism that uses less storage. As the number of nodes increases, it does not directly lead to an increase in the number of keys in the network.
- (5)
- Efficiency: Wireless sensor networks must consider storage capacity, processing power, and communicational capability. The critical distribution mechanism should manage the number of keys, overly complex key computation, and excessive key exchanges between nodes. We use a group key distribution model and implement computationally efficient symmetric encryption to protect data and minimize computational overhead. WSN may encounter issues after use, such as node power depletion and the addition of new nodes. During re-initialization, group changes, and other unexpected errors may cause the number of nodes to change. When nodes are added or removed, the network membership changes, and new keys need to be generated and distributed. The capability of adding and removing nodes is therefore necessary. This paper proposes a mechanism for dynamic node management and key distribution, which consists of three parts: node addition, node and key deletion, and key update.
- ■
- Node addition: After a specific period of network usage, some nodes may have depleted their power, and the system may deploy new nodes to replace the old ones to maintain the operation of the wireless sensor network. When a new node joins the network, the base station assigns a key partition block to that node and notifies all nodes in the network, including the new node. The node is then added to a designated group. If the group has reached its maximum size, other groups that can admit the node are identified or the grouping process is re-executed. Otherwise, the new node and its neighbors generate the group key, establish a data transmission channel within the group, and complete the node addition process.
- ■
- Node and key deletion: When a node depletes its power or experiences a failure, the base station removes that node from the network and broadcasts the node’s ID to all nodes in the network for deletion. Additionally, the base station deletes all related key information of the node, including the key partition block and the group key, to ensure the security of future data transmissions. After node deletion, the child nodes point to the parent node, and a new group key is generated.
- ■
- Key update: This mechanism applies to the subsequent stages of node addition and node and key deletion. Therefore, when a node joins or leaves a group, new keys can be generated using the previously described group key parameter allocation method.
Furthermore, aggregate nodes, which perform aggregation function calculations, have higher power consumption than regular nodes. Accordingly, the base station may designate nodes with sufficient power as new aggregate nodes to maintain the network lifetime. Since our grouping method is based on aggregate nodes, grouping must be performed for the new aggregate nodes, and the group keys for each group are generated according to our key update mechanism.
Additionally, if the network experiences poor transmission path efficiency, high packet loss, or nodes not returning data to the aggregate node or base station, the base station can designate a path for data transmission through other nodes. As changing paths may result in different group traversals, the base station can execute the key update mechanism to generate new group keys.
- (6)
- Data freshness: Ensure that each data record is up to date and prevent replay attacks. Users include a random number in each request packet, combining it with key shares or group key parameters. This ensures that each generated group key is unique for every request.
4. Results
In this study, we used a tree topology to simulate a WSN environment. The simulated network has a tree structure in which simulated sensor nodes are connected like the branches of a tree. The tree structure network has three branches, and 1000 nodes were implanted randomly in the network with an increment of 100. Each sensor node was assumed to transmit one data. The sensor nodes were grouped into 10, 15, 20, 25, and 50 using TDG, BUG, and ABG. The aggregators were the reference of node grouping because power volume and memory space are critical resources for sensor nodes. The aggregator proportion was set from 10% to 50%. Space consumption can be evaluated from the number of group key parameters needed to be stored in the node. Table 1 lists the network parameter setting.

Table 1.
Network parameter setting.
Encryption and decryption follow the same estimation rules. Figure 9 shows the encryption and decryption procedures and how to estimate the number of encryption and decryption operations. Data are transmitted from one sensor node (Node1) to the target node (Aggregator). The data may be transmitted between the nodes from different groups. The data transmitted from Node1 to the aggregator passes through the node from three different groups (Figure 10), and they need three encryptions and two decryptions. We infer that one node transmits data to the aggregator through nodes from different t groups, and t + 1 encryptions and t decryption are needed. The node from the same bottom level (Node6–7) must be aggregated as one aggregator (Aggregator2) using the aggregate function, and the data are encrypted as one data. The aggregator (Aggregator2) transmits the data to the previous level (depth = 2), repeating the aggregation procedure until the data are transmitted to the top level (depth = 1). Thus, one encryption is needed. The aggregator needs to decrypt each child non-aggregator node (green node). If one aggregator has y child non-aggregator nodes, it needs y decryption.
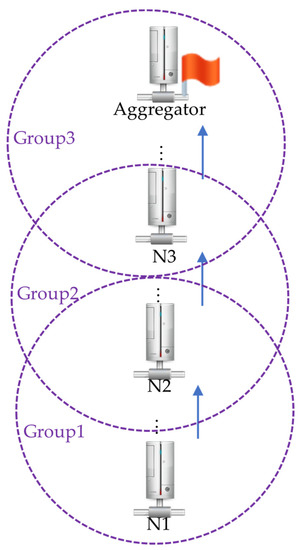
Figure 9.
Data transmission to the aggregator.
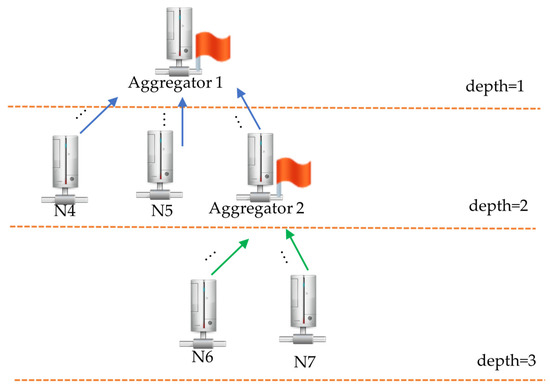
Figure 10.
Data receival by the aggregator.
In this experiment, we simulated wireless sensor networks using C programming language by randomly deploying 100–1000 nodes in a tree structure with 100-node increments in each simulation, and the degree of the tree was set to three. The aggregator nodes accounted for 10–50% of all network nodes. Based on the algorithm used for calculating the number of encryption and decryption operations in the simulations, we inferred that as the number of groups between transmitting and aggregator nodes increases, the number of encryption and decryption operations required for data transmission by a given node increases. We assumed that each node would transmit a piece of data, and the maximum group size was set to 10, 15, 20, 25, and 50 individuals. The experimental parameters included the number of encryption and decryption operations required for the entire network to transmit data to a base station and the average number of group key parameters that the nodes need to store.
After reading data, nodes perform encryption before transmitting the data to the upper layer. Notably, there exist two cases that require additional decryption and encryption operations during the transmission. The first case pertains to data transmission from one group to another: when the connecting node receives the data, it is decrypted using the current group key and then encrypted using the next group key until all data are transmitted to the base station. The second case pertains to data aggregation: upon receiving the data, the aggregator node decrypts the data, performs aggregation with other data to reduce packet size, and encrypts the aggregated result for further transmission. In this case, if the data aggregator and connecting nodes are the same, the number of encryption and decryption operations required to transmit the data to the base station will be reduced. This is the primary concept behind the proposed algorithm that performs grouping based on the aggregator nodes. In this study, we used a three-depth tree structure network as an instance (Figure 10). The maximum number of groups was nine. The sensor nodes were grouped using TDG, BUG, and ABG. The most significant results determined by different grouping algorithms are the number of encryption and decryption. Generally, most nodes perform encryption for sensed data only once and send them to BS or relay the encrypted data to BS without decryption, except for the following boundary and aggregator nodes. These two nodes decrypt and then encrypt received data using the group key(s) and neighboring group key, respectively. The boundary node is responsible for inter-group connections. If the sensed data go through b boundary nodes before reaching the aggregator, there would be b encryption and b−1 decryption executed in the boundary nodes. Before executing the aggregation function, the aggregator decrypts all received data from its child nodes and executes encryption once. Table 2 lists the grouping results from the experiment under the same conditions.

Table 2.
Grouping results.
We used the saved percentage, which compares control and experimental methods (Equation (7)), as criteria to evaluate the performance of the algorithms.
where NExperimental indicates the number of encryption and decryption operations using ABG algorithm. NControl represents the number of encryption and decryption operations using TDG algorithm or BUG algorithm.
We evaluated the three network grouping algorithms under different network scales, including the number of sensor nodes and group size. The number of sensor nodes was auto-increased in increments of 100 until 1000 nodes were reached. The maximum number of group members was set to 10, 15, 20, and 25 (Figure 11). When the node grouping method was constrained by a maximum of 10 nodes of a group, ABG could reduce the number of encryptions and decryptions by 16% and 18% compared with those of TDG and BUG, respectively. The maximum number of upward group adjustments was 25. ABG could also reduce the number of encryptions and decryptions required for TDG and BUG by 22% and 28%, respectively. When more aggregation nodes also served as boundary nodes simultaneously, the number of encryption and decryption decreased further. Thus, if a network allows severe nodes of group members, ABG would have better computation performance than TDG and BUG. When a maximum of 50 group members were considered, ABG could reduce the encryption and decryption by 35% and 36% compared with those of TDG and BUG, respectively.
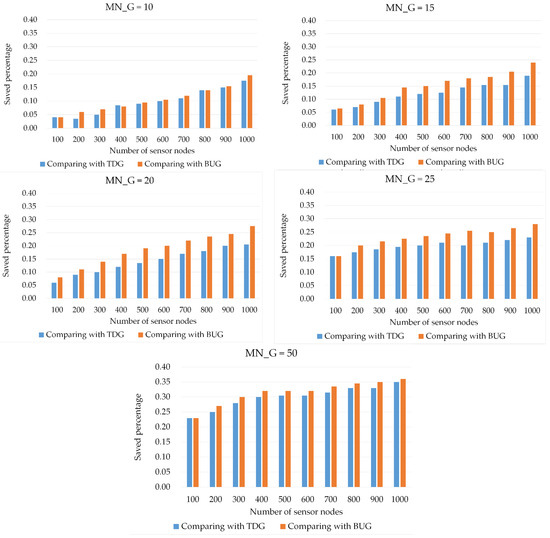
Figure 11.
Comparison between the percentage reduction in the number of encryption and decryption for different network scales.
We investigated the influence of encryption and decryption using the group algorithms between different proportions of aggregator nodes, and the results are shown in Figure 12. TDG, BUG, and ABG were used to group 1000 nodes in the network. When a network allows fewer group members, more groups are created. Also, only a few nodes can share the same key in the group; thus, the security level of the entire network can be increased. Contrarily, when a large number of nodes exist in each group, all nodes can share the same key in the group. Thus, the number of encryptions and decryptions can be reduced, but the security level of the network reduces. Therefore, choosing an appropriate MN_G is an important issue when launching WSN applications. Herein, the proposed ABG could further reduce the number of encryptions and decryptions when the percentage of aggregators occupied in the network approached 30% with MN_G = 10, 15, 20, and 25. When the percentage was over 30%, the grouping results for all MN_G values were similar. Thus, the number of encryption and decryption operations was also similar.
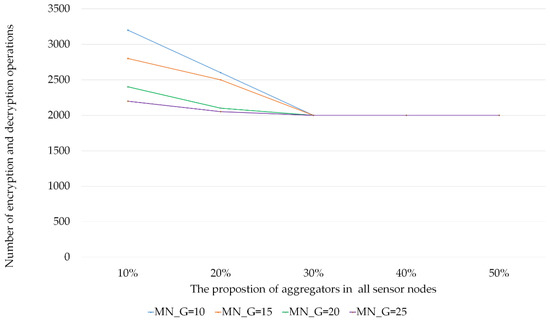
Figure 12.
Influence of the number of aggregators on the number of encryptions and decryptions.
In the proposed scheme, the memory consumption for each node is attributed mainly to the storing of the group key parameter. Unlike normal nodes in WSNs, the boundary node has more than one group key parameter to create correspondent group keys and render secure communication among different groups. When the maximum number of group members is small, more groups will be created, resulting in more boundary nodes. The aggregators have two types of arrangements: neighboring and non-neighboring. Theoretically, to reduce storage requirements, the group sizes should be as close to the maximum number of group members as possible so that the group number can be lowered to reduce the requirement for deploying boundary nodes. For ABG, since the addition of sensor nodes to one group stops when the aggregation node is met, the group size in each group is likely lower than the maximum number of group members. Thus, more groups are generated, and more boundary nodes would be created accordingly, resulting in more storage requirements for group key parameters. This problem can be alleviated by evenly distributing the network aggregators and preventing them from being close to one another. For MN_G = 6 (Figure 13a), with neighboring aggregators in the network, only three nodes were in Group 1. With non-neighboring aggregators, there were six nodes in Group 1 (Figure 13b). The results show that the average storage of group key parameters for ABG with the neighboring aggregator arrangement is smaller than that of TDG and BUG.
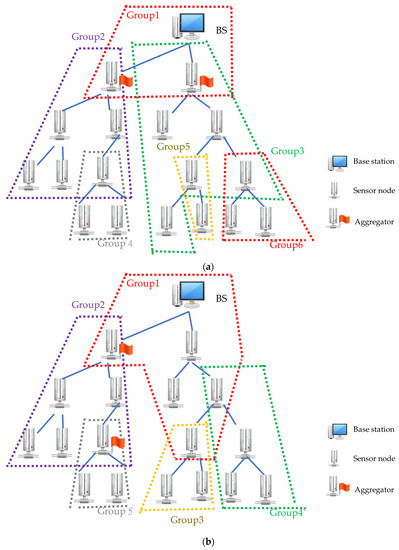
Figure 13.
Aggregator arrangements: (a) neighboring and (b) non-neighboring.
5. Conclusions
There is an increasing number of sensor nodes in WSNs. The sensor node grouping directly affects the communication efficiency of WSNs. Herein, we developed a grouping method for the key distribution of implicit certificates in WSNs to enhance computing performance. Further, we propose a novel key distribution mechanism for WSN applications. Following the management mechanism along with its above-average performance on storage requirement, the resilience of node capture, key connectivity, and scalability, we developed an efficient network grouping strategy, ABG, which can minimize encryptions and decryptions by combining data aggregation and inter-group communication (both of which require encryptions and decryptions for the sensed data) in the same node. We investigated the influence of the number of aggregators in the network on the number of encryptions and decryptions. We found that ABG can reduce EN compared to other grouping algorithms. Moreover, the average storage of group key parameters for ABG with a neighboring aggregator arrangement is also smaller than that of TDG and BUG. The performance evaluation results suggest that the proposed scheme can be employed in ubiquitous WSN application domains. Experimental design conditions include same power, memory capacity, CPU processing power, and communicational capability, and the results depend on these conditions. Thus, if the conditions are changed, the results may differ: there are the experiment’s limitations.
In our future studies, in addition to investigating the encryption and decryption operations issues, we will investigate other issues, such as the average storage of group key parameters and the effect of non-neighboring and neighboring aggregators on encryption and decryption. This will provide a more efficient way to communicate and secure data in WSN. This study proposed an experimental environment that may not adapt to the actual network environment. In the future, a system simulation method, such as steady-state simulation, is expected to be employed in the experiment to make the investigation fit the realistic network environment.
Author Contributions
Conceptualization, R.-I.C.; data curation, C.-W.C.; formal analysis, C.-W.C.; funding acquisition, R.-I.C. and Y.-H.H.; investigation, R.-I.C., C.-W.C. and Y.-H.H.; methodology, R.-I.C. and C.-W.C.; software, R.-I.C. and C.-W.C.; supervision, R.-I.C. and Y.-H.H.; validation, Y.-H.H.; writing—original draft, R.-I.C. and Y.-H.H.; writing—review and editing, R.-I.C. and Y.-H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Taiwan National Science and Technology Council (NSTC), under Grant no. 110-2410-H-002-094-MY2, 111-2221-E-224-033-MY2 and MOE “Teaching Practice Research” Subsidies Program grant number PBM1110139.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hasan, M. State of IoT 2022: Number of Connected IoT Devices Growing 18% to 14.4 billion Globally. IoT Analytics. Available online: https://iot-analytics.com/number-connected-iot-devices/ (accessed on 18 May 2022).
- Akyildiz, I.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. J. Comput. Netw. 2022, 38, 393–422. [Google Scholar] [CrossRef]
- Li, W.; Kara, S. Methodology for monitoring manufacturing environment by using wireless sensor networks (WSN) and the internet of things (IoT). Procedia CIRP 2017, 61, 323–328. [Google Scholar] [CrossRef]
- García-Hernández, C.F.; Ibargüengoytia-González, P.H.; García-Hernández, J.; Pérez-Díaz, J.A. Wireless Sensor Networks and Applications: A Survey. Int. J. Comput. Sci. Netw. Secur. 2007, 7, 264–273. [Google Scholar]
- Culler, D.; Estrin, D.; Srivastava, M. Guest Editors’ Introduction: Overview of Sensor Network. IEEE Comput. Soc. 2004, 37, 41–49. [Google Scholar] [CrossRef]
- Zahariadis, T.; Trakadas, P.; Leligou, H.; Papadopoylos, K.; Ladis, E.; Tselikis, C.; Vangelatos, C.; Besson, L.; Manner, J.; Loupis, M.; et al. Securing wireless sensor networks towards a trusted Internet of Things. In Towards the Future Internet—A European Research Perspective; IOS Press: Amsterdam, The Netherlands, 2009; pp. 47–56. [Google Scholar]
- Cheng, S.; Lai, Y.; Wang, C.; Lin, R. Hierarchical data aggregation model and group management for wireless sensor network. In Proceedings of the 2009 the Fourth International Conference on Communications and Networking, Xi’an, China, 26–28 August 2009. [Google Scholar]
- Ren, X.; Yu, H. Security Mechanisms for Wireless Sensor Networks. Int. J. Comput. Sci. Netw. Secur. 2006, 6, 155–161. [Google Scholar]
- Belinda, M.; Dhas, C. A Study of Security in Wireless Sensor Networks. Masaum J. Rev. Surv. 2009, 1, 91–95. [Google Scholar]
- Wander, A.S.; Gura, N.; Eberle, H.; Gupta, V.; Shantz, S.C. Energy Analysis of Public-Key Cryptography for Wireless Sensor Networks. In Proceedings of the IEEE Pervasive Computing and Communication, Kauai, Hawaii, 8–12 March 2005; pp. 324–328. [Google Scholar]
- Amin, F.; Jahangir, A.H.; Rasifard, H. Analysis of Public-Key Cryptography for Wireless Sensor Networks Security. Int. J. Comput. Syst. Sci. Eng. 2009, 5, 107–112. [Google Scholar]
- Parakh, A.; Kak, S. Online Data Storage using Implicit Security. Inf. Sci. 2009, 179, 3323–3331. [Google Scholar] [CrossRef]
- Chang, C.C.; Arafa, S.; Muftic, S. Key Establishment Protocol for Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Mobile Ad-Hoc and Sensor Systems, Pisa, Italy, 8–11 October 2007. [Google Scholar]
- Chang, R.-I.; Tsai, J.-H.; Wang, C.-H. Edge Computing of Online Bounded-Error Query for Energy-Efficient IoT Sensors. Sensors 2022, 22, 4799. [Google Scholar] [CrossRef]
- Jones, J.; Haas, Z.J. Predeployed Secure Key Distribution Mechanisms in Sensor Networks: Current State-of-the-Art and a New Approach using Time Information. IEEE Wirel. Commun. 2008, 15, 42–51. [Google Scholar]
- Dustin, M.; Shankarappa, J.; Petrowski, M.; Weerasingha, H.; Fu, H. Analysis of Key Management in Wireless Sensor Networks. In Proceedings of the IEEE Electro/Information Technology Conference, Chicago, IL, USA, 17–20 May 2007. [Google Scholar]
- Cheng, Y.; Agrawal, D.P. Efficient Pairwise Key Establishment and Management in Static Wireless Sensor Networks. In Proceedings of the Mobile Ad Hoc and Sensor System Conference, Washington, DC, USA, 25–27 May 2005. [Google Scholar]
- Eschenauer, L.; Gligor, V. A Key-Management Scheme for Distributed Sensor Networks. In Proceedings of the 9th ACM Conference on Computer and Communications Security, Washington, DC, USA, 18–22 November 2002; pp. 41–47. [Google Scholar]
- Du, W.; Deng, J.; Han, Y.S.; Chen, S.; Varshney, P.K. A Key Management Scheme for Wireless Sensor Networks Using Deployment Knowledge; IEEE Infocom: Hong Kong, China, 2004. [Google Scholar]
- Liu, D.; Ning, P.; Du, W. Group-Based Key Pre-distribution in Wireless Sensor Networks. In Proceedings of the 4th ACM Workshop on Wireless Security (WiSe’05), Cologne, Germany, 2 September 2005; pp. 11–20. [Google Scholar]
- Alshammari, M.R.; Elleithy, K.M. Efficient and secure key distribution protocol for wireless sensor networks. Sensors 2018, 18, 3569. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, U.; Shafi, S. A provable and secure key exchange protocol based on the elliptical curve diffe–hellman for wsn. In Advances in Big Data and Cloud Computing: Proceedings of ICBDCC18; Springer: Singapore, 2019; pp. 363–372. [Google Scholar]
- Lin, H.Y. Integrate the hierarchical cluster elliptic curve key agreement with multiple secure data transfer modes into wireless sensor networks. Connect. Sci. 2022, 34, 274–300. [Google Scholar] [CrossRef]
- Tehseen, M.; Javed, H.; Shah, I.H.; Ahmed, S. A lightweight key negotiation and authentication scheme for large scale wsns. In Recent Trends and Advances in Wireless and IoT-Enabled Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 225–235. [Google Scholar]
- Elhoseny, M.; Hassanien, A.E.; Elhoseny, M.; Hassanien, A.E. Secure data transmission in WSN: An overview. In Dynamic Wireless Sensor Networks: New Directions for Smart Technologies; Springer: Berlin/Heidelberg, Germany, 2019; pp. 115–143. [Google Scholar]
- Robinchandra Singh, U.; Roy, S. Survey on key management schemes and cluster based routing protocols in wireless sensor network. Int. J. Comput. Intell. IoT 2019, 576–594. [Google Scholar]
- Chen, Z.; Chen, S.; Xu, H.; Hu, B. A security scheme of 5G ultradense network based on the implicit certificate. Wirel. Commun. Mob. Comput. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Mehmood, G.; Khan, M.S.; Waheed, A.; Zareei, M.; Fayaz, M.; Sadad, T.; Kama, N.; Azmi, A. An Efficient and Secure Session Key Management Scheme in Wireless Sensor Network. Complexity 2021, 2021, 6577642. [Google Scholar] [CrossRef]
- Vijayan, K.; Raaza, A. A novel cluster arrangement energy efficient routing protocol for wireless sensor networks. Indian J. Sci. Technol. 2016, 9, 1–9. [Google Scholar] [CrossRef]
- Srinivas, K.; Sagar, K. Secure-Key Management Protocols for Wireless Sensor Networks in IoT. Ind. Eng. J. 2022, 15. [Google Scholar]
- Fereidooni, H.; Marchal, S.; Miettinen, M.; Mirhoseini, A.; Möllering, H.; Nguyen, T.D.; Rieger, P.; Sadeghi, A.-R.; Schneider, T.; Yalame, H.; et al. SAFELearn: Secure aggregation for private federated learning. In Proceedings of the 2021 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 27 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 56–62. [Google Scholar]
- Guan, Z.; Zhang, Y.; Zhu, L.; Wu, L.; Yu, S. EFFECT: An efficient flexible privacy-preserving data aggregation scheme with authentication in smart grid. Sci. China Inf. Sci. 2019, 62, 32103. [Google Scholar] [CrossRef]
- Przydatek, B.; Song, D.; Perrig, A. SIA: Secure information aggregation in sensor networks. In Proceedings of the 1st ACM Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003. [Google Scholar]
- Przydatek, B.; Chan, H.; Perrig, A.; Song, D. SIA: Secure information aggregation in sensor networks. J. Comput. Secur. 2007, 15, 69–102. [Google Scholar]
- Li, H.; Lu, R.; Zhou, L.; Yang, B.; Shen, X. An Efficient Merkle-Tree-Based Authentication Scheme for Smart Grid. IEEE Syst. J. 2013, 8, 655–663. [Google Scholar] [CrossRef]
- Nesa, N.; Banerjee, I. A lightweight security protocol for IoT using Merkle hash tree and chaotic cryptography. Adv. Comput. Syst. Secur. 2020, 10, 3–16. [Google Scholar]
- So, J.; Güler, B.; Avestimehr, A.S. Turbo-aggregate: Breaking the quadratic aggregation barrier in secure federated learning. IEEE J. Sel. Areas Inf. Theory 2021, 2, 479–489. [Google Scholar] [CrossRef]
- Bhushan, S.; Kumar, M.; Kumar, P.; Stephan, T.; Shankar, A.; Liu, P. FAJIT: A fuzzy-based data aggregation technique for energy efficiency in wireless sensor network. Complex Intell. Syst. 2021, 7, 997–1007. [Google Scholar] [CrossRef]
- Sanli, H.O.; Ozdemir, S.; Cam, H. SRDA: Secure Reference-Based Data Aggregation Protocol for Wireless Sensor Networks. In Proceedings of the IEEE Vehicular Technology Conference, Los Angeles, CA, USA, 26–29 September 2004; pp. 4650–4654. [Google Scholar]
- Girao, J.; Westhoff, D. CDA: Concealed Data Aggregation for Reverse Multicast Traffic in Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2005. [Google Scholar]
- Ozdemir, S.; Xiao, Y. Secure Data Aggregation in Wireless Sensor Networks: A Comprehensive Overview. Comput. Netw. 2009, 53, 2022–2037. [Google Scholar] [CrossRef]
- Jiao, R.; Ouyang, H.; Lin, Y.; Luo, Y.; Li, G.; Jiang, Z.; Zheng, Q. A computation-efficient group key distribution protocol based on a new secret sharing scheme. Information 2019, 10, 175. [Google Scholar] [CrossRef]
- Harn, L.; Hsu, C.; Xia, Z. General logic-operation-based lightweight group-key distribution schemes for Internet of Vehicles. Veh. Commun. 2022, 34, 100457. [Google Scholar] [CrossRef]
- Madden, S.; Franklin, M.J.; Hellerstein, J.M.; Hong, W. TAG: A Tiny Aggregation Service for Ad-Hoc Sensor Networks. In Proceedings of the 5th Symposium on Operating Systems Design and Implementation, Boston, MA, USA, 9–11 December 2002; pp. 131–146. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).