Abstract
Hardware-in-the-loop testing is usually a part of the design cycle of control systems. Efficient and fast models can be created in a Hardware Description Language (HDL), which is implemented in a Field-Programmable Gate Array (FPGA). Control engineers are more skilled in higher-level approaches. HDL models derived automatically from schematics have noticeably lower performance, while HDL models derived from their equations are faster and smaller. However, even models translated automatically into HDL using the equations might be worse than manually coded models. A design workflow is proposed to achieve manual-like performance with automatic tools. It consists of the identification of similar operations, forcing signal signedness, and adjusting to multiplier input sizes. A detailed comparison was performed between three workflows: (1) translation of high-level MATLAB code, (2) translation of a Simulink model, and (3) working directly in the HDL. Sources of inefficiency were shown in a buck converter, and the process was validated in a full-bridge with electrical losses using a Runge–Kutta method. The results showed that the proposed approach delivered code that performed very close to a reference VHDL implementation, even for complex designs. Finally, the model was implemented in an off-the-shelf FPGA board suitable for a hardware-in-the-loop test setup.
1. Introduction
Hardware-In-the-Loop (HIL) techniques contribute greatly to the testing stages of complex systems because they minimize the risk of injuries or equipment breakdown [1,2]. In these techniques, an element of the real system is replaced by a real-time model. A model of a plant provides the same feedback to the controller as the real element. In power electronics, a HIL model enables safe testing without using live parts until the design is sufficiently tested [3]. It also enables the testing of controllers using a virtual plant before constructing the converter.
The models operate in real-time and must calculate their states with high precision. Either commercial systems can be used (such as Opal-RT, dSPACE, and Typhoon HIL) or Field Programmable Gate Array (FPGA) devices [4,5,6] programmed in a Hardware Description Language (HDL), such as Verilog or VHDL.
The use of HIL elements is one step in the V-shaped development cycle of complex systems, as shown in [1]. A power engineer typically builds the model in a high-level language. Manual translation into a HIL implementation requires HDL skills, which means additional effort or using automatic tools.
Several works have shown the use of commercial tools for generating high-performance HIL models in FPGAs: electrical and mechanical components of a wind energy conversion system in [7], in a photovoltaic system in [8], or in electrical networks in [9].
In these cases, the processing elements are generated using automated workflows, but the authors do not analyze how far away they are from the best possible performance, typically obtained by manual HDL design. In [10,11], the authors state that automatic generation is faster and less error-prone for power electronic designers, although no comparison was made against a model generated manually. In [12,13,14], this comparison was made, and the authors showed that the automated model uses more resources than the manual model; however, they did not analyze the source of the disparity. In [15], the authors showed that the model generated automatically requires more than double the number of multiplier elements, without giving any explanation. Some workflows have been proposed, such as [16]; however, they are oriented toward FPGA experts, and they did not check if the VHDL code generated was optimum. In the VHDL code generation step (Figure 2 in [16]), after automatic translation, no verification of the quality of the translation was made.
Until now, the choice for the designer was either to obtain a very efficient model through manual design or a worse one with automatic translation. The first choice requires high effort and HDL skills. The second choice requires less effort and time, but may lead to suboptimal models. This might not be apparent, since extra resource usage can be offset by using more powerful hardware. However, in the end, this means that either HIL models overspecify the hardware requirements or that a larger-than-necessary portion of the existing hardware is used, taking up resources that could be dedicated, for example, to making the simulation more precise. The ultimate consequence is a higher cost of the simulation, a loss of precision, or even both.
This paper proposes a design workflow for automatic model generation that aims to achieve the best of automatic and manual approaches: high efficiency, low effort, easy addition of interfaces, no need to program in a low-level HDL, and compatibility with complex models and different numerical methods.
As shown in Figure 1, to build an efficient HIL model, the first choice is between a commercial system or an ad hoc one. Ad hoc systems offer the best performance and flexibility. In these, the model is characterized either at the schematic level or the state equation level. The MATLAB/Simulink Simscape library allows for modeling at the schematic level. This is less demanding, but offers less control to the designer.
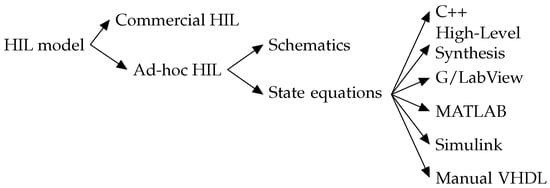
Figure 1.
Decision tree for implementation of a HIL model.
High-Level Synthesis and G/LabView require less effort, but as Table 7 in [17] showed, their results were not satisfactory. High-Level Synthesis causes high resource utilization [18], and G/LabView delivers worse results. Therefore, the candidate approaches use Simscape to derive the equations from schematics or calculating the equations, either manually or starting from the MATLAB or Simulink models.
The buck and full-bridge schematics were modeled into the HDL using Simscape, with an acceptable maximum speed, but much higher resource utilization compared to other approaches. Simscape always considers first-order losses, which exacerbates the resource utilization issue. Table 1 presents the implementation results, including the VHDL and MATLAB code from [17]. The table shows the utilization of Look-Up Tables (LUTs), Flip-Flops (FFs), Digital Signal Processors (DSPs) and a minimum simulation step using the Forward Euler numerical method and floating-point arithmetic. The conclusion was that direct translation from a Simscape schematic always leads to inefficient results, both in resources and speed, while translation from MATLAB code may also lead to such inefficiencies. Therefore, the possible causes of inefficiency were explored in this work.

Table 1.
Resource utilization and speed with floating-point models generated from manual VHDL and translation from MATLAB code, both from Table 7 in [17] and from Simscape.
The poor results of the C++, High-Level Synthesis, and G/LabView approaches, together with the lack of control over the internals of the Simscape model and its high resource utilization led to the choice of MATLAB/Simulink high-level approaches for this work, as detailed in Section 2.
The rest of the paper is structured as follows: Section 2 shows the proposed design workflow. Section 3 compares the automatic and manual design approaches and identifies the sources of inefficiencies with a simple model. Once the proposed design workflow has been analyzed with a simple model, Section 4 validates the proposal in a complex model, a full-bridge converter with losses and pipelined operation. Section 5 shows its implementation in an FPGA. Finally, Section 6 summarizes the results, and Section 7 provides the conclusions.
2. Proposed Design Workflow
In the classical process, which led to a HIL model, the MATLAB or Simulink model was used as the input to the automatic-code-generation tool (Figure 2). Here, additional intermediate steps are proposed (Figure 3). These steps will ensure that the inputs to the automatic-code-generation tool are optimized.
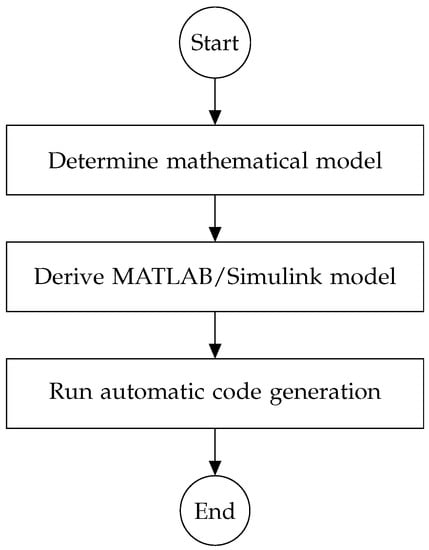
Figure 2.
Typical design workflow for automatic code generation.
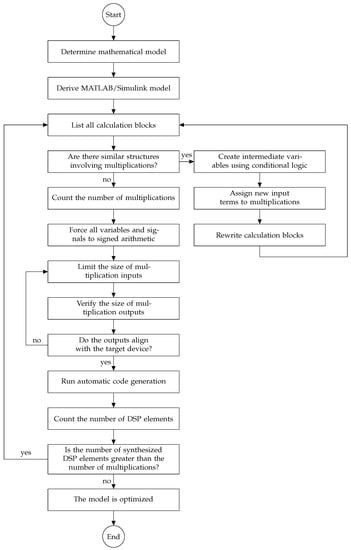
Figure 3.
Proposed design workflow to achieve an efficient model with automatic code generation.
These steps will be familiar to expert HDL designers. However, the objective of this work was to propose a method that does not require knowledge of HDL design processes and is powerful enough to ensure an efficient HIL model.
The following requirements were considered:
- It must be compatible with existing automatic workflows;
- It must not change the initial mathematical model;
- It must not require knowledge of hardware description languages by the power engineer;
- Any modifications to the algorithm design must be understandable to the power engineer;
- It must not require knowledge of the inner structure of the target device;
- It must not require knowledge of HDL design and optimization processes;
- It must be simple enough to make it worth using so that the performance improvement in the final model is obtained at the price of a small additional effort;
- It must be compatible with different numerical methods;
- It must be compatible with complex architectures, such as pipelined operation;
- It must achieve similar occupation figures in the target device compared to manual design;
- It must achieve a similar speed to that achieved by manual design.
The process can be divided into four major stages: code rewriting, signal forcing, adjustment to the multiplier size, and verification.
In the code rewriting step, the designer must make a list of all the calculation blocks, compare them side-by-side, and determine if they have similar structures. For those that are similar, the designer must create intermediate variables or signals that take their value depending on some conditions. The objective is to replace several multiplications with only one, having all inputs activated or not depending on the model conditions. Once this optimization is performed, the designer must count the number of multiplications. This will be used in a later stage.
After that, all variables and signals are forced to signed arithmetic to avoid uncontrolled addition of bits. Then, in the third stage, the sizes of the variables or signals used at the multiplications must be listed and trimmed to adjust to the device multiplication elements. This is the only step where some knowledge of the target device is required, namely the input and output signal sizes of the multiplication elements. However, this information is present in any datasheet and does not require deep knowledge.
The output size of the multiplication signals must be then checked. If they are greater than the device size, the previous step must be repeated iteratively until the outputs are in line with the device multiplier outputs.
An additional step serves to verify that the translation has delivered an optimized model. This was achieved by comparing the number of multipliers needed by the target device against the number of multiplications counted after optimization of the calculation structures. In the case of Xilinx devices, the multiplier elements are DSP structures. If the number of multiplier elements is the same as the number of multiplications, this means that the automatic code generation did not create overhead and the model is optimized. Then, the automatic code generation can be launched.
The workflow as presented complies with Requirements 1 to 6 stated above. The modifications are easy to follow and are performed on the very same MATLAB or Simulink model created by the designer, and not at the HDL level. They do not change the model and require only knowledge of the multiplier elements of the target device. The rest of the requirements were validated by the results shown in Section 4 and Section 5.
3. Characterization in a Buck Converter
The initial study was performed with the synchronous buck converter shown in Figure 4. The topology is simple enough to allow manual inspection and comparison of the HDL code generated in the different approaches. Once the methodology has been analyzed and understood, it is applied to a more complex converter in Section 4.
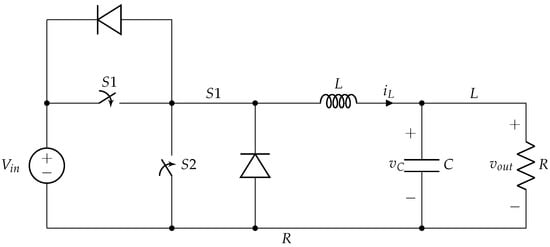
Figure 4.
Synchronous buck circuit chosen for HIL implementation.
The synchronous buck converter operates by alternately closing Switches S1 and S2, with the duty cycle determined by the relation. To avoid short-circuiting the source, dead times were introduced between opening one switch and closing the other, during which Diodes D1 and D2 provide a path for the inductor to discharge.
Three operating modes can be identified in the circuit:
- Mode 1: S1 is closed and S2 open or S1 and S2 are open (dead time), and the inductor current () is negative (D1 in the conduction state).
- Mode 2: S1 is open and S2 closed and during a dead time in which (D2 in the conduction state).
- Mode 3: if the inductor becomes discharged during a dead time, there is no current flow through the inductor.
The circuit equations were derived from the behavior of the inductor and the capacitor and the converter’s operating modes. Solving for the state variables and , three sets of ordinary differential equations were obtained. Table 2 shows the equations that apply to each case.

Table 2.
Buck circuit equations for each operation mode.
To avoid miscalculations during a change from Mode 1 or 2 to Mode 3 during a dead time, Reference [19] suggested different techniques, including saturating the inductor current to zero amperes. This is a simple and effective solution when using the Forward Euler method, as in this case.
The model calculates in real-time the solution of these equations. The Forward Euler method is commonly used since its implementation is straightforward. Methods such as the second- or fourth-order Runge–Kutta method are more accurate, but more complex [4,9]. The fixed-step Forward Euler method makes the following approximation, for small values of :
Substituting (1) and (2) for each mode, the changes in the state variables and during one step are calculated numerically with the pseudocode shown in Algorithm 1.
Parameters , , and are constants. The divisions are performed only once by the user before the simulation. This pseudocode will be the basis for each of the design flows analyzed. The parameters of the proposed buck converter are summarized in Table 3.
| Algorithm 1 Calculation of the following value of and with the Euler method using a simple saturation method. | ||
| 1: | Constant declaration | |
| 2: | ||
| 3: | ||
| 4: | ||
| 5: | function calculateStep() | |
| 6: | if OR AND AND then | ▹ Mode 1 |
| 7: | ||
| 8: | ||
| 9: | else if OR AND AND then | ▹ Mode 2 |
| 10: | ||
| 11: | ||
| 12: | else if then | ▹ Mode 3: during a dead time |
| 13: | ||
| 14: | ||
| 15: | end if | |
| 16: | ||
| 17: | ||
| 18: | if AND AND then | ▹ iL crosses zero during a dead time |
| 19: | ||
| 20: | end if | |
| 21: | end function | |

Table 3.
Parameters of the proposed buck converter.
3.1. HDL Model Design Workflows
The three HIL workflows start from the same model (Algorithm 1) and have each a different initial implementation: (1) MATLAB code, (2) Simulink block design, and (3) manual VHDL code. This implementation was simulated with floating point. Then, it was converted into fixed point to optimize the performance. Although commercial HIL systems usually use floating point and some ad hoc HIL systems also use them [20,21], most ad hoc systems use fixed point.
3.1.1. Conversion of MATLAB Code into VHDL
A MATLAB function implements the state equations and calculates the values of the state variables and one step at a time, with persistent variables to keep their values. Another function served as a test bench, providing stimuli and recording the output. The code is then converted into a fixed-point version using the fixed-point conversion of the HDL Code Generation Workflow, with the user adjusting the size until the required precision is achieved. The HDL Coder then transforms the fixed-point code into synthesizable VHDL code. The initial MATLAB function resembles Algorithm 1, with an if–then–else block calculating and , detecting if crosses zero during a dead time and setting it to zero if so, then storing variables for the next calculation cycle.
3.1.2. Model-Based Design with Simulink
Simulink is a modeling and simulation environment for model-based engineering. It allows for the graphical design of systems by connecting blocks. The HDL Coder Simulink library must be used to ensure blocks can be translated into the HDL. The Simulink model shown in Figure 5 consists of four subsystems: the mode selector, Euler calculation blocks for and , and the saturation detector during a dead time. The parameters , , and are input constants, and the state of the switches and and the input voltage are the input signals. The mode selector block takes the inputs of the states of the switches , , and and produces an output (1, 2, 3), which represents the operation mode. This output is used as the input by other calculation blocks.
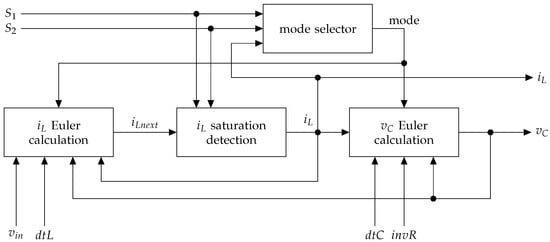
Figure 5.
Overview of the buck converter Simulink model.
The block that calculates using the Forward Euler method (see Figure 6) consists of an element that calculates , according to the operation mode, which is added to the value of obtained via a feedback loop through a unit delay. In this case, the function f calculates as follows: , with taking the value of or zero depending on the mode signal. The Euler solver block available in Simulink was not used because it did not allow for easy assignment of as an external signal. By proceeding as explained, can be set externally by assigning the corresponding values to the signals and .
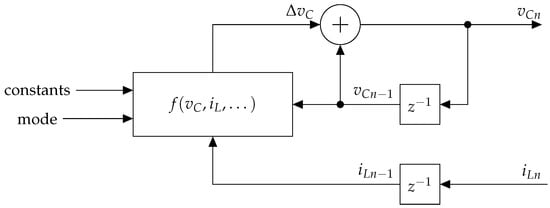
Figure 6.
Close-up view of the Euler calculation block of Figure 5.
A similar structure is used to calculate an intermediate value for the inductor current, . This signal is then fed into the saturation detector block. The detector checks if changes sign within a dead time, and if so, it sets the output to zero until one of the switches is activated again. Otherwise, the output keeps the value of .
The steps for obtaining the HDL code are similar to those of the MATLAB approach from Section 3.1.1. The Simulink model is converted into fixed point, and the HDL Coder automatically generates the HDL code.
3.1.3. Reference Implementation in VHDL
The VHDL code followed the approach proposed in [22]. This procedure yielded results similar to the assisted translation by the MATLAB tools described in Section 3.1.1 and Section 3.1.2, but it required more manual work. A unified set of sizes (see Table 4) was used for the three workflows for a fair comparison.

Table 4.
Size of variables and constants used for the buck model.
3.2. Implementation
3.2.1. Generation of VHDL Code from MATLAB
Following the process explained in Section 3.1.1, the MATLAB code equivalent to Algorithm 1 was translated into fixed point and then into VHDL code for the FPGA—a Xilinx Zynq xc7z020clg400-1 in this case. This is a low-cost FPGA that includes an embedded Advanced RISC Machine (ARM) processor, although it is not used by the model. The sizes of the variables and constants are shown in Table 4. Negative values for integers mean that the leftmost bit stored lies at the right of the decimal point. The first row in Table 5 contains the results of the implementation using Xilinx Vivado.

Table 5.
Resource usage and maximum speed for the buck converter.
3.2.2. Generation of VHDL Code from Simulink
The proposed workflow for the Simulink model described in Section 3.1.2 was followed, and the VHDL code was created. The signal sizes also followed Table 4. The second row in Table 5 shows the implementation results. The maximum speed was similar in both cases; the MATLAB-originated code had a higher usage of DSPs.
3.2.3. Initial Comparison
The maximum speed was similar, but there was a significant difference in resource utilization, especially the DSPs. The resource usage was influenced by the variable sizes and the number of operations in the FPGA; multiplication operations are usually assigned to DSP slices. The VHDL code was analyzed in both cases to determine the number of operations implemented and their origin in the high-level model.
In the first case (MATLAB-generated code), the VHDL architecture was equivalent to the original high-level code, while in the second case (Simulink-generated code), each block in the model was translated into VHDL code. A direct comparison between the two types of VHDL code is not possible, but there was a correlation between the number of arithmetic operations and DSP usage. Table 6 compares the number of operations in each model and the resulting VHDL code.

Table 6.
Operations in the MATLAB and Simulink models and their VHDL code, before optimization of the MATLAB code.
Further examination of the generated VHDL code revealed that certain lines of Algorithm 1 (e.g., Lines 7 and 10) were translated into separate signals, which required separate computing resources on the FPGA. Additionally, Line 13 has a structure similar to the previously mentioned lines, except for the variable , which is absent and produces a different signal. This implied that the additional signals and calculations were responsible for the increased resource usage.
3.2.4. Revised Algorithmic Model
To optimize Algorithm 1, algebraic operations should be avoided. One way is to limit the if–then–else block to only assignments, with the circuit operation mode (1, 2, or 3) as the output. Intermediate variables are then used to store values that depend on the operating mode, and the algebraic operations that calculate and should appear only once. Algorithm 2 illustrates this optimized approach.
This alternative made the architecture similar to the Simulink-based approach: the if–then–else block resembles the mode selector block, whose output drives the switching of signals, which in turn are used to calculate and .
| Algorithm 2 Optimized version of Algorithm 1, taking the multiplications out of the if–then blocks. Changes in red. | ||
| 1: | Constant declaration | |
| 2: | ||
| 3: | ||
| 4: | ||
| 5: | function calculateStep() | |
| 6: | ||
| 7: | if OR AND AND then | |
| 8: | ||
| 9: | else if OR AND AND then | |
| 10: | ||
| 11: | else if then | |
| 12: | ||
| 13: | end if | |
| 14: | if OR then | |
| 15: | ||
| 16: | else | |
| 17: | ||
| 18: | end if | |
| 19: | ||
| 20: | if then | |
| 21: | ||
| 22: | else if then | |
| 23: | ||
| 24: | else | |
| 25: | ||
| 26: | end if | |
| 27: | ||
| 28: | ||
| 29: | ||
| 30: | if AND AND then | ▹ iL crosses zero during a dead time |
| 31: | ||
| 32: | end if | |
| 33: | end function | |
The revised pseudocode contains only three multiplication operations, four additions or subtractions, and one sign change. As a result, it generates optimal VHDL code, yielding similar occupation and speed results as the Simulink-based approach, as shown in Table 7. While there were negligible differences in the maximum achievable speed, the overhead was due to the generation of extra signals in parallel calculation paths, which caused additional resource usage. However, this had no timing influence as the logic performed these calculations in parallel, and the calculation path had the same length.

Table 7.
Resource usage and maximum speed for the buck model.
3.2.5. Reference Implementation in VHDL
The VHDL implementation followed the structure presented in Section 3.1.3, considering the signal sizes of Table 4. The results are shown in the fourth row of Table 7. This workflow generates the least use of resources, as the VHDL designer only uses what is necessary for directly implementing the algorithm in the low-level language. Despite this, the maximum speed achieved was similar to other methods, indicating that automatic tools can translate arithmetic operations into high-performing HDL code with an efficient computation path.
3.3. Code Metrics and Resource Usage
Metrics can be used to compare the VHDL code complexity and overhead generated by the automatic translation. The number of lines of code is frequently used in software [23] and can be applied to VHDL code. It serves to give an idea of the overhead added by the translation, but this overhead does not necessarily lead to additional logic usage. The other proposal (additions/subtractions, multiplications, if–then–else blocks, number of signals and variables) has a direct relation with resource usage. A higher number in any of them will imply more resource usage. These metrics, shown in Table 8, allow for a detailed analysis of the VHDL code complexity.

Table 8.
VHDL code metrics of the three design flows.
These code metrics alone do not explain why the MATLAB and Simulink models create a higher usage of resources. The number of signals and variables can be assumed to be correlated with the higher LUTs and FFs usage. However, there are three multiplications in the code, and they translate into 12 DSPs instead of 9, as in the case of the manual VHDL code.
The inspection of the generated code showed that the signals grew in intermediate calculations and the inputs to the multipliers were not optimized. Unsigned signals may grow by one bit if they intervene in calculations with signed signals. Thus, with the automated tools, the user cannot determine the exact size of the multiplier inputs unless an intermediate variable is created or a conversion block is placed before the multiplication.
The embedded DSP blocks in the target FPGA include multipliers with one input of 25 bits and the other one of 18 bits. Both are signed inputs. If more bits are used in any multiplication, the synthesis tool will use two or more DSP blocks for a single multiplication. This will not only increase the necessary resources (DSP blocks), but also the delay because it will include the delay of both DSP blocks.
4. Validation in a More Complex Circuit
This section presents a more complex model to validate the proposed design workflow. Specifically, a more complex design was used both to verify Requirements 7 to 11 and to test if just following the proposed workflow from Figure 3 is enough to achieve a HIL model with a performance similar to that of a model created manually, that is if the proposed workflow is sufficient to ensure an optimized real-time model without knowledge of HDL design. A full-bridge converter with first-order electrical losses, shown in Figure 7, was chosen, using the second-order Runge–Kutta method. This method provides high accuracy even with higher simulation steps. It requires two calculations during each computation cycle, instead of one, so it is a candidate for pipelined implementation. As it is more complex, an automated workflow would surely be preferred.
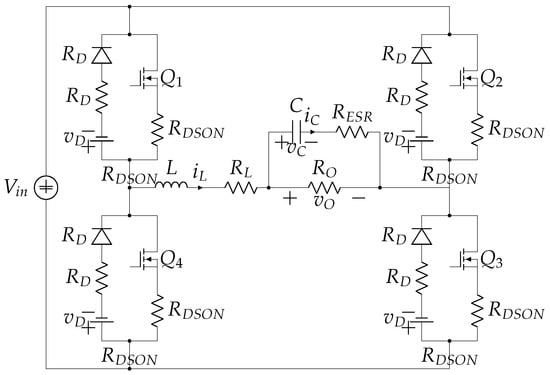
Figure 7.
Full-bridge converter with losses chosen for the verification of the proposed workflow.
4.1. Full-Bridge Converter Equations
The initial equations describing the circuit behavior [13] were rewritten to apply the second-order Runge–Kutta method:
The values for the and terms are:
The terms , , , and are the series resistance of the inductor, diode, metal–oxide–semiconductor field-effect transistor (MOSFET), and capacitor, respectively, and . The forward voltage of the diode is . The terms , , and vary depending on the operating conditions of the circuit. Their values are driven by the state of the switches to and the sign of inductor current according to Table 9. The rest of the terms remain constant during circuit operation. The equation for can be written as follows:

Table 9.
Parameters , , and according to switches’ states and inductor current sign.
4.2. Second-Order Runge–Kutta Model with K-Calculator
The second-order Runge–Kutta method uses a two-step approximation for the calculation of the state variables. For the proposed full-bridge, the terms are calculated as follows:
The values of the state variables at the next time step are then given by:
The implementation of the full-bridge uses a K-calculator similar to the one proposed in [19]. The K-calculator is a computing block that produces the different terms of the Runge–Kutta method— terms when the inputs are zero and when the inputs are the terms. This allows for calculating these terms iteratively reusing hardware elements. The K-calculator implements these equations:
4.3. Full-Bridge MATLAB Model
The MATLAB code was based on the initial code for the Forward Euler method used in [13], moving the multiplications out of the if–then blocks to avoid hardware duplication. The procedural code with two calls to a K-calculator function was rewritten to implement a pipelined operation with a state machine:
- State 0: Calculates and .
- State 1: The K-calculator computes and (13) and (14). In parallel, is calculated based on the stored values of and .
- State 2: The K-calculator computes and (15) and (16).
- State 3: The new values of and are calculated.
The K-calculator function is called once outside the if–then blocks for hardware reuse. States 1 and 2 have a maximum latency due to two sequential multiplications. Fixed-point conversion was performed using the HDL Code Generation Workflow advisor. The input signal sizes were limited to 25 or 18 bits with the sign bit to avoid extra DSP synthesis, as proposed in Section 2.
4.4. Full-Bridge Simulink Model
The Simulink model uses a pipelined configuration with four states, similar to the MATLAB model. Figure 8 shows a simplified version of the model with four blocks, one for each state. These perform the and calculation, the K-calculation, the accumulation of parameters, and the assignment of values to the state variables and . Conversion blocks are used at the inputs to ensure proper variable sizes and adapt variables before multiplication. For instance, and are adjusted to 25 bits before being multiplied to calculate when (10) is implemented. This ensures the minimum number of DSPs.
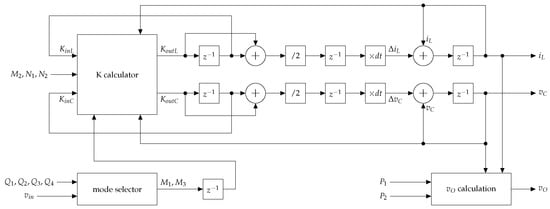
Figure 8.
Overview of the Simulink model of the full-bridge rectifier with losses. Enabling ports of unit delays are controlled by the state counter (not shown).
4.5. Full-Bridge Native VHDL Model
The native VHDL model of the full bridge converter contains one procedure, two processes, and the K-calculator in combinatorial logic. The procedure calculates variables and . The first process contains the state machine operations. It calls the procedure to calculate and in the first state of each iteration. It sets the correct inputs to the K-calculator (either zero or the values from the first cycle) and calculates the update of the state variables in the last state of the iteration. The second process updates the registered outputs.
4.6. Summary of the Full-Bridge Model Results
The three approaches showed similar results in terms of maximum speed and device usage, with all requiring 12 DSPs. Regarding the LUTs, the VHDL offered significantly better results. The maximum clock speed ranged from 19 to ns. Using the four-stage pipelining, a real-time result would be produced every 80 ns with the Runge–Kutta method, which is about five-times slower than the initial Euler method. However, since the results were more accurate, the overall system performance would be better. Table 10 summarizes the results of the three approaches and shows a comparison with the method proposed in [17], Table 6. The model required more resources because the numerical method was more complex, but there was little variation between automatic and manual designs, as opposed to the two comparable models created in [17].

Table 10.
Resource usage and maximum speed for the full-bridge model (Rows 1 to 3) and comparison with the method proposed in [17] (Rows 4 and 5).
Table 11 compares the metrics of the three design flows of the full-bridge model. The semi-automatically generated VHDL code was more complex. However, the parameters with a direct influence on hardware occupation and performance were similar to those of manually written VHDL code. The manual VHDL code had 14 multiplications, instead of 12, but it finally used 12 DSPs. This was because the K-calculator in the VHDL code was written following Equations (19) and (20), which allowed the synthesis tool to generate the correct optimization and produce only 2 DSPs for the 4 multiplication terms.

Table 11.
Metrics’ comparison for the full-bridge model with losses.
These results showed that the proposed workflow effectively achieved a translation into an efficient model. Even when handling a more complex model that typically is designed by HDL experts, the iterative optimizations of the MATLAB and Simulink code resulted in very efficient HDL models, totally comparable to the manual model in terms of speed and resource usage. This is remarkable because the manual model was generated with more effort and required knowledge of the VHDL. This was spared for the case of the MATLAB and Simulink models.
5. Experimental Results
The final step was implementing the system in hardware. As explained in Section 3.2.1, a Zynq device was used. In the implemented design, the programmable logic was used to run the model in real-time, and the processor communicated with an external computer for configuration.
The Simulink block design (Section 4.4) was modified by adding Advanced eXtensible Interface (AXI) ports for the initial configuration, and the VHDL code was automatically generated again to produce an Intellectual Property (IP) core. A block design was created in Vivado to integrate the generated IP core into the Zynq processing system. The full-bridge converter model (parameters shown in Table 12) ran in real-time with a clock speed of 22 ns. As Table 13 shows, the FPGA usage and clock speed were higher than the theoretical minimum (Table 10) due to the addition of the AXI interfaces and the integration with the processor.

Table 12.
Parameters of the proposed full-bridge converter.

Table 13.
Resource usage of the bare and complete full-bridge model.
The results were extracted with an Integrated Logic Analyzer. Figure 9 shows a transient from a duty cycle of 50% to 75%. Only one point per switching cycle was extracted to remove the switching ripple, although smaller steps were calculated internally. The model can calculate values properly and can be used for hardware-in-the-loop design and testing workflows as proposed in Section 1.
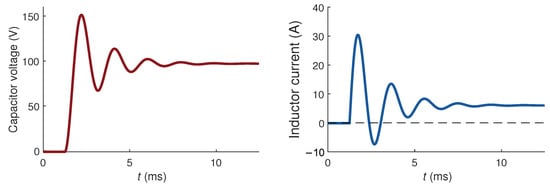
Figure 9.
Transition from 50% duty cycle to 75% duty cycle calculated in real-time.
6. Discussion
This paper focused on implementing models using their equations rather than directly translating schematics to HDL code, which can have low performance and high hardware usage. The results showed that semi-automatically generated models achieve high efficiency if the proposed method is followed.
The maximum speed was similar in all cases. DSP usage is critical in HIL applications, and an unoptimized algorithm could double the number of DSPs used, but the achievable speed of the non-optimized approach was still similar to the optimized one. The best results came from the HDL code generation approach, but it was also the most-complex and required manual conversion into fixed point. Besides, the inclusion of AXI interfaces required knowledge of the protocols and their implementation. Finally, pipelined designs increase the complexity, increasing the risk of incorrect implementation. All this makes the proposed workflow very attractive for designers who are not experts in HDL, since the effort of low-level HDL tasks with little added value is eliminated. At the same time, the designer can rest assured that the model obtained automatically has optimum performance. The price for this is careful work with the MATLAB or Simulink model. However, such a model is well known by the designer, so it requires little effort and creates low risk.
The recommended workflow proved to be compatible with complex models with pipelined architectures and several numerical methods. The power electronics designer can generate an efficient real-time model by following simple changes to the MATLAB or Simulink implementation. No knowledge of the target device is necessary, except for the multiplier input and output signal sizes. Modifications take place in a scope well known to the designer, the MATLAB or Simulink model: inspection of the calculation blocks, creation of new signals based on logical conditions, which depend on the circuit operation modes well known to him/her, adjustment of the variable sizes to those required by the device, and verification that the number of multiplier elements is in line with the calculations in the MATLAB/Simulink design.
The proposed steps were enough to ensure optimum code translation. They can be added to an existing design workflow, and the overhead due to the extra work and iterations is outweighed by the security that a very efficient model is generated.
Further work should be dedicated to validating the workflow in other disciplines using HIL. It can also be extended to other fields such as digital control systems, where engineers do not necessarily know an HDL, but know very well the equations that model the behavior of the system. It has to be determined if the proposed steps are enough also in other model types to produce efficient HDL code, that is to check if FPGA parameters other than multipliers impact the real-time model performance. In addition, the proposed method could be a candidate itself for automatic implementation, reducing even more effort for designers. For this, deeper formalization and generalization of the steps are needed.
7. Conclusions
A modification to the design workflow of HIL models is proposed, which leads to the automatic generation of very efficient models. It eliminates the need for designing at the HDL level and delivers results very close to those of manual designs. It was analyzed in a simple design and validated in a more complex one.
The proposal presented here eliminates the need to choose between either having an efficient model or producing it in an automated way.
For a typical power designer, who has little or no knowledge of an HDL, applying the proposal to MATLAB- and Simulink-based approaches delivers well-performing code, with additional use of resources, but with the same maximum speed. This is a promising path because it allows circuit designers to generate models with very good real-time behavior in automated workflows.
Author Contributions
Conceptualization, R.S., A.S. and A.d.C.; formal analysis, R.S., A.S. and A.d.C.; investigation, R.S., A.S. and A.d.C.; methodology, R.S. and A.d.C.; resources, R.S. and A.S.; software, R.S. and A.S.; supervision, A.S. and A.d.C.; validation, R.S., A.S. and A.d.C.; visualization, R.S.; writing—original draft, R.S.; writing—review and editing, R.S., A.S. and A.d.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Madrid Government (Comunidad de Madrid-Spain) under the Multiannual Agreement with Universidad Autónoma de Madrid in the line for the Excellence of the Universitary Teaching Staff, in the context of the V PRICIT (Regional Programme of Research and Technological Innovation).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mihalič, F.; Truntič, M.; Hren, A. Hardware-in-the-Loop Simulations: A Historical Overview of Engineering Challenges. Electronics 2022, 11, 2462. [Google Scholar] [CrossRef]
- Kirei, B.S.; Farcas, C.A.; Chira, C.; Ilie, I.A.; Neag, M. Hardware Emulation of Step-Down Converter Power Stages for Digital Control Design. Electronics 2023, 12, 1328. [Google Scholar] [CrossRef]
- Aiello, G.; Cacciato, M.; Scarcella, G.; Scelba, G. Failure analysis of AC motor drives via FPGA-based hardware-in-the-loop simulations. Electr. Eng. 2017, 99, 1337–1347. [Google Scholar] [CrossRef]
- Yushkova, M.; Sanchez, A.; de Castro, A. Strategies for choosing an appropriate numerical method for FPGA-based HIL. Int. J. Electr. Power Energy Syst. 2021, 132, 107186. [Google Scholar] [CrossRef]
- Razzaghi, R.; Mitjans, M.; Rachidi, F.; Paolone, M. An automated FPGA real-time simulator for power electronics and power systems electromagnetic transient applications. Electr. Power Syst. Res. 2016, 141, 147–156. [Google Scholar] [CrossRef]
- Liu, C.; Ma, R.; Bai, H.; Li, Z.; Gechter, F.; Gao, F. Hybrid modeling of power electronic system for hardware-in-the-loop application. Electr. Power Syst. Res. 2018, 163, 502–512. [Google Scholar] [CrossRef]
- Iranian, M.E.; Mohseni, M.; Aghili, S.; Parizad, A.; Baghaee, H.R.; Guerrero, J.M. Real-Time FPGA-Based HIL Emulator of Power Electronics Controllers Using NI PXI for DFIG Studies. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2005–2019. [Google Scholar] [CrossRef]
- Selvamuthukumaran, R.; Gupta, R. Rapid prototyping of power electronics converters for photovoltaic system application using Xilinx System Generator. IET Power Electron. 2014, 7, 2269–2278. [Google Scholar] [CrossRef]
- Parizad, A.; Mohamadian, S.; Iranian, M.E.; Guerrero, J.M. Power System Real-Time Emulation: A Practical Virtual Instrumentation to Complete Electric Power System Modeling. IEEE Trans. Ind. Inform. 2019, 15, 889–900. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Town, G.E. Design of FPGA-controlled power electronics and drives using MATLAB Simulink. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, Australia, 3–6 June 2013; pp. 571–577. [Google Scholar] [CrossRef]
- Alecsa, B.; Cirstea, M.N.; Onea, A. Simulink Modeling and Design of an Efficient Hardware-Constrained FPGA-Based PMSM Speed Controller. IEEE Trans. Ind. Inform. 2012, 8, 554–562. [Google Scholar] [CrossRef]
- Bonny, T. Chaotic or Hyper-chaotic Oscillator? Numerical Solution, Circuit Design, MATLAB HDL-Coder Implementation, VHDL Code, Security Analysis, and FPGA Realization. Circuits Syst. Signal Process. 2021, 40, 1061–1088. [Google Scholar] [CrossRef]
- Zamiri, E.; Sanchez, A.; de Castro, A.; Martínez-García, M.S. Comparison of Power Converter Models with Losses for Hardware-in-the-Loop Using Different Numerical Formats. Electronics 2019, 8, 1255. [Google Scholar] [CrossRef]
- Costas, L.; Colodrón, P.; Rodríguez-Andina, J.J.; Fariña, J.; Chow, M.Y. Analysis of two FPGA design methodologies applied to an image processing system. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 3040–3044. [Google Scholar] [CrossRef]
- Rosado-Muñoz, A.; Bataller-Mompeán, M.; Soria-Olivas, E.; Scarante, C.; Guerrero-Martínez, J.F. FPGA Implementation of an Adaptive Filter Robust to Impulsive Noise: Two Approaches. IEEE Trans. Ind. Electron. 2011, 58, 860–870. [Google Scholar] [CrossRef]
- Karimi, S.; Poure, P.; Saadate, S. An HIL-Based Reconfigurable Platform for Design, Implementation, and Verification of Electrical System Digital Controllers. IEEE Trans. Ind. Electron. 2010, 57, 1226–1236. [Google Scholar] [CrossRef]
- Zamiri, E.; Sanchez, A.; Yushkova, M.; Martínez-García, M.S.; de Castro, A. Comparison of Different Design Alternatives for Hardware-in-the-Loop of Power Converters. Electronics 2021, 10, 926. [Google Scholar] [CrossRef]
- Lamo, P.; Ruiz, G.A.; Azcondo, F.J.; Pigazo, A.; Brañas, C. Impact of the Noise on the Emulated Grid Voltage Signal in Hardware-in-the-Loop Used in Power Converters. Electronics 2023, 12, 787. [Google Scholar] [CrossRef]
- Saralegui, R.; Sanchez, A.; de Castro, A. Modeling of Deadtime Events in Power Converters with Half-Bridge Modules for a Highly Accurate Hardware-in-the-Loop Fixed Point Implementation in FPGA. Appl. Sci. 2021, 11, 6490. [Google Scholar] [CrossRef]
- Sanchez, A.; Todorovich, E.; de Castro, A. Impact of the hardened floating-point cores on HIL technology. Electr. Power Syst. Res. 2018, 165, 53–59. [Google Scholar] [CrossRef]
- Liu, J.; Dinavahi, V. Nonlinear Magnetic Equivalent Circuit-Based Real-Time Sen Transformer Electromagnetic Transient Model on FPGA for HIL Emulation. IEEE Trans. Power Deliv. 2016, 31, 2483–2493. [Google Scholar] [CrossRef]
- Sanchez, A.; de Castro, A.; Garrido, J. A Comparison of Simulation and Hardware-in-the- Loop Alternatives for Digital Control of Power Converters. IEEE Trans. Ind. Inform. 2012, 8, 491–500. [Google Scholar] [CrossRef]
- Perez-Cham, O.E.; Montalvo, C.S.; Nunez-Varela, A.S.; Puente, C.; Ontanon-Garcia, L.J. Source Code Metrics to Predict the Properties of FPGA/VHDL-Based Synthesized Products. In Proceedings of the 2018 6th International Conference in Software Engineering Research and Innovation (CONISOFT), San Luis Potosi, Mexico, 24–26 October 2018; pp. 93–98. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).