Optimal Allocation of IaaS Cloud Resources through Enhanced Moth Flame Optimization (EMFO) Algorithm

Abstract

A new generation of computing resources is available to customers via IaaS, PaaS, and SaaS administrations, making cloud computing the most significant innovation in recent history for the general public. A virtual machine (VM) is configured, started, and maintained across numerous physical hosts using IaaS. In many cases, cloud providers (CPs) charge utility customers who have registered their premises with the utility registration authorities. Given the opposing aims of increasing customer demand fulfillment while decreasing costs and optimizing asset efficiency, efficient VM allocation is generally considered as one of the most difficult tasks for CPs to overcome. This paper proposes the Enhanced Moth Flame Optimization (EMFO) algorithm to provide a unique strategy for assigning virtual machines to suit customer requirements. The recommended approach is applied on Amazon’s EC2 after three distinct experiments are assumed. The utility of the proposed method is further shown by the use of well-known optimization techniques for effective VM allocation. The app was created using a Java-based programming language and then run on the Netbeans IDE 12.4 platform.

1. Introduction

Cloud computing is an internet-based platform that supports several tenants and provides on-demand access to digital services from a variety of cloud service providers, all of which are constrained by quality of service (QoS) requirements. This service includes computer hardware for users, an operating system for communication, networks for resource sharing, resource storage, a database for resource management, and on-demand user applications. For the most part, cloud computing may be broken down into three major categories: Infrastructure as a Service (IaaS), Platform as a Service (PaaS), and Software as a Service (SaaS) [1]. IaaS is used in [2] to provide on-demand access to shared resources without disclosing the location or hardware details. Images of servers, queueing and other resources are also made available to users. Finally, IaaS gives people full control over the server infrastructure, not just applications or containers. It is hard to manage resources [3], network infrastructure [4], virtualization, and multi-tenancy [5] in cloud systems.

Resources in the form of virtual machines may be rented from IaaS providers such as Amazon EC2 and IBM Smart Cloud Enterprise [6]. An example of a pay-per-use public cloud is provided by Amazon EC2, which is described in [7]. Co-locating network I/O Apps together may result in significant performance gains, according to research [8]. However, they failed to demonstrate how this method might be used to improve cloud-based decision-making. The authors of [9] propose some complementary works to be carried out to enhance and continue verifying the infrastructure in tenant-based resource allocation paradigm. A separate platform, such as HPC or situations such as online transactional applications, should be deployed over the cloud infrastructure. Assuming that processing power and bandwidth are both provided concurrently for each request and leased out on an hourly basis, ref. [10] has presented an efficient joint technique for allocating multiple resources. Each service request has its own set of assigned resources. “Virtual machines” (VMs) of varying sizes and budgets are used as the primary computational components in [11]. VMs are dynamically allocated and also distributed, and workloads are scheduled on the most cost-effective ones. One study [12] has provided a method for allocating data for cloud computing resource management. A problem is that they do not account for things such as cloud provider hourly billing rates, VM startup times, and workflow.

It has been suggested in this work that Enhanced Moth Flame Optimization (EMFO) be implemented in order to address the issues raised in the literature. EMFO allocates resources in the most efficient manner while taking into account the profit, execution time, maximum resource usage, and resilience. The following are the key contributions that are anticipated as a result of the proposed work:

(i)

Using suitable cost functions and operational limitations, implemented MFO for efficient resource allocation in an IaaS cloud environment.

(ii)

For improved search capabilities, migration and curvilinear properties are added into MFO.

(iii)

The quantitative performance of the EMFO is examined under a number of various conditions and settings.

(iv)

A comparative performance analysis of the various strategies described in the literature is also provided.

The rest of this work is organized as follows: Section 2 reviews pertinent literature; The suggested system model, which incorporates application and execution models, is discussed in Section 3; Section 4 covers the suggested EMFO search approach; Section 5 analyzes the simulation findings for the test instances examined; Section 6 summarizes the work and makes a recommendation for further expansion.

2. Related Works

An IaaS cloud’s power usage was reduced by optimizing the mapping between a virtual machine and a physical server in [13]. A hybrid cloud environment is used to develop an integer programming model for the issue of resource allocation in an infrastructure as a service (IaaS) cloud [14]. This challenge is addressed via the use of a self-adaptive learning PSO (SLPSO)-based scheduling technique. A new generation of renewable energy-aware and thermal-aware virtual machine migration algorithms is described in [15]. These algorithms take into consideration the temperature consequences of mixed cooling systems, which include both CARC and air economizer. The stochastic search method is used to identify the best solution for maximizing the consumption of renewable energy in a joint optimal planning approach.

It is proposed in [16] to conduct an investigation on profit maximization for the provider by taking advantage of changeable energy costs. To assess the impact of energy and carbon-aware dynamic VM placement on cloud providers’ costs, ref. [17] examines and contrasts numerous energy-aware and carbon-aware dynamic resource allocation. Energy efficiency, including the availability of renewable energy sources and changes in energy use, has a substantial impact on the reduction of carbon footprint. Mixed Integer is used to express the reliability-aware server consolidation strategy in [18]. The linear programming mathematical model considers energy and reliability expenses to lower total DC expenditures. In more recent years, researchers have looked at the use of random search algorithms to tackle the resource allocation issue in cloud systems. When it comes to scheduling activities in datacenters, the authors of [19] employ simulated annealing (SA), a well-known randomized search method. SA’s lightweight nature, as well as its scalability and capacity to schedule activities across clusters of hundreds of servers, is one of its most often touted advantages. Furthermore, this solution does not permit the reallocation of virtual machines via migration.

For the challenge of virtual machine placement in datacenters, the authors of [20] use a genetic algorithm to combine the quick filtering and sorting capabilities of MapReduce with a genetic algorithm. Content-based VM selection and migration using fixed and dynamic threshold algorithms are being assessed [21] for server consolidation via VM migration, with the goal of minimizing the amount of memory data transmitted by utilizing content similarity. The ABBSH scheduling algorithm, which is mindful of renewable energy and power costs, is suggested in [22] for scheduling batch jobs. It also takes into account the work deadline to cope with renewable energy’s intermittent nature while preserving service-level agreements (SLAs). An energy-aware task-based virtual machine consolidation approach [23] is recommended to manage jobs with variable resource needs throughout execution. VMs and their workloads are categorized into four categories based on how much CPU, memory, I/O, and communication they use, with the goal of minimizing both the duration of the VMs’ lifespan and the amount of energy they consume. When compared to other approaches such as FCFS, Round-Robin, and EERACC, the experimental findings demonstrate that the suggested technique produces superior outcomes. Because of the reduced availability and dependability of the system, resource consolidation via live migration is a time-consuming operation that may result in SLA violations.

Ant Colony Optimization is used to optimize VM placement and consolidation for energy consumption and system dependability in order to establish a healthy balance between these two competing goals [24]. The resource utilization-aware energy efficient server consolidation algorithm (RUAEE) is a novel method [25] that aims to limit the number of live migrations of VMs during the consolidation process, lowering energy consumption and service-level agreement violations. The authors of [26] illustrate how group technology may manage resource allocation effectively to increase system efficiency while limiting investment costs. Resource consolidation is accomplished via the employment of a discrete cuckoo optimization method based on the Jaccard similarity coefficient grouping approach. A Multi-objective Ant Colony Optimization (MACO) strategy for virtual machine placement and consolidation is proposed in [27], which is energy-aware and QoS-aware. The proposed technique tries to achieve a trade-off between energy efficiency system performance and SLA compliance while maintaining system reliability. It is hypothesized in [28] that a prediction-based workflow-scheduling algorithm could discover the best-fit virtual machine and ensure optimum resource usage while fulfilling the timeline and budget constraints. The authors of [29] explain how a multi-resource-based VM placement strategy was built using the nova scheduler to improve CPU usage and execution performance on a VM. Two consolidation-based energy-efficient solutions were developed in [30] to reduce energy use and related SLA violations while also improving on the existing energy-conscious task consolidation (ECTC) and maximum utilization (MaxUtil) methodologies. Using a dynamic resource management approach for cloud spot markets, the authors of [31] have come up with a technique that effectively controls unused cloud resources in order to boost income.

The Resource Intensity Aware Load Balancing (RIAL) technique described in [32] has used to transfer VMs from congested physical machines (PMs). It is one of a kind since it weighs resources based on their resource intensity. The more time-consuming a resource is, the more important it is in a project management system. Because it utilizes the weights when deciding which VMs to migrate and which destination PMs to use, RIAL speeds up the process of getting to a load-balanced state and does so at a cheaper cost. One study [33] proposes a sophisticated scheduling method in combination with a load balancing strategy based on binary JAYA to improve resource utilization while simultaneously lowering the degree of energy consumption and makepan. According to [34], a fair and efficient online auction is developed for dynamic resource scaling and pricing, in which cloud users continually bid for resources in the future with increasing amounts, in accordance with their preferences for scaling up or out. For social welfare maximization, they looked at server energy cost reduction and discovered a crucial characteristic of the objective function, submodularity. A unique competitive analytic approach was used to handle the problem of submodular function optimization with non-linear constraints. With a variety of constraints on multiprocessor computing systems in mind, a quantum-inspired binary chaotic salp swarm method (QBCSSA) has been developed [35] to deal with the scheduling issue. In [36], a flower pollination strategy is employed to tackle the IaaS cloud VM allocation problem. Private cloud and external cloud cost characteristics are taken into account for an efficient VM allocation in the proposed study. It has been discovered that many of the optimization techniques offered to solve the VM allocation issue suffer from algorithm specific parameters, fail to provide global optimum solutions, demand extra execution time, and lag in their consistency in offering solutions and scalability.

The suggested work aims to enhance the performance of the algorithms described in the literature by offering maximum profit, optimum run time, resilience with better scalability, and improved convergence characteristics. Enhanced Moth Flame Optimization (EMFO) is presented in this work to address the issue of optimal resource allocation in IaaS administration. MFO [37] has a simple structure and a good selection capability for the given VM allocation problem compared to other algorithms such as SLPSO, SPSO-SA, CPLEX, and ACO. As described in the EMFO model, the classical MFO is combined with migrating [38] and descending curvilinear [39] qualities in order to increase the pace of searching and guarantee the global optimum solution is found.

3. System Model

3.1. Application Model

Many of the competing aims discussed in the introduction suggest that efficient VM allocation is a complex problem. In addition, the goals of the challenge change depending on how the system model’s architecture behaves. This research investigates problem-solving from the perspective of IaaS providers to maximize profit. Figure 1 depicts the diagrammatic form of the suggested system model.

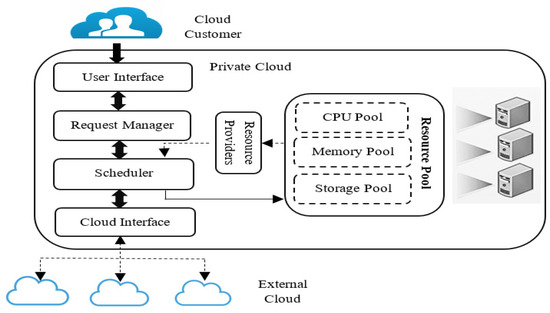
Figure 1. Proposed system model with private and external clouds.

Many service providers in the public cloud allow consumers to choose the cloud provider that most suits their needs. Individual public cloud service providers are referred to as “private clouds” in [15]. In each private cloud, consumers are given a price tag for the various services they may get from the cloud. On-demand resource allocation is possible in the private cloud thanks to an optimized scheduler. Customers’ needs may be unmet if the private cloud’s infrastructure is not up to snuff. A lack of infrastructure on the part of the service provider might result in the loss of clients. With the agreed rate, additional private clouds may be hired to provide resources in the public cloud. When it comes to hiring resources, optimum scheduler once again chooses the most suited private cloud inside the public cloud environment. When adopted to optimize resources in both private and public clouds, the optimum scheduler assumes all the duty. Both users and service providers gain from this, and no requests go unmet. The EMFO method used in this study provides the most efficient scheduler for the resources.

This work aims to find the best way to allocate resources for a pool of independent jobs on batch workloads. Data processing, memory, simulation packages, etc. are all examples of tasks. The issue statement is based on the premise that the cloud environment’s resource parameters, and requests are made accessible to the developer. Table 1 and Table 2 provide definitions for terminology relating to resources and workloads that are evaluated over the course of this research. The resource parameters shown in Table 1 include private clouds (PC), virtual machines (VM), price (p), cost (c), CPU, and RAM. The workloads and their associated expressions are detailed in Table 2. In terms of workloads, each application has a strict deadline for fulfilling all of the prerequisites before it can be filed. Each program is constrained by a stringent deadline (D_l) and runtime (r_l), as well as a collection of tasks (T_l,p). The suggested work aims to maximize PC1′s profit while allocating the ‘l’ applications to PC_n (n = 1, 2, …, l). Tasks linked with an associated application should be completed in a sequential manner to ensure that no task is interrupted. Each task must be assigned to one PC_n. The process running on PC₁ should not use more resources than the machine has available for a particular time period; also, PC_n (n = {2, 3, …, l}) has infinite resources.

Table 1. Definitions of resources.

Parameters	Definitions	Expressions	Details
Private Clouds	PC	{PC1, PC2, …, PCn}	Cloud environment with ‘n’ private clouds
Virtual Machines	VM	{VM1, VM2, …, VMm}	Each physical machine has ‘m’ virtual machines
Price	p	pn	Price of nth private cloud
Cost	c	cn,m	Cost of mth virtual machine in nth private cloud
CPU	cpu	cpun,m	Number of CPU of mth virtual machine in nth private cloud
		cputotal,n	Total number of CPUs in nth private cloud
Memory	mry	mryn,m	Memory size of mth virtual machine in nth private cloud
		mrytotal,n	Total memory size of nth private cloud

Table 2. Definitions of batch of workloads.

Parameters	Definitions	Expressions	Details
Applications	A	{A1, A2, …, Al}	For any instance ‘l’ requested applications
Tasks	T	{Tl,1, Tl,2, …, Tl,p}	Application ‘l’ has ‘p’ number of tasks
Deadline	D	{D1, D2, …, Dl}	Deadline of applications {1, 2, …., l}
Runtime	r	{r1, r2, …, rl}	Runtime of each task of applications {1, 2, …, l}
Deadline Threshold	S		Maximum Deadline

3.2. Execution Model

The proposed approach is focused on batch workloads, namely a collection of discrete activities, each of them may be large-scale data processing, scientific simulation, or image/video rendering. This sort of bag-of-tasks is often used in corporate applications such as consumer behavior mining or sensor data analysis of forecasting machine failures in IT infrastructure. Strongly connected activities, complicated processes, and online transaction processing are examples of workloads that are not addressed by this approach. Each submitted application consists of a number of embarrassingly simultaneous and independent tasks, all of which must be completed by a specified deadline. Each job must be completed in a single VM instance type. The fundamental purpose of VM allocation is to optimize private cloud profit (PC_profit) and to guarantee that no request goes unsatisfied at any point in time. Profitability is determined by a good accounting of the private cloud provider’s revenue (PC_revenue) and the entire cost of supplying the customer’s applications (PC_cost). The mathematical equation for calculating the profit margin on private clouds is provided below.

Maximize

$$P{C}_{profit}=P{C}_{revenue}-P{C}_{cost}$$

(1)

where

$$P{C}_{revenue}={{\displaystyle \sum }}_{i=1}^l{{\displaystyle \sum }}_{j=1}^m{T}_i{x}_{ij}{r}_{i }{p}_j$$

(2)

$$P{C}_{cost}={{\displaystyle \sum }}_{i=1}^l{{\displaystyle \sum }}_{l=1}^{T_i}{{\displaystyle \sum }}_{j=1}^m{{\displaystyle \sum }}_{k=1}^n{y}_{ilk}{x}_{ij}{c}_{kj}{r}_i$$

(3)

Subject to

$${{\displaystyle \sum }}_{k=1}^n{y}_{ipk}=1, \forall i \in \left\{1, 2, \dots \dots , l\right\}, p \in \left\{ 1, 2, \dots ., T_k\right\}$$

(4)

$${{\displaystyle \sum }}_{s=1}^{d_i}{w}_{ips}=y_{ip1}{r}_i,\forall i \in \left\{1, 2, \dots \dots , l\right\}, p\in \{ 1, 2, \dots ., T_i\}$$

(5)

$$st{s}_{ip}\ge 1,\forall i \in \left\{1, 2, \dots \dots , l\right\}, p\in \left\{ 1, 2, \dots ., T_i\right\}$$

(6)

$$\begin{array}{c}st{s}_{ip}\le d_i-r_i+1, \forall i \in \left\{1, 2, \dots \dots , l\right\}, p \in \{ 1, 2, \dots ., T_i\}\\ \left(s\le st{s}_{ip}-1\right) \vee \left(s\ge d_i-r_i\right)\vee \left(\left(s\ge st{s}_{ip}\right)\wedge \left(s\le st{s}_{ip}+r_i-1\right)\wedge \left(w_{ips}=y_{ip1}\right)\right)\end{array}$$

(7)

$$\forall s\in \left\{1, 2, \dots d_i\right\},i \in \left\{1, 2, \dots \dots , l\right\}, p \in \left\{ 1, 2, \dots ., T_i\right\}$$

(8)

$${{\displaystyle \sum }}_{i=1}^l{{\displaystyle \sum }}_{p=1}^{T_i}{{\displaystyle \sum }}_{j=1}^m{w}_{ips}{x}_{ij}cp{u}_j\le tota{l}_{cpu}, \forall s\in \left\{1, 2, \dots S\right\}$$

(9)

$${{\displaystyle \sum }}_{i=1}^l{{\displaystyle \sum }}_{p=1}^{T_i}{{\displaystyle \sum }}_{j=1}^m{w}_{ips}{x}_{ij}me{m}_j\le total\_mem ,\forall s\in \left\{1, 2, \dots S\right\}$$

(10)

$$y_{ipk}\in \left\{0, 1\right\},\forall i\in \left\{1, 2, \dots \dots , l\right\}, p \in \left\{ 1, 2, \dots ., T_i\right\}, k \in \left\{1, 2, \dots \dots , n\right\}$$

(11)

$$z_{ips}\in \left\{0, 1\right\}, \forall i\in \left\{1, 2, \dots \dots , l\right\}, p\in \left\{ 1, 2, \dots ., T_i\right\}, s \in \left\{1, 2, \dots \dots ,S\right\}$$

(12)

$$st{s}_{ip}\in \left\{1, 2, \dots ., S\right\},\forall i\in \left\{1, 2, \dots \dots , l\right\}, p \in \left\{ 1, 2, \dots ., T_i\right\}$$

(13)

In accordance with constraint (4), each job will be precisely assigned to one cloud service provider. Constraint (5) guarantees that each activity is completed before the deadline set out for it. Because of constraints (6)–(8), it is guaranteed that each job is non-preemptable, which means that a task is completed without interruption. Constraints (9) and (10) are applied to private cloud in order to guarantee that it does not consume more CPUs and memory than it has available in any one slot. Lastly, (11)–(13) provide definitions for the choice factors. We can see from the phrasing that the issue is one of work allocation. Using a mathematical programming technique to solve such issues requires a significant amount of processing time for a large-scale challenge. This characteristic precludes the use of mathematical programming in this case, where tasks must be planned in real time. Table 3 contains the definitions of the decision variables that were examined.

Table 3. Decision variables.

Variables	Definitions
$x_{ij}$	$x_{ij}$=1, if the ith application uses jth VM type, otherwise ‘0’
$st{s}_{ip}$	Start time slot of task tip
$y_{ipk}$	$y_{ipk}$= 1, if the task tip is allocated to kth PC, otherwise ‘0’
$w_{ips}$	$w_{ips}$ = 1, if the task tip is allocated to time slot ‘s’ of PC1, otherwise ‘0’

4. Proposed Search Strategy

4.1. Standard MFO (SMFO)

The moth–flame optimization (MFO) technique, invented by Seyedali Mirjalili, was initially unveiled in 2015, and it is a revolutionary nature-inspired population-based strategy based on evolutionary computing ideas. Moths and flames are two fundamental components of the MFO approach, with moths indicating fitness values calculated by using randomly generated variables for each population of each iteration and flames reflecting the best solutions at the finish of each iteration.

Moths regarded of as a matrix, which can be represented in the following way:

$$M=\left[\begin{array}{cc}\begin{array}{cc}{M}_{1,1}& M_{1,2}\\ M_{2,1}& M_{2,2}\end{array}& \begin{array}{cc}\cdots & M_{1,d}\\ \cdots & M_{2,d}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ M_{n,1}& M_{n,2}\end{array}& \begin{array}{cc}\cdots & ⋮\\ \cdots & M_{n,d}\end{array}\end{array}\right]$$

(14)

where ‘n’ and ‘d’ represent the number of moths and control variables of the problem, respectively. Accordingly, the fitness values of the individual moths form an array which can be described as follows:

$$OM=\left[\begin{array}{c}\begin{array}{c}O{M}_1\\ O{M}_2\end{array}\\ ⋮\\ O{M}_n\end{array}\right]$$

(15)

In the above equation, OM_n holds the fitness value of the n_th moth. Similarly, the flames have the same structure as the moths and can be described as follows:

$$F=\left[\begin{array}{cc}\begin{array}{cc}{F}_{1,1}& F_{1,2}\\ F_{2,1}& F_{2,2}\end{array}& \begin{array}{cc}\cdots & F_{1,d}\\ \cdots & F_{2,d}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ F_{n,1}& F_{n,2}\end{array}& \begin{array}{cc}\cdots & ⋮\\ \cdots & F_{n,d}\end{array}\end{array}\right]$$

(16)

The corresponding fitness values of the flames are stored in an array such as moths:

$$OF=\left[\begin{array}{c}\begin{array}{c}O{F}_1\\ O{F}_2\end{array}\\ ⋮\\ O{F}_n\end{array}\right]$$

(17)

In the above equation, OF_n holds the fitness value of the n_th flame. The MFO algorithm’s convergence is achieved through its unique three-dimensional approach of solving the non-linear problem, which is represented as:

$$MFO=\left(I,P,T\right)$$

(18)

In Equation (18), the random moths and their respective fitness levels are stored in the function ‘I.’ A moth’s last known location in a search region is stored in function ‘P’. When the halting criteria are met, function ‘T’ closes off the solution process.

When updating the progress of moths, this method makes use of a logarithmic spiral.

$$\left(M_i,F_j\right)=D_i{e}^{bt}cos\left(2\pi t\right)+F_j$$

(19)

$$D_i=\left|F_j-M_i\right|$$

(20)

where $D_i$ represents the distance of i_th moth with respect to j_th flame, ‘b’ is a co-efficient of the logarithmic spiral and $t \in \left[-1,-2\right].$

During the iterations, the number of flames decreases to better identification of the perfect solution:

$$flameno=round\left(n-l\frac{n-1}{T}\right)$$

(21)

where ‘l’ and ‘T’ represents the current and maximum iterations, respectively.

All occupations in MFO are represented as moths that fly about in search space, always updating their position based on their own and the flames’ experiences. Each moth’s priorities are used to allocate work to a private cloud or an ECs, as stated. By using a moth (a collection of priorities), MFO hopes to optimize the distribution of cloud resources. The suggested approach’s search capacity is increased by both the logarithmic spiral adaptation’s frequent updating of the number of participating flames and the progress updating of the moths’ positions.

4.2. Enhanced MFO (EMFO)

Scientific and technical areas have avoided classical MFO because of its incapacity to deal with a broad variety of challenges. Additionally, it is easy to become stuck in local optimums for certain difficult jobs. The optimal solution to the VM allocation problem is not easy to find. As a result, a more powerful and resilient MFO is needed to handle this problem effectively. It is possible to avoid local optimization by increasing the diversity of moths and flames. When searching for flames and moths, MFO is paired with migrating and descent curvilinear to keep track of their position.

4.2.1. Migration Principle

This is used to alleviate the strain of selecting the best moth from a limited population by regenerating a fresh population of individuals with a broad range of moths. On the basis of the best individual M_i,b, a new generation of moths is created. In this case, the d_th individual’s i_th moth is transformed into the following:

$$M_{i,d}=\{\begin{array}{c}{M}_{i,b}+{\alpha }_{i,d}\left(M_{d,min}-M_{i,b}\right) if {ά}_{i,d}<\frac{M_{i,b}-M_{d,min}}{M_{d,max}-M_{i,b}}\\ M_{i,b}+{\alpha }_{i,d}\left(M_{h,max}-M_{i,b}\right) otherwise\end{array}$$

(22)

where both ${\alpha }_{i,d}$ and ${ά}_{i,d}$ refer to uniformly distributed random numbers. This heterogeneous population is then used as initial choice parameters to avoid the local optimum places. The equation for carrying out the migration is presented in expression (23), which is carried out only if the moth population density ($\rho$) is smaller than the tolerance of the moth population diversity (${\epsilon }_1$).

$$\rho =\frac{{{\displaystyle \sum }}_{\begin{array}{c}i=1\\ i\ne b\end{array}}^n{{\displaystyle \sum }}_{h=1}^d{\eta }_z}{d\left(n-1\right)}<{\epsilon }_1$$

(23)

where

$${\eta }_z=\{\begin{array}{c}1 if \left|\frac{M_{i,d}-M_{i,b}}{M_{i,b}}\right|\\ 0 otherwise \end{array}>{\epsilon }_2$$

(24)

The parameter ${\epsilon }_2$ denotes the moth diversity relative to the best individual, while ${\eta }_z$ denotes the scale index. The cycle is repeated until there is no progress in the best individual. In Equation (23), ‘b’ is an integer variable which refers the location of best moth, ‘h’ and ‘d’ are the integer variables which refers the h_th and d_th generation of moths, and ‘n’ is an integer variable which refers the total number of moths.

4.2.2. Descending Curvilinear Principle

This idea has been tweaked to make it easier to find the best solution faster. Because of the high number of random states in moth swarm behavior, it must be checked repeatedly, which results in an algorithm that is very time-consuming. Improved convergence of the adaptive flame number and the algorithm’s convergence speed are achieved by changing the update process from linear (21) to curved descent. The following is the new formula for the number of adaptive flames.

$$flameno=round\left(\frac{T}{l+\left( \frac{T}{n} \right)}\right)$$

(25)

The pseudocode of the proposed EMFO algorithm is detailed below.

Input:Maximal iteration number (MAXIT), Number of Control variables (d)   Number of Moths (n), iterCount = 0 Output: OptimalSolution //Execute the following steps if (iterCount< MAXIT) { //Preparation phase of Moths   M(n,d) = random()       // Prepare the matrix for moths [M](n*d) (14)   Obj(M(n))          // Find the fitness value for moths [OM](n*1) (15) //Preparation phase of Flames   F(n,d) = random()       // Prepare the matrix for flames [F](n*d) (16)   Obj(F(n))          // Find fitness value for flames [OF](n*1) (17) // interaction phase of Moths and flames   D = f(F,M)          //Find distance of moths (20) // updation phase of Moths   S = f(F,M)          // Find logarithmic spiral for moths (19)   M = f(S)           //Update position of moths   finalM = best(M)       //Collect best Moths // Migration operation   M = f(finalM)         // Diverse moths using (22),(23) and (24) // limiting the flow of flames for further iterations   F = f(n,l,T)          // Curvilinear reduction of flames (25)   iterCount = iterCount + 1    //Increment the generation count } Display finalM

5. Results and Discussions

5.1. Technical Specifications of the Study

A private cloud and ECs are being built, with three distinct kinds of VMs used for testing the effectiveness of the proposed algorithm on the actual infrastructure. In this work, two types of resources, namely CPU and RAM, have been chosen since they are the most often used configuration factors when selecting a VM instance in the cloud. Table 4 shows the amount of CPUs and accessible RAM for the different VM instance types, as well as the cost and price of private cloud and ECs for each kind [15]. Additional versatility is provided by three kinds of virtual machines (ECs) based on the three VM instance types, which allow for a greater variety of ECs and VMs.

Table 4. Details of the resources.

VM Instance Types			Private Clouds		ECs Price (p)
Name	CPU (cpu)	Memory in GB (mry)	Cost (c)	Price (p)	TypeA	TypeB	TypeC
VM_type1	1	1.7	0.03	0.08	0.085	0.07	0.10
VM_type2	4	7.5	0.12	0.32	0.34	0.36	0.40
VM_type3	8	15	0.24	0.64	0.68	0.70	0.72

The task model is constructed with three different problem instances. Table 5 details factors such as the tasks, VM type, and deadline for each application for the instances, as well as the required amount of needed resources of applications. The characteristics of the applications are chosen at random within the given range based on the instance type; for example, for type 1, the number of tasks for each application is chosen between 1 and 5. The suffix ‘U’ indicates that the value chosen from the supplied range must be an integer amount. The search space is decreased by reducing each application’s deadline to a maximum of 5 h. In addition, each task of the application may choose one of the three VM instance kinds. To guarantee that the deadline of each program is longer than its runtime, the runtime of each application is maintained below the deadline for the instance types. For instance types 1, 2, and 3, the number of applications is set to 8, 5, and 10, correspondingly. Furthermore, the required number of CPUs and memory for type 1 is restricted to 20 units and 40 GB, respectively. The other two instance types, on the other hand, are restricted to 512 units and 1024 GB.

Table 5. Details of the applications.

	Instance Type 1			Instance Type 2 and 3
Parameters	Values	Resources	Number	Values	Resources	Number
Tasks	U [1, 5]	CPU (cpu)	20	U [1, 50]	CPU (cpu)	512
VM type	U [1, 3]	Memory (mry)	40 GB	U [1, 3]	Memory(mry)	1024 GB
Deadline (hrs.)	U [1, 5]			U [1, 168]

5.2. Performance Evaluation

When it comes to scheduling work for each of the three issue scenarios, the suggested EMFO is used to arrange them in the most efficient manner possible, given the resources available in each case. A comparison is made between the performance of EMFO and the performance of other suggested algorithms such as CPLEX [15], SLPSO-SA [15], CEDWS [29], and IFPA [33] when the task and resource settings are the same. Literature references are used to determine the algorithm-specific parameters of the various algorithms. A PC equipped with a 64-bit Intel Core i5 CPU working at 2.93 GHz and 8 GB of RAM, running Windows 10, has been utilized to assess the strategies. The algorithms are developed in MATLAB R2017a and validated on this computer, which serves as a simulation platform for the techniques.

5.2.1. Instance Type 1

The proposed EMFO is executed for 10 runs for the optimal task scheduling of instance type 1 by properly picking the random integer values for the tasks, VM type, deadline, and runtime. The average runtime and average profit during each run are recorded, which are shown in Table 6. It is evident from the table that during every new execution, the proposed algorithm brings the optimal solution with minimum runtime. Additionally, the proposed algorithm produces a maximum profit of 4.9767 and minimum profit of 4.88 with execution times of 12.55 s and 15.79 s, respectively.

Table 6. Profit and runtime during different executions for instance type 1.

Runs	1	2	3	4	5	6	7	8	9	10
Profit (PCprofit)	4.9157	4.9030	4.8837	4.9196	4.8794	4.8800	4.9767	4.9553	4.9233	4.9115
Runtime (s)	12.20	11.35	11.80	15.20	10.71	15.79	12.55	11.18	11.34	9.71

The obtained results are compared with the results of the literature, which is shown in Table 7. Parameters such as average profit, average runtime, standard error, and standard deviation [15] are considered for the effective comparison of the algorithms. In terms of average profit, it is evident from Table 7 that the EMFO algorithm introduced outperforms all other existing algorithms. While SLPSO-SA and CPLEX make profits of 4.9080 and 4.9100, respectively, EMFO achieves an average profit of 4.9148. There is a clear difference in dependability between the three methods based on their standard deviation and standard error. Additionally, the solution technique’s average runtime is faster than both SLPSO-SA and CEDWS. IFPA and CPLEX take up the least processing time on average compared to the other algorithms. This work also compares the algorithm convergence characteristics to show that the suggested EMFO is effective. SLPSO-SA, IFPA, CEDWS, and EMFO algorithms are used for the comparison. Figure 2 shows the simulation results for each method. Convergence is better with the EMFO approach than any other optimization method shown in Figure 2. Both SLPSO-SA and EMFO have essentially identical linear features; however, the algorithms CEDWS and IFPA have different characteristics and generate profits that are less than 4.85 and 4.825 percent, respectively, compared to SLPSO-SA and EMFO.

Table 7. Comparison of simulation results of instance type 1.

Algorithms	Average Profit	Average Runtime	Standard Error	Standard Deviation
SLPSO-SA	4.9080	29.55	0.0020	0.0060
CPLEX	4.9100	0.98	0.0003	0.0008
IFPA	4.8240	0.86	0.0014	0.0372
CEDWS	4.8500	14.6	0.0025	0.0091
EMFO	4.9148	12.18	0.0009	0.0038

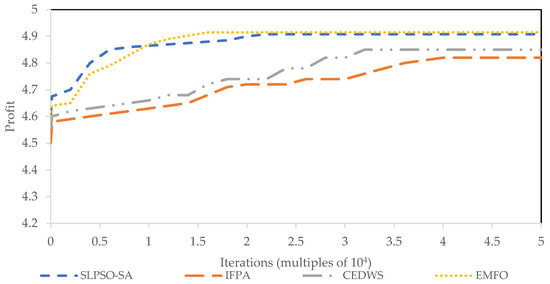
Figure 2. Convergence characteristics of algorithms for instance type 1.

5.2.2. Instance Type 2 and 3

The algorithms under consideration in this work are run for instance types 2 and 3 in the same way as they were for the prior instance, with the exception of the CPLEX. Table 8 shows the average profit, the execution time, the standard deviation, and the standard error that are acquired. It can be seen from the table that the suggested algorithm generates a higher profit than previous algorithms, with an average profit of 3587.182 for instance type 2 and 4327.64 for instance type 3 recorded. The algorithms used by SLPSO-SA, IFPA, and CEDWS result in profit reductions of 2.08%, 8.52%, and 6.48% for type 2, and 4.11%, 5.97%, and 5.15% for type 3, according to the results of the comparison. Furthermore, the suggested technique has a much shorter runtime than previous algorithms, with a recorded value of 2368.49 s for type 2 compared to other algorithms. In contrast, when it comes to type 3, the SLPSO-SA algorithm has taken the shortest amount of time when compared to EMFO. The CEDWS algorithm is more profitable than the IFPA method. However, the IFPA solution process beats CEDWS due to its unique nature, which takes the least amount of runtime to produce the best solution. Standard error and standard deviation are used to evaluate the trustworthiness of all algorithms, and these values are calculated from a large number of executions. The EMFO algorithm has emerged as the most trustworthy algorithm, followed by the IFPA, SLPSO-SA, and CEDWS algorithms.

Table 8. Comparison of simulation results of instance type 2 and 3.

	Instance Type 2				Instance Type 3
Algorithms	Average Profit	Average Runtime	Standard Error	Standard Deviation	Average Profit	Average Runtime	Standard Error	Standard Deviation
SLPSO-SA	3512.48	2874.27	0.0491	0.0620	2814.78	4265.80	0.0280	0.0513
IFPA	3281.25	4772.86	0.0352	0.0551	2760.17	6923.77	0.0215	0.0420
CEDWS	3354.62	3964.14	0.0567	0.0784	2784.30	7264.91	0.0530	0.0691
EMFO	3587.182	2368.49	0.0245	0.0537	2935.56	4327.64	0.0086	0.0347

Using the same working circumstances and a set number of iterations, the algorithms’ convergence properties are evaluated. Figure 3 and Figure 4 show the convergence characteristics of the algorithms for type 2 and type 3, respectively. According to Figure 3 and Figure 4, the SLPSO-SA algorithm obtains a greater convergence rate than the EMFO technique while having a lower profit margin than the EMFO method. Furthermore, for type 2, SLPSO-SA obtains the optimal solution before half of the total number of iterations; however, for type 3, SLPSO-SA finds the optimal solution after a large number of iterations. A further point to note is that for both instance types, the IFPA and CEDWS algorithms exhibit the same convergence characteristics, but with lower profits than the EMFO approach.

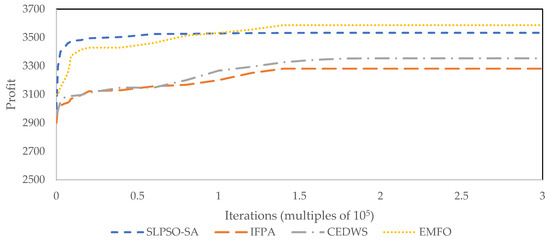
Figure 3. Convergence characteristics of algorithms for instance type 2.

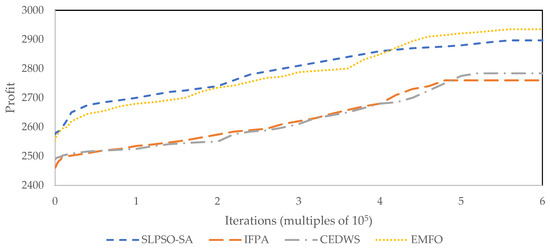
Figure 4. Convergence characteristics of algorithms for instance type 3.

6. Conclusions and Future Work

This research attempts to build an improved moth–flame optimization technique for VM allocation in an IaaS context with the goal of increasing cloud providers’ revenues. It has been put to the test on three separate tasks of varying difficulty to see how well it handles a range of circumstances. To validate the effectiveness, the acquired results of several algorithms were compared. Based on the comparison, it is evident that the suggested algorithm produces superior outcomes in a variety of situations. The algorithm’s dependability is further tested using the standard deviation and standard error of profit for a certain number of runs. The notions of migration and descending curvilinear has been nicely incorporated into the standard MFO, resulting in a considerable reduction in runtime. The inclusion of high-level SLA to the proposed work will provide the highest levels of service security and dependability. Additionally, the current work may be incorporated to handle concerns such as energy management and fault tolerance.