Context Aware Recommender Systems: A Novel Approach Based on Matrix Factorization and Contextual Bias

Abstract

In the world of Big Data, a tool capable of filtering data and providing choice support is crucial. Recommender Systems have this aim. These have evolved further through the use of information that would improve the ability to suggest. Among the possible exploited information, the context is widely used in literature and leads to the definition of the Context-Aware Recommender System. This paper proposes a Context-Aware Recommender System based on the concept of embedded context. This technique has been tested on different datasets to evaluate its accuracy. In particular, the use of multiple datasets allows a deep analysis of the advantages and disadvantages of the proposed approach. The numerical results obtained are promising.

1. Introduction

The Internet of Things (IoT) [1,2,3,4] allows the digitalization of the daily experience and the collection of an enormous number of data that involves the Big Data management problem. The Big Data [5] term denotes a structured or not growing data set selected through complex algorithms [6]. The main features of Big Data are volume, variety, and velocity [7]. Data mining techniques can acquire relevant data and deal with the Big Data problem [8]. Among all of the used tools, the data mining field widely exploits Recommender Systems (RSs) [9].

RSs can analyze and filter information to provide support to the user in the selection phase [10,11]. RSs work on three main elements: system users, items to suggest, and transactions, interactions between users and the systems. Among the various transaction forms, rating or utility function [10] plays a central role and represents a user evaluation about an item that the system can suggest. Formally, the rating is a function that has as domain the Cartesian product of the users set U, and the items set I, and has as a codomain the real numbers set $\mathbb{R}$.

$$r : \left(u,i\right) \in U\times I\mapsto {\widehat{r}}_{ui}=r\left(u,i\right) \in \mathbb{R}$$

(1)

The Recommender Systems’ [12,13] principal utility is the prevision of items to suggest to individual users that users do not interact with, or rather the images of couples $\left(u,i\right) \in U\times I$ that the system ignores. The techniques used to provide these forecasts classify Recommender Systems.

Content-based RSs [14,15,16] aim to create profiles (features vectors) that represent system entities (user, item). Profiles allow the calculation of the affinity between a user and an item of the system, for instance, through the cosine similarity [17,18].

Collaborative Filtering RSs [19,20,21] are recommendation methods based on the knowledge of ratings provided by users. Known ratings are collected in a matrix $R\in {\mathbb{R}}^{m\times n}$, where the value m represents the number of users and the value n consists in a number of items. Collaborative techniques are divided into two groups: Memory-Based and Model-Based. Memory-Based Collaborative Filtering RSs [22] generate rating forecasts through the creation of Neighborhoods [23] that are groups of users (User-Based) [22] or of items (Item-Based) [24]. Model-Based Collaborative Filtering RSs [25,26] aim to build a mathematical model of the problem through the use of factorization techniques on the rating matrix R [27,28,29].

Hybrid Recommender Systems [30,31,32] exploit multiple recommendation techniques to generate more reliable rating forecasts. Moreover, they aim to overcome singular methodologies limits as, for instance, cold start [33,34], scalability [34,35,36], and sparsity [34,36,37].

Many methods aim to improve Recommender Systems performance. These methods exploit machine learning [38] and deep learning [39] techniques, ontologies [40], and context awareness [41,42] to provide more reliable rating forecasts. This paper focuses on Context-Aware Recommender Systems (CARSs) [43].

Context denotes “any information useful to characterize the situation of an entity that can affect the way users interact with systems” [44,45,46], where Recommender System entities are users and items [47]. In CARSs, contextual information involves the rating variation. For instance, an outdoor archaeological site has different ratings on rainy days to sunny ones.

Based on the information that characterizes the context, it can be divided into individual, location, time, activity, and relational context [47]. The individual concerns the entities (user, item) of the Reccomender systems, the location gives information on the physical or virtual location of an entity, the time context is based on a specific time or a time interval, activity concerns the entities tasks, and relational notifies social or functional relations among all entities. This general classification can be adapted to the application fields. For instance, in a musical application, the context classification includes features related to the device with which users interact and focuses on the achievement and the activity of users [48].

The strategies of contextual information integration into Recommender Systems are shown in Figure 1 and described in the following:

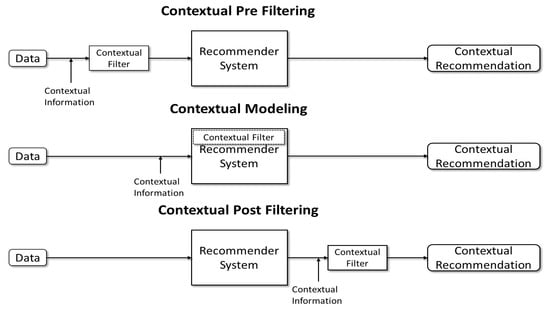
Figure 1. Summary of the contextual information introduction in the Recommendation Phase.

• Contextual Pre-Filtering: contextual information is exploited for data filtering and, subsequently, is elaborated by the Recommender System. In Content-Based RSs, this strategy involves the creation of multiple profiles based on the contexts related to each user and each item. The Pre-Filtering consists of the selection of the proper features vector provided in the recommendation phase. In Collaborative Filtering RSs, this strategy elaborates the ratings related to the determined contextual dimension [47,49];
• Contextual Post-Filtering: contextual information is exploited after the recommendation phase to select the proper rating forecasts related to the context [47,49];
• Contextual Modeling: the recommendation phase integrates contextual information to calculate contextually consistent rating forecasts. In Content-Based RSs, contextual information entails the change of the formula related to the user/item affinity calculation in the determined context. In Collaborative Filtering RSs, Heuristic-Based methods are applied in the Memory-Based RSs, and tensor factorization and properly integrated matrix factorization techniques are exploited in Model-Based RSs [47,49,50].

This paper aims to introduce a novel Contextual Modeling recommendation method that exploits matrix factorization and contextual biases. The proposed approach evaluates context as tensor representation does, then all contexts are considered as ordered tuples and not individually. We define this context representation as embedded context that aims to consider all the contextual information simultaneously. For instance, a user can watch a movie ‘alone’ and ‘at home’, as shown in Figure 2. In this case, the individual evaluation of the companion context value alone can take into account all the values of location context and not only the value ‘at home’; likewise, the singular evaluation of the location context ‘at home’ evaluates all possible values of the companion context and not only the value ‘alone’. Instead, the embedded context allows elaborating the location and companion contexts only for the proper values.

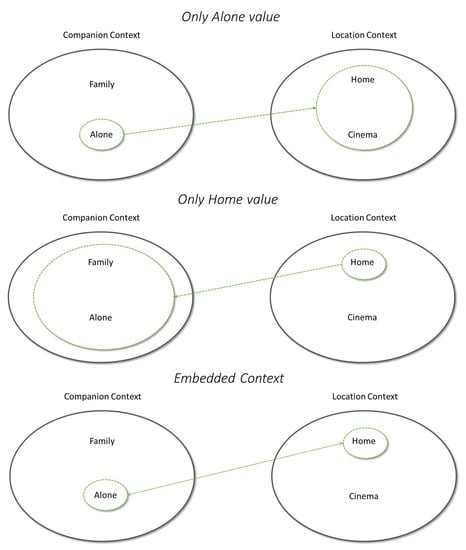
Figure 2. Summary of the embedded context idea based on the example provided.

The paper structure is as follows: Section 2 focuses on the Context-Aware Recommender Systems literature, Section 3 aims to describe the proposed approach defined Contextual Bias Matrix Factorization (CBMF) and deeply describes the embedded context, in Section 4 numerical results related to the method accuracy are discussed, and finally, Section 5 contains conclusions and future works.

2. Related Works

Over time, the various Recommender Systems application fields allow the development of several contextual recommendation methods and testify the RSs’ adaptability to different domains.

Missaoui et al. [51] propose the LOOKER system, implemented to recommend for travels in Tunisia. The system is based on a Content-Based Recommender System and exploits time and location contexts integrated through the Contextual Pre-Filtering strategy.

Shin et al. [52] provide a Content-Based recommendation approach based on a Contextual Modeling strategy for context integration. This approach evaluates the time context through the creation of users and items profiles that include contextual information. These contextual profiles allow the calculation of similarity in the specific considered context.

Chang et al. [53] aim to propose points of interest (POI) recommendations through the construction of a dataset that includes the information taken by Instagram. The recommendation method exploits location context and works through a Context-Aware hierarchical POI Embedding model (CAPE).

Xu et al. [54] propose a Memory-Based RS that integrates contextual information through a Contextual Post-Filtering strategy and exploits the location context related to geolocalization of users’ photos.

Karatzoglou et al. [55] develop a Context-Aware Recommender System that integrates context through a Contextual Modeling strategy. The recommendation method exploits a machine learning approach based on High-Order Singular Value Decomposition (HOSVD) [56,57].

Baltrunas et al. [58,59] propose a Context-Aware Collaborative Filtering RS with Contextual Pre-Filtering strategy. This method, defined Item-Splitting, is based on the division of the available ratings related to an item based on the context values in which users express ratings. This approach allows the selection of the proper ratings based on contextual information, and the recommendation technique only works on the proper contextual information.

The development of the division on the matrix rows, instead of matrix columns, brings us to the definition of the User-Splitting technique [60,61]. The division applied on rows and columns of the rating matrix allows us to define the User-Item-Splitting technique [61]. Moreover, to avoid the overgrowth of the computation cost, the User-Splitting and the Item-Splitting techniques only exploit one context dimension; instead, the User-Item-Splitting technique takes advantage of two context dimensions, one applied on the rating matrix rows and another on the rating matrix columns. To clarify these approaches, Table 1 introduces some contextual information.

Table 1. Example of contextual information.

Location Context	Companion Context
Home (H)	Alone (A)
Cinema (C)	Family (F)

For instance, the User-Item-Splitting method considers the companion context for the users and the location context for the items. Then, each user u is evaluated as the user in the companion context values ‘Alone’ and ‘Family’. Analogously, each item becomes the item in the location context values ‘Home’ and ‘Cinema’. Table 2 shows an example of the rating matrix provided by the User-Item-Splitting method.

Table 2. Example of User-Item-Splitting that uses the contextual information of Table 1.

	${\mathit{i}}_1$-Home	${\mathit{i}}_1$-Cinema	⋯
$u_1$-Alone	${\widehat{r}}_{u_1,i_1,A,H}$	${\widehat{r}}_{u_1,i_1,A,C}$	⋯
$u_1$-Family	${\widehat{r}}_{u_1,i_1,F,H}$	${\widehat{r}}_{u_1,i_1,F,C}$	⋯
⋮	⋮	⋮	⋱

Baltrunas et al. [62] propose a Contextual Modeling approach defined Context-Aware Matrix Factorization (CAMF). This approach calculates the rating forecast on k contextual dimension according to relation (2) where $\overline{r}$ denotes the mean of all items, $p_u·q_i$ expresses the user/item affinity, $b_u$ indicates the decontextualized user bias, and the elements $B_{iz{c}_z}$ denote the bias related to the context dimension z.

$${\widehat{r}}_{ui{c}_1\dots c_k}=\overline{r}+p_u·q_i+b_u+\sum _{z=1}^k{B}_{iz{c}_z}$$

(2)

The selection of the context dimensions on which the system calculates rating forecast allows us to define of different CAMF methods:

• CAMF-C: one contextual dimension is considered ($k=1$);
• CAMF-CI (CAMF Context-Item): considered contextual information is related to items as shown by relation (2). CAMF-CI approach involves the increasing of parameters the system must calculate;
• CAMF-CC: CAMF-CI contextual dimensions are selected to reduce the computation cost related to rating forecast calculation;
• CAMF-CU (Context-User) [61]: contextual information is related to users instead of items in order to calculate rating forecasts;
• CAMF-CUCI [61]: contextual information is related to both users and items.

For instance, the CAMF-CI approach applied to Table 1 contextual information calculates rating forecasts through relation (3).

$${\widehat{r}}_{ui{c}_1{c}_2}=\overline{r}+p_u{q}_i+b_u+B_{i,1,c_1}+B_{i,2,c_2}\begin{array}{c}{c}_1\in \left\{\mathrm{H},\mathrm{C}\right\}\\ c_2\in \left\{\mathrm{A},\mathrm{F}\right\}\end{array}$$

(3)

Jeong et al. [63] exploits two techniques: an Autoencoder that allows learning context from data, and a Deep Learning approach that provides the suggestions. In particular, the Autoencoder acquires the context data from an internal layer. The union of Autoencoder unsupervised learning and the supervised Deep Learning approach allow us to determine the rating forecasts. The experimental results are obtained from three datasets through the precision metric.

Lakehal et al. [64] utilize as inputs of a Hybrid Recommender System the user context dimension, the device capability, and the rule item dimension. In particular, rules can be related to user location, user role, or the combination of both of them. A learning phase anticipates the recommendation phase in order to collect rules from platforms and social media with the ratings that users give to them. A pre-elaboration of data allows the analysis and classification of rules through an Ontology. The first two steps of the recommendation phase consist of the calculation of rules’ similarity and their probability in the specific context. Then, the inputs of the Recommender system are ready for the score elaboration. Then, the scores relate to rules, allowing the organization of the rules that are filtered through the device capability. Finally, the new rule is selected and memorized in the Ontology proper class.

Polignano et al. [65] utilize the emotional context to improve the Recommender System suggestions into the music field. They create a contextual profile that contains the six Ekman basic emotions. These features are associated with the user’s preferences and can be compared with other emotional features through the cosine similarity. Likewise, emotional features are associated with items. The output calculation exploits the mean of the similarity between items’ emotions and users’ emotions.

Another application in the music field is provided by Sánchez-Moreno et al. [66] that exploits the time context to determine suggestions. Specifically for the music field, they study the time effect on recommendations and acquire implicit feedback from the preferences variation over time.

Also, Wang et al. [67] propose a Reccomender system application in the music domain. They develop a three-phase Reccomender system that exploits content and context to provide suggestions. In the first phase, defined Heterogeneous Information Network (HIN), exploits a graph that represents users, session, music, and content sets as nodes, and the edges provide the weighted connection among them. The second phase, defined Content- and Context-Aware Music Embedding, aims to extract information from HIN and learn features vectors. The learning exploits Convolutional Neural Networks and an attention mechanism. Finally, the recommendation phase integrates the users’ historical, contextualized preferences, and the similarity with the learned vectors.

The coming section introduces the proposed approach defined Contextual Bias Matrix Factorization (CBMF) and describes the embedded context concept.

3. CBMF: Contextual Bias Matrix Factorization

Classical Recommender Systems that do not consider context exploit the rating matrix R described in relation (4) to represent known ratings. The rating matrix has two dimensions related to the cardinality of the users set U, and the items set I.

$$R={\left(r_{ui}\right)}_{u \in U,i \in I}\in {\mathbb{R}}^{m\times n}m=\left|U\right|n=\left|I\right|$$

(4)

The rating matrix R element $r_{ui}$ is related to user u and the item i and non zero if it is known otherwise $r_{ui}$ is usually equal to 0.

In the Context-Aware Recommender Systems field, the rating matrix R two-dimensionality is not enough to represent known ratings. Then, the tensor $\mathcal{R}$ described in relation (5) allows the rating representation in the CARS case.

$$\mathcal{R}={\left(r_{ui{c}_1\dots c_k}\right)}_{u\in U,i\in I,c_1\in C_1,\dots ,c_k\in C_k}\in {\mathbb{R}}^{m\times n\times w_1\times \dots \times w_k}$$

(5)

$$m = \left|U\right|,n = \left|I\right|,w_j = \left|C_j\right|j = 1,\dots ,k$$

(6)

The tensor dimensions are related to the cardinality of the users set U, the items set I, and the cardinality of contexts sets $C_1,\dots ,C_k$ that contains the values assumed by the relative context. The tensor element $r_{ui{c}_1\dots c_k}$ expresses the rating of the user u about the item i in the contextual information $c_1\in C_1,\dots ,c_k\in C_k$ and is non-zero if it is known, otherwise $r_{ui{c}_1\dots c_k}$ is usually equal to 0.

The tensor $\mathcal{R}$ allows the collection of the rating in the exact contextual scope represented by all values assumed by each context $C_1,\dots ,C_k$. This tensorial representation of the context is the basis of the embedded context concept exploited by the proposed approach Contextual Bias Matrix Factorization (CBMF).

Due to the high computation cost and the great quantity of memory requested by tensor decompositions, CBMF exploits matrix factorization and contextual bias based on the embedded context that considers the context in all values assumed by each context simultaneously.

To clarify the embedded context concept, Table 3 introduces the embedded context based on Table 1 contextual information and allows to understand how CBMF differs from other recommendation methods, for instance, User-Item-Splitting represented in Table 2 and CAMF-CI shown in relation (3).

Table 3. List of Embedded Contexts based on contextual information of Table 1.

Embedded Context
(Home, Alone)
(Home, Family)
(Cinema, Alone)
(Cinema, Family)

From the provided example, the evaluation of the embedded context, related to the tensorial representation of the context, is the same as the evaluation of one context composed by the tuple composed by all values assumed by each context dimension. Then, in the example related to Table 3, the three dimensions tensor in which the context takes on four embedded context values instead of a tensor of dimension four.

To improve the comprehension of the embedded context concept, the example related to Figure 2 can explore it. The tensor related to the particular case has four dimensions as in relation (7). The first dimension is related to the number of system users, the second to the number of system items, and the third and the fourth concern the number of contexts values.

$$\overline{\mathcal{R}}=\left({\overline{\mathcal{R}}}_{ui{c}_1{c}_2}\right) \in {\mathbb{R}}^{m\times n\times 2\times 2}m = \left|U\right|n = \left|I\right|$$

(7)

The embedded context allows the definition of a new three-dimensional tensor $\tilde{\mathcal{R}}$, defined in relation (8), where the unique contextual dimension contains all the combinations of contextual information related to the two contexts of the example. Indeed, Table 3 describes the values of the embedded context.

$$\tilde{\mathcal{R}}=\left({\tilde{\mathcal{R}}}_{uic}\right) \in {\mathbb{R}}^{m\times n\times 4}$$

(8)

In particular, if the system makes recommendations based on only the companion context ‘alone’, it will calculate the mean of location context values. Indeed, in the rating forecast related to ‘home’, contextual information considers a mean of all values contained in the tensor $\overline{\mathcal{R}}$ for location context, as in relation (9).

$${\widehat{\mathcal{R}}}_{u,i,alone}=\frac{1}{2}\left({\overline{\mathcal{R}}}_{u,i,alone,home}+{\overline{\mathcal{R}}}_{u,i,alone,cinema}\right)$$

(9)

The same reasoning applies if the system calculates rating forecasts based on ‘home’ value for location context. The embedded context evaluates the relationships between the location and companion contexts in the contextual information evaluated. This approach allows the systems not to lose the effects of contexts combination on rating forecasts. The presence of more contextual values for the unconsidered context implies the mean on more values than the particular case taken into account. Table 4 summarizes the typologies of rating forecasts calculation based on the evaluated contextual information.

Table 4. Summary of the typologies of rating forecasts based on evaluated contextual information.

Context	Contextual Information	Rating Forecast
Companion	Alone	$\frac{1}{2}\left({\overline{\mathcal{R}}}_{u,i,alone,home}+{\overline{\mathcal{R}}}_{u,i,alone,cinema}\right)$
Location	Home	$\frac{1}{2}\left({\overline{\mathcal{R}}}_{u,i,alone,home}+{\overline{\mathcal{R}}}_{u,i,family,home}\right)$
Embedded Context	Alone, Home	${\overline{\mathcal{R}}}_{u,i,alone,home}$

This introductory example aims to underline that the objective of the proposed approach consists of evaluating all the contextual information to avoid losing information related to context.

Let be the system user u, the item i, and the contextual information c related to the embedded context. Contextual Bias Matrix Factorization method elaborates the rating forecasts through relation (10).

$${\widehat{r}}_{uic}={\overline{r}}_c+b_{uc}+b_{ic}+p_u·q_i$$

(10)

The parameter ${\overline{r}}_c$ is the mean related to all available ratings of all users and items in the embedded context c; $b_{uc}$ is the contextual bias of user in the embedded context c; $b_{ic}$ is the contextual bias related to the item i in the embedded context c; and $p_u·q_i$ expresses the user/item affinity.

The main feature of the proposed approach is the introduction of the context into the mean ${\overline{r}}_c$ and the biases $b_{uc}$ and $b_{ic}$. Moreover, the principal difference between the proposed approach and the other methods consists of the context evaluation. Instead of considering a contextualized bias related to a single context, the proposed approach aims to consider the combination of all contexts to avoid losing the contextual information specificity. Moreover, the context introduction into users and items bias allows us to avoid the employment of tensor factorizations. Moreover the bias employment can improve the serendipity of the proposed approach [68].

The application of the CBMF method implies the calculation of the needed parameters. For instance, in the example related to the context information of Table 1, the method needs to calculate the parameter shown by Table 5.

Table 5. Parameters required to obtain the ratings forecasts based on the CBMF method related to Table 3 embedded contexts.

Embedded Context	Mean	Bias User	Bias Item
(Home, Alone)	${\overline{r}}_{\left(H,A\right)}$	$b_{u,\left(H,A\right)}$	$b_{i,\left(H,A\right)}$
(Home, Family)	${\overline{r}}_{\left(H,F\right)}$	$b_{u,\left(H,F\right)}$	$b_{i,\left(H,F\right)}$
(Cinema, Alone)	${\overline{r}}_{\left(C,A\right)}$	$b_{u,\left(C,A\right)}$	$b_{i,\left(C,A\right)}$
(Cinema, Family)	${\overline{r}}_{\left(C,F\right)}$	$b_{u,\left(C,F\right)}$	$b_{i,\left(C,F\right)}$

The current Section has introduced the embedded context concept and how the CBMF method calculates rating forecasts. The coming section provides the numerical experiments aimed to evaluate the accuracy of the proposed approach.

4. Numerical Results

The focus of this section is the introduction of the numerical experiments related to Contextual Bias Matrix Factorization (CBMF). Four subsections compose the current section: the first subsection aims to present the accuracy measures, the second subsection introduces the exploited datasets, the third subsection presents the limitations of the proposed approach related to the lack of contextual information, and, finally, the fourth subsection shows the domain in which CBMF works best.

The CBMF method exploits the Singular Value Decomposition [69] to calculate the user/item affinity through the algorithm Bias Stochastic Gradient Descent (BSGD) [70]. The parameter related to the BSGD algorithm are experimentally setted and assumed the values:

• five latent factors;
• $0.001$ learning rate;
• $\lambda =0.005$;
• 20 interactions.

Moreover, the dataset allows the calculation of contextual biases $b_{uc}$ e $b_{ic}$ related to relation (10). If the biases are zero elements after the training phase, they assume the mean value showed by relations (11) and (12).

$$\forall i\in I \mathrm{if} \left(b_{ic}=0\right)\mathrm{then} b_{ic}^{new}=\frac{1}{\left|\{b_{lc}:b_{lc}\ne 0,l\in I\}\right|}\sum _{s\in I}{b}_{sc}$$

(11)

$$\forall u\in U \mathrm{if} \left(b_{uc}=0\right)\mathrm{then} b_{uc}^{new}=\frac{1}{\left|\{b_{zc}:b_{zc}\ne 0,z\in U\}\right|}\sum _{s\in U}{b}_{sc}$$

(12)

Then, if there are not known ratings in a specific embedded context c related to an item i, the embedded context bias considers the mean of the biases for all items. Likewise, if there are not known ratings for the calculation of the embedded context bias related to the user u, it assumes a value equal to the mean of the known bias of all users in the specific embedded context. Finally, to make the numerical results more reliable, the experimental phase exploits the Cross-Validation k-Fold [71] method with the division of the dataset into five parts.

4.1. Accuracy Evaluation Metrics

The experimental phase exploits two accuracy metrics: the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) [72,73,74].

Let be D the dataset expressed by relation (13) that contains the available ratings related to k contextual dimensions, and let be ${\widehat{\mathcal{R}}}_{ui{c}_1,\dots ,c_k}$ the rating forecasts provided by the CBMF method. The MAE is calculated through relation (14) and the RMSE is calculated through relation (15).

$$D=\{\left(u,i,c_1,\dots ,c_k\right) \in U\times I\times C_1,\times \cdots \times C_k:\exists {\mathcal{R}}_{ui{c}_1,\dots ,c_k}\}$$

(13)

$$\mathrm{MAE}=\frac{1}{\left|D\right|}\sum _{\left(u,i,c_1,\dots ,c_k\right)\in D}|{\mathcal{R}}_{ui{c}_1,\dots ,c_k}-{\widehat{\mathcal{R}}}_{ui{c}_1,\dots ,c_k}|$$

(14)

$$\mathrm{RMSE}=\sqrt{\frac{1}{\left|D\right|}\sum _{\left(u,i,c_1,\dots ,c_k\right)\in D}{\left({\mathcal{R}}_{ui{c}_1,\dots ,c_k}-{\widehat{\mathcal{R}}}_{ui{c}_1,\dots ,c_k}\right)}^2}$$

(15)

4.2. Datasets

This Subsection focuses on the description of the exploited datasets. The evaluated datasets are DePaulMovie, LDOS-CoMoDa, InCarMusic, and Travel-STS.

• De Paul Movie Dataset [49,75,76] is a movies dataset composed of:

  –

  5043 ratings divided into:

  ∗

  1448 ratings without a specific context;

  ∗

  3595 contextual ratings.

  –

  3 contextual dimensions:

  • Location: Home, Cinema;
  • Companions: Alone, Family, Friends;
  • Time: Weekend, Weekday.

• LDOS-CoMoDa [49,77] is a movies dataset composed of:

  –

  2296 ratings related to 121 users an 1232 movies divided into:

  ∗

  44 ratings without a specific context;

  ∗

  2252 contextual ratings.

  –

  12 contextual dimensions:

  • Time (4): Morning, Afternoon, Evening, Night;
  • Daytype (4): Working day, Weekend, Holiday;
  • Season (4): Spring, Summer, Autumn, Winter;
  • Location (3): Home, Public place, Friend’s house
  • Weather (5): Sunny, Rainy, Stormy, Snowy, Cloudy;
  • Social (7): Alone, My partner, Friends, Colleagues, Parents, Public, My family;
  • Emotion (7): Sad, Happy, Scared, Surprised, Angry, Disgusted, Neutral;
  • Dominant Emotion (7): Sad, Happy, Scared, Surprised, Angry, Disgusted, Neutral;
  • Mood (3): Positive, Neutral, Negative;
  • Physical (2): Healthy, Ill;
  • Decision (2): User decided which movie to watch, User was given a movie;
  • Interaction (2): first interaction, n-th interaction.

• InCarMusic [49,76,78] is a music dataset composed of:

  –

  4012 ratings related to 42 users and 139 items divided into:

  ∗

  1003 ratings without a specific context;

  ∗

  3009 contextual ratings.

  –

  8 contextual dimensions:

  • Driving style (2): Relaxed driving, sport driving;
  • Landscape (4): Coast line, Country side, Mountains, Urban;
  • Mood (4): Active, Happy, Lazy, Sad;
  • Natural phenomena (4): Afternoon, Day time, Morning, Night;
  • Road type (3): City, Highway, Serpentine;
  • Sleepiness (2): Awake, Sleepy;
  • Traffic conditions (3): Free road, Lots of cars, Traffic jam;
  • Weather (4): Cloudy, Rainy, Snowing, Sunny.

• Travel-STS [49,76,79] is a dataset composed of:

  –

  2534 ratings related to 325 users and 249 items divided into:

  ∗

  1146 ratings without a specific context;

  ∗

  1388 contextual ratings.

  –

  14 contextual dimensions:

  • Distance (2): Far away, Near by;
  • Time available (3): Half day, One day, More than one day;
  • Temperature (6): Burning, Hot, Warm, Cool, Cold, Freezing;
  • Crowdedness (3): Crowded, Not crowded, Empty;
  • Knowledge of surroundings (3): New to area, Returning visitor, Citizen of the area;
  • Season (4): Spring, Summer, Autumn, Winter;
  • Budget (3): Budget traveler, Price for quality, High spender;
  • Daytime (5): Morning, Noon, Afternoon, Evening, Night;
  • Weather (6): Clear sky, Sunny, Cloudy, Rainy, Thunderstorm, Snowing;
  • Companion (5): Alone, Friends, Family, Partner, Children;
  • Mood (4): Happy, Sad, Active, Lazy;
  • Daytype (2): Weekday, Weekend;
  • Travel goal (9): Visiting friends, Business, Religion, Health care, Social event, Education, Landscape, Hedonistic, Sport;
  • Means of transport (4): No transportation means, Bicycle, Car, Public transport.

The DePaulMovie dataset contains all the contextual information related to the known ratings contextual dimensions. Instead, in the LDOS-CoMoDa and Travel-STS datasets, available ratings do not present some contextual information. To overcome the problem of a lack of contextual information, the experimental results in these datasets exploit the information lack as a value. Then, lack of contextual information is one of the values that one of the components of the embedded context tuple can assume. Finally, the InCarMusic dataset contains the contextual information related to one contextual dimension for each known rating in the dataset.

The exploited tool is MatLab for the accuracy evaluation on datasets DePaulMovie, LDOS-CoMoDa, InCarMusic, and Travel-STS. The Import Data functionality of MatLab allows us to acquire files related to these datasets and convert them into numerical matrices. Then, the matrices elaboration enables calculation of the accuracy of these datasets through the Cross-Validation k-fold technique.

4.3. Limits of the Embedded Context

The provided definition of embedded context as a unique contextual dimension composed of the combination of the values that contextual dimensions assume has to deal with a problem: the contextual dimension increase implies a high increase in the possible combination that composes the embedded context.

The study on the LDOS-CoMoDa dataset allows the analysis of the proposed approach behavior on 12 contextual dimensions in the case of a lack of contextual information. This study is focused on the CBMF method accuracy on the single contexts and on a group of contexts selected based on the number of contextual information values as shown below:

• Contextual dimensions 9-Mood (3), 10-Physical (2), 11-Decision (2), and 12-Interaction (2): contextual dimensions that contain a low number of contextual information for each node;
• Contextual dimensions 1-Time (4), 2-Daytype (4), 3-Season (4), and 4-Location (3): contextual dimensions that have a medium number of contextual information for each node;
• Contextual dimensions 5-Weather (5), 6-Social (7), 7-Emotion (7), and 8-Dominant Emotion (7): contextual dimensions that present a high number of contextual information for each node.

Table 6 presents the experimental results provided by the division into groups of contextual dimensions. Instead, Table 7 provides the accuracy measure results on the single contextual dimensions.

Table 6. Numerical results of the experiments tested on the LDOS-CoMoDa dataset based on the division into groups of contextual dimensions.

Contexts	# Contexts	Values	# Embedded Context	MAE	RMSE
10	1	2	2	0.8344	1.0877
10-11	2	4	4	0.8643	1.0967
10-11-12	3	6	8	0.8288	1.0764
9-10-11-12	4	9	24	0.8281	1.0826
1	1	4	4	0.8493	1.0990
1-2	2	8	16	0.8621	1.1159
1-2-3	3	12	64	0.8856	1.1457
1-2-3-4	4	15	192	0.8907	1.1440
7	1	7	7	0.7380	0.9711
7-8	2	14	49	0.7265	0.9556
6-7-8	3	21	343	0.7352	0.9646
5-6-7-8	4	26	1715	0.7695	0.9992
All	12	50	7,902,720	0.8386	1.0680

Table 7. Results related to single contexts of the LDOS-CoMoDa dataset.

Contextual Dimensions	# Values	MAE	RMSE
Time	4	0.8493	1.0990
Daytipe	4	0.8568	1.1012
Season	4	0.8307	1.0738
Location	3	0.8490	1.0923
Weather	5	0.8569	1.1130
Social	7	0.8608	1.1107
Emotion	7	0.7380	0.9711
Dominant Emotion	7	0.7374	0.9771
Mood	3	0.8515	1.1008
Physical	2	0.8344	1.0877
Decision	2	0.8408	1.0799
Interaction	2	0.8253	1.0630

From Table 6, numerical results return that the increase in the number of exploited contextual dimensions does not imply the accuracy measure improvement. Moreover, accuracy measure results related to Table 7 suggest that the increase in the amount of contextual information does not return a reduction in the MAE and the RMSE values. In fact, for instance, node 12 related to the context Interaction has two pieces of contextual information and obtains a better accuracy measure than the accuracy of contexts Time, Daytype, Season, Weather, and Social, which all have more contextual information.

The results from this dataset imply that the proposed approach reliability is not related to the contextual information quantity of a single contextual dimension but to the influence that contextual ratings suffer in the specific context. However, these results have to be deeply studied through other datasets that present a similar structure to LDOS-CoMoDa.

In the application field, where sensors allow collecting a large number of contextual information related to various contextual dimensions, the CBMF method needs to select the proper contextual dimensions to avoid the increase in embedded context and obtain only the contexts that affect the contextual rating variation. One of the possible tools that allows the contextual dimensions selection is the Context Dimension Tree [11] that consists of a non-oriented acyclic graph that allows context management.

From Table 6, the combination of Emotion and Dominant Emotion context dimensions returns the best accuracy, measuring results among all the considered combinations of contexts. Then, the proposed approach only exploits these contextual dimensions to the comparison with other methods. This study aimed at the contextual dimensions selection is consistent with the study of Zheng et al. [61] about the role of the emotions in Context-Aware Recommender Systems.

The comparison methods are Item-Splitting, User-Splitting, CAMF-C, CAMF-CI, and CAMF-CU, as described in Section 2. Zheng et al. [61] provide RMSE results related to the comparison methods on the LDOS-CoMoDa dataset. Table 8 presents the best results of each comparison method provided by Zheng et al. [61]. CAMF-C, CAMF-CI, and CAMF-CU return the best results on Emotion and Dominant Emotion contexts instead, using Item-Splitting and User-Splitting to analyze all contextual dimensions. CBMF is the third-best method among all methods of Table 8, despite the problems described before on the LDOS-CoMoDa dataset. The proposed approach of RMSE is worst than CAMF-CU and User-Splitting methods but is better than CAMF-C, Item-Splitting, and CAMF-CI methods.

Table 8. Numerical Results of the methods on the LDOSCoMoDa dataset.

Method	Context	RMSE
CAMF-C	Emotions Only	0.968
CAMF-CI	Emotions Only	1.019
CAMF-CU	Emotions Only	0.902
Item-Splitting	All Contexts	1.011
User-Splitting	All Contexts	0.913
CBMF	Emotions Only	0.956

Then, Table 9 compares the same methods with the proposed approach. In the case of unknown contextual information, the Root Mean Squared Error results return the same difficulties of the proposed approach. The methods CAMF-CI and Item-Splitting return better accuracy performance than CBMF. Instead, the proposed approach obtains a lower RMSE than the other comparison methods CAMF-C, CAMF-CU, and User-Splitting.

Table 9. Numerical Results of the methods on the Travel-STS dataset.

Method	RMSE
CAMF-C	1.1989
CAMF-CI	1.0978
CAMF-CU	1.1264
Item-Splitting	1.1045
User-Splitting	1.1287
CBMF	1.1126

The results obtained from the LDOS-CoMoDa and Travel-STS datasets suggest that the proposed approach can mediate between the case in which context affects more users than items and the vice-versa. However, this assertion needs more experiments for confirmation.

4.4. Advantages of Embedded Context

After the previous subsection which has analyzed the proposed approach limits, this subsection focuses on the advantages of Contextual Bias Matrix Factorization methods through the accuracy measure study on the DePaulMovie dataset. Initially, Table 10 shows the accuracy results related to the single contextual dimensions and all combinations of the contextual dimensions as in the LDOS-CoMoDa dataset.

Table 10. Numerical Results of CBMF method on the De Paul Movie dataset.

Contexts	MAE	RMSE
Time	0.9419	1.1823
Location	0.9073	1.1425
Companions	0.8410	1.0909
Time-Location	0.8153	1.0671
Time-Companions	0.7463	0.9988
Location-Companions	0.7257	0.9802
Time-Location-Companions	0.6591	0.9186

The DePaulMovie dataset contains all the contextual information related to Location, Companions, and Time contexts for each available contextual rating, and, in this case, the increase in the evaluated context returns an accuracy measure enhancement. The experimental results on the DePaulMovie dataset suggest that the CBMF method improves the accuracy when all contextual information is available. Instead, the proposed approach accuracy worsens when there is a lack of contextual information, according to the previous analysis on the LDOS-CoMoDa dataset.

Table 11 returns the numerical results related to the MAE and the RMSE of the Contextual Bias Matrix Factorization method on DePaulMovie, LDOS-CoMoDa, Travel-STS, and InCarMusic datasets. This Table aims to summarize the results but cannot represent a comparison among datasets due to their different specifications.

Table 11. Accuracy of the CBMF methods on the datasets DePaulMovie, LDOS-CoMoDa, STS-Travel, and InCarMusic.

Dataset	MAE	RMSE
DePaulMovie	0.6591	0.9186
LDOS-CoMoDa	0.8386	1.0680
STS-Travel	0.9284	1.1126
InCarMusic	1.2901	1.5207

The accuracy measures value related to DePaulMovie confirms the proper behavior of the proposed approach when all contextual information is known, according to the results obtained into Table 10. Instead, the results provided by the method on the Travel-STS and LDOS-CoMoDa datasets return the proposed approach’s difficulties in the contextual information lack. In fact, in the case of LDOS-CoMoDa, the proposed approach is overcome by other comparison methods. Finally, on the InCarMusic dataset, the embedded context concept is not achievable due to the structure of the InCarMusic dataset because it presents only one known contextual dimension among all dataset available contexts. In fact, the accuracy results obtained from InCarMusic are inadequate.

Now Table 12 compares the CBMF method with CAMF-CI, CAMF-CU, CAMF-C, CAMF-CUCI, Item-Splitting, and User-Splitting on the DePaulMovie dataset where the proposed approach works best. The CARSKit [75] provides the MAE and the RMSE results related to comparison methods.

Table 12. Comparison between the proposed approach and other CARS techniques on De Paul Movie dataset.

	MAE	RMSE
CAMF-CI	0.7122	0.9660
CAMF-CU	0.6682	0.9198
CAMF-C	0.7029	0.9571
CAMF-CUCI	0.6753	0.9206
Item-Splitting	0.7185	1.0362
User-Splitting	0.7361	1.0588
CBMF	0.6591	0.9186

Table 12 confirms that the proposed approach provides the best accuracy measures results when the CBMF method works in the best situation. The Mean Absolute Error and the Root Mean Square Error related to the Contextual Bias Matrix Factorization method are better than the accuracy values of the comparison methods.

4.5. CBMF Evaluation through the Normalized Discounted Cumulative Gain Metric

The final part of this section aims to introduce an additional test to evaluate the quality of the suggestions provided by the proposed approach. The Normalized Discounted Cumulative Gain (NDCG) [80,81] achieves this purpose and allows the evaluation of the Top-N Recommendation developed by CBMF.

To define the NDCG, the definitions of Discounted Cumulative Gain (DCG) and the Ideal Discounted Cumulative Gain (IDCG) are needed.

$${\mathrm{DCG}}_N=\sum _{p=1}^N\frac{r\left(p\right)}{{log}_2\left(p+1\right)}$$

(16)

The DCG is represented in formula (16) where N is the number of the recommendation in the list provided by the proposed approach and $r\left(p\right)$ consists of the relevance of the item at the position p. The IDCG represents DCG of the ideal ordering. Then, the NDCG is defined in formula (17).

$${\mathrm{NDCG}}_N=\frac{{\mathrm{DCG}}_N}{{\mathrm{IDCG}}_N}$$

(17)

Figure 3 shows the experimental results that aim to testify the quality of the suggestions. In particular, the NDCG results on DePaulMovie are $0.7643,0.7681,$ and $0.7704$ related to $N=5,10,$ and 15, respectively. On LDOS-CoMoDa the results are $0.7079,0.6978,$ and $0.7098$, and on Travel-STS they are $0.7145,0.7209,$ and $0.7410$, respectively.

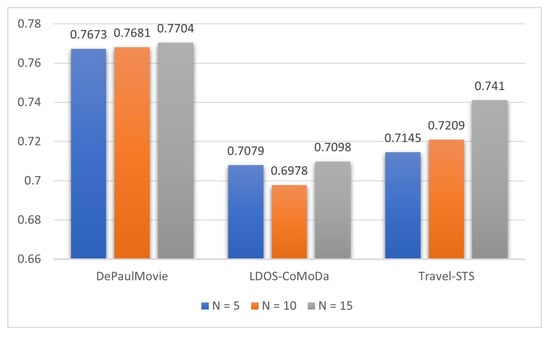
Figure 3. Results of the proposed approach on datasets DePaulMovie, LDOS-CoMoDa, and Travel-STS related to Normalized Discounted Cumulative Gain metric and the values $N=5,10,15$.

Table 13 presents the results obtained by the proposed approach and the comparison methods on datasets LDOS-CoMoDa and Travel-STS. The quality analysis of provided recommendation suggests that on LDOS-CoMoDa the best performance is obtained by the CAMF-CU method. Moreover, the User-Splitting and CBMF methods have similar results for the value $N=5$, but the first provides better results than CBMF for $N=10$ and $N=15$ values. Instead, the proposed approach results overcame those of CAMF-CI, CAMF-C, and Item-Splitting.

Table 13. Results on LDOS-CoMoDa and Travel-STS datasets related to Normalized Discounted Cumulative Gain metric and the values $N=5,10,15$.

Method	LDOS CoMoDa			Travel STS
	NDCG @5	NDCG @10	NDCG @15	NDCG @5	NDCG @10	NDCG @15
CAMF-CI	0.6988	0.7003	0.7015	0.7217	0.7302	0.7416
CAMF-CU	0.7188	0.7195	0.7203	0.7044	0.7088	0.7129
CAMF-C	0.6711	0.6722	0.6719	0.6812	0.6847	0.6851
Item-Splitting	0.6654	0.6632	0.6675	0.7011	0.7027	0.7035
User-Splitting	0.7089	0.7124	0.7126	0.7149	0.7216	0.7311
CBMF	0.7079	0.6978	0.7098	0.7145	0.7209	0.7410

The results of Travel-STS return that the CAMF-CI method provides the best recommendations quality. However, the result for the value $N=15$ differs slightly from those of the proposed approach. Then, CBMF and Item-Splitting provide results in which CBMF overcame Item-Splitting for values $N=15$, but the NDCG coefficient of the proposed approach is lower than the Item-Splitting method for values $N=5$ and $N=15$. Finally, the results of the proposed approach are better than those of the methods CAMF-CU, CAMF-C, and User-Splitting on the Travel-STS dataset.

These results confirm the difficulties of the CBMF method when there is unknown contextual information. However, the quality of the recommendation when the limits of the proposed approach arise are satisfactory.

Table 14 provides the results of the recommendation quality on the DePaulMovie dataset. In this case, the NDCG values of CBMF overcome the results of the others methods. These results confirm the accuracy results obtained in Table 12. In fact, on the DePaulMovie dataset, the proposed approach has the best results. These results suggest that the knowledge of all contextual information consists of the best application case of the proposed approach. However, this assertion should be confirmed through further studies on datasets similar to DePaulMovie.

Table 14. Results on DePaulMovie dataset related to Normalized Discounted Cumulative Gain metric and the values $N=5,10,15$.

Method	NDCG@5	NDCG@10	NDCG@15
CAMF-CI	0.7111	0.7149	0.7158
CAMF-CU	0.7249	0.7320	0.7324
CAMF-C	0.7188	0.7190	0.7193
CAMF-CUCI	0.7312	0.7374	0.7499
Item-Splitting	0.6748	0.6832	0.6878
User-Splitting	0.6956	0.7012	0.7077
CBMF	0.7643	0.7681	0.7704

5. Conclusions and Future Works

This paper describes the Contextual Bias Matrix Factorization method and tests it on DePaulMovie, LDOS-CoMoDa, Travel-STS, and InCarMusic datasets to determine the advantages and disadvantages of the proposed approach. In particular, in the best application case, the CBMF method returns better accuracy results than the comparison methods. Future works will focus on the evaluation of other metrics with different accuracy to evaluate other aspects of the recommendation method. Among all possible metrics, Novelty and Diversity will be tested. In particular, novel metrics that allow the evaluation of more aspects can be exploited [82]. Moreover, machine learning techniques will be exploited to calculate contextual biases. This technique should improve the deal with the scalability of the proposed approach. In particular, we will initially develop the update formulas related to Stochastic Gradient Descent for the Adaline method application in the case of regression, and then an Artificial Neural Network will be implemented. Moreover, the best structure of an Artificial Neural Network had to be studied for this recommendation method. For this purpose, we will move from MatLab to Python, developing the proposed approach through the appropriate libraries available.

Other future works concern the application of the proposed approach into a case of study for applications in the Cultural Heritage field.