Improving Characteristics of LUT-Based Three-Block Mealy FSMs’ Circuits

Abstract

One of the very important problems connected with FPGA-based design is reducing the hardware amount in implemented circuits. In this paper, we discuss the implementation of Mealy finite state machines (FSMs) by circuits consisting of look-up tables (LUT). A method is proposed to reduce the LUT count of three-block circuits of Mealy FSMs. The method is based on finding a partition of set of internal states by classes of compatible states. To reduce the LUT count, we propose a special kind of state code, named complex state codes. The complex codes include two parts. The first part includes the binary codes of a state as the element of some partition class. The second part consists of the code of corresponding partition class. Using complex state codes allows obtaining FPGA-based FSM circuits with exactly four logic blocks. If some conditions hold, then any FSM function from the first and second blocks is implemented by a single LUT. The third level is represented as a network of multiplexers. These multiplexers generate either additional variable encoding collections of outputs or input memory functions. The fourth level generates FSM outputs. An example of synthesis and experimental results is shown and discussed. The experiments prove that the proposed approach allows reducing hardware compared to such methods as auto and one-hot of Vivado, JEDI. Further, the proposed approach produces circuits with fewer LUTs than for three-level Mealy FSMs based on joint use of several methods of structural decomposition. The experiments show that our approach allows reducing the LUT counts on average from 11 to 77 percent. As the complexity of an FSM increases, the gain from the application of the proposed method grows; the same is true for both the FSM performance and power consumption.

1. Introduction

The behavior of a sequential device can be represented by the model of a Mealy finite state machine (FSM) [1,2]. This stimulates constant development of various methods of designing Mealy FSM logic circuits [2,3]. As a rule, these methods are aimed at optimizing one or more basic characteristics of resulting FSM circuits [4]. There are three basic characteristics, namely: (1) the chip area occupied by an FSM circuit), (2) the operating frequency, and (3) the power consumption; however, as a rule, it is impossible to optimize these three characteristics at the same time. For example, a decrease in the required internal resources (the required chip area) is often associated with a decrease in the maximum operating frequency [2]. As it is known, the occupied chip area significantly affects other characteristics of an FSM circuit [5]. At the same time, it is important that reducing the area as little as possible increases the delay time of the circuit. As it is known [6], the major challenge in the LUT-based FSM design is developing a low-area circuit without the compromising an FSM performance. In this paper, we propose a method to create Mealy FSMs whose three-level circuits are implemented using internal resources of field-programmable gate arrays (FPGAs) [7,8]. The proposed approach belongs to methods of structural decomposition [2].

Recently, more and more digital systems are implemented using FPGA chips [9]. The analysis of VLSI’ market shows that Xilinx [10] is the largest manufacturer of FPGA chips. This fact explains the orientation of our article to FPGAs of Xilinx. We discuss a case when an FSM circuit is implemented using internal resources of FPGAs such as look-up table (LUT) elements, programmable flip-flops, inter-slice multiplexers, programmable interconnects, synchronization tree, and programmable input–outputs.

Our current article is devoted to improving the LUT count of three-block LUT-based Mealy FSM circuits obtained with the simultaneous usage of the replacement of FSM inputs and the encoding of collections of FSM outputs [11]. The resulting FSM circuits have three blocks of LUTs; each block has a unique system of inputs and outputs. When certain conditions are met, the circuit of some (or even all) logic block is synthesized using the methods of functional decomposition [12,13]. Such blocks are represented by circuits having several levels of LUTs. This leads to significant decrease in the FSM operating frequency. Moreover, the interconnection system of a multi-level block becomes dramatically more complex, which leads to a further decrease in the FSM performance. This is why it is so important to reduce the number of levels in each logic block of FSM circuits.

The main contribution of this paper is a novel design method aimed at reducing the number of LUTs and their levels in circuits of three-block LUT-based Mealy FSMs. The reduction diminishes the total number of LUTs in an FSM circuit compared to this number for equivalent FSMs based on the functional decomposition. To apply our method, it is necessary to construct classes of compatible states. This in turn leads to an increase in the number of state variables compared to their minimum number. To reduce the number of state variables, we propose a new type of state codes. We name them complex state codes (CSC). A CSC of any state includes two parts. The first part is a code of a class of compatible states including the particular state. The second part is a code of this state as an element of a particular class. Our method produces four-block FSM circuits. In the best case, each block is represented by a single-level LUT-based circuit. As experimental results show, the proposed approach also provides the performance at the level of three-block FSMs and reduces the power consumption. These phenomena are additional positive qualities of the proposed method.

The further text of the paper includes five sections. Section 2 shows the background of LUT-based Mealy FSMs. Section 3 analyses the related works. The main idea of the proposed method is shown in Section 4. An example of a CSC-based FSM synthesis is shown in Section 5. Section 6 analyses the results of experiments. The paper ends with a short conclusion.

2. Basic Information

A Mealy FSM logic circuit can be represented by two systems of Boolean functions (SBFs) [14]. One of these SBFs represents FSM outputs connected with operational units of a particular digital system. The second SBF represents input memory functions (IMFs). The arguments of these SBFs are external FSM inputs and internal state variables. The inputs form a set $X=\{x_1,\dots ,x_L\}$; the IMFs create a set $\Phi =\{D_1,\dots ,D_R\}$. An FSM circuit is represented by the following SBFs:

$$Y=Y(T,X);$$

(1)

$$\Phi =\Phi (T,X).$$

(2)

The state variables $T_r\in T$ encode internal states from a set $A=\{a_1,\dots ,a_M\}$. To encode M states, the minimum number of state variables is determined as [1]

$$R=\lceil lo{g}_{2}M\rceil .$$

(3)

Each state $a_m\in A$ is represented by a binary code $K\left(a_m\right)$ having R bits. These codes are kept into the state code register (RG). In this article, we discuss a case when the RG has informational inputs of D type. This is the most common case [15]. The systems (1) and (2) determine so called P Mealy FSM [2] shown in Figure 1.

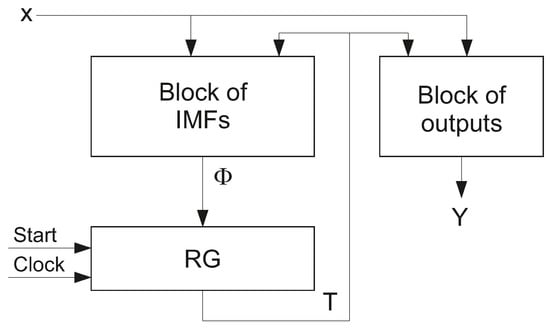
Figure 1. Structural diagram of P Mealy FSM.

In Figure 1, the block of IMFs is implemented using SBF (2); the block of outputs is based on SBF (1). The state register has R D flip-flops. The r-th flip-flop keeps the state variable $T_r\in T$. The pulse $Start$ allows clearing the content of RG. This pulse loads a code of the initial state $a_1\in A$ into RG. As a rule, the code $K\left(a_1\right)$ consists of zeros. The pulse $Clock$ shows an instant when the RG content can be changed by current IMFs.

As a rule, an FSM is represented by either a state transition table (STT) [1] or a state transition graph (STG) [5]. To obtain the systems (1) and (2), it is necessary to form an FSM direct structure table (DST) [14]. In this article, we start from the STG. Next, this graph is transformed into the equivalent STT. Using the STT, we construct the DST.

An STG is a directed graph whose nodes correspond to FSM states. Interstate transitions are represented by edges of STG. Each edge is marked by a combination of inputs causing a particular transition and collection of outputs (COs) generated during this transition. An STT is a representation of STG as a list of interstate transitions. An STT includes five columns with: a current state $a_m$; a state of transition $a_T$; an input signal $X_h$ which is a conjunction of some inputs (or their complements) determining this particular transition; CO $Y_h$ generated during this transition; h is a number of transition ($h\in \{1,\dots ,H\}$) [1].

A DST includes the columns with state codes and IMFs [14]. These columns are: the code of the current state $K\left(a_m\right)$, the code of the next state $K\left(a_T\right)$, and a collection of IMFs $D_h\subseteq \Phi$ equal to 1 to load the code of the next state into the state register RG.

In this paper, we consider a case when internal resources of FPGA chips are used for implementing SBFs (1) and (2). An FSM circuit is implemented using configurable logic blocks (CLB) of FPGAs produced by Xilinx [10]. A circuit is represented as a network of CLBs connected with help of a programmable routing matrix [16]. In this paper, we discuss a case when CLBs include LUTs, multiplexers, and programmable flip-flops. Using the notation [17], we denote as $I_L$-LUT a single-output LUT with $I_L$ inputs. If a Boolean function depends on up to $I_L$ arguments, then it is represented by a single-LUT logic circuit. If the number of LUT inputs is less than the number of arguments, then a circuit has more than a single level of LUTs. To implement multi-level circuits, the methods of functional decomposition (FD) are used [18,19]. As a rule, the FD-based circuits have the complicated systems of “spaghetti-type” interconnections [2].

We discuss a case when each CLB is a part of slice [10]. The slice includes internal multiplexers. They can be used for changing the number of LUT inputs within one slice. The internal multiplexers are connected with LUTs by a system of fast inter-slice interconnections. Due to this, the delay time for 6-, 7-, and 8-input LUTs is practically the same for SLICEL of Virtex-7 [20,21]. This approach makes it possible to flexibly adapt the LUT parameters to the characteristics of the function being implemented. For example, the SLICEL of Virtex-7 includes four 6-LUTs, 8 flip-flops, and 27 multiplexers [20]. Each 6-LUT can be used as two 5-LUTs with shared inputs. This explains the presence of eight flip-flops in each SLICEL. Using internal multiplexers allows combining two 6-LUTs into a single 7-LUT. Next, four 6-LUTs can be combined into a single 8-LUT. The control inputs of multiplexers can be used as inputs of 7- and 8-LUTs. Each SLICEL possesses special carry chains used for organization of fast multi-bit adders. It is worth noting that these circuits can be used to implement arbitrary logic circuits [22,23].

In this paper, we use multiplexers to generate functions (1) and (2). We denote a multiplexer having K data inputs as $K-MX$. Using a single 6-LUT, we can implement a circuit of $4-MX$. It has two control inputs and four data inputs. Further, we can organize an $8-MX$ with the help of two 6-LUTs. Its circuit has only slightly bigger delay than a circuit of a $4-MX$ [20]. It is possible due to using fast interconnections inside a slice. If a $16-MX$ has the control inputs $T1-T4$, then its circuit includes four 6-LUTs controlled by $T3-T4$. To implement a $32-MX$, two slices and inter-slice interconnections are used. As a result, a $32-MX$ is much slower than a $16-MX$.

In LUT-based FSMs, the flip-flops of RG are distributed among LUTs generating functions (1). Due to this, the RG is “hidden” inside the slices where the IMFs are generated. There are two blocks in an LUT-based P Mealy FSM (Figure 2).

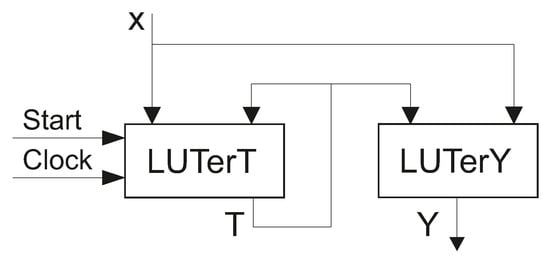
Figure 2. Structural diagram of LUT-based P Mealy FSM.

In this paper, we denote as LUTer a logic block consisting of LUT-based CLBs. In the P Mealy FSM (Figure 2), a $LUTerY$ implements SBF (1) and $LUTerT$ implements SBF (2). To control the RG, the pulses $Start$ and $Clock$ are used.

If each function from systems (1) and (2) depends on not more than $I_L$ arguments, then both blocks of LUT-based P Mealy FSM (Figure 2) are represented by single-level circuits. For Xilinx-based solutions, an LUT has 6 inputs [10]. There is no point in increasing this value, because $I_L=6$ provides the best balance for such LUT characteristics as the occupied chip area, performance and consumed power [16]; however, even for FSMs with average complexity [14], it could be up to 40 arguments in functions (1) and (2). Obviously, there is a distinct imbalance between such big number of arguments in SBFs representing FSM circuits and a fairly small value of LUT inputs. This imbalance requires improving synthesis methods of LUT-based FSMs.

Denote as $NA\left(f_i\right)$ the number of literals in a sum-of-product of function $f_i\in \Phi \cup Y$. If the condition

$$NA\left(f_i\right)>I_L$$

(4)

holds, then it is impossible to represent the function $f_i\in \Phi \cup Y$ by a single-level circuit. In this case, it is very important to optimize the system of connections between different slices of an FSM circuit. This follows from the fact that more than 70% of the power consumption is due to the interconnections [2]. Moreover, time delays of the interconnection system are starting to play a major role in comparison with CLB delays [18]. The results of research [2] show that the optimization of interconnections leads to increasing the maximum operating frequency and reducing the power consumption of LUT-based FSM circuits. This can be performed, for example, using various methods of structural decomposition [2].

3. Related Work

There are a huge number of methods for improving characteristics of circuits targeting LUT-based FSMs. The survey of these methods can be found, for example, in [2,12]. These methods should be applied if the condition (4) holds [2]. These methods can improve either the LUT count or the maximum operating frequency or the power consumption [24]. Sometimes, these methods are looking for a solution that allows joint improvement of more than only one FSM circuit’s characteristic. In this paper, we propose a method for decreasing the number of LUTs (this is an LUT count) of FPGA-based Mealy FSMs.

This task can be solved using various methods of state assignment [25,26,27]. In these methods, the number of bits in the state codes ranges from the minimum determined by formula (3) to the maximum determined by the total number of states, M. If $R=M$, then this is a one-hot state assignment. These approaches are used in both academic and industrial CAD tools. The examples of academic systems are SIS [28] and ABC by Berkeley [29,30]. The examples of industrial systems are Vivado [31] of Xilinx and Quartus of Intel (Altera) [32].

Now, there is no single universal method of state encoding that provides the best possible characteristics of FSM circuits. The applicability of a particular method can be judged both by the required number of state variables (R) and by the number of FSM inputs (L). As follows from [33], the one-hot codes improve FSM characteristics if $R>4$. The rather small value of $I_L$ increases the influence of the value of L on the characteristics of LUT-based FSM circuits [2]. It is shown in [34] that it is better to use the codes with the minimum number of bits ($R=\lceil lo{g}_{2}M\rceil$), if $L>10$.

So, in one case, it is better to use the one-hot state codes, and, in the other case, it is better to use the maximum binary state assignment with $R=\lceil lo{g}_{2}M\rceil$; therefore, it makes sense to compare several state assignment methods for the same FSM and find a method with the best characteristics. Due to this, we have compared the FSMs circuits produced by our proposed approach with FSM circuits produced by four other methods of state assignment. As a base for comparison, we use: the method of maximum state assignment Auto used in the CAD tool Vivado [31] by Xilinx; one-hot state assignment used in Vivado; the algorithm JEDI [28] which is one of the best methods of binary state assignment [19]. Our choice of Vivado is dictated by the fact that it operates with FPGAs of Xilinx. Further, we compared FSM circuits produced by our approach with three-block FSM circuits [11].

In this paper, we propose a method leading to four-block FSM circuits. It belongs to the methods of structural decomposition (SD) [2]. The main idea of these methods is the elimination of the direct connection between FSM outputs $y_n\in Y$ and IMFs $D_r\in \Phi$, on the one hand, and FSM inputs $x_l\in X$ and state variables $T_r\in T$, on the other hand. The SD leads to an increase in the total number of implemented functions having significantly fewer arguments than functions (1) and (2). These methods are analyzed, for example, in [2].

In [11], we have proposed an optimization method based on the combined use of two structural decomposition methods. These methods are the replacement of FSM inputs and encoding of collections of outputs. This approach leads to so called $MPY$ Mealy FSMs. Let us discus these two methods.

The first method is based on the replacement of inputs $x_l\in X$ by additional variables $p_g\in P=\{p_1,\dots ,p_G\}$, where $G\ll L$. The method uses the fact that transitions from any state $a_m\in A$ depend on $L_m$ inputs, where $L_m\ll L$ [14]. In the case of LUT-based FSMs, the variables $p_g\in P$ are generated by an additional block $LUTerP$. This block implements the system

$$P=P(T,X).$$

(5)

The second method is based on the fact that only a limited set of outputs is formed during transitions from any FSM state. Each transition is accompanied by generating some CO $Y_q\subseteq Y$, where $q\in \{1,\dots ,Q\}$. Each CO $Y_q\subseteq Y$ is encoded by a binary code $K\left(Y_q\right)$ having $R_Y$ bits, where

$$R_Y=\lceil lo{g}_{2}Q\rceil .$$

(6)

To encode these COs, additional variables $z_r\in Z=\{z_1,\dots ,z_{RY}\}$ are used.

In $MPY$ FSMs, a special block $LUTerY$ generate FSM outputs as functions

$$Y=Y\left(Z\right).$$

(7)

The variables $z_r\in Z$ and IMFs are generated by a block $LUTerTZ$:

$$Z=Z(T,P).$$

(8)

$$\Phi =\Phi (T,P).$$

(9)

So, the structural diagram of an LUT-based $MPY$ Mealy FSM includes three blocks connected in series (Figure 3).

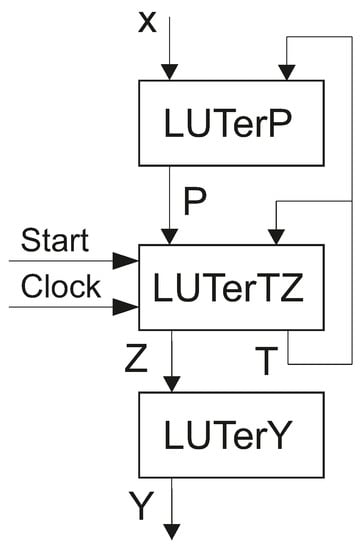
Figure 3. Structural diagram of LUT-based $MPY$ Mealy FSM.

There is a hidden register RG inside the block $LUTerTZ$. This explains why pulses $Clock$ and $Start$ enter the block $LUTerTZ$. Obviously, the informational inputs of D flip-flops are connected with IMFs $D_r\in \Phi$.

As shown in [11], such joint usage of two methods of SD leads to a significant decrease in the LUT count compared with other investigated methods; however, the gain in LUTs is significantly reduced if the condition (4) is met for the functions $f_i\in \Phi \cup Z$, where these systems are represented as (8) and (9). In this case, the circuit of $LUTerTZ$ is designed using the methods of functional decomposition [13]. As a result, there are several levels of LUTs in the circuit of $LUTerTZ$ with all the negative consequences.

The proposed method is an evolution of methods of twofold state assignment [17]. These methods are based on construction a partition ${\Pi }_A$ of the set of states by the classes of compatible states: ${\Pi }_A=\{A^1,\dots ,A^J\}$. Each state $a_m\in A$ determines a set $X\left(a_m\right)$ including FSM inputs causing transitions from this state. Inside each class, the states are encoded using maximum binary codes. If a set $A^j\in {\Pi }_A$ includes $M_j$ elements, then it is enough

$$R_j=\lceil lo{g}_2(M_j+1)\rceil$$

(10)

variables to encode these states by maximum binary codes. One additional code corresponds to the relation $a_m\notin A^j$.

We use the same definition of compatible states as the one propose in the paper [17]. The states $a_m\in A^j$ are compatible if

$$R_j+L_j\le I_L.$$

(11)

In (11), the symbol $L_j$ stands for the number of inputs determining transitions from states $a_m\in A^j$. These inputs form a set of inputs $X^j\subseteq X$.

To create the partition ${\Pi }_A=\{A^1,\dots ,A^J\}$ with minimum number of classes, J, we use the method from [17]. Each class $A^j\in {\Pi }_A$ consists of compatible states. Each class $A^j\in {\Pi }_A$ determines local sets of inputs $X^j\subseteq X$ and outputs $Y^j\subseteq Y$. If outputs $y_n\in Y$ are generated during transitions from states $a_m\in A^j$, then they are included into a set $Y^j\subseteq Y$.

In the case of twofold state assignment, each state $a_m\in A$ has two codes [17]. The code $K\left(a_m\right)$ determines the state $a_m\in A$ as an element of the set A. The extended state code (ESC) [35]$C\left(a_m\right)$ determines this very state an element of a compatibility class $A^j\in {\Pi }_A$. Each class $A^j\in {\Pi }_A$ determines a collection of partial functions generating by a block $LUTerj$. These partial functions are partial outputs $y_n\in Y^j$ and partial IMFs $D_r\in {\Phi }^J$. The set ${\Phi }^j\subseteq \Phi$ includes IMFs generating during the transitions from the states $a_m\in A^j$. These partial functions are denoted as $y_n^j$ and $D_r^j$. Because of (11), each partial function is represented by a single LUT.

An ESC consists of J fields. The j-th field has $R_j$ bits and corresponds to the class $A^j\in {\Pi }_A$. So, there are $R_E=R_1+R_2+...+R_J$ bits in ESCs. If the relation $a_m\in A^j$ holds, then only bits from the j-th field differ from zeros.

In [17], it is propose to produce ESCs by the transforming state codes $K\left(a_m\right)$ kept into RG. Unfortunately, the transformation requires an additional block of CLBs which consumes some internal resources of a chip and decreases the performance of a resulting FSM circuit. The improvement of this approach is proposed in [35]. In this case, the codes $C\left(s_m\right)$ are generated in parallel with FSM outputs. This approach allows eliminating the block of code transformation; however, this approach also has some drawbacks. Firstly, there are $R_E$ flip-flops in the RG. Secondly, the total number of LUTs generating IMFs is increased by $R_E-R$ compared to the previous approach.

The experiments [35] show that using only ESCs allows increasing performance up to 15.9% compared with equivalent FSMs based on the twofold state assignment. The growth of operating frequency is accompanied by a slight growth in the LUT count (up to 7.7%). In this paper, we propose a method of reducing the LUT count in $MPY$ Mealy FSM. The method is based on the replacing ESCs by complex state codes proposed in this paper.

4. Main Idea of the Proposed Method

The proposed method is based on finding a partition ${\Pi }_C=\{A^1,\dots ,A^{J_C}\}$ of the set A by $J_C$ classes of compatible states. The same state variables are used for encoding states from different compatibility classes. The states are encoded by codes $C\left(a_m\right)$ using $R_A$ state variables:

$$R_A=max(\lceil lo{g}_2{M}_1\rceil ,...,\lceil lo{g}_2{M}_{J_C}\rceil ).$$

(12)

A code $C\left(a_m\right)$ determines the state $a_m\in A$ as the element of a particular class of ${\Pi }_C$. The classes $A^j\in {\Pi }_C$ are encoded by class codes $K\left(A^j\right)$. These codes include $R_C$ bits:

$$R_C=\lceil lo{g}_2{J}_C\rceil .$$

(13)

We propose to represent FSM states $a_m\in A$ by the complex state codes denoted as $CSC\left(a_m\right)$. For any state $a_m\in A^j$, a CSC is a concatenation of the class code $K\left(A^j\right)$ and a state code $C\left(a_m\right)$:

$$CSC\left(a_m\right)=K\left(A^j\right)*C\left(a_m\right).$$

(14)

In (14), the sign “*” denotes the concatenation of the codes. There are $R_B$ state variables in CSCs. The value of $R_B$ is determined as

$$R_B=R_C+R_A.$$

(15)

To encode the classes, we use the variables from the set $T_C=\{T_1,\dots ,T_{RC}\}$. To encode states as elements of classes $A^j\in {\Pi }_C$, we use $R_C$ variables from the set $T_A=\{T_{RC+1},\dots ,T_{RB}\}$. Together, these sets form a set $T=T_C\cup T_A$ having $R_B$ elements.

The proposed method of state assignment is aimed at the reducing LUT count for LUT-based circuits of $MPY$ FSMs. The method is based on the joint application of: (1) the replacement of FSM inputs; (2) the encoding of collections of outputs; (3) the encoding of states by complex state codes. As a result, we propose to replace $MPY$ FSMs by $M{P}_{C}Y$ FSMs. The subscript “C” means that the complex state codes are used in $MPY$ FSM. There is the structural diagram of $M{P}_{C}Y$ FSM shown in Figure 4.

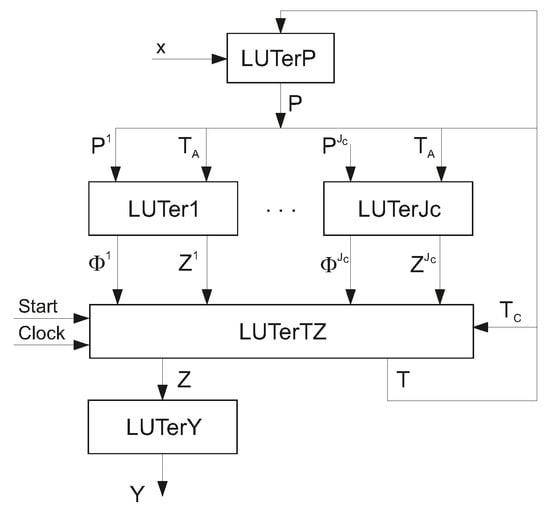
Figure 4. Structural diagram of LUT-based $M{P}_{C}Y$ Mealy FSM.

There are four levels of logic blocks in $M{P}_{C}Y$ FSMs. The first level is represented by LUTerP. This block implements the SBF (5).

The second level includes $J_C$ blocks $LUTerj$, where $j\in \{1,\dots ,J_C\}$. A class $A^j\in {\Pi }_C$ determines three sets of variables. The set $P^j\subseteq P$ includes additional variables $p_g\in P$ determining transitions from the states $a_m\in A^j$. The set ${\Phi }^j$ contains IMFs generated during the transitions from the states $a_m\in A^j$. The set $Z^j$ consists of the variables $z_r\in Z$ equal to 1 in codes of COs produced during the transitions from the states $a_m\in A^j$ determined by each class $A^j\in {\Pi }_C$. Each block $LUTerj$ produces the following partial functions:

$${\Phi }^j={\Phi }^j(T_A,P^j);$$

(16)

$$Z^j=Z^j(T_A,P^j).$$

(17)

The block $LUTerTZ$ represents the third logic level. It consists of $R_Y+R_B$ multiplexers generating IMFs $D_r\in \Phi$ and additional variables $z_r\in Z$. The data inputs of these multiplexers are the partial functions (16) and (17). To select a particular partial function, we use the class variables $T_r\in T_C$. So, the multiplexers generate the following SBFs:

$$D_r=D_r(T_C,D_r^1,\dots ,D_r^{J_C})(r\in \{1,\dots ,R_B\});$$

(18)

$$z_r=z_r(T_C,z_r^1,\dots ,z_r^{J_C})(r\in \{1,\dots ,R_Y\}).$$

(19)

The functions (18) enter the inputs of the flip-flops that make up the hidden register RG. Due to this, the control signals $Clock$ and $Start$ enter this block.

The fourth logic level is represented by the block $LUTerY$. It implements the SBF (7).

So, there are four levels of logic blocks in the circuits of $M{P}_{C}Y$ Mealy FSMs. In the best case, each block is represented by a single-level LUT-based circuit.

In this paper, we propose a synthesis method for LUT-based $M{P}_{C}Y$ Mealy FSMs. We start the synthesis process from an FSM state transition graph. The proposed method includes the following steps:

(1)

Creating the state transition table of Mealy FSM.

(2)

Constructing the partition ${\Pi }_C$ of the set of states by classes of compatible states.

(3)

Encoding of FSM states by complex state codes $CSC\left(a_m\right)$.

(4)

Executing the replacement of FSM inputs by additional variables $p_g\in P$.

(5)

Creating SBF (5) representing $LUTerP$.

(6)

Encoding of collections of outputs by codes $K\left(Y_q\right)$.

(7)

Creating SBF (7) representing $LUTerY$.

(8)

Creating direct structure table of $M{P}_{C}Y$ Mealy FSM.

(9)

Creating tables of blocks of partial functions $LUTer1$–$LUTer{J}_C$.

(10)

Creating SBFs (16) and (17) representing the second level of $M{P}_{C}Y$ Mealy FSM logic circuit.

(11)

Creating table of $LUTerTZ$.

(12)

Creating SBFs (18) and (19) representing the third level of the logic circuit.

(13)

Implementing the LUT-based circuit of $M{P}_{C}Y$ Mealy FSM using internal resources of a particular FPGA chip.

The partition ${\Pi }_C$ is created using the method [17]. This approach allows minimizing LUT counts in the resulting Mealy FSM circuits. If it is possible, each class of compatible states should include the maximum possible number of states. This helps minimizing the number of classes (and the blocks of the second level of logic). In turn, this optimizes the number of LUTs in the circuit of $LUTerTZ$. Any multiplexer from this block is implemented as a single LUT if the following condition takes place:

$$R_C+J_C\le I_L.$$

(20)

Even if condition (20) is violated, then the multiplexers could be implemented as single-level circuits. This is possible, if the number of partial functions for a given function $f_i\in \Phi \cup Y$ does not exceed the value $I_L-R_C$. Otherwise, the internal multiplexers of CLBs are used for generating functions (18) and (19).

5. Example of Synthesis

We use the symbol $M{P}_{C}Y\left(S_a\right)$ to show that the model of $M{P}_{C}Y$ Mealy FSM (Figure 4) is used to implement the circuit of an FSM $S_a$. Consider an FSM $S_0$ represented by its STG (Figure 5). Let us synthesize the circuit of Mealy FSM $M{P}_{C}Y\left(S_0\right)$ using 5-LUTs.

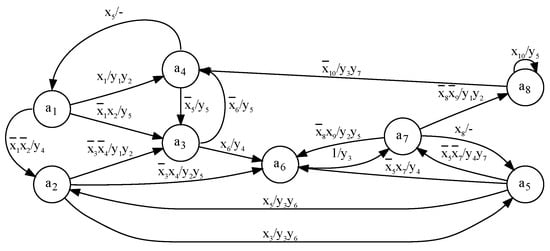
Figure 5. The state transition graph of Mealy FSM $S_0$.

Step 1. The h-th edge of an STG is transformed into a row of an STT [14]. There are 19 edges in the STG (Figure 5). So, it should be $H=19$ rows in the corresponding STT. The transformation is executed in a trivial way [1]. Table 1 is a resulting STT of FSM $S_0$. The following sets can be derived from Table 1: the set of states $A=\{a_1,\dots ,a_8\}$, the set of inputs $X=\{x_1,\dots ,x_{10}\}$, and the set of outputs $Y=\{y_1,\dots ,y_7\}$. This gives the following parameters: $M=8$, $L=10$, and $N=7$.

Table 1. State transition table of Mealy FSM $S_0$.

${\mathit{a}}_{\mathit{m}}$	${\mathit{a}}_{\mathit{T}}$	${\mathit{X}}_{\mathit{h}}$	${\mathit{Y}}_{\mathit{h}}$	h
$a_1$	$a_4$	$x_1$	$y_1{y}_2$	1
	$a_3$	$\overline{x_1}{x}_2$	$y_5$	2
	$a_2$	$\overline{x_1}\overline{x_2}$	$y_4$	3
$a_2$	$a_5$	$x_3$	$y_3{y}_6$	4
	$a_6$	$\overline{x_3}{x}_4$	$y_2{y}_5$	5
	$a_3$	$\overline{x_3}\overline{x_4}$	$y_1{y}_2$	6
$a_3$	$a_6$	$x_6$	$y_4$	7
	$a_4$	$\overline{x_6}$	$y_5$	8
$a_4$	$a_3$	$\overline{x_5}$	$y_5$	9
	$a_1$	$x_5$	–	10
$a_5$	$a_2$	$x_5$	$y_3{y}_6$	11
	$a_6$	$\overline{x_5}{x}_7$	$y_4$	12
	$a_7$	$\overline{x_5}\overline{x_7}$	$y_4{y}_7$	13
$a_6$	$a_7$	1	$y_3$	14
$a_7$	$a_5$	$x_8$	–	15
	$a_6$	$\overline{x_8}{x}_9$	$y_2{y}_5$	16
	$a_8$	$\overline{x_8}\overline{x_9}$	$y_1{y}_2$	17
$a_8$	$a_8$	$x_{10}$	$y_5$	18
	$a_4$	$\overline{x_{10}}$	$y_3{y}_7$	19

Step 2. Using the methods [17], we can obtain the partition ${\Pi }_C=\{A^1,A^2\}$ with $J_C=2$. There are the following classes of this partition: $A^1=\{a_1,\dots ,a_4\}$ and $A^2=\{a_5,\dots ,a_8\}$. So, there is $M_1=M_2=4$. Using (12), we can obtain the value $R_A=max(\lceil lo{g}_2{M}_1\rceil ,\lceil lo{g}_2{M}_2\rceil )=2$. Using (13), we can obtain the value $R_C=1$. Now, we have the sets $T=\{T_1,T_2,T_3\}$, $T_C=\left\{T_1\right\}$, and $T_A=\{T_3,T_4\}$.

Step 3. As known [2], the state codes do not affect the number of LUTs in circuits of FSMs based on twofold or extended state codes [35]. So, the states can be encoded in the arbitrary way. For our example, one of the possible outcomes of the state assignment is shown in Figure 6.

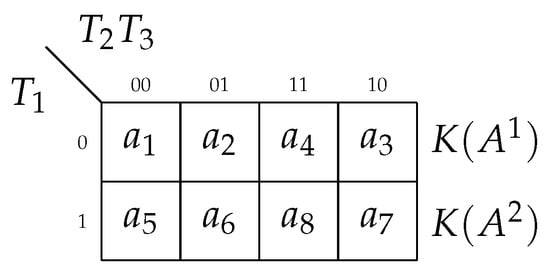
Figure 6. Complex state codes of Mealy FSM $M{P}_{C}Y\left(S_0\right)$.

The following class and state codes can be found from Figure 6: $K\left(A^1\right)=0$ and $K\left(A^2\right)=1$, $C\left(a_1\right)=C\left(a_5\right)=00,\dots ,C\left(a_4\right)=C\left(a_8\right)=11$. Using the codes of classes of compatible states $K\left(A^j\right)$ and state codes $C\left(a_m\right)$ gives the following complex state codes: $CSC\left(a_1\right)=000,CSC\left(a_2\right)=001,\dots ,CSC\left(a_4\right)=011,$ and $CSC\left(a_8\right)=111$.

Step 4. To execute the replacement, we should find the minimum value of additional variables, G. To do it, we use the methods from [14]. It is necessary to analyze sets $X\left(a_m\right)\subseteq X$ including FSM inputs which determine the transitions from states $a_m\in A$ [2]. These sets can be found using either the STG (Figure 5) or STT (Table 1). In the discussed case, there are the following sets: $X\left(a_1\right)=\{x_1,x_2\},X\left(a_2\right)=\{x_3,x_4\},X\left(a_3\right)=\left\{x_6\right\},X\left(a_4\right)=\left\{x_5\right\},X\left(a_5\right)=\{x_5,x_7\},X\left(a_6\right)=\varnothing ,X\left(a_7\right)=\{x_8,x_9\},$ and $X\left(a_8\right)=\left\{x_{10}\right\}$. If $L\left(a_m\right)$ is a number of elements in the set $X\left(a_m\right)\subseteq X$, then $L\left(a_1\right)=L\left(a_2\right)=L\left(a_5\right)=L\left(a_7\right)=2,$$L\left(a_3\right)=L\left(a_4\right)=L\left(a_8\right)=1,L\left(a_6\right)=0$.

The value of G is equal to the maximum value of $L\left(a_m\right)$. Obviously, there is $G=2$. So, it is enough $G=2$ additional variables to replace $L=10$ inputs: $P=\{p_1,p_2\}$.

The columns of table of inputs’ replacement are marked by FSM states $a_m\in A$, the rows are marked by additional variables $p_g\in P$. If an input $x_l\in X$ is replaced by a variable $p_g\in P$ in a state $a_m\in A$, then this input is written at the intersection of the corresponding column and row. Using methods from [14] gives the table of replacement (Table 2).

Table 2. Replacement of inputs for Mealy FSM $M{P}_{C}Y\left(S_0\right)$.

	A	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$	${\mathit{a}}_6$	${\mathit{a}}_7$	${\mathit{a}}_8$
P
$p_1$		$x_1$	$x_3$	$x_6$	–	$x_7$	–	$x_8$	$x_{10}$
$p_2$		$x_2$	$x_4$	–	$x_5$	$x_5$	–	$x_9$	–

Step 5.Table 2 is a base for finding SBF (5). The following SBF can be derived from Table 2:

$$\begin{array}{ccc}\hfill & & p_1=A_1{x}_1\vee A_2{x}_3\vee A_3{x}_6\vee A_5{x}_7\vee A_7{x}_8\vee A_8{x}_{10};\hfill \\ & & p_2=A_1{x}_2\vee A_2{x}_4\vee A_4{x}_5\vee A_5{x}_5\vee A_7{x}_9.\hfill \end{array}$$

(21)

In (21), the symbol $A_m$ stands for a conjunction of state variables corresponding to the state $a_m\in A$. Obviously, each of Equation (21) can be implemented as $8-MX$.

Step 6. There are $Q=9$ different collections of outputs in STT (Table 1). They are the following: $Y_1=\varnothing ,Y_2=\{y_1,y_2\},Y_3=\left\{y_5\right\},Y_4=\left\{y_4\right\},Y_5=\{y_3,y_6\},Y_6=\{y_2,y_5\},Y_7=\{y_4,y_7\},Y_8=\left\{y_3\right\},Y_9=\{y_3,y_7\}$.

To optimize the circuit of $LUTerY$, it is necessary to encode COs in a way minimizing the total number of literals in SBF (7) [2]. Each literal determines an interconnection between $LUTerTZ$ and $LUTerY$. Using the approach from [2], we can encode the COs as it is shown in Figure 7.

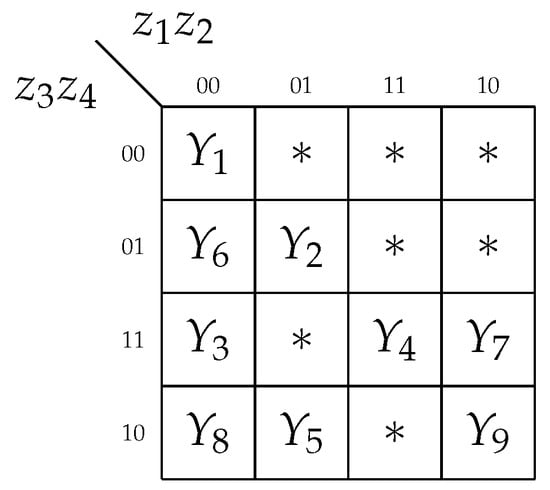
Figure 7. Outcome of encoding of COs for Mealy FSM $M{P}_{C}Y\left(S_0\right)$.

Step 7. Using contents of COs and their codes (Figure 7) gives the following SBF:

$$\begin{array}{ccc}\hfill & & y_1=Y_2=z_2\overline{z_3};y_5=Y_3\vee Y_6=\overline{z_1}\overline{z_2}{z}_4;\hfill \\ & & y_2=Y_2\vee Y_6=\overline{z_3}{z}_4;y_6=Y_5=\overline{z_1}{z}_2{z}_3;\hfill \\ \hfill & & y_3=Y_5\vee Y_8\vee Y_9=z_3\overline{z_4};y_7=Y_7\vee Y_9=z_1\overline{z_2}.\hfill \\ & & y_4=Y_4\vee Y_7=z_1{z}_4;\hfill \end{array}$$

(22)

There are 16 literals in (22). The maximum number of literals is equal to $N{R}_Y=7·4=28$. So, due to encoding shown in Figure 7, the number of literals (and interconnections) has almost halved.

Step 8. The DST of $MPY$ Mealy FSM is constructed using the initial STT, codes of states and COs, and a table of replacement of inputs. A DST includes the following columns: $a_m$, $K\left(a_m\right)$, $a_T$, $K\left(a_T\right)$, $P_h$, ${\Phi }_h$, $Z_h$, h. The columns of state codes include codes from Figure 6. The column $P_h$ is constructed using the initial STT and table of replacement of inputs (Table 2). The column ${\Phi }_h$ includes IMFs equal to 1 for loading the code $K\left(a_T\right)$ into state register. The column $Z_h$ includes variables $z_r\in Z$ equal to 1 in the code $K\left(Y_q\right)$ of CO written in the h-th row of STT. This column is constructed using the initial STT and codes of COs (Figure 7).

In the discussed case, the DST is represented by Table 3. Let us analyze the first row of Table 3. There is the input $x_1$ in this row of Table 1. As follows from Table 2, the input $x_1$ is replaced by the additional variable $p_1$ in the state $a_1$. For this row, there is the following relation: $a_T=a_4$. As follows from Figure 6, there is $K\left(a_4\right)=011$. Due to this, column ${\Phi }_h$ of Table 3 contains $D_2=D_3=1$ in row $h=1$. In row 1 of Table 1, there is the CO $Y_2$ in column $Y_h$. As follows from Figure 7, there is $K\left(Y_2\right)=0101$. Due to this, column $Z_h$ of Table 3 contains $z_2=z_4=1$ in row $h=1$. All other rows of Table 3 are constructed in the same way.

Table 3. Direct structure table of Mealy FSM $U_4\left(S_1\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{K}\left({\mathit{a}}_{\mathit{m}}\right)$	${\mathit{a}}_{\mathit{T}}$	$\mathit{K}\left({\mathit{a}}_{\mathit{T}}\right)$	${\mathit{P}}_{\mathit{h}}$	${\Phi }_{\mathit{h}}$	${\mathit{Z}}_{\mathit{h}}$	h
$a_1$	000	$a_4$	011	$p_1$	$D_2{D}_3$	$z_2{z}_4$	1
		$a_3$	010	$\overline{p_1}{p}_2$	$D_2$	$z_3{z}_4$	2
		$a_2$	001	$\overline{p_1}\overline{p_2}$	$D_3$	$z_1{z}_2{z}_3{z}_4$	3
$a_2$	001	$a_5$	100	$p_1$	$D_1$	$z_2{z}_3$	4
		$a_6$	101	$\overline{p_1}{p}_2$	$D_1{D}_3$	$z_4$	5
		$a_3$	010	$\overline{p_1}\overline{p_2}$	$D_2$	$z_2{z}_4$	6
$a_3$	010	$a_6$	101	$p_1$	$D_1{D}_3$	$z_1{z}_2{z}_3{z}_4$	7
		$a_4$	011	$\overline{p_1}$	$D_2{D}_3$	$z_3{z}_4$	8
$a_4$	011	$a_3$	101	$p_2$	$D_2$	$z_3{z}_4$	9
		$a_1$	000	$\overline{p_2}$	–	–	10
$a_5$	100	$a_2$	001	$p_2$	$D_3$	$z_2{z}_3$	11
		$a_6$	101	$\overline{p_2}{p}_1$	$D_1{D}_3$	$z_1{z}_2{z}_3{z}_4$	12
		$a_7$	110	$\overline{p_2}\overline{p_1}$	$D_1{D}_2$	$z_1{z}_3{z}_4$	13
$a_6$	101	$a_7$	110	1	$D_1{D}_2$	$z_3$	14
$a_7$	110	$a_5$	100	$p_1$	$D_1$	–	15
		$a_6$	101	$\overline{p_1}{p}_2$	$D_1{D}_3$	$z_4$	16
		$a_8$	111	$\overline{p_1}\overline{p_2}$	$D_1{D}_2{D}_3$	$z_2{z}_4$	17
$a_8$	111	$a_8$	111	$p_1$	$D_1{D}_2{D}_3$	$z_3{z}_4$	18
		$a_4$	011	$\overline{p_1}$	$D_2{D}_3$	$z_1{z}_3$	19

Step 9. These tables are constructed using the classes $A^j\in {\Pi }_C$, DST of $MPY$ Mealy FSM, codes $C\left(a_m\right)$ and $CSC\left(a_m\right)$. For the discussed example, there is $J_C=2$. So, there are two blocks ($LUTer1$ and $LUTer2$) generating the partial functions (16) and (17). The transitions from the states from the class $A^1\in {\Pi }_C$ are represented by Table 4, for the class $A^2\in {\Pi }_C$ by Table 5.

Table 4. Table of $LUTer1$ of Mealy FSM $M{P}_{C}Y\left(S_0\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{C}\left({\mathit{a}}_{\mathit{m}}\right)$	${\mathit{a}}_{\mathit{T}}$	$\mathbf{CSC}\left({\mathit{a}}_{\mathit{T}}\right)$	${\mathit{P}}_{\mathit{h}}^1$	${\Phi }_{\mathit{h}}^1$	${\mathit{Z}}_{\mathit{h}}^1$	h
$a_1$	00	$a_4$	011	$p_1$	$D_2{D}_3$	$z_3{z}_4$	1
		$a_3$	010	$\overline{p_1}{p}_2$	$D_2$	$z_3{z}_4$	2
		$a_2$	001	$\overline{p_1}\overline{p_2}$	$D_3$	$z_1{z}_2{z}_3{z}_4$	3
$a_2$	01	$a_5$	100	$p_1$	$D_1$	$z_2{z}_3$	4
		$a_6$	101	$\overline{p_1}{p}_2$	$D_1{D}_3$	$z_4$	5
		$a_3$	010	$\overline{p_1}\overline{p_2}$	$D_2$	$z_2{z}_4$	6
$a_3$	10	$a_6$	101	$p_1$	$D_1{D}_3$	$z_1{z}_2{z}_3{z}_4$	7
		$a_4$	011	$\overline{p_1}$	$D_2{D}_3$	$z_3{z}_4$	8
$a_4$	11	$a_3$	010	$p_2$	$D_2$	$z_3{z}_4$	9
		$a_1$	000	$\overline{p_2}$	–	–	10

Table 5. Table of $LUTer2$ of Mealy FSM $M{P}_{C}Y\left(S_0\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{C}\left({\mathit{a}}_{\mathit{m}}\right)$	${\mathit{a}}_{\mathit{T}}$	$\mathbf{CSC}\left({\mathit{a}}_{\mathit{T}}\right)$	${\mathit{P}}_{\mathit{h}}^2$	${\Phi }_{\mathit{h}}^2$	${\mathit{Z}}_{\mathit{h}}^2$	h
$a_5$	00	$a_2$	001	$p_2$	$D_3$	$z_2{z}_3$	1
		$a_6$	101	$\overline{p_2}{p}_1$	$D_1{D}_3$	$z_1{z}_2{z}_3{z}_4$	2
		$a_7$	110	$\overline{p_2}\overline{p_1}$	$D_1{D}_2$	$z_1{z}_3{z}_4$	3
$a_6$	01	$a_7$	110	1	$D_1{D}_2$	$z_3$	4
$a_7$	10	$a_5$	100	$p_1$	$D_1$	–	5
		$a_6$	101	$\overline{p_1}{p}_2$	$D_1{D}_3$	$z_4$	6
		$a_8$	111	$\overline{p_1}\overline{p_2}$	$D_1{D}_2{D}_3$	$z_2{z}_4$	7
$a_8$	11	$a_8$	111	$p_1$	$D_1{D}_2{D}_3$	$z_3{z}_4$	8
		$a_4$	011	$p_2$	$D_2{D}_3$	$z_1{z}_3$	9

There is a transparent correspondence between Table 3, on the one hand, and tables of $LUTer1$ (Table 4) and $LUTer2$ (Table 5), on the other hand. There are $H_1=10$ rows in Table 4 and $H_2=9$ rows in Table 5. Obviously, the following equality takes place: $H_1+H_2=H=19$.

Step 10. The following sets can be found from Table 4 and Table 5: $P^1=P^2=P$, ${\Phi }^1={\Phi }^2=\Phi$, and $Z^1=Z^2=Z$. It means that each $LUTerj$ contains $R_B+R_Y=7$ 5-LUTs. Together, this gives 14 5-LUTs in the mutual circuit of $LUTer1$ and $LUTer2$.

The functions (16) and (17) are constructed in the trivial way. For example, the following SBF of partial functions $D_1^1,D_1^2,z_1^1$, and $z_1^2$ can be derived from Table 4 and Table 5:

$$\begin{array}{ccc}\hfill & & D_1^1=\overline{T_2}{T}_3{p}_1\vee \overline{T_2}{T}_3\overline{p_1}{p}_2\vee T_2\overline{T_3}{p}_1;\hfill \\ & & D_1^2=\overline{T_2}\overline{T_3}\overline{p_2}\vee \overline{T_2}{T}_3\vee T_2\overline{T_3}\vee T_2{T}_3{p}_1.\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill & & z_1^1=\overline{T_2}\overline{T_3}\overline{p_1}\overline{p_2}\vee T_2\overline{T_3}{p}_1;\hfill \\ & & z_1^2=\overline{T_2}\overline{T_3}\overline{p_2}\vee T_2{T}_3{p}_2.\hfill \end{array}$$

(24)

All other partial functions are created in the same manner.

Step 11. The table of $LUTerTZ$ is constructed using sets ${\Phi }^j$ and $Z^j$ where $j\in \{1,\dots ,J_C\}$. The table contains the columns "Function" and "j". For our example, this block is represented by Table 6.

Table 6. Table of $LUTerTZ$ of Mealy $M{P}_{C}Y\left(S_0\right)$.

Function	j
	1	2
$D_1$	1	1
$D_2$	1	1
$D_3$	1	1
$z_1$	1	1
$z_2$	1	1
$z_3$	1	1
$z_4$	1	1

For example, the IMF $D_1$ appears in both tables. Due to this, there are ones in columns with $j=1$ and $j=2$. All other rows are filled used the similar analysis.

Step 12. The SBFs (18) and (19) representing the third level of the logic circuit are constructed in the trivial way. They include two components: (1) conjunctions of variables $T_r\in T_C$ corresponding to class codes and (2) corresponding partial functions. For example, functions $D_1$ and $z_1$ are represented by the following SBF:

$$\begin{array}{ccc}\hfill & & D_1=\overline{T_1}{D}_1^1\vee T_1{D}_1^2;\hfill \\ & & z_1=\overline{T_2}{z}_1^1\vee \overline{T_1}{z}_1^2.\hfill \end{array}$$

(25)

All other functions (18) and (19) are constructed in the same manner.

Step 13. To implementing the LUT-based circuit of Mealy FSM $M{P}_{C}Y\left(S_0\right)$, it is necessary to use some CAD tools. In the case of FPGAs from Virtex-7, the system Vivado [31] should be used; for our simple example we can design this circuit manually.

As follows from (21), there are nine literals in the sum-of-products of $p_1$ and eight literals in the sum-of-products of $p_2$. The circuit should be implemented using LUTs with $I_L=5$ inputs. So, the condition (4) holds. To implement the circuit of $LUTerP$, it is necessary to apply the methods of FD [12,13]. As a result, we obtain a two-level circuit of $LUTerP$ including six LUTs.

In the discussed case, each function $f_i\in Z\cup \Phi$ is represented by $J_C=2$ partial functions. Further, the condition (11) holds for the blocks of ${\Pi }_C$. Due to this, there are enough $2(R_B+R_Y)=14$ 5-LUTs for implementing the circuits of $LUTer1$-$LUTer2$. Since $(R_B+R_Y)=7$, there are seven LUTs in the circuit of $LUTerTZ$. As follows from (22), there are seven LUTs in the circuit of $LUTerY$.

So, there are 34 5-LUTs in the circuit of Mealy FSM $M{P}_{C}Y\left(S_0\right)$. This circuit has five levels of LUTs (Figure 8).

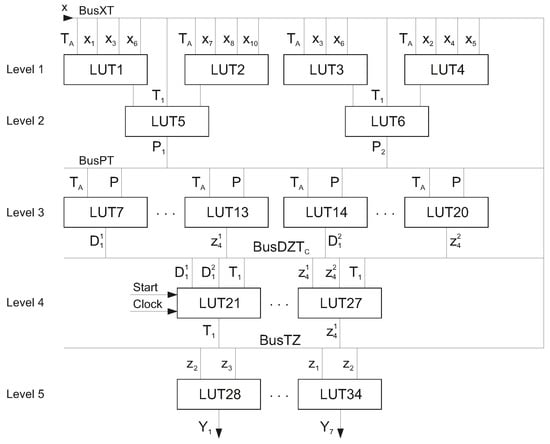
Figure 8. Logic circuit of Mealy FSM $M{P}_{C}Y\left(S_0\right)$.

In this circuit, $LUTerP$ is represented by LUT1–LUT6. This circuit has two levels of LUTs shown in Figure 8. The $BusXT$ delivers the inputs $x_l\in X$ and state variables $T_r\in T_A$ for generating the additional variables $p_g\in P$. These variables enter $BusPT$ to be transformed into the partial functions (16) and (17). The transformation is executed by $LUTer1$ and $LUTer2$. These blocks include elements LUT7–LUT20. The fourth level of the FSM circuit is represented by LUT21–LUT27. The IMFs are generated by LUT21–LUT23. The outputs of these LUTs are connected with flip-flops implementing the register RG. The flip-flops are controlled by the pulses $Start$ and $Clock$. The variables $z_r\in Z$ are generated by LUT24–LUT27. The outputs of $LUTerTZ$ form the $BusTZ$. At last, level five consists of seven LUTs (LUT28–LUT34) creating the circuit of $LUTerY$.

We compared the characteristics of the 5-LUT-based circuits of $M{P}_{C}Y\left(S_0\right)$ and $MPY\left(S_0\right)$ FSMs. In both cases, there is the same number of flip-flops in the state register ($R=R_B=3$). In the case of $MPY\left(S_0\right)$, there are six LUTs in the $LUTerP$ and seven LUTs in $LUTerY$. There are two levels of LUTs in the circuit of $LUTerP$. So, these subcircuits are the same for $M{P}_{C}Y\left(S_0\right)$ and $MPY\left(S_0\right)$. There are two levels of LUTs in the circuit of $LUTerTZ$ of $MPY\left(S_0\right)$. This block’s circuit includes 24 LUTs. So, there are $6+24+7=37$ LUTs in the circuit of $MPY\left(S_0\right)$.

Thus, for the FSM $S_0$, the transition from model $MPY\left(S_0\right)$ to model $M{P}_{C}Y\left(S_0\right)$ allows you to reducing the LUT count by 1.088 times. Note that both circuits have the same number of logical levels; therefore, the model proposed in this article allows reducing the number of LUTs without reducing the operating frequency compared to the circuit of equivalent $MPY\left(S_0\right)$ FSM. In the next Section, we compare some FSM models with the one proposed in this article.

6. Experimental Results

In this Section, we show the results of experiments which have been conducted to compare characteristics of $M{P}_{C}Y$ Mealy FSMs with characteristics of FSM circuits based on some other models. To conduct the experiments, we use: (1) the internal resources of Virtex-7; (2) the benchmark FSMs from the library [36]; (3) the industrial package Vivado [31]. The library [36] includes 48 benchmarks represented in the format KISS2. The benchmarks have a wide range of basic characteristics (numbers of states, inputs, and outputs). They are used very often by different researchers to compare area and time characteristics of FSMs obtained using various synthesis methods. The characteristics of benchmarks are shown Table 7.

Table 7. Characteristics of benchmark Mealy FSMs [36].

Benchmark	L	N	$\mathit{R}+\mathit{L}$	$\mathit{M}/\mathit{R}$	H	Category
bbara	4	2	8	12/4	60	1
bbsse	7	7	12	26/5	56	1
bbtas	2	2	6	9/4	24	0
beecount	3	4	7	10/4	28	1
cse	7	7	12	32/5	91	1
dk14	3	5	8	26/5	56	1
dk15	3	5	8	17/5	32	1
dk16	2	3	9	75/7	108	1
dk17	2	3	6	16/4	32	0
dk27	1	2	5	10/4	14	0
dk512	1	3	6	24/5	15	0
donfile	2	1	7	24/5	96	1
ex1	9	19	16	80/7	138	2
ex2	2	2	7	25/5	72	1
ex3	2	2	6	14/4	36	0
ex4	6	9	11	18/5	21	1
ex5	2	2	6	16/4	32	0
ex6	5	8	9	14/4	34	1
ex7	2	2	12	17/5	36	1
keyb	7	7	12	22/5	170	1
kirkman	12	6	18	48/6	370	2
lion	2	1	5	5/3	11	0
lion9	2	1	6	11/4	25	0
mark1	5	16	10	22/5	22	1
mc	3	5	6	8/3	10	0
modulo12	1	1	5	12/4	24	0
opus	5	6	10	18/5	22	1
planet	7	19	14	86/7	115	2
planet1	7	19	14	86/7	115	2
pma	8	8	14	49/6	73	2
s1	8	7	14	54/6	106	2
s1488	8	19	15	112/7	251	2
s1494	8	19	15	118/7	250	2
s1a	8	6	15	86/7	107	2
s208	11	2	17	37/6	153	2
s27	4	1	8	11/4	34	1
s386	7	7	12	23/5	64	1
s420	19	2	27	137/8	137	4
s510	19	7	27	172/8	77	4
s8	4	1	8	15/4	20	1
s820	18	19	25	78/7	232	4
s832	18	19	25	76/7	245	4
sand	11	9	18	88/7	184	3
shiftreg	1	1	5	16/4	16	0
sse	7	7	12	26/5	56	1
styr	9	10	16	67/7	166	2
tma	7	9	13	63/6	44	2

We executed the experiments using a personal computer with the following characteristics: CPU: Intel Core i7 6700 K 4.2@4.4 GHz, Memory: 32 GB RAM 2400 MHz CL15. Further, we used the Virtex-7 VC709 Evaluation Platform (xc7vx690tffg1761-2) [37] and CAD tool Vivado v2019.1 (64-bit) [31]. There is $I_L=6$ for FPGAs of Virtex-7. To obtain the results of experiments, the reports produced by Vivado are used. To enter Vivado, we use thed CAD tool K2F [2].

We compared three basic characteristics of resulting FSM circuits. These parameters are: (1) the LUT count; (2) the time of cycle; (3) the power consumption. In addition, two integral characteristics were investigated, namely: (1) the area-time products and (2) the area-time-power products. To conduct the experiments, five FSM models were used. They are: (1) Auto of Vivado (it uses binary state codes); (2) one-hot of Vivado; (3) JEDI; (4) $MPY$-based FSMs; (5) $M{P}_{C}Y$-based FSMs proposed in this article. Obviously, the first three methods are based on the model of P FSM shown in Figure 2.

Based on the methodology [35], we divide the benchmark FSMs [36] by five categories. To divide the benchmarks, we use the relation between the values of $R+L$ and $I_L$. There is $I_L=6$ for LUTs of Virtex-7. We use this value to divide the benchmarks by the categories.

The benchmarks belong to category of trivial FSMs (category 0), if the following condition holds: $R+L\le 6$. This category includes the following 11 benchmarks: $bbtas,dk17,dk27,$$dk512,ex3,ex5,lion,lion9,mc,modulo12,$ and $shiftreg$. The benchmarks belong to category of simple FSMs (category 1), if there is $R+L\le 12$. The category 1 consists of the benchmarks bbara, bbsse, beecount, cse, dk14, dk15, dk16, donfile, ex2, ex4, ex6, ex7, keyb, mark1, opus, s27, s386, s840, and $sse$. The benchmarks belong to category of average FSMs (category 2), if $R+L\le 18$. The category 2 contains the benchmarks ex1, kirkman, planet, planet1, pma, s1, s1488, s1494, s1a, s208, styr, and $tma$. The benchmarks belong to category of big FSMs (category 3), if the following condition takes place: $R+L\le 24$. The category three includes only the benchmark $sand$. The category of very big FSMs (category 4) includes benchmarks satisfying relation $R+L>24$. The benchmarks s420, s510, s820, and s832 belong to this category.

The results of experiments are shown in Table 8, Table 9, Table 10, Table 11 and Table 12. There is the same organization of these tables. The investigated methods are listed in the table columns. The table rows contain the names of benchmarks. Inside each table, the benchmarks are listed in alphabetical order, and sorted by ascending category number. The rows “Total” contain results of summation of values for each column. The row “Percentage” includes the percentage of summarized characteristics of FSM circuits produced by other methods respectively to $M{P}_{C}Y$-based FSMs. We use the model of P Mealy FSM as a starting point for methods Auto, one-hot, and JEDI. The basic data (the LUT count, time, and power consumption) are taken from reports of Vivado. Next these data were used to obtain the integral characteristics.

Table 8. Experimental results (LUT counts).

Benchmark	Auto	One-Hot	JEDI	$\mathit{MPY}$	Our Approach	Category
bbtas	5	5	5	8	8	0
dk17	5	12	5	8	8	0
dk27	3	5	4	7	7	0
dk512	10	10	9	12	12	0
ex3	9	9	9	11	11	0
ex5	9	9	9	10	10	0
lion	2	5	2	6	6	0
lion9	6	11	5	8	8	0
mc	4	7	4	6	6	0
modulo12	7	7	7	9	9	0
shiftreg	2	6	2	4	4	0
bbara	17	17	10	10	9	1
bbsse	33	37	24	26	21	1
beecount	19	19	14	14	12	1
cse	40	66	36	33	30	1
dk14	16	27	10	12	10	1
dk15	15	16	12	6	7	1
dk16	15	34	12	11	10	1
donfile	31	31	24	21	18	1
ex2	9	9	8	8	8	1
ex4	15	13	12	11	10	1
ex6	24	36	22	21	19	1
ex7	4	5	4	6	6	1
keyb	43	61	40	37	34	1
mark1	23	23	20	19	16	1
opus	28	28	22	21	19	1
s27	6	18	6	6	7	1
s386	26	39	22	25	23	1
s8	9	9	9	9	9	1
sse	33	37	30	26	22	1
ex1	70	74	53	40	34	2
kirkman	42	58	39	33	29	2
planet	131	131	88	78	68	2
planet1	131	131	88	78	68	2
pma	94	94	86	72	64	2
s1	65	99	61	54	51	2
s1488	124	131	108	89	81	2
s1494	126	132	110	90	79	2
s1a	49	81	43	38	32	2
s208	12	31	10	9	9	2
styr	93	120	81	70	61	2
tma	45	39	39	30	27	2
sand	132	132	114	99	91	3
s420	10	31	9	8	8	4
s510	48	48	32	22	19	4
s820	88	82	68	52	46	4
s832	80	79	62	50	42	4
Total	1808	2104	1489	1323	1188
Percentage,%	152.19	177.10	125.34	111.36	100.00

Table 9. Experimental results (the latency time for all benchmarks, nsec).

Benchmark	Auto	One-Hot	JEDI	$\mathit{MPY}$	Our Approach	Category
bbtas	4.898	4.898	4.852	4.991	5.013	0
dk17	5.018	5.988	5.015	5.003	5.075	0
dk27	4.854	4.953	4.898	5.085	5.150	0
dk512	5.095	5.095	5.006	5.150	5.208	0
ex3	5.132	5.132	5.108	5.230	5.372	0
ex5	5.548	5.548	5.520	5.616	5.690	0
lion	4.940	4.902	4.942	4.996	5.025	0
lion9	4.871	5.399	4.845	5.022	5.155	0
mc	5.085	5.116	5.079	5.177	5.278	0
modulo12	4.831	4.831	4.828	4.972	4.824	0
shiftreg	3.807	3.794	3.620	3.896	3.978	0
bbara	5.171	5.171	4.712	4.945	4.997	1
bbsse	6.367	5.913	5.484	5.518	5.809	1
beecount	6.002	6.002	5.338	5.401	5.461	1
cse	6.829	6.111	5.614	5.708	5.875	1
dk14	5.218	5.792	5.159	5.258	5.298	1
dk15	5.194	5.395	5.132	5.202	5.258	1
dk16	5.892	5.721	5.073	5.146	5.244	1
donfile	5.434	5.435	4.910	4.977	5.045	1
ex2	5.036	5.036	4.997	5.042	5.072	1
ex4	5.526	5.627	5.186	5.259	5.370	1
ex6	5.897	6.105	5.663	5.839	5.912	1
ex7	4.999	4.979	4.985	5.047	5.096	1
keyb	6.392	6.970	5.937	6.172	6.240	1
mark1	6.158	6.158	5.676	5.876	5.920	1
opus	6.017	6.017	5.608	5.705	5.830	1
s27	5.032	5.222	5.022	5.099	5.195	1
s386	5.947	5.765	5.582	5.655	5.874	1
s8	5.555	5.588	5.518	5.611	5.788	1
sse	6.367	5.913	5.726	5.878	6.086	1
ex1	6.625	7.155	5.654	5.484	5.235	2
kirkman	7.073	6.494	6.382	5.983	5.521	2
planet	7.535	7.535	5.344	5.288	5.234	2
planet1	7.535	7.535	5.344	5.288	5.234	2
pma	6.841	6.841	5.888	5.612	5.370	2
s1	6.830	7.361	6.363	6.164	5.743	2
s1488	7.220	7.579	6.362	5.941	5.809	2
s1494	6.694	6.861	6.085	5.805	5.557	2
s1a	6.520	5.669	5.911	5.611	5.517	2
s208	5.736	5.667	5.594	5.503	5.339	2
styr	7.267	7.697	6.866	6.178	5.908	2
tma	6.102	6.766	6.092	5.659	5.554	2
sand	8.623	8.623	7.885	6.864	6.558	3
s420	5.751	5.667	5.642	5.341	5.193	4
s510	5.629	5.629	5.512	5.338	5.257	4
s820	6.579	6.529	5.663	5.496	5.288	4
s832	6.863	6.526	5.754	5.373	5.169	4
Total	278.536	280.710	257.378	255.403	254.625
Percentage,%	109.39	110.24	101.08	100.31	100.00

Table 10. Experimental results (Total On-Chip Power, Watts).

Benchmark	Auto	One-Hot	JEDI	$\mathit{MPY}$	Our Approach	Category
bbtas	0.533	0.533	0.533	0.661	0.661	0
dk17	1.901	1.935	1.891	2.363	2.363	0
dk27	1.168	0.854	1.158	1.459	1.459	0
dk512	1.496	1.496	1.345	1.708	1.708	0
ex3	0.391	0.391	0.391	0.501	0.501	0
ex5	0.387	0.387	0.385	0.496	0.496	0
lion	0.542	0.629	0.547	0.711	0.711	0
lion9	0.733	0.97	0.728	0.939	0.939	0
mc	0.447	0.561	0.443	0.567	0.567	0
modulo12	0.559	0.559	0.563	0.715	0.715	0
shiftreg	0.523	0.603	0.512	0.645	0.645	0
bbara	0.569	0.569	0.488	0.399	0.379	1
bbsse	2.22	1.206	1.713	1.522	1.474	1
beecount	1.631	1.631	1.021	0.835	0.793	1
cse	0.958	1.019	0.891	0.683	0.649	1
dk14	2.959	3.33	2.952	2.892	2.747	1
dk15	1.403	1.905	1.399	1.312	1.246	1
dk16	2.967	2.742	2.512	2.335	2.218	1
donfile	0.709	0.709	0.603	0.478	0.454	1
ex2	0.368	0.386	0.342	0.267	0.254	1
ex4	1.562	1.241	1.187	0.923	0.877	1
ex6	2.269	3.85	2.242	1.975	1.879	1
ex7	0.992	1.181	0.994	0.998	0.968	1
keyb	1.093	1.071	1.075	0.796	0.748	1
mark1	1.445	1.445	1.227	1.087	1.011	1
opus	1.344	1.344	1.283	1.121	1.064	1
s27	0.756	1.95	0.765	0.564	0.525	1
s386	1.251	1.393	1.121	0.998	0.938	1
s8	0.736	0.805	0.732	0.682	0.662	1
sse	1.22	1.296	1.089	0.907	0.862	1
ex1	4.102	2.968	2.342	1.728	1.589	2
kirkman	1.693	1.844	1.439	1.127	1.048	2
planet	4.122	4.122	2.456	2.028	1.906	2
planet1	4.122	4.122	2.456	2.028	1.906	2
pma	1.37	1.37	1.253	0.803	0.739	2
s1	2.685	3.13	2.518	2.048	1.925	2
s1488	3.982	4.096	3.548	1.883	1.751	2
s1494	3.079	3.178	2.982	2.358	2.169	2
s1a	1.322	2.01	1.208	0.885	0.832	2
s208	1.367	2.82	1.249	0.957	0.871	2
styr	4.044	4.771	3.187	2.632	2.448	2
tma	1.589	1.314	1.321	0.918	0.845	2
sand	1.149	1.149	0.988	0.617	0.557	3
s420	1.337	2.82	1.286	0.892	0.794	4
s510	1.543	1.543	1.091	0.852	0.767	4
s820	2.054	1.801	1.463	0.843	0.742	4
s832	2.096	2.087	1.828	0.932	0.829	4
Total	76.788	83.136	64.747	55.070	52.231
Percentage,%	147.02	159.17	123.96	105.44	100

Table 11. Experimental results (area-time products).

Benchmark	Auto	One-Hot	JEDI	$\mathit{MPY}$	Our Approach	Category
bbtas	24.49	24.49	24.26	39.92	40.10	0
dk17	25.09	71.86	25.08	40.03	40.60	0
dk27	14.56	24.76	19.59	35.60	36.05	0
dk512	50.95	50.95	45.06	61.80	62.49	0
ex3	46.19	46.19	45.97	57.53	59.10	0
ex5	49.93	49.93	49.68	56.16	56.90	0
lion	9.88	24.51	9.88	29.97	30.15	0
lion9	29.23	59.39	24.23	40.18	41.24	0
mc	20.34	35.81	20.32	31.06	31.67	0
modulo12	33.82	33.82	33.80	44.75	43.41	0
shiftreg	7.61	22.76	7.24	15.58	15.91	0
bbara	87.91	87.91	47.12	49.45	44.97	1
bbsse	210.11	218.78	131.62	143.46	121.98	1
beecount	114.04	114.04	74.74	75.62	65.53	1
cse	273.17	403.32	202.11	188.38	176.25	1
dk14	83.49	156.39	51.59	63.10	52.98	1
dk15	77.91	86.32	61.58	31.21	36.81	1
dk16	88.38	194.52	60.87	56.60	52.44	1
donfile	168.45	168.48	117.85	104.52	90.80	1
ex2	45.32	45.32	39.97	40.34	40.58	1
ex4	82.89	73.15	62.23	57.85	53.70	1
ex6	141.53	219.78	124.58	122.61	112.33	1
ex7	20.00	24.90	19.94	30.28	30.58	1
keyb	274.85	425.18	237.49	228.38	212.17	1
mark1	141.63	141.63	113.52	111.65	94.72	1
opus	168.47	168.47	123.37	119.80	110.77	1
s27	30.19	93.99	30.13	30.59	36.37	1
s386	154.62	224.84	122.80	141.36	135.10	1
s8	49.99	50.29	49.66	50.50	52.10	1
sse	210.11	218.78	171.79	152.83	133.89	1
ex1	463.76	529.48	299.66	219.37	178.00	2
kirkman	297.07	376.62	248.91	197.43	160.11	2
planet	987.11	987.11	470.24	412.44	355.89	2
planet1	987.11	987.11	470.24	412.44	355.89	2
pma	643.04	643.04	506.39	404.06	343.70	2
s1	443.96	728.74	388.14	332.86	292.90	2
s1488	895.31	992.88	687.11	528.75	470.55	2
s1494	843.43	905.66	669.34	522.44	439.01	2
s1a	319.49	459.18	254.18	213.23	176.55	2
s208	68.83	175.68	55.94	49.53	48.05	2
styr	675.82	923.65	556.17	432.45	360.41	2
tma	274.59	263.87	237.60	169.76	149.95	2
sand	1138.23	1138.23	898.91	679.57	596.76	3
s420	57.51	175.68	50.78	42.73	41.55	4
s510	270.19	270.19	176.39	117.45	99.87	4
s820	578.95	535.39	385.09	285.78	243.23	4
s832	549.04	515.56	356.77	268.64	217.11	4
Total	12,228.61	14,168.64	8859.93	7540.03	6641.23
Percentage,%	184.13	213.34	133.41	113.53	100.00

Table 12. Experimental results (area-time-power products).

Benchmark	Auto	One-Hot	JEDI	$\mathit{MPY}$	Our Approach	Category
bbtas	13.05	13.05	12.93	26.39	26.51	0
dk17	47.70	139.04	47.42	94.58	95.94	0
dk27	17.01	21.15	22.69	51.93	52.60	0
dk512	76.22	76.22	60.60	105.56	106.73	0
ex3	18.06	18.06	17.98	28.82	29.61	0
ex5	19.32	19.32	19.13	27.86	28.22	0
lion	5.35	15.42	5.41	21.31	21.44	0
lion9	21.42	57.61	17.64	37.73	38.73	0
mc	9.09	20.09	9.00	17.61	17.96	0
modulo12	18.90	18.90	19.03	32.00	31.04	0
shiftreg	3.98	13.73	3.71	10.05	10.26	0
bbara	50.02	50.02	23.00	19.73	17.04	1
bbsse	466.45	263.85	225.47	218.35	179.80	1
beecount	186.00	186.00	76.31	63.14	51.97	1
cse	261.70	410.99	180.08	128.66	114.39	1
dk14	247.05	520.76	152.28	182.48	145.53	1
dk15	109.31	164.44	86.15	40.95	45.86	1
dk16	262.23	533.37	152.91	132.17	116.32	1
donfile	119.43	119.45	71.06	49.96	41.22	1
ex2	16.68	17.50	13.67	10.77	10.31	1
ex4	129.48	90.78	73.87	53.40	47.10	1
ex6	321.14	846.15	279.31	242.16	211.06	1
ex7	19.84	29.40	19.82	30.22	29.60	1
keyb	300.41	455.36	255.30	181.79	158.70	1
mark1	204.66	204.66	139.29	121.36	95.76	1
opus	226.43	226.43	158.29	134.30	117.86	1
s27	22.82	183.29	23.05	17.25	19.09	1
s386	193.43	313.20	137.66	141.08	126.73	1
s8	36.80	40.49	36.35	34.44	34.49	1
sse	256.34	283.54	187.08	138.62	115.41	1
ex1	1902.35	1571.49	701.79	379.07	282.84	2
kirkman	502.94	694.49	358.19	222.50	167.80	2
planet	4068.89	4068.89	1154.90	836.42	678.33	2
planet1	4068.89	4068.89	1154.90	836.42	678.33	2
pma	880.97	880.97	634.51	324.46	253.99	2
s1	1192.03	2280.97	977.34	681.70	563.84	2
s1488	3565.11	4066.82	2437.87	995.65	823.93	2
s1494	2596.92	2878.19	1995.98	1231.90	952.21	2
s1a	422.36	922.96	307.05	188.71	146.89	2
s208	94.09	495.41	69.87	47.40	41.85	2
styr	2733.03	4406.71	1772.50	1138.20	882.29	2
tma	436.33	346.73	313.87	155.84	126.71	2
sand	1307.82	1307.82	888.12	419.30	332.40	3
s420	76.89	495.41	65.30	38.11	32.99	4
s510	416.91	416.91	192.44	100.06	76.60	4
s820	1189.16	964.23	563.39	240.91	180.48	4
s832	1150.78	1075.98	652.18	250.38	179.98	4
Total	30,285.77	36,295.13	16,766.68	10,481.70	8538.73
Percentage,%	354.69	425.06	196.36	122.75	100.00

Let us analyze the experimental data taken from reports of Vivado. These tables contain the following data: (1) the LUT counts (Table 8); (2) the minimum time of cycle (Table 9); (3) the total On-Chip Power (Table 10); (4) the area-time products (Table 11); (5) the area-time-power products (Table 12). In addition, we compared each of the characteristics for each category; however, in order to avoid a significant increase in the size of the article, we did not show the corresponding tables. We just showed the results of these comparisons.

As follows from Table 8, the $M{P}_{C}Y$–based FSMs require fewer LUTs than it is for other investigated counterparts. Using the proposed approach, we can obtain circuits having 52.19% less 6-LUTs than it is for equivalent Auto–based FSMs; 77.1% less 6-LUTs than for equivalent one-hot–based FSMs; 25.34% less 6-LUTs than for equivalent JEDI–based FSMs. Our approach produces circuits having on average 11.36% less 6-LUTs than the circuits of $MPY$-FSMs.

Using Table 8, we can compare LUT counts for different categories of benchmark FSMs. Comparing the results for category 0 shows that both multi-level approaches ($MPY$ and $M{P}_{C}Y$) lose out to the other methods. This loss is 30.4% compared to auto-based FSMs, 3.4% compared to one-hot-based FSMs, and 31.5% compared to JEDI-based FSMs. We explain this by the fact that condition (4) is not satisfied for benchmark FSMs of the category 0. This means that only a single LUT is needed to implement any function for systems (1) and (2). Obviously, for category 0, the replacement of inputs should not be performed for both $MPY$ and $M{P}_{C}Y$ FSMs; however, the encoding of output collections is always performed for these multi-level FSMs. Due to this, for the category 0, the multi-level FSMs have higher LUT counts than they are for other investigated design methods. Let us point out, that equivalent $MPY$- and $M{P}_{C}Y$-FSMs have the same LUT counts for this category.

Starting from category 1, the condition (4) is met. At the same time, it makes sense to use structural reduction methods instead of methods of functional decomposition. For this category, using the complex state codes in $MPY$ FSMs allows obtaining FSM circuits with fewer LUTs than it is for other methods used in our experiments. This gain is 40.0% compared to auto-based FSMs, 81.1% compared to one-hot-based FSMs, 16.2% compared to JEDI-based FSMs, and 11.0% compared to $MPY$ FSMs.

As follows from this part of research, the winnings increase with the increase in the category number. The gain in LUTs increases up to 65.64% (for categories 2–4) compared to auto-based FSMs. The gain increases up to 65.64% (for categories 2–4) compared to one-hot-based FSMs. Comparison with JEDI-based FSMs shows that the gain increases up to 34.86% (for categories 2–4). At last, compared to $MPY$-based FSMs, the gain increases from 8.44% (for categories 0–1) to 12.73% (for categories 2–4).

As follows from Table 9, the $M{P}_{C}Y$-based FSMs are faster than their investigated counterparts. They require a cycle time 9.39% less than the equivalent auto-based FSMs, 10.24% less than one-hot-based FSMs, and 1.08% less than the equivalent JEDI-based FSMs. win 18.73%. They also marginally benefit (0.31%) in relation to $MPY$ FSMs. It follows from this that our approach allows reducing the number of LUTs without losing performance. As we have already noted, this is the greatest challenge associated with the optimization of chip area occupied by an FSM circuit. So, our approach allows overcoming this obstacle.

Using Table 9, we have compared time characteristics for different categories of benchmark FSMs. Comparing the results for category 0 shows that $M{P}_{C}Y$-based FSMs lose out to the other methods. This loss is 3.23% compared to auto-based FSMs, 0.2% compared to one-hot-based FSMs, 3.68% compared to JEDI-based FSMs, and 1.13% compared to $MPY$-based FSMs. As it is for LUT counts, we explain this by the fact that condition (4) is not satisfied for benchmarks of this category. Starting from category 1, the condition (4) is met. This allows obtaining some gain compared to FSMs based on both Auto (3.48%) and one-hot (3.37%); however, other models provide better performance than our approach (3.84% compared to JEDI and 1.93% compared to $MPY$).

Starting from the category 2, our approach gives better results compared to all other investigated methods. This gain for the category 2 is the following: (1) 24.17% compared to Auto; (2) 25.96% compared to one-hot; (3) 8.88% compared to JEDI; (4) 3.78% compared to $MPY$ FSMs. For the category 3, the gain increases. It is the following: (1) 31.49% compared to Auto; (2) 31.49% compared to one-hot; (3) 20.24% compared to JEDI; (4) 4.76% compared to $MPY$ FSMs. Further, there is a gain for category 4; however, the gain is less than for category 3. It is the following: (1) 18.73% compared to Auto; (2) 16.48% compared to one-hot; (3) 7.96% compared to JEDI; (4) 3.07% compared to $MPY$ FSMs. We explain this decrease in winnings by an increase in the number of levels in the circuits of $M{P}_{C}Y$-based FSMs compared to their number for category 3; however, the following conclusion can be drawn: the proposed approach allows obtaining faster LUT-based FSM circuits starting from category 2.

The Vivado provides us by information about the total on-chip power. We combine these reports in Table 10. As follows from Table 10, the $M{P}_{C}Y$-based FSMs consume less energy than their investigated counterparts. On average, they provide the following gain in power consumption: (1) 47.02% compared to auto-based FSMs; (2) 59.17% compared to one-hot-based FSMs; (3) 23.96% compared to JEDI-based FSMs; (4) 5.44% compared to $MPY$ Mealy FSMs.

Using Table 10, we have compared total on-chip power for each category. Comparing the results for category 0 shows that $M{P}_{C}Y$-based FSMs lose out to the other methods. This loss is 19.37% compared to auto-based FSMs, 17.6% compared to one-hot-based FSMs and 21.08% compared to JEDI-based FSMs. The same data are correct for $MPY$ FSMs; however, starting from the category 1, our approach allows designing circuits consuming less power. The winnings grow as the category number grows. With respect to auto-based FSMs, our method provides the following gain: (1) 33.95% for the category 1; (2) 85.68% for the category 2; (3) 106.28% for the category 3; (4) 124.46% for the category 4. With respect to one-hot-based FSMs, our method provides the following gain: (1) 47.22% for the category 1; (2) 98.26% for the category 2; (3) 106.28% for the category 3; (4) 163.44% for the category 4. With respect to JEDI-based FSMs, the proposed method provides the following gain: (1) 19.69% for the category 1; (2) 43.98% for the category 2; (3) 77.38% for the category 3; (4) 80.97% for the category 4. Further, there is the following gain compared to $MPY$-based FSMs: (1) 5.20% for the category 1; (2) 7.58% for the category 2; (3) 10.77% for the category 3; (4) 12.36% for the category 4. So, the proposed organization of the FSM circuit allows reducing the power consumption, starting with simple FSMs (category 1).

Using data from Table 8, Table 9 and Table 10, we can calculate the values for two integral characteristics. One of them is an area-time product [6,38], the second is an area-time-power product. The smaller the values of these products, the better the quality of the resulting FSM circuit [6]. As it is the case in many articles [6,38], we estimate the area of an FSM circuit by its LUT count.

As follows from Table 11, the $M{P}_{C}Y$-based FSMs have better area-time characteristics than their investigated counterparts. On average, they provide the following gain: (1) 84.13% compared to auto-based FSMs; (2) 113.34% compared to one-hot-based FSMs; (3) 33.41% compared to JEDI-based FSMs; (4) 13.53% compared to $MPY$ Mealy FSMs. Using Table 11, we have compared area-time characteristics for each category of benchmark FSMs. As in the previous cases, for category 0 our approach gives the worst results; however, starting from category 1, the benefits of our approach are steadily increasing.

Comparing the results for category 0 shows that $M{P}_{C}Y$-based FSMs lose out to the other methods. This loss is 31.8% compared to auto-based FSMs, 2.88% compared to one-hot-based FSMs, 33.33% compared to JEDI-based FSMs, and 1.1% compared to $MPY$ FSMs; however, starting from category 1, our approach allows designing circuits having smaller values of area-time products than they are for all other approaches. With respect to auto-based FSMs, our method provides the following gain: (1) 46.49% for the category 1; (2) 107.13% for the category 2; (3) 90.73% for the category 3; (4) 141.9% for the category 4. With respect to one-hot-based FSMs, our method provides the following gain: (1) 88.39% for the category 1; (2) 139.36% for the category 2; (3) 90.73% for the category 3; (4) 148.74% for the category 4. With respect to JEDI-based FSMs, the proposed method provides the following gain: (1) 11.42% for the category 1; (2) 45.42% for the category 2; (3) 50.63% for the category 3; (4) 61.03% for the category 4. Further, there is the following gain compared to $MPY$-based FSMs: (1) 8.74% for the category 1; (2) 16.92% for the category 2; (3) 13.88% for the category 3; (4) 18.75% for the category 4. So, the proposed organization of the FSM circuit allows reducing the values of area-time products, starting with simple FSMs (category 1).

As follows from Table 12, the $M{P}_{C}Y$-based FSMs have much smaller values of area-time-power products than they are for their investigated counterparts. On average, they provide the following gain: (1) 254.69% compared to auto-based FSMs; (2) 325.06% compared to one-hot-based FSMs; (3) 96.36% compared to JEDI-based FSMs; (4) 22.75% compared to $MPY$ Mealy FSMs. Using Table 12, we have compared area-time-power products for each category of benchmark FSMs. As in the previous cases, for category 0 our approach gives the worst results; however, starting from category 1, the benefits of our approach are steadily increasing.

Comparing the results for category 0 shows that $M{P}_{C}Y$-based FSMs lose out to the other methods. This loss is 45.51% compared to auto-based FSMs, 10.12% compared to one-hot-based FSMs, 48.69% compared to JEDI-based FSMs, and 1.13% compared to MPY FSMs; however, starting from category 1, our approach allows designing circuits having smaller values of area-time-power products than they are for all other approaches. With respect to auto-based FSMs, our method provides the following gain: (1) 104.39% for the category 1; (2) 301.21% for the category 2; (3) 293.45% for the category 3; (4) 502.86% for the category 4. With respect to one-hot-based FSMs, our method provides the following gain: (1) 194.34% for the category 1; (2) 376.56% for the category 2; (3) 293.45% for the category 3; (4) 528.13% for the category 4. With respect to JEDI-based FSMs, the proposed method provides the following gain: (1) 36.51% for the category 1; (2) 112.16% for the category 2; (3) 167.19% for the category 3; (4) 213.43% for the category 4. Further, there is the following gain compared to $MPY$-based FSMs: (1) 15.65% for the category 1; (2) 25.71% for the category 2; (3) 26.14% for the category 3; (4) 33.91% for the category 4. So, the proposed organization of the FSM circuit allows reducing the values of area-time-power products, starting with simple FSMs (category 1).

The main goal of the proposed approach is the reducing LUT counts in FPGA-based circuits of Mealy FSMs. The results of experiments (Table 8) show that this goal has been achieved. Obviously, this gain is achieved by using complex state codes in $MPY$ FSMs. Using these codes leads to introducing an additional level of LUTs forming the partial functions. It was natural to expect that the introduction of this additional level would lead to a decrease in performance; however, as follows from Table 9, our approach leads to slower FSM circuits only for FSMs from categories 0–1. As the complexity of FSMs increases, our approach begins to give a win in terms of minimum cycle time. Moreover, the proposed approach allows reducing the power consumption of resulting FSM circuits (starting from the category 1). The same is true for the integral characteristics of FSM circuits (the area-time and area-time-power products). These phenomena are positive side effects associated with our approach.

So, the results of our experiments show that the proposed approach can be used instead of other models starting from the simple FSMs (category 1). Our approach allows improving LUT counts starting from the simple FSMs. The same is true for the power consumption. Further, starting from the category 2, the proposed method allows improving the minimum cycle time compared with other investigated methods. In our research, we use the chip xc7vx690tffg1761-2 by Virtex-7 (Xilinx); however, this chip has no unique architecture of CLBs. This very architecture of CLBs is used in all chips of the 7th generation of Xilinx chips. Due to this, the results of our experiments show that the proposed approach can be used for improving LUT counts for designs based on any FPGA chip of the 7th generation. Moreover, all Xilinx FPGA families have one fundamental property in common: an extremely limited number of LUT inputs. This leads to the need to develop FSM synthesis methods aimed at reducing the influence of this factor on the characteristics of the LUT-based FSM circuits. The results of our research show that the proposed method allows solving this problem better than some well-known methods combining various approaches of state assignment (auto, one-hot, and JEDI) and functional decomposition, as well as our previous method based on structural decomposition ($MPY$ FSMs).

7. Conclusions

Modern FPGA chips include more than 7.5 billion transistors [8]. They have proved to be a very effective means of implementing a variety of digital systems. There is a serious drawback inherent in FPGAs, namely, a rather small number of LUT inputs. This leads to the need of using various methods of functional decomposition under the design of LUT-based FSM circuits. As a result, the LUT-based circuits of rather complex FSMs are presented in the form of multi-level networks with a complex system of spaghetti-type interconnections [2]. This disadvantage can be overcome due to applying methods of structural decompositions [2,35]. This leads to FSM circuits with predicted number of levels and regular systems of interconnections [2].

Our research [2,35] shows that SD-based Mealy FSM circuits have better characteristics than their FD-based counterparts. As a rule, the combined use of methods of SD allows obtaining a greater gain in the number of LUTs than from the use of each of these methods separately [2]. In [11], we proposed to use two methods of SD, namely, the replacement of inputs and encoding of collections of outputs; however, even in this case, some parts of the resulting FSM circuits can have more than a single level of LUTs. In this article, we discuss just such a case.

To diminish the number of LUTs and their levels, we use the ideas [17]. These methods are based on finding a partition of states by classes of compatible states; however, in contrast to the known methods [17], we have replaced known extended state codes by the complex state codes, which have not been known before. The complex state codes are represented by concatenations of class codes and the codes of FSM states as elements of these classes. This approach leads to four-level FSM circuits, which require fewer LUTs than their counterparts based on methods [11]. There is a gain in the LUT count around 11.36% relative to three-level $MPY$ FSM circuits [11]. Moreover, our approach provides a very small increase in the FSM performance (on average, only 0.31%) and a decrease in the power consumption (on average by 5.79%) for the benchmarks from the library [36]. In our opinion, the proposed method can be applied instead of LUT-based MPY Mealy FSMs.