Heuristic Strategy of Service Function Chain Deployment Based on N-Base Continuous Digital Coding in Network Function Virtualization Environment

Abstract

As a novel network architecture, network function virtualization (NFV) greatly improves the flexibility and scalability of service provision. Deploying the service function chain (SFC) in an NFV environment needs to coordinate the instantiation of the virtual network function descriptor, network function embedding, and traffic steering, which also improves the complexity of the problem. Although heuristic algorithms are widely used to optimize this problem, due to the lack of complete SFC deployment solution space and digital coding scheme, the time complexity of the algorithm is difficult to meet the requirements. Therefore, this paper studies the digital coding scheme of the heuristic SFC deployment to improve time efficiency without reducing performance. Firstly, we model the SFC deployment as a 0–1 integer linear programming, considering the above factors, and then design a continuous digital solution space construction scheme based on N-Base coding (NBACO-SS) to optimize the above problems. NBACO-SS uses integer size and carry to map the complex SFC deployment to simple digital coding, evaluates the continuity of solution space through the Manhattan distance, and optimizes the continuity through the ant colony algorithm. Based on NBACO-SS, we reconstruct two heuristic algorithms to solve the SFC deployment problem. Experimental results demonstrate that NBACO-SS can improve the time efficiency by 20% without reducing the total network service traffic.

1. Introduction

Network function virtualization (NFV) [1] is a novel network architecture, which decouples software and hardware, and realizes the network functions originally realized by expensive special hardware with virtualization technology on the commercial server (such as the firewall, WAN accelerator, and traffic Monitor), which is called virtual network function (VNF). This new network architecture makes the deployment of network services more flexible and scalable and greatly reduces the capital expenditure and operative costs of network operators. Although NFV provides great flexibility for service deployment, network operators face some new challenges in deploying and managing user services. Generally, user service traffic needs to pass through a set of network functions in an orderly way and is defined as a service function chain (SFC) [2]. SFC deployment in the NFV environment needs to coordinate the resource allocation of instantiated VNF (selecting appropriate the virtual network function descriptor), network function embedding, and traffic routing between VNFs. How to realize fast, scalable, and flexible SFC deployment is a new challenge; this problem has proved to be an NP-hard problem [3].

To optimize the above SFC deployment problem and find a near-optimal solution in a reasonable time, many scholars have established the mathematical model of SFC deployment [4,5,6,7,8,9,10,11,12,13], and designed heuristic solutions (individual-based [14,15,16,17,18,19], population-based [20,21,22,23], and others [24,25,26,27,28,29,30,31,32,33]). However, most of these models ignore the constraints of computer architecture on hardware resource allocation; that is, VNF cannot be instantiated with resources of any size, but need to meet certain specification constraints. These resource specifications are pre-defined in the virtual network function descriptor (VNFD) [34], and the types of VNFDs that service providers can provide are limited for effective management. At the same time, the description of the underlying network resources, service delay, and traffic routing in these SFC deployment models is not perfect. For example, user delay and traffic processing scalability of VNF are not considered in [4,5,6], and the optimization objective also lacks the consideration of resource competition among different users. On the other hand, heuristic algorithms are used to optimize the SFC deployment problem, which can effectively reduce the time complexity. However, these schemes only combine the local optimization avoidance strategy of heuristic algorithms with the deployment of SFC, and the lack of systematic analysis of SFC deployment solution space and the corresponding digital-domain mapping scheme. Therefore, the operations, such as instantiation VNFD selection, network function embedding, and traffic routing cannot be described abstractly, which makes the algorithm design complex. At the same time, the size of neighborhood space cannot be accurately judged in the search process, or described with concise digital operations, so that the time complexity cannot be further improved.

In this paper, a mathematical model of SFC deployment considering multiple factors is established. Based on the model, the digital coding strategy of SFC deployment is studied, and a complete and continuous digital domain solution space is constructed to further improve the efficiency of the heuristic algorithm. The contributions of this paper are summarized as follows:

• We make an in-depth analysis on the problems of instantiation VNFD selection, network function embedding, and traffic steering in SFC deployment, and establish a 0–1 integer linear programming (ILP) model considering the above factors. The goal of the model is to maximize the total network service traffic. The problem is proved to be an NP-hard problem by reducing it to a knapsack loading problem.
• We analyze the solution space of the SFC deployment problem in detail and design a continuous digital solution space construction scheme based on N-Base coding (NBACO-SS). By using integer size and carry, the complex SFC deployment is abstracted and mapped to a simple digital domain coding, and the continuity of solution space is evaluated by Manhattan distance. The problem is compared with the traveling salesman problem (TSP), and an ant colony algorithm is used to optimize the continuity of solution space and make it close to the theoretical optimum. We also reconstruct an affinity-based simulated annealing deployment algorithm and a tabu search deployment algorithm, based on NBACO-SS.
• Through extensive experiments, we prove that NBACO-SS can effectively improve the continuity of solution space and approach the theoretical optimization when the solution space is small. At the same time, the reconstructed heuristic SFC deployment strategies can improve the time efficiency by about 20% without reducing the total network service traffic. We also obtain the optimal number of service traffic steering paths in distributed network architecture.

The rest of this paper is structured as follows. Section 2 reviews the related work. Then, Section 3 formulates the mathematical model of SFC deployment. Section 4 describes the proposed NBACO-SS method and two reconstructed heuristic algorithms, and Section 5 discusses the test scenarios and evaluation of the proposed algorithm. Finally, the paper is summarized in Section 6.

2. Related Work

The related work falls into the following two categories: (1) SFC deployment mathematical model and (2) heuristic algorithm for SFC deployment optimization.

2.1. SFC Deployment Mathematical Model

SFC is an important use case of the NFV scenario [35], and its deployment is also one of the major challenges in the research of NFV [36]. Many scholars have studied the deployment of SFC and established mathematical models. Aiming at minimizing the consumption of network bandwidth resources and improving bandwidth utilization, a mathematical model is established for the placement of VNF and traffic steering of SFC in [4,5]. In the model, the constraints of node calculation, memory resources, link bandwidth capacity, and SFC traffic traversal sequence are considered. In [6], aiming at maximizing the total service traffic, the virtual network function placement and routing path selection of SFC were studied, and the SFC deployment model was established considering the resource constraints, such as link, VNF, and VM, etc., and it was proved to be an NP-hard problem by reducing the model to a EDP problem. However, the above model simplifies the VNF, does not consider the scalability of VNF for traffic processing, and ignores the user service delay limit [7]. Considering the transmission delay between data centers and minimizing the total delay of SFC, a mixed-integer linear programming (MILP) model is established, and it is transformed into a linear programming model by the restriction of decision variables. In [8], aiming at minimizing the total delay of SFC, the similarity between SFC and the shortest path tour problem is studied, and two novel ILP models are established for the service path and function placement based on the proposed augmented network. The author of [9] studied the SFC deployment problem in the environment of time-varying workloads and basic resource consumption of VNF instantiation, and established the ILP model to minimize the number of physical machines used. The author of [10] studied the differentiated routing and load balancing of SFC requests with different types of traffic. Aiming at minimizing the resource consumption cost of SFC requests, a binary linear programming model considering the constraints of bandwidth, flow table, CPU and delay was established. The above models assume that the network functions of SFC can only be deployed on one VNF. Considering the multi-instance deployment problem of SFC, the mixed-integer programming model and linear programming model are established respectively in [11,12] for the selection and mapping of VNFs and the traffic steering between upstream and downstream. In [13], the scheduling of VNF was studied, and a MILP model was established which includes three stages: network function mapping, traffic routing, and service schedule; a linear programming lower bound and an ILP upper bound of the MILP model are given by the column generation method.

The above model does not consider the differences of the underlying resource requirements of instantiating different VNFD templates of the same type of VNF; however, in the real NFV environment, VNF instantiation has such resource constraints that the integrity of the model is defective.

2.2. Heuristic Algorithm for SFC Deployment Optimization

The SFC deployment problem is an NP-hard problem. Heuristic algorithms are usually used to obtain a near-optimal solution in an acceptable time. Many scholars have designed heuristic optimization schemes for this problem.

In terms of individual-based heuristic algorithm design, [14], firstly, compares the advantages and disadvantages of the heuristic algorithm and greedy algorithm in the online mapping and scheduling of VNF, and the performance of three greedy algorithms and a tabu search algorithm is analyzed. In [15], an affinity-based simulated annealing algorithm (ABSA) is proposed to minimize the delay of SFC by deploying network functions on the same underlying node as much as possible and finding the optimal solution through the simulated annealing algorithm. The authors of [16,17] also used the tabu search algorithm to optimize the VNF management and migration in the large-scale distributed NFV environment and designed a variety of basic neighborhood operations, and they achieved effective performance improvement. The simulated annealing heuristic algorithm is used to optimize the delay and bandwidth consumption of SFC deployment in [18], and two neighborhood update strategies of randomly selecting or exchanging the deployment location of Middlebox are designed. Compared with the benchmark algorithm, the end-to-end delay and bandwidth consumption are reduced by 22% and 38%. The authors of [19] aimed at the embedding problem of SFC and used the tabu search algorithm to optimize the bandwidth occupation of the network resources. The algorithm obtains the neighborhood by randomly changing the deployment location of VNF, which improves the acceptance rate of service requests. The above heuristic deployment algorithms do not consider the digital coding mapping strategy.

The population-based heuristic algorithm is also widely used in SFC deployment. The authors of [20] aimed at the problem of content caching and service provision in the fog network in order to optimize the function mapping and virtual content placement; an ant colony-based heuristic algorithm is proposed to reduce the time complexity of this NP-hard problem. The authors of [21] proposed a multi-objective service path construction algorithm based on discrete particle swarm optimization (MOPSO); a particle position initialization and update strategy (PIFC) is proposed based on the further study of the evaluation criteria of candidate nodes and paths, which accelerated the convergence speed of the program. The algorithm optimizes the quality of service paths and improves the success rate of service path construction and long-term average revenue. To solve the problem of VNF placement in a network function virtualization environment, in [22], an integer-coding gray wolf optimizer algorithm was designed considering the constraints of computing, storage, IO, and bandwidth resources of the underlying network. By assigning integer numbers to the underlying nodes, the deployment positions of service functions on the underlying nodes are coded as the gray wolf positions, and a new location update strategy of the wolf group was proposed. The scheme minimizes the end-to-end delay of SFC deployment and achieves better fitness than other heuristic algorithms. The author of [23] decomposes the dynamic VNF deployment problem into SFC scheduling and mapping sub-problems, establishes a dynamic scheduling model of second-order queue, and proposes a dynamic VNF placement algorithm consisting of two genetic algorithms to optimize the above problems. In the algorithm, the gene position of the chromosome is encoded as the number of VNF for each type. The above heuristic algorithms use some simple digital mapping strategies, but ignore the continuity and size of solution space and simplify the routing of traffic.

In addition to the above general heuristic algorithms, there are other heuristic algorithms to optimize the deployment of SFC. A heuristic algorithm is proposed to coordinate the composition and embedding of SFC (CoordVNF) in [24,25]. CoordVNF adopts the concept of backtracking to recursively find an effective embedding scheme [5]. Aiming at the problem of SFC deployment and path selection, a heuristic scheme based on the longest function allocation sequence is proposed to optimize the VNF reuse and bandwidth resource saving. This scheme can reduce the number of deployed VNFs and link bandwidth requirements, and serve more requests than other algorithms. The author of [26], aiming at the problem of cross-domain SFC partition and service sub-chain mapping, proposed a Viterbi heuristic algorithm, which can dynamically change the emission probability to obtain the near-optimal solution of minimizing the end-to-end delay of SFC deployment in large-scale networks. In [27], a Viterbi heuristic strategy is also proposed to reduce the complexity of VNF migration, determine the best migration strategy, and reduce energy consumption. The above algorithm also does not consider the digital domain operation of heuristic service function chain deployment.

Heuristic algorithms are widely used in the research of SFC deployment to simplify the complexity of the problem. The heuristic strategy in the above design lacks a complete solution space and digital coding scheme for the SFC deployment problem, which makes the algorithm design complicated and the time complexity difficult to meet the requirements.

3. System Model and Problem Description

The SFC deployment model in the NFV scenario is shown in Figure 1, which is divided into three layers: network function virtualization infrastructure (NFVI), virtual network function, and user service. Three factors are considered in the model: the selection of instantiation VNFD on NFVI, the mapping of the user network function, and the selection of the traffic steering path. Table 1 summarizes the notations used in this paper.

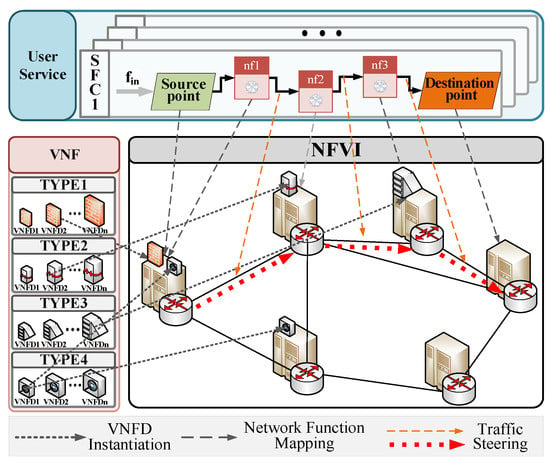
Figure 1. The overall system model of service function chain deployment.

Table 1. Notations in the paper.

Function	Notation	Definition
NFVI	$G^S=(N^S,E^S)$	Network function virtualization infrastructure, consisting of physical nodes and physical links
	$n_i^s$$, e_{ij}^s$	$\mathrm{A} \mathrm{physical} \mathrm{node} \mathrm{and} \mathrm{a} \mathrm{physical} \mathrm{link} \mathrm{connecting} \mathrm{nodes} n_i^s$$\mathrm{and} n_j^s$
	$ca{p}^r\left(n_i^s\right)$	$\mathrm{Number} \mathrm{of} \mathrm{resources} \mathrm{of} \mathrm{type} \mathrm{r} \mathrm{contained} \mathrm{by} \mathrm{node} n_i^s$
	$bw(e_{ij}^s)$$, delay(e_{ij}^s)$	$\mathrm{Bandwidth} \mathrm{and} \mathrm{transmission} \mathrm{delay} \mathrm{of} \mathrm{link} e_{ij}^s$
VNF	$F$$, f_i\in F$	A collection of VNF types and a specific type of VNF
	$coef{f}^r( f_i)$$, ratio( f_i)$	Resource demand coefficient and traffic-scaling factor of VNF type $f_i$
	$f_{\mathrm{j}}^k$	$k$-th $\mathrm{VNFD} \mathrm{of} \mathrm{VNF} \mathrm{type} f_j$
	$re{s}^r(f_j^k)$	$\mathrm{Number} \mathrm{of} \mathrm{resources} \mathrm{of} \mathrm{type} r$ needed to instantiate the VNFD
User Service	$G^V$$, G_j^V=\left(N_{{}^j}^V,E_{{}^j}^V\right)$	User service requirements and a specific user service SFC j
	$\{S_j,n_{j1}^v,n_{j2}^v,\cdots ,n_{ji}^v,\cdots ,D_j\}$	The source, network function set, and destination node of SFC j.
	$n_{j0}^v, n_{j(\left|N_{{}^j}^V\right|-1)}^v$	Another representation of source node and target node of SFC j
	${\mu }_{ji}^l$	$\mathrm{Whether} n_{ji}^v$$\mathrm{needs} \mathrm{a} \mathrm{VNF} \mathrm{of} \mathrm{type} f_l$
	${\mathrm{e}}_{ji}^v\in E_{{}^j}^V\left(0\le i<\left|E_{{}^j}^V\right|\right)$	$\mathrm{The} \mathrm{virtual} \mathrm{link} \mathrm{connecting} \mathrm{network} \mathrm{function} n_{ji}^v$$\mathrm{and} n_{j(i+1)}^v$
	$F(G_{{}^j}^V)$$, D(G_{{}^j}^V)$	Traffic requirements and delay limits of an SFC
	$re{s}^r(n_{ji}^v)$$, traffic({\mathrm{e}}_{ji}^v)$	Resource requirements of SFC
	$M=\left|G_j^V\right|-2$	The number of network functional requirements in an SFC
Traffic Steer	$\mathsf{\Gamma }$	The path set of all nodes in the network
	${\tau }_{pq}$$, {\tau }_{pql}$$, {\tau }_{{}_{pql}}^z$	$\mathrm{The} \mathrm{path} \mathrm{set} \mathrm{between} \mathrm{nodes} n_p^s$$\mathrm{and} n_q^s$, l-th $\mathrm{path} \mathrm{in} \mathrm{the} \mathrm{set} \mathrm{and}$ z-th node on the path
	${\sigma }_{pql}^{ij}$	$\mathrm{Whether} {\tau }_{pql}$$\mathrm{contains} \mathrm{the} \mathrm{adjacent} \mathrm{path} e_{ij}^s$
	$D\left({\tau }_{pql}\right)$$, N_l$	$\mathrm{Delay} \mathrm{and} \mathrm{number} \mathrm{of} \mathrm{nodes} \mathrm{of} \mathrm{the} \mathrm{routing} \mathrm{path} {\tau }_{pql}$
Decision variable and the Algorithm	${\eta }_i^{jk}$$, {\chi }_{ji}^p$$, {\gamma }_{ji}^{pql}$	Binary decision variable
	$\mathsf{\Phi }$	The total deployment traffic
	$z_1{z}_2\cdots z_M$	M-Bit N-Base number
	$Z=\{Z_1,Z_2,\cdots ,Z_i,\cdots \}$	All deployment schemes of an SFC in a single routing link
	$D(Z)$	The sum of Manhattan distances between digital coding schemes

3.1. Network Function Virtualization Infrastructure (NFVI)

The NFVI is modeled as an undirected graph $G^S=(N^S,E^S)$, where $N^S$ represents the set of physical nodes and $E^S$ represents the set of physical links. For the consistent network architectures of multi-access edge computing (MEC) and distributed data centers, each node, $n_i^s\in N^S$, has the same type and contains switching and forwarding capabilities. $R$ represents the resources set contained by physical nodes, such as CPU, MEMORY, and STORAGE. For any resource, $r\in R$ and $ca{p}^r\left(n_i^s\right)$ represent the number of resources of type $r$ contained by node $n_i^s$. $e_{ij}^s\in E^S$ represents a physical link between the adjacent nodes $n_i^s, n_j^s$, and $bw(e_{ij}^s)$; $delay(e_{ij}^s)$ represents the bandwidth and transmission delay of link $e_{ij}^s$ [37,38]. It is assumed that the internal bandwidth of the same node is large enough to support the internal business requirements of the node without considering the internal delay of the node [6].

3.2. Virtual Network Function (VNF)

VNFs are defined as a software entity that implements different traffic processing functions on NFVI. VNF can be instantiated in the form of a virtual machine for higher resource independence or as a container virtualization for greater flexibility [39], both of which will occupy NFVI node resources. $F$ represents a collection of VNF types, and $f_i\in F$ represents a specific type of VNF, which can provide a specific traffic processing service (such as a firewall). Considering the difference in resource consumption of data packets processed by different types of VNFs, we assume a linear relationship between traffic and required resources [7] and use the resource demand coefficient $coef{f}^r( f_i)$ to represent the resource consumption capacity of different VNFs, that is, for any size of traffic $t_{\mathrm{in}}$, the required resource $c_r$ of type $r$ and of VNF $f_i$, is demonstrated in (1).

$$c_r=coef{f}^r(f_i)\cdot t_{\mathrm{in}}\hspace{1em}\hspace{1em}(r\in R),$$

(1)

Considering the packet processing methods of different VNF, such as the adding and deleting of headers, compression of redundant data, and discarding part of data packets, these will change the size of traffic [40]. $ratio( f_i)$ is defined as the traffic scaling factor of VNF $f_i$; the traffic size after the $f_i$ processing is shown in (2).

$$t_{\mathrm{out}}=ratio( f_i)\cdot t_{\mathrm{in}},$$

(2)

Considering the limitation of computer hardware resource architecture, VNF can only be instantiated with specific resources (for example, 2 CPU cores and 4G memory; 2.1 CPU and 4.1G memory are usually not allowed). The VNFD regulates the occupation limit of VNF to the underlying resources. Through VNFD, a VNF with a specific size can be instantiated on the underlying node. For effective management, the number of VNFD types provided by the data center is also limited. $f_{\mathrm{j}}^k$ is the $k$-th VNFD of VNF type $f_j$, and $re{s}^r(f_j^k)$ is the number of resources of type $r$ needed to instantiate the template. It is assumed that there is at most one VNF of the same type on a physical node and the remaining resources in the VNF instance can be shared by different users with the same type of service function requirements [24,27], but the total service demand resources cannot exceed the total VNF resources to ensure service QoS and resource security.

3.3. User Service

User service requirements can be represented by a set of SFCs $G^V$, where $G_j^V\in G^V$ represents the $j$-th SFC, which includes source, target nodes, and a group of ordered network functions, and can be represented by a directed graph, $G_j^V=\left(N_{{}^j}^V,E_{{}^j}^V\right)$. $N_j^V=\{S_j,n_{j1}^v,n_{j2}^v,\cdots ,n_{ji}^v,\cdots ,D_j\}$ represents the source, network function set, and destination node of SFC $j$. For convenience, $n_{j0}^v, n_{j(\left|N_{{}^j}^V\right|-1)}^v$ are used to represent the source and destination node. $E_j^V$ represents the virtual link set connecting the network function. In node set $N_j^V$, $n_{ji}^v$$(1\le i<\left|N_{{}^j}^V\right|-1)$ means that traffic needs to pass through the $i$-th network function, and it needs to be mapped to only one VNF of type $f(n_{ji}^v)\in F$, and ${\mu }_{ji}^l$ means whether $n_{ji}^v$ needs a VNF of type $f_l$. ${\mathrm{e}}_{ji}^v\in E_j^V\left(0\le i<\left|E_{{}^j}^V\right|\right)$ is the virtual link connecting the network function $n_{ji}^v$ and $n_{j(i+1)}^v$. For any SFC $G_j^V$, $F(G_j^V)$ and $D(G_j^V)$ represent the traffic requirements and delay limits. Therefore, according to the type of network functions and the size of traffic required by the SFC, the formula for the bandwidth demand of the virtual link, ${\mathrm{e}}_{ji}^v$, is as follows:

$$traffic({\mathrm{e}}_{ji}^v)={\displaystyle \prod _{x=0}^{i}ratio( f(n_{jx}^v))\cdot F(G_{{}^j}^V)} (ratio( f(n_{j0}^v))=1),$$

(3)

Therefore, we can also get the demands of the network function, $n_{ji}^v$, for $r(r\in R)$ types of resources, as follows:

$$\begin{array}{ll}re{s}^r(n_{ji}^v)& =traffic({\mathrm{e}}_{j(i-1)}^v)\cdot k_{f(n_{ji}^v)}^r\\ & =k_{f(n_{ji}^v)}^r\cdot F(G_{{}^j}^V)\cdot {\displaystyle \prod _{x=0}^{i-1}ratio( f(n_{jx}^v))}\left(1\le i<\left|N^V\right|-1, \forall r\in R\right)\end{array}$$

(4)

3.4. Traffic Steer

The shortest path algorithm is most commonly used for the traffic steering of SFC. Although the shortest path can reduce service delay and save the network bandwidth, it has certain limitations. This paper models the traffic routing problem and considers multiple routing paths in the network. $\mathsf{\Gamma }=({\tau }_{11},{\tau }_{12},\cdots ,{\tau }_{pq},\cdots )$ is defined as the path set of all nodes in the network, ${\tau }_{pq}$ represents the path set between the nodes $n_p^s$ and $n_q^s$, which are arranged in a positive delay order, ${\tau }_{pql}$ is the $l$-th $(1\le l\le \left|{\tau }_{pq}\right|)$ path in the set, and ${\tau }_{{}_{pql}}^z$ is the $z$-th node on the path. Note that ${\tau }_{pql}$ is composed of a series of end-to-end adjacent paths. For the convenience of calculation, the binary variable ${\sigma }_{pql}^{ij}$ is defined to indicate whether ${\tau }_{pql}$ contains the adjacent path $e_{ij}^s$. For the traffic steering problem of SFC, all the above routing paths will be considered comprehensively. The delay formula of the routing path is referred to (5).

$$D\left({\tau }_{pql}\right)={\displaystyle \sum _{e_{ij}^s\in E^S}{\sigma }_{pql}^{ij}\cdot delay(e_{ij}^s)},$$

(5)

3.5. Decision Model and Optimization Objective

The SFC deployment problem can be regarded as the mapping of the SFC-directed graph set, $G^V$, on the undirected graph of the underlying network $G^S$ and the selection of the VNFD instantiation on the nodes under the requirements of service delay and traffic. Instantiating appropriate VNFD templates on nodes can meet the needs of user services and reduce resource fragmentation. The mapping of user services on the underlying network should not only consider the resource constraints of the underlying network but also coordinate the resource competition between SFCs. To sum up, this problem needs to consider the selection of instantiated VNFD, user service function mapping and traffic steering, and the resource competition among different SFCs. The above operations are usually realized by the NFV management and orchestration module (MANO); therefore, the implementation of the fast and flexible SFC deployment strategy can provide support for an efficient orchestrator. We establish the above problem as a 0–1 integer linear programming (0–1 ILP) model and define the Boolean decision variables ${\eta }_i^{jk}$, ${\chi }_{ji}^p$, and ${\gamma }_{ji}^{pql}$.

$${\eta }_i^{jk}=\{\begin{array}{l}1\hspace{1em}\hspace{1em}\mathrm{if} f_j^k \mathrm{is} \mathrm{instantiated} \mathrm{on} n_i^s\\ 0\hspace{1em}\hspace{1em}\mathrm{if} f_j^k \mathrm{is} \mathrm{not} \mathrm{instantiated} \mathrm{on} n_i^s\end{array},$$

(6)

$${\chi }_{ji}^p=\{\begin{array}{l}1\hspace{1em}\hspace{1em}\mathrm{if} n_{ji}^v \mathrm{is} \mathrm{mapped} \mathrm{to} n_p^s\\ 0\hspace{1em}\hspace{1em}\mathrm{if} n_{ji}^v \mathrm{is} \mathrm{not} \mathrm{mapped} \mathrm{to} n_p^s\end{array},$$

(7)

$${\gamma }_{ji}^{pql}=\{\begin{array}{l}1{\hspace{1em}\hspace{1em}\mathrm{if} \mathrm{e}}_{ji}^v \mathrm{is} \mathrm{mapped} \mathrm{to} {\tau }_{pql}\\ 0{\hspace{1em}\hspace{1em}\mathrm{if} \mathrm{e}}_{ji}^v \mathrm{is} \mathrm{not} \mathrm{mapped} \mathrm{to} {\tau }_{pql}\end{array},$$

(8)

${\eta }_i^{jk}$ indicates whether VNF with type and descriptor $f_j^k$ is instantiated on the physical node $n_i^s$, ${\chi }_{ji}^p$ indicates whether the $j$-th network function requirement $n_{ji}^v$ of SFC $G_j^V$ is mapped on the underlying node $n_p^s$, and ${\gamma }_{ji}^{pql}$ indicates whether the virtual link ${\mathrm{e}}_{ji}^v$ of SFC $G_j^V$ is routed through the link ${\tau }_{pql}$.

The optimization objective is to maximize the deployment traffic of user service under the condition of limited underlying network resources, so as to maximize the interests of service providers. Considering that the number of network functions required by the user SFC is different, and the traffic-scaling coefficient of different network functions is different, the total network traffic is defined as the total bandwidth of the virtual link, and the calculation formula is referred to in (9).

$$\begin{array}{ll}\hfill \mathsf{\Phi }& ={\displaystyle \sum _{G_j^V\in G^V}{\displaystyle \sum _{{\mathrm{e}}_{ji}^v\in E_{{}^j}^V}traffic({\mathrm{e}}_{ji}^v)}}\\ & ={\displaystyle \sum _{G_j^V\in G^V}{\displaystyle \sum _{{\mathrm{e}}_{ji}^v\in E_{{}^j}^V}{\displaystyle \prod _{x=0}^{i}ratio( f(n_{jx}^v))\cdot F(G_{{}^j}^V)}}}\end{array}$$

(9)

The above optimization objectives not only consider the user service traffic requirements, but also consider the number and type of network function required, which effectively prevents the service requirements containing less network functions from being preferentially deployed. Therefore, the optimization objective of the SFC deployment problem is to maximize the total deployment traffic without violating the user service requirements and the underlying resource constraints:

$$\mathrm{maximize}\hspace{1em}\mathsf{\Phi },$$

(10)

Subject to:

(1) Each network function of SFC needs to be deployed on a physical node;

$${\displaystyle \sum _{n_p^s\in N^S}{\chi }_{ji}^p}=1 \forall G_j^V\in G^V, \forall n_{ji}^v\in N_j^V,$$

(11)

(2) Each virtual link of SFC needs to be mapped on a routing link;

$${\displaystyle \sum _{{\tau }_{pq}\in \mathsf{\Gamma }}{\displaystyle \sum _{{\tau }_{pql}\in {\tau }_{pq}}{\gamma }_{ji}^{pql}}}=1 \forall G_j^V\in G^V, \forall {\mathrm{e}}_{ji}^v\in E_j^V,$$

(12)

(3) At most one VNF of the same type can be instantiated on each node;

$${\displaystyle \sum _{f_{{}_j}^k\in f_j}{\eta }_i^{jk}}\le 1 \forall n_i^s\in N^S, \forall f_j\in F,$$

(13)

(4) Resource constraints of NFVI nodes;

$${\displaystyle \sum _{f_j\in F}{\displaystyle \sum _{f_{{}_j}^k\in f_j}re{s}^r(f_j^k)\cdot {\eta }_i^{jk}}}\le ca{p}^r(n_i^s) \forall n_i^s\in N^S, \forall r\in R,$$

(14)

(5) Bandwidth limitation of NFVI links;

$$\begin{array}{l}{\displaystyle \sum _{E_{{}^j}^V\in G^V}{\displaystyle \sum _{{\mathrm{e}}_{ji}^v\in E_{{}^j}^V}\left({\displaystyle \sum _{{\tau }_{pq}\in \mathsf{\Gamma }}{\displaystyle \sum _{{\tau }_{pql}\in {\tau }_{pq}}traffic({\mathrm{e}}_{ji}^v)\cdot {\sigma }_{pql}^{mn}\cdot {\gamma }_{ji}^{pql}}}\right)}}\\ \le bw(e_{mn}^s) \forall e_{mn}^s\in E^S\end{array}$$

(15)

(6) Resource limitation of VNFs;

$$\begin{array}{l}{\displaystyle \sum _{N_{{}^j}^V\in G^V}{\displaystyle \sum _{n_{ji}^v\in N_{{}^j}^V}re{s}^r(n_{ji}^v)\cdot }{\mu }_{ji}^l\cdot {\chi }_{ji}^p}\cdot \le {\displaystyle \sum _{f_{{}_l}^k\in f_l}re{s}^r(f_l^k)\cdot {\eta }_p^{lk}}\\ \forall n_p^s\in N^S, \forall f_l\in F, \forall r\in R\end{array}$$

(16)

(7) Delay limit of SFCs;

$${\displaystyle \sum _{{\mathrm{e}}_{ji}^v\in E_{{}^j}^V}{\displaystyle \sum _{{\tau }_{pql}\in {\tau }_{pq}}{\gamma }_{ji}^{pql}\cdot D\left({\tau }_{pql}\right)}}\le D(G_j^V) \forall G_j^V\in G^V,$$

(17)

(8) SFC deployment restriction; both ends of the virtual link mapping routing path must be the deployment location of the corresponding virtual node.

$$\begin{array}{l}{\displaystyle \sum _{m=1}^{\left|N^S\right|}{\displaystyle \sum _{l=1}^{\left|{\tau }_{pml}\right|}{\gamma }_{ji}^{pml}}}-{\displaystyle \sum _{m=1}^{\left|N^S\right|}{\displaystyle \sum _{l=1}^{\left|{\tau }_{mql}\right|}{\gamma }_{ji}^{mql}}}={\chi }_{ji}^{\mathrm{p}}-{\chi }_{j(i+1)}^q\\ \forall n_p^s,n_q^s\in N^S, \forall G_j^V\in G^V, \forall {\mathrm{e}}_{ji}^v\in E_{{}^j}^V\end{array}$$

(18)

The above SFC deployment model, considering the selection of instantiated VNFD, user service function mapping, and traffic routing, is a 0–1 ILP problem. By reducing it to a knapsack loading problem (KLP), it can be proved that this problem is an NP-hard problem (Theorem 1). Since it is very difficult to solve the above NP-hard problem, in the next section, a solution space composition scheme based on N-Base continuous digital coding is designed, and the SFC heuristic deployment algorithm is combined to solve the above problem.

Proof of Theorem 1.

The above SFC deployment problem is reduced to KLP to prove its NP-hard property. □

Each SFC $G_j^V$ in the service set is simplified to only need to go through a network function $n_{j1}^v$, and the type is $f_1\in F$. Meanwhile, the adjacent node bandwidth $bw(e_{ij}^s)$ of NFVI is set to infinity and the link delay $delay(e_{ij}^s)=0$. In this case, there is no need to consider the link bandwidth and delay constraints, and the only limiting factor is node resources. The above problem is simplified as loading $\left|G^V\right|$ boxes with the limit of $re{s}^r(n_{j1}^v)$ on the NFVI node $N^S$ to obtain the maximum traffic. The problem is simplified as a typical knapsack loading problem.

4. Heuristic SFC Deployment Algorithm Based on N-Base Continuous Digital Coding

Heuristic algorithms are one of the most effective methods to solve optimization problems, especially for large-scale scenes. Because of its strong search ability and the strategy of preventing local optimization, it can often get an acceptable solution in a relatively fast time. Based on the detailed study of the SFC deployment model and heuristic algorithm, this paper proposes a heuristic SFC deployment scheme based on N-Base continuous digital coding. In this scheme, the solution space of the SFC deployment problem is mapped to a group of N-Base codes in the digital domain, and the continuity of solution space is further improved through ant colony optimization. The solution realizes the deployment operation of SFC at the digital level, which can effectively improve the simplicity and speed of heuristic algorithms.

4.1. Construction of Continuous Solution Space Based on N-Base Coding and Ant Colony Optimization (NBACO-SS)

4.1.1. Solution Space Generation Scheme Based on N-Base Coding

Considering the deployment of SFC $G_j^V$ on the underlying network $G^S$, its network function requirements can only be mapped on the routing path set ${\tau }_{pq} (p,q={\displaystyle \sum _{n_m^s\in N^S}{\chi }_{j0}^m\cdot }{n}_m^s, {\displaystyle \sum _{n_m^s\in N^S}{\chi }_{j(\left|N_{{}^j}^V\right|-1)}^m\cdot }{n}_m^s)$. Because the traffic needs to pass through the network function set in turn, the deployment position of the network function on the underlying link is limited, and this restriction happens to be represented numerically. Define $M=\left|G_j^V\right|-2$, that is, the number of network functional requirements in the SFC, and $N_l=\left|{\tau }_{pql}\right|$ is defined as the number of physical nodes passing through the $l$-th path from the source node to the target node. Then the M-Bit N-Base number $z_1{z}_2\cdots z_M\left(0\le z_1\le z_2\cdots \le z_M\le N_{l-1}\right)$ represents a deployment scheme of $G_j^V$ on ${\tau }_{pql}$, and the corresponding decision relationship is as follows:

$$\{\begin{array}{l}{\chi }_{ji}^m=1\hspace{1em}(m={\tau }_{{}_{pql}}^{z_i})\\ {\gamma }_{ji}^{mnl}=1\hspace{1em}(m={\tau }_{{}_{pql}}^{z_i},n={\tau }_{{}_{pql}}^{z_{i+1}})\end{array}(1\le i\le M) ,$$

(19)

After all the SFCs deployment codes are determined, the decision variable ${\eta }_i^{jk}$ can be determined by choosing to instantiate the VNFD $f_j^k$, whose resources are larger than and closest to the needs on the node $n_i^s$.

By coding the natural number from 0 to $N^M-1$ according to the M-Bit N-Base number, we can get the set of all deployment schemes of SFC in a single routing link ${\tau }_{pql}$, and record it as $Z=\{Z_1,Z_2,\cdots ,Z_i,\cdots \}$, where $Z_i$ is the $i$-th deployment scheme of SFC. Algorithm 1 shows the calculation method of the N-Base coding solution space (NB-SS).

Figure 2 shows the solution space of $M=2$ and $N=3$. All deployment schemes $Z_1~Z_6$ can be obtained by counting from 0 to 8. We can see that carrying from low bit to high bit leads to certain discontinuity. For example, two network functions are moved in $Z_3\to Z_4$, and this discontinuity will affect the selection of neighbors. We use $D(Z)$ to represent the continuity of the deployment scheme set, and its value is the sum of Manhattan distances between digital coding schemes. The formula is as follows:

$$D(Z)={\displaystyle \sum _{i=1}^{\left|Z\right|-1}d(Z_{i-1},Z_i)} d(i,j) \mathrm{is} \mathrm{the} \mathrm{Manhattan} \mathrm{Distance} \mathrm{between} i \mathrm{and} j,$$

(20)

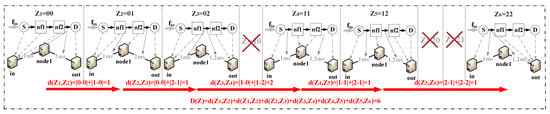
Figure 2. All SFC deployment schemes when $M=2$ and $N=3$.

The upper limit of the theoretical value of the above continuity can be deduced as Equation (21), and the corresponding physical meaning is that only one NF deployment position is moved to the adjacent node in each step.

$$D{(Z)}_{\min }={\displaystyle \sum _{i=1}^{\left|Z\right|-1}\min (d(Z_{i-1},Z_i)})=|Z|-1,$$

(21)

Algorithm 1: NB-SS algorithm

Input: NF number: M, path length: N Output: deploy solutions: Z,  Require: count ← 0, Z ← Ø, z ← zeros (N) 1: While count < N^M − 1 do          /* Traverse all integers in 0~N^M − 1 */ 2:    data ← count, i ← 0 3:    While data > 0 do          /* Converts count to base N */ 4:       z[M – 1 − i] ← data%M 5:       data ← [data/N] 6:       i++ 7:     end while 8:      if z[0] < z[1] … < z[M − 1]    /* Restrictions on the NF deployment order */ 9:       add z to Z 10:   end if 11:   count++ 12: end while 13: return Z

4.1.2. Solution Space Continuity Optimization Based on Ant Colony Optimization Algorithm

To alleviate the discontinuity of solution space caused by carrying in N-Base coding, the coding sequence of solution space can be rearranged. As shown in Figure 3, the sum of the Manhattan distances of the two arrangements is 12 and 10, respectively ($M=3,N=3$). When the number of $M$ and $N$ is relatively large (such as $M=N=5$, there will be 126 deployment schemes), it is difficult to find the optimal continuity scheme. Inspired by TSP, we take each deployed coding scheme as a city and use the Manhattan distance between deployment coding schemes as the distance between cities. We can model the above continuity optimization problem as an acyclic TSP, and take Equation (20) as the optimization objective, and optimize the problem through the ACO algorithm to obtain the near-optimal continuity [41]. The N-Base coding solution space construction based on the ant colony optimization algorithm (NBACO-SS) is shown in Algorithm 2.

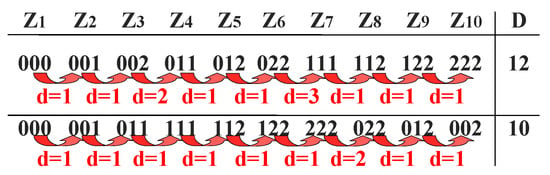
Figure 3. Sum of Manhattan distances for different solution space arrangements ($M=3, N=3$).

The NBACO-SS algorithm abstracts the SFC deployment problem as an integer coding calculation problem, so an NBACO-SS library can be established in advance after determining the scale of NFVI and the length range of SFCs to reduce the coding and ACO time.

Algorithm 2: NBACO-SS algorithm

Input: NF number: M, path length: N Output: deploy solutions: Z,  Require: Initialize solution Z0 ← N-base-SS (M, N)  best_distance ← +∞, city_num ← len(Z) 1: ants ← Generating_ant_colony() /* Generated ant colony */ 2: While not stop do 3:    for ant in ants       /* traverse ant colony */ 4:       citys ← Z0, out ← Ø 5:       while citys != Ø 6:          city ← Select_city(ant, citys) /* select the next city */ 7:          Move(ant)          /* move the ant */ 8:          add city to out          /* store cities that have passed */ 9:        end while 10:       dis ← D(out)          /* Calculate the Manhattan distance according to Equation (20) */ 11:       if dis < best_distance       /* Update optimal solution */ 12:          best_distance, Z ← dis, out 13:       end if 14:     end 15:     Update_pheromone()          /* Update pheromone */ 16: end while 17: return Z

4.2. Heuristic SFC Deployment Algorithm Based on N-Base Continuous Digital Coding

In this paper, we combine the continuous digital coding strategy with the existing heuristic algorithm and reconstruct the tabu search embedding algorithm and affinity-based simulated annealing algorithm based on NBACO-SS.

4.2.1. Affinity-Based Simulated Annealing Algorithm on N-Base Continuous Digital Coding Solution Space (NB-ABSA)

NB-ABSA algorithm is based on an affinity-based simulated annealing embedding algorithm (ABSA) proposed in [15], and NBACO-SS is used to build a complete SFC deployment solution space and deployment coding scheme. For any group of SFC $G^V=\{G_{{}^1}^V,G_2^V,\cdots ,G_j^V\}$, its deployment scheme in NBACO-SS solution space is $\mathrm{X}=\{x_1,x_2,\cdots ,x_j\}$, where $x_j=(l,j)$ represents its deployment scheme on the $l$-th path ${\tau }_{pql}$ of path set ${\tau }_{pq} (p,q={\displaystyle \sum _{n_m^s\in N^S}{\chi }_{j0}^m\cdot }{n}_m^s, {\displaystyle \sum _{n_m^s\in N^S}{\chi }_{j(\left|N_{{}^j}^V\right|-1)}^m\cdot }{n}_m^s)$. In the affinity-based deployment scheme, the network functions of the same SFC are deployed on the same node as much as possible to reduce the occupation of traffic bandwidth. This affinity can be measured by the mode function $Mode\left(Z_j\right)$. The larger its value is, the more network functions of the same SFC are deployed on the same node.

The pseudo-code of the NB-ABSA algorithm is shown in Algorithm 3. Lines 1–5 use the affinity-based approach [15] to generate a deployment scheme for each SFC and find its corresponding code in the NBACO-SS space. Lines 8–16 perform neighborhood update operations. The affinity-based approach is used to generate the neighborhood set for each SFC that has been successfully deployed in $G^V$, and tries to deploy unsuccessful SFC with the affinity-based approach, and the maximum fitness and corresponding neighborhood are calculated. Lines 17–21 update the optimal solution according to the metropolis criterion. Line 22 is the cooling function.

Algorithm 3: NB-SS-ABSA algorithm

Input:$\mathrm{SFCs}: G^V$$, \mathrm{NFVI}: G^{\mathrm{S}}$, NBACO-SS library: Γ Output: deploy solutions: X,  Require: temperature ← T0, cooling_rate ← α  X ← Ø, best_fit ← 0 1: for sfc in $G^V$ 2:    sol ← Affinity_Based_Approach(sfc)/* Affinity based deployment strategy */ 3:    x ← Solution_to_num(Γ, sol)    /* Encode the Solution into the Number */ 4:    X ← update x to X 5: end 6: While temperature > 1 do 7:    temp_sol ← Ø, temp_fit ← 0 8:    for sfc in $G^V$ 9:       if sfc is deployed successfully 10:          sol ← Affinity_Based_Approach(sfc) 11:          fit ← Calculated_fitness()   /* calculate fitness */ 12:          if fit > temp_fit 13:             temp_fit ← fit, temp_sol ← sol 14:          end if 15:       end 16:    end 17:    if e(temp_fit- best_fit) > rand(0,1)   /* Metropolis criterion */ 18:       x ← Solution_to_num(Γ, temp_sol) 19:       best_fit ← temp_fit 20:       update x to X 21:    end if 22:    temperature ← temperature•(1-cooling_rate)   /* reduce temperature */ 23: end while 24: return X, best_fit

4.2.2. Tabu Search-Embedding Algorithm on N-Base Continuous Digital Coding Solution Space (NB-ETS)

The NB-ETS algorithm is based on a tabu search SFC-embedding algorithm proposed in paper [19], which uses NBACO-SS to construct a complete SFC deployment solution space coding and realize a neighborhood update and tabu list in the digital domain. For any set of SFC $G^V=\{G_{{}^1}^V,G_2^V,\cdots ,G_j^V\}$, NB-ETS adopts the same scheme as the NB-ABSA algorithm to construct a deployment scheme $\mathrm{X}=\{x_1,x_2,\cdots ,x_j\}$. When a tabu list $TabuList=[T_1,T_2,\cdots ,T_j]$ is constructed, a separate table item $T_j=[x_{j1},x_{j2},\cdots ,]$ is constructed for each SFC, which represents a group of historical deployment schemes of SFC $G_j^V$.

The pseudo-code of the NB-ETS algorithm is shown in Algorithm 4. Lines 1–6 randomly generate the deployment scheme for each user SFC and calculate the fitness. Lines 8–10 randomly select a successfully deployed SFC and find the neighborhood in NBACO-SS. The neighborhood update operation is performed on Lines 11–15, and the fitness is calculated. Line 18 judges whether the neighborhood is in the tabu list. If it is in the tabu list, the optimal solution with the suboptimal solution in Line 19–20 is replaced. Line 22 updates the tabu list and removes the first item if the maximum length is exceeded.

Algorithm 4: NB-SS-ETS algorithm

$\mathbf{Input}\mathbf{:} \mathrm{SFCs}: G^V$$, \mathrm{NFVI}: G^{\mathrm{S}}$, NBACO-SS library: Γ Output: deploy solutions: X,  Require: TabuList ← Ø, best_fit ← 0  X ← Ø, i ← 0 1: for sfc in $G^V$ 2:    x ← Random.choice(Γ, sfc)   /* randomly select the scheme code from Γ */ 3:    Deploy_sfc_by_solution(x)   /* deploy SFC according to code x */ 4:    update x to X 5: end 6: best_fit ← Calculated_fitness()   /* calculate fitness */ 7: While i < N do 8:    sfc ← Random.choice($G^V$)   /* randomly select a SFC */ 9:    neighbors ← GetNeighbors(Γ, sfc)  /* Get neighborhood */ 10:    fit_list ← Ø 11:    for neighbor in neighbors 12:       Deploy_sfc_by_solution(neighbor) 13:       fit ← Calculated_fitness()    /* calculate fitness */ 14:       add fit to fit_list 15:    end 16:    temp_fit ← max(fit_list)       /*get the maximum fitness and index */ 17:    x ← fit_list.Index(best_fit) 18:    while x in TabuList[sfc] do     /* Check if x is in the taboo list */ 19:       temp_fit ← next_max(fit_list) 20:       x ← fit_list.Index(temp_fit) 21:    end while 22:    update x to TabuList[sfc]       /* update TabuList */ 23:    if   temp_fit > best_fit 24:       best_fit ← temp_fit 25:       update x to X 26: end while 27: return X, best_fit

5. Performance Evaluation

This chapter compares the performance of our proposed heuristic SFC deployment algorithm based on N-Base continuous digital coding with the heuristic algorithm without digital coding proposed in paper [15] and paper [19]. The ABSA algorithm proposed in paper [15] considers the affinity of network functions of SFC, and deploys the network function with the traffic relation on the same node as possible, and uses a simulated annealing algorithm to find the optimal solution. The ETS algorithm proposed in the paper [19] is a completely random tabu search deployment algorithm. In this paper, the NBACO-SS is used to reconstruct the two algorithms in the unified digital solution space, which effectively reduces the complexity of the algorithm and improves the efficiency of operation. We first describe the simulation environment, then give the simulation results of the algorithm and make a comparative analysis.

5.1. Simulation Environment and Design

The simulation environment used is SFCSim [42], an open-source NFV resource allocation simulation software, which is based on the NetworkX network simulation library and can realize complex network simulations. Two real network topologies, NSFNET and CERNNET2, are used in the simulation. The NSFNET network contains 14 nodes and 17 links and there are a lot of loops in the network for traffic routing decisions. The CERNNET2 network contains 21 nodes and 23 links, which has a larger network scale but fewer loops compared with the NSFNET network. The number of core resources of NFVI nodes conform to the uniform distribution $U(10,30)$, the importance of nodes in the network topology is evaluated according to the degree of nodes, and the resources are allocated according to the degree in turn. The link bandwidth resource is fixed at 10 Gbps, and the link delay conforms to the uniform distribution $U(0.5 \mathrm{ms},1.5 \mathrm{ms})$.

Network services provide 8 types of VNF. The traffic-scaling factor of VNF conforms to a uniform distribution $U(0.5,1.5)$, and the resource coefficient of processing per Gbps traffic conforms to a uniform distribution $U(1,2)$. According to the configuration of the cloud server by cloud infrastructure (such as Alibaba Cloud and HUAWEI Cloud, etc.), each VNF contains five VNFD, and the node core resources occupied by instantiating each template are 2, 4, 8, 16, and 24, respectively. In addition, the user services contain 100 SFCs, and the source and destination nodes are randomly generated in the network topology. The traffic demand conforms to the uniform distribution $U(2 \mathrm{Gbps},4 \mathrm{Gbps})$, and the delayed demand conforms to the uniform distribution $U(5 \mathrm{ms},10 \mathrm{ms})$. The types of virtual network functions that the traffic needs to pass through are between 1 and 5.

In this paper, we will compare the simulation iteration time and the maximum service traffic of the four heuristic algorithms in the above simulation environment.

5.2. Simulation Results

5.2.1. Continuity Evaluation of NBACO-SS

Figure 4 shows that the Manhattan distance continuity of the digital solution space constructed by the NBACO-SS algorithm varies with the length of the user SFC and compares it with the theoretical boundary value calculated by Equation (21) and the NB-SS algorithm without ACO. Note that most of the theoretical boundary values are unreachable according to the Euler Path Theorem, but they can be used as the reference value for algorithm performance evaluation. It can be observed from Figure 4 that the Manhattan distance D(z) increases rapidly with the increase of SFC length and the number of nodes on the routing path. This is because the total number of codes, $N^M$, is a power function and an exponential function with $N$ and $M$, respectively. Therefore, the solution space composed of qualified codes will also increase rapidly, and Manhattan distance $D(Z)$ will increase accordingly. ACO can greatly improve the continuity of solution space based on NB-SS strategy, especially when the number of NF is less than five and the number of routing nodes is less than six; when the solution space scale is small, and the ant colony algorithm can converge in a faster time, it can approach the theoretical boundary value.

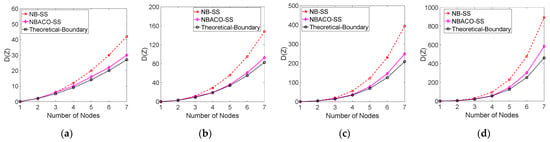
Figure 4. Simulation of solution space continuity of NBACO-SS algorithm: (a) length = 4; (b) length = 5; (c) length = 6; (d) length = 7.

5.2.2. Performance Evaluation of Heuristic Deployment Scheme Based on NBACO-SS

Figure 5 shows the time performance of the heuristic deployment scheme based on NBACO-SS, which is defined as the search time of the algorithm under different iterations. To obtain accurate experimental data, we conducted five experiments at each experimental point and obtained the average results within 80% confidence. The parameter controlling the NB-ABSA algorithm is the cooling rate α. The smaller the α, the slower the temperature reduction and the greater the number of iterations. Figure 5a,b are the simulation results of the NB-ETS algorithm and NB-SBSA algorithm, respectively. We can see that with the deepening of algorithm search time, the proposed NBACO-SS strategy can effectively reduce the simulation time of SFC deployment algorithms. This is because a complete solution space can reduce the repeated search operation, and the coding based on the digital domain can effectively reduce the time efficiency of memory storage, comparison, and search operations of heuristic SFC deployment algorithms. Figure 6 quantifies the time efficiency improvement of our proposed strategy (time efficiency is defined as the ratio of search time improved by the new algorithm to the original algorithm). For two completely different heuristic algorithms, simulated annealing and tabu search, the heuristic deployment scheme based on NBACO-SS can improve the time efficiency by about 20%.

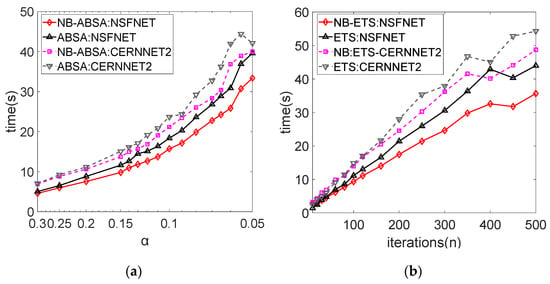
Figure 5. Time performance of heuristic SFC deployment algorithm based on NBACO-SS: (a) NB-ABSA; (b) NB-ETS.

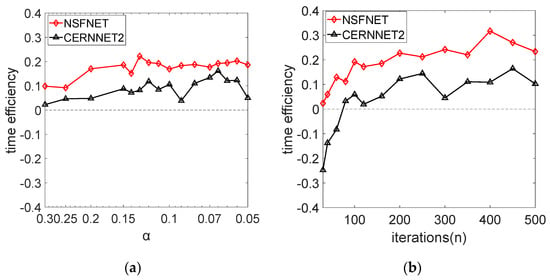
Figure 6. Time efficiency optimization of heuristic SFC deployment algorithm based on NBACO-SS: (a) NB-ABSA; (b) NB-ETS.

Table 2 shows the simulation results of the total service traffic of the four algorithms in two network topologies varying with the number of routing paths. It can be observed from the table that the heuristic deployment scheme based on NBACO-SS achieves almost the same total service traffic as the original deployment scheme, but NBACO-SS can effectively improve the execution speed of the algorithm, and the algorithm can get the optimal solution faster.

Table 2. Network service traffic of heuristic SFC deployment algorithm based on NBACO-SS.

Network/Path Number		NB-ABSA	ABSA	NB-ETS	ETS
NSFNET	1	190	190.6	196.8	194.7
	2	194.9	195.4	209.4	209.5
	3	193	192.6	210.1	209.7
	4	189.4	190.5	211.9	211.8
	5	189.3	189.6	210.9	211.6
CERNNET2	1	241.2	242.2	247.3	241.9
	2	240.8	238.7	261.4	260.9
	3	240.1	240.3	264.6	263.1
	4	238.8	239.2	266.4	264.3
	5	238.9	239.5	264.3	262.7

Finally, we simulate the change of total network service traffic and algorithm convergence time with the number of routing paths. From Figure 7a, we can observe that selecting the routing path other than the shortest path can slightly improve the service traffic, but when considering too many paths, the total service traffic will decrease. This is because the more routing paths considered, the lower the quality of the path and the more bandwidth resources consumed; it will also enlarge the solution space and improve the probability of getting into the suboptimal solution and the search time. Figure 7b demonstrates that with the increase of the number of routing paths, the convergence time of the algorithm increases rapidly, and this increasing trend slows down with the increase of paths. This is because the overall quality of routing paths decreases, and the heuristic algorithm will automatically exclude some poor search space. Therefore, it is more appropriate to choose 2–3 of the shortest routing paths when considering traffic routing paths.

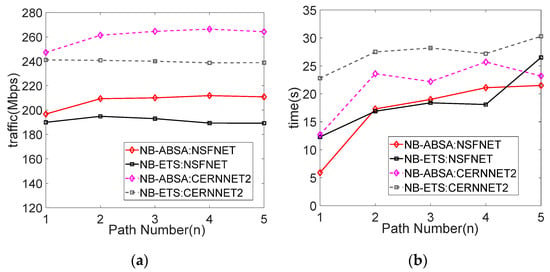
Figure 7. The total network service traffic and algorithm convergence time vary with the number of routing paths: (a) traffic; (b) time.

6. Conclusions and Future Work

In this paper, we propose a new continuous digital coding strategy for heuristic SFC deployment algorithms. We model the deployment of SFC into a 0–1 ILP model. For the first time, the instantiated VNFD selection, network function embedding, and traffic steering are considered in the model, and the problem is reduced to a KLP to prove that it is an NP-hard problem. Based on the model, we conduct a detailed analysis of the solution space of the SFC deployment problem and propose a concise and complete solution space composition strategy based on N-Base continuous digital coding. NBACO-SS maps the complex SFC deployment problem to a simple digital domain-coding problem by using integer size and carry and evaluates the continuity of solution space through Manhattan distance. Finally, the solution space continuity is improved by TSP and ACO. Based on NBACO-SS, a simulated annealing algorithm (NB-ABSA) and a tabu search algorithm (NB-ETS) are reconstructed to solve the above SFC deployment problem. The simulation results demonstrate that compared with the original algorithm, the heuristic SFC deployment algorithm based on NBACO-SS can improve the time efficiency by about 20% without reducing the total network service traffic. At the same time, choosing the traffic steering path beyond the shortest path can slightly improve the service traffic, but it will also increase the size of the solution space, in order to improve the probability of falling into the suboptimal solution and the search time; therefore, it is more appropriate to choose 2–3 of the shortest paths, as the traffic steering paths in distributed network architectures, such as MEC and distributed micro-data centers. As future work, we plan to use the established model to compare and analyze the SFC deployment in two different VNFD resource granularity architectures, the container and virtual machine, and design an SFC deployment scheme that can effectively reduce resource fragmentation based on NBACO-SS and heuristics.