A Secure Personal Health Record Sharing System with Key Aggregate Dynamic Searchable Encryption

Abstract

Recently, as interest in individualized health has increased, the Personal Health Record (PHR) has attracted a lot of attention for prognosis predictions and accurate diagnoses. Cloud servers have been used to manage the PHR system, but privacy concerns are evident since cloud servers process the entire PHR, which contains the sensitive information of patients. In addition, cloud servers centrally manage the PHR system so patients lose direct control over their own PHR and cloud servers can be an attractive target for malicious users. Therefore, ensuring the integrity and privacy of the PHR and allocating authorization to users are important issues. In this paper, we propose a secure PHR sharing system using a blockchain, InterPlanetary File System (IPFS), and smart contract to ensure PHR integrity and secure verification. To guarantee the patient’s authority over the management of his/her own PHR, as well as provide convenient access, we suggest a key aggregate dynamic searchable encryption. We prove the security of the proposed scheme through informal and formal analyses including an Automated Verification of Internet Security Protocols and Applications (AVISPA) simulation, Burrows–Abadi–Needham (BAN) logic, and security-model-based games. Furthermore, we estimate the computational costs of the proposed scheme using a Multiprecision Integer and Rational Arithmetic Cryptographic Library (MIRACL) and compare the results with those of previous works.

1. Introduction

With the increasing interest in and efforts to manage one’s health and prevent disease, the Personal Health Record (PHR) has attracted a lot of attention from various parties such as academia, industries, and the government. According to the International Organization for Standardization (ISO), a PHR is the representation of information related to health, which can be standalone or an integration of health information from multiple sources. The ISO also indicates that individuals should be allowed to manage, control, and access their own PHRs [1]. This means that the PHR is a patient-oriented system [2] and patients may want to share their PHRs with users such as medical professionals for prognosis predictions, accurate diagnoses, and health consulting. Due to the storage requirements and maintenance costs, patients often outsource their PHRs to third-party cloud servers. There are some cloud-based healthcare applications such as MTBC PHR [3], CapzulePHR [4], and My Medical [5]

However, cloud servers can be an attractive target for malicious users since a PHR contains the sensitive information of a patient [6]. If malicious users abuse or modify a PHR, the patient’s life could be put in danger or compromised due to misdiagnosis. Patients must be able to decide which users can access their PHRs. Attribute-based searchable encryption (ABSE), which is the integration of attribute-based encryption (ABE) and searchable encryption (SE), has been utilized to satisfy these requirements. ABSE provides fine-grained search control by regulating how authorized users acquire trapdoors to search for encrypted PHRs [7]. However, ABSE does not ensure patient-oriented sharing since it requires a trusted third party (TTP) to set up the system and allocate keys to entities. In addition, the decryption key size in ABSE is non-constant, which means that as the amount of data to be decrypted increases, the size of the decryption key increases [8]. To solve this problem, key aggregate searchable encryption (KASE) has been proposed for the data owner (e.g. patient), which generates system parameters and allocates decryption keys to users [9]. In addition, in KASE, the decryption key is a single constant aggregate key that has compacted the decryption keys corresponding to the data. Therefore, KASE is suitable for a PHR sharing system since it ensures the patient’s authority over his/her PHR and solves the key management problem.

Although cryptosystems are used in cloud-based systems for the privacy of patients, there are still non-negligible drawbacks. Storing PHRs on cloud servers means that patients delegate the management rights to the cloud server so patients lose their self-determined control over their personal information [10]. In addition, cloud servers are organized centrally, where storage is typically owned and managed by a single entity. Since cloud servers are usually not credible, they can steal or reveal PHRs by dishonestly performing malicious operations and can provide forged search results to users [11]. So, the existence of a centralized cloud server leads to the single-point-of-failure problem.

Researchers have considered a blockchain as a prospective solution to handle the problems in cloud-based systems [12,13,14,15]. A blockchain is a peer-to-peer (P2P) decentralized network that provides transparency, provenance, auditability, and security features, which are advantageous in data-sharing applications [16]. A blockchain eliminates the need for a third party by making the system secure and completely decentralized. However, there are limitations for managing all PHRs on the network since storing large volumes of data is expensive for a blockchain [17,18]. In addition, it does not guarantee scalability, which is an important challenge in blockchains. In order to alleviate the storage problem of blockchains, an InterPlanetary File System (IPFS) has been introduced. An IPFS is a distributed content-addressable file system, where for each uploaded PHR, IPFS allocates a unique hash as an identifier. By storing this identifier on the blockchain and using it as a pointer, the IPFS can overcome the storage limitations inherent in blockchains.

In this paper, we propose a secure PHR sharing system by applying a blockchain and an IPFS. We use KASE to ensure that patients retain authority over their records. However, existing KASE schemes do not consider dynamic data search sharing tasks, which can incur considerable computational costs since users must make repeated data request trapdoors. Therefore, we suggest a key aggregate dynamic searchable encryption using a Linear Secret Sharing Scheme (LSSS). The proposed system can ensure patient-oriented sharing.

1.1. Motivation, Methodology, and Contributions

A PHR contains the sensitive information of patients so it is necessary to restrict access to users. ABSE has been utilized as a solution but it does not ensure that patients maintain authority over data management. In addition, ABSE suffers from key management problems since the number of keys linearly increases depending on the complexity of the corresponding access policy. Researchers have utilized KASE as a countermeasure but their proposed schemes did not consider dynamic searches, which cause severe computational costs for data requests. In addition, they still depend on cloud servers for data management, which eliminates patients’ self-determined control over their personal information. Guaranteeing patients’ rights and reducing unnecessary communication between users in PHR sharing systems are indeed challenges. Therefore, we propose a secure PHR sharing system model. We utilize a blockchain and an IPFS to share the PHRs in a decentralized manner and handle the problems in cloud-based systems. We combine the KASE and LSSS to provide convenient keyword searches for users to obtain data. The proposed scheme provides essential security requirements such as the right to manage personal data, data integrity, transparency, and mutual authentication so our scheme has novel aspects compared to other previous works. The main contributions are summarized as follows.

• We propose a secure PHR sharing system that ensures patients’ authority over their personal records by suggesting a key aggregate dynamic searchable encryption. Thus, patients can manage and regulate access to their own PHRs.
• We provide dynamic searches for allowing users to obtain specific PHRs with low computational costs. We support dynamic searches using LSSS. In the proposed scheme, users can generate a trapdoor with various keywords at the same time to acquire a PHR.
• The proposed scheme utilizes a blockchain to provide data integrity and prevent the single point of failure. In addition, we utilize a smart contract to realize the secure and effective keyword searches and trapdoor verification.
• We store PHRs using an IPFS, which is a decentralized data storage system. Since the IPFS is a content-addressable protocol generating unique hash values for stored PHRs, it ensures the security of PHRs and avoids duplications.

1.2. Organization

The rest of the paper is organized as follows. We briefly cover previous works in Section 2. Section 3 presents the system models and interprets the conceptual aspect to assist with understanding this paper. Section 4 proposes a secure PHR sharing scheme. We prove the security of the proposed scheme in Section 5 and Section 6, including the BAN logic, AVISPA simulation tool, INDistinguishability against the Chosen Plaintext Attack (IND-CPA), INDistinguishability against the Chosen Keyword Attack (IND-CKA), and INDistinguishability against the Keyword Guessing Attack (IND-KGA). We analyze and compare the performance of the proposed scheme and existing schemes in Section 7. Section 8 presents the conclusions of this paper.

2. Related Works

Over the past few years, many studies have been conducted on secure PHR sharing using access control cryptosystems. In 2013, Li et al. [19] proposed a cloud-computing-based PHR sharing system using ABE since PHRs should only be available to authorized users. In 2015, Liu et al. [20] proposed a PHR sharing system based on cloud computing that employed ciphertext-policy attribute-based signcryption scheme. They suggested a method where the data owner signs the PHR with his/her own private key to protect the unauthorized modification of the PHR. They claimed that this scheme provided confidentiality through indistinguishable against chosen ciphertext attacks. However, Rao [21] proved that Lie et al.’s claim was incorrect and ccould not offer confidentiality in indistinguishability of ciphertexts under a selective encryption predicate and adaptive chosen ciphertext attack (IND-sEP-CCA2) security model. To supplement this problem, Rao proposed a cloud-based PHR sharing system that provides confidentiality using the IND-sEP-CCA2 model. However, these schemes [19,20,21] did not consider dynamic keyword search processes to access PHRs, which can cause considerable computational costs to users.

To address this problem, Zhang et al. [22] proposed a cloud-based PHR sharing system that provided dynamic keyword searches. However, Peng et al. [23] mentioned that Zhang et al.’s scheme was inefficient for queries since the ciphertexts of different data owners were matched against the same query. By considering these problems, Peng et al. suggested an enhanced scheme based on [22]; however, Sun et al. [24] mentioned that Peng et al.’s scheme was vulnerable to keyword guessing and equivalence test attacks. Liu et al. [25] presented an ABSE-based signcryption scheme for PHR sharing using LSSS. Xu et al. [26] proposed a PHR sharing system that used two cloud servers. They mentioned that privacy issues can occur in single-server system since cloud servers can compromise stored data using secret keys. However, they still suffered from the single-server problem since the whole system regarding or relevant to the sensitive PHR information was stored on a cloud server. This means that cloud servers can collude to abuse the stored PHRs. In addition, these existing schemes [22,23,25,26] managed PHRs on centralized cloud servers, thus they can also suffer from the single-point-of-failure problem.

To overcome this problem, Wang et al. [27] presented a blockchain-based PHR sharing system. They stored the verification values on the blockchain to match the search results from the cloud server. Zhang et al. [28] proposed a blockchain-based hierarchical PHR sharing system. They considered search result auditing and verification through the blockchain by regarding the cloud server and auditor as malicious entities. They also allowed the users to delegate decryption keys hierarchically to their groups for alleviating the burden of the key distribution task of authority. However, in this system, users delegated decryption keys to their groups without mutual authentication, which could lead to PHR leak problems. Zhang et al. [29] proposed a distributed PHR sharing scheme based on ABE and a blockchain. They adopted both a blockchain and cloud servers to overcome the limited storage capacity of the blockchain. However, these schemes [27,28,29] still used cloud servers to manage the enormous volumes of PHRs, thus the single-point-of-failure problem remained due to the centralized nature of the cloud server.

To mitigate these issues, Madine et al. [30] proposed a blockchain-based PHR architecture with an IPFS. In addition, Wang et al. [31] proposed a PHR sharing system using a consortium blockchain and an IPFS. They also utilized a smart contract to realize personalized access control. Wu et al. [32] suggested a blockchain-enabled PHR sharing system with access control. They considered mutual evaluation for the individual-centric transaction network and access control decisions. Hussien et al. [33] suggested a blockchain-based access control scheme for PHR sharing. However, existing PHR sharing schemes [30,31,32,33] rely on TTP to share PHRs, which does not guarantee a patient-centered system.

In 2020, Niu et al. [34] proposed a blockchain-based medical data sharing system using KASE in the Internet of Things environment. However, their scheme was vulnerable to privileged-insider attacks and did not provide secure mutual authentication. In addition, they did not consider dynamic keywords, which incurred significant computational costs to users. Niu et al. also relied on cloud servers to store data, which led to the single-point-of-failure problem. Thus, we propose a fully decentralized secure PHR sharing scheme that ensures patients’ self-determined control over their personal information. In addition, the proposed scheme realizes convenient PHR searches using key aggregate dynamic searchable encryption.

3. Preliminaries

In this section, we present the system models and cover the conceptual aspect referred to in this paper.

3.1. System Models

We consider the following network, threat, and security models to design and analyze the proposed scheme.

3.1.1. Network Model

The proposed secure PHR sharing model is depicted in Figure 1. In this figure, we have four entities: data owner, data user, IPFS, and blockchain.

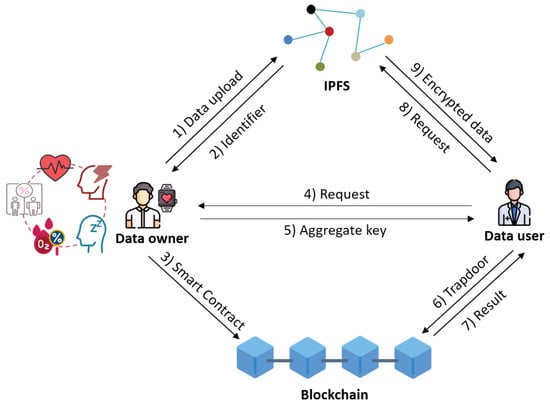
Figure 1. Network model of the proposed scheme.

• Data owner (DO): The $DO$ manages his/her own PHR for self-directed health care. The $DO$ generates the system parameters for his/her own PHR and controls the access rights of the $DU$ using an aggregate key. The $DO$ uploads the encrypted PHR to the IPFS and generates and uploads the smart contract to the blockchain for realizing the secure verification of the trapdoor.
• Data user (DU): The $DU$ is the person that wants to access the PHR of the $DO$. To obtain the read rights of the PHR, the $DU$ requests the aggregate key from the $DO$. The $DU$ can obtain the aggregate key by mutual authentication with the $DO$. The $DU$ can request and receive the PHR by communicating with the blockchain and IPFS. For the PHR decrypted using the aggregate key, the $DU$ can verify the integrity through the received verification value from the blockchain.
• IPFS: IPFS is a P2P decentralized database. In the proposed system, the IPFS stores the encrypted PHR of the $DO$ and returns a unique hash address for the stored PHR as an identifier. In addition, when the $DU$ requests the PHR through the identifier, the IPFS returns the corresponding results to the $DU$.
• Blockchain: The architecture of the blockchain is a public permissionless blockchain since all network parties can access the smart contract in the blockchain. The proposed system employs the Practical Byzantine Fault Tolerance (PBFT) consensus algorithm for the validation of transactions and generation of blocks. The blockchain implements the stored smart contract when the $DU$ sends the trapdoor. Then, the blockchain transmits the identifier and verification value as a result.

The overall communication flows of the network are summarized as follows.

1

The $DO$ generates the system parameters for his/her own PHR and the $DO$ and $DU$ generate their own public and private key pairs with the system parameters. Then, the $DO$ encrypts the PHR and uploads it to the IPFS.

2

The IPFS stores the received PHR. Then, the IPFS generates and sends an unique hash address as an identifier for the received PHR to the $DO$. The $DO$ calculates the keyword ciphertexts corresponding to the PHR and verification values. Then, the $DO$ generates the smart contract using the keyword, identifier, and verification value, and uploads the smart contract to the blockchain.

3

The $DU$ requests the aggregate key for reading the $DO$’s PHR by sending the $DU$’s credentials.

4

The $DO$ verifies the $DU$’s credentials, and if the $DU$ is valid, the $DO$ generates and sends the aggregate key and secret value to the $DU$.

5

The $DU$ generates the trapdoor using the keyword and received secret value. Then, the $DU$ sends the trapdoor to the blockchain to obtain the identifier and verification value for the encrypted PHR.

6

The blockchain checks the validity of the $DU$, and if the $DU$ is validated, the blockchain sends the corresponding PHR’s identifier and verification values to the $DU$ as a result.

7

The $DU$ sends a request for the PHR to the IPFS using the received identifier.

8

The IPFS sends the encrypted PHR to the $DU$ by matching the identifier in the database. The $DU$ decrypts the received PHR using the aggregate key. Then, the $DU$ checks whether the PHR is the data of the $DO$ using the verification value. If it is correct, the process is successfully completed.

3.1.2. Threat Model

We adopt the broadly accepted Dolev–Yao (DY) threat model [35] to evaluate the security of the proposed scheme. In the DY model, each network entity communicates and exchanges messages through an insecure channel. This model also recognizes that an adversary $\mathcal{A}$ can eavesdrop or intercept the transmitted messages between the network entities. With this message, $\mathcal{A}$ can modify, forge, and insert the malicious content into the messages and delete or replay them during communication. $\mathcal{A}$ can perform various attacks such as impersonation, replay, and man-in-the-middle (MITM) attacks [36,37].

3.1.3. Security Model

Under the threat model in Section 3.1.2, the scheme must satisfy the following security requirements:

• Data privacy: The PHR contains the sensitive information of the $DO$. If the PHR is leaked, the $DO$’s life life could be put in danger or compromised. The PHR ciphertext does not reveal any information about the plaintext to the adversary. Thus, data confidentiality and integrity must be ensured in the PHR sharing system. We prove data privacy using the IND-CPA model.
• Ciphertext privacy: The keyword ciphertext does not expose any information about the corresponding keywords to the adversary who is the unauthorized user. We prove ciphertext privacy using the IND-CKA model.
• Trapdoor privacy: For secure PHR sharing, only the authorized $DU$ can access the PHR, i.e., the trapdoor with the received secret values can be generated. The trapdoor does not disclose any information about the corresponding keywords to the adversary who is not authorized by the $DO$. Using the IND-KGA model, we demonstrate that the proposed scheme ensures trapdoor privacy.

In our scheme, games using the IND-CPA, IND-CKA, and IND-KGA models are defined as follows.

Definition 1

(Data privacy). We denote the semantic security for data privacy using the following IND-CPA model. In this game, the advantage of the adversary is defined as $Ad{v}_{\mathcal{A}}^{IND-CPA}=|Pr[{\delta }^{\prime }=\delta ]-\frac{1}{2}|$. This game is secure against IND-CPA if $|Pr[{\delta }^{\prime }=\delta ]-\frac{1}{2}|\le \epsilon$ is satisfied for all attacks, where ε is a negligible probability.

• Init.Adversary $\mathcal{A}$ selects a challenge set $S^{*}\subseteq \{1,\dots ,n\}$ that $\mathcal{A}$ wants to attack.
• Setup.Simulator $\mathcal{X}$ executes the setup phase and sends the public parameters to $\mathcal{A}$.
• Phase 1.$\mathcal{A}$ queries the aggregate key $AK$ for set $S^{\prime }\subseteq S^{*}$ to $\mathcal{X}$. Then, $\mathcal{X}$ performs the aggregate key request phase and sends $AK$ to $\mathcal{A}$.
• Challenge.$\mathcal{A}$ picks two plaintext $PH{R}_0$ and $PH{R}_1$, where $|PH{R}_0|=|PH{R}_1|$, from a set of possible plaintexts belonging to class $i^{*}$ and submits them to $\mathcal{X}$. $\mathcal{X}$ flips the coin $\delta \in \{0,1\}$, encrypts $PH{R}_{\delta }$ in the data upload phase and sends the ciphertext to $\mathcal{A}$.
• Phase 2.$\mathcal{A}$ repeatsPhase 1for $S^{\prime }\subseteq \overline{S^{*}}$, that is, the aggregate sets that contain data classes apart from those in the target set $S^{*}$.
• Guess.$\mathcal{A}$ outputs a guess ${\delta }^{\prime }$ of δ to $\mathcal{X}$. If ${\delta }^{\prime }=\delta$, $\mathcal{A}$ wins the game.

Definition 2

(Ciphertext privacy). Here, we demonstrate the game for ciphertext privacy using the IND-CKA model. The adversary’s advantage in this game is defined as $Ad{v}_{\mathcal{A}}^{IND-CKA}=|Pr[{\delta }^{\prime }=\delta ]-\frac{1}{2}|$. If $|Pr[{\delta }^{\prime }=\delta ]-\frac{1}{2}|\le \epsilon$ is met, this game is secure against the IND-CKA model.

• Init.Adversary $\mathcal{A}$ chooses a challenge set $S^{*}\subseteq \{1,\dots ,n\}$ that $\mathcal{A}$ wants to attack.
• Setup.Simulator $\mathcal{X}$ executes the setup phase and returns the public parameters to $\mathcal{A}$.
• Phase 1.First, $\mathcal{A}$ sends an aggregate key request query to $\mathcal{X}$. $\mathcal{X}$ implements the aggregate key request phase and returns $AK$ to $\mathcal{A}$. Then, $\mathcal{A}$ transmits the trapdoor query for the keyword $w_l$. If $S^{*}\subseteq S$, $\mathcal{X}$ executes the data request phase and responds with the trapdoor.
• Challenge.$\mathcal{A}$ chooses two keywords $w_0$ and $w_1$, where $|w_0|=|w_1|$ and of a challenge set $S^{*}$, to $\mathcal{X}$. $\mathcal{X}$ flips the coin $\delta \in \{0,1\}$ and responds with the ciphertext for $w_{\delta }$ in the data upload phase to $\mathcal{A}$.
• Phase 2.$\mathcal{A}$ repeatsPhase 1with the restriction that neither $w_0$ nor $w_1$ are used.
• Guess.$\mathcal{A}$ outputs a guess ${\delta }^{\prime }$ of δ to $\mathcal{X}$. If ${\delta }^{\prime }=\delta$, $\mathcal{A}$ wins the game.

Definition 3

(Trapdoor privacy). Here, we demonstrate the game using the IND-KGA model to prove trapdoor security. In this game, $Ad{v}_{\mathcal{A}}^{IND-KGA}=|Pr[{\delta }^{\prime }=\delta ]-\frac{1}{2}|$ is the advantage of $\mathcal{A}$. If $Ad{v}_{\mathcal{A}}^{IND-KGA}\le \epsilon$, this game is secure against the IND-KGA model. This game for the proposed scheme is defined as follows.

• Init.Adversary $\mathcal{A}$ gives to the simulator $\mathcal{X}$ a challenge set $S^{*}\subseteq \{1,\dots ,n\}$.
• Setup.$\mathcal{X}$ executes the setup phase and returns the results to $\mathcal{A}$.
• Phase 1.$\mathcal{A}$ first sends an aggregate key request query to $\mathcal{X}$. $\mathcal{X}$ executes the aggregate key request phase and sends $AK$ to $\mathcal{A}$. Then, $\mathcal{A}$ sends the ciphertext query for the keyword $w_l$. If $S^{*}\subseteq S$, $\mathcal{X}$ executes the data upload phase and responds with the ciphertext.
• Challenge.$\mathcal{A}$ submits two equal-length keywords $w_0$ and $w_1$ to $\mathcal{X}$ within $S^{*}$. $\mathcal{X}$ flips the coin $\delta \in \{0,1\}$ and responds with the trapdoor for $w_{\delta }$ in the data request phase to $\mathcal{A}$.
• Phase 2.$\mathcal{A}$ repeatsPhase 1with the restriction that neither $w_0$ nor $w_1$ are used.
• Guess.$\mathcal{A}$ outputs a guess ${\delta }^{\prime }$ of δ to $\mathcal{X}$. If ${\delta }^{\prime }=\delta$, $\mathcal{A}$ wins the game.

3.2. Bilinear Maps

A bilinear map is a pairing-based cryptosystem. Let $\mathcal{G}$ and ${\mathcal{G}}_T$ be the multiplicative cyclic groups with a large prime order q. The bilinear map $e:\mathcal{G}\times \mathcal{G}\to {\mathcal{G}}_T$ satisfies the following properties.

• Bilinearity: For $\forall a,b\in \mathcal{G}$ and $\forall x,y\in {\mathcal{Z}}_q^{*}$, we have $e(a^x,b^y)=e{(a,b)}^{xy}$.
• Non-degeneracy: $\exists a,b\in \mathcal{G}$, $e(a,b)\ne 1$.
• Computability: $\forall a,b\in \mathcal{G}$, $e(a,b)$ can be computed in polynomial time.

3.3. Linear Secret-Sharing Scheme (LSSS)

A secret-sharing scheme $\Pi$ [38] realizing access policies on a set of parties $\mathcal{P}$ is linear over $Z_q$ if the following conditions are satisfied:

• For each party, the shares of a secret $s\in Z_q$ form a vector over $Z_q$.
• There is an $l\times \varphi$ matrix $\mathcal{M}$ called the share-generating matrix on $\Pi$ and a function $\rho$ that maps each row of $\mathcal{M}$ to a specific party in $\mathcal{P}$. During the generation of the shares, we give consideration to the column vector $\overrightarrow{v}={(s,r_2,\dots ,r_{\varphi })}^{\perp }$, where $r_2,\dots ,r_{\varphi }\in Z_q$. Then, l shares a vector of s, which is equal to $\mathcal{M}·\overrightarrow{v}$. In addition, the share ${\lambda }_j={\mathcal{M}}_j·\overrightarrow{v}$ belongs to $\rho \left(j\right)$, where ${\mathcal{M}}_j$ is the jth row of $\mathcal{M}$.

We denote that ${\mathbf{A}}_s$ is an authorized set of the access structure $\mathcal{T}$, ${\mathbf{A}}_s\in \mathcal{T}$, and I is defined as the set of rows where labels of I are in S, such as $I=\left\{i\right|i\in \{1,\dots ,l\},\rho \left(i\right)\in S\}$. Then, there exists coefficients ${\left\{b_i\right\}}_i\in I$ that recover secret s by ${\sum }_{i\in I}{b}_i{\lambda }_i={\sum }_{i\in I}{b}_i(\mathcal{M}·\overrightarrow{v})={\sum }_{i\in I}\left(b_i{\mathcal{M}}_i\right)·\overrightarrow{v}=(1,0,\dots ,0)·(s,r_2,\dots ,r_{\varphi })=s$.

3.4. Computational Assumption

Let $e:\mathcal{G}\times \mathcal{G}\to {\mathcal{G}}_T$ be a bilinear map, g be a generator of $\mathcal{G}$, and $a,b,c,z\in Z_q^{*}$ be chosen randomly. With this establishment, the assumptions used in this paper are defined as follows.

3.4.1. Decisional Diffie–Hellman (DDH) Assumption

The DDH assumption is that it is difficult for a probabilistic polynomial time adversary $\mathcal{A}$ to distinguish $(g^a,g^b,g^{ab})$ from $(g^a,g^b,g^z)$. The advantage $\epsilon$ of $\mathcal{A}$ is defined as follows:

$$|Pr[\mathcal{A}(g^a,g^b,g^{ab})=1]-Pr[\mathcal{A}(g^a,g^b,g^z)=1]|\ge \epsilon$$

If there is no way that $\mathcal{A}$ can decide whether $g^z=g^{ab}$, that is, deciding whether $z=ab$ or $z\in Z_q^{*}$ with a non-negligible advantage, the DDH assumption holds.

3.4.2. Decisional Bilinear Diffie–Hellman (DBDH) Assumption

Under the DBDH assumption, an adversary $\mathcal{A}$ cannot distinguish $(g^a,g^b,g^c,e{(g,g)}^{abc})$ from $(g^a,g^b,g^c,e{(g,g)}^z)$ in probabilistic polynomial time. The advantage $\epsilon$ of $\mathcal{A}$ is defined as follows.

$$|Pr[\mathcal{A}(g^a,g^b,g^c,e{(g,g)}^{abc})=1]-Pr[\mathcal{A}(g^a,g^b,g^c,e{(g,g)}^z)=1]|\ge \epsilon$$

If $\mathcal{A}$ cannot decide whether $e{(g,g)}^z=e{(g,g)}^{abc}$, which is determining whether $z=abc$ or $z\in Z_q^{*}$ with a non-negligible advantage, the DBDH assumption is valid.

3.5. Blockchain

A blockchain is a distributed ledger technology that maintains a list of growing records. These records called blocks are chronologically linked using the cryptographic hashes of the previous blocks along with the timestamps and lists of transactions. Due to its chained structure, any included data cannot be changed unconstitutionally without the modification of all subsequent frames. In addition, each node of the blockchain network holds a copy of the chain to prevent a single point of failure. These properties make it difficult to change the transaction history, and the blockchain provides traceability, accountability, transparency, and provenance. Depending on the requirements and goals to be met, the blockchain can be classified into public/private and permissionless/permissioned types [39,40].

• Public permissionless blockchain: every node can participate in the consensus process, read and write the transactions, and maintain the ledgers.
• Public permissioned blockchain: the nodes are permitted to read or convert the state of the ledger with approved performing consensus, that is, only authorized nodes in the network can write in the ledger.
• Private permissionless blockchain: only authorized nodes are allowed to participate; the read and write abilities are owned by authorized nodes; all transactions can be conducted privately, and if necessary, the transaction can be opened for verification.
• Private permissioned blockchain: only authorized nodes can access, perform operations over the distributed ledger, and participate in the consensus process.

A smart contract is a computerized transaction protocol that executes the terms of a contract [41]. If a specific pre-defined condition is met, the smart contract is automatically implemented on the blockchain, and the contact with the smart contract is documented on the blockchain as a transaction. The smart contract can realize interoperability and flexible control over the blockchain system. Therefore, the proposed system adopted a blockchain and a smart contract to ensure the integrity of PHRs and provide secure verification mechanisms. The proposed scheme employed a public permissionless blockchain since anyone could access the blockchain. In addition, we adopted the PBFT consensus algorithm to realize consistency and synchronization in terms of transaction validation, block generation, and the voting process in the distribution network.

3.6. InterPlanetary File Systems

An InterPlanetary File System (IPFS) [42] is a P2P distributed file system for storing and accessing files. When content is uploaded to the IPFS, the IPFS returns a unique hash of content, called a content identifier (CID). The CID indicates the content address in the IPFS, which is based on the content itself, rather than the location of the content. Thus, anyone who has the CID can access the corresponding content. Since the IPFS connects all computing devices to share and access files, there are no authorized nodes, which eliminates the no single-point-of-failure problem and the nodes do not need to trust each other. Content-based addressing in an IPFS is constructed using the SHA-256 cryptographic hash, and this hash function creates an identifier for a certain file in the InterPlanetary Name System (IPNS). With this unique feature, the IPFS can maintain the same path for updated files with identifiers.

4. Proposed Scheme

We propose a secure PHR sharing scheme with key aggregate dynamic searchable encryption. The proposed scheme comprises six phases: the setup, key-generation, data upload, aggregate key request, data retrieval, and data request phases. The notations used in this paper can be found in Table 1 and the six phases are described in the following subsections.

Table 1. Notation.

Notation	Description
$DO$, $DU$	Data owner/data user
$(s{k}_o,p{k}_o)$	Data owner’s private key and public key
$(s{k}_u,p{k}_u)$	Data user’s private key and public key
n	Maximum number of PHRs
m	Maximum number of keywords
W	Keyword set for document
$W^{\prime }$	Search keyword set
I	Index of search keyword set
$PH{R}_i$	i-th PHR
w	Keyword
$\alpha ,t,r_o,r_u,R_u$	Random number
$T_1,T_2,T_3$	Timestamp
$▵T$	Maximum transmission delay
$AK$	Aggregate key
$T{r}_{y1},T{r}_{y2}$	Trapdoor
e	Bilinear map $e:\mathcal{G}\times \mathcal{G}\to {\mathcal{G}}_T$
h	One-way hash function ${\{0,1\}}^{*}\to Z_q$
$\left|\right|$	Concatenation operator
⊕	Bitwise exclusive-or operator

4.1. Setup Phase

The $DO$ generates the bilinear parameters $(q,\mathcal{G},{\mathcal{G}}_T,e)$ and sets the maximum number of PHRs and keywords as n and m, respectively. Then, the $DO$ chooses a generator $g\in \mathcal{G}$, a random number $\alpha \in Z_q$, and a hash function $h:{\{0,1\}}^{*}\to Z_q$. The $DO$ computes $g_i=g^{{\alpha }^i}\in \mathcal{G}$ for $i=\{1,\dots ,n,n+2,\dots ,2n\}$. Finally, the $DO$ publishes $\{q,\mathcal{G},{\mathcal{G}}_T,e,g,n,m,{\left\{g_i\right\}}_{1\le i\le 2n,i\ne n+1},h\}$.

4.2. Key Generation Phase

In this phase, the $DO$ and $DU$ generate the private and public key pairs for secure PHR sharing. The $DO$ and $DU$ compute $(s{k}_o,p{k}_o)=(s{k}_o,g^{s{k}_o})$ and $(s{k}_u,p{k}_u)=(s{k}_u,g^{s{k}_u})$, respectively.

4.3. Data Upload Phase

The $DO$ uploads the PHR to the IPFS for health care. This phase is briefed in Figure 2 and the detailed steps are given below.

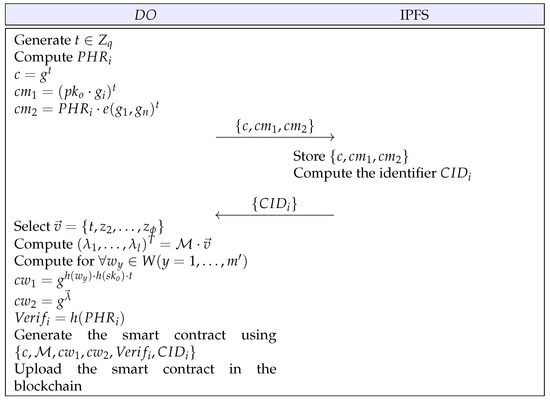
Figure 2. Data upload phase.

Step 1: 

The $DO$ generates $t\in Z_q$ and computes $c=g^t$, $c{m}_1={(p{k}_o·g_i)}^t$, $c{m}_2=PH{R}_i·e{(g_1,g_n)}^t$ for the $PH{R}_i$. Then, the $DO$ sends $\{c,c{m}_1,c{m}_2\}$ to the IPFS.

Step 2: 

The IPFS stores $\{c,c{m}_1,c{m}_2\}$ in the database and computes the identifier $CI{D}_i$. Then, the IPFS sends $\left\{CI{D}_i\right\}$ to the $DO$.

Step 3: 

The $DO$ selects $\overrightarrow{v}=\{t,z_2,\dots ,z_{\varphi }\}$, where $z_2,\dots ,z_{\varphi }\in Z_q$, and $l\times \varphi$ matrix $\mathcal{M}$. The $DO$ computes ${({\lambda }_1,\dots ,{\lambda }_l)}^T=\mathcal{M}·\overrightarrow{v}$, and calculates $c{w}_1=g^{h\left(w_y\right)·h\left(s{k}_o\right)·t}$, $c{w}_2=g^{\overrightarrow{\lambda }}$, $Veri{f}_i=h\left(PH{R}_i\right)$ for $\forall w_y\in W(y=1,\dots ,m^{\prime })$, where $m^{\prime }$ is the number of keywords about $PH{R}_i$. Then, the $DO$ generates the smart contract using $\{c,\mathcal{M},c{w}_1,c{w}_2,Veri{f}_i,$$CI{D}_i\}$ and uploads it to the blockchain.

4.4. Aggregate Key Request Phase

The $DU$ requests the aggregate key to the $DO$ for reading the PHR. Figure 3 indicates this phase and the details are as follows.

Figure 3. Aggregate key request phase.

Step 1: 

The $DU$ generates $r_u$ and $T_1$. The $DU$ computes $PI{D}_u=h(I{D}_u\left|\right|s{k}_u)$, $TI{D}_u=h\left(I{D}_u\right)\oplus r_u$, $U_1=g^{\left(TI{D}_u\right|\left|s{k}_u\right)}$, $U_2=p{k}_o^{\left(TI{D}_u\right|\left|s{k}_u\right)}$, $VI{D}_u=PI{D}_u\oplus h\left(U_2\right)$, $Si{g}_u=h(PI{D}_u\left|\right|U_2\left|\right|p{k}_u\left|\right|T_1)·s{k}_u\left(modq\right)$. Then, the $DU$ sends $\{U_1,VI{D}_u,Si{g}_u,T_1,S\}$ to the $DO$ through a public channel.

Step 2: 

After receiving the message, the $DO$ checks $|T_1-T_1^{*}|\le ▵T$. Then, the $DO$ computes $U_2^{*}=U_1^{s{k}_o}$, $PI{D}_u^{*}=VI{D}_u\oplus h\left(U_2^{*}\right)$, and checks $g^{Si{g}_u}\stackrel{?}{=}p{k}_u^{h\left(PI{D}_u^{*}\right|\left|U_2^{*}\right|\left|p{k}_u\right|\left|T_1\right)}$. If it is correct, the $DO$ computes $PI{D}_o=h(I{D}_o\left|\right|s{k}_o)$, $TI{D}_o=h\left(I{D}_o\right)\oplus r_o$, $O_1=g^{\left(TI{D}_o\right|\left|s{k}_o\right)}$, $O_2=U_1^{\left(TI{D}_o\right|\left|s{k}_o\right)}$, $VI{D}_o=PI{D}_o\oplus h\left(O_2\right)$, $Si{g}_o=h(PI{D}_o\left|\right|PI{D}_u^{*}\left|\right|O_2\left|\right|T_2)·s{k}_o\left(modq\right)$, $V_{ou}=h(PI{D}_o\left|\right|PI{D}_u^{*}\left|\right|O_2\left|\right|T_2)$, $AK={\prod }_{j\in S}{g}_{n+1-j}^{s{k}_o}$, $O_3=\left(AK\right||h\left(s{k}_o\right))\oplus h(O_2\left|\right|PI{D}_o\left|\right|PI{D}_u^{*})$. Then, the $DO$ sends $\{O_1,Si{g}_o,VI{D}_o,V_{ou},O_3,T_2\}$ to the $DU$.

Step 3: 

Upon receiving the message, the $DU$ checks $|T_2-T_2^{*}|\le ▵T$. Then, the $DU$ computes $O_2^{*}=O_1^{\left(TI{D}_u\right|\left|s{k}_u\right)}$, $PI{D}_o^{*}=VI{D}_o\oplus h\left(O_2^{*}\right)$, $V_{ou}^{*}=h(PI{D}_o^{*}\left|\right|PI{D}_u\left|\right|O_2^{*}\left|\right|T_2)$, and checks whether $g^{Si{g}_o}\stackrel{?}{=}p{k}_o^{h\left(PI{D}_o^{*}\right|\left|O_2^{*}\right|\left|p{k}_o\right|\left|T_2\right)}$ and $V_{ou}^{*}\stackrel{?}{=}{V}_{ou}$. If it is valid, the $DU$ obtains the secret values by computing $\left(AK\right||h\left(s{k}_o\right))=O_3\oplus h(O_2^{*}\left|\right|PI{D}_o^{*}\left|\right|PI{D}_u)$.

4.5. Data Retrieval Phase

The $DU$ requests the PHR’s location to the blockchain. The proposed scheme considers the dynamic search for the convenience of the PHR search so the $DU$ sends the trapdoor to the blockchain only once. Figure 4 denotes this phase, and we interpret the detailed steps below.

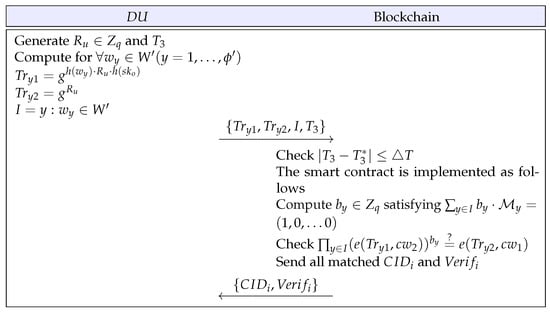
Figure 4. Data retrieval phase.

Step 1: 

The $DU$ generates $R_u\in Z_q$ and $T_3$, and computes $T{r}_{y1}=g^{h\left(w_y\right)·R_u·h\left(s{k}_o\right)}$, $T{r}_{y2}=g^{R_u}$ for $\forall w_y\in W^{\prime }(y=1,\dots ,{\varphi }^{\prime })$, where ${\varphi }^{\prime }$ is the number of search keywords. Then, the $DU$ sends $\{T{r}_{y1},T{r}_{y2},I,T_3\}$ to the blockchain, where $I=y:w_y\in W^{\prime }$.

Step 2: 

With the received message, the blockchain checks $|T_3-T_3^{*}|\le ▵T$ and implements the smart contract. The blockchain computes $b_y\in Z_q$ satisfying ${\sum }_{y\in I}{b}_y·{\mathcal{M}}_y=(1,0,\dots 0)$ and checks whether ${\prod }_{y\in I}{\left(e(T{r}_{y1},c{w}_2)\right)}^{b_y}\stackrel{?}{=}e(T{r}_{y2},c{w}_1)$. If it is correct, the blockchain sends all matched $CI{D}_i$ and $Veri{f}_i$ to the $DU$.

4.6. Data Request Phase

The $DU$ requests the PHR to the IPFS with the received identifier. Then, the $DU$ decrypts the encrypted PHR using the aggregate key. We denote this phase in Figure 5, and describe the detailed steps below.

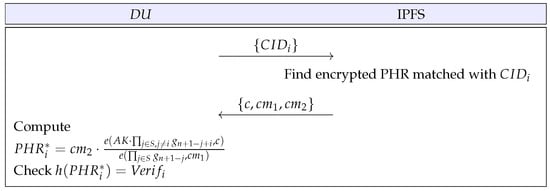
Figure 5. Data request phase.

Step 1: 

The $DU$ sends the identifier $CI{D}_i$ to the IPFS for the PHR that the $DU$ wants.

Step 2: 

The IPFS finds the encrypted document, which is matched with $CI{D}_i$. Then, the IPFS sends $\{c,c{m}_1,c{m}_2\}$ to the $DU$.

Step 3: 

After receiving the message, the $DU$ computes $PH{R}_i^{*}=c{m}_2·\frac{e(AK·{\prod }_{j\in S,j\ne i}{g}_{n+1-j+i},c)}{e({\prod }_{j\in S}{g}_{n+1-j},c{m}_1)}$. Then, the $DU$ checks whether $h\left(PH{R}_i^{*}\right)=Veri{f}_i$. If it is valid, the $DU$ obtains the right PHR, and the process of the proposed PHR sharing system is successfully completed.

5. Informal Security Analysis

We indicate the security features of the proposed scheme, including impersonation, replay, MITM, and insider attacks. In addition, we prove that the proposed scheme ensures correctness, perfect forward secrecy, anonymity, and mutual authentication.

5.1. Impersonation Attack

An adversary $\mathcal{A}$ tries to masquerade as the $DU$ to obtain $PH{R}_i$. In this case, $\mathcal{A}$ needs $CI{D}_i$ and $AK$ corresponding to $PH{R}_i$. As mentioned in Section 3.1.2, $\mathcal{A}$ can utilize the transmitted message. $\mathcal{A}$ eavesdrops $\{U_1,VI{D}_u,Si{g}_u,T_1,S\}$ and $\{T{r}_{y1},T{r}_{y2},I,T_3\}$. Then, $\mathcal{A}$ attempts to send $\{U_1^{\prime },VI{D}_u^{\prime },Si{g}_u^{\prime },T_1^{\prime },S^{\prime }\}$ and $\{T{r}_{y1}^{\prime },T{r}_{y2}^{\prime },I^{\prime },T_3^{\prime }\}$ to obtain $AK$ and $CI{D}_i$, respectively. However, it is impossible for $\mathcal{A}$ since $\mathcal{A}$ did not have knowledge about the $DU$’s real identity $I{D}_u$ and the secret key $s{k}_u$. Thus, the proposed scheme is secure against the impersonation attacks.

5.2. Replay Attack

With the ability described in Section 3.1.2, $\mathcal{A}$ intercepts the transmitted messages. $\mathcal{A}$ interrupts $\{U_1,VI{D}_u,Si{g}_u,T_1,S\}$ and $\{T{r}_{y1},T{r}_{y2},I,T_3\}$ and resends them to the $DO$ and blockchain for obtaining the $PH{R}_i$. However, the $DO$ and blockchain check the transmission delay time and the freshness of the message, which is encrypted with random nonces $\{r_u,R_u\}$ so $\mathcal{A}$ cannot obtain the $PH{R}_i$. Therefore, our scheme has resistance against replay attacks.

5.3. Man-in-the-Middle (MITM) Attack

In this attack, $\mathcal{A}$ interrupts the transmitted messages $\{U_1,VI{D}_u,Si{g}_u,T_1,S\}$ and $\{T{r}_{y1},T{r}_{y2},I,T_3\}$ and modifies them to $\{U_1^{\prime },VI{D}_u^{\prime },Si{g}_u^{\prime },T_1^{\prime },S^{\prime }\}$ and $\{T{r}_{y1}^{\prime },T{r}_{y2}^{\prime },I^{\prime },T_3^{\prime }\}$. Unfortunately, it is computationally impossible for $\mathcal{A}$ since these messages are made up of the $DU$’s identity $I{D}_u$, secret key $s{k}_u$, and aggregate key $AK$. Hence, the proposed scheme prevents the MITM attack.

5.4. Insider Attack

This attack supposes that $\mathcal{A}$ is an insider that receives the authorization from the $DO$. $\mathcal{A}$ attempts to impersonate another legitimate $DU$ to know what kind of person the $DU$ is by obtaining the $PH{R}_i$. For this, $\mathcal{A}$ endeavors to generate the messages $\{U_1,VI{D}_u,Si{g}_u,T_1,S\}$ and $\{T{r}_{y1},T{r}_{y2},I,T_3\}$ with the $DU$’s $I{D}_u$ and $s{k}_u$. However, $\mathcal{A}$ cannot compute them since the corresponding values of the $DU$ are unknown. Thus, the proposed scheme is secure against the insider attacks.

5.5. Correctness

5.5.1. Dynamic Keyword

In Section 4.5, the blockchain checks whether the $DU$ sends the correct trapdoor using the aggregate key. We prove it arithmetically as follows.

$$\begin{array}{cc}\hfill \prod _{y\in I}e{(T{r}_{y1},c{w}_2)}^{b_y}& =e{(g^{h\left(w_y\right)·R_u·h\left(s{k}_o\right)},g^{\overrightarrow{\lambda }})}^{b_y}\hfill \\ \hfill & =e{(g,g)}^{h\left(w_y\right)·R_u·h\left(s{k}_o\right)·\overrightarrow{\lambda }·b_y}\hfill \\ \hfill & =e{(g,g)}^{h\left(w_y\right)·R_u·h\left(s{k}_o\right)·(\mathcal{M}·\overrightarrow{v})·b_y}\hfill \\ \hfill & =e{(g,g)}^{h\left(w_y\right)·R_u·h\left(s{k}_o\right)·({\sum }_{y\in I}{b}_y·{\mathcal{M}}_y)·\overrightarrow{v}}\hfill \\ \hfill & =e{(g,g)}^{h\left(w_y\right)·R_u·h\left(s{k}_o\right)·(1,0,\dots ,0)·\overrightarrow{v}}\hfill \\ \hfill & =e{(g,g)}^{h\left(w_y\right)·R_u·h\left(s{k}_o\right)·t}\hfill \\ \hfill & =e(g^{R_u},g^{h\left(w_y\right)·h\left(s{k}_o\right)·t})=e(T{r}_{y2},c{w}_1)\hfill \end{array}$$

5.5.2. PHR

As described in Section 4.6, the $DU$ can obtain the PHR of the $DO$ by decrypting with the aggregate key $AK$. Then, the $DU$ compares the obtained PHR with $Veri{f}_i$ to determine whether it is the correct value. For correctness, the $PH{R}_i$ can be obtained as follows.

$$\begin{array}{cc}\hfill PH{R}_i^{*}& =c{m}_2·\frac{e(AK·{\prod }_{j\in S,j\ne i}{g}_{n+1-j+i},c)}{e({\prod }_{j\in S}{g}_{n+1-j},c{m}_1)}\hfill \\ \hfill & =c{m}_2·\frac{e({\prod }_{j\in S}{g}_{n+1-j}^{s{k}_o}·{\prod }_{j\in S,j\ne i}{g}_{n+1-j+i},g^t)}{e({\prod }_{j\in S}{g}_{n+1-j},{(p{k}_o·g_i)}^t)}\hfill \\ \hfill & =c{m}_2·\frac{e({\prod }_{j\in S}{g}_{n+1-j+i},g^t)}{e({\prod }_{j\in S}{g}_{n+1-j+i},g^t)}·\frac{1}{e(g_{n+1},g^t)}\hfill \\ \hfill & =PH{R}_i·\frac{e{(g_1,g_n)}^t}{e(g_{n+1},g^t)}=PH{R}_i\hfill \end{array}$$

5.6. Perfect Forward Secrecy

In this attack, $\mathcal{A}$ can have the keys $s{k}_u$ of the $DU$. With this value, $\mathcal{A}$ tries to acquire the $PH{R}_i$. For this, $\mathcal{A}$ needs the aggregate key $AK$ so $\mathcal{A}$ makes effort to generate the message $\{U_1,VI{D}_u,Si{g}_u,T_1,S\}$. Nevertheless, $\mathcal{A}$ cannot calculate it since $\mathcal{A}$ did not have knowledge about the $DU$’s real identity $I{D}_u$ and secret key $s{k}_u$. For this reason, our scheme provides the perfect forward secrecy.

5.7. Anonymity

In the proposed scheme, each entity cannot trust each other so they hide the real identity $\{I{D}_o,I{D}_u\}$ with $\{s{k}_o,r_o,s{k}_u,r_u\}$ and perform the mutual authentication through the pseudo identity $\{PI{D}_o,PI{D}_u\}$. Although $\mathcal{A}$ tries to obtain the real identity from the pseudo identity, it is computationally impossible because of the collision-resistant property of the hash function. Therefore, the proposed scheme ensures the anonymity of each entity.

5.8. Mutual Authentication

In Section 4.4, it was shown that the $DO$ and $DU$ check the validity of each other before issuing the aggregate key $AK$. The $DU$ generates the signature $Si{g}_u$ that can represent the $DU$ and sends $\{U_1,VI{D}_u,Si{g}_u,T_1,S\}$ to the $DO$. After checking the transmission delay time, the $DO$ checks whether $g^{Si{g}_u}\stackrel{?}{=}p{k}_u^{h\left(PI{D}_u^{*}\right|\left|U_2^{*}\right|\left|p{k}_u\right|\left|T_1\right)}$. If it is correct, the $DU$’s validity is verified from the $DO$. Then, the $DO$ sends $\{O_1,Si{g}_o,VI{D}_o,V_{ou},O_3,T_2\}$ with the signature $Si{g}_o$. With the received message, the $DU$ checks whether $g^{Si{g}_o}\stackrel{?}{=}p{k}_o^{h\left(PI{D}_o^{*}\right|\left|O_2^{*}\right|\left|p{k}_o\right|\left|T_2\right)}$ and $V_{ou}^{*}\stackrel{?}{=}{V}_{ou}$. If this condition is approved, the validity of the $DO$ is verified to the $DU$. Consequently, the $DO$ and $DU$ mutually authenticate so the proposed scheme provides mutual authentication.

6. Formal Security Analysis

In this section, we conduct a formal analysis to evaluate the security of the proposed scheme using the AVISPA simulation tool, BAN logic, IND-CPA, IND-CKA, and IND-KGA.

6.1. AVISPA Simulation Tool

AVISPA is a security analysis tool for protocols in security-sensitive wireless environments [43]. For confirming security, many authentication schemes have been widely used [44,45,46]. We simulated the proposed scheme with the AVISPA tool based on the DY threat model to identify the security issues against replay and MITM attacks. To analyze our scheme, we shaped the actions of each participant using High-Level Protocols Specification Language (HLPSL), a role-based language. The HLPSL2IF translator coverts HLPSL into Intermediate Format (IF) and inputs the IF into the back-end. Then, the back-ends outputs the Output Format (OF) as the security analysis results against four components including the On-the Fly-Model-Checker (OFMC), SAT-based Model-Checker (SATMC), CL-based Attack Searcher (CL-AtSe), and Tree-Automata-based Protocol Analyzer (TA4SP).

We simulated the proposed scheme on the OFMC and CL-AtSe back-ends since they provide bitwise exclusive-OR operations. The simulated results on the OFMC and CL-AtSe were identified as SAFE or UNSAFE by estimating the security issues against replay and MITM attacks. In Figure 6, the OF indicates that the proposed scheme is “SAFE” in both the OFMC and CL-AtSe back-ends. Therefore, our scheme completely attains the specific security goals and withstands the attacks in a wireless environment.

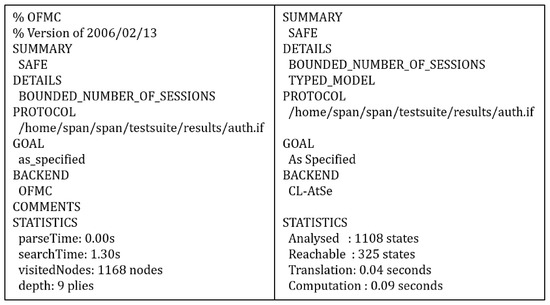
Figure 6. AVISPA evaluation results.

6.2. Formal Security Analysis using BAN Logic

BAN logic is a mathematical proof method for secure mutual authentication, which is widely used in authentication schemes [47,48,49]. We proved that the proposed scheme provides mutual authentication in Section 4.4. We describe the notations of BAN logic in Table 2, indicate the goals of this analysis, present all considered assumptions, and provide corresponding proof.

Table 2. BAN Logic Notation.

Notation	Description
$scky$	Secret key
$K|\equiv Y$	Kbelieves statement Y
$\#Y$	Statement Y is fresh
$K◃Y$	Kreceives statement Y
$K|\sim Y$	K once said Y
$K\Rightarrow Y$	Kcontrols statement Y
$<Y{>}_S$	Statement Y is combined with secret statement S
${\left\{Y\right\}}_{scky}$	Statement Y is masked by $scky$
$K\stackrel{scky}{⟷}Q$	K and Q share $scky$ to communicate with each other

6.2.1. Rules

The rules of the BAN logic are as follows.

• Message meaning rule ($MMR$):

  $$\frac{K|\equiv K\stackrel{scky}{⟷}Q,K◃{\left\{Y\right\}}_{scky}}{K|\equiv Q|\sim Y}$$
• Nonce verification rule ($NVR$):

  $$\frac{K|\equiv \#(Y),K|\equiv Q|\sim Y}{K|\equiv Q|\equiv Y}$$
• Jurisdiction rule ($JR$):

  $$\frac{K|\equiv Q|\Rightarrow Y,K|\equiv Q|\equiv Y}{K|\equiv Y}$$
• Freshness rule ($FR$):

  $$\frac{K|\equiv \#(Y)}{K|\equiv \#(Y,S)}$$
• Belief rule ($BR$):

  $$\frac{K|\equiv (Y,S)}{K|\equiv Y}$$

6.2.2. Goals

We establish the goals for proving mutual authentication as follows:

Goal 1: 

$DO|\equiv DO\stackrel{AK}{⟷}DU$

Goal 2: 

$DU|\equiv DO\stackrel{AK}{⟷}DU$

Goal 3: 

$DO|\equiv DU|\equiv DO\stackrel{AK}{⟷}DU$

Goal 4: 

$DU|\equiv DO|\equiv DO\stackrel{AK}{⟷}DU$

6.2.3. Idealized Forms

The idealized forms in the proposed scheme are as follows:

$M_1$:

$DU\to DO:{\{U_2,T_1\}}_{PI{D}_u}$

$M_2$:

$DO\to DU:{\{AK,O_2,T_2\}}_{PI{D}_o}$

6.2.4. Assumptions

The assumptions to achieve the BAN logic are as follows:

$A_1$:

$DO|\equiv (DO\stackrel{PI{D}_u}{⟷}DU)$

$A_2$:

$DO|\equiv \#(T_1)$

$A_3$:

$DU|\equiv (DO\stackrel{PI{D}_o}{\leftrightarrow }DU)$

$A_4$:

$DU|\equiv \#(T_2)$

$A_5$:

$DO|\equiv DU\Rightarrow (DU\stackrel{AK}{\leftrightarrow }DO)$

$A_6$:

$DU|\equiv DO\Rightarrow (DU\stackrel{AK}{\leftrightarrow }DO)$

6.2.5. Proof

We prove the guarantee of mutual authentication by attaining the goals using notations, idealized forms, and assumptions. We execute the proof according to the following steps:

Step 1: 

$S_1$ can be obtained from $M_1$.

$$S_1:DO◃{\{U_2,T_1\}}_{PI{D}_u}$$

Step 2: 

$S_2$ can be obtained by applying the $MMR$ with $A_1$.

$$S_2:DO|\equiv DU|\sim {\{U_2,T_1\}}_{PI{D}_u}$$

Step 3: 

$S_3$ can be gained from the $FR$ with $S_2$ and $A_2$.

$$S_3:DO|\equiv \#(U_2,T_1)$$

Step 4: 

$S_4$ can be acquired by applying the $NVR$ with $S_2$ and $S_3$.

$$S_4:DO|\equiv DU|\equiv (U_2,T_1)$$

Step 5: 

$S_5$ can be obtained from $M_2$.

$$S_5:DU◃{\{AK,O_2,T_2\}}_{PI{D}_o}$$

Step 6: 

$S_6$ can be gained from $MMR$ with $S_5$ and $A_3$.

$$S_6:DU|\equiv DO|\sim {\{AK,O_2,T_2\}}_{PI{D}_o}$$

Step 7: 

$S_7$ can be obtained by applying $FR$ with $S_6$ and $A_4$.

$$S_7:DU|\equiv \#(AK,O_2,T_2)$$

Step 8: 

$S_8$ can be obtained from $NVR$ with $S_6$ and $S_7$.

$$S_8:DU|\equiv DO|\equiv (AK,O_2,T_2)$$

Step 9: 

$S_9$ and $S_{10}$ can be obtained from $S_4$ and $S_8$ since $O_3=\left(AK\right||h\left(s{k}_o\right))\oplus h(O_2\left|\right|PI{D}_o\left|\right|PI{D}_u)$.

$S_9:DO|\equiv DU|\equiv \left(DO\stackrel{AK}{⟷}DU\right)$(Goal 3)

$S_{10}:DU|\equiv DO|\equiv \left(DO\stackrel{AK}{⟷}DU\right)$(Goal 4)

Step 10: 

$S_{11}$ and $S_{12}$ can be obtained by applying $JR$ from $S_9$, $S_{10}$, $A_5$, and $A_6$.

$S_{11}:DO|\equiv \left(DU\stackrel{AK}{⟷}DO\right)$(Goal 1)

$S_{12}:DU|\equiv \left(DO\stackrel{AK}{⟷}DU\right)$(Goal 2)

Therefore, the $DO$ and $DU$ authenticate securely in the aggregate key request phase of the proposed scheme.

6.3. IND-CPA Security

Theorem 1.

When an adversary $\mathcal{A}$ can win the game with a non-negligible advantage ε in a probability polynomial time, $\mathcal{A}$ can solve the DBDH assumption’s difficult problem with $\epsilon /2$.

Proof. 

We prove this security game according to Definition 1 and Section 3.4.2. Assume there is $\mathcal{A}$ that can break our scheme with advantage $\epsilon$. Then, we build a simulator $\mathcal{X}$ to play the DBDH game with advantage $\epsilon /2$. The simulation process is as follows. Challenger $\mathcal{B}$ randomly selects a random number $a,b,c,z\in Z_q$ and a generator $g\in \mathcal{G}$. Then, $\mathcal{B}$ randomly tosses a coin to obtain a random value $\mu \in \{0,1\}$. $\mathcal{B}$ sets if $\mu =0$, then $Z=e{(g,g)}^{abc}$, which is $(g^a,g^b,g^c,e{(g,g)}^{abc})$; otherwise $Z=e{(g,g)}^z$, which means $(g^a,g^b,g^c,e{(g,g)}^z)$. Then, $\mathcal{B}$ sends the results to $\mathcal{X}$ that plays the DBDH game.

Init. The simulator $\mathcal{X}$ runs the adversary $\mathcal{A}$ to create a challenge set $S^{*}\subseteq \{1,\dots ,n\}$ that $\mathcal{A}$ wants to attack. Then, $\mathcal{A}$ sends it to $\mathcal{X}$.

Setup.$\mathcal{X}$ computes the public parameters ${\{g_i=g^{{\alpha }^i}\}}_{1\le i\le 2n,i\ne n+1}$ and sets the instance of the DBDH game as ${\alpha }^1=a$ and ${\alpha }^n=b$. Then, $\mathcal{X}$ sends the public parameters to $\mathcal{A}$.

Phase 1.$\mathcal{A}$ requests an aggregate key $AK$ for $S\subseteq S^{*}$. $\mathcal{X}$ computes $AK={\prod }_{j\in S}{g}_{n+1-j}^{s{k}_o}$. Then, $\mathcal{X}$ sends $AK$ to $\mathcal{A}$.

Challenge.$\mathcal{A}$ submits two equal-length plaintext $PH{R}_0$ and $PH{R}_1$ to $\mathcal{X}$ with $S^{*}$. $\mathcal{X}$ randomly flips a coin to obtain $\delta \in \{0,1\}$. We set if $\mu =0$, then $Z=e{(g,g)}^{abc}$. In this case, we let $t=c$ be the instance of the DBDH game, then $e{(g,g)}^{abc}=e{(g,g)}^{ab·t}=e{(g^a,g^b)}^t=e{(g_1,g_n)}^t$ and $c_{m2}=PH{R}_{\delta }·e{(g,g)}^{abc}$. Otherwise, if $\mu =1$, then $Z=e{(g,g)}^z$ and $c_{m2}=PH{R}_{\delta }·e{(g_1,g_n)}^z$. $\mathcal{X}$ computes $c=g^t$, $c{m}_1={(p{k}_o·g_i)}^t$ and sends $\{c,c{m}_1,c{m}_2\}$ to $\mathcal{A}$.

Phase 2.$\mathcal{A}$ repeats Phase 1 to obtain the aggregate key, which is associated with the data sets $S\subseteq \overline{S^{*}}$.

Guess.$\mathcal{A}$ guesses ${\delta }^{\prime }$ of $\delta$. If ${\delta }^{\prime }=\delta$, we set $\mathcal{X}$ outputs 0, otherwise, it outputs 1. $\mathcal{X}$ outputs 0 means that $Z=e{(g,g)}^{abc}$ and $\mathcal{A}$ can obtain the practical ciphertext. Then, the advantage is $\epsilon$ and we can obtain $Pr[{\delta }^{\prime }=\delta |Z=e{(g,g)}^{abc}]=\frac{1}{2}+\epsilon$. $\mathcal{X}$ outputs 1 means that $Z=e{(g,g)}^z$ and $\mathcal{A}$ obtains invalid ciphertext. So, there is no advantage in guessing the correct ${\delta }^{\prime }$ and $\mathcal{A}$ obtains $Pr[\delta \ne \delta |Z=e{(g,g)}^z]=\frac{1}{2}$. Therefore, the probability $Pr$ of a successful game is

$$\begin{array}{cc}\hfill Pr& =\frac{1}{2}Pr[\mathcal{A}(g,g^a,g^b,g^c,e{(g,g)}^{abc})=1]\hfill \\ \hfill & +\frac{1}{2}Pr[\mathcal{A}(g,g^a,g^b,g^c,e{(g,g)}^z)=1]-\frac{1}{2}\hfill \\ \hfill & =\frac{1}{2}Pr[{\delta }^{\prime }=\delta |Z={(g,g)}^{abc}]\hfill \\ \hfill & +\frac{1}{2}Pr[{\delta }^{\prime }\ne \delta |Z=e{(g,g)}^z]-\frac{1}{2}\hfill \\ \hfill & =\frac{1}{2}\times (\frac{1}{2}+\epsilon )+\frac{1}{2}\times \frac{1}{2}-\frac{1}{2}\hfill \\ \hfill & =\frac{\epsilon }{2}\hfill \end{array}$$

(1)

Therefore, our scheme ensures IND-CPA security. □

6.4. IND-CKA Security

Theorem 2.

If an adversary $\mathcal{A}$ can win the game with a non-negligible advantage ε in a probability polynomial time, $\mathcal{A}$ can solve the DDH assumption’s difficult problem with $\epsilon /2$.

Proof. 

Let an adversary $\mathcal{A}$ break our scheme with advantage $\epsilon$. Then, we construct a simulator $\mathcal{X}$ to play the DDH game with advantage $\epsilon /2$. The simulation process is described as follows. Challenger $\mathcal{B}$ randomly selects $a,b,z\in Z_q$ and a generator $g\in \mathcal{G}$. Then, $\mathcal{B}$ randomly tosses a coin to obtain a random value $\mu \in \{0,1\}$. If $\mu =0$, then $Z=g^{ab}$, which is $(g^a,g^b,g^{ab})$; otherwise $Z=g^z$, which means $(g^a,g^b,g^z)$. Then, $\mathcal{B}$ sends the results to $\mathcal{X}$ that plays the DDH game.

Init. The simulator $\mathcal{X}$ executes the adversary $\mathcal{A}$ to create a challenge set $S^{*}\subseteq \{1,\dots ,n\}$. Then, $\mathcal{A}$ sends it to $\mathcal{X}$.

Setup.$\mathcal{X}$ generates the public parameters ${\left\{g_i\right\}}_{1\le i\le 2n,i\ne n+1}$. Then, $\mathcal{X}$ returns them to $\mathcal{A}$.

Phase 1.$\mathcal{A}$ requests the aggregate key $AK$ for $S\subseteq S^{*}$. $\mathcal{X}$ computes $AK={\prod }_{j\in S}{g}_{n+1-j}^{s{k}_o}$. Then, $\mathcal{X}$ sends $AK$ to $\mathcal{A}$. In addition, $\mathcal{A}$ sends the trapdoor query for the keyword $w_l$. If $S^{*}\subseteq S$, $\mathcal{X}$ executes the data request phase and sends $\{T{r}_{y1},T{r}_{y2}\}$ to $\mathcal{A}$.

Challenge.$\mathcal{A}$ submits two keywords $w_0$ and $w_1$, where $|w_0|=|w_1|$ and of a challenge set $S^{*}$ to $\mathcal{X}$. $\mathcal{X}$ randomly tosses a coin to obtain $\delta \in \{0,1\}$. If $\mu =0$, then $Z=g^{ab}$. In this case, we let $t=ab$, then $g^{ab}=g^t$ and $c=g^t=g^{ab}$, $c{w}_1=g^{h\left(w_y\right)·h\left(s{k}_o\right)·t}=g^{h\left(w_y\right)·h\left(s{k}_o\right)·ab}$. Otherwise, if $\mu =1$, then $Z=g^z$ and $c=g^t=g^z$, $c{w}_1=g^{h\left(w_y\right)·h\left(s{k}_o\right)·t}=g^{h\left(w_y\right)·h\left(s{k}_o\right)·z}$. Then, $\mathcal{X}$ computes $c{w}_2=g^{\overrightarrow{v}}$ and sends $\{c,c{w}_1,c{w}_2\}$ to $\mathcal{A}$.

Phase 2.$\mathcal{A}$ repeats Phase 1 to obtain the aggregate key and trapdoor under the restriction that neither $w_0$ nor $w_1$ are used.

Guess.$\mathcal{A}$ guesses ${\delta }^{\prime }$ of $\delta$. If ${\delta }^{\prime }=\delta$, $\mathcal{X}$ outputs 0, otherwise, it outputs 1. In addition, $\mathcal{X}$ outputs 0 is the representation of $Z=g^{ab}$ and $\mathcal{A}$ can obtain the practical ciphertext. Then, the advantage is $\epsilon$ so we can obtain $Pr[{\delta }^{\prime }=\delta |Z=g^{ab}]=\frac{1}{2}+\epsilon$. $\mathcal{X}$ outputs 1 is the indication that $Z=g^z$ and $\mathcal{A}$ obtains invalid ciphertext. So, there is no advantage in guessing the correct ${\delta }^{\prime }$ and $Pr[{\delta }^{\prime }\ne \delta |Z=g^z]=\frac{1}{2}$ can be obtained. So, the probability $Pr$ of a successful game is

$$\begin{array}{cc}\hfill Pr& =\frac{1}{2}Pr[\mathcal{A}(g,g^a,g^b,g^{ab})=1]\hfill \\ \hfill & +\frac{1}{2}Pr[\mathcal{A}(g,g^a,g^b,g^z)=1]-\frac{1}{2}\hfill \\ \hfill & =\frac{1}{2}Pr[{\delta }^{\prime }=\delta |Z=g^{ab}]+\frac{1}{2}Pr[{\delta }^{\prime }\ne \delta |Z=g^z]-\frac{1}{2}\hfill \\ \hfill & =\frac{1}{2}\times (\frac{1}{2}+\epsilon )+\frac{1}{2}\times \frac{1}{2}-\frac{1}{2}\hfill \\ \hfill & =\frac{\epsilon }{2}\hfill \end{array}$$

(2)

Therefore, our scheme ensures IND-CKA security. □

6.5. IND-KGA Security

Theorem 3.

The difficult problem of the DDH assumption can be solved when an adversary $\mathcal{A}$ can win the game with ε in a probability polynomial time. Then, a non-negligible advantage is $\epsilon /2$.

Proof. 

Suppose that an adversary $\mathcal{A}$ can break our scheme with advantage $\epsilon$. Then, we form a simulator $\mathcal{X}$ to play the DDH game with advantage $\epsilon /2$. The simulation process is described as follows. Challenger $\mathcal{B}$ randomly selects $a,b,z\in Z_q$ and $g\in \mathcal{G}$. Then, $\mathcal{B}$ randomly tosses a coin to obtain a random value $\mu \in \{0,1\}$. If $\mu =0$, then $Z=g^{ab}$, which is $(g^a,g^b,g^{ab})$; otherwise $Z=g^z$ which means $(g^a,g^b,g^z)$. Then $\mathcal{B}$ sends the results to $\mathcal{X}$ that plays the DDH game.

Init. The simulator $\mathcal{X}$ executes the adversary $\mathcal{A}$ to create a challenge set $S^{*}\subseteq \{1,\dots ,n\}$. Then, $\mathcal{A}$ sends it to $\mathcal{X}$.

Setup.$\mathcal{X}$ generates the public system parameters ${\left\{g_i\right\}}_{1\le i\le 2n,i\ne n+1}$. Then, $\mathcal{X}$ returns them to $\mathcal{A}$.

Phase 1.$\mathcal{A}$ requests aggregate key $AK$ for $S\subseteq S^{*}$. $\mathcal{X}$ computes $AK={\prod }_{j\in S}{g}_{n+1-j}^{s{k}_o}$. Then, $\mathcal{X}$ sends $AK$ to $\mathcal{A}$. In addition, $\mathcal{A}$ sends the ciphertext query for the keyword $w_l$. If $S^{*}\subseteq S$, $\mathcal{X}$ executes Data upload phase and sends $\{c,c{w}_1,c{w}_2\}$ to $\mathcal{A}$.

Challenge.$\mathcal{A}$ submits two equal-length keywords $w_0$ and $w_1$ to $\mathcal{X}$ within $S^{*}$. $\mathcal{X}$ randomly tosses a coin to obtain $\delta \in \{0,1\}$. If $\mu =0$, then $Z=g^{ab}$. In this case, we let $R_u=ab$, then $g^{ab}=g^{R_u}$ and $T{r}_{y1}=g^{ab·h\left(w_{\delta }\right)·h\left(s{k}_o\right)}$, $T{r}_{y2}=g^{ab}$. Otherwise, if $\mu =1$, then $Z=g^z$ and $T{r}_{y1}=g^{z·h\left(w_{\delta }\right)·h\left(s{k}_o\right)}$, $T{r}_{y2}=g^z$. Then, $\mathcal{X}$ sends $\{T{r}_{y1},T{r}_{y2}\}$ to $\mathcal{A}$.

Phase 2.$\mathcal{A}$ repeats Phase 1 to obtain the aggregate key under the restriction that neither $w_0$ nor $w_1$.

Guess.$\mathcal{A}$ guesses ${\delta }^{\prime }$ of $\delta$. If ${\delta }^{\prime }=\delta$, $\mathcal{X}$ outputs 0, otherwise, it outputs 1. In addition, $\mathcal{X}$ outputs 0 is the representation of $Z=g^{ab}$, and $\mathcal{A}$ can obtain the practical trapdoor. Then, the advantage is $\epsilon$, so we can get $Pr[{\delta }^{\prime }=\delta |Z=g^{ab}]=\frac{1}{2}+\epsilon$. $\mathcal{X}$ outputs 1 is the indication that $Z=g^z$, and $\mathcal{A}$ obtains invalid trapdoor. So, there is no advantage in guessing the correct ${\delta }^{\prime }$, and it can be obtained $Pr[{\delta }^{\prime }\ne \delta |Z=g^z]=\frac{1}{2}$. So, the probability $Pr$ of a successful game is

$$\begin{array}{cc}\hfill Pr& =\frac{1}{2}Pr[\mathcal{A}(g,g^a,g^b,g^{ab})=1]\hfill \\ \hfill & +\frac{1}{2}Pr[\mathcal{A}(g,g^a,g^b,g^z)=1]-\frac{1}{2}\hfill \\ \hfill & =\frac{1}{2}Pr[{\delta }^{\prime }=\delta |Z=g^{ab}]+\frac{1}{2}Pr[{\delta }^{\prime }\ne \delta |Z=g^z]-\frac{1}{2}\hfill \\ \hfill & =\frac{1}{2}\times (\frac{1}{2}+\epsilon )+\frac{1}{2}\times \frac{1}{2}-\frac{1}{2}\hfill \\ \hfill & =\frac{\epsilon }{2}\hfill \end{array}$$

(3)

Therefore, our scheme ensures IND-KGA security. □

7. Security and Performance Analysis

In this section, we compare the security and performance of the proposed scheme to the related schemes [25,28,31] in terms of security features, computational costs, and communication costs.

7.1. Security Features

We present the security properties of the proposed scheme and existing schemes [25,28,31]. As shown in Table 3, the related schemes suffer from security vulnerability problems, including perfect forward secrecy and mutual authentication. In contrast, our scheme is secure against various attacks in DY threat model, and ensures perfect forward secrecy, anonymity, mutual authentication, correctness, access control, dynamic search, data verification, and the $DO$’s authority over his/her own PHR. Therefore, our scheme provides more security features compared to the related schemes.

Table 3. Security Features.

Security Features	Liu et al. [25]	Zhang et al. [28]	Wang et al. [31]	Ours
$S{F}_1$	∘	∘	∘	∘
$S{F}_2$	∘	∘	∘	∘
$S{F}_3$	∘	∘	∘	∘
$S{F}_4$	∘	∘	∘	∘
$S{F}_5$	×	×	×	∘
$S{F}_6$	−	∘	∘	∘
$S{F}_7$	×	×	×	∘
$S{F}_8$	∘	∘	∘	∘
$S{F}_9$	∘	∘	∘	∘
$S{F}_{10}$	∘	∘	∘	∘
$S{F}_{11}$	×	×	×	∘
$S{F}_{12}$	×	×	×	∘

∘: Secure; ×: Insecure; −: Not considered; SF₁: Impersonation attack; SF₂: Replay attack; SF₃: MITM attack; SF₄: Insider attack; SF₅: Perfect forward secrecy; SF₆: Anonymity; SF₇: Mutual authentication; SF₈: Correctness; SF₉: Access control; SF₁₀: Dynamic search; SF₁₁: Data verification; SF₁₂: DO’s authority over his/her own PHR.

7.2. Computational Costs

We conducted a testbed experiment on cryptographic computation using MIRACL [50] on a personal computer (PC). The detailed performance of the PC was “Ubuntu 18.04.4 LTS with memory 8GiB, processor: Intel Core i7-4790 @ 3.60GHz × 4, CPU Architecture: 64-bit”. We measured the average run time of 100 runs for a hash operation $T_h\approx$ 0.003 ms, a bilinear pairing operation $T_b\approx$ 6.575 ms, a scalar point multiplication operation $T_{sm}\approx$ 2.373 ms, an exponentiation operation $T_e\approx$ 0.819 ms, an addition operation $T_a\approx$ 0.013 ms, and a symmetric key encryption/decryption $T_s\approx$ 0.001 ms. Table 4 shows the measurement results. $\alpha$ is the number of search keywords and $\beta$ is the size of the PHR dataset. The compared schemes provide a dynamic keyword search, and some schemes [28,31] do not consider data verification. Thus, to verify the performance of the dynamic keyword search, Figure 7 denotes the results obtained for different numbers of returned PHRs: $\beta =1$, $\beta =10$, $\beta =30$, and $\beta =50$. As shown in Figure 7, the existing schemes [25,28,31] exhibited higher computational costs than the proposed scheme. Furthermore, they did not satisfy some security features, such as mutual authentication and perfect forward secrecy. In contrast, the proposed scheme has lower computational costs and provides many security features that are not provided by the existing schemes.

Table 4. Computational Costs Comparison.

Scheme	Total Execution Time (ms)
[25]	$\alpha (4T_h+10T_b+10T_e+13T_{sm})+\beta (T_h+2T_b+4T_e+4T_{sm})\approx 104.801\alpha +25.921\beta$
[28]	$\alpha (4T_h+13T_b+22T_e+17T_{sm}+T_a)+\beta (T_h+T_e+T_s+2T_{sm})\approx 143.859\alpha +5.569\beta$
[31]	$\alpha (T_h+13T_b+19T_{sm}+5T_e+2T_a)+\beta T_s\approx 134.686\alpha +0.001\beta$
Ours	$\alpha (T_h+4T_b+8T_e+4T_{sm})+\beta (2T_b+3T_{sm})\approx 22.732\alpha +21.343\beta$

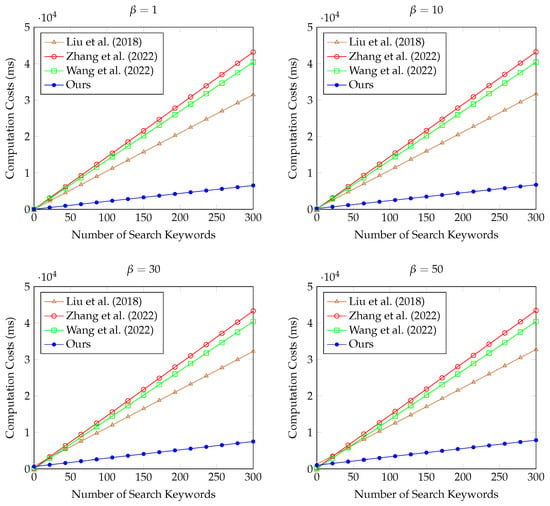
Figure 7. Computation costs comparison as the number of search keywords increases [25,28,31].

7.3. Communication Costs

The communication costs of the proposed scheme are compared with [25,28,31]. We set the bit size of the hash function, identity, timestamp, random number, index, an elliptic curve point, $\mathcal{G}$, ${\mathcal{G}}_T$, symmetric encryption/decryption, and attribute set to 160 bits, 128 bits, 32 bits, 160 bits, 32 bits, 320 bits, 512 bits, 1024 bits, 256 bits, and 32$\mathcal{T}$ bits, respectively. Table 5 indicates the comparison results of the communication costs. In the data retrieval and request phases, the exchanged messages $\{T{r}_{y1},T{r}_{y2},I,T_3\}$, $\{CI{D}_i,Veri{f}_i\}$, $\left\{CI{D}_i\right\}$, and $\{c,c{m}_1,c{m}_2\}$ needed 1088 bits, 320 bits, 160 bits, and 2048 bits, respectively. The existing schemes [25,28,31] had higher costs than the proposed scheme. Therefore, we have lower costs and ensure more security requirements than the existing schemes [25,28,31].

Table 5. Communication Costs Comparison.

Scheme	Communication Costs	Number of Messages
[25]	2$\mathcal{T}$ + 5792 bits	2
[28]	$\mathcal{T}$ + 7552 bits	5
[31]	$\mathcal{T}$ + 4576 bits	5
Ours	3616 bits	4

8. Conclusions

We proposed a secure PHR sharing system by applying a blockchain and an IPFS to ensure integrity and solve the single-point-of-failure problem. We suggested key aggregate dynamic searchable encryption using LSSS to provide the authority of data owners and reduce the unnecessary computation for users. In addition, we considered mutual authentication and data verification to realize securing sharing between network entities. With the proposed scheme, the data owner can encrypt and upload his/her own PHR with unique system parameters and assign the read rights to data users with an aggregate key through mutual authentication. The data user can obtain the encrypted PHR by communicating with the blockchain and IPFS, and the data user can verify the integrity of the decrypted PHR ciphertext with the aggregate key. We proved the security of the proposed scheme through information and formal analyses including BAN logic, the AVISPA tool and the IND-CPA, IND-CKA, and IND-KGA models. In addition, we performed a comparison of previous works using MIRACL. We demonstrated that our scheme provides more efficient and secure sharing compared to existing schemes. As a result, the proposed scheme provides essential security requirements such as rights related to personal data, data integrity, transparency, mutual authentication, and convenience of search so our scheme has novelty compared to other previous works. Therefore, the proposed scheme can be applied in a practical PHR sharing system and will ensure secure and efficient sharing by providing the authority of the patient and ensuring the confidence of the data user. Since the scope of the proposed scheme is how data owners share their PHR without TTP, we focused on the method of secure PHR sharing through mutual authentication. So, we have an issue to overcome in terms of verifying the identity before mutual authentication between the data owner and user. In the future, we will cover the identity verification for more systematic patient-oriented systems. In addition, we plan to test the proposed scheme on the blockchain and IPFS implementations. Then, we will evaluate the feasibility of the proposed scheme in a practical PHR sharing system.