Abstract
In this paper, we show that an additional inductor–capacitor–inductor filter can increase the oscillation amplitude of the enhanced swing Colpitts oscillator (ESCO), and call this topology the more enhanced swing Colpitts oscillator (mESCO). When it is connected with a rectifier, the DC–DC boost conversion ratio can be increased, especially for low-voltage sensor ICs or energy harvesting. This paper focuses on the electrical characteristics of mESCO. The oscillation frequency was modeled as a function of the circuit parameters of mESCO. The common gate voltage gain (ACG), defined by the ratio of the drain voltage amplitude to the source voltage amplitude of the switching MOSFET of mESCO, was also modeled under the assumption that all the circuit elements are ideal. The model was validated with a SPICE simulation. For ACG < 1.5, the model was in good agreement with the SPICE results within 10%. In addition, the drain voltage amplitude vda was modeled by assuming that the average transconductance of the MOSFET in a half cycle is null when the long-channel Shockley model is used. vda needs to be sufficiently high to have a large DC–DC boost conversion ratio. The model can predict the tendency that vda increases as ACG approaches unity. We found that the voltage difference of the drain voltage amplitude to the source voltage amplitude is a constant even when the circuit parameters, and thereby ACG are varied.
1. Introduction
Battery-free IoT sensor modules are required to eliminate battery replacement to reduce costs. Wireless power transfer (WPT) charges the modules with electromagnetic waves [1,2,3,4]. An energy transducer (ET) transforms environmental energy such as lights, heat flow, and vibration into electric power [5,6]. Those techniques can remove the batteries out of the modules. Circuit designs have improved the power efficiency of power converters even with low power received via WPT and ET. Multisine WPT can increase the peak power with the same average transmitter power, resulting in improvement in power efficiency [7,8,9]. Figure 1 graphically explains how it works. Each of the N multisine waves has power of 1/N to attain the same power as the conventional continuous wave. At the receiving antenna, the peak voltage amplitude can be theoretically increased by a factor of with beating multisine waves when the input impedance is common for N multisine waves with different frequencies. Due to the nonlinearity of the rectifying diode, the multisine waves can output more averaged current than the continuous wave.
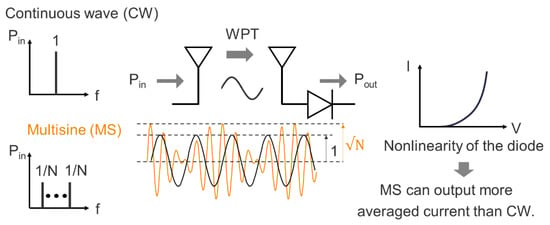
Figure 1.
Efficiency improvement in wireless power transfer with multisine electromagnetic waves.
The Colpitts oscillator is one of the oscillator circuit topologies that provides a carrier frequency for wireless communication [10,11,12,13]. The phase noise of the oscillator is a critical factor limiting the sensitivity of wireless communication. It is important to increase the output voltage amplitude of the oscillator to reduce the phase noise. In order to increase the voltage amplitude, an enhanced swing Colpitts oscillator (ESCO) was proposed [14,15,16,17,18]. What about adding beating to the ESCO to further increase the output voltage amplitude in DC–DC boost converter applications for low-voltage sensor ICs or energy harvesting? In this paper, we show that an additional inductor–capacitor–inductor filter can increase the oscillation amplitude of the ESCO, and call this topology the more enhanced swing Colpitts oscillator (mESCO). Rectifiers were connected with the output terminals of ESCO and mESCO to output boosted voltages, called ER (ESCO followed by rectifier) and mER (mESCO followed by rectifier), respectively. A SPICE simulation was run to compare the performance of ER and mER. The result showed that mER output a higher open circuit voltage and higher output current at a certain voltage than ER.
The rest of the paper discusses a circuit analysis of the mESCO. The oscillation frequency is shown as a function of the circuit parameters of mESCO. The common gate voltage gain ACG, defined by the ratio of the drain voltage amplitude to the source voltage amplitude of the switching MOSFET of mESCO, was modeled under the assumption that all the circuit elements are ideal. The drain voltage amplitude vda was also modeled by assuming that an averaged transconductance of the MOSFET in a half cycle is null when the long-channel Shockley model is used. vda needs to be sufficiently high to have a large DC–DC boost conversion ratio. The model can predict the tendency that vda increases as ACG approaches unity. We also found that the voltage difference of the drain voltage amplitude to the source voltage amplitude is a constant even when the circuit parameters, and thereby ACG, are varied. The paper is organized as follows: Section 2 proposes the mESCO and mER. The performance of mER is compared with that of ER. Section 3 analyzes the oscillation frequency, common gate voltage gain, and drain voltage amplitude of mESCO. The models are validated with SPICE simulation. The conclusion is given in Section 4.
2. More Enhanced Swing Colpitts Oscillator (mESCO), and DC–DC Converter with mESCO and Rectifier (mER)
Let us consider on-chip DC–DC boost converters composed of an oscillator whose peak output voltage is higher than the input DC voltage VIN and a rectifier to supply power to building blocks in sensor/RF IC, as shown in Figure 2. When the decoupling capacitor CDEC is too large to stabilize the input power rails, the oscillator runs with the DC supply voltage, as shown in Figure 2a. On the other hand, if CDEC is set to a relatively small value, the AC component adds to the DC supply voltage to create beat tones into the oscillator, as shown in Figure 2b.
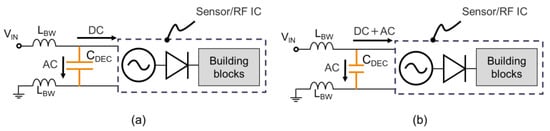
Figure 2.
(a) Relatively large decoupling capacitor to filter out the AC component; (b) relatively small decoupling capacitor to create beat tones into the oscillator.
Figure 3a illustrates a boost converter (ER) with an enhanced swing Colpitts oscillator (ESCO) followed by a rectifier to drive the load RL. The drain voltage of M1 exceeds VIN. M2 transfers the current when the peak drain voltage of M1 is higher than the target voltage VOUT. To increase the VSS of the ESCO, a small decoupling capacitor is connected between the VIN and VSS through the parasitic inductance of bonding wires, as shown in Figure 3b. Additional oscillation at VSS increases the drain voltage of M1, resulting in a higher output current at the same VOUT as ER.
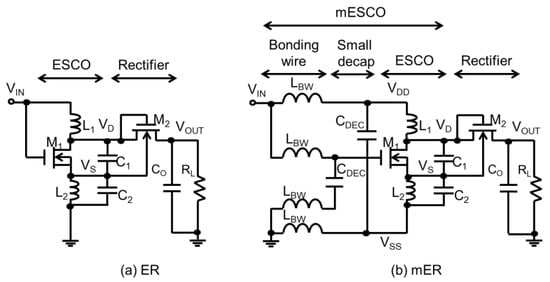
Figure 3.
(a) Enhanced swing Colpitts oscillator (ESCO) followed by rectifier (ER); (b) ER with LC filter (more enhanced swing Colpitts oscillator followed by rectifier (mER).
A SPICE simulation was run with VIN = 0.3 V, LBW = 2 nH, CDEC = 25 pF, L1 = 0.239 nH, L2 = 2.93 nH, C1 = 4 pF, and C2 = 1.5 pF. The parameters L1, L2, C1, and C2 are common to both circuits. The SPICE model in 65 nm CMOS was used in this study. Figure 4a shows the waveform of VD and VS of ER and mER when the outputs are open. The highest peak voltages of VD were 1.08 V with ER and 2.01 V with mER. In mER, the peak voltages were alternately high and low. Figure 4b shows the VOUT vs. IOUT of ER and mER. In addition to an increase in the maximum attainable output voltage, mER can have a larger output current at any operating output voltage than ER. In Section 3, a circuit analysis for mESCO is conducted.
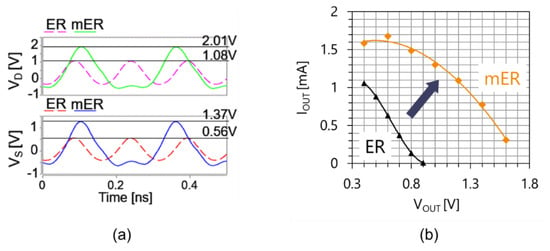
Figure 4.
Comparison of mESCO with ESCO; (a) waveform of VD and VS when the outputs are open, (b) VOUT − IOUT.
3. Circuit Analysis of mESCO
Let us define the notation of voltages in this work, as shown in Figure 5. The DC offset and voltage amplitude are described by VX and vxa, respectively. The voltage differences from the ground and DC offset are described by Vx and vx as a function of phase θ, respectively.
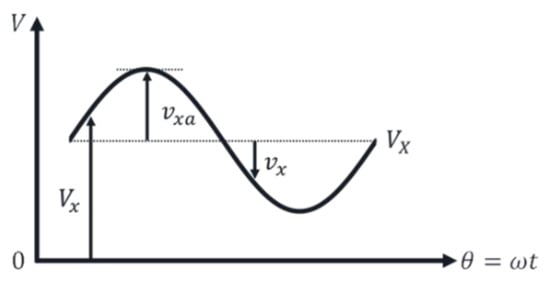
Figure 5.
Notation of voltages in this work.
3.1. Oscillation Frequency
The oscillation frequency of ESCO was modeled in [16] by ignoring any real part of impedance and conductance, assuming the ESCO operates in steady state. We can similarly formulate the oscillation frequency of mESCO. Figure 6 shows the circuit reduction of mESCO from Figure 6a through Figure 6g. A small-signal equivalent circuit of Figure 6a is reduced to Figure 6b. Introducing Ltb for the series connection of Lt and Lb with Ltb = Lt + Lb, and eliminating M1 results in Figure 6c under the assumption that any real part of impedance and conductance is omitted for a simple model. When the impedances of the parallel connections of Ltb and CIN and of L2 and C2 are capacitive, they can be replaced with single capacitors Ceq1 and Ceq2, respectively, by using the formula shown in Figure 6d, where ω is the angular velocity of a signal of interest. Likewise, when the impedance of the series connection of L1 and C1 is inductive, we can replace it with a single inductor Leq, by using the formula shown in Figure 6e. Thus, the circuit shown in Figure 6c is reduced to Figure 6f using Leq, Ceq1 and Ceq2. Finally, we can obtain an LC circuit as shown in Figure 6g, where Ceq = Ceq1 + Ceq2. Thus, (1)–(4) hold for mESCO.
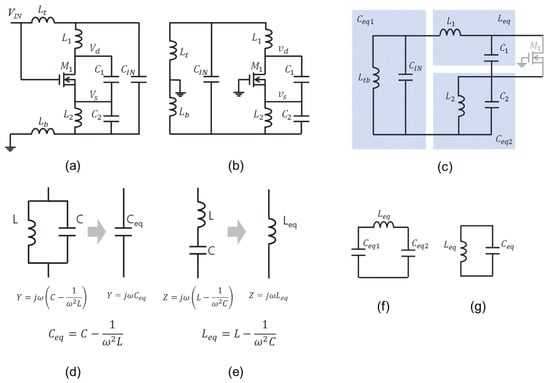
Figure 6.
Circuit reduction of mESCO from (a) through (g); (a) original mESCO, (b) small-signal equivalent circuit of (a), (c) omitting M1, (d) equivalent capacitance of L and C connected in parallel, (e) equivalent inductance of L and C connected in series, (f) circuit reduced from (c) with (d) and (e), and (g) circuit reduced from (f).
A fundamental frequency is given by the solution in cubic Equation (5) in terms of f2, and thereby can be resolved with three different values. To validate the models proposed in Section 3 with SPICE simulation, the nominal condition shown in Table 1 was used. The values of the inductors and capacitors were much larger than the ones fabricated in a single chip because the SPICE model in 180 nm CMOS was used for M1. For parameter response on electrical characteristics, the remaining ones except for the sweeping parameter were set as shown in Table 1.

Table 1.
Nominal condition to validate the models proposed in Section 3 with SPICE simulation.
The numerical solutions under wide ranges of circuit parameters were in good agreement with the SPICE results within 10% at most, as shown in Figure 7. Among the three solutions, the highest one was selected because the other two frequencies are too low to have Leq and Ceq positive values.
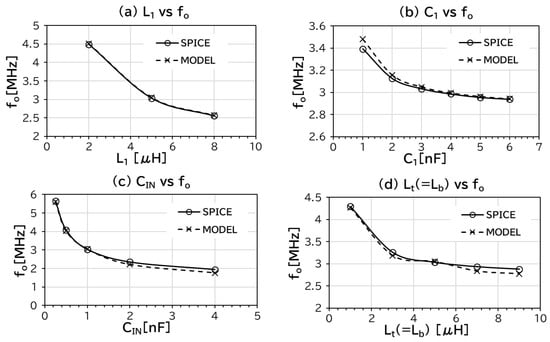
Figure 7.
Operation frequency as a function of each circuit parameter. (a) L1 vs. fo, (b) C1 vs. fo, (c) CIN vs. fo, (d) Lt(=Lb) vs. fo.
3.2. Common-Gate Voltage Gain
For DC–DC boost converters to have large boost ratios, a large voltage amplitude at the drain of M1 is required. Let us determine a common gate voltage gain ACG as a function of the circuit parameters first. As performed for modeling the operation frequency of mESCO, a circuit transformation was produced from an original circuit diagram of mESCO as shown in Figure 8a to its small-signal equivalent circuit as shown in Figure 8b, and then a circuit model of mESCO as shown in Figure 8c.
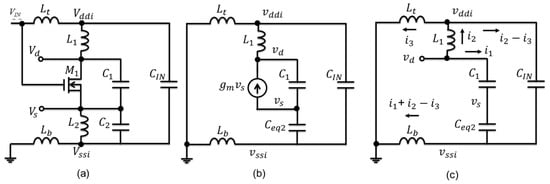
Figure 8.
Circuit transformation: (a) an original circuit diagram of mESCO, (b) its small-signal equivalent circuit, and (c) a circuit model of mESCO to extract its common-gate voltage gain ACG.
When vd is forced, what voltage appears at vs? Seven variables (four voltages and three currents) among six equations were applied, as shown by (6)–(11).
Therefore, an equation can relate any two variables. After some calculations, (12) was derived for the common gate voltage gain ACG. With (13)–(18), (12) provides a value for ACG when the circuit parameters are given.
where Ceq2 is given by (2). β, LX, and CX, defined by (16), (17), and (18), respectively, were used to calculate TSQ1-3. Figure 9 shows ACG as a function of each design parameter. The tendencies of ACG vs. L1 (a) and C1 (b) are matched with those for ESCO [16]. As expected, the smaller the CIN, the closer to unity for ACG in (c). (This tendency validated increasing the drain voltage amplitude with a smaller CIN in the following sub-section, as expected in Section 1). There were substantial discrepancies in ACG between the model and SPICE results for CIN > 2 nF. A physical background is required here, but its investigation will be conducted in future work. Figure 9d suggests that Lt and Lb can be minor contributors to ACG, resulting in no significant impact on the drain voltage amplitude, as discussed in the following subsection. In summary, the model calculation results were in good agreement with the SPICE results, except for CIN > 2 nF.
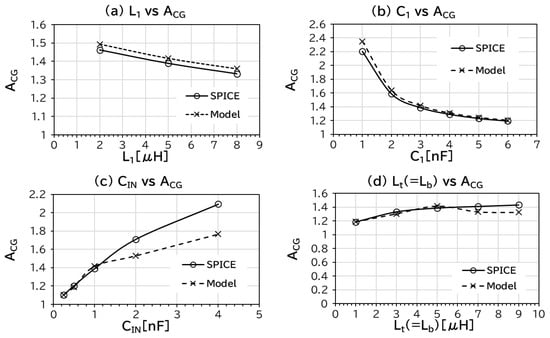
Figure 9.
ACG as a function of each design parameter. (a) L1 vs. ACG, (b) C1 vs. ACG, (c) CIN vs. ACG, (d) Lt(=Lb) vs. ACG.
3.3. Drain Voltage Amplitude vda
In this subsection, the drain voltage amplitude vda is modeled. In reality, there was a distortion in Vd and Vs due to the nonlinear behavior of the transconductance and drain conductance of M1, but it was assumed for simplicity in this study that the AC components of Vd and Vs are modeled with sinusoidal waveforms whose amplitudes are vda and vsa, respectively, as shown in Figure 10.
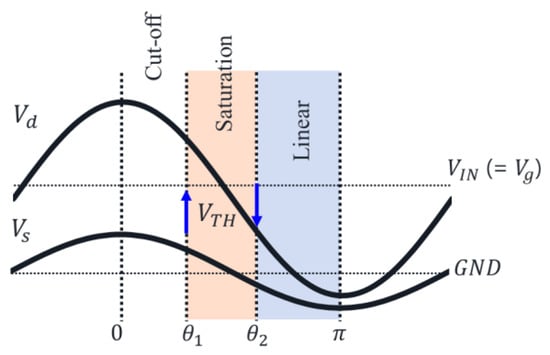
Figure 10.
Waveform of Vd and Vs and operation modes in one cycle.
Vd has an offset voltage of VIN. Thus, Vd and Vs can be written as (19) and (20), respectively.
When vsa is large enough, M1 operates in three different modes, i.e., in cut-off, saturation, and linear operation modes. θ1 is the boundary between cut-off and saturation, resulting in (21), where VTH is the threshold voltage of M1. θ2 is the boundary between saturation and linear, resulting in (22).
Let us assume a simple Shockley model for M1, as described in (23) and (24), where Ids_sat and Ids_lin are the drain current in saturation and liner modes, respectively, and k is a proportional coefficient of the drain current.
The transconductance is expressed by (25) and (26) in saturation and liner modes, respectively.
Let us assume (27) holds when mESCO runs in steady state, where the peak drain voltage does not change by cycle, because when the left side value of (27) is positive, the amplitude increases by a cycle; whereas when it is negative, the amplitude decreases by a cycle.
Using (21), (22), (25) and (26), (27) resulted in (28).
Equation (28) shows that vda is a function of ACG, VIN and VTH. Therefore, the model was compared with the SPICE results in terms of vda vs. ACG, as shown in Figure 11a. Dots in colors show the SPICE results where the circuit parameters are varied as much as the ones in Figure 9. Because the SPICE model for NMOSFET used in this study has no breakdown at high drain voltages, all the simulated data were plotted. However, because there is a strict specification for the maximum voltages in reality, it can limit the design space for the circuit parameters. Even though the model result has an offset from the trend curve of the SPICE results, the model well-represents the tendency that vda is determined by ACG rather than individual circuit parameters. It is interesting to note that the data points of vda and vsa are plotted on a linear line with a slope of 1.00 for both the SPICE results and model calculated results with a slightly different offset of 1.05 and 1.25 V for the SPICE results and model calculated results, respectively, as shown in Figure 11b.
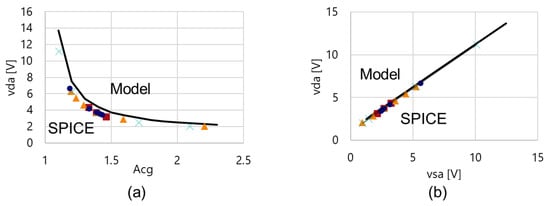
Figure 11.
(a) ACG vs. vda and (b) vsa vs. vda.
Figure 12a,b show the waveforms for voltage, current, and gm in cases of ACG = 1.2 and 1.8, respectively. The waveform for gm in Figure 12a suggests that gm in a linear operation can partially contribute to surplus for a very large voltage amplitude. For a relatively low voltage swing in Figure 12b, positive and negative gm appear in the saturation and linear regions, respectively.
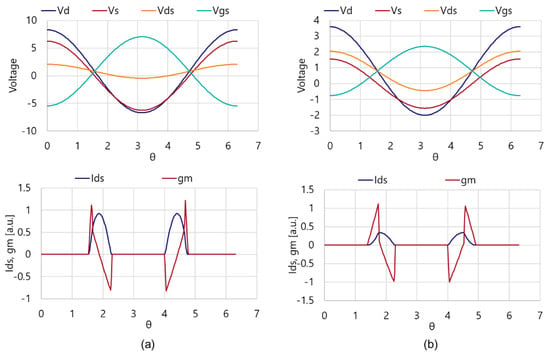
Figure 12.
Waveform in cases of ACG = 1.2 (a) and 1.8 (b).
To compare the vda of mESCO with that of ESCO, SPICE simulations and model calculations based on [16] were made with the same parameter conditions for L1, C1, and VIN as mESCO. Figure 13 shows the comparison results. Even though the model accuracy of (28) for mESCO is not as sufficient as that of [16] for ESCO, the trend over circuit parameters represents the SPICE results. With the same values for L1, L2, C1, and C2 as those of ESCO, mESCO has a 2× or larger vda than ESCO.
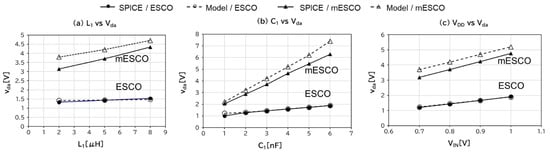
Figure 13.
vda of ESCO and mESCO as a function of L1 (a), C1 (b), and VIN (c).
The data in Figure 13 are placed in a single vda−ACG graph as shown in Figure 14. mESCO, as well as ESCO, has a unified characteristic curve. It is essential to design mESCO and ESCO with ACG as close to unity as possible to have a large vda.
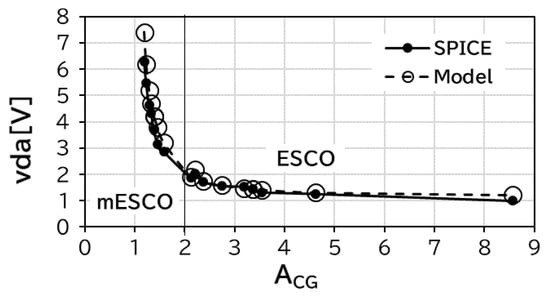
Figure 14.
vda of ESCO and mESCO as a function of ACG.
4. Conclusions
We found that an additional L–C–L filter for ESCO, called mESCO, increased the peak drain voltage, which will contribute to increasing the boost ratio when it is used in DC–DC boost converter applications. In this study, the operation frequency, common gate voltage gain, and drain voltage amplitude were analyzed with simple proposed models for mESCO. Even though the frequency model potentially has three different frequencies as a solution, the lower two components were not allowed because an equivalent inductor and capacitor would have had negative inductance and capacitance, respectively. The highest frequency was matched with the SPICE results in wide circuit parameter ranges. The common gate voltage gain was also modeled with a simple circuit transformation. The model calculation results are in good agreement with the SPICE results within a 10% error, except for large CIN. In addition, the drain voltage amplitude was modeled with an assumption that the average transconductance of the switching transistor over a half cycle is null. Even with a simple Shockley model, the drain voltage amplitude was successfully modeled so that it is a function of the common gate voltage gain rather than individual circuit parameters. This fact is valid for ESCO as well as mESCO. In wide ranges of L1, C1, and VIN, the drain voltage amplitude of mESCO was 2× or larger than that of ESCO. ESCO and mESCO had the same trend in the drain voltage amplitude over the common gate voltage gain.
Further experiments to validate the model and SPICE results and an application of mESCO to DC–DC boost converters will be conducted in the future. When a rectifier is added to mESCO for the DC–DC boost converter, it would have another impedance at the drain of the switching transistor, potentially yielding a loss in the drain voltage amplitude and thereby a degradation of the output power of the DC–DC converter. One would need to analyze its impact to design a DC–DC converter with sufficient output power.
Author Contributions
Conceptualization, T.T.; methodology, T.N. and T.T.; software, T.N.; validation, T.N. and T.T.; formal analysis, T.N. and T.T.; investigation, T.N. and T.T.; writing—original draft preparation, T.N.; writing—review and editing, T.T.; funding acquisition, T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI grant number 22K04042.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by JSPS KAKENHI grant number 22K04042.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| ACG | Common gate voltage gain |
| CDEC | Decoupling capacitor |
| ER | ESCO followed by rectifier |
| ESCO | Enhanced swing Colpitts oscillator |
| ET | Energy transducer |
| IoT | Internet of Things |
| LBW | Inductance of bonding wires |
| mER | mESCO followed by Rectifier |
| mESCO | more Enhanced Swing Colpitts Oscillator |
| SPICE | Simulation Program with Integrated Circuit Emphasis |
| vda | Drain voltage amplitude |
| VIN | Input DC voltage |
| VOUT | Output DC voltage |
| VX | DC offset |
| Vx | Voltage difference from ground |
| vx | Voltage difference from the DC offset |
| Vxa | Voltage amplitude |
| WPT | Wireless power transfer |
| θ | Phase |
References
- Shinohara, N. Power without wires. IEEE Microw. Mag. 2011, 12, S64–S73. [Google Scholar] [CrossRef]
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, A. Wireless power transfer and applications to sensor networks. IEEE Wirel. Commun. 2013, 20, 140–145. [Google Scholar] [CrossRef]
- Amar, A.B.; Kouki, A.B.; Cao, H. Power approaches for implantable medical devices. Sensors 2015, 15, 28889–28914. [Google Scholar] [CrossRef] [PubMed]
- Qian, L.; Cui, K.; Xia, H.; Shao, H.; Wang, J.; Xia, Y. An Inductive Power Transfer System for Powering Wireless Sensor Nodes in Structural Health Monitoring Applications. IEEE Trans. Microw. Theory Tech. 2022, 70, 3732–3740. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy Harvesting From Human and Machine Motion for Wireless Electronic Devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Kazmiersuki, T.; Beedy, S. Energy Harvesting Systems: Principles, Modeling and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–78. [Google Scholar]
- Trotter, M.S.; Griffin, J.D.; Durgin, G.D. Power-optimized waveforms for improving the range and reliability of RFID systems. In Proceedings of the 2009 IEEE International Conference on RFID, Orlando, FL, USA, 27–28 April 2009; pp. 80–87. [Google Scholar] [CrossRef]
- Boaventura, A.S.; Carvalho, N.B. Maximizing DC power in energy harvesting circuits using multisine excitation. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Collado, A.; Georgiadis, A. Optimal Waveforms for Efficient Wireless Power Transmission. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 354–356. [Google Scholar] [CrossRef]
- Clarke, K.K.; Hess, D.T. Communication Circuits: Analysis and Desig; Addison-Wesley Publishing Company: Boston, MA, USA, 1971; Chapter 6. [Google Scholar]
- Zhang, M.; Du, L.; Fang, Z.; Zhao, Z. A sensitivity-enhanced film bulk acoustic resonator gas sensor with an oscillator circuit and its detection application. Micromachines 2017, 8, 25. [Google Scholar] [CrossRef]
- Sharma, S.; Gao, H.; Hueber, G.; Mazzanti, A. A Magnetically Coupled Dual-Core 154-GHz Class-F Oscillator with -177.1 FoM and -87 dBc/Hz PN at 1-MHz Offset in a 22-nm FDSOI with Third-Harmonic Extraction. In Proceedings of the 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Honolulu, HI, USA, 12–17 June 2022; pp. 12–13. [Google Scholar] [CrossRef]
- Liu, S.-H.; Hung, C.-M.; Chuang, H.-R.; Huang, T.-H. A W-band Push-Push VCO with Gm-Boosted Colpitts Topology in 90-nm CMOS Technology. In Proceedings of the 2021 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Hualien, Taiwan, 25–27 August 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Troedsson, N.; Sjoland, H. An ultra low voltage 2.4 GHz CMOS VCO. In Proceedings of the RAWCON 2002 IEEE Radio and Wireless Conference (Cat. No.02EX573), Boston, MA, USA, 11–14 August 2002; pp. 205–208. [Google Scholar] [CrossRef]
- Hsieh, H.; Lu, L. A High-Performance CMOS Voltage-Controlled Oscillator for Ultra-Low-Voltage Operations. IEEE Trans. Microw. Theory Tech. 2007, 55, 467–473. [Google Scholar] [CrossRef]
- Brown, T.W.; Farhabakhshian, F.; Roy, A.G.; Fiez, T.S.; Mayaram, K. A 475 mV, 4.9 GHz Enhanced Swing Differential Colpitts VCO With Phase Noise of -136 dBc/Hz at a 3 MHz Offset Frequency. IEEE J. Solid-State Circuits 2011, 46, 1782–1795. [Google Scholar] [CrossRef]
- Machado, M.B.; Schneider, M.C.; Galup-Montoro, C. On the Minimum Supply Voltage for MOSFET Oscillators. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 347–357. [Google Scholar] [CrossRef]
- Lim, B.-M.; Seo, J.-I.; Lee, S.-G. A Colpitts Oscillator-Based Self-Starting Boost Converter for Thermoelectric Energy Harvesting With 40-mV Startup Voltage and 75% Maximum Efficiency. IEEE J. Solid-State Circuits 2018, 53, 3293–3302. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).