Abstract
Crowdsensing uses the sensing units of many participants with idle resources to collect data. Since the budget of the platform is limited, it is crucial to design a mechanism to motivate participants to lower their bids. Current incentive mechanisms assume that participants’ gains and losses are absolute, but behavioral economics shows that a certain reference point determines participants’ gains and losses. Reference dependence theory shows that the reference reward given by a platform and the reward obtained before will greatly affect the decision-making of the participant. Therefore, this paper proposes a participants’ decision-making mechanism based on the reference dependence theory. We set a reference point to reduce the participants’ bids, improving the platform’s utility. At the same time, risk preference reversal theory shows that participants evaluate the benefits based on the relative value of the rewards rather than the absolute value. Therefore, this paper proposes a winner selection mechanism based on the risk preference reversal theory. Theoretical analysis and simulations demonstrate that this paper’s incentive mechanism can guarantee the platform’s utility and improve the task completion rate.
1. Introduction
Crowdsensing is an emerging interactive sensing technology [1]. The technology is widely used in embedded devices and mobile devices for completing various sensing tasks such as traffic detection [2,3] and environmental monitoring [4,5]. Because crowdsensing uses the idle resources of participants to collect data, the cost of data collection is very low [6]. For example, [7] used taxi drivers at work to collect data. The location of the task needs to be consistent with the trajectory of the taxi so that the idle resources of the driver can be effectively utilized. Therefore, tasks can be allocated more efficiently through the model where drivers provide biddings.
Platform’s utility is an essential issue in crowdsensing [8]. When participants complete the crowdsensing task, they will consume resources such as computing and storage. Therefore, the platform must use a suitable incentive mechanism to compensate participants and ensure participation rates [9]. However, the goal of crowdsensing is to collect data at a lower cost than fixed sensors, so the platform’s budget is limited. The limited budget cannot recruit enough participants to complete the task, reducing the feasibility of crowdsensing applications. For example, crowdsensing can detect PM2.5 (fine particulate matter) and help draw a city’s air quality distribution map [10] to advise urban management. However, the city may make one-sided decisions if the number of participants is low and coverage is low. Crowdsensing can also collect the data of parking lots through onboard cameras. This crowdsensing application cannot be successful if the participants do not install cameras in their cars [11] without sufficient rewards. Therefore, it is necessary to design an incentive mechanism to motivate participants with a limited budget. Many studies discussed how to improve the utility of the platform with limited budgets [12,13,14,15]. Because the improvement of the platform’s utility means that the platform can motivate more participants to participate in the task, which will improve the probability of the success of the crowdsensing application.
However, the current platform’s utility-oriented incentive mechanisms have two problems: (1) when analyzing the participants’ decision-making, these mechanisms only consider the influence of participants’ intrinsic drives, i.e., the difference between the tasks’ reward and cost [16,17,18]. At the same time, these mechanisms set the goals of maximizing participants’ benefits. However, the reference dependence theory of behavioral economics shows that people are influenced by reference points when they make decisions [19]. Therefore, participants’ decisions are influenced not only by intrinsic drives but also by reference points. If the incentive mechanism only considers the intrinsic drive, the expected result will deviate from the actual one, and the incentive mechanism cannot achieve the best performance. At the same time, the platform cannot identify future potential participants in the incentive mechanisms that do not consider the reference points. Therefore, the incentive mechanism based on the reference dependence theory can perform better. (2) Current incentive mechanisms do not consider the impact of risk on participants’ decision-making [20,21,22]. When selecting participants, these mechanisms tend to select those who have a lower cost in completing the tasks. As for the same reward, these participants with a lower cost are more likely to continue participating in the task. However, the risk preference reversal Theory in behavioral economics shows that the reward has a different value for participants with varying types of risk [23]. Therefore, the incentive mechanisms that do not consider the risk preference will miss those most suitable participants. Suppose the incentive mechanism considers the influence of risk preference on the participants. In that case, it will be more likely to select the right participants, which in turn can improve the final CRoT.
In summary, reference points will affect participants’ decisions on whether to participate in the tasks. Therefore, by setting reasonable reference points, the platform can change participants’ decisions and thus achieve the expected goals. This paper uses the reference dependence theory of behavioral economics to design a participant’s decision mechanism. Through this mechanism, the platform can pick out participants with real potential. These potential participants will have higher expectations when facing the same task. These participants are like gamblers who think a lottery ticket with a high probability of not winning is valuable. For those low-reward tasks that ordinary participants are unwilling to do, these potential participants will have a greater probability of participating in the task. This will effectively increase the participation rate. At the same time, we take risks into the mechanism setting, which can guarantee the completion rate of tasks to a greater extent, especially for tasks requiring timeliness. For example, before the deadline of a task, if the participants are unwilling or unable to complete the task due to uncertainty, the platform needs to spend more money to motivate other temporary participants, which will greatly increase the cost of the platform. If risks are considered in the mechanism, those participants who are more robust in the face of risks can be selected. In that case, the platform’s utility and the completion rate of tasks will be effectively improved.
The Incentive Mechanism Based on Behavioral Economics (IMBE) proposed in this paper includes Participant Decision Mechanism Based on Reference Dependency (PDRD) and Winner Selection Mechanism Based On Risk Preference Reversal (WSRPR). These two mechanisms aim to improve the overall task completion rate and guarantee the platform’s utility.
The main contributions of this paper are as follows:
- A participant decision mechanism based on reference dependency called PDRD is proposed. This mechanism cultivates new and old participants to form reference points by setting internal and external reference rewards. It increases the expected reward of participants. In addition, a competition mechanism is designed based on the alternative participants. In the mechanism, the optimal decision of the participants is to lower their bids to improve the platform’s utility.
- A winner selection mechanism based on risk preference reversal called WSRPR is proposed. The mechanism calculates the value function of participants with different risk preferences for rewards and evaluates the variability of participants’ risk preferences. We design a winner selection algorithm to change the risk preferences of participants, so that the platform can select more potential participants. The algorithm enables participants to have higher values, which can increase the probability of participants participating in the task and improve the task completion rate.
The remainder of this paper is organized as follows. Section 2 introduces the existing incentive mechanisms and some studies in behavioral economics. Section 3 presents the system model of crowdsensing, and Section 4 describes the specific process of the IMBE. In Section 5, the IMBE is evaluated and analyzed by the experimental simulation. Finally, this paper summarizes the whole mechanism in Section 6.
2. Related Work
In this section, we introduce current incentive mechanisms based on traditional economics and explain the relevant concepts in behavioral economics.
2.1. Incentive Mechanisms Based on Traditional Economics
Currently, the existing incentive mechanisms in crowdsensing can be divided into monetary incentive mechanisms [24,25,26,27,28,29,30] and non-monetary incentive mechanisms [31,32,33,34]. Next, these two mechanisms will be introduced.
2.1.1. Monetary Incentive Mechanism
Monetary incentive mechanisms usually use rewards to motivate participants to achieve the platform’s goals, which is most widely used in crowdsensing [24]. Some monetary incentive mechanisms use the method of auction. Ji proposed a reverse auction, the mechanism takes the participant with the smallest bid as the winner to improve the platform’s utility and the task’s completion rate [25]. Yang proposed a two-way auction-based incentive mechanism to increase the overall task completion rate [26]. Gao paid old participants compensation based on the VCG (Vickrey–Clark–Groves) auction to ensure the participation rate of the old participants [27]. Some incentive mechanisms use the method of game theory. Kim designed an incentive mechanism based on reinforcement learning and game theory to motivate participants to increase the participation rate [28]. Pouryazdan proposed a scheme based on the perfect equilibrium of the coalition game and subgame to improve the platform’s utility and the participation rate [29]. Yang designed a platform-centered incentive mechanism based on the Stackelberg game model [30]. In the mechanism, the participants maximize their benefits according to their needs.
2.1.2. Nonmonetary Incentive Mechanism
Non-monetary incentive mechanisms usually use methods other than rewards to motivate participants to achieve platform goals. Some non-monetary incentive mechanisms use games to motivate participants. Jordan proposed a game approach to motivate participants [31]. Mccall incorporated a gamification-based badge scheme and a participant ranking scheme. Some incentive mechanisms make the participants who participate in the platform tasks gain a sense of accomplishment by setting the reputation value to motivate participants to participate in the task continuously [32]. Bigwood solved the problem of selfish participants’ reluctance to participate in tasks by introducing reputation values [33]. Sun proposed the concept of heterogeneous belief values to maximize social welfare and to increase task completion rate [34].
No matter what kind of classification these incentive mechanisms belong to, there are two problems with these incentive mechanisms.
First, these incentive mechanisms only consider the impact of intrinsic drives on participants’ decisions. For example, Ji and Yang assumed that the benefit is the only consideration for participants to make task decisions when designing auction mechanisms [25,26]. Participants will select a task as long as the benefit meets their expectations. These mechanisms often fail to achieve the expected results in reality. This is because if the platform has been paying participants with high reward and then suddenly reduces the reward at some point, participants will not accept the reduced reward, even though the reduced reward also meets their expectations. This extrinsic reference can affect the effectiveness of the mechanism. The same problem exists in the studies of Jordan and Mccall [31,32]. The two mechanisms only considered the impact of rankings on participants but not the rest of the participants. Therefore, if the influence of external reference on the participant’s decision is ignored, the expected incentive results will not be achieved.
Second, these incentive mechanisms do not consider the effect of risk on participants’ decisions. For example, Pouryazdan took the benefit of participants as the goal when designing the mechanism [29]. The study assumed that the higher the benefits of participants, the greater their satisfaction and the greater their probability of participating in tasks. However, behavioral economics points out that participants’ reward utility is not only determined by benefits, but also by their risk preference. For a risk-averse participant, even if faced with a task with high benefit, he will choose to give up the task because of the high variability of the task’s reward. If participants are evaluated only by their benefit, the platform will not find the potential participants, and the incentive effect will not meet expectations. Yang designed game mechanisms and assumed that participants are homogeneous so that the same game reward delivery mechanism will have the same incentive effect on participants [30]. However, behavioral economics’ risk preference reversal theory shows that the same reward will have different values for participants with different risk preferences. Therefore, using the same reward mechanism for all participants would make the incentive effect not meet expectations.
In summary, the presence of reference rewards and risk preferences can cause deviations between participants’ decisions and optimal decisions, which in turn affect the incentive effect. Therefore, this paper applies the reference dependence theory and the risk preference reversal theory of behavioral economics to construct an incentive mechanism, which aims to secure the platform’s utility and improve the task completion rate.
2.2. The Current Study of Reference Dependency
Reference dependency theory shows that people will be influenced by reference points when making decisions [35]. Mark classified reference points as external reference points and internal reference points [36]. External reference points are generated through the stimulation of external reference information, while internal reference points are generated through the decision maker’s previous experience [37]. Internal reference points are essentially participants’ predictions for the future based on their past experiences [38]. Reference points have been widely used in healthcare and finance [39]. Holte used reference dependence theory to design an incentive mechanism for “pay for performance” for physicians [40]. In [41], the relationship between consumers’ consumption decisions and information disclosure order was studied using reference dependence theory. Soetevent investigated how insurance companies encourage consumers to participate in the claim of loss compensation under the role of reference dependence [42].
Stores and insurance companies use reference dependence theory to motivate people to consume. The PDRD proposed in this paper is similar to the incentive methods of stores and insurance companies. The PDRD changes the participants’ decisions by setting reference points, which can guarantee the platform’s utility and increase the task completion rate.
2.3. The Current Study of Risk Preference Reversal
The risk preference reversal theory in behavioral economics shows that people make decisions based not only on absolute returns but also on their risk preferences. It was found that people’s preferences for risk are classified as risk aversion, risk neutral, and risk lover. When faced with increasing or decreasing reward, these types of participants have different valuation methods for value [23]. People’s risk preference types are variable [35], and the risk preference factor that measures the degree of people’s risk preferences is shown in Formula (1).
where denotes the first-order derivative of the value function, and denotes the second-order derivative.
Kahneman defined the value function [43], as shown in Figure 1 below. In Figure 1, the center of the coordinates is a reference. The decision maker calculates the value using the value curve graph on the right side of the coordinates when he considers himself to gain and using the left side when he considers himself to lose.
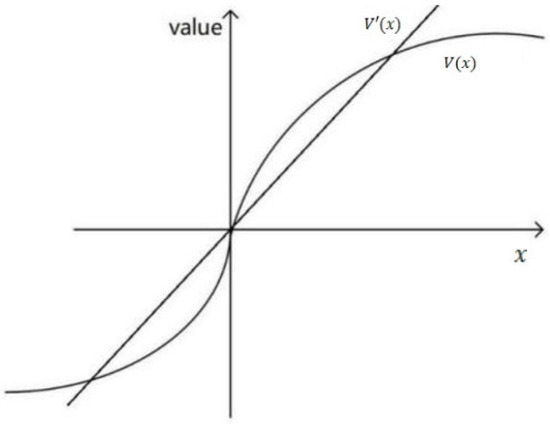
Figure 1.
The diagram of the value function.
Traditional economics uses the straight line in Figure 1 when calculating the value function of a participant , i.e., participant value is linearly related to the amount of gain/loss. In contrast, behavioral economics states that the value function of participants is nonlinear, and [23] gives the value function as shown in Formula (2):
where represents the decision maker’s gain/loss. When is greater than 0, the decision maker is in a gain state. On the contrary, the decision maker is in a loss state. The parameters and determine the concavity of the value function, and the parameter determines the slope of the value function, which reflects the decision maker’s sensitivity to losses.
In this paper, the reward for the participants to complete the task is fixed, and the cost of completing the task is uncertain. Furthermore, because net benefit = reward − cost, the participant’s net benefit is risky. According to Formulas (1) and (2), since the risk is reflected in the change of net benefit, the risk preference factor is related to the change of net benefit.
Risk preference reversal theory has been applied in many fields. For example, [44] found that agents’ risk preferences directly affect the optimal incentives and risk sharing between principals and agents. Ji used the risk preference reversal theory to design incentives to regulate workers’ safety behavior [45]. Enguix designed a rational compensation policy based on the degree of risk preferences of banking managers [46].
The WSRPR proposed in this paper is similar to the above incentive mechanisms. We can analyze participants’ decision-making more accurately by classifying participants according to their risk preferences. The WSRPR can thus improve the task completion rate.
3. System Model
3.1. Physical Model
Figure 2 shows the physical model of IMBE. The circular area in the figure shows the area for the crowdsensing task. There are multiple task areas in the figure, and the quality of task completion in each area is related to the number of participants who complete the task in that area. The more participants, the higher the quality of task completion in that area. The IMBE mainly acts on the interaction between participants and the platform. The platform encourages participants to participate in tasks through the IMBE to improve the quality of task completion. The main interaction is divided into six steps, which are described as follows:
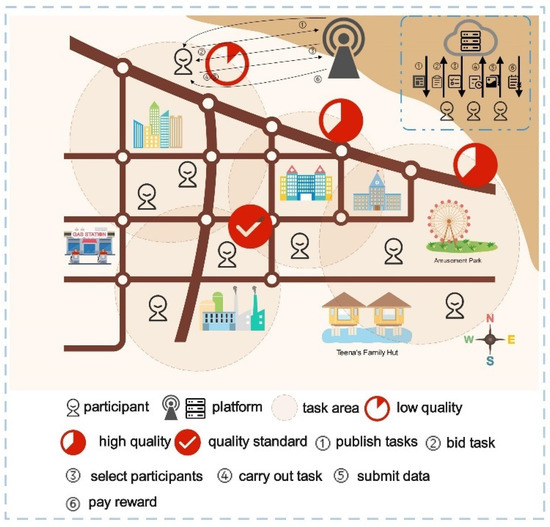
Figure 2.
Physical model.
Step 1. Platform publishes tasks: The platform publishes the task set Step 2. Participant bids: Participant bid for tasks in the jth round according to their conditions, such as cost, willingness to participate, task value, etc. Let as the bid price of participant . At the same time, the platform includes all bidding participants into the candidate set .
Step 3. Platform selects the winners: The platform selects the winners of the jth round from the set according to certain rules and includes the final selected participants into the winner set .
Step 4. Participants complete the task: Participants in complete the sensing tasks assigned by the platform.
Step 5. Participants submit data: Participants submit the collected data to the platform after completing the tasks of the jth round.
Step 6. The platform pays reward: The platform rewards all participants who have completed the tasks according to certain rules.
In the six steps of the above interaction, we assume that the platform’s server is safe and reliable. The storage of participants’ information and data transmission are safe, and there will be no leakage of participants’ privacy.
Next, we will define some key parameters that appear in the paper.
Definition 1 (External reference reward).
The reward’s reference value is provided by the platform for new participants. The external reference reward is the reward that a new participant expects to receive when participating in the task of the jth round (i.e., the first round thatparticipate in the task).
Definition 2 (External reference factor ).
The impact of the external reference reward on the decision of new participants.
Definition 3 (Internal reference reward).
The reward standard is set by the platform for old participants (not first-time participants who participate in task) who are to participate in the next round of tasks.
Definition 4 (Internal reference factor).
The impact of the internal reference reward on the bid prices of old participants.
Some additional parameters and related descriptions covered in this paper are given in Table 1.

Table 1.
Parameter table.
3.2. Logic Model of IMBE
Figure 3 shows the logic model of IMBE. IMBE mainly acts on steps 2, 3, and 5, which are the most critical steps in the physical model in Section 3.1.
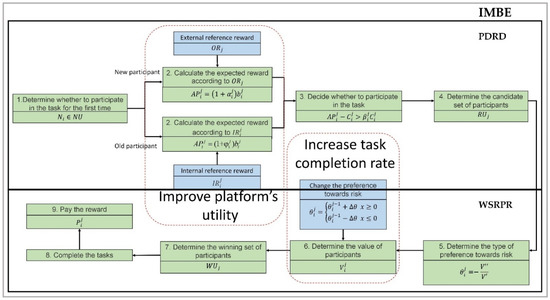
Figure 3.
Logic model of IMBE.
This section proposes the incentive mechanism called IMBE based on reference dependence and risk preference, which works mainly in the phases of participant selection of tasks, platform selection of participants, and platform payment of rewards.
First, the PDRD acts. In step 1, the platform classifies participants into new and old participants based on whether has participated in the tasks before. In step 2, the platform calculates the expected reward of participants using external reference reward and internal reference reward . In step 3, the platform determines whether the participant can participate in the task based on the expected reward and decides which participants will be placed into the candidate set based on the expected reward of the participant. In the PDRD, participants will lower their bids to be able to join the candidate set, which will increase the platform’s utility.
Then, the WSRPR follows. In step 5, the platform determines the participant’s risk preference and the value function of the participant in step 6 based on the type of the participant. After ranking participants’ value functions in step 7, the platform selects participants with the larger value function into the winning set . In this process, participants will change their risk preferences to be selected into the winning set, increasing the final task completion rate. Finally, in step 8, the participants complete the tasks, and in step 9, the platform pays to participants.
To sum up, in the PDRD, the platform will select more potential participants according to the indicator of expected reward, which is designed according to the reference dependence theory. Then, the platform puts these participants into the candidate set. These participants were more likely to participate in the task even when faced with low pay. In the WSRPR, the platform will select more potential participants according to the indicator of the value function, which is designed according to the risk preference theory. Then, the platform puts them into the winner set. These participants were more likely to participate in tasks even when faced with risky situations. Therefore, the platform can incentivize these participants to complete tasks with less reward, which will increase the platform’s utility.
4. The Incentive Mechanism Based on Behavioral Economics
4.1. The Detail of PDRD
Participants will choose whether to participate in the task according to their expected rewards. As seen in Section 2.2, reference points can make participants overestimate their actual benefits, motivating them to lower their bids per round and increase the platform’s utility. This section describes the effect of reference points on new and old participants, external reference rewards and internal reference rewards separately. In particular, the platform classifies participants who have never participated in a task as new participants and puts them into the new participant set , and classifies participants who have participated in the task as old participants and puts them into the old participants set .
4.1.1. Setting of External Reference Reward
According to the reference dependence theory in Section 2.2, participants’ expected rewards are not constant and can be changed by external factors. The expectations for rewards of new and old participants are different and need to be discussed separately. This section first discusses the setting of external reference rewards that affect new participants.
The platform gives an external reference reward to all new participants. As seen from Section 2.2, the external reference points of participants are generated based on the stimulus of external reference information. New participants who have never participated in a task before have no reference standard for the reward. Thus, they need to rely on the platform to generate a reference value. The reference value is based on the market price and the platform’s budget. The range of external reference values has an impact on the evaluation of decision makers, so we set the range of external reference rewards for new participants in the jth round of tasks as shown in Formula (3):
where the parameter represents the total budget of the platform and the parameter represents the number of participants involved in the sensing task.
the cost of participating in the task of jth round. Since it is necessary to ensure that the expected return of participants is positive, the external reference reward given by the platform to new participants must be greater than the cost of participants. At the same time, to keep the reward within the budget of the platform, the external reference reward must be smaller than the average budget of the platform for each participant, that is, .
The range of the external reference rewards for participants was discussed above. Next, we set an external reference factor to measure the impact of on a new participant’s decision. The external reference factor should be related to , where is the difference between the external reference reward and the bid price . The larger , the larger the expected reward of the participant, the larger the external reference factor. Therefore, this paper defines the external reference factor as shown in Formula (4):
As the growth of has an upper limit, and the growth rate of decreases over time, so we define the function as shown in Formula (5):
Bringing into Formula (4), we can obtain the final expression of the reference factor:
As a result, can be used to quantify the influence of external reference rewards on participants’ decisions, which supports the later discussion of participants’ decisions.
4.1.2. Setting of Internal Reference Reward
The previous section discussed the external reference rewards set for new participants, and this section discusses the internal reference rewards for old participants. For old participants who have participated in the task before, the external reference rewards have less impact on them. The expected rewards for participating in the task are related to the experience of previously completed tasks. Therefore, this section describes the setting of internal reference rewards for old participants.
For an old participant , they will form their expectations of reward. Accordingly, the platform sets the internal reference reward for old participants to discuss the decision-making of old participants.
For each old participant , the platform defines the internal reference reward as shown below:
where the parameter represents the bid of the old participant in the jth round, and represents the internal reference factor. The next step is to discuss the setting of the internal reference factor.
As seen from Formula (7), the internal reference reward of the old participant in the jth round of the task is adjusted by the bid price . The internal reference factor is used to reflect the degree of adjustment of the internal reference reward.
When the internal reference reward of the participant in the (j − 1)th round is less than the mean reward , the internal reference factor has a positive incentive effect on the participant , and vice versa. At the same time, there are certain upper and lower bounds for the change of internal reference factor , and the change rate gradually tends to 0. Thus, we set the definition of the internal reference factor as follows:
4.1.3. Participant’s Decision-Making
This section discusses participants’ decision-making based on the reference dependence discussed above. We will describe the incentive effect of the internal and external reference rewards on the decision-making of new and old participants.
The conditions for a participant to participate in the task can be represented by the following Formula (9):
where represents the actual reward of the participant in the jth round, represents the cost of the participant , and represents the expected reward rate of the participant . The cost of the participant to complete the task includes definite costs and uncertain costs. The definite costs include energy consumption for positioning and transmitting data, which can be calculated and provided by the platform [47,48]. The uncertain costs include the cost required for the participant to reach the task location and the time cost, etc., which need to be evaluated by the participant [49,50]. Participants decide to participate in the task only when the real reward exceeds the expected reward.
Next, we introduce the concept of expected reward to analyze the participant’s decisions. We define the expected reward as the expected reward of participant in the jth round.
Since the expected rewards of new and old participants have different reference points, they need to be discussed separately.
The expected rewards of new participants are discussed first. For new participants, the conditions for their participation in a new round of tasks are as follows:
The expression of the expected reward is given by the following Formula (11):
After substituting Formula (11) into Formula (10), the new condition can be obtained as follows:
By comparing Formula (12) with Formula (9), we can find that . Since , the bids of the new participant under the external reference reward must be smaller than the reward received by the participant without the mechanism, i.e., . In other words, the PDRD can motivate new participants to reduce their bids, which is beneficial to improving the platform’s utility.
For old participants, the expected reward is given by the following Formula (13):
After substituting Formula (13) into the decision condition of Formula (10), the new decision condition can be obtained as the following Formula (14):
Similarly, we find that under the PDRD, the old participants will also reduce their bids, improving the platform’s utility.
The above section discusses the effect of reference rewards on the decision of new and old participants. Then, we can judge whether the participant can join the candidate set of a participant.
4.1.4. Setting of the Reference Reward
Finally, to facilitate the discussion of new and old participants, we set the reward reference value for evaluating the reward assigned to participants in the jth round.
The formula of the reward reference value is defined as follows:
Substituting the formulas of the external reference factor and internal reference factors into Formula (15), the complete formula of can be obtained as the following Formula (16):
The definition of facilitates the design of the following payment mechanism.
4.2. The Detail of WSRPR
The variable risk preference theory in behavioral economics points out that participants’ variable preference for risk affects their decisions. Based on the theory, we designed the winner selection mechanism WSRPR.
4.2.1. Setting of Risk Preference
According to the risk preference theory, participants are divided into risk aversion, risk neutrality, and risk lover according to the types of risk preference. Risk preference factors are designed to measure participants’ degree of risk preference. This part first introduces the risk preference factor.
It can be seen from Section 2.3 that when facing uncertainty, participants will make decisions according to their risk preference. Participants with different risk preferences have different preferences for different tasks. Therefore, we designed the risk preference factor of participants according to the value function discussed in Section 2.3, which can be used to evaluate the type and degree of risk preference of participants. We define the risk preference factor of participant in the jth round as Formula (17):
where is the second derivative of the value function of participant in the jth round. is the first derivative of the value function. The setting of the value function will be introduced in Section 4.2.2.
Next, we discuss the range of risk preference factors of participants with different risk preference types according to the risk preference theory.
For participants who are risk lovers, the value function is a convex function [23], i.e., . In addition, the value increases gradually with the increase of income, i.e., . According to the definition of the risk preference factor, the risk preference factor of participants who are risk lovers is . Similarly, for risk averse participants, the risk preference factor is , while for risk neutral participants, the risk preference factor is .
This section discusses the range of risk preference factors of different types of participants. Next, we can discuss the value functions of different types of participants.
4.2.2. Participant’s Value Function
In this section, we will discuss the setting of the value function of different types of participants and the relevant properties of the value function.
The value function in behavioral economics reflects the participants’ evaluation of the value of completing the task. This paper sets as the basis for selecting participants. Participants with higher value functions will be preferentially selected. We define as Formula (18):
where the parameters , and . represents the expected benefit of participant . In Formula (18), for the participants who participate in the task, the reward is a gain, and for the participants who do not participate in the task, this part of the reward that is not received is a loss. To further refine the value function, we need to discuss whether the participants will participate in the task.
Formula (14) represents the condition for the old participant to decide to participate in the task. We substitute the expression of the internal reference factor into Formula (14) to obtain the condition for the participant to decide to participate in the task as the following Formula (19):
Substituting Formulas (8) and (19) into Formula (18), we can obtain the value function as follows:
It can be seen from Formula (20) that when , the platform will meet the requirement of the participants who show risk aversion, i.e., , when , the platform will not meet the requirement of the participant who are risk lovers, i.e., . Therefore, the platform will prioritise the participants with risk aversion as the winners.
4.2.3. Risk Preference Reversal
It can be seen from the previous section that participants who are risk lovers will feel loss when they are unable to get the reward, and then, they may change their risk preference. This section discusses the change in participants’ risk preference based on the risk preference reversal theory in behavioral economics. We use the following Formula (21) to express this change:
when the risk preference factor increases, the risk aversion degree of participants gradually increases. When it decreases, the risk lover degree of participants gradually increases. Changes in participants’ risk preference are mainly divided into (1) participants changed from risk aversion to risk lover or (2) participants changed from risk lover to risk aversion. Next, the two types of situations are described respectively:
(1) Participants change from risk aversion to risk lover. In this case, the platform continues to meet the participants’ internal reference reward until the participants’ internal reference reward exceeds the average reward. As the platform has always met the participants’ requirements for reward in the first few rounds, the degree of participants’ risk aversion gradually increases. When the internal reference reward of the participants is greater than the budget ceiling of the platform, the participants generate a negative value function, and the type of risk preference of the participants will change from risk aversion to risk lover. At this time, the platform will not select this participant.
(2) Participants change from risk lover to risk aversion. When the participant is a risk lover, the value generated by the participant is negative. We can know from Formula (20) that the negative participant value generated by the loss of the participants under the same reward is greater than the positive participant value generated by the reward, which indicates that the participants attach great importance to the loss. To avoid the loss of the participants, the platform will reduce the participants’ internal reference reward until the reference reward is less than the platform budget, and the platform will reconsider selecting the participants. When participants re-enter the alternative set, they will produce positive value.
After discussing participants’ change of risk preference, we next discuss how the platform selects participants in the alternative set to generate the winning participant set.
4.2.4. Winner Selection Algorithm Based on Risk Preference Reversal
In this section, we will select appropriate participants from the platform task candidate set and put them into the winner set to prepare for completing the platform task according to the behavior decision-making methods of different participants discussed earlier. Algorithm 1 shows the process of finding the winner set .
| Algorithm 1. Winner Selection Algorithm Based on Risk Preference Reversal. |
| input: candidate set:, mean reward: |
| output: winner set: |
| 1: For |
| 2: For |
| 3: ; |
| 4: End For |
| 5: For |
| 6: ; |
| 7: If |
| 8: ; |
| 9: End If |
| 10: End For |
| 11: End For |
In Algorithm 1, lines 2–4 traverse the for each round and calculate the participant’s value . Then, lines 5–9 sort these participants’ values from high to low according to the number of participants required for the platform in the jth round. The participants whose value is ranked in the top and whose bid price is less than the reward in the traditional mechanism are put into the winner set in turn. By repeating this process times, the set of all winner participants in the rounds of the platform can be obtained.
After the platform selects the winning participants, the participants will complete the corresponding tasks published by the platform.
4.2.5. Platform’s Utility
The platform’s utility can be used to measure the benefits ability of the platform, i.e., the difference between the total value brought to the platform by each round of participants after completing the task and the remuneration paid to the participants. The higher the utility of the platform, the more the platform can recruit more participants to complete the task, which will improve the task completion rate. We define the platform’s utility as the following Formula (22):
where represents the value of the task completed by participant in the jth round task, and represents the reward paid by platform to participant after completing the jth round task.
Based on Formula (22), we discuss the relationship between the platform’s utility of the DSTA [51] and the PDRD in this paper.
Note that the platform’s utility under PDRD is , and its expression is: . Note that the platform’s utility under the DSTA is , and its expression is . In the PDRD, the decision-making condition for new participants to participate in a new round of tasks is . In the PDRD, the decision-making condition for old participants to participate in a new round of tasks is . For the participants in the DSTA, their decision conditions for participating in a new round of tasks are: . Take the new participant as an example. At this time, we assume that when makes participant decisions according to two different mechanisms and algorithms under the same initial conditions, the costs and of the j round task of the participant under the two mechanisms and algorithms are the same, the expected returns and are the same. Based on this, we observe the left-hand side and of the two inequalities, and we can conclude that the following equation holds when all the above parameters are equal: . Since the external reference factor satisfies for the participant , under the two algorithms, the participant’s quotation satisfies . It can be found that the PDRD reduces the bid of the participants. The remuneration given to the participant by the PDRD is less than or equal to the participant’s quotation. In contrast, the remuneration given by the platform to the participant in the DSTA is the participant’s quotation. Therefore, we can conclude that the reward paid by the platform to the participants under the PDRD is less than that paid by the platform to the participants under the DSTA. According to Formula (26), when the task value is equal, the less the reward to the participants, the greater the platform’s utility. At the same time, the actual reward of the participants of the PDRD is always less than the actual reward under the DSTA. Therefore, we can obtain that the platform’s utility under the PDRD is greater than that under the DSTA algorithm, i.e., .
It can be seen from the above that under the IMBE, the platform can obtain higher benefits, which also shows that it can recruit more participants to complete tasks, thereby improving the final task completion rate.
5. Simulations and Evaluations
The IMBE is simulated and compared with the DSTA (Duration-Sensitive Task Allocation) [51] in the section. The DSTA mechanism aims to maximize the number of completed tasks under certain constraints and transform the optimization problem into a constrained submodular optimization problem. The DSTA mechanism proposed an efficient greedy heuristic algorithm based on the utility function to solve the optimization problem. Experiments show that compared with the latest mechanisms [52,53,54], DSTA can improve the number of tasks completed. Therefore, we choose the DSTA as the comparison mechanism.
5.1. Simulation Settings
Table 2 shows the initial settings for the simulation experiments. In the simulation, we set up a 25 km × 25 km area for the experiment. The distribution of tasks conforms to a uniform distribution [55,56], and the distribution of participants conforms to a clustered distribution [57]. The initial settings of the parameters and in the value function are the theoretical values in behavioral economics [23]. We use the JAVA language to simulate, and take the average value by simulating 100 times as the result of the simulation.

Table 2.
Experimental parameter settings.
5.2. Discussion on the Effect of the IMBE
Figure 4 shows the reference value of the participant’s reward under the PDRD. The reference value of the reward directly affects the reward the participant can get. In the experiment, we first determined the maximum reference value of the participant’s reward and then traversed the reference value of each participant’s reward. At the same time, the ratio of the reward reference value of these participants to the maximum reward reference value is within the range of (0,1). In Figure 4, the reward reference value of participant 11 among participants in the current round is the largest. In addition, the reward reference value of participant 7 and participant 19 is 0, indicating that these two participants did not participate in the platform task.
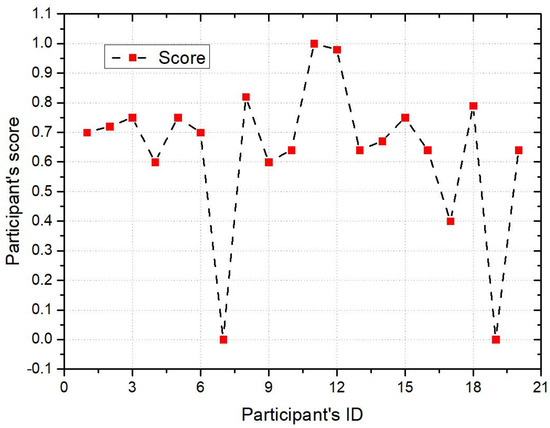
Figure 4.
Reward reference value.
Next, Figure 5 shows the value of participants under the WSRPR mechanism. The participant value reflects the possibility of the participant participating in the task. It is also an important reference indicator for the platform to determine the winning participants. The experiment collected the participant value of 20 participants. As seen from the figure, most participant values are mainly concentrated between (6,8). Participant 17 has the lowest value, and the value is 4. According to the theory of risk preference reversal, the participant may be a risk lover. The platform will not select this participant to enter the winning set. Participants 11 and 12 have the largest participant value, both exceeding 10. They may be risk aversive, and the platform will prioritize them into the winning participant set.
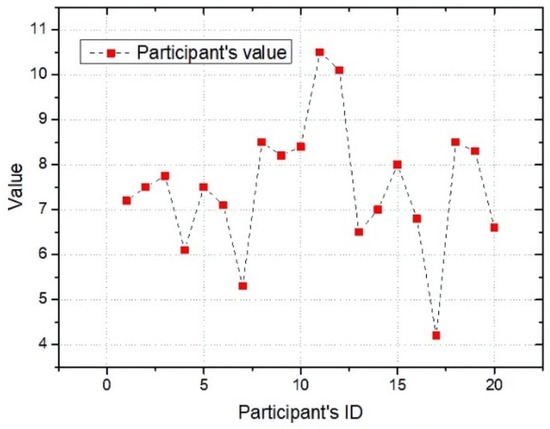
Figure 5.
Participant value.
Figure 6 shows the analysis of participant value under the WSRPR. The Y-axis is the factor of the value function, and the x-axis is the rounds. It can be found that the round has a smaller impact on the participant value, while the impact factor has a greater effect on the value function. It can be found that the value function of participants mainly depends on their preference for reward. In addition, in the whole process of completing the task, the value of participants will not fluctuate greatly. It will be relatively stable, which is conducive to the platform’s incentives for participants.
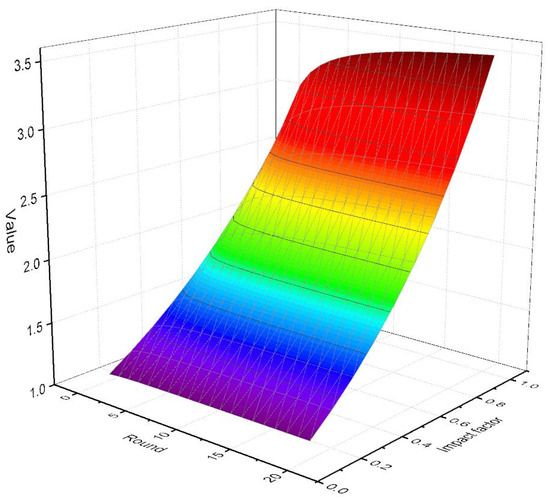
Figure 6.
Participant value analysis.
5.3. Comparison with DSTA
In this section, we will compare the results of the IMBE and the DSTA.
Figure 7 shows the rewards paid by the platform for each completed task. The number of tasks in the current round is 50, and the rewards that need to be paid to participants range from 0 to 10. It can be seen from the figure that the platform will pay more in the DSTA than in the PDRD. For example, for the participants, the reward for task 23 under the PDRD is 4.8, and the reward for task 23 under the DSTA is 7.9. This further proves that under the PDRD, the platform can motivate participants to complete tasks with less reward, which improves the platform’s utility.
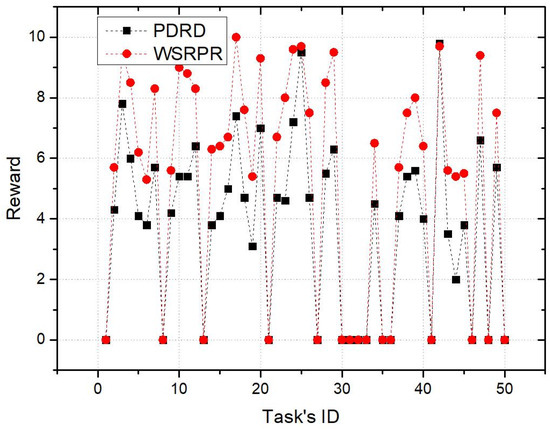
Figure 7.
Comparison of reward.
Figure 8a shows the platform’s utility under the two mechanisms. In addition, the experiment collected 20 rounds of the platform’s utility of PDRD and DSTA, in which the value of each platform task is 30 per round. It can be seen from the figure that the platform’s utility of PDRD is higher than that of DSTA, which indicates that PDRD can effectively improve the platform’s utility.
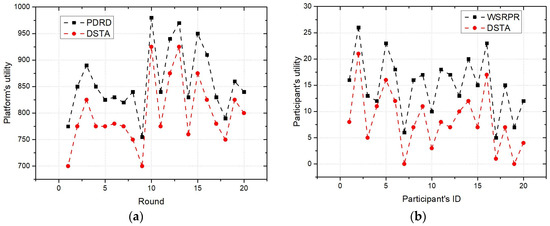
Figure 8.
(a) Comparison of platform’s utility, (b) comparison of participant utility.
Finally, Figure 8b compares participants’ utility. It can be seen from the figure that under the WSRPR, the utility of all 20 participants is greater than that of the participants under the DSTA. At the same time, it can be found that compared with the DSTA, the WSRPR has a similar trend in the participant’s utility, which is the impact of the reward reference value on the participants. It can be seen from the figure that the total participants’ utility under the WSRPR is greater than that under the DSTA.
6. Conclusions
This paper proposes an IMBE based on behavioral economics to solve the low platform’s utility resulting in a low task completion rate. The IMBE includes the PDRD and WSRPR. PDRD uses external and internal reference rewards, respectively, to form a reference point for new and old participants and motivate participants to lower their bids. Participants’ lower bids increase the utility of the platform. Thus, under the same budget limit, more participants can be motivated to participate in the task, and the final task completion rate can be improved. In the WSRPR, according to the risk preference of different participants, we design a value function based on risk preference reversal to evaluate the participants’ potential for participating in the task. The platform can choose those more potential participants under the condition of paying the same reward, which can improve the participants’ utility and increase the task completion rate. The simulation results show that, through this mechanism, participants reduce the bid price, guarantee the platform’s utility, increase the participants’ utility, and improve the overall task completion rate. At the same time, the effects of different parameters in the mechanism are discussed. Next, we will further apply our incentive mechanism to real crowdsensing applications. We hope to optimize the parameter settings in the incentive mechanism through the feedback of the incentive mechanism in the real environment to achieve better incentive effect.
Author Contributions
R.P., H.X. and J.L. designed the project and drafted the manuscript, as well as collected the data. W.H. and M.P. wrote the code and performed the analysis. All participated in finalizing and approved the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Hunan Provincial Natural Science Foundation of China (2020JJ5770, 2021JJ30869) and in part by Changsha Municipal Natural Science Foundation kq2014136.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lin, Y.; Cai, Z.; Wang, X.; Hao, F.; Wang, L.; Sai, A.M.V.V. Multi-Round Incentive Mechanism for Cold Start-Enabled Mobile Crowdsensing. IEEE Trans. Veh. Technol. 2021, 70, 993–1007. [Google Scholar]
- Liu, Z.; Jiang, S.; Zhou, P.; Li, M. A Participatory Urban Traffic Monitoring System: The Power of Bus Riders. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2851–2864. [Google Scholar]
- Feng, Z.; Zhu, Y.; Zhang, Q.; Ni, L.; Vasilakos, A.V. TRAC: Truthful Auction for Location-Aware Collaborative Sensing in Mobile Crowdsourcing. In Proceedings of the 2014 33rd IEEE Annual Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 1231–1239. [Google Scholar]
- Hasenfratz, D.; Saukh, O.; Walser, C.; Hueglin, C.; Fierz, M.; Arn, T.; Beutel, J.; Thiele, L. Deriving high-resolution urban air pollution maps using mobile sensor nodes. Pervasive Mob. Comput. 2015, 16, 268–285. [Google Scholar]
- Hu, Y.; Dai, G.; Fan, J.; Wu, Y.; Zhang, H. BlueAer: A fine-grained urban PM 2.5 3D monitoring system using mobile sensing. In Proceedings of the 2016 35th IEEE Annual International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Wei, X.; Yang, Y.; Jiang, W.; Shen, J.; Qiu, X. A Blockchain Based Mobile Crowdsensing Market. China Commun. 2019, 16, 31–41. [Google Scholar] [CrossRef]
- Restuccia, F.; Ferraro, P.; Silvestri, S.; Das, S.K.; Re, G.L. IncentMe: Effective Mechanism Design to Stimulate Crowdsensing Participants with Uncertain Mobility. IEEE. Trans. Mob. Comput. 2019, 18, 1571–1584. [Google Scholar] [CrossRef] [Green Version]
- Yucel, F.; Yuksel, M.; Bulut, E. IncentMe: Coverage-Aware Stable Task Assignment in Opportunistic Mobile Crowdsensing. IEEE Trans. Veh. Technol. 2021, 70, 3831–3845. [Google Scholar] [CrossRef]
- Sun, P.; Wang, Z.; Wu, L.; Feng, Y.; Pang, X.; Qi, H.; Wang, Z. Towards Personalized Privacy-Preserving Incentive for Truth Discovery in Mobile Crowdsensing Systems. IEEE. Trans. Mob. Comput. 2021, 21, 352–365. [Google Scholar]
- Guo, H.; Dai, G.; Fan, J.; Wu, Y.; Shen, F.; Hu, Y. A Mobile Sensing System for Urban PM2.5 Monitoring with Adaptive Resolution. J. Sens. 2016, 2016, 7901245. [Google Scholar]
- Munneke, M.; Nijkrake, M.; Keus, S.H.J.; Bloem, B.R.; Kwakkel, G.; Berendse, H.M.; Roos, R. A process evaluation of ParkNet implementation. Parkinsonism Relat. Disord. 2007, 13, S181. [Google Scholar]
- Jiang, W.; Chen, P.; Zhang, W.; Sun, Y.; Chen, J. Mobile Crowdsensing User Recruitment Algorithm Based on Combination Multi-Armed Bandit. J. Electron. Inf. Technol. 2022, 44, 1119–1128. [Google Scholar]
- Jiang, W.; Chen, P.; Zhang, W.; Sun, Y.; Chen, J.; Qing, W. User Recruitment Algorithm for Maximizing Quality under Limited Budget in Mobile Crowdsensing. Discret. Dyn. Nat. Soc. 2022, 2022, 4804231. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, W.; Chen, P.; Chen, J.; Sun, Y.; Yang, Y. Quantity sensitive task allocation based on improved whale optimization algorithm in crowdsensing system. Concurr. Comput. Pract. Exp. 2021, 2021, e6637. [Google Scholar] [CrossRef]
- Li, F.; Zhao, J.; Yu, D.; Cheng, X.; Lv, W. Harnessing Context for Budget-Limited Crowdsensing with Massive Uncertain Workers. IEEE ACM Trans. Netw. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Wang, E.; Yang, Y.; Lou, K. User Recruitment for Optimizing Requester’s Benefit in Self-Organized Mobile Crowdsensing. IEEE Access 2018, 6, 17518–17526. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, D.; Bhuiyan, M.D.Z.A.; Xu, M.; Wang, G.; Lv, P. Towards Benefit Optimization during Online Participant Selection in Compressive Mobile Crowdsensing. ACM Trans. Sens. Netw. 2019, 15, 38. [Google Scholar] [CrossRef]
- An, B.; Xiao, M.; Liu, A.; Xie, X.; Zhou, X. Crowdsensing Data Trading based on Combinatorial Multi-Armed Bandit and Stackelberg Game. In Proceedings of the 2021 37th IEEE International Conference on Data Engineering, Chania, Greece, 19–22 April 2021; pp. 253–264. [Google Scholar]
- Tapas, P.; Pillai, D. Prospect theory: An analysis of corporate actions and priorities in pandemic crisis. Int. J. Innov. Sci. 2021, 1, 1–15. [Google Scholar] [CrossRef]
- Yang, J.; Fu, L.; Yang, B.; Xu, J. Participant Service Quality Aware Data Collecting Mechanism with High Coverage for Mobile Crowdsensing. IEEE Access 2020, 8, 10628–10639. [Google Scholar] [CrossRef]
- Jaimes, L.G.; Vergara, I.J.; Raij, A. A Location-based Incentive Algorithm for Consecutive Crowd Sensing Tasks. IEEE Lat. Am. Trans. 2016, 14, 811–817. [Google Scholar] [CrossRef]
- Gao, G.; Wu, J.; Yan, Z.; Xiao, M.; Chen, G. Unknown Worker Recruitment with Budget and Covering Constraints for Mobile Crowdsensing. In Proceedings of the 2019 IEEE 25th International Conference on Parallel and Distributed Systems, Tianjin, China, 4–6 December 2019; pp. 539–547. [Google Scholar]
- Mellers, A.B.; Chang, S.-J. Representations of Risk Judgments. Organ. Behav. Hum. Decis. Processes 1994, 57, 167–184. [Google Scholar] [CrossRef]
- Koutsopoulos, I. Optimal Incentive-driven Design of Participatory Sensing Systems. In Proceedings of the 2013 32nd IEEE INFOCOM Conference, Turin, Italy, 14–19 April 2013; pp. 1402–1410. [Google Scholar]
- Ji, G.; Yao, Z.; Zhang, B.; Li, C. A Reverse Auction-Based Incentive Mechanism for Mobile Crowdsensing. IEEE Internet Things J. 2020, 7, 8238–8248. [Google Scholar] [CrossRef]
- Yang, D.; Fang, X.; Xue, G. Truthful Incentive Mechanisms for K-Anonymity Location Privacy. In Proceedings of the 2013 32nd IEEE INFOCOM Conference, Turin, Italy, 14–19 April 2013; pp. 2994–3002. [Google Scholar]
- Gao, L.; Hou, F.; Huang, J. Providing Long-Term Participation Incentive in Participatory Sensing. In Proceedings of the 2015 34th IEEE Conference on Computer Communications, Hong Kong, China, 26 April–1 May 2015; pp. 1–9. [Google Scholar]
- Kim, S. Effective crowdsensing and routing algorithms for next generation vehicular networks. Wirel. Netw. 2019, 25, 1815–1827. [Google Scholar]
- Pouryazdan, M.; Kantarci, B. On Coalitional and Non-Coalitional Games in the Design of User Incentives for Dependable Mobile Crowdsensing Services. In Proceedings of the 2020 IEEE International Conference on Service Oriented Systems Engineering, Oxford, UK, 3–6 August 2020; pp. 1–9. [Google Scholar]
- Yang, D.; Xue, G.; Fang, X.; Tang, J. Crowdsourcing to Smartphones: Incentive Mechanism Design for Mobile Phone Sensing. In Proceedings of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, 22–26 August 2012; pp. 173–184. [Google Scholar]
- Jordan, K.O.; Sheptykin, I.; Grüter, B. Identification of structural landmarks in a park using movement data collected in a location-based game. ACM 2013, 13, 1–8. [Google Scholar]
- Mccall, R.; Koenig, V. Gaming concepts and incentives to change driver behaviour. In Proceedings of the 2012 11th Annual Mediterranean Ad Hoc Networking Workshop, Ayia Napa, Cyprus, 19–22 June 2012; pp. 1–6. [Google Scholar]
- Bigwood, G.; Henderson, T. IRONMAN: Using Social Networks to Add Incentives and Reputation to Opportunistic Networks. In Proceedings of the IEEE Third International Conference on Privacy, Boston, MA, USA, 9–11 October 2011; pp. 65–72. [Google Scholar]
- Sun, J. An Incentive Scheme Based on Heterogeneous Belief Values for Crowd Sensing in Mobile Social Networks. In Proceedings of the IEEE Global Communications Conference, Atlanta, GA, USA, 9–13 December 2013; pp. 1717–1722. [Google Scholar]
- Dong, Z.Y. Behavioral Economics; Peking University Press: Beijing, China, 2005; pp. 75–81. [Google Scholar]
- Mark, S.; Winer, R.S. An Empirical Analysis of Price Endings with Scanner Data. J. Consum. Res. 1997, 24, 57–67. [Google Scholar]
- Briesch, R.A.; Krishnamurthi, L.; Mazumdar, T. A Comparative Analysis of Reference Price Models. J. Consum. Res. 1997, 24, 202–214. [Google Scholar]
- Epley, N.; Gilovich, T. When effortful thinking influences judgmental anchoring: Differential effects of forewarning and incentives on self-generated and externally-provided anchors. J. Behav. Decis. Mak. 2005, 18, 199–212. [Google Scholar]
- Hardie, B.; Johnson, E.J.; Fader, P. Modeling Loss Aversion and Reference Dependence Effects on Brand Choice. Mark. Sci. 1993, 12, 378–394. [Google Scholar]
- Holte, J.H.; Sivey, P.; Abelsen, B.; Olsen, J.A. Modelling Nonlinearities and Reference Dependence in General Practitioners’ Income Preferences. Health Econ. 2016, 25, 1020–1038. [Google Scholar] [PubMed]
- Liu, X. Disclosing information to a loss-averse audience. Econ. Theory Bull. 2018, 6, 63–79. [Google Scholar]
- Soetevent, A.; Zhou, L. Loss Modification Incentives for Insurers under Expected Utility and Loss Aversion. Econ.-Neth. 2016, 164, 41–67. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect Theory of Decisions Under Risk. Econometrica 1979, 47, 263–292. [Google Scholar]
- Zhang, G.-M. Principal-Agent Model and Risk Analysis under Asymmetric Information Condition. In Proceedings of the 18th International Conference on Management Science and Engineering, Rome, Italy, 13–15 September 2011; pp. 187–191. [Google Scholar]
- Ji, L.; Liu, W.; Zhang, Y. Research on the Tournament Incentive Mechanism of the Safety Behavior for Construction Workers: Considering Multiple Heterogeneity. Front. Psychol. 2021, 12, 796295. [Google Scholar] [PubMed]
- Enguix, L. The New EU Remuneration Policy as Good but Not Desired Corporate Governance Mechanism and the Role of CSR Disclosing Marginal values analysis for chemical industry. Sustainability 2021, 13, 5476. [Google Scholar]
- Balasubramanian, N.; Balasubramanian, A.; Venkataramani, A. Energy consumption in mobile phones: A measurement study and implications for network applications. In Proceedings of the 9th ACM SIGCOMM Internet Measurement Conference, Chicago, IL, USA, 4–6 November 2009; pp. 280–293. [Google Scholar]
- Ma, H.D.; Zhao, D. Mobile Crowd Sensing Network; Tsinghua University Press: Beijing, China, 2019. [Google Scholar]
- Duan, L.; Kubo, T.; Sugiyama, K.; Huang, J.; Hasegawa, T.; Walrand, J. Incentive mechanisms for smartphone collaboration in data acquisition and distributed computing. In Proceedings of the IEEE INFOCOM Conference, Orlando, FL, USA, 25–30 March 2012; pp. 1701–1709. [Google Scholar]
- Lee, J.; Hoh, B. Dynamic Pricing Incentive for Participatory Sensing. Pervasive Mob. Comput. 2010, 6, 693–708. [Google Scholar]
- Lai, C.; Zhang, X. Duration-Sensitive Task Allocation for Mobile Crowd Sensing. IEEE Syst. J. 2020, 14, 4430–4441. [Google Scholar]
- Wang, J.; Wang, F.; Wang, Y.; Wang, L.; Qiu, Z.; Zhang, D.; Guo, B.; Lv, Q. HyTasker: Hybrid Task Allocation in Mobile Crowd Sensing. IEEE. Trans. Mob. Comput. 2020, 19, 598–611. [Google Scholar]
- Wang, J.; Wang, Y.; Zhang, D.; Wang, F.; Xiong, H.; Chen, C.; Lv, Q.; Qiu, Z. Multi-Task Allocation in Mobile Crowd Sensing with Individual Task Quality Assurance. IEEE. Trans. Mob. Comput. 2018, 17, 2101–2113. [Google Scholar]
- Wang, J.; Wang, Y.; Zhang, D.; Wang, L.; Xiong, H.; Helal, A.; He, Y.; Wang, F. Fine-Grained Multitask Allocation for Participatory Sensing with a Shared Budget. IEEE Internet Things J. 2016, 3, 1395–1405. [Google Scholar]
- Hu, A.; Gu, Y. Mobile crowdsensing tasks allocation for mult-parameter bids. In Proceedings of the 3rd IEEE Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 3–5 October 2017; pp. 489–493. [Google Scholar]
- Zhang, X.; Xue, G.; Yu, R.; Yang, D.; Tang, J. Robust Incentive Tree Design for Mobile Crowdsensing. In Proceedings of the 37th IEEE International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 458–468. [Google Scholar]
- Liu, J.; Yang, Y.; Li, D.; Deng, X.; Huang, S.; Liu, H. An Incentive Mechanism Based on Behavioural Economics in Location-based Crowdsensing Considering an Uneven Distribution of Participants. IEEE. Trans. Mob. Comput. 2020, 21, 44–62. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).